Graphical abstract
Keywords: Roller compaction, Design space prediction, Solid fraction, Throughput
Abstract
This work presents a new model based approach to process design and scale-up within the same equipment of a roller compaction process. The prediction of the operating space is not performed fully in-silico, but uses low-throughput experiments as input. This low-throughput data is utilized in an iterative calibration routine to describe the behavior of the powder in the roller compactor and improves the predictive quality of the mechanistic models at low and high-throughput. The model has been validated with an experimental design of experiments of two ibuprofen formulations. The predicted sweet spots in the operating space are in good agreement with the experimental results.
Abbreviations
roller diameter [m] [cm]
roller width [m] [cm]
roller gap [m] [mm]
roller force [N] [N]
- SCF
specific compaction force [N/m] [N/cm]
roller speed [1/s] [rpm]
screw speed [1/s] [rpm]
true density [kg/m3] [g/cm3]
effective angle of internal friction [rad] [°]
wall friction angle [rad] [°]
screw constant [kg] [g]
compressibility factor [-]
pre-consolidation solid fraction [-]
in-gap ribbon solid fraction [-]
ribbon solid fraction [-]
ribbon thickness [m] [mm]
relaxation factor [-]
feeding screw mass flow rate [kg/s] [kg/h]
mass flow rate between rolls [kg/s] [kg/h]
observed mass throughput [kg/s] [kg/h]
feed pressure [Pa] [kPa]
maximum pressure at roller gap [Pa] [kPa]
force factor [kg/s] [kg/h]
angular position at roller, at gap [rad] [°]
nip angle [rad] [°]
shear stress [Pa] [kPa]
- RSD
residual standard deviation [-]
1. Introduction
Dry granulation technology via roller compaction (RC) is increasingly applied in the pharmaceutical industry to produce solid oral dosage forms, mainly tablets, as well as capsules and sachets (Chang et al., 2008, Lopes et al., 2016). The granulation step primarily addresses the poor flowability of powders and other issues, such as dustiness, low bulk density and propensity for segregation. Unlike wet granulation, RC does not require solvents and a drying step to remove them, which is especially advantageous for moisture- and heat-sensitive active pharmaceutical ingredients (APIs). Moreover, since RC involves fewer processing steps, it is suitable for continuous processing lines (Kleinebudde, 2004, Miller, 2005, Guigon et al., 2007, Leane et al., 2015, Rowe et al., 2013, Martinetz et al., 2018). However, an RC process poses several challenges. Firstly, roller compaction formulations generally require higher amounts of excipients and therefore lower drug loading compared to wet granulation. The exact formulation also depends on the compactability of the API. Secondly, the powder blend compressibility may be compromised when forming granules that are subsequently compressed into tablets (Sun and Kleinebudde, 2016).
During the compaction process development, a special emphasis is made on maintaining the same product quality, e.g., during scale-up and technology transfer (Nesarikar et al., 2012, Souihi et al., 2015, Perez-Gago et al., 2017). To that end, current approaches often rely on labor-intensive experimental trials to explore the full design space for various throughputs or even various types of equipment, resulting in considerable material and operational costs (Kleinebudde, 2004, Teng et al., 2009). Additionally, since in the early stages of drug product development the available quantities of API are limited, process design has to be performed either via model compounds mimicking the API or via reduced flow rates on the equipment. As a result, complex interactions between the material attributes and process parameters may hinder extracting relevant information from the experiments performed (Michrafy et al., 2017).
The aim of this work is to reduce the material consumption in a systematic design of experiment (DoE). A mechanistic approach based on the models described by (Johanson, 1965) and (Reynolds et al., 2010) has been developed in order to replace the experiments with higher throughput and material consumption (high roller and screw speeds) with model predictions. The key is an iterative calibration sequence that employs the experimental data at low throughput to improve the predictions at both low and high throughputs. This approach has been validated by comparing the resulting operating space with a fully experimentally obtained one.
2. Roller compaction modeling
2.1. Working principle and relevant models
Fig. 1 shows a schematic diagram of an RC process. First, the material is fed into the hopper (1) and transported by the conveyer screws (2 and 3) onto two counter-rotating rollers (5). By applying a specific compaction force, the material is compressed into a so-called ribbon. It is subsequently milled into granules (6) using various mills and milling parameters, which are known to affect the properties of final granules (Perez-Gandarillas et al., 2016). Ribbon density or solid fraction, defined as the mass of material per volume of ribbon, is commonly considered a critical quality attribute (CQA) of an RC process (Vervaet and Remon, 2005, Fonteyne et al., 2015, Park et al., 2018). The ribbon solid fraction is actively measured and controlled in a continuous manufacturing process (Gupta et al., 2005, Singh et al., 2012). In order to predict the ribbon density, only a small fraction of the RC process has to be modeled (rectangular region (5) in Fig. 1)
Fig. 1.
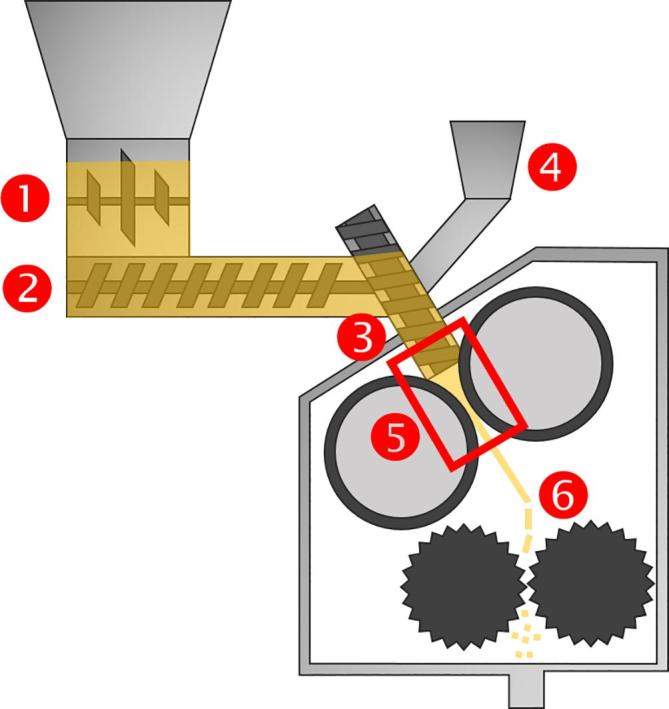
Schematic of a roller compactor. (1) inlet funnel with agitator; (2) feed screw; (3) tamp screw; (4) small quantity inlet funnel; (5) rollers; and (6) rotor miller. The mechanistic model describes the region of between the rollers.
The process parameters of interest during the compaction step are the roller speed NR, screw speed NS, specific compaction force between the rollers (SCF), and gap width S (Inghelbrecht and Remon, 1998, Vervaet and Remon, 2005, Dumarey et al., 2011, Csordas et al., 2018). The roller gap and force are often correlated with the screw speed of the feed, depending on the control scheme and the equipment manufacturer (Guigon and Simon, 2003, Rowe et al., 2017). There are two major operation modes:
-
•
Gap-controlled mode (also termed ‘automatic mode’). The operator can set the roller speed, the roller force and the roller gap width. The screw speed is the machine’s response via an internal feedback loop to obtain the desired roller gap and force. This is the most common operation mode for industrial processes.
-
•
Screw-controlled mode (also termed ‘manual mode’). The operator can set the roller speed, the roller force and the screw speed. The parameters selected and the characteristics of the material compressed result in a certain roller gap.
Depending on the control mode of the roller compactor, an appropriate process model should be selected: Johanson’s model is better suited for the gap-controlled mode, whereas Reynolds’ model is better for the screw-controlled mode.
However, applying these models directly usually leads to an overestimation of the ribbon density (Dec et al., 2003, Bi et al., 2014). One way to improve the results is a better prediction of the stresses acting on the powder between the rolls. (Katashinskii, 1966) developed an analytical model that considers the stress gradient in trapezoidal “slabs” in the roller region. With better computational resources it became possible to solve the pressure distribution with the finite element method (FEM) (PM Modnet Modelling Group, 1999, Wang and Karabin, 1994), or even a combined approach of discrete element method (DEM) and FEM simulations (Mazor et al., 2018). While these methods give and in-depth insight to the roller compaction process, performing FEM simulations for every process condition and powder blend is not feasible.
One source of discrepancy between the predictions of Johanson’s and Reynolds’ model and the ribbon density measurements is the different compaction behavior of the powder in the roller compactor compared to uniaxial compression tests (Reynolds et al., 2010). (Reimer and Kleinebudde, 2019) demonstrated that the roller compactor and a compaction simulator lead to different ribbon densities and built a model to account for that difference.
In addition to the differences in the compaction behavior, the mechanistic models predict strictly speaking not the solid fraction of the final ribbon (), but the solid fraction density in the roller gap (). In this case, the elastic recovery of the ribbon is neglected.
In this work, roller compaction experiments at low screw speeds have been utilized to calibrate a compaction profile that relates the maximum pressure in the roller gap to the final ribbon density. (Sajjia et al., 2017) used a similar approach to predict the ribbon densities in screw-controlled mode. Section 2.4 introduces a calibration routine for ribbon density and throughput in both gap-controlled and screw-controlled mode.
2.2. Prediction of ribbon density and throughput in the gap-controlled mode
Johanson’s model is one of the first mechanistic models of an RC process. It accounts for the powder properties (compaction profile, angle of friction) and the geometry of the rolls (width, diameter, and gap) but neglects the roller and screw speeds (Johanson, 1965). It is well-suited for predicting the ribbon density in the gap-controlled mode since the actively-controlled process parameters (the gap and the roller force) are input for the model, whereas the changing process parameter (screw speed) is neglected. Once the ribbon density is known, it is possible to predict the throughput based on the geometrical considerations and the roller speed. However, the throughput calculation was not part of Johanson’s initial work.
Johanson categorized the regions containing the compacted material into a slip region (1), where the rollers move faster than the powder, and a nip region, where there is no slip between the roller and the powder (2) as shown in Fig. 2.
Fig. 2.
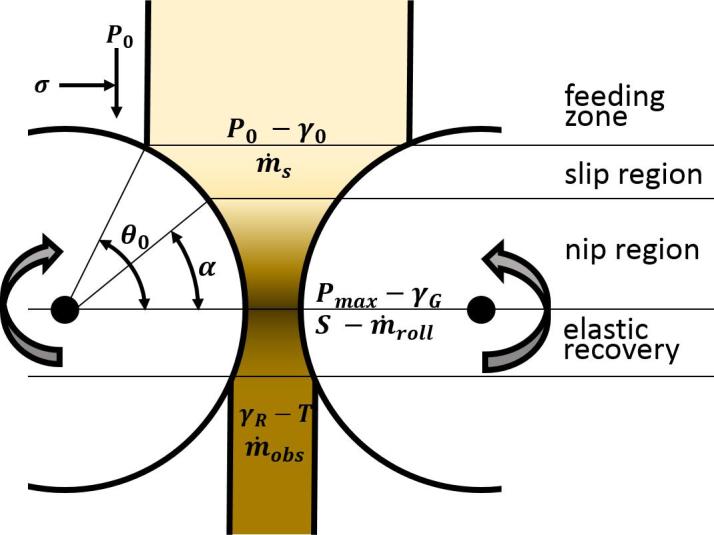
Schematic diagram of the compaction process showing the feeding zone and the nip and slip regions. The powder has the maximum density at the gap. Past the roller gap, there is a region of elastic recovery where ribbon thickness T increases while reducing the ribbon density to its final value . The mass flow can be predicted in the feeding zone using either the screw mass flow rate () or the gap geometry and the roller speed (). Experimentally, it is the throughput observed after the ribbon relaxation ().
The stress gradients in the nip region are higher than those in the slip region, indicating that most of the compaction takes place in the nip region. Based on the geometrical considerations, it is possible to define a normalized stress gradient in the nip region and the slip region . The stress is applied in horizontal direction, i.e. normal to the direction of the initial feed pressure . Johanson derived expressions for both stress gradients as:
| (1) |
| (2) |
where
| (3) |
| (4) |
Nip angle is defined as an angular roller position () in which the material transforms from the slip condition to the non-slip condition, i.e., the boundary between the slip and nip regions. At this point, the stress gradients of the slip and nip regions are equal. Therefore, nip angle can be calculated by applying this condition based on Eqs. (1) and (2):
| (5) |
Eq. (5) shows that the nip angle solely depends on material-related parameters, such as effective angle of internal friction , wall friction angle (ΦW) and compressibility constant (K).
To link peak pressure exerted on the material at the minimum roller gap S with the roller force, Johanson applies an analytical expression of roller force as follows:
| (6) |
where W is the roller width, D is the roller diameter and is an integral over the nip region, as shown below: Because the pressures in the slip region are small compared to the nip region, it can be neglected in the calculation of the roller force (Johanson, 1965)
| (7) |
Johanson described his model as an initial value problem: if feeding pressure in the beginning of the slip region is known, integrating over the stress gradients in Eqs. (1), (2) makes it possible to obtain , the maximum pressure applied to the powder in the roller gap. Once is known, roller force can be extracted using Eqs. (6), (7). In contrast to older systems, nowadays modern roller compactors can measure and actively control their roller force either directly or using some parameter that can easily be converted into the roller force, e.g., the hydraulic roller pressure. In this case, equipment suppliers provide a conversion factor to translate the roller pressure into the roller force.
If roller force is known, Eqs. (6) and (7) can be used to extract the peak pressure . There is no need to assume feeding pressure and numerically integrate over the stress gradients (which can still be used to obtain nip angle , as shown in Eq. (5)).
Assuming that material compression follows a compression power law, ribbon solid fraction at the gap can be calculated as:
| (8) |
where is the compressibility constant of the material and is the pre-consolidation solid fraction. Incorporating Eqs. (6) and (7) into Eq. (8) expresses the relationship between process output (ribbon solid fraction) and process parameters (roller force, minimum roller gap, roller diameter, roller width) as follows:
| (9) |
(Reynolds et al., 2010) considered the mass balance around the roller gap. If the roller speed, the roller geometry, the true density of powder and the solid fraction of the ribbon are known, the mass throughput can be calculated as:
| (10) |
2.3. Prediction of ribbon density and throughput in the screw-controlled mode
Johanson’s model can be used for equipment in the gap-controlled mode. However, since the roller speed and screw speed are not considered process parameters in terms of predicting the ribbon solid fraction, the model cannot be used for equipment in the screw-controlled operation mode. Reynolds et al. addressed this issue by solving the mass balance around the roller gap as a function of roller width, roller speed and feeding screw speeds (Reynolds et al., 2010).
Reynolds assumed a linear relationship between the mass flow on the feeding screw and the screw speed:
| (11) |
where is the screw constant which depends on the powder properties and screw geometry and can be established via a linear regression between the throughput and the screw speed. For the purposes of the model, is treated as constant material parameter.
Mass flow in the roller gap is given by Eq. (10). An effective gap size can be obtained by setting and solving for a non-dimensional gap S/D:
| (12) |
Substituting for in Eq. (9) makes it possible to calculate the final ribbon density in the screw-controlled mode at the cost of having to use a calibration factor .
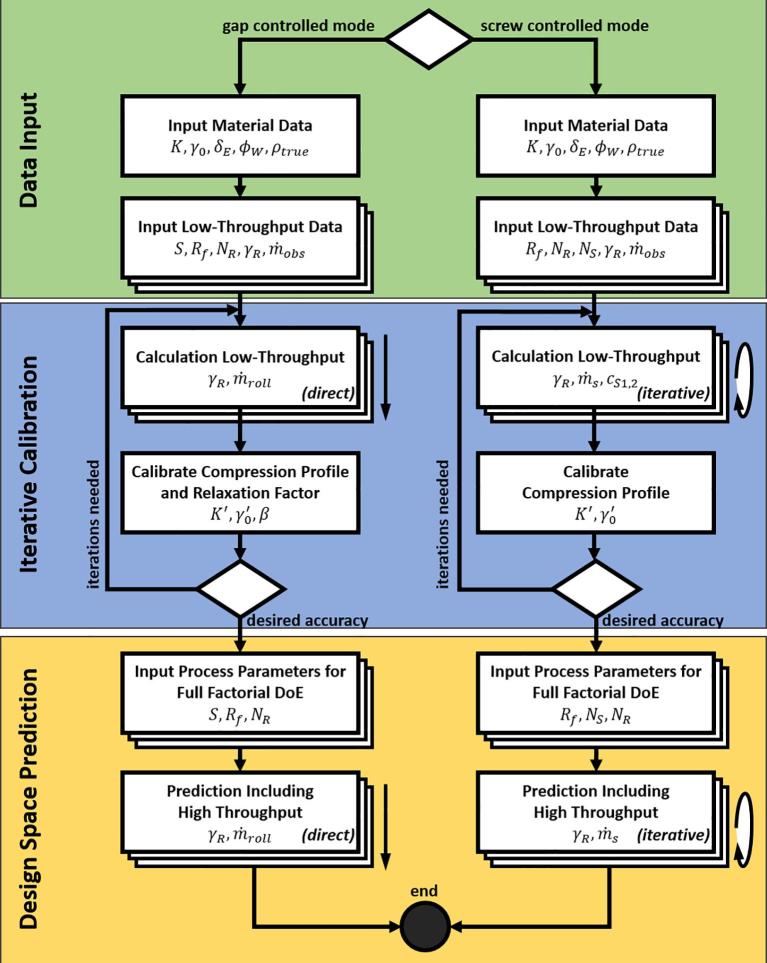
Eq. (12) assumes that the ribbon solid fraction – the output of the model – is known. Thus, has to be computed numerically in an iterative manner rather than via a single analytical expression. Let us assume to be the ribbon solid fraction that is used to calculate the effective gap size and to be the result of Eq. (9). The iteration varies in the expected range and calculates . Only if the value of has been assumed correctly, it matches the result of the calculation . The result of the iteration is then the value of that produced the minimal deviation between and .
The accuracy of this iteration can be chosen freely by setting the step size of between potential candidates: A step size of 0.001 will produce results accurate to 0.1% points of ribbon solid fraction. This iteration is denoted by the small loop symbol in the screw controlled branch in the flow chart in Fig. 3. In contrast, there is no iteration needed to solve for the ribbon density in gap controlled mode: a single evaluation of Eq. (9) suffices.
Fig. 3.
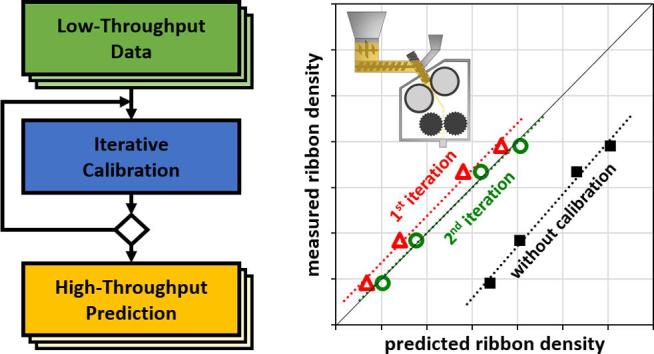
Flow chart of the final model. The operation mode decides the process parameters and the model used for predicting solid fraction and throughput. The required material properties are the same. The iterative calibration loop predicts solid fraction for the known low-throughput process conditions and corrects the compression profile to match the low throughput data. With the calibrated compression profile, the rest of the DoE (with high roller speed and throughput) is predicted.
The throughput is simply calculated based on the two input parameters, screw speed and screw constant, given by Eq. (11).
2.4. Iterative calibration in low-throughput experiments
The previous sections addressed the prediction of ribbon density and throughput using a single set of process parameters in the gap- or screw-controlled mode. However, there are two sources of discrepancies between the predicted and measured results which are unaccounted for by the models:
First, the compaction behavior of powders in a roller compactor is typically different from that in the uniaxial compression test, requiring a different set of parameters to describe the compression profile (Reynolds et al., 2010). This means that even if the calculation of peak pressure is correct, the resulting predicted ribbon density in the roller gap will not match the experimental one. Second, the elastic recovery of the ribbon must be considered. The measured ribbon thickness is greater than roller gap size . Thus, the predicted ribbon density in the gap does not match the experimentally-obtained ribbon density . Both of the above factors influence the prediction of ribbon density and resulting throughput. Several theoretical and empirical efforts have been undertaken to account for the elastic recovery and to improve the compression profile in a roller compactor (Cunningham, 2005, Peter et al., 2010).
The objective of this work is to develop a model for the operating space under the assumption that low-throughput measurements are available. The rationale behind such a strategy is that low-throughput is generally associated with low API consumption. As such, the low-throughput data can be used to calibrate the models in order to improve the ribbon density and throughput predictions at both low and high throughputs.
The first step is calibration of the compression profile, i.e., finding a pair that matches the powder behavior in the roller compactor. Since the compressibility factor is used not only in the compression profile computation in Eq. (8) but also in the peak pressure calculation in Eqs. (6) and (7), the most suitable compression profile must be established iteratively.
Step 1: Defining initial K and γ0
In the beginning of the iteration process, to determine the final values of K and γ0, the initial values of K and γ0 have to be defined. They can be obtained from uniaxial compression experiments or chosen arbitrarily within their expected range. The closer the initial choice of K and is to the final values, the fewer iterations are required.
Step 2. Calculation of peak pressures
For each data point in the low-throughput measurements, the peak pressure is obtained by solving Eq. (7) either directly (gap-controlled mode) or iteratively by substituting Eq. (12) (screw-controlled mode).
Step 3. Regression to improve K and γ0
An improved compression profile with can be established via a linear regression over the logarithmic form of the compression profile:
| (13) |
using predicted peak pressures and measured ribbon densities .
Step 4. Check ribbon densities and repeat
The improved compression profile is then used to predict ribbon densities . If the predicted values match the measured data with the desired accuracy, stop the iteration. If not, assign and and repeat with Step 2.
Since in the screw-controlled operation mode the throughput is a direct result of the screw speed and the screw constant, no further calibration is required for the throughput prediction.
In the gap-controlled mode, the throughput prediction can be made based on the ribbon geometry and the roller speed (Eq. (10)). However, the model is calibrated with the density of relaxed ribbon rather than the ribbon density in gap that is generally higher (Nkansah et al., 2008, Gamble et al., 2010). As such, elastic recovery β can be introduced to back-calculate the ribbon density in the gap using the relaxed ribbon density predicted by the model:
| (14) |
β can be determined by plotting the process throughput (kg/h) over the calculation of mass flow rate exiting the rollers (Eq. (14)). β is the slope of the regression line (with y = 0 intercept).
Alternatively, β can be determined via the ratio of measured ribbon thickness (T) and the roller gap (S) using the low-speed experiments, as shown in Eq. (15). With regard to the prediction of high throughput, it is assumed that increasing the roller speed does not have a significant impact on the ribbon relaxation.
| (15) |
2.5. Determining the screw constant
In the screw-controlled mode, can be calculated via Eq. (11). The screw constant can be calculated using two approaches. First, the screw constant cS1 can be calculated based on the experimentally observed throughput () as follows:
| (16) |
Secondly, the screw constant cS2 can be calculated using the mass balance, as proposed by (Reynolds et al., 2010):
| (17) |
In this work, cS1 and cS2 are compared to evaluate how accurately they can predict the throughput.
2.6. In silico design space exploration
The previous sections contained equations for predicting the ribbon solid fraction and the throughput as a function of material properties and RC process parameters. These correlations are leveraged to define a design space for the formulation using a specific roller compactor.
Fig. 3 shows a roadmap for developing and experimentally confirming this design space. RC experiments are performed at low throughput to generate data for calculating the compression properties of a powder blend via iteration using the applicable RC mechanistic model (see previous section). The data obtained allows running the design of experiments (DoEs) in silico and determining the in silico design space for various process parameters (roller gap, screw speed, roller speed) as a function of process output (ribbon solid fraction and throughput).
Since this design space is obtained in silico, it has to be experimentally confirmed in the center and along the extremes. In this work, a full factorial DoE was performed both in silico and experimentally to evaluate the model’s predictive capabilities for the ribbon solid fraction and throughput. This model-based approach involves less experimental work. The experimental methodology is explained below.
For a gap-controlled RC process, two to four roller compactor experiments are required. A minimum roller speed (NR) is used in every run to minimize the consumption of material. Ideally, all four combinations of minimum and maximum roller gap (S) and compaction force (SCF) are performed experimentally. The number of experiments can be further reduced to two, if necessary. In this case, the experiments should cover the process conditions with minimum and maximum expected ribbon density: highest roller gap with lowest compaction force, and lowest roller gap with highest compaction force. A minimum of two experiments is needed to uniquely define the compression profile with the two parameters K and .
The two measured process outputs are the ribbon solid fraction and the throughput. The iterative calibration method yields an improved compression profile and elastic recovery parameter . These calibrated values are subsequently used for the high-throughput prediction purposes.
The ideal set of low throughput experiments in screw-controlled mode consists of four operating points, similar to the gap-controlled mode. The roller speed NR is set to the minimum to minimize material consumption. Specific compaction force (SCF) and screw-to-roller-speed ratios (NS/NR) are set two the highest and lowest values expected in the operating space. If desired, the number of experiments can be further reduced to two. Again, the two operating conditions should result into the highest and lowest ribbon density: high compaction force with high screw-to-roller speed ratios, and low compaction force with low NS/NR ratios.
In screw controlled mode, there are two ways to calculate the screw constant. The screw constant obtained from Eq. (16) is denoted cs1, the screw constant obtained from Eq. (17) is denoted cs2. The influence on the results is discussed in the Results section.
Full factorial DoEs have been performed experimentally. The critical process parameters are:
-
-
In the gap-controlled mode: roller gap, compaction force and roller speed.
-
-
In the screw-controlled mode: screw-to-roller-speed ratio, compaction force and roller speed.
The predicted operating space relies on the low-throughput (low NR) results and has been validated with the fully experimentally obtained operating space. The virtual DoEs use either the modified Johanson model for the gap-controlled operation mode or Reynolds’ model for the screw-controlled operation mode to reflect the critical process parameters as input parameters to the model. The key modification to models found in literature is the differentiation between in-gap ribbon density and final ribbon density . This relationship can be established using the iterative calibration in the previous section. Table 1 provides an overview of which input parameters are required in each RC operation mode. The process is shown graphically in Fig. 3.
Table 1.
Overview of model parameters.
| Gap-Controlled Mode | Screw-Controlled Mode | |
|---|---|---|
| Compression profile | ||
| Powder Characterization | ||
| RC geometry | ||
| Process Parameters | ||
| Modified by Iterative Calibration | ||
| Calculation of | direct | iterative |
3. Experimental and analytical work
3.1. Materials
Ibuprofen (Janssen Pharmaceutical, Beerse, Belgium) was used as a model API, mannitol (Pearlitol® 200 SD Roquette GmbH, Frankfurt, Germany) and microcrystalline cellulose (Avicel® PH-101, FMC Bioploymer, Brussels, Belgium) as a filler/binder, and magnesium stearate (Parteck LUB MST, Merck KGaA, Darmstadt, Germany) as a lubricant.
Two formulations were created. Each consisted of 49.75 %w/w API (Ibuprofen), 49.75 %w/w excipient (microcrystalline cellulose in the IbuMCC formulation, mannitol in the IbuMannitol formulation), and 0.5% w/w lubricant (magnesium stearate in both formulations).
The formulations were blended in a Bohle LM40 (L.B. Bohle Maschinen + Verfahren GmbH, Ennigerloh, Germany) bin blender. After 18 min of blending, magnesium stearate was added and the blending continued for additional 2 min. The blender was operated at 20 rpm.
4. Methodology
4.1. Density measurement
Pycnometric density of raw excipients was determined using an AccuPyc® 1330 helium pycnometer (Micromeritics, Norcross, USA). Three measurements were performed each time. The pycnometric density of the formulation was calculated as weighted harmonic mean of raw materials as:
| (18) |
where is the number of components, is the index of the component, is the density of the -th component, and is the fraction of the -th component. The individual fractions sum up to 1.
4.2. Shear cell measurement
The angle of internal friction powders and granules was measured in a ring shear tester (RST-01, Dr. Schulze Schuettguttechnik, Wolfenbuettel, Germany). The samples were carefully filled into the measuring cell to avoid measurement artefacts. Prior to each measurement, a smooth surface was created with a spoon. A normal stress of 5000 Pa was applied for pre-shearing. Stresses of 1000, 2000, 3000, 4000 Pa were used for shear deformation in the ascending order. Subsequently, the measuring point at 1000 Pa was repeated to establish potential changes in the samples. Based on the results, the effective angle of internal friction was calculated by the software of the ring shear tester.
4.3. Compressibility measurement
A rotary die tablet press equipped with 8 mm flat-faced punches was applied for the compressibility analysis (PRESSIMA, IMA Pharma, Bologna, Italy). 200 ± 2 mg of each formulation was weighed by hand, and at least 11 tablets were compressed at 2.5 kN, 5 kN, 7.5 kN, 10 kN, 12.5 kN and 15 kN. Tablet height, width, diameter, mass and breaking strength were analyzed using a SmartTest 50 (SOTAX AG, Lörrach, Germany), n = 6 for IbuMannitol and n = 10 for IbuMCC.
4.4. Roller compaction trials
For RC trials, a Gerteis MINI-PACTOR® (Gerteis Maschinen + Process Engineering AG, Jona, Switzerland) equipped with knurled rolls and rim roller sealing was used. The roller diameter was 25 cm and the roller width was 2.5 cm. The adjustable settings were the roller speed (NR), the roller gap (S) and the specific compaction force (SCF). When the process settings were changed, samples were drawn only after the process equilibrium was reached. Gap-controlled operation mode was used while recording the equilibrium screw speed of the equipment. 490 g to 800 g of IbuMCC ribbons and 140 g to 410 g of IbuMannitol ribbons were collected. A 23 full factorial design with three repetitions at the center point was used. Table 3 shows the DoE, Table 2 shows the process settings used for the different formulations.
Table 3.
Process settings used in the DoE for IbuMCC and IbuMannitol formulations.
| roll speed | gap width | specific compaction force | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NR (rpm) |
S (mm) |
SCF (kN/cm) |
|||||||
| Level | −1 | 0 | +1 | −1 | 0 | +1 | −1 | 0 | +1 |
| IbuMCC | 1 | 2 | 3 | 2 | 3 | 4 | 5 | 7 | 9 |
| IbuMannitol | 1 | 2 | 3 | 2 | 3 | 4 | 2 | 3.5 | 5 |
Table 2.
Full factorial DoE with 11 experimental runs. The critical process parameters are the roll speed NR, the gap width S, and the specific compaction force SCF. The simulated values used the experimental runs at low throughput (NR level = –1) for calibration, whereas the high the results for higher throughput (NR levels = 0 and +1) were fully predicted.
| Run # | NR | S | SCF | role in simulation |
|---|---|---|---|---|
| 1 | –1 | –1 | –1 | used for calibration |
| 2 | +1 | –1 | –1 | fully predicted |
| 3 | –1 | +1 | –1 | used for calibration |
| 4 | +1 | +1 | –1 | fully predicted |
| 5 | –1 | –1 | +1 | used for calibration |
| 6 | +1 | –1 | +1 | fully predicted |
| 7 | –1 | +1 | +1 | used for calibration |
| 8 | +1 | +1 | +1 | fully predicted |
| 9 | 0 | 0 | 0 | fully predicted |
| 10 | 0 | 0 | 0 | fully predicted |
| 11 | 0 | 0 | 0 | fully predicted |
β, cS1 and cS2 were calculated using the experimental data obtained from the four RC experiments carried out at a roller speed of 1 rpm and Eqs. (15), (16) and (17), respectively. The average of the four values obtained was subsequently used as the model’s input.
4.5. Envelope density analysis
Dust from the ribbons was carefully removed with a brush. The mass of 2 to 3 g of ribbons was determined using an analytical balance. The ribbons were filled into a GeoPyc 1360 (Micromeritics, Norcross, USA) powder pycnometer. Large ribbons were broken into smaller pieces if they failed to fit into the measurement chamber that had a diameter of 25.4 mm. The consolidation force was 51 N, and the conversion factor was 0.5153 cm3/mm. The solid fraction was calculated using the true density of formulation, the sample mass and the envelope density. The samples were measured in triplicate.
5. Results and discussion
5.1. Formulation characterization
IbuMCC and IbuMannitol are two different formulations chosen to contain a plastically-deforming filler and a brittle filler, respectively (Table 2). Table 4 shows that IbuMCC has a lower compressibility factor (K, obtained in the uniaxial compression test), indicating that lower pressure was required to achieve the same degree of densification. True densities and pre-consolidation densities of the two formulations were similar, while the effective angle of internal friction of IbuMCC was higher due to higher cohesion forces of MCC. The angle of wall friction was not experimentally determined, and a value of 15° was assumed for both formulations since the value generally ranges between 10° and 20° (Nesarikar et al., 2012, Souihi et al., 2015, Perez-Gago et al., 2017). Our previous studies (not shown) indicated that the effect of this parameter on the prediction of solid fraction is minimal.
Table 4.
Properties measured for IbuMCC and IbuMannitol formulations. The wall friction angle is an input parameter for the model and has been estimated based on literature values, e.g. (Nesarikar et al., 2012).
| IbuMCC | IbuMannitol | |
|---|---|---|
| True density (g/cm3) | 1.299 | 1.269 |
| Effective angle of internal friction (δE) | 44° ± 2° | 36° ± 1° |
| Compressibility factor [K] (out-of-die) | 7.84 | 10.29 |
| Pre-consolidation relative density [γ0] (out-of-die) | 0.504 | 0.548 |
| Angle of wall friction (ΦW) | 15° | 15° |
5.2. Determining K and γ0
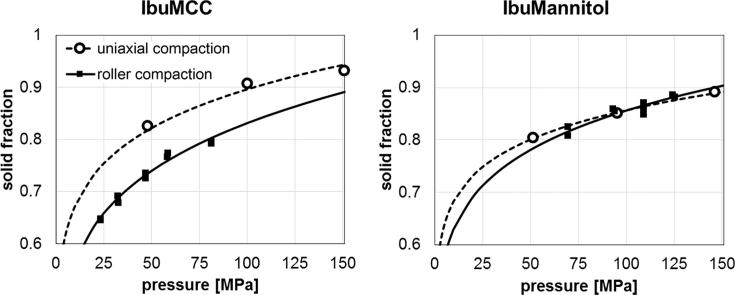
The compression profile obtained from the tableting experiments is only an estimate of the compression profile in the roller compactor. Fig. 4 compares the compression profiles for both formulations. The uniaxial compression profile is direcly obtained from the tableting data, the RC profile is the result of the calibration routine. IbuMCC is significantly less compressible in the RC compared to the tableting machine. The compression profiles of IbuMannitol match in the range from 60 to 130 MPa.
Fig. 4.
Comparison of compression profiles obtained from the tableting data (dashed line, ○) and the roller compaction process (solid line). Because no pressure measurement is available during the RC process, the measured ribbon densities are plotted over the predicted pressures (■).
Fig. 5 shows the influence of the different compression profiles and compares predicted and observed ribbon solid fraction of IbuMCC obtained in the low throughput (NR = 1 rpm) RC experiments. The initial values of K (7.84) and γ0 (0.5) estimated based on the uniaxial compression test resulted in over-prediction of the ribbon solid fraction using Johanson’s model (■). The iteration process described in the section above was performed to obtain the final values of K and γ0.
Fig. 5.
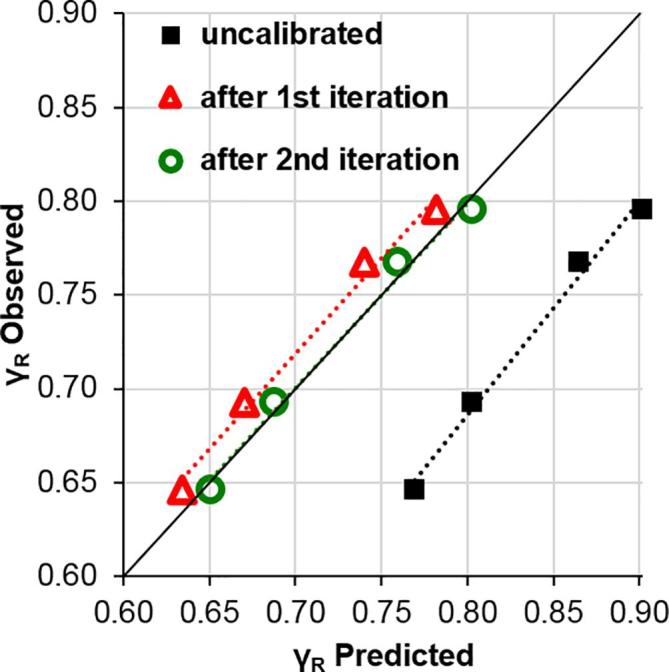
Initial prediction (■), the prediction after one iteration ( ) and the ribbon solid fraction prediction after a second iteration (
) and the ribbon solid fraction prediction after a second iteration ( ).
).
Since the screw speed was monitored during the experiment, the same process was repeated for Reynolds’ model (simulating the screw-controlled operation mode). The throughput measured in the RC experiments at a roller speed of 1 rpm was used to obtain the value of β and cS1.
Table 5 presents the K and γ0 values obtained after the calibration routine for both models (Johanson and Reynolds) representing the two modes of operation: gap and screw controlled, respectively. In screw controlled mode, the two equations for calculating the screw constant are compared: cS1 from Eq. (16) and cS2 from Eq. (17). The compression profile of the IbuMCC formulation shows a large deviation from the uniaxial compression test (see Fig. 4), indicating different compression behavior of a blend when compacted by a uniaxial compression machine and a roller compactor. In the calculations for predicting the ribbon solid fraction and throughput, the values of K and γ0 from the iteration were used. The iteration relates the pressure in the roller gap to the solid fraction of the final ribbon, after relaxation. To offset this effect, the parameter γ0, which is classically related to the preconsolidation density, also changed during the iteration.
Table 5.
List of material properties obtained from the calibration routine.
| IbuMCC | IbuMannitol | |
|---|---|---|
| K (gap-controlled) | 5.94 | 7.57 |
| K (screw cS2) | 5.76 | 7.46 |
| K (screw cS1) | 5.74 | 7.39 |
| γ0 (gap-controlled) | 0.383 | 0.466 |
| γ0 (Screw cS1) | 0.382 | 0.466 |
| γ0 (Screw cS2) | 0.376 | 0.463 |
| cS1 (g) ± std. | 2.61 ± 0.11 | 2.98 ± 0.10 |
| cS2 (g) ± std. | 2.08 ± 0.09 | 2.37 ± 0.13 |
| β ± std. | 1.259 ± 0.036 | 1.257 ± 0.088 |
The section below presents the results of predicting the ribbon solid fraction and the throughput. The mean %Error was calculated to provide a parameter of the model’s accuracy as:
| (19) |
5.3. Predicting the ribbon solid fraction
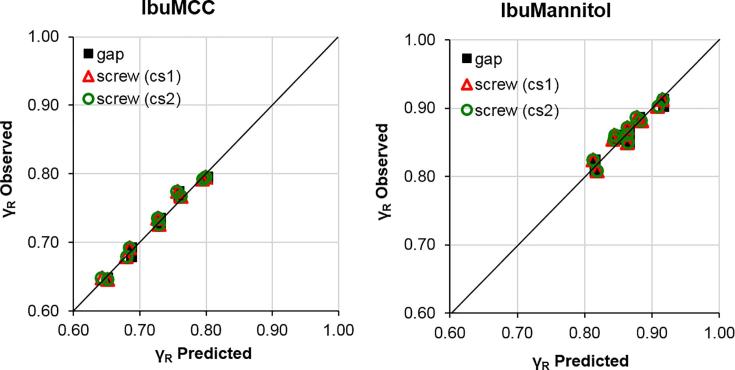
Fig. 6 shows the predicted ribbon solid fraction plotted against the experimentally observed ribbon solid fraction for IbuMCC and IbuMannitol performed in gap-controlled mode, indicating that both models predicted the ribbon solid fraction well. This was confirmed by a low-average error percentage of the ribbon solid fraction prediction stated in Table 6 (0.8–1.0% for both formulations, regardless of the model and the screw constant calculation).
Fig. 6.
Prediction of ribbon solid fraction for formulations IbuMCC and IbuMannitol using the gap-controlled operation model (■) and the screw-controlled operation model using either cS1 ( ) or cS2 (
) or cS2 ( ) as the model input.
) as the model input.
Table 6.
Experimentally observed ribbon solid fraction and the prediction error for the IbuMCC and IbuMannitol formulations. The predictions used the calibrated compression profile . The two methods to calculate the screw constant in screw-controlled mode are compared ( and ). Runs marked with an asterisk (*) were used in the calibration sequence.
| Run # | IbuMCC |
IbuMannitol |
||||||
|---|---|---|---|---|---|---|---|---|
| Obs. γR | Gap | Screw cS1 | Screw cS2 | Obs. γR | Gap | Screw cS1 | Screw cS2 | |
| 1* | 0.692 | 0.687 | 0.684 | 0.684 | 0.860 | 0.848 | 0.843 | 0.845 |
| 2 | 0.679 | 0.688 | 0.679 | 0.680 | 0.855 | 0.849 | 0.843 | 0.844 |
| 3* | 0.646 | 0.651 | 0.651 | 0.651 | 0.808 | 0.816 | 0.818 | 0.819 |
| 4 | 0.648 | 0.651 | 0.643 | 0.642 | 0.825 | 0.816 | 0.813 | 0.813 |
| 5* | 0.796 | 0.803 | 0.800 | 0.800 | 0.913 | 0.918 | 0.916 | 0.917 |
| 6 | 0.793 | 0.803 | 0.795 | 0.795 | 0.903 | 0.918 | 0.908 | 0.909 |
| 7* | 0.767 | 0.759 | 0.762 | 0.762 | 0.882 | 0.882 | 0.885 | 0.884 |
| 8 | 0.774 | 0.760 | 0.757 | 0.755 | 0.886 | 0.881 | 0.878 | 0.877 |
| 9 | 0.736 | 0.732 | 0.728 | 0.728 | 0.861 | 0.866 | 0.863 | 0.863 |
| 10 | 0.726 | 0.732 | 0.728 | 0.728 | 0.871 | 0.866 | 0.863 | 0.863 |
| 11 | 0.736 | 0.732 | 0.728 | 0.728 | 0.849 | 0.866 | 0.863 | 0.863 |
| Mean %Error | 0.9 | 0.8 | 0.9 | 0.9 | 1.0 | 1.0 | ||
5.4. Prediction of throughput
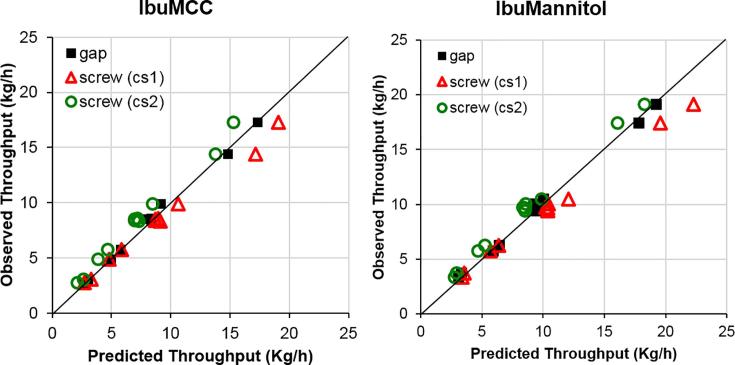
Fig. 7 shows the predicted throughput plotted over the experimentally observed throughput. An accurate throughput prediction was achieved in the gap-controlled mode. In the screw-controlled mode with screw constant cS2 the throughput was lower than the observed one for every single data point.
Fig. 7.
Prediction of throughput for the IbuMCC and IbuMannitol formulations in the gap-controlled model with relaxation factor β (■) and the screw-controlled model with either cS1 ( ) or cS2 (
) or cS2 ( ).
).
The predictions in the screw-controlled mode with cS1 were accurate at low-throughput data points (up to 10 kg/h). However, at higher predicted throughputs the corresponding observed value was lower. Table 7 shows that the average error percentage for cS2 is much higher than the one for the throughput prediction in the gap-controlled mode.
Table 7.
Experimentally observed throughput and the prediction error for the IbuMCC and IbuMannitol formulations. The predictions used the calibrated compression profile and the relaxation factor in gap-controlled mode. The two methods to calculate the screw constant in screw-controlled mode are compared ( and ). Runs marked with an asterisk (*) were used in the calibration sequence.
| Run # | IbuMCC |
IbuMannitol |
||||||
|---|---|---|---|---|---|---|---|---|
| Observed Throughput | Gap | Screw cS1 | Screw cS2 | Observed Throughput | Gap | Screw cS1 | Screw cS2 | |
| 1* | 2.77 | 2.61 | 2.67 | 2.14 | 3.31 | 3.09 | 3.37 | 2.77 |
| 2 | 8.54 | 7.85 | 8.70 | 6.97 | 10.06 | 9.28 | 10.45 | 8.58 |
| 3* | 4.87 | 4.95 | 4.82 | 3.86 | 5.72 | 5.94 | 5.68 | 4.66 |
| 4 | 14.38 | 14.86 | 17.17 | 13.75 | 17.42 | 17.81 | 19.54 | 16.04 |
| 5* | 3.07 | 3.06 | 3.28 | 2.62 | 3.73 | 3.34 | 3.54 | 2.91 |
| 6 | 9.91 | 9.16 | 10.61 | 8.49 | 10.50 | 10.02 | 12.04 | 9.88 |
| 7* | 5.79 | 5.78 | 5.83 | 4.67 | 6.27 | 6.42 | 6.38 | 5.24 |
| 8 | 17.28 | 17.34 | 19.07 | 15.27 | 19.12 | 19.25 | 22.25 | 18.26 |
| 9 | 8.32 | 8.34 | 8.95 | 7.17 | 9.69 | 9.46 | 10.35 | 8.52 |
| 10 | 8.40 | 8.34 | 8.95 | 7.17 | 9.42 | 9.46 | 10.35 | 8.52 |
| 11 | 8.57 | 8.34 | 8.95 | 7.17 | 9.72 | 9.46 | 10.35 | 8.52 |
| av. %Error | 2.8 | 6.2 | 15.7 | 4.0 | 7.1 | 12.9 | ||
Predictions for the screw-controlled mode using screw constant cS1 are on average approximately 25% higher than those using cS2 since the latter does not account for the ribbon relaxation and roller surface effects. Generally, the throughput prediction using screw constant cS1 results in over-prediction, cS2 to under-prediction at high throughputs (Fig. 7). The average error is smaller for screw constant cS1.
A classical assumption is that the screw constant is independent from screw speed (Reynolds et al., 2010). To verify, the screw constant cs1 has been calculated at different operating conditions with the experimentally observed throughput and screw speed (Eq. (17)). Fig. 8 shows that the screw constant cS1 (Eq. (17)) changes as a function of screw speed. At high screw speeds, the amount of formulation that is transported by each rotation of the screw decreases due to at least one of the following phenomena: First, at high screw speeds the feeding of the screw from the hopper is less effective. Secondly, at high screw speeds there might be higher powder slippage on the screw surface, resulting in a lower transport efficiency.
Fig. 8.
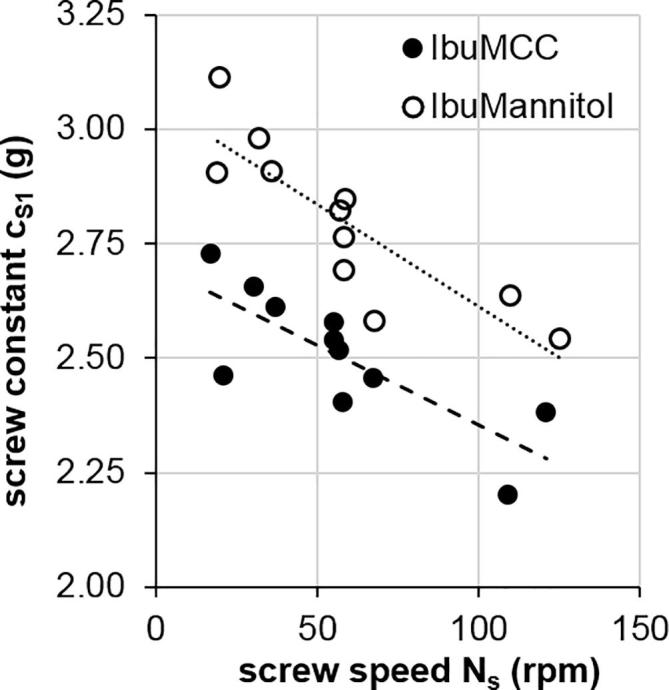
cS1 calculated using Eq. (16) at every experimental point for both formulations. The efficiency of transporting material decreases with increasing screw speeds, indicated by a decreasing cS1 value.
A possible expansion to the model could incorporate the change of the screw constant with screw speed. The advantage would be an improved predictability at high throughputs. However, the cost is one additional experiment at high throughout in order to calibrate the behavior of the screw constant at high screw speeds.
5.5. Design space prediction
In this section, multiple linear regression (MLR) was used to obtain the design space for both formulations. The design space obtained experimentally was then compared to the predicted one in the gap-controlled mode.
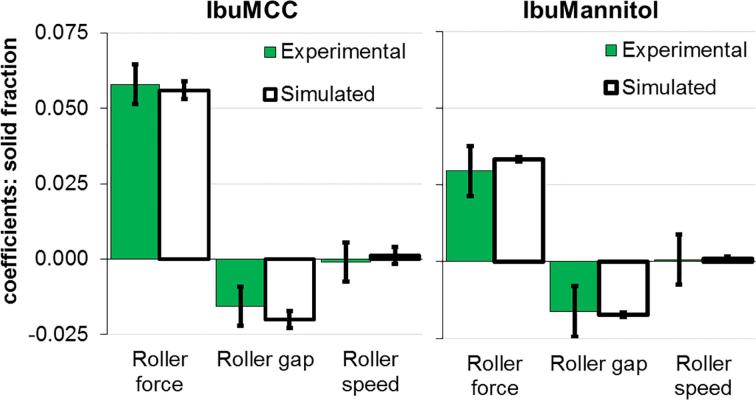
Fig. 9 shows the scaled and centered coefficient plots of the solid fraction response for both formulations. The factor interactions were insignificant and were excluded from Fig. 9 and from the final model. The coefficient plots for both formulations show that the roller speed factor is small and insignificant in terms of predicting the solid fraction in both formulations. As such, it was excluded from the final model. The confidence intervals of the coefficients for simulated data are narrower compared to experimental data. When evaluating the experimental data, there are two effects that might increase the confidence interval: (1) the experimental error which is evaluated from the triplicate center point and (2) the deviation from the experimental data points from the regression surface. The results from the model are perfectly reproducible, and thus the confidence intervals only describe the deviation between results and regression surface (2). The coefficients obtained using the data from the simulated DoE are very close to those obtained using the experimental values.
Fig. 9.
Scaled and centered coefficients for ribbon solid fraction for the IbuMCC and IbuMannitol formulations using experimental and simulated data. N = 11.
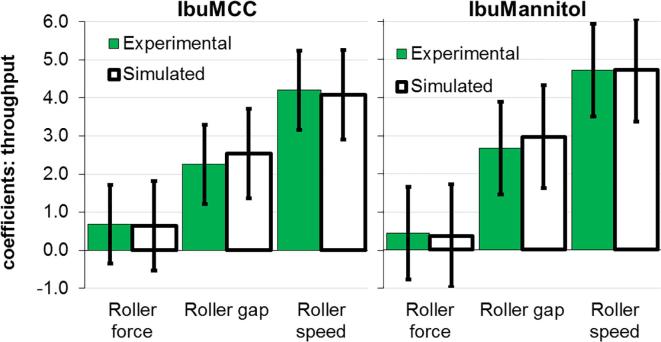
Fig. 10 shows the scaled and centered coefficients of the throughput prediction. The factor interactions were found to be insignificant and are not shown here. Since the roller force was found to be statistically insignificant for both formulations, it was removed and the model was refitted. This result is somewhat unexpected since the SCF is the main parameter that affects the ribbon density which is used for the throughput prediction in Eq. (10).
Fig. 10.
Scaled and centered coefficients for throughput for the IbuMCC and IbuMannitol formulatios using experimental and simulated data. N = 11.
The regression analysis parameters goodness of fit (R2) and goodness of prediction (Q2) are listed in Table 8. The regression models for the solid fraction response were especially well- fitted with the simulated data, with R2 and Q2 being > 0.995 for both formulations. The regression models for the throughput response showed a very similar quality of fit, with Q2 and R2 being practically the same in all DoEs. Thus, the regression model is a good approximation for arbitrary operating points within the design space. The difference between running the mechanistic model at operating points within the design space and using the regression model is thus expected to be small. The RSD in the analysis of variance (ANOVA) at a 95% confidence level is shown in Table 8.
Table 8.
Quality parameters of regression for simulated and experimental data for both formulations: goodness of fit R2, goodness of prediction Q2 and standard deviation of residuals (RSD).
| Solid fraction |
Throughput |
|||||||
|---|---|---|---|---|---|---|---|---|
| IbuMCC |
IbuMannitol |
IbuMCC |
IbuMannitol |
|||||
| Exp. | Sim. | Exp. | Sim. | Exp. | Sim. | Exp. | Sim. | |
| R2 | 0.985 | 0.997 | 0.930 | 1.000 | 0.958 | 0.957 | 0.968 | 0.968 |
| Q2 | 0.972 | 0.995 | 0.872 | 0.999 | 0.924 | 0.923 | 0.945 | 0.950 |
| RSD | 7.4x10−3 | 3.2x10−3 | 9.2x10−3 | 7.6x10−4 | 5.7x10−2 | 5.8x10−2 | 4.8x10−2 | 5.0x10−2 |
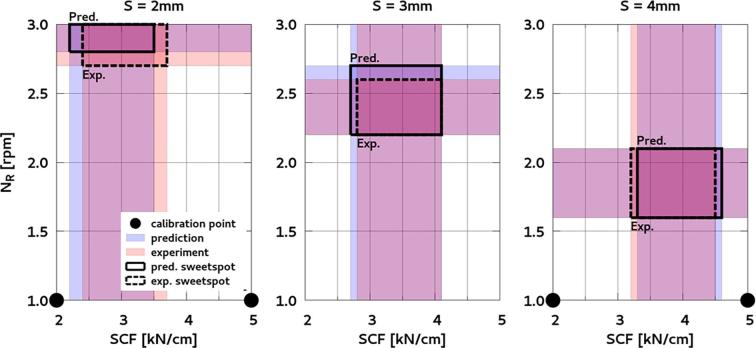
The proposed regression models can be used to predict design space for the desired ribbon solid fraction and throughput. Fig. 11 provides a visual comparison between the simulated and experimental design space, showing the region of operability (or sweet spot) that IbuMCC requires for obtaining a target ribbon solid fraction of 0.725 (min = 0.700, max = 0.750) and a throughput of 10 kg/h (min = 9 kg/h, max = 11 kg/h). The target solid fraction of 0.725 has been chosen as compromise between ribbon strength (high solid fractions preferred) and tabletability of the granules (low levels of pre-compaction preferred). The target throughput of 10 kg/h is the throughput of the complete continuous production line and variations between the different unit operations have to be minimized.
Fig. 11.
Graphical exploration around the optimal point (γR = 0.725; = 10 kg/h) comparing the MLR model based on the experimental data with the MLR model based on the simulated data for IbuMCC. The four experimental data points used to calibrate the mechanistic model are marked ●.
Fig. 11 indicates that the design spaces obtained based on the simulated and experimental DoEs are very similar. This offers a considerable reduction of experimental efforts and material consumption related to spot- checking the sweet spot in the center and along the extremes. The sweet spot analysis for the IbuMannitol formulation provides a similarly good prediction, because the correlation coefficients match between simulation and experiment (Fig. 9 for ribbon density, Fig. 10 for throughput).
Robustness of dry granulation process is a key element in process validation that should be ensured within the drug product development stage. The presented approach has the value of providing in-silico design spaces allowing a robustness simulation based on mechanistic modeling using limited number of real experiments. Additionally, the key input to this model can be communicated directly from the RC to predict the solid fraction of the ribbon being produced in real-time. This will eventually enable the application of RC model as a soft sensor in the strive towards robust and reliable RC processes, ensuring high quality product and increased economic profit.
6. Conclusion
In practice, RC mechanistic models are highly sensitive to the compressibility factor (K) and the pre-consolidation density (γ0). Characterizing these properties in tableting machines delivers inaccurate results. The exact compression profile of the formulation depends on the equipment used. This is reflected by different and values for the same formulation in different equipment types, resulting in additional trials and formulation consumption. Thus, in this work, we introduced a roadmap to the RC process development and scale-up on the same equipment. The key is an iteration process for calibrating the K and γ0 values, which can reduce the material amount required, the number of RC experiments and the material characterization efforts at a low software expense.
Additionally, we proposed a simple method that uses the RC throughput to calculate the volume relaxation that the ribbon experiences after exiting the rollers. This parameter (β) can be used to predict the throughput with an acceptable accuracy.
We demonstrated that, based on a limited number of experiments, a design space for a broad range of throughputs can be predicted with a high accuracy. It may be used in the future as a soft sensor for RC processes operating in continuous manufacturing lines for in-line adjustment of throughput while maintaining the desired ribbon solid fraction. In order to calibrate the model for a new material in gap-controlled mode, it is necessary to perform the calibration routine to extract the compression profile and the relaxation factor . Then it is possible to reliably predict the ribbon density with Eq. (9) and the throughput with Eq. (14). With a better prediction of the ribbon density and throughput, the process can be controlled better.
Acknowledgements
The Research Center Pharmaceutical Engineering is funded by the Austrian COMET program under the auspices of the Austrian Federal Ministry of Transport, Innovation and Technology (bmvit), the Austrian Federal Ministry of Economy, Family and Youth (bmwfj) and by the State of Styria (Styrian Funding Agency SFG). COMET is managed by the Austrian Research Promotion Agency FFG.
References
- Bi M., Alvarez-Nunez F., Alvarez F. Evaluating and Modifying Johanson’s Rolling Model to Improve its Predictability. J. Pharm. Sci. 2014;103:2062–2071. doi: 10.1002/jps.24012. [DOI] [PubMed] [Google Scholar]
- Chang C.K., Alvarez-Nunez F.A., Rinella J.V., Jr., Magnusson L.-E., Sueda K. Roller Compaction, Granulation and Capsule Product Dissolution of Drug Formulations Containing a Lactose or Mannitol Filler, Starch, and Talc. AAPS PharmSciTech. 2008;9:597–604. doi: 10.1208/s12249-008-9088-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csordas K., Wiedey R., Kleinebudde P. Impact of roll compaction design, process parameters, and material deformation behaviour on ribbon relative density. Drug Dev. Ind. Pharm. 2018;44:1295–1306. doi: 10.1080/03639045.2018.1446444. [DOI] [PubMed] [Google Scholar]
- Cunningham J.C. Drexel University; 2005. Experimental studies and modeling of the roller compaction of pharmaceutical powders (PhD Thesis) [Google Scholar]
- Dec R.T., Zavaliangos A., Cunningham J.C. Comparison of various modeling methods for analysis of powder compaction in roller press. Powder Technol. 2003;130:265–271. [Google Scholar]
- Dumarey M., Wikström H., Fransson M., Sparén A., Tajarobi P., Josefson M., Trygg J. Combining experimental design and orthogonal projections to latent structures to study the influence of microcrystalline cellulose properties on roll compaction. Int. J. Pharm. 2011;416:110–119. doi: 10.1016/j.ijpharm.2011.06.018. [DOI] [PubMed] [Google Scholar]
- Fonteyne M., Vercruysse J., De Leersnyder F., Van Snick B., Vervaet C., Remon J.P., De Beer T. Process Analytical Technology for continuous manufacturing of solid-dosage forms. TrAC, Trends Anal. Chem. 2015;67:159–166. [Google Scholar]
- Gamble J.F., Tobyn M., Dennis A.B., Shah T. Roller compaction: application of an in-gap ribbon porosity calculation for the optimization of downstream granule flow and compactability characteristics. Pharm. Dev. Technol. 2010;15:223–229. doi: 10.3109/10837450903095342. [DOI] [PubMed] [Google Scholar]
- Guigon P., Simon O. Roll press design—influence of force feed systems on compaction. Powder Technol. 2003;130:41–48. [Google Scholar]
- Guigon P., Simon O., Saleh K., Bindumadhavan G., Adams M.J., Seville J.P.K. Roll pressing. In: Salmon A.D., Hounslow M.J., Seville J.P.K., editors. Granulation, Handbook of Powder Technology. Elsevier; Amsterdam; Boston: 2007. [Google Scholar]
- Gupta A., Peck G.E., Miller R.W., Morris K.R. Real-time near-infrared monitoring of content uniformity, moisture content, compact density, tensile strength, and young’s modulus of roller compacted powder blends. J. Pharm. Sci. 2005;94:1589–1597. doi: 10.1002/jps.20375. [DOI] [PubMed] [Google Scholar]
- Inghelbrecht S., Remon J.P. The roller compaction of different types of lactose. Int. J. Pharm. 1998;166:135–144. [Google Scholar]
- Johanson J.R. A Rolling Theory for Granular Solids. J. Appl. Mech. 1965;32:842. [Google Scholar]
- Katashinskii V.P. Analytical determination of specific pressure during the rolling of metal powders. Soviet Powder Metallurgy and Metal Ceramics. 1966;5:765–772. [Google Scholar]
- Kleinebudde P. Roll compaction/dry granulation: pharmaceutical applications. Eur. J. Pharm. Biopharm. 2004;58:317–326. doi: 10.1016/j.ejpb.2004.04.014. [DOI] [PubMed] [Google Scholar]
- Leane M., Pitt K., Reynolds G. The Manufacturing Classification System (MCS) Working Group A proposal for a drug product Manufacturing Classification System (MCS) for oral solid dosage forms. Pharmaceutical Dev. Technol. 2015;20:12–21. doi: 10.3109/10837450.2014.954728. [DOI] [PubMed] [Google Scholar]
- Lopes D.G., Garsuch V., Becker K., Paudel A., Stehr M., Zimmer A., Salar-Behzadi S. Improving the granule strength of roller-compacted ibuprofen sodium for hot-melt coating processing. Int. J. Pharm. 2016;510:285–295. doi: 10.1016/j.ijpharm.2016.06.049. [DOI] [PubMed] [Google Scholar]
- Martinetz M.C., Karttunen A.-P., Sacher S., Wahl P., Ketolainen J., Khinast J.G., Korhonen O. RTD-based material tracking in a fully-continuous dry granulation tableting line. Int. J. Pharm. 2018;547:469–479. doi: 10.1016/j.ijpharm.2018.06.011. [DOI] [PubMed] [Google Scholar]
- Mazor A., Orefice L., Michrafy A., de Ryck A., Khinast J.G. A combined DEM & FEM approach for modelling roll compaction process. Powder Technol. 2018;337:3–16. [Google Scholar]
- Michrafy, A., Zavaliangos, A., Cunningham, J.C., 2017. Dry granulation process modeling. In: Predictive Modeling of Pharmaceutical Unit Operations. Elsevier, pp. 71–97. https://doi.org/10.1016/B978-0-08-100154-7.00004-1.
- Miller, R., 2005. Roller Compaction Technology. In: Parikh, D. (Ed.), Handbook of Pharmaceutical Granulation Technology, Third Edition. Informa Healthcare, pp. 159–190. https://doi.org/10.1201/9780849354953.ch6.
- Nesarikar V.V., Patel C., Early W., Vatsaraj N., Sprockel O., Jerzweski R. Roller compaction process development and scale up using Johanson model calibrated with instrumented roll data. Int. J. Pharm. 2012;436:486–507. doi: 10.1016/j.ijpharm.2012.06.027. [DOI] [PubMed] [Google Scholar]
- Nkansah P., Wu S.-J., Sobotka S., Yamamoto K., Shao Z.J. A Novel Method for Estimating Solid Fraction of Roller-Compacted Ribbons. Drug Dev. Ind. Pharm. 2008;34:142–148. doi: 10.1080/03639040701484387. [DOI] [PubMed] [Google Scholar]
- Park S.-Y., Galbraith S.C., Liu H., Lee H., Cha B., Huang Z., O’Connor T., Lee S., Yoon S. Prediction of critical quality attributes and optimization of continuous dry granulation process via flowsheet modeling and experimental validation. Powder Technol. 2018;330:461–470. [Google Scholar]
- Perez-Gago A., Reynolds G., Kleinebudde P. Impact of roll compactor scale on ribbon density. Powder Technol. 2017 [Google Scholar]
- Perez-Gandarillas L., Perez-Gago A., Mazor A., Kleinebudde P., Lecoq O., Michrafy A. Effect of roll-compaction and milling conditions on granules and tablet properties. Eur. J. Pharm. Biopharm. 2016;106:38–49. doi: 10.1016/j.ejpb.2016.05.020. [DOI] [PubMed] [Google Scholar]
- Peter S., Lammens R.F., Steffens K.-J. Roller compaction/Dry granulation: use of the thin layer model for predicting densities and forces during roller compaction. Powder Technol. 2010;199:165–175. [Google Scholar]
- PM Modnet Modelling Group Comparison of computer models representing powder compaction process: State of the art review. Powder Metall. 1999;42:301–311. [Google Scholar]
- Reimer H.L., Kleinebudde P. Hybrid modeling of roll compaction processes with the Styl’One Evolution. Powder Technol. 2019;341:66–74. [Google Scholar]
- Reynolds G., Ingale R., Roberts R., Kothari S., Gururajan B. Practical application of roller compaction process modeling. Comput. Chem. Eng. 2010;34:1049–1057. [Google Scholar]
- Rowe, J.M., Charlton, S.T., McCann, R.J., 2017. Development, Scale-Up, and Optimization of Process Parameters. In: Developing Solid Oral Dosage Forms. Elsevier, pp. 869–915. https://doi.org/10.1016/B978-0-12-802447-8.00032-7.
- Rowe J.M., Crison J.R., Carragher T.J., Vatsaraj N., Mccann R.J., Nikfar F. Mechanistic Insights into the Scale-Up of the Roller Compaction Process: A Practical and Dimensionless Approach. J. Pharm. Sci. 2013;102:3586–3595. doi: 10.1002/jps.23659. [DOI] [PubMed] [Google Scholar]
- Sajjia M., Shirazian S., Egan D., Iqbal J., Albadarin A.B., Southern M., Walker G. Mechanistic modelling of industrial-scale roller compactor ‘Freund TF-MINI model’. Comput. Chem. Eng. 2017;104:141–150. [Google Scholar]
- Singh R., Ierapetritou M., Ramachandran R. An engineering study on the enhanced control and operation of continuous manufacturing of pharmaceutical tablets via roller compaction. Int. J. Pharm. 2012;438:307–326. doi: 10.1016/j.ijpharm.2012.09.009. [DOI] [PubMed] [Google Scholar]
- Souihi N., Reynolds G., Tajarobi P., Wikström H., Haeffler G., Josefson M., Trygg J. Roll compaction process modeling: Transfer between equipment and impact of process parameters. Int. J. Pharm. 2015;484:192–206. doi: 10.1016/j.ijpharm.2015.02.042. [DOI] [PubMed] [Google Scholar]
- Sun C.C., Kleinebudde P. Mini review: Mechanisms to the loss of tabletability by dry granulation. Eur. J. Pharm. Biopharm. 2016;106:9–14. doi: 10.1016/j.ejpb.2016.04.003. [DOI] [PubMed] [Google Scholar]
- Teng Y., Qiu Z., Wen H. Systematical approach of formulation and process development using roller compaction. Eur. J. Pharmaceutics Biopharmaceutics. 2009;73:219–229. doi: 10.1016/j.ejpb.2009.04.008. [DOI] [PubMed] [Google Scholar]
- Vervaet C., Remon J.P. Continuous granulation in the pharmaceutical industry. Chem. Eng. Sci. 2005;60:3949–3957. [Google Scholar]
- Wang P.T., Karabin M.E. Evolution of porosity during thin plate rolling of powder-based porous aluminum. Powder Technol. 1994;78:67–76. [Google Scholar]