Graphical abstract
Keywords: Protein formulations, Viscosity, Electroviscous effect, Drug delivery, High concentration, Subcutaneous injection, Electrostatic interaction
Abstract
Subcutaneous delivery of highly concentrated protein formulations is paramount for reducing healthcare cost and improving patient compliance, where reducing the solution viscosity of formulations is critical for drug delivery. The objective of this paper is to provide some mechanistic understanding about the contribution of electrostatic repulsion to the viscosity of protein solutions at high concentrations, along with the effect of excipients such as salts on relative viscosity. Proteins are treated as charged colloids in this paper. At high concentrations, the electrical double layer starts to overlap, and secondary electroviscous effect becomes significant in addition to primary electroviscous effect. In other words, the hydrodynamic volume of proteins plays a great role in influencing their solution viscosity because of the excluded volume effect. Currently, it is hypothesized that the high viscosity of concentrated protein solutions is attributed to formation of clusters due to either electrostatic attraction or hydrophobic interactions, especially for monoclonal antibodies, in which anybody molecules in high concentration formulations may form networks. Consequently, viscosity reduction in the presence of inorganic or organic salts in these formulations is due to breaking up of these networks. In this review, authors hope to provide another point of view based on the effect of the electrostatic repulsion on the excluded volume-hydrodynamic volume. Finally, authors hope the proposed theoretical framework can be used to guide excipient selection in the product development of highly concentrated proteins.
1. Introduction
Developing drug products consisting of highly concentrated protein solutions is of importance in the biopharmaceutical industry, particularly in conjunction with delivery devices (Shire, 2015). This is because drug products containing highly concentrated protein solutions can enable subcutaneous delivery of protein therapeutics using syringes or autoinjectors, which may bring several advantages in dose administration, including self-administration, increased patient comfort, improved patient compliance, and reduced healthcare costs due to the avoidance of intravenous infusions. As delivery of biologics via devices is becoming increasingly popular, it is demanding to formulate proteins at high concentrations to meet the volume requirement of devices. However, proteins in concentrated solutions can display many undesirable physical properties such as forming reversible or irreversible aggregates (Harn et al., 2007). Additionally, highly concentrated protein solutions may be very close to their solubility limits under certain solution conditions such as solution pH, ionic strength, buffer species, etc. (Salinas et al., 2010). Finally, protein solutions of high concentration generally result in high viscosity, which poses challenges in manufacturing and delivery of biologics (Joshi et al., 2014).
Protein solutions of high viscosity can significantly impede the process development for drug substances and drug products. For drug substance development, high viscosity can present significant challenges in filtration and thus purification (Shire, 2009). Similarly, for drug product development protein solutions with high viscosity often encounter various issues during mixing and vial filling, which can generate non-uniform products because of insufficient mixing and/or inaccurate filling (Shire, 2009). As for drug administration, while formulations of highly concentrated proteins provide options for outpatient or self-administration therapies because they can supply a single dose in a volume amenable to syringe or autoinjector usage, it significantly increases the force requirement of dosing devices due to high viscosity. High viscosity also causes great concerns regarding the syringeability of many protein therapeutics because syringes currently available on the market can only function within certain limits of solution viscosity values, in which 30–50 cP is a common viscosity limit above which it would require much higher injection forces (Burckbuchler et al., 2010). Needle gauge is a key factor for syringeability of highly concentrated protein formulations. While fine needles cause less injection pain, it requires relatively much high injection forces. Various approaches have been taken to overcome the challenges in administering the drug products with high protein concentrations in terms of reducing formulation viscosity (Mitragotri et al., 2014). The viscosity of highly concentrated mAb formulations may be lowered by adding salts or other excipients (Wang et al., 2015). Some commonly used excipients include L-arginine HCl and sodium chloride, as well as other inorganic salts (Sudrik et al., 2017). Nonetheless, although many approaches have been empirically attempted to reduce the solution viscosity of highly concentrated protein formulations, there is still a lack of fundamental understanding on the correlation of formulation viscosity with concentrations of salts or other excipients (Wang, 2015).
Mechanistically, the rapid increase of solution viscosity with concentration has been investigated for various protein solutions (Zhang and Liu, 2017). Second virial coefficient (B22) along with diffusion interacting parameter (kD) has been measured to correlate the solution viscosity with intermolecular interactions (Connolly et al., 2012). Hypothetically, the high viscosity of protein solutions with concentrated antibodies is assumed to be caused by formation of clusters due to electrostatic attraction as suggested in literature (Inoue et al., 2014). Any reduction in solution viscosity by increasing ionic strength or addition of hydrophobic ions is attributed to breaking down of electrostatic attraction. Additionally, electroviscous effect (primary electroviscous) is typically considered as a minor factor whereas formation of transient networks is assumed to be the major contributor for significant viscosity increase (Inoue et al., 2014). However, this conjecture cannot explain the fact that presence of different ion species can lower viscosity in varied magnitude, and in the case of adding Na2SO4 viscosity was increased (Zhang and Liu, 2017).
In this paper, we focus on understanding how electroviscous forces influence the solution viscosity of protein formulations. Prior to discussing electroviscous effect (including primary, secondary, and tertiary electroviscous effects), we first introduce the role of electrostatic interaction in stabilizing protein formulations. Additionally, a few common rheological models in terms of volume fraction (ϕ), including one with an electroviscous factor (p), are introduced. Furthermore, the theoretical foundation of electroviscous effect for charged colloids will be brought in to facilitate data interpretation. Because there is a lack of systematic research regarding the effect electroviscous force on the protein solution viscosity, experimental results from inorganic/organic charged colloids are also encompassed for discussion. Moreover, to explain the viscosity reduction by salt addition, we center on the impact of reducing electrostatic repulsion (molecular separation) on the excluded volume (secondary electroviscous effect). Finally, authors hope this paper can stimulate more research in this area because of its significance in the development of drug products of biologics.
2. Viscosity and protein-protein interactions
Proteins are macromolecules with complex physical structures and diverse surface properties. The solution behavior of proteins at high concentrations including viscosity is often significantly different from that at low concentrations largely because of the presence of protein-protein interactions (PPIs) (Saluja and Kalonia, 2008). Since PPIs contribute significantly to the non-ideality of solution behavior of proteins at high concentrations, they are frequently evaluated. Thermodynamically, B22 (osmotic secondary virial coefficient) has been measured to assess the effect of non-specific PPIs in solution where a positive B22 suggests repulsive interactions while negative values are indicative of protein-protein attractions (Roberts et al., 2014). Although B22 has been used to analyze the aggregation tendency of proteins as well as formation of clusters, it has not been very successful in predicting the viscosity behavior of protein solutions at high concentrations (Chi et al., 2003, He et al., 2011, Saito et al., 2012). Recently, protein interaction parameter (kD) which can be more conveniently measured using dynamic light scattering is frequently used to evaluate PPIs and correlate with the aggregation and cluster formation propensity of proteins (Connolly et al., 2012, Lehermayr et al., 2011, Saito et al., 2012). While these thermodynamic parameters can provide some insight into PPIs, the interpretation of the rheological behaviors of highly concentrated protein solutions is still very challenging.
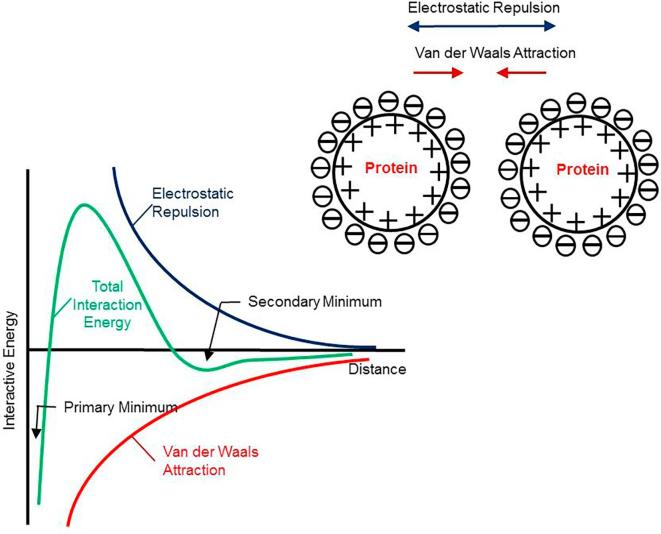
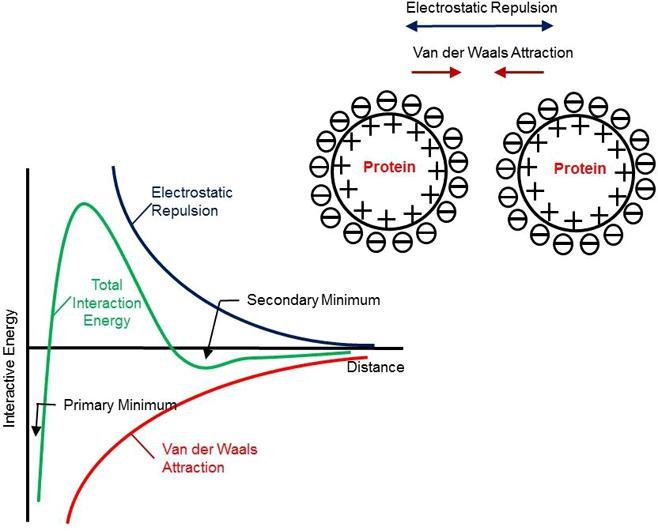
The surface effective charge (surface potential) of therapeutic proteins in formulations is influenced by solution pH, ionic strength, surfactants, and binding of ligands (Pace et al., 2009). When solution pH is away from the pI of a protein, protein molecules bear a net charge although locally either positive or negative charge can be present due to the heterogeneity of surface charge distribution. This net charge, positive or negative, determines the surface effective charge of protein macroions and consequently the formation electrical double layer (EDL). A common electrostatic theory, known as Derjaguin, Landau, Verwey, and Overbeek (DLVO) theory in colloid science, has been commonly used to describe the forces involved in complex colloids such as proteins. According to DLVO, stability of colloidal particles is determined by the overall balance between the long-range electrostatic repulsion and short-range Van der Waals attraction. Fig. 1 depicts a typical potential energy diagram based on DLVO.
Fig. 1.
A schematic depicting the balance between electrostatic repulsion and van Der Waals attraction for colloids (DLVO theory).
Proteins in solution are typically stabilized by electrostatic repulsion. The solution viscosity of proteins is mostly attributed to the excluded volume of proteins with EDL included, in the absence of major PPI such as Hoffmeister effect. Increasing ionic strength by adding salts reduces electrostatic repulsion, which decreases the effective excluded volume, and ultimately lowers the solution viscosity (Heinen et al., 2012). Since Van der Waals attraction dominates at short distance, PPIs in highly concentrated formulations will be greatly augmented when electrostatic repulsion is significantly weakened due to EDL compression in the presence of high concentration salts (Neergaard et al., 2013). In this case, proteins in formulations are at risk of forming aggregates, flocs or other networked structures, causing physical instability concern. Studies showed that the long-range electrostatic repulsion usually dominates at low ionic strength, while the short-range attractive forces become prominent above a critical ionic strength. Furthermore, surface effective charge or surface potential greatly influences electrostatic interaction (Roberts et al., 2014). As shown in Fig. 1, the energy barrier created by electrostatic repulsion, which prevents two protein molecules from approaching each other, abates when EDL is compressed (Leckband and Sivasankar, 1999). In other words, Van der Waals attraction governs and mediates the aggregation process of protein molecules. In addition to the electrostatic repulsion and Van der Waals attraction, it has been shown that non-classic DLVO forces such as the hydration force and hydrophobic interaction, also contribute to protein-protein interaction (Leckband and Sivasankar, 1999). These forces are very significant at short separation distance when protein molecules are near each other in highly concentrated solutions (Leckband and Sivasankar, 1999). These forces are often included in extended DLVO theory. However, in this paper we will focus on discussing the impact of the electrostatic force on the viscosity behavior of protein solutions in the presence of electrolytes.
2.1. Viscosity of protein formulations
The apparent viscosity of protein formulations, which can be measured using a rheometer, is typically influenced by the following elements: molecular structure, particle shape, and particle morphology, as well as external factors such as the solution pH and ionic strength, along with temperature and pressure (Jezek et al., 2011, Mezger, 2011). The most commonly used viscosity equation for protein solutions is Huggins Equation, an empirical expression related the reduced viscosity of a dilute solution to protein concentration in solution as described below (Pamies et al., 2008):
| (1) |
where is the specific viscosity of macromolecular solutions over concentration, is the intrinsic viscosity, and is a dimensionless (Huggins) constant (Sandler et al., 1998). The concentration term in Huggins equation is expressed as mass per volume while for macromolecules in solution their hydrodynamic volume greatly contributes to solution viscosity. Thus, using volume fraction to express viscosity is more appropriate. Huggins equation is most applicable in the dilute concentration regime where Huggins profile varies linearly with concentration. For proteins, their concentration regime in solution is protein and physical-state dependent in which the physical properties of proteins such as surface charge as well as folded or denatured can significantly influence this regime. As noted later in this paper, the electrostatic repulsive interactions among proteins are included in the kH term in Huggins equation (see discussion on secondary electroviscous effect) although inexplicitly. Einstein derived the first viscosity expression (η: apparent viscosity; η0: the apparent viscosity of the medium) in terms of volume fraction (ϕ) for dilute colloidal dispersions of spherical particles as shown in Eq. (2) (Einstein, 1911):
| (2) |
Since Einstein equation is only valid for dilute suspensions at low concentrations, much of work had been done to extend this equation to non-dilute systems at high solid contents. Mooney derived an empirical formula for hard spheres in the absence of interactions, with only consideration of excluded volume effect (Pindrus et al., 2017). For non-spherical particles such as mAb solutions, the revised Mooney equation is shown below:
| (4) |
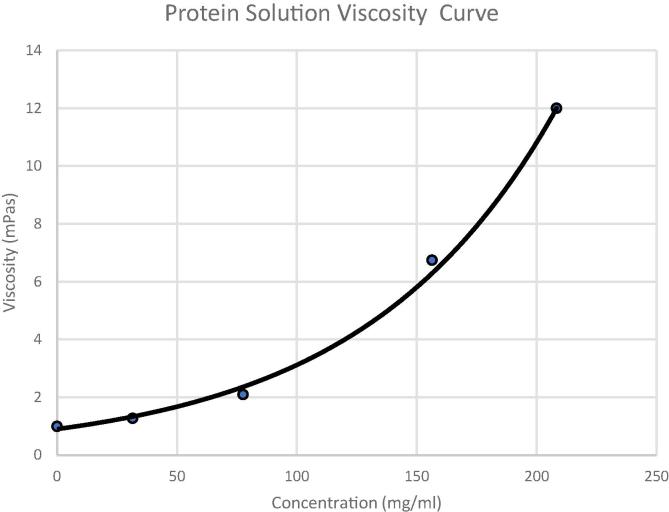
where is the solution viscosity, and is the viscosity of the medium used. Additionally, c is the concentration of proteins while is again the intrinsic viscosity of the protein solution. Furthermore, k are a crowding factor and the Simha parameter (shape dependent). Fig. 2 shows a typical viscosity-concentration profile for protein solutions-well-fit for Moony equation, where the viscosity is observed to increase exponentially with concentration beyond certain concentrations. However, the concentration approaches the maximum as the Figure shows. In this regime, movement of neighboring particles is significantly impeded because of the self-crowding factor near the maximum concentration (∼25% in terms of volume fraction or about 300–400 mg/mL in concentration for some proteins (Gonçalves et al., 2016). Moreover, other rheological models, also in volume fraction, include the one derived by Irvin Krieger and Thomas Dougherty (Krieger and Dougherty, 1959).
| (3) |
where is the maximum volume fraction of solid content in a suspension, denoting the maximum free space that particles are allowed for moving around in the suspension. Here, [η] (the intrinsic viscosity) is a shape dependent parameter, typically 2.5 for spheres. For protein solutions of non-spherical shape of particles with strong electrostatic interactions, both shape and electroviscous parameters need to be included. In this case, a modified Einstein equation is frequently employed to model the relative viscosity as the following (Monnery et al., 1991, Simha, 1940):
| (5) |
where S is the shape factor (1 for spheres), and p is a coefficient accounting for the electrostatic interaction (electroviscous effect). Since S is a complicated function, we will not further discuss it in this paper. Most importantly, p depends on the zeta potential of colloidal particles and ionic strength of the medium, along with volume fraction. For protein formulations, electroviscous effect plays a great role in influencing their solution viscosity, in which reducing p can enable product development. For dilute solutions of proteins (ϕ ≪ 0.2 for most of proteins), primary electroviscous effect is dominant, and secondary and ternary electroviscous effects will become evident as the solution concentration increases (ϕ ∼ 0.25). The latter is very important for protein formulations at high concentrations.
Fig. 2.
Solution viscosity as a function of concentration, data were excerpt from the cited reference (Kanai, et al., 2008) with no added salt in a mAb solution.
3. Electroviscous effect
3.1. Theoretical background
Biological therapeutics, including proteins, DNAs, RNAs, and Cells, are charged colloids formulated in buffer solutions with sugars and other additives (Wang and Singh, 2013). During manufacturing the rheological behavior of these formulations is significantly influenced by electroviscous effect (EE), especially for formulations of highly concentrated proteins (ϕ ∼ 0.25; 300–400 mg/mL for some proteins) at which EDL starts to overlap (Tomar et al., 2016). Therefore, one of effective strategies for lowering formulation viscosity is to reduce electrostatic repulsion through addition of salts. As reported in literature, flow of charged particles is influenced by both surface charges of colloidal particles and the ionic strength of the medium, in addition to shear rate (van de Ven, 2001). As for protein colloids, because of the presence of electrical double layers around proteins, their solution viscosity is consequently increased due to the overlaps of electrical double layers and rise of energy dissipation under shear. Shear thinning generally reduces formulation viscosity; for protein colloids with thick EDL viscosity is inversely proportional to Peclet number (Russel, 1978). This effect was termed as electroviscous effect (EE) (p in Eq. (5)), as reported in 1930s (Mosteller, 1964). Typically, EE can be categorized as primary, secondary, and tertiary, which will be discussed in the following sections.
3.1.1. Primary electroviscous effect
Primary electroviscous effect (PEE) is commonly referred to as the viscosity increase due to distortion of EDL (counter ions)-rise of energy dissipation. Smoluchowski published the first equation on the relative viscosity of charged colloids as a function of the solution properties as shown in Eq. (6) (Smoluchowski, 1916)
| (6) |
where ηrel, ϕ, τ0, η0, ε, a, and ς are the relative viscosity, volume fraction, conductivity, and viscosity and permittivity of the medium (solvent), as well as the radius and the zeta potential of colloidal particles. In Eq. (6), represents electroviscous effect (p) in Eq.5. Eq. (6) works well for charged colloids of thin electrical double layers (κa ≫ 1) at high ionic strength. However, for proteins in solution with a typical ionic strength of 0.01 M (κ−1 = 3 nm) (antibodies in 0.01 histidine buffer), κa can range from 1 to about 3, given that the radius of proteins varies from 3 nm to 10 nm. Thus, Smoluchowski’s formula is not applicable to protein solutions. Booth developed an equation which can be applied in a wide range of κa with limited zeta potentials (Booth, 1950). The most recent analysis on PEE, covering a wide range of κa and zeta potential, was developed by Watterson and White (Watterson and White, 1981; . Based on the derivation from Watterson and White, the electroviscous term for charged colloids is approximated as:
| (7) |
where e, ni∝, zi, and λi are the electrical charge of an electron, the bulk ion concentration of type i, the valence of ion i, and a parameter related conductance defined by Eq. (8)
| (8) |
where NA is the Avogadro’s number, e is the electrical charge and zi is the valence of the ion i, as well as Λi0 is the limiting conductance of the ith ionic species.
| (9) |
Z(κa) value varies with the thickness of EDL. For a thick double layer (Booth, 1950),
| (10) |
| (11) |
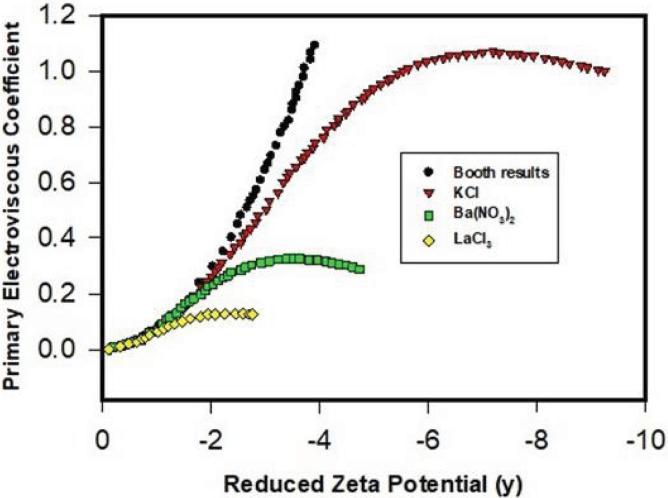
Watterson and White predict that primary electroviscous factor decreases significantly with increasing ionic strength (κa). In practice, for protein formulations with concentration much <0.25 (ϕ), PEE is usually significant at low ionic strength (much <0.01 M or κa < 1). As for the surface charge effect, Watterson and White indicates that PEE (electroviscous factor P) increases with zeta potential in which the magnitude of the increase in PEE varies with κa-thus the ionic strength of protein solutions, where impact of zeta potential on PEE is especially significant for thick EDL such as κa = 0.25 (see Fig. 3). According to the above analysis, increasing in ionic strength-decreasing in EDL and thus increasing in κa-lowers PEE. In other words, addition of salts in protein solutions evidently decreases PEE. However, proteins with larger zeta potentials display greater PEE, thereby potentially raising solution viscosity. Furthermore, presence of different ion species in formulations such as buffer species (phosphate buffer vs. histidine buffer), especially their valence, can significantly influence PEE (see Fig. 4). Specially, presence of high valency ions in protein formulations can significantly increase ionic strength and hence reduce κ−1, thereby mitigating PEE viscosity. In Fig. 4, high valency cations such as Ba2+ and La3+ can suppress the increase of electroviscous factor with zeta potential where suppression is closely related to the ion valency. This is practically an effective approach to alleviate PEE. Examples of impact of ion valency on the solution viscosity will be discussed later. As the theory indicated, PEE is only pronounced for dilute protein solutions. For concentrated protein solutions, secondary electroviscous effect due to protein-protein interaction becomes influential.
Fig. 3.
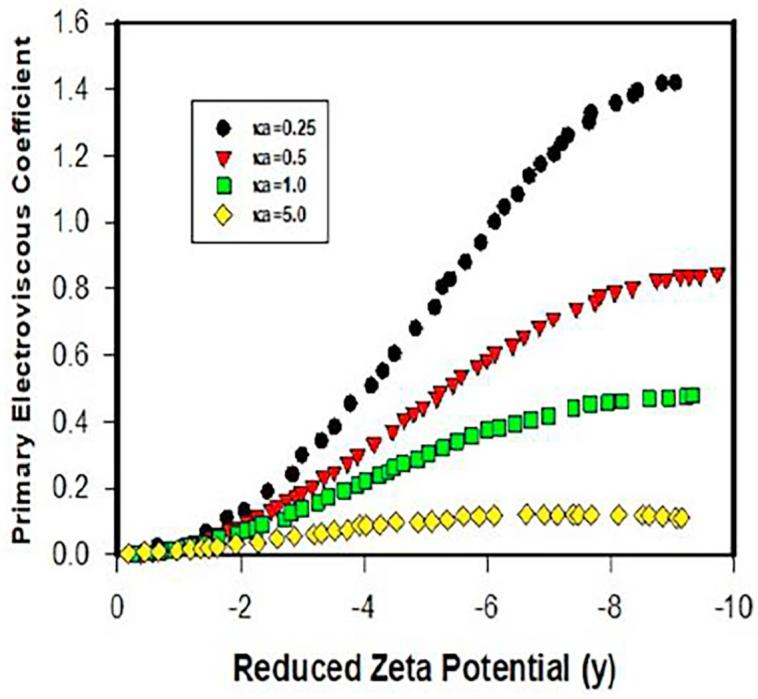
Predicted primary electroviscous parameter (viscosity increase) as a function of zeta potential at varied ionic strength (Watterson and White, 1981) (y = δ/kT) indicating increase of primary electroviscous coefficient with surface potential; this effect is more pronounced for thick double layers (κa).
Fig. 4.
Predicted effect of ion valency on primary electroviscous parameter (p = viscosity increase) in a range of zeta potential (Watterson and White, 1981) (y = δ/kT): 1:1 KCl, 2:1 Ba(NO3)2, 3:1 LaCl3 at fixed κa = 5; for high valency ions increase of p with zeta potential is less than low valency ions.
3.1.2. Secondary electroviscous effect
Impact of secondary electroviscous effect (SEE) on the viscosity of highly concentrated protein formulations is of importance in developing protein formulations. Because of the “crowding effect” in highly concentrated protein formulations, molecules start to lose their freedom of motion due to a space limitation, and thus the interaction owing to particle-particle contact (proportional to ϕ2) becomes dominant. In this case, the expression for ηrel is extended to beyond the first term in ϕ. Theoretical analysis of SEE of charged colloids was performed by Chan et al., 1966, Russel, 1980). For simplicity, here we only introduce the expression derived by Chan et al. As reported by Chan et al., the two charged latex particles (polystyrene) approaching experienced a strong electrostatic repulsion which consequently increased the particle–particle separation distance. Because of electrostatic repulsion, the formed doublet particles have a larger apparent center-to-center distance, causing a larger energy dissipation when rotating in a shear field (Chan et al., 1966). By balancing the hydrodynamic force with electrostatic repulsion while neglecting Van der Waals force and Brownian motion, Chan et al. expressed k2-the second coefficient in the relative viscosity expression (ηr = η0 + k1ϕ + k2 ϕ2) as:
| (13) |
where is the distance between two particles closest approached-depending on their effective surface charge (zeta potential) and ionic strength, and a is the radius of colloidal particles. As shown in Eq. (13), is a significant factor in influencing SEE. k2 is also closely related to the Huggins constant (kH) as kH = k22/k1 (Blachford et al., 1969). According to Eq. (13),is determined by electrostatic repulsion in which high ionic strength can significantly suppress the repulsion and reduce . Furthermore, high valency ions such as Na2SO4 are effective in reducingdue to significant increase in ionic strength. In summary, reduction in due to suppression of electrostatic repulsion can greatly lower k2 and kH. Russel, However, took a different mathematical approach, in which dimensionless quantity was used (Russel, 1980). Although Russel’s formula has included the Brownian motion force, his expression is confounded with many parameters, making the interpretation of viscosity dependence on zeta potential and κa very challenging. Hence, we will not discuss it in this paper.
3.1.3. Tertiary electroviscous effect and others
Tertiary electroviscous effect (TEE) denotes the impact of conformational and other structural changes such as denaturation of proteins on solution viscosity (Hunter, 2013). Because TEE involves changing protein conformations, along with other modifications of physical state such as formation of aggregates, it is very challenging to predict TEE theoretically. This is especially true for formulations of highly concentrated proteins. Overall, TEE is associated with significant changes of physical state or structures of proteins (secondary, tertiary, or quaternary), as well as formation of aggregates, flocs, and gels. These may be caused by ion binding and Van der Waals attraction.
3.2. Viscosity and electroviscous effect
The current supposition for the high viscosity observed in concentrated protein solutions such as monoclonal antibodies (mAbs) is that proteins self-associate at high concentrations to form reversible clusters through electrostatic attraction (Roberts et al., 2014). In presence of salts solution viscosity is reduced because salts can disrupt electrostatic attraction through ion binding and breakup of clusters (Roberts et al., 2014). In most literature, electroviscous effect-mainly primary electroviscous effect-is generally not considered. In this paper, we will attempt to explain the effect of salts (ionic strength) and types of salts in reducing the viscosity of protein solutions on the basis of electroviscous effect (DLVO theory). We mainly focus on SEE because in the concentration regime of around 25% in ϕ (300–400 mg/mL for some proteins) protein molecules are very close to each other so that EDL starts to overlap (Gonçalves et al., 2016). So, addition of salts in protein formulations can be an effective way to reduce viscosity, in some cases resulting in an order of magnitude reduction. Even though primary electroviscous effect is always present, its contribution to solution viscosity in highly concentrated protein formulations is probably negligible. However, at concentration much less than ϕ = 0.25, proteins are not in contact and PEE appears to be very important. Reduction of PEE by addition of salts has been predicted by Watterson as described before. Nonetheless, at ϕ ≪ 0.25 viscosity of protein formulations is not a significant concern for delivery. So, as an alternative model this approach has the advantage used available colloidal theory to understand the viscosity behavior of protein solutions. Especially, for concentrated protein formulations where SEE can be dominating, reducing the electrostatic repulsion by increasing ionic strength is able to compress EDL and increase free space for particle motion (decreasing the excluded volume) (Esfandiary et al., 2015). Other factors to be discussed include the effect of ion binding, ion species, ion size, as well as the hydrophobic forces resulted from the ligands of organic salts.
3.3. Inorganic salts
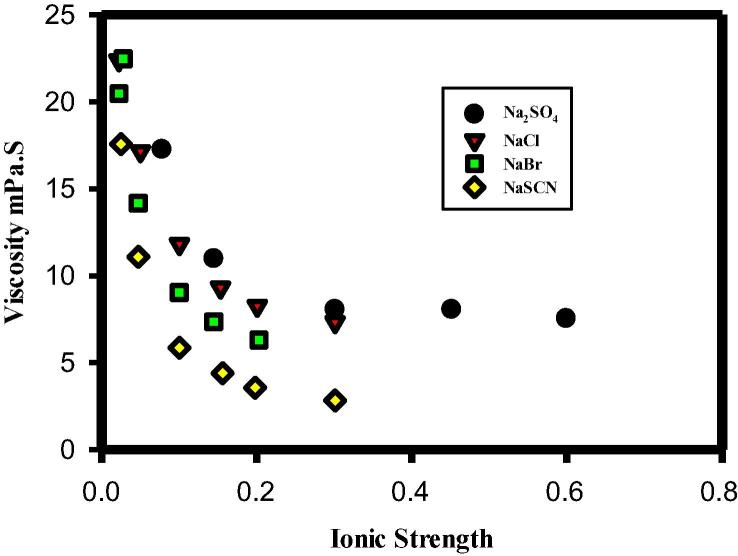
Bringing down the solution viscosity of protein formulations through addition of salts is a common practice in the biotech/pharmaceutical industry. For globular proteins, (DLVO) is frequently used to interpret their solution behaviors including viscosity when electroviscous effect is significant (Bauer et al., 2017, Yadav et al., 2011). Experimentally, impact of EE on suspension viscosity has been investigated for many colloidal systems (Castellanos et al., 2016, Heinen et al., 2012, Manley and Mason, 1954, Rubio Hernández et al., 2002). Chan et al. used sulfonated polystyrene latex particles to study the influence of PEE on viscosity by varying ionic strength, and their results (PEE) were shown to be comparable (with experimental error) to the theoretical predictions from the equations of Smoluchowski and Booth (Chan and Goring, 1966). As for concentrated protein formulations, electroviscous effect (it is really referred to PEE in many papers) is considered not important, completely neglecting SEE (Zhang and Liu, 2017). Experimentally significant reduction in viscosity is commonly observed when salt concentration is raised as shown in Fig. 5, Fig. 6 where viscosity reduction with salts is shown. Particularly, viscosity reduction displayed in Fig. 5 is not significant because protein formulations are not highly concentrated. As suggested by many authors, the hypothesis for this is that the high viscosity observed for protein solutions is caused by clusters formed due to PPIs, and the networked clusters are disrupted in the presence of ions. Although this explanation seems plausible, it cannot explain the fact that viscosity reduction is ion species specific as shown in both figures which will be expounded later. Here, we attempt to employ DLVO theory (electroviscous effect) to interpret these results. For dilute protein solutions, the viscosity reduction by raising salt concentration is generally not significant which we will not focus on in this paper. However, large reduction in viscosity was observed for highly concentrated protein formulations when salts were present as shown in Fig. 6 (Zhang and Liu, 2017). In this case viscosity reduction is hypothetically attributed shortening the particle-particle separation due to EDL compression, which decreases the excluded volume and enhances solution fluidity. As shown in the theoretical section, SEE was analyzed by Chan et al., in which k2 (kH-the Huggins’s viscosity constant) is proportional to the fifth power of separation distance (k2 = (1 + δ/a)5. Thus, reduction in separation distance (δ) can greatly lower the viscosity of protein formulations. This explains why addition of salts to protein formulations frequently results in viscosity reduction. Furthermore, as noted in Fig. 6, presence of Na2SO4 in mAb solutions has actually raised the solution viscosity, which cannot be explained based on formation of clusters and networks in which addition of salts presumably breaks protein-protein clusters or networks. In contrast, according to DLVO model Na2SO4 in protein solutions may reduce the electrostatic repulsion between proteins to such extent that the stabilization force (potential barrier) is eliminated and Van der Waals forces become dominant. A similar case was observed for suspensions of cellulose Nano crystallites with Na2SO4 (Beck and Bouchard, 2016). As reported by the authors, the viscosity of the cellulose suspensions was noted to rapidly rise when the amount of Na2SO4 was increased beyond a critical concentration. This is because electrostatic repulsion was swamped due to EDL compression. At high Na2SO4 concentrations, formation of gel was observed. Overall, modulating solution viscosity through varying ionic strength can be interpreted as a reduction of electrostatic repulsion due to EDL compression, and thereby excluded volume is lowered and more space is freed for flow. Other factors impacting EDL structures including modification of hydration layers by ions will be discussed below.
Fig. 5.

Viscosity of antibody solutions verses salt concentration of different salts (Liu and Shire, 2005) showing the impact of ion types along with their valency and amino acid.
Fig. 6.
Decrease of solution viscosity of antibody formulations as a function of ionic strength in the presence of various salts (Zhang and Liu, 2017) showing the effect of ion species and ion valency.
Ion species and ion size, known for influencing hydration of proteins and other colloids, can also affect the viscosity of protein solutions (Ben-Yaakov et al., 2011, Salis and Ninham, 2014). In Fig. 6, the impact of ion species on protein viscosity is shown where NaSCN is noted as the most effective salt in reducing viscosity, followed by NaBr and NaCl. To explain the order of viscosity reduction by different ions shown in Fig. 6, self-association model based on electrostatic attraction appears to be inadequate because neither ion size nor ion species are accounted in the model. Nor is the argument according to PEE in which only zeta potential and ionic strength were taken into consideration. However, as reported by Dong and Gray (1997), ion size in cellulose suspensions can affect the repulsive interactions between charged cellulose crystallites, which impacted the critical concentration for phase separation (Table 1). In other words, a high observed concentration for phase separation is an indication of excluded volume reduction-a thin EDL. In Table 1 the suspension of Cs+ displays the highest critical concentration for phase separation, suggesting that in the presence of Cs+ cellulose crystallites have the smallest excluded volume-the thinnest EDL. To expound this, we need to explore the relationship between hydration and effective charge as well as hydrodynamic volume due to hydration (Davies, 1962). For inorganic cations such as Na+, K +, and Cs+, their hydration number and hydrated ion size decrease with increasing effective charge in the order Na+ > K+ > Cs+. When these hydrated cations bind to the surfaces of negatively charged particle, the repulsive hydration force between particles generated follows the order Na+ > K+ > Cs+. Thus, the suspensions of cellulose crystallites with NaCl have the highest excluded volume, consequently displaying the lowest critical concentration for phase separation. The same argument can be applied to mAb solutions of various anions as exhibited in Fig. 6. The weak repulsive force from low hydration number of NaSCN and NaBr may produce a short separation distance (a small δ), resulting in less excluded volume and less viscosity. This is consistent with Chan’s model, in which k2 and kH decrease significantly with δ. Furthermore, impact of surface water on the structure of EDL-consequently on the suspension viscosity-was also reported for colloidal suspensions of poly (methyl methacrylate-co-methacrylic acid) (PMMMA) (Chen et al., 2013). Authors concluded that for PMMMA suspensions the most contributing factor to viscosity seems to be surface water (tertiary electroviscous effect). Besides hydration, hydrophobic interaction can also impact PPIs and thus the solution viscosity of proteins as discussed below.
Table 1.
Effect of cationic counter ions on the critical concentration for phase separation.
| Inorganic counter ions |
Organic counter ions |
||
|---|---|---|---|
| Suspension | Critical concentration for phase separation (%) | Suspension | Critical concentration for phase separation (%) |
| S-H | 4.9 | S-H | 4.9 |
| S-Na | 5.3 | S-NH4 | 5.2 |
| S-K | 5.4 | S-Tri-MA | 5.5 |
| S-Cs | 5.9 | S-Tri-EA | 6.0 |
S stands for sulfate which came from hydrolysis of cellulose using sulfuric acid. In her 1996 paper, the effect of NaCl and KCl salts on phase separation of cellulose crystallites was used.
3.4. Organic salts and amino acids
Organic salts including ((NH4+)2SO4, sodium p-toluenesulfonate, sodium benzoate, sodium p-hydroxybenzoate, trimethylphenylammonium chloride, and trimethylphenylammonium bromide have been tested for their effectiveness in reducing the solution viscosity of mAb formulations (Du and Klibanov, 2011, Larson et al., 2017, Wang et al., 2015). As reported by Kilibanov et al., hydrophobic salts, whether cationic or anionic salts, can significantly reduce the viscosity of mAb formulations. They suggest that mechanistically viscosity reduction by organic salts is due to breaking-up of the transient networks of proteins through the hydrophobic interaction of hydrophobic counterions with proteins. Generally, organic salts with hydrophobic ligands are more effective in reducing viscosity. While organic salts have been shown to be more effective than inorganic salts in reducing viscosity, no rheological measurements such as viscoelastic properties are reported to demonstrate the formation of networked structures. Additionally, no aggregation was observed. So, in this case it is also possible that the reduction in viscosity is due to a decrease of the excluded volume for hydrophobic ligands can greatly reduce the repulsion between proteins, which rendering mAb molecules flowing well as hydrophobic ion are known to impact EDL structures. A similar observation was made by Dong and Gray for cellulose crystallites in terms of the critical concentrations for phase separation, where increase of the critical concentration for phase separation with increasing the size of organic cation was noted (see Table 1). This observation can be elucidated by the hydrophobic interaction of organic salts with crystallites. It has been shown that hydrophobic interaction of ligands with particle surfaces can change the EDL structure including hydration (Scheu et al., 2013). Because hydrophobic interaction can alter the EDL structure and weaken the repulsive force between crystallites, the excluded volume is reduced. So, reduction of the excluded volume results in increasing the critical concentration for phase separation. The same argument can be applied to protein solutions. In the presence of organic hydrophobic ions, because of alteration of the EDL structures of proteins, the electrostatic repulsive force is reduced, so the excluded volume is thus greatly lowered which ultimately enhances the fluidity of protein solutions. Similarly, according to Chan’s argument the reduction of separation distance (δ), due to weakening of electrostatic repulsion, can greatly lower solution viscosity.
Amino acid salts such as arginine HCl are frequently added to protein formulations to lower viscosity. Although their effectiveness in reducing viscosity is protein dependent, studies showed that arginine HCl and lysine HCl, two commonly used amino acid additives, appear to behave like inorganic salts such as NaCl (Chi et al., 2003, Wang et al., 2015) Fig. 5. It has been suggested that adding arginine HCl in protein solutions may reduce electrostatic repulsions, consequently shortening the separation distance (δ) of proteins and decreasing the excluded volume) so that the free space for particle flow is increased. Thus, presence of amino acid such as arginine HCl essentially reduces the electroviscous effect, especially SEE. Compared with organic salts, amino acid salts are generally less effective in lowering viscosity. This is because amino acid salts are hydrophilic with limited effect on EDL, similar to NaCl, while hydrophobic ligands of organic salts can significantly alter EDL structure. Additionally, the common amino acid salts such as arginine HCl and lysine HCl do not appear to exhibit ion binding effect.
3.5. Ion binding effect
Ion binding is an omnipresent phenomenon for proteins in solution. Ion binding at protein surfaces can significantly affect the physical and chemical properties as well as the physical state of therapeutic proteins (Du and Klibanov, 2011, Kunz and Neueder, 2010). Ion binding to proteins can either increase their stability by enhancing hydrogen bonding (kosmotropic ions) or decrease protein stability by promoting denaturation (chaotropic ions) as indicated by Hoffmeister effect (Esfandiary et al., 2015b). However, specific ion effects are not typically included in the conventional electrostatic theory (DLVO theory) (Liu et al., 2014), rendering the classical DLVO theory less applicable to proteins. Concerning the impact of ion binding on solution viscosity, kosmotropic ions may have less effect relative to chaotropic ions since the latter can destabilize the structures of proteins and cause formation of aggregates or flocs (tertiary electroviscous effect). With regard to the effect of ion binding on the effective surface charge, Gokarn et al. have demonstrated that the reduction of the effective charge of proteins is in the order of I− > Br− > Cl− > F− (Kunz and Neueder, 2010). Similarly, adsorption of organic ligands can decrease the zeta potential in which hydrophobic (long alkyl chain) ligands appeared to be more effective in reducing zeta potential (Gokarn et al., 2011). Since ion binding/adsorption of organic ligands can affect the effective surface charge/potential, it is likely that ion biding essentially changes the electrostatic repulsion, which lowers the solution viscosity of proteins. Additionally, at extreme cases ion binding can also significantly change the protein structures besides impacting EDL as guanidine HCl and other denaturants can denature proteins (Kanai et al., 2008). However, at low concentrations they can reduce the viscosity of protein solutions (Kanai et al., 2008). Practically, mechanistic understanding of ion binding is very important for optimizing protein formulations in terms of selecting a buffer system which has a favorable effect in increasing formulation stability and reducing viscosity.
4. Conclusions
In developing formulations of highly concentrated proteins, electroviscous effect which is protein dependent is an important factor to consider in reducing formulation viscosity. Protein can be significantly different even they have similar primary structures. As the theory predicted, viscosity reduction is mainly achieved by decreasing SEE effect. Tertiary electroviscous effect, which is due to the alteration of protein conformations or gelation, should be absolutely avoided. Although addition of salts generally lowers the viscosity of protein solutions, selection of salt species can be intriguing where specific ion effect needs to be taken into consideration. While organic salts are generally effective in reducing the solution viscosity of protein formulations, lack of mechanistic understanding still prevents us from using them effectively. For the development of formulations of highly concentrated proteins, it is desirable to investigate the impact of ions on the electrical properties of proteins since physical stability is closely relates to the electrical properties of proteins. Since SEE is significant in highly concentrated formulations (ϕ ∼ 0.25), compressing EDL through addition of salts (organic or inorganic) is most likely effective. However, one should be cautious about the amount of salts added for over-addition of salts can destabilize the repulsive potential and cause formation of aggregates or denaturation of proteins. At ϕ ≪ 0.25, SEE is not significant while PEE is predominant. Typically, in dilute solutions of proteins, viscosity is less of a concern. Overall, this paper provides another framework to examine the viscosity issue in developing highly concentrated protein formulations.
Conflict of Interest
There is no conflict of interest involved in this manuscript.
Acknowledgement
Authors thank Dr. Scott Hart for reviewing the entire manuscript and the support of DPST management for completing this work.
References
- Bauer K.C., Suhm S., Wöll A.K., Hubbuch J. Impact of additives on the formation of protein aggregates and viscosity in concentrated protein solutions. Int. J. Pharm. 2017;516:82–90. doi: 10.1016/j.ijpharm.2016.11.009. [DOI] [PubMed] [Google Scholar]
- Beck S., Bouchard J. Ionic strength control of sulfated cellulose nanocrystal suspension viscosity. TAPPI J. 2016;15(6):363–372. [Google Scholar]
- Ben-Yaakov D., Andelman D., Podgornik R., Harries D. Ion-specific hydration effects: extending the Poisson-Boltzmann theory. Curr. Opin. Colloid Interface Sci. 2011;16:542–550. [Google Scholar]
- Blachford J., Chan F.S., Goring D.A.I. Secondary electroviscous effect. Paths of approach of two charged spheres in a viscous medium. J. Phys. Chem. 1969;73:1062–1065. [Google Scholar]
- Booth F. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society; 1950. The electroviscous effect for suspensions of solid spherical particles; pp. 533–551. [Google Scholar]
- Burckbuchler V., Mekhloufi G., Giteau A.P., Grossiord J.L., Huille S., Agnely F. Rheological and syringeability properties of highly concentrated human polyclonal immunoglobulin solutions. Eur. J. Pharm. Biopharm. 2010;76:351–356. doi: 10.1016/j.ejpb.2010.08.002. [DOI] [PubMed] [Google Scholar]
- Castellanos M.M., Clark N.J., Watson M.C., Krueger S., McAuley A., Curtis J.E. Role of molecular flexibility and colloidal descriptions of proteins in crowded environments from small-angle scattering. J. Phys. Chem. B. 2016;120:12511–12518. doi: 10.1021/acs.jpcb.6b10637. [DOI] [PubMed] [Google Scholar]
- Chan F.S., Goring D.A.I. The primary electroviscous effect in a sulfonated polystyrene latex. J. Colloid Interface Sci. 1966;22:371–377. [Google Scholar]
- Chan F.S., Blachford J., Goring D.A.I. The secondary electroviscous effect in a charged spherical colloid. J. Colloid Interface Sci. 1966;22:378–385. [Google Scholar]
- Chen M., Riddles C.J., Van De Mark M.R. Electroviscous contribution to the rheology of colloidal unimolecular polymer (CUP) particles in water. Langmuir. 2013;29:14034–14043. doi: 10.1021/la4026552. [DOI] [PubMed] [Google Scholar]
- Chi E.Y., Krishnan S., Kendrick B.S., Chang B.S., Carpenter J.F., Randolph T.W. Roles of conformational stability and colloidal stability in the aggregation of recombinant human granulocyte colony-stimulating factor. Protein Sci. 2003;12:903–913. doi: 10.1110/ps.0235703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connolly B.D., Petry C., Yadav S., Demeule B., Ciaccio N., Moore J.M.R., Shire S.J., Gokarn Y.R. Weak interactions govern the viscosity of concentrated antibody solutions: high-throughput analysis using the diffusion interaction parameter. Biophys. J. 2012;103:69–78. doi: 10.1016/j.bpj.2012.04.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies C.W. Butterworths; London: 1962. Ion Association. [Google Scholar]
- Dong X.M., Gray D.G. Effect of counterions on ordered phase formation in suspensions of charged rodlike cellulose crystallites. Langmuir. 1997;13:2404–2409. [Google Scholar]
- Du W., Klibanov A.M. Hydrophobic salts markedly diminish viscosity of concentrated protein solutions. Biotechnol. Bioeng. 2011;108:632–636. doi: 10.1002/bit.22983. [DOI] [PubMed] [Google Scholar]
- Einstein A. Berichtigung zu meiner Arbeit:, Eine neue Bestimmung der Moleküldimensionen”. Ann. Phys. 1911;339:591–592. [Google Scholar]
- Esfandiary R., Parupudi A., Casas-Finet J., Gadre D., Sathish H. Mechanism of reversible self-association of a monoclonal antibody: role of electrostatic and hydrophobic interactions. J. Pharm. Sci. 2015;104:577–586. doi: 10.1002/jps.24237. [DOI] [PubMed] [Google Scholar]
- Gokarn Y.R., Fesinmeyer R.M., Saluja A., Razinkov V., Chase S.F., Laue T.M., Brems D.N. Effective charge measurements reveal selective and preferential accumulation of anions, but not cations, at the protein surface in dilute salt solutions. Protein Sci. 2011;20:580–587. doi: 10.1002/pro.591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonçalves A.D., Alexander C., Roberts C.J., Spain S.G., Uddin S., Allen S. The effect of protein concentration on the viscosity of a recombinant albumin solution formulation. RSC Adv. 2016;6:15143–15154. [Google Scholar]
- Harn N., Allan C., Oliver C., Middaugh C.R. Highly concentrated monoclonal antibody solutions: direct analysis of physical structure and thermal stability. J. Pharm. Sci. 2007;96:532–546. doi: 10.1002/jps.20753. [DOI] [PubMed] [Google Scholar]
- He F., Woods C.E., Becker G.W., Narhi L.O., Razinkov V.I. High-throughput assessment of thermal and colloidal stability parameters for monoclonal antibody formulations. J. Pharm. Sci. 2011;100:5126–5141. doi: 10.1002/jps.22712. [DOI] [PubMed] [Google Scholar]
- Heinen M., Zanini F., Roosen-Runge F., Fedunová D., Zhang F., Hennig M., Seydel T., Schweins R., Sztucki M., Antalík M. Viscosity and diffusion: crowding and salt effects in protein solutions. Soft Matter. 2012;8:1404–1419. [Google Scholar]
- Hunter R.J. Academic press; 2013. Zeta Potential in Colloid Science: Principles and Applications. [Google Scholar]
- Inoue N., Takai E., Arakawa T., Shiraki K. Arginine and lysine reduce the high viscosity of serum albumin solutions for pharmaceutical injection. J. Biosci. Bioeng. 2014;117:539–543. doi: 10.1016/j.jbiosc.2013.10.016. [DOI] [PubMed] [Google Scholar]
- Jezek J., Rides M., Derham B., Moore J., Cerasoli E., Simler R., Perez-Ramirez B. Viscosity of concentrated therapeutic protein compositions. Adv. Drug Delivery Rev. 2011;63:1107–1117. doi: 10.1016/j.addr.2011.09.008. [DOI] [PubMed] [Google Scholar]
- Joshi V., Shivach T., Kumar V., Yadav N., Rathore A. Avoiding antibody aggregation during processing: establishing hold times. Biotechnol. J. 2014;9:1195–1205. doi: 10.1002/biot.201400052. [DOI] [PubMed] [Google Scholar]
- Kanai S., Liu J.U.N., Patapoff T.W., Shire S.J. Reversible self-association of a concentrated monoclonal antibody solution mediated by Fab-Fab interaction that impacts solution viscosity. J. Pharm. Sci. 2008;97:4219–4227. doi: 10.1002/jps.21322. [DOI] [PubMed] [Google Scholar]
- Krieger I.M., Dougherty T.J. A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 1959;3:137–152. [Google Scholar]
- Kunz W., Neueder R. An attempt of a general overview. Specific Ion Effects. 2010:3–54. [Google Scholar]
- Larson A.M., Weight A.K., Love K., Bonificio A., Wescott C.R., Klibanov A.M. Bulky polar additives that greatly reduce the viscosity of concentrated solutions of therapeutic monoclonal antibodies. J. Pharm. Sci. 2017;106:1211–1217. doi: 10.1016/j.xphs.2017.01.018. [DOI] [PubMed] [Google Scholar]
- Leckband D., Sivasankar S. Forces controlling protein interactions: theory and experiment. Colloids Surf., B. 1999;14:83–97. [Google Scholar]
- Lehermayr C., Mahler H.-C., Mäder K., Fischer S. Assessment of net charge and protein–protein interactions of different monoclonal antibodies. J. Pharm. Sci. 2011;100:2551–2562. doi: 10.1002/jps.22506. [DOI] [PubMed] [Google Scholar]
- Liu X., Li H., Li R., Xie D., Ni J., Wu L. Strong non-classical induction forces in ion-surface interactions: general origin of Hofmeister effects. Sci. Rep. 2014;4:5047. doi: 10.1038/srep05047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J., Shire S.J. Google Patents; 2005. Reduced-viscosity Concentrated Protein Formulations. [Google Scholar]
- Manley R.S.J., Mason S.G. The viscosity of suspensions of spheres: a note on the particle interaction coefficient. Can. J. Chem. 1954;32:763–767. [Google Scholar]
- Mezger T.G. Vincentz Network; 2011. The Rheology Handbook: For Users of Rotational and Oscillatory Rheometers. [Google Scholar]
- Mitragotri S., Burke P.A., Langer R. Overcoming the challenges in administering biopharmaceuticals: formulation and delivery strategies. Nat. Rev. Drug Discovery. 2014;13:655–672. doi: 10.1038/nrd4363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monnery W.D., Mehrotra A.K., Svrcek W.Y. Modified shape factors for improved viscosity predictions using corresponding states. Can. J. Chem. Eng. 1991;69:1213–1219. [Google Scholar]
- Mosteller, F., 1964. An Introduction to Physical Biochemistry.
- Neergaard M.S., Kalonia D.S., Parshad H., Nielsen A.D., Møller E.H., van de Weert M. Viscosity of high concentration protein formulations of monoclonal antibodies of the IgG1 and IgG4 subclass–prediction of viscosity through protein–protein interaction measurements. Eur. J. Pharm. Sci. 2013;49:400–410. doi: 10.1016/j.ejps.2013.04.019. [DOI] [PubMed] [Google Scholar]
- Pace C.N., Grimsley G.R., Scholtz J.M. Protein ionizable groups: pK values and their contribution to protein stability and solubility. J. Biol. Chem. 2009;284:13285–13289. doi: 10.1074/jbc.R800080200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pamies R., Hernández Cifre J.G., del Carmen López Martínez M., García de la Torre J. Determination of intrinsic viscosities of macromolecules and nanoparticles. Comparison of single-point and dilution procedures. Colloid Polym. Sci. 2008;286:1223–1231. [Google Scholar]
- Pindrus M.A., Shire S.J., Yadav S., Kalonia D.S. Challenges in determining intrinsic viscosity under low ionic strength solution conditions. Pharm. Res. 2017;34:836–846. doi: 10.1007/s11095-017-2112-8. [DOI] [PubMed] [Google Scholar]
- Roberts D., Keeling R., Tracka M., Van Der Walle C.F., Uddin S., Warwicker J., Curtis R. The role of electrostatics in protein–protein interactions of a monoclonal antibody. Mol. Pharm. 2014;11:2475–2489. doi: 10.1021/mp5002334. [DOI] [PubMed] [Google Scholar]
- Rubio Hernández F.J., Gómez-Merino A.I., Ruiz-Reina E., Garcıa-Sánchez P. An experimental test of Booth's primary electroviscous effect theory. J. Colloid Interface Sci. 2002;255:208–213. doi: 10.1006/jcis.2002.8656. [DOI] [PubMed] [Google Scholar]
- Russel W.B. Bulk stresses due to deformation of the electrical double layer around a charged sphere. J. Fluid Mech. 1978;85:673–683. [Google Scholar]
- Russel W.B. Review of the role of colloidal forces in the rheology of suspensions. J. Rheol. 1980;24:287–317. [Google Scholar]
- Saito S., Hasegawa J., Kobayashi N., Kishi N., Uchiyama S., Fukui K. Behavior of monoclonal antibodies: relation between the second virial coefficient (B 2) at low concentrations and aggregation propensity and viscosity at high concentrations. Pharm. Res. 2012;29:397–410. doi: 10.1007/s11095-011-0563-x. [DOI] [PubMed] [Google Scholar]
- Salinas B.A., Sathish H.A., Bishop S.M., Harn N., Carpenter J.F., Randolph T.W. Understanding and modulating opalescence and viscosity in a monoclonal antibody formulation. J. Pharm. Sci. 2010;99:82–93. doi: 10.1002/jps.21797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salis A., Ninham B.W. Models and mechanisms of Hofmeister effects in electrolyte solutions, and colloid and protein systems revisited. Chem. Soc. Rev. 2014;43:7358–7377. doi: 10.1039/c4cs00144c. [DOI] [PubMed] [Google Scholar]
- Saluja A., Kalonia D.S. Nature and consequences of protein–protein interactions in high protein concentration solutions. Int. J. Pharm. 2008;358:1–15. doi: 10.1016/j.ijpharm.2008.03.041. [DOI] [PubMed] [Google Scholar]
- Sandler S.R., Karo W., Bonesteel J.A., Pearce E.M. Elsevier Science; 1998. Polymer Synthesis and Characterization: A Laboratory Manual. [Google Scholar]
- Scheu R.d., Chen Y., Subinya M., Roke S. Stern layer formation induced by hydrophobic interactions: a molecular level study. J. Am. Chem. Soc. 2013;135:19330–19335. doi: 10.1021/ja4102858. [DOI] [PubMed] [Google Scholar]
- Shire S.J. Formulation and manufacturability of biologics. Curr. Opin. Biotechnol. 2009;20:708–714. doi: 10.1016/j.copbio.2009.10.006. [DOI] [PubMed] [Google Scholar]
- Shire S. Elsevier Science; 2015. Monoclonal Antibodies: Meeting the Challenges in Manufacturing, Formulation, Delivery and Stability of Final Drug Product. [Google Scholar]
- Simha R. The influence of Brownian Movement on the viscosity of solutions. J. Phys. Chem. 1940;44:25–34. [Google Scholar]
- Smoluchowski M.v. Theoretische bemerkungen über die viskosität der kolloide. Kolloid-Zeitschrift. 1916;18:190–195. [Google Scholar]
- Sudrik C., Cloutier T., Pham P., Samra H.S., Trout B.L. Preferential interactions of trehalose, L-arginine.HCl and sodium chloride with therapeutically relevant IgG1 monoclonal antibodies. MAbs. 2017;9:1155–1168. doi: 10.1080/19420862.2017.1358328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomar D.S., Kumar S., Singh S.K., Goswami S., Li L. Molecular basis of high viscosity in concentrated antibody solutions: strategies for high concentration drug product development. MAbs. 2016;8:216–228. doi: 10.1080/19420862.2015.1128606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Ven T.G.M. Electroviscous phenomena in colloidal dispersions. Chem. Eng. Sci. 2001;56:2947–2955. [Google Scholar]
- Wang W. Advanced protein formulations. Protein Sci. 2015;24:1031–1039. doi: 10.1002/pro.2684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W., Singh M. Wiley; 2013. Biological Drug Products: Development and Strategies. [Google Scholar]
- Wang S., Zhang N., Hu T., Dai W., Feng X., Zhang X., Qian F. Viscosity-lowering effect of amino acids and salts on highly concentrated solutions of Two IgG1 monoclonal antibodies. Mol. Pharm. 2015;12:4478–4487. doi: 10.1021/acs.molpharmaceut.5b00643. [DOI] [PubMed] [Google Scholar]
- Watterson I.G., White L.R. Primary electroviscous effect in suspensions of charged spherical particles. J. Chem. Soc., Faraday Trans. 2: Mol. Chem. Phys. 1981;77:1115–1128. [Google Scholar]
- Yadav S., Sreedhara A., Kanai S., Liu J., Lien S., Lowman H., Kalonia D.S., Shire S.J. Establishing a link between amino acid sequences and self-associating and viscoelastic behavior of two closely related monoclonal antibodies. Pharm. Res. 2011;28:1750–1764. doi: 10.1007/s11095-011-0410-0. [DOI] [PubMed] [Google Scholar]
- Zhang Z., Liu Y. Recent progresses of understanding the viscosity of concentrated protein solutions. Curr. Opin. Chem. Eng. 2017;16:48–55. [Google Scholar]