Probabilistic estimation of residential air exchange rates for population-based human exposure modeling

Abstract

Residential air exchange rates (AERs) are a key determinant in the infiltration of ambient air pollution indoors. Population-based human exposure models using probabilistic approaches to estimate personal exposure to air pollutants have relied on input distributions from AER measurements. An algorithm for probabilistically estimating AER was developed based on the Lawrence Berkley National Laboratory Infiltration model utilizing housing characteristics and meteorological data with adjustment for window opening behavior. The algorithm was evaluated by comparing modeled and measured AERs in four US cities (Los Angeles, CA; Detroit, MI; Elizabeth, NJ; and Houston, TX) inputting study-specific data. The impact on the modeled AER of using publically available housing data representative of the region for each city was also assessed. Finally, modeled AER based on region-specific inputs was compared with those estimated using literature-based distributions. While modeled AERs were similar in magnitude to the measured AER they were consistently lower for all cities except Houston. AERs estimated using region-specific inputs were lower than those using study-specific inputs due to differences in window opening probabilities. The algorithm produced more spatially and temporally variable AERs compared with literature-based distributions reflecting within- and between-city differences, helping reduce error in estimates of air pollutant exposure.

INTRODUCTION

Previous exposure assessment panel studies have observed considerable seasonal, between-home and between-city variability in residential air pollutant infiltration,^{1, 2, 3} likely as a result of differences in residential air exchange rates (AERs). AERs have been shown to vary widely both between- and within-urban areas due to differences in housing characteristics, seasonal trends dependent on meteorological conditions, and occupant behaviors such as air conditioning (AC) use or opening of windows.^{1, 4, 5} Recent studies have found that residential AER significantly modified the associations between air pollution and adverse health effects.^{6, 7, 8, 9} Therefore, improving AER prediction methods through evaluation and refinement of existing tools will be highly valuable.¹⁰

Human exposure models that incorporate factors such as time-location-activity budgets and penetration of ambient pollutants to the indoor environment are increasingly being used to characterize exposures for air pollution health studies.^{6, 11} One example is the Stochastic Human Exposure and Dose Simulation (SHEDS) model, a population-based exposure model that uses a probabilistic approach to estimate personal exposures for simulated individuals based on ambient concentrations, literature-based distributions of residential AERs, and pollutant infiltration parameters, and time spent in various microenvironments (e.g. home, office, school, and vehicle) from a large database of human activity diaries.^{12, 13, 14} The predicted distribution of exposures provides a range in exposures for the general population or subpopulation of interest, and the likelihood of exposures above a particular level.¹³

Previous applications of SHEDS have used literature-based^{12, 13, 14} input distributions of residential AERs that vary by season and region of the country. However, Isaacs et al.¹⁵ identified key influential factors in their analysis of residential AER measurements (outdoor temperature, central AC prevalence, and home age), which are consistent with the theoretical understanding of AER that may provide more appropriate characterization of AER variability for exposure simulations.¹⁵ A modified version of the Lawrence Berkeley National Laboratory (LBNL) Infiltration model that estimates residential AERs based on these factors, including meteorology, census-tract level housing characteristics,^{16, 17} information on the prevalence of AC, and assumptions on AC use vs the opening of windows6 was recently developed and applied to predict AERs at more temporally (i.e. daily) and spatially (e.g. zip-code or census tract) resolved level.^{7, 18}

The first objective of this paper is to describe the adaptation of the aforementioned LBNL model into a new algorithm for SHEDS that stochastically estimates residential AER with improved characterization of spatial and temporal variability. The probabilistic approach required development of distributions for each input parameter of the LBNL model based on the available data. The second objective is to evaluate the distributions of AERs estimated using the new algorithm. Modeled AERs are evaluated against measured AERs from exposure panel studies conducted in four US cities (Elizabeth, NJ, Houston, TX, and Los Angeles, CA and Detroit, MI)^{19, 20} using study-specific information on prevalence of AC and probability of open windows as input. The algorithm is also applied using publicly available input data, generally only representative of a region of the United States, and differences in the estimated AERs assessed vs utilizing study-specific input data. Finally distributions of AERs generated with the new algorithm are compared with those generated using literature-based AER distributions as input to demonstrate the advantages of the approach.

MATERIALS AND METHODS

The SHEDS model estimates daily personal exposure for a representative set of simulated individuals from a defined population over a specified time period. The residential AER algorithm developed for SHEDS is based on a modified version of the LBNL Infiltration model¹⁸ and stochastically samples from distributions for the various input parameters of the AER equations assigned to each simulated individual based on the census tract for the residence. The following describes the equations, parameters, and the input distributions for application of the algorithm to different cities as well as the evaluation of the model output, and the methods used to compare model results.

SHEDS AER Algorithm

Residential AERs for each simulated individual are calculated as the total airflow (Q_tot) in m³/s divided by the volume of the house (V) (Equation (1).

$$\text{AER}= \frac{Q_{\text{tot}}}{V}$$ (1)

Breen et al.21 extended the LBNL infiltration model to include both airflow due to infiltration (Q_f) and natural ventilation (Q_nat) in the calculation of Q_tot²¹ (Equation (2).

$$Q_{\text{tot}}=\sqrt{Q_{\text{f}}^2+Q_{\text{fnat}}^2}$$ (2)

Q_f is considered as the airflow through small unintentional openings in the building envelope, due to housing characteristics, while Q_nat accounts for large controllable openings, such as open windows.

Q_f (m³/h) is calculated for each individual residence from the effective leakage area (ELA), the specific infiltration (s, defined below), and a factor converting s from m/s to m/h (Equation (3).

$$Q_{\text{f}}=\text{ELA }\times \text{s }\times 3600$$ (3)

The ELA (m²) of the building, represents all of the leakage pathways in the building, and is defined as:

$$\text{ELA }=\frac{\text{NL }\times A_{\text{f}}}{1000}{\left(\frac{2.5}{H}\right)}^{0.3}$$ (4)

where NL (unitless) is the normalized leakage, A_f is the floor area of the house (m²) and H is the total height of the house (m). For this application, we assumed a height of 5 m (2-story homes). The regressions developed by Chan et al.¹⁶ are used to predict NL based on the year a house was built, its floor area, and whether the house is occupied by individuals whose income is below the national poverty level. These equations are given below.

$${\text{NL}}_{\text{lowincome}}=\text{exp}(11.1-5.37\times {10}^{-3}\cdot \text{YearBuilt}-4.18\times {10}^{-3}\cdot {\text{A}}_f$$ (5)

$${\text{NL}}_{\text{lowincome}}=\text{exp}(20.7-1.07\times {10}^{-2}\cdot \text{YearBuilt}-2.20\times {10}^{-3}\cdot {\text{A}}_f$$ (6)

where NL_lowincome and NL_conventional are the normalized leakage for low income and conventional homes, respectively. A home is defined as low income or conventional based on the poverty status of the occupants. Year Built is the year the home was built.

The specific infiltration (s; m/s) is driven by the stack effect (or the indoor–outdoor temperature difference, f_s; m/s/degrees Kelvin^0.5), and is proportional to the square root of the temperature difference. The wind effect (or wind-induced infiltration airflow, f_w; unitless) arises from the dynamic wind pressure on the building, and is proportional to the wind speed. Equation (7) presents the equation for s.

$$s = \sqrt{{\text{f}}_{\text{s}}^2\times \Delta T +{\text{f}}_{\text{w}}^2\times {\text{ v}}^2}$$ (7)

ΔT is the inside outside temperature difference in degrees K; and v² is the square of the wind speed (m/s). The equations for the stack and wind effect are shown in Supplementary Equations (S1) and (S2), respectively in Supplementary Information.

It is also important to capture the effect of window opening on AER, particularly during the warmer months. Q_nat is a combination of ventilation airflow due to wind (Q_v,w; m³/s) and the ventilation airflow due to the stack effect (Q_v,s; m³/s) (Equation 8).

$$Q_{\text{nat}}=\sqrt{Q_{v,w}^2+Q_{v,s}^2}$$ (8)

Supplementary Equations (S3) and (S4) in Supplementary Information present the ventilation airflows due to wind and stack effects, respectively. These equations incorporate the effect of open windows. If the windows are closed, then Q_nat is equal to zero.

SHEDS uses a probabilistic approach to randomly sample from input distributions to characterize population variability. The key input parameters in the AER equations above requiring distributions include: (a) joint probabilities of year built, floor area, and household poverty status for calculation of ELA in determining Q_f and (b) for determining Q_nat, joint probability of AC in the home by year built and household poverty status, and probability of open windows by presence of AC in the home and outdoor temperature, which are used together to define area of intentional openings (A_v) for Supplementary Equations (S2) and (S3).

Application to Measurement Study Areas

Measured AERs from the Relationship of Indoor, Outdoor, and Personal Air (RIOPA) studies in Elizabeth, NJ, Houston, TX, and Los Angeles, CA,19and from the Detroit Exposure and Aerosol Research Study (DEARS) in Detroit, MI²⁰ were used to evaluate the SHEDS AER algorithm. AER measurements for homes in DEARS were 24 h samples, whereas RIOPA AER measurements were 48 h samples. SHEDS was applied separately to each of these cities using population demographic data from the US Census for census tracts that overlaid the RIOPA and DEARS study areas. For each city, a representative sample of 10,000 simulated individuals living in single-family homes was generated, with each simulated individual assigned a home census tract within the study area. Daily AER was estimated for all years sampled during DEARS and RIOPA for each city, which included 2004–2007 for Detroit, MI, and 1999–2001 for Elizabeth, NJ, Houston, TX, and Los Angeles, CA.

Joint probabilities of housing characteristics needed as input for calculation of ELA were developed by combining US Census data from both the American Community Survey (ACS)²² and the American Housing Survey (AHS).²³ ACS data for each Public Use Microdata Area (PUMA) within the DEARS and RIOPA study areas stratified by the number of rooms by year built and poverty status but lacked house size information, whereas the broader-scale AHS (metropolitan statistical area or region of the country) provided data for relating house size to number of rooms, year built, and poverty status. Details on how the probabilities were developed can be found in Supplementary Information. Within SHEDS, each simulated individual was assigned a PUMA based on overlap with the home census tract, and housing characteristics were randomly assigned based on the PUMA-specific joint probabilities from the ACS data. House size was then randomly assigned based on the joint probabilities from the AHS data for the housing characteristics of each simulated individual.

To incorporate the effect of open windows when calculating Q_nat, the probability that an individual opens their windows was based on the presence of AC in the home and the outdoor temperature. Two sets of probability distributions were developed, which included “study-specific” inputs derived from the self-reported conditions for presence of AC and open windows in the RIOPA19 or DEARS20 data sets for each city, and “regional” inputs derived from AHS data on AC in the home by year built and household poverty status, along with literature values for window opening behavior by AC status and outdoor temperature category.²⁴ The “study-specific” input distributions are provided in Supplementary Tables S3 and S4; “regional” input distributions are presented in Supplementary Table S5. Within SHEDS, each simulated individual was randomly assigned an AC status from the joint probability of AC in the home by year built and household poverty status, then open windows were assigned for each date simulated from the joint probabilities of open windows by AC status and outdoor temperature category (Supplementary Table S6).

Finally, the temperature and wind speed data inputs were taken from the nearest National Weather Service (NWS) Automated Surface Observing System (ASOS) site for each city.

SHEDS was first applied for each city using the “study-specific” inputs for evaluation of the modeled AER with measured AER data from each study. The SHEDS AER algorithm was also applied for the same simulated individuals for each city using the “regional” inputs to assess differences in the modeled AER due to type of input data available. A third SHEDS simulation was also performed for the same simulated individuals for Elizabeth, NJ using the original algorithm that randomly sampled AER from region and season-specific AER input distributions obtained from Murray and Burmaster.²⁵ This study developed empirical AER distributions for different regions of the United States by season based on data collected from 2844 households in different US states using a perflourocarbon tracer technique. The distributions were estimated for each season in four US regions defined by the number of annual heating degree days and Region 2 distributions were selected for Elizabeth, NJ (see Supplementary Table S9)

Data Analysis

For all comparisons, the SHEDS modeled AERs were averaged across the simulated individuals within each census tract for each day. Similarly, daily census tract-averaged AERs were calculated for census tracts that had multiple AER measurements from multiple homes.

Daily modeled census tract-averaged AERs were compared with the Detroit AER from DEARS, while the model output for the RIOPA study cities was averaged to match the 48 h RIOPA AER measurements. Although both studies included various housing types (e.g. single-family homes, apartments, and townhomes), the SHEDS AER algorithm is specific for single-family homes, so the modeled to measured comparisons are restricted to that category. Only the SHEDS modeled AERs that matched the measured AERs by census tract and day were used in this evaluation.

Since only a few homes were typically sampled within a census tract on the same day during the studies, the measured AERs may not be representative of the entire census tract. Therefore, distributions of the measured and modeled census tract-averaged daily AER were calculated as well as for the ratio of the measured to modeled AER. The mean, median, 75th percentile, and 95th percentile of the measured and modeled AERs were compared.

The temporal patterns of the AERs were also compared using the ratios of the measured AERs to the modeled AERs by season. Since seasonal temperatures varied widely among the cities the following temperature categories based on quartiles of the daily temperatures from the study observations were used: cold (<10.3 °C), cool (≥10.3 °C and <17 °C), warm (≥17 °C and <22.4 °C), and warmest (≥22.4 °C).

For examining differences between the modeled AERs calculated using “study-specific” (those collected as part of either the RIOPA of DEARS study) vs “regional” (generated using ACS and AHS data) inputs the overall distributions were compared as well as how well the modeled AERs utilizing the regional data sources captured the temporal and spatial patterns produced using the study-specific data. AERs were categorized based on the temperature classes used to determine the probabilities of AC use and the opening of windows. These include temperature (T)<17  °C, 17 °C≤T≤22.5 °C, 22.5 °C<T≤24 °C, and T>24 °C.

Finally, the Elizabeth, NJ study area was used to illustrate the spatial distributions produced by the SHEDS AER algorithm using “regional” input data, compared with the original algorithm that randomly sampled from residential AER distributions from Murray and Burmaster.²⁵ To characterize the spatial patterns, the SHEDS modeled AER from each algorithm was averaged over all days for each census tract and separately by season. Seasons were defined as in Murray and Burmaster as follows, winter: December, January, and February; spring: March, April, and May; summer: June, July, and August; and fall: September, October, and November.²⁵

RESULTS

A probabilistic approach for estimation of daily residential AER was implemented in the SHEDS population-based exposure model for air pollutants, and applied to four US cities to (a) evaluate the model results against AER measurement data, (b) compare modeled AER using different sources for inputs, and (c) contrast the predictive AER algorithm with the previous SHEDS approach using AER data distributions as input.

Comparison of Measured and Modeled AERs using Study-Specific Inputs

Table 1 presents the summary statistics for the measured and modeled AER overall and by temperature category. Overall, modeled AER was similar in magnitude to the measured AER. However, the model consistently underestimated the measured AERs in Detroit, Elizabeth and Los Angeles and overestimated the AERs in Houston. Median ratios were 1.4 for Detroit and Elizabeth, 0.78 for Houston, and 1.2 for Los Angeles. The range of ratios across census tract was much narrower in Houston than in the other cities (Supplementary Figure 1S). The coefficient of variability was 2–5 times lower for the modeled AERs compared with the measured AERs. As stated previously, the measured AERs may include extreme values not captured by our model decreasing the observed variability.

Table 1:

Summary statistics of daily census tract-averaged measured AERs and modeled AERs (1/h) using study-specific inputs overall and by temperature categories.^a

Temperature category	City	Measured AER				Modeled AER
		N	Mean (SD)	Median (CV)	Range	N	Mean (SD)	Median (CV)	Range
Overall	Detroit	608	1.58 (1.60)	1.47 (1.01)	0.08–17.0	608	0.83 (0.20)	0.81 (0.24)	0.27–1.57
	Elizabeth	43	1.37 (1.21)	0.94 (0.88)	0.11–4.48	43	0.87 (0.24)	0.89 (0.28)	0.48–1.28
	Houston	96	0.55 (0.42)	0.43 (0.76)	0.11–2.43	89	0.59 (0.21)	0.54 (0.36)	0.31–1.49
	LA	81	1.40 (1.01)	0.98 (0.72)	0.20–4.75	79	0.89 (0.36)	0.80 (0.40)	0.391–2.12
Cold	Detroit	251	1.12 (0.67)	0.94 (0.60)	0.22–3.66	251	0.82 (0.13)	0.81 (0.16)	0.50–1.18
	Elizabeth	18	1.60 (1.41)	0.87 (0.73)	0.33–4.47	18	1.03 (0.17)	1.04 (0.17)	0.80–1.28
	Houston	12	0.84 (0.41)	0.81 (0.49)	0.25–1.36	11	0.69 (0.18)	0.67 (0.26)	0.47–1.10
	LAb	1	0.57 (NA)	NA	NA	1	1.36 (NA)	NA	NA
Cool	Detroit	8	1.67 (1.03)	1.50 (0.61)	0.08–3.15	8	0.34 (0.05)	0.32 (0.15)	0.27–0.45
	Elizabeth	11	1.22 (1.08)	1.02 (0.89)	0.25–4.22	11	0.80 (0.16)	0.76 (0.20)	0.58–1.08
	Houston	15	0.57 (0.44)	0.47 (0.77)	0.13–1.71	14	0.60 (0.09)	0.59 (0.15)	0.48–0.79
	LA	20	1.02 (0.56)	0.80 (0.55)	0.23–2.29	19	0.88 (0.26)	0.83 (0.30)	0.51–1.26
Warm	Detroit	94	2.03 (2.45)	1.30 (1.21)	0.12–17.1	94	0.82 (0.25)	0.81 (0.30)	0.39–1.33
	Elizabeth	8	0.89 (0.35)	0.91 (0.39)	0.11–1.33	8	0.55 (0.09)	0.53 (0.16)	0.48–0.73
	Houston	16	0.46 (0.20)	0.49 (0.43)	0.18–0.86	15	0.79 (0.34)	0.66 (0.43)	0.36–1.49
	LA	40	1.42 (1.14)	0.88 (0.80)	0.20–4.75	40	0.95 (0.43)	0.87 (0.45)	0.39–2.12
Warmest	Detroit	255	1.87 (1.74)	1.47 (0.93)	0.13–9.6	255	0.85 (0.22)	0.80 (0.26)	0.45–1.56
	Elizabeth	6	1.58 (1.53)	1.08 (0.96)	0.25–4.48	6	0.94 (0.18)	0.98 (0.19)	0.62–1.13
	Houston	53	0.51 (0.44)	0.38 (0.86)	0.11–2.44	49	0.51 (0.12)	0.49 (0.24)	0.31–0.97
	LA	20	1.77 (1.00)	1.58 (0.56)	0.54–4.10	19	0.74 (0.20)	0.69 (0.27)	0.42–1.22

Abbreviations: AERs, air exchange rates; CV, coefficient of variations; LA, Los Angeles.

^aCold <10.3 °C; ≥10.3 °C cool <17 °C, ≥17 °C warm <22.4 °C; and warmest ≥22.4 °C.

^bOnly 1 value so unable to calculate statistic.

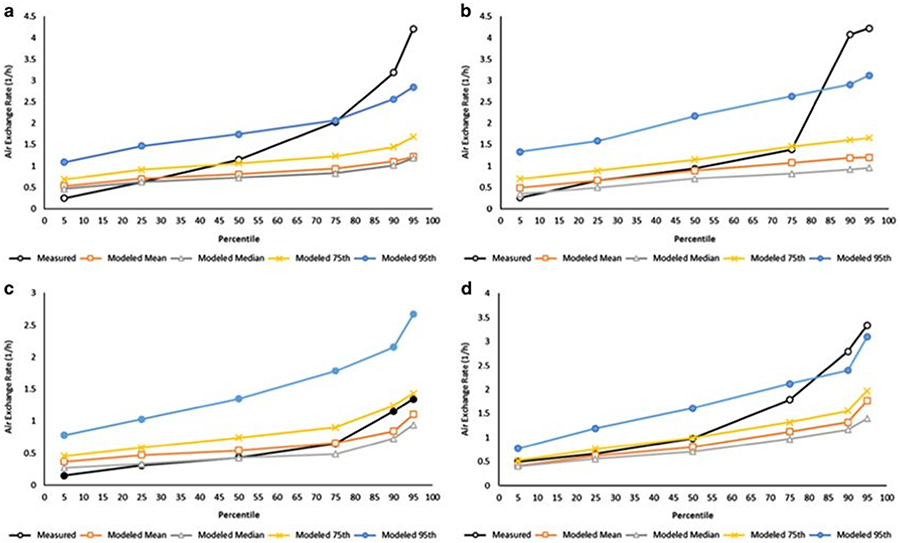
In addition, the measured AERs may not be representative of the entire census tract which the model algorithm is intended to characterize. Figure 1 compares the distributions of the measured AERs with the mean, median, 75th percentile, and 95th percentile of modeled AERs. Using a Wilcoxon rank-sum test, the distributions of the measured AER in Detroit, Elizabeth, and Los Angeles were not statistically different from the distributions of the modeled 75th percentile AERs. The measured AER distributions in Houston were not statistically different from the median modeled AER distributions.

Fig 1.

Comparison of the distributions of the measured AERs with the mean, median, 75th percentile, and 95th percentile of modeled AER values of each census tract for (a) Detroit, (b) Elizabeth, (c) Houston, and (d) Los Angeles.

Differences between the measured and modeled AERs by temperature category were also examined; however, this is limited by the small number of observations for some temperature categories (Table 1). Of note, although the number of AER measurements in Detroit is much larger than in other cities, the number of different homes measured is ~100 due to multiple days of sampling for each home. Comparison of ratios of the measured to modeled AERs by temperature category was limited to categories with >10 values and are presented in Supplementary Figure 2S. In Detroit and Los Angeles, the majority of ratios are above 1 for all temperate categories indicating that the model underestimated the measurement, but higher ratios tended to occur for warmer days. For Houston, the majority of ratios were below 1 for the cool, warm, and warmest temperature categories but higher ratios tended to occur with cold temperatures. Finally, the median ratio was below 1 in Elizabeth for the cold temperature category with the opposite true for the other categories.

Comparison of Modeled AERs using Study-Specific vs Regional Inputs

For evaluation of the modeled AER against measured AER above, “study-specific” probabilities of AC use and window opening were developed based on data from the homes in each study for the model inputs. Availability of this type of data is typically limited; therefore, model inputs were generated based on publically available data for the corresponding regions of the United States and model results compared to assess the impact of using “regional” inputs.

Summary statistics for the modeled AERs derived from “study-specific inputs” and “regional inputs” are presented in Table 2. On average, AERs simulated from study-specific inputs are higher than those modeled using regional-input data with median ratios (AERs from study-specific inputs/AERs from regional inputs) of 1.1, 1.3, 1.1, and 1.7 for Detroit, Elizabeth, Houston, and Los Angeles, respectively. Examining by temperature class related to AC use, the AERs were similar between the inputs in warmer weather (22.5 °C<T≤24 °C and T>24 °C) whereas the AERs generated with the study-specific inputs were greater in colder weather (T<17 °C and 17 °C≤T≤22.5 °C) than those generated with the regional data. The coefficient of variations (CV) are also similar between input category results as well as across cities and temperature classes.

Table 2:

Comparison of distributions of AERs (1/h) simulated using study-specific inputs vs regional inputs overall and by AC use temperature class.

AC use temperature (T) class	City	Study-specific inputs			Regional inputs
		N	Mean (SD)	Median (CV)	Range	N	Mean (SD)	Median (CV)	Range
Overall	Detroit	203,079	0.78 (0.24)	0.76 (0.31)	0.16–3.0	203,079	0.68 (0.21)	0.67 (0.31)	0.12–3.1
	Elizabeth	143,576	0.85 (0.26)	0.82 (0.31)	0.16–2.7	143,576	0.69 (0.21)	0.66 (0.30)	0.21–2.4
	Houston	287,152	0.68 (0.28)	0.61 (0.41)	0.15–3.1	287,152	0.62 (0.24)	0.58 (0.39)	0.07–3.0
	LA	127,136	0.89 (0.29)	0.85 (0.33)	0.15–2.7	127,136	0.55 (0.24)	0.48 (0.44)	0.09–2.2
T <17 °C	Detroit	129,965	0.75 (0.20)	0.74 (0.27)	0.16–2.3	129,965	0.69 (0.18)	0.69 (0.26)	0.16–1.4
	Elizabeth	90,128	0.92 (0.26)	0.90 (0.28)	0.24–3.0	90,128	0.62 (0.16)	0.61 (0.26)	0.21–1.6
	Houston	72,819	0.70 (0.24)	0.66 (0.34)	0.18–2.8	73,098	0.46 (0.14)	0.44 (0.30)	0.13–1.6
	LA	57,784	0.88 (0.26)	0.83 (0.30)	0.33–2.4	57,784	0.40 (0.09)	0.38 (0.23)	0.16–0.86
17 °C≤T≤22.5 °C	Detroit	40,449	0.80 (0.31)	0.76 (0.39)	0.21–3.0	40,449	0.59 (0.22)	0.55 (0.37)	0.17–3.1
	Elizabeth	24,366	0.64 (0.20)	0.61 (0.31)	0.16–2.2	24,366	0.69 (0.21)	0.67 (0.30)	0.24–2.4
	Houston	68,382	0.86 (0.34)	0.81 (0.40)	0.15–3.1	68,644	0.61 (0.25)	0.57 (0.41)	0.07–2.4
	LA	52,561	0.93 (0.32)	0.91 (0.34)	0.15–2.7	52,561	0.63 (0.21)	0.61 (0.33)	0.09–2.2
22.5 °C<T≤24 °C	Detroit	11,537	0.86 (0.26)	0.81 (0.30)	0.35–2.1	11,537	0.79 (0.23)	0.74 (0.29)	0.26–2.1
	Elizabeth	8908	0.86 (0.20)	0.83 (0.23)	0.33–1.7	8908	0.90 (0.22)	0.88 (0.24)	0.41–2.0
	Houston	22,446	0.91 (0.29)	0.86 (0.32)	0.26–2.9	22,532	0.92 (0.30)	0.87 (0.33)	0.17–3.0
	LA	8373	0.86 (0.29)	0.81 (0.34)	0.30–2.0	8373	0.88 (0.29)	0.84 (0.33)	0.23–2.1
T >24 °C	Detroit	21,128	0.88 (0.25)	0.84 (0.28)	0.32–2.1	21,128	0.75 (0.21)	0.72 (0.28)	0.28–2.3
	Elizabeth	20,174	0.78 (0.19)	0.76 (0.24)	0.30–1.6	20,174	0.88 (0.22)	0.85 (0.25)	0.37–2.0
	Houston	122,409	0.53 (0.14)	0.51 (0.26)	0.18–1.7	122,878	0.66 (0.19)	0.63 (0.29)	0.17–2.5
	LA	8418	0.74 (0.22)	0.71 (0.30)	0.29–1.6	8418	0.78 (0.25)	0.77 (0.32)	0.24–1.9

Abbreviations: AC, air conditioning; AERs, air exchange rates; CV, coefficient of variations; LA, Los Angeles.

Comparison of Modeled AER using Regional Inputs vs AER Distributions as Input

Before the incorporation of the AER algorithm in SHEDS, simulated individuals were randomly assigned AER for each season from a set of empirical distributions of AER for the appropriate region of the United States. Model results from the AER algorithm were compared with those from the prior approach to demonstrate the impact of accounting for differences in the physical factors influencing AER variability across census tracts (e.g. home age and size) and over time (e.g. temperature and wind speed) in the new algorithm.

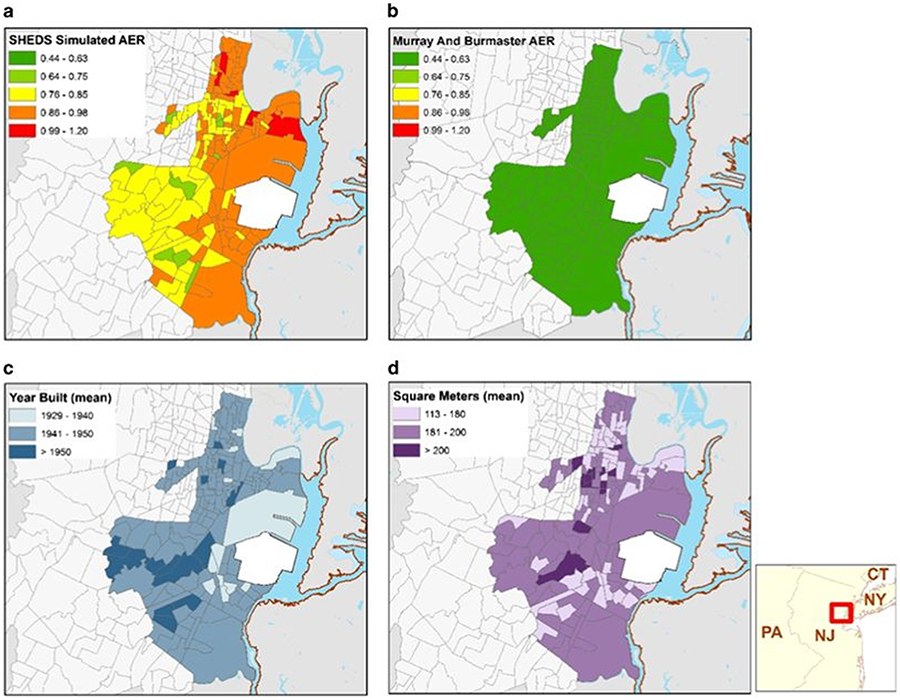
To illustrate the spatial differences, Figure 2 presents the census tract-averaged AERs for Elizabeth, NJ estimated from the new algorithm using regional inputs (Figure 2a) and those estimated using the prior AER (Murry–Burmaster(M–B)) input distributions (Figure 2b). AER estimated using the new algorithm exhibited considerably more spatial variability than those using the M–B AER input distributions. As shown in Figure 2c and d, the spatial variability in AER from the new algorithm is consistent with the pattern of differences in housing characteristics, such as home age (Figure 2c) and home size (Figure 2d) across census tracts. Higher AERs are expected in census tracts with an older housing stock and larger homes.

Fig 2.

Maps of (a) SHEDS simulated AERs (1/h), (b) Murray and Burmaster AERs (1/h), (c) Year Home built, and (d) Home Size (square meters) across census tracts in Elizabeth.

In addition, increased temporal variability was observed for AER estimated from the new algorithm as shown in the monthly means and CV (Table 3). AERs estimated using the algorithm are greater than those using the M–B AER input distributions except for the summer months (i.e. June, July, and August). The monthly CVs produced from the algorithm are 2–4 times higher than those produced from the prior approach illustrating the impact of accounting for daily changes in meteorology on AER with the new algorithm.

Table 3:

Comparison of monthly mean and coefficient of variation of AERs (1/h) estimated using Murry–Burmaster distributions vs new AER algorithm for Tract ID 340130000900 in Elizabeth, NJ.

Month	Murray–Burmaster		New algorithm
	Mean	CV	Mean	CV
1	0.56	11	0.73	20.6
2	0.56	11.1	0.69	18.8
3	0.43	13.8	0.68	21.5
4	0.43	14.3	0.57	21.8
5	0.43	13.7	0.59	39
6	0.84	12.5	0.8	30.6
7	0.84	12.2	0.83	28.5
8	0.84	12.5	0.83	25.2
9	0.36	8.55	0.68	37.3
10	0.36	8.57	0.55	29.9
11	0.36	8.52	0.58	24.6
12	0.56	10.9	0.69	21.9

Abbreviations: AERs, air exchange rates; CV, coefficient of variations.

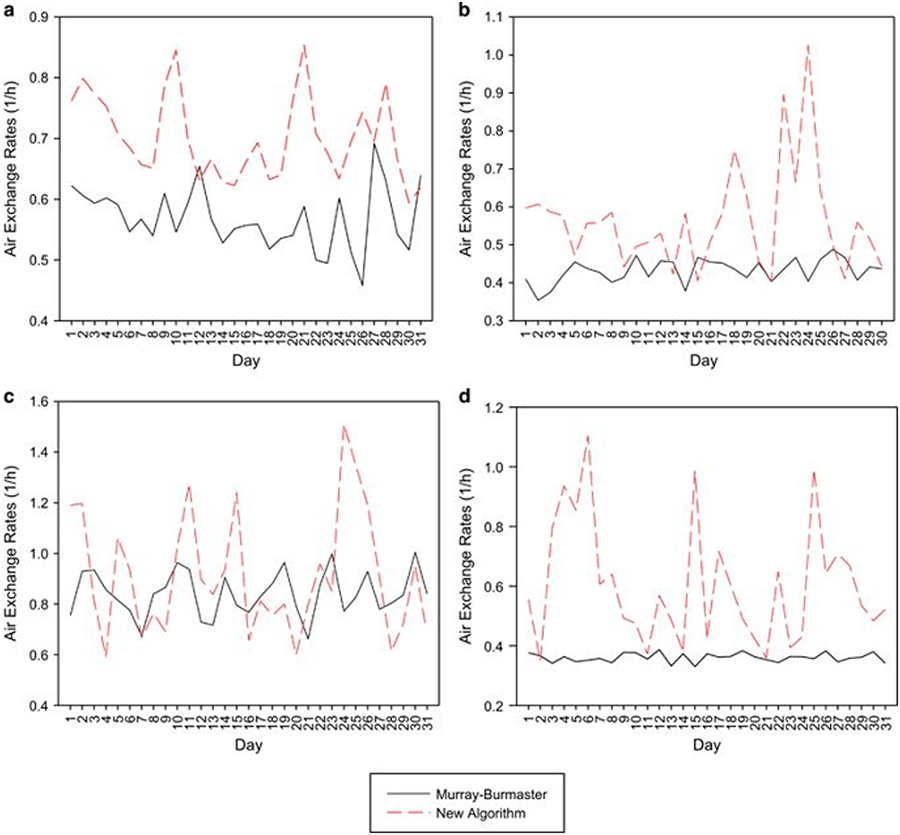
Day-to-day variations in AERs are also more pronounced with the new algorithm, as shown in time-series plots of AERs (Figure 3) comparing results for one census tract during 4 months representing different seasons. In concurrence with Table 3, the day-to-day fluctuations are greater for the AERs generated using the new algorithm; however, the magnitude of these differences depended on the season. During April (spring) and October (fall), the M–B distributions produced very little daily variations in AERs whereas the AERs estimated using the algorithm showed significant day-to-day fluctuations. The differences in the fluctuations were less during January and July. These variations in temperature and subsequent occupant behaviors may not be well represented by the M–B empirical distributions.

Fig 3.

Time series of AERs for Tract ID 34013000900 in (a) January 2001, (b) April 2001, (c) July 2001, and (d) October 2001.

DISCUSSION

This paper presents a new algorithm for estimating AERs using a modified version of LBNL Infiltration model that can be incorporated into stochastic population-based exposure models. In the first analysis, study-specific data were utilized to develop probabilities of AC use and window opening. The distributions of measured AERs were statistically the same as the 75th percentiles of the modeled AERs for Detroit, Elizabeth, and Los Angeles, and for the median modeled distributions in Houston. Study-specific data will not always be available so these probabilities were also generated using regional-input data that is publically available. Overall AERs estimated using study-specific inputs were higher than those estimated from regionally-available data. Before the incorporation of the new AER algorithm, literature-based distributions were used to estimate AERs for SHEDS relying on empirical distributions rather than mechanistic modeling. The algorithm produced more spatially and temporally variable AERs compared with literature-based distributions reflecting within- and between-city differences.

Differences between the measured and modeled AERs could be due to factors related to the stochastic sampling of home characteristics resulting in differences in the home age or size between the measured and modeled homes, as well as occupant behaviors not captured in the algorithm. However, a consistent pattern across cities was not observed. The age for the measured and modeled homes was similar except in Los Angeles, which had a larger percentage of newer homes (1995 or newer) than the RIOPA homes compared with the simulations. For the RIOPA cities, measured homes were smaller on average than modeled homes (data not available for DEARS). The means and medians for the modeled AERs were similar, ranging from a 2–10% difference, while the difference between the measured means and medians ranged from 6% to 31%, suggesting that there are extreme values (i.e. very high AERs) not being captured by the algorithm. These higher values may be caused by occupant behaviors such as window fan use and opening of doors. For example, in Detroit measured AERs were significantly higher (P<0.05, Wilcoxon–Mann Whitney test) in homes using window fans (mean=2.84 h⁻¹) compared with homes not using a window fan (mean=1.25 h⁻¹).

Differences between AER estimated using the “study-specific” and “regional” inputs appear to be due to the differences in the probabilities for open windows. Overall, model inputs for assigning presence of AC in the home were very similar between the two data sources (Supplementary Table S7). The window opening probabilities by AC status used as “regional” inputs were derived from homes in Ohio²⁴ and may not be representative of window opening behavior in all other regions of the country. The probability of window opening by AC status and temperature class do have noticeable differences between the two input data sets that parallel differences in the modeled AER (Supplementary Table S8). For example, in the T<17°C category the probability of open windows for the regional-input data was 0 regardless of AC status whereas there was some window openings in the study-specific input data, particularly for Los Angeles homes which is reflected in the higher AERs generated from the study-specific data (Table 2).

The window opening probabilities derived from Johnson et al.²⁶ were the only published data in the appropriate format available in addition to the RIOPA and DEARS data. Although this type of data is scarce, there may be more region and/or city-specific information that is publically available.

This new algorithm will also account for spatial and temporal variability not captured by literature-based distributions. Variability in home characteristics (e.g. air tightness and presence of AC), operation (e.g. use of AC and/or air filters and opening of windows), and occupant activities (e.g. cooking and candle burning) can result in substantial spatial variability in outdoor air pollution exposure and intake in-homes that experience similar outdoor concentration profiles.¹⁵ Temporal variability in AERs is driven by diurnal and seasonal variability in outdoor air pollutant concentrations and the atmospheric conditions (temperature, wind, pressure, etc), affecting in-home exposures.²⁷

The goal of developing a new AER algorithm for SHEDS was to estimate more temporally and spatial resolved AERs. There are however some limitations with our method. First, the equations from the LBNL model16are based on single-family detached homes and may not be as applicable to other housing types such as apartment buildings. Exclusions of other types of housing may make it difficult to assess residential AERs for certain populations, or locations with primarily apartments, for example low socioeconomic status (SES) homes. Similarly, census tracts with lower SES homes may also have different activity patterns. As more data are collected on different building types and different group’s activity patterns, adjustments can be incorporated into the algorithm and input databases.

The algorithm also contains several assumption such as a constant internal temperature and building height. For temperature what is driving the AERs is the indoor–outdoor temperature difference, which is greater during the winter and summer months. Second, differences between the measured and modeled AERs indicated that our approach may not be able to estimate extreme values due to unmeasured occupant behaviors. However, these extreme values are most likely not representative of the census tract. Our approach may therefore do a better job estimating AERs on a census-tract and/or population basis. Further validation is needed comparing the results from the probabilistic model to longitudinal AER measurements representative of a census tract. These measurement data are not currently available. Finally, a significant data gap is information on opening windows behavior. There is limited publicly available data and available data may not be applicable to all geographical regions of the country. This is illustrated in the differences in the window opening probabilities between the study-specific and regional-input data and the resulting differences in the AERs. The window opening probabilities is a user-defined portion of the algorithm; therefore, more representative data can be utilized in the future to calculate these input probabilities.

In conclusion, exposure models that account for the variability in factors such as infiltration of outdoor air indoors have recently been applied to better characterize exposures for epidemiological studies. Appropriate population distributions for AER are required for modeling reasonable estimates of total population exposures to outdoor air pollutants. There are currently limited data available on AERs for exposure modeling. Previously, input distributions created from region- and season-specific empirical data have been used in SHEDS. This results in AERs only exhibiting temporal variability on a seasonal basis and little or no intra-urban spatial variability. We therefore developed a generalizable algorithm to estimate AERs for a population based on a mechanistic model. The AERs estimated from this algorithm will allow for day-to-day fluctuations in AERs and incorporate differences between census tracts. Information on the within- and between-home variability of AER is necessary to better characterize exposure and not accounting for this variability may cause substantial exposure misclassification in epidemiological studies.