Abstract
On a springy new indoor track at Harvard University runners can run faster than they can on standard tracks. The design of the track was arrived at through a close analysis of the mechanics of human running.
Keywords: track & field surface compliance, force reduction, human locomotion dynamics, injury reduction, speed enhancement, muscle physiology
INTRODUCTION
In October of last year Harvard University opened a new indoor sports facility housing a six-lane 220-yard running track. The track has a supporting substructure consisting primarily of wood and a synthetic surface covering. Most people find running on the track a pleasant and unusual experience. It feels particularly springy and therefore is comfortable to run on, and members of the Harvard track team have sustained considerably fewer injuries since they began practicing on the track. What is most remarkable, however, is that an analysis of the 1977–78 records of Harvard runners and their competitors shows that the track substantially enhances a runner’s performance, reducing the time of, say, a well-run mile by several seconds. By all estimations the new track is fast.
Background
One of the most important parameters of track design is compliance, and it is mainly in this respect that the new track differs from other indoor tracks. Just how compliant—or, alternatively, how stiff—should a track be? In 1976, when the new track was being designed, the Harvard track coach, Bill McCurdy, and the Harvard Planning Office sought our advice on this question. At that time there was no information available concerning the effect of a given track surface on running speed and comfort. It is intuitively clear, however, that running on a compliant surface such as grass is less conducive to injury than running on a hard surface such as asphalt. Indeed, if comfort were the only consideration, all tracks would be extremely springy, perhaps as springy as a diving board. Intuition also suggests, however, that on a springy track the time spent rebounding from the surface is increased, so that a runner is slowed down. Hence if a running track is to be fast, its compliance must be limited.
One might therefore suppose the hardest track surfaces are the fastest, but that is not the case. A compliant surface acts as a spring, and we found that if the stiffness of the spring is closely tuned to the mechanical properties of the human runner, the runner’s speed can be increased. In other words, there is a specific intermediate track compliance at which running speed is optimized. At that optimum compliance the runner stepping down onto the track stores elastic energy in its surface, much as a pole vaulter stores elastic energy in bending a fiberglass pole, which is recovered as the pole propels him upward. A track whose compliance is in the theoretically optimum range can be called a tuned track.
A tuned track is special only in that its properties are particularly compatible with those of the runner. Hence our first step in designing such a track was to develop a model of the mechanics of running, one that was complex enough to be realistic but simple enough to be mathematically manageable. Running speed is determined by several parameters. With the physiological simplifications introduced in the model it was possible to derive mathematical expressions for those parameters as functions of track stiffness. In this way we were able to predict the effect various track compliances would have on running speed. Our final step was to test the model predictions with runners and experimental tracks. The ultimate test was provided by the new Harvard track, whose wood substructure is designed to achieve a compliance in the range we found to be optimum. The results of these tests, which are discussed below, are in good agreement with the theoretical predictions.
Literature Review - Figures 1, 2, 3, 4
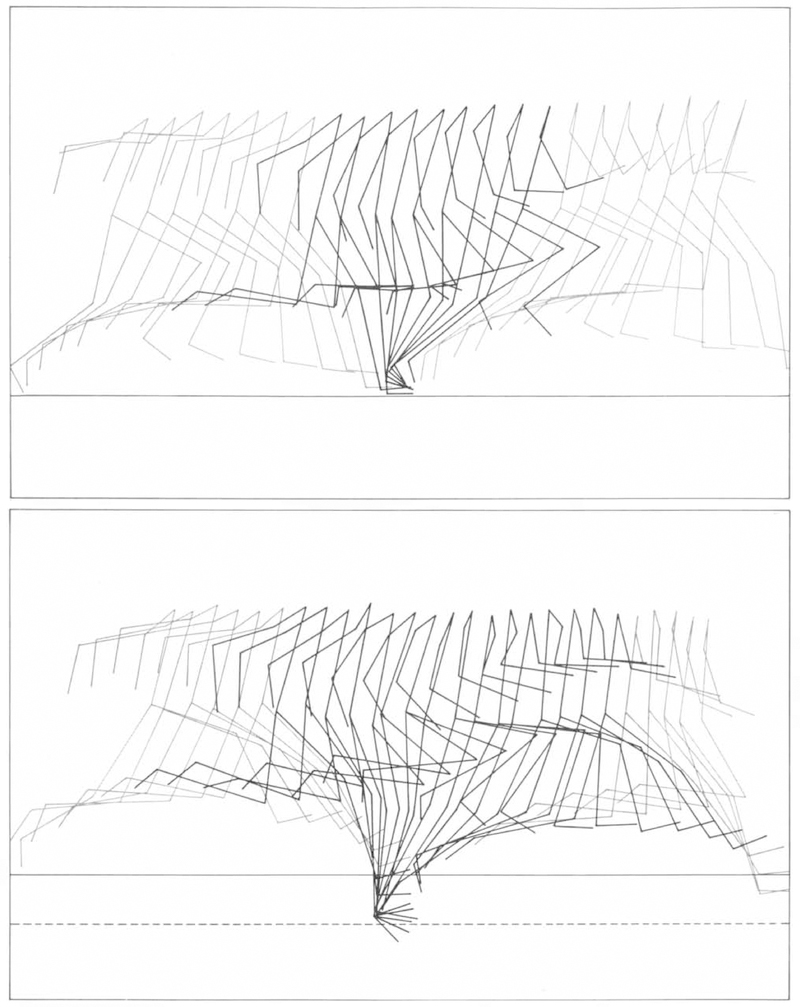
Figure 1.
COMPUTER SEQUENCES showing running positions are obtained by digitizing the points marking a runner’s major limb joints in a motion picture of running and then connecting those points on a digital plotter. In the sequences shown here the points mark the runner’s right hip, shoulder, ear, elbow, wrist, knees, ankles and big toes. The same runner is shown on a hard, or stiff, surface (top) and on a soft, or springy, one (bottom). Running speed can be viewed as the ratio of the runner’s step length (the distance the body travels while one foot is on the ground) to his ground-contact time Ref. [1] (the time the foot is on the ground). The sequences show that a runner’s step length and ground-contact time are both increased on a soft surface, with the net result that his running speed is decreased. A very hard surface, however, is not the fastest The authors found that there is a range of intermediate track stiffnesses at which running speed is enhanced. The computer analysis for this illustration was performed in the Gait Analysis Laboratory of the Children’s Hospital Medical Center in Boston.
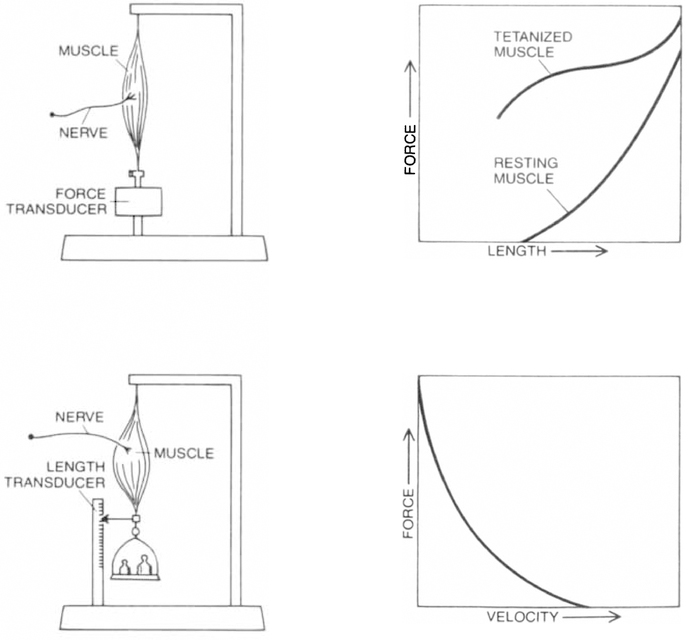
Figure 2.
MUSCLE REMOVED FROM THE BODY of a frog and held at constant length in an apparatus that measures force (top) develops more force at greater lengths, whether it is resting (engaged in minimal electrochemical activity) or tetanized (engaged in sustained electrochemical activity). A mechanical device that develops more force at greater lengths is a coiled spring. When the muscle is allowed to shorten-and pick up a weight so that its shortening-velocity can be measured (bottom), it is discovered that if the amount of force developed-in the muscle (the weight lifted) is decreased, the shortening velocity is increased. The mechanical device that creates such a damping effect is a dashpot, or shock absorber. In the authors’ mechanical model they represented muscles employed in running as spring connected in parallel with dashpot.
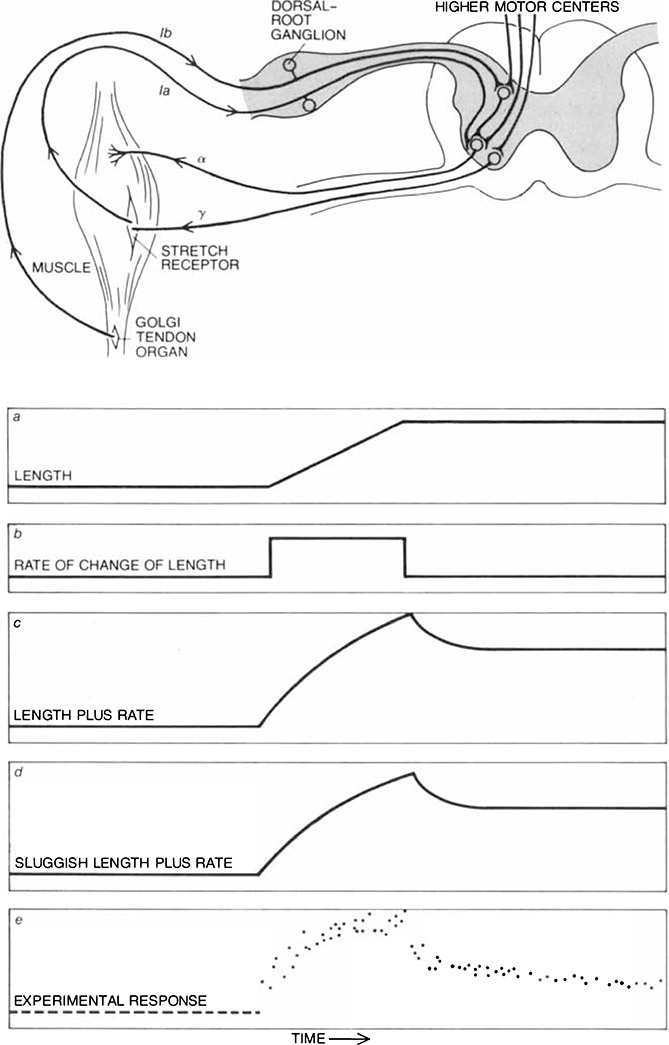
Figure 3.
MUSCLES IN THE BODY are regulated by the feedback-control system of the reflexes: commands in the form of electrochemical impulses are sent to the muscles along the axon, or long fiber, of the specialized nerve cells in the spinal cord called alpha motoneurons; information about muscle activity is sent back to the central nervous system by stimulus-sensitive receptors. Impulses from the receptors travel along the fibers of nerve cells found in the part of the peripheral nervous system known as the dorsal-root ganglion. These pathways can be divided into two types: the Ia pathways innervate stretch receptors (shown greatly enlarged here), which are primarily sensitive to changes in muscle length, and the Ib pathways innervate the receptors called Golgi tendon organs (also shown greatly enlarged), which are primarily sensitive to changes in muscle force. The stretch receptors also act as muscles, innervated by the nerve cells called gamma motoneurons. In addition the stretch receptors are rate sensitive, that is, they are responsive to the rates of change in their stimuli. The rate sensitivity of the reflexes is another way the muscle system is damped. The graphs in the lower part of the illustration show how this phenomenon affects the stretch receptors called spindle organs. When a spindle organ is steadily lengthened starting from a resting position, the magnitude of its response is proportional not to the sum (c) of the “ramp” function representing the change of length (a) and the step function representing the change of rate (b) but to a damped, or sluggish, version of the sum (d, e). These findings suggest that dashpot introduced into the model of running to represent the force-velocity relation of muscle also serves to represent the rate sensitivity of reflexes. Graphs are adapted from work of Tristan D. M. Roberts Ref. [4] of University of Glasgow.
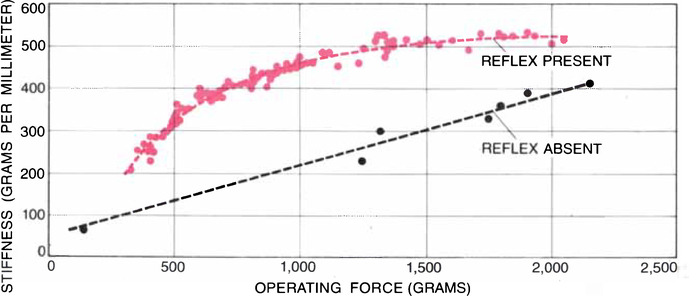
Figure 4.
STIFFNESS OF AN ISOLATED MUSCLE (the change in the force developed by the muscle when it is stretched, divided by its change in length) increases as the muscle is stretched. Recent results indicate that in the body the reflexes maintain the stiffness of an actively contracting muscle at an almost constant level. J. A. Hoffer and S. Andreassen Ref. [2] of the University of Alberta measured the increase in the stiffness of the cat soleus muscle (a plantar-flexor muscle in the ankle) as a function of force. When the pathways leading from the receptors back to the central nervous system were severed, the stiffness rose in proportion to the force exerted by the muscle (broken black line). With those pathways intact, however, the muscle stiffness was higher. (A closed-loop negative-feedback control system is always stiffer than an open-loop one.) After rising with low forces the stiffness reached a plateau at moderate and high forces (broken color curve). These findings suggest that spring, which has constant stiffness, is a suitable representation of the muscles involved in running, particularly in moderate-to-large range of forces.
Running is essentially a series of bounds. As the runner’s foot strikes the running surface the antigravity muscles that support his skeleton contract and ultimately reverse the downward velocity of his body. To understand how our model was devised and why the tuned track works, it is necessary to understand how the physiological properties of these muscles and the reflexes that control them determine the functioning of the runner as a mechanical system.
Consider first an isolated muscle, removed from an animal and placed in an apparatus that measures its force at a constant length. With its blood supply cut off, a muscle from a mammal such as a rat will quickly fatigue and die, but in a suitably oxygenated bath a muscle from a small amphibian such as a frog will remain alive for hours or even days. A muscle that is not being stimulated to contract is said to be resting. When the force developed in the resting muscle is plotted against the length of the muscle, the force-length relation curves upward, that is, the force increases with length. The slope dF/dx of the force-length curve is the stiffness of the muscle, and the curve shows that it too increases with length. (Resting muscle is stiffer at greater lengths for the same reason a nylon stocking feels stiffer as it is stretched. As the muscle is lengthened more of the collagen fibers in the connective tissue associated with it become taut and begin bearing load.)
If a resting muscle is given a small electric shock‚ either directly or through the nerve that supplies it‚ the force in the muscle rises above the resting level and then quickly drops. This momentary rise in force, called a twitch, is the basic event in muscle contraction. In a sustained activity such as running, a train of twitches can merge at an elevated level of force; in this state the muscle is said to be tetanized. The force-length curve for tetanized muscle shows that, as in resting muscle, force increases with length. The same property is exhibited by a mechanical system: a coiled spring. It was this fact that suggested to us a model of running in which the muscles would be represented by springs.
The difference in force between tetanized muscle and resting muscle is termed developed tension. An important phenomenon having to do with developed tension is observed when tetanized muscle is placed in another type of apparatus: one in which the muscle is allowed to shorten and pick up a weight so that its shortening velocity can be determined. This experiment reveals that the shortening velocity does not increase throughout the shortening period; rather, after a brief starting period the muscle shortens at a constant speed. When the shortening velocity is measured with different weights, it becomes apparent that muscle shortens more rapidly when it is working against lighter weights. It is as if a damping element—a dashpot, or shock absorber—were subtracting some of the developed tension. When the damping phenomenon was first discovered some 50 years ago, it was suggested that something like a mechanical dash-pot was actually present in muscle, but it is now clear that the damping effect is a property of the force-generating mechanism itself, specifically of the interaction of actin and myosin, the contractile proteins of muscle.
Hence an isolated muscle shortening against a constant load behaves like a damped spring, or, more precisely, like a stretched spring acting in parallel with a dashpot. In the body, however, the functioning of the muscles is controlled by the nervous system. It is conceivable that under such conditions the spring-and-dashpot system might not apply. What we found is that with certain elaborations the model derived from the inherent properties of isolated muscles also describes muscles and reflexes as they function in the feedback control system of the body. (It should be noted that a mathematically linear spring, which has constant stiffness at any length, is utilized in the model, even though an isolated muscle acts as a mathematically nonlinear spring, which has variable stiffness. Recent experiments concerning reflexes, which we shall discuss, serve to justify this simplification.)
Muscle fibers receive their commands, or electrochemical stimuli, directly from the specialized nerve cells in the spinal cord called alpha motoneurons, Figure 3. The traffic of impulses along the axon, or long fiber, of an alpha motoneuron is efferent: it moves outward from the spinal cord and the rest of the central nervous system. Information comes back to the central nervous system along afferent pathways whose nerve-cell bodies are found in the dorsal-root ganglion: a swelling of the peripheral nerve just outside the spinal cord. The fibers of these nerve cells terminate in receptors that are specialized to respond most effectively to certain types of stimuli. Receptors in the locomotor system provide the central nervous system with the information that makes smooth movement possible. In control engineering the route from a receptor to the central nervous system over afferent pathways and from the central nervous system to an effector organ (such as a muscle) over efferent pathways is called a feedback loop; in physiology it is called a reflex arc.
For example, when a physician strikes the large tendon below a patient’s kneecap with a hammer, he is testing the muscle-control system known as the stretch reflex. When the hammer strikes the tendon, the quadriceps group of muscles is stretched momentarily. As the muscles lengthen, stretch receptors in them (spindles) also lengthen and transmit a burst of impulses. This information travels along an afferent pathway to the quadriceps alpha motoneurons, eliciting the kick that tells the physician the patient’s neuromuscular wiring is in good condition.
Two groups of afferent pathways designated Ia and Ib are the most important ones in the muscle-control system. The Ia pathways innervate the stretch receptors. Since stretch receptors are connected in parallel with muscles, they are primarily sensitive to muscle length. For example, in the stretch-reflex test an increase in the length of the quadriceps muscles sends information along an afferent Ia pathway. The Ib pathways innervate the receptors known as Golgi tendon organs, which are mainly sensitive to muscle force.
Stretch receptors respond to dynamic stimuli as well as static ones: they are sensitive to the rates of change in the strength of stimuli as well as to the changes themselves. In mechanical terms the stretch receptors encode and send back to the spinal cord not only position information but also velocity information.
Consider a spindle-organ receptor that is being steadily lengthened. The rate of change in length begins at zero, rises to a constant level and then falls back to zero when the lengthening stops. Experimental results show that the magnitude of the spindle response is proportional not to the sum of the “ramp” function representing the change in length and the step function representing the rate of change in length but to a sluggish version of the sum. The sluggishness is due partly to a property of all muscles, including spindles, known as series elasticity, and partly to the dashpot property of the receptors. In other words the sluggishness is an intrinsic property of the rate sensitivity of the reflex.
The spindle organ is itself composed of muscle cells and is separately innervated by the nerve cells called gamma motoneurons. Hence the length at which it sends a given intermediate frequency of impulses to the spinal cord can be changed by input from the higher motor centers. That makes the spindle organ a specialized type of strain gauge: a length-reporting device that converts mechanical stretch into nerve impulses, which in this case can be recalibrated to accommodate large-scale changes such as a change in the position of the body.
Consider again the stretch-reflex arc, where the final response to an imposed lengthening of muscle was the patient’s kick reaction. Because the imposed muscle lengthening ultimately produced this muscle shortening, the reflex arc is a negative-feedback control system. Both the length and the rate of change of the length of the quadriceps muscles are reported along the Ia pathway as negativefeedback signals. Considering the mass of the leg, one can correctly predict that the normal overall response to the hammer blow will be a heavily damped, decaying oscillation of the knee angle, with the velocity feedback from the muscle giving rise to the damping effect. If the stretch receptor were sensitive only to muscle length, there would be no feedback damping, and in the absence of friction the oscillation would continue indefinitely.
What is the control function of the Golgi tendon organs, the group of receptors sensitive to muscle force? For many years it was believed their only role was to turn off the alpha-motoneuron activity and cause a muscle to relax whenever a critical muscle force, which might be capable of injuring the muscle, was exceeded. Newer evidence shows, however, that feedback from the Golgi tendon organs may also help to modify the stretch reflex in such a way that muscle stiffness, rather than muscle force or length, is the controlled property. J. A. Hoffer and S. Andreassen Ref. [2] Figure 4 of the University of Alberta measured the increase in the overall stiffness of the plantar-flexor muscles in the ankle of the cat as a function of muscle force. In their first set of experiments the afferent pathways carrying information from the muscle spindles and Golgi tendon organs were intact. At low forces stiffness rose with force, but at moderate and large forces it reached a plateau. In their second set of experiments the afferent pathways were severed: the stiffness of the same muscles was always lower (because a closed-loop negative-feedback control system is always stiffer than an uncontrolled system), but it continued to increase no matter how much force was applied. In other words, through the regulation of the muscle spindles and Golgi tendon organs, muscle stiffness at all forces except very low ones was moderately independent of muscle force.
Materials & Methods - Figures 5, 6, 7
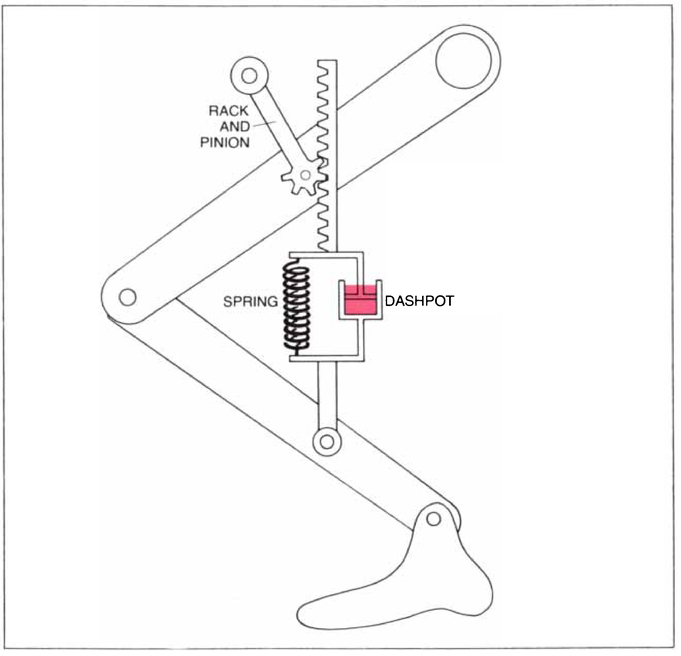
Figure 5.
MODEL OF THE MUSCLES AND REFLEXES involved in running consists of a rack-and-pinion element connected in series with a damped spring. The dashpot damping effect is created by a piston moving in a cylinder containing a viscous fluid such as oil (color). In the model the rack and pinion represents the role of movement commands from higher motor centers, the spring represents the muscle stiffness (assumed to be constant) and the dashpot represents both the force-velocity relation of muscle and the rate sensitivity of the reflexes. In other words, the setting up of leg positions is modeled by the motion of the rack and pinion, but the reaction to external force disturbances, such as the impact of the track on the contact leg, is modeled by the deflection of the damped spring. Hence the leg and hip positions at the beginning and end of the ground-contact phase, which determine step length, depend only on the movement of the rack and pinion, whereas the body motion during that phase, which determines ground-contact time, depends only on the deflection of the damped spring. With these simplifications, once runner’s inherent spring stiffness Ref. [3] and damping constants have been determined experimentally, effect of track stiffness on ground-contact time and step length can be calculated.
Figure 6.
MODEL RESULTS WERE TESTED with runners on tracks of various degrees of stiffness. In the experimental setup shown here a force platform under one of the panels of the track (not visible) records the beginning and end of a ground-contact phase. The results are plotted on the oscilloscope shown at the bottom of the photograph. Running speed is recorded with the electronic timer at the lower right and the two pairs of timing lights arranged on each side of the track. (The lights are placed at the level of the runner’s neck to avoid the triggering of false timing readings by the runner’s arms and legs.) The running trials were also recorded on high-speed motion-picture film.
Figure 7.
RUNNING FILMS show that whether a runner is on a fairly stiff wood track (top) or on a soft pillow track (bottom) the trajectory of his head is nearly level. Therefore for the purposes of the model it can be assumed that the hip follows a level path no matter what surface runner is on. Assumption simplifies calculation of effect of track stiffness on the step length (see bottom illustration on opposite page).
We were able to get similar results with the reflexes controlling the antigravity muscles of the human leg. In our experiments weight lifters bearing loads of up to twice their body weight on their shoulders executed small bouncing motions on a long plank. The subjects kept their knees bent to the extent they would in running. Knowing the total mass of the subject and the weight (and therefore the force exerted on the muscles), the effective mass of the plank and the natural frequency of vibration, we could use a simple mathematical procedure to calculate the stiffness of the subjects. We found that at knee-flexion angles in the range appropriate for running, the controlled, or reflex, stiffness is virtually independent of load and consequently of muscle force.
The observation that the reflexes maintain muscle stiffness at an almost constant level turns out to have considerable practical value. Remember that the problem with using a mathematically linear spring to represent the muscles involved in running was that the spring has constant stiffness and the muscles do not. The results of the experiments imply that the change in muscle stiffness with muscle force observed in experiments with isolated muscles can be ignored. Actually during the first quarter or so of the ground-contact period in a running step the reflexes have not had time to act, and so’ the intrinsic properties of the muscles alone determine the stiffness and damping of the leg. In the second half of the contact period, however, the stiffness and damping are almost certainly under reflex control and therefore are reasonably well represented by a damped linear spring.
We are now able to complete our model of the mechanics of running, Figure 5. We shall view the muscles and reflexes of the leg as a system consisting of a rack-and-pinion element acting in series with a damped spring [Fig. 5]. The rack-and-pinion element is included to emphasize the role of movement commands descending from higher motor centers; the spring represents the assumed constant stiffness of the muscles and reflexes, and the dashpot damping mechanism represents the intrinsic force-velocity property of the muscles and the rate sensitivity of the reflexes. In other words, the setting up of leg positions is modeled by the motion of the rack and pinion, and the effect of external force disturbances such as the impact of the track on the runner’s leg is modeled by the deflection of the damped spring. As we shall now show, the simplifications introduced by the model make it possible to calculate a runner’s speed on a track of arbitrary compliance with only a few items of information: the runner’s mass, the length of his leg, his spring stiffness and his step length and top running speed on a hard surface.
What value of track compliance—if any—will optimize running speed? For our purposes the most useful way to measure running speed is as the ratio of step length (the distance the body moves forward while one foot is on the ground) to ground-contact time (the time the foot is on the ground). On a tuned track the ground-contact time should be minimized and the step length should be maximized. In the model it is primarily the runner’s mass and the motion of the damped spring that determine the body motion during the ground-contact phase and therefore the ground-contact time; it is the motion of the rack-and-pinion element that determines the leg and hip positions at the beginning and end of the ground-contact phase and therefore the step length.
RESULTS - Figures 8, 9, 10, 11, 12
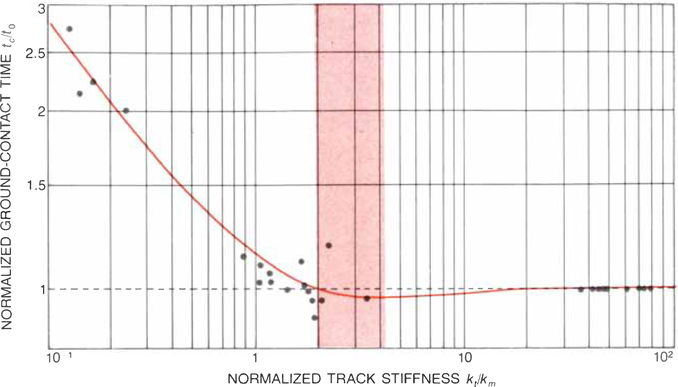
Figure 8.
GROUND-CONTACT TIME can be derived from the model as a function of track stiffness. In this graph of the function, normalized, or dimensionless, values of each parameter have been used so that theoretical results (curve) can be compared with experimental findings for many runners (black dots). Ground-contact time bas been normalized by dividing the time on a compliant surface tc by the time on a hard surface t0; track stiffness bas been normalized by dividing the track stiffness kt by the runner’s stiffness km. Because of the damping of human muscle ground-contact time does not decrease continuously as track stiffness increases but reaches minimum at stiffnesses between two and four times that of average athelete (color).
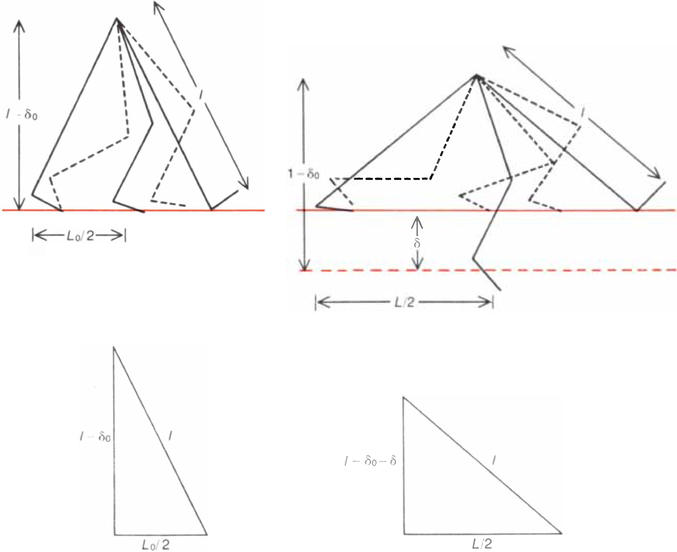
Figure 9.
STEP LENGTH IS LONGER on a compliant surface (right) than on a hard one (left) because the bending angle of the hip joint is greater, as is shown by these schematic representations of a runner on the two surfaces. At the beginning and end of either running step the contact leg (solid black line) is fully extended, with length l. After heel contact (leg position farthest to the right) the contact leg moves back (to the left) as the swing leg moves forward. At mid-stance, when the body has traveled a distance of half a step length, the contact leg is flexed, that is, shortened by a distance of δ0, which is taken to be independent of the track compliance. Hence on a hard surface, which has step length L0, the distance from the hip to the track surface is l − δ0. On a compliant surface, however, the flexed contact leg sinks below the undeflected track surface (solid color line). It is as if the runner were moving across a hypothetical surface (broken color line) a distance S below the undeflected surface, where S depends on the compliance of the track and the mass of the runner. Therefore the distance from the hip to the undeflected surface on a compliant track is l − δ0 − δ. The right triangles below each figure in the illustration show how these factors result in a greater step length L on a compliant surface. Since the distance S is equal to the runner’s weight divided by the track stiffness, and since L0 and l can be measured directly, the step length on a track of arbitrary stiffness can be calculated by applying Pythagorean theorem to the two triangles.
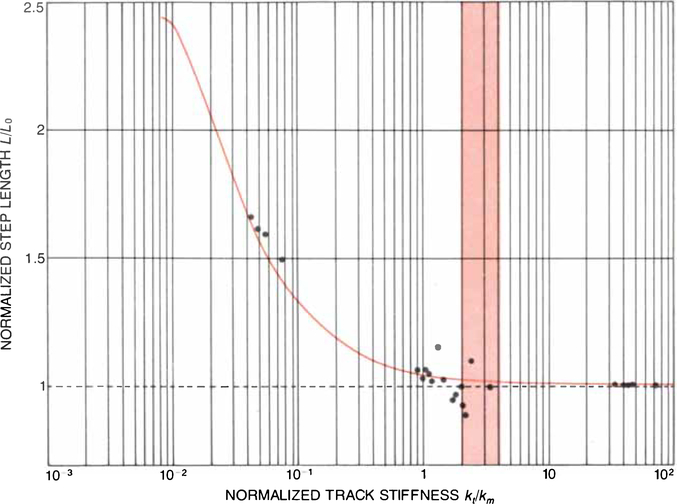
Figure 10.
MODEL PREDICTIONS of the effect of track stiffness on step length (curve) are in close agreement with experimental findings (black dots). Step length is greatest on softer surfaces, where ground-contact time is also greatest. In the range of stiffnesses where ground-contact time is minimized and therefore optimum with respect to running speed (color) step length is still slightly increased over its hard-surface value. Hence in that range, and particularly in the low end of the range, running speed is enhanced. (In the graph step length has been normalized by dividing step length L on a surface of arbitrary stiffness by step length L0 on a hard surface; track stiffness has been normalized by dividing track stiffness kt by runner’s stiffness km)
Figure 11.
INDOOR TRACK AND TENNIS FACILITY at Harvard University opened in October of last year. Its six-lane 220-yard track features banked turns, a polyurethane top surface and a substructure made primarily of wood. The substructure is designed to convey a stiffness between two and three times the stiffness of an average athlete. Stiffness is in the low end of the range authors found to be optimum with respect to running speed. Facility was designed and built by T.A.C., Inc., and the Turner Construction Company of Boston.
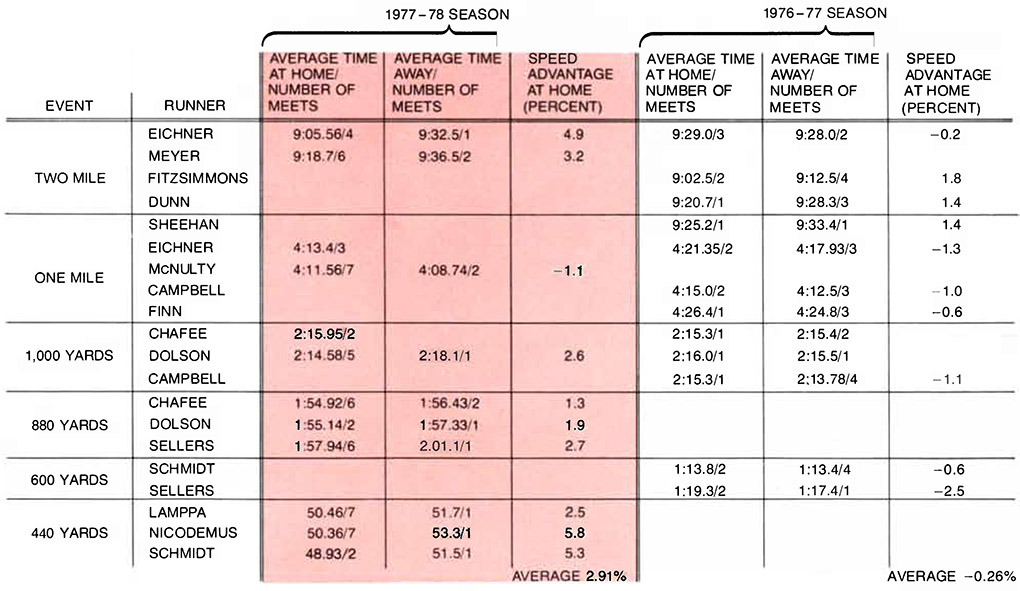
Figure 12 Table I.
HARVARD TEAM’S TRACK RECORDS for the first season on the new track (color) show that the track substantially enhances running performance. Each Harvard runner’s performance on the new track is compared with his performance at the Intercollegiate Athletic Association of America and the Heptagonal meets, which were run on standard tracks. The new track conveyed an average speed advantage of nearly 3 percent. Further analysis of these statistics shows the probability is about 93 percent that any given individual will run faster on the new track. Similar statistics are given for preceding year (white), when Harvard team’s home meets were run on cinder track.
Consider first the relation of track stiffness to ground-contact time. To derive an expression for ground-contact time as a function of track stiffness it is necessary to assign to a runner a spring stiffness and also to determine the extent to which the combined effects of the force-velocity relation and the velocity feedback from the reflexes act to damp his spring. We observed that once a runner’s muscles have guided his foot into contact with the ground their most important role is to contract as forcefully and as soon as they can in order to reverse the downward velocity of the body. For this reason we chose to make the somewhat arbitrary assumption that the rack and pinion cannot be disturbed by external forces while the foot is on the ground, so that the ground-contact time on a hard surface depends entirely on the runner’s mass and the properties of the damped spring. Hence the numerical values denoting the runner’s spring stiffness and damping can be derived from the measurement of his ground-contact time when he is running on a hard surface. (The matter is complicated by the fact that a runner’s spring stiffness is affected by his effort. Muscle strength varies greatly among runners, and the stronger a runner is, the more muscle fibers he can recruit in parallel and the stiffer his spring is. For this reason we chose to determine a runner’s spring stiffness by measuring his ground-contact time as he was running at top speed on a hard surface.)
Once a runner’s stiffness and damping constants have been determined it is a straightforward matter to calculate how his ground-contact time is changed on tracks of various stiffnesses. This result was the most important in predicting the effect of track stiffness on running speed. It can be assumed the runner is tuned to the track so that he rebounds from it in half a period of the lowest natural mode of vibration. As intuition suggests, the calculations show that the ground-contact time on soft surfaces is long. If there were no damping element in the spring of human muscle, the ground-contact time would decrease continuously from that value as track compliance decreases, reaching a minimum at the compliance of infinitely hard surfaces. In that case a running surface such as concrete would be the fastest. Our findings show, however, that the ground-contact time does not decrease over the entire range of compliances. Since the runner is a damped system, his ground-contact time reaches a minimum at an intermediate compliance; at a track stiffness between two and four times greater than the runner’s the ground-contact time is shorter than it is on harder surfaces. Therefore on tracks of precisely the right stiffness enhanced speeds should be possible.
To check these results we built several test tracks, Figure 6, ranging from wood tracks with an adjustable compliance to pillows or large foam-rubber blocks laid end to end Figure 7. Test subjects were not given any information concerning our expectations. They were simply instructed to run at top speed, first on an experimental track and then on the concrete floor beside it. The trials were recorded with motion-picture cameras in order to measure the ground-contact time. Photoelectric timers and a precision force platform were also used. On all the tracks the measurements agreed well with the model predictions, Figure 8.
Running speed is not entirely determined by ground-contact time, however; step length is also an important factor. Remember that step length is the distance traveled while the foot is on the ground, as opposed to the distance between footprints, which is stride length. We noticed that as our subjects ran on the more compliant experimental tracks, such as the one consisting of foam-rubber pillows, their step length was greater. The explanation of this phenomenon has to do with the position of the contact leg at the beginning and the end of the contact phase. At those points the leg is fully extended, and it can be assumed there are no loads acting on the spring, that is, the geometry of the leg as it strikes the ground depends solely on the rack-and-pinion element, Figure 9.
For our investigations of the rack-and-pinion motion we made another assumption based on a feature we observed in the running films. No matter how hard or soft the running surface was, the trajectory of each runner’s head was nearly level, as if his postural controllers were trying to give the acceleration-sensing mechanism of the inner ear a smooth ride. In any case it is certain that at the frequency in question, with the modest value of the acceleration due to gravity and the short time between footfalls, the vertical motion of the body’s center of mass cannot be great. Hence we chose to assume that the hip follows a level path whether the runner is on a hard surface or a soft one.
The step length on a track of arbitrary compliance can be calculated as follows. In each running step one of the runner’s legs makes contact with the ground as the other swings over the running surface. As the swing leg moves forward it stays above the undeflected surface of the track, whether the track is hard or soft. On a hard track the contact leg also stays above the surface. On a soft track, however, the contact leg sinks below the surface. Therefore it is necessary to visualize the runner moving across a hypothetical surface a distance below the undeflected one, where δ is the average track deflection over a complete stride cycle. (The stride cycle includes not only the ground-contact phase but also the aerial phase; if the runner were standing motionless on the compliant track, he would be standing in a well of depth δ.)
At the beginning (and end) of the contact phase the runner’s contact leg is fully extended, and we shall call the full hip-to-heel length l, Figure 9. At mid-stance, when a distance of half a step has been traveled, the contact leg is flexed, shortened by, say, a length of δ0 on a hard track, so that the distance between the hip and the hard-track surface is l − δ0. Assuming that the hip follows a level path, this situation is described by a right triangle with hypotenuse l and sides l − δ0 and L0/2, where L0 is the step length on a hard surface. On a compliant track, however, the comparable triangle has sides l, L/2 and l − δ0 − δ. where L is the step length and l − δ0 − δ is the distance from the hip to the undeflected track surface. The average deflection S is determined by two measurable quantities: the runner’s body weight and the track stiffness. The leg length l and the step length on a hard track L0 can be measured directly. Hence by applying the Pythagorean theorem to the two triangles it is a simple matter to calculate what a runner’s step length will be on a track of arbitrary stiffness.
CONCLUSIONS
We found that the model predictions agreed well with our experimental measurements of step length on compliant surfaces, Figure 10. Just as we had calculated, the foam-rubber surface increased a subject’s step length by approximately 50 percent, partly compensating for the more than 100 percent increase in ground-contact time with the same surface. The net effect was that the runners were slowed to only about 70 percent of their hard-surface speed; if their step length had stayed constant on the foam rubber, they would have been slowed to about 50 percent of that speed, Figure 11.
Thus step length is most increased (a desirable effect) in the range of track compliances where ground-contact time is increased (an undesirable effect). It turns out. However, that in the range of compliances that are optimum with respect to ground-contact time, step length is still slightly increased over its hard-surface value. Therefore in this range of compliances—at a stiffness slightly more than twice the stiffness of the runner—the two factors determining running speed come together in an optimum way. Our model results showed that on tracks in this range of compliances the combined effect of decreased ground-contact time and increased step length should lead to a speed enhancement of between 2 and 3 percent, Figure 12, Table I.
At the end of the 1977–78 track season, the first season the track was in service, we compared the overall performance of members of the Harvard track team on the new track with their performance at the Intercollegiate Amateur Athletic Association of America championships held at Princeton University and the Heptagonal championships held at Cornell University. The Princeton and Cornell tracks are almost identical with the new Harvard track in size, but both of those tracks have a hard substructure with a synthetic top surface. (The Harvard track is also the only one of the three with banked turns. There is disagreement over the value of this feature of track design: banked turns increase the comfort and safety of running at high speeds, but they work to the disadvantage of runners moving at speeds lower than those for which the banking was designed: a fast quarter-mile.)
The analysis of the track records leaves little doubt about the effects of the tuned track. Although the two meets away from Harvard were championships, where runners are challenged to make their best showing, every Harvard runner except one ran his best time of the year on the new Harvard track. The runners’ average speed advantage on the new track was 2.91 percent, which is in close agreement with the predictions derived from our model. In the preceding year the team ran an average .26 percent slower at home (on a cinder track) than they did away, and so it seems unlikely that these statistics reflect a home advantage. Moreover, similar statistics on 11 of the top runners from four other institutions show that they experienced the same kind of improvement, running an average of 2.12 percent faster on the new Harvard track than they did at the championships.
In the same season an individual Harvard runner’s best time on the new track was an average of 3.87 percent faster than his best time off it and an average 2.04 percent faster than his best time of the preceding season. In terms of competition, however, the real advantage of a properly tuned track is probably not its speed enhancement; after all, the opposing teams run faster on it too. It is the comfort and safety of a tuned track that gives the home team an edge, enabling them to train much harder than they could on an ordinary track. A coach who can train ambitiously without fear of injuring his runners during practice can build a better team. Far fewer runners have been injured on the new track, although the Harvard team trained very hard last year.
In view of the discussion so far it may come as a surprise that no one expects a world record to be set on the Harvard track. That is because the International Amateur Athletic Federation does not recognize records for indoor running. Indoor tracks must usually be fitted into existing structures and so there is little standardization of design; for example, the length of such tracks and the radii of their turns vary greatly. Hence official world records can be set only on outdoor tracks.
No outdoor track of the optimum mechanical design has yet been built. If such a track is built, we predict that the world record for the mile could be improved by as much as seven seconds. The opportunity stands as a challenge.
Reference List
- [1].Cavagna GA, Thys H and Zamboni A, 1976. The sources of external work in level walking and running. The Journal of Physiology (Lond.), 262(3), pp. 639–657. DOI: 10.1113/jphysiol.1976.sp011613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Hoffer JA and Andreassen S, 1978. Factors affecting the gain of the stretch reflex and soleus muscle stiffness in premammillary cats. Annual Meeting of the Society for Neuroscience. DOI: 10.1152/jn.1981.45.2.267 [DOI] [Google Scholar]
- [3].Nichols TR and Houk JC, 1976. Improvement in linearity and regulation of stiffness that results from actions of stretch reflex. Journal of Neurophysiology, 39(1), pp. 119–142. DOI: 10.1152/jn.1976.39.1.119 [DOI] [PubMed] [Google Scholar]
- [4].Roberts TDM, 1963. Rhythmic excitation of a stretch reflex, revealing (a) hysteresis and (b) a difference between the responses to pulling and to stretching. Quarterly journal of experimental physiology and cognate medical sciences, 48(4), pp.328–345. [DOI] [PubMed] [Google Scholar]