Adaptive Changes in Cardiac Fibroblast Morphology and Collagen Organization as a Result of Mechanical Environment

Abstract

There is a growing body of work in the literature that demonstrates the significant differences between 2D versus 3D environments in cell morphologies, spatial organization, cell–ECM interactions, and cell signaling. The 3D environments are generally considered more realistic tissue models both because they offer cells a surrounding environment rather than just a planar surface with which to interact, and because they provide the potential for more diverse mechanical environments. Many studies have examined cellular-mediated contraction of 3D matrices; however, because the 3D environment is much more complex and the scale more difficult to study, little is known regarding how mechanical environment, cell and collagen architecture, and collagen remodeling are linked. In the current work, we examine the spatial arrangement of neonatal cardiac fibroblasts and the associated collagen organization in constrained and unconstrained collagen gels over a 24 h period. Collagen gels that are constrained by their physical attachment to a mold and similar gels, which have been detached (unconstrained) from the mold and subsequently contract, offer two simple mechanical models by which the mechanisms of tissue homeostasis and wound repair might be examined. Our observations suggest the presence of two mechanical regimes in the unconstrained gels: an outer ring where cells orient circumferentially and local collagen aligns with the elongated cells; and a central region where unaligned stellate/bipolar cells are radially surrounded by collagen, similar to that seen throughout constrained gels. The evolving organization of cell alignment and surrounding collagen organization suggests that cellular response may be due to the cellular perception of the apparent stiffness of local physical environment.

Introduction

Fibroblasts have long been recognized as the cells responsible for the synthesis and remodeling of extracellular matrices (ECM) in a variety of tissues. Fibroblast-induced mechanical deformation of the collagen network within the ECM represents a mechanism by which cells can assess their environment, transmit information between one another over large distances, and establish physical (microstructural) patterns [1]. It is well established that adherent cells respond to their mechanical environment, actively probing it and using the information to adjust their position, orientation, and morphology [1–4]. As a result of this cellular activity the structure and properties of the collagenous network of the ECM are also altered through remodeling, again in response to functional requirements based on environmental cues. Remodeling of collagen is a complex process consisting of the deposition of new collagen as well as the degradation of existing matrix and plays an important role in aspects of development, as well as in tissue maintenance, angiogenesis, wound contraction, inflammatory responses, and metastasis [5].

To recapitulate the mechanically induced remodeling process in vitro, numerous studies have examined the contraction of 3D collagen gels by fibroblasts. The roles of angiotensin II [6] and IGF1 [7], LPA [8] and PDGF [9] in collagen remodeling have been examined using this assay. Previous studies have also shown that the presence of ascorbic acid in culture media is critical for the production and secretion of collagen by cardiac fibroblasts [10]; however, the role of this molecule in contraction of collagen gels by cardiac fibroblasts is poorly understood. Integrins, transmembrane receptors responsible for attaching cells to collagen and other ECM components, have also been shown to be critical for collagen remodeling by cardiac fibroblasts [9, 11]. Studies of changes in collagen density during the contraction process have shown that decreases in density correlate with an increased ability of cells to contract the collagen matrix [12]. Other studies have employed the collagen gel contraction assay as a model system for related studies. Aggregates of ligament fibroblasts on collagen gels have demonstrated that these cells, in the absence of an opposing force, generate higher order collagen patterning by pulling the collagen toward the aggregate, thus producing radially oriented collagen [13]. Fibroblasts embedded within a 3D collagen matrix require cell–cell contacts to fully contract collagen gels, although the density of the cells appears to vary throughout the gel from high density on the edges to low density in the center of the gels [14]. While many of these studies have characterized cell behavior in freely contracting gels, during the majority of remodeling events which occur in vivo, boundary conditions will be such that the area undergoing remodeling will be, at least partially, physically restrained.

The goal of this study was to examine how cardiac fibroblast morphology and orientation, and collagen organization are affected by global mechanical environment, through the use of models of both constrained (attached) and freely contracting gels. Examining deformation within the contracting collagen gels yielded two distinct environments: the edges of the gels, which experienced a significant amount of displacement during the contraction process, and the gel centers, which experience little if any displacement. Cardiac fibroblasts on the edges of contracting gels oriented parallel to the free edge while those in the center of contracting gels, and throughout attached gels, were randomly oriented. The observed morphologies of these fibroblasts also depended upon their position within the gels as well as the global mechanical environment of the gel. Understanding the impact of local mechanical environments on cell behavior will have significant implications for measures aimed at controlling the remodeling process or tailoring the design of engineered replacement tissues.

Materials and Methods

Isolation, Culture, and Preparation of Collagen Gels Containing Neonatal Cardiac Fibroblasts

Cardiac fibroblasts were isolated from 3 day neonatal rat hearts (Harlan Sprague-Dawley) as previously described [15]. Briefly, hearts were dissected, minced, and digested with collagenase (100 U/ml; Worthington, Lakewood, NJ) and fibroblasts isolated through selective attachment. Fibroblasts were maintained in culture in Dulbecco’s Modified Eagle’s Medium (DMEM; Sigma Chemical Co., St. Louis, MO) containing 10% fetal bovine serum (FBS; Atlanta Biological, Atlanta, GA), 5% newborn calf serum (NBS; GibcoBRL, Rockville, MD), 100 U/ml penicillin G and 100 μg/ml streptomycin (Sigma) and used prior to passage four. Three-dimensional collagen gels [10] were prepared using an 8:1:1 (v/v/v) ratio of 3.1 mg/ml bovine collagen type I (Inamed Biomaterials, Fremont, CA), 1X MEM (Sigma), 0.2 N HEPES pH 9.0 (Sigma). Cardiac fibroblasts were added to the collagen solution such that the final cell concentration was 200,000 cells per 1 ml gel. The gels were cast in a 24-well tissue culture plate and allowed to polymerize in a 37°C humidified incubator under 5%CO₂ for approximately 1 h before media was added to each gel. In addition to normal media, some gels were cultured in media supplemented with 50 μg/ml ascorbic acid [10, 16] and 292 μg/ml glutamine [16, 17]. After polymerization, gels were either allowed to remain attached to the well or physically detached from the well and allowed to float freely in the culture media.

Measurement of Fibroblast-Induced Collagen Gel Deformation

For bulk deformation measurements during collagen gel contraction, black polystyrene beads (100 μm; DukeScientific Corporation, Fremont, CA) were first coated with collagen (50 μg/ml) for 48 h and then mixed into the gel solution described above prior to polymerization. After the polymerization was complete, half of the gels were dissociated from the walls of the well plate and half left attached. The gels containing beads were imaged at time zero, the undeformed configuration, and after 24 h, capturing the deformed configuration. Images were collected using a PULNiX progressive Scan TM-9701 camera with a Schneider-KREUZNACH XENOPLAN 1:10.14/11 telecentric lens directly connected to a computer and ImageAcqRR software. Calculation of displacement and approximate strains in the collagen gels during contraction was accomplished using the digital image correlation software Vic-2D^©(Correlated Solutions, Columbia, SC).

Staining of Collagen Gels for Confocal Microscopy

Collagen gels were fixed in 2% paraformaldehyde followed by rinsing in PBS (10 mM PBS, 0.138 M NaCl, 2.7 mM KCl, pH 7.4; Sigma). Cells were permeablized by treatment with PBS containing 0.1% Triton X-100 (Sigma) and 0.01 M glycine and subsequently blocked in PBS containing 1% bovine serum albumin (BSA). Alexa 488 phalloidin (Molecular Probes; Eugene, OR) diluted 1:100 in 1% BSA/PBS was added to the gels to visualize the actin cytoskeleton, and gels were incubated for 30 min and were extensively rinsed in PBS containing 0.01% sodium azide to remove unbound stain. Gels were mounted under gasket slides (EMS; Washington, PA) in DABCO and imaged using a Zeiss LSM 510 META confocal scanning laser microscope using an argon laser and a PlanNeoflaur 10× air objective (N.A. = 0.3) and a Achroplan 40× water immersion objective (N.A. = 0.8) at room temperature. During image acquisition the location of the image collected relative to the edge or center and direction (top, bottom, left, or right) of the gel was noted. Collagen was visualized directly by imaging in reflection mode [18] with the 40× water immersion objective.

Image Analysis—Cell Alignment

In order to quantify the degree of alignment resulting from gel contraction, a statistical analysis was performed on the lower magnification (10×) confocal images using software developed by the Cardiac Mechanics Research Group at the University of California, San Diego (http://cmrg.ucsd.edu). This software employs an automated gradient detection algorithm to scan digital images and develop local averages of trends in angular orientation within the image. Its output, in terms of circular statistics, provides a mean vector whose direction, θ,(‒ 90 ≤ θ ≤90), represents the mean orientation within the image and whose length, r, (0 ≤ r ≤ 1), is an indication of concentration about the mean, either a random distribution (r = 0) or a perfectly aligned sample (r = 1). If the data are sufficiently concentrated, (large r) about the mean direction (θ), this indicates that the cells exhibit alignment. The data on cell alignment are bimodal in the sense that the cells do not distinguish direction, only alignment, e.g. +90° is the same as ‒90°. The Pearson product moment correlation coefficient, a dimensionless index that ranges from [‒1.0 to 1.0], was used to calculate correlations between the mean angular alignment directions, as calculated from the UCSD software, and the circumferential direction recorded during imaging.

Image Analysis—Collagen Microstructure

The image analysis software NIH ImageJ–FracLac2.5 was used to assess two metrics associated with the cell– collagen microstructures: fractal dimension and lacunarity. Fractal dimension is a measure of the complexity of the image, based on its complexity as a self-similar structure. Self-similarity is a measure of the degree to which a structural pattern is preserved at all scales, i.e., a line cut up produces more lines, a square can be divided into self-similar smaller squares, ferns display smaller frond patterns at smaller and smaller scales, etc. The fractal dimension is generally defined as the ratio of the log of the number of self-similar pieces to the log of the magnification factor (which produced the smaller pieces). In the simplest cases a line has a fractal dimension of 1, a planar square of 2, and a cube of 3. A larger fractal dimension implies more complexity. The analysis in this work was done using the Standard Box Count option of the FracLac plugin, which calculates dimension by overlaying the image with a series of increasingly smaller square grids, and counting the number of grid squares required to cover the image at each step. The images were converted to grayscale by the ImageJ software and analyzed in this mode.

Lacunarity is a refinement to the classification of fractal. It characterizes texture of the fractal, specifically the presence and size distribution of holes, a “gappiness” property. Generally, an image with a large lacunarity has large spaces between elements, one with smaller lacunarity is more statistically homogeneous and it is somewhat more translationally invariant. Two images can have the same fractal dimension but different lacunarity.

Statistical Analysis

Significance testing was done using the Student’s t-test and an ANOVA test. Significant differences were obtained when P < 0.05. Box plots were used to illustrate the five numbers which summarize the statistical characterization;bars extend from the smallest observation to the largest observation, box top and bottom edges lie at the lower quartile and upper quartile lines, and the line within the box is the mean value.

Results

Gel Contraction

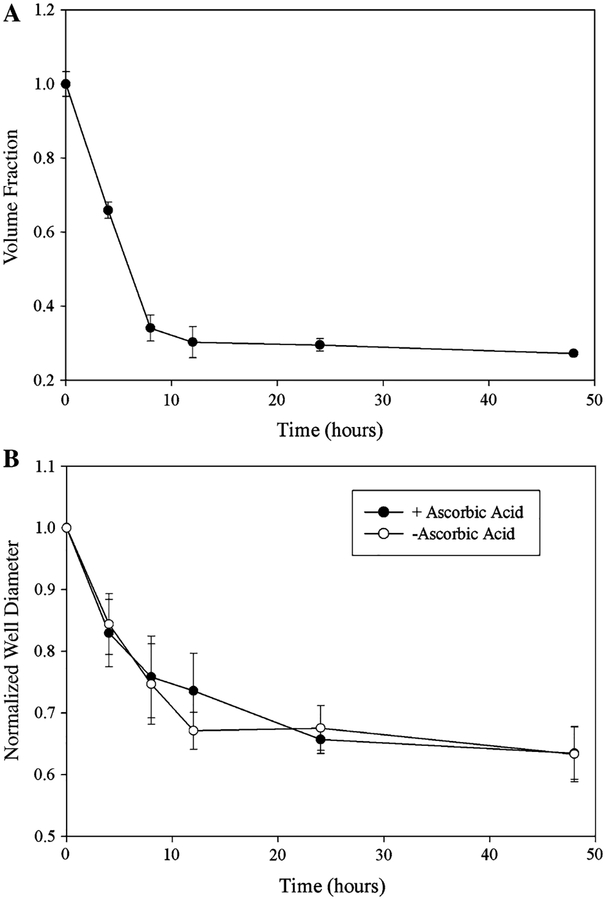
In this study, two global mechanical environments were considered: detached/floating gels and attached/constrained gels (Fig. 1). During polymerization collagen gels attach to the walls of polystyrene plates. Floating gels are the result of detaching the gels from well walls and bottom by running a pipette tip around and under the gel. Constrained gels remain attached to both well walls and bottom. Contraction of collagen gels by neonatal cardiac fibroblasts was monitored at multiple time points during the contraction process (0, 4, 8, 12, 24, and 48 h) by measuring the volumes of the gels and tracking changes in gel diameter. Figure 2 shows that over time, as the detached gels decrease in diameter, there is a corresponding decrease in gel volume. The most significant changes in detached gel volume (Fig. 2a) and diameter (Fig. 2b) occur in the first 12 h, whereas in the attached gels, there is no change in gel diameter throughout the entire time course of the study. The addition of ascorbic acid to culture media had little effect on the bulk gel contraction (Fig. 2b).

Fig. 1.

Collagen gel contraction assay. Collagen gels containing cardiac fibroblasts were polymerized and either remained attached to the walls of a 24-well plate (constrained; top row) or physically detached (free-floating in culture media; bottom row). The left column has images of gels taken 4 h after polymerization and the middle column are images after 24 h. Schematic in the right column illustrates a side-on view of the collagen gels within the well

Fig. 2.

Contraction of collagen gels by cardiac fibroblasts. (a) The volume of fibroblast populated collagen gels, as determined by the volume of buffer displaced by the gels, decreased throughout the course of the contraction with the most significant decreases occurring in the first 12 h. (b) Gel diameter also decreased during the observation period, paralleling observed volume changes, with the greatest decrease in gel diameter in the first 12 h. The addition of ascorbic acid, a cofactor necessary for the modification and assembly of collagen, to culture media did not alter the rate of gel contraction. Both figures represent an n = 3 gels from three independent experiments and error bars represent standard deviations

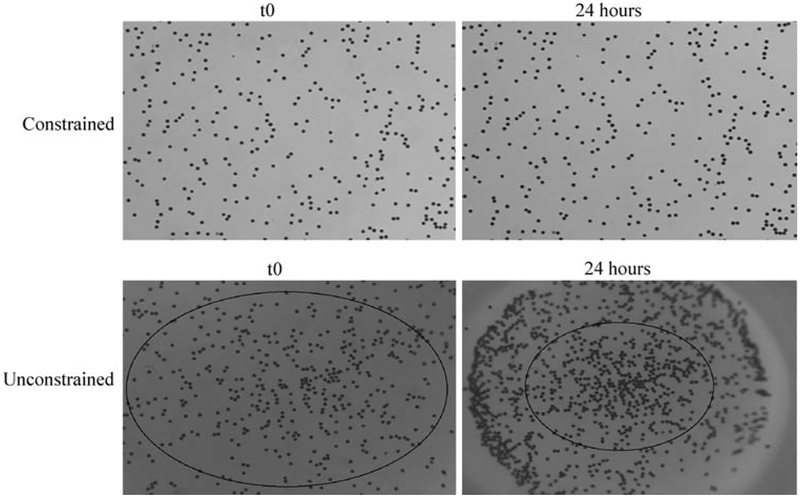
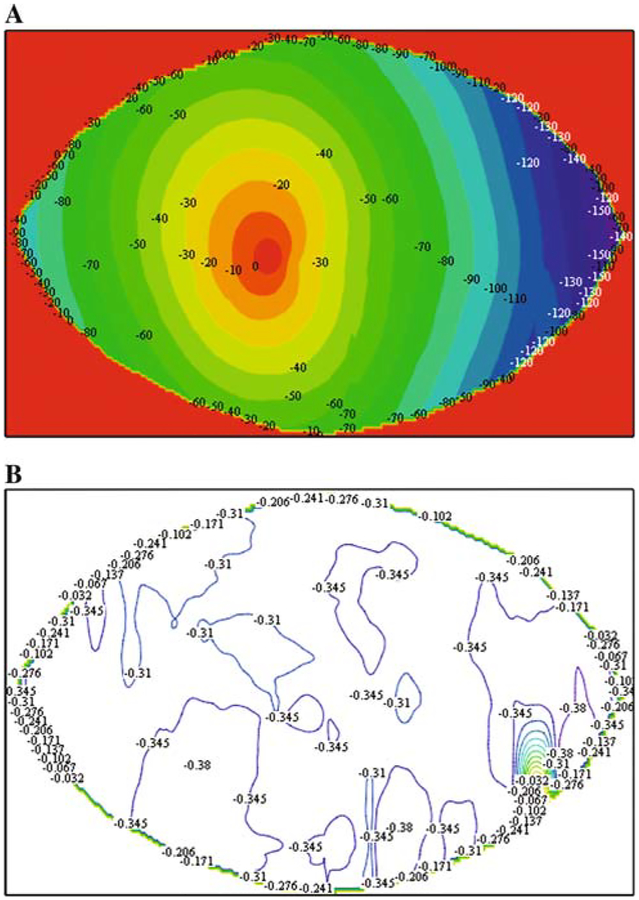
To mechanically characterize the bulk deformation of the collagen gels during the contraction process, polystyrene beads were embedded in attached and detached collagen gels as described above. Figure 3 shows the pattern of beads at time zero (after polymerization) and 24 h later in representative attached and detached gels. Due to the inability of the telecentric lens to zoom, images were collected from the centers of the gels. While the spatial distribution of beads remained essentially unchanged in attached gels (Fig. 3), the proximity of beads to one another decreased in the freely contracting gels (Fig. 3). Using Vic2D^©, the radial displacement and radial and circumferential strains were calculated using images collected before (undeformed; time zero) and after (deformed; 24 h) gel contraction. Figure 4a shows the associated radial displacement field and calculated strains for detached collagen gels. At this scale no circumferential displacement, which might be visualized as in-plane swirling or twisting, is apparent (i.e., a point initial at position (r, θ) moves to a position (r — dr, θ)). The radial displacement field is largely axisymmetric, independent of h. The radial strain, calculated as a gradient of displacement, predicts a relatively uniform strain field, as shown in Fig. 4b.

Fig. 3.

Determination of global collagen gel deformation by cardiac fibroblasts. Polystyrene beads were added to fibroblasts populated collagen gels prior to polymerization and imaged at t₀ (immediately after polymerization) or 24 h later. There is virtually no displacement of beads in constrained gels after 24 h (top right) compared to the significant displacement of beads observed in the unconstrained gel (bottom right)

Fig. 4.

Global displacement and strain fields in a contracting collagen gel. (a) Using Vic2D and images such as those shown in Fig. 3, the degree of bead displacement during gel contraction was calculated. This plot illustrates that displacement is greatest on the edges of the gel and lower, essentially zero, at the center of the gels. (b) Using Vic2D a strain map was calculated from the measured displacements; the strain field, strains are essentially a normalization with respect to the original distance between beads, are relatively uniform across the contracting collagen gels. The numerical approximation used to calculate strains from displacements results in some variations across the field

Cardiac Fibroblast Alignment

To examine fibroblast distribution within the collagen gels during contraction, gels were fixed, stained, and sub-sequently imaged at time zero—initially after the polymerization of the gels, and at 4, 8, 12, and 24 h. The planar images were selected at regions of densest cell population. Because, as shown in Fig. 2, the most significant deformation in the detached gels occurs by 8–12 h, with minimal changes after that time, the analysis focused on samples from the 8 and 12 h times. For analysis of cell alignment, images were collected at each time point from the center and edges of both attached and detached gels using a 10× objective.

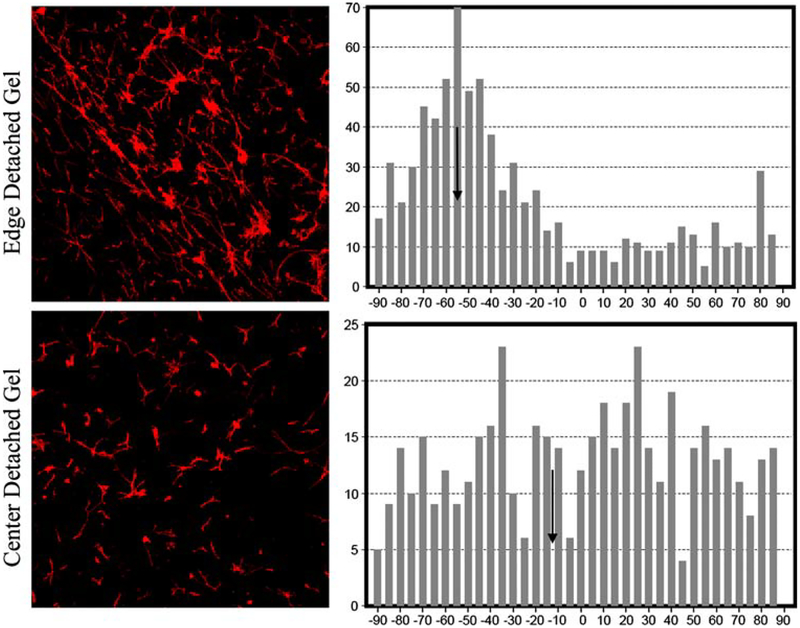
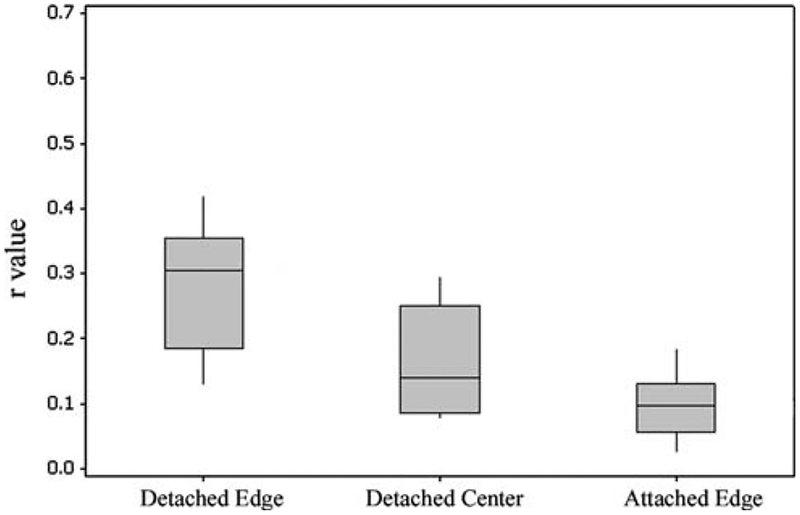
Deformation of the gels results in compaction of both the gel matrix and cells. In order to quantify the degree of cellular alignment resulting from this deformation, an automated statistical analysis (described above) was per-formed on the 10× confocal images. From the output a mean angular orientation θ and length r were calculated. Mean r values were calculated from images, taken at 8 and 12 h, of edge detached, center detached, and edge attached. Figure 5 shows patterns of cell alignment, and the corresponding histograms of alignment distributions, for representative edge and center cells in the detached gels. The cells in the top row (detached edge) have a measured r value of 0.421 with a mean angle θ = ‒55°; those on the bottom row (detached center) have an r value of 0.077 with a mean angle of θ = 11.5°, indicating less alignment in the gel’s central cell population. Similarly, the broader peak around the mean value (bottom row histogram) indicates less alignment. Box plots of r values for detached edge, detached center, and attached edge samples are shown in Fig. 6. Differences between mean r values of edge detached (0.303) and center detached (0.156) and edge detached (0.303) and edge attached (0.097) were significant (P < 0.05). The differences between the means of center detached (0.156) and edge attached (0.097) cell alignments were also significant (P < 0.05). Three-wayANOVA analysis indicates that all three means are significantly different. This suggests that the alignment of fibroblasts within contracting gels is affected by the position of the cells within the gel (edge versus center) as well as the mechanical environment of the gel (attached versus detached). Cardiac fibroblasts were most aligned at the edges of detached gels, least aligned at the edges of the attached gels.

Fig. 5.

Illustration of circular statistics used to analyze cell alignment. Cardiac fibroblasts were stained with Alexa488 phalloidin and confocal images collected. Representative images of 12 h detached gels illustrating two levels of alignment: Top row showing aligned cells from the edge (within 2 mm of the physical edge of the gel) of a detached gel r = 0.421 and bottom row cells from the center of a detached gel exhibit less alignment r = 0.077. Mean directions indicated by arrows inset on histogram; bars represent the number of cells with a given alignment. Narrower peak (upper histogram) around the mean indicates greater degree of alignment. Table 1 shows the results of this analysis for multiple time points using six gels per time point

Fig. 6.

Analysis of cell alignment. Mean values of length of alignment vector, r, compared for edge detached versus center detached, edge detached versus edge attached, and center detached versus edge attached. In all cases, the mean values are significantly different with P < 0.05. Each bar represents the analysis of between 2–3 images per gel with 3–6 gels per condition

Along the edges of detached gels, cardiac fibroblasts appear oriented along the circumference. To verify this observation, fibroblast alignment was correlated to the relative orientation of the image to the free edge of the gel. During image collection, the radial direction was recorded for each edge image and the corresponding circumferential direction for each image defined as the perpendicular to this direction. Table 1 shows the mean directions for six representative samples (n = 4, 2–3 images per gel), from each time point and the statistical correlation (1 is perfect positive correlation, 0 un-correlated) between alignment and the circumferential direction. As anticipated, a high degree of correlation was found between the alignment direction and the orientation of the circumferential edge of the gel. The lower correlation at the 4 h time point also suggests that the alignment increases with the level of contraction. As anticipated, a high degree of correlation was found between the alignment direction and the circumferential edge of the gel.

Table 1.

Correlation of angle alignment with circumferential direction (gel geometry)

A. Edge samples from detached gels	B. Calculated mean direction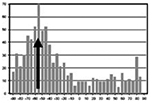	C. Corresponding circumferential θ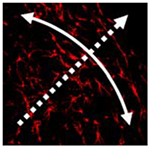	D. Correlation coefficient between columns B and C
4 h
1	6.69	0
2	−24.46	90
3	23.43	45
4	87.34	90
5	−8.51	0
6	−47.82	−45	0.76
8 h
1	−76.67	−90
2	68.18	45
3	−58.01	−45
4	−30.91	−45
5	78.39	90
6	53.4	45	0.98
12 h
1	−51.34	−45
2	−55.14	−45
3	−62.22	−90
4	89.98	90
5	−72.42	−67.5
6	−72.42	−22.5	0.92
24 h
1	−76.54	−90
2	−54.19	−90
3	−53.3	−45
4	3.89	0
5	54.2	45
6	58.98	67.5	0.97

Note: Based on the mean alignment direction of six samples from each time point (data are representative of n = 4, 2–3 images per gel.), statistical correlations coefficients were calculated of cellular alignment with circumferential (gel perimeter) direction along gel edge. A value of 1 is perfect positive correlation, 0 indicates uncorrelated

Cardiac Fibroblast Morphology

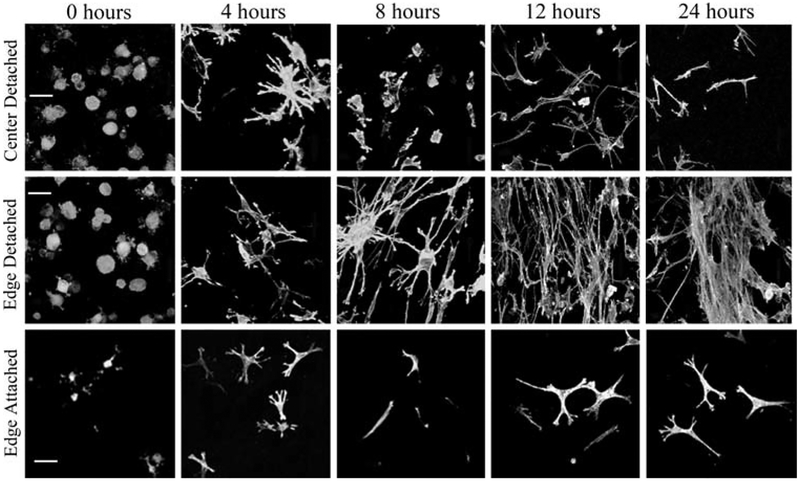
To examine changes in cardiac fibroblast morphology during compaction of the gel, 10 × confocal images were collected using confocal microscopy to show the distribution of the cells fluorescently stained with Alexa488 phalloidin. Figure 7 shows the evolution of cell morphology over time at the edges and in the center of the detached contracting gels. At time zero, immediately following polymerization when the gels are disassociated from the well walls, all cells, regardless of location within the gel, exhibited a rounded morphology. Fibroblasts located on the edges of detached gels adopt a dendritic morphology by 4 h of matrix compaction, which transitions into a bipolar morphology by 8 h. This bipolar morphology is maintained by the cells during continued compaction of the collagen gel. These cells are largely parallel to the freely contracting edge of the collagen gel. In contrast, fibroblasts located in the center of a detached gel have a mixed morphology with initially both bipolar and dendritic shapes observed; however, the bipolar morphology appears to dominate. From 8 to 12 h, fibroblasts exhibit a dendritic shape which by 24 h has become bipolar, similar to what was observed in cells located at the edge of detached gels at this time. Fibroblasts located at the edge of attached gels are morphologically similar to cells located in the center of detached gels in that a mixture of dendritic and bipolar cells is present 4 h into the compaction process. However, in these cultures, the dendritic morphology again dominates. After 8 h in culture, the bipolar phenotype dominates but is replaced by dendritic-shaped cells by 12 h in culture and this phenotype is maintained at 24 h.

Fig. 7.

Cardiac fibroblast morphology during collagen gel contraction. Representative confocal Z-series collected with a 40 × objective of fibroblasts in contracting collagen gels illustrating that cardiac fibroblast morphology changes with time and position in the gel. Columns (left-right) are t₀,4 h, 8 h, 12 h, and 24 h. Rows are (top) center detached, (middle) edge detached, and (bottom) edge attached. Cells along detached edges show alignment, increased density, and elongated phenotype of the cells. Cells in the center of the gels show a more random orientation. Scale bar = 100 μm

Collagen Organization

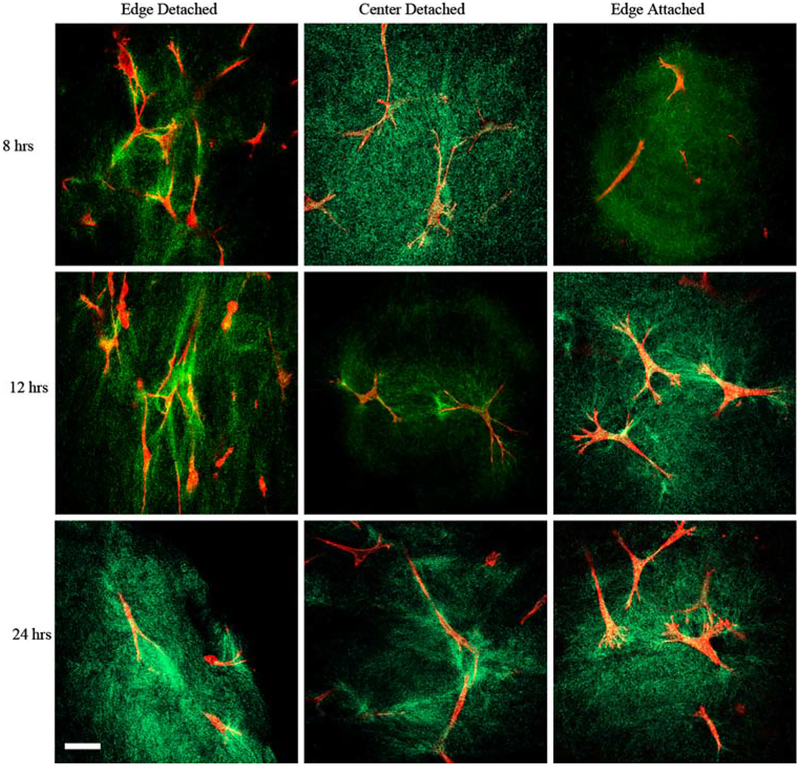
High magnification images (40×), using fluorescence (for cells) and reflection (for collagen), offer visual evidence of the difference in the cell–collagen microstructure along the edges of the contracting and constrained gels (representative images shown in Fig. 8). Specifically, within the 8–24 h time frame of the contracting gels, after most of the contraction is finished, visual inspection suggests that the collagen is aligned with the long axis of the cells. In contrast, in attached gels from the same time period, the collagen appears radially aligned around the edges of the cells. Within these attached gels, the collagen has a more uniform density in appearance and collagen links between cells are in evidence, but no preferential directional orientation of the collagen is observed. The detached gels often had uneven densities of collagen and collagen alignment appears to be influenced more by the deformation of compaction than cell–cell connections. Cell–collagen images from the center of the detached gels did not appear to show collagen aligned with the cells and the collagen often displayed a semi-radial arrangement around the cell boundary, similar to that seen in the attached gels, but they also showed the uneven density seemingly more characteristic of the edges of detached gels.

Fig. 8.

Confocal reflection microscopy of collagen in compacting collagen gels. High magnification (40 ×) confocal images of fluorescence (cells) and reflection (collagen). Representative images from 8 to 24 h range, columns (left-right)—edge detached, center detached, and edge attached. Alignment of collagen with cells is visible in images of cells at detached edge. Radial organization around cell boundary is clearly seen in images of the attached edges. Collagen surrounding cells in the center of detached gels exhibits radial organization. Scale bar = 1 μm

Quantitatively it was possible to distinguish between the cell–collagen microstructure based on image analysis of the fractal dimension and lacunarity using the NIH ImageJ software FracLac. The fractal dimension was not significantly different between the edges and centers of detached gels (2.83 ± 0.030 versus 2.84 ± 0.024). When comparing the edges or centers of the detached gels to edges of attached gels, however, a significant difference in the fractal dimension was observed. In Fig. 8, representative images from 8, 12, and 24 h, edge detached, center detached, and edge attached gels are shown. The average fractal dimension was larger from the detached gel samples, on average 2.83 ± 0.013, whereas a lower average fractal dimension of 2.77 ± 0.030 was calculated for the attached gel edges (P < 0.005). The narrow spread of the data in both instances implies that the values are distinct as well as statistically significantly different. Since the fractal dimension of surfaces is usually assumed to lie in the range between 2 and 3 [19], it might be argued that the relatively small difference between these fractal dimensions, although they do not overlap, does not indicate a dramatic difference in architecture.

The lacunarity was larger in the edge detached gel images, on average 0.088 ± 0.032, than in the center detached gels0.065 ± 0.022, again distinct values, but in this case not significantly different. The attached gels showed greater lacunarity, significantly different (P < 0.01) from both the detached gel regions on average 0.146 ± 0.032. These values suggest that the detached gels show fewer holes than the attached gels, which is likely due to the increasing density of cells and collagen resulting as the gel contracts.

Discussion

The 3D collagen gel model has long been used to investigate how cells respond to their extracellular environment under a variety of biological conditions. It has been demonstrated that the ability to contract and remodel collagen matrices is independent of proliferative capability [20] and can be influenced by a number of growth factors [21]. With respect to mechanical factors, the 3D environment provides more in vivo like interactions between cells and the collagen and departs from a 2D system, which, since it provides a rigid support for cells, alters how they perceive their local mechanical environment [22].

The cell-mediated contraction of the detached gels represents a fairly rapid mechanical event, with the most significant change in gel diameter occurring within the first 12 h and maximal contraction reached within 24 h. The physical decrease in gel diameter is matched by a decrease in volume, indicating that contraction occurs as least in part by exclusion of fluid from the collagen matrix. The two models, attached versus detached, can be distinguished mechanically by using simple models, i.e., if it is assumed that the endogenous traction forces of the cells are the same under both conditions and that the gel/cell material is statistically homogeneous (homogeneous over a large scale), then the attached gels can be described as strain free. Large-scale deformation is prevented by a balance between the endogenous traction forces of the cells and the constraining force of the fixed boundary. Cells in this situation develop an equilibrium balance of isometric tension. In contrast, at the global level, the detached gels can be described as stress free. The contraction (deformation) is not being resisted, until a limiting, optimal or incompressible density is reached, and so no stress results. In a homogeneous material the strain would be uniform at all scales. In reality, it is possible that local variations and inhomogeneities may be significant, but this serves as a general classification.

In the data presented here, these macroscale displacements vary linearly as a function of radial position throughout the detached gels as evidenced by the displacement of marker beads used to monitor the bulk contraction. Displacements are largest at the outer edge and decrease toward the center of the gel. Normalization of this displacement by the original distance between beads demonstrates that the result is a relatively uniform strain field (gradients of displacement) throughout the plane of the contracting gel.

This suggests two distinguishable regimes in the mechanical environment within the contracting gel model: edge and center. Near the edge of contracting gels, cell traction forces are sufficient to deform the gel and pull the gel edge radially inward. The edge is unattached and the cells are near the interface of the gel and the media solution, therefore it would be relatively easy to ‘squeeze’ the interstitial fluid out of the gel and contract the collagen network without a significant build-up of hydrostatic pressure. In the center of the detached gels there is significantly more gel material to shift, representing an inertia mass component, which would more successfully resist the same magnitude of cell traction forces than the unconstrained collagen network at the edge of the gel. Additionally, attempts to contract the gel in this region may encounter an increased pressure due to compression of the interstitial fluid, which may not easily flow out of the gel. In a pure radial displacement field with no rigid body motion (translational shifts), a center position would experience no displacement. With respect to displacement fields this is a mechanical environment similar to that of the cells in an attached gel at all radial distances from the center. So, in addition to classifying the two systems by their idealized mechanical zero stress or zero strain fields, a distinction can also be made within the zero stress model (detached) as to magnitudes of displacements, i.e., displacement of the edge or in the center and a comparison drawn between the centers of detached gels and the zero strain model (attached gels).

Dermal fibroblasts have been shown to orient themselves within thin collagen films in a process that appeared to depend upon film geometry and cell density [23]. In rectangular films, cells aligned parallel to the long axis of the film, whereas in attached circular and square films the cells were more randomly oriented. In thin collagen films with free edges, cells aligned parallel to the free edge, an alignment mirrored by collagen orientation. In contrast, another study using dermal fibroblasts found that cells were randomly oriented within a fully attached square gel but displayed a significant alignment at the free edges compared to cells in the center of these gels [4]. The use of 3D, fibrin microspheres has demonstrated that the initial position of a fibroblast within the matrix can effect the alignment of the cells within the matrix [24]. Dermal fibroblasts uniformly distributed throughout the sphere exhibited a random orientation, whereas cells located in the outer shell of concentric microspheres align circumferentially after compaction while cells originally embedded in the center of the microsphere adopt a radial alignment. In the absence of compaction, fibroblasts embedded in the outer shell of the concentric spheres maintained their initial random orientation. The production of a contact guidance field, due to the alignment of fibers during the compaction process, is largely responsible for the observed preferential orientations of fibroblasts observed in contracting models [25]. Studies of embryonic chicken fibroblast cultured in collagen membranes have also shown preferential cell alignment, again along the free edge of the membrane, and suggest that this alignment is a result of cells responding to the greatest resistance to cell traction/spreading whereas cells in the center of the membranes perceive uniform resistance to cell spreading and randomly orient themselves [26].

The studies described herein observed similar behavior of cardiac fibroblasts in 3D collagen gels. Cardiac fibroblasts at the edges of a detached collagen gel, where the matrix deformation as well as the resistance to cell spreading is the greatest, orient parallel to the freely contracting edge. Cells in the center of detached gels, which experience little or no displacement, display no preferential orientation. The ability of cells to orient themselves appears to depend less on the strain, which in the case presented here was shown to be relatively uniform, than upon the absolute position of the cells relative to the contracting edge of the gel, i.e. displacement. When collagen gels were constrained at the edges and allowed to contract in the z-direction, therefore becoming thinner but maintaining their original diameter, dermal fibroblasts oriented in radial and circumferential directions [27], behavior which was later recapitulated in a model of adherent collagen gels [25]. This model, however, does not describe the orientation of cells within contracting gels. This observed orientation of dermal fibroblasts is in contrast to the orientation of the cardiac fibroblasts observed in attached collagen gels in this work, which were randomly oriented at the constrained edge. Unlike the previous study, the attached collagen gels used in this study were constrained on all but their upper surface, therefore little change in gel thickness was observed. These observed differences between dermal and cardiac fibroblast behavior may represent a true variation in response from cells representing different in vivo environments or may be due to differences in the experimental environment.

Previous work has established that the most significant differences between cell morphologies in floating versus constrained cell populated collagen gels are the initial appearance of dendritic cell extensions in the former [28, 29]. It has been hypothesized that these dendritic configurations correspond to mechanisms associated with motility, and while they do not result in focal adhesions, they may translocate the surrounding collagen fibrils. Grinnell and collaborators [21, 28, 30] have identified two cell morphologies that can be linked to the constrained and unconstrained systems, respectively: stellate (star shaped) or bipolar (cells with two principle extensions, i.e. bar-like shape) forms, characteristic of the taut, braced cells in isometric tension within constrained gels and cells with dendritic extensional networks, usually associated with cell motility and initially present in unconstrained gels. In order to initiate contraction, cells in detached gels develop more stellate/bipolar configurations, which result in focal adhesions and allow the cells to contract the collagen. In constrained gels the cells rapidly adopt stellate/bipolar shapes, associated with focal adhesions and indicative of a state of isometric tension. Initially the cardiac fibroblasts also developed fairly obvious dendritic configurations in the edge cells of the detached gels, fewer in the center cells, and virtually none in the attached gels. The morphology of the center detached cells were more like the edge cells observed in the attached gels, which established, and maintained, strongly defined stellar shapes early in the time line.

The collagen network in the center of the gel may not be constitutively stiffer—in the sense of different intrinsic material properties that are the result of differences in density or microstructural anisotropy, but cells at the center may perceive a greater apparent stiffness characterized by how difficult the gel is to deform. If the cells encounter sufficient resistive force then their local environment may be less distinguishable from that of cells in a constrained gel. In this case they may be able to establish isometric tension, which is generally assumed to result in stellate or bipolar shapes. Physics suggests that eventually the contraction of the gel will be large enough that the cell traction forces will not be able to compress the collagen network further and the edge cells would also establish some level of isometric tension, although the geometry of the packing arrangement, which occurs with contraction, may be the dominating factor defining their morphology. Cell geometries along the edges and the centers of gels may also evolve subsequent to the completed contraction.

The idea of a perceived apparent stiffness can also be applied to evaluations of the alignment of the edge cells. Cells in populations, not single cells but at scales below bulk tissue, have been observed to align their long axis along lines of greatest tension [4]. Edge cells in contracting gels, testing the apparent stiffness in radial and circumferential directions (corresponding to the geometry of the circular gels), would assess the circumferential stiffness as greater than the radial stiffness. Cell forces applied in the circumferential direction would encounter a resistive force, whereas cell forces applied in the radial direction would encounter less resistance from the unattached edge and are able to shift the gel matrix easily, an apparently less stiff direction. It would, therefore, be expected that the cells would align circumferentially, as observed in this work.

The fractal dimension as well as the lacunarity of the cell–collagen microstructure, likely dominated by the architecture of the collagen, is distinguishably different between the detached and attached gels, exhibiting significantly different fractal dimensions (higher in detached gels) and significantly different lacunarity (lower in detached gels), i.e., more complexity and fewer gaps. While it is difficult to specifically quantify geometric components that may contribute equally to fractal dimension, a measure of complexity as defined by self-similarity, the architecture of the collagen network in the detached gels is evolving due to two mechanisms, the physical compaction due to the contraction as well as the local rearrangement of collagen by the cells. Therefore it would be expected then that the resulting architecture of the detached gels would be more complex than that of the attached gel. With respect to lacunarity, the “fewer” holes characterization of the detached gels as compared to the attached gels also makes intuitive sense. Image analysis, however, was not able to distinguish between the two suggested regimes in the detached gels—edges and centers.

With respect to alignment, collagen fibers associated with cells in the edges of detached gels were observed to be strongly aligned with the cells; organized in the circumferential direction corresponding to the perceived “stiffer” direction. The radial contraction of the gel contributes to this effect, but collagen alignment is apparent even at early stages and in regions where the cells are not densely packed due to contraction. Cells at the center of detached gels and along the edges of the attached gels exhibit visual similarities with respect to how the collagen fibers are aligned along the plane of view. Both show collagen fibers organized radially around the cell with denser collagen regions between neighboring cells. This again suggests more firmly anchored, tethered cells; the collagen following/or supporting the cell generated radial isometric tensile forces.

The architecture of cell–collagen gels functions at the bulk level of the gel as a structural entity, and at the cell level as a means of providing anchorage and facilitating cell–cell interactions. As an adaptive system its evolving multi-scale design must be based on assessment by the cells of their environment; certainly biochemical signals and built-in cellular functions are significant factors, however, it is apparent that local mechanical environments also play a key role in triggering or facilitating these adaptive processes. Contraction of collagen gels by cardiac fibroblasts will, over time, result in a stiffer, more compacted, collagen network, change the proximity of cells to one another, and allow cells to establish taut anchorages to the collagen network. If the fibroblasts cannot contract the surrounding matrix, firm anchorages will develop earlier, cell connections may need to be facilitated more by migration, than deformation, and the density of the collagen will be influenced more by additional collagen production and deposition. Under either condition cells respond with differing morphologies and differing organization of their surrounding collagen. This suggests a large potential impact for relatively subtle changes in the mechanical environment to be used as tools for modulating collagen remodeling during scar formation, such as after a myocardial infarction, or tissue engineering strategies.