Abstract
Gamma oscillations are readily observed in a variety of brain regions during both waking and sleeping states. Computational models of gamma oscillations typically involve simulations of large networks of synaptically coupled spiking units. These networks can exhibit strongly synchronized gamma behavior, whereby neurons fire in near synchrony on every cycle, or weakly modulated gamma behavior, corresponding to stochastic, sparse firing of the individual units on each cycle of the population gamma rhythm. These spiking models offer valuable biophysical descriptions of gamma oscillations; however, because they involve many individual neuronal units they are limited in their ability to communicate general network-level dynamics. Here we demonstrate that few-variable firing rate models with established synaptic timescales can account for both strongly synchronized and weakly modulated gamma oscillations. These models go beyond the classical formulations of rate models by including at least two dynamic variables per population: firing rate and synaptic activation. The models’ flexibility to capture the broad range of gamma behavior depends directly on the timescales that represent recruitment of the excitatory and inhibitory firing rates. In particular, we find that weakly modulated gamma oscillations occur robustly when the recruitment timescale of inhibition is faster than that of excitation. We present our findings by using an extended Wilson-Cowan model and a rate model derived from a network of quadratic integrate-and-fire neurons. These biophysical rate models capture the range of weakly modulated and coherent gamma oscillations observed in spiking network models, while additionally allowing for greater tractability and systems analysis.
NEW & NOTEWORTHY Here we develop simple and tractable models of gamma oscillations, a dynamic feature observed throughout much of the brain with significant correlates to behavior and cognitive performance in a variety of experimental contexts. Our models depend on only a few dynamic variables per population, but despite this they qualitatively capture features observed in previous biophysical models of gamma oscillations that involve many individual spiking units.
Keywords: gamma oscillations, rate model, Wilson-Cowan model
INTRODUCTION
Gamma oscillations (30–120 Hz) are a prominent feature of local field potential recordings from awake mammals, with correlates to visual perception (Fries 2009; Gray and Singer 1989; Taylor et al. 2005), audition (Haenschel et al. 2000), olfaction (Freeman 1978), motor control (Schoffelen et al. 2005), and learning and memory (Bieri et al. 2014; Colgin et al. 2009; Dvorak et al. 2018). There is a great deal of experimental work suggesting that inhibition plays a crucial role in gamma oscillations (Bartos et al. 2007; Traub et al. 2001, 2004), supporting early hypotheses (Dunin-Barkowski 1978; Freeman 1975). Numerous theoretical studies of large networks of coupled, spiking neuronal units have provided basic understanding and insights into how the dynamics of inhibition plays a synchronizing role and how the inhibitory timescale regulates the gamma frequency (Börgers and Kopell 2003; Brunel and Wang 2003; Gerstner 2000; Whittington et al. 2000), but these many-unit models do not lend themselves to easy analysis as few-variable mean-field models do. Although mean-field firing rate models were developed in general settings (Dafilis et al. 2009; Ledoux and Brunel 2011; Wilson and Cowan 1972) and for particular applications (Jansen and Rit 1995), they are not often specifically designed to describe gamma oscillations. In part, this is because these formulations typically do not explicitly represent synaptic dynamics. The classic Wilson-Cowan model has a single firing rate variable for each population (Wilson and Cowan 1972). Furthermore, gamma rhythms that involve strongly synchronized epochs of excitatory spiking events (Buzsáki and Wang 2012; Kopell et al. 2010; Wang 2010) would violate the assumption of asynchronous firing present in mean-field reductions. Here we present a mean-field model that overcomes these limitations by including an additional variable for synaptic activation. These models are able to capture epochs of tight synchrony and explicitly represent synaptic dynamics in their formulation.
Spiking models of gamma oscillations have typically been studied in specific regimes. Here we highlight two. In the first, the strong-synchrony regime, individual neuronal units align temporally with the network rhythm and fire on nearly every cycle, with silence between these population events (Kopell et al. 2010; Wang and Buzsáki 1996; Whittington et al. 2000). In the second, the weakly modulated regime, gamma cycling is apparent at the population level but neurons exhibit fractional participation on each cycle (Brunel and Hakim 1999, 2008; Tikidji-Hamburyan et al. 2015) and fire at a lower overall rate than the network rhythm. These models of weakly modulated gamma can either show little neural activity between the pulsatile-like firing epochs in each cycle (Brunel and Hakim 2008) or show firing probability modestly fluctuating about a mean firing rate (Brunel and Hakim 1999; Brunel and Wang 2003; Tikidji-Hamburyan et al. 2015). In the weakly modulated regime, these spiking network models account for features of gamma observed in vivo, with neurons firing sparsely with loose phase-locking to the network gamma rhythm (Fujisawa et al. 2008; Greenberg et al. 2008; Tukker et al. 2007).
Analyses of these spiking network models typically describe transitions into and out of oscillatory states, along with how different neuronal subtypes may impact the robustness of these oscillations (Brunel 2000; Brunel and Hansel 2006; Brunel and Wang 2003; Hansel and Mato 2003; Tikidji-Hamburyan et al. 2015; Wallace et al. 2011; Zillmer et al. 2009). Importantly, gamma oscillations observed in vivo are categorized by a broad gamma band (Bragin et al. 1995). This feature is much more readily described by stochastic spiking gamma models and suggests that at the onset of a gamma oscillation the amplitude is small.
Another categorization of spiking gamma models is according to whether or not the excitatory population is necessary for the oscillatory behavior. In the strongly synchronized regime that depends on the excitatory population [so-called PING (pyramidal interneuron network gamma)] (Börgers and Kopell 2003; Whittington et al. 2000), a brief epoch of excitation recruits inhibition that in turn silences the network until the inhibitory conductance subsides and the excitatory units (assumed to be intrinsically oscillatory) fire again, initiating the next cycle. Alternatively, without excitation, an inhibitory-only spiking network model can generate near-synchronous gamma [so-called ING (interneuron network gamma)] (Traub et al. 2004; Wang and Buzsáki 1996; Whittington et al. 2000). This is somewhat counterintuitive behavior, as one may expect inhibition to produce clusters that fire in antiphase. Synchrony through mutual inhibition occurs if synaptic inhibition decays slowly (to set the timescale of cycling) and rises sufficiently slowly or with an explicit delay (see Van Vreeswijk et al. 1994; Wang and Rinzel 1992). Although it is unclear whether exhibitory (E)-inhibitory (I)-based or I-I-based gamma mechanisms play a more important role in in vivo recordings (Bartos et al. Jonas 2007; Le Van Quyen et al. 2016; Tiesinga and Sejnowski 2009; Whittington and Traub 2003), we focus on the former in this article.
In this article, we show that few-variable rate models, with dynamical variables for firing rate and for synaptic activation, can generate E-I gamma oscillations and capture features of spiking network models including both strongly synchronized and weakly modulated regimes. We consider two different frameworks: a Wilson-Cowan-like formulation with intuitive appeal and ad hoc plausibility (Keeley et al. 2017) and a rate formulation with exact correspondence to a network of heterogeneous quadratic integrate-and-fire (QIF) units (Coombes and Byrne 2019; Laing 2017; Luke et al. 2013; Montbrió et al. 2015). In each framework, the two gamma regimes can be tuned in by adjusting the timescales for the firing rate dynamics; weakly modulated network gamma is found when the firing rate of the inhibitory population is recruited faster than that of the excitatory population, and strongly synchronized gamma oscillations are seen for the reverse. In both frameworks, network oscillations arise when a steady state loses stability via Hopf bifurcation as drive to the excitatory population increases. The small-amplitude oscillation that emerges from the bifurcation persists over a substantial range of values of the drive in the weakly modulated regime, but for the strongly synchronous case the oscillation amplitude rises sharply to become a strongly synchronous E-I rhythm as drive increases. We compare the rate model dynamics for the macroscopic (mean field) variables to averaged quantities from spiking networks and suggest that some dynamical features and insights from the rate models can be extended to spiking network models of excitatory and inhibitory populations.
RATE MODEL WITH SYNAPTIC DYNAMICS
First, we propose a two-population rate model with an excitatory and an inhibitory population. This general form contains essential components to demonstrate an E-I-based gamma oscillation (Whittington et al. 2000), i.e., an excitatory and an inhibitory population reciprocally connected, with E-E self-connectivity in the excitatory population and external drives IE and II provided to the respective populations. The dynamic model is formulated in the following expressions:
| (1) |
| (2) |
Here, each population is described by a firing rate variable ra(t) and a synaptic variable sa(t), where a = {E,I}. The synaptic activity is driven by the population firing rate, scaled by a parameter γa, saturating at a value of 1, and with synaptic decay time constant and background synaptic drive . Note that the synaptic rise time constant is given by /γa. The time-varying rate is a function of synaptic connectivity weights wab (where a and b = {E,I}) and a sigmoidal nonlinearity f. As is customary in neural population models, we neglect possible differences for synaptic activation dynamics onto self- or cross-population targets. That is, sI is not different for inhibitory inputs to excitatory and inhibitory cells; only the weights differ (Brunel and Wang 2003; Hansel and Mato 2003; Kopell et al. 2010).
Typically, E-I gamma oscillations are synchronized by the inhibitory population (Van Vreeswijk et al. 1994), which is true for spiking models as well as our rate model. An example raster plot of a simple leaky integrate-and-fire (LIF) stochastic E-I spiking network is shown alongside a given trajectory for our rate model (Fig. 1). Here, because of sparse connectivity and noisy upstream inputs, the participation of neurons is random within each cycle of the oscillation. This is in contrast to other models where neurons spike on every cycle (Kopell et al. 2010; Whittington et al. 2000).
Fig. 1.
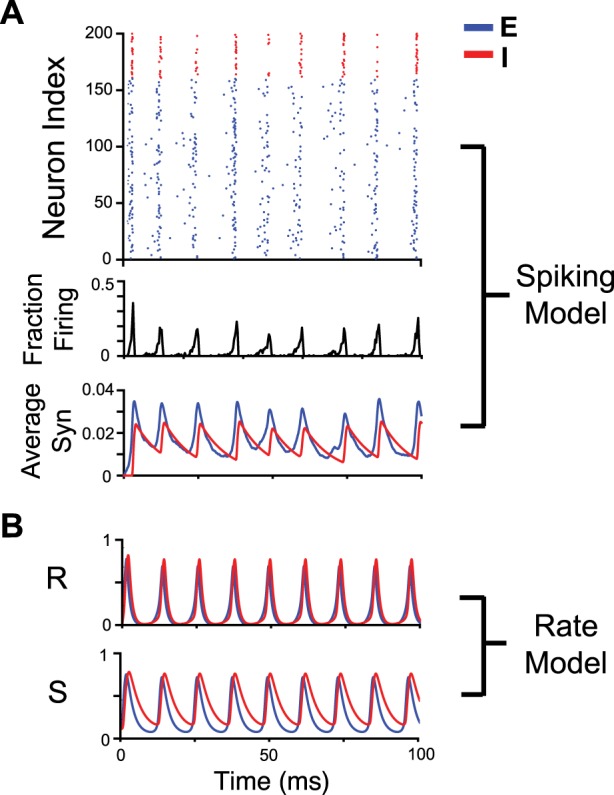
Stochastic spiking excitatory (E)-inhibitory (I) oscillatory model with fractional participation of neurons alongside time courses of the synaptic and rate variables of an E-I rate model. A, top: raster plot of 200 leaky integrate-and-fire neurons (160 excitatory and 40 inhibitory). The network received excitatory input from upstream Poisson spiking units. Bottom: histogram of spiking from all units and average synaptic activity averaged for excitatory and inhibitory populations. B: rate (r) and synaptic (s) dynamic variables from an E-I rate model with parameters tuned to match that of the spiking model. Note how the rate variable and spiking histogram demonstrates fractional participation of neurons for each cycle in the oscillation. Network rate exhibits more sharp peaks than synaptic activity for both rate and spiking models.
The average time course of the synaptic activity averaged across all units in the network and the histogram of the number of cells spiking at each moment in time (bin width 0.8 ms) qualitatively correspond to the rate and synaptic time courses of the idealized E-I gamma rate model. The relative peakiness of the rate variable and the relative smoothness of the synaptic variable capture the actual dynamics of the spiking stochastic oscillator model. Both of these models easily exhibit rhythmic activity at gamma frequencies for reasonable parameter choices (for more details on rate model parameter choices, see appendix).
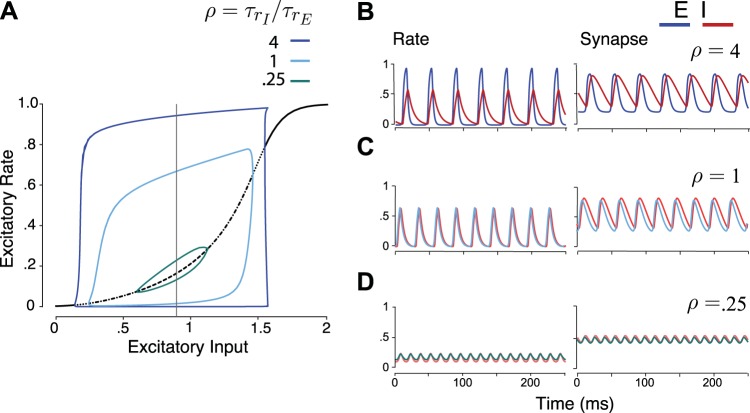
This rate model’s oscillation properties can be examined through an exploration of the bifurcations of the system. Here we visualize this by increasing the input parameter, IE, and plotting the solution of the excitatory rate variable, rE (Fig. 2A). Given sufficiently strong connectivity weights, the model exhibits a Hopf bifurcation at a certain threshold of input to the excitatory population, indicating the onset of an oscillatory solution. For synaptic and rate timescales on the order of a few milliseconds, the period of this oscillation corresponds to realistic gamma oscillation values.
Fig. 2.
Bifurcation diagram and respective time courses of an excitatory (E)-inhibitory (I) rate model, for 3 values of the ratio of rate timescales for the E and I populations. A: bifurcation plots of the 4-variable E-I gamma model (Eqs. 1 and 2) showing the rate variable rE of the excitatory population vs. excitatory input, IE. Steady-state rate (black) is flanked by maximum and minimum amplitudes of oscillation. The steady state transitions from stable (solid) to unstable for different ratios of time constants, ; ρ = 0.25 (dotted), ρ = 1 (dot-dashed), ρ = 4 (dashed). Thin vertical black line corresponds to input value (IE = 0.9) for example time traces. Colors illustrate oscillation amplitude profiles for varying ρ. The time constant values are = 8 ms and = 2 ms (ρ = 0.25), = = 5 ms (ρ = 1), and = 2 ms and = 8 ms (ρ = 4) for the E and I rate variables with the synaptic timescales fixed to 3 ms (E) and 10 ms (I). The oscillation amplitude near onset changes more abruptly as ρ increases, i.e., the inhibitory rate timescale becomes larger than the excitatory rate timescale. B–D: example time courses for IE = 0.9 (thin vertical black line in A) for both rate and synapse variables. Oscillation becomes more PING-like as the ratio of inhibitory to excitatory rate timescales increases.
Because there are four relevant timescales to the system (2 per population), for illustrative purposes we hold the synaptic timescales fixed to biophysically plausible values (3 ms for the E synapses and 10 ms for the I synapses) (Angulo et al. 1999; Bartos et al. 2001) and examine the bifurcations as we vary the ratio of the firing rate timescales, . The sum of the rate timescales was fixed ( + = 10 ms) to counteract the effect of timescale increases on the population firing frequency, i.e., increasing will increase the frequency, but decreasing will slow it down. For a variety of ρ values, the system moves from a stable steady state to an unstable steady state flanked by a stable oscillatory attractor. The amplitude profile of this oscillation is noted by blue lines in Fig. 2A. This bifurcation amplitude profile becomes more steeply modulated as we increase the timescale of the inhibitory population relative to the timescale of the excitatory population (i.e., increase ρ). For large ρ, the system behaves as a strongly synchronized, pulsatile oscillator (Fig. 2B). The firing rate of the E population rises sharply and quickly, recruiting the I population, which then silences the E population. These sharply synchronous events are akin to PING-like gamma oscillations. For smaller ρ, the E and I populations begin to align their phases and the E population becomes less tightly aligned to the population rhythm (Fig. 2C). For very small ρ, the system oscillates with a small amplitude around some mean firing rate (Fig. 2D). This mean fluctuation around the steady firing rate is akin to stochastic oscillator spiking models (Brunel and Hakim 2008; Brunel and Wang 2003). Oscillations for these parameter choices are in the gamma range, with values of 27 Hz, 37 Hz, and 68 Hz for values of ρ = 4, 1, and 0.25, respectively. Interestingly, interneurons thought to participate in gamma exhibit fast rate responses (Hasenstaub et al. 2016), as is the case for small ρ values in our model.
We note also that if we vary the synaptic timescales the extent to which the oscillatory amplitude increases at bifurcation depends on the extent to which both the inhibitory timescales are larger than excitatory timescales. That is, oscillations become more PING-like if inhibitory synapses are further slowed down with respect to excitatory synapses and less PING-like if synaptic timescales are brought together (not shown). For simplicity and because of known biological properties (Angulo et al. 1999; Bartos et al. 2001), we keep synaptic timescales constant for our demonstrations and vary only the ratio of the rate timescales. To understand the approximate overall dynamics (rate and synapse) per population, it is possible to linearize about the steady state and examine the eigenvalues of the population (see appendix).
RATE MODEL DERIVED FROM A SPIKING NETWORK
Recent advances in the field of self-organized systems have led to the derivation of an exact mean-field reduction for a network of θ neurons (Laing 2014; Luke et al. 2013). In general, this approach can be applied to any spiking neuron model where the synaptic coupling function is a sinusoidal function of the oscillator’s phase (Ashwin et al. 2016; Montbrió et al. 2015). Byrne and Coombes (Byrne et al. 2017; Coombes and Byrne 2019) demonstrated that a network of QIF neurons of the form
| (3) |
can be reduced to a simple four-dimensional system when the evolution of the synaptic variable s is chosen to mimic that of a second-order synapse. Note that this model includes a reset condition: when vi(t) > vth, vi(t) = vreset (these values are set to +∞ and −∞, respectively). Here, we will assume a first-order synapse to mirror the setup of the ad hoc model. Hence, the reduced system used here is three dimensional. The background drives ηi are chosen from a Lorentzian distribution with center η0 and half-width Δ (heterogeneity parameter), τ corresponds to the effective integration time constant of the cell, gsyn represents the synaptic conductance, and vsyn is the synaptic reversal potential. All variables and parameters (bar time constants) are dimensionless.
Byrne and Coombes described the reduced system in terms of the complex-valued Kuramoto parameter Z. In this article, we wish to explore the dynamics of the population rate r and mean voltage V, so we use the conformal mapping derived by Montbrió et al. (2015),
| (4) |
where W = πτr + iV. This allows us to describe the mean-field behavior as follows:
| (5) |
| (6) |
| (7) |
where s0 corresponds to a constant external synaptic input and k is the coupling strength. It is interesting to note that the evolution of the mean voltage V takes a form similar to the voltage of the individual neurons vi, with an additional negative term keeping it from diverging to infinity. This term represents the reset condition.
This framework can easily be extended to two populations, as
| (8) |
| (9) |
| (10) |
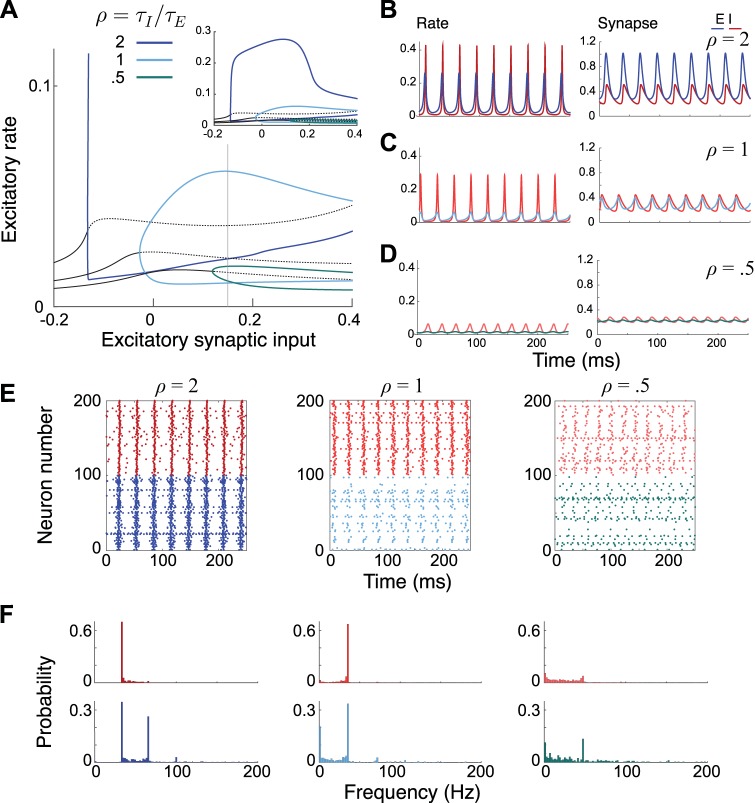
where a = {E,I}. As in the previous section, we fix the synaptic time constants to biologically plausible values ( = 3 ms, = 10 ms) and vary the integration time constants, while keeping their sum fixed (τE + τI = 12 ms), to examine the bifurcation properties of the system. Manipulating the integration time constants τa in this model is akin to manipulating the time constants for firing rate recruitment in the previous section. However, these time constants correspond to the effective integration time constants of the excitatory and inhibitory neurons themselves; hence, changing these values can lead to changes in the steady-state value of the population firing rates. All other parameters, as well as details on the numerical schemes, are given in the appendix. The system undergoes a Hopf bifurcation as the drive to the excitatory synapse, , is increased (Fig. 3A); this is robust to choices in the ratio of time constants ρ = τI/τE. Increasing ρ leads to more abrupt increases in firing rate at the bifurcation. For ρ = 2, the system produces a highly synchronized γ rhythm, with sharp peaks in the firing rate (Fig. 3B). Reducing ρ = 0.5 produces lower-amplitude, more modulated oscillations (Fig. 3D).
Fig. 3.
Behavior of the 2-population quadratic integrate-and-fire (QIF) model for 3 values of the ratio of the integration time constants, ρ = τI/τE. A: bifurcation diagram of the system described by Eqs. 8–10, showing the firing rate of the excitatory population as a function of the drive to the excitatory synapses . Solid (dashed) black line represents the stable (unstable) steady state. Curves illustrate the minimum and maximum amplitude of the oscillations for various values of ρ. As in Fig. 2, the amplitude increase becomes more abrupt as ρ is increased. Inset: zoomed-out version of the entire bifurcation profile showing peak amplitude values. B–D: example time courses of the firing rate and synapses for the mean-field model, taken for = 0.15 (gray vertical line in A). E: raster plots of the individual neuron firing rates for a network of spiking QIF neurons. The raster plots show a random sample of 10% of the neurons in the network. The parameters are chosen to match those in A–D. F: distribution of firing rates of individual neurons in corresponding simulations. Neurons fractionally participate in oscillations with smaller ρ values, but the overall population frequency remains relatively constant. The integration time constants are given as τE = 8 ms and τI = 4 ms (ρ = 0.5), τE = τI = 6 ms (ρ = 1), and τE = 4 ms and τI = 8 ms (ρ = 2).
The benefit of this model is that it is an exact representation of a network of spiking QIF neurons. We simulated a network of QIF neurons using the same parameters as those in Fig. 3, A and B, to examine how the microscopic dynamics change under these conditions. The raster plots in Fig. 3E show a sample of 100 excitatory and 100 inhibitory neurons for a network with 1,000 of each. Reducing ρ leads to a reduction in overall firing as well as more firing between population events. We can also examine the firing rates of the individual neurons in the populations by plotting their distributions (Fig. 3F). For ρ = 2, we observe that both sets of neurons have a large peak at the population firing frequency as well as smaller peaks at multiples of this frequency for the excitatory cells. As ρ is reduced there are more cells with firing rates lower than the population rate, especially at ρ = 0.5, where the peak at the population frequency is small and the majority of the cells have firing rates lower than this value. This is akin to the behavior described by Brunel and Wang for LIF neurons (Brunel and Wang 2003), where the cells fire sparsely at a frequency lower than the population firing frequency. Here, there are still a number of neurons firing at and above the population firing frequency, but we do have sparse firing with population oscillations in the gamma range.
It is also possible to track within-population synchrony in the QIF mean-field description, by examining the order parameter Z = ReiΨ, where R is the within-population synchrony and Ψ is the average phase of the oscillators (Byrne et al. 2017; Coombes and Byrne 2019). When the model is tuned to exhibit strongly modulated gamma (Fig. 3E, left), the within-population synchrony will be almost 1. In the modulated gamma case (Fig. 3E, right), the within-population synchrony is lower, with smoother increases/decrease between population events. In this way, we can use the mean-field description to characterize elements of the spiking model that could not be captured in previous rate models.
DISCUSSION
We demonstrated that firing rate models of gamma oscillation can have qualitative features like those of spiking gamma models. Unlike spiking network models, these few-parameter rate models are tractable and allow for standard dynamical systems analysis of network behavior. We explored two rate model frameworks, distinguished from the classical Wilson-Cowan description (Wilson and Cowan 1972), by representing each neuronal population, excitatory and inhibitory, with at least two dynamic variables: the firing rate or firing probability per unit time r(t) and synaptic activity s(t), each with their individual timescales. One framework is an enhanced Wilson-Cowan-like description, and the other is an explicit derivation from a spiking QIF network that includes an additional voltage variable, V(t), per population. These rate models, depending upon parameter settings, can support weakly modulated gamma rhythms or strongly synchronized gamma rhythms robustly over a range of parameter conditions. The onset of oscillations was shown to occur through a Hopf bifurcation. Here, we fixed the synaptic timescales to physiologically justified values (3 ms for excitatory and 10 ms for inhibitory) and varied the time constants for the recruitment of network activity, r(t), within a biologically plausible range (2–8 ms). We demonstrated that these weakly or strongly modulated oscillations can be manipulated simply by altering these recruitment timescales in the system. In particular, we found that by using either interneurons with a comparatively small rate recruitment timescale or excitatory neurons with a large rate recruitment timescale we facilitate supercritical Hopf bifurcations and generate low-coherence, small-amplitude oscillations.
Synchronous gamma rhythm (PING).
The PING rhythm is characterized by brief epochs of near-synchronous excitatory firing that recruit inhibition, which in turn quench excitation. Hence, inhibitory synaptic dynamics determine the timescale for the next excitatory epoch (Börgers and Kopell 2003; Kopell et al. 2010). Theoretical studies of PING have been predominantly focused on networks of spiking neurons. We illustrated that it is not necessary to track the individual spiking units and their synaptic currents to model PING, which had previously been assumed essential. The tractability of the rate models allowed us to easily demonstrate that oscillations emanate from a Hopf bifurcation, when the control parameter, stimulus intensity, passes a critical value.
We demonstrated that these PING-like oscillations emerge with an amplitude that is small at emergence but grows abruptly with stimulus intensity, leading to a strongly synchronized PING-like rhythm (Figs. 2 and 3). The prominence of PING occurs in both models when the excitatory recruitment time constant is smaller than that for the inhibitory population, i.e., inhibition is slower. We note that this PING-like behavior is also seen if both excitatory and inhibitory recruitment are fast compared with the synaptic dynamics, essentially reducing to a two-variable, sE(t) and sI(t), Wilson-Cowan-like model (Keeley et al. 2017). In this case, these PING-like oscillations with small and may also coexist with a steady state over a considerable range of excitatory input. The Hopf bifurcations in this regime may also be subcritical with a steep dependence of amplitude on input. Whether such bistability is functionally meaningful or whether it might occur with robustness in other parameter regimes or in spiking models are interesting issues to consider. This feature of bistability diminishes as the recruitment timescale slows, as seen in Figs. 2 and 3. For further description of the bistable behavior in this parameter range, see the appendix.
Modulated gamma rhythm.
The rate models presented here also account for weakly modulated gamma rhythms, characterized by small-amplitude cycling of network activity at gamma frequencies (Börgers et al. 2005; Tikidji-Hamburyan et al. 2015). This corresponds to our rate and synaptic variables oscillating with a small amplitude around some mean values. When the mean values were low (as in Fig. 2D, Fig. 3D, Fig. 3E, right, and Fig. 3F, right), the models demonstrated “weak gamma”: individual cells fire at much lower rates than the network gamma rhythm, with fractional network participation per cycle (Börgers et al. 2005). This behavior is realized via a supercritical Hopf bifurcation and is robust over a range of stimulus intensities, when the excitatory recruitment rate timescale is larger than the inhibitory one, i.e., when the inhibitory r(t) is fast and the excitatory r(t) is slow. Interestingly, parvalbumin-positive interneurons, implicated in gamma in a number of experimental studies (Bartos et al. 2007; Sohal et al. 2009; Wulff et al. 2009), do indeed fit the mold of a fast rate response to input and a strong synaptic effect (Hasenstaub et al. 2016), suggesting that timescales of this form lead to realistic small-amplitude gamma oscillations. When inhibitory recruitment is fast, the excitatory cell firing is not able to rise quickly before the inhibitory population is recruited (as occurs in the strongly synchronous behavior). Instead, as excitation is recruited, inhibition immediately follows. This allows for nearly in-phase E and I activity that oscillates around some mean rate with small amplitude. This modulated behavior is close to what is observed in vivo (Buzsáki and Wang 2012) and is the form of many of the more recent stochastic spiking-gamma models (Tikidji-Hamburyan et al. 2015). In fact, these cell-based stochastic spiking models for weak gamma have nearly in-phase behavior (Brunel and Wang 2003), whereas highly synchronous models show E activity preceding I activity (Kopell et al. 2010). This suggests that incorporating additional variables into the rate model frameworks is valuable for demonstrating this realistic gamma behavior and for tuning between the regimes of weak and strong gamma.
Relationship to spiking models.
The QIF framework carries the advantage of a direct link between the macroscopic mean-field variables and the microscopic spiking network (Coombes and Byrne 2019; Luke et al. 2013; Montbrió et al. 2015). This linkage is global with respect to coupling weights and input. Hence, we can predict from the rate model the firing rate, mean voltage, and within-population synchrony of the QIF network. For the LIF model we do not have a global direct linkage, but local mean-field analyses exist for describing the onset of network oscillations. Brunel and Wang identified the occurrence of Hopf bifurcation for weakly modulated network gamma with low cellular rate for an excitatory-inhibitory network (Brunel and Wang 2003). This treatment seeks instabilities of the asynchronous state, and as such the behavior is guaranteed accurate only close to the instability onset. Such an analysis was also performed by Hansel and Mato for the QIF model, but their analysis was also valid only at the onset of oscillations (Hansel and Mato 2003). This connection between the macroscopic and microscopic dynamics is consistent with our findings for the Wilson-Cowan-like rate model. In particular, small-amplitude network oscillations about a low cellular firing rate occur when the system is poised at the foot of the cellular input-output relation. Intuition suggests that this represents the scenario in which the individual neurons are poised below their deterministic threshold and fire on occasional cycles of the gamma rhythm (Brunel and Wang 2003), as is the case in the QIF framework. Furthermore, such behavior, in the Wilson-Cowan-like model, suggests that increasing the effective rate recruitment timescale of the excitatory population relative to the inhibitory population, in an LIF network, encourages smaller-amplitude oscillations about a mean firing rate, with a smoothly modulated amplitude profile.
Limitations.
The idealized rate models outlined here have limitations in their mapping to gamma phenomena observed in vivo. In particular, the network oscillations are perfectly regular; we did not consider the effects of correlated network noise or time-varying input amplitude. Even in the QIF network when the individual units are not necessarily firing periodically, we still observe regular network gamma oscillations. Thus these models do not capture the broadband gamma oscillations observed in in vivo recordings (Bragin et al. 1995; Buzsáki and Wang 2012).
Additionally, both rate model frameworks assumed asynchronous spiking, a natural feature for units with type 1 excitability (Rinzel and Ermentrout 1998) that do not show preferred spike timing. Such rate-model descriptions apply to a number of previous spiking models (Börgers et al. 2005; Börgers and Kopell 2003; Wang and Buzsáki 1996). These spiking or rate models do not capture the features and consequences of intrinsic resonance that have been identified in some experimental and computational studies of fast-spiking-like inhibitory interneurons and gamma rhythmicity (Mancilla et al. 2007; Tikidji-Hamburyan et al. 2015). The incorporation of intrinsic resonance and type 2 excitability for interneurons into a rate framework and consideration therein of possible advantages for robustness of gamma remain challenges for future efforts.
Moreover, the rate and synapse model is limited in that there can be no oscillations without some autocatalytic effect in E synapse recruitment; that is, wEE > 0 is necessary in order to find oscillations. In a spiking network model wEE = 0 does not preclude network oscillations; the spikes, by way of regenerative sodium current, inherently provide autocatalysis (Kopell et al. 2010). Likewise, in the QIF-rate model reduction there can still be gammalike rhythms with wEE = 0 since there is an exact correspondence with a spiking model. In the rate and synapse model, however, without the wEE there is no way to develop coordination of the E units and hence the sharply timed quenching effect from inhibitory firing.
Finally, the QIF reduction presented here assumes all-to-all coupling, which is physiologically unrealistic. However, all-to-all coupling is not an unreasonable assumption when considering small densely connected areas of cortex (Deco et al. 2008). Recent work has shown that a similar reduction may also be performed in modular networks (Chandra et al. 2017) as well as spatially extended networks (Byrne et al. 2019; Laing 2014). The cost of such extensions is a more complicated system of reduced equations.
Strictly inhibitory network models.
In this article, we focus on mechanisms with interacting excitatory-inhibitory populations for gamma oscillations. However, there are numerous theoretical and in vitro studies of inhibitory-only networks that can produce gamma oscillations (Tikidji-Hamburyan et al. 2015; Wang and Buzsáki 1996; Whittington and Traub 2003). Spiking network models with cellular mechanisms that have synchronization effects for inhibition, such as synaptic rise times as well as slow decay times, gap junctions, or propagation delays, were found to support ING rhythms (Traub et al. 2001; Whittington and Traub 2003). Wilson-Cowan-like rate models for inhibitory-only networks have been developed through the inclusion of a mean voltage variable or a delay (Keeley 2016). The QIF mean-field model allows for oscillations in the single inhibitory population case, and such a network was studied in Coombes and Byrne (2019) and Byrne et al. (2017). Although this inhibitory-only-based approach is an important piece to understanding the variety of gamma features observed, it is outside of the scope of the present article.
Predictions.
We showed that increasing the recruitment timescale for inhibition with respect to excitation in models of gamma led to more coherent and stronger network oscillations. In contrast, speeding up the recruitment of inhibition promoted weakly modulated network gamma oscillations. We expect that this result generalizes not just to the QIF framework but also to other spiking models such as LIF. Although previous work in spiking models has explored the nature of synaptic timescales in E and I populations and their relationship to oscillations (Brunel and Wang 2003; Hansel and Mato 2003), our work uses few-variable rate models and focuses on differing rate recruitment timescales, or the speed with which neural firing responds to inputs. We found a general feature in these models that increasing recruitment timescales of the inhibitory neurons, or decreasing recruitment timescales of the excitatory population, sharpens the synchrony of gamma oscillations. This suggests that the excitability of excitatory and inhibitory neuronal populations significantly affects their oscillatory behavior in the gamma regime.
Conclusions.
We demonstrated that rate models reliably approximate the gamma behavior of networks of spiking neurons. These tractable models are easy to analyze, provide valuable insight into the bifurcation and oscillatory features of the system, and, moreover, readily encapsulate a variety of features seen in spiking models. In particular, we highlighted that by introducing separate rate and synaptic timescales to the Wilson-Cowan framework, we alter the amplitude profiles and oscillatory behavior of the gamma into weakly and strongly modulated regimes, two distinct features observed in existing spiking network models of gamma oscillations. We reinforced this finding by illustrating that it also applies to a QIF rate model, which has an exact mapping to spiking neurons.
GRANTS
S. Keeley was supported by National Institutes of Health (NIH) Grant 5F32 MH-115445-02. A. Fenton is supported by NIH Grant R01 NS-105472. Á. Byrne was supported by the Swartz Foundation.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
S.K. and Á.B. performed simulations; J.R. analyzed data; J.R. interpreted results of simulations; S.K. and Á.B. prepared figures; S.K. drafted manuscript; S.K., Á.B., A.F., and J.R. edited and revised manuscript; S.K. approved final version of manuscript.
APPENDIX
Timescales of a rate and synapse formulation.
For our rate and synapse model, we fix the synaptic timescales such that the inhibitory population timescale is larger than the excitatory population (10 ms and 3 ms, respectively). We find that when the converse is true for the rate timescales (i.e., excitatory timescale > inhibitory timescale), the population firing rate exhibits small-amplitude, weakly modulated oscillations. Alternatively, if the inhibitory rate timescale is, as it is for the synapses, larger than the excitatory rate timescale, the oscillation is coherent and has a large amplitude. That is, if the larger of the timescales for each population are similar, smaller-amplitude oscillations are more readily observed. This suggests that within each population the dominant timescale may play a significant role in determining that population’s dynamics. Here, we calculate an “effective” timescale within each subpopulation (E and I) of our four-variable gamma model that corresponds to the slower timescale of its dynamic variables. We illustrate this for a single excitatory population by linearizing the dynamics about the steady state. For small perturbations around the steady state, the dependence of the firing rate dynamics on the synaptic drive is linear, with proportionality constant α. For ease, we drop the “E” subscript notation, and for notational convenience we let , . The system is thus
| (A1) |
| (A2) |
with eigenvalues
| (A3) |
We then make an approximation by estimating the eigenvalues for different relationships of τr and τs. When the rate timescale is much longer (τr >> τs, i.e., β >> 1), the eigenvalues can be shown to be λ1 ≈ −β − αγ, λ2 ≈ −1 + αγ. Here, we limit recurrent excitation so that αγ < 1, which guarantees that the system exhibits a steady-state solution. This means that the timescales of the solutions to this system are
| (A4) |
| (A5) |
These solutions represent the timescales of the two eigenvectors of our linearized E subsystem. Hence, by making τr large the solutions to the system show a long timescale proportional to τr. Following the same logic, it can be shown that for β << 1 small responses around the steady state decay with rates
| (A6) |
| (A7) |
These results indicate that the timescale of the E subsystem can be realized by making either τr or τs large. This slow timescale is increased by an additional factor of .
The same can be shown for the I subsystem, but here the effective slowness of the larger τ is scaled downward by a factor of . Hence, when rate and synaptic timescale deviate significantly, the relaxation of each subpopulation can be approximated by either its rate or synaptic timescale, whichever is larger.
Simulation parameter values.
Rate and synapse model parameter values for the rate and synapse E-I simulations for Fig. 2 are as follows. The f-I sigmoids are governed by a threshold θ and slope κ according to F(I) = 1/{1+ exp[−κ(I − θ)]}. Here, θE = 0.2 and θI = 0.4, and κE = κI = 0.1. Connectivity weights for all simulations are wEE = wEI = 3.5, wII = 3, and wIE = 5. Input current to the excitatory population is a free parameter, and there is no input into the inhibitory population. γE = 4 and γI = 8, and background synaptic drive and .
In the QIF framework, the conductance strengths are given as , , , and and the synaptic reversal potentials as = 8 and = −15. The background drives are chosen from Lorentzian distributions with centers = 2.5 and = 1.65 and half-width ΔE = 0.8 and ΔI = 0.2. The synaptic variables are tuned to have coupling strengths kE = 5 and kI = 5 and external drive = 0.15, = 0.1. Simulations were performed in MATLAB with an Euler scheme with step size dt = 0.01 ms. Bifurcation diagrams were computed in XPPAUTO (Ermentrout 2002). For the spiking neuron simulations, we used Ornstein-Uhlenbeck noise with mean 0 and timescale τ = 5 ms for both populations. The system was evaluated with a Euler-Maruyama scheme with dt = 0.01 ms.
Additional simulations for rate model with synaptic dynamics.
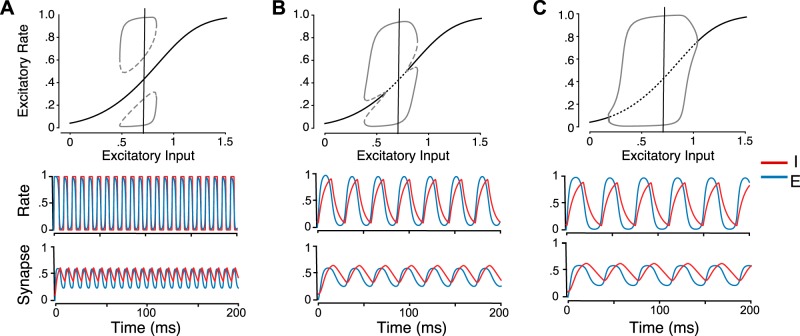
Here we demonstrate that for a range of parameter values our model demonstrates coherent PING-like oscillations with a co-occurring stable steady state. The extent of this bistability can be tuned by manipulating only timescales. Moreover, the coexistence of stable coherent oscillations and a stable steady state can exist over the entire range of input (IE). Examples in Fig. A1 illustrate these model features.
Fig. A1.
Oscillation and bifurcation properties of the rate and synapse model with parameters modified from those used in Fig. 2. A: oscillatory solutions exist and appear as an isola, where a stable oscillatory state exists over a range of input values and coexists with a stable steady state over the entire range. B: bistability arises here through subcritical Hopf bifurcations. C: oscillations emerge via supercritical Hopf bifurcations. Gray dotted lines correspond to unstable oscillation amplitudes, solid gray lines to stable oscillation amplitudes, solid black lines to stable steady state, and dotted black lines to unstable steady state. Rate and synaptic time courses for each of the models are shown at bottom. These time courses reflect an input current, IE of 0.7, to the excitatory population, indicated by the vertical lines in the bifurcation plots. Parameter values for the 3 cases are A: = 1, = 8, = = 0.1, B: = 3, = 8, = 2, = 6, and C: = 3, = 10, = 2, = 8. All other values are the same for the rate and synapse as for Fig. 2 except for the following: γE = 1 and γI = 2, wEE = 5.
REFERENCES
- Angulo MC, Rossier J, Audinat E. Postsynaptic glutamate receptors and integrative properties of fast-spiking interneurons in the rat neocortex. J Neurophysiol 82: 1295–1302, 1999. doi: 10.1152/jn.1999.82.3.1295. [DOI] [PubMed] [Google Scholar]
- Ashwin P, Coombes S, Nicks R. Mathematical frameworks for oscillatory network dynamics in neuroscience. J Math Neurosci 6: 2, 2016. doi: 10.1186/s13408-015-0033-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartos M, Vida I, Frotscher M, Geiger JR, Jonas P. Rapid signaling at inhibitory synapses in a dentate gyrus interneuron network. J Neurosci 21: 2687–2698, 2001. doi: 10.1523/JNEUROSCI.21-08-02687.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat Rev Neurosci 8: 45–56, 2007. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
- Bieri KW, Bobbitt KN, Colgin LL. Slow and fast γ rhythms coordinate different spatial coding modes in hippocampal place cells. Neuron 82: 670–681, 2014. doi: 10.1016/j.neuron.2014.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Börgers C, Epstein S, Kopell NJ. Background gamma rhythmicity and attention in cortical local circuits: a computational study. Proc Natl Acad Sci USA 102: 7002–7007, 2005. doi: 10.1073/pnas.0502366102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Börgers C, Kopell N. Synchronization in networks of excitatory and inhibitory neurons with sparse, random connectivity. Neural Comput 15: 509–538, 2003. doi: 10.1162/089976603321192059. [DOI] [PubMed] [Google Scholar]
- Bragin A, Jandó G, Nádasdy Z, Hetke J, Wise K, Buzsáki G. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci 15: 47–60, 1995. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comput Neurosci 8: 183–208, 2000. doi: 10.1023/A:1008925309027. [DOI] [PubMed] [Google Scholar]
- Brunel N, Hakim V. Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural Comput 11: 1621–1671, 1999. doi: 10.1162/089976699300016179. [DOI] [PubMed] [Google Scholar]
- Brunel N, Hakim V. Sparsely synchronized neuronal oscillations. Chaos 18: 015113, 2008. doi: 10.1063/1.2779858. [DOI] [PubMed] [Google Scholar]
- Brunel N, Hansel D. How noise affects the synchronization properties of recurrent networks of inhibitory neurons. Neural Comput 18: 1066–1110, 2006. doi: 10.1162/neco.2006.18.5.1066. [DOI] [PubMed] [Google Scholar]
- Brunel N, Wang XJ. What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J Neurophysiol 90: 415–430, 2003. doi: 10.1152/jn.01095.2002. [DOI] [PubMed] [Google Scholar]
- Buzsáki G, Wang XJ. Mechanisms of gamma oscillations. Annu Rev Neurosci 35: 203–225, 2012. doi: 10.1146/annurev-neuro-062111-150444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrne Á, Avitabile D, Coombes S. Next-generation neural field model: the evolution of synchrony within patterns and waves. Phys Rev E 99: 012313, 2019. doi: 10.1103/PhysRevE.99.012313. [DOI] [PubMed] [Google Scholar]
- Byrne Á, Brookes MJ, Coombes S. A mean field model for movement induced changes in the β rhythm. J Comput Neurosci 43: 143–158, 2017. doi: 10.1007/s10827-017-0655-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandra S, Hathcock D, Crain K, Antonsen TM, Girvan M, Ott E. Modeling the network dynamics of pulse-coupled neurons. Chaos 27: 033102, 2017. doi: 10.1063/1.4977514. [DOI] [PubMed] [Google Scholar]
- Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, Moser MB, Moser EI. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature 462: 353–357, 2009. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- Coombes S, Byrne A. Next generation neural mass models. In: Nonlinear Dynamics in Computational Neuroscience, edited by Torcini A, Corinto F. Cham, Switzerland: Springer, 2019. [Google Scholar]
- Dafilis F, Frascoli F, Cadusch MP, Liley D. Chaos and generalised multistability in a mesoscopic model of the electroencephalogram. Physica D 238: 1056–1060, 2009. doi: 10.1016/j.physd.2009.03.003. [DOI] [Google Scholar]
- Deco G, Jirsa VK, Robinson PA, Breakspear M, Friston K. The dynamic brain: from spiking neurons to neural masses and cortical fields. PLOS Comput Biol 4: e1000092, 2008. doi: 10.1371/journal.pcbi.1000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunin-Barkowski WL. Information Processes in Neural Structures. Moscow: Nauka, 1978. [Google Scholar]
- Dvorak D, Radwan B, Sparks FT, Talbot ZN, Fenton AA. Control of recollection by slow gamma dominating mid-frequency gamma in hippocampus CA1. PLoS Biol 16: e2003354, 2018. doi: 10.1371/journal.pbio.2003354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout GB. Simulating, Analyzing, and Animating Dynamical Systems: A Guide To XPPAUT for Researchers and Students. Philadelphia, PA: Society of Industrial & Applied Mathematics, 2002. [Google Scholar]
- Freeman WJ. Mass Action in the Nervous System. New York: Academic, 1975. [Google Scholar]
- Freeman WJ. Spatial properties of an EEG event in the olfactory bulb and cortex. Electroencephalogr Clin Neurophysiol 44: 586–605, 1978. doi: 10.1016/0013-4694(78)90126-8. [DOI] [PubMed] [Google Scholar]
- Fries P. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu Rev Neurosci 32: 209–224, 2009. doi: 10.1146/annurev.neuro.051508.135603. [DOI] [PubMed] [Google Scholar]
- Fujisawa S, Amarasingham A, Harrison MT, Buzsáki G. Behavior-dependent short-term assembly dynamics in the medial prefrontal cortex. Nat Neurosci 11: 823–833, 2008. doi: 10.1038/nn.2134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W. Population dynamics of spiking neurons: fast transients, asynchronous states, and locking. Neural Comput 12: 43–89, 2000. doi: 10.1162/089976600300015899. [DOI] [PubMed] [Google Scholar]
- Gray CM, Singer W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc Natl Acad Sci USA 86: 1698–1702, 1989. doi: 10.1073/pnas.86.5.1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenberg DS, Houweling AR, Kerr JN. Population imaging of ongoing neuronal activity in the visual cortex of awake rats. Nat Neurosci 11: 749–751, 2008. doi: 10.1038/nn.2140. [DOI] [PubMed] [Google Scholar]
- Haenschel C, Baldeweg T, Croft RJ, Whittington M, Gruzelier J. Gamma and beta frequency oscillations in response to novel auditory stimuli: a comparison of human electroencephalogram (EEG) data with in vitro models. Proc Natl Acad Sci USA 97: 7645–7650, 2000. doi: 10.1073/pnas.120162397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansel D, Mato G. Asynchronous states and the emergence of synchrony in large networks of interacting excitatory and inhibitory neurons. Neural Comput 15: 1–56, 2003. doi: 10.1162/089976603321043685. [DOI] [PubMed] [Google Scholar]
- Hasenstaub A, Otte S, Callaway E. Cell type-specific control of spike timing by gamma-band oscillatory inhibition. Cereb Cortex 26: 797–806, 2016. doi: 10.1093/cercor/bhv044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen BH, Rit VG. Electroencephalogram and visual evoked potential generation in a mathematical model of coupled cortical columns. Biol Cybern 73: 357–366, 1995. doi: 10.1007/BF00199471. [DOI] [PubMed] [Google Scholar]
- Keeley S. Firing Rate Models Elucidate Competitive Gamma Mechanisms in the Hippocampus (PhD thesis). New York: New York Univ., Center for Neural Science, 2016. [Google Scholar]
- Keeley S, Fenton AA, Rinzel J. Modeling fast and slow gamma oscillations with interneurons of different subtype. J Neurophysiol 117: 950–965, 2017. doi: 10.1152/jn.00490.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopell N, Börgers C, Pervouchine D, Malerba P, Tort A. Gamma and theta rhythms in biophysical models of hippocampal circuits. In: Hippocampal Microcircuits, edited by Cutsuridis V, Graham B, Cobb S, Imre V. New York: Springer, 2010. p. 423–457. [Google Scholar]
- Laing CR. Derivation of a neural field model from a network of theta neurons. Phys Rev E Stat Nonlin Soft Matter Phys 90: 010901, 2014. doi: 10.1103/PhysRevE.90.010901. [DOI] [PubMed] [Google Scholar]
- Laing CR. Phase oscillator network models of brain dynamics. In: Computational Models of Brain and Behavior, edited by Moustafa AA. Hoboken, NJ: Wiley, 2017, p. 505–517. doi: 10.1002/9781119159193.ch37. [DOI] [Google Scholar]
- Le Van Quyen M, Muller LE 2nd, Telenczuk B, Halgren E, Cash S, Hatsopoulos NG, Dehghani N, Destexhe A. High-frequency oscillations in human and monkey neocortex during the wake-sleep cycle. Proc Natl Acad Sci USA 113: 9363–9368, 2016. doi: 10.1073/pnas.1523583113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledoux E, Brunel N. Dynamics of networks of excitatory and inhibitory neurons in response to time-dependent inputs. Front Comput Neurosci 5: 25, 2011. doi: 10.3389/fncom.2011.00025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luke TB, Barreto E, So P. Complete classification of the macroscopic behavior of a heterogeneous network of theta neurons. Neural Comput 25: 3207–3234, 2013. doi: 10.1162/NECO_a_00525. [DOI] [PubMed] [Google Scholar]
- Mancilla JG, Lewis TJ, Pinto DJ, Rinzel J, Connors BW. Synchronization of electrically coupled pairs of inhibitory interneurons in neocortex. J Neurosci 27: 2058–2073, 2007. doi: 10.1523/JNEUROSCI.2715-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montbrió E, Pazó D, Roxin A. Macroscopic description for networks of spiking neurons. Phys Rev X 5: 021028, 2015. doi: 10.1103/PhysRevX.5.021028. [DOI] [Google Scholar]
- Rinzel J, Ermentrout GB.. Analysis of neural excitability and oscillations. In: Methods in Neuronal Modeling (2nd ed.), edited by Koch C, Segev I. Cambridge, MA: MIT Press, 1998, p. 251–292. [Google Scholar]
- Schoffelen JM, Oostenveld R, Fries P. Neuronal coherence as a mechanism of effective corticospinal interaction. Science 308: 111–113, 2005. doi: 10.1126/science.1107027. [DOI] [PubMed] [Google Scholar]
- Sohal VS, Zhang F, Yizhar O, Deisseroth K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature 459: 698–702, 2009. doi: 10.1038/nature07991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor K, Mandon S, Freiwald WA, Kreiter AK. Coherent oscillatory activity in monkey area v4 predicts successful allocation of attention. Cereb Cortex 15: 1424–1437, 2005. doi: 10.1093/cercor/bhi023. [DOI] [PubMed] [Google Scholar]
- Tiesinga P, Sejnowski TJ. Cortical enlightenment: are attentional gamma oscillations driven by ING or PING? Neuron 63: 727–732, 2009. doi: 10.1016/j.neuron.2009.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tikidji-Hamburyan RA, Martínez JJ, White JA, Canavier CC. Resonant interneurons can increase robustness of gamma oscillations. J Neurosci 35: 15682–15695, 2015. doi: 10.1523/JNEUROSCI.2601-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traub RD, Bibbig A, LeBeau FE, Buhl EH, Whittington MA. Cellular mechanisms of neuronal population oscillations in the hippocampus in vitro. Annu Rev Neurosci 27: 247–278, 2004. doi: 10.1146/annurev.neuro.27.070203.144303. [DOI] [PubMed] [Google Scholar]
- Traub RD, Kopell N, Bibbig A, Buhl EH, LeBeau FE, Whittington MA. Gap junctions between interneuron dendrites can enhance synchrony of gamma oscillations in distributed networks. J Neurosci 21: 9478–9486, 2001. doi: 10.1523/JNEUROSCI.21-23-09478.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tukker JJ, Fuentealba P, Hartwich K, Somogyi P, Klausberger T. Cell type-specific tuning of hippocampal interneuron firing during gamma oscillations in vivo. J Neurosci 27: 8184–8189, 2007. doi: 10.1523/JNEUROSCI.1685-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Vreeswijk C, Abbott LF, Ermentrout GB. When inhibition not excitation synchronizes neural firing. J Comput Neurosci 1: 313–321, 1994. doi: 10.1007/BF00961879. [DOI] [PubMed] [Google Scholar]
- Wallace E, Benayoun M, van Drongelen W, Cowan JD. Emergent oscillations in networks of stochastic spiking neurons. PLoS One 6: e14804, 2011. doi: 10.1371/journal.pone.0014804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev 90: 1195–1268, 2010. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J Neurosci 16: 6402–6413, 1996. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Rinzel J. Alternating and synchronous rhythms in reciprocally inhibitory model neurons. Neural Comput 4: 84–97, 1992. doi: 10.1162/neco.1992.4.1.84. [DOI] [Google Scholar]
- Whittington MA, Traub RD. Interneuron diversity series: inhibitory interneurons and network oscillations in vitro. Trends Neurosci 26: 676–682, 2003. doi: 10.1016/j.tins.2003.09.016. [DOI] [PubMed] [Google Scholar]
- Whittington MA, Traub RD, Kopell N, Ermentrout B, Buhl EH. Inhibition-based rhythms: experimental and mathematical observations on network dynamics. Int J Psychophysiol 38: 315–336, 2000. doi: 10.1016/S0167-8760(00)00173-2. [DOI] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J 12: 1–24, 1972. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wulff P, Ponomarenko AA, Bartos M, Korotkova TM, Fuchs EC, Bähner F, Both M, Tort AB, Kopell NJ, Wisden W, Monyer H. Hippocampal theta rhythm and its coupling with gamma oscillations require fast inhibition onto parvalbumin-positive interneurons. Proc Natl Acad Sci USA 106: 3561–3566, 2009. doi: 10.1073/pnas.0813176106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zillmer R, Brunel N, Hansel D. Very long transients, irregular firing, and chaotic dynamics in networks of randomly connected inhibitory integrate-and-fire neurons. Phys Rev E Stat Nonlin Soft Matter Phys 79: 031909, 2009. doi: 10.1103/PhysRevE.79.031909. [DOI] [PubMed] [Google Scholar]