Revisiting atelectasis in lung units with low ventilation/perfusion ratios

Abstract

Patients on high inspired O₂ concentrations are at risk of atelectasis, a problem that has been quantitatively assessed using analysis of ratio of ventilation to perfusion (V̇a/Q̇) equations. This approach ignores the potential of the elastic properties of the lung to support gas exchange through “apneic” oxygenation in units with no tidal ventilation, and is based on an error in the conservation of mass equations. To fill this gap, we correct the error and compare the pressure drops associated with apneic gas exchange with the pressure differences that can be supported by lung recoil. We analyze a worst case scenario: a small test unit in the Weibel model A tree structure with zero tidal ventilation, 100% inspired O₂, the rest of the lung being normally ventilated tidally. We first computed the gas flux to the (unventilated) test unit and estimated the associated pressure drops. We then computed the difference in local gas pressure relative to the surrounding lung that would cause the unit to collapse. We compared these two, and finally computed the degree of airway narrowing that would effect change from the stable (apneic gas exchange) regime to the unstable regime leading to collapse. We find that except under extreme conditions of loss of airway caliber exceeding roughly 90%, lung recoil is sufficient to maintain oxygenation through convective transport alone. We further argue that the fundamental V̇a/Q̇ equations are invalid in these circumstances, and that the issue of atelectasis in low V̇a/Q̇ will require modifications to account for this additional mode of gas exchange.

NEW & NOTEWORTHY Breathing high concentrations of oxygen increases the likelihood of atelectasis because of oxygen absorption, which is thought to be inevitable in regions with relatively low ventilation/perfusion ratios. However, airspaces of the lung resist collapse because of the forces of interdependence, and can, with low or even zero active tidal ventilation, draw in an inspiratory flow of oxygen sufficient to replace the oxygen consumed, thus preventing collapse of airspaces served by all but the most narrowed airways.

INTRODUCTION

Some 40 years ago, Dantzker et al. (2) considered the potential for atelectasis in lung units with low ventilation perfusion ratios (V̇a/Q̇). In a seminal paper, assuming the standard model of the relationships between gas and blood transport as linked to V̇a/Q̇, they concluded that lung units with values of V̇a/Q̇ below a critical value of ~0.06 (taken from Fig. 5 in Ref. 2) would collapse. To be sure, there is no question that for lung units that are closed, absorption atelectasis occurs, the rate of which increases with higher fraction of inspired oxygen ($\text{F}{\mathrm{I}}_{O_2}$); see, e.g., Rothen et al. (9). In what follows, let us distinguish between what we denote “active” or tidal ventilation, meaning convective transport of gas through inspiratory and expiratory volumetric changes of a lung unit, and “passive” ventilation, meaning convective flow secondary to O₂ absorption, without any volume changes in that unit. In the extreme case of zero tidal ventilation, this is the phenomenon of apneic gas exchange. Thus in particular, if active tidal ventilation is low, e.g., secondary to narrowing of bronchial or bronchiolar lumens, or even zero, the possibility remains that if the airways remain even marginally patent, the lowered alveolar gas pressure secondary to O₂ absorption may be supported by local lung recoil associated with parenchymal tethering or interdependence. This in turn may be sufficient to support passive ventilation and prevent atelectasis and alveolar collapse. Here we revisit the question of atelectasis risk from this rather different perspective, and specifically inquire what narrowing or loss of conducting airway lumen would still permit adequate gas exchange in that unit, without a necessary consequence of local collapse and atelectasis.

The issue of “apneic oxygenation” is older still than Dantzker et al. (2). In a remarkable study, Frumin et al. (3) demonstrated adequate oxygenation in subjects undergoing minor operations for time periods from 30 to 60 min when the airway opening was supplied from a reservoir bag containing 100% O₂ and with no active ventilation from the bag. It is clear from that study that sufficient pressure drops can exist (from airway opening to terminal air space) to promote passive convective transport of reservoir gas to the gas exchanging regions of the lung. In this study, CO₂ was allowed to rise and constituted a limiting factor. With extracorporeal CO₂ scrubbing, Nielsen et al. (7) in a more recent study found adequate apneic oxygenation in an experimental pig model for >3 h on 100% O₂. These results suggest that adequate oxygenation is indeed possible through simple passive inspiratory flow driven by the pressure difference from the airway opening to the alveoli because of O₂ absorption. Note that in this model, with the convention that alveolar ventilation is that gas expired from a lung unit, V̇a/Q̇ is strictly zero.

From the point of view of lung units with very low or even zero tidal ventilation, to the extent that the remaining lung provides adequate CO₂ elimination, we can therefore reexamine whether local lung recoil is adequate to support passive transport in some lung unit sufficient to replace the absorbed O₂, thus preventing distal atelectasis.

In our analysis, we make the following specific assumptions:

• • We consider a small test unit of 1% lung volume, with zero tidal ventilation; hence a local V̇a/Q̇ of zero (explicitly less than the critical value of 0.06 in Ref. 2).
• • The test unit’s perfusion is normal.
• • The rest of the lung has normal tidal ventilation, with V̇a/Q̇ ≈ 1.
• • Inspired gas is 100% O₂, representing a “worst case” scenario.
• • We will keep all calculations to one or at most two decimal places, as further precision is not important for examining the essence of gas transport in this context.
• • We argue that since the rest of the lung is normal, total CO₂ exchange is not significantly compromised, and that the average gas composition seen just proximal to our small test unit is roughly the average of inspired and alveolar gas from the remaining lung.

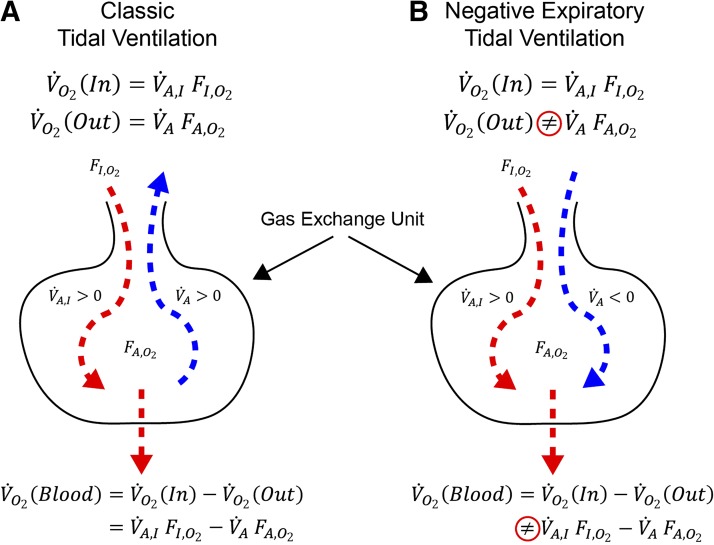
Note that here, as in Dantzker et al. (2), we explicitly distinguish inspiratory (active) ventilation, denoted V̇_AI, from expiratory (active) ventilation, usually denoted simply V̇_A. In the case of the lung unit with zero active ventilation, the analysis in Dantzker et al. (2) predicts that expiratory active ventilation is actually negative. We argue that if this were the case, then the use of the classical conservation equation:

$${\dot{V}}_{\text{AI}}{\mathrm{F}}_{I{O}_2}-{\dot{V}}_A{F}_{A{O}_2}=\dot{Q}({\mathrm{C}}_{a{O}_2}-{\mathrm{C}}_{\overline{V}{O}_2})={\dot{V}}_{O_2,blood}$$ (1)

is incorrect. This equation is simply an expression stating that net transport to blood is equal in steady state to “in” (V̇_AIF_IO2) minus “out” (V̇_AF_AO2), given that both V̇_AI and V̇_A are positive. When the solution to Eq. 1 implies a negative expiratory ventilation for the apneic unit (V̇_A < 0), the second term on the left hand side does not represent an expiratory flow of O₂ at its alveolar fraction, but rather a passive inspiratory flow of O₂ at an O₂ fraction given by a mixture of gas from neighboring units. This concept is shown pictorially in Fig. 1.

Fig. 1.

Illustration of the concept that transport to blood is equal to ventilation “in” minus ventilation “out.” Cartoon A is classical and correctly expresses conservation of mass. In this case V̇o₂(blood) = V̇o₂(In) − V̇o₂(Out). Cartoon B shows the circumstance when predicted expiratory tidal ventilation is negative. In this case ${\dot{V}}_{O_2}(Out)\ne {\dot{V}}_A{F}_{A,O_2}$, and Eq. 1 (from which the negative V̇_A was computed) is no longer valid.

METHODS AND RESULTS

The logical flow of our arguments respecting the extent to which local lung recoil can support gas exchange is as follows:

1. We estimate the convective flux required to satisfy that unit with respect to O₂ uptake by blood.

2. We inquire what the Poiseuille pressure drop would be to support such bulk transport.

3. We then compare this pressure drop to that which can be supported by the mechanical properties of the lung through parenchymal tethering or interdependence. (Note that collapse is dominated by shear deformation, which in turn is a function of local lung recoil.)

4. Finally, we compute the amount of narrowing that could exist, consistent with the pressures being sustained by the interdependence of the surrounding parenchyma.

Convective flux.

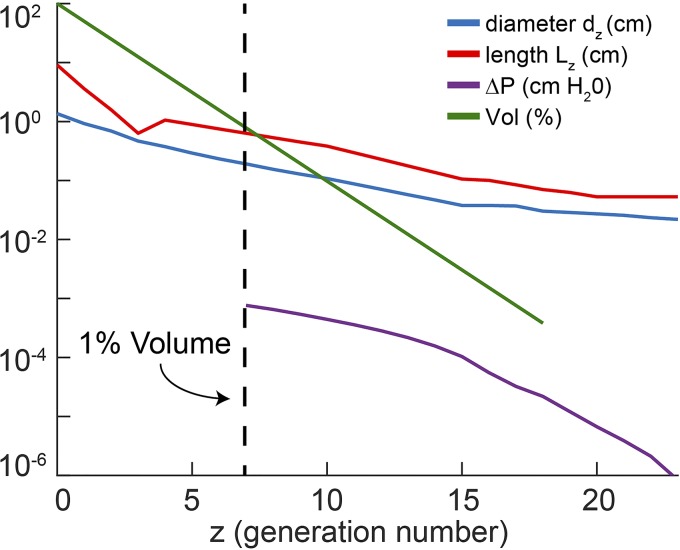
First, consider the effect of breathing 100% O₂ on mixed venous blood. As our unit is small (1% of total lung volume), and the remaining lung is taken to be normal, CO₂ transport is largely unaffected, and mixed venous Pco₂ will approximate normal conditions of 45 Torr. With 100% O₂ in the inspired gas, alveolar Po₂ (in the normal lung with negligible shunt) and arterial Po₂ will rise from 100 Torr to ~670 Torr. Considering the poor solubility of O₂ in blood, this amounts to a very small increase in content (holding metabolic rate and cardiac output fixed) such that mixed venous Po₂ rises only modestly, to no more than 50 Torr. To the extent that the gas seen at the proximal end of the unit is a mixture of inspired and expired gas from the remaining lung, and if transport is dominated by passive (inspiratory) convection, it follows that alveolar gas in the unit will have a Po₂ in the range of mid-600s Torr and Pco₂ around the mixed venous point of 45 Torr, respectively. Given this high level of Po₂, net oxygen consumption in the unit (here we assume normal blood flow) will be roughly normal, and will therefore be proportional to its volume, i.e., 1% of the normal V̇o₂, or ~2.5 ml/min. (This is an upper bound for flux in the unit; a unit that is collapsing will have commensurately increased tissue thickness separating gas from blood, which would only decrease local diffusing capacity and reduce the local oxygen consumption proportionately.) As shown in Fig. 2, the volume of our unit at risk of collapse corresponds to a unit served roughly by generation 7 (2⁻⁷ ≈ 0.01), which in the Weibel A model (13) represents the beginning of the terminal bronchioles. This is shown in the green curve of Fig. 2, together with bronchial lengths and diameters (corrected for a functional residual capacity of 40% TLC by geometric similarity).

Fig. 2.

Diameters d_z (blue) and lengths L_z (red) diameters of the bronchial tree in the Weibel A model. Generation z = 0 is the trachea. Green line is the volume served by a bronchus at generation z, given by 2^−z, expressed in percent of total lung volume. Dotted line shows that our unit of 1% volume is served by a bronchus at generation 7. Purple curve shows the cumulative pressure drop during apneic ventilation ΔP(z) in cmH₂O from generation z distally to generation 23. It is given by $\Delta P(z)={\displaystyle \sum _{n=z}^{23}\Delta P_n}$, where ΔP_n are the individual pressure drops at generation n.

Pressure drop.

We now compute the pressure drop within each generation during apneic ventilation, assuming Poiseuille flow, for which ΔP_n = 8μL_nV̇_n/(π(d_n/2)⁴, where μ = 2 × 10⁻⁴ poise, L_n, d_n are bronchial lengths and diameters, V̇_n = V̇₀2⁻ⁿ is the volume flow in that airway due solely to O₂ transport, and where V̇₀ is basal metabolic rate of 250 ml O₂/min. The cumulative pressure drop beginning at each generation and ending at the termination of the Weibel model distally is also shown in Fig. 2 as the purple curve. The pressure drop from generation 7 to the terminal alveoli is on the order of 0.001 cmH₂O; this very low pressure drop is traceable to the fact that the convective flow is only some 4% of tidal flow (i.e., the ratio of a typical oxygen consumption of 0.25 l/min to a typical minute ventilation of 6 l/min) and to the smaller resistance distal to generation 7.

Pressure drops associated with collapse.

We know that the mechanical forces required to collapse a lung unit are approximately characterized by the shear modulus, e.g., where for a spherical terminal unit, the decrease in volume is related to the decrease in transmural pressure (i.e., internal gas pressure relative to pleural pressure) by ΔV/V = 3Δr/r = −3ΔP/4G (10), where G is the shear modulus of the lung. G is known to be closely approximated by G ≈ 0.7P_el(L), where P_el(L) is elastic lung recoil (4). This notion suggests that for ΔP close to G, there will be a risk of collapse (ΔV/V ≈ 1). This relation between strain and stress is strictly true only for small degrees of collapse; large deformations are more complex and require more (negative) pressure to effect collapse, significantly associated both with finite deformation and with strain stiffening. Suppose we take an (underestimate) of a factor of 2 for this stiffening effect. Then if P_el(L) is on the order of 2 cmH₂O at functional residual capacity during quiet breathing, we would require a pressure drop from the terminal gas space to the surrounding parenchyma of roughly 4 cmH₂O to effect collapse. It is clear that this is much larger than the pressure drop required to support bulk transport to replace absorbed O₂ (Fig. 2).

Degree of bronchial narrowing leading to collapse.

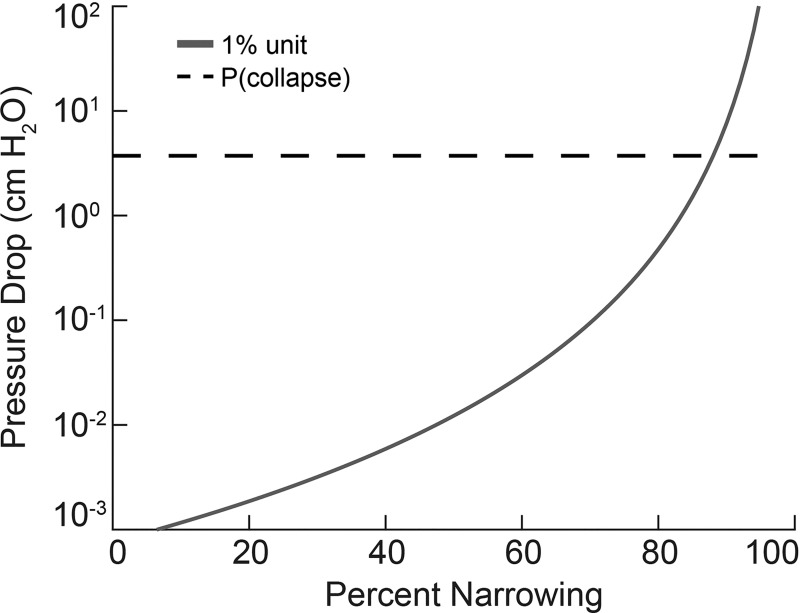
The ideas elaborated above apply only for normal bronchi serving our hypothetical 1% unit with zero tidal ventilation. It remains to calculate the degree of diameter reduction (narrowing from constriction, partial mucus plugging, etc.) that would be necessary to reach the critical pressure drop of roughly 4 cmH₂O. This is shown in Fig. 3, where we have assumed a homogeneously distributed narrowing throughout the whole pathway of our unit from generation 7 to the terminal air space.

Fig. 3.

Cumulative pressure drop from generation 7 (corresponding to a bronchus serving the apneic unit 1% volume) to generation 23, as a function of the degree of diameter narrowing α (expressed in percent), given by ΔP(7)/(1−α/100)⁴.ΔP(z) is defined in the legend to Fig. 2. Pressure required for collapse (dashed line) is estimated in the text (Pressure drops associated with collapse) to be around 4 cmH₂O.

Here we see both the trivial magnitude of pressure drop for normal airways (where the percent narrowing is near zero), as well as the sharply increasing ΔP as luminal diameter is decreased; this behavior is due to the inverse fourth power of radius effect on resistance, and hence on pressure drop. The conclusion from these data is that even for markedly narrowed airways, there is insufficient pressure drop with passive ventilation to affect collapse. Importantly, we find that it is only when the percent constriction exceeds ~90% that the threshold for collapse is crossed. A factor of 10 in narrowing, through the same fourth-power dependence of resistance, would reduce its tidal V̇a/Q̇ as conventionally estimated to ≈0.0001. We conclude that for regions with V̇a/Q̇ greater than this, passive convection driven by oxygen absorption alone could affect bulk inspiratory flow appropriate to local oxygen consumption and thus prevent collapse.

DISCUSSION

We draw several conclusions from these analyses. First, contrary to prior results (2), we find that airways serving a small unit that remains patent, even to the extent of ~90% constriction or obstruction, have pressure drops associated with passive apneic oxygen flow that can be supported through the unit’s mechanical interdependence with the surrounding parenchyma. Second, we believe it is clear from this example that the classical V̇a/Q̇ concepts and equations are incomplete, and in extreme cases of near complete absence of tidal ventilation, are actually incorrect. While they are in large measure valid over a very wide range of conditions, it is in extreme conditions such as very low V̇a/Q̇ where other effects cannot be neglected, and in particular, the possibility of supporting pressure differences through interdependence sufficient to effect bulk inspiratory flow supporting local oxygen consumption. We conclude that the conservation equations (Eq. 1) fundamental to the V̇a/Q̇ analysis must be modified when active tidal ventilation to any unit is sufficiently small or even zero as in the case analyzed here.

With respect to such a modification, if predicted expiratory V̇_A < 0, it is clear that it is not transporting gas with an alveolar oxygen fraction ${\mathrm{F}}_{A,O_2}$. But we note that one cannot “fix” this simply by replacing the oxygen fraction used there by some mixture of inspired and expired O₂ fractions at the proximal end of, e.g., the apneic unit described above. We believe it is true that such a mixture does represent a source term (as we have done here), but one cannot then use this with what is an incorrect quantification of the negative expiratory ventilation. We would that it were possible to construct a corrected version of the V̇a/Q̇ equations, but we cannot do this yet. In addition to the issue of quantifying the inspired concentration from neighboring units, a more difficult problem is whether the direction of convective flow to a low V̇a/Q̇ unit during the expiratory phase is inspiratory or expiratory. This is not easy to quantify; it depends on the competition between pure active tidal flow in the expiratory direction and passive flows in the inspiratory direction due to O₂ gradients, and this may vary over the expiratory phase of the respiratory cycle. Finally, we note that the classical conservation equations rest on a fractionation of tidal ventilation into dead space and alveolar ventilation. This approximation is largely legitimate under normal circumstances, insofar as the transition from pure bulk convection to pure diffusion is rather abrupt spatially. But in the extreme case analyzed here, this is no longer true. Indeed, with pure apneic ventilation, dead space is in fact zero; all gas presenting at the airway opening ultimately takes part in oxygen exchange.

Similar issues arise in the implementation of the multiple inert gas elimination technique (MIGET; 12), which is based on the same conservation laws as given in Eq. 1, modified to relate content through inert gas solubilities. In this technique, active tidal expiration is necessary to measure the local gas concentration arising from the alveolar space. But if this situation is compromised through passive convective flow supporting local O₂ consumption sufficient to prevent alveolar gas from reaching the airway opening, then such units will be in effect invisible to the MIGET technique. As such (or indeed if the sign is predicted to be ultimately negative), this realization invites similar modifications to the foundations of MIGET and in the interpretation of units with very low V̇a/Q̇.

We emphasize that the analysis done here is a worst case scenario. To the extent that inspired oxygen is less than 100% (common but not always done in clinical practice), and to the extent that positive end-expiratory pressure is employed in optimizing ventilator strategy, the risk of atelectasis is lower. Our approach has the consequence that the estimates given above, where airway narrowing exceeding 90% would lead to potential collapse, are conservative in the sense that commensurately greater narrowing would be necessary to increase atelectatic risk under these more common circumstances. Along the lines of modifications necessary in low V̇a/Q̇ units, we also note that even if there is positive expiratory active tidal ventilation, it may be sufficiently low that ventilation remains dominated by the inspiratory passive ventilation. Combining nonzero active tidal ventilation with its passive complement remains an open and potentially difficult question.

Even apart from the fact that our analysis was done on 100% O₂, our model here is in some respects artificial. Pathologies affecting only a small unit such that it is apneic (or one with V̇_AI/Q̇ < 0.06), isolated from the rest of a lung that was normal, are surely uncommon. Another factor that we have ignored is whether airways per se can narrow to a degree such as 90%. Indeed the presence of airway liquid instabilities have been firmly established, with the consequence that with narrowing beyond a certain point airways will suffer the formation of liquid bridges, and unless these are resolved will contribute to distal atelectasis (6, 11). And of course, with surfactant dysfunction or airway hyperresponsiveness, this phenomenon is likely to be exacerbated with consequent increased risk of atelectasis.

Further limitations of this model include the following considerations. First, if many such units are compromised, there will necessarily be a commensurate compromise to CO₂ transport, acid/base balance, and consequences of this. Including the combined effects of a distributed collection of compromised units on overall transport would seem to be a difficult problem, and is certainly beyond the scope of this simple model. Note that we have also only described a situation with a very low recoil, essentially the case with no positive end-expiratory pressure. In that spirit, however, we note that we are presenting again a kind of “worst case,” wherein the lower lung volumes and lower recoil would facilitate airway closure and subsequent atelectasis. In addition, we acknowledge that there may be cyclic behavior of airways that remain patent on inspiration but collapse on expiration. This is a complicated question regarding the interaction of bronchi and the tethering parenchyma, and is beyond the scope of this paper. On the other hand, we do know that the effects of airway wall stiffness cannot be neglected. Bates and Lauzon (1) have shown that in rats and rabbits, wall stiffness can be significantly greater than the elastic stiffness of the parenchyma. To the extent that this finding is true, it follows that our estimate of a collapsing stress given in Fig. 3 is actually an underestimate of the pressures necessary to effect collapse. As such, apneic units are even more protected against collapse than what would be suggested here.

Finally, we note a curious consequence of our analysis. It is conventional wisdom that low V̇a/Q̇ units are a source of venous admixture, or equivalently, a kind of shunt wherein venous blood with low Po₂ fails to get oxygenated with consequent arterial hypoxemia. In units that collapse, this concept is valid. However, in what we have described here, quite the contrary is true. For example, our apneic unit with zero active or tidal V̇a/Q̇, when airways remain patent (with narrowing below the critical level in Fig. 3) continues to have a very high Po₂, given the mixed Po₂ from inspired and expired gas from the neighboring normal lung presenting at the unit’s proximal end. As such, with normal septal architecture, the end capillary blood from the unit will achieve full oxygenation and not contribute at all to venous admixture or shunt.

To be sure, atelectasis can and does occur, and is a serious clinical problem. Alveolar collapse is surely true in cases of complete bronchial closure (5, 8) where there remains a closed gas pocket, secondary to a wide range of pathologies that can contribute to closure. These factors would certainly include surfactant dysfunction, local loss of tethering tissue surrounding emphysematous bullae, etc. In addition, hyperoxia has been associated with airway inflammation, which may ultimately contribute to airway closure and atelectasis. But we suggest that an atelectatic consequence to V̇a/Q̇ ratios below a critical value is not inevitable when the mechanics of lung and the viability of passive apneic oxygenation are included in the analysis.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.P.B. and S.H.L. conceived and designed research; J.P.B., A.M., and S.H.L. analyzed data; J.P.B. prepared figures; J.P.B. drafted manuscript; J.P.B., A.M., and S.H.L. edited and revised manuscript; J.P.B., A.M., and S.H.L. approved final version of manuscript.