Differential activation of lumbar and sacral motor pools during walking at different speeds and slopes

Abstract

Organization of spinal motor output has become of interest for investigating differential activation of lumbar and sacral motor pools during locomotor tasks. Motor pools are associated with functional grouping of motoneurons of the lower limb muscles. Here we examined how the spatiotemporal organization of lumbar and sacral motor pool activity during walking is orchestrated with slope of terrain and speed of progression. Ten subjects walked on an instrumented treadmill at different slopes and imposed speeds. Kinetics, kinematics, and electromyography of 16 lower limb muscles were recorded. The spinal locomotor output was assessed by decomposing the coordinated muscle activation profiles into a small set of common factors and by mapping them onto the rostrocaudal location of the motoneuron pools. Our results show that lumbar and sacral motor pool activity depend on slope and speed. Compared with level walking, sacral motor pools decrease their activity at negative slopes and increase at positive slopes, whereas lumbar motor pools increase their engagement when both positive and negative slope increase. These findings are consistent with a differential involvement of the lumbar and the sacral motor pools in relation to changes in positive and negative center of body mass mechanical power production due to slope and speed.

NEW & NOTEWORTHY In this study, the spatiotemporal maps of motoneuron activity in the spinal cord were assessed during walking at different slopes and speeds. We found differential involvement of lumbar and sacral motor pools in relation to changes in positive and negative center of body mass power production due to slope and speed. The results are consistent with recent findings about the specialization of neuronal networks located at different segments of the spinal cord for performing specific locomotor tasks.

INTRODUCTION

The final output of the locomotor circuitry comprising supraspinal, sensory, and central pattern generator (CPG) signals is represented by the spatiotemporal modulation of α-motoneuron (MN) activity (Brown 1914; Grillner 1981; Kiehn 2016). In the course of evolution, motor circuits in the spinal cord were assembled to meet specific body movement requirements and specific spatial arrangement and biomechanical function of limb muscles (Jessell et al. 2011). A sequential trunk muscle activation for the undulatory body movements (de Sèze et al. 2008) was replaced by more complex and discrete bursts of limb MN activity related to specific kinematic and kinetic events (Lacquaniti et al. 2012). Each human lower limb contains >50 muscles, and corresponding MNs are grouped in motor columns (Sharrard 1964) whose spatiotemporal organization is precisely orchestrated during development (Dewitz et al. 2018). Furthermore, motor pool topography contributes to sensory-motor connectivity in the spinal cord (Jessell et al. 2011).

In recent years, there has been growing interest in understanding the functional organization of the spinal locomotor output in the context of neuromodulation of the spinal circuitry (Taccola et al. 2018; Wenger et al. 2016), differential impairment of lumbar and sacral motor pools in gait pathologies (Coscia et al. 2015; Grasso et al. 2004; Martino et al. 2018), and adaptation to different biomechanical requirements (Allen and Franz 2018; Chvatal et al. 2011; Ivanenko et al. 2008; MacLellan et al. 2012; Martino et al. 2015; Santuz et al. 2018). Furthermore, selective stimulation of spinal motor pools represents a promising tool to restore the functioning of the spinal pattern generation circuitry in both animals (Capogrosso et al. 2016; Wenger et al. 2016) and humans (Angeli et al. 2018; Gerasimenko et al. 2015; Solopova et al. 2017; Wagner et al. 2018). Overall, these findings highlight the importance of investigating the functional segmental organization and biomechanical functions of lumbar and sacral motor pools.

Only a few studies have attempted to evaluate the relationship between the spatiotemporal organization of the spinal motor output and biomechanics in human locomotion (Cappellini et al. 2010; La Scaleia et al. 2014; MacLellan et al. 2012; Martinez-Valdes et al. 2018; Yokoyama et al. 2017). During walking, the spatiotemporal organization of the spinal motor pools fluctuates roughly in phase with the motion of the center of body mass (COM) (Cappellini et al. 2010), with bursts of activity around touchdown and foot liftoff (La Scaleia et al. 2014). In particular, biomechanical mechanisms of locomotion, such as inverted pendulum walking dynamics, are related to specific spatiotemporal organization of motor pool activity in the spinal cord (Cappellini et al. 2010). To further investigate the relationships between bursts of MN activity and biomechanical functions, here we examine how the spatiotemporal dynamics of motor pool activity is related to human walking on different slopes and at different speeds.

Recently, we reported modifications in walking biomechanics with slopes (Dewolf et al. 2017, 2018). The changes in the mechanical demands induced modifications in the neuromuscular control during slope compared with level walking (Janshen et al. 2017; Rozumalski et al. 2017; Saito et al. 2018). In particular, Lay et al. (2007) observed nonuniform changes in the muscle activity patterns across negative and positive slopes compared with level walking, suggesting that new control strategies are needed for walking on slopes. Furthermore, we reported a speed-dependent modification in the walking pattern on slopes (Dewolf et al. 2018), reflecting that there is no simple scaling of spinal motor output activity with speed and slope but the involvement of somewhat different neural circuits (Yokoyama et al. 2017).

In light of the above-mentioned considerations and a differential biomechanical function of lower limb muscles (Pickle et al. 2016), we expect that modifications in the spatiotemporal organization of motor pool activity in the lumbar and sacral spinal cord would be related to biomechanical changes due to slope and speed. A better understanding of the outputs of MN pools during different locomotor conditions may provide further insights into interspecies comparison (Carlson-Kuhta et al. 1998; Smith et al. 1998; Yakovenko et al. 2002) and into modularity of neural control in humans with changes in environmental demands (La Scaleia et al. 2014; Santuz et al. 2018). Knowledge about how the nervous system adapts to such demands in normal subjects can provide a basis for understanding deficits in patient populations and may thus have important clinical implications (Cappellini et al. 2016; Grasso et al. 2004; Wagner et al. 2018).

Specifically, we addressed the question of whether the pools of α-MNs are recruited in the same chronological order and relative intensity or are differentially activated as a function of speed and slope. The former case would be implied by the hypothesis that there exists a leading oscillator in the lumbar spinal cord that propagates motor bursts to more caudal segments by means of traveling waves of activity (Cazalets et al. 1995; Cuellar et al. 2009; Saltiel et al. 2016). The latter case, instead, would be implied by the hypothesis that there exist multiple generators of locomotor activity that can operate quasi-independently of each other (Grillner 1981; Hägglund et al. 2013).

The identification of CPGs in humans remains difficult, but one can obtain critical insights by describing the spatiotemporal activation of MN pools during locomotion (Ivanenko et al. 2006a). Spatiotemporal maps of activation are derived from recording electromyogram (EMG) activity profiles from several muscles of the lower limbs during walking and combining these profiles with known lumbosacral segmental organization of MN pools Kendall et al. 1993; Sharrard 1964).

We asked subjects to walk on an instrumented treadmill on inclined surfaces at different imposed velocities. Then, we assessed the spatiotemporal modulation of the MN output by mapping the activity patterns from a large number of simultaneously recorded muscles onto the anatomical rostrocaudal location of the MN pools in the spinal cord, which offers a compact representation of the total motor output (Ivanenko et al. 2006a, 2013b; O’Donovan et al. 2008; Monaco et al. 2010; Warp et al. 2012; Yakovenko et al. 2002). Then, we related the spatiotemporal modulation of the MNs to the kinetics of the COM, to explore relationships between changes in the mechanics of walking and changes in its motor control. In addition, we decomposed the coordinated muscle activation profiles into a small set of common factors. Such factor analysis identified the major neuromuscular activation patterns, allowing further assessment of differential changes in the motor output of the lumbosacral cord as a function of speed and slope.

METHODS

Participants and Experimental Protocol

We recorded surface EMGs at the same time and on the same subjects as in previous studies (Dewolf et al. 2017, 2018). Ten healthy subjects (6 men, 4 women; age: 22.2 ± 2.4 yr, mass: 69.2 ± 14.4 kg, height: 1.75 ± 0.10 m, means ± SD) walked on an instrumented treadmill at seven different inclinations (0°, ±3°, ±6°, and ±9°). Six of them walked on all slopes, two walked at 0° and ±6°, and two walked at 0° and ±9°. At each slope, subjects walked at seven different speeds ranging between 0.56 m/s (2 km/h) and 2.22 m/s (8 km/h); some subjects were not able to walk at 2.22 m/s at all slopes. Between 6 and 36 strides per trials were recorded, and a total of 8,864 strides were analyzed. Before participation, subjects gave written informed consent. The study followed the guidelines of the Declaration of Helsinki, and the procedures were approved by the Research Ethics Committee of the Université catholique de Louvain (Ref. No. 2015/06JUL/372).

Data Recordings

We recorded kinematic data at 100 frames/s with a high-speed video camera (Basler A501k; resolution 1,280 × 1,024 pixels, aperture time 3 ms) fixed on the ground 3 m to the side of the treadmill, perpendicular to the plane of progression. Reflective markers were placed on one side of the subject over the following landmarks: the chin-neck intersect, greater trochanter, lateral femoral epicondyle, lateral malleolus, heel, and fifth metatarsophalangeal joint. The instrumented treadmill measured the normal, parallel, and lateral components of the ground reaction force exerted by the tread belt on the feet. The force signals were digitized by a 16-bit analog-to-digital converter at 1,000 Hz. The vertical (v), fore-aft (y), and lateral components of force and velocity of the COM were then computed with the methods described in Dewolf et al. (2016).

We recorded EMG activity at 2,000 Hz by means of surface electrodes (using the Trigno Wireless EMG System; Delsys, Boston, MA; bandwidth of 20–450 Hz, overall gain of 1,000) from 16 muscles on the right side of each subject. These included one muscle from the lower back [erector spinae (ES) at L₂ level], two muscles from the buttocks [gluteus maximus (Gm) and gluteus medius (Gmed)], eight muscles from the thigh [sartorius (SART), tensor fasciae latae (TFL), adductor longus (ADD), vastus medialis (VM), vastus lateralis (VL), rectus femoris (RF), biceps femoris long head (BF), semitendinosus (ST)], and five muscles from the shank [tibialis anterior (TA), medial gastrocnemius (MG), lateral gastrocnemius (LG), soleus (SOL), peroneus longus (PERL)]. After preparing the shaved skin with fine sandpaper, ether, and alcohol, we placed EMG electrodes (5-mm bar electrodes with a 10-mm interelectrode distance) based on suggestions from SENIAM (http://www.seniam.org), the European project on surface EMG. To this end, we located the muscle bellies by means of palpation and oriented the electrodes along the main direction of the fibers (Kendall et al. 2005; Winter 1991). We verified electrode position and signal quality by visually inspecting the EMG signals while subjects contracted each instrumented muscle and then also visually inspected EMG signals from the walking trials. Some EMG signals from these walking trials were not usable and were thus removed on a subject-specific basis. On average we analyzed 15.3 muscle EMGs from each subject in each condition.

Data Analysis

General gait parameters.

The stride was defined as the period between two right foot contacts (FCs). FC and toe-off (TO) were defined based on the displacement of the center of pressure on the belt (Meurisse et al. 2016). The stride frequency (f) was calculated as the inverse of the time between two successive right FCs. We calculated the beginning of the step-to-step transition phase measuring the index of the minimum (t_v) of the vertical velocity of the COM V_v, as defined by Adamczyk and Kuo (2009). The duration of the double contact phase (t_DC) was determined as the time between FC and TO of the contralateral foot. Both t_v and t_DC were normalized relative to the stride duration.

Terminology for mechanical power.

The mechanical power during walking can be estimated on one hand from the power done to move the COM relative to the surroundings plus the power done on/by the environment and on the other hand as the power developed to the move of the body segments relative to the COM. This division of the power into two parts was proposed for the first time by Fenn (1930) and was improved and popularized by Cavagna et al. (1963). In this “classical” division, the two parts are called external and internal power, respectively. However, this terminology can be misleading, since the terms “external and internal power” are used differently by many authors, as discussed in detail in van der Kruk et al. (2018). Furthermore, this terminology may be confusing because the internal and external powers are both performed “internally,” i.e., within the body (mostly by muscle). To avoid any ambiguity, the terms used are clearly defined in the following section.

COM and peripheral power.

The COM power, Ẇ_com, referred as external power by Cavagna et al. (1963), can be computed by (Gosseye et al. 2010)

$${\dot{\text{W}}}_{\text{com}}=FV$$ (1)

where F and V are the force vector and the velocity vector of the COM, respectively. The pattern of fluctuation of the COM power during walking typically presents one major peak of negative power (Ẇ⁻) and two major peaks of positive power (${\dot{\text{W}}}_1^{+}$ and ${\dot{\text{W}}}_2^{+}$) (Cavagna et al. 1976). Here, the maximum of each of these three peaks were measured across all conditions.

To compute the peripheral power Ė_per, as named by van der Kruk et al. (2018) or Zelik and Kuo (2012) but also referred to as internal power by Cavagna and Kaneko (1977), the body was subdivided into seven rigid segments (trunk + arms + head, thighs, shanks, and feet) as in Davis et al. (1991), the position of the COM of the body was calculated from the position of the center of mass and the mass of each segment, as obtained from anthropometric tables (Dempster and Gaughran 1967). The translational and rotational velocity of the segments relative to the COM was then computed (Willems et al. 1995). Ė_per was then estimated as the time derivative of changes in the sum of the translational and rotational energy of each segment relative to the COM (E_per), computed as

$${\text{E}}_{\text{per}}={\displaystyle {\sum }_{i=1}^7\frac{{\text{m}}_i{v}_{i,\text{com}}^2+{\text{I}}_i{\text{ω}}_i^2}{2}}$$ (2)

where m_i is the mass of the ith segment, v_i,com is the linear velocity of the center of mass of the ith segment relative to the COM, I_i is the moment of inertia, and ω_i is the angular velocity of the ith segment around its center of mass.

EMG activity and bilateral activation.

The raw EMG signals were high-pass filtered (30 Hz) and then rectified and low-pass filtered with a zero-lag third-order Butterworth filter (10 Hz) to obtain the EMG envelopes. To reduce residual baseline noise, which appears as offsets in these envelopes, we subtracted the minimum signal from each envelope (Cappellini et al. 2016; La Scaleia et al. 2014). The timescale was normalized by interpolating individual gait cycles over 400 points (i.e., each 0.25% of the stride). For each subject and for each condition, the average EMG activity was calculated across all gait cycles. To obtain an estimate of the total muscle activity across speeds and slopes, we summed the average EMG activity of all muscles after normalizing them to muscle physiological cross-sectional area (PCSA; Ward et al. 2009).

Neuromuscular control of ipsilateral EMG activities has been previously considered during slope walking (e.g., Janshen et al. 2017; Rozumalski et al. 2017; Saito et al. 2018). In this study, we considered instead the functional implications of bilateral muscle activities. The rationale for the bilateral analysis is that the COM motion results from muscle activities of both legs rather than activities of only one leg. To obtain an estimate of the EMG activity of the left side of the subjects, right average EMG activity was half-cycle shifted, assuming perfect symmetry of bilateral activations (Burnett et al. 2011; Pierotti et al. 1991). Bilateral recording of EMG activities of 15 leg muscles has been previously reported for different locomotor conditions and found to be roughly symmetrical (Cappellini et al. 2010). The activity of the left and right leg muscles was then collapsed within one gait cycle defined for the right leg. The EMG signal from each of the 32 muscles (i.e., 16 measured on right side and 16 projected to estimate left side) was then normalized to its peak value across all conditions for each participant.

Bilateral basic activation patterns were extracted with the nonnegative matrix factorization (NNMF) algorithm (Cappellini et al. 2016; Martino et al. 2015). For every subject, slope, and speed, the average muscle activation profiles were concatenated into an m × n matrix (M), where m indicates the number of muscles (32) and n is the number of time-normalized samples (400). The NNMF algorithm was applied to M to identify the underlying basic activation patterns P and the associated weighting coefficients C (Lee and Seung 2001) as follows:

$$\mathbf{M}=P\text{×}C+\mathbf{e}$$ (3)

where e is the residual error matrix. The algorithm searches for an approximate solution to minimize the root-mean-square error between M and P × C. For a given number of motor components (see below), the factorization uses an iterative method starting from randomly chosen initial conditions for P and C (Gizzi et al. 2011; Ivanenko et al. 2005; Sartori et al. 2013). Because the root-mean-square error may have local minima, the best solution was selected out of 100 iterations to find C and P from multiple random starting values. The degree of similarity between basic patterns across subjects was evaluated based on the best-matching scalar product of weighting coefficients normalized to Euclidean norm (Cheung et al. 2005; Martino et al. 2015).

The goodness of the pattern decomposition was assessed in terms of the percentage of variance accounted for (VAF; Torres-Oviedo et al. 2006):

$$\text{VAF}=\text{1}-\text{SSE/TSS}$$ (4)

where SSE is the sum of squared errors between the experimental and reconstructed excitations and TSS is the total sum of squares after subtraction of the mean from each EMG envelope (Martino et al. 2015). The number of motor components was an input parameter for the NNMF algorithm and was fixed as 4 (as in our previous study, Dominici et al. 2011), because it accounted for >80% of total variance and adding an additional component increased VAF by <5% (see results).

Spinal maps.

To characterize the spatiotemporal patterns of the spinal motor output, the bilateral average EMG activities were mapped onto the estimated rostrocaudal location of the MN pools in the human spinal cord from the L₂ to S₂ segments based on Kendall’s myotomal charts as in Ivanenko et al. (2006a, 2013b). In brief, the maps were constructed by adding up the contributions of each muscle to the total activity at each spinal segment. The motor output pattern of each spinal segment S_j was estimated according to the following equation (La Scaleia et al. 2014):

$$S_j=\frac{{\sum }_{i=1}^{m_j}\left(\frac{k_{ji}}{n_i}\right)\times {\text{EMG}}_i}{{\sum }_{i=1}^{m_j}\left(\frac{k_{ji}}{n_i}\right)}\times {\text{MN}}_j$$ (5)

where EMG_i represents the subject-specific envelope of muscle activity, k_ji is a weighting coefficient for the ith muscle (k_ji = 1, 0.5, or 0 if the jth spinal level is a major, minor, or no source of MN for this muscle, respectively, according to Kendall’s charts), m_j is the number of muscles innervated by the jth spinal segment, and n_i is the total number of spinal levels that innervate the ith muscle, again accounting for major and minor sources. To account for size differences in MN pools at each spinal level, this fractional activity value was then multiplied by the segment-specific number of MNs (MN_j), taken from Tomlinson and Irving (1977).

To obtain the averaged (across subjects) spinal maps at each speed and slope, we calculated the spinal motor output for each subject based on averaged normalized EMG patterns and then averaged spinal maps across subjects. To compute the relative activation of the lumbar and sacral segments in each walking condition, we averaged the motor output patterns over the gait cycle in the upper part of the lumbar (sum of the activity from L₂ to L₄) and the sacral (sum of activity from S₁ to S₂) segments. Because of its intermediate position, spinal segment L₅ has not been taken into account.

Statistics

Data were grouped into speed-slope classes. For each variable studied, to obtain one value per subject in each speed-slope class, the data measured on each stride of a given trial were averaged. The mean and standard deviation of the population were then computed in each speed-slope class (grand mean). Similarly, the curves obtained on each stride of a given subject in a speed-slope class were averaged (mean curve). Then, the mean curves of all the subjects were averaged in each speed-slope class (ensemble averaged). After checking for normality of data distribution, the variables were analyzed across all conditions by using a repeated-measures ANOVA with post hoc Bonferroni correction to assess the difference between conditions (PASW Statistics 19, SPSS, IBM). An α threshold of 0.05 was used throughout to assess statistical significance.

Both for temporal basic activation patterns and weighting coefficient, similarities between level and slope walking at each speed of progression were assessed by measuring the scalar product between data of individual subjects walking on slope and the average data across subjects walking on the level. Similarities between level and slope walking at different speeds were assessed by correlating the time curves of basic muscle activation pattern, of COM and peripheral power, and of lumbar and sacral segment motor output during walking on a slope with the time curves during walking on the level. Therefore, we measured the Pearson correlation between curves of individual subjects walking on a slope and the average curve (across subjects) obtained during level walking. To average the individual correlations across subjects, we averaged the Fisher’s z-transformed r and back-transformed the average z value.

RESULTS

Gait Parameters and Mechanical Power

The step frequency f increases with speed (ANOVA; F = 605.7, P < 0.001) but is not significantly affected by the slope of the terrain (Bonferroni post hoc; P > 0.344), except at −9°, where f is slightly greater than on the level (Fig. 1B), especially at slow walking speeds. These results are in accordance with Kawamura et al. (1991) and Sun et al. (1996). The relative duration of stance and swing phases is also affected by the speed of progression since t_DC decreases with increasing speed (ANOVA; F = 204.3, P < 0.001). t_DC is not affected by the slope of the terrain (Bonferroni post hoc; P > 0.062), except at −9°, where t_DC is slightly shorter than on the level, especially at slow walking speed. The time (t_v) between FC and the minimum of the vertical component of velocity of the COM changes with gait speed (ANOVA; F = 40.3, P < 0.001) but also with slope (ANOVA; F = 189.6, P < 0.001). At slow speed, t_v occurs around FC at all slopes. As speed increases, t_v occurs later on negative slopes and earlier both on the level and on positive slopes.

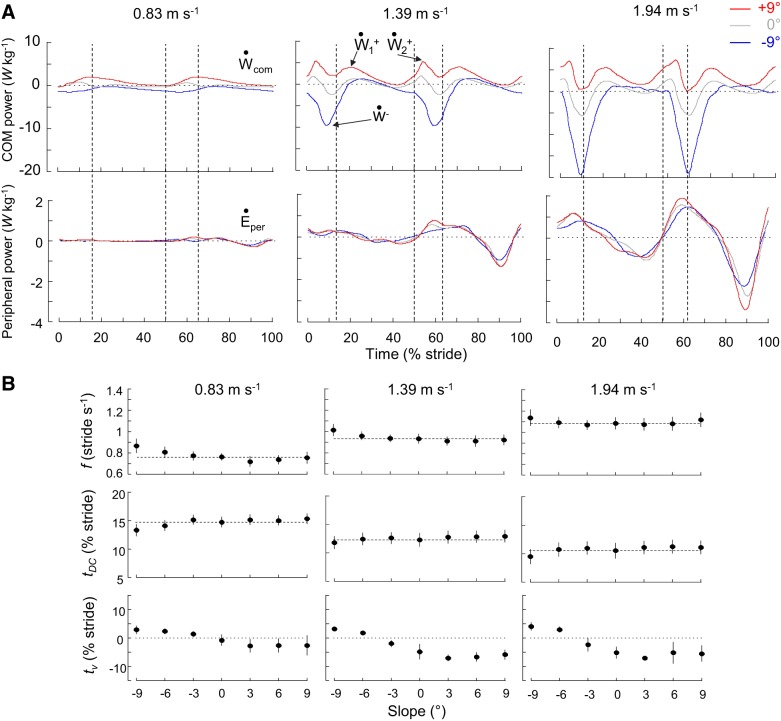
Fig. 1.

Center of body mass (COM) and peripheral power and stride parameters during walking at 0.83, 1.39, and 1.94 m/s on different slopes. A: ensemble-averaged time curves (see methods) of the mass-specific COM (top) and peripheral (bottom) powers (also referred to as external and internal power) during walking at 0.83, 1.39, and 1.94 m/s on a −9°, 0°, or +9° slope. Time is expressed as % of stride period (0% and 100% of stride correspond to the right foot contact). Vertical dashed lines correspond to foot contact (50% of stride corresponds to the left foot contact) and toe-off. Note that at a given speed curves of the peripheral power are similar across slopes, whereas curves of the COM power change drastically with slope. Ẇ_com, COM power; ${\dot{\text{W}}}_{\text{com}}^{+}$, positive portion; ${\dot{\text{W}}}_{\text{com}}^{-}$, negative portion; Ė_per, peripheral power. B: gait parameters (means ± SD) as a function of slope in the 3 speed-classes. Gait parameters are, from top to bottom: stride frequency (f), relative duration of the double contact phase (t_DC), and the time between touchdown and the minimum vertical velocity of the COM (t_v). t_DC and t_v are expressed in % of stride period. The horizontal dashed lines correspond to level walking. Symbols and bars represent the grand mean and the SD (when the length of the bar exceeds the size of the symbol).

The Ė_per curves are highly affected by the speed of progression but are similar across slopes (Fig. 1A): the correlation coefficient (r²) of the time course between Ė_per on slopes and Ė_per on the level is 0.88 ± 0.07 at 0.83 m/s, 0.93 ± 0.05 at 1.39 m/s, and 0.93 ± 0.07 at 1.94 m/s. The Ẇ_com curves are highly affected by both speeds and slopes: the correlation coefficient between Ẇ_com curves on slopes and Ẇ_com on the level is 0.38 ± 0.44 at the slowest speed and increases up to 0.83 ± 0.17 at the highest speed (Fig. 1A).

The modifications of the gait dynamics with slope are thus mainly linked to modifications of Ẇ_com. In level and downhill walking, the Ẇ_com-time curves display one peak of negative power (Ẇ⁻) occurring ~10% after FC. At low walking speeds, the magnitude of this peak is slightly greater when walking downhill than when walking on the level. When speed increases, the magnitude of this peak changes (F_3,215 = 236.09, P < 0.001) at a faster rate in downhill walking than on the level. During level and uphill walking, the Ẇ_com-time curves display two peaks of positive power.

At all slopes, the magnitude of ${\dot{\text{W}}}_1^{+}$ is greater than the magnitude of ${\dot{\text{W}}}_2^{+}$. When walking uphill at slow speeds, the magnitude of these two peaks is greater than on the level (${\dot{\text{W}}}_1^{+}$ F_3,215 =284.46, P < 0.001 and ${\dot{\text{W}}}_2^{+}$ F_3,215 = 171.44, P < 0.001). When speed increases, these two peaks increase (F_6,215 = 218.59 and F_6,215 = 161.01, P < 0.001) at a faster rate in uphill walking than on the level (F_6,215 = 102.81, P < 0.001). When walking downhill, both ${\dot{\text{W}}}_1^{+}$ and ${\dot{\text{W}}}_2^{+}$ decrease with increasing slope. Note that on steep negative slopes ${\dot{\text{W}}}_2^{+}$ tends to disappear.

EMG Activity

Figure 2A illustrates the ensemble-averaged EMG envelopes when walking on the level and on a +9° and a −9° slope. EMGs are visually consistent with those reported in the literature for level walking (Ivanenko et al. 2006a; Winter 1991) and inclined walking (Lange et al. 1996; Sun et al. 1996).

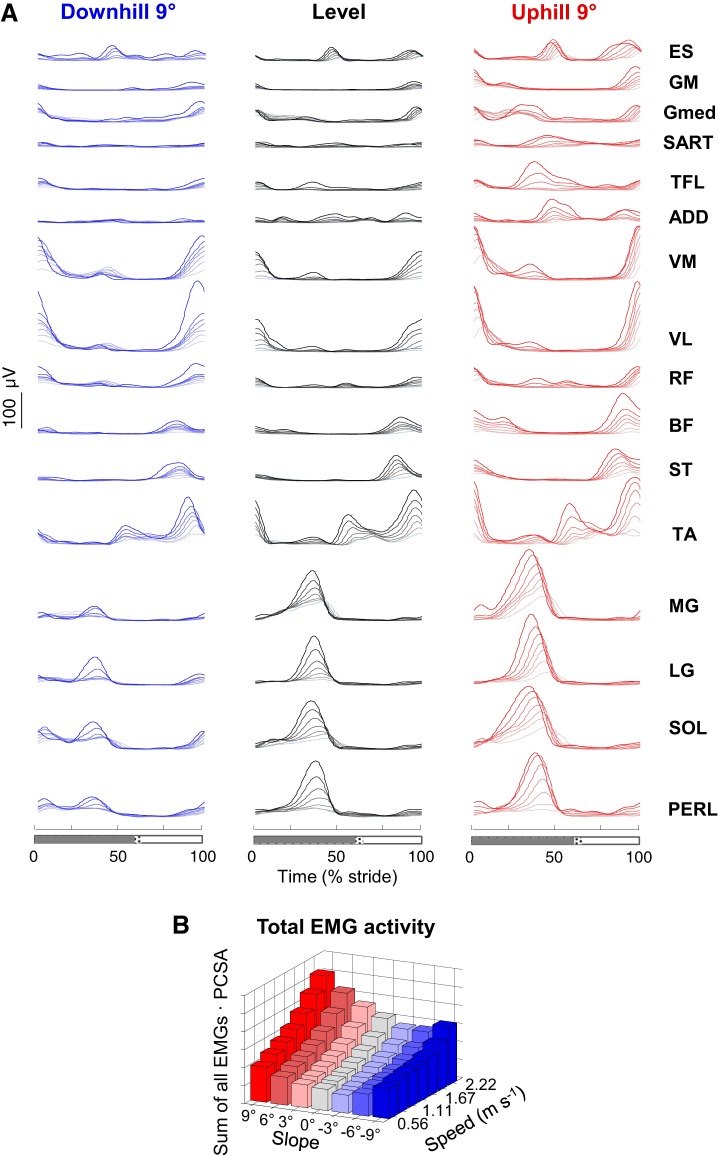
Fig. 2.

Ensemble-averaged electromyogram (EMG) patterns during walking at different speeds and slopes. A: ensemble-averaged EMG patterns during walking at different speeds (color intensity increases with speed) on a −9° slope (left), on the level (center), and on a +9° slope (right). ES, erector spinae; GM, gluteus maximus; Gmed, gluteus medius; SART, sartorius; TFL, tensor fascia latae; ADD, adductor longus; VM, vastus medialis; VL, vastus lateralis; RF, rectus femoris; BF, biceps femoris; ST, semitendinous; TA, tibialis anterior; MG, gastrocnemius medialis; LG, lateral gastrocnemius; SOL, soleus; PERL, peroneus longus. Stance (gray bar) and swing (white bar) are shown at bottom. As the relative duration of stance varied with speed, a hatched region also indicates an amount of variability in the stance phase duration across speeds. B: total EMG activity normalized to the physiological cross-sectional area (PCSA) of muscles (Ward et al. 2009) at all speeds and slopes. Note a minimum between −3° and −6° slope depending on the walking speed.

In all muscles, the mean EMG amplitude changes with the speed of progression (ANOVA; F_6,355 > 3.7, P < 0.002) and with the slope of the terrain (ANOVA; F_6,355 > 11.9, P < 0.001). When speed increases, muscle activities increase. By contrast, the changes across positive or negative slopes are different: for +9° uphill walking the average EMG amplitude of all muscles over the gait cycle is increased compared with level walking (Bonferroni post hoc ;P < 0.001), whereas on a −9° slope the average amplitude of some EMGs is reduced with slope (ADD, ST, TA, MG, LG, PERL; Bonferroni post hoc; P < 0.032) and the amplitude of other EMGs is increased (TFL, VM, VL, RF; Bonferroni post hoc; P < 0.001). As a result, the summed average EMG activity of all muscles normalized to the cross-sectional area have a minimum at a slope ranging between −3° at slow speeds and −6° at high speeds (Fig. 2B).

When walking on a slope, there are also deviations from EMG bursting patterns observed during level walking. Indeed, additional bursts of activity appear in uphill and downhill walking. For instance, an additional burst of activity appears in the distal extensors (MG, LG, SOL, PERL) at the onset of stance at negative slopes, which is normally absent during level walking.

Bilateral Basic Activation Patterns

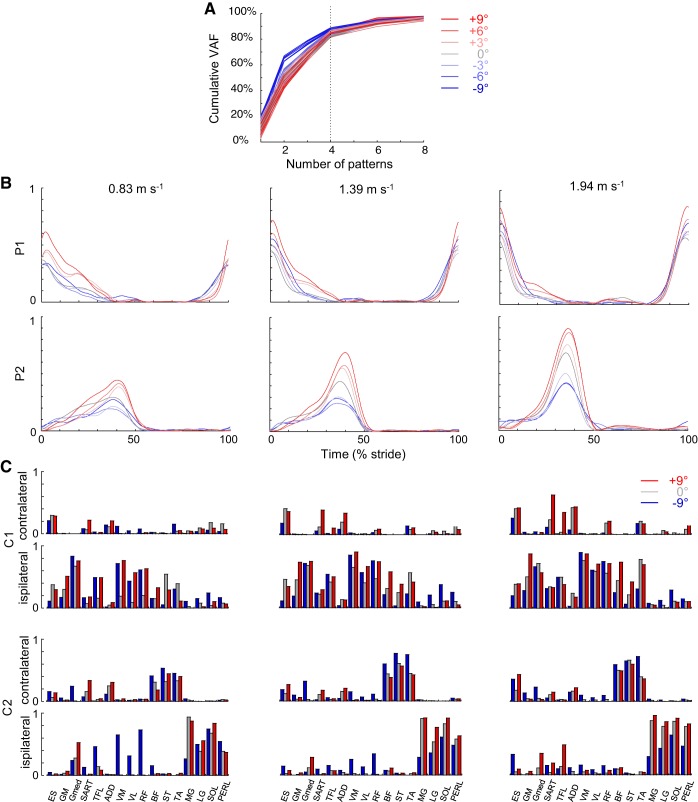
Analysis of dimensionality with the NNMF method shows that bilateral EMG activity changes during slope walking are captured by a small number of motor modules (Fig. 3). The percent total VAF by four basic patterns is equal to 85.1 ±4.9% (mean ± SD) (Fig. 3A). Adding an additional component increased VAF by only 4.2 ± 2.0%. A small but significant effect of speed is observed on the VAF (F_6,360 = 3.8, P = 0.001): the VAF decreases with increasing speed, from 0.56 to 2.22 m/s. Note that the VAF was greater in downhill walking than on the level or uphill walking.

Fig. 3.

Bilateral basic muscle activation patterns assessed by nonnegative matrix factorization (NNMF). A: cumulative % of variance accounted for (VAF) explained by basic electromyogram (EMG) patterns at all speeds and slopes. B: basic activation patterns during walking at 0.83, 1.39, and 1.94 m/s on different slopes. Each curve represents the ensemble-averaged pattern for a specific slope. The basic patterns are named in a “chronological” order (P1 appears around foot contact, whereas P2 appears at the end of single stance, etc.). Since P3 and P4 were half-cycle-shifted copies of P1 and P2, we illustrate only P1 and P2 (accordingly, the associated weighting coefficients of P1 and P2 are the same as for P3 and P4 but reversed for the ipsilateral and contralateral legs). C: corresponding group mean weights (synergies; C1 and C2) for ipsilateral and contralateral leg muscles in −9° downhill, level, and +9° uphill walking. The gait cycle starts with the right foot contact, whereas the NNMF analysis was performed for bilateral EMG envelopes, so that weights for the ipsilateral and contralateral leg muscles are different. ES, erector spinae; GM, gluteus maximus; Gmed, gluteus medius; SART, sartorius; TFL, tensor fascia latae; ADD, adductor longus; VM, vastus medialis; VL, vastus lateralis; RF, rectus femoris; BF, biceps femoris; ST, semitendinous; TA, tibialis anterior; MG, gastrocnemius medialis; LG, lateral gastrocnemius; SOL, soleus; PERL, peroneus longus.

Because the timing of four main activity peaks during walking is temporally synchronized on opposite sides of the body, two patterns (P3 and P4) are phase shifted by one half-cycle from the other two (P1 and P2). Accordingly, the associated weighting coefficients of P1 and P2 are the same as for P3 and P4 but reversed for the ipsilateral and contralateral legs. Therefore, only the basic activation patterns P1 and P2 and the corresponding weightings (muscle synergies) are reported in Fig. 3, B and C. Although both slope and speed affect the associated weighting coefficients (Fig. 3C), the timing of activity peaks (Fig. 3B) is relatively invariant across speeds and slopes: pattern P1 occurs around FC, whereas pattern P2 occurs during the second part of single stance. However, the shape and the amplitude of the basic activation patterns (Fig. 3B) are modified with speed and slope. The peak magnitude of all basic patterns increases with speed (ANOVA; F_6,360 >75.9, P < 0.001) and on positive slopes compared with on the level (Bonferroni post hoc; P < 0.037). On negative slopes, the maximum of P1 increases whereas the maximum of P2 decreases compared with on the level (Bonferroni post hoc; P < 0.001).

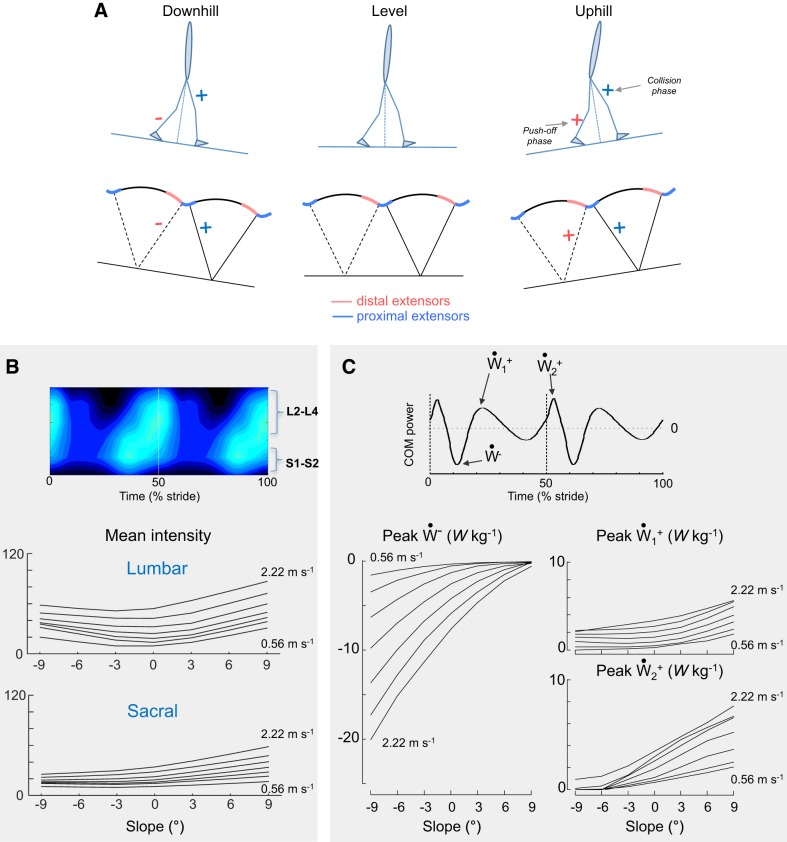
Spinal Maps

Figure 4 presents the average segmental MN output over one gait cycle. Qualitative similarities in temporal profile are observed across speeds and slopes. In particular, two major “spots” of activity are present: the first burst around FC mainly localized on the lumbar segment and the second burst during the second part of single stance mainly localized on the sacral segment.

Fig. 4.

Bilateral spatiotemporal spinal motor outputs computed from ensemble-averaged electromyograms (EMGs) during walking at different speeds and slopes. Motor output (reported in % of maximal activation) is plotted as a function of gait cycle, the vertical white dotted line corresponding to half (50%) of gait cycle. Note that the intensities of both the lumbar and the sacral segments increase monotonically with speed, but that these intensities change differently on positive and on negative slopes.

In contrast to the qualitatively similar temporal characteristics, there are substantial differences in the intensity of spinal activation across slopes. In particular, the most striking feature in the spinal maps is a systematic change in the lumbar and sacral segmental outputs. The mean motor output intensity of the total lumbar (L₂–L₄) and sacral (S₁–S₂) MN activation increases with speed of locomotion (lumbar F_6,360 = 80.8, P < 0.001; sacral F_6,360 = 67.1, P < 0.001). These intensities are also affected by the slope of the terrain (lumbar F_6,360 = 54.4, P < 0.001; sacral F_6,360 =79.5, P < 0.001): compared with the level, the maximal intensity of the lumbar MN activation increases in both positive and negative slopes whereas the maximal intensity of the sacral MN activation increases in uphill walking and slightly decreases in downhill walking. Note that the effect of speed on sacral activity is more marked on a positive than a negative slope (F_6,360 = 1.76, P < 0.006).

Correspondence Between Mechanical Power and Spinal Maps

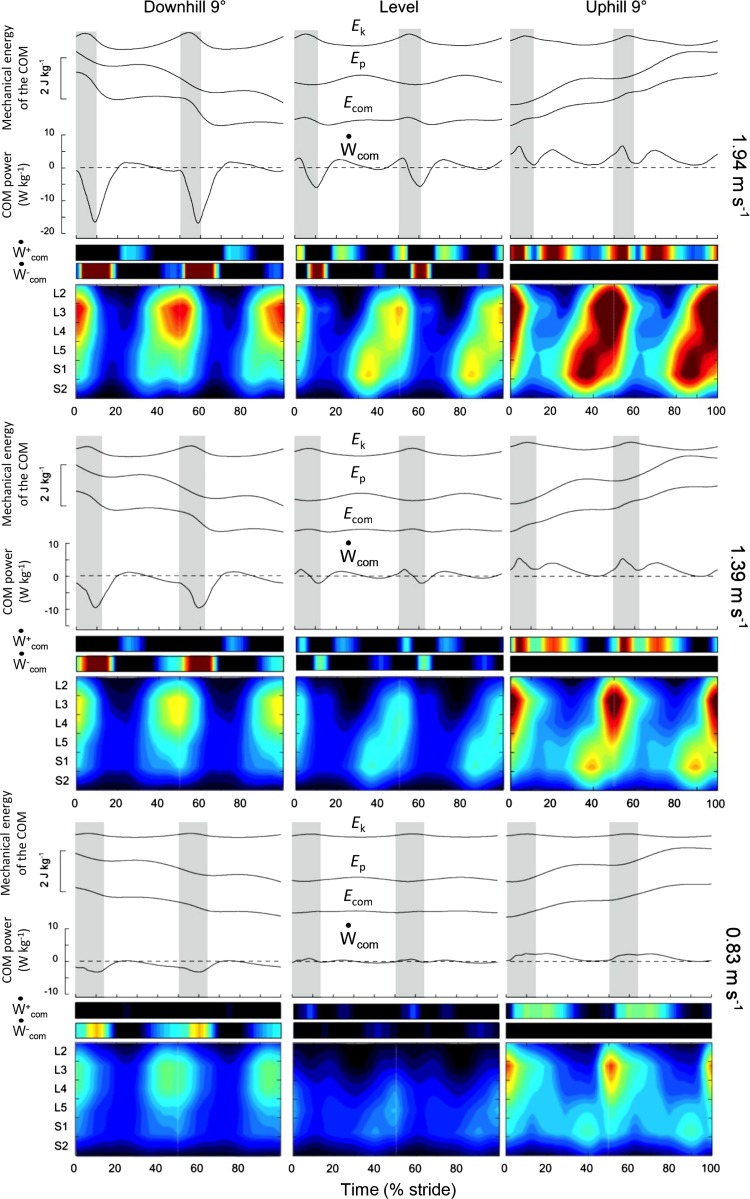
Since Ė_per curves are similar across slopes (Fig. 1A), the modifications of spinal motor output are mainly related to changes in Ẇ_com-time curves. During level walking, the Ẇ_com-time curves during each step tend to follow a consistent pattern of fluctuations (Fig. 1A and Fig. 5). A phase of negative power (Ẇ⁻) presenting a peak ~10% after FC occurs after the collision with the ground. Ẇ⁻ is followed by a first phase of positive power (${\dot{\text{W}}}_1^{+}$; Fig. 6C). The phases Ẇ⁻ and ${\dot{\text{W}}}_1^{+}$ contribute to the vertical redirection of the COM after FC and are designated as the Collision phase. A second phase of positive power (${\dot{\text{W}}}_2^{+}$; Fig. 6C) starts at the end of single stance, and its peak occurs close to the bottom of the COM trajectory. This phase accelerates the COM and is designated as the Push-off phase.

Fig. 5.

Mechanical energy of the center of body mass (COM) motion and spinal maps during walking at 0.83, 1.39, and 1.94 m/s on a −9° slope (left), on the level (center), and on a +9° slope (right). Top: the ensemble-averaged mass-specific mechanical energy-time curves of the COM during a stride. E_k, the kinetic energy of the COM; E_p, its gravitational potential energy; E_com, the total energy of the COM (E_com = E_k + E_p). Middle: the COM power (Ẇ_com, black curves) and its positive (${\dot{\text{W}}}_{\text{com}}^{+}$) and negative (${\dot{\text{W}}}_{\text{com}}^{-}$) portions (color scale). Gray zones correspond to the double contact periods. Bottom: color plots refer to the bilateral spinal maps of motoneuron activity (the same format as in Fig. 4).

Fig. 6.

Differential changes in the lumbar and sacral spinal locomotor output and center of body mass (COM) power. A: schematic representation of changes in the proximal and distal extensor muscles with slope. + and − signs mean that the muscular activity increases/decreases compared with level walking. B: changes in the mean intensity of the estimated upper lumbar (L₂+L₃+L₄) and sacral (S₁+S₂) segments with walking speed and slope. C: changes in the positive (${\dot{\text{W}}}_{\text{1}}^{+}$ and ${\dot{\text{W}}}_{\text{2}}^{+}$) and negative (Ẇ⁻) peaks of the COM power with speed and slope. Since there are 2 peaks of Ẇ_com in most conditions (see Figs. 1 and 5), the amplitude of both the first ${\dot{\text{W}}}_{\text{1}}^{+}$ and second ${\dot{\text{W}}}_{\text{2}}^{+}$ peaks was evaluated (right).

We observe a systematic temporal correspondence between the major loci of MN activity and the fluctuations of Ẇ_com (Fig. 5 and Fig. 6). Note that a temporal delay occurs between MN activations and the peaks of Ẇ_com. First, there is a temporal correspondence between the MN activity of the lumbar locus and the occurrence of the Collision phase. This first locus is associated with EMG activity in proximal lower limb and ankle dorsiflexor muscles. The lumbar segment activation increases with slopes in both downhill and uphill walking. Ẇ⁻ increases on a negative slope, whereas ${\dot{\text{W}}}_1^{+}$ increases on a positive slope. As a result, there is increasing MN activity in the lumbar locus during the Collision phase. Second, there is a systematic temporal correspondence between the MN activity of the sacral locus and the occurrence of the Push-off phase. When slope changes from −9° to +9°, both the sacral spinal activity and ${\dot{\text{W}}}_2^{+}$ increase, suggesting monotonic changes in the Push-off phase between a steep negative and a steep positive slope.

Differential Effect of Speed

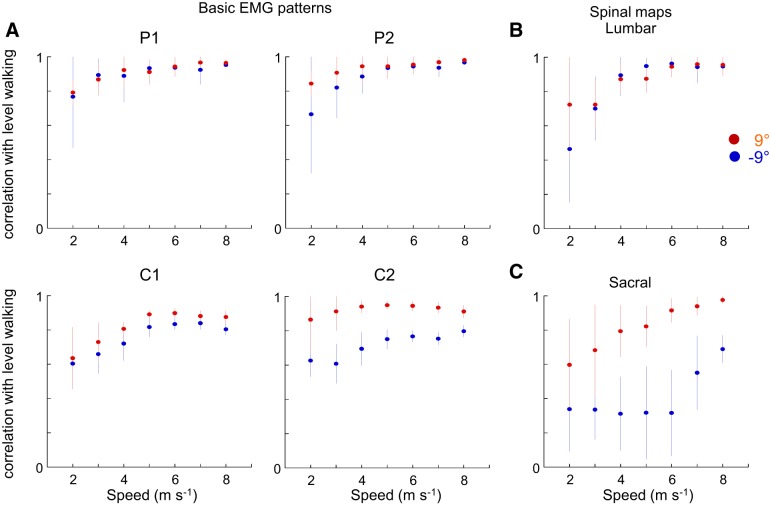
Changes in the motor pattern due to inclination of the terrain depend on walking speed. Indeed, the correlation between basic activation patterns (P1 and P2 and C1 and C2) on a steep slope and the same patterns on the level is smaller at slow than at fast speeds (Fig. 7A). The same observation can be made for the lumbar and sacral segment activities (Fig. 7B).

Fig. 7.

Differential effect of speed during walking on ±9° slopes. A, top: correlation between basic muscle activation patterns (P1 and P2) on a slope and basic muscle activation patterns on the level, as a function of speed. Bottom: correlation between muscle synergies (C1 and C2) on a slope and muscle synergies on the level. B: correlation between lumbar activity (L₂+L₃+L₄) when walking on a slope and lumbar activity when walking on the level. C: correlation between sacral activity (S₁+S₂) when walking on a slope and sacral activity when walking on the level. Patterns, synergies, and lumbar and sacral activities from individual subjects walking on a slope are correlated with the grand mean of these variables obtained during level walking. Points and bars represent the mean correlation ± SD of the correlation coefficients (see methods).

DISCUSSION

In this study, we examined neuromechanical relationships between lower limb muscle activity, associated spinal motor pool activation, and COM kinetics in humans walking at different speeds on different slopes. Spinal maps (Fig. 4 and Fig. 5) showed four major loci of activity associated with the major kinetic events of the Collision and Push-off phases (Fig. 5 and Fig. 6). Furthermore, the results supported our expectation that walking on negative and positive slopes at different speeds is characterized by a different involvement of the lumbar and sacral motor pools (Fig. 6). Statistical analysis of bilateral muscle activity patterns confirmed a similar temporal organization of the major bursts of activity but showed differential changes in the amplitude of basic activation patterns as a function of speed and slope (Fig. 3). Below, we discuss the changes of the segmental spinal motor output in relation to power production, supporting the idea that multiple generators of locomotor activity are differentially activated as a function of speed and slope.

EMG Patterns and General Biomechanical Characteristics of Walking on Slopes

During walking, muscles consume metabolic energy for positive and negative work related to raising/lowering and accelerating/decelerating the body’s center of mass and limb segments during each stride (Minetti et al. 1993). When walking on a slope, the COM dynamics undergo significant modifications (Dewolf et al. 2017), mainly linked to modification of COM power due to changes in the COM gravitational potential energy. These different biomechanical demands on slopes require changes in the activity from lower limb muscles. In line with several previous studies in both humans and quadrupeds (Carlson-Kuhta et al. 1998; Hunter et al. 2010; Lay et al. 2007; Pickle et al. 2016; Smith et al. 1998), slope-related changes of EMG activity are highly nonlinear, in contrast to the quasi-linear changes with speed (Fig. 2A). For instance, during uphill walking, the mean activity of all muscles increases. Compared with uphill walking, downhill walking is characterized by greater modifications of the motor output: some muscles show limited changes, whereas others systematically increase or decrease their activity when the slope becomes steeper (Fig. 2A).

Because of the force-velocity relationship, the muscle force produced for a given activation as well as the corresponding metabolic cost depend on the mode of contraction (concentric or eccentric). Furthermore, subjects’ individual differences in PCSA and in thickness of subcutaneous adipose tissue have not been taken into account in this study. Therefore, the sum of PCSA-normalized average EMG activity of all muscles should only be considered as a qualitative parameter, particularly when related to energy consumption. Regardless of those limitations, the overall estimated intensity of EMG activity normalized to the cross-sectional area of muscles shows monotonic changes with speed and presents a minimum around a −3 to −6° slope, depending on walking speed (Fig. 2B). This slope is close to the metabolic optimum slope of approximately −6° (Hunter et al. 2010; Minetti et al. 1993).

Sequential Activation of Lumbar and Sacral Segments

We previously reported that the segmental spinal motor output in humans reveals temporal similarities for disparate walking behaviors, exhibiting peaks around foot strike (Collision) and foot lift (Push-off) for each lower limb (La Scaleia et al. 2014). Moreover, net spinal motor output contributes to mechanical work, mainly during the step-to-step transition to raise/accelerate the COM (Bianchi et al. 1998). The motor patterns on both sides exhibit bursts of activity around foot liftoff of the trailing limb and touchdown of the leading limb (Ivanenko et al. 2006b; La Scaleia et al. 2014, Olree and Vaughan 1995; MacLellan et al. 2014). Accordingly, basic bilateral muscle activation patterns (Fig. 3) show four major loci of activity: these peaks are synchronized on opposite sides of the body so that two patterns (P3 and P4) are phase shifted by a half-cycle from the other two (P1 and P2). These four basic patterns account for ~85% of the total EMG variance of recorded muscles (Fig. 3A); the remaining (~15%) activity is likely related to the natural EMG variability and/or online control of postural/kinematic disturbances and corresponding variability in the sensory feedback. Although this bilateral temporal “program” is rather invariant across speeds and slopes, the shape/amplitude of the basic activation patterns (Fig. 3B) and the associated weighting coefficients (Fig. 3C) change with speed and slope. In particular, the amplitude of the first basic component P1 increases in both uphill and downhill walking, whereas the amplitude of P2 increases during uphill but decreases during downhill walking (Fig. 3).

Slope-related changes in motor patterns were previously discussed in terms of unit burst generators (Grillner 1981) for the control of extensor/flexor muscles of the hip, knee, ankle, or foot (Smith et al. 1998) and of the joint torques (Lay et al. 2007; Pickle et al. 2016). Whereas a comparative analysis of joint powers with the motor pool activation would be meaningful in terms of understanding the contribution of individual joints and muscle groups to the biomechanics of walking on slopes, the lower limb EMG activities are not easily related to joint moments, especially during uphill walking (Lay et al. 2007). Indeed, several muscles are bi- or multiarticular, acting on several joints simultaneously. Some muscles may also generate a noticeable lateral force component (Dostal et al. 1986). Moreover, just because of physics, a torque exerted at one joint may also affect angular motion of dynamically coupled joints of the limb (Ivanenko et al. 2013a; Zajac et al. 2003).

The novelty of our study consists in an integrative approach to evaluation of the bilateral spatiotemporal organization of the spinal motor output linked to specific kinetic events. Indeed, both stance- and swing-related muscle activities contribute to the spinal motor output (Ivanenko et al. 2008; Marsh et al. 2004). When multimuscle EMG activity is mapped onto the rostrocaudal location of the MN pools, the bilateral spinal maps show four major loci of activity at all slopes and speeds (Fig. 4 and Fig. 5). The most striking feature in the spinal maps is a systematic change in the lumbar and sacral segmental output (Fig. 4). Figure 6A schematically summarizes the main findings. Although the overall activity of sacral motor pools decreases on negative slopes and increases on positive slopes, the lumbar motor pools monotonically increase their engagement at all slopes with regard to level walking.

Relationship Between Spinal Motor Pool Activation and Biomechanics of Bipedal Gait

Peripheral power (also referred to as internal power) to move the limbs relative to the COM is rather independent of slope (Minetti et al. 1993; Fig. 1A) whereas COM power (also referred to as external power) accounts for most differences in the energetics of walking on slopes (Fig. 1A). Therefore, it is not surprising that the loci of MN activity precede the major peaks in the COM power (Fig. 5). Some temporal delays between muscle power and activation should be expected given the electromechanical delays, elastic energy storage, dynamic coupling, and velocity dependence of muscle-tendon unit functioning plus limb inertia. However, when analyzing both the biomechanical and neurophysiological aspects of gait, our findings point toward the link between segmental motor pool activation and the mechanics of bipedal gait, which presumably reflects the functional grouping of spinal MNs adopted during evolution (Jessell et al. 2011).

On the whole, there are monotonic changes in the sacral spinal activity and in the magnitude of the second peak of positive power (${\dot{\text{W}}}_2^{+}$). This Push-off phase mainly corresponds to the peak of positive ankle joint power of the trailing limb at the end of stance (Franz and Kram 2014; Lay et al. 2007; Yang et al. 2019) to accelerate the COM and swing limbs (e.g., Zelik and Adamczyk 2016). Push-off before contralateral limb foot strike may reduce the energy lost because of collision with the ground and in turn the metabolic cost of walking (Kuo 2001). On positive slopes, the sacral spinal activity and ${\dot{\text{W}}}_2^{+}$ increase and t_v (i.e., the time at which V_v is minimal) appears earlier (Fig. 1B). Similar increase is also observed in the amplitude of the second basic bilateral activation pattern P2 (Fig. 3B). P2 involves primarily the ankle dorsiflexor and knee flexor of the leading limb and the ankle plantar flexors of the trailing limb (Fig. 3C), which is related to the greater ankle joint power observed at the end of stance (Lay et al. 2006, 2007; Pickle et al. 2016; Yang et al. 2019). On negative slopes, the decrease in the distal extensor muscle activity results in a decrease in the sacral spinal activity and in the amplitude of P2 (Fig. 3B). Furthermore, ${\dot{\text{W}}}_2^{+}$ tends to disappear, which is related to the reduction of the positive ankle joint power of the trailing limb at the end of stance (Lay et al. 2006, 2007; Pickle et al. 2016; Yang et al. 2019). As a result, t_v occurs after FC (Fig. 1B) and a greater collision with the ground occurs at FC.

In the lumbar segment, the MN activation increases when the slope becomes steeper (Fig. 6B). This activity is associated with a peak of negative power Ẇ⁻ followed by the first peak of positive power ${\dot{\text{W}}}_1^{+}$. In uphill walking, the lumbar spinal activity increases and is associated with an increase in the amplitude of the first basic bilateral activation pattern P1, involving primarily hip and knee extensors of the leading limb and ankle dorsiflexors of the trailing limb (Fig. 3B). The positive power ${\dot{\text{W}}}_1^{+}$ during the Collision phase also increases to complete the vertical lift and corresponds essentially to greater peaks of positive hip and knee joint power of the leading limb at early stance (Franz and Kram 2014; Lay et al. 2006, 2007). In downhill walking, the lumbar spinal activity and the amplitude of P1 increase and are associated with an increase in Ẇ⁻ during the Collision phase. This negative power is mainly done to decelerate and lower the COM, via a greater peak of negative knee joint power of the leading limb (Lay et al. 2006, 2007; Pickle et al. 2016) and via soft tissue deformations (Honert and Zelik 2019; Zelik and Kuo 2010).

A comparison of different human gaits and developmental considerations further highlights the link between global biomechanical parameters, such as COM dynamics, and functional spinal cord topography. In neonate stepping, sequential activation of spinal segments and bursts of activity around touchdown and foot liftoff are not yet developed and both lumbar and sacral motor pools are simultaneously activated during midstance (Ivanenko et al. 2013b). In addition, neonates cannot develop enough COM positive and negative power (Dominici et al. 2011; Forssberg 1985), and forward progression needs to be accomplished by the experimenter or by using a moving treadmill belt. In adults, the rostrocaudal displacements of the center of bilateral MN activity mirror the changes in the mechanical energy of the COM motion during both forward and backward walking, as well as in running (Cappellini et al. 2010). During walking on the slippery surface, the shear forces were reduced and the center of MN activity and the kinetic energy oscillations decreased in parallel (Cappellini et al. 2010).

The present results corroborate recent findings about the specialization of neuronal networks located at different segments of the spinal cord for performing specific locomotor tasks. For example, Minassian et al. (2017) suggest that the lumbar pattern generator activity may represent the major oscillator “pacemaker,” and Cazalets and Bertrand (2000) show that the sacral generator may play a more subordinate role, e.g., for adaptation to specific foot-support interactions (Selionov et al. 2009). Moreover, the locomotor neural networks do not seem to fully overlap at the same spinal segments for different locomotor tasks. For instance, in the cat the neuronal networks responsible for forward locomotion are distributed broadly in the lumbosacral segments, whereas networks generating backward locomotion are limited to the caudal part of the spinal cord (Merkulyeva et al. 2018). In addition, substantial reorganization of spinal locomotor networks is observed when moving on slopes (Carlson-Kuhta et al. 1998; Smith et al. 1998), somewhat similar to that observed in human. Indeed, based on anatomical models of the organization of the MN pools within the cat lumbar enlargement (Yakovenko et al. 2002), in downhill walking the modifications of stance-related muscle activities suggest that the motor output of the lower lumbar and sacral segments is reduced whereas that of the upper lumbar segment is increased. In uphill walking, the activities of stance-related muscles increase, suggesting an increase of the upper and lower lumbar segments. Furthermore, when comparing slow and fast speeds of progression, there is no simple scaling of MN and interneuron activity but involvement of rather different neural circuits. This was demonstrated in a variety of animal species (Bellardita and Kiehn 2015; McLean et al. 2008; Yokoyama et al. 2017). Here we observed that, with regard to level walking, modification of basic activation patterns and spinal motor output to slopes is greater at slow speeds than at high speeds (Fig. 7). This is consistent with different telescopic limb behavior on slopes at slow and fast speeds of progression (Dewolf et al. 2018).

Limitations of Study

There are several assumptions implicit in our methods. First, the rectified EMG does not provide a direct measure of the net firing of MNs in the spinal cord (Martinez-Valdes et al. 2018). However, this estimate is reasonable because mean EMG tends to increase fairly linearly with the net motor unit firing rate (Day and Hulliger 2001). Second, we do not take into account some minor interindividual anatomical variability in the spinal maps of MN that has been documented previously (Stewart 1992). Indeed, we used anatomical charts of MN localization in the lumbosacral cord derived from the literature (Kendall et al. 2005) to estimate spatiotemporal maps of activation, since we had no direct estimates of MN localization in our subjects. However, using electrical epidural stimulation of the lumbosacral cord with selective engagement of specific dorsal roots and the corresponding myotomes, Wagner et al. (2018) have recently confirmed Kendall’s charts in spinal cord-injured patients undergoing rehabilitation. Third, our analysis focuses on consistent and reproducible patterns of muscle activation across various steps; the averaging procedure addresses that issue. Another limitation is that we recorded only a subset of muscles, whereas each lower limb contains >50 muscles and most of them are active during walking (Ivanenko et al. 2006a; La Scaleia et al. 2014; Zelik et al. 2015). Nevertheless, although including more muscles may affect the analysis of muscle synergies (Zelik et al. 2014), it is worth noting that the recorded set of muscles constitutes a large part of the total cross-sectional area of lower limb muscles (Ward et al. 2009). Furthermore, the reconstruction of the spinal motor output from multimuscle EMG recordings is relatively insensitive to the subset of muscles analyzed, provided that the key muscles that we studied here are included (La Scaleia et al. 2014). In particular, the major part of MN activity is organized in bursts (Fig. 4) with tightly coupled phasing in all spinal segments and across the midline (Ivanenko et al. 2006a; Kiehn 2016).

Despite these limitations, our results show changes in the spinal motor output when walking at different slopes and speeds. A striking feature of walking on slopes is the differential involvement of the lumbar and sacral motor pools in relation to changes in the mechanical demand. Such investigations of spatiotemporal patterns of spinal cord activations and their dependence on the walking environment may also have important clinical implications. For instance, differential spinal cord segment stimulation (epidural or transcutaneous) is a promising tool to restore the functioning of the spinal pattern generation circuitry in both animals (Capogrosso et al. 2016; Wenger et al. 2016) and humans (Angeli et al. 2018; Gill et al. 2018; Solopova et al. 2017; Wagner et al. 2018), and such stimulation techniques should take into account differential activation of spinal segments to selectively drive neuroprostheses depending on walking conditions, such as changes in slope.

GRANTS

This study was funded by the Université catholique de Louvain, the Fonds de la Recherche Scientifique (Belgium), the Italian Ministry of Health (IRCCS Fondazione Santa Lucia Ricerca corrente), the Italian Space Agency (Grant I/006/06/0 and MARS-PRE), the Italian Ministry of University and Research (PRIN Grants 2015HFWRYY_002 and 2017CBF8NJ_005), and the Horizon 2020 Robotics Program (ICT-23-2014 under Grant Agreement 644727-CogIMon).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Y.I., K.E.Z., F.L., and P.A.W. conceived and designed research; K.E.Z., F.L., and P.A.W. performed experiments; A.H.D., Y.I., and K.E.Z. analyzed data; A.H.D., Y.I., F.L., and P.A.W. interpreted results of experiments; A.H.D. and Y.I. prepared figures; A.H.D. and Y.I. drafted manuscript; A.H.D., Y.I., K.E.Z., F.L., and P.A.W. edited and revised manuscript; A.H.D., Y.I., K.E.Z., F.L., and P.A.W. approved final version of manuscript.