Estimation of indirect social genetic effects for skin lesion count in group-housed pigs by quantifying behavioral interactions

Abstract

Mixing of pigs into new social groups commonly induces aggressive interactions that result in skin lesions on the body of the animals. The relationship between skin lesions and aggressive behavioral interactions in group-housed pigs can be analyzed within the framework of social genetic effects (SGE). This study incorporates the quantification of aggressive interactions between pairs of animals in the modeling of SGE for skin lesions in different regions of the body in growing pigs. The dataset included 792 pigs housed in 59 pens. Skin lesions in the anterior, central, and caudal regions of the body were counted 24 h after pig mixing. Animals were video-recorded for 9 h postmixing and trained observers recorded the type and duration of aggressive interactions between pairs of animals. The number of seconds that pairs of pigs spent engaged in reciprocal fights and unilateral attack behaviors were used to parametrize the intensity of social interactions (ISI). Three types of models were fitted: direct genetic additive model (DGE), traditional social genetic effect model (TSGE) assuming uniform interactions between dyads, and an intensity-based social genetic effect model (ISGE) that used ISI to parameterize SGE. All models included fixed effects of sex, replicate, lesion scorer, weight at mixing, premixing lesion count, and the total time that the animal spent engaged in aggressive interactions (reciprocal fights and unilateral attack behaviors) as a covariate; a random effect of pen; and a random direct genetic effect. The ISGE models recovered more direct genetic variance than DGE and TSGE, and the estimated heritabilities $\left({\widehat{h}}_D^2\right)$ were highest for all traits (P < 0.01) for the ISGE with ISI parametrized with unilateral attack behavior. The TSGE produced estimates that did not differ significantly from DGE (P > 0.5). Incorporating the ISI into ISGE, even in a small dataset, allowed separate estimation of the genetic parameters for direct and SGE, as well as the genetic correlation between direct and SGE $\left({\widehat{r}}_{ds}\right)$, which was positive for all lesion traits. The estimates from ISGE suggest that if behavioral observations are available, selection incorporating SGE may reduce the consequences of aggressive behaviors after mixing pigs.

INTRODUCTION

In swine production systems, animals may be periodically remixed into new groups throughout their productive life to facilitate management. Mixing unfamiliar pigs into new social groups is usually followed by a period of physically damaging aggression that is more intense in the first few days postmixing (Turner et al., 2009). One of the consequences of damaging aggression is the occurrence of skin lesions that may have a negative impact on the welfare, productivity, and health of individual pigs (Turner et al., 2009; Camerlink et al., 2013; Wurtz et al., 2017; Peden et al., 2018). Management changes that reduce aggression are costly to implement, and a breeding solution to this problem may be valuable (Peden et al., 2018). The presence of skin lesions (i.e., fresh wounds) is commonly associated with an individual being the recipient of damaging aggression. However, a positive genetic correlation exists between delivery of aggression in single-sided attacks and the number of lesions on the front body region of the pig that attacks, suggesting that the same pig can have a genetic predisposition to deliver and receive aggression (Turner et al., 2008, 2009). Examining the relationship between damaging aggressive behavior and skin lesions improves our understanding of the genetics of aggressive interactions in group-housed pigs. Thus, it is essential to elicit better models to analyze these 2 traits simultaneously.

So far, the joint analysis of behavioral variables (i.e., time spent delivering attacks) and lesion counts have been performed using bivariate classical animal models (Turner et al., 2008, 2009). However, such an approach does not explicitly model the effect of the delivery of aggression by one individual on the count of lesions produced on the skin of the animal delivering aggression and of its group mates. A way to explicitly model the effect of the aggressor on the recipients is by fitting social genetic effect models (SGE, Griffing, 1967, 1968a, 1968b; Moore et al., 1997). In an SGE model, 2 types of genetic effects are estimated: the direct effect, which is the effect of the animal’s genotype on its own phenotype and the SGE, which is the effect of the animal’s genotype on its group mates. These models have been applied to describe genetic effects of competition and aggression (Muir 2005; Bergsma et al., 2008; Ellen et al., 2008; Alemu et al., 2014). A common assumption in these models is that the interactions between social group mates are uniform (Bijma et al., 2007). Specifically, the non-zero elements of the incidence matrix of the social effect (Z_S), are values equal to one in the columns that relate the individual phenotype to the SGE of all its group mates. In other words, the model does not explicitly consider variation in the intensity of interaction among individuals. However, considering the results of Büttner et al. (2015) and Foister et al. (2018) who reported strong evidence of unequal distribution of aggressive interactions in dyads, a model that explicitly accounts for such data when available has potential to recover more variation, while in the absence of detailed data on social interactions, a traditional social effects model will be more convenient. A notorious problem associated with uniform interactions in Z_S is that the common environmental effect may be partially confounded with the social effect, which may render some variance components nonestimable (Arango et al., 2005; Van Vleck and Cassady, 2005; Van Vleck et al., 2007). The partial confounding between social effects and common environmental effects can sometimes be avoided by deliberate allocation of genetic groups and families across social groups (Bijma, 2010). But this solution may not always be available in some industry settings.

An alternative way to deal with the potential lack of identifiability of the (co)variance components for SGE has been addressed by Cantet and Cappa (2008), who propose to replace non-zero elements of Z_s with an estimate of the pairwise intensity of social interactions (ISI) between individuals (Cappa and Cantet, 2008). This approach has been used successfully in tree breeding, where the intensity of competition between trees can be easily modeled based on the distance and relative location of each pair of individuals, but it is harder to implement in animals that perform more complex social interactions. Ragab et al. (2019) first attempted to use a nonuniform Z_s matrix for data on feeding behavior in pigs. However, those authors did not explicitly use pairwise behavior records. Using direct observations of behavioral pairwise interactions between animals in a social group to parametrize who propose to replace non-zero elements of has 2 potential benefits: 1) avoiding the confounding of SGE and some common environmental effects and 2) explicitly modeling the causal effect of aggressive interactions on the number of skin lesions that an animal receives on itself and delivers to its group mates.

The goal of the current research is to employ SGE models with ISI to incorporate records of aggressive behavior into the analysis of skin lesion traits in grow-finishing pigs immediately after mixing. By doing so, we can effectively separate SGE from direct genetic effects and from common environmental effects. Moreover, we show that these models recover more variance than models that only include direct genetic effects and models with SGE that assume uniform interactions among group members. Finally, we explain how the direct and SGE are correlated with each other and how these models separate the effect that delivering aggression has on the animal’s own phenotype and on the phenotype of the animal’s group mates.

MATERIALS AND METHODS

All animal protocols were approved by the Institutional Animal Care and Use Committee (Animal Use Form number 01/14-003-00).

Experimental Population

The experimental population used for the current analyses is described in detail in Wurtz et al. (2017). Briefly, animals were housed at the Michigan State University Swine Teaching and Research Center, East Lansing, MI. The dataset consisted of 792 Yorkshire pigs (406 gilts, 386 barrows) with mean age of 66.75 d (SD ±3.02) and mean weight 27.13 kg (SD ±3.6) for gilts and mean age of 66.80 d (SD ±3.11) and mean weight 27.01 kg (SD ±4.49) for barrows that were strategically remixed into new groups of single-sex familiar and unfamiliar animals going into the growth-finishing stage. Animals were regrouped into 59 pens (10 to 15 pigs per pen with at least 2 and no more than 6 familiar pigs, while the rest were unfamiliar) over 7 replicates, resulting in an average of 3.6 ± 0.8 familiar pigs per finisher pen.

Lesion Counting

Lesion scoring was performed by 3 trained observers and consisted of counting the total number of skin lesions immediately prior to mixing and 24 h postmix. The trait was recorded on both sides of the body on 3 body regions: anterior, central, and caudal. A lesion was counted when a single and continuous scratch was noticed fresh (within the last 24 h), regardless of severity. Fresh lesions were judged based on redness and development of scabbing (Wurtz et al., 2017).

Behavioral Observations

Animals were video-recorded for 9 h postmixing (5 h immediately after mixing and 4 h to the next morning) and 21 trained observers characterized in detail damaging and nondamaging aggressive behaviors. Records included the initial and end times of fights between pairs of pigs, and the identity of the pig that started the aggressive interaction. The ethogram of aggressive interactions allowed for classifying and encoding 8 types of behavior. In the current study, the focus was on 2 forms of unidirectional interaction (Attack and Single Bite) and 1 bidirectional interaction (Reciprocal Fight). An attack was coded when a pig inflicted damaging aggression for a minimum of 1 s, while the recipient pig did not return damaging aggression during the event. A single bite was recorded when a pig delivered a knock with the head or snout against the head, neck, or body of a recipient animal with the mouth open, and it occurred at least 5 s before or after a period of damaging aggression. On the other hand, an event was coded as a reciprocal fight when pairs of pigs engaged in damaging aggression for a minimum duration of 3 s.

Genotyping and Data Editing

For all data analyses, the total number of animals in the pedigree was 2149, from which 1082 were genotyped with the GeneSeek Genomic Profiler for Porcine HD version 1 commercial BeadChip (Neogen Corporation – GeneSeek Operations, Lincoln, NE). Initial genotyping returned 68,516 markers. After quality control of genotypes, markers were removed when displaying more than 10% missing data, which resulted in a loss of 4275 SNP. In addition, 3 animals were removed for having more than 10% missing SNP. The SNP from the X chromosome as well as markers whose minor allele frequency was less than 5% (n = 13,310) were also excluded, as were a further 1470 SNP according to the procedure suggested by Forneris et al. (2015), leaving a total of 49,461 SNP markers available for the analyses of 1079 animals. In brief, the last step consisted of estimating the heritability of allelic dosage at every SNP conditional upon available pedigree information and testing the null hypothesis that the heritability is equal to 1.0. For those markers where the hypothesis is rejected, there is strong evidence of non-Mendelian segregation. The properties of this method have been reported in detail in the original paper.

Quantitative Genetics Models for Direct and Social Interaction Effects

Two model equations were used for estimating the variance components and the breeding values for both direct and social genetic effects.

The model equation for DGE can be written as

$$y=X\beta +Z_d{a}_d+Z_p{p}_p+e$$ [1]

whereas the model equation for TSGE and ISGE is equal to

$$y=X\beta +Z_d{a}_d+Z_s{a}_s+Z_p{p}_p+e$$ [2]

In Eq. [1] and [2], y is an n × 1 vector of log-transformed lesion counts, i.e., y_i = log (1 + lesion count_i) of animal i, and X is the n × p incidence matrix relating the records to the vector of fixed effects β of order p, which included the sex of the animal (gilt or barrow), the replicate (7 levels), the premixing lesion count, the observer effect (6 levels), the weight of the pig as a covariate, and the total time that the animal spent engaged in aggressive interactions as a covariate. The need for and use of the total time as a covariate is extensively discussed in the results section. Matrix Z_d of order n × q (q is the number of pigs in pedigree) relates records in y to the random vector of additive genetic effects $a_d\left(q\times 1\right)$. The distribution of the direct breeding values was assumed to be $a_d~N(0,G{\sigma }_d^2)$, where G is the genomic relationship matrix that was computed after VanRaden (2008). To such purpose, genotypes were expressed as allelic dosage and stored in the marker matrix M, with dimensions n (number of individuals with records, 1079) by m (number of SNP, 49,461). Once M was calculated, G was computed by multiplying the standardized marker matrix Z by its transpose. The resulting matrix product contains estimates of the realized genomic relationships between any pair of pigs. The scalar ${\sigma }_d^2$ is the additive genetic variance; p_p is an s × 1 vector of random pen effects or contemporary groups, such that $p_p~N(0,I{\sigma }_d^2)$, where ${\sigma }_p^2$ is the variance of pen effects, and the n × s matrix Z_p relates records in y to the vector of pen effects p. The incidence matrix of social effects Z_s (n × q) relates records with the social interaction effects in a_s, and is described in detail below. Social interaction effects in a_s (q × 1) follows the Gaussian specification such as $a_s~N(0,G{\sigma }_s^2)$. The scalar ${\sigma }_s^2$ is the variance of the social interaction breeding values. The same q individuals displaying direct breeding values in a_d are also included in a_s. Note that all animals with recorded phenotypes for lesion counts were also genotyped. Finally, Z_d is an identity matrix, e (n × 1) is the random vector of independent errors distributed as $N(0,I{\sigma }_e^2)$, and ${\sigma }_e^2$ is the error variance.

The resulting covariance matrix of breeding values has a Kronecker structure as $G{\sigma }_d^2$ and $G{\sigma }_s^2$, are the respective covariance matrix for direct and social interaction effects, whereas the covariance between direct and social genetics effects is $G{\sigma }_{ds}$. The scalar ${\sigma }_{ds}$ is the covariance between direct and social breeding values, a parameter whose sign and magnitude are central to predict the response to selection including social interaction effects. With all these specifications, the covariance matrix of breeding values for direct and social interaction effects is written in a more compact manner as follows:

$$Var\left[\begin{array}{c}{a}_d \\ a_s\end{array}\right]=\left[\begin{array}{cc}{\sigma }_d^2& {\sigma }_{ds}\\ {\sigma }_{ds}& {\sigma }_s^2\end{array}\right]\otimes G=G_0\otimes G$$

The Matrix Z_s of Social Interaction Breeding Values

The identifiability of social interaction effects (SI) in the model associated with the column space of matrix Z_s (Cantet and Cappa, 2008). Non-zero elements in any row reflect the “intensity or strength” of the SI between any pair of individuals within the same pen, at the time they were located together (Cantet and Cappa, 2008; Cappa and Cantet, 2008; Bijma, 2014). We compared 2 different type of structures for Z_s, according to the models TSGE and ISGE, to estimate the (co)variance components for lesion counts traits of pigs immediately postmixing.

The first structure corresponds to the TSGE model, and Z_s was computed as described by Bijma et al. (2007) by assuming uniform interactions within groups. Therefore, letting i,j be the index describing a pair of individuals in Z_s, the diagonal elements should be zero, i.e., $Z_{s_{i,j}}=0$, as individuals do not display a SI with themselves, whereas the off-diagonals are $Z_{s_{i,j}}=1$, if i and j belong to the same group, or $Z_{s_{i,j}}=0$ if i,j are in different groups. As a result, Z_s is a block-diagonal matrix with the number of blocks equal to the number of groups, and each group may have a number of individuals that is different from the number of animals in every other group.

The other matrix structure for Z_s is the one from the ISGE models and was originally discussed by Cappa and Cantet (2008) for the estimation of dispersion parameters with competition effects in forest trees. The parametrization accounts for the number and position of competitors in tree breeding and it requires the specification of the intensity of competition (IC) effect. This number can be interpreted as a weighting factor that expresses how intense pairs of individuals compete in relation to all other animals in the group. It can be chosen to represent extreme patterns in which only particular individuals display competition behavior whereas the remaining animals do not. Cantet and Cappa (2008) argue that this type of structure on Z_s plays a role in the identifiability of the (co)variance components in animal models with competition effects. The first reason is that this structure for Z_s avoids collinearity between X and Z_s, and also because the use of different values for ICs avoids the confounding between the pen effects and social breeding values. Without proper identifiability of SI effects, estimates of heritabilities and genetic correlations between direct and SI effects may be grossly underestimated (Cappa and Cantet, 2008). In this paper, we focus on noncompetitive social interactions, and thus, we replace the concept of IC with intensity of social interaction (ISI), but the statistical interpretation and modeling of effects remain identical to those originally presented by Cantet and Cappa (2008). The calculus of ISI requires interactions to be expressed as a continuous variable that can be measured differentially for every pair of individuals in a group. Thus, we propose to employ the total time (in seconds) of aggressive interactions that take place between any pair of animals within groups over a 9-h postmix period as a measure of the intensity of social interaction. Z_s was constructed as a block-diagonal matrix, where each block represents a social group. Thus, the ISI for an i,j pair of pigs was taken to be the total time in seconds of aggressive interactions between pig i and pig j belonging to the same social group: $Z_{s{*}_{ij}}$ = time engaged in aggressive interaction. The standardization of Z_s (see Cantet and Cappa, 2008; Bijma, 2014) was accomplished with the use of the following formula:

$$Z_{sij}=\frac{z_{s{*}_{i,j}}}{\sqrt{{\displaystyle {\sum }_{j=1}^q\left(z_{s{*}_{i,j}}^2\right)}}}$$ [3]

At row i in the Z_s matrix, the time $Z_{s{*}_{ij}}$ is divided by the square root of the sum of all q squared elements ($Z_{s{*}_{ij}}^2$) in the same row, most of them being equal to zero.

Estimation of (co)variance Components

The (co)variance components for all 3 models were estimated by Restricted Maximum Likelihood (REML, Patterson and Thompson, 1971) using the EM (Expectation-Maximization; Dempster et al., 1977) algorithm through in-house developed functions implemented in R. The algorithm required us to first set up the following set of mixed model equations (Henderson, 1984) to obtain solutions for fixed effects, direct and social breeding values, and pen effects from model [2]

$$\left(\begin{array}{cccc}{X}^{\prime }X& X^{\prime }{Z}_d& X^{\prime }{Z}_s& X^{\prime }{Z}_p\\ {Z^{\prime }}_{d}X& {Z^{\prime }}_d{Z}_d+g^{11}{G}^{-1}& {Z^{\prime }}_d{Z}_s+g^{12}{G}^{-1}& Z_d{Z}_p\\ {Z^{\prime }}_{s}X& {Z^{\prime }}_s{Z}_d+g^{21}{G}^{-1}& {Z^{\prime }}_s{Z}_s+g^{22}{G}^{-1}& {Z^{\prime }}_s{Z}_p\\ {Z^{\prime }}_{p}X& {Z^{\prime }}_p{Z}_d& {Z^{\prime }}_s{Z}_s& {Z^{\prime }}_s{Z}_p+I\left(\frac{{\sigma }_e^2}{{\sigma }_p^2}\right)\end{array}\right)\left(\begin{array}{c}\widehat{\beta }\\ {\widehat{\alpha }}_d\\ {\widehat{\alpha }}_d\\ {\widehat{p}}_p\end{array}\right)=\left(\begin{array}{c}{X}^{\prime }y\\ {Z^{\prime }}_{d}y\\ {Z^{\prime }}_{s}y\\ {Z^{\prime }}_{p}y\end{array}\right)$$ [4]

Matrix G⁻¹ is the inverse of the genomic relationship matrix (VanRaden, 2008), and

$$\left(\begin{array}{cc}{g}^{11}& g^{12}\\ g^{21}& g^{22}\end{array}\right)=G_0^{-1}{\sigma }_e^2$$

The estimating equations of the EM algorithm for the (co)variance parameters ${\sigma }_d^2$, ${\sigma }_s^2$, ${\widehat{\sigma }}_{ds}$, ${\sigma }_p^2$, ${\sigma }_e^2$ are developed in Supplementary Appendix 1[A]. The variances of the REML estimators and their standard errors were calculated as follows. Let $\theta ={\left({\sigma }_d^2,{\sigma }_s^2,{\sigma }_{ds}^2,{\sigma }_p^2,{\sigma }_e^2\right)}^{\prime }$ be the vector of (co)variance components of model [2], Harville (1977) derived formulae to calculate the information matrix I(θ). of REML estimates of θ. The inverse of the information matrix is the asymptotic covariance matrix of REML estimates (Harville, 1977; Searle et al, 1992). Being a covariance matrix, I(θ) and its inverse are positive definite, a useful property that enables us to check whether the (co)variance components in model [2] were identifiable (Cantet and Cappa, 2008).

Estimation of Heritability (${\widehat{h}}_D^2$) for Lesion Counts Traits

The count of skin lesions 24 h postmixing in pigs has been shown to be associated with aggressive interactions, and the locations of lesions on the body have been associated with engaging in delivery of aggression and reciprocal fights (primarily anterior lesions), or receiving aggression (primarily caudal lesions; Turner et al., 2008; 2009; Wurtz et al., 2017). As a preliminary analysis, we fitted 2-trait models (see Supplementary Appendix 2) to estimate direct heritabilities and genetic and phenotypic correlations between lesion count traits with each other and between lesion count traits and behavioral traits.

This modeling can be seen as a classical genetic model where the behavioral trait (time engaged in aggression) and its consequence (lesion count) are treated as 2 traits in a bivariate analysis (Turner et al., 2009). This model collapses the fighting time that is observed on a dyadic basis (for pairs of animals) into a single vector of total count per animal. It also ignores the causal relationship between fights and lesions. Our modeling, using social interaction effects, avoids these shortcomings.

More importantly, we used SGE models (TSGE, ISGE) to estimate variance components, heritability and their standard errors of model lesion counts in different regions of body in pigs at the finishing stage 24 h postmixing. This modeling does not collapse behavioral data, but it keeps it in the dyadic scale in which they are observed. Furthermore, our models explain variance in lesion counts as a function of direct genetic effects and SGE whose intensity is quantified by the dyadic behavioral trait “time spent engaged in mutual aggression.”

The lesion count traits in each region of the body (anterior, central, caudal) were analyzed with univariate models by 3 separate analyses (one for each trait), with the DGE, TSGE, and ISGE models. The heritability for direct genetic effects (${\widehat{h}}_D^2$) was estimated as the ratio between the additive genetic variance (${\sigma }_u^2$) and the phenotypic variance (${\sigma }_P^2$):

$${\widehat{h}}_D^2=\frac{{\sigma }_u^2}{{\sigma }_P^2}=\frac{{\widehat{\sigma }}_d^2}{{\widehat{\sigma }}_d^2+{\widehat{\sigma }}_{pen}^2+{\widehat{\sigma }}_e^2}$$ [5]

Where ${\widehat{\sigma }}_d^2$, ${\widehat{\sigma }}_{pen}^2$, and ${\widehat{\sigma }}_e^2$ are the estimated variance components for the direct additive genetic variance, pen variance, and error variance, respectively.

Data and Code Availability

All data and codes used to generate the presented results are freely available at: https://github.com/steibelj/ISGE_MSU.

RESULTS AND DISCUSSION

The REML estimates of the (co)variance components, heritabilities, and genetic correlations for all 6 models (DGE, TSGE, ISGE based on unilateral interactions and ISGE based on bilateral interactions) of analysis of lesion counts at different parts of the body observed 24 h after mixing, are displayed in Table 1. As described in the Methods, for the ISGE models, there are model-specific covariates representing the total time spent by an animal engaged in the corresponding aggressive interaction. For instance, in ISGE, for reciprocal fights, the covariate represented the total time that an individual spent engaged in reciprocal fights with any social group mate. It is important to include the covariate to account for a mean effect of time engaged in social interactions on the lesion count, because the Z_s matrix is standardized by row and does not account for such mean effect. Moreover, it was necessary to include similar covariates in DGE and TSGE to compare models with similar fixed effects. Consequently, 2 DGE and TSGE models were fitted, one using total time engaged in attacks and another one using total time engaged in reciprocal fights. Model comparisons between DGE, TSGE, and ISGE were made between models with identical fixed effects formulations. Estimates presented in Table 1 were obtained from a subset of the data employed by Wurtz et al. (2017), who estimated $h_D^2$ equal to 0.32, 0.15, and 0.16 for anterior, central, and caudal lesions. Wurtz et al. (2017) used a similar model to DGE in Table 1, except that their model did not include the covariate for the total time engaged in aggression because at the moment of submission such data were not available. Moreover, comparing the estimates from Wurtz et al. (2017) to the ones for DGE in Table 1 we can evaluate the effect of including the covariate in the model. In general, when the covariate was total time engaged in attack, the estimated $h_D^2$ did not differ from that obtained with the model without the covariate, but when total time of reciprocal fight was used as a covariate, the estimated heritability reported in Table 1 was significantly lower. This can be explained by the results of the bivariate analyses presented in Table 2 (methods described in Supplementary Appendix 2). The genetic correlations $({\widehat{r}}_g)$ between total attacks and lesion counts were non significantly different from zero as the magnitude of the estimate (−0.24 to 0.24) was similar to the magnitude of the corresponding standard error (0.28 to 0.38), while genetic correlations between lesion counts and reciprocal fights were larger in magnitude (0.72 to 0.89) and significantly different from zero (SE: 0.07 to 0.16). This raises a question of the appropriateness of including a covariate that is genetically correlated with the response variable. On one hand, as explained before, it is necessary to adjust the mean lesion count for the total level of fights that an individual has engaged in. On the other hand, for the particular case of reciprocal fighting, this may come at the cost of removing not only residual but also some genetic variance.

Table 1.

Estimated variance components and heritability of lesions in different regions of the body of pigs at the finisher stage 24 h postmixing as estimated by 6 models (SE in parentheses)¹

Model	Covariate	Trait	${\widehat{\sigma }}_d^2$	${\widehat{\sigma }}_s^2$	${\widehat{\sigma }}_{ds}$	${\widehat{\sigma }}_{\mathrm{pen}}^2$	${\widehat{\sigma }}_e^2$	${\widehat{h}}_D^2$
DGE	tRF	Anterior	0.059 (0.017)			0.033 (0.010)	0.21 (0.015)	0.19 (0.055)
		Central	0.014 (0.09)			0.051 (0.013)	0.20 (0.009)	0.05 (0.035)
		Caudal	0.028 (0.015)			0.081 (0.020)	0.28 (0.018)	0.073 (0.03)
DGE	tAT	Anterior	0.11 (0.028)			0.026 (0.010)	0.27 (0.022)	0.28 (0.063)
		Central	0.037 (0.015)			0.06 (0.016)	0.23 (0.016)	0.11 (0.044)
		Caudal	0.039 (0.018)			0.092 (0.023)	0.30 (0.020)	0.091 (0.04)
TSGE	tRF	Anterior	0.057 (0.010)	0.025NS (0.012)	−0.0004NS (0.015)	0.001 (0.011)	0.21 (0.014)	0.20 (0.036)
		Central	0.015 (0.0075)	0.032 NS (0.013)	0.0007 NS (0.011)	0.016 (0.013)	0.20 (0.012)	0.064 (0.031)
		Caudal	0.033 (0.013)	0.041 NS (0.020)	0.016 NS (0.017)	0.034 (0.021)	0.27 (0.017)	0.096 (0.038)
TSGE	tAT	Anterior	0.10 (0.017)	0.030 NS (0.017)	−0.026 NS (0.029)	0.007 (0.016)	0.26 (0.021)	0.28 (0.044)
		Central	0.033 (0.010)	0.020 NS (0.016)	−0.008 NS (0.015)	0.045 (0.018)	0.23 (0.015)	0.10 (0.034)
		Caudal	0.037 (0.016)	0.038 NS (0.023)	0.0019 NS (0.020)	0.057 (0.025)	0.30 (0.020)	0.09 (0.040)
ISGE-Reciprocal Fights	tRF	Anterior	0.084 (0.008)	0.040* (0.013)	0.051* (0.010)	0.026 (0.013)	0.18 (0.013)	0.29 (0.031)
		Central	0.019 (0.007)	0.023* (0.011)	0.015* (0.007)	0.044 (0.014)	0.19 (0.012)	0.075 (0.027)
		Caudal	0.037 (0.011)	0.064* (0.019)	0.040* (0.011)	0.047 (0.019)	0.24 (0.016)	0.11 (0.035)
ISGE-Attacks	tAT	Anterior	0.155 (0.014)	0.051* (0.017)	0.077* (0.015)	0.020 (0.014)	0.22 (0.017)	0.38 (0.037)
		Central	0.051 (0.009)	0.048* (0.016)	0.036* (0.010)	0.042 (0.016)	0.20 (0.014)	0.17 (0.032)
		Caudal	0.049 (0.014)	0.068* (0.021)	0.031* (0.014)	0.057 (0.021)	0.26 (0.018)	0.13 (0.038)

*P < 0.01, ^NSP > 0.5.

1${\widehat{\sigma }}_d^2$ direct genetic variance, ${\widehat{\sigma }}_s^2$ social genetic variance, ${\widehat{\sigma }}_{ds}$ covariance genetic direct-social, ${\widehat{\sigma }}_{\mathrm{pen}}^2$ pen variance, ${\widehat{\sigma }}_e^2$, error variance, ${\widehat{h}}_D^2$, heritability. DGE: direct genetic additive model, TSGE: traditional social genetic effect model, ISGE-Reciprocal Fights: Intensity-based social genetic effect model with Reciprocal Fight behavior, ISGE-Attacks: Intensity-based social genetic effect model with Attack and Single Bite behaviors. t_RF: total time that the animal spent engaged in reciprocal fight behavior, t_AT: total time that the animal spent engaged in attack behavior.

Table 2.

Heritability (on diagonal) and genetic (above diagonal) and phenotypic (below diagonal) correlations between lesion count traits recorded 24 h postmixing and aggressive behavioral traits (SE in parentheses)

Trait		Lesion count			Behavioral trait
		Anterior	Central	Caudal	Reciprocal fight	Received attacks
Lesion count	Anterior	0.27 (0.06)			0.89 (0.07)	−0.22 (0.28)
	Central		0.12 (0.04)		0.77 (0.14)	−0.24 (0.38)
	Caudal			0.11 (0.04)	0.72 (0.16)	0.24 (0.34)
Behavioral trait	Reciprocal fight	0.63 (0.02)	0.47 (0.03)	0.39 (0.03)	0.16 (0.05)	−0.59 (0.34)
	Received attacks	0.12 (0.03)	0.11 (0.04)	0.12 (0.04)	0.10 (0.04)	0.06 (0.03)

Turner et al. (2009) also obtained ${\widehat{h}}_D^2$ for lesion counts in the 3 regions of a pig. Our estimated value of $h_D^2$ was generally smaller than those reported by Turner et al. (2009), who obtained $h_D^2$ estimates equal to 0.26, 0.25, and 0.21 for anterior, central, and caudal lesion counts, respectively and by Desire et al. (2015) who reported $h_D^2$ estimates of 0.08, 0.11, and 0.12 for anterior, central, and caudal regions of the body. However, those authors did not include the covariate for total time, which absorbs both residual and genetic additive variation, especially for reciprocal fights. For all 3 traits, the estimated variance components with DGE did not significantly differ from the usual model with direct and SGE (TSGE). The estimated residual variance (${\widehat{\sigma }}_e^2$) and the additive genetic variance for direct effects ${\widehat{\sigma }}_d^2$ from DGE were similar to the estimates with TSGE when comparing models with the same covariate structure. As a consequence, the values of ${\widehat{h}}_D^2$ from both models were alike. On the other hand, the estimated variance components for social additive effects (${\widehat{\sigma }}_s^2$), and the covariance between direct and social additive effects ${\widehat{\sigma }}_{ds}$) with TSGE were not significantly different (P > 0.5) from zero in all traits analyzed, when testing with the likelihood ratio statistics. This is a consequence of the non-zero elements in any row of Z_s to be equal for all pigs within the same social group and the small sample size, in such a way that there is not enough information in the data to disentangle SGE from pen effects (Cantet and Cappa, 2008); a confounding that may persist even when treating pen effects as random. This indecisive estimation of ${\sigma }_s^2$ and ${\sigma }_{\mathrm{ds}}$ in TSGE has been previously reported. Arango et al. (2005) estimated a value of ${\sigma }_s^2$ not significantly different from zero, whereas they were not able to estimate ${\sigma }_{\mathrm{ds}}$ for ADG in pigs. By simulating a pig production system, Van Vleck and Cassady (2005) observed very large standard errors of the estimated (co)variance components when all pens had an equal number of pigs, and pen effects were viewed as a random effect in the model. Moreover, Van Vleck et al. (2007) estimated an almost zero value for ${\sigma }_s^2$ and negative values for ${\sigma }_{\mathrm{ds}}$ while analyzing ADG of Hereford bulls.

Interestingly enough, the estimates of the additive variance for SGE and of the covariance between direct and SGE were significantly different from zero (P < 0.01), for all traits and in both ISGE models. The values of ${\widehat{\sigma }}_s^2$ ranged from 0.023 to 0.064 when Z_s was calculated using data from reciprocal fights, and from 0.048 to 0.068 when the incidence matrix of SGE was proportional to the time spent receiving attacks. Estimates of ${\sigma }_{\mathrm{DS}}$ were positive for the 3 lesion count traits and ranged between 0.015 and 0.051 for reciprocal fights, whereas for attack behavior, ${\widehat{\sigma }}_{ds}$ ranged from 0.031 to 0.077.

Significative differences were observed between the magnitude of the estimates of the variance components and heritability for the 3 lesion counts traits (Table 1) with ISGE compared to the estimates from DGE. Including social genetic effects using the intensity of social interactions produced a larger estimate of ${\sigma }_d^2$, a smaller estimate of ${\sigma }_e^2$and, consequently, a larger estimate of heritability from ISGE when compared with estimates of the same parameters from DGE. This difference in the magnitude of the estimates was more pronounced for anterior lesion counts where ${\widehat{\sigma }}_e^2$ was equal to 0.27 in DGE and 0.22 in ISGE (using attacks to model ISI), whereas ${\widehat{\sigma }}_d^2$ increased from 0.11 in DGE to 0.15 in ISGE (also with attacks). On defining ${\widehat{h}}_D^2=\raisebox{1ex}{${\widehat{\sigma }}_d^2$}\!\left/ \!\raisebox{-1ex}{$\left({\widehat{\sigma }}_d^2+{\widehat{\sigma }}_{pen}^2+{\widehat{\sigma }}_e^2\right)$}\right.$, the value of ${\widehat{h}}_D^2$ increased from 0.28 in DGE to 0.38 in ISGE, a value 35% higher. This increase in estimated direct additive genetic variability while fitting SGE with an informative Z_s is intermediate compared to previously published works. For instance, in tree breeding Cappa and Cantet (2008) found significantly larger increases in recovered direct variance. For the diameter at breast height of Loblolly pines (Pinus taeda L.), they used a model where off-diagonal elements of Z_s were inversely proportional to the distance among trees and found 83% higher ${\widehat{\sigma }}_d^2$ in ISGE than in DGE. However, Ragab et al. (2019) using data on ADG of Duroc pigs estimated 14% higher ${\widehat{\sigma }}_d^2$ from ISGE than from DGE, which is a modest increase compared to our results. In that research, the non-zero elements of any row of Z_s were proportional to the pairwise Euclidean distances between animals computed for several feeding behavior variables.

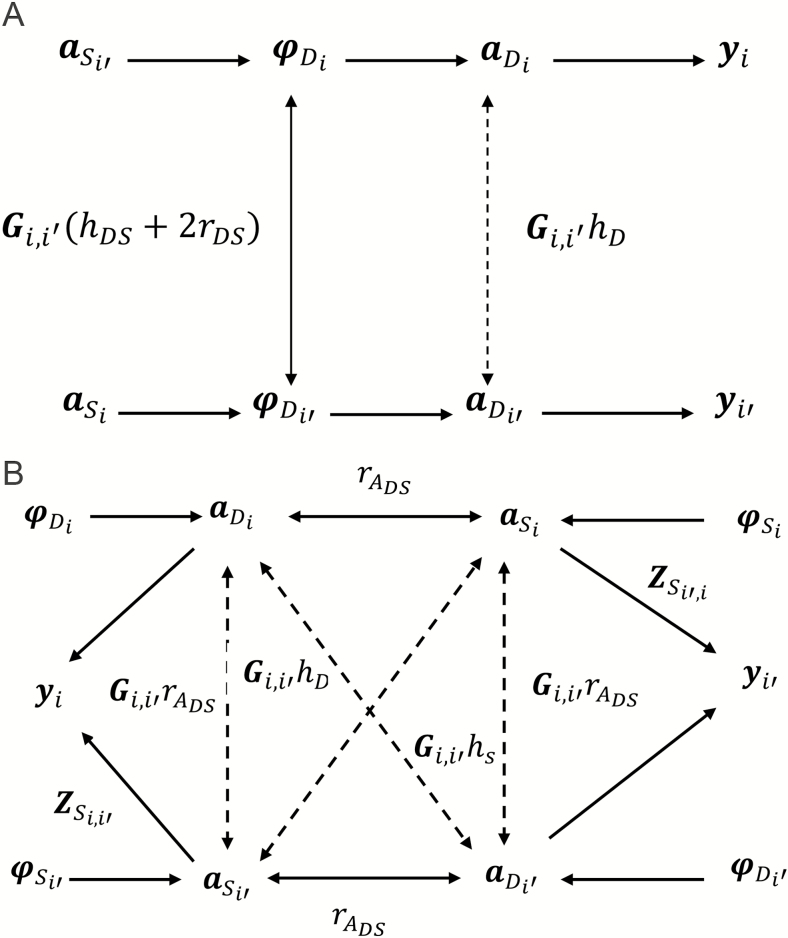
An explanation for the increased additive genetic variability recovered by the ISGE model compared with the variance from the DGE model can be deduced from Figs 1a and b. Figure 1a displays a path coefficient diagram (Wright, 1921) depicting the DGE for the phenotypes of 2 related individuals (y_i and y_i’) in the same social group, whereas Fig. 1b shows the same phenotypes under ISGE. For animals i and i’, their direct and social breeding values and Mendelian residual effects, respectively are a_Di , a_Di’, a_Si , a_Si’, φ _Di , φ _Di’, φ _Si , and φ _Si’. One-headed arrows indicate causation; double-headed arrows indicate correlation (Wright, 1921). The values over or alongside the arrows are those of the path coefficients. The intensity of social interaction (ISI) or Z_s in Fig. 1b are path coefficients or partial regression coefficients. Under the Gaussian specification of direct and SGE breeding values, partial and conditional variances and covariances are equal (Baba et al., 2004), so that the ISI are parameters of the conditional distribution of an SGE given the SGE of all remaining interacting animals and the inference from a path coefficient diagram is similar to the one from an acyclic mixed graph (Fox et al., 2015). Actually, the DGE and ISGE below can be expressed as direct acyclic graphs or DAG (Rosa et al., 2011). By including the parental breeding values of i and i’ for direct and social effects in Fig. 1b, all double arrows (correlations) disappear and single (causal) arrows explain the observed relationships. Thus, the extra variability is the result of the partial covariance between Mendelian residuals in DGE being projected into ISGE: by fitting the SGE in ISGE, the Mendelian residuals become independent. This fact is overlooked when fitting direct effects only; a similar situation occurs when maternal effects are ignored and is partially responsible for the genetic variability. Hence, when fitting SGE with ISI into ISGE, the fraction of variability for direct effects that is in common with the indirect effect is expressed in the non-zero elements of Z_s, and it is available for selection purposes.

Figure 1.

(a) Path coefficient diagram or acyclic mixed graph of DGE. (b) Path coefficient diagram or acyclic mixed graph of ISGE. y_i, y_i′ = phenotypes of two related individuals; aD, a_D′ = Direct Breeding Values for animals i and i’; aS, a_S′ = Social Breeding Values for animals i and i’; ${\phi }_{D_i},{\phi }_{D_{i^{\prime }}}$ = Mendelian residual for animals i and i’; G_i,i߰ = genomic relationship between animals i and i’; r_DS = correlation between direct and social effects; h_D = square root of direct heritability; h_S= square root of $h_S^2$, where $h_S^2=\frac{{\widehat{\sigma }}_S^2}{{\widehat{\sigma }}_S^2+{\widehat{\sigma }}_e^2+{\widehat{\sigma }}_{pen}^2}$; $r_{A_{DS}}$= correlation between genetic direct and social breeding values; $Z_{S_{i,i^{\prime }}}$ = square root of the direct heritability; $Z_{S_{i^{\prime },i}}$, = intensity of social interaction between animals i and i’.

The estimates of the additive genetic correlation between direct and social effects (${\widehat{r}}_{DS}$) and their standard errors are displayed in Table 3. The values of ${\widehat{r}}_{DS}$ from ISGE in reciprocal fights were highly positive: 0.877, 0.70, and 0.82 for the estimated values of the Anterior, Central, and Caudal parts of the body, respectively. On the other hand, for attacks, we observed ${\widehat{r}}_{DS}$ = 0.86 for the Anterior, ${\widehat{r}}_{DS}$ = 0.73 for the Central, and ${\widehat{r}}_{DS}$ = 0.53 for the Caudal body regions. Alemu et al. (2014) obtained positive values of ${\widehat{r}}_{DS}$ ranging from 0.55 to 0.99 for lesion counts at different parts of the body in mink. Positive values of ${\widehat{r}}_{DS}$ indicate that the genotypes that display more aggressive social behavior tend to display more frequent lesion counts in any part of their bodies and cause more lesions to their pen mates. It is also interesting to note that when Z_s is proportional to reciprocal fights, the correlation between direct and SGE is close to unity. In the case where the ISI was parameterized as a function of unilateral attacks, the correlation was smaller. This makes sense from the behavioral point of view, as it is expected that in a reciprocal fight an animal will receive a number of lesions proportional to the number of lesions that it delivers. But in the case of single-sided attacks, one animal attacks another one to deliver lesions so the number of lesions that the first animal receives depends on the reaction of the recipient: in some cases, the recipient will turn around and retaliate and sometimes it will not, resulting in a lower ${\widehat{r}}_{DS}$.

Table 3.

Estimated correlation between Direct and Social genetic effects and standard error in the models with social effects¹

Model	Covariate	Trait	${\widehat{r}}_{DS}$	SE
TSGE	tRF	Anterior	−0.010NS	0.40
		Central	0.30NS	0.50
		Caudal	0.42NS	0.44
TSGE	tAT	Anterior	−0.45NS	0.41
		Central	−0.30NS	0.59
		Caudal	0.051NS	0.54
ISGE-Reciprocal Fights	tRF	Anterior	0.877*	0.12
		Central	0.70*	0.29
		Caudal	0.82*	0.18
ISGE-Attacks	tAT	Anterior	0.86*	0.13
		Central	0.73*	0.17
		Caudal	0.53*	0.21

*P < 0.01, ^NSP > 0.5.

1${\widehat{r}}_{DS}$ correlation genetic Direct-Social. TSGE: traditional social genetic effect model, ISGE-Reciprocal Fights: Intensity-based social genetic effect model with Reciprocal Fight behavior, ISGE-Attacks: Intensity-based social genetic effect model with Attack and Single Bite behaviors, t_RF: total time that the animal spent engaged in reciprocal fight behavior, t_AT: total time that the animal spent engaged in attack behavior.

The ability of the ISGE to estimate covariance components in this data ultimately has a profound impact on the ability to predict social breeding values. In the current dataset (small sample size and specific allocation of animals to pens), the TSGE does not allow a reliable prediction of social genetic effects (their associated variance is not different from zero), while the ISGE allows recovery of some social genetic component and, thus, predicts social genetic effects better. Once obtained, these estimates of social genetic effects would be treated identically to those obtained from the TSGE (Bijma et al., 2007; Bergsma et al., 2008; Ellen et al., 2008) to predict social breeding values and total breeding values, because the intensity of interaction is not relevant for selection purposes.

In summary, we successfully estimated genetic (co)variance components in different animal models including direct and social effects in pigs. This was accomplished by measuring dyadic interactions for the total time pairs of animals were engaged in aggressive behavior; a laborious task requiring many hours of watching and registering video recordings of the pigs. However, these data allowed calculation of an informative matrix Z_s, which permitted disentangling SGE from social group effects, as suggested by Cantet and Cappa (2008). As a result, more additive variability was recovered from using such Z_s in ISGE than from the (co)variance components estimated through TSGE. Our estimates from ISGE suggest that if behavioral observations are available, selection incorporating social genetic effects may greatly reduce the consequences of damaging aggressive behavior after mixing pigs in new social groups.