Genotype by environment interactions for performance and thermoregulation responses in growing pigs

Abstract

Heat stress affects pig health, welfare, and production, and thus the economic viability of the pig sector in many countries. Breeding for heat tolerance is a complex issue, increasingly important due to climate change and the development of pig production in tropical areas. Characterizing genetic determinism of heat tolerance would help building selection schemes dedicated to high performance in tropical areas. The main objective of our study was to estimate the genetic parameters for production and thermoregulation traits in two highly related growing pig populations reared in temperate (TEMP) or tropical humid (TROP) environment. Pigs came from a backcross population between Large White (LW, heat sensitive) and Creole (CR, heat tolerant) pigs. Phenotypic data were obtained on a total of 1,297 pigs using the same procedures in both environments, for body weight (BW, at weeks 11 and 23), daily feed intake (ADFI), backfat thickness (BFT, at weeks 19 and 23), cutaneous temperature (CT, at weeks 19 and 23), and rectal temperature (RT, at weeks 19, 21, and 23). Feed conversion ratio (FCR) and residual feed intake (RFI) were computed for the whole test period (11 to 23 wk). Criteria comparing the fits to the data revealed genotype × environment (G × E) interactions for most traits but not for FCR. The variance components were obtained using two different methods, a restricted maximum likelihood method and a Bayesian Markov chain Monte Carlo method, considering that traits are either similar or different in each environment. Regardless of the method, heritability estimates for production traits were moderate to high, except for FCR (lower than 0.18). Heritability estimates for RT were low to moderate, ranging from 0.04 to 0.34. The genetic correlations of each trait between environments generally differed from 1, except for FCR and ADG. For most thermoregulation traits, they also did not differ significantly from zero, suggesting that the main genetic bases of heat tolerance may vary in different environment. Within environments, the unfavorable genetic correlations between production traits and RT suggest an antagonism between the ability to maintain inner temperature and the ability to increase ADFI and ADG. However, greater RT were also associated to leaner pigs and better feed efficiency. Nevertheless, due to large inaccuracies of these estimations, larger cohorts would be needed to decide about the best breeding schemes to choose for tropical pig production.

INTRODUCTION

Heat stress (HS) decreases pig farms profitability in tropical areas. Temperate countries are also affected during summer. In the United States, the estimated annual losses in pig industry due to HS are about $300 million (St-Pierre et al., 2003). These costs are related to the negative effects of HS on animal health, welfare, and reproduction (Mayorga et al., 2019). Improved strategies to mitigate the impact of HS effect are needed, and they are becoming more important with climate change. Nutritional strategies (e.g., feed with a low extra-heat increment) and/or heat abatement solutions (e.g., cooling option) are available and are cost-effective opportunities to improve pig performance in HS. An additional solution would be to propose animals better adapted to HS (Hoffmann, 2010). The genetic solution to reduce HS in pigs would allow animals to keep their performance under HS. According to Renaudeau et al. (2004), such genetic improvement could be related to changes in heat sensitivity threshold, and in improvement in thermoregulation efficiency, which is true if these traits have a genetic determinism. Heat-tolerant genotypes have been reported in other species, for example, in cattle (Nguyen et al., 2017), small ruminants (Menendez-Buxadera et al., 2012), and poultry (Mignon-Grasteau et al., 2015). In pigs, studies have shown that Creole (CR) pigs (local tropical breed) have better heat tolerance than Large White (LW) pigs (Renaudeau et al., 2006), but lower (re)production performances (Gourdine et al., 2006). A backcross population with these two breeds (LW and CR) was set up to characterize the genetic variability of heat tolerance in growing pigs in two contrasted climatic environments: temperate (TEMP) and tropical humid (TROP) conditions (Rosé et al., 2017). The aims of this study were: 1) to estimate genetic parameters of production and thermoregulation traits in TEMP and TROP environments, and 2) to quantify the level of genetic by environment (G × E) interactions.

MATERIALS AND METHODS

All measurements and observations on animals were performed in accordance with the current law on animal experimentation and ethics (Authorizations CE2012-9 and 69-2012-2 from the Animal Care and Use Committee of Poitou-Charentes and of French West Indies and Guyana, respectively), under the direction of Y. Billon and J. Fleury (INRA-PTEA; authorization number by the French Ministry of Agriculture and Fisheries: 17015 and 971-2011-03 7704, respectively).

Experimental Design

Data used in this study were obtained in a backcross (BC) population (3/4 LW and ¼ CR breed). Detailed description of the population and the two environments has been provided in Rosé et al. (2017). In a few words, a total of 634 BC pigs from 60 LW sows (raised in 11 contemporary batches) and 664 BC from 70 LW sows (12 batches) were obtained in TEMP (INRA experimental facility Le Magneraud, GenESI, Surgères, Charentes, France; 46°N, 0.45°W) and TROP (INRA experimental facility PTEA, Petit-Bourg, Guadeloupe, French West Indies; 16°N, 61°W) conditions, respectively. The effect of the combination of the surrounding temperature and humidity was quantified by the calculation of a thermal humidity index (THI). Based on the THI calculations, pigs raised in TROP conditions were exposed to heat stress during the experiment as the mean daily THI fluctuated during the test period between 23.2 and 26.8°C in TROP conditions and between 22.8 and 24.4°C in TEMP conditions. Backcross growing pigs in the two farms were related via the same 10 F1 CR × LW boars sired with genetically related LW sows (same sires and maternal grand-sires). A common trait recording protocol was developed during the growing period from weeks 11 to 23 in both TEMP and TROP conditions. At week 10, 60 pigs from eight litters were chosen to balance by sire line and by sex. Pens of 10 pigs of the same sex (females and castrated males) were evaluated. Pigs were fed ad libitum, with a commercial feed formulated with the same characteristics in the two farms (15.7 MJ ED/kg, 17% of digestible crude protein). Animals had a free access to water.

Phenotypic Records

Production traits

All animals were weighed at week 11 (BW₁₁) and week 23 (BW₂₃). Average daily gain (ADG) was calculated between weeks 11 and 23. Backfat thickness was measured at week 19 (BFT₁₉) and week 23 (BFT₂₃) as the average of six ultrasonic measurements (Agroscan, E.C.M, Angoulême, France) on six different sites, measured directly above the point of the elbow, last rib (P2 site), and last lumbar vertebra locations, respectively, and taken 5 cm off the midline on each side of the pig. Single place electronic feeders (ACEMA 128, ACEMO, Pontivy, France) were available to record individual feed intake during the test. To maximize the number of pigs with feeding measurements, during the 12 weeks of test pigs had access to automatic feeders for three periods of 2 weeks, which alternated with periods of 2 weeks fed with conventional collective feeders. Hence, average daily feed intake (ADFI) was available for two groups of pigs: those with records for period 1 (weeks 11–12, 15–16, and 19–20) and those with records for period 2 (weeks 13–14, 17–18, and 21–22). According to Schulze et al. (2001), the first 2 days of record should be excluded for avoiding bias information due to period of adaptation to the change from collective feeders to electronic feeders. In a preliminary analysis, we compared feeding data by excluding either the first day or the first 2 days of record. Only the exclusion of the first day of record is needed for obtaining reliable feed intake information because the readaptation of pigs to electric feeders was not necessary. We calculated feed conversion ratio (FCR) as ADFI divided by ADG. The residual feed intake (RFI) was computed for each animal as the deviation between recorded ADFI and average daily feed intake predicted by a multiple regression of ADFI on ADG between weeks 11 and 23, BFT23, and the average metabolic body weight during the test, as described in Rosé et al. (2017).

Thermoregulation traits

Rectal temperature was measured in the morning at week 19 (RT₁₉), week 21 (RT₂₁), and week 23 (RT₂₃) with digital thermometers (Microlife Corp., Paris, France). The cutaneous temperature was measured on the back at the P2 site at week 19 (CT₁₉) and wk 23 (CT₂₃) using a skin surface thermocouple probe (type K, model 88002K-IEC; Omega Engineering, Inc., Stamford, CT) connected to a microprocessor based handheld thermometer (model HH-21; Omega Engineering, Inc.). The relative gradient between the rectal and the cutaneous temperature was computed for each week of measurement (GRAD₁₉ and GRAD₂₃) as (RT_x − CT_x) / RT_x where x is either 19 or 23.

Within each environment, extreme values were checked for all traits and records differing by more than three phenotypic SD from the mean (i.e., outliers) were excluded. The resulting number of records for each trait is given in Table 1. Shapiro–Wilks test of normality were performed and the assumption of normality was accepted for all studied traits (P > 0.10).

Table 1.

Number of records, mean, and phenotypic SD of the traits recorded according to the environment (temperate vs. tropical)

Trait1		Temperate		Tropical
	n	Mean	SD	n	Mean	SD
BW11, kg	633	31.3	4.2	664	21.1	4.6
BW23, kg	633	103.4	9.9	664	85	11.4
BFT23, mm	627	20.6	3.7	664	15.6	3.0
ADG, g/d	633	832	95	664	758	101
ADFI, kg/d	625	2.21	0.46	660	1.78	0.41
RFI, g/d	619	−52	373	660	4	275
FCR	625	2.66	0.51	660	2.45	0.62
RT19, °C	630	39.5	0.38	663	39.7	0.37
RT21, °C	632	39.4	0.40	664	39.5	0.38
RT23, °C	627	39.3	0.40	663	39.4	0.31
CT19, °C	633	35.1	0.90	664	36.1	0.80
CT23, °C	632	35.2	1.01	664	35.7	0.79
GRAD19	630	0.11	0.02	663	0.09	0.02
GRAD23	626	0.12	0.03	663	0.09	0.02

¹BW₁₁, body weight at week 11; BW₂₃, body weight at week 23; BFT₂₃, back fat thickness at week 23; ADG = average daily weight gain; ADFI = average daily feed intake; RFI, residual feed intake; FCR, feed conversion ratio; RT₁₉, rectal temperature at week 19; RT₂₁, rectal temperature at week 21; RT₂₃, rectal temperature at week 23; CT₁₉, cutaneous temperature at week 19; CT₂₃, cutaneous temperature at week 23; GRAD₁₉ = (RT₁₉ − CT₁₉) / RT₁₉; GRAD₂₃ = (RT₂₃ − CT₂₃) / RT₂₃.

Statistical Analyses

REML and MCMC models

Pedigree information of seven ancestral generations comprising 1,490 individuals was available with a total of 161 dams and 30 sires. Production and thermoregulation traits were analyzed using single (i.e., the trait is considered without G × E interactions, hence without taking into account TEMP and TROP as two different environments) and bivariate (i.e., a same trait considered as different in TEMP and TROP) animal linear mixed models. To assess the robustness of the generated results from the animal models, we used two methods. The animal models were implemented both with ASREML version 4 (Gilmour et al., 2009) using the REML procedure, and with the MCMCglmm R package (Hadfield, 2010). Bayesian and frequentist frameworks are not directly comparable. The general principles of REML and MCMC models are well described by Sorensen and Gianola (2002). The idea in the Bayesian approach used in MCMC models is to combine the knowledge before the data are observed (prior probability distribution) with the information coming from the data (posterior distribution). In REML approach (frequentist), inferences are made only with the posterior probability distribution.

Single animal models

The general single trait animal model can be written as:

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{y}=\mathbf{X}\beta +\mathbf{Z}\mathit{a}+\mathbf{Z}\mathbf{c}+\mathit{e}}\end{array}}$$ (1)

where y is the vector of observations for the trait recorded, β is the vector of fixed effects with design matrix X, $a$ is the vector of additive genetic effects, c is the vector of permanent environmental effects of litter, and $\mathit{e}$ is a vector of residuals. The matrix Z is the incidence matrix relating observations to animals. The fixed effects used are the effects of the sex (2 levels), the batch within farm (23 levels), and the period (2 levels, for ADG, ADFI, and FCR), and the covariate of the age at measurement (for BW₁₁, BW₁₉, and BW₂₃) or of the BW (BW₁₁ for ADG, ADFI, RFI, and FCR; BW₁₉ for RT₁₉, CT₁₉, and GRAD₁₉; and BW₂₃ for BFT₂₃, RT₂₃, CT₂₃, and GRAD₂₃). In REML single trait animal models, the three random effects have the following distribution: $a$ ~ N(0, A${\sigma }_a^2$), $\mathit{c}$ ~ N(0, I${\sigma }_c^2$) and $e$ ~ N(0, I${\sigma }_e^2$), where ${\sigma }_a^2$ is the direct additive genetic variance, ${\sigma }_c^2$ is the variance due to permanent environmental effects due to litter effects and where ${\sigma }_e^2$ is the residual variance. From a frequentist point of view (REML analysis), the parameters that are inferred are ${\sigma }_a^2$, ${\sigma }_c^2$, and ${\sigma }_e^2$. From a Bayesian approach (MCMC analysis), the vector β is also an random variable and β ~ N(µ, ${\sigma }_{\beta }^2$) where µ is the overall mean and ${\sigma }_{\beta }^2$ is the variance of the fixed effects. To carry out MCMC analysis, flat priors are assigned to the parameters β, ${\sigma }_a^2$, ${\sigma }_c^2$, and ${\sigma }_e^2$. The prior specification follows inverse Wishart distribution, which is a classical choice for avoiding the prior to largely influence the estimated posterior distribution.

Bivariate animal models

The most common bivariate animal model was given by:

$${\displaystyle \begin{array}{l}{\displaystyle \left[\begin{array}{l}{\mathit{y}}_1\\ {\mathit{y}}_2\end{array}\right]=\left[\begin{array}{ll}{\mathit{X}}_1& {\displaystyle 0}\\ 0& {\displaystyle {\mathit{X}}_2}\end{array}\right]\left[\begin{array}{l}{\mathit{\beta }}_1\\ {\mathit{\beta }}_2\end{array}\right]+\left[\begin{array}{ll}{\mathit{Z}}_1& {\displaystyle 0}\\ 0& {\displaystyle {\mathit{Z}}_2}\end{array}\right]\left[\begin{array}{l}{\mathit{a}}_1\\ {\mathit{a}}_2\end{array}\right]+\left[\begin{array}{ll}{\mathit{Z}}_1& {\displaystyle 0}\\ 0& {\displaystyle {\mathit{Z}}_2}\end{array}\right]\left[\begin{array}{l}{\mathit{c}}_1\\ {\mathit{c}}_2\end{array}\right]+\left[\begin{array}{l}{\mathit{e}}_1\\ {\mathit{e}}_2\end{array}\right]}\end{array}}$$ (2)

where y₁ and y₂ are vectors of phenotypic value for the traits recorded in TEMP and TROP, respectively; X₁ and X₂ are incidence matrices for TEMP and TROP, respectively; β₁ and β₂ are vectors of systematic effects in the corresponding environment. Note that for Bayesian (MCMC) models, β is a random variable, β _i ~ N(µ, Σ_βi); Z₁ and Z₂ are matrices of random additive genetic [$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]$ ~ N(0, A$\left[\begin{array}{cc}{\sigma }_{a1}^2& {\sigma }_{a12}\\ {\sigma }_{a12}& {\sigma }_{a2}^2\end{array}\right]$)] and permanent environment due to litter effects [$\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]$ ~ N(0, $\left[\begin{array}{cc}{\sigma }_{c1}^2& 0\\ 0& {\sigma }_{c2}^2\end{array}\right]$)] effects in TEMP and TROP, respectively; Z₁ and Z₂ are incidence of random effects in TEMP and TROP, respectively, and e₁ and e₂ are vectors of random residual effects [$\left[\begin{array}{c}{e}_1\\ e_2\end{array}\right]$ ~ N(0, I$\left[\begin{array}{cc}{\sigma }_{c1}^2& 0\\ 0& {\sigma }_{c2}^2\end{array}\right]$)] in TEMP and TROP, respectively. The fixed effects used in single trait models were the same in bivariate models. For MCMC analysis, two-dimensional inverted Wishart distributions are assigned as prior for $\left[\begin{array}{c}\text{}\beta \text{}{}_1\\ \text{}\beta \text{}{}_2\end{array}\right]$, $\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]$, $\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]$, and $\left[\begin{array}{c}{e}_1\\ e_2\end{array}\right]$.

Model comparisons

With ASREML, first variance components were estimated with univariate models, under the null hypothesis of no interaction between TEMP and TROP. Second, bivariate analyses (full model) described in equation 2 were applied. In this latter analysis, heritabilities within each environment and genetic correlations across environments were estimated for all traits. The bivariate analysis of each trait was compared with the corresponding null model with the Akaike information criteria (AIC) and the Bayesian information criteria (BIC): $\mathrm{A}\mathrm{I}\mathrm{C}=-2l_R+2t$ and $\mathrm{B}\mathrm{I}\mathrm{C}=-2l_R+t\log \gamma$, where t is the number of variance parameters in the model, γ = n − p is the residual degrees of freedom where n is the number of observations and p is the number of parameters, and l_R is the REML log-likelihood of the model. Models with smaller AIC and BIC should be preferred to models with greater AIC and BIC. Consequently, smaller AIC and BIC in bivariate analysis than in the null model would indicate significant interaction between TEMP and TROP for the analyzed trait. Next, all combinations of two traits were analyzed to estimate genetic correlations between different traits within and between environments.

For MCMCglmm analyses, a total of 1,000,000 iterations were generated and the burn-in of initial iterations to be discarded was 500,000, with a thinning interval of five iterations. This resulted in a final set of 100,000 independent samples. The convergence was checked by the Geweke’s convergence diagnostic (Geweke, 1992), using the coda R package (Plummer et al., 2006) and by graphical check using the trace of variances. The autocorrelation of the Markov chain samples was checked and effective sample size was estimated. The variance components were obtained from the posterior distribution using the interval with the highest posterior density (HPD). As with the frequentist approach, we compared the full models (considering the environment interaction for a given trait) with the null models, using in MCMC models the deviance information criterion (DIC) for each model $\mathrm{D}\mathrm{I}\mathrm{C}=D\left(\overline{\theta }\right)+2p_D$, where $D\left(\overline{\theta }\right)$ is a point estimate of the deviance obtained by replacing the parameters with their posterior mean estimates in the likelihood function, and $p_D$ denotes the effective number of parameters in the model (Torres et al., 2018). The DIC was calculated for each model. The model with the smallest value was preferred.

Calculation

Whatever the method used (REML or MCMC), the heritability ($h_x^2$) and genetic correlation ($r_g)$between TEMP and TROP for a trait were calculated as:

$${\displaystyle \begin{array}{l}{\displaystyle h_x^2=\frac{{\sigma }_{ax}^2}{{\sigma }_{ax}^2+{\sigma }_{cx}^2+{\sigma }_{ex}^2}\mathrm{a}\mathrm{n}\mathrm{d}{r}_g=\frac{{\sigma }_{a12}}{\sqrt{{\sigma }_{a1}^2\times {\sigma }_{a2}^2}}}\end{array}}$$ (3)

where x is either the TEMP or TROP environment in bivariate analyses, ${\sigma }_a^2$ is the additive genetic variance, ${\sigma }_c^2$ is the permanent environment variance, ${\sigma }_e^2$ is the residual variance, ${\sigma }_{a1}^2$ is the additive genetic variance for the trait in TEMP, ${\sigma }_{a2}^2$ is the additive genetic variance for the same trait in TROP and σ _a12 is the additive genetic covariance between trait in TEMP and the same trait in TROP. For MCMC analyses, the formulae in equation 3 were applied to each sample of the posterior distribution, and then posterior means and standard deviations of the parameters were generated. The statistical significance of the heritability estimates and the genetic correlations was assessed using CI. If unity (respectively zero) is in the CI, the difference between the heritability estimate or the genetic correlation and unity (respectively zero) is not significant. To assess the robustness and sensitivity between the 10 sire families (i.e., the 10 F1 CR × LW boars), posterior median of boar’s breeding values were estimated for those traits for which G × E interactions were found significant in MCMC analyses. The sire families were ranked according to the difference between their estimated breeding values in TEMP and in TROP. For a given trait, scores were then assigned to boars, from 1 (i.e., the boar with the smallest difference in estimated breeding values between TEMP and TROP) to 10 (i.e., the boar with the greatest difference in estimated breeding values between TEMP and TROP).

RESULTS AND DISCUSSION

Pig Characteristics

We previously showed with the same experimental design that the temperature and humidity index had a significant difference of 2.4°C between TEMP and TROP, pointing out that pigs reared in TROP were heat-stressed most of the time (Rosé et al., 2017). In this previous article, all production and thermoregulation traits were significantly affected by the environment (P < 0.05). In summary, for all thermoregulatory body measures (RT, CT), greater values were found for pigs in TROP than in TEMP (on average 35.9 vs. 34.8°C for CT, and 39.5 vs. 39.3°C for RT, respectively). These thermoregulatory responses suggesting that TROP pigs were partly unable to lose the entire heat load by sensible pathways (Renaudeau et al., 2007). Consequently, lower performance was observed in pigs reared in the TROP environment as compared with TEMP: TROP pigs exhibited lower values for BW (−18% of BW23), for ADFI (−20%), for ADG (−9.6%), and for BFT (−24%) compared with TEMP ones. As observed in our study, it has been already established that chronic heat stress induces a feed intake reduction, resulting in a growth rate reduction (Renaudeau et al., 2011).

Heritabilities And G × E For Production Traits

All REML models have converged and the convergence diagnostics used in MCMC models have not revealed any convergence problems. The parameters used in MCMC models (number of iterations, burnin and thin) lead to effective sample sizes greater than 80,000 and 1,500 for fixed and random effects, respectively (results not shown). Because the models with smallest values for AIC are also those with smallest values for BIC, we chose to present only the BIC results in Table 2. With the exception of FCR and ADG, the full REML models had the smallest BIC compared with the null models (Table 2). They were therefore preferred to the null models that have no G × E interactions. The same was observed with MCMC models when comparing DIC, except for FCR. The model comparisons thus pointed out significant G × E interactions for all production traits, except for FCR, and potentially limited for ADG. These results are in line with those of Rosé et al. (2017) who indicated significant sire family × environment interactions for production and thermoregulation.

Table 2.

Bayesian information criteria (BIC) for REML analyses, and deviance information criteria (DIC) for MCMC analyses, for the null (no G × E interaction) and the full (G × E interaction) models

	REML model		MCMC model
	BIC		DIC
Trait1	Null model	Full model	Null model	Full model
BW11	5,036	4,876a	6,903	6,395a
BW23	7,187	7,155a	9,204	8,889a
BFT23	4,040	3,873a	6,029	5,620a
ADG	12,569a	12,670	14,841	14,804a
ADFI	17,823	16,397a	18,845	18,621a
RFI	16,048	15,972a	18,433	18,273a
FCR	732a	847	813a	1,486
RT19	1,460	1,412a	965	912a
RT21	1,330	1,265a	1,109	1,086a
RT23	1,638	1,470a	870	715a
CT19	527a	635	2,828	2,825
CT23	599a	657	2,869	2,795a
GRAD19	−8,189	−8,758a	−6,742	−9,356a
GRAD23	−5,969	−6,153a	−6,602	−9,312a

¹BW₁₁, body weight at week 11; BW₂₃, body weight at week 23; BFT₂₃, back fat thickness at week 23; ADG, average daily weight gain; ADFI, average daily feed intake; RFI, residual feed intake; FCR, feed conversion ratio; RT₁₉, rectal temperature at week 19; RT₂₁, rectal temperature at week 21; RT₂₃, rectal temperature at week 23; CT₁₉ = cutaneous temperature at week 19; CT₂₃, cutaneous temperature at week 23; GRAD₁₉ = (RT₁₉ − CT₁₉) / RT₁₉; GRAD₂₃ = (RT₂₃ − CT₂₃) / RT₂₃.

^aValue for the full model lower by 10 units than the null model.

Relatively large SE (REML) and posterior SD (MCMC) were found for heritabilities within environments, and for genetic correlations (Table 3). It is well known that the larger the sample size, the more accurate an estimate of heritability will generally be. In addition, genetic correlations are seldom very accurate with small sample sizes like those in this study, as precise standard errors require good estimates of the genetic variances and covariances of the traits (Falconer and Mackay, 1996). Nevertheless, general trends can be outlined. Low to moderate heritability (between 0.13 ± 0.07 and 0.35 ± 0.14) were found for feed intake, and low to high heritability (between 0.16 ± 0.09 and 0.58 ± 0.18) for BFT and BW, which is consistent with values generally reported in the literature (Whittemore, 2007). Heritabilities were comparable between environments (Table 3). In the present study, we observed a low to moderate heritability for ADFI (between 0.13 ± 0.07 and 0.35 ± 0.14) and FCR (between 0.10 ± 0.05 and 0.18 ± 0.09). According to the literature in TEMP environments, the heritability for ADFI and FCR are moderate to high (ranging from 0.21 ± 0.06 to 0.48 ± 0.06 for ADFI and between 0.30 ± 0.03 and 0.40 ± 0.06 for FCR; Saintilan et al., 2013; Jiao et al., 2014). Similarly, the heritability for ADFI and FCR are moderate to high in TROP environments (0.37 ± 0.09 and 0.32 ± 0.04, respectively; Akanno et al., 2013). Our low estimates for feed intake traits could come from the fact that individual feeding measures were only available during 50% of the total growth period. Furthermore, as the genetic correlation between TEMP and TROP for FCR was high and not significantly different from 1, it can be hypothesized that the animal models struggle to estimate two components. The same result was observed for ADFI in REML models. However, the heritability estimates for ADFI and FCR with univariate models (considered as a same trait in TEMP and TROP together, or one model by environment) were close to the values found in bivariate models, ranging from 0.07 ± 0.05 and 0.18 ± 0.05 (results not shown).

Table 3.

Heritability estimates (±SE) for production traits in temperate and tropical climates, SD for the animal effect (σ _a) and genetic correlation between environments, obtained from REML estimations and from MCMC computations (posterior SD in parentheses)

	REML model					MCMC model1
	Temperate		Tropical			Temperate		Tropical
Trait2	h 2 (SE)	${\sigma }_a$ 3	h 2 (SE)	${\sigma }_a$ 3	$r_g$ 4	h 2 (SE)	${\sigma }_a$ 3	h 2 (SE)	${\sigma }_a$ 3	$r_g$ 4
BW11	0.37 ± 0.17	2.41	0.39 ± 0.17	2.67	0.56 ± 0.18	0.58 ± 0.18	3.04	0.64 ± 0.17	3.52	0.58 ± 0.33a
BW23	0.39 ± 0.16	6.10	0.46 ± 0.15	7.70	0.43 ± 0.37a	0.24 ± 0.13a	5.18	0.31 ± 0.15	6.53	0.16 ± 0.26a
BFT23	0.33 ± 0.11	2.08	0.28 ± 0.12	1.57	0.55 ± 0.15	0.35 ± 0.15	2.23	0.16 ± 0.09	1.18	0.21 ± 0.23a
ADG	0.47 ± 0.16	62.9	0.33 ± 0.13	58.8	0.77 ± 0.18b	0.25 ± 0.12	51.2	0.24 ± 0.12	48.2	0.35 ± 0.22a
ADFI	0.15 ± 0.09a	0.17	0.18 ± 0.10a	0.16	0.65 ± 0.28b	0.35 ± 0.14	0.28	0.13 ± 0.07a	0.15	0.18 ± 0.25a
RFI	0.11 ± 0.06a	123	0.12 ± 0.07a	96.8	0.52 ± 0.23	0.37 ± 0.13	205.4	0.11 ± 0.05	101.7	0.20 ± 0.26a
FCR	0.10 ± 0.05	0.15	0.13 ± 0.09a	0.20	0.99 ± 0.30b	0.18 ± 0.09	0.22	0.10 ± 0.05	0.22	0.66 ± 0.20b

¹Posterior inferences for the mean and SD of the parameters.

²BW₁₁, body weight at week 11; BW₂₃, body weight at week 23; BFT₂₃, back fat thickness at week 23; ADG, average daily weight gain; ADFI, average daily feed intake; RFI, residual feed intake; FCR, feed conversion ratio.

³SD for the animal effect.

⁴Genetic correlation for a trait between TEMP and TROP climates.

^aValue not significantly different from 0.

^bValue not significantly different from 1 using confidence intervals.

Our study indicates no G × E interactions for FCR and to a lesser extent for ADG traits. Our findings go partly against the previous results obtained by Rosé et al. (2017) who found moderate to strong G × E interactions for ADG. The discrepancy is explained by the statistical model and the information used to estimate G × E. In our study, we used the pedigree as the main information to connect individuals whereas Rosé et al. (2017) used the sire family as fixed effect. Recently, Godinho et al. (2019) reported G × E interaction of about 0.64 ± 0.25 for ADG between purebred pigs in TEMP (The Netherlands, France, and Canada) and TROP (Brasil), but the authors pointed out that the estimate should be interpreted with caution due to convergence issues. For all the other production traits (i.e., except for FCR and ADG), the genetic correlations between TEMP and TROP were significantly different from 1, indicating that the genetic mechanisms underlying the traits partially differed between environments. Indeed, with the REML method, greater genetic correlations were obtained for the same traits, but they are significantly different from 1. In MCMC models, weak to medium genetic correlations, not significantly different from zero, were observed for BW, BFT, ADFI, and RFI. This was consistent with the information criteria comparisons of the null and full models (Table 2).

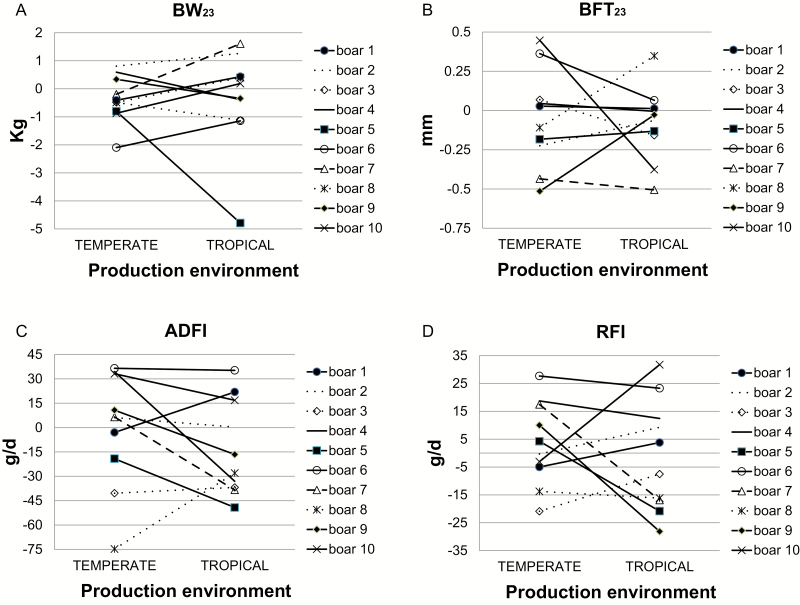
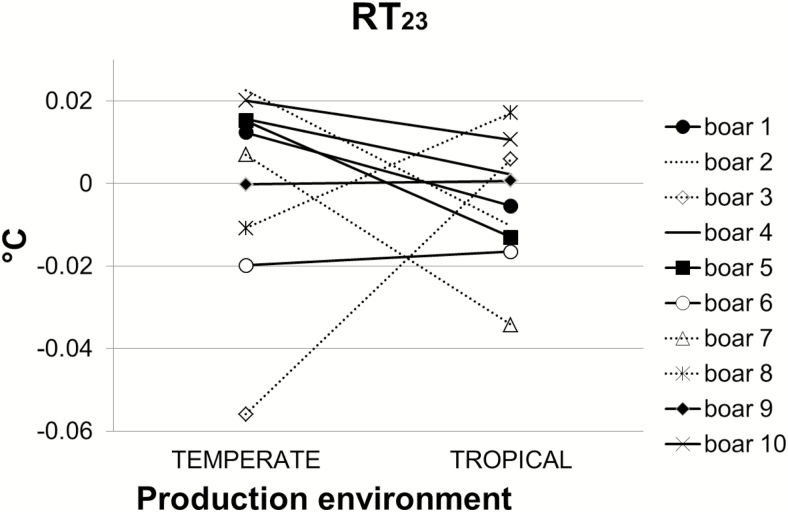
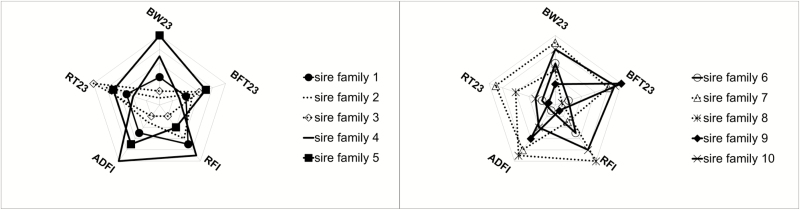
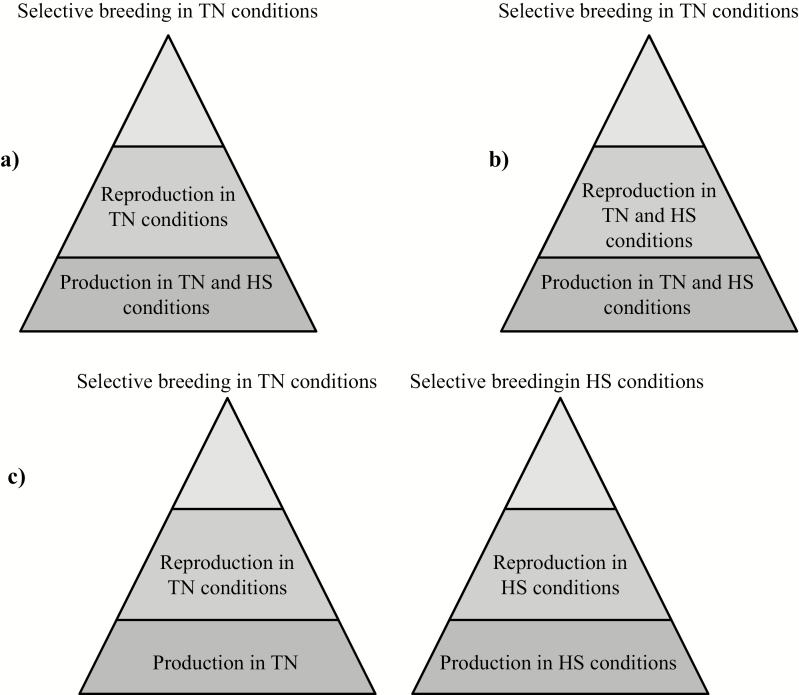
Consequently, the major genetic progress on performance traits carried out due to selection in TEMP would not necessarily translate into TROP environment. Furthermore, these G × E interactions suggest that the genetic control of some production trait differs according to the climatic environment. Differences in the ranking of boars’ breeding values in the two environments are presented in Figure 1 (for some production traits) and in Figure 2 (for RT₂₃). These figures show that some re-ranking of the boars’ breeding values did occur. For instance, the best boar for BW₂₃ in TROP (the sire family 7) may increase BW₂₃ (+1.6 kg) whereas the corresponding value of −0.2 kg in TEMP decrease the trait (Figure 1a). The worst boar for BFT₂₃ in TEMP (the sire family 10; +0.45 mm) is ranked in the best two boars in TROP (−0.38 mm; Figure 1a). In Figure 1b, the sire family 3 has low rank, and the sire family 6 has high rank for ADFI and RFI, respectively, in both environments. The best sire family for RT₂₃ in TEMP (the sire family 3; −0.05°C) is ranked 8 in TROP (+0.01°C). One of the two lowest ranked sire families for RT₂₃ in TEMP (the sire family 10; +0.02°C) is ranked the same as the sire family 3 in TROP (Figure 2). Figure 3 represents the score of the 10 sire families for the following traits: BW₂₃, BFT₂₃, ADFI, RFI, and RT₂₃. For a given trait, score 1 (and conversely, score 10) was assigned to the family with the lowest (and conversely, the highest) estimated breeding values’ difference between TEMP and TROP environments. Thus, in Figure 3, the closest to the center, the pentagon of the sire family is, the more robust the family is. Based on the five traits studied, it is not so obvious to find a sire family robust for all traits. For instance, the family 3 is one of the most robust for BW₂₃, ADFI, and RFI but one of the most sensitive for RT₂₃ and BFT₂₃. The family 9 is one of the most robust for BW₂₃, RT_23, and RFI but one of the most sensitive for ADFI and BFT₂₃. In contrast, families 7 and 5 are considered the most sensitive. However, in the present study, due to the relatively large uncertainty for our estimates, interpretation from our results should be taken with caution. Worldwide, pigs are generally selected under optimal temperate conditions and under constantly improving management. These nucleus units are generally not exposed to HS, so the selection produces animals with high performance but not necessarily selected for better response to HS. As pointed out by Misztal (2017), selection mainly on production traits has produced animals with high performance and in general with smaller environmental flexibility. Furthermore, the best genotypes from the selection environment could not be the best in the target environment, such as the tropical one. Hence, in presence of not negligible G × E interactions, selection programs should take these interactions into account for improving selection efficiency (Knap, 2005; Knap and Su, 2008). Taking into account G × E interactions could thus be important when choosing the best genotypes for pig farms in hot climates. Figure 4 illustrates three possible pyramidal selection schemes according to the level of G × E interactions. On one hand, if G × E interactions between thermoneutral farms and hot farms are small (i.e., as long as the genetic correlation between environments is greater than 0.75 according to Mulder et al. (2006) or Vargas and van Arendonk (2004)), it is possible to combine data from the whole production systems and perform a single breeding program (Figure 4a). On the other hand, if G × E interactions are strong (i.e., the genetic correlation between environments is lower than 0.50), separate selection programs are needed (Figure 4c). Figure 4b consists in an intermediate situation for which G × E interactions are weak to moderate. In this case, the phenotypic information obtained from multiplication farms located in different environments could improve the selection programs. Lewis and Bunter (2011) found high genetic correlations between seasons for performance of lactating sows, and the authors suggested that the determination of breeding values specific to production environments would not be necessary. In contrast, Bloemhof et al. (2012) found sensitive and heat-robust lines in relation to sow reproduction performance, suggesting that we need to consider G × E interactions in breeding schemes. Based on the low genetic correlation between TEMP purebred and TROP crossbred pigs for growth and carcass traits, Godinho et al. (2019) suggested that selection to improved growth and carcass performance of crossbred pigs in TROP based only on the performance of purebred animals in TEMP would compromise the genetic progress.

Figure 1.

Differences in ranking of the 10 boars’ posterior median breeding values in temperate and tropical environment for (a) BW and backfat thickness at the end of test period (week 23; BW at 23 wk of age [BW₂₃] and BFT at 23 wk of age [BFT₂₃]) and (b) daily feed intake (ADFI) and residual feed intake (RFI) during the overall test period.

Figure 2.

Differences in ranking of the 10 boars’ posterior median breeding values in temperate and tropical environment for rectal temperature measured at the end of test period (week 23; RT₂₃).

Figure 3.

Assessment of robustness and sensitivity in the 10 sire families according to their score (from 1, the most robust, to 10, the most sensitive) on boars’ posterior median breeding values differences between temperate and tropical environments on BW and backfat thickness at week 23 (BW at 23 wk of age [BW₂₃] and BFT at 23 wk of age [BFT₂₃]), and daily feed intake (ADFI) and residual feed intake (RFI) during the overall test period, and rectal temperature measured at week 23 (RT₂₃). The closer to the center the sire family pentagon is, the more robust it is.

Figure 4.

Three possible pyramidal selection schemes according to the magnitude of G × E interactions between thermoneutral (TN) and heat stress (HS) conditions; (a) current situation of pig breeding; (b) a pyramidal device that takes into consideration the phenotypic information obtained from multiplication farms located in different environments (case of weak to moderate G × E interactions); (c) case where the G × E interactions are strong and where it becomes essential that the environment of selection is not different from the environmental conditions of production.

Heritabilities and G × E for Thermoregulation Traits

Model comparisons with BIC or DIC (Table 2) showed lower values for the full models as compared with the null models, except for CT. This indicated evidence of G × E interactions for rectal temperatures, which might not exist for cutaneous temperatures.

Heritability estimates for rectal temperature ranged from 0.04 ± 0.05 to 0.34 ± 0.12 (Table 4). Values found in the literature do not show such a low bound, ranging from 0.11 to 0.37 in bovine and poultry (Taouis et al., 2002; Prayaga and Henshall, 2005; Dikmen et al., 2012). Our estimates were also lower than those reported for rectal temperature in lactating sows reared in a tropical environment (0.35 ± 0.09; Gourdine et al., 2017), and for change in rectal temperature in crossbred gilts exposed to chronic heat stress (greater than 0.49; Kim et al., 2018). Lower heritability values could be explained by the small number of RT measurements for each individual. First, estimates depend on the accuracy of the measurement, and second, they depend on the timing of the measurement. It is known that the phenotypic variance of RT can vary during the day. Indeed, Renaudeau (2016) have shown that the internal temperature of pigs varies according to a circadian bi-phasic rhythm in thermoneutral conditions, whereas in a HS situation (32°C), a single phase is observed with maximum values obtained at 22:00. Finally, the discrepancy between our heritability estimates for RT and those in the literature could be explained by the fact that we studied growing pigs while Gourdine et al. (2017) and Kim et al. (2018) studied lactating sows. The sow’s metabolism is highly demanded during lactation, and sow’s rectal temperature may result from individual metabolic differences under genetic control more directly than that of growing pigs. Furthermore, our results suggest that the effect of environment, both in TEMP and TROP, affecting internal temperature is important in growing pigs, more than the genetic effects.

Table 4.

Heritability estimates (±SE) for thermoregulation traits in temperate and tropical climates, SD for the animal effect (σ _a) and genetic correlation between environments, obtained from REML estimations and from MCMC computations (posterior SD in parentheses)

Trait2			REML model					MCMC model1
	Temperate		Tropical		$r_g$ 4	Temperate		Tropical
	h 2 (SE)	${\sigma }_a$ 3	h 2 (SE)	${\sigma }_a$ 3		h 2 (SE)	${\sigma }_a$ 3	h 2 (SE)	${\sigma }_a$ 3	$r_g$ 4
RT19	0.04 ± 0.05a	0.07	0.17 ± 0.07	0.14	0.94 ± 0.49a,b	0.13 ± 0.07a	0.14	0.12 ± 0.07a	0.13	0.10 ± 0.20
RT21	0.09 ± 0.06a	0.12	0.07 ± 0.05a	0.10	0.65 ± 0.49a,b	0.15 ± 0.07	0.16	0.11 ± 0.05	0.14	0.09 ± 0.23a
RT23	0.07 ± 0.06a	0.10	0.08 ± 0.06a	0.09	0.93 ± 0.49a,b	0.34 ± 0.12	0.25	0.10 ± 0.05	0.10	0.10 ± 0.26a
CT19	0.03 ± 0.04a	0.13	0.02 ± 0.04a	0.10	0.77 ± 0.96a,b	0.11 ± 0.05	0.30	0.06 ± 0.03	0.20	0.06 ± 0.30a
CT23	0.07 ± 0.05a	0.25	0.06 ± 0.05a	0.18	0.91 ± 0.92a,b	0.36 ± 0.10	0.57	0.07 ± 0.03	0.21	0.37 ± 0.29a
GRAD19	0.05 ± 0.04a	0.004	0.05 ± 0.05a	0.004	0.45 ± 0.96a,b	0.01 ± 0.01a	0.002	0.01 ± 0.01a	0.002	0.00 ± 0.04a
GRAD23	0.03 ± 0.03a	0.004	0.03 ± 0.03a	0.003	0.09 ± 0.91a,b	0.01 ± 0.01a	0.003	0.01 ± 0.01a	0.002	0.00 ± 0.04a

¹Posterior inferences for the mean and SD of the parameters.

²RT₁₉, rectal temperature at week 19; RT₂₁, rectal temperature at week 21; RT₂₃, rectal temperature at week 23; CT₁₉, cutaneous temperature at week 19; CT₂₃, cutaneous temperature at week 23; GRAD₁₉ = (RT₁₉ − CT₁₉) / RT₁₉, GRAD₂₃ = (RT₂₃ − CT₂₃) / RT₂₃.

³SD for the animal effect.

⁴Genetic correlation for a trait between TEMP and TROP climates.

^aValue not significantly different from 0.

^bValue not significantly different from 1 using confidence intervals.

For cutaneous temperatures and the gradients between rectal and cutaneous temperatures, heritability estimates were low in both environments. Moreover, the average values obtained for GRAD₁₉ and GRAD₂₃ traits were close to zero with the two methods of estimation. To our knowledge, this is the first time that heritability for cutaneous temperature has been estimated in growing pigs. In crossbred gilts, Kim et al. (2018) reported that change in skin temperature from thermoneutral to HS conditions was not heritable. On the contrary, Gourdine et al. (2017) have shown that skin temperature of lactating sows reared in tropical humid conditions was moderately heritable (0.34 ± 0.12). In laying hens, surface temperature measured by infrared thermography on unfeathered zone (comb and shank) had low to moderate heritabilities, ranging from 0.15 ± 0.01 to 0.22 ± 0.01 at 18 or 28°C, with no difference depending on the environment (Loyau et al., 2016). The measurement of cutaneous temperature from infrared thermometer is an indicator of heat dissipation through the sensible pathway. Furthemore, skin temperature is the result of heat transport from the core to the periphery of the pig body and outdoor climatic conditions. In addition, in our study, CT was measured in a single point (always the same) and it is well known from infrared thermography that the body temperature is very heterogeneous on the animal’s surface (Dela Ricci et al., 2019). Measuring the whole body temperature with an infrared thermography camera could better estimate heat dissipation in pigs. Heat can also be dissipated through respiratory pathway, which has not been measured in our conditions due to technical issues for measuring animals in groups. However, it is well known that evaporative heat loss becomes increasingly important as HS becomes more pronounced (Mount et al., 1979). Gourdine et al. (2017) and Kim et al. (2018) estimated heritability for respiratory rate of about 0.39 in lactating sows (in chronic HS) and in gilts (change from thermoneutrality to acute HS), respectively. As a consequence, skin temperature would not be the best indicator of heat loss and taking into account respiratory rate might provide better knowledge than cutaneous temperature to improve thermolysis.

The genetic correlations for rectal temperature between TEMP and TROP environment did not differ from zero with the REML and MCMC estimations, suggesting that the genetic mechanisms involved in the expression of inner temperature may be partially different, depending on the studied environment (Table 4). However, the REML estimates did not differ from 1 either due to large SE. Models information criteria confirm significant G × E for RT and GRAD₁₉ and GRAD₂₃, but no conclusion for CT could be achieved. In TEMP, rectal temperature may only be indicative of the digestive and maintenance metabolism, while in TROP, HS may interact with those regulations, making it a genetically different trait.

Genetic Correlations Between Production and Thermoregulation Traits

In the present study, as the heritability estimates for GRAD₁₉ and GRAD₂₃ were very low, the genetic correlations between production and thermoregulation traits were calculated only for RT and CT (Table 5 and 6). The genetic correlation estimates were obtained with very large inaccuracies (CV varied in absolute values between 18% and 100%, with a median value of 43% for MCMC models). For most traits’ combinations, at least one estimate did not differ significantly from 1, and another did not differ significantly from 0. Consequently, interpretations of such genetic correlations should be taken with caution. However, general trends can be seen both with REML and MCMC models. Most of genetic correlations between BW and RT were negative (81% of the 16 estimations). The same trend was observed for the genetic correlations between ADFI and RT, between ADG and RT, BFT₂₃ and RT, RFI and RT, and FCR and RT, suggesting that greater rectal temperature would be associated with lower feed intake and growth rate (unfavorable), but also better feed efficiency and increased leanness. This result suggests that a fast growth associated to high feeding level has an unfavorable relationship with the ability to dissipate heat, certainly due to more active metabolism, such as higher metabolic energy for maintenance or higher lean deposition rate. However, the correlations with feed efficiency suggest that some compromise could be found. As reviewed by Renaudeau et al. (2004), there is an antagonism between the ability to maintain or to slowly increase inner temperature, and the ability to maintain production levels in spite of HS. At the selection level, a breeding program aiming at increasing the level of production would tend to decrease the average value of the inner temperature, and thus the capacity of the pig to increase its body temperature to favor heat loss. Similarly, a selection to increase the average value of rectal temperature would tend to decrease the level of production.

Table 5.

Genetic correlations between thermoregulation and production traits within temperate or tropical climates and their SE, obtained from a REML algorithm

	RT19		RT23		CT19		CT23
Trait1	Temperate	Tropical	Temperate	Tropical	Temperate	Tropical	Temperate	Tropical
BW11	−0.75 ± 0.35a	−0.13 ± 0.05	−0.46 ± 0.20	−0.05 ± 0.05b	−0.30 ± 0.13	−0.99 ± 0.21a	−0.20 ± 0.07	−0.30 ± 0.17b
BW23	−0.65 ± 0.25a	−0.22 ± 0.14b	−0.25 ± 0.41a,b	0.06 ± 0.04b	0.41 ± 0.14	0.78 ± 0.32a	0.74 ± 0.18	−0.10 ± 0.09b
BFT23	0.05 ± 0.05b	−0.62 ± 0.25a	−0.68 ± 0.31a	−0.27 ± 0.17b	−0.09 ± 0.05	−0.82 ± 0.15ba	−0.24 ± 0.09b	−0.90 ± 0.34a
ADG	−0.93 ± 0.31a	−0.14 ± 0.05	−0.42 ± 0.21	−0.25 ± 0.14b	0.46 ± 0.12	0.82 ± 0.25a	0.87 ± 0.17a	0.44 ± 0.22
ADFI	0.29 ± 0.14	−0.43 ± 0.21	−0.91 ± 0.35a	−0.42 ± 0.25b	−0.36 ± 0.18	0.90 ± 0.33a	0.43 ± 0.14a	0.36 ± 0.12
RFI	−0.99 ± 0.25a	−0.23 ± 0.15b	−0.76 ± 0.14a	−0.26 ± 0.14b	−0.13 ± 0.08b	−0.91 ± 0.29a	0.01 ± 0.05b	−0.60 ± 0.14
FCR	−0.19 ± 0.47a,b	−0.53 ± 0.42a	−0.72 ± 0.39a,b	−0.43 ± 0.48a,b	−0.11 ± 0.44b	−0.90 ± 0.40a	−0.37 ± 0.39a,b	−0.16 ± 0.55a,b
RT19			0.98 ± 0.24a	0.90 ± 0.25a	0.13 ± 0.04	0.83 ± 0.18a	0.35 ± 0.10	0.44 ± 0.20
RT23	0.98 ± 0.24a	0.90 ± 0.25a			0.14 ± 0.08b	0.55 ± 0.14a	0.16 ± 0.05	0.26 ± 0.11
CT19	0.13 ± 0.04	0.83 ± 0.18a	0.14 ± 0.08b	0.55 ± 0.14			0.89 ± 0.26a	0.99 ± 0.19a
CT23	0.35 ± 0.10	0.44 ± 0.20	0.16 ± 0.05	0.26 ± 0.11	0.89 ± 0.26a	0.99 ± 0.19a

¹BW₁₁, body weight at week 11; BW₂₃, body weight at week 23; BFT₂₃, back fat thickness at week 23; ADG, average daily weight gain; ADFI, average daily feed intake; RFI, residual feed intake; FCR, feed conversion ratio; RT₁₉, rectal temperature at week 19; RT₂₁, rectal temperature at week 21; RT₂₃, rectal temperature at week 23; CT₁₉, cutaneous temperature at week 19; CT₂₃, cutaneous temperature at week 23; GRAD₁₉, (RT₁₉ − CT₁₉) / RT₁₉, GRAD₂₃ = (RT₂₃ − CT₂₃) / RT₂₃.

^aValue not significantly different from 1 (P < 0.05).

^bValue not significantly different from 0 (P < 0.05).

Table 6.

Posterior mean and SD of genetic correlations between thermoregulation and production traits within temperate or tropical climates, obtained using an MCMC procedure

Trait1	RT19		RT23		CT19		CT23
	Temperate	Tropical	Temperate	Tropical	Temperate	Tropical	Temperate	Tropical
BW11	−0.80 ± 0.15a	−0.01 ± 0.22b	−0.89 ± 0.15a	0.09 ± 0.18	−0.65 ± 0.16	−0.56 ± 0.21	−0.63 ± 0.15	−0.58 ± 0.16
BW23	−0.18 ± 0.25b	−0.11 ± 0.33b	0.02 ± 0.16b	−0.06 ± 0.13b	0.82 ± 0.11	0.01 ± 0.22b	0.16 ± 0.23b	−0.14 ± 0.19b
BFT23	0.11 ± 0.21b	−0.28 ± 0.15b	−0.43 ± 0.16	−0.30 ± 0.14	0.05 ± 0.27b	−0.55 ± 0.17	0.09 ± 0.28b	−0.49 ± 0.18
ADG	−0.24 ± 0.34b	−0.26 ± 0.34b	−0.03 ± 0.42b	−0.07 ± 0.37b	0.88 ± 0.09	0.81 ± 0.16	0.88 ± 0.10	0.63 ± 0.29a
ADFI	−0.10 ± 0.26b	−0.34 ± 0.23b	−0.13 ± 0.27b	−0.21 ± 0.24b	−0.22 ± 0.24b	0.03 ± 0.34b	0.17 ± 0.35b	0.06 ± 0.35b
RFI	−0.84 ± 0.28a	−0.93 ± 0.11a	−0.78 ± 0.35a	−0.90 ± 0.16a	−0.87 ± 0.27a	−0.92 ± 0.15a	−0.69 ± 0.44a	−0.91 ± 0.18a
FCR	−0.09 ± 0.19b	−0.24 ± 0.27b	−0.24 ± 0.27b	−0.23 ± 0.26b	−0.26 ± 0.32b	−0.25 ± 0.30b	−0.27 ± 0.32b	−0.25 ± 0.30b
RT19	1	1	0.32 ± 0.09	0.76 ± 0.09	0.53 ± 0.25	0.92 ± 0.04a	0.32 ± 0.31b	0.25 ± 0.29b
RT23	0.32 ± 0.09	0.76 ± 0.09	1	1	0.05 ± 0.35b	0.27 ± 0.28b	0.37 ± 0.30b	0.84 ± 0.07
CT19	0.53 ± 0.25	0.92 ± 0.04a	0.05 ± 0.35b	0.27 ± 0.28b	1	1	0.55 ± 0.27	0.69 ± 0.19
CT23	0.32 ± 0.31b	0.25 ± 0.29b	0.37 ± 0.30b	0.84 ± 0.07	0.55 ± 0.27	0.69 ± 0.19	1	1

¹BW₁₁, body weight at week 11; BW₂₃, body weight at week 23; BFT₂₃, back fat thickness at week 23; ADG, average daily weight gain; ADFI, average daily feed intake; RFI, residual feed intake; FCR, feed conversion ratio; RT₁₉, rectal temperature at week 19; RT₂₁, rectal temperature at week 21; RT₂₃, rectal temperature at week 23; CT₁₉, cutaneous temperature at week 19; CT₂₃, cutaneous temperature at week 23; GRAD₁₉ = (RT₁₉ − CT₁₉) / RT₁₉, GRAD₂₃ = (RT₂₃ − CT₂₃) / RT₂₃.

^aValue not significantly different from 1 (P < 0.05).

^bValue not significantly different from 0 (P < 0.05).

There are very few studies dealing with G × E interactions in growing pigs under HS (Godinho et al., 2019), in comparison with studies in poultry (Mignon-Grasteau et al., 2015), dairy cattle (Hayes et al., 2009), and beef cattle (Santana et al., 2013). This is probably due to the lack of tight genetic relationships between growing pigs raised in contrasted environments, and also due to the absence of a significant number of observations allowing accurate quantification of G × E interactions. In other species, genetic correlations between performance traits and rectal temperatures are generally unfavorable and moderate to high (Taouis et al., 2002; Prayaga and Henshall, 2005; Dikmen et al., 2012), so our results were in general accordance with these findings.

Concerning cutaneous temperatures, no general trend could be outlined between or within environment, as the genetic correlations between production and CT were either positive or negative with high inaccuracies, depending on the production trait and the environment considered. The genetic correlations between RT and CT were positive and generally high, ranging from 0.05 ± 0.35 to 0.99 ± 0.19, with a median value of 0.62, and lower values in TEMP than in TROP. These results could be expected as TROP pigs experienced heat stress more often than TEMP pigs (Rosé et al., 2017). Actually, the greater correlations between RT and CT in TROP than in TEMP reflect the heat transfer from the core to the skin of TROP pigs due to HS.

Experimental Design Used to Estimate Genetic Parameters for Heat Tolerance

As previously outlined, in this study we used a backcross population (3/4 Large White and ¼ Creole breed) to estimate the genetic parameters for heat tolerance. The genetics of Large White breed are world widely distributed in pig commercial farms via terminal crossbreeding, but to our knowledge the Creole breed is mainly reared in small family farming systems from rural communities (Burgos-Paz et al., 2013). Consequently, our studied BC population was not representative of the commercial lines generally based on pure breeds such as Large White, Landrace, Duroc, and Pietrain. For instance, Kim et al. (2018) used commercial crossbred gilts (PIC × Duroc) to estimate the heritability of thermoregulation traits. In the same way, Zumbach et al. (2008) studied commercial crossbred growing pigs [Duroc × (Landrace × Large White)] to evaluate the genetic component of heat tolerance. Recently, Godinho et al. (2019) reported G × E interactions between TEMP and TROP for growth and carcass traits in purebred and crossbred growing pigs. Hence, the genetic variability observed in the present study may not be consistent with that observed in commercial pig populations, and our interpretations on selection strategies must be taken with caution.

Conclusions

In the present study on growing pigs, the low to moderate heritabilities for thermoregulation traits, and their genetic correlations with production traits imply that there is some genetic variation in pig thermotolerance that can be exploited to improve heat tolerance. Moreover, for most traits, the genetic correlation estimates were different from 1 between the environments, showing the existence of G × E interactions and suggesting that the genetic mechanisms underlying the traits would be partially different depending on the environment. Our study questions the breeding strategies to improve the performance of pigs reared in tropical area and the need to include G × E interactions into the breeding scheme. As expected, with our small sample size relatively to several studies dealing with estimation of genetic parameters in growing pigs, our estimates were obtained with high inaccuracies. Our conclusion should thus be validated on larger number of animals. The accuracy of our results could be improved by including genomic information. Further studies involving genomic analysis for deciphering chromosomic regions related with heat tolerance are in course and they can be promising to this topic.