MULTiPly: a novel multi-layer predictor for discovering general and specific types of promoters

Abstract

Motivation

Promoters are short DNA consensus sequences that are localized proximal to the transcription start sites of genes, allowing transcription initiation of particular genes. However, the precise prediction of promoters remains a challenging task because individual promoters often differ from the consensus at one or more positions.

Results

In this study, we present a new multi-layer computational approach, called MULTiPly, for recognizing promoters and their specific types. MULTiPly took into account the sequences themselves, including both local information such as k-tuple nucleotide composition, dinucleotide-based auto covariance and global information of the entire samples based on bi-profile Bayes and k-nearest neighbour feature encodings. Specifically, the F-score feature selection method was applied to identify the best unique type of feature prediction results, in combination with other types of features that were subsequently added to further improve the prediction performance of MULTiPly. Benchmarking experiments on the benchmark dataset and comparisons with five state-of-the-art tools show that MULTiPly can achieve a better prediction performance on 5-fold cross-validation and jackknife tests. Moreover, the superiority of MULTiPly was also validated on a newly constructed independent test dataset. MULTiPly is expected to be used as a useful tool that will facilitate the discovery of both general and specific types of promoters in the post-genomic era.

Availability and implementation

The MULTiPly webserver and curated datasets are freely available at http://flagshipnt.erc.monash.edu/MULTiPly/.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The first and most critical step of gene expression is the initiation of transcription, requiring a dynamic cooperation between the RNA polymerase (RNAP) and the promoter (Ramprakash and Schwarz, 2008). Promoters are chromosome regions that facilitate the transcription of particular genes, and they are located proximal to the transcription start sites of genes, towards the 5′ region of the sense strand. In bacteria, the promoter is recognized by the RNA polymerase and correlated function-specific sigma factors that are labelled on the basis of their molecular weights (${\sigma }^{24}$,${\sigma }^{28}$,${\sigma }^{32}$,${\sigma }^{38}$,${\sigma }^{54}$ and ${\sigma }^{70}$), which in turn are often brought to the promoter by regulatory proteins that bind to specific sites nearby (Barrios et al., 1999; Helmann and Chamberlin, 1988; Towsey et al., 2008). The types of promoters are defined according to how the σ factors identify the promoter.

The precise recognition of promoters is crucial to regulation of the expression of each gene and each transcription unit in the genome. However, the precise prediction of promoters remains a challenging task, because individual promoters usually differ from the consensus at one or even more positions (Mrozek et al., 2014, 2016).

In recent years, a number of computational methods have been developed to rapidly differentiate DNA sequences as promoters or non-promoters, aimed at complementing with experimental efforts and overcoming certain experimental bottlenecks. For instance, position weight matrices (PWMs) were used to predict ${\sigma }^{70}$ promoters in Escherichia coli, based on the conservation of the -10 and -35 hexamers (with the consensus sequences ‘TATAAT’ and ‘TTGACA’, respectively) and the distribution of promoters from the start of the gene (Hertz and Stormo, 1996; Huerta and Collado-Vides, 2003); however, the latter approach achieved a relatively lower accuracy. In 2009, Kemal, a new method that integrated feature selection and a fuzzy-AIRS classifier system to predict E.coli promoter gene sequences was proposed (Polat and Güneş, 2009). More recently, with machine learning techniques booming, many promoter prediction tools have been developed and made available, including 70ProPred, iPro54-PseKNC, iPromoter-2L and bTSSfinder (He et al., 2018; Liang et al., 2017; Lin et al., 2014, 2017; Liu et al., 2018; Shahmuradov et al., 2017). We note that, amongst previously developed tools, only iPromoter-2L is able to predict whether a query sequence sample is a promoter or not (Task 1), and identify which specific promoter type it would belong to if it is identified as a promoter (Task 2). iPromoter-2L reached an overall accuracy of 81.68% for identifying promoters and non-promoters on the 5-fold cross-validation test. However, with respect to the prediction of specific promoter types, except for the identification of the ${\sigma }^{24}$ promoter, the performance results on other types of promoters were not entirely satisfactory. For ${\sigma }^{28}, {\sigma }^{32}, {\sigma }^{38} \mathrm{a}\mathrm{n}\mathrm{d} {\sigma }^{54}$ promoters, iPromoter-2L achieved a specificity (Sp) of higher than 99%, but achieved a much worse sensitivity (Sn) of lower than 54%. In addition, for ${\sigma }^{70}$ promoter prediction, the Sn was 95.34%, while the Sp was only 59.35%. A major reason for the observed large discrepancy might be attributed to the different numbers of the six distinct types of promoters.

To address this complexity and improve the effectiveness of promoter prediction, in this work, we developed MULTiPly, a multi-layer two-task predictor designed to both recognize the promoters and identify their specific types in E.coli. Firstly, both the sequences themselves and the information measures including k-tuple nucleotide composition (KNC), dinucleotide-based auto covariance (DAC) and the global information of the whole samples including bi-profile Bayes (BPB) and k-nearest neighbour feature (KNN), were taken into consideration; subsequently, the F-score feature selection method was applied to identify the optimal feature combination. To overcome the complexity associated with the analysis of varying numbers of samples for six types of known promoters, the method learns to differentiate between one (positive) promoter subset and the joint set of all other promoter subsets with less samples than the positive dataset (negative). We established a total of five binary sub-classifiers in the second task according to the dataset size. In the first sub-classifier, the largest subset $S^{+}\left({\sigma }^{70}\right)$ was regarded as the positive class, while the union of the other five types of promoter samples were considered as negative samples to train the classifier for identifying the ${\sigma }^{70}$ promoters. Then, we successively deemed ${S^{+}(\sigma }^{24})$, ${S^{+}(\sigma }^{32})$, $S^{+}\left({\sigma }^{38}\right)$ and ${S^{+}(\sigma }^{28})$ as the positive class, and the rest promoters that were not classified jointly as the negative class. Comprehensive benchmarking experiments using 5-fold cross-validation, jackknife test and independent test based on our newly constructed independent test dataset consistently showed the effectiveness of the proposed MULTiPly approach, especially for distinguishing specific types of promoters.

2 Materials and methods

As suggested in a series of recent publications (Chen et al., 2018a,b,c; Cheng et al., 2018a,b; Li et al., 2018a,b; Song et al., 2018a,b,c), we followed the guidelines of Chou’s 5-step rule (Chou, 2011), in an effort to make the presentation of this paper more clear and transparent, enable others to repeat analysis steps, and ensure that the proposed predictor can be easily and widely used by the majority of experimental scientists. The five detailed steps include: (i) construct a valid benchmark dataset and an independent test dataset; (ii) extract the features that can truly reflect their intrinsic correlations with the target to be predicted; (iii) introduce a powerful algorithm (or prediction engine) to operate the prediction; (iv) properly perform cross-validation tests to objectively evaluate the predictor’s accuracy; (v) establish a user-friendly web-server as an implementation of the predictor that is freely accessible to the wider research community. A graphical illustration of the five steps involved in the development of MULTiPly is shown in Figure 1.

Fig. 1.

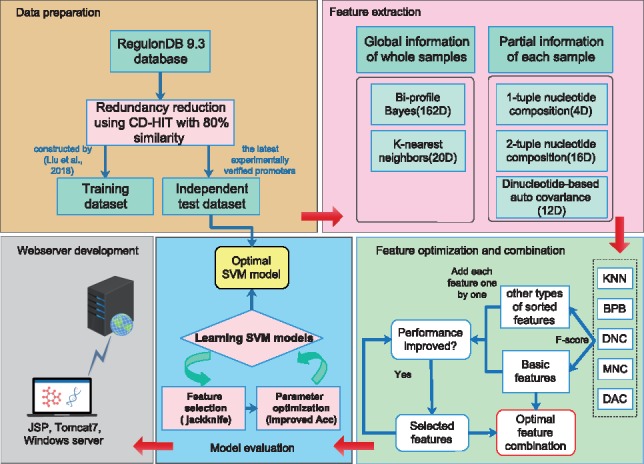
The overall framework of MULTiPly. The five steps are formulated and illustrated according to Chou’s 5-step rule (Chou, 2011)

2.1 Datasets

The models of MULTiPly were trained using a most-recent dataset, constructed in (Liu et al., 2018a,b). All collected promoter samples were experimentally verified (each with 81 bp) and retreived from the RegulonDB database (Version 9.3). RegulonDB (available at http://regulondb.ccg.unam.mx/) is one of the most useful public resources on bacterial gene regulation in the model organism E.coli K-12. If a reported promoter belonged to two sigma types, we accordingly assigned it to the type that had a larger number of experimentally verified sequences. After the raw data processing, the final benchmark dataset $S$ was defined as follows:

$$\left\{\begin{array}{c}S=S^{+}\cup S^{-}\\ S^{+}=S^{+}\left({\sigma }^{24}\right)\cup S^{+}\left({\sigma }^{28}\right)\cup S^{+}\left({\sigma }^{32}\right)\cup S^{+}\left({\sigma }^{38}\right)\cup S^{+}\left({\sigma }^{54}\right)\cup S^{+}\left({\sigma }^{70}\right)\end{array}\right.\mathrm{ }$$ (1)

where $S^{+}$ denotes the positive dataset containing 2860 promoter sequences, $S^{-}$ denotes the negative dataset containing 2860 non-promoter sequences, while the symbol $\cup$ denotes the ‘union’ in the Set Theory. $S^{+}$ contains all six types of promoter sequences; specifically, there existed 484 promoter sequences of${\sigma }^{24}$, 134 of ${\sigma }^{28}$, 291 of ${\sigma }^{32}$, 163 of ${\sigma }^{38}$, 94 of ${\sigma }^{54}$ and 1694 of ${\sigma }^{70}$, respectively. The length of each sequence in our used datasets is 81. As RegulonDB was updated in 18/06/2018, we collected the recently experimentally verified promoter samples from the current version of RegulonDB (Version 10.0) as the independent test dataset, which was denoted as $S_{test}$, to test the performance of MULTiPly. Lastly, a total of 54 promoter sequences were collected in $S_{test}$, including 46 sequences of ${\sigma }^{70}$, 1 of ${\sigma }^{24}$, 2 of ${\sigma }^{32}$, 4 of ${\sigma }^{38}$ and 1 of ${\sigma }^{28}$.

2.2 Feature extraction strategy

In general, feature extraction refers to the formulation of an effective mathematical expression representing a nucleotide sequence. In this study, features were extracted incorporating both global features (i.e. BPB and KNN features) and local (i.e. KNC and DAC features) features, in order to derive more representative and useful information from promoter and non-promoter samples. BPB features reflect the nucleotide distribution within the whole samples, while KNN features describe whether each sample sequence is more similar to the positive or negative samples. KNC was used to encode the compositions of nucleotides and di-nucleotides in a single DNA sample. DAC measures the correlation between two di-nucleotides which have the similar physicochemical index. The feature extraction procedures are described in the following sections.

2.2.1 Bi-profile bayes (BPB)

BPB has proven useful for improving the prediction performance of machine learning-based models in a number of different bioinformatics studies, such as predicting protein methylation sites (Shao et al., 2009), caspase cleavage sites (Song et al., 2010, 2012a,b; Wang et al., 2014) and strong and weak enhancer (Jia and He, 2016). BPB considers the position-specific information from both positive and negative training samples simultaneously. The latter is the main reason why BPB outperforms other feature encoding schemes in many cases.

Each of the DNA samples S can be expressed as:

$$\mathrm{S}=R_1{R}_2{R}_3\dots R_i\dots R_L (i=1,\mathrm{ }2,\mathrm{ }3,\dots ,L)$$ (2)

where $R_i$ is one of the nucleotides A, G, C and T; i represents a nucleotide position, and L denotes the length of the nucleotide sequence. In this study, L = 81, which is the same as that used in previous works (Liu et al., 2018a,b). The sequence S is encoded as a feature vector $V_{BPB}=\left(p_1,p_2,\dots ,p_L,p_{L+1},\dots p_{2L}\right),$where $p_i(\mathrm{i}\hspace{0.5em}=\hspace{0.5em}1,\mathrm{ }2,\mathrm{ }\dots ,\mathrm{ }L)$ represents the posterior probability of each nucleotide at the ith position in all positive samples, and $p_i(\mathrm{i}=L+1,\mathrm{ }L+2,\dots ,\mathrm{ }2L)$ denotes the posterior probability of each nucleotide at the ith position in all negative samples. When the numbers of positive and negative samples were equal and sufficiently large, the frequency of each nucleotide at each position would be a close approximation to the true probability of the occurrence. Accordingly, the posterior probabilities of the positive and negative samples were calculated as the occurrence frequencies for each nucleotide to appear at each position in the positive and negative training datasets, respectively. The dimension of the BPB feature vector was 162, the 1st–81th features were derived from the overall probability distribution of the positive samples, while the 82th–162th features were derived from the overall probability distribution of the negative samples.

2.2.2 KNN features

In the fields of bioinformatics and computational biology, the KNN features have been successfully applied to the analysis and prediction of protein, DNA and RNA sequences (Chen et al., 2013; Jia et al., 2016, 2018; Li et al., 2018a,b; Wang et al., 2017). By extracting relevant features from similar sequences in both the positive and negative datasets using the KNN algorithm, the KNN scores could capture the local sequence similarity in the promoter and non-promoter samples (Gao et al., 2010).

For two local sequences $P_1$ and $P_2$, the distance $\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\left(P_1,P_2\right)$ can be defined as follows:

$$\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\left(P_1,P_2\right)=\sum _{i=1}^{L}Sim(P_1\left(i\right),P_2(i\left)\right)\mathrm{ }$$ (3)

where L represents the number of nucleotides in a DNA sequence (L = 81 in this study), while $P_1\left(i\right) \mathrm{a}\mathrm{n}\mathrm{d} P_2\left(i\right)$ denote the nucleotides at the ith position of sequences $P_1$ and $P_2$, respectively. For two nucleotides a and b, their similarity score is defined as (Jia et al., 2018)

$$\mathrm{S}\mathrm{i}\mathrm{m}\left(\mathrm{a},\mathrm{ }\mathrm{b}\right)=\left\{\begin{array}{c}+2, if a=b;\\ -1, otherwise.\end{array}\right.$$ (4)

For a query DNA sequence (potential promoter or non-promoter sequence), the local sequence similarity would be first considered. Then, the KNN scores were calculated based on the proportion of the positive and negative samples in the set of k neighbours, respectively. The detailed procedures for calculating the KNN scores are described as follows: (i) form a comparison set that contains all the positive and negative samples; (ii) calculate the distances between a query sequence and the other samples in the comparison set; (iii) sort the distances in the ascending order and generate the top k nearest neighbours; (iv) calculate the KNN scores, which is the percentage of the positive neighbours in its k nearest neighbours. To obtain the best features, different values of k (k = 10, 20, 30… 200) were assessed in this study. More specifically, if the dimension of KNN features was d (1 ≤ d ≤ 20), the numbers of 10, 20, …, 10d neighbours would be successively selected.

2.2.3 k-tuple nucleotide composition (KNC)

The type and position of nucleotides within a DNA sequence contained crucial information. Accordingly, strategies for extracting such information in an effective manner have been extensively researched in a number of previous studies. The KNC can characterize the occurrence frequency and the permutation order of nucleotides in each sequence, and this measure has been widely used in many previous studies (Chen et al., 2015; Ioshikhes et al., 1996; Jia et al., 2013; Kabir and Hayat, 2016; Li et al., 2015a,b). After various trials, the 1-tuple (mononucleotide) and 2-tuple (dinucleotide) compositions (referred to as MNC and DNC, respectively) were determined to construct the feature vector. The MNC feature vector can be formulated as follows:

$$\mathrm{D}={\left[\mathrm{f}\left(\mathrm{A}\right),\mathrm{ }\mathrm{f}\left(\mathrm{C}\right),\mathrm{ }\mathrm{f}\left(\mathrm{G}\right),\mathrm{ }\mathrm{f}\left(\mathrm{T}\right)\right]}^{\text{'}}$$ (5)

where $\mathrm{f}\left(i\right)$ represents the frequency of occurrence of each nucleotide. The DNC feature vector can be defined as follows:

$$\mathrm{D}={\left[f\left(AA\right),f\left(AC\right),f\left(AG\right),f\left(AT\right),\dots ,f\left(TT\right)\right]}^{\mathrm{\text{'}}}$$ (6)

where $\mathrm{f}\left(i\right)$ represents the frequency of occurrence of each dinucleotide $i$.

2.2.4 Dinucleotide-based auto-covariance (DAC)

DAC measures the correlation between two di-nucleotides separated by a distance ($\mathrm{\lambda })$along the sequence with the same physicochemical index (Dong et al., 2009; Guo et al., 2008; Liu et al., 2015, 2017a,b). It can be calculated as:

$$\mathrm{D}\mathrm{A}\mathrm{C}\left(\mathrm{u},\mathrm{\lambda }\right)={\sum }_{i=1}^{L-\lambda -1}(P_u\left(R_i{R}_{i+1}\right)-{\overline{P}}_u)(P_u\left(R_{i+\lambda }{R}_{i+\lambda +1}\right)-{\overline{P}}_u)/(L-\lambda -1)$$ (7)

where u is a physicochemical index, L is the length of the promoter sequence S, $P_u\left(R_i{R}_{i+1}\right)$ denotes the numerical value of the physicochemical index u for the dinucleotide $R_i{R}_{i+1}$ at the position i, and ${\overline{P}}_u$ is the average value for the physicochemical index u along the whole sequence, which is defined as:

$${\overline{P}}_u=\sum _{j=1}^{L-1}{P}_u\left(R_j{R}_{j+1}\right)/(L-1)$$ (8)

In such a way, the length of the DAC feature vector can be defined as $N\mathrm{*}\mathrm{\Lambda }$, where N is the number of physicochemical indices while $\mathrm{\Lambda }$ is the maximum of $\mathrm{\lambda }$ ($\mathrm{\lambda }\hspace{0.5em}$= 1, 2…$\mathrm{\Lambda }$). In this study, we selected six physicochemical indices, including Base stacking, Dinucleotide GC content, A-philicity, Rise, Roll and Stability and set the parameter $\mathrm{\Lambda }$ as 2. The feature vector can then be generated using the very powerful, publicly available Pse-in-One web server, documented in the literature (Friedel et al., 2009; Liu et al., 2017a,b).

2.3 Feature optimization

When multiple features are incorporated to train a model, the dimension of the resulting hybrid feature vectors becomes very large. As the initial features might contain redundant and noisy information, we presumed that this could exert a negative effect on model training. Therefore, to filter out the noisy and irrelevant features and select a subset of optimal features, the most important features were identified by a feature selection method known as F-score (Bui, 2016; Lin and Ding, 2011; Zuo and Jia, 2017). The F-score of the jth feature is defined as:

$$\mathrm{F}-\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\left(\mathrm{j}\right)=\frac{{({{\displaystyle \stackrel{-}{x}}}_j^{\left(+\right)}-{{\displaystyle \stackrel{-}{x}}}_j)}^2+{({{\displaystyle \stackrel{-}{x}}}_j^{\left(-\right)}-{{\displaystyle \stackrel{-}{x}}}_j)}^2}{\frac{1}{m^{+}-1}\sum _{k=1}^{m^{+}}{({{\displaystyle \stackrel{-}{x}}}_{k,j}^{\left(+\right)}-{{\displaystyle \stackrel{-}{x}}}_j^{\left(+\right)})}^2+\frac{1}{m^{-}-1}\sum _{k=1}^{m^{-}}{({{\displaystyle \stackrel{-}{x}}}_{k,j}^{\left(-\right)}-{{\displaystyle \stackrel{-}{x}}}_j^{\left(-\right)})}^2}$$ (9)

where ${{{\displaystyle \stackrel{-}{x}}}_j, {\displaystyle \stackrel{-}{x}}}_j^{\left(+\right)}$ and ${{\displaystyle \stackrel{-}{x}}}_j^{\left(-\right)}$ denote the average values of the jth feature in the combined (i.e. positive and negative), the positive and the negative datasets, respectively. $m^{+}$ denotes the number of positive samples,$m^{-}$ denotes the number of negative samples, ${{\displaystyle \stackrel{-}{x}}}_{k,j}^{\left(+\right)}$ denotes the jth feature of the kth positive instance, and ${{\displaystyle \stackrel{-}{x}}}_{k,j}^{\left(-\right)}$ denotes the jth feature of the kth negative instance. A feature with a larger F-score value indicates that such feature can distinguish well between the positive and negative samples, and thus is regarded as being more useful for classification.

2.4 Model training

Support vector machine (SVM) is a powerful and popular supervised machine-learning method, and can be used to solve both linear and nonlinear data classification, regression and prediction tasks (Jia and Yun, 2017; Jia et al., 2013; Wee and Low, 2012; Ying and Keong, 2004; Zhang et al., 2007; Zou et al., 2016). In this study, SVM was trained with the LIBSVM package (Chang and Lin, 2011) to build the model to differentiate both promoter and non-promoter samples. We adopted the radial basis function (RBF) $K\left(x_i,x_j\right)=\mathrm{e}\mathrm{x}\mathrm{p}{(-\gamma \left|x_i-x_j\right|}^2)$ as the kernel function. Based on 5-fold cross-validation test, the penalty parameter C and kernel parameter γ were optimized for different types of input features using the SVMcg function of the LIBSVM package. This procedure was conducted for each task separately. In the first task, different types of feature sets (i.e. BPB, MNC, DNC, KNN and DAC) as well as their combined feature sets were evaluated by means of jackknife and cross-validation. Finally, the optimal parameters $\mathrm{C}\hspace{0.5em}=\hspace{0.5em}32$ and $\mathrm{\gamma }\hspace{0.5em}=\hspace{0.5em}0.01056$ were identified, and assigned for the prediction of promoters and non-promoters. In the second task, there were five binary sub-classifiers all of which had distinct parameters from each other. Among those five sub-classifiers, $\mathrm{C}\hspace{0.5em}=\hspace{0.5em}1.4142$ and $\mathrm{\gamma }\hspace{0.5em}=\hspace{0.5em}0.01121$ were the final parameters used for the first sub-classifier, $\mathrm{C}\hspace{0.5em}=\hspace{0.5em}2.8284$ and $\mathrm{\gamma }\hspace{0.5em}=\hspace{0.5em}2$ for the second sub-classifier, $\mathrm{C}\hspace{0.5em}=\hspace{0.5em}5.6569$ and $\mathrm{\gamma }\hspace{0.5em}=\hspace{0.5em}1$ for the third sub-classifier, $\mathrm{C}\hspace{0.5em}=\hspace{0.5em}32$ and $\mathrm{\gamma }\hspace{0.5em}=\hspace{0.5em}0.25$ for the fourth sub-classifier and $\mathrm{C}\hspace{0.5em}=\hspace{0.5em}1.4142$ and $\mathrm{\gamma }\hspace{0.5em}=\hspace{0.5em}2$ for the fifth sub-classifier.

2.5 Performance assessment

To examine the combination of the optimal features and evaluate the prediction performance of the trained models, 5-fold cross-validation, jackknife and independent dataset tests were performed in the present study, as suggested in a number of previous studies (Chen et al., 2017, 2018a,b,c; Chou and Zhang, 1995; Jia et al., 2015; Li et al., 2015a,b, 2016, 2018a,b; Song et al., 2018a,b,c). In addition, we also calculated four commonly used performance measurements, i.e. Sensitivity (Sn), Specificity (Sp), Accuracy (Acc) and the Matthew’s Correlation Coefficient (MCC), which are respectively defined as:

$$\left\{\begin{array}{c} \\ \begin{array}{c}\mathrm{S}\mathrm{n}=1-\frac{N_{-}^{+}}{N^{+}}\mathrm{ }0\mathrm{ }\le \mathrm{S}\mathrm{n}\le 1\mathrm{ }\\ \begin{array}{cc}\begin{array}{cc}\mathrm{S}\mathrm{p}=1-\frac{N_{+}^{-}}{N^{-}}& \mathrm{ }0\le \mathrm{S}\mathrm{p}\le 1\end{array}\mathrm{ }& \mathrm{ }\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}\begin{array}{cc}\mathrm{A}\mathrm{c}\mathrm{c}=\mathrm{ }\mathrm{\Lambda }=1-\frac{N_{-}^{+}+N_{+}^{-}}{N^{+}+N^{-}\mathrm{ }}& \mathrm{ }0\le \mathrm{A}\mathrm{c}\mathrm{c}\le 1\mathrm{ }\end{array}\end{array}\mathrm{ }\\ \begin{array}{cc}\mathrm{ }\mathrm{M}\mathrm{C}\mathrm{C}=\mathrm{ }\frac{1-\left(\frac{N_{-}^{+}}{N^{+}}+\frac{N_{+}^{-}}{N^{-}}\right)}{\sqrt{\left(1+\frac{N_{+}^{-}-N_{-}^{+}}{N^{+}}\right)\mathrm{ }\left(1+\frac{N_{-}^{+}-N_{+}^{-}}{N^{-}}\right)}}\mathrm{ }& -1\le \mathrm{M}\mathrm{C}\mathrm{C}\le 1\mathrm{ }\end{array}\end{array}\end{array}\right.\left(10\right)$$

where $N^{+}$ represents the total number of positive samples, $N_{-}^{+}$ represents the total number of false negatives, $N^{-}$ represents the total number of negative samples, while $N_{+}^{-}$ represents the total number of false positives, respectively.

2.6 Multiple classification process

MULTiPly is a two-task seamless predictor. The role of the first task is to distinguish a query DNA sequence as a promoter or non-promoter, which is a classic binary classification problem. The second task is to further predict which of the six types of promoters the identified promoter in the first task belongs to. Therefore, this second task is a multi-classification problem. As revealed in the process of constructing the benchmark dataset, the numbers of examples included in the six promoter subsets were quite unbalanced. For example, the largest promoter subset $S^{+}\left({\sigma }^{70}\right)$ contained 1694 samples while the smallest promoter subset $S^{+}\left({\sigma }^{54}\right)$ contained only 94 samples. To overcome the data imbalance problem, we developed five binary sub-classifiers. In the first sub-classifier, the subset $S^{+}\left({\sigma }^{70}\right)$ was regarded as the positive dataset, while the subset ${S^{+}\left({\sigma }^{24}\right)\cup S}^{+}\left({\sigma }^{28}\right)\cup S^{+}\left({\sigma }^{32}\right)\cup S^{+}\left({\sigma }^{38}\right)\cup S^{+}\left({\sigma }^{54}\right)$ was regarded as the negative dataset. In this way, a query DNA sequence sample can be classified as belonging to the ${\sigma }^{70}$ promoter class or to the non-${\sigma }^{70}$ promoter class. If the query sequence was classified as the non-${\sigma }^{70}$ promoter class, the next sub-classifier was started. To train the second sub-classifier, the subset $S^{+}\left({\sigma }^{24}\right)$ was considered as positive samples and the subset $S^{+}\left({\sigma }^{28}\right)\cup S^{+}\left({\sigma }^{32}\right)\cup S^{+}\left({\sigma }^{38}\right)\cup S^{+}\left({\sigma }^{54}\right)$was considered as negative samples. Similar to our description above, the second sub-classifier can predict the query DNA sequence as belonging to the ${\sigma }^{24}$ promoter or non-${\sigma }^{24}$ promoter class. This process was proceeded until the fifth sub-classifier, the subset $S^{+}\left({\sigma }^{28}\right)$ was regarded as the positive dataset and $S^{+}\left({\sigma }^{54}\right)$ regarded as the negative dataset, respectively. Through the subsequent evaluation, standard performance measures indicate the above approach based on the five binary sub-classifiers could not only address the data imbalance problem but, as a by-product, could also accurately predict which of the six types the identified promoter belonged to. The flowchart of this multi-layer classifier is shown in Figure 2.

Fig. 2.

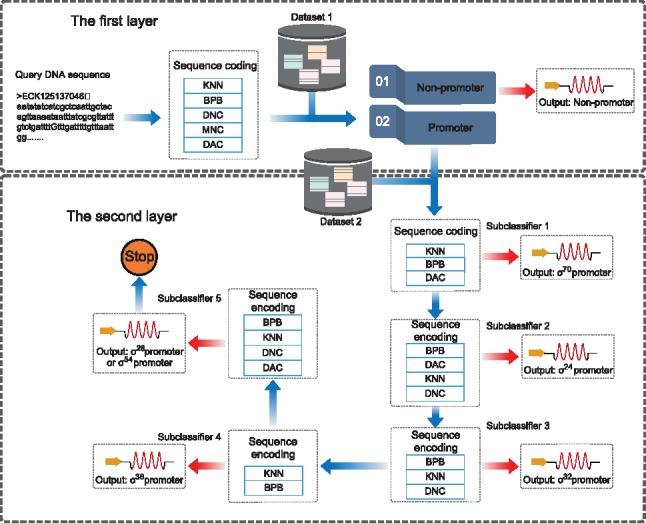
The flowchart of the proposed multi-layer classifier

3 Results and discussion

3.1 Selection of the basic features

The combination of different heterogeneous features often leads to different prediction results; accordingly, how to effectively select the basic and essential features to incorporate into the model is a crucial but hard problem to solve. In this study, features that achieved the best prediction performance were chosen as the basic features. Since the dimension of BPB was large, we sorted the 162 components of the characteristic vector using the F-Score, and then chose a step size of 10 entries in the vector to increase the number of components. The other features types were selected using a step size of 2 according to the F-Score. Selection of the optimal feature combination was based on the jackknife test that had the only output result making it easy to compare to (Chou, 2011).

The detailed performance results for the selection of single feature types are given in the Supplementary Tables S1 and S2. For the sake of convenience and intuitive understanding, Tables 1 and 2 show the best performance results for all single types of features, and the corresponding feature dimension at which the best performance was achieved. For the first task, the KNN features with 15 dimensions [KNN (15) for short] were regarded as the basic features, and were then incorporated into the BPB with a step size of 10 entries to further improve the prediction performance. Supplementary Table S3 showed that for KNN(15) combined with BPB of 130 dimension [BPB(130)], the MCC value improved to some extent (for brevity, the encoding scheme was represented by KNN(15)+BPB(130), so on and so forth). Next, KNN(15)+BPB(130) were further incorporated with the component of DNC one by one, and as a result KNN(15)+BPB(130)+DNC(9) reached the best performance with an Acc of 86.80% and an MCC of 0.7360. This process was terminated at the feature combination KNN(15) + BPB(130) + DNC(9) + MNC(1) + DAC(10), which reached a Sn of 87.27%, a Sp of 86.57%, an Acc of 86.92% and an MCC of 0.7385.

Table 1.

The best performance achieved by single type of features for the first task

Features	Dimension	Sn(%)	Sp(%)	Acc(%)	MCC
KNN	15	85.56	86.68	86.12	0.7224
BPB	120	82.03	81.40	81.71	0.6343
DNC	12	74.86	80.84	77.85	0.558
MNC	4	73.25	80.59	76.92	0.5399
DAC	12	74.48	76.15	75.31	0.5064

Table 2.

The best performance achieved by single types of features for the second task

Sub-classifier	Features	Dimension	Sn (%)	Sp (%)	Acc(%)	MCC
1st	KNN	15	90.26	75.64	84.30	0.6723
	BPB	162	88.55	76.76	83.74	0.6609
	DNC	4	89.08	29.67	64.86	0.237
	MNC	3	88.84	27.10	63.67	0.2055
	DAC	12	90.2	24.01	63.22	0.1925
2nd	KNN	3	86.36	91.06	89.11	0.7754
	BPB	130	89.05	92.67	91.17	0.8179
	DNC	8	21.9	90.32	61.92	0.1698
	MNC	3	2.89	98.24	58.66	0.0378
	DAC	12	33.06	84.31	63.04	0.2037
3rd	KNN	11	80.07	86.7	83.87	0.6696
	BPB	80	83.51	87.47	85.78	0.7094
	DNC	10	26.80	85.93	60.7	0.159
	MNC	2	1.72	99.49	57.77	0.0592
	DAC	6	13.75	92.58	58.94	0.1038
4th	KNN	5	82.82	89.04	86.45	0.7206
	BPB	70	82.21	86.40	84.65	0.6850
	DNC	14	42.33	78.51	63.43	0.2238
	MNC	3	26.99	87.28	62.15	0.1806
	DAC	12	49.08	75.00	64.19	0.2488
5th	KNN	1	96.27	82.98	90.79	0.8107
	BPB	140	94.78	91.49	93.42	0.8641
	DNC	10	79.10	60.64	71.49	0.4046
	MNC	3	91.04	7.45	56.58	−0.0269
	DAC	10	76.12	58.51	68.86	0.3509

The purpose of the second task is to predict the specific subtype that a predicted promoter belonged to. To select an optimal combination of features for each of the sub-classifiers, we employed the same strategy and method as described for the first task. The detailed results on the jackknife test are shown in Supplementary Table S4.

For the first sub-classifier, to identify ${\sigma }^{70}$ promoters, the feature combination of KNN(15) + BPB(130) + DAC(6) yielded an Acc of 85.24% and an MCC of 0.6923, respectively. For the second sub-classifier, to identify ${\sigma }^{24}$promoters, BPB(130) +KNN(17)+DAC(1)+ DNC(12) achieved an Acc of 91.68% and an MCC of 0.8286, respectively. The prediction performance for the third sub-classifier, to identify ${\sigma }^{32}$promoters, reached an Acc of 87.98% and an MCC of 0.7534, respectively, based on the feature combination of BPB(80)+ KNN(15)+DNC(2). The fourth sub-classifier, to identify ${\sigma }^{38}$promoters, achieved an Acc of 86.96% and an MCC of 0.7331, respectively, based on only two types of features, KNN(5)+BPB(80). For the last sub-classifier, to distinguish ${\sigma }^{28}$ and ${\sigma }^{54}$ promoters, it used the feature combination of BPB(140)+KNN(3)+DNC(1)+DAC (3) and yielded an Acc of 95.18% and an MCC of 0.9003, respectively.

For dimensionality reduction, we followed two rules: (i) if two kinds of feature combinations achieved the same Acc value, we selected the dimensional features that achieved the larger Sn; and (ii) if all performance indices were identical, we selected the features with the fewest dimensions. Supplementary Tables S5 and S6 provide the best performance results for each combination, for the purpose of easing the interpretation of performance trends.

3.2 Comparison with existing methods on the same training dataset

In general, if one uses different training datasets and validation methods to compare the performance of different prediction tools, the results will vary greatly among them (Li and Lin, 2006; Lin et al., 2014; Liu et al., 2018; Silva et al., 2014; Song, 2012a,b). Therefore, to avoid bias, we applied the same training dataset used in (Liu et al., 2018). The results are shown in Figure 3, which indicate that MULTiPly uniformly achieved a superior performance compared with all other methods. Specifically, the Sn was 7.79% higher than the second-best predictor, iPromoter-2L. Note that only two methods iPromoter-2L and MULTiPly were able to recognize the specific types of promoters. As such, we were more interested in comparing the performance of the two methods for the second task. As shown in Figure 4 and Supplementary Table S7, MULTiPly achieved better MCCs for all six types of promoters, implying that Sn and Sp values were not extremely different, as a higher Sn (or Sp) and a lower Sp (or Sn) at the same time would lead to a lower MCC value. However, the only exception for MULTiPly was in the case of differentiating ${\sigma }^{70}$ promoters, for which the value of Sn was 90.43%, which was 13.5% higher than the value of Sp. In contrast, iPromoter-2L had a larger divergence between the Sn and Sp values: when either its Sn (or Sp) was over 95%, the other measurement was lower than 60% at the same time.

Fig. 3.

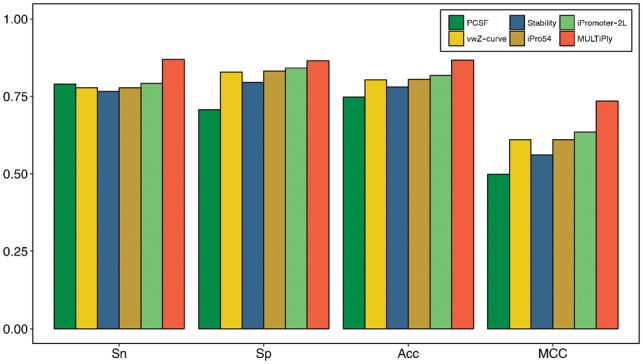
Performance comparison results between MULTiPly, PCSF, vwZ-curve, Stability, iPro54 and iPromoter-2L for identifying promoters for the first task on 5-fold cross-validation test

Fig. 4.

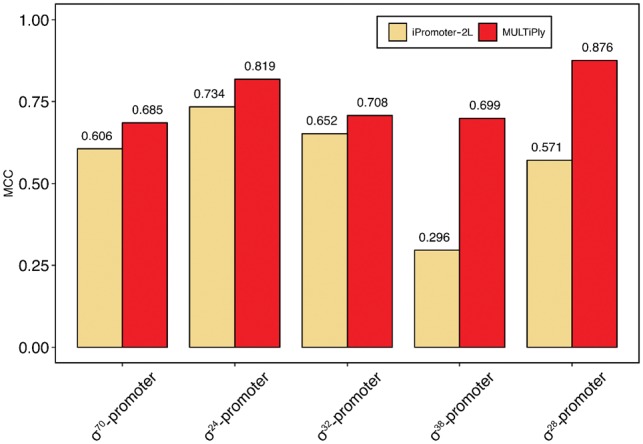
Performance comparison between MULTiPly and iPromoter-2L for the second task in terms of MCC on 5-fold cross-validation test

To further illustrate the effectiveness of the developed MULTiPly method, we assessed and compared its performance with a direct multi-class SVM classifier (Supplementary Table S8). It can be seen that for ${\sigma }^{32}, {\sigma }^{38}$and ${\sigma }^{28}$ types of promoters, none of the promoters were predicted correctly by the multi-class SVM classifier. The worse performance of the multi-class SVM classifier might be explained by the fact that it did not consider the effects brought upon by different numbers of different types of known promoters.

3.3 Performance comparison on the independent test dataset

We compared the proposed MULTiPly method with other existing methods (Li and Lin, 2006; Lin et al., 2014; Liu et al., 2018; Silva et al., 2014; Song, 2012a,b) on an independent test dataset containing 54 newly found promoters. Because no web servers were available for PSCF, vwZ-curve and Stability, we only compared the prediction performance of iPro54, iPromoter-2L and MULTiPly. Performance comparison results between the three methods are provided in Table 3. For the first task, iPro54 only correctly predicted 22 promoter sequences, while iPromoter-2L and MULTiPly achieved the best performance, with all promoter sequences being correctly predicted. Next, we further compared the performance of MULTiPly and iPromoter-2L for the second task of identifying the specific type of promoters. In this regard, iPromoter-2L and MULTiPly achieved a similar performance across all types of promoters (Table 3).

Table 3.

Performance comparison between MULTiPly, iPromoter-2L and iPro54 for identifying promoters and their types on the independent test dataset

Promoter	Method	TPa	FNb
promoter	iPro54	22	32
	iPromoter-2L	54	0
	MULTiPly	54	0
${\mathrm{\sigma }}^{70}$-promoter	iPromoter-2L	44	2
	MULTiPly	43	3
${\mathrm{\sigma }}^{24}$-promoter	iPromoter-2L	1	0
	MULTiPly	1	0
${\mathrm{\sigma }}^{32}$-promoter	iPromoter-2L	1	1
	MULTiPly	1	1
${\mathrm{\sigma }}^{38}$-promoter	iPromoter-2L	1	3
	MULTiPly	1	3
${\mathrm{\sigma }}^{28}$-promoter	iPromoter-2L	1	0
	MULTiPly	1	0

^aTP represents the number of predicted $\left({\sigma }^i\right)$-promoter sequences.

^bFN represents the number of predicted non-$\left({\sigma }^i\right)$-promoter sequences, where i = 70, 24, 32, 38 or 28.

3.4 Performance comparison with other machine learning classifiers

Based on the feature combination determined by SVM, we compared the prediction performance between six commonly used machine learning algorithms, including random forest (RF) (Breiman, 2001; Wei et al., 2018a,b,c), naive Bayes (NB) (Rish, 2001), Ensemble for Boosting (Maclin and Opitz, 1999), discriminant analysis (Cao and Sanders, 1996), gradient boosting decision tree (GBDT) (Friedman, 2001) and SVM (Feng et al., 2018; Wei et al., 2018a,b,c). We performed jackknife tests to examine if there was still room for performance improvement. By and large, the quantity of trees has a bearing on the performance of the RF algorithm. As a consequence, we set out to search for the optimal RF parameters in the two-task predictor. The results are shown in Supplementary Table S9. For GBDT, the learning rate for every tree was set to 0.1, the boosting number was set to 1000 and the depth for every tree was set to 3, respectively. Through a comprehensive performance comparison of these algorithms, we verified the correctness and effectiveness of the SVM classification model, reflected by its higher MCC values. The results are shown in Supplementary Table S10. However, it is worth noting that for the identification of promoters and non-promoters, as well as ${\mathrm{\sigma }}^{70}$-promoters and ${\mathrm{\sigma }}^{32}$-promoters, the other classifiers instead of the SVM also achieved similar prediction results. Overall, while the results are very promising, it seems that there could be further room for the performance improvement through continued tests and research.

3.5 Web server implementation

As pointed out in Chou and Shen (2009) and suggested in a number of recent publications (see, e.g. Chen et al., 2018a,b,c; Cheng et al., 2018a,b; Feng et al., 2017; Liu et al., 2017a,b; Qiu et al., 2018; Su et al., 2018; Wei et al., 2018a,b,c; Xiao et al., 2017; Xu et al., 2017), user-friendly and publicly accessible web servers represent the future direction for the development of practically useful prediction methods and bioinformatics tools. As a matter of fact, a great variety of practically useful web servers have significantly increased the impact of bioinformatics on medical science (Chou, 2015), driving medicinal chemistry into an unprecedented revolution (Chou, 2017). In view of this, we have implemented and made available the MULTiPly (http://flagshipnt.erc.monash.edu/MULTiPly/) web server via which users can readily obtain their desired prediction results of potential promoters.

The MULTiPly web server was implemented using MATLAB and Java Server Pages, managed by Tomcat 8 and configured on a 64-bit windows server equipped with an 8-core CPU, 1TB hard disk and 32 GB memory. The web server requires DNA sequences in the FASTA format as the input. Supplementary Figure S1 shows an example of the prediction webpages of the web server with the detailed prediction outputs.

4 Conclusion

In this study, we present MULTiPly, a novel bioinformatics tool for identifying bacterial promoters and the specific promoter types they belong to. MULTiPly is capable of recognizing the specific type of promoters in a layer-by-layer manner, which overcomes the complexity brought upon by different numbers of available types of promoters in the datasets. Extensive benchmarking experiments on 5-fold cross-validation and jackknife tests demonstrate the strategy used by MULTiPly is effective and can deal with the data imbalance problems. We expect that MULTiPly will be used as a useful tool for expediting the discovery of both general and specific types of promoters in the future.

Funding

This work was supported by Fundamental Research Funds for the Central Universities (No. 3132016306, 3132018227), the National Natural Science Foundation of Liaoning Province (20180550307) and the National Scholarship Fund of China for Studying Abroad. JS was supported by grants from the National Health and Medical Research Council of Australia (NHMRC) (APP490989, APP1127948 and APP1144652), the Australian Research Council (ARC) (LP110200333 and DP120104460), the National Institute of Allergy and Infectious Diseases of the National Institutes of Health (R01 AI111965), a Major Inter-Disciplinary Research (IDR) project awarded by Monash University and the Collaborative Research Program of Institute for Chemical Research, Kyoto University (2018-28). TML and AL were supported in part by the Informatics Institute of the School of Medicine at UAB.

Conflict of Interest: none declared.