Protein Melting Temperature Cannot Fully Assess Whether Protein Folding Free Energy Underlies the Universal Abundance–Evolutionary Rate Correlation Seen in Proteins

Abstract

The protein misfolding avoidance hypothesis explains the universal negative correlation between protein abundance and sequence evolutionary rate across the proteome by identifying protein folding free energy (ΔG) as the confounding variable. Abundant proteins resist toxic misfolding events by being more stable, and more stable proteins evolve slower because their mutations are more destabilizing. Direct supporting evidence consists only of computer simulations. A study taking advantage of a recent experimental breakthrough in measuring protein stability proteome-wide through melting temperature (T_m) (Leuenberger et al. 2017), found weak misfolding avoidance hypothesis support for the Escherichia coli proteome, and no support for the Saccharomyces cerevisiae, Homo sapiens, and Thermus thermophilus proteomes (Plata and Vitkup 2018). I find that the nontrivial relationship between T_m and ΔG and inaccuracy in T_m measurements by Leuenberger et al. 2017 can be responsible for not observing strong positive abundance–T_m and strong negative T_m–evolutionary rate correlations.

Introduction

After decades of protein evolutionary studies, the major sequence evolutionary rate (ER) constraint has been discovered to be gene expression (Sharp 1991; Pál et al. 2001; Rocha and Danchin 2004; Lemos et al. 2005; Drummond et al. 2006). A strong negative expression–ER correlation is observed in organisms’ proteomes from the three kingdoms of life (Drummond and Wilke 2008; Zhang and Yang 2015). However, it is unknown why this correlation is universal. The first mechanism proposed is the protein misfolding avoidance hypothesis (MAH). Originally formulated by Drummond et al. (2005) as the translational robustness hypothesis and later modified (Yang et al. 2010; Serohijos et al. 2012), MAH claims that proteins with high abundance (A) are under strong selection to stably fold ($\mathrm{\Delta }G\mathrm{}=G^{\mathrm{fold}}-G^{\mathrm{unfold}}$) because misfolded proteins are toxic to the cell. Greater stability ensures fewer misfolded proteins (m) by the following equation, derived from equilibrium statistical mechanics and which assumes two-state folding (Drummond and Wilke 2008):

$$\begin{array}{c}m=A_{\text{tot}}-A\\ =\frac{A}{P_{\text{nat}}}-A\\ =A\left(1+{\mathrm{e}}^{\beta \Delta G}\right)-A=A{\mathrm{e}}^{\beta \Delta G}\end{array}.$$ (1)

The parameter β is the inverse energy of the environment and is equal to 1/(k_bT), where k_b is the Boltzmann constant and T is the ambient temperature. Misfolded proteins in the MAH framework are considered to be equally toxic, regardless of differing protein identities (Drummond and Wilke 2008; Geiler-Samerotte et al. 2011). An organism’s proteins with the same abundance are under the same selection to stably fold according to MAH. Although gene expression and protein abundance are not interchangeable (Greenbaum et al. 2003; Taniguchi et al. 2010), data from the relatively recent advent of experimental techniques to measure abundance on the proteome scale have demonstrated a universal A–ER correlation as well (Drummond et al. 2006; Plata and Vitkup 2018; Razban et al. 2018).

Since its original proposal, MAH assumptions have been refined. Mistranslation was first thought to be the main physical driver of misfolding (Drummond et al. 2005; Drummond and Wilke 2008). Later, Yang et al. (2010) showed that misfolding of correctly synthesized proteins also contributes to explaining the A–ER correlation, when explicitly modeling misfolding of mistranslated and correctly translated lattice proteins in computer simulations. Yang et al. (2010) coined the name MAH to encompass the greater breadth.

Another assumption altered is the relationship between ΔG and ER, in light of abundance. A paradox in MAH is that more stable proteins are more robust to misfolding in the cell but also fix fewer mutations (Drummond et al. 2005). One would instead expect that an increased robustness to misfolding would lead to greater tolerance for mutations and hence a higher chance for mutations to fix, since such proteins should be able to tolerate more mutations before losing marginal stability. The paradox was first resolved by distinguishing between mutations that cause a loss of protein function and mutations that are more generic. The former determines ER for low A; the latter, for high A (Wilke and Drummond 2006). Although their model recapitulates the A–ER correlation, Wilke and Drummond (2006) note that their model predicts an exponential decline in ER with increasing A, rather than the experimentally observed power law.

Serohijos et al. (2012) suggested another resolution by showing that more stable proteins evolve more slowly in simulations if there exists a sufficiently strong anticorrelation between $\mathrm{\Delta }{G}_{\mathrm{wild}-\mathrm{type}}$ and $\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\mathrm{single}\mathrm{}\mathrm{mutant}}-\mathrm{\Delta }{G}_{\mathrm{wild}-\mathrm{type}}$. Such anticorrelation arises from the fact that random mutations attempted in a very stable protein are more likely to be destabilizing and thus less likely to fix than random mutations on a less stable protein. Serohijos et al. (2012) argued that previous computer simulations (Drummond and Wilke 2008; Yang et al. 2010) in support of MAH unknowingly satisfied this condition by using sequence-based models of lattice proteins. Serohijos et al. (2012)’s resolution of the paradox is superior to that of Wilke and Drummond (2006) because Serohijos et al. (2012) recapitulated the known power-law dependence between A and ER.

Figure 1 summarizes MAH expected correlations between protein properties (horizontal arrows) and the assumptions underlying them (vertical arrows). Single-sided, rather than double-sided, arrows are used because causation is implied in MAH’s explanation of why higher A causes lower ER. Figure 1 reflects the current formulation of MAH; it is a synthesis of its initial proposal as the translational robustness hypothesis (Drummond et al. 2005; Drummond and Wilke 2008) with later developments (Yang et al. 2010; Serohijos et al. 2012).

Fig. 1.

The protein misfolding avoidance hypothesis (MAH). Horizontal arrows denote expected correlations between protein properties. Vertical arrows denote the assumptions underlying their respective horizontal arrow. Throughout the text, ΔG is defined such that more stable proteins have more negative ΔG values. If T_m is substituted in place of ΔG, correlations described here would have opposite signs because more stable proteins have more positive T_m values.

Although MAH correlations are exhibited in different simulation frameworks (Wilke and Drummond 2006; Drummond and Wilke 2008; Yang et al. 2010; Serohijos et al. 2012), explicit experimental support is lacking. Yang et al. (2010) and Plata et al. (2010) used limited ΔG data from the Protein Thermodynamic database (ProTherm) (Gromiha et al. 2016) for 5 Saccharomyces cerevisiae and 23 Escherichia coli proteins, respectively, and found no correlation between A and ΔG. On the other hand, indirect support for MAH has been reported elsewhere. Highly expressed proteins in several proteomes, including E. coli, S. cerevisiae, and Homo sapiens, were shown to have sequences similar to those of thermophiles. Highly expressed proteins in S. cerevisiae also showed some enhanced features of proxies for ΔG, such as strength of hydrogen bonds and interatomic contacts, both calculated by Eris (Serohijos et al. 2013). However, more direct experimental support than those presented in and Serohijos et al. (2013) is still needed to prove that more abundant proteins are more stable, as posited by MAH.

The scarcity of proteome-wide data on ΔG limited the ability to test key predictions stemming from MAH. This situation seems to have changed with the recent advance of proteome-wide measurements of melting temperature (T_m) (Leuenberger et al. 2017). Using T_m as a proxy for ΔG, MAH can be indirectly assessed experimentally with hundreds of proteins per organism. In Leuenberger et al. (2017), support for MAH was shown for E. coli when parsing proteins in three bins based on T_m. When considering each protein as an individual data point, Plata and Vitkup (2018) found the MAH-consistent positive correlation between ln A and T_m to be weakly significant and the T_m–ln ER correlation to be nonexistent for the E. coli proteome. (The natural logarithm (ln) of A and ER are taken because the observed power-law dependence of A–ER becomes linear for ln A–ln ER, yielding more informative Pearson correlation coefficients.) More discouragingly, the three other organisms for which proteome-wide T_m was measured—S. cerevisiae, H. sapiens, and Thermus thermophilus—demonstrated none of the MAH-consistent correlations, even though they demonstrated the universal negative correlation between ln A and ln ER (Plata and Vitkup 2018).

Based on the analysis of correlations between T_m and other protein properties, Plata and Vitkup (2018) have raised doubts concerning the validity of MAH. However, it is unclear whether limitations from using T_m as a proxy for ΔG could be responsible for the apparent lack of support for MAH. As shown in figure 1, MAH posits ΔG, not T_m, to be the confounding physical variable. Plata and Vitkup (2018) took T_m and ΔG measurements from ProTherm and reported a T_m–ln −ΔG Pearson correlation of 0.75 when including multiple measurements per protein as individual data points, and 0.48 for one averaged T_m and one averaged ΔG measurement per protein. Both correlations are significant, with P values of 2E-40 and 3E-8, respectively (Plata and Vitkup 2018).

It remains unclear whether the correlation between T_m and ΔG is large enough such that MAH can be assessed with T_m. In this article, I investigate the relationship between the two protein stability measurements with respect to MAH. In the first part of my results, I consider whether ln A–T_m and T_m–ln ER correlations directly correspond to ln A–ΔG and ΔG–ln ER correlations, respectively. In the second part, I carefully obtain a simpler relationship between T_m and ΔG that can be currently evaluated with experimental data, starting from the canonical equation relating the two stability metrics and employing two approximations. With my derived relationship, in the third part I create a ΔG variable that is consistent with MAH by construction. I study how correlations are affected when transforming the perfect, MAH-consistent ΔG into T_m.

Results

Correlations Are Generally Not Transitive

A common misconception is that Pearson correlation coefficients (r) are transitive: if X and Y positively correlate, and Y and Z positively correlate, then X and Z must also positively correlate (Castro Sotos et al. 2009). As a counterexample, Langford et al. (2001) tabulated the number of base hits, triples and home-runs of New York Yankees’ players in the 2000 regular season. Although base hits and triples positively correlate, and base hits and home-runs positively correlate, triples and home-runs were found to negatively correlate! This surprising negative correlation can be reconciled by noting that players hitting home-runs are bigger and more powerful, whereas players getting triples are more agile and run faster to third base.

Notwithstanding the hitting records of the Yankees’, there can be specific pairs of correlations in which the assumption of transitivity is valid. To identify cases in which r is transitive, Langford et al. (2001) derived an equation characterizing the range in possible r_YZ, depending on r_XY and r_XZ values.

$$r_{X\mathrm{Y}}{r}_{\mathit{XZ}}-\sqrt{\left(1-r_{\mathit{XY}}^2\right)\left(1-r_{\mathit{XZ}}^2\right)}\le r_{\mathit{YZ}}\le r_{\mathit{XY}}{r}_{\mathit{XZ}}+\sqrt{\left(1-r_{\mathit{XY}}^2\right)\left(1-r_{\mathit{XZ}}^2\right)}.$$ (2)

A three-dimensional plot of the volume enclosed by equation (2) demonstrates that for large and positive r_XY and r_XZ, I can count on r_YZ being large and positive too (supplementary fig. S1). However, when r_XY and r_XZ become smaller in magnitude, then I cannot narrowly define r_YZ. In this case, r_YZ could be negative or positive, regardless of r_XY and r_XZ signs.

I can apply equation (2) for correlations between T_m and protein properties to define a range of possible corresponding correlations between ln −ΔG and protein properties. Inserting T_m for X, ln −ΔG for Y and ln A for Z in equation (2), I find r(ln −ΔG, ln A)’s range given Plata and Vitkup (2018)’s reported r(T_m, ln −ΔG), and r(T_m, ln A) for the respective organism.

$$r\left(T_{\mathrm{m}},\ln -\mathrm{\Delta }G\right)r\left(T_{\mathrm{m}},\ln A\right)-\sqrt{\left[1-{r\left(T_{\mathrm{m}},\ln -\mathrm{\Delta }G\right)}^2\right][1-{r\left(T_{\mathrm{m}},\ln A\right)}^2]}\le r\left(\ln -\mathrm{\Delta }G,\ln A\right)\le r\left(T_{\mathrm{m}},\ln -\mathrm{\Delta }G\right)r\left(T_{\mathrm{m}},\ln A\right)+\sqrt{\left[1-{r\left(T_{\mathrm{m}},\ln -\mathrm{\Delta }G\right)}^2\right][1-{r(T_{\mathrm{m}},\ln A)}^2]}.$$ (3)

Inserting r(T_m, ln −ΔG) = 0.75 and r(T_m, ln A) = 0.09 from figure 1 in Plata and Vitkup (2018) into equation (3), E. coli r(ln −ΔG, ln A) is calculated to range from −0.59 to 0.73. That is, the resulting r(ln −ΔG, ln A) correlation could be as low as −0.59—in strong variance with MAH—around 0, just like r(T_m, ln A), or as high as 0.73—in complete support of MAH. Known correlations of T_m with other protein properties poorly define resulting ln −ΔG correlations, even though r(T_m, ln −ΔG) is relatively large. Equation (2) demonstrates that T_m as a proxy for ln −ΔG narrowly identifies r(ln −ΔG, ln A) only if r(T_m, ln −ΔG), as well as r(T_m, ln A) are close to 1. Strong T_m correlations are capable of proving or disproving MAH because such correlations (e.g., |r(T_m, ln A)| ∼ 1) lead to ranges in the corresponding ΔG correlations which are strong as well.

By the same logic as in equation (3), an inequality characterizing r(ln −ΔG, ln ER) can be derived from r(T_m, ln −ΔG) and r(T_m, ln ER). From figure 2 in Plata and Vitkup (2018), r(T_m, ln ER) = 0.045, making E. coli r(ln −ΔG, ln ER) range from −0.63 to 0.69. Again, I am unable to reject MAH because of T_m correlations. I perform the same procedure for S. cerevisiae and H. sapiens T_m correlations and find similarly large ranges in corresponding ln −ΔG correlations that cannot discount MAH (fig. 2). No A data set could be found for T. thermophilus (Materials and Methods), thus it is not included in my analyses.

Fig. 2.

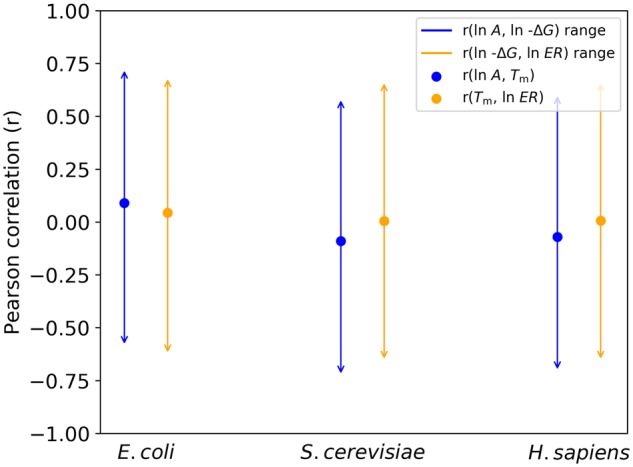
Wide ranges of Pearson correlation coefficients for ln −ΔG with ln A and ln ER from corresponding T_m correlations with ln A and ln ER demonstrate that T_m measured by Leuenberger et al. (2017) cannot assess the protein MAH. Ranges are obtained by evaluating equation (2) with r(T_m, ln −ΔG) = 0.75 from supplementary figure 1a, and r(T_m, ln A) and r(T_m, ln ER), which are represented as dots, taken from figures 1 and 2, respectively, of Plata and Vitkup (2018).

Although r(T_m, ln −ΔG) is reported in Plata and Vitkup (2018), r(T_m, −ΔG) = 0.76 is essentially identical to r(T_m, ln −ΔG) = 0.75. Therefore, ranges illustrated in figure 2 for r(ln −ΔG, ln A) and r(ln −ΔG, ln ER) are essentially identical to ranges for r(ln A, −ΔG) and r(−ΔG, ln ER) when r(T_m, −ΔG) is employed.

Relationship between T_m and ΔG

The previous subsection highlighted that possible ranges for ΔG correlations could be broad given those involving T_m measured by Leuenberger et al. (2017). Equation (2) considers all possible relationships between variables. If I could find an equation relating T_m to ΔG, I could obtain narrower ranges for ln A–ΔG and ΔG–ln ER correlations from corresponding ln A–T_m and T_m–ln ER correlations, respectively. Under the experimentally validated assumption that the change in heat capacity at constant pressure (ΔC_p) is independent of temperature during protein folding, Becktel and Schellman (1987) derived a relationship between T_m and ΔG in terms of ΔC_p and the change in enthalpy (ΔH_m) at T_m, using the Gibbs–Helmholtz equation.

$$\Delta G=-\Delta H_{\mathrm{m}}\left(1-\frac{T}{T_{\mathrm{m}}}\right)+\Delta C_{\mathrm{p}}\left(T_{\mathrm{m}}-T+T\ln \frac{T}{T_{\mathrm{m}}}\right).$$ (4)

As seen in equation (4), the dependence between ΔG and T_m involves two other protein-specific variables: ΔH_m and ΔC_p. Generally, no simple monotonic relationship exists between T_m and ΔG. I find a weakly significant T_m–ΔG correlation r = −0.36 (P value = 0.02) when taking the T_m, ΔH_m, and ΔC_p reported for 43 proteins in Rees and Robertson (2001, table 1A) and calculating ΔG according to equation (4) (supplementary fig. S2A).

After employing two biologically motivated approximations, I obtain an equation that is evaluable proteome-wide, while maintaining the original accuracy of equation (4) (Materials and Methods).

$$\Delta G\approx -N[2.92+0.058\mathrm{}\left(T_{\mathrm{m}}-\mathrm{}333\right)]\frac{T_{\mathrm{m}}-T}{T}\frac{\mathrm{kJ}}{\mathrm{mol}}.$$ (5)

My analytical foray has failed to yield a monotonic relationship between ΔG and T_m because the number of residues (N) in a protein confounds the relationship. However, I can still narrow down the ΔG correlation ranges I found in the previous subsection from corresponding T_m correlations by evaluating equation (5) with T_m from Leuenberger et al. (2017) and N from the Universal Protein Resource (UniProt Consortium 2018). In figure 3, no MAH-consistent correlations are recovered with ΔG(T_m, N) across E. coli, S. cerevisiae, and H. sapiens proteomes.

Fig. 3.

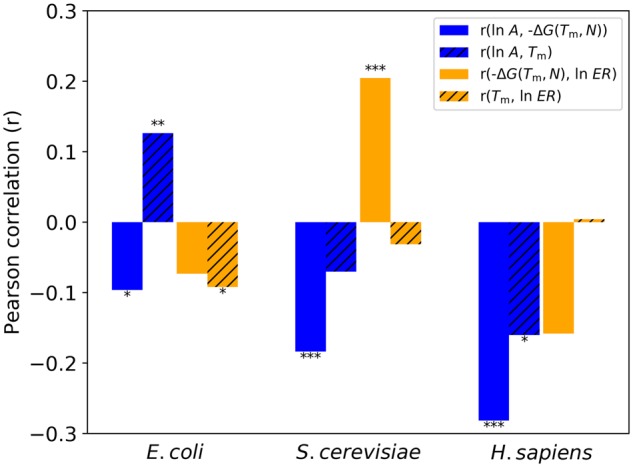
My derived ΔG(T_m, N) does not recover any MAH-consistent correlations. Corresponding T_m correlations have dashed lines and are derived from my curated data sets, with T_m from Leuenberger et al. (2017) (Materials and Methods). Asterisks above or below bar plots denote P value ranges: x < 10⁻¹⁰, ***<0.001, **<0.01, and *<0.05.

In many cases, correlations opposite of MAH expectations are seen in figure 3. For all three organisms, a significant negative r(ln A, −ΔG) is seen, which is opposite of MAH expectations. The r(ln A, −ΔG) correlation is driven by the significant negative r(ln A, N) correlation seen for all three organisms (supplementary fig. S4). This correlation is consistent with the gene length–expression correlation previously reported for H. sapiens (Chiaromonte et al. 2003; Grishkevich and Yanai 2014). For S. cerevisiae, a significant positive r(−ΔG, ln ER) is seen, which is again opposite of what I would expect from MAH because a significant positive r(N, ln ER) correlation is present. Escherichia coli and H. sapiens do not have significant r(N, ln ER), thus no significant r(−ΔG, ln ER) is seen (supplementary fig. S4).

Analyzing the Perfect MAH Correlate with T_m

It remains unclear whether the lack of MAH-consistent correlations is due to possible inaccuracies in T_m measurements by Leuenberger et al. (2017) or the fundamental inaccuracy in T_m representing ΔG being confounded by N. In other words, could perfectly accurate T_m measurements ever result in correlations consistent with MAH?

To free ourselves from having to know proteome-wide protein stabilities, I take advantage of a previously derived equation relating ΔG and ln A within the MAH framework (Serohijos et al. 2013) (supplementary eq. S2, Supplementary Material online). For completeness, I should also explicitly define ln ER as a function ΔG^MAH, however, to do so requires an equation relating ln ER and ΔG, which is currently unknown. Thus, I limit my analysis to just half of the MAH—the ln A–ΔG correlation.

Expressing equation (5) in terms of T_m and then evaluating the resulting expression using ΔG^MAH (supplementary eq. S3), there exists no T_m values that are in better agreement with MAH because the ΔG^MAH that T_m approximates is constructed to yield r(ln A, −ΔG^MAH) = 1. I analyze the ln A–$T_{\mathrm{m}}^{\mathrm{MAH}}$ correlation and find a strong MAH-consistent correlation across all three organisms (fig. 4). Even for S. cerevisiae and H. sapiens which exhibit negative ln A–T_m correlations with Leuenberger et al. (2017) data, MAH-consistent positive ln A–$T_{\mathrm{m}}^{\mathrm{MAH}}$ correlations are seen. The r(ln A, $T_{\mathrm{m}}^{\mathrm{MAH}}$) value is directly the result of the r($T_{\mathrm{m}}^{\mathrm{MAH}}$, ΔG^MAH) value, that is, r(ln A, $T_{\mathrm{m}}^{\mathrm{MAH}}$) = r($T_{\mathrm{m}}^{\mathrm{MAH}}$, −ΔG^MAH) because r(ln A, −ΔG^MAH) = 1 (eq. 2). I conclude that perfectly accurate T_m could in principle yield MAH-consistent correlations.

Fig. 4.

Utilizing the quoted equation for ΔG^MAH, my derived $T_{\mathrm{m}}^{\mathrm{MAH}}$ recovers MAH expected correlations. Corresponding T_m correlations have dashed lines and are derived from my curated data sets, with T_m from Leuenberger et al. (2017) (Materials and Methods). X marks and asterisks above or below bar plots denote P value ranges: xx < 10⁻⁵⁰, x < 10⁻¹⁰, ***<0.001, **<0.01, and *<0.05. No r($T_{\mathrm{m}}^{\mathrm{MAH}}$, ln ER) correlations are presented because no equation exists to describe the MAH expected ΔG–ln ER relationship.

In light of finding $T_{\mathrm{m}}^{\mathrm{MAH}}$ correlations consistent with MAH, does the lack of MAH-consistent correlations in the Leuenberger et al. (2017)T_m data set indicate that MAH is wrong? Leuenberger et al. (2017) reported that T_m from their study had a Pearson correlation coefficient of 0.36 (P value = 3E-4) with experimental T_m measurements listed in ProTherm for E. coli proteins. T_m in ProTherm can be assumed to more accurately characterize a protein’s T_m in isolation because differential scanning calorimetry, the standard protocol for T_m measurement (Robertson and Murphy 1997), is used. T_m in Leuenberger et al. (2017) employs a novel technique to measure T_m proteome-wide by employing limited proteolysis coupled with mass spectroscopy on cell extracts. The relatively low correlation between Leuenberger et al. (2017)T_m values and ProTherm T_m values signifies that supplementary equation (S3), is not valid as written for Leuenberger et al. (2017)T_m because of uncertainty in T_m measurements. To make my previous analysis comparable to the Leuenberger et al. (2017)T_m data set, I explicitly account for the inaccuracy in measurements by defining,

$$T_{\mathrm{m}}^{\alpha }=T_{\mathrm{m}}^{\mathrm{MAH}}+\mathrm{\alpha }N(0,\mathrm{}1).$$ (6)

$T_{\mathrm{m}}^{\alpha }$ represents Leuenberger et al. (2017)T_m, $T_{\mathrm{m}}^{\mathrm{MAH}}$ refers to ideally accurate T_m consistent with MAH as described previously, and α × N(0, 1) captures the inaccuracy between the two variables. N(0, 1) is the normal distribution with a mean of 0 and variance of 1. The noise strength α modulates the variance. The added α × N(0, 1) term is appropriate because the histogram of residuals from linearly fitting Leuenberger et al. (2017)T_m to ProTherm T_m resembles a normal distribution centered at 0 (Leuenberger et al. 2017), a general property of accurate linear relationships (Anscombe 1973).

I can analytically solve for α in terms of r($T_{\mathrm{m}}^{\mathrm{MAH}}$, $T_{\mathrm{m}}^{\alpha }$) starting from the definition of the Pearson correlation coefficient and employing properties of the covariance (Cov) (Rice 2007). Then, writing down r(ln A, $T_{\mathrm{m}}^{\alpha }$) in terms of r(ln A, $T_{\mathrm{m}}^{\mathrm{MAH}}$) and inserting the expression for α (supplementary eqs. S4 and S5),

$$r\left(\ln A,T_{\mathrm{m}}^{\alpha }\right)=r\left(\ln A,T_{\mathrm{m}}^{\mathrm{MAH}}\right)\mathrm{}r\left(T_{\mathrm{m}}^{\mathrm{MAH}},T_{\mathrm{m}}^{\alpha }\right).$$ (7)

Inserting r(ln A, $T_{\mathrm{m}}^{\mathrm{MAH}}$) = 0.36 (fig. 4) and r($T_{\mathrm{m}}^{\mathrm{MAH}}$, $T_{\mathrm{m}}^{\alpha }$) = 0.36 (Leuenberger et al. 2017) for E. coli into equation (7), yields r(ln A, $T_{\mathrm{m}}^{\alpha }$) = 0.13. My r(ln A, $T_{\mathrm{m}}^{\alpha }$) for E. coli is identical to what I find for r(ln A, T_m) = 0.13 using the Leuenberger et al. (2017) data set (Materials and Methods). My analysis demonstrates the possibility that MAH may be completely true, however the imperfect T_m–ΔG relationship and inaccurate Leuenberger et al. (2017)T_m values reduce the MAH expected positive correlation between ln A and T_m.

It would be useful to compare these results for E. coli to those for S. cerevisiae and H. sapiens, however, it is difficult to repeat this analysis for these organisms because there are few reported S. cerevisiae and H. sapiens T_m measurements in ProTherm. Regardless, my approach of adding noise to $T_{\mathrm{m}}^{\mathrm{MAH}}$ (eq. 6) would not be able to recapitulate the opposite than MAH expected ln A–T_m correlations observed for S. cerevisiae and H. sapiens using Leuenberger et al. (2017)T_m (Materials and Methods). The addition of noise to a perfect MAH correlate cannot explain this result because added noise only erases any correlation present; it cannot recreate a significant correlation in the opposite direction. An important assumption is that Leuenberger et al. (2017)T_m must actually relate to ΔG according to equation (4). The negative ln A–T_m correlation for S. cerevisiae and H. sapiens could be the result of some variable confounding the T_m measurement, rather than disproving MAH. I propose that this confounding variable weakly affects E. coli because a significant r($T_{\mathrm{m}}^{\mathrm{MAH}}$, $T_{\mathrm{m}}^{\alpha }$) is found.

What could be confounding Leuenberger et al. (2017)T_m measurements and why would it affect organisms unequally? Leuenberger et al. (2017) attributed discrepancies between their T_m measurements and those of ProTherm to their measurements being made in the cellular milieu. The methodology developed by Tan et al. (2018) specifies how the cellular milieu could be responsible for the discrepancy between ProTherm and Leuenberger et al. (2017)T_m values. Tan et al. (2018) used heat to induce protein aggregation and to subsequently identify proteins involved in protein complexes for H. sapiens. Tan et al. (2018) briefly noted that thermally induced protein aggregation could affect Leuenberger et al. (2017)T_m measurements since lysed cell samples must be exposed to wide temperature ranges to measure T_m. Indeed, using a similar experimental technique as Leuenberger et al. (2017) to measure T_m, Becher et al. (2018) did find individual H. sapiens proteins in complexes having similar T_m values to each other.

I find that the number of stable protein–protein interactions (PPIs) are right shifted for S. cerevisiae and H. sapiens compared with that of E. coli (median PPI for E. coli = 8, S. cerevisiae = 16, and H. sapiens = 25), consistent with previous reports (Reid et al. 2010; Schad et al. 2011). Escherichia coli T_m from Leuenberger et al. (2017) would more likely correspond to T_m in ProTherm because cellular PPI effects on stability are less prevalent than in S. cerevisiae and H. sapiens. In supplementary figure S5, I reanalyze the Leuenberger et al. (2017)T_m data set by only including proteins with PPIs less than or equal to the median PPI found for the proteome of the respective organism, hoping to recover the weakly consistent MAH correlations seen in E. coli, in S. cerevisiae and H. sapiens as well. However, MAH-consistent correlations are not recovered for S. cerevisiae and H. sapiens. For E. coli, the MAH-consistent ln A–T_m correlation is retained, however, the MAH-consistent T_m–ln ER correlation is lost. This seems to be the result of E. coli proteins with more PPIs evolving slower (Razban et al. 2018).

Further study is required to elucidate whether measured T_m values of protein complexes are strongly influenced by current experimental methods, or are biologically significant. It remains unknown whether the stability of the protein in isolation, or the stability of the protein in the midst of other proteins and metabolites present in the cell, is more biologically important in light of evolution. Simulation frameworks testing MAH have only considered the former case. It would be insightful to elucidate how MAH correlations obtained from simulations change when considering PPIs on an individual protein’s ΔG.

Discussion

My analysis of MAH with recent proteome-wide T_m measurements (Leuenberger et al. 2017) finds MAH not necessarily invalidated by experimental evidence. Simply put, MAH does not posit T_m to be the biophysical property underlying the negative A–ER correlation. Although T_m and ΔG are both metrics for protein stability, I show that the two are not interchangeable in assessing MAH by noting that,

• Pearson correlation coefficients of T_m with ln A or ln ER do not directly correspond to those of ΔG because Pearson correlation coefficients are generally not transitive (fig. 2).

and finding that,

• T_m is capable of reproducing MAH-consistent correlations when T_m is a proxy for the perfect MAH-consistent ΔG (fig. 4). However, inaccuracies in Leuenberger et al. (2017)T_m measurements are too large to reproduce strong MAH-consistent correlations for E. coli and any MAH-consistent correlations for S. cerevisiae and H. sapiens.

Results supporting my claim are obtained for all three organisms’ proteomes for which A, T_m, and ER experimental measurements are currently available—E. coli, S. cerevisiae, and H. sapiens. I consider the T_m–ln −ΔG correlation of 0.75 reported in Plata and Vitkup (2018) in the “Correlations Are Generally Not Transitive” subsection, although I demonstrate that its true value is likely much lower and that the T_m–ln −ΔG relationship is unfounded in the “Relationship between T_m and ΔG” subsection. No explicit T_m–ln −ΔG dependence is present in equation (4), the canonical equation relating T_m and ΔG. A more appropriate comparison is T_m–ΔG, supported analytically by equation (8) when assuming ΔH_m to be constant.

Leuenberger et al. (2017)’s study has provided insight into proteome-wide trends in stability, such as structure and sequence signatures of stable and unstable proteins, how PPI networks relate to temperature induced cell death, and intrinsically disordered protein structures in the context of the cellular matrix. My analysis demonstrates that one area the T_m data cannot be freely extended towards is testing MAH. T_m measured by any experimental technique, not just that from Leuenberger et al. (2017) has a ceiling in its correlation magnitude for capturing corresponding ΔG correlations (fig. 4). Recent advances in proteome-wide T_m measurements (Becher et al. 2018; Mateus et al. 2018) may lead to stronger MAH support than that found with Leuenberger et al. (2017), however, I expect no r(ln A, T_m) calculated from other T_m data sets to exceed r(ln A, $T_{\mathrm{m}}^{\mathrm{MAH}}$).

Other known proxies for ΔG exist, but they correlate at least just as poorly as T_m does with ΔG. As noted in Materials and Methods, Robertson and Murphy (1997) found thermodynamic terms making up ΔG: ΔH_m, ΔC_p and entropy, to correlate strongly with N. Combining these linear fits with N leads to an equation for ΔG at any T, only as a function of N (Ghosh and Dill 2009). However, the correlation between ΔG and N is not found bioinformatically (supplementary fig. S6A) because the thermodynamic terms that make up ΔG are orders of magnitude larger. When subtracting large terms from each other, noise in those large terms suppresses any signal in the resultant value (Ghosh and Dill 2009).

I attempt to use contact density calculated for proteins with solved structures listed in the Protein Data Bank (Berman et al. 2000) as a proxy for stability (England et al. 2003; England and Shakhnovich 2003; Choi et al. 2017). Using ΔG assembled from ProTherm and reported in Plata and Vitkup (2018, supplementary figure 1b), I find no significant correlation between ΔG and contact density (supplementary fig. S6B). I also computationally calculate ΔG using FoldX, although FoldX was only trained to make accurate single mutant ΔΔG predictions (Guerois et al. 2002). If accurate ΔGs could be derived from FoldX, I could then test MAH bioinformatically with computationally calculated ΔGs. A significant Spearman rank correlation is observed between ΔG^FoldX and ΔG^ProTherm. However, FoldX-calculated ΔGs are unrealistic, with outputted ΔGs ranging from −200 to 900 kcal/mol (supplementary fig. S6C).

Only accurate ΔG measurements can fully assess whether MAH expected correlations, so far only seen in simulations, extend to reality. Currently, it is difficult to assess the validity of MAH compared with other alternative hypotheses proposed more recently to explain the universal A–ER correlation (Tartaglia et al. 2007; Cherry 2010b; Plata et al. 2010; Yang et al. 2012; Park et al. 2013; Kepp and Dasmeh 2014). Unlike MAH, experimental support in the S. cerevisiae proteome has already been found for alternative hypotheses, such as experimentally determined PPI partners (Chatr-aryamontri et al. 2017) for the protein misinteraction avoidance hypothesis (Yang et al. 2012), and experimental measurements of mRNA folding strengths (Zur and Tuller 2012) for the mRNA folding hypothesis (Park et al. 2013).

Materials and Methods

Bioinformatics Data

Escherichia coli and S. cerevisiae data sets, except for $T_{\mathrm{m}}$ from supplementary table S3 of Leuenberger et al. (2017), are taken from ProteomeVis (Razban et al. 2018). Because only proteins with a Protein Data Bank structure have biophysical properties listed on the ProteomeVis web app, I access the complete data sets on ProteomeVis’ GitHub page. Abundance in ProteomeVis was originally reported in parts per million, however, here we use absolute abundance because that is the biologically relevant unit.

Homo sapiens data are currently not reported on ProteomeVis, and I use the same strategies employed in ProteomeVis’ data curation to pick A and ER data sets. My chosen A data set (Beck et al. 2011) has the largest coverage and is the most accurate that explicitly measures absolute abundance from a single reference, according to the Protein Abundances Across Organisms database (PaxDb) (Wang et al. 2015) (accessed April 2019). The A data set corresponds to expressed proteins in the U2OS (human osteosarcoma) cell line. Homo sapiens ER data are taken from the same overall data set that E. coli and S. cerevisiae ER data originate (Zhang and Yang 2015). ER in this article is the sequence identity between aligned, orthologous protein sequences (Zhang and Yang 2015). It was shown that this metric correlates very well with nonsynonymous substitutions per nonsynonymous site (d_N) (Razban et al. 2018). I avoid using d_N/d_S as the metric for ER because d_S has been shown to be selected (Wall et al. 2005; Jacobs and Shakhnovich 2017) and its selection pressure may differ from that of d_N, in light of MAH (Drummond and Wilke 2008). Because I compare ERs across proteins in a proteome, I do not need to normalize by divergence time, which d_S is assumed to capture when considering d_N/d_S. PPIs for H. sapiens are taken from the same database as for E. coli and S. cerevisiae, the IntAct database (Orchard et al. 2014).

As of April 2019, I could not find any protein abundance data for T. thermophilus, thus I did not include it in my analyses. Plata and Vitkup (2018) resorted to employing mRNA abundance, also called gene expression, as a proxy for protein abundance for T. thermophilus. I hesitate to do the same given the relatively poor correlation found between mRNA and protein abundance for E. coli (Taniguchi et al. 2010) and S. cerevisiae (Greenbaum et al. 2003; Lahtvee et al. 2017).

I reproduce the weak positive Pearson correlation coefficient between ln A and T_m for E. coli (table 1) that Plata and Vitkup (2018) reported. I also find a negative T_m–ln ER correlation that is barely significant for E. coli, consistent with Plata and Vitkup (2018) when they included ribosomal proteins in their analysis. In general, I include all proteins that have measurements for all three protein properties—A, T_m, and ER—regardless of protein function. Both correlations for S. cerevisiae are not significant (table 1), however, Plata and Vitkup (2018) found a weakly significant negative ln A–T_m correlation that goes against MAH expectations. The same observation was seen for H. sapiens (Plata and Vitkup 2018), which ProteomeVis recapitulates.

Table 1.

Pearson Correlation Coefficients (r) and P Values in Parentheses between Two Variables When Including All Proteins with Experimental Data for the Three Protein Properties: Abundance (A), Melting Temperature (T_m), and Evolutionary Rate (ER).

	r(ln A, Tm)	r(Tm, ln ER)	r(ln A, ln ER)	N
E. coli	0.13 (0.004)	−0.09 (0.03)	−0.32 (4E-15)	577
S. cerevisiae	−0.07 (0.1)	0.03 (0.5)	−0.39 (5E-18)	468
H. sapiens	−0.16 (0.03)	0.004 (0.96)	−0.18 (0.02)	175

Note.—n = numbers of data points.

My A and ER data sets are different from those employed by Plata and Vitkup (2018), in terms of their source and units. Plata and Vitkup (2018) utilized whole organism integrated A data sets reported by PaxDb in units of parts per million for all three organisms. The metric of ER used by Plata and Vitkup (2018) is d_N, which they generate themselves by running PAML (Yang 2007) on pairs of orthologous gene sequences for all three organisms. Nonetheless, my reported correlations are roughly consistent with those reported by Plata and Vitkup (2018) for the three organisms considered. This indicates that reported correlations are not biased by any specific curation procedure in selecting A and ER data sets.

My employed data sets can be downloaded from the Supplementary Material online.

Approximating Equation (4) Such That It Is Evaluable Proteome-Wide While Still Maintaining Accuracy

As an attempt to obtain a simpler ΔG–T_m relationship that is physically motivated, I approximate equation (4) by writing T_m = T + δ_m and Taylor expanding to first order around δ_m/T = 0. The approximation is not drastic because temperatures in equation (4) are in Kelvin (T ∼ 300 K) and proteins have a mean stability of 333 K (Robertson and Murphy 1997), making δ_m/T ≪ 1.

$$\begin{array}{c}\Delta G=-\Delta H_{\mathrm{m}}\hspace{0.17em}\left(1-\frac{T}{T+{\delta }_{\mathrm{m}}}\right)\hspace{0.17em}+\hspace{0.17em}\Delta C_p\left({\delta }_{\mathrm{m}}+T\ln \frac{T}{T+\delta }\right)\\ =-\Delta H_{\mathrm{m}}\left[1-{\left(1+\frac{{\delta }_{\mathrm{m}}}{T}\right)}^{-1}\right]+\Delta C_p\left[{\delta }_{\mathrm{m}}-T\ln \left(1+\frac{{\delta }_{\mathrm{m}}}{T}\right)\right]\\ \approx -\Delta H_{\mathrm{m}}\left[1-\left(1-\frac{{\delta }_{\mathrm{m}}}{T}\right)\right]+\hspace{0.17em}\Delta C_p\left[{\delta }_{\mathrm{m}}-T\left(\frac{{\delta }_{\mathrm{m}}}{T}\right)\right]\\ =-\Delta H_{\mathrm{m}}\frac{{\delta }_{\mathrm{m}}}{T}=-\Delta H_{\mathrm{m}}\frac{T_{\mathrm{m}}-T}{T}\end{array}$$ (8)

Equation (8) demonstrates that ΔC_p can be neglected to first order in δ_m/T. When fitting ΔG to the right-hand side of the final expression in equation (8) (which I define as x₁) with the Rees and Robertson (2001, table 1A) data set, I find r = 0.91 (P value = 2E-17) with a best-fit line of ΔG = 0.43 × x₁ − 5.9 kJ/mol (supplementary fig. S2B). If equation (8) is perfectly valid, ΔG = 1 × x₁ + 0. I reason that the imperfection is a result of the δ_m/T ≪ 1 approximation. When only considering half the data set with lower T_m, equation (8) holds stronger with r(x₁, ΔG) = 0.95 (5E-11) and a best-fit line of ΔG = 0.61 × x₁ + 0.08 kJ/mol. The slope in this case is closer to 1 and the intercept is nearly 0 because the δ_m/T ≪ 1 approximation is less severe for proteins with lower T_m.

Although equation (8) is simpler than equation (4), equation (8) still does not guarantee a monotonic relationship between T_m and ΔG because in the equation, ΔG still depends on one other protein property besides T_m: ΔH_m. Moreover, ΔG cannot be evaluated explicitly because proteome-wide ΔH_m values are currently unknown. A previous study found ΔH and ΔC_p to scale with the number of residues (N) in a protein (Robertson and Murphy 1997) at 333 K, where ΔH(T = 333 K) = 2.92N kJ/mol and ΔC_p = 0.058N kJ/mol. Thus, ΔH_m = ΔH(T = 333 K) + ΔC_p (T_m − 333 K) = 2.92N + 0.058N (T_m − 333 K). Compact and cubic lattice proteins, the simplest model that captures contacts present in globular proteins that are important for assuming native conformations (Shakhnovich 1997), can motivate the N dependence. The energy of folded lattice proteins scales with the number of contacts and the number of contacts can be shown to scale as 2N as N approaches infinity for compact and cubic lattice proteins (supplementary eq. S1, Supplementary Material online). I assume that ΔH_m ∼ energy of the folded lattice protein (Gin et al. 2009; Best et al. 2013). Because ΔC_p is the temperature derivative of ΔH_m, the N scaling immediately follows. Inserting the ΔH_m(T_m, N) relationship into equation (8) yields equation (5).

When fitting ΔG to the right-hand side of equation (5) (which I define as x₂) with Rees and Robertson (2001, table 1A), I find r = 0.80 (9E-11) with a best-fit line of ΔG = 0.38 × x₂ − 9.67 kJ/mol (supplementary fig. S2C). r(x₂, ΔG) is not drastically smaller than the previous r corresponding to equation (8) (r = 0.91). The slight loss in accuracy is acceptable given that ΔG no longer depends on ΔH_m and depends on N, a protein property that is known proteome-wide.

In principle, I could omit the first approximation altogether, and plug in N-dependent values directly into equation (4). When doing so, the corresponding correlation with ΔG is similar to that seen for r(x₂, ΔG), r = 0.82 (3E-11). This makes sense because equation (5) only has one protein-specific value that is approximated by N, whereas equation (4) has two. The inaccuracy from employing N as a proxy for both ΔH_m and ΔC_p terms in equation (4) is similar to employing N as a proxy for just ΔH_m in equation (5) after approximating equation (4). Besides depending less on the assumption that thermodynamic properties making up ΔG scale with N, I keep the first approximation because the resulting equation relating ΔG and T_m is simpler and has the added benefit of being analytically invertible, that is, I can write T_m as a function of ΔG (supplementary eq. S3). Results discussed are presented only for equation (5), however they remain unaltered if I employ N as a proxy for both ΔH_m and ΔC_p terms in equation (4).

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.