Functional data analysis for computational biology

Abstract

Supplementary information: Supplementary data are available at Bioinformatics online.

To the Editor: How the many players of the genome and epigenome orchestrate transcriptional regulation, as well as other molecular mechanisms related to development or diseases, remains an unresolved question in biology. Most sequencing-based genomic or epigenomic assays generate high-resolution data suitable to be represented as 1D curves over the genome (e.g. ChIP-seq) or 2D heatmaps over 3D space (e.g. chromosome conformation capture techniques such as Hi-C). Functional data analysis (FDA), a repertoire of statistical methods that considers data as evaluations of curves (mathematical functions) over a discrete grid, plays a critical role in exploiting the output of Next generation sequencing (NGS) assays, and allows sophisticated biological interpretation of shape information. However, despite its potential, FDA has not received much attention compared to machine learning in general, or deep learning—which has become increasingly popular. Obstacles to the spread of FDA in computational biology include, but are not limited to, the paucity of user-friendly software specifically designed for omics applications, the absence of functional analogues to some of the classical multivariate techniques, and the complexities of interpreting curvature and derivatives which are keys in FDA but not even defined in multivariate analysis.

NGS data are subject to several problems such as missing values, correlations among neighbouring genomic positions, and non-trivial technology-specific noise sources. Many standard statistical methods, as well as some machine learning methods, rely on rather simplistic specifications of correlations and noise—and are not robust if these specifications are not accurate. FDA is an appealing option for overcoming these problems. Correlations among neighbouring measurements can in fact be advantageous in FDA—which smooths such measurements into curves, effectively reducing the dimension of the data. Importantly, the dimension of smooth data representations can be controlled selecting the type and number of basis functions employed, while roughness penalties (e.g. on the total curvature of a function) allow continuous control over smoothness. By representing the data as functions, FDA also alleviates the impact of non-trivial noise and ‘fills in’ missing values, improving statistical power. In addition to improving signal-to-noise ratios, and hence power, smoothing can unveil information and biological insights missed by multivariate techniques, as long as the assumption of smoothing is reasonable (Froslie et al., 2013).

FDA has begun to appear in the computational biology/bioinformatics and ‘omics’ literature during the last 5 years. We identified three main research directions in which leveraging shape information already proved to be effective. These directions could, and in our opinion should, be expanded to encompass a wider range of techniques and applications of interest to the research community.

1. Shapes of the genomic landscape. Recent techniques profile a very large number of features at increasing levels of resolution, generating a multifaceted, fine-detail map of the genomic landscape which includes, e.g. interspersed repeat densities, replication timing, recombination rates, mutation rates, etc. Using the shapes of the genomic landscape increases power and accuracy in contrasting genomic regions and loci of interest (Cremona et al., 2018). For instance, the flanks of old and young endogenous retroviruses can be contrasted against background regions to investigate their integration and fixation preferences in mammalian genomes (Campos-Sanchez et al., 2016). Contrasting shapes is also useful in a variety of other applications, e.g. to study how polymerization speed and error rates are affected by non-B DNA (Guiblet et al., 2018) (Fig. 1A).

2. Shapes of the epigenome. NGS techniques produce nucleotide or quasi-nucleotide resolution signals for the epigenome. Shape information is useful at every step of epigenomic data analysis, from the pre-processing of sequenced reads to the study of cellular processes and functions. It has been used to improve binding site detection (Mendoza-Parra et al., 2013; Wu and Ji, 2014), as well as to compare ChIP-seq profiles between different replicates, conditions and/or times (Madrigal, 2017; Schweikert et al., 2013). Techniques have been developed for clustering ChIP-seq peaks characterized by different shapes (Cremona et al., 2015; Parodi et al., 2017), and for exploiting shape variation and co-variation in the identification of histone mark effects in gene regulation, and between histone modifications and DNA binding proteins (Madrigal, 2017; Madrigal and Krajewski, 2015). Additional work is needed to analyze sparse data in single-cell epigenomics (Kelsey et al., 2017) (Fig. 1B), incorporate shape in the analysis of chromatin spatial organization, and integrate 1D epigenomic profiles with 3D information.

3. Shapes of phenotypes. Information in shapes can be leveraged in traditional longitudinal and biometric studies, such as growth curves and gene expression trajectories. Complex phenotypes represented as functional outcomes, in combination with DNA sequencing data, can dramatically increase power and accuracy for detecting relevant variants in genome-wide association studies (Reimherr and Nicolae, 2014) and for associating microbiota composition to child weight gain (Craig et al., 2018). Among the most recent developments in this field are techniques for feature selection in models where a functional outcome is regressed against a very large number of potential predictors (e.g. single nucleotide polymorphisms) (Foygel-Barber et al., 2017). These techniques can be generalized for contemporary biomedical imaging, representing quantitative complex phenotypes as functions; Examples include 2D or 3D imaging of tissues, organs or body parts (Huang et al., 2017; Kang et al., 2017) (Fig. 1C).

Fig. 1.

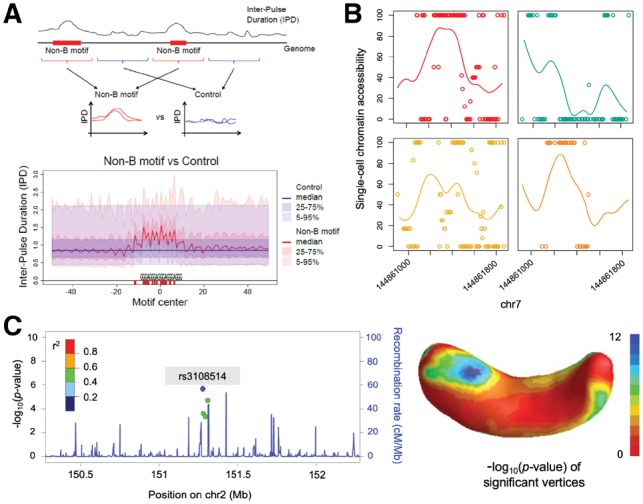
Examples of FDA in computational biology. (A) Comparison of polymerase speed data (inter-pulse duration) between non-B DNA and control regions, using a functional hypothesis test (Guiblet et al., 2018). (B) Estimated coverage profile of scNMT-seq single-cell chromatin accessibility data for four mouse embryonic stem cells facilitated by sparse functional principal component analysis on a population of 69 cells (Madrigal et al., 2018). (C) Integration of genetic data and neuroimaging using a functional genome-wide association analysis framework (SNP rs3108514 for right hippocampus surface) (Huang et al., 2017)

We also believe that the scope of FDA could be broadened to other areas of computational biology, with methods that target specifically data generated by novel assay techniques. The Human Cell Atlas will soon release millions (perhaps a billion) of single-cell datasets (Rozenblatt-Rosen et al., 2017). Based on recent contributions (Clark et al., 2018) (Fig. 1B) we anticipate that, because of severe sparsity, FDA will be even more useful in single-cell epitranscriptomics or epigenomics than it has been to date.

FDA models could also be used to study dynamics in time series for NGS data, including transcriptomic measures such as RNA velocity—the time derivative of RNA abundance (La Manno et al., 2018). With the popularization of chromatin conformation capture and data becoming more spatio-temporal in nature, investigating variation in the shape of DNA, spatial smoothing, building predictive models and integrating derivative information into these models are challenges that could be addressed using FDA. Development of informative summary statistics, exploratory techniques and rigorous inferential methods will all be necessary.

Finally, representing the evolution of shapes over time can be critically important also for phenotypes and genomic landscape (e.g. temporal change in the 3D shape of an imaged tumour mass; temporal change in the landscape of mutations, transcription factor binding, methylation and gene expression, of a cancer genome). FDA methods able to include temporal evolution in the analysis will be extremely useful in this context.

For all these reasons, we believe there is ample room for FDA in computational biology. We hope that an increasing number of researchers in the community will start using and developing FDA methods in many different settings, generating novel biological insights. In the Supplementary Material, we provide a list of online resources, books and software as a starting point for those interested in FDA.

Funding

This work was supported by the Eberly College of Science and the Institute of CyberScience. The Pennsylvania State University; the National Center for Research Resources and the National Center for Advancing Translational Sciences [NIH Grant UL1TR000127] (the content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH); and the Tobacco Settlement and CURE funds, PA Department of Health (the Department specifically disclaims responsibility for any analyses, interpretations or conclusions).

Conflict of Interest: none declared.