Conditions for eradicating hepatitis C in people who inject drugs: A fibrosis aware model of hepatitis C virus transmission

Abstract

It is estimated that 80% of new hepatitis C virus (HCV) infections occur among people who inject drugs (PWID). Eradicating HCV from this population is key for the complete eradication of the disease, and the advent of simple to use, high efficacy treatments could conceivably make this scenario possible. This paper presents a mathematical model where transmission of HCV is studied in a simulated population of PWID where fibrosis progression is explicitly tracked. The stability thresholds that determine whether HCV will remain endemic or become eradicated were established numerically, and analytically on a reduced version of the model. Conditions on testing and treatment rates for eradication to occur were determined, within the context of the new high efficacy therapies. The results show that HCV eradication in the PWID population of the Vancouver, BC test scenario is achievable, but testing and especially treatment rates will need to increase significantly from current rates. Parameter estimates were drawn from published data.

1. Introduction

The hepatitis C virus (HCV) is a major global health concern, with estimates of up to 3% of the world population being infected (Lavanchy, 2009). In North America, HCV has become the most prevalent blood-borne disease, with 1 in 100 infected and 15,106 people dying of HCV in the US in 2007 alone (Ly et al., 2012). Between 80% and 90% of new cases occur in people who inject drugs (PWID), where HCV prevalence is estimated to be 67% (Nelson et al., 2011), however only 1–2% of infected PWID are treated each year (Alavi et al., 2013; Iversen et al., 2014). A cure for HCV has been available for more than 10 years, but up to 2012 the standard of care was a lengthy (48 weeks) interferon and ribavirin-based treatment, which had numerous side effects and a high pill burden, and a success rate of around 50%, depending on the HCV genotype. The treatment length, tolerability issues and pill burden resulted in a high barrier to access treatment for the population most vulnerable to the disease.

Over the past three years we have seen the emergence of direct acting antiviral treatments (DAA) for HCV. These new therapies target specific parts of the HCV virus, and they are revolutionizing the treatment of HCV. The first two approved treatments (boceprevir and telaprevir) reduced treatment length to 24 weeks with improved efficacy in genotype 3 patients, however, they were still used in conjunction with pegylated interferon and ribavirin. Patient tolerance of side-effects was a significant issue (Hézode et al., 2013). Recently, the so-called second generation DAA treatments are starting to become available, with cure rates above 90% even on previous non-responders, coinfected patients with HIV, and people with advanced liver disease. Tolerability has improved, but the treatment response depends on the HCV genotype, and concerns have been raised about antiviral resistance. The US FDA and Canadian Pharmacare recently approved the first all oral, one pill a day HCV treatment that is interferon and ribavirin-free, but is limited to genotype 1 infections. There are increasing expectations that in the near future we will have interferon and ribavirin-free, one pill a day, pangenotypic treatments with efficacies above 90% and minimal side effects (Feeney and Chung, 2014). The HCV treatment landscape is in the process of changing dramatically and efforts are needed to predict the effects of these new treatments and develop strategies on how to best deliver this life-saving but highly expensive treatment.

Mathematical models have previously been used to understand the effects that new therapies and harm reduction efforts will have on the course of the HCV epidemic (Elbasha, 2013; Kwon et al., 2009; Martin et al., 2013; Razavi et al., 2014; Lima et al., 2015). The performance and tolerability of the new therapies have the potential to greatly increase access to treatment, and could eventually lead to the eradication of the epidemic. In this work we present a mathematical model for HCV transmission designed for PWID populations. Key features in the model are: (a) fibrosis progression is explicitly modeled, with mortality rates adjusted for fibrosis level, allowing the study of policy scenarios to treat individuals based on fibrosis level; (b) the model accounts for the delay from infection to diagnosis due to testing practices; (c) reinfection is explicitly modeled, and reinfection risk reduction due to engagement in harm reduction. The model was calibrated with data from the PWID population of British Columbia (BC), Canada. In this work, we analyzed the stability properties of the solutions to the model with the goal of understanding the conditions necessary to eradicate the HCV epidemic. An extended version of this model (Lima et al., 2015), commissioned by the BC Minister of Health, was used to study the effect of the new therapies on incidence, prevalence, and mortality.

1.1. Study design

We designed a deterministic mathematical multigroup model with 35 ordinary differential equations (ODE): seven main compartments with five sub-compartments each. The numerical and analytical aspects were coded in Python 2.7 (Rossum, 1995). The numerical simulations were done using the numpy and scipy libraries (Jones et al., 2001), and the symbolic algebra was done using the sympy library. The numerical integration of the ODE system was done using the vode integrator, an implicit Adams method. Solutions were evaluated at multiple step sizes to ensure proper convergence. Data outputs were obtained by linearly interpolating the integration data and evaluating it at yearly intervals. The force of infection (β) and the mortality rate parameters (μ) were fit to known prevalence and incidence rates at the endemic steady state equilibrium via a Powell hybrid optimization algorithm. Parameters for the model were obtained from the available literature and are listed with references in Table 1.

Table 1.

Parameters used in the numerical simulations.

Symbol	Explanation	Baseline value [range]	Reference
ρ	Proportion achieving SVR	0.9[0.75–0.95]	Feeney and Chung (2014)
1/ω	Treatment duration	12 [8–16] weeks	Lawitz et al. (2013)
χ0	Relative infectivity while chronically infected	0.10	Kleinman et al. (2009)
χ1	Relative infectivity while on treatment	[$0-\frac{{\chi }_0}{2}$]	Kleinman et al. (2009)
θ	Spontaneous clearance proportion	0.25 [0.22–0.29]	Grebely et al. (2014a); Micallef et al. (2006)
1/δ	Duration of acute phase	6 months	Mondelli et al. (2005)
ζ	Proportion not eligible for treatment	0.2 [0.2–0.5]	Remis (2010)
εΓ	Reinfection risk reduction	0.79 [0.48–0.92]	Turner et al. (2011)
κ	Proportion moving into risk reduction after achieving SVR	0.45 [0.4–0.6]	Turner et al. (2011), UHRI, (2013)
γ	Loss of individuals from the risk reduction compartment	60 per 1000 PW1D per year	Dalgard (2005)
τ	Testing rate	140 per 1000 PW1D per year	Alavi et al. (2013), Grebely et al. (2009)
σCa	Treating rate, Ca compartment	8 per 1000 PW1D per year	Alavi et al. (2013), Grebely et al. (2013)
σCn	Treating rate, Cn compartment	ασCa	Alavi et al. (2013), Grebely et al. (2013)
α	Treatment rate reduction for Cn due to treatment ineligibility	0.75	Hull et al. (2012), Alavi et al. (2013), UHRI, (2013)
β	Average contact rate	Fit to reproduce prevalence data
μPWID	BC PW1D mortality rate	Fit to reproduce incidence data	Puri et al. (2014)
mLD	Standardized mortality ratio for liver disease	8.44 [7.5–10]	Yu et al. (2013)
μ	Fibrosis-dependent mortality rate	μPWID at F0 to μPWIDmLD at F4 0.8 to 6.9 per PY
f01	Fibrosis progression rate Fi to Fi+1	0.067 [0.054–0.109]	Razavi et al. (2014), Thein et al. (2008)
f12		0.049 [0.039–0.068]
f23		0.069 [0.055–0.113]
f34		0.051 [0.041–0.125] degrees per year
ψ	Fibrosis regression rate, Fi to Fi−1	0.2[0.18–0.22] degrees per year	George et al. (2009), Shiratori et al. (2000)

2. Model description

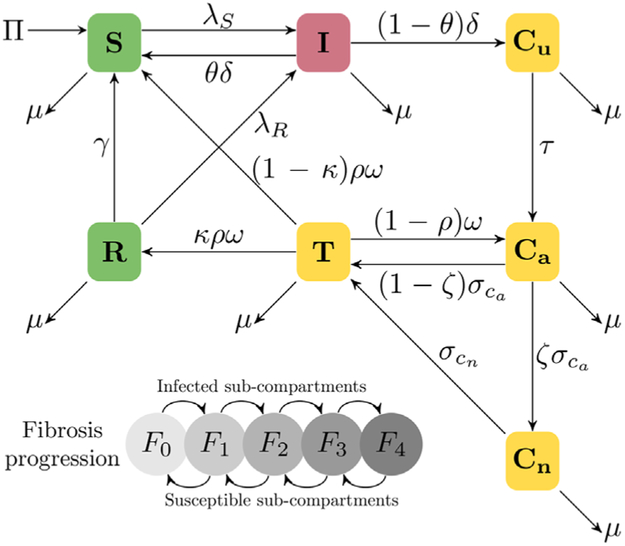
The seven main compartments in the ODE system allocate the susceptible and infected populations as susceptibles (S), acutely infected (I), chronic infected and unaware (C_u), chronic aware (C_a), chronic not eligible for treatment (C_n), on treatment (T), and engaged into risk reduction (R). The five sub-compartments in each main compartment correspond to the five liver fibrosis progression stages, F0–F4 according to the METAVIR scoring system (Bedossa and Poynard, 1996). A diagram for the model can be seen in Fig. 1.

Fig. 1.

Flow diagram for the HCV model specified in Eqs. (1a)-(1g). In the major compartments, susceptible individuals (S) become acutely infected (I) according to a transmission rate λ_S, and subsequently progress to chronic unaware (C_u) at a rate δ, they are then tested at a rate τ to become chronic aware (C_a), and a proportion ζ is deemed ineligible for treatment (C_n) and the rest are treated (T) at a rate σ_Ca. We allow the possibility of new treatments being able to treat the population ineligible for treatment (at a rate σ_Cn). Of those who get cured, defined as achieving a sustained virologic response (SVR) 12–24 weeks after finishing treatment, a proportion κ lower their reinfection risk (R), but they can drop out of the compartment to become susceptible once again at a rate γ. At each major infected compartment, individuals progress across fibrosis stages F0→F4, and in the uninfected compartments reverse the progression F4→F0. Mortality depends on the fibrosis stage; all deaths were reincorporated to the model via the recruitment term Π to keep the population constant.

The equations describing the above system are:

$$\frac{d\mathbf{S}}{dt}=\Pi +\rho (1-\kappa )\omega \Omega \mathbf{T}+\gamma \mathbf{R}+\theta \delta \mathbf{I}+\Psi \mathbf{S}-({\lambda }_S+\mu )\mathbf{S},$$ (1a)

$$\frac{d\mathbf{I}}{dt}={\lambda }_S\mathbf{S}+{\lambda }_R\mathbf{R}-(\delta +\mathbf{F}+\mu )\mathbf{I},$$ (1b)

$$\frac{d{\mathbf{C}}_{\mathbf{u}}}{dt}=(1-\theta )\delta \mathbf{I}-(\tau +\mathbf{F}+\mu ){\mathbf{C}}_{\mathbf{u}},$$ (1c)

$$\frac{d{\mathbf{C}}_{\mathbf{a}}}{dt}=\tau {\mathbf{C}}_{\mathbf{u}}+(1-\rho )\omega \mathbf{T}-({\sigma }_{c_a}+\mathbf{F}+\mu ){\mathbf{C}}_{\mathbf{a}},$$ (1d)

$$\frac{d{\mathbf{C}}_{\mathbf{n}}}{dt}=\zeta {\sigma }_{c_a}{\mathbf{C}}_{\mathbf{a}}-({\sigma }_{c_n}+\mathbf{F}+\mu ){\mathbf{C}}_{\mathbf{n}},$$ (1e)

$$\frac{d\mathbf{T}}{dt}=(1-\zeta ){\sigma }_{c_a}{\mathbf{C}}_{\mathbf{a}}+{\sigma }_{c_n}{\mathbf{C}}_{\mathbf{n}}-(\omega +\mu )\mathbf{T},$$ (1f)

$$\frac{d\mathbf{R}}{dt}=\rho \kappa \omega \Omega \mathbf{T}+\Psi \mathbf{R}-(\gamma +{\lambda }_R+\mu )\mathbf{R},$$ (1g)

where

$$\begin{gathered} \Pi =({\Pi }_0,0,0,0,0{)}^T, \\ {\Pi }_0=\mu \cdot (\mathbf{S}+\mathbf{I}+{\mathbf{C}}_{\mathbf{u}}+{\mathbf{C}}_{\mathbf{a}}+{\mathbf{C}}_{\mathbf{n}}+\mathbf{T}+\mathbf{R}), \\ {\lambda }_S=\beta \sum _{i=0}^4(I_i+{\chi }_0(C_{ui}+C_{ai}+C_{ni})+{\chi }_1{T}_i)∕N, \\ {\lambda }_R=(1-{\epsilon }_r){\lambda }_S, \\ N=\sum _{i=0}^4(S_i+I_i+C_{ui}+C_{ai}+C_{ni}+T_i+R_i)=18,068, \end{gathered}$$

with Π being the recruitment of new individuals into the system, designed to keep the total population (N) constant; λ_S and λ_R are the force of infection terms from the S and R compartments, respectively. Infectivity is modeled to be highest in the acute compartment (I), decrease in the chronic compartments (C_u, C_a, C_n), and to be lowest while on treatment (T) (Elbasha, 2013; Kleinman et al., 2009). The transition matrices Ψ and F represent the decrease (Marcellin et al., 2013) and increase (Thein et al. 2008) in fibrosis level due to being in a non-infected or infected compartment, respectively. The Ω matrix models a decrease of one fibrosis level upon successfully completing treatment.

$$\begin{gathered} \Omega =\left(\begin{array}{ccccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),\Psi =\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill \psi \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\psi \hfill & \hfill \psi \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\psi \hfill & \hfill \psi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\psi \hfill & \hfill \psi \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\psi \hfill \end{array}\right), \\ \mathbf{F}=\left(\begin{array}{ccccc}\hfill f_{01}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -f_{01}\hfill & \hfill f_{12}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -f_{12}\hfill & \hfill f_{23}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -f_{23}\hfill & \hfill f_{34}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -f_{34}\hfill & \hfill 0\hfill \end{array}\right). \end{gathered}$$

2.1. Parameter values

A summary of parameter estimates with references can be found in Table 1. Parameters were obtained from relevant biological HCV treatment literature sources, and from studies with PWID whenever possible. The proportion of PWID in treatment that achieve SVR (ρ) was set to 90% for the simulations for 2015 onwards, and in determining the baseline steady state we used 55% up to 2012, and 75% from 2012 to 2015. Treatment duration (1/ω) was set at 12 weeks for 2015 onwards, 48 weeks up to 2012, and 24–48 weeks depending on genotype for 2012–2015. The proportion of the population that spontaneously clears the disease while on the acute stage (Grebely et al., 2014a), as well as the duration of the acute stage (Mondelli et al., 2005) have been well studied, and established at 25% and 6 months, respectively (parameters θ and δ). There is conflicting evidence as to whether acutely infected individuals are more infective than chronically infected individuals (Kleinman et al., 2009; Hajarizadeh et al., 2015). Mathematical models for HCV with relative risks of infection as low as 1% have been used in Elbasha (2013), and equal for all stages in Martin et al. (2013); for this work we used a more conservative value for the relative infectivity parameters (χ₀ and χ₁) between those two extremes.

Reinfection rates of PWID in Vancouver are 3.2 cases per 100 person-years (PY), and 5.3 for PWID reporting injection drug use (Grebely et al., 2010). For the 2006–2012 period, HCV incidence of new infections was 3.1 per 100 PY and 4.9 for individuals injecting during follow-up (Grebely et al., 2014b). From this data, it appears that curing HCV does not confer significant immunity against reinfection. On the other hand, harm reduction efforts (opiate substitution therapy and needle and syringe programs) can reduce infection risks by nearly 80% (Turner et al., 2011). Reinfection risk reduction (ε_r) for individuals in the risk reduction compartment (R) was set to 0.79, 95% CI: [0.48–0.92]. The proportion of the population that after achieving SVR engages in harm reduction strategies (κ) was estimated based on the Urban Health Research Initiative report on the drug situation in Vancouver (UHRI, 2013). The number of people on OST is similar to numbers reported for various places in the UK (Turner et al., 2011). The rate at which PWID drop out of the harm reduction compartment (γ) was estimated from Dalgard (2005), where five years after successful treatment, 33% of the patients had returned to using drugs.

There is evidence that the PWID population is relatively well tested. In Alavi et al. (2013), it was estimated that 86% of the population at risk was tested for HCV between 2003 and 2009, yielding an average yearly testing rate (τ) of 14%. The percentage of the population that gets evaluated for HCV treatment (σ), however, is very low, at 0.81% yearly over the same time period. The proportion of people ineligible for treatment (ζ) was taken, conservatively due to the low treatment rates, to be 75% and 50% for the up to 2012 and 2012–2015 time periods, respectively. There is evidence that with the new all oral DAAs it will be possible to treat individuals with advanced fibrosis/cirrhosis (Feeney and Chung, 2014), hence we lowered ζ to 20% for 2015 onwards based on the number of people with severe liver complications (Remis, 2010). The reduced treatment rate for the population previously deemed ineligible for treatment was based on the unstable housing and drug use patterns (UHRI, 2013; Alavi et al., 2013), which act as counter-indications for the use of the drugs in the Canadian HCV guidelines (Hull et al., 2012). It was taken to be 10% up to 2012 and 20% for the 2012–2015 period, and 75% CI:[0.60–0.90] for 2015 onwards. The average contact rate (β) was set by optimizing the model to satisfy an endemic equilibrium with a 65% prevalence rate at 2012, and β was kept constant afterwards.

The mortality rates for the sub-compartments were generated by linearly interpolating between the background mortality rate μ_PWID (for F0) and adjusted with the liver-disease SMR (for F4) (Yu et al. 2013).

Fibrosis progression was modeled to occur in all infected compartments, where individuals would go from fibrosis level f_i to f_i+1 over time. The upper values in the fibrosis progression ranges were taken from the Thein et al. (2008) meta-analysis, and the lower values from recent data from Razavi et al. (2014). Fibrosis regression was modeled for all non-infected compartments, with the fibrosis regression rate parameter fixed at 0.20, or regression of one fibrosis level every 5 years when cured. Fibrosis was assumed to not vary while on treatment.

3. Results

3.1. Existence and uniqueness of endemic and disease-free solutions

With a constant total population N, it is possible to solve the system and obtain the disease-free solution. By setting the variables representing infected states (I, C_u, C_a, C_n, T) to zero, from Eq. (1b) we get that R=0, and from Eq. (1a) we can see that S_i=0 for 1 ≤ i ≤ 4. Given that the total population N is constant, we have then that S₀ = N is the only disease-free equilibrium.

It should be possible in theory to solve the system to obtain an alternative solution representing an endemic equilibrium. One way to do it would be by setting the system to zero and using the fact that the variables I, C_u, C_n, T, and the parameters λ_R, λ_S can be expressed linearly in terms of C_a. The variables S,R can then be solved in terms of C_a. Finally, the equilibrium value or values of C_a can be obtained using the constant population constraint.

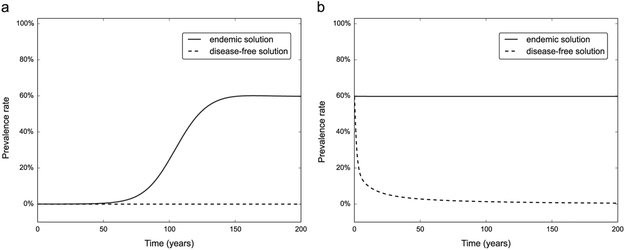
While it is possible to obtain analytical forms for the endemic solutions, the large number of equations and parameters makes it impractical. The existence of the two solutions can be shown numerically by integrating the system for different parameter sets. Fig. 2 shows the prevalence of HCV positive individuals in the model population at both the disease-free and endemic equilibriums. Both equilibrium solutions can lose their stability and transition to the other equilibrium solution (disease-free to endemic in Fig. 2a, and vice versa in Fig. 2b when changing parameters past a stability threshold. A more detailed analysis of the stability of the system is discussed in Section 3.2. In order to display the two solutions, we integrated the ODE system on parameter ranges reflecting both an aggressive HCV testing and treatment program and the baseline low coverage scenario.

Fig. 2.

Existence of the disease-free and endemic solutions, and change in stability. (a) Two long term integrations of the ODE system (1) with initial conditions set to the disease-free equilibrium plus low amplitude random noise. Simulating aggressive testing and treatment rates of σ = 0.7, τ = 0.7 the disease-free equilibrium (dotted line) is stable throughout the simulation. Decreasing the parameters to the low coverage baseline scenario (σ = 0.008, τ = 0.14), the disease-free equilibrium loses stability and a stable endemic solution (solid line) appears. (b) We repeated the experiment starting with the endemic solution as initial conditions, again testing both sets of parameters. The endemic solution remains stable with the baseline parameters, and loses its stability and transitions to the disease-free solution in the aggressive testing and treatment scenario.

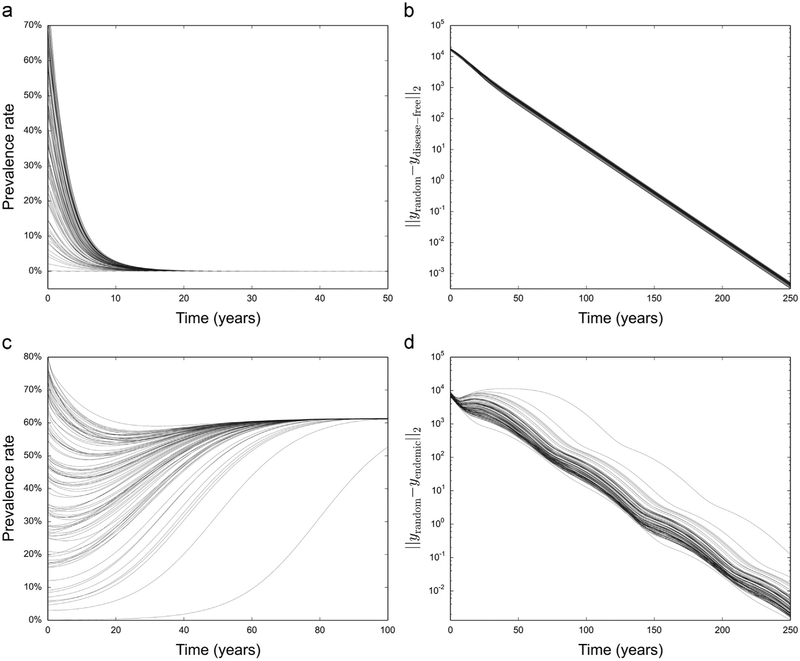
We know that there is only one disease-free solution (S₀ = N), while the uniqueness of the endemic solution is inferred from numerical simulations. We generated 100 different random initial conditions on both the aggressive testing and treatment scenario and the low uptake baseline scenario, and integrated the system for 250 years. In all cases we saw convergence to the expected equilibrium solution (Fig. 3a and c). We also measured the norm of the difference between the equilibrium solutions and the solutions generated from random initial conditions and saw exponential convergence for both scenarios (Fig. 3b and d), suggesting the existence of a unique globally stable solution for each parameter set.

Fig. 3.

Long-term simulations with random initial conditions, with parameters for both an endemic solution and a disease-free solution. (a) We used 100 sets of random initial conditions with the system parameters simulating an aggressive testing and treatment scenario. (b) Norm of the difference between the solutions and the disease-free solution as time increases. (c) Repeat with model parameters reflecting the baseline low coverage scenario. Solutions all converge to the endemic solution, with similar exponential convergence (d) as in the disease-free scenario.

3.2. Stability of the equilibrium solutions

To determine the stability of the solutions, we calculated the eigenvalue with largest real value from the Jacobian of the system evaluated at the equilibrium points. This parameter is often referred to as the Malthusian or intrinsic growth rate and labeled as r₀ (Anderson and May, 1979). It shares with the basic reproductive ratio R₀ the property of defining the parameter space where equilibrium solutions in the system are stable or unstable. An equilibrium solution with r₀ < 0 is stable, and unstable if r₀ > 0, with r₀ = 0 being the stability threshold. This is analogous to R₀ < 1, R₀ > 1 and R₀ = 1. A key advantage of using r₀ over the basic reproductive ratio (R₀) to study the stability of solutions is that r₀ can be calculated for both the disease-free and the endemic equilibrium solutions. In contrast, the basic reproductive ratio R₀ is only applicable to the disease-free equilibrium.

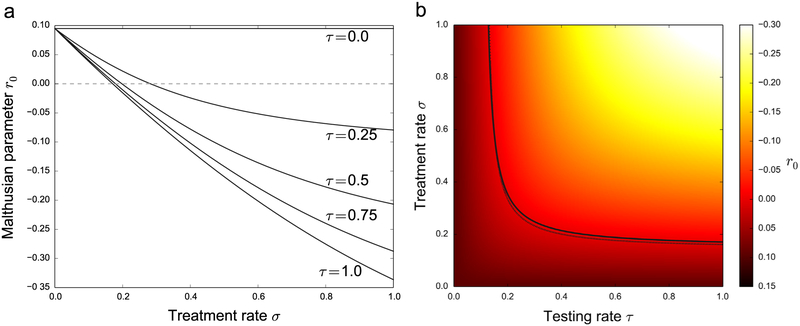
The stability of the disease-free equilibrium was determined as a function of the testing and treatment rate parameters (τ, σ). Fig. 4 shows the estimated r₀ for different values of the (τ, σ) parameters. The solid line in the figure on the right is the threshold r₀ = 0, and the dotted line close to it is the analytical approximation to the stability threshold derived in Eq. (3) below.

Fig. 4.

The stability of the disease-free equilibrium as a function of the testing and treatment rates (τ, σ). (a) r₀ is plotted against σ for 5 fixed values of τ. (b) Color map of the same data over σ and τ. The solid line in (b) represents the numerically computed stability threshold r₀ = 0, and the dotted line is the R₀ = 1 threshold computed from the analytical approximation in Eq. (3).

We determined an analytical approximation to the stability threshold by calculating the basic reproductive number R₀ for a simplified scalar model without fibrosis stages.

$$\begin{gathered} \frac{dS}{dt}=\Pi +\rho (1-\kappa )\omega T+\gamma R+\theta \delta I-({\lambda }_S+\mu )S, \\ \frac{dI}{dt}={\lambda }_{S}S+{\lambda }_{R}R-(\delta +\mu )I, \\ \frac{d{C}_u}{dt}=(1-\theta )\delta I-(\tau +\mu )C_u, \\ \frac{d{C}_a}{dt}=\tau C_u+(1-\rho )\omega T-({\sigma }_{c_a}+\mu )C_a, \\ \frac{d{C}_n}{dt}=\zeta {\sigma }_{c_a}{C}_a-({\sigma }_{C_n}+\mu )C_n, \\ \frac{dT}{dt}=(1-\zeta ){\sigma }_{c_a}{C}_a+{\sigma }_{C_n}{C}_n-(\omega +\mu )T, \\ \frac{dR}{dt}=\rho \kappa \omega T-(\gamma +{\lambda }_R+\mu )R, \end{gathered}$$ (2)

The simplified scalar model has seven equations instead of the 35 in the multigroup model, with the mortality μ being the average of the fibrosis-dependent mortality parameters of the multigroup model. Furthermore, R₀ can be computed using only the four equations from the infection subsystem (I, C_u, C_a, and C_n) using the next-generation method (Diekmann et al., 2012; Van den Driessche and Watmough, 2002). The next-generation matrix is defined as the product of the matrices F and V⁻¹; the F matrix describes infection transmission, and the V matrix all other transitions across compartments. This result was then compared with the numerically calculated stability threshold for r₀ since the stability thresholds for both r₀ (r₀ = 0) and R₀ (R₀ = 1) occur in the same parameter space (Diekmann et al., 2009).

The F, V, and V⁻¹ matrices are given by

$$\begin{gathered} \mathbf{F}=\beta \left(\begin{array}{cccc}\hfill 1\hfill & \hfill {\chi }_0\hfill & \hfill {\chi }_0\hfill & \hfill {\chi }_0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right), \\ \mathbf{V}=\left(\begin{array}{cccc}\hfill \delta +\mu \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \delta (1-\theta )\hfill & \hfill \theta +\mu \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\tau \hfill & \hfill {\sigma }_{C_a}+\mu \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -{\sigma }_{C_a}\hfill & \hfill {\sigma }_{C_n}+\mu \hfill \end{array}\right), \\ \eta =(\delta +\mu )(\tau +\mu )({\sigma }_{C_a}+\mu )({\sigma }_{C_n}+\mu ), \\ {\mathbf{V}}^{-1}=\left(\begin{array}{cccc}\hfill \frac{1}{\delta +\mu }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{\delta (1-\theta )}{(\delta +\mu )(\tau \mu )}\hfill & \hfill \frac{1}{\tau +\mu }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{({\sigma }_{C_n}+\mu )\delta (1-\theta )\tau }{\eta }\hfill & \hfill \frac{\tau }{(\tau +\mu )({\sigma }_{C_a}+\mu )}\hfill & \hfill \frac{1}{{\sigma }_{C_a}+\mu }\hfill & \hfill 0\hfill \\ \hfill \frac{\delta (1-\theta )\tau {\sigma }_{C_a}\zeta }{\eta }\hfill & \hfill \frac{(\delta +\mu )\tau {\sigma }_{C_a}\zeta }{\eta }\hfill & \hfill \frac{{\sigma }_{C_a}\zeta }{({\sigma }_{C_a}+\mu )({\sigma }_{C_n}+\mu )}\hfill & \hfill \frac{1}{{\sigma }_{C_n}+\mu }\hfill \end{array}\right) \end{gathered}$$

The basic reproductive number is defined as the spectral radius of FV⁻¹. Given that FV⁻¹ has only one non-zero eigenvalue, with corresponding eigenvector e = [1, 0, 0, 0]^T, we get

$$\begin{gathered} R_0=\rho ({\mathbf{FV}}^{-1})=\beta \left(\frac{1}{\delta +\mu }+\frac{{\chi }_0\delta (1-\theta )}{(\delta +\mu )(\tau +\mu )}+\frac{{\chi }_0\delta (1-\theta )\tau }{(\delta +\mu )(\tau +\mu )({\sigma }_{C_a}+\mu )} \\ +\frac{{\chi }_0\delta (1-\theta )\tau {\sigma }_{C_a}\zeta }{(\delta +\mu )(\tau +\mu )({\sigma }_{C_a}+\mu )({\sigma }_{C_n}+\mu )}\right) \end{gathered}$$ (3)

Using Eq. (3), the equilibrium threshold can be calculated with any zero-finding algorithm. For ranges between 0 and 100 per 100 PWID per year in both the testing and treatment parameters (τ and σ), we determined the analytical approximation for the stability threshold and plotted the results overlaid on top of the numerical estimation in Fig. 4b (dotted line), overlaid on the numerical estimate of r₀ for the disease-free solution in the full multigroup model.

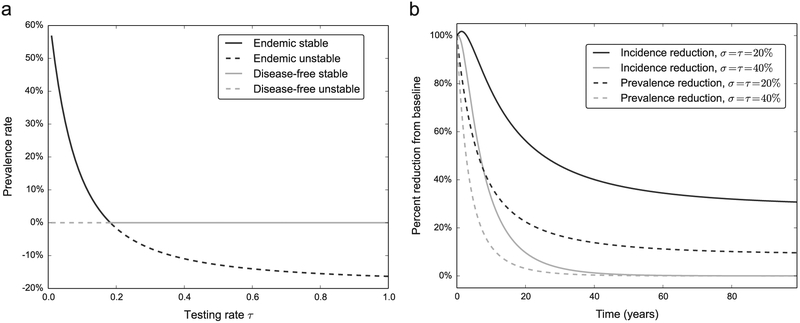
The stability of the endemic solution was determined by generating a bifurcation diagram for the full multigroup model, with the testing rate τ as the free parameter. Starting with the endemic solution with a σ = 0.4 and τ = 0.14, a pseudo arc-length continuation algorithm (Keller, 1987) followed the endemic solution. In this parameter set, when τ ≃ 0.2 a transcritical bifurcation occurs and the endemic and disease-free solutions exchange stability. Consequently, an unstable endemic solution with negative prevalence values will coexist with the now stable disease-free solution (Fig. 5a).

Fig. 5.

Solutions on both sides of the endemic threshold. (a) Bifurcation diagram showing the exchange of stability between the disease-free equilibrium and the endemic equilibrium when undergoing a transcritical bifurcation. The treatment rate parameter is fixed at σ = 0.4 on these curves for a varying testing rate. (b) Change in incident cases and prevalence rate with τ and σ in both sides of the endemic equilibrium (dark lines are endemic stable, gray lines are disease-free stable). As expected, both the number of incident cases and the prevalence rate drop to zero in the disease-free scenario (gray lines), and remain above zero.

We looked at the effect on the number of incident cases and the prevalence rate in the PWID population of interventions that increase the testing and treatment rates; τ and σ were chosen to be both below the endemic threshold (stable endemic) and above the endemic threshold (stable disease-free) (Fig. 5b). Both interventions are significantly above the baseline level of σ = 0.008 and τ = 0.14, therefore in all scenarios we observe reductions in the number of incident cases and the prevalence rate, however when τ and σ lie above the stability threshold in Fig. 4b, both epidemic parameters drop to zero. It is worth noting that the number of incident cases below the epidemic threshold (solid dark line) shows a spike above the baseline level in the first three years. This is due to the fact that the population that is cured can become reinfected and the sudden increase in the susceptible population results in a temporary increase in incident cases.

3.3. Sensitivity analysis

We performed a univariate sensitivity analysis with r₀ as the target variable. The sensitivity coefficients measure relative changes in the target variable subject to changes in the model parameters. The magnitude of the coefficient reflects how sensitive the target variable is to changes in a specific parameter, and the sign of the coefficient establishes a positive or negative association. The coefficients were determined in parameter sets that result in both a stable and unstable disease-free equilibrium (the testing and treatment rate parameters [τ, σ] fixed at [0.5, 0.2] and [0.5,0.7], which yield r₀=0.040 and r₀ = −0.074, respectively). For a parameter p, the sensitivity parameter is determined by the formula

$$S_{r_0,p}=\frac{p}{r_0}\frac{\mathrm{d}{r}_0}{\mathrm{d}p}.$$ (4)

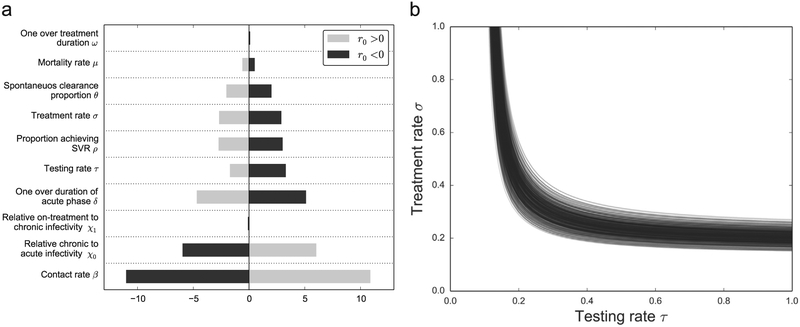
The sensitivity coefficients were calculated from the numerical algorithm used to calculate r₀ for the full multigroup model. Fig. 6a shows the sensitivity coefficients for the ten most sensitive parameters.

Fig. 6.

Sensitivity analysis when determining r₀. (a) The sensitivity parameter when calculating r₀ (Eq. (4)) with model parameters for both a stable and unstable disease-free equilibrium. (b) We performed 500 runs calculating the stability threshold r₀ = 0 on the (τ, σ) parameter space using Latin hypercube sampling on the parameter ranges from Table 1.

In order to characterize the uncertainty in our parameter estimations, we performed a multivariate sensitivity calculation; we did 500 numerical calculations of the stability threshold based on Latin hypercube sampling of the parameter uncertainty ranges in Table 1. The resulting curves are shown in Fig. 6b.

4. Discussion and conclusions

In this paper we presented a deterministic mathematical model of HCV transmission, with fibrosis progression taken into consideration. The model simulates realistic features of the HCV epidemic among PWID, including reinfection, time to diagnosis, and risk reduction after successfully clearing the disease. We described the existence of both disease-free solution and endemic solutions, independent of initial conditions. We derived an analytical approximation of the basic reproductive number R₀ of the disease-free solution, which had a high agreement with the numerical approximation to the stability threshold on the full system. Simulating the new DAA treatments, we determined the parameter space of treatment and testing rates that would result in an r₀ < 0 (R₀ < 1), ultimately leading to the eradication of HCV. The stability of the disease-free solution was analyzed with respect to the testing and treatment rates (τ and σ respectively), and we generated a complete picture in the (τ, σ) parameter space of the regions where the disease-free solution was stable and unstable. From a parameter set where the endemic solution was stable, we generated a bifurcation diagram with the testing rate τ as the bifurcation parameter and found that the endemic solution exchanges stability with the disease-free solution across the stability threshold r₀ = 0 via a transcritical bifurcation.

The analytical approximation in Eq. (3) showed that the R₀ parameter depends linearly on the contact rate β, and in the univariate sensitivity analysis it showed up as the most sensitive parameter, followed by the duration of the acute phase. From a policy perspective, this shows that efforts to reduce the contact rate, e.g. via harm reduction efforts, will have a big effect in pushing the disease into the eradication window. We assumed that infected individuals are most infective during the acute phase, therefore detecting and treating individuals in the acute phase will have a large effect on the epidemic. It has also been shown that individuals treated early have the best outcomes (Jaeckel et al., 2001).

It is important to discuss the limitations of this model. Continuous deterministic models such as this one present a number of caveats: homogeneous mixing across compartments does not account for high and low risk behavior among PWID, this is a feature that can be added to the model at a later point, and it was shown in Martin et al. (2013) that the gap between high and low risk for transmission in Vancouver is relatively small compared to other cities (1.4–0.4, versus 3.6–0.4 for Edinburgh and Melbourne); residence times across compartments are distributed exponentially, and the continuous nature of the model makes it unsuitable for modeling small populations. We added heterogeneity to the model by separating the major compartments according to fibrosis level, mortality rates increase significantly with increased fibrosis levels, and treatment policies often use the fibrosis level as a determinant for treatment. The model does not specifically account for patients developing resistance to the treatments, becoming immune after spontaneously clearing the disease, or developing super-infections, but the results from the multivariate sensitivity analysis (Fig. 6b) show a relatively narrow stability threshold band, implying that the results from the model will not vary much even if a moderate number of individuals are subject to either of those conditions. Other known vectors of HCV transmission are unsafe therapeutic injections and contaminated blood transfusions, in which our model does not account for, since the focus is on the PWID population, and it was assumed that most HCV infections among PWID are due to unsafe drug use.

The model was calibrated with data from PWID cohorts in British Columbia, Canada, where HCV prevalence is around 65%. The baseline data for the testing and treatment rates for 2012 was of 0.8% and 14%, respectively. The characteristics of the new DAA treatments will make it possible to treat more PWID individuals, and our simulations provide thresholds to aim for (Fig. 4) in order to eradicate the HCV epidemic. Our model showed that besides increasing treatment coverage, decreasing the time to access treatment is crucial for destabilizing the endemic solution, eventually leading to the eradication of the HCV epidemic.

HIGHLIGHTS.

• We developed a deterministic compartmental model of HCV disease transmission.

• The model targets people who inject drugs, explicitly tracking the fibrosis level.

• We determined the stability of the model, both numerically and analytically.

• By increasing testing and treatment we could potentially eradicate the epidemic.