TensorView: A Software Tool for Displaying NMR Tensors

Abstract

The representation of NMR tensors as surfaces on three-dimensional molecular models is an information-rich presentation that highlights the geometric relationship between tensor principal components and the underlying molecular and electronic structure. Here we describe a new computational tool, TensorView, for depicting NMR tensors on the molecular framework. This package makes use of the graphical interface and built-in molecular display functionality present within the Mathematica programming environment and is robust for displaying tensor properties from a broad range of commercial and user-specific computational chemistry packages. Two mathematical forms for representing tensor interaction surfaces are presented, the popular ellipsoidal construct and the more technically correct “ovaloid” form. Examples are provided for chemical shielding and shift tensors, dipole-dipole and quadrupolar couplings, and atomic anisotropic displacement parameters (thermal ellipsoids) derived from NMR crystallography.

Graphical Abstract

Introduction

Visualizing NMR tensors as surfaces on molecular models is an information-rich presentation that highlights the geometric relationship between tensor principal components and essential aspects of the underlying molecular and electronic structure [1–10]. These relationships are particularly important in applications of “NMR-assisted crystallography,” which often combine solid-state nuclear magnetic resonance with computational methods to build and test atomic-resolution models of structure and dynamics [11–25]. Enabling these computationally-aided approaches has been the remarkable success of first-principles computational chemistry at modeling solid-state structure and calculating – with high accuracy – the corresponding NMR properties such as chemical shielding/shift, and dipole-dipole, J, and quadrupolar couplings [15,26–34]. The anisotropic nature of these tensor properties provides a critical link between the orientation of the molecular frame, to which these properties are tied, and NMR observables measured in the laboratory frame.

Here we describe a new software tool for depicting NMR tensors on three-dimensional molecular models. This package, TensorView, makes use of the graphical interface, tools, and molecular display functionality present within the Mathematica programming environment [35], combined with user input of interaction tensors and molecular coordinates. TensorView is not an automated program for displaying tensors generated in computational packages, but involves direct, relatively straightforward input and modification by the user. The merit of this approach is that with some basic familiarity with Mathematica, users can display tensor properties from a broad range of commercial and user‐specific computational chemistry packages – all that is required is a molecular coordinate file (in a standard format) and the matrix representation of the tensor in the same coordinate frame.

Several general features that are important to the description and display of second-rank Cartesian tensors are first discussed using the chemical shielding interaction as an example. These include the mathematical form of the corresponding term in the NMR Hamiltonian, conventions regarding the principal axis system (PAS), and the uniqueness of Euler angle parameterizations that relate the PAS and molecular frames. Two options for representing tensor surfaces are presented, the popular ellipsoidal construct [1] and the more technically correct “ovaloid” form [2,3,6,7]. Abbreviated examples for the chemical shift, dipole-dipole, and quadrupolar interactions are then presented, followed by considerations for displaying atomic anisotropic displacement parameters derived from NMR crystallography experiments [36,37].

Given the important link between molecular/electronic structure and NMR tensor properties, a number of programs for displaying tensors have been developed [4–6,9,10]. In addition, many groups have developed in-house software or adapted other programs for this purpose. Our goals with TensorView are to provide the following: a well-documented, easy-to-use computational environment for displaying NMR tensors regardless of which programs (or experiments) were used to generate them; the option for displaying tensors in either the ellipsoidal or ovaloid form; and the flexibility to adapt to new applications. Displaying atomic anisotropic displacement parameters with TensorView began as one instance of the latter [37].

Graphical Representation of Second-Rank Cartesian Tensors: Chemical Shielding as Example

In this section we derive the equation for a chemical shielding surface in terms of the tensor principal components and the orientation of the principal axis system (PAS) relative to the molecular frame. Our goal is an equation for the shielding surface written in the molecular coordinate frame so that it can be graphed directly on three-dimensional structural models.

Chemical Shielding Hamiltonian

The chemical shielding interaction results from currents in the electron density induced by the external magnetic field, which in turn produce an additional magnetic field that interacts with a nuclear spin. This interaction is described by the following term in the NMR Hamiltonian (written in the laboratory frame), [38]

$$\begin{gathered} H_{\text{CS}}/\hslash =\gamma \overrightarrow{I}\cdot \mathbf{\sigma }\cdot \overrightarrow{B} \\ =\gamma \left(\begin{array}{ccc}{I}_x& I_y& I_z\end{array}\right)\cdot \left(\begin{array}{ccc}{\sigma }_{xx}& {\sigma }_{xy}& {\sigma }_{xz}\\ {\sigma }_{yx}& {\sigma }_{yy}& {\sigma }_{yz}\\ {\sigma }_{zx}& {\sigma }_{zy}& {\sigma }_{zz}\end{array}\right)\cdot \left(\begin{array}{c}0\\ 0\\ B_z\end{array}\right), \\ =\gamma \left(I_x{\sigma }_{xz}{B}_z+I_y{\sigma }_{yz}{B}_z+I_z{\sigma }_{zz}{B}_z\right) \\ \stackrel{\begin{array}{l}\text{secular}\\ \text{approx}\end{array}}{=}\gamma B_z{\sigma }_{zz}{I}_z={\omega }_0{\sigma }_{zz}{I}_z \end{gathered}$$ (1)

where γ is the gyromagnetic ratio, $\overrightarrow{I}$ is the spin angular momentum vector operator, σ is the chemical shielding tensor (a second-rank Cartesian tensor [39]), and $\overrightarrow{B}$ is the static magnetic field, which defines the laboratory-frame z-axis. In the final line, the secular approximation [40] has been taken, in which the components that do not commute with the Zeeman interaction are discarded. This leads to a spectral frequency that is proportional to ${\sigma }_{zz}$, the zz-component of the shielding tensor in the laboratory frame.

The chemical shielding interaction is anisotropic, it depends not only on the local chemical and electronic structure, but also on orientation in the magnetic field. The shielding tensor (like all tensors we will consider here) is fixed relative to the molecular frame. When the molecule reorients, the laboratory-frame components of this tensor are modulated and the spectral frequency changes. One useful way to visualize the chemical shielding tensor is to draw a surface rigidly attached to the molecular framework so that the distance from the tensor/atom center to any point on the surface is equal to the shielding when the magnetic field is applied along that direction in space. This is what we are representing when we draw a shielding surface on a molecular model such as the example shown in Figure 1A.

Figure 1:

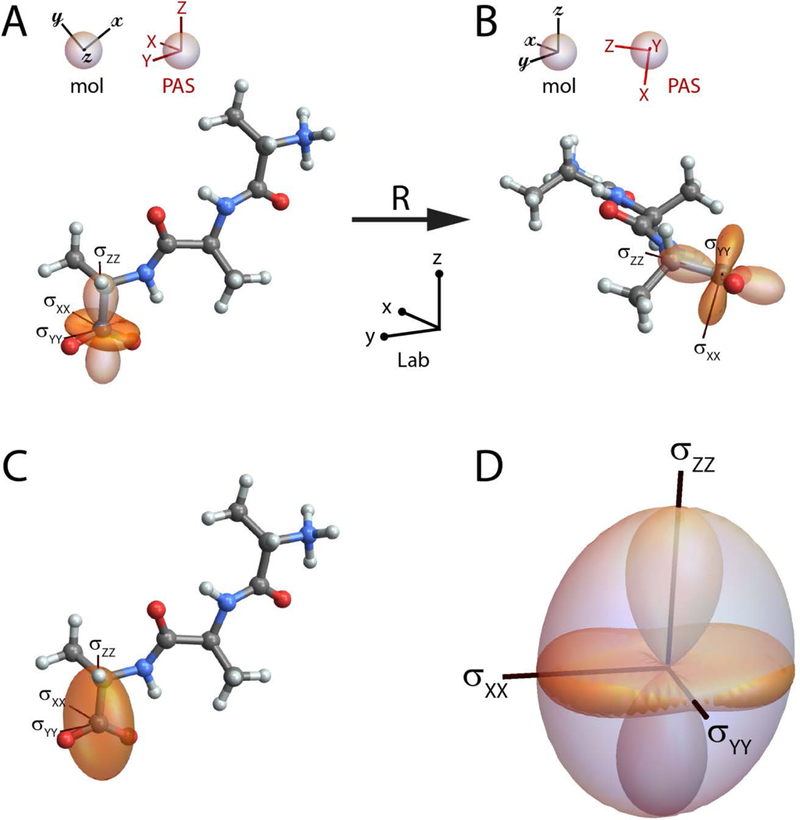
(A) The chemical shielding surface for the carboxylate carbon in the tripeptide Ala-Ala-Ala. The shielding surface is shown using the ovaloid representation, in which the radius from the center of the tensor to a point on the surface is proportional to the chemical shielding when the magnetic field is aligned along that direction in space; the sign of the shielding is indicated by the shading of the surface (orange is positive, light orange is negative). In (A) the principal axes (with principal components σ_XX=66.8 ppm, σ_YY=43.7 ppm, and σ_ZZ=−83.2 ppm) are aligned with the laboratory frame, while in (B) the tripeptide has been rotated to align the molecular (mol) and laboratory frames. (C) The ellipsoidal representation of the carboxylate shielding tensor. (D) Overlay of the ovaloid and ellipsoidal shielding surfaces; the principal axis system and magnitude of the principal components are preserved in the ellipsoidal representation, but the precise correspondence of the surface with shielding is lost. All molecular models are drawn with atom types designated using the standard CPK color scheme (H, white; C, gray; N, blue; O, red).

Principal Axis System and Euler Angle Conventions

The chemical shielding tensor contains 9 independent elements,

$$\mathbf{\sigma }=\left(\begin{array}{ccc}{\sigma }_{xx}& {\sigma }_{xy}& {\sigma }_{xz}\\ {\sigma }_{yx}& {\sigma }_{yy}& {\sigma }_{yz}\\ {\sigma }_{zx}& {\sigma }_{zy}& {\sigma }_{zz}\end{array}\right),$$ (2)

and can be decomposed into symmetric and antisymmetric parts

$$\begin{gathered} \mathbf{\sigma }={\mathbf{\sigma }}^S+{\mathbf{\sigma }}^A \\ {\mathbf{\sigma }}^S=\frac{1}{2}\left(\mathbf{\sigma }+{\mathbf{\sigma }}^T\right)=\left(\begin{array}{ccc}{\sigma }_{xx}& \frac{1}{2}\left({\sigma }_{xy}+{\sigma }_{yx}\right)& \frac{1}{2}\left({\sigma }_{xz}+{\sigma }_{zx}\right)\\ \frac{1}{2}\left({\sigma }_{xy}+{\sigma }_{yx}\right)& {\sigma }_{yy}& \frac{1}{2}\left({\sigma }_{yz}+{\sigma }_{zy}\right)\\ \frac{1}{2}\left({\sigma }_{xz}+{\sigma }_{zx}\right)& \frac{1}{2}\left({\sigma }_{yz}+{\sigma }_{zy}\right)& {\sigma }_{zz}\end{array}\right) \\ {\mathbf{\sigma }}^A=\frac{1}{2}\left(\mathbf{\sigma }-{\mathbf{\sigma }}^T\right)=\left(\begin{array}{ccc}0& \frac{1}{2}\left({\sigma }_{xy}-{\sigma }_{yx}\right)& \frac{1}{2}\left({\sigma }_{xz}-{\sigma }_{zx}\right)\\ -\frac{1}{2}\left({\sigma }_{xy}-{\sigma }_{yx}\right)& 0& \frac{1}{2}\left({\sigma }_{yz}-{\sigma }_{zy}\right)\\ -\frac{1}{2}\left({\sigma }_{xz}-{\sigma }_{zx}\right)& -\frac{1}{2}\left({\sigma }_{yz}-{\sigma }_{zy}\right)& 0\end{array}\right) \end{gathered}$$ (3)

where σ^T is the transpose of σ. σ^A does not contribute to the observed spectral frequency – its zz-component is zero for all orientations of the molecule – so the antisymmetric components are often ignored. When a chemical shielding tensor is input into TensorView, it is symmetrized, and below we assume we are working only with the symmetric form.

Because the symmetric part of the shielding tensor is also Hermitian, it has real eigenvalues and a complete, orthonormal basis (i.e., coordinate system) in which the tensor is diagonal. These are referred to as the principal components (PC) and the principal axis system (PAS), respectively, and correspond to the axes shown on the shielding surfaces in Figure 1. There are two popular conventions for labeling the principal components of the shielding tensor [41]. In the “Mehring” convention, [1] the components are labeled ${\sigma }_{\text{11}},{\sigma }_{\text{22}},\text{and}{\sigma }_{\text{33}}$ and ordered with ${\sigma }_{\text{11}}\le {\sigma }_{\text{22}}\le {\sigma }_{\text{33}}$. This gives the following shielding tensor in the PAS

$${\mathbf{\sigma }}_{\text{M}}^{\text{PAS}}=\left(\begin{array}{ccc}{\sigma }_{11}& 0& 0\\ 0& {\sigma }_{22}& 0\\ 0& 0& {\sigma }_{33}\end{array}\right).$$ (4)

In the “Haeberlen” convention, the components are designated ${\sigma }_{\text{XX}},{\sigma }_{\text{YY}},\text{and}{\sigma }_{\text{ZZ}}$ and ordered such that $\left|{\sigma }_{\text{YY}}-{\sigma }_{\text{iso}}\right|\le \left|{\sigma }_{\text{XX}}-{\sigma }_{\text{iso}}\right|\le \left|{\sigma }_{\text{ZZ}}-{\sigma }_{\text{iso}}\right|$, where ${\sigma }_{\text{iso}}=\frac{1}{3}\left({\sigma }_{\text{XX}}+{\sigma }_{\text{YY}}+{\sigma }_{\text{ZZ}}\right)$ is the isotropic shielding [40]. It is customary that uppercase letters designate the PAS frame, while the lowercase letters in Equations (1)–(3) indicate the lab frame. In the Haeberlen convention,

$${\mathbf{\sigma }}_{\text{H}}^{\text{PAS}}=\left(\begin{array}{ccc}{\sigma }_{XX}& 0& 0\\ 0& {\sigma }_{YY}& 0\\ 0& 0& {\sigma }_{ZZ}\end{array}\right),$$ (5)

which may have elements swapped relative to ${\mathbf{\sigma }}_{\text{M}}^{\text{PAS}}$. In TensorView, the user chooses either “Mehring” or “Haeberlen” for the PAS convention, which sets the PC and axis labels accordingly.

The PAS and molecular frames have a fixed relative orientation. Figure 1A is drawn with the PAS aligned with the laboratory frame, while Figure 1B shows the molecular and laboratory frames aligned. The molecular frame is arbitrary, in that a different orientation could have been used to specify the coordinates for the first-principles calculation. But whatever orientation was used to calculate the interaction tensor is taken from that point on to define the molecular frame. The molecules in Figures 1A and 1B are related by a rotation, defined by a matrix R, that acts on the initial lab-frame atomic coordinates, $\overrightarrow{q}$, to give the final lab-frame coordinates, ${\overrightarrow{q}}^{\prime }$

$${\overrightarrow{q}}^{\prime }=\mathbf{R}\overrightarrow{q}.$$ (6)

The components of the chemical shielding tensor viewed in the laboratory frame are different for these two orientations, but given the initial lab-frame shielding tensor, σ, and the rotation matrix, the transformed shielding tensor, ${\mathbf{\sigma }}^{\prime }$, can be calculated

$${\mathbf{\sigma }}^{\prime }=\mathbf{R}\mathbf{\sigma }{\mathbf{R}}^{-1}.$$ (7)

When two coordinate frames are coincident, the components of the shielding tensor written in both frames are equal. This allows the two lab-frame shielding tensors in Figures 1A and 1B to be equated with σ = σ^PAS and σ′ = σ^mol, respectively, in Equation (7).

Equation (6) completely determines the rotation matrix R in terms of the 9 matrix elements that take vector $\overrightarrow{q}$ to ${\overrightarrow{q}}^{\prime }$. This rotation can be parameterized in terms of a rotation matrix operator and a set of 3 Euler angles, $\mathrm{\Omega }=\left\{\alpha ,\beta ,\gamma \right\}$. There is considerable confusion in the literature regarding the various conventions and corresponding forms for the rotation operator, and a detailed discussion of this topic is given in our earlier paper on tensors and rotations in NMR [42] and by Bouten [43], who points out several well-hidden errors in classic texts. TensorView makes use of the right-handed, active rotation convention to describe the rotation and orientation of an object defined by the positon of its body-fixed axes (XYZ) relative to a stationary, space-fixed reference frame (xyz; Figure 2). The Euler angles $\mathrm{\Omega }=\left\{\alpha ,\beta ,\gamma \right\}$ parameterize this transformation in terms of three successive rotations about the object’s body-fixed axes as shown in the upper pathway of Figure 2. From initial coincidence of the two frames, the object is first rotated about its body-fixed Z-axis by angle α, using a right-hand rule in which a positive rotation angle results in counterclockwise motion about the axis. Next, the object is rotated about its body-fixed Y-axis (in its new orientation in the space-fixed frame) by angle β. Finally, the object is rotated about its body-fixed Z-axis (in its final orientation) by angle γ. For completeness, it is noted that this same net transformation can be recast in terms of three successive rotations performed entirely with respect to the space-fixed axes (Figure 2, lower path): first a rotation about the z-axis by angle γ; second, a rotation about the space-fixed y axis by angle β; third, a rotation about the space-fixed z axis by angle α. The body-fixed and space-fixed rotations are rigorously equivalent [44], and both are parameterized by the same Euler angles $\mathrm{\Omega }=\left\{\alpha ,\beta ,\gamma \right\}$. Which perspective is more natural will depend on context, but in either case the rotation operator R is given by

$$\mathbf{R}={\mathbf{R}}_{\text{A}}\left(\alpha ,\beta ,\gamma \right)=\left(\begin{array}{ccc}\cos \alpha \cos \beta \cos \gamma -\sin \alpha \sin \gamma & -\cos \alpha \cos \beta \sin \gamma -\sin \alpha \cos \gamma & \cos \alpha \sin \beta \\ \sin \alpha \cos \beta \cos \gamma +\cos \alpha \sin \gamma & -\sin \alpha \cos \beta \sin \gamma +\cos \alpha \cos \gamma & \sin \alpha \sin \beta \\ -\sin \beta \cos \gamma & \sin \beta \sin \gamma & \cos \beta \end{array}\right).$$ (8)

Figure 2:

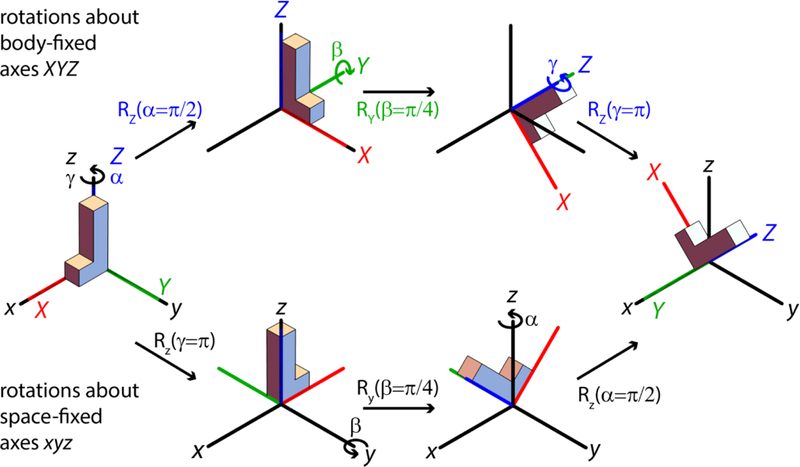
TensorView makes use of the active rotation convention to describe the rotation and orientation of an object defined by the final position of its body-fixed axes (XYZ) relative to a stationary, space-fixed reference frame (xyz). The Euler angles $\mathrm{\Omega }=\left\{\alpha ,\beta ,\gamma \right\}$ parameterize this transformation by the three successive rotations shown along the upper pathway: first an α-rotation about the object’s body-fixed Z-axis (using a right-hand rule); second, a β-rotation about its body-fixed Y-axis (in its new orientation in the space-fixed frame); third, a γ-rotation about its body-fixed Z-axis (in its final orientation). The same net transformation can be effected by three successive rotations performed entirely with respect to the space-fixed axes (bottom path): first, a γ-rotation about the z-axis; second a β-rotation about the space-fixed y axis; and finally an α-rotation about the space-fixed z axis. It is important to note the inversion in order for the α and γ rotations along the space-fixed pathway.

To determine the relative orientation of the PAS and molecular frames, TensorView first solves for and orders the PC, and then searches for the Euler angles that take the shielding tensor from its initial orientation with the PAS and laboratory frames aligned (σ = σ^PAS ; Figure 1A) to its final orientation with respect to the coincident laboratory and molecular frames (σ′ = σ^mol; Figure 1B),

$${\mathbf{\sigma }}^{\text{mol}}={\mathbf{R}}_{\text{A}}\left(\alpha ,\beta ,\gamma \right){\mathbf{\sigma }}^{\text{PAS}}{\mathbf{R}}_{\text{A}}^{-1}\left(\alpha ,\beta ,\gamma \right).$$ (9)

The solution to this equation, and therefore the choice of PAS in the molecular frame, is not unique. Figure 3 illustrates the problem: while the alignment of the principal axes (the lines they fall on) are well-defined, the orientations (direction of the axes) are not – even with the constraint that they satisfy the right-hand rule. In general, for any solution $\left\{\alpha ,\beta ,\gamma \right\}$ to equation (9), the sets of Euler angles $\left\{\alpha ,\beta ,\gamma +\pi \right\}$, $\left\{\alpha +\pi ,\pi -\beta ,\pi -\gamma \right\}$, and $\left\{\alpha +\pi ,\pi -\beta ,2\pi -\gamma \right\}$ are also solutions. This means that the orientation of the same tensor can be described by four sets of Euler angles, each giving a different principal axis system. By default, TensorView searches for the PAS defined by Euler angles in the range $0\le \alpha \le 2\pi ,0\le \beta \le \frac{\pi }{2},\text{and}0\le \gamma \le \pi$. The user can modify these in the global settings at the top of the notebook.

Figure 3:

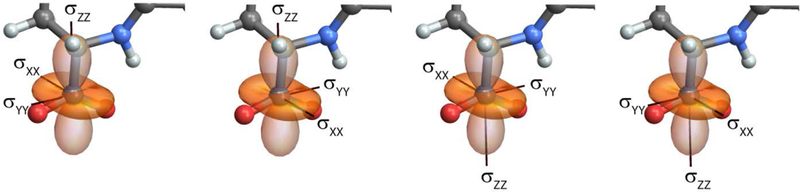
Four choices for the PAS in the molecular frame. The default in TensorView is to choose the PAS defined by Euler angles in the range $0\le \alpha \le 2\pi ,0\le \beta \le \frac{\pi }{2},\text{and}0\le \gamma \le \pi$.

Shielding Surfaces as Ovaloids and Ellipsoids

It is the tensor’s laboratory-frame zz-component that determines the spectral frequency. For a molecule in which the molecular and lab frames are aligned (Figure 1B), the zz-component is given by

$$\begin{gathered} {\sigma }_{\text{zz}}={\left[{\mathbf{R}}_{\text{A}}\left(\alpha ,\beta ,\gamma \right){\mathbf{\sigma }}^{\text{PAS}}{\mathbf{R}}_{\text{A}}^{-1}\left(\alpha ,\beta ,\gamma \right)\right]}_{zz} \\ ={\sigma }_{ZZ}{\cos }^2\beta +{\sigma }_{XX}{\sin }^2\beta {\cos }^2\gamma +{\sigma }_{YY}{\sin }^2\beta {\sin }^2\gamma \end{gathered}$$ (10)

where $\mathrm{\Omega }=\left\{\alpha ,\beta ,\gamma \right\}$ are the Euler angles that parametrize the orientation of the PAS as viewed from within the molecular/lab frame. One approach to turning this into an equation for the full shielding surface is to recognize that the value of the surface at polar angles (θ,φ), defined relative to an origin at the atom/tensor center, corresponds to the zz-component that the shielding tensor would have if this new axis were aligned with the laboratory z-direction. This can be accomplished by rotating the shielding tensor back by the same angles, (θ,φ), giving the following equation for the shielding surface in the molecular coordinate frame:

$$\begin{gathered} S\left(\theta ,\phi \right)={\left[{\mathbf{R}}_{\text{A}}^{-1}\left(\phi ,\theta ,0\right){\mathbf{R}}_{\text{A}}\left(\alpha ,\beta ,\gamma \right){\mathbf{\sigma }}^{\text{PAS}}{\mathbf{R}}_{\text{A}}^{-1}\left(\alpha ,\beta ,\gamma \right){\mathbf{R}}_{\text{A}}\left(\phi ,\theta ,0\right)\right]}_{zz} \\ ={\sigma }_{XX}{\left[\sin \beta \cos \gamma \cos \theta +\sin \gamma \sin \left(\alpha -\phi \right)\sin \theta -\cos \beta \cos \gamma \cos \left(\alpha -\phi \right)\sin \theta \right]}^2+ \\ {\sigma }_{YY}{\left[\sin \beta \sin \gamma \cos \theta +\cos \gamma \sin \left(\alpha -\phi \right)\sin \theta -\cos \beta \sin \gamma \cos \left(\alpha -\phi \right)\sin \theta \right]}^2+ \\ {\sigma }_{ZZ}{\left[\cos \beta \cos \theta +\cos \left(\alpha -\phi \right)\sin \beta \sin \theta \right]}^2 \end{gathered}$$ (11)

This is the shielding surface shown in Figures 1A and 1B. This form for the shielding surface has been noted by multiple authors [2,3,6] (although not always written down explicitly) and is exact – it is derived from the chemical shielding tensor, and the value that the surface takes (i.e., the radius from the origin to the surface) is proportional to the true shielding for a static magnetic field aligned along that direction in space.

Figures 1A and 1B show the chemical shielding surface (Equation (11)) for the terminal carboxylate in the tripeptide Ala-Ala-Ala. This first-principles shielding tensor was calculated in Gaussian09 using the “NMR” keyword and the Gaussian output and molecular structure files are included in the Supplementary Material. The tensor has principal values σ_XX=66.8 ppm, σ_YY=43.7 ppm, and σ_ZZ=−83.2 ppm, labeled in the Haeberlen convention. The functional form for the shielding surface in Equation (11) can accommodate both positive and negative principal components, as reflected in the change in shading and zero-crossings for the shielding surface. As pointed out by Radeglia, the shielding surface can be thought of as the addition of three perpendicular unit bodies (one for each of the principal components) that have the shape of the squared p-orbitals and are weighted by the principal components [3]. Radeglia refers to the shape of the shielding surface as an “ovaloid,” although a general mathematical definition for an ovaloid does not appear to have been universally agreed upon. Even still, we adopt this terminology here and in the TensorView notebook. For reference, the Supplementary Material includes a pictorial dictionary of ovaloid surfaces with varying principal components (both magnitude and sign).

The ovaloid representation of the shielding surface has not been as widely adopted for displaying tensors as the “ellipsoidal” representation popularized by Mehring [1]. The ellipsoidal form is not exact, but does provide a useful and perhaps slightly less cluttered visualization of the tensor and PAS. In this representation, the principal axes of the tensor are aligned along the axes of a three-dimensional ellipsoid. In the PAS, the equation for the ellipsoidal surface is

$$\frac{X^2}{{\sigma }_{XX}^2}+\frac{Y^2}{{\sigma }_{YY}^2}+\frac{Z^2}{{\sigma }_{ZZ}^2}=1.$$ (12)

The corresponding ellipsoidal shielding surface in spherical coordinates, $S_{\text{PAS}}^{\text{E}}\left(\theta ,\phi \right)$, can be derived by substituting the spherical form of the Cartesian coordinates into (12) and solving for the radius,

$$S_{\text{PAS}}^{\text{E}}\left(\theta ,\phi \right)=\frac{\left|{\sigma }_{XX}{\sigma }_{YY}{\sigma }_{ZZ}\right|}{\sqrt{{\sigma }_{XX}^2{\sigma }_{YY}^2{\cos }^2\theta +{\sigma }_{YY}^2{\sigma }_{ZZ}^2{\sin }^2\theta {\cos }^2\phi +{\sigma }_{XX}^2{\sigma }_{ZZ}^2{\sin }^2\theta {\sin }^2\phi }}.$$ (13)

In the molecular frame, the ellipsoidal surface is rotated, but the functional form can again be found by rotating the coordinate system in the opposite sense. This gives in Cartesian coordinates

$$\begin{gathered} 1=\frac{{\left[x\left(\cos \alpha \cos \beta \cos \gamma -\sin \alpha \sin \gamma \right)+y\left(\sin \alpha \cos \beta \cos \gamma +\cos \alpha \sin \gamma \right)-z\sin \beta \cos \gamma \right]}^2}{{\sigma }_{XX}^2}+ \\ \frac{{\left[-x\left(\cos \alpha \cos \beta \sin \gamma +\sin \alpha \cos \gamma \right)+y\left(-\sin \alpha \cos \beta \sin \gamma +\cos \alpha \cos \gamma \right)+z\sin \beta \sin \gamma \right]}^2}{{\sigma }_{YY}^2}+ \\ \frac{{\left[x\cos \alpha \sin \beta \cos \gamma +y\sin \alpha \sin \beta +z\cos \beta \right]}^2}{{\sigma }_{ZZ}^2} \end{gathered}$$ (14)

with the corresponding shielding surface in spherical coordinates

$$\begin{array}{l}{S}^{\text{E}}\left(\theta ,\phi \right)=\left|{\sigma }_{XX}{\sigma }_{YY}{\sigma }_{ZZ}\right|/\{{\sigma }_{XX}^2{\sigma }_{YY}^2{\left[\cos \theta \cos \beta +\sin \theta \cos \left(\phi -\alpha \right)\sin \beta \right]}^2+\\ {\sigma }_{YY}^2{\sigma }_{ZZ}^2{\left[\sin \theta \cos \left(\phi -\alpha \right)\cos \beta \cos \gamma -\cos \theta \sin \beta \cos \gamma +\sin \theta \sin \left(\phi -\alpha \right)\sin \gamma \right]}^2+\\ {\sigma }_{XX}^2{\sigma }_{ZZ}^2{\left[-\sin \theta \cos \left(\phi -\alpha \right)\cos \beta \sin \gamma +\cos \theta \sin \beta \sin \gamma +\sin \theta \sin \left(\phi -\alpha \right)\cos \gamma \right]}^2{\}}^{1/2}\end{array}$$ (15)

The ellipsoidal shielding surface for the Ala-Ala-Ala carboxylate is shown in Figure 1C. Again, it is emphasized that the ellipsoidal representation is not exact – the radius from the origin to the surface is no longer proportional to the true shielding for all directions in space. But the orientation of the PAS and the absolute values of the PC are still faithfully represented. Cases in which different PC have opposite signs are a particular problem for the ellipsoidal representation as this sign information is lost (Equation (15)), and the surface would be the same if the sign of any of the components were inverted. Mehring suggests adding a constant to all PC, which would give them the same sign [1]; we do not do that here to preserve the magnitudes of the PC and recommend the ovaloid form instead. Figure 1D shows an overlap of the ellipsoidal and ovaloid surfaces, emphasizing the equivalence of the PAS and magnitude of the PC, but also underscoring the dramatic differences between the surfaces.

The TensorView Mathematica Notebook

The graphics in Figure 1 were generated using the TensorView1.4.1.nb Mathematica notebook (Supplementary Material). Before moving on to additional examples, we take an introductory look at this notebook and the steps necessary to generate shielding surface plots. While a current Mathematica license is required to edit and run the notebook, the free Wolfram CDF player can be used to view it. To begin, it is assumed that the following are available as the result of a first-principles calculation:

1. The coordinates of the molecule or region of interest for an extended solid; we call the frame in which these coordinates are written the “molecular frame.” For TensorView, the coordinates need to be saved in a structure file that can be read into Mathematica. We make use of the protein data bank format (.pdb), but alternate formats such as XYZ molecular geometry (.xyz) and MDL MOL format (.mol/.mol2) can also be natively imported.

2. The tensor components in the same molecular frame. For first-principles calculations, this means that the NMR properties should be calculated on the coordinate/structure file supplied above. Note that programs such as Gaussian [45] may rotate input structures before properties are calculated, so consistency should be checked.

TensorView requires relatively straightforward input and modification by the user. Specifically, the first two cells in each section need to be edited to specify a new molecule, tensor, and display options; the final three cells are then executed to align the tensor and generate the display. The following summarizes the options and functions of each cell in the chemical shielding example; a screen shot of the first two cells is shown in Figure 4.

Figure 4:

The first two cells in the chemical shielding section of the TensorView notebook. Cell 1 specifies the directory location and structure file, tensor components, and the coordinates for placing the tensor. Cell 2 includes options for the PAS convention, tensor type, tensor scaling, and display colors. Only the first two cells in each section need to be edited; the remaining cells are then executed to align the tensor and generate the display. The full TensorView1.4.1.nb notebook is included in the Supplementary Material.

Cell 1: In the first cell, the following are specified:

• (a)The directory location and structure file. These are used to import the molecular structure as the graphics object, pMolecule.
• (b)The chemical shielding tensor elements, in the format XX = number; XY = number; …
• (c)The atomic coordinates for placing the tensor, atomcoord (in units of Å). Note that the working units for molecular structures in Mathematica are pm, so these values will eventually be converted.

Cell 2: In Cell 2, options are set for the following:

• (a)The PAS convention: PAS = “Haeberlen” or “Mehring”
• (b)The choice of chemical shift (Shift = True) or chemical shielding tensor (Shift = False). A reference value must be entered for the shift tensor (ref ).
• (c)The scaling of the tensor surface, where tensorscale is the length (in pm) of the largest tensor principal component.
• (d)The colors for the positive and negative shielding surfaces, the principal axes, and flags for displaying the PAS and PAS labels.

Cell 3: In cell 3, TensorView solves for the PC and the Euler angles that specify the orientation of the PAS in the molecular frame.

Cell 4: Evaluating this cell generates the ellipsoidal and ovaloid shielding surfaces as the graphics objects pShieldingTensorE and pShieldingTensorO, respectively.

Cell 5: In this final cell, graphics objects for the molecular structure and shielding surface(s) are combined and displayed using the Show[graphics_1, graphics_2, …] command. The output graphics can be manipulated using left-click and drag to rotate, with the addition of Ctrl and Shift for zoom and pan. Right-clicking brings up a menu with options for exporting graphics.

Additional Examples

TensorView can be adapted for the display of any second-rank tensor property. Additional examples are provided below for the chemical shift, quadrupolar coupling/electric field gradient, dipole-dipole coupling, and atomic anisotropic displacement parameters; options specific to a given interaction and several auxiliary TensorView functions are described.

Chemical Shift

Experimental NMR spectra are generally presented on the chemical shift scale relative to a standard compound, and the components of the chemical shift tensor (δ), not the shielding tensor (σ), reported. The two tensors are related through the isotropic shielding of a reference compound, [38]

$$\begin{gathered} \mathbf{\delta }={\sigma }_{\text{ref}}\mathbf{1}-\mathbf{\sigma } \\ =\left(\begin{array}{ccc}{\delta }_{xx}& {\delta }_{xy}& {\delta }_{xz}\\ {\delta }_{yx}& {\delta }_{yy}& {\delta }_{yz}\\ {\delta }_{zx}& {\delta }_{zy}& {\delta }_{zz}\end{array}\right)=\left(\begin{array}{ccc}{\sigma }_{\text{ref}}-{\sigma }_{xx}& -{\sigma }_{xy}& -{\sigma }_{xz}\\ -{\sigma }_{yx}& {\sigma }_{\text{ref}}-{\sigma }_{yy}& -{\sigma }_{yz}\\ -{\sigma }_{zx}& -{\sigma }_{zy}& {\sigma }_{\text{ref}}-{\sigma }_{zz}\end{array}\right) \end{gathered}$$ (16)

An appropriate reference must be specified to display a first-principles chemical shift tensor in TensorView. Ideally, this reference would be determined computationally at the same level of theory (i.e., method and basis set) as the shielding tensor [33]; when not available, reference values determined with similar computational parameters can be substituted. In TensorView, the principal axes for chemical shift are chosen to coincide with those for chemical shielding. This means that the ordering of the chemical shift PC is reversed in Mehring’s notation, with ${\delta }_{\text{11}}\ge {\delta }_{\text{22}}\ge {\delta }_{\text{33}}$, while the PC in Haeberlen’s notation still satisfy $\left|{\delta }_{\text{YY}}-{\delta }_{\text{iso}}\right|\le \left|{\delta }_{\text{XX}}-{\delta }_{\text{iso}}\right|\le \left|{\delta }_{\text{ZZ}}-{\delta }_{\text{iso}}\right|$.

Figure 5 shows the chemical shift tensor for the C-terminal carboxylate group of the tri-peptide Ala-Ala-Ala introduced above, using the ¹³C chemical shielding reference ${\sigma }_{\text{ref}}$ = 173 ppm from [33] to convert from chemical shielding to chemical shift on the TMS scale. In this case, the principal components are labeled using the Mehring convention and a different orientation of the PAS was purposefully chosen. Note that even though all principal components are positive, the ovaloid shielding surface still does not reduce to an ellipse but is “peanut” shaped. This is indeed the correct form of the shift surface. This display highlights the relationship between the chemical shift tensor and the underlying molecular/electronic framework, with δ₁₁ practically collinear with the C-C bond, and δ₃₃ nearly perpendicular to the carboxylate plane. Carboxylate tensors are sensitive to chemical environment, with δ₁₁ showing a characteristic change of +15 ppm upon protonation and δ₂₂ tracking hydrogen bonding; δ₃₃ and δ_iso show little variation with protonation state or hydrogen bonding [46].

Figure 5:

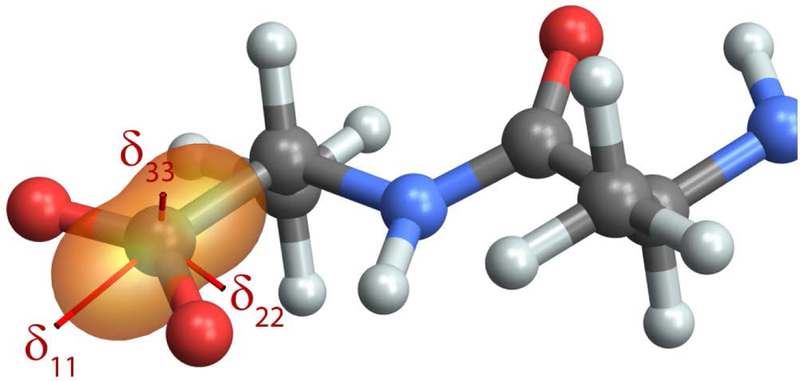
The first-principles chemical shift surface for the terminal carboxylate in Ala-Ala-Ala, calculated in Gaussian09. For carboxylate tensors, δ₁₁ and δ₂₂ show a characteristic response to protonation and hydrogen bonding, respectively, while δ₃₃ and δ_iso are relatively insensitive to chemical environment.

Quadrupolar Coupling and Electric Field Gradient Tensor

The non-spherical charge distribution of nuclei with spin greater than 1/2 gives rise to a nuclear electric quadrupole moment that interacts with the electric field gradient (EFG) at the nucleus. The energy of this interaction is described by the nuclear quadrupolar Hamiltonian [38]

$$\begin{gathered} H_{\text{Q}}^{}/\hslash =\frac{eQ}{2I\left(2I-1\right)\hslash }\overrightarrow{I}\cdot \mathbf{V}\cdot \overrightarrow{I} \\ =\frac{eQ}{2I\left(2I-1\right)\hslash }\left(\begin{array}{ccc}{I}_x& I_y& I_z\end{array}\right)\cdot \left(\begin{array}{ccc}{V}_{xx}& V_{xy}& V_{xz}\\ V_{yx}& V_{yy}& V_{yz}\\ V_{zx}& V_{zy}& V_{zz}\end{array}\right)\cdot \left(\begin{array}{c}{I}_x\\ I_y\\ I_z\end{array}\right), \\ \stackrel{\text{PAS}}{=}\frac{3eQ}{2I\left(2I-1\right)\hslash }{V}_{zz}\frac{3I_z^2-I\left(I+1\right)+\frac{V_{xx}-V_{yy}}{V_{zz}}\left(I_x^2-I_y^2\right)}{6} \end{gathered}$$ (17)

where the final equality holds in the PAS of the EFG tensor. In these expressions, Q is the nuclear electric quadrupole moment, e is the fundamental electric charge, and V is the traceless and symmetric EFG tensor. When the strength of the quadrupolar interaction is small compared to the Larmor frequency, this expression can be further simplified by taking the secular approximation, giving the first-order quadrupolar Hamiltonian

$$\begin{gathered} H_Q^{(1)}/\hslash =\frac{3eQ}{2I\left(2I-1\right)\hslash }{V}_{zz}\frac{3I_z^2-I\left(I+1\right)}{6} \\ ={\omega }_Q^{\left(1\right)}\frac{3I_z^2-I\left(I+1\right)}{6} \end{gathered}$$ (18)

and the first-order quadrupolar coupling, ${\omega }_Q^{\left(1\right)}$, which is proportional to the lab-frame zz-component of the EFG tensor. For the quadrupolar coupling interaction, it is the electric field gradient (EFG) tensor that determines the spatial dependence of the interaction. In the PAS,

$${\mathbf{V}}^{\text{PAS}}=\left(\begin{array}{ccc}{V}_{XX}& 0& 0\\ 0& V_{YY}& 0\\ 0& 0& V_{ZZ}\end{array}\right)$$ (19)

and TensorView adopts the IUPAC recommendation that the principal values be designated such that $\left|V_{ZZ}\right|>\left|V_{YY}\right|>\left|V_{XX}\right|$ [41], which is neither the Haeberlen nor the Mehring convention.

Because the EFG tensor is symmetric, TensorView requires only the six independent components be entered. The units are arbitrary, as the axes will be scaled for display. The relevant EFG tensor is traceless, but different computational programs report traceless EFG tensors, finite trace EFG tensors, or both. Either can be entered as TensorView will subtract the isotropic value to generate the traceless form.

Figure 6 displays the EFG tensor for a backbone amide deuterium in Ala-Ala-Ala, calculated in Gaussian09 using the “PROP” keyword. This visualization immediately draws attention to the fact that V_ZZ is essentially collinear with the N-D bond [47], with a small perturbation due to the presence of the neighboring carbonyl group. Motions that modulate the orientation of this bond lead to dynamically-averaged EFG tensors with characteristic line shapes that can be fit to parameterize and test models for the dynamics [48].

Figure 6:

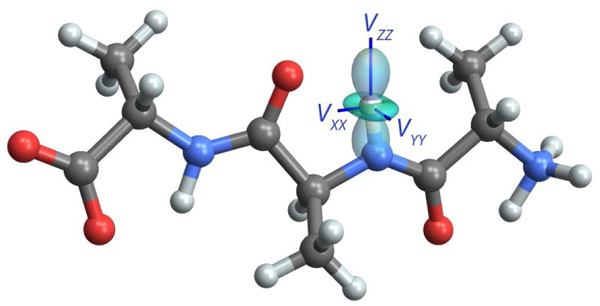
The first-principles EFG tensor for a backbone amide deuterium in Ala-Ala-Ala, calculated in Gaussian09 using the “PROP” keyword. V_ZZ is nearly aligned with the N-D bond and V_YY is perpendicular to the amide plane. Molecular motions that modulate the orientation of the EFG tensor have a profound effect on the deuterium NMR line shape.

Dipole-Dipole Coupling

The distance and orientation dependence of the direct magnetic-dipole-magnetic-dipole coupling interaction has made it a particularly important property for NMR studies of structure and dynamics [49]. The dipole-dipole coupling between two nuclear spins, I and S, is given by the following term in the NMR Hamiltonian [38]

$$\begin{gathered} H_{\text{D}}/\hslash =\overrightarrow{I}\cdot \mathbf{D}\cdot \overrightarrow{S} \\ =\left(\begin{array}{ccc}{I}_x& I_y& I_z\end{array}\right)\cdot \left(\begin{array}{ccc}{D}_{xx}& D_{xy}& D_{xz}\\ D_{yx}& D_{yy}& D_{yz}\\ D_{zx}& D_{zy}& D_{zz}\end{array}\right)\cdot \left(\begin{array}{c}{S}_x\\ S_y\\ S_z\end{array}\right) \\ \stackrel{\begin{array}{l}\text{sec approx/}\\ \text{homonuclear}\end{array}}{=}{D}_{zz}\frac{3I_z{S}_z-I•S}{2} \\ \stackrel{\begin{array}{l}\text{sec approx/}\\ \text{heteronuclear}\end{array}}{=}{D}_{zz}{I}_z{S}_z \end{gathered}$$ (20)

The strength and orientation dependence of the dipolar interaction is carried by the dipole-dipole coupling tensor, D, which depends on the gyromagnetic ratios, ${\gamma }_I$ and ${\gamma }_S$, and the length and orientation of the internuclear vector, $\overrightarrow{r}={\overrightarrow{r}}_S-{\overrightarrow{r}}_I=\left(x,y,z\right)$, [50]

$$\mathbf{D}=-\frac{{\mu }_0}{4\pi }\frac{{\gamma }_I{\gamma }_S\hslash }{r^3}\left(\begin{array}{ccc}\frac{3x^2}{r^2}-1& \frac{3xy}{r^2}& \frac{3xz}{r^2}\\ \frac{3xy}{r^2}& \frac{3y^2}{r^2}-1& \frac{3yz}{r^2}\\ \frac{3xz}{r^2}& \frac{3yz}{r^2}& \frac{3z^2}{r^2}-1\end{array}\right).$$ (21)

The dipole-dipole tensor is traceless and symmetric, and in the PAS

$${\mathbf{D}}^{\text{PAS}}=\left(\begin{array}{ccc}-d& 0& 0\\ 0& -d& 0\\ 0& 0& 2d\end{array}\right),$$ (22)

where $d=-\frac{{\mu }_0}{4\pi }\frac{{\gamma }_I{\gamma }_S\hslash }{r^3}$ is the dipole-dipole coupling constant. IUPAC recommends that the dipole-dipole coupling tensor principal values be designated with the Haeberlen convention: $\left|D_{ZZ}\right|\ge \left|D_{XX}\right|=\left|D_{YY}\right|$ [41].

TensorView calculates the reduced dipole-dipole coupling tensor D/d directly from the atomic coordinates supplied by the user. The dipolar coupling PAS Z-axis falls along the internuclear vector, and the Euler angles are chosen so that it points from the “atom of interest” (placed at the center of the tensor) to its dipole coupled partner. Because D_XX = D_YY, the γ Euler angle is arbitrary and set to 0.

Figure 7 shows the NH and CH dipole-dipole coupling tensors for two adjacent backbone amide and alpha carbon sites on the Ala-Ala-Ala tripeptide. When viewed down the N-C^α bond, the relative orientation of these tensors defines the H^N-N-C^α-H^α torsion angle, φ^H, which can be related back to the protein backbone dihedral angle φ (φ ≈ φ^H+60^o) [51]. In this example, tensor scalings proportional to the size of the dipole-dipole coupling constants have been incorporated. so that the relative magnitude of the interactions can be inferred visually. Due to the larger gyromagnetic ratio for carbon compared to nitrogen, the CH dipole-dipole coupling is ~2.15 times greater than the NH coupling.

Figure 7:

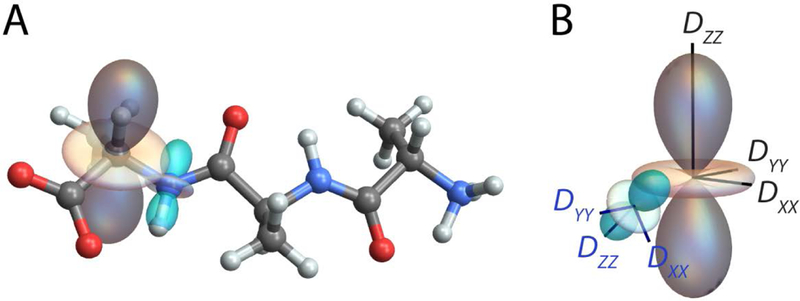
(A) TensorView display of the NH (cyan) and CH (gray) dipole-dipole coupling tensors for adjacent amide and alpha carbon sites. When viewed along the N-C^α bond, these tensors define the peptide backbone torsion angle φ^H. (B) The orientation of the NH dipolar PAS in the CH PAS frame.

TensorView contains two auxiliary functions for quantifying relative orientation. The first, torsion[x₁,x₂,x₃,x₄], returns the x₁-x₂-x₃-x₄ torsion angle; for the H^N-N-C^α-H^α torsion above, φ^H=122.7^O. The second, EulerRel[Ω₁ Ω₂], returns the Euler angles positioning PAS 2 (defined by laboratory frame Euler angles Ω₂) within the reference frame of PAS 1 (defined by laboratory frame Euler angles Ω₁). The relative alignment of two principal axis systems is particularly important for modeling solid-state NMR line shapes under the influence of multiple tensor interactions, such as two dipole-dipole couplings [51,52], or simultaneous chemical shift and dipolar [53] or quadrupolar [54] coupling. For the dipole-dipole tensors in Figure 7, the orientation of the NH PAS in the CH PAS frame is given by Euler angles {α,β,γ}={167.2°, 125.5°, 356.6°}.

Atomic Anisotropic Displacement Parameters

In addition to the second-rank Cartesian tensors that describe the spatial dependence of NMR interactions, TensorView can display other tensor properties derived from NMR and complementary experiments. One particularly relevant property for NMR crystallography is atomic anisotropic displacement parameters (ADP) [36,37]. X-ray crystal structures commonly include ADP as “thermal ellipsoids,” which describe uncertainties in atomic position reflecting both thermal motion and static disorder [55]. Recently it has been demonstrated that methods in NMR crystallography can also provide ADP by sampling atomic positional variations using molecular mechanics [36] and Monte Carlo [37] methods. Remarkably, the ADP from NMR crystallography of powdered samples were smaller than those obtained from X-ray and even neutron diffraction studies involving single crystals. In cases with known crystal structures, programs such as ORTEP [56] can be used for the ellipsoidal representations of ADP derived from either diffraction or NMR. However, NMR crystallography can provide ADP for structures having no known crystal structure, and in these cases TensorView provides an alternative way to visualize these properties.

ADP are parameterized by a mean-square displacement (MSD) tensor, U, which has units of length-squared and defines a three-dimensional Gaussian probability distribution $p\left(\overrightarrow{x}\right)$ for the atomic displacements $\overrightarrow{x}$ relative to the mean [55]

$$\begin{gathered} p\left(\overrightarrow{x}\right)=\sqrt{\frac{\det \left({\mathbf{U}}^{-1}\right)}{8{\pi }^3}}\exp \left(-\frac{{\overrightarrow{x}}^T.{\mathbf{U}}^{-1}.\overrightarrow{x}}{2}\right) \\ \stackrel{\text{PAS}}{=}\sqrt{\frac{1}{8{\pi }^3{\text{U}}_{11}{\text{U}}_{22}{\text{U}}_{33}}}\exp \left[-\frac{1}{2}\left(\frac{x^2}{{\text{U}}_{11}}+\frac{y^2}{{\text{U}}_{22}}+\frac{z^2}{{\text{U}}_{33}}\right)\right] \end{gathered}$$ (23)

where the second equality holds in the PAS of U, in which

$${\mathbf{U}}^{\text{PAS}}=\left(\begin{array}{ccc}{U}_{11}& 0& 0\\ 0& U_{22}& 0\\ 0& 0& U_{33}\end{array}\right)$$ (24)

The ellipsoidal surface in the PAS

$$\frac{x^2}{{\text{U}}_{11}}+\frac{y^2}{{\text{U}}_{22}}+\frac{z^2}{{\text{U}}_{33}}=k^2$$ (25)

encloses 19.9%, 73.9%, and 97.1% of the atomic displacements for k=1, 2, and 3, respectively, and correspond to the ORTEP ellipsoids shown on crystal structures (the default is typically k=1, 19.9%). ADP are mapped onto the rotated ellipsoids displayed in TensorView by passing elements $k\sqrt{U_{ii}}$ in the function call (compare the form of equations (25) and (12)). By construction, the mean-square-displacement (MSD) tensor and the related root-mean-square-displacement (RMSD) tensor are second-rank Cartesian tensors and can also be directly plotted using the ovaloid representation. The units of the RMSD tensor make it the more natural choice for display on molecular models. Following the standard convention in crystallography, however, it is recommended that atomic anisotropic displacement parameters be represented as ellipsoids.

Figure 8 shows the ADP ellipsoidal surface (19.9% enclosure) for the carboxylic acid hydrogen atom in the A₂ polymorph of palmitic acid, making use of the MSD tensor from [37]. Displaying the ADP ellipsoid allows one to immediately observe the large out-of-plane OH hydrogen atom displacement that is a hallmark of COOH vibrations. It also conveys information about the relatively small thermal ellipsoid volume – especially given that the site characterized is a hydrogen atom.

Figure 8:

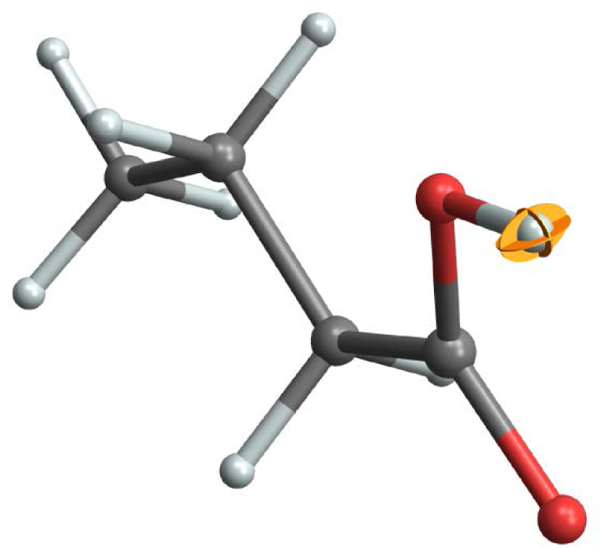
The anisotropic displacement parameters (thermal ellipsoid) for the carboxylic acid hydrogen of palmitic acid derived from NMR-crystallography [37]. The ellipsoid is drawn to enclose 19.9% of the atomic displacements and is shown in “principal ellipse” form. The molecular model is rendered with a 50% scaling of the ball-and-stick radii.

For generating ADP plots in TensorView, the units of the MSD matrix should first be converted to pm², the probability contour chosen by specifying k, and no additional scaling applied so that the surface faithfully corresponds to the enclosed probability stated. At the 19.9% contour level, the ADP surface is comparable in size to the default sphere used to represent hydrogen atoms in ball-and-stick models. One alternative for better visualization is to display the molecule in wireframe format, while a second is to shrink the radii used to display the atoms and bonds. The TensorView function skinny[graphic, scale_factor] (defined in the notebook initialization cells) can be used for the latter.

Conclusion

The TensorView Mathematica notebook provides a flexible computational environment for displaying NMR tensors and related properties on the molecular framework. Worked examples for the chemical shielding/shift, dipole-dipole, electric field gradient, and atomic anisotropic displacement tensors demonstrate the information-rich nature of these representations, highlighting the geometric relationship between principal components/axes and the underlying molecular structure. TensorView requires the user to supply a molecular coordinate file that can be imported into Mathematica and tensor components in the same frame. Direct modification of the notebook has the advantage that with some familiarity with Mathematica, tensor properties from a broad range of commercial or user-specific computational chemistry packages can be entered and displayed. We anticipate that TensorView could easily be adapted to display additional second-rank Cartesian tensor properties relevant to magnetic resonance, such as g-tensors, pseudocontact shift surfaces, and diffusion tensors.

Appendix: Software Implementations and Distribution

Additional Software Implementations: TensorView.py

Mathematica is required to take full advantage of the features in TensorView. However, a beta version of TensorView written in Python (TensorView.py) is also described and distributed as part of the Supplementary Material. This limited implementation generates formatted output that can be inserted into PDB files and used to display NMR tensors in programs such as Chimera [57] and the Cambridge Crystallographic Data Centre (CCDC) Mercury Viewer [58]. This approach co-opts the thermal ellipsoid display option within these programs for depicting NMR tensors. In its current beta release, the user must supply the tensor in its desired final form (i.e., shift tensor properly referenced, EFG tensor traceless, full dipolar tensor), and make simple edits to the PDB files. Only the ellipsoidal representation is supported.

Software Download

The most recent version of TensorView and example files can be downloaded from the Mueller Group website (research.chem.ucr.edu/groups/mueller or by following the links from chem.ucr.edu). A working copy of Mathematica is required to make full use of the TensorView.nb notebook, while the free Wolfram CDF player can be used to view it. The Python implementation requires an external program such as Chimera for display.