Towards a Unified Model of Event-Related Potentials as Phases of Stimulus-to-Response Processing

Abstract

This study demonstrates the utility of combining principles of connectionist theory with a sophisticated statistical approach, structural equation modeling (SEM), to better understand brain-behavior relationships in studies using event-related potentials (ERPs). The models show how sequential phases of neural processing measured by averaged ERP waveform components can successfully predict task behavior (response time; RT) while accounting for individual differences in maturation and sex. The models assume that all ERP measures are affected by individual differences in physical and mental state that inflate measurement error. ERP data were collected from 154 neurotypical children (7–13 years, M = 10.22, SD = 1.48; 74 males) performing a cued Go/No-Go task during two separate sessions. Using SEM, we show a latent variable path model with good fit (e.g., χ²(51) = 56.20, p = .25; RMSEA = .03; CFI = .99; SRMR = .06) yielding moderate-to-large predictive coefficients from N1 through the E-wave latent variables (N1 β = −.29 ➔ P2 β = −.44 ➔ N2 β = .28 ➔ P3 β =.64➔ E-wave), which in turn significantly predicted RT (β =.34, p = .02). Age significantly related to N1 and P3 latent variables as well as RT ( β =.31, −.58, & −.40 respectively), and Sex significantly related to the E-wave latent variable and RT ( β =.36 & .21 respectively). Additionally, the final model suggested that individual differences in emotional and physical state accounted for a significant proportion of variance in ERP measurements, and that individual states systematically varied across sessions (i.e., the variance was not just random noise). These findings suggest that modeling ERPs as a system of inter-related processes may be a more informative approach to examining brain-behavior relationships in neurotypical and clinical groups than traditional analysis techniques.

1. Introduction

The purpose of the present study is to demonstrate the utility of combining principles of connectionist theory (Hebb, 1949; McNaughton & Nadel, 1990; Raftopoulos, 1997) with a sophisticated statistical approach, structural equation modeling (SEM), in order to better understand brain-behavior relationships in studies using event-related potentials (ERPs). The conceptual models we propose to evaluate and compare are shown in Figure 1. In our proposed models, the components of the averaged ERP waveform obtained from each individual during a contingent negative variation (CNV) ERP paradigm (e.g., Bender et al., 2004; Segalowitz & Davies, 2004; Taylor, Gavin & Davies, 2016; Walter et al., 1964) represent sequential phases of neural activity for processing a stimulus in order to produce an appropriate behavior, much akin to the concept of phase sequences proposed by connectionist theory (Bear & Cooper, 1990; Laufs et al., 2003; Lowe et al., 2016; McNaughton & Nadel, 1990; Raftopoulos, 1997).

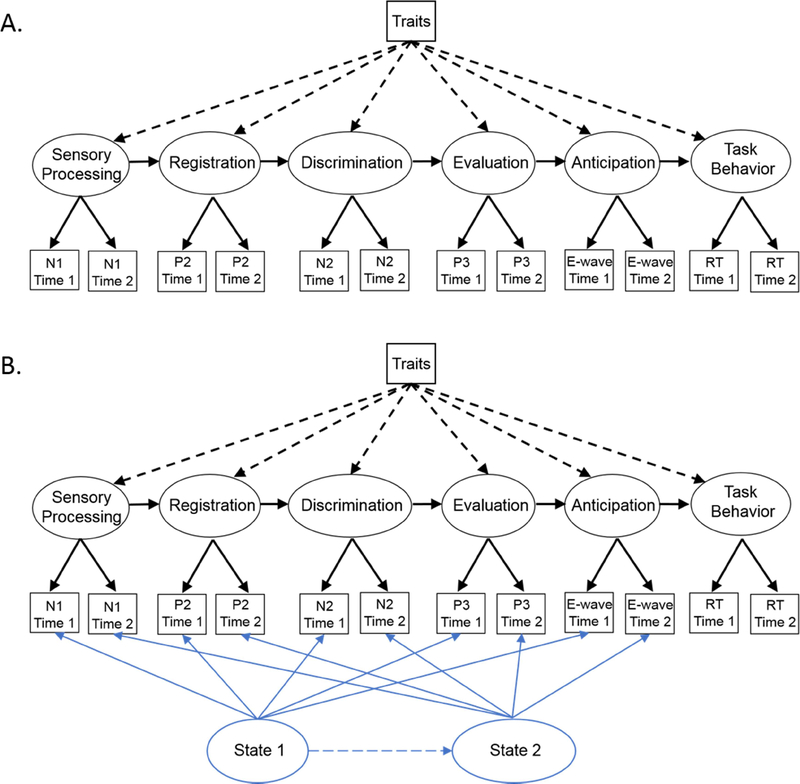
Figure 1.

The two conceptual models being evaluated in this study. Model “A” depicts how both trait characteristics of the individual and a task behavior (e.g. response time) may relate to brain activity. State effects for manifest variable are assumed to be random and therefore are subsumed in the residual variances of the manifest measures. Model “B” assumes the same relationships between trait characteristics, task behavior, and brain activity as “A” but includes the assumption that nonrandom state effects are measurable for each assessment session. In both models, components from averaged ERPs of correct trials in the contingent negative variation (CNV) ERP paradigm and the averaged response time obtained in two separate sessions serve as the manifest variables (squares) used to create the latent variables (ovals). Solid arrows show relationships expected to be statistically significant and dashed arrows depict relationships that may or may not be statistically significant depending on nature of the cognitive task, the specific parameters of the task, and the characteristics of the participants.

Connectionist theory provides a framework for understanding complex neural dynamics, from early sensory processing through increasingly complex cognitive and behavioral domains (Bear & Cooper, 1990; Hebb, 1949; Laufs et al., 2003; Lowe et al., 2016; Raftopoulos, 1997). Among its assumptions, connectionist theory offers the concept of “phase sequences”, which are neural state trajectories underlying sensory-motor events (Hebb, 1949; McNaughton & Nadel, 1990). In essence, phase sequences are cascades of neural activity which activate in certain patterns in order to produce a specific cognitive or behavioral response. Neurons, their inputs (e.g., sensory information), and their outputs (e.g., motor responses) are all dynamically-interacting parameters that form systems of cognitive and behavioral functioning; in short, each stage in the process is conceived as directly affecting the next stage in the neural processing sequence leading to observable behaviors. This cascading, systematic view of processing is a core principle in the conceptualization of our proposed model of ERPs.

The general model we propose (Figure 1) is also an outgrowth of our previous work and others’ to evaluate the psychometric properties of ERP components and efforts to establish brain-behavior relationships using regression approaches. In general, test-retest reliability of ERP component amplitudes, but not latencies, tends to be relatively high among adult samples, even over long period of time as demonstrated by Cassidy, Robertson, and O’Connell (2012). However, a growing body of evidence indicates that the test-retest reliability of ERP components commonly used in brain-behavior relationship research is moderate at best in groups of interest for developmental and clinical investigations, such as neurotypical children, and adults and children with neuropsychological diagnoses (e.g., Foti et al., 2016; Hämmerer, Li, Völkle, Müller, & Lindenberger, 2013; Meyer, Bress, & Proudfit, 2014; Segalowitz & Barnes, 1993; Taylor et al., 2016). Such weak effects are inadequate for use in diagnostics, or for measuring development over time. In fact, in order to be relevant for such use, many researchers agree that the psychometric properties of a measure being used as a dependent variable should include reliability coefficients upwards of r = .80, though greater than .90 is preferred (for reviews, see Clayson & Miller, 2017; Hopkins, Stanley, & Hopkins, 1990; McCauley & Swisher, 1984; Salvia & Ysseldyke, 1981). Inadequate stability of dependent measures may explain, at least in part, why researchers have struggled to identify viable brain-behavior relationships in such groups.

To conceptualize why a psychophysiological measure (PM) may have low test-retest reliability, Gavin and Davies (2008) suggested that any PM, including an ERP component, is comprised of the combined variance from multiple sources: (1) the stimulus processing involved in eliciting the component; (2) the state of the individual participant during measurement such as current mood or sleepiness; (3) the trait characteristics of the individual such as general attention abilities, maturation level, or sex; (4) the signal processing techniques employed to calculate the ERP component including variability in the number of segments used in averaging of ERP signals; and (5) measurement error (ME), which is any other unaccounted-for variance. Such a model can be simply written as in equation (1) below (reprinted from Gavin and Davies, 2008, p. 428), and this type of conceptual model allows for the use of multiple regression techniques to understand the variation of brain activity across individuals performing a given task, particularly when examining performance repeated on two or more occasions. These concepts are similar to those discussed in classical test theory (CTT) and the revision of latent state-trait theory (LST-R) where distinctions are made between “an attribute of a person (a trait), an attribute of a person-in-a-situation (a state), and observable measures that may reflect both these components, but that typically also contain method effects and measurement error” (Steyer, Mayer, Geiser, & Cole, 2015 pp. 72–73).

$$\text{PM}={\text{Effect}}_{\text{STIMULUS}}+{\text{Effect}}_{\text{STATE}}{+\text{Effect}}_{\text{TRAIT}}+{\text{Effect}}_{{\text{PM}}_{-}}{}_{\text{PROCESSING}}+\text{ME}$$ (1)

As the simplified model proposed by Gavin and Davies (2008) suggests, when researchers fail to account for one or more of these other potential sources of individual differences that are contributing to an ERP component measure, the researchers are compounding the unaccounted-for individual effects into the ME term. Implicit in discussions of CTT and LST-R theories, methodological effects are often considered to be minimal or even zero if the same exact experimental protocol is applied consistently to each participant as was done in this current study. Given the assumption that methodological effects inconsequential, these theories and our models focus on state and trait effects which are assumed to be potentially larger and, if not adequately controlled for methodologically or statistically, get summed into the measurement error term. The larger measurement error term may result in increased type I or type II errors. For instance, if a significant statistical relationship is found between a physiological measure and a functional behavior, this relationship could be explained by either the stimulus effect or the undefined measurement error. Thus, it is important to reduce the amount of measurement error in analyses by accounting for the variance of factors that are often folded into measurement error if the study’s conclusions are to be as unambiguous as possible. By reducing measurement error, researchers may increase their ability to detect effects of interest in the data, such as the effect of the stimulus or other experimental manipulations. Researchers may implement behavioral controls during data collection to reduce or minimize the contribution of variance due to differences in the state of participants within a group, or between sessions for an individual participant (Gavin & Davies, 2008). Additionally, researchers can utilize statistical methods to account for such sources of variance after data collection is complete.

To explore statistical methods for controlling state effects (Effect_STATE) in ERP components, Taylor et al. (2018) used SEM techniques to establish a model of brain-behavior relationships between latent variables. Children in the study completed a visual, cued Go/No-Go task (Segalowitz & Davies, 2004; Taylor, Gavin & Davies, 2016) while EEG data were recorded during two separate sessions. Participants saw either a “Go” or a “No-Go” conditional cue stimulus (250 ms) exactly two seconds before seeing a target stimulus, which prompted a motor response in the form of a button press for “Go” trials. The study explored whether a latent variable defined by combining the E-wave component of the averaged ERP derived from each of the two sessions could be used to predict response times acquired in the task, also defined as a latent variable derived from the two sessions. When creating latent variables in this manner, only the common variance of the ERP component across the sessions is retained. Variance that might be due to changes in the individual’s emotional or physical state in each session (i.e., Effect_STATE) is treated as random, residual variance. Thus, the analysis controls for potentially confounding sources of variance, such as state effects and measurement error. The latent variable approach in defining the E-wave significantly improved the amount of variance explained in response times beyond what was accounted for by using univariate analyses (Taylor et al., 2018). However, the effect was still small and failed to reach statistical significance. It is possible that examining a single ERP component in isolation may not be sufficient for explaining task behaviors. Earlier phases of neural processing represented by other ERP components that occur before the E-wave may be important contributors to behavioral performance.

The conceptual models shown in Figure 1 expand on the previous work by Taylor et al. (2018) by utilizing the same latent variable approach by modeling the full time-course of an averaged ERP as a phased sequence of neural activity leading to a task behavior in accordance with principles of connectionist theory (Hebb, 1949; McNaughton & Nadel, 1990; Raftopoulos, 1997). Specifically, the models use repeated measures of multiple ERP components to create latent variable constructs that successively predict one another in chronological order, culminating in the prediction of task behaviors during the ERP paradigm. Each stage of processing may represent specific, cognitively-based constructs of brain activity needed to produce successful task behavior. For illustrative purposes the stages are conceptualized here as: processing the sensory information of the stimulus cue during the N1 component (Sensory Processing; Hillyard, Hink, Schwent, & Picton, 1973; Kappenman & Luck, 2012; Kauramäki, Jääskeläinen, & Sams, 2007; Luck, 1995); matching the stimulus to stored information during the P2 component (Registration; Adams et al., 2017; Davies et al., 2010; Davies & Gavin, 2007); discriminating between stimuli in order to initiate a behavior during the N2 component (Discrimination; Enoki, Sanada, Yoshinaga, Oka, & Ohtahara, 1993; Patel & Azzam, 2005; Heil et al., 2000; Moon et al., 2014); evaluation of the decision regarding behavior to engage in during the P3 component (Evaluation; Polich, 1993, 2007; Sato et al., 2005; Verleger et al., 2005; Wu & Zhou, 2009); and anticipating the onset of the second stimulus signaling the required response during the E-wave (Anticipation; Hämmerer et al., 2010; Segalowitz & Davies, 2004; Walter et al., 1964). Thus, the proposed models assess to what extent more resource-intensive processing in one phase of processing, represented by larger ERP amplitudes, predicts the intensity of processing at the chronologically subsequent phase.

The proposed models also specify how both trait characteristics of the individual (i.e., attributes that each individual has prior to task participation) and task behavior (i.e., response time of button pressing) are related to brain activity which is measured as indicator variables then modeled as latent variables. Individual traits, which may include general attention abilities, maturation level (e.g., age), or sex are considered to relate to one or more of the steps in the brain activity in a predictive manner because 1) traits are already established at the time of engagement of the task, 2) traits are not likely to be substantially modified during the brief period of the task itself, and 3) each trait can be tested for its degree of influence on each neural processing step. Because the behavior at the end of each trial of the ERP task is a product of processing the stimuli within a trial, the steps of brain processing are modeled as predictors of the task behavior, such as a timely button press. The latent variable model in Figure 1A assumes that the confounding individual state effects and any individual methodological effects are randomly distributed across ERP components and sessions. Thus, state and method effects are removed from the latent variables and contribute only to residual variances. Figure 1B, however, suggests that the effect of individual states within each session (e.g., fatigue, anxiety, task strategy, etc.) significantly contribute to the composition of averaged ERPs and may change systematically across sessions. In other words, this second model hypothesizes that state effects are not random and should not be considered as contributing to general measurement error.

The model in Figure 1B is variant of the model by Eid, Holtmann, Santangelo, & Ebner-Priemer (2017; see their figure on page 290) that describes an indicator-specific trait variable and congeneric measurement structure for the latent occasion specific variables. In the Eid, et al. (2017) model latent occasion variables are the latent state measures derived from all the indicator variables obtained at a measurement period and latent trait measures are derived by combining multiple instances of each indicator variable across the measurement periods. In the proposed model here in Figure 1B, each of the two latent “state” variables are also derived from all the indicator variables obtained at a given measurement period and each of the neural latent variables are derived by combining multiple instances of each indicator variable, the ERP component measures. In addition, the proposed model includes measures of one or more “traits” that each individual brings to the study prior to measurement of brain activity; i.e., additional traits at time zero that may also relate to or help explain the effects of one or more of the neural latent traits on subsequent stages of information processing.

The present study examined the validity of multiple models where time-ordered latent trait variables of neural processing predict a latent measure of task behavior while accounting for additional trait effects that the individual has established prior to the first task session (specifically, age and sex of the individual). We began by assessing the viability of manifest-level path models in which ERP components predicted RT, with one model for each session. We then examined the viability of latent variable models of neural processing by testing the models outlined in Figures 1A and 1B. We compared model fit indices of the nested models to determine whether the addition of the state-based latent variables improved overall model fit.

2. Methods

2.1. Participants

Data were collected from a total of 154 neurotypical children between the ages of 7 and 13 years (74 males; M = 10.22 years, SD = 1.48) during two sessions scheduled one-to-two weeks apart (note: this is an extension of the sample in Taylor et al., 2018). Data were collected in two separate waves (Wave 1: n = 57; Wave 2: n = 97). Procedural differences in data collection procedures between the two waves are described in detail below. In prior work, we excluded participants who did not have enough ERP data following data reduction procedures (e.g., Taylor et al., 2016; Taylor et al., 2018). However, in the present study no participants were excluded based on performance due to the use of full information maximum likelihood (FIML) to estimate model parameters. Details are described in the missing data section below. Participants had no neurological or developmental diagnoses, nor were they currently taking any psychopharmaceutical medications, as reported by parents. Parents of children signed informed consent forms, and child participants signed assent forms. Children received their choice of a t-shirt or cocoa mug after completing their first visit, and their choice of a t-shirt, cocoa mug, or $10 after their second visit. All procedures were approved by the local university institutional review board.

2.2. Procedure

Participants completed two EEG recording sessions scheduled one or two weeks apart with the second session being at the same time and day of the week as the first session. Participants were seated in a comfortable chair at a table in front of a computer screen. Two research assistants placed the EEG cap and sensors on the participant. For each participant, the same EEG cap was used for each session, and measurements were performed to assure proper placement each time. Next a research assistant gave participants a brief training on how to reduce production of artifacts from eye blinks and muscle movements. Then, three minutes of eyes-opened resting EEG were recorded while participants stared at a fixation point on the screen. Participants then performed a total of three EEG paradigms lasting approximately one hour. One of the ERP tasks was split such that half of the trials were presented before, and half were presented after the third paradigm. Only the visually-cued Go/No-Go paradigm, which was the third paradigm, will be discussed in this study. Participants were given a short break of 2 to 4 minutes between each paradigm. Following EEG data collection and removal of the EEG cap and sensors, children completed a battery of behavioral assessments of attention and executive function abilities which will not be discussed further in this study. In total, each session lasted approximately two hours.

2.3. Visually-Cued Go/No-Go Paradigm

During each trial of the cued Go/No-Go task, children saw a sequence of two stimuli (Segalowitz & Davies, 2004). First, a circle, either red or green, was displayed in the center of the screen for 250ms (i.e., the conditional or cue stimulus). Then the screen went blank for 1750ms before a picture of a car appeared in the center of the screen with a duration of 250ms (i.e., the imperative or target stimulus). If the circle at the beginning of the trial was green, children were instructed to press a button placed on the table in front of them as quickly as possible after the car appeared on the screen (i.e., a Go trial). However, if the circle was red, the children were instructed not to press the button (i.e., a NoGo trial). The task consisted of 40 Go and 40 NoGo trials presented in a pseudorandom order with a variable inter-trial interval of 2000–7000ms. The same task was performed during both sessions.

This cued Go/No-Go task was selected for this study because the task is relatively simple while requiring cognitive processing to appropriately respond, and the period between the cue and target stimuli was approximately 2 seconds allowing time for stimulus processing to complete. The relative simplicity of the task assured that all participants could complete the task, while requiring the participants to engage in cognitive processing on each trial, allowing us to investigate stages of cognitive processing leading to a behavior (i.e., button press). The 2-second interval between stimuli allowed separation of the stages of processing. In a traditional, speeded Go/No-Go task, a response may occur during the time window of the N2 or P3 component, thus that stage of processing may be confounded preventing these two stages to be properly represented in the overall model.

2.4. Electrophysiological Recording

EEG recordings were obtained using the BioSemi ActiveTwo system with a Lycra head cap (BioSemi, Inc., Amsterdam, The Netherlands). For children in Wave 1, active EEG was recorded from 32 Ag-AgCl sintered electrodes with an additional pin-type Ag/AgCl electrode placed at FCz for a total of 33 scalp sites. EEG data recorded from the additional 97 children in Wave 2 were collected using a 64-channel BioSemi ActiveTwo system with Ag/AgCl sintered electrodes. Scalp electrodes for recordings in both waves were positioned according to a modified 10–20 system (American Electroencephalographic Society nomenclature guidelines, 1994) with additional common mode sense (CMS) and driven right leg (DRL) sensors which were used to generate a common reference voltage (https://www.biosemi.com/faq/cms&drl.htm). For participants in both waves, an additional six sensors were placed on the face (on the left supra- and infra-orbital regions, and on the left and right outer canthi) to record eye movements and both the left and right earlobes to provide sites for offline re-referencing. Data were collected at a sampling rate of 1024Hz.

2.5. Electrophysiological Data Reduction

Using BrainVision Analyzer 2 software (Brain Products GmbH, Munich, Germany; www.brainproducts.com), data from the continuous EEG recording were re-referenced to the averaged voltage of the two earlobe electrodes, filtered with a .03 to 30Hz bandpass filter (12dB/octave), and then segmented from 200ms prior to the cue stimulus onset to 2250ms after the cue stimulus onset. Only correct Go trials were examined in this study. Correct Go trials were any trials in which a green circle appeared before the car, and the button was pressed after the car appeared. Baseline correction was performed on each segment using the EEG data from −200 – 0ms relative to the cue stimulus onset. A regression procedure used to remove eye blinks was applied to retained segments (Segalowitz, 1996). Following the regression procedure, segments were baseline corrected again using the −200 to 0ms window and then underwent an artifact rejection procedure to remove segments with voltages exceeding ±100μV. For each participant, an averaged ERP was calculated for each session.

The averaged ERPs were processed using a MATLAB routine which allows for automatic scoring and visual inspection of ERP component peaks, and, when necessary, allows for manual marking of component peaks. All ERP component measurements were reviewed by one trained research assistant. The averaged amplitude in the time window of the E-wave were measured via the MATLAB routine. The N1 was defined as the most negative amplitude in the 70–170ms window, P2 as the most positive peak in the 150–300ms window, N2 as the most negative amplitude in the 250–400ms window, and P3 as the most positive peak in the 400–650ms window (see Figure 2). The E-wave was measured as the averaged amplitude in the 1800–2000ms window. All ERP component time windows were selected based on prior research and modified to accommodate the variability inherent in data collected from children (e.g., Hämmerer et al., 2010; Kappenman & Luck, 2012; Kropp et al., 2000; Taylor et al., 2016).

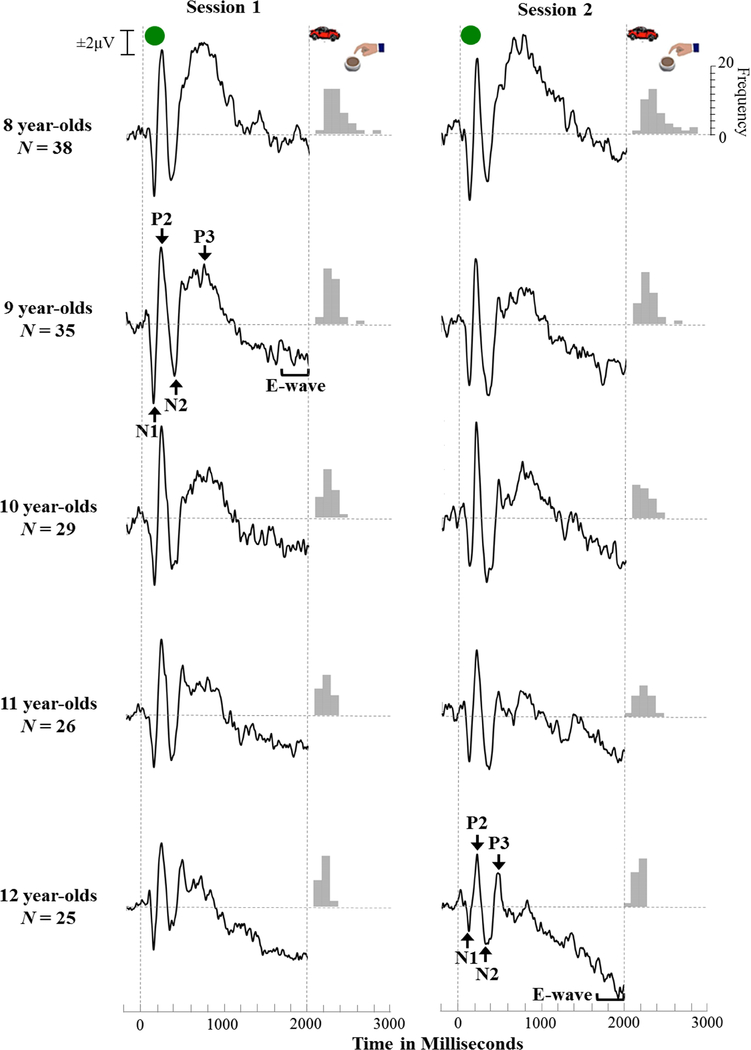
Figure 2.

The grand averaged event-related potentials (ERPs) for session 1 and session 2 Go trials separated by age group. All ERP images were derived at site Cz. The frequency distribution of average response times for each session and age group is shown to the right of each ERP. Note: there were very few children that were 7- or 13-years-old, and those children’s data were grouped with the 8- and 12-year-olds’ data, respectively. Note: The data shown in the figure represent the data included in the models: all children’s response times, and only the averaged ERPs for children who had adequate data for that session are included in each figure. N’s for each age group indicate the total number of children in that age group.

Despite literature indicating varying scalp sites for maximal peak measurement of the different ERP components, we only utilized measurements taken from Cz in our models. As we built our models, we did attempt to include mixtures of measurements from different scalp sites in the creation of latent variables, but the models did not converge; in fact, the models would only converge if we created latent variables using measurements from a single site. It is likely that the influences of temporally- and spatially-varying signals introduced too little common variance among the manifest variables, thereby creating additional challenges for model convergence. By utilizing a single site, we were able to control for some of those effects and examine relative changes in voltage over time at a single site, which had similar influences of spatially- and temporally-based variance. We selected Cz because 1) it is the central location on the scalp, 2) all components of interest are visible and measurable at this scalp site (see Figure 2), and 3) Cz is the site commonly used for measuring the E-wave component of the CNV.

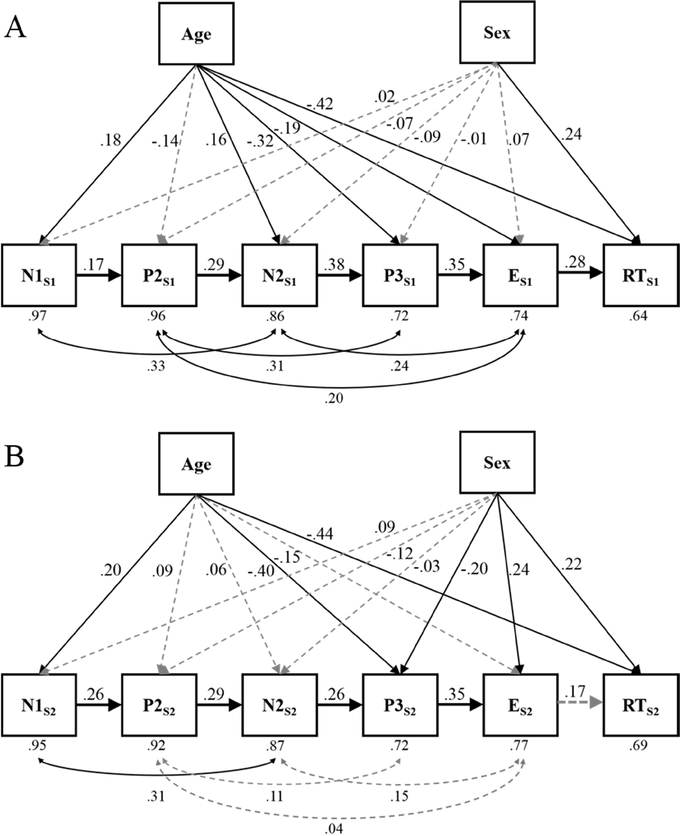
Figure 3.

The two manifest path models of neural processing predicting a task behavior (e.g. response time) while controlling for variance attributed to two trait characteristics of the individuals (Age and Sex): A depicts outcomes for Session 1 Go trials; and B depicts outcomes for Session 2 Go trials. Gray dotted arrows indicate non-statistically significant relationships, i.e., p > .05. Residual variances are reported below each variable. All reported coefficients are standardized.

In addition to ERP component measures, averaged response times (RT) were derived for correct Go trials for each participant. RTs were calculated as the amount of time between the onset of the target stimulus (i.e., the car) and the participant’s button press for each trial. Then, an averaged RT was computed for each session separately, for each individual participant. While the RT values were measured and reported in the tables with milliseconds as the unit (see Table 1), within the models averaged RTs were linearly transformed by dividing each participant’s average RT by 100 in order to reduce its variance values and contribute to creating more homogenous variance across all measures.

Table 1.

Means and standard deviations of baseline-to-peak Go trial ERP component amplitudes in microvolts, and averaged response times (RT) in milliseconds for each session.

	Session 1	Session 2	Difference	Test-retest Reliability
	M (SD)	M (SD)	t	r
N1	−6.86 (4.55)	−6.51 (4.42)	−.86	.60***
P2	9.06 (4.85)	8.35 (5.46)	1.48	.59***
N2	−7.05 (6.40)	−8.06 (6.20)	1.61	.53***
P3	10.78 (6.19)	8.68 (5.30)	3.27**	.41***
E-wave	−2.30 (5.07)	−4.03 (5.24)	2.89**	.35***
RT	290.76 (103.64)	288.02 (127.39)	.44	.81***

Note:

^*p < .05

^**p < .01

^***p < .001

N = 96 due to listwise deletion for analyses in SPSS.

2.6. Data Analysis

2.6.1. Missing Values

If a child had fewer than 12 correct Go segments (i.e., fewer than 30% of possible Go trials) remaining following EEG data reduction procedures, ERP component amplitudes were not measured for that session. Measuring averaged ERPs comprised of relatively few trials (i.e., fewer than 12 in this case) could potentially introduce additional confounds into the data, including a poor signal-to-noise ratio. It is noteworthy that all children did perform the task well enough to be included in the study (i.e., all children correctly performed more than 12 Go trials each session). For participants that had less than 12 trials in the averaged ERP, the loss of data was primarily due to movement artifacts (e.g., eye blinks). A total of 30 children in session 1, and 45 children in session 2 had fewer than 12 segments. Of these, 18 participants had too few segments during both session 1 and session 2 and thus only had age, sex, and RT data to contribute to the models. Overall, the children who had too few segments to reliably measure averaged ERP components during either session tended to be younger (M = 9.78 years, SD = 1.27), with 62.5% of the children with too few segments being below the sample mean age. One child who had sufficient trials to measure averaged ERP components did not have an identifiable N1 component for session 1. Missing data was handled in Mplus version 8.1 using FIML estimation. We conducted all analyses with and without the FIML estimation, and the conclusions drawn were the same regardless. Thus, we report the analyses that utilized FIML estimation due to the statistical power gained by including all participants’ data.

2.6.2. Descriptive Statistics

Analyses began with basic descriptive statistics for each dependent measure, including ERP component amplitudes as well as averaged RTs during the task. We also completed a series of paired-samples t-tests and explored test-retest reliability via Pearson product-moment correlations to examine any changes in the measures across sessions in accordance with prior literature (Taylor et al., 2016; Taylor et al., 2018). The analyses were also meant to demonstrate and confirm the inherent variability present in ERP data collected from children. In addition, we performed Pearson product-moment correlations to examine the interrelationships among the measures of interest (ERP component amplitudes, RTs, age, and sex) to set the foundation for building models of brain processing and task behavior. All initial descriptive analyses were completed using SPSS version 24.

2.6.3. Manifest-Level Path Models

Following descriptive analyses, we developed two path models that represented the sequence of neural processing in the averaged ERPs for each session. The goal was to determine whether the full sequence of neural processing, modeled with manifest variables, could successfully predict the task behavior measure (i.e., RT). In the model applied to each session, a single ERP component amplitude was used to predict the next in chronological order such that N1 ➔ P2 ➔ N2 ➔ P3 ➔ E-wave ➔ RT. The exact age (i.e., to the hundredths of a year) and sex (coded “0 = male”, “1 = female”) were modeled as predictors of each ERP component and to RT. Subsequent to our hypothesized conceptual model structure, we considered additional correlations between non-adjacent ERP components (e.g., N1 and N2) in accordance with the bivariate correlation structure identified in our descriptive statistics (described in detail in the Results section). In the manifest-level models, all parameters were freely estimated (i.e., no paths were constrained).

2.6.4. Latent Variable Path Model with No State Effects

After the manifest variable path models, we fit a latent variable path model. Latent variables are derived from the common variance of multiple manifest variables, and the resulting latent variable is free of measurement error (i.e., any variance that is not common among the manifest variables is removed). Thus, unlike the manifest level path model, the latent variable definition should also remove state-specific effects (i.e., Effect_STATE) which varied across the two sessions (see Figure 1A). We defined a latent variable by the combination of measurements from each of the two sessions for each dependent measure (e.g., session 1 and session 2 N1 amplitudes combined into a latent “N1” variable). The factor loading of each “session 1” manifest variable was constrained to “1” to identify each latent variable. All other paths and parameters were freely estimated. The latent variable path was modeled similarly to the manifest variable paths. Each latent variable derived from a set of ERP components predicted the next in chronological order (N1 ➔ P2 ➔ N2 ➔ P3 ➔ E-wave ➔ RT) to model the sequence of neural processing leading to the task behavior. Exact age and sex were modeled as predictors to all latent variables.

2.6.5. Latent Variable Path with State Effects

In order to test whether measurement error removed from the latent variable path was random from one session to the next, we fit a final latent variable model including session-specific latent state variables. The model included the latent variable path as described previously (N1 ➔ P2 ➔ N2 ➔ P3 ➔ E-wave ➔ RT) with exact age and sex as predictors of each latent variable. In addition, we derived two latent variables, one for each session (“State1” and “State2”), representing state effects present in the ERP component measures (see Figure 1B). Thus, all five ERP components measured within a single session were used to derive a single state latent variable. State1 was modeled as a predictor of State2 to determine to what extent state effects were random or systematic across sessions.

All models were examined for model fit. To evaluate overall model fit, we used the model fit criteria suggested by Hu and Bentler (1999), including comparative fit index (CFI) > .95, root mean square error of approximation (RMSEA) < .06, and standardized root mean square residual (SRMR) < .08. We also examined the chi-square test of model fit, where a non-statistically significant test indicates perfect fit of the model to the data. In all cases, only the best-fitting models are reported. Because the two latent variable models were nested, we assessed whether the addition of latent state effects significantly improved model fit using a chi-square difference test.

3. Results

3.1. Descriptive Statistics

Means and standard deviations, paired-samples t-tests, and test-retest reliability indices of ERP component amplitude measures and averaged RTs are shown in Table 1. The data indicated that the N1, P2, and N2 ERP component amplitudes, and RTs were similar across sessions. The P3 component was significantly larger (more positive) in session 1 than in session 2, and the E-wave was significantly larger (more negative) in session 2 than in session 1. With respect to test-retest reliability, all components and RTs were significantly and moderately reliable across sessions. The findings related to E-wave and RT test-retest reliabilities are in accordance with previous work that had a smaller sample size (Taylor et al., 2016; Taylor et al., 2018). The bivariate correlations among ERP component amplitude measures, age, sex, and RTs within a given session are shown in Table 2.

Table 2.

Correlations between all variables of interest to be inserted into the model structures (ERP amplitudes in μV; reaction times in ms; ages in years). ERP amplitudes were all measured at site Cz. Note: Analyses were done using pairwise deletion in order to exemplify the most accurate intercorrelations present within the data set; models employed FIML estimation to complete missing records.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1. N1S1	–
2. P2 S1	.13	–
3. N2 S1	.36***	.32***	–
4. P3 S1	.058	.40***	.40***	–
5. ES1	.011	.32***	.38***	.46***	–
6. N1 S2	.61***	.076	.20*	−.14	.040	–
7. P2 S2	.06	.59***	.15	.22*	.33*	.22*	–
8. N2 S2	.26*	.16	.56***	.19	.30*	.41***	.39***	–
9. P3 S2	.027	.13	.21*	.41***	.28*	−.066	.22*	.26**	–
10. E S2	.079	.13	.22*	.19	.35***	.099	.12	.05**	.36***	–
11. RT S1	.023	.067	.008	.036	.36***	−.005	.010	.011	.14	.33**	–
12. RT S2	.15	.019	.070	−.018	.25**	.034	−.053	.008	.10	.31**	.81***	–
13. Age	.18*	−.11	.11	−.23**	−.26**	.23*	−.058	.021	−.38***	−.27**	−.48***	−.47***	–
14. Sex	.022	−.058	−.094	−.071	.69	.091	−.099	−.053	−.27**	.13	.22**	.21*	.075	–

^*p < .05

^**p < .01

^***p < .001

p’s uncorrected for multiple tests.

Note: S1 = session 1; S2 = session 2; E = E-wave amplitude; RT = reaction time; sex is coded as follows: 0 = “male”, 1 = “female”

3.2. Age Represents Maturation of Brain and Behavior

Examination of the grand averaged ERPs and RTs separated by age group showed developmental trends from 8 to 12 years of age. Changes in ERP morphology are shown in Figure 2 with grand averages organized by age groups. Specific correlation coefficients describing the relationship of age with each ERP component and averaged response time are reported in Table 2. The ERP morphology was generally more organized with less variability in older children compared to younger children. Additionally, the 12-year-old children seemed to have earlier, narrower P3 components compared to the younger children in the sample, and also had the most negative (adult-like) E- wave components out of all age groups. Younger children’s E-wave components were much less negative with many tracings resting near baseline, especially in the first session.

With respect to RTs, older children tended to have a narrower distribution that clustered closer to the onset of the imperative stimulus when compared to younger age groups (see Figure 2). In contrast, the younger children had much more dispersed distributions of average RTs. The data suggest a developmental trend (r = −.48, p <.001) such that older children tended to perform more consistently, and more quickly than younger children in this sample. Collectively, these findings support the use of age as a predictor of both ERP component amplitudes and RTs among children in the sample; it seems that age, which is a trait-level indicator of maturation across multiple domains of functioning, does indeed have an influence on neural processing and task behaviors measured during the cued Go/No-Go task.

3.3. Manifest Paths

To determine if the significant bivariate correlations found in session 1 between non-adjacent ERP components (see Table 2) were independent of effects of confounding trait measures, four correlations were added to the model evaluated at each session: N1 with N2, P2 with P3, P2 with the E-wave, and N2 with the E-wave. The same correlational relationships were estimated in both the session 1 and session 2 models for the sake of symmetry and cross-comparison of the parameter estimates. Examination of the model fit statistics for each of the path models revealed that fit indices did meet the criteria set by Hu and Bentler (1999). Chi-square p values were .35 and .29, RMSEA values were .03 and .04, CFI values were 1.00 and .99, and SRMR values were .03 and .04 for session 1 and session 2, respectively. It is noteworthy that in each of the established manifest-level path models, the manifest variables had large residual variances. The data suggest that a significant proportion of the variance in neural processing was not being explained in the models (R²’s = .034 - .36 for session 1; R²’s = .053 - .31 for session 2).

The predictive coefficients indicated differences across sessions (see Figures 3A and 3B). Both of the models showed that one phase of processing significantly predicted the next from N1 through the E-wave. However, while the E-wave did significantly predict RT in session 1, (ß = .28, p = .001), it did not significantly predict RT in session 2 (ß = .17, p = .059). Additionally, for session 1 all four of the correlations between the non-adjacent ERP components were significant; for session 2 only the correlation between N1 and N2 was significant (see lines with double arrows below the manifest variables in Figures 3A and 3B). The positive coefficients between each measure of brain activity shown in Table 2 and in the positive coefficients in the manifest models in Figure 3 suggest an underlying positive manifold between all ERP amplitudes; i.e., participants with greater positive ERP components showed smaller negative ERP components. Whether this person-specific overall shift in voltage represents a true property of the person or some methodological artefact is unknown and difficult to ascertain give the present data. However, the structural equation models suggest the positive manifold holds over two separate measurement occasions and that the covariances are not likely accounted for by artefacts of the recording situation.

Considering the effects of trait variables, age was a significant predictor of all variables except for the P2 in the session 1 model. Older children tended to have smaller ERP component amplitudes and tended to respond faster than their younger peers during the Go/No-Go task. Session 2 results followed the same pattern as session 1, with significant age effects on only N1, P3, and RT. The only significant effect of sex in session 1 was on RT, with males responding faster than females. Session 2 data revealed additional sex effects, indicating that males tended to have larger P3 and E-wave component amplitudes in addition to faster response times when compared to females.

3.4. Latent Variable Path without State Effects

In order to better manage sources of variance in the data, including state-specific effects that may vary across sessions, we developed a latent variable model to examine the sequence of neural processing. Each latent variable was derived from the combination of the two sessions of a single ERP component measure (e.g., N1 latent variable form by N1_S1 and N1_S2). Thus, for instance, the N1 latent variable was comprised of only the variance in the N1 measure that was common across both sessions, removing the influence of measurement error and state-specific effects that varied across sessions (see Figure 4).

Figure 4.

The latent variable model of neural processing predicting a task behavior (e.g. response time) while controlling for variance attributed to two trait characteristics of the individuals (Age and Sex). Gray dotted arrows indicate non-statistically significant relationships, i.e., p > .05. Residual variances are reported below each manifest variable, and disturbances are reported at the upper left of each latent variable. All reported coefficients are standardized. Note: S1 = session 1 measure, S2 = session 2 measure; E_S1 = E-wave amplitude in session 1, E_S2 = E-wave amplitude in session 2.

Unlike the manifest-level analyses, model fit statistics for this latent-variable path model did not meet the criteria for “good fit” as defined by Hu and Bentler (1999); χ²(61) = 146.24, p < .001, RMSEA = .10, 90% CI [.08, .12], p < .001; CFI = .85; SRMR = .08. Importantly, the model fit indices suggested that there were non-trivial relationships in the model that were not yet accounted for in our conceptual model. However, the latent variables were well-defined, with each manifest variable significantly loading onto its respective latent variable (see Figure 4). The latent path did reveal significant predictive relationships from one phase of processing to the next from the N1 through RT. Examination of trait effects showed significant associations between age and the N1, N2, P3, and RT latent variables. The data suggested that older children had smaller ERP component amplitudes and faster response times than younger children. In addition, there were significant sex effects suggesting that males tended to have larger E-waves and faster response times than females.

3.5. Latent Variable Path with State Effects

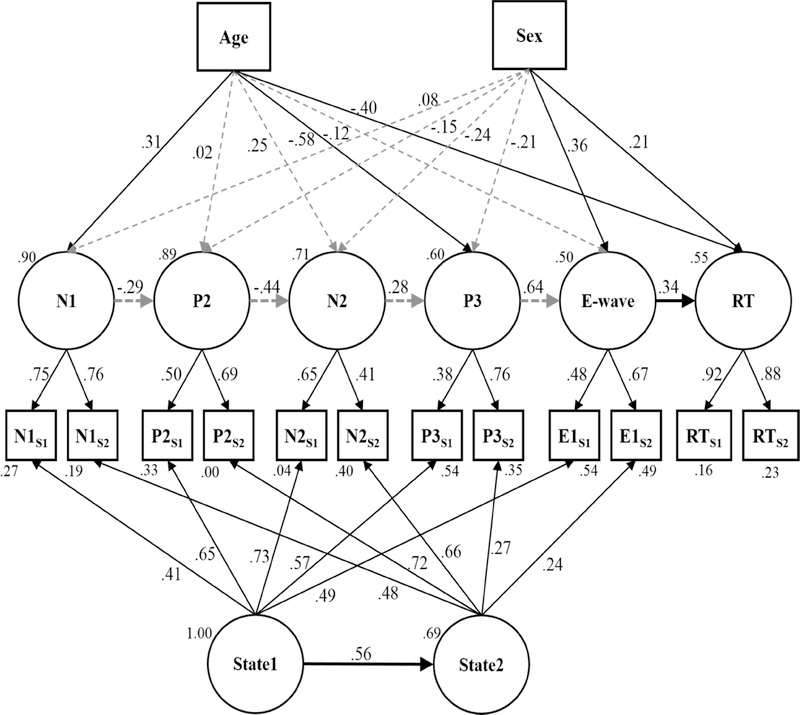
The final model we tested included the latent variable path described above along with the addition of two latent variables representing individual states that may vary from one session to the next (i.e., “State1” and “State2”). The purpose was to determine whether the measurement error subsumed in the residual variances was purely random, or whether a portion of that variance may represent states that shifted systematically across sessions (see Figure 5).

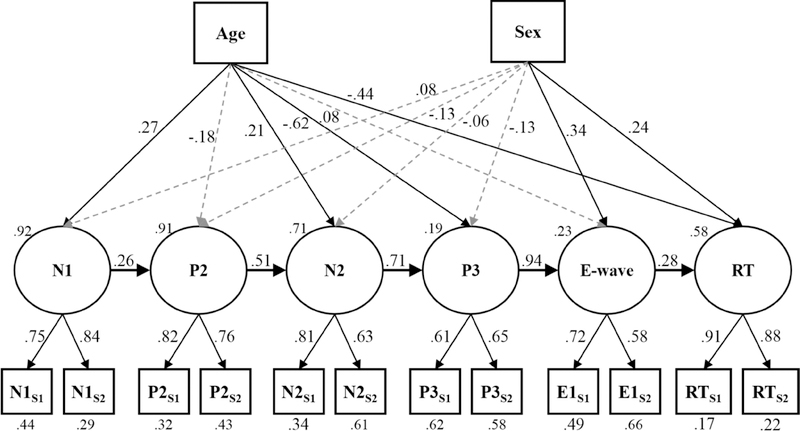
Figure 5.

The latent variable model of neural processing predicting a task behavior (e.g. response time) while controlling for variance attributed to changes in individual states between the sessions as well variance due to two trait characteristics of the individuals (Age and Sex). Gray dotted arrows indicate non-statistically significant relationships, i.e., p > .05. Residual variances are reported below each manifest variable, and disturbances are reported at the upper left of each latent variable. All reported coefficients are standardized. Note: S1 = session 1 measure, S2 = session 2 measure, E_S1 = E-wave amplitude in session 1, E_S2 = E-wave amplitude in session 2.

This model yielded excellent fit statistics, χ²(50) = 56.19, p = .25, RMSEA = .03, 90% CI [.00, .06], p = .84; CFI = .99; SRMR = .06. However, there was one instance of a Heywood case: the P2 component amplitude measured in session 2 had a negative residual variance. Examination of the 95% confidence interval around the estimated residual variance included 0 (estimate: −.46; 95% CI [−17.75, 16.84]), which implied that the problem may be due to random, normative sampling error rather than model misspecification (e.g., Van Driel, 1978). Thus, we re-ran the model with the residual variance for the P2 amplitude in session 2 fixed to 0 per recommendations in the literature (e.g., Chen, Bollen, Paxton, Curran, & Kirby, 2001; Dillon, Kumar, & Mulani, 1987; Gerbing & Anderson, 1987). After adding the constraint, parameter estimates in the resultant model were similar to the original model prior to fixing P2 amplitude to 0, and fit indices remained excellent, χ²(51) = 56.20, p = .25, RMSEA = .03, 90% CI [.00, .06], p = .84; CFI = .99; SRMR = .06. A comparison of the present model against the latent variable path analysis without state effects showed that adding in the latent state variables significantly improved model fit, Δχ²(10) = 90.04, p < .001.

Examination of the model showed that all manifest-level variables significantly loaded onto their respective latent variables (see Figure 5). However, there was a breakdown of the latent variable path such that only the E-wave significantly predicted RT. The predictions from N1 to P2 (ß = −.29, p = .065) and from P3 to the E-wave (ß = .64, p = .064) approached statistical significance. Although the path analysis only trended toward significance for most relationships, the data did reveal a sensible pattern of predictions across phases of neural processing during the task given the ideas presented in connectionist theory. A larger N1 amplitude was associated with a larger P2, and a larger P2 was associated with a larger N2. Then, a smaller N2 was associated with a larger P3. Larger P3 components trended toward predicting smaller E-waves, and larger E-wave amplitudes predicted faster response times during the Go/No-Go task. However, these paths should be interpreted with caution given that, in the present study, they do not reach statistical significance. Thus, to further explore the phenomenon, we tested variations of the model in Figure 5 to determine whether the temporal ordering of latent ERP component variables impacted the overall model, despite the non-statistically significant predictive coefficients.

In our first set of analyses, we temporally scrambled the order of the latent ERP component variables, retaining the overall structure of the model presented in Figure 5. A robust shift in Akaike’s Information Criterion (AIC; e.g., > 10) would indicate that altering the temporal ordering of the ERP component variables significantly harmed model fit. Table 3 below summarizes the model variants we tested along with their AIC and Δ AIC values relative to the model we present in Figure 5. The findings suggested that some models approached the criterion level with one model unable to converge, and others showed smaller relative shifts in AIC. It is worth noting that all of the models which converged produced multiple errors of non-positive definite matrices. Given these mixed, and possibly untrustworthy findings, we pursued a second set of analyses.

Table 3.

Additional models tested to confirm the necessary temporal ordering of latent ERP component variables.

Temporally-scrambled models of latent ERP component variables
Model Tested		AIC	Δ AIC
Original Model (see Figure 5)		7662.41	—
P2 ➔ P3 ➔ E-wave ➔ N1 ➔ N2 ➔ RT		7668.20	−5.78
E-wave ➔ P2 ➔ N1 ➔ P3 ➔ N2 ➔ RT		7671.38	−8.97
N1 ➔ N2 ➔ E-wave ➔ P2 ➔ P3 ➔ RT		7670.98	−8.57
N1 ➔ P3 ➔ N2 ➔ P2 ➔ E-wave ➔ RT		7660.44	1.98
P2 ➔ E-wave ➔ N2 ➔ P3 ➔ N1 ➔ RT		7668.41	−6.00
P3 ➔ N1 ➔ E-wave ➔ N2 ➔ P2 ➔ RT		7668.22	−5.80
N2 ➔ P2 ➔ N1 ➔ E-wave ➔ P3 ➔ RT		7666.54	−4.13
E-wave ➔ N1 ➔ P3➔ N2 ➔ P2 ➔ RT		7668.12	−5.71
P2 ➔ N2 ➔ N1 ➔ E-wave ➔ P3 ➔ RT		7662.40	0.01
P3 ➔ P2 ➔ N1 ➔ E-wave ➔ N2 ➔ RT		(No convergence)
Single latent ERP component variable omitted from sequence
Model Tested	Latent Variable Removed	AIC	Δ AIC
Original Model (see Figure 5)		7662.41	—
P2 ➔ N2 ➔ P3 ➔ E-wave ➔ RT	N1	(No convergence)
N1 ➔ N2 ➔ P3 ➔ E-wave ➔ RT	P2	(No convergence)
N1 ➔ P2 ➔ P3 ➔ E-wave ➔ RT	N2	(No convergence)
N1 ➔ P2 ➔ N2 ➔ E-wave ➔ RT	P3	7665.49	−3.08
N1 ➔ P2 ➔ N2 ➔ P3 ➔ RT	E-wave	7679.22	−16.81

In our second set of analyses, we used the model in Figure 5 as our base, keeping all latent variables in their temporal order except for one. The one latent variable we left out of the path was still included in the model and free to correlate with RT, but it was not part of the predictive path of latent ERP components. Not only does this approach test whether each latent variable in the predictive path is important to establishing the model, it also retains the theoretical lens of connectionist theory as well as the field’s traditional interpretation of ERP components as a representation of temporally-specific phases of neural processing. In other words, the models we tested in this second set of analyses suggest that any one latent ERP component variable may be related to the task behavior (RT), but may not be part of the predictive, systematic path as we have hypothesized based on the field’s classical interpretations and the connectionist theoretical perspective.

The models generally corroborate our (and the field’s) stance on the importance of the fully-recognized temporal ordering of the ERP components: three out of five models did not converge (see Table 3). Of the two models that did converge, only one model yielded good fit without a robust shift in AIC. Considering both the mixed results from the temporally-scrambled models, which produced multiple errors, and the relatively straightforward findings of the second set of models in which a latent variable was left out of the full path, we feel that we have provided sufficient evidence to support our nuanced interpretation of the predictive paths presented in our model in Figure 5.

The results of our hypothesized model shown in Figure 5 also yielded several significant trait effects that the individual brought to the first task session (i.e., age and sex). Age was a significant predictor of N1, P3, and RT latent variables, indicating that older children tended to have larger N1 amplitudes, smaller P3 amplitudes, and faster RTs than their younger peers. Additionally, there were significant sex effects on the E-wave and RT latent variables, showing that males tended to have more negative E-waves and faster RTs than females. There were trends toward significance for an age effect on the N2 (ß = .25, p = .085), and for a sex effect on the P3 (ß = −.21, p = .065).

Considering the latent state variables, State1 significantly predicted State2. The finding suggests that 1) there was a source of variance that was common across all ERP components measured within a single session, and 2) a significant proportion of that variance was systematic across sessions; that is, there are consistent individual differences in ERP amplitudes across the two measurement occasions. The model suggests that the supposed measurement error comprising the residual variances in the latent path model without latent state variables was not all random. Rather, there may have been an organized shift in the way the task was processed at the neural level across sessions, which contributed a significant amount of variance to the ERP component measurements.

Because the final model may not be considered a faithful representation of a LST-R model given the regressing of State2 onto State1, two additional models were tested. Firstly, instead of regressing one state on another, a latent trait variable was defined by the two latent state variables, with factor loadings fixed at 1. This model had the same fit values as reported above (χ2(51) = 56.20, p = .29; RMSEA = .03, 90% CI [.00, .06]; CFI = .99; SRMR = .06). Further examination of the variance explained by the higher-order latent trait versus the two latent states suggested that the trait accounted for significantly more variance in the manifest variables for session 1 (60.22%) and session 2 (51.27%) than either of the two latent states (15.84% and 23.72% for sessions 1 and 2, respectively). These data further confirmed the conclusion that the variance across sessions was systematic and likely represented an organized shift in voltages rather than a more random change in individual states (e.g., hunger, mood). The second tested model, which correlated the states rather than regressing one onto the other, also showed the same fit values. Thus, while these two models may represent valid variations of the original model from a statistical view point, the original model shown in Figure 5 was hypothesized a priori based on theories, traditional interpretation of ERP components, and the time order of occurrence of the manifest variables.

4. Discussion

The current investigation presents a unified model of ERP components that describes how systematic phases of brain activity from stimulus onset to response processing can predict a behavioral measure of the task in neurotypical children. Additionally, by including trait measures that each individual brings to the study prior to measurement of brain activity, the model explores how the traits might relate to one or more the brain measures representing processing phases as well as the task behavior. Inclusion of traits as predictive measures in the model also serves as a statistical control to account for some of variance found in physiological measures of each processing phase contributed by each trait.

The first step in the modeling effort began as a path analysis using manifest level variables. Analysis of each session separately revealed that both manifest path models achieved acceptable levels of model fit. The models showed that ERP components can be modeled as successive stages of processing in which one component predicts the next in chronological order beginning with the N1 and ending with the E-wave (see Figure 3). Furthermore, as expected, all of the coefficients of these predictions were found to be statistically significant. Importantly, the neural processing measured as the positive peak in the 400–650 ms window following the stimulus (i.e., P3) significantly predicted a phase of neural processing nearly 1000 ms later (i.e., the E-wave). In addition, the neural processing represented by the E-wave measure when modeled at the manifest level was found to significantly predict averaged RTs in the first session (p = .001) though not for the second session (p = .059). The two traits, Age and Sex, differentially related to ERP components, but the pattern of significant effects was not consistent across sessions.

While all the significant predictive coefficients of the ERP component and RT manifest variables ranged from .17 to .38, they had large residual variances, suggesting that the influence of measurement error may have been obscuring the ability to detect stronger relationships between brain activity and the task behavior. These findings may be explained in part by the ideas presented by Gavin and Davies (2008), namely that all psychophysiological measures, including ERP components, are comprised of multiple sources of variance. While the manifest path models attempted to control for two trait measures, other possible sources of variance were not controlled for or removed, and these resulting variances may still have been contributing to the measurement error term. For instance, state-specific effects that may have varied across sessions (e.g., strategies used to perform the task, fatigue, mood, etc.) or data processing effects (e.g., differences in the number of segments in each averaged ERP across subjects and sessions) could have confounded the measurements, thus leading to large residual variances and low predictive power.

4.1. The Benefits of a Latent Variable Approach

In order to reduce measurement error to obtain a better estimate the true nature of brain-behavior relationships in the data, the first theoretically-driven latent variable model was tested (see Figure 4). Latent variables were comprised of the common variance among the same ERP component or RT measure obtained during two separate sessions. Thus, use of latent variables effectively removes any state-dependent effects that may have varied across sessions, as well as any other sources of measurement error such as unintended methodological effects that may occur when processing physiological signals (e.g., individual participants may vary in the number of segments used to compute the averaged ERP).

Like the manifest path models, the first latent variable path analysis (see Figure 4) assessed the predictive relationship from one phase of processing to the next while controlling for variance related to two trait measures. In other words, model assessed to what extent more resource-intensive processing in one phase of processing, represented by larger ERP amplitudes, predicted the intensity of processing at the chronologically subsequent phase while accounting for variance contributed by traits of the individual. Though the model fit statistics for this latent-variable path model did not meet the criteria for good fit, several important pieces of information can be gleaned from the results. First, the latent variables were well-defined, with each manifest variable significantly loading onto its respective latent variable. Moderate-to-strong significant predictive coefficients (i.e., .26 to .94) from one phase of processing to the next suggested that, like the manifest path models, each ERP latent variable may represent related, sequential stages of information processing. In addition, the E-wave latent variable at the end of the sequence of neural processing predicted task behavior (i.e., RT); there was a significant, moderate prediction to RT by the latent E-wave variable in the present study (β = .28). Another advantage to the latent variable path approach is that one can more directly examine additional effects of trait variables on the underlying constructs represented by the latent variables in a similar manner as conducted with manifest variables. The significant patterns of predictive relationships of Age to the latent variables of N1, N2, P3 and RT, and of Sex to E-wave and RT are more similar to those of the manifest path model for the second session than those of the first session. But most importantly, the model fit indices suggested that there were non-trivial relationships in the model that were not yet accounted for in our conceptual model. Therefore, a second latent variable model was evaluated.

The first latent variable model assumed that any state effects within each latent variable were small and random within and across participants. This assumption was tested in the final model by including two additional latent state variables to the first latent model. Each new latent variable was derived from the variance common across all ERP components measured within a session (see Figure 5). Analysis of this final model revealed that all of the fit criteria suggested by Hu and Bentler (1999) were met. Both of the latent state variables were well-defined, with each manifest variable significantly loading onto its respective latent variable. Despite the addition of the state latent variables to the model, the latent variables of the ERP components remained well-defined with each manifest variable significantly loading onto its respective latent variable. The prediction of RT by the latent E-wave variable remained statistically significant (β = .34, p = .02). The effect was also an improvement over prior work showing only weak predictive ability from neural processing to task behavior (see Taylor et al., 2018). However, the addition of the state latent variables did result in smaller predictive coefficients between all the latent ERP components which were no longer statistically significant. This suggests that significant relationships between the latent ERP variables found in the latent path model without latent state variables (Figure 4) may have been spurious and driven more by the effects of the previously-unaccounted for latent state variables. However, it is also possible that the relative simplicity of the task itself introduced variability in the ERP component measures which may not exist in more cognitively-demanding tasks, such as a speeded Flanker task. Studies in adults have shown that increasing task difficulty, to an extent, can actually increase ERP component amplitudes and reduce variability in performance (e.g., Benikos, Johnstone, & Roodenrys, 2006). Several of the predictive paths in the present study did still approach statistical significance (i.e., N1 ➔ P2 and P3 ➔ E-wave), thus with some reduction in variability, researchers may be able to detect significant effects in the path, even with latent state variables.

The findings highlight the importance of considering state effects when analyzing and interpreting ERP data. In the present study, state effects most likely represented a systematic shift in ERP component amplitudes across sessions. Our follow-up analysis in which we examined a “pure” LST model indicated that a higher-order latent trait variable defined by the two latent states accounted for significantly more variance in the manifest variables than either latent state. Prior work has shown that ERP amplitudes can systematically shift following practice on a task regardless of changes in behavioral performance, providing evidence of neural plasticity as a function of learning or shifts in strategy (e.g., Pauli et al., 1994; Romero, McFarland, Faust, Farrell, & Cacace, 2008; Taylor, Gavin, & Davies, 2016). Future research may consider further exploring the nature of the shift in voltages between visits using refined techniques such as multilevel SEM. Such an approach may provide additional insights into learning at the neural level within- and between visits.

Also, when state effects were accounted for, the patterns of significant predictive relationships of two traits of Age and Sex were reduced slightly. Age predicted the latent variables of N1, P3 and RT but no longer N2. Sex predicted the latent E-wave and RT but no longer predicted P3. Thus, one might conclude that using a latent variable approach in which state-dependent effects are removed from the measures may provide a unique new view of the nature of brain-behavior relationships.

4.2. Understanding Individual Levels of Maturation from a New Perspective

Using bivariate correlations, the data indicated a significant relationship between the trait measure of individual levels of maturation (i.e., the Age variable) and the N1, P3, E-wave, and RT in both sessions (see Table 2). However, both at the manifest variable and latent variable levels, using a path analysis approach revealed a slightly different pattern of maturation effects (see Figures 3, 4, and 5). Despite what the bivariate correlations showed, and the prior work by other research groups that showed maturational effects of CNV amplitude (e.g., Hämmerer et al., 2010; Jonkman, 2006; Jonkman et al., 2003; Segalowitz & Davies, 2004; Taylor et al., 2016), our latent path models show no significant direct effect of maturation on the E-wave component of the CNV. Rather, the models suggest that maturation effects on the E-wave are mediated through the P3 component. This finding illustrates how relying on simple correlations rather than examining more comprehensive models may affect interpretations of brain-behavior relationships. The path analysis takes into account the variability of the prior components, including their unique Age effects. Specifically, when the effects of latent P3 variable are removed from the latent E-wave, it is only the N1 and P3 components along with RT that are significantly related to the Age variable. Thus, while the E-wave component appears to become more negative as the children become older as shown in Figure 2, our models suggest that this maturational effect that researchers previously identified using bivariate correlations is actually accounted for (i.e., mediated) by the maturational effects present in prior phases of neural processing, principally the P3 component. Thus, the path analyses in the present study showed no additional significant effect of age on the E-wave above and beyond what was already explained in the chronologically earlier component of the ERP. Thus, if investigators are interested in developmental effects or maturational differences between groups of children using ERP methodology, the investigator should consider using the related N1 or P3 ERP measures rather than the CNV measure alone in their statistical analyses.

Interestingly, the significant Age effects in path models also indicate that there were consistent unique maturation effects that account for variance in N1 and P3 components, and in RT. The data suggest that the age effects were not accounted for by prior phases of neural processing and may represent several different aspects of cognitive and behavioral maturation. In fact, Johnson and de Haan (2011) argue that Age may not be a single, non-changing construct; rather, the researchers suggest that Age can be conceptualized as unique maturation within a number of constructs, such as attention, motor control, and executive function. Thus, any single Age effect present in the path models may indicate development of any number of cognitive and behavioral abilities that are otherwise unaccounted for in the present models.

Additionally, the latent path models revealed significant Sex effects on the E-wave and RT latent variables, showing that males tended to have a more negative E-wave component and a faster RT than females. While the bivariate correlation of Sex with RT was significant, the bivariate correlation of Sex with the E-wave was not (r values of .04 and .13 for sessions 1 and 2, respectively). Interestingly, in the manifest path model for the first session the sex effect on the E-wave was minor and non-significant (β = .07, p = .36) but in the second sessions it was significant (β = .24, p = .005). This Sex effect on the E-wave is accounted for in part in the final latent path model by the difference of the loading factors of the E-wave on to the latent state variable; .49 vs .24 for session 1 and 2 respectively. Our findings support previous reports of developmental sex differences in the amplitude of ERP components and RT (Davies, Segalowitz, & Gavin, 2004; Dykiert, Der, Starr, & Deary, 2012; Gavin, Lin & Davies, 2019). In addition, by using SEM analyses, our results demonstrate that state effects should be included to fully comprehend the sex differences on the e-wave component.

4.3. Functional Associations of the Latent ERP Variables

Based on the functional associations established in the literature and reviewed in the Introduction, the sequence of neural processing may be labeled with more cognitively-specific constructs in place of the simple ERP component labels. For instance, rather than N1 ➔ P2 ➔ N2 ➔ P3 ➔ E-wave ➔ RT, one might suggest that the model could be conceptualized as Sensory ➔ Registration ➔ Discrimination ➔ Evaluation ➔ Anticipation ➔ Task Behavior (see Figure 1). We can assess the extent to which this suggested labeling scheme representing phases of neural processing is appropriate by employing more complex models. Specifically, future research could examine whether each phase of neural processing maps onto different cognitive constructs, like attention and executive function, assessed using additional behavioral measures. Such a model could also indicate whether the effect of Age is better conceptualized as maturation within specific cognitive abilities rather than as a simple unitary construct representing general development over time. However, more complex models require additional participants beyond that used in the present study.

4.4. Future Directions

The present study investigated only one of many possible brain-behavioral models that might be postulated to account for the brain activity observed during the multiple stages of cognitive processing from the presentation of a simple stimulus leading to a behavioral response. A number of variations to the base model or alternate models should also be explored. For instance, while our processing steps started with the N1 component, there are a number of other sensory-based components that occur chronologically earlier than the N1, such as the N20 and P50 (for a review, see Kappenman & Luck, 2012) that could be added to the model. Furthermore, the present study investigated the sequence of processing of cognitive ERP components based only on peak amplitude measured at a single scalp site, one of the most basic (and most common) measures of brain activity. Other approaches to measuring brain activity that might be more closely related to specific neural networks should be explored as well. In addition, given the limitation of sample size, the present study only investigated how two trait measures, Age and Sex, might relate to each stage of brain processing. In a similar manner, one or more other traits such as cognitive control, attentional abilities, and presence or absence of neurologically based diagnostic categories could be explored beyond the model presented here. However, as stated before, developing more complex models by increasing the number of variables and the number relationships in a model requires corresponding increases in the sample size to adequately evaluate the model.

4.5. Conclusions

The present study demonstrated the utility of combining principles of connectionist theory with sophisticated statistical approaches for understanding brain-behavior relationships in typically-developing children. The findings suggest that ERP components leading up to the task behavior can be conceptualized and modeled as phase sequences of neural processing in accordance with connectionist theory (Hebb, 1949; Landa et al., 2014; McNaughton & Nadel, 1990; Raftopoulos, 1997). To the best of our knowledge, this is the first investigation to model ERPs as a full sequence of systematic neural processing leading to task behavior. By modeling the full time course of an ERP as a phase sequence of neural processing, and by utilizing a latent variable path analysis approach, we were able to detect strong, stable predictive relationships between chronologically-ordered ERP components. Moreover, using a sequence of neural processing measures while accounting for trait and state measures, we were able to significantly predict task behaviors. Our findings highlighted the importance of considering multiple sources of variance, particularly state effects, when measuring and interpreting ERP components. In addition, we were able to detect unique effects of the Age and Sex variables on ERP components that may be confounded by more traditional analysis techniques like bivariate correlations. The established latent variable model holds promise for future work in exploring the functional associations of each phase of neural processing, which could be useful for better understanding brain and behavioral relationships across development and in clinical populations.

Highlights.

• Brain-behavior relationships are demonstrated using structural equation modeling

• Sequential phases of neural processing significantly predict response time

• The traits of age and sex significantly and differentially relate to ERP components

• State of individual participants accounted for variance in neural processing