Changes in shear wave propagation within skeletal muscle during active and passive force generation

Abstract

Muscle force can be generated actively through changes in neural excitation, and passively through externally imposed changes in muscle length. Disease and injury can disrupt force generation, but it can be challenging to separate passive from active contributions to these changes. Ultrasound elastography is a promising tool for characterizing the mechanical properties of muscles and the forces that they generate. Most prior work using ultrasound elastography in muscle has focused on the group velocity of shear waves, which increases with increasing muscle force. Few studies have quantified the phase velocity, which depends on the viscoelastic properties of muscle. Since passive and active forces within muscle involve different structures for force transmission, we hypothesized that measures of phase velocity could detect changes in shear wave propagation during active and passive conditions that cannot be detected when considering only group velocity. We measured phase and group velocity in the human biceps brachii during active and passive force generation and quantified the differences in estimates of shear elasticity obtained from each of these measurements. We found that measures of group velocity consistently overestimate the shear elasticity of muscle. We used a Voigt model to characterize the phase velocity and found that the estimated time constant for the Voigt model provided a way to distinguish between passive and active force generation. Our results demonstrate that shear wave elastography can be used to distinguish between passive and active force generation when it is used to characterize the phase velocity of shear waves propagating in muscle.

1. Introduction

Muscle can generate force actively through neural excitation or passively when stretched. Both methods contribute to our ability to interact with the physical world, and pathological disruptions to active and passive force generation can profoundly alter on functional abilities. Hence, many have estimated the influence of pathology on muscle force generation during a variety of tasks (Boyaci et al.; Moreau et al., 2012). Unfortunately, it can be challenging to separately identify passive from active contributions to net muscle force. The objective of this study was to determine if ultrasound-based shear wave elastography can be used for this purpose.

Passive tension develops when muscle is stretched beyond its slack length, due to loading of structures within the myofilaments (Granzier and Labeit, 2007) and the extracellular matrix (Gillies and Lieber, 2011). Active tension is generated by myosin-actin cross-bridges and transmitted through extracellular structures (Hill, 1968; Street, 1983). The shared structures contributing to passive and active forces in muscle make it challenging to distinguish them from each other. This can be an impediment to assessing the relative importance of changes in neural control from changes in muscle composition following disease or injury. For example, diseases such as cerebral palsy can affect passive and active structures, leading to altered material properties and impaired force generation (Lee et al., 2016; Tisha et al., 2018). Increases in collagen (Alnaqeeb et al., 1984; Ochala et al., 2004) and intramuscular fat (Sions et al., 2012) that accompany aging can also affect material properties and force generation, as can changes to the active structures associated with aging and immobilization (Balagopal et al., 1997; D’Antona et al., 2003; Gracies, 2005; Sions et al., 2012). While these structural changes to muscle have been well documented, their contributions to impairment remain difficult to quantify. Techniques that quantify passive and active contributions to muscle force could help resolve this challenge.

Ultrasound elastography is a non-invasive imaging technique for characterizing the material properties of biological tissues. There is a direct relationship between shear wave velocity and the material properties of unstressed, homogenous, isotropic materials. Unfortunately, none of these assumptions apply to muscle, with its long contractile fibers surrounded by a complex extracellular matrix. Furthermore, shear wave propagation depends not only on material properties of a tissue, but also stresses within that tissue (Hug et al., 2015; Martin et al., 2018). For these reasons, the precise relationship between the material properties of muscle, the force it is generating, and shear wave propagation remains unknown. Studies of passive muscle have examined changes in shear wave speed that depend on muscle length (Maisetti et al., 2012) and pathology (Brandenburg et al., 2016; Du et al., 2016; Jakubowski et al., 2018; Jakubowski et al., 2017; Lee et al., 2016; Rasool et al., 2018; Vigotsky et al., 2018). Studies of active muscle have reported changes with the level of activation (Nordez and Hug, 2010; Yoshitake et al., 2014). Most prior work has focused on the shear wave group velocity, but the viscoelastic properties of muscle result in shear wave dispersion that cannot be quantified by group velocity alone. Phase velocity, often parameterized using a Voigt model with viscous and elastic elements, can be used to describe shear wave dispersion (Gennisson et al., 2010; Hoyt et al., 2008). Hoyt et al. reported increased elasticity and viscosity of the Voigt parameters for several muscles but only considered a single level of contraction (Hoyt et al., 2008). Gennisson et al. examined a range of muscle forces but not in a manner that facilitated normalized comparison between subjects (Gennisson et al., 2010).

Our objective was to determine if ultrasound shear wave elastography could be used to distinguish between actively and passively generated forces within skeletal muscle. This was studied in the human biceps by measuring the phase velocity of propagating shear waves over a range of muscle forces. Muscle force was regulated either by changes in voluntary activation or through passive changes in muscle length. Phase velocity was characterized using a Voigt model and compared to characterizations available from the more commonly used group velocity. Our hypothesis was that the parameters of the Voigt model would allow us to distinguish between passive and actively generated forces. Our results have implications for separating these components of the net muscle force during a variety of normal and pathological conditions.

2. Methods

2.1. Participants

Sixteen healthy adults (10 for the main experiment, 6 for the control experiment) participated in this study (7 male and 9 female, age: 26 ± 4 years, height: 1.70 ± 0.1 m, body mass: 64 ± 11 kg). The group had no history of upper extremity injury or musculoskeletal disease. All subjects provided informed consent prior to data collection. The collection protocols were approved by the Northwestern University Institutional Review Board (STU00200422-MOD0002).

2.2. Experimental setup

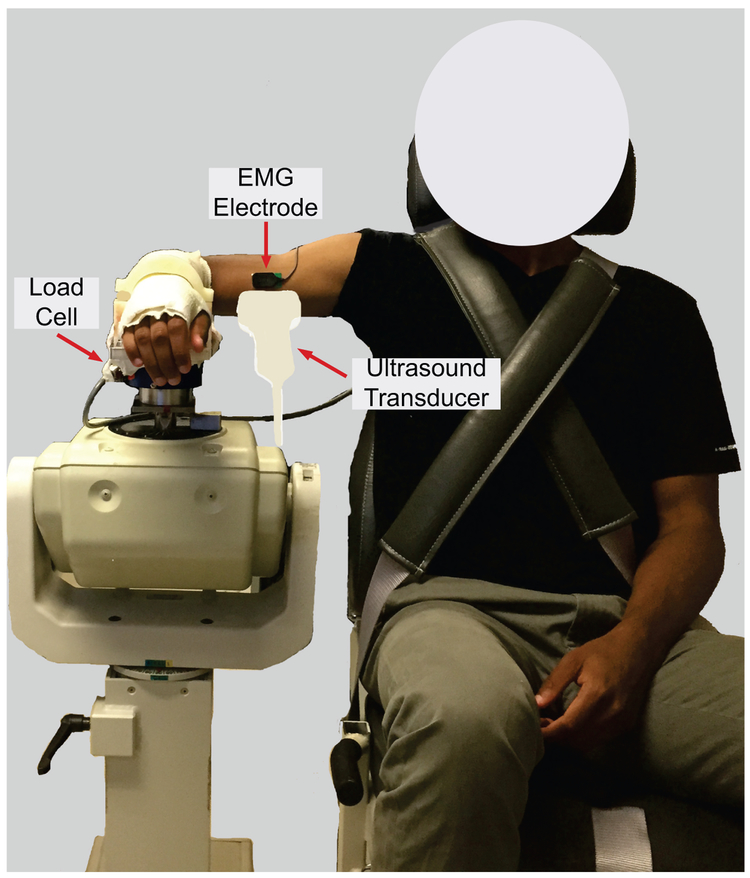
Subjects were seated in an adjustable chair (Biodex, Shirley, NY) with the trunk secured, shoulder abducted to 90° in the frontal plane, and forearm pronated to 90° (Fig. 1). Various elbow angles were used, as described in the protocols below. The forearm and wrist were fixed in a custom-made fiberglass cast attached to a six degrees of freedom load cell (Model 45E15A-U760-A, JR3, Inc., Woodland, CA) used to measure elbow moments. A single differential bar electrode (Delsys, Inc., Natick, MA) was placed on the belly of biceps brachii to monitor electromyographic (EMG) activity throughout the experiment.

Figure 1.

Experimental setup for data acquisition.

Ultrasound elastography measurements were made using an Aixplorer system (SuperSonic Imagine, Aix-en-Provence, France) with a linear transducer array (SL 15-4, Vermon, Tours, France) to induce shear waves and measure their resulting propagation. The transducer probe was hand-held and aligned with the fascicle plane using even, minimal contact pressure between the transducer and the skin to minimize the effect of contact pressure on shear wave measurement (Kot et al., 2012). Simultaneous B-mode imaging ensured that data were collected within the fascicle plane. Shear waves were induced by a standard sequence of focused ultrasound pulses (Bercoff et al., 2004), using the “MSK/Foot-Ankle” mode of the Aixplorer system. Measurements were obtained from a 10 mm × 25 mm (transverse × axial) region of interest (ROI) within the biceps brachii. The top of the ROI was about 3 mm below the aponeurosis.

2.3. Protocol and Data Acquisition

Two experiments were performed. The primary experiment (10 subjects) was designed to test independently the influence of muscle activation and passive stretching on shear wave velocity. The second experiment was designed to assess interactions between these variables.

2.3.1. Primary Experiment

At the beginning of each experiment, we collected three trials of maximum voluntary contraction (MVC) for elbow flexion with the elbow flexed at 90°. MVCs were used to scale subject effort during trials that required muscle activation. Ultrasound data were collected at different active and passive muscle forces as regulated with changes in activation level and muscle length, respectively.

In active conditions, subjects performed isometric elbow flexion (90° of flexion) at activation levels of 0, 10, 20, and 30% MVC. Real-time feedback of elbow torque was provided to assist with task completion. Subjects were required to maintain the desired torque within 5% MVC. The standard deviation of the measured torque was less than 0.8% MVC across all collected trials. These activation levels were chosen to prevent muscle fatigue and to avoid saturation of the shear wave velocity measurements.

For passive conditions, muscle force was regulated by changing the elbow angle (80°, 90°, 135°, and 180°) while shoulder posture remained constant, thereby changing length of the biceps brachii. Our convention was to measure the inner angle of the elbow so that 180° corresponds to full extension. Seven repetitions were made for each passive and active condition. Elbow torque and biceps brachii EMG were not recorded during passive trials in the primary experiment.

2.3.2. Control Experiment

A control experiment (6 subjects) was run to determine if the results of our primary experiment were applicable to different joint angles. In addition, EMGs and joint torques were recorded during the active and passive conditions, allowing us to confirm that the biceps brachii remained inactive during passive conditions. In the control experiment, we collected ultrasound data at elbow angles of 90° and 150° for the full range of activation levels (0, 10, 20, and 30 % MVC) tested in our primary experiment. Otherwise, the protocol for the control experiment was identical to that for the primary experiment.

2.4. Data Analysis

We used two measures from the ultrasound system. The first was shear group velocity (V_g), representing the propagation speed of the shear wave pulse at each pixel in the ROI (Fig. 2); results from all values (198 × 50 matrix) within the ROI were averaged to provide a single measure from each trial. The second measure was a high-speed (8 kHz) movie of tissue displacement used to calculate phase velocity, representing the frequency-dependent propagation of shear waves. Each pixel in the shear wave movie can be represented by a tissue displacement field u(x, z, t, n); x represents lateral position along the fascicles, z represents depth from the transducer, t is time, and n is push beam. Each image in the movie was averaged over the z-axis to improve signal-to-noise ratio, resulting in an averaged displacement field u(x, t, n). A Fourier transform was used to obtain a frequency-domain representation of the displacement field U(x, w, n), summarized by its amplitude A(x, w, n) and phase φ(x, w, n) at each angular frequency w. The phase velocity V_ϕ (w) can be estimated by changes in phase with distance (Chen et al., 2004).

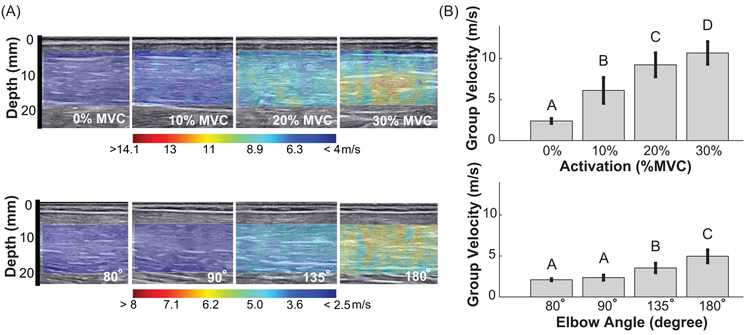
Figure 2.

(A) Example of shear wave group velocity color map superimposed on the B-mode image of biceps brachii muscle belly, as function of (Top) muscle activation at 0%, 10%, 20% and 30% MVC and (Bottom) passive elbow extension to angles of 80°, 90°, 135°, and 180°. Note the different scales for passive and active conditions. (B) Shear wave group velocity averaged across all subjects; error bars show standard deviations. Groups that do not share a letter indicate statistical difference (p < 0.05).

$$V_{\varnothing }(\omega )=\frac{\omega \Delta x}{\Delta \phi (x,\omega ,n)}$$ (1)

A Voigt model, consisting of an elastic spring and a viscous dashpot arranged in parallel, was fit to phase velocity (Chen et al., 2004; Gennisson et al., 2010; Hoyt et al., 2008). Assuming a planar shear wave propagating in an isotropic and homogenous Voigt material, the equation governing the phase velocity can be expressed as:

$$V_{\varphi }(\omega )=\sqrt{\frac{2({{\mu }_0}^2+{\omega }^2{{\mu }_1}^2)}{\rho ({\mu }_0+\sqrt{{{\mu }_0}^2+{\omega }^2{{\mu }_1}^2)}}}$$ (2)

where ρ is the density of muscle, w is the angular frequency, μ₀ is the shear elasticity, and μ₁ is the shear viscosity. Density ρ was assumed to be fixed at 1060 kg/m³ (Mendez and Keys, 1960). A nonlinear least-square algorithm (lsqcurvefit; Mathworks, Natick, MA) was used to estimate μ₀ and μ₁ from V_ϕ (w) for all experimental conditions. The strain response of a viscoelastic material is time-dependent. For a Voigt model, this time-dependence can be characterized by the time constant $\tau =\frac{{\mu }_1}{{\mu }_0}$. Phase velocity is influenced by the intrinsic material properties of muscle and muscle tension (Hug et al., 2015; Martin et al., 2018). Parameters of the estimated Voigt model must be interpreted in this context and not considered a direct measure of the intrinsic material properties of muscle.

2.5. Statistical Analysis

Our objective was to evaluate how viscoelastic parameters of a Voigt model characterizing shear wave propagation vary with active and passive changes in muscle force. We used linear mixed-effect models to evaluate this relationship. Separate models were used for active and passive conditions in the primary experiment. Activation level (0%, 10%, 20%, 30% MVC) was treated as a fixed factor for the active condition; elbow angle (80°, 90°, 135°, 180°) was a fixed factor for the passive condition. Subjects were treated as a random factor for both conditions. Shear elasticity, shear viscosity, time constant and shear wave group velocity were dependent factors. We observed unequal variances across treatment groups. Therefore, the variance for each group was estimated as part of the mixed-effect model. Tukey’s post hoc test was used to evaluate the difference between levels of all significant factors.

Given that group velocity is often used to estimate shear elasticity assuming that ${\mu }_0=\rho \times V_g^2$, we compared the relationship between the group velocity estimated elasticity and the elasticity estimated from fitting a Voigt model to the phase velocity. Though this relationship between group velocity and shear elasticity is commonly used, it is important to remember that tension can also lead to changes in shear wave propagation (Hug et al., 2015; Martin et al., 2018). Nevertheless, this equation provides a simple means to compare our measures of group velocity with the parameters of the Voigt model fit to our phase velocity dispersion curves.

A linear mixed-effect model was also used to analyze control experiment results. Since a full-factorial design was used in the control experiment, a single model was used, with activation level and elbow angle treated as fixed factors and subjects as a random factor. The remainder of the analysis was as described for the primary experiment.

Statistics were performed in MATLAB (2014a, Mathworks, Natick, MA) and R (Version 3.0.2, RStudio Inc., Vienna, Austria). Significance was evaluated against a p value of 0.05.

3. Results

In our primary experiment, shear wave group velocity increased monotonically with activation and muscle length for all subjects (Fig. 2). There was a significant effect of activation (p < 0.001) on group velocity, and the values at each activation level differed significantly (all p < 0.001). There was also a significant effect of joint angle (p < 0.001) on group velocity, with significant difference between the group velocity measured at all joint angles (all ρ < 0.001), except between 80° and 90° (p = 0.643). The lack of a significant difference between these shortest muscle lengths may result from the muscle remaining slack in both postures.

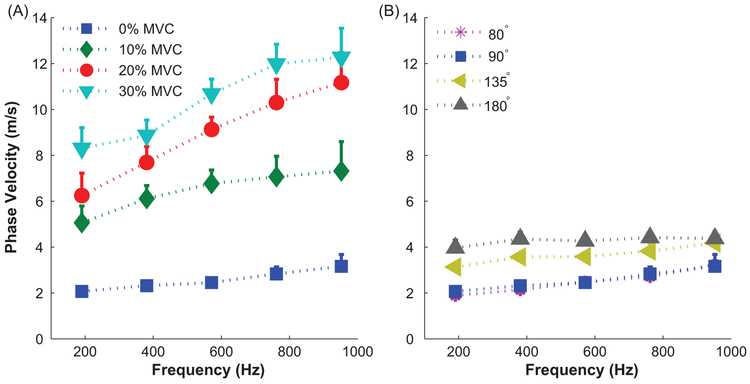
Phase velocity also changed with changes in passive and active muscle forces. The frequency dependence of the phase velocity dispersion curves was more pronounced during active changes in muscle force than during passive changes (Fig. 3). A Voigt model was fit to each dispersion curve (average R² = 0.86 ± 0.16, active; average R² = 0.74 ± 0.24, passive). The lower R² for the passive curves resulted from nearly flat curves across the measured frequencies.

Figure 3.

Mean shear wave dispersion curve in biceps brachii for a representative subject. Error bars are +1 standard deviation. (A) Increases in muscle force with activation. All measurements made with the elbow extended to 90 deg. (B) Increases in muscle force with passive stretching.

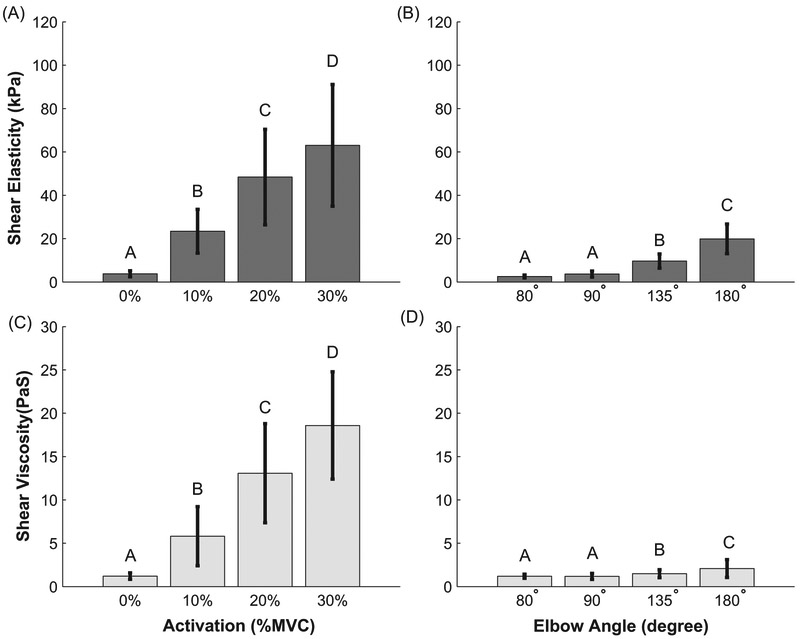
The shear elasticity and viscosity parameters fit to the phase velocity dispersion curves changed significantly with active and passive changes in muscle force (Fig. 4). During active changes in force, the shear elasticity (p < 0.001) and shear viscosity (p < 0.001) increased significantly with increased activation level. There were significant differences in elasticity and viscosity between all activation levels. Under passive force modulation, we found a significant effect of joint angle on shear elasticity (p < 0.001) and shear viscosity (p < 0. 001), except for between the joint angles of 80° and 90° (p ~1, both parameters).

Figure 4.

Mean shear elasticity and shear viscosity extracted from Voigt model fit to the dispersion curves. Error bars show +/− 1 standard deviation. Figures (A) and (C) correspond to active conditions. Figures (B) and (D) correspond to passive conditions. Groups that do not share a letter indicate statistical difference (p<0.05).

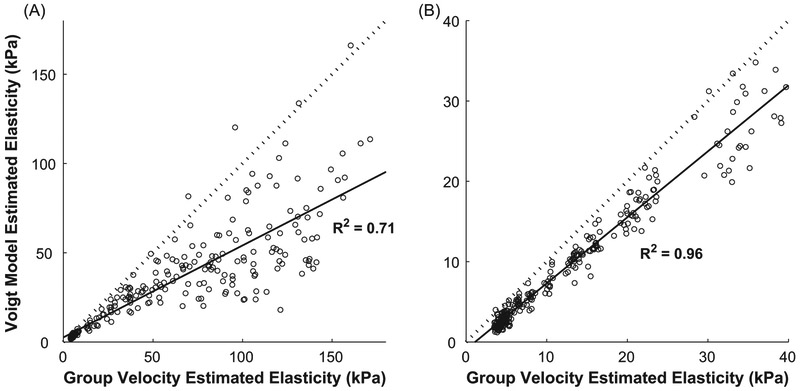
The elasticity estimated from the measured group velocity was correlated with the elasticity of the Voigt model fit to the phase velocity dispersion curves (p < 0.001, R² = 0.71 for active, R² = 0.96 for passive), but these values were different (Fig. 5). The slope of the relationship was lower for the active (0.51 ± 0.02) than the passive (0.82 ± 0.01) conditions, demonstrating that there are differences in the estimates of shear elasticity obtained from group velocity and phase velocity and that these differences are greatest for active muscles.

Figure 5.

Comparison of the elasticity estimated from the measured group velocity to that estimated from the Voigt model for active conditions (A) and passive conditions (B). The solid line shows the least square fit to the data. The dashed line has a slope of 1.0, which would indicate perfect correspondence between the two estimates of elasticity.

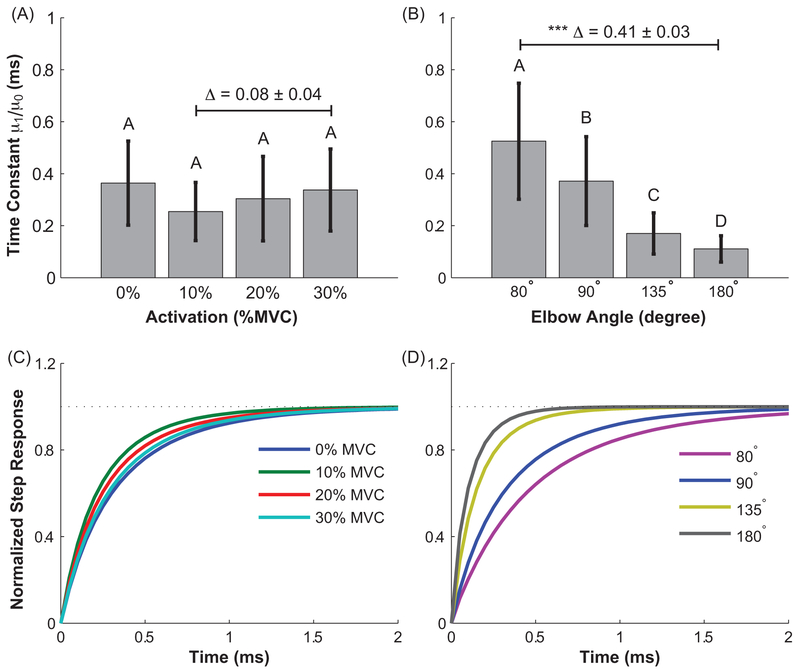
The viscoelastic time constant for the estimated Voigt models changed significantly with increases in passive (p < 0.001) but not active muscle forces (p = 0.08). Passive differences were significant across all elbow angles (Figs. 6 a & b). The differences were visualized by simulating the strain response of the Voigt model to a step change in stress; simulated responses were normalized to their maximum value to facilitate comparisons across experimental conditions (Figs. 6 c & d). We observed similar strain responses across all activation levels. In contrast, a much faster strain response was observed at longer (180°) than shorter (80°) passive muscle lengths.

Figure 6.

The time constant of the Voigt model for active (A and C) and passive (B and D) conditions. Top row shows the average results across all subjects. The error bar indicates the standard deviation across subjects. Δ indicates the mean difference between the selected groups. Groups that do not share a letter indicate statistical difference. The bottom row illustrates the simulated step response of the average estimated Voigt models for each experimental condition.

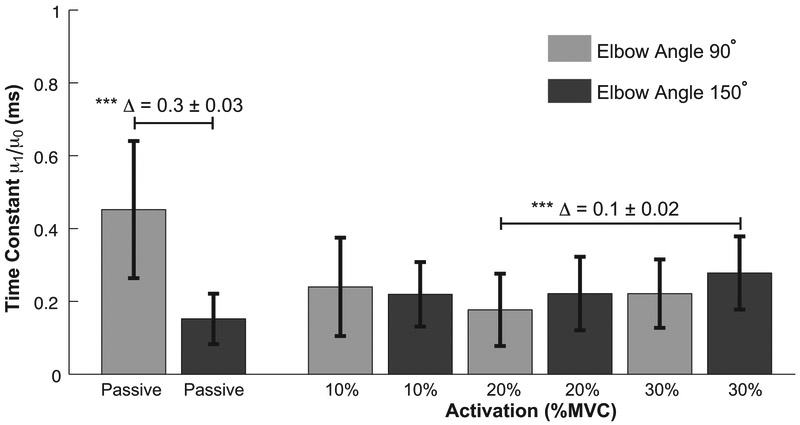
The results of the control experiment were largely consistent with those reported above for the primary experiment. While changes in passive muscle length had a large effect on the viscoelastic time constant (p ~ 0; Δ = 0.3 ± 0.03), the estimated time constant was similar across all active conditions at both joint angles (Fig. 7). The only statistically significant difference in the active conditions was between the time constants estimated at 20% MVC and 90°, and that estimated at 30% MVC and 150° (p < 0.001, Δ = 0.1 ± 0.02).

Figure 7.

The time constant of the Voigt model for passive and all active conditions at elbow angles 90° and 150°. The error bar indicates the standard deviation across subjects. Δ indicates the mean difference between the selected groups. The groups with statistical difference are indicated (*** p < 0.001).

The biceps brachii remained inactive during the passive experiments. The average EMG recorded across all subjects and postures was 0.28 ± 0.27% MVC. Finally, the elbow torque changed by an average of 0.5 ± 0.2 Nm as the elbow was extended from 90° to 150°. When normalized by strength, this corresponded to 1.4 ± 0.4% MVC. Hence, the change in muscle force during the passive conditions was much smaller than that in the active conditions.

4. Discussion

This study examined if shear wave ultrasound elastography could be used to distinguish between actively and passively generated forces in muscle. We found that shear wave group velocity and phase velocity increased with passively and actively generated increases in force, but that more information can be obtained from phase velocity. Phase velocity was characterized by a Voigt model with elastic and viscous components, both which increased with muscle force. However, there were distinct differences in how phase velocity changed during active and passive force generation. The ratio of viscosity to elasticity remained nearly constant during active contractions but decreased significantly for increasing passive force. These results demonstrate that shear wave elastography is sensitive to the different mechanisms responsible for transmitting actively and passively generated muscle forces and suggest that it may be possible to distinguish which mechanisms are responsible for the net forces present during more functionally relevant conditions.

The measured shear waves were used to estimate group velocity and phase velocity. Phase velocity was parameterized over the frequency range of our measurements (~200-1000 Hz) using a Voigt model. We observed increases in group velocity with muscle length and activation, consistent with previous studies (Bouillard et al., 2011; Maisetti et al., 2012; Sasaki et al., 2014). Often it is assumed that group velocity is a proxy for elasticity $({\mu }_0=\rho \times V_g^2)$. Our results demonstrate that there are substantial differences between shear elasticity estimated from group velocity and that estimated from phase velocity (Fig. 5); only the latter accounts for the viscoelastic properties of muscle. When viscosity is negligible, shear elasticity estimated from phase velocity will equal that estimated from group velocity. The relationship between group velocity and phase velocity depends on the mechanical properties of the material and the frequency content of the propagating waves. We explored this relationship for our measurements (Supplementary materials) and found that errors are strongly dependent on the material viscosity. Materials with a large time constant (ratio of viscosity to elasticity) exhibit a larger error between the true elasticity of the material and that estimated from group velocity. These results suggest that group velocity should be interpreted carefully when used to estimate material properties of viscoelastic tissues such as muscle. Preferably, phase velocity would be used instead.

The elasticity of the Voigt models increased with increasing active and passive forces. Under active conditions, shear elasticity increased ~16-fold from passive to 30% MVC, an increase comparable to that reported for the brachialis by Gennisson (Gennisson et al., 2010), the only study we know that made similar measure of viscoelasticity. During passive conditions, shear elasticity increased ~ 8-fold as the elbow was extended from 80° to 180°. This is slightly larger than reported by Gennisson, possibly reflecting differences in passive properties of brachialis and biceps brachii.

Shear viscosity also increased with increasing active and passive forces. In active conditions, viscosity increased ~16-fold from passive to 30% MVC. The shear viscosity reported by Gennisson was more variable and lower in magnitude than we observed (Gennisson et al., 2010), possibly reflecting the larger range of activations we tested. Furthermore, Gennisson used constant loads not normalized to subject strength, likely leading to more variable muscle stresses than in our experiment. During passive stretching, shear viscosity increased ~ 2-fold across the tested range of elbow angles. Gennisson did not demonstrate a significant effect of length on shear viscosity but did note a trend towards increasing shear viscosity with increased brachialis length.

The time constant of the estimated Voigt models varied differently in active and passive conditions. It decreased significantly as passive tension increased from biceps lengthening (Figs. 6B & 6D). The nonlinear change in biceps length with elbow angle (Murray et al., 1995) may have contributed to the unequal changes in the time constant between 90° and 135° compared to that between 135° and 180°. Regardless, this implies a more elastic behavior as biceps was lengthened. In contrast, the time constant remained nearly invariant during active contractions (Figs. 6A & 6C), due to proportional increases in elasticity and viscosity. This relationship held even at longer muscle lengths where active and passive forces were present (Fig. 7). It remains to be seen if this finding holds for muscles with substantially more passive force than the biceps has within its physiological range.

The differential changes in shear wave propagation may result from different structures transmitting force during active and passive conditions. Both titin and the extracellular matrix (ECM) have been suggested to be the primary load bearing structure within whole muscle during passive stretching and both exhibit elastic properties (Freundt and Linke, 2019; Lieber and Friden, 2019). The small changes in viscosity with passive loading are consistent with the strain-insensitive behavior of viscosity at the single fiber level (Meyer et al., 2011). The increase in elasticity during activation is likely due to increasing numbers of attached crossbridges (Ford et al., 1981). The corresponding increase in viscosity may result from the sliding of actin and myosin filaments (Moss and Halpern, 1977) or be a byproduct of crossbridge cycling (Schoenberg, 1985).

4.1. Limitations

There are several limitations to consider when interpreting our findings. The first is that we used a Voigt model to parameterize the phase velocity dispersion curves. It was chosen based on previous work (Chen et al., 2004; Gennisson et al., 2010; Hoyt et al., 2008), its simple composition with only two parameters (μ₀, μ₁), and because it fit the data well. Alternative rheological models, including fractional power models, have also been used to characterize biological tissue including muscle (Dai et al., 2015; Klatt et al., 2010; Sack et al., 2013), sometimes exhibiting superior fits than a Voigt model (Yasar et al., 2013). Our ultrasound system limited the frequency resolution of our measurements (Fig. 3), making it difficult to assess these more complex models.

The interpretation of the shear moduli parameters estimated from elastography remains an active area of research for muscle. Due to the heterogenous, non-isotropic structure of muscle and the load-dependence of shear wave propagation (Martin et al., 2018), it is unlikely that the parameters estimated by shear wave elastography can be directly interpreted as the mechanical properties of muscle. Still, our results demonstrate that they provide useful information about muscle state even if the direct connection to muscle mechanics remains unclear at this time.

Finally, our measurements were made only in the human biceps brachii. It is not yet clear how changes in muscle architecture influence shear wave propagation.

4.2. Conclusions

We evaluated how shear wave propagation in muscle is altered by changes in passive and active muscle force. We used a Voigt model to characterize phase velocity dispersion curves and compared those results to commonly used estimates of group velocity. We demonstrated through experiments and a theoretical analysis that measures of group velocity can overestimate the shear elasticity of muscle, particularly during active contractions. We also showed that the parameters of an estimated Voigt model provide a means to distinguish between forces that are generated passively and those generated actively. This distinction can be made by examining the viscoelastic time constant for the estimated Voigt models. It remains to be seen if this approach can be extended to conditions in which substantial passive and active forces are present simultaneously in muscle.