A Varying-Coefficient Generalized Odds Rate Model with Time-Varying Exposure: An Application to Fitness and CVD Mortality

Summary:

Varying-coefficient models have become a common tool to determine whether and how the association between an exposure and an outcome changes over a continuous measure. These models are complicated when the exposure itself is time-varying and subjected to measurement error. For example, it is well known that longitudinal physical fitness has an impact on cardiovascular disease (CVD) mortality. It is not known, however, how the effect of longitudinal physical fitness on CVD mortality varies with age. In this paper, we propose a varying-coefficient generalized odds rate model that allows flexible estimation of age-modified effects of longitudinal physical fitness on CVD mortality. In our model, the longitudinal physical fitness is measured with error and modeled using a mixed effects model, and its associated age-varying coefficient function is represented by cubic B-splines. An expectation-maximization (EM) algorithm is developed to estimate the parameters in the joint models of longitudinal physical fitness and CVD mortality. A modified pseudo-adaptive Gaussian–Hermite quadrature method is adopted to compute the integrals with respect to random effects involved in the E-step. The performance of the proposed method is evaluated through extensive simulation studies and is further illustrated with an application to cohort data from the Aerobic Center Longitudinal Study.

1. Introduction

Physical inactivity, mainly due to a sedentary lifestyle, has been shown to have a positive association with cardiovascular disease (CVD) mortality (Blair et al., 1996; Kohl 3rd, 2001; Mora et al., 2007; Nocon et al., 2008). The Aerobic Center Longitudinal Study (ACLS) involves patients in the Cooper Clinic in Dallas, TX, who attended periodic preventive medical examinations, along with health and lifestyle behaviors consultation. The longitudinal measurements of cardiorespiratory fitness (“fitness”), an objective measure for physical activity (PA, of Sports Medicine, 2013), provides a unique opportunity to advance the current understanding of the association between longitudinal fitness and CVD mortality.

Using a total of 3,980 patients enrolled in the study from 1970 ~ 1980 with follow-up till 2003, we first explore the association between the baseline fitness and CVD mortality using the proportional hazards (PH) (Cox, 1972) model. Adjusting for age, gender, BMI, family history of CVD, and smoking status, the results from the PH model are summarized in Table 1. It shows that baseline fitness has an inverse association with CVD mortality (coefficient= −0.013), but the effect is not significant (p value= 0.572). However, if we consider age as an effect modifier of fitness and include “age×fitness” in the model, we find the interaction term is significant (p value= 0.050). This indicates that the effect of fitness on CVD mortality changes over age, which can be depicted through an age varying coefficient.

Table 1.

Fit PH Models for ACLS Baseline Data

	Without Interaction			With Interaction
Variable	Estimate	StDev	P value	Estimate	StDev	P value
BMI	0.103	0.030	0.001	0.110	0.030	0.000
FamilyCVD	0.124	0.168	0.462	0.133	0.168	0.427
Smoke	0.218	0.233	0.349	0.230	0.233	0.323
Female	−0.342	0.371	0.356	−0.348	0.371	0.347
AGE	0.117	0.011	0.000	0.181	0.035	0.000
Fitness	−0.013	0.023	0.572	0.192	0.107	0.072
AGE×Fitness	-	-	-	−0.004	0.002	0.050

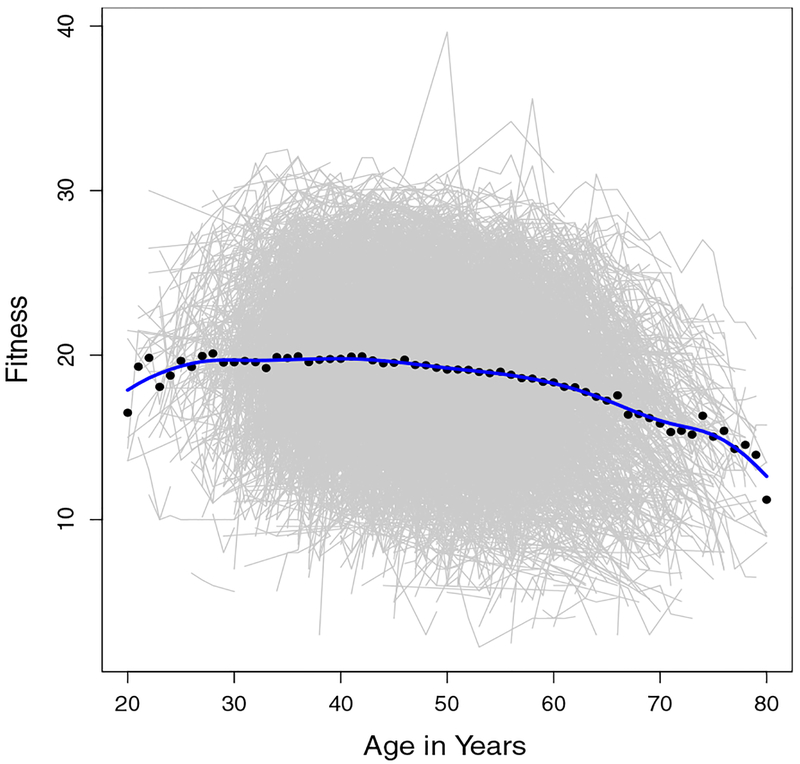
Moreover, it is well-known that there are changes in the overall level of fitness with age. Figure 1 displays the fitness profiles for all participants in the ACLS by age. It can be seen that the mean fitness is around 20 and gradually decreases with age. Changes in fitness that occur during follow-up may have important influence on CVD mortality but cannot be detected when the analysis relies on a single baseline assessment. Additionally, even though the standard exercise test is an objective measure of PA which is superior to self-report, the values still appear to be subjected to measurement error. This measurement error could be due to true measurement error in the equipment or small biological fluctuations in the subjects fitness level on the day of measurement (e.g., a bad night of sleep). We seek a model that allows for a time-varying effect of fitness on CVD mortality, where fitness is subject to measurement error.

Figure 1.

Profile Plots of Longitudinal Fitness. (This figure appears in color in the electronic version of this article.)

In practice it is challenging to capture the association between a time-varying covariate and a survival outcome with a varying-coefficient model. Previous studies focused on either estimation of varying coefficients for time-independent variables (Cai and Sun, 2003; Tian et al., 2005), or fixed coefficients for time-dependent variables (Fisher and Lin, 1999; Zeng and Lin, 2006). To the best of our knowledge, there is no literature on survival models that consider both a time-varying covariate and its varying-effect over another variable. What complicates our situation more is that the exposure of interest is an endogeneous covariate, which are time-dependent measures that typically require the subject to survive to be measured and commonly measured with error (Rizopoulos, 2012), so that the previous methods do not apply.

The most popular tools in modeling the association between a survival outcome and an endogeneous covariate with measurement error are joint models. Specifically, a mixed effects model with normal random effects is commonly assumed for the longitudinal observations, and standard survival models are used for the survival outcome. There have been plenty of work on joint models which combine the linear mixed model with PH model (e.g.,Wulfsohn and Tsiatis (1997); Bycott and Taylor (1998); Zeng et al. (2005); Zeng and Cai (2005)). Furthermore, the proportional odds (PO) joint model has also been studied in the literature when the PH assumption is violated (Andrinopoulou et al., 2014). Under the Bayesian framework, Köhler et al. (2017) and Andrinopoulou et al. (2017) studied the nonlinear effect of the longitudinal predictor using P-splines. Various extensions of joint models have been made to account for complex data structures in practice, with considerations of multiple longitudinal outcomes (Song et al., 2002; Brown et al., 2005; Rizopoulos and Ghosh, 2011; Moreno-Betancur et al., 2017), competing risks (Elashoff et al., 2008; Huang et al., 2011), and cure rate models (Yu et al., 2004; Brown and Ibrahim, 2003). More overviews and extensions can be found in Tsiatis and Davidian (2004) and Rizopoulos (2012).

The existing joint models do not allow varying coefficients, so they cannot be used to estimate the age-related association between fitness and CVD mortality. Therefore, we develop a novel joint modeling framework considering the following three features: (1) longitudinal process of fitness, (2) survival process of CVD mortality, and (3) the age-related fitness effects. For the longitudinal process, we assume a flexible pre-specified time function with random coefficients to accommodate subject-specific longitudinal trajectories. For the survival process, we propose to incorporate the generalized odds rate (GOR) model (Dabrowska and Doksum, 1988; Scharfstein et al., 1998; Zhou et al., 2017a), including the PH model and the PO model (Bennett, 1983) as special cases. To investigate the age-related fitness effect on CVD mortality, we include a novel age-dependent varying coefficient for longitudinal fitness in the survival model. The proposed model can improve the understanding of how age-related fitness affects CVD mortality, which can provide direct guidance in behavior consultation.

The rest of the article is organized as follows. We first introduce the notations and model definitions in Section 2. The estimation procedures for the proposed joint model are discussed in Section 3, where the details of the expectation-maximization (EM) algorithm and the corresponding variance estimation are presented in Section 3.3 and Section 3.4, respectively. The results of extensive simulation studies are performed in Section 4. To study the nonlinear age-dependent effect of fitness on CVD mortality, we apply the proposed methods to the ACLS data in Section 5. The final discussion and conclusions are summarized in Section 6.

2. Model and Notation

Consider a longitudinal study of n subjects. Let T_i denote the failure time of interest for subject i, i = 1, … , n. Let Z_i denote a vector of baseline covariates of subject i, A_i(s) denote their age at time s, and W_i(·) denote the true underlying time-varying exposure process, such as the longitudinal physical fitness process in our application. Note that A_i ≡ A_i(0) is the baseline age and A_i(s) = A_i+s. The filtration of W_i(·) is denoted by ${\mathcal{W}}_i(t)=\left\{W_i(s):s⩽t\right\}$. Let 0Λ_i(t) denote the conditional cumulative hazard function of T_i given Z_i, A_i and ${\mathcal{W}}_i(\cdot )$. We propose the following varying-coefficient generalized odds rate model for Λ_i(t):

$${\Lambda }_i(t)\equiv \Lambda \left\{t|{\mathit{Z}}_i,A_i,{\mathcal{W}}_i(\cdot )\right\}=G_r\left({\int }_0^t{\lambda }_0(s)\text{exp}\left[{\mathit{Z}}_i^{\prime }\mathit{\beta }+\psi \left\{A_i(s)\right\}{W}_i(s)\right]ds\right),$$ (1)

where λ₀(t) is an unspecified baseline hazard function, β is a vector of coefficients for Z_i, ψ {A_i(s)} is an age-varying smooth coefficient function for W_i(s), and G_r{·} is a pre-specified increasing transformation function indexed by a non-negative argument r. In particular, in our implementation, we take the transformation function as G_r(x) = r⁻¹ log(1 + rx) when r > 0 and G_r(x) = x when r = 0, which reduces to a PH model with r = 0 and a PO model with r = 1 (Zeng et al., 2016). In addition, we approximate the smooth coefficient function using cubic B-splines, i.e. $\psi (a)={\sum }_{l=1}^L{\mathit{\gamma }}_l{B}_l(a)$, where B_l(·), l = 1, ⋯ , L, are the B-spline basis functions.

The whole trajectory of the true longitudinal exposure W_i(·) is usually not obtainable in practice. Instead, we can only observe Y_i ≡ (Y_i,1, ⋯, Y_i,mi), where Y_i,j = Y_i(t_i,j), j = 1, … , m_i, are m_i contaminated measurements of W_i(·), at a sequence of intermittent observation times t_i (t_i,1, … , t_i,mi), with 0 ⩽ t_i,1 < ⋯ < t_i,mi. We assume the following random effects model for Y_i(t):

$${\mathit{Y}}_i(t)=W_i(t)+{ϵ}_i(t)\equiv g(t{)}^{\prime }{\mathit{b}}_i+{ϵ}_i(t),$$ (2)

where g(t) is a d-dimensional vector of known functions of t, for example, g(t) = (1, t)′ corresponds to a linear function of t with d = 2, b_i = (b_i1, … , b_id) is a d-dimensional vector of random effects assumed to follow a multivariate normal distribution with mean μ and variance-covariance matrix D, and the error process ϵ_i(t) is an independent mean-zero normal process with variance σ².

3. Estimation Procedure

3.1. Complete Likelihood Function

In the presence of censoring, we observe V_i = min(T_i, C_i) and δ_i = I(T_i ⩽ C_i), i = 1, … , n, where C_i is the right censoring time of subject i and is assumed to be independent of T_i given Z_i and A_i. The observed data for subject i can be denoted as O_i = (V_i, δ_i, A_i, Z_i, t_i, Y_i) and the parameters to be estimated include θ = (β, γ, λ₀, μ, D, σ²), where γ = (γ₁, … , γ_L) is a vector of coefficients for the B-spline functions. Note that given random effects b_i, Y_i(·) is independent of T_i, C_i, A_i and Z_i. Therefore, the conditional cumulative hazard function of T_i given Z_i, A_i and ${\mathcal{W}}_i(\cdot )$ is the same as that of T_i given Z_i, A_i and b_i, denoted by Λ(t|Z_i, A_i, b_i). Let S(t|Z_i, A_i, b_i) = exp{−Λ(t|Z_i, A_i, b_i)} denote the corresponding conditional survival function of T_i given Z_i, A_i and b_i. Under the proposed model (1), the survival function S(t|Z_i, A_i, b_i) = exp{−Λ(t|Z_i, A_i, b_i)} can be written as

$$S\left(t|{\mathit{Z}}_i,A_i,{\mathit{b}}_i\right)=\{\begin{array}{ll}\text{exp}\left[-{\int }_0^t{\lambda }_0(s)\text{exp}\left\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+\psi \left(A_i+s\right)\times W_i(s)\right\}ds\right],\hfill & r=0,\hfill \\ {\left[1+r{\int }_0^t{\lambda }_0(s)\text{exp}\left\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+\psi \left(A_i+s\right)\times W_i(s)\right\}ds\right]}^{-1/r},\hfill & r>0.\hfill \end{array}$$

Let S(t|Z_i, A_i, ϕ_i, b_i) denote the frailty model with

$$S\left(t|{\mathit{Z}}_i,A_i,{\varphi }_i,{\mathit{b}}_i\right)=\text{exp}\left(-{\varphi }_i{\int }_0^t{\lambda }_0(s)e^{{\mathit{Z}}_i^{\prime }\mathit{\beta }}\text{exp}\left[\psi \left\{A_i(s)\right\}{W}_i(s)\right]ds\right),$$

and ϕ_i is a frailty variable with gamma distribution. It is easy to show that S(t|Z_i, A_i, b_i) = ∫ S(t|Z_i, A_i, ϕ_i, b_i)f(ϕ_i)dϕ_i, where f(·) is the density function of a gamma distribution with mean 1 and variance r. Thus, the conditional survival function S(t|Z_i, A_i, b_i) is equivalent to the marginal distribution of gamma frailty model.

The complete likelihood function of θ given the observed data O ≡ (O₁, … , O_n), the frailty terms ϕ ≡ (ϕ₁, …, ϕ_n) and the random effects b = (b₁, … , b_n) can be written as:

$$\begin{array}{l}{\mathcal{L}}_c(\mathit{\theta }|\mathit{O},\mathit{\varphi },\mathit{b})=\prod _{i=1}^{n}p\left(V_i,{\delta }_i|{\varphi }_i,{\mathit{b}}_i;\mathit{\beta },\mathit{\gamma },{\lambda }_0\right)\times p\left({\mathit{Y}}_i|{\mathit{b}}_i;{\sigma }^2\right)\times p\left({\mathit{b}}_i|\mathit{\mu },\mathit{D}\right)\times f\left({\varphi }_i\right)\\ =\prod _{i=1}^n{\left\{{\varphi }_i{\lambda }_0\left(V_i\right)e^{{\mathit{Z}}_i^{\prime }\mathit{\beta }}\eta \left(V_i|A_i,{\mathit{b}}_i;\mathit{\gamma }\right)\right\}}^{{\delta }_i}\times \text{exp}\left\{-{\varphi }_i{\int }_0^{V_i}{\lambda }_0(s)e^{{\mathit{Z}}_i^{\prime }\mathit{\beta }}\eta \left(s|A_i,{\mathit{b}}_i;\mathit{\gamma }\right)ds\right\}\\ \times {\left(2\pi {\sigma }^2\right)}^{-\frac{m_i}{2}}\text{exp}\left\{-\frac{1}{2{\sigma }^2}{\left({\mathit{Y}}_i-{\mathit{G}}_i{\mathit{b}}_i\right)}^{\prime }\left({\mathit{Y}}_i-{\mathit{G}}_i{\mathit{b}}_i\right)\right\}\\ \times {\left(2\pi \right)}^{-\frac{d}{2}}|\mathit{D}{|}^{-\frac{1}{2}}\text{exp}\left\{-\frac{1}{2}{\left({\mathit{b}}_i-\mathit{\mu }\right)}^{\prime }{\mathit{D}}^{-1}\left({\mathit{b}}_i-\mathit{\mu }\right)\right\}\times f\left({\varphi }_i\right),\end{array}$$ (3)

where G_i = (g(t_i,1), …, g(t_i,mi))′ and η (s|A_i, b_i; γ) = exp[ψ{A_i(s)}g(s)′b_i].

The observed likelihood function $\mathcal{L}(\mathit{\theta }|\mathit{O})$ can be derived by integrating the frailty terms ϕ and the random effects b out of (3). Direct maximization of the observed likelihood $\mathcal{L}(\mathit{\theta }|\mathit{O})$ is difficult due to the integrals with respect to the random effects and frailties. Therefore, we develop an EM algorithm to estimate the model parameters, including both finite and infinite dimensional parameters.

3.2. Conditional Expectations

After dropping the terms that do not contain θ, the complete log-likelihood function can be written as the summation of three distinct parts, i.e. $l^c(\mathit{\theta }|\mathit{\varphi },\mathit{b})=l_1^c\left({\lambda }_0,\mathit{\beta },\mathit{\gamma }|\mathit{\varphi },\mathit{b}\right)+l_2^c\left({\sigma }^2|\mathit{b}\right)+l_3^c(\mathit{\mu },\mathit{D}|\mathit{b})$, where

$$\begin{array}{l}{l}_1^c\left({\lambda }_0,\mathit{\beta },\mathit{\gamma }|\mathit{\varphi },\mathit{b}\right)=\sum _{i=1}^n{\delta }_i\left[\text{log}\left\{{\lambda }_0\left(V_i\right)\right\}+{\mathit{Z}}_i^{\prime }\mathit{\beta }+\text{log}\left\{\eta \left(V_i|A_i,{\mathit{b}}_i;\mathit{\gamma }\right)\right\}\right]-{\varphi }_i{\int }_0^{V_i}{\lambda }_0(s)e^{{\mathit{Z}}_i^{\prime }\mathit{\beta }}\eta \left(s|A_i,{\mathit{b}}_i;\mathit{\gamma }\right)ds,\\ l_2^c\left({\sigma }^2|\mathit{b}\right)=\sum _{i=1}^n-\frac{m_i}{2}\text{log}\left({\sigma }^2\right)-\frac{1}{2{\sigma }^2}{\left({\mathit{Y}}_i-{\mathit{G}}_i{\mathit{b}}_i\right)}^{\prime }\left({\mathit{Y}}_i-{\mathit{G}}_i{\mathit{b}}_i\right),\text{ and }\\ l_3^c(\mathit{\mu },\mathit{D}|\mathit{b})=\sum _{i=1}^n-\frac{1}{2}\text{log}(\left|\mathit{D}\right|)-\frac{1}{2}{\left({\mathit{b}}_i-\mathit{\mu }\right)}^{\prime }{\mathit{D}}^{-1}\left({\mathit{b}}_i-\mathit{\mu }\right).\end{array}$$

Let Q(θ; θ^(k)) denote the conditional expectation of the complete log-likelihood function l^c(θ\ϕ, b) given observed data O = (O₁, …, O_n) and current estimates θ^(k). Similar to previous arguments, Q(θ; θ^(k)) can be written as the summation of three distinct parts,

$$\begin{array}{l}Q\left(\mathit{\theta };{\mathit{\theta }}^{(k)}\right)=E_{\mathit{b}}\left[E_{\varphi }\left\{l^c(\mathit{\theta }|\mathit{\varphi },\mathit{b})|\mathit{O},\mathit{b}\right\}|\mathit{O},{\mathit{\theta }}^{(k)}\right]\\ =E_{\mathit{b}}\left[E_{\varphi }\left\{l_1^c\left({\lambda }_0,\mathit{\beta },\mathit{\gamma }|\mathit{\varphi },\mathit{b}\right)|\mathit{b},\mathit{O},{\mathit{\theta }}^{(k)}\right\}|\mathit{O},{\mathit{\theta }}^{(k)}\right]\\ +E_{\mathit{b}}\left\{l_2^c\left({\sigma }^2|\mathit{b}\right)|\mathit{O},{\mathit{\theta }}^{(k)}\right\}+E_{\mathit{b}}\left\{l_3^c(\mathit{\mu },\mathit{D}|\mathit{b})|\mathit{O},{\mathit{\theta }}^{(k)}\right\}\\ =Q_1\left({\lambda }_0,\mathit{\beta },\mathit{\gamma };{\mathit{\theta }}^{(k)}\right)+Q_2\left({\sigma }^2;{\mathit{\theta }}^{(k)}\right)+Q_3\left(\mathit{\mu },\mathit{D};{\mathit{\theta }}^{(k)}\right).\end{array}$$

To evaluate the conditional expectation Q(θ; θ^(k)), we need to calculate both E(ϕ_i|b_i, O_i, θ^(k)) and the conditional expectations of functions of b_i given O_i and current estimate θ^(k). The conditional distribution of ϕ_i given b_i, O_i and θ^(k) is

$$p\left({\varphi }_i|{\mathit{b}}_i,{\mathit{O}}_i\right)\propto {\varphi }_i^{{\delta }_i}\times \text{exp}\left\{-{\varphi }_i{\int }_0^{V_i}{\lambda }_0(s)e^{{\mathit{Z}}_i^{\prime }\mathit{\beta }}\eta \left(s|A_i,{\mathit{b}}_i;\mathit{\gamma }\right)ds\right\}\times f\left({\varphi }_i\right).$$

Plugging in the density for Gamma(1/r, r) and doing some algebra, it can be shown that the resulting conditional distribution is a gamma distribution with shape parameter δ_i + 1/r and scale parameter ${\left\{1/r+{\int }_0^{V_i}{\lambda }_0(s)e^{{\mathit{Z}}_i^{\prime }\mathit{\beta }}\eta \left(s|A_i,{\mathit{b}}_i;\mathit{\gamma }\right)ds\right\}}^{-1}.$

Expectations with respect to the conditional distribution of b_i given O_i and θ^(k) can be approximated using a modified version of adaptive Gaussian–Hermite (GH) quadrature. Details can be found in Appendix A.

3.3. EM Algorithm

An EM algorithm is derived to obtain the maximum likelihood estimator (MLE) of θ. The algorithm is described as follows.

Initialization: obtain initial values θ⁽⁰⁾ based on the following two-step approach:

Step 1: Fit the mixed effect model Y(t) = g(t)′b + ϵ(t) based on the data (t_i, Y_i), i = 1, …, n, and set the estimated mean and covariance matrix of b as μ⁽⁰⁾ and D⁽⁰⁾, and the estimated variance of error term as (σ²)⁽⁰⁾. This can be realized by using the “nlme” package (Pinheiro et al., 2016) (https://cran.r-project.org/web/packages/nlme/) in R (R Core Team, 2013).

Step 2: For a pre-specified r, fit the GOR model only with Z as the covariates, and set the estimated regression coefficients as β⁽⁰⁾ and estimated baseline cumulative hazard function as ${\Lambda }_0^{(0)}(t)$. This can be done using the R package “TransModel” (Zhou et al., 2017b) (https://cran.r-project.org/web/packages/TransModel/index.html). The initial values for γ⁽⁰⁾ are set to be 0.

In the kth iteration,

E-step: Compute the conditional expectations described in Section 3.2 based on O and current estimate θ^(k) using adaptive GH quadrature.

M-step: Maximize the expectation of the log-likelihood functions, Q₁(λ₀(·), β , γ; θ^(k)), Q₂(σ²; θ^(k)) and Q₃(μ, D; θ^(k)), respectively, and update the parameters as θ^(k+1). The details are below.

1. By solving the partial derivative of Q₁(λ₀(·), β, γ; θ^(k)) with respective to λ₀(·), we obtain

   $${\tilde{\lambda }}_0(t;\mathit{\beta },\mathit{\gamma })=\frac{\sum _{i=1}^n{\delta }_{i}I\left(V_i=t\right)}{\sum _{i=1}^{n}I\left(V_i⩾t\right)e^{{\mathit{Z}}_i^{\prime }\mathit{\beta }}{E}_{{\mathit{b}}_i}\left\{E\left({\varphi }_i|{\mathit{b}}_i,{\mathit{O}}_i,{\mathit{\theta }}^{(k)}\right)\eta \left(t|A_i,{\mathit{b}}_i;\mathit{\gamma }\right)|{\mathit{\theta }}^{(k)},{\mathit{O}}_i\right\}}$$

   as a function of (β, γ). Apply the Newton–Raphson algorithm to maximize the expectation of the profile log-likelihood function, $Q_1\left({\tilde{\lambda }}_0(t;\mathit{\beta },\mathit{\gamma }),\mathit{\beta },\mathit{\gamma };{\mathit{\theta }}^{(k)}\right)$ to obtain the updates β^(k+1) and γ^(k+1). Then, the baseline hazard function can be updated by ${\lambda }_0^{(k+1)}(t)={\tilde{\lambda }}_0\left(t;{\mathit{\beta }}^{(k+1)},{\mathit{\gamma }}^{(k+1)}\right)$. More details can be found in Appendix B.
2. From Q₂(σ²; θ^(k)) and Q₃(μ, D; θ^(k)), we update with the following formula

   $$\begin{array}{l}{\mathit{\mu }}^{(k+1)}=\sum _{i=1}^{n}E\left\{{\mathit{b}}_i|{\mathit{\theta }}^{(k)},{\mathit{O}}_i\right\}/n,{\mathit{D}}^{(k+1)}=\sum _{i=1}^{n}E\left({\mathit{b}}_i{\mathit{b}}_i^{\prime }|{\mathit{\theta }}^{(k)},{\mathit{O}}_i\right)/n,\text{\hspace{1em} and }\\ {\left({\sigma }^2\right)}^{(k+1)}=\frac{\sum _{i=1}^n\sum _{j=1}^{m_i}E\left\{{\left({\mathit{Y}}_i-{\mathit{G}}_i{\mathit{b}}_i\right)}^{\prime }\left({\mathit{Y}}_i-{\mathit{G}}_i{\mathit{b}}_i\right)|{\mathit{\theta }}^{(k)},{\mathit{O}}_i\right\}}{\sum _{i=1}^n{m}_i}.\end{array}$$

   Iterate the E-step and M-step until ∑(θ^(k+1)−θ^(k))² < 0.001. From our numerical experience, the above algorithm usually converges within 100 iterations.

Remarks: Following the proof in Kim et al. (2017), the consistency of the MLEs, $\widehat{\mathit{\theta }}$, $\widehat{\psi }$, $\widehat{\Lambda }$, and the asymptotic normality and the semiparametric efficiency of $\widehat{\mathit{\theta }}$ can be established given the conditions listed in the supporting information.

3.4. Variance Estimation

After the EM algorithm converges, we have the maximum likelihood estimate $\widehat{\mathit{\theta }}$. Let θ* = θ \ λ₀ denote the vector of finite dimensional parameters. Suppose the length of the vector θ* is m. The m × m variance-covariance matrix of ${\widehat{\mathit{\theta }}}^{*}$ can be estimated by inverting the observed information matrix based on the profile likelihood.

To be specific, we define $pl\left({\mathit{\theta }}^{*}\right)={\text{max}}_{{\lambda }_0}{n}^{-1}{\sum }_{i=1}^{n}p{l}_i\left({\mathit{\theta }}^{*},{\lambda }_0\right)$ as the logarithm of the profile likelihood for θ*, where pl_i(θ*, λ₀) denote the logarithm of the observed likelihood for subject i, i = 1, …, n. Let I(θ*) = {v_ll′}, l, l′ = 1, …, m, denote the observed information matrix for ${\widehat{\mathit{\theta }}}^{*}$. The element v_ll′ can be approximated by the second-order numerical difference of pl(θ*) (Murphy and Van der Vaart, 2000; Zeng and Cai, 2005; Zeng et al., 2005). Specifically,

$$v_{l{l}^{\prime }}=\frac{{\left\{q\left({\widehat{\mathit{\theta }}}^{*}+h_n{e}_l\right)-q\left({\widehat{\mathit{\theta }}}^{*}\right)\right\}}^{\prime }\left\{q\left({\widehat{\mathit{\theta }}}^{*}+h_n{e}_{l^{\prime }}\right)-q\left({\widehat{\mathit{\theta }}}^{*}\right)\right\}}{h_n^2},$$

where $q\left({\widehat{\mathit{\theta }}}^{*}\right)=\left(p{l}_1\left({\widehat{\mathit{\theta }}}^{*}\right),\cdots ,p{l}_n\left({\widehat{\mathit{\theta }}}^{*}\right)\right)$ is the vector of profile likelihood functions being evaluated at ${\widehat{\mathit{\theta }}}^{*}$, e_l is the unit vector of length m that has the lth element being 1 and other elements being 0, and $h_n=\mathit{O}(1/\sqrt{n})$ is a pre-specified constant that is bounded by $1/\sqrt{n}$.

4. Simulation Study

To study the properties of the proposed methods simulation studies were ran. We generated data for the proposed joint models from the following varying-coefficient GOR model

$$S\left(t|{\mathit{Z}}_i\right)=\{\begin{array}{l}\text{exp}\left[-{\int }_0^t{\lambda }_0(s)\text{exp}\left\{{\mathit{Z}}_i\mathit{\beta }+\psi \left(A_i+s\right)\times W_i(s)\right\}ds\right],r=0,\hfill \\ {\left[1+r{\int }_0^t{\lambda }_0(s)\text{exp}\left\{{\mathit{Z}}_i\mathit{\beta }+\psi \left(A_i+s\right)\times W_i(s)\right\}ds\right]}^{-1/r},r>0.\hfill \end{array}$$

The baseline hazard function λ₀(·) is chosen to be Weibull with the shape and scale parameters set at 2. The varying coefficient function is chosen as ψ (a) = −0.2 sin(a). Baseline standardized age A_i is generated from a standard normal distribution and two baseline covariates are included: Z₁ follows Uniform (0,2) and Z₂ follows Bernoulli (0.5). Coefficients for Z = (Z₁,Z₂) are β = (1,−1). Different GOR models with the transformation parameter r = 0, 0.5, 1 and 2 are considered.

A linear function for the fitness over time is assumed, i.e., W_i(t) = b_i0 + b_i1t. The random effects b_i = (b_i0, b_i1) ~ N(μ, D), where μ = (2, 1) and the covariance matrix D = {v_ij} is assumed to be v_ij = I(i = j) + 0.5I(i ≠ j), that is, the variances are 1 and the covariance is 0.5. The error terms is assumed to follow the normal distribution with mean zero and variance σ² = 0.5.

The censoring time C is generated from the uniform distribution, U(0, a), where a is adjusted to have 50% censoring rate. Subject i is assumed to have visits 0 ⩽ t_i1 < ⋯ < t_imi < min{T_i, C_i}, and the length between two consecutive visits are set to be 0.1. Sample size of n = 500 is used and 1000 replications are conducted for each setting. We use 5 nodes in our adaptive GH quadrature method and L = 3 knots at the percentiles of observed age for the B-splines to estimate the varying coefficient function ψ(·).

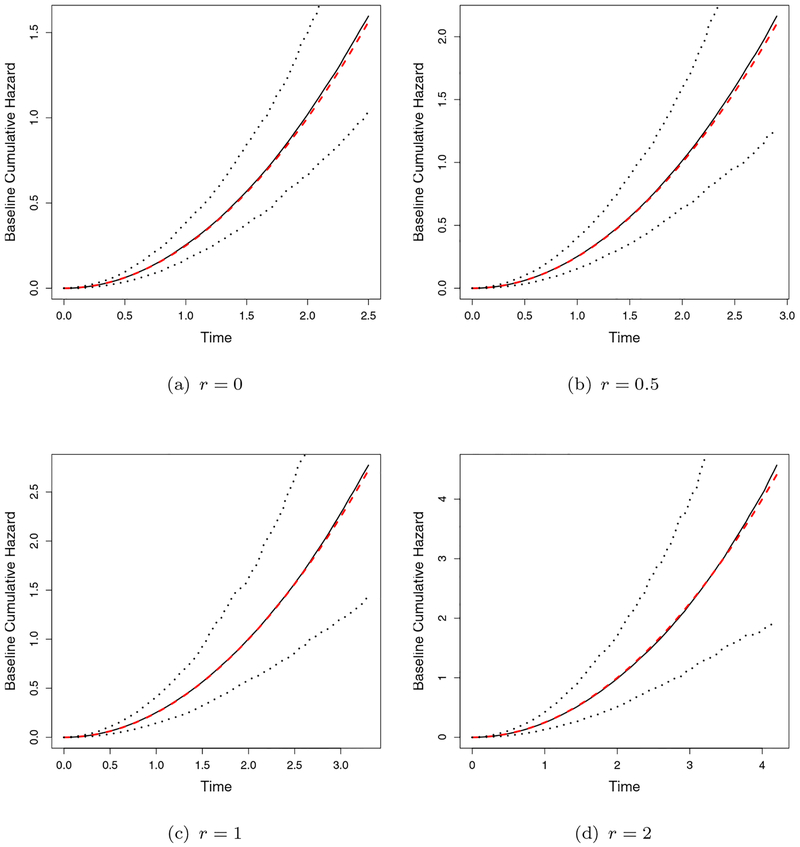
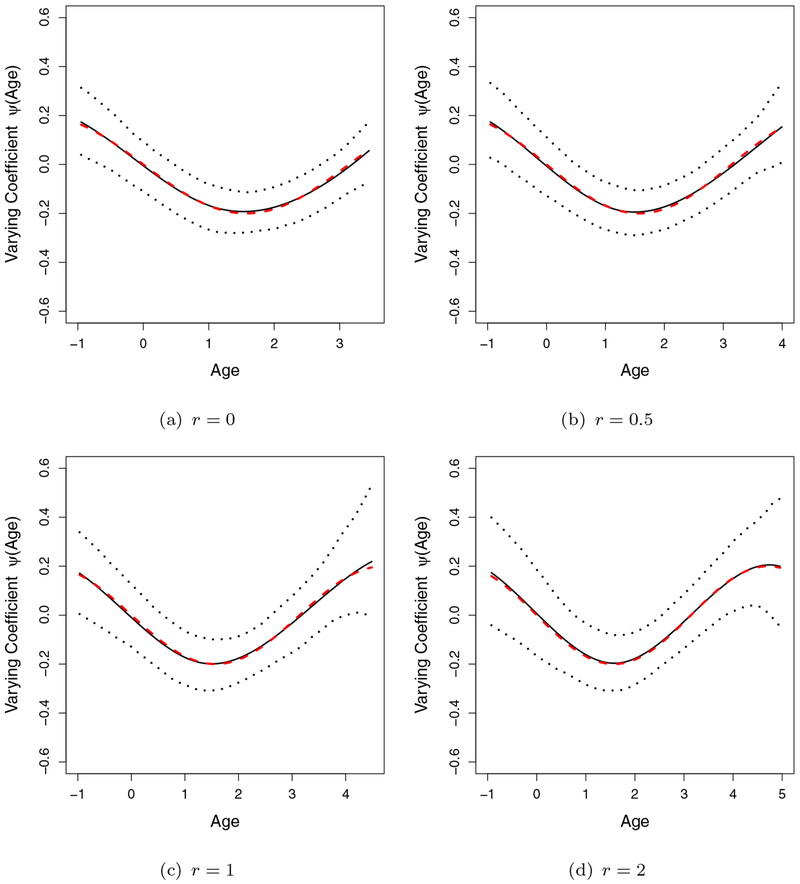
The simulation results are summarized in Table 2, where we report the bias, empirical standard deviation (StDev), mean of the estimated standard error (StdErr) and the coverage probability (CP) of 95% Wald confidence intervals. The bias of all the parameters is small, the estimated standard errors based on the profile likelihood are close to the empirical estimates and the CP is close to the nominal level 0.95. The estimated baseline cumulative hazard functions and the varying coefficient functions ψ(·) are compared with the true curves in Figures 2 and 3, respectively, overlaid with 2.5th and 97.5th quantiles of the estimates. All the curves are found to be close to the true values.

Table 2.

Simulation Results

Variable	Bias	StDev	StdErr	CP	Bias	StDev	StdErr	CP
	r=0				r=0.5
β1	0.005	0.125	0.124	0.944	−0.003	0.139	0.145	0.954
β2	−0.013	0.138	0.141	0.948	−0.005	0.169	0.165	0.946
μ0	−0.001	0.047	0.048	0.952	0.003	0.046	0.048	0.964
μ1	−0.006	0.059	0.060	0.952	−0.008	0.058	0.057	0.944
σ2	−0.004	0.010	0.010	0.934	−0.005	0.009	0.010	0.912
v11	−0.007	0.069	0.075	0.968	−0.011	0.074	0.073	0.940
vl2	0.012	0.066	0.065	0.940	0.014	0.062	0.062	0.952
v22	−0.008	0.099	0.099	0.938	−0.005	0.098	0.093	0.944
	r=1				r=2
β1	0.009	0.170	0.164	0.942	0.000	0.203	0.194	0.946
β2	−0.007	0.188	0.187	0.946	0.025	0.228	0.223	0.940
μ0	0.000	0.049	0.048	0.946	0.002	0.047	0.047	0.944
μ1	−0.003	0.060	0.056	0.926	−0.001	0.058	0.054	0.926
σ2	−0.006	0.009	0.009	0.886	−0.006	0.008	0.008	0.884
v11	−0.008	0.071	0.072	0.942	−0.017	0.069	0.071	0.932
vl2	0.021	0.062	0.062	0.938	0.013	0.058	0.059	0.964
v22	0.007	0.092	0.091	0.948	−0.007	0.087	0.084	0.924

Figure 2.

Estimated Baseline Cumulative Hazard Curves (solid lines are the mean of estimates, dashed lines are the true curve and the dotted lines are the 2.5 and 97.5 quantiles of the estimates).(This figure appears in color in the electronic version of this article.)

Figure 3.

Estimated Varying Coefficient Curves ψ (A(t)) (solid lines are the mean of estimates, dashed lines are the true curve and the dotted lines are the 2.5 and 97.5 quantiles of the estimates). (This figure appears in color in the electronic version of this article.)

The Akaike information criterion (AIC) can be used to select appropriate transformation parameter r and knots L in practice. To evaluate its performance, we do a small cross validation for the setting of r = 1. We search among the grids with r = 0, 1, 2 and L = 3, 5, 7 based on AIC. Proportions of selecting each grid are reported in Table 3 for sample sizes n = 200 and 500. As we can see from the result, when we have small sample such as 200, the PH model is more likely to be selected. The proportion of selecting the true r reaches to72.9% as sample size increases to 500.

Table 3.

Cross validation based on AIC

	n = 200				n = 500
	L = 3	L = 5	L = 7	Row sums	L = 3	L = 5	L = 7	Row sums
r = 0	27.2	25.8	4.0	57.0	16.3	3.1	1.6	21.0
r = 1	20.2	16.0	2.7	38.9	57.7	11.0	4.2	72.9
r = 2	2.1	1.6	0.4	4.1	4.7	1.0	0.3	6.0

More simulation settings are conducted and results are summarized in the supporting information. First, we investigate more settings with regard to different functions for the baseline distribution, different sample sizes and censoring, which give similar findings. Second, we evaluate the impact of the initial value. We conduct simulation studies using the initial values from the linear mixed model and PH moded separately, and simulation results are similar. Third, a setting with conditionally independent censoring, where C is generated based on A, is also considered in the supporting infomation, and the results are found to be similar.

5. Application to the ACLS Data

In order to assess the longitudinal effect of fitness on the CVD mortality, we apply the proposed model to the subset of ACLS Data set. We include patients who were enrolled between 1970 and 1980, and were followed till the end of 2003. Fatal outcomes (e.g. CVD mortality) were extracted from mortality surveillance, principally through the National Death Index. The main exposure variable is the cardiorespiratory fitness (fitness), which is quantified as the maximal treadmill time in minutes during a symptom limited exercise test. As an objective measure of physical activity, fitness is a more reliable measure of recent activity levels than self-reported values. Other potential confounders we adjust in the model include gender, BMI, smoking status and family history of CVD. There are a total of 3,980 patients with 437 females and 3,543 males. The number of follow-up visits for all participants ranges from 3 to 30 with median number of follow up being equal to 5. Among all participants, 145 participants died from CVD by the end of year 2003.

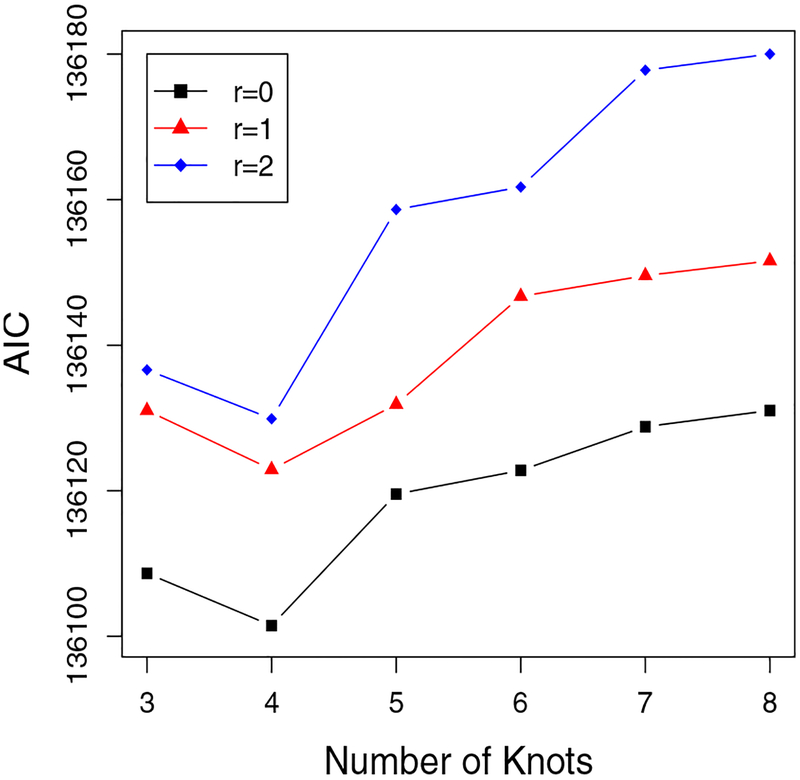
We assume a linear form for the fitness trajectory over time. Similar to the simulation, we use GH quadrature with 5 nodes for the approximation in the E-step, which gives similar results to those using a larger number of nodes. We apply cubic B-splines with L knots being placed at percentiles of observed age to estimate the varying coefficient, where the number L is selected based on the AIC. For illustration, in Figure 4 we plot the AIC versus number of knots for three different models: a PH model (r = 0), a PO model (r = 1) and a variant of PO model (r = 2). Based on the curves, the PH model with 4 knots results in the smallest AIC.

Figure 4.

ACLS Data: Choose Knots and r Based On AIC. (This figure appears in color in the electronic version of this article.)

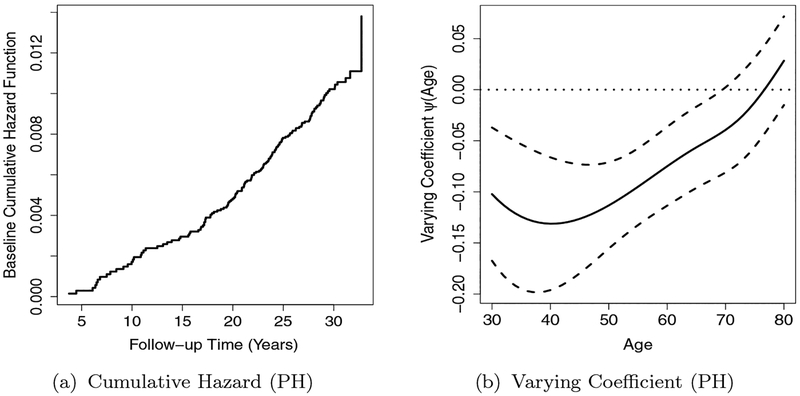
We summarize the estimated coefficients in the PH model with 4 knots in Table 4. Based on the results, higher BMI will increase the risk of CVD mortality and females generally have lower risk of dying from CVD. Smoking and family history are positively associated with a risk of dying from CVD. All the terms in the longitudinal process are found to be highly significant, indicating a significant decreasing linear trend of fitness with time. The baseline cumulative hazard curve is plotted in Figure 5(a), which is a step function with jumps at the event times.

Table 4.

ACLS Data: Parameter Estimates

	PH Model
Parameter	Estimate	StDev	P value
BMI	0.092	0.029	0.002
FamilyCVD	0.198	0.179	0.269
Smoke	0.167	0.234	0.476
Female	−0.442	0.386	0.253
μ0	18.337	0.073	< 0.001
μ1	0.063	0.005	< 0.001
σ2	3.984	0.022	< 0.001
v11	19.056	0.508	< 0.001
vl2	−0.280	0.026	< 0.001
v22	0.052	0.002	< 0.001

Figure 5.

ACLS Data: Estimated Baseline Cumulative Hazard and Age-dependent Varying Coefficient for Fitness.

Based on the estimated γ coefficients in B-splines, we also can test the hypothesis “H₀: the varying coefficient is constant with age”, which is equivalent to H₀₁ : M₁γ = 0, where

$$M_1=\left(\begin{array}{ccccc}1& -1& 0& 0& 0\\ 0& 1& -1& 0& 0\\ 0& 0& 1& -1& 0\\ 0& 0& 0& 1& -1\end{array}\right)$$

The test statistic $\left(M_1\widehat{\mathit{\gamma }}\right){\left(M_1\widehat{V_{\mathit{\gamma }}}{M}_1^{\prime }\right)}^{-1}{\left(M_1\widehat{\mathit{\gamma }}\right)}^{\prime }$ follows a chi-squared distribution with 4 degree of freedom under H₀₁, where $\widehat{V_{\mathit{\gamma }}}$ is the estimated covariance matrix of $\widehat{\mathit{\gamma }}$ The calculated test statistic value is 138.12, which yields a highly significant p-value. Therefore, we can conclude that the fitness effect on CVD mortality is significantly non-constant with age.

The age-dependent varying coefficient is illustrated in Figure 5(b) along with its 95% pointwise confidence intervals, which shows a clear pattern of the effect of fitness on CVD mortality with age.

In addition, based on the estimated point-wise confidence intervals for the varying coefficient, there is a negative association between fitness and CVD mortality for the age period of study. Based on the curve, physical activity has significant protective effects on CVD mortality till age 70, and no significant impact from 70 to 80. An explanation for this finding could be that after 70, age genetic factors take over as the dominate reason for CVD related mortality, and that the individuals’ physical activity is not a significant factor. The protective effect of physical activity is the strongest around age 40, suggesting that more exercise during middle-aged population is the most effective in reducing CVD associated mortality. Note that the standard errors reported are from the optimal selected model and no post-model selection effects have been adjusted here.

6. Discussion

We proposed a joint model with an age-dependent varying coefficient for GOR model with a longitudinal endogenous covariate measured with error. The age-related varying coefficient was flexibly modeled with cubic B-splines. The function g(t) presents how individual longitudinal observations change over time. In practice, the individual longitudinal profile can be plotted along with the smoothed curve. The plot can be used to provide evidence for a linear, quadratic or other forms of change. Then, the linear, quadratic or cubic spline function of t will be suggested for g(t). The EM algorithm is applied in estimating the proposed joint model, while the variance of the estimates are approximated based on a profile likelihood function. The estimation methods are discussed and evaluated by simulation studies.

The ACLS dataset is used to illustrate the usage of the model, where we study the longitudinal effect of fitness on the CVD mortality. The effect of fitness on CVD mortality is found to change over age, and the trajectory can be clearly described by the estimated varying coefficient curve as illustrated in Section 5.

Aging is the most important factor in many chronic diseases. The change in age-related behavior plays an important role in disease development and corresponding disease-related mortality. The proposed model can be broadly used in modeling survival outcomes with time-varying effects of longitudinal predictors, and helps improving the understanding of the real impact of some age-related chronic behaviors on survival outcomes.