Assessing Pharmacokinetic Marker Correlates of Outcome, with Application to Antibody Prevention Efficacy Trials

Abstract

The Antibody Mediated Prevention (AMP) efficacy trials are the first studies to evaluate whether passive administration of a broadly neutralizing monoclonal antibody (mAb) can prevent HIV acquisition. The trials randomize 4600 HIV-negative volunteers to receive 10 infusions of the mAb VRC01 or placebo. The primary objective compares the incidence of HIV infection between the study groups. The secondary objective assesses whether and how a marker defined as the serum concentration of VRC01 over time associates with the instantaneous rate of HIV infection, using a two-phase sampling design, a pharmacokinetic (PK) model for the time-concentration curve, and an estimator of HIV infection times. While a Cox model with a time-dependent covariate constitutes an important approach to this problem, the low inter-individual vs. intra-individual marker variability limits its power, motivating us to develop two alternative methods that condition on outcome status: 1) an indirect method that checks whether HIV-infected cases have unexpectedly long times from the most recent infusion to the estimated infection date; and 2) a direct method that checks whether the marker itself is unexpectedly low at estimated infection dates. In simulations and a pseudo AMP application, we find that method 2) (but not 1) has greater power than the Cox model. We also find that the quality of the infection time estimator majorly impacts method performance and thus incorporating details of an optimized estimator is critical. The methods apply more generally for assessing a time-dependent longitudinal marker as a correlate of risk when the marker trajectory is modeled pharmacokinetically.

1. Introduction

The HIV pandemic continues to incur a large burden of morbidity and mortality. While a highly efficacious preventive vaccine is likely required to end the pandemic, only one modestly efficacious vaccine has been identified.¹ Over the past decade, many anti-HIV antibodies have been isolated from HIV infected individuals that broadly neutralize most strains of HIV. Several of these broadly neutralizing monoclonal antibodies (mAbs) have been developed for potential use to prevent HIV infection via passive administration and has generated optimism that highly efficacious vaccines that elicit broadly neutralizing antibodies against HIV can be developed.^2,3

The first studies to evaluate HIV prevention efficacy of a mAb began in March of 2016, the Antibody Mediated Prevention (AMP) studies of the VRC01 mAb. AMP consists of two linked efficacy trials in two cohorts at high risk of acquiring HIV infection: (1) men and transgender persons who have sex with men in the U.S., Peru, Brazil, and Switzerland; and (2) women in sub-Saharan Africa. The two AMP trials have identical study designs and harmonized protocols, which we refer to collectively as AMP. AMP randomizes HIV negative volunteers in 1:1:1 allocation to one of three study arms– 10 mg/kg VRC01 (low dose), 30 mg/kg VRC01 (high dose), or placebo– each administered via infusion every 8 weeks for 10 infusions. The primary objective compares the cumulative incidence of HIV infection by the Week 80 study visit between the two VRC01 study groups pooled versus the placebo group. The secondary objective assesses the association of the serum concentration of VRC01 over time in VRC01 recipients with the instantaneous rate of HIV infection. Identification of an association would aid HIV vaccine development by setting a bar for the required potency of a vaccine-induced immune response to putatively achieve a high level of protection, thus helping define study endpoints in Phase 1 and 2 trials that vet candidate HIV vaccines for their potential efficacy. Using AMP as an illustration, we develop and evaluate statistical methods for assessing a time-dependent longitudinal biomarker–whose value changes over time in a cyclical fashion and can be appropriately modeled with a population pharmacokinetic (PK) model– as a correlate of risk of an interval censored failure time.

Appropriate statistical methods need to account for the following statistical issues. First, because the longitudinal marker of interest is costly to measure, it is measured in VRC01 group participants using a sub-sampling design such as classic case-cohort (e.g., Self-Prentice⁴) or case-control/two-phase sampling (e.g., Breslow et al.⁵). AMP plans two-phase sampling, measuring the marker in all participants experiencing the primary endpoint HIV infection by Week 80 (cases), and in a stratified random sample of participants who complete follow-up to Week 80 HIV negative (controls). In controls, the marker is measured every 4 weeks from Week 0 to Week 80 plus at 5 days post second infusion, and in cases the marker is measured on the same schedule up until HIV infection diagnosis. Second, for all participants in the case-control sample, a PK model is used to estimate the true serum concentrations S(t) of VRC01 over continuous time t since study entry, which has an error term due to the fact that S(t) is only measured at discrete time points. The PK model also needs to account for the heterogeneity among participants in the timing and number of infusions received, which occurs due to variability in days between infusion visits and to missed infusions. Third, the time from enrollment until HIV-1 infection is interval censored given the periodic HIV diagnostic tests (administered every 4 weeks in AMP), which means that S(t) at the HIV infection date has an additional source of uncertainty.

One direct approach to studying the association question of interest would link S(t) modeled by a PK model with the hazard of HIV infection via a Cox proportional hazards model and use joint longitudinal survival modeling methods that account for the error in estimation of S(t); however to our knowledge the literature for these methods [e.g., work by Wu⁶ and later references] has not considered a PK model for S(t). While this approach is worth pursuing given its interpretability, when we discovered that an approximate joint modeling method [regression calibration applied with the Self-Prentice⁴ and Lin⁷ Cox models for a case-cohort or two-phase sampled time-dependent covariate] had surprisingly low power for AMP, we launched new research to consider alternative methods that instead of modeling the infection hazard conditional on S(t), turn the problem around and model S(t) conditional on HIV infection time. This affords multiple simplifications as described below, yielding two methods of study– one that assesses if HIV infections tend to occur late in infusion intervals (when concentrations S(t) must be low), and a second that assesses if S(t) at HIV infection tends to be low compared to expected levels of S(t) at times of HIV exposures. This alternative approach also advantageously allows use of measurement error methods that directly account for uncertainty due to the interval censoring of HIV infection times, something not done by existing joint modeling methods. In particular, the new approaches modularly incorporate a model for predicting HIV infection dates of cases from collected data including on HIV-1 diagnostics, HIV-1 viral loads, and intra-host diversification of HIV-1 sequences. Moreover, the first of the alternative approaches has resource advantage of not needing any measurements of S(t).

The article is organized as follows. Section 2 defines the target parameters and associated hypothesis tests of interest. Section 3 summarizes the PK model of mAb concentration S(t) over time. Section 4 describes the two newly proposed methods for estimating the target parameters and obtaining confidence intervals and p-values. Section 5 compares power and precision of the two new methods – plus a comparison with two alternative methods (a Cox model that handles two-phase sampling and a case-only sign test) – via a simulation study of AMP. Section 6 illustrates application of the methods to a pseudo-example data set representative of what is anticipated from AMP. Section 7 concludes with discussion.

2. Target Parameters and Hypothesis Tests

The methods we develop restrict the analysis to participants assigned to receive VRC01. For simplifying the methods exposition we do not account for assignment to low or high dose VRC01, although the inferential methods account for this factor through stratification/covariate-adjustment, and we also account for dose in the Simulations and Application.

2.1. Notation

We first define the failure time information. Let T be the time from enrollment to HIV infection, and C be the time from enrollment to right-censoring, defined as loss to follow-up or reaching the final follow-up visit at time τ without any HIV positive test results (τ = Week 80 for AMP). Let T^dx be the time from enrollment to HIV infection diagnosis (based on a positive HIV test result at a study visit), where generally T^dx > T because infection dates cannot be observed due to the periodic HIV tests. Let Y = I(T ≤ τ) be the indicator of infection occurrence during study follow-up. Let X = min(T,C), X^dx = min(T^dx,C), Δ = I(T ≤ C), and Δ^dx = I(T^dx ≤ C). Note that “cases” are participants with T^dx ≤ τ and “observed cases” are participants with Δ^dx = 1. We assume that for every observed case, an interval [L, U] can be determined such that T lies within [L, U] with probability 1. (A critical methodological issue is estimation of L and U, which we address in the Simulations and Supplement E.) Thus T is interval censored, whereas T^dx is subject to right censoring. Let Y^obs = 0 define “eligible controls” – participants who reach the final follow-up visit τ HIV negative (defined by Y^obs = 1 − (1 − Δ^dx)I(C = τ)) – which constitutes the set from which controls are sampled for a case-control study.

We next define other variables. Let Z be baseline covariates. Suppose N_max infusions are planned and no more than N_max infusions are actually administered. Let N be the number of infusions actually received, with $T^{inf}(\tau )={\left(T_1^{inf},\cdots ,T_N^{inf}\right)}^T$ the set of infusion times (since enrollment) with $0=T_1^{inf}<T_2^{inf}<\cdots <T_N^{inf}\le \tau$. Here we assume infusions do not occur after HIV infection, which is approximately true in AMP because infusions are discontinued after HIV infection diagnosis. Let $\text{939547}$ be a participant’s average of his/her infusion interval times. For cases let T^diff be the time elapsed between HIV infection and the most recent infusion before infection: $T^{diff}=\left(T-T_N^{inf}\right)$. To define the longitudinal VRC01 concentration marker process data, let $\tilde{S}(\tau )=\left\{S(u),0\le u\le \tau \right\}$ with S(u) the marker value at time u, and let $\overline{S}(\tau )=\frac{1}{X^{dx}}{\int }_0^{X^{dx}}S(t)dt$ be a participant’s average log-transformed concentration during his/her follow-up period. Participants eligible for measurement of $\tilde{S}(\tau )$ are cases and eligible controls, from which participants are randomly sampled for measurement of the marker (the “case-control sample”). Let ϵ be the indicator that a participant is selected into the case-control sample. For participants with ϵ = 1, suppose M_max measurements of the marker are planned and no more than M_max measurements are made. The marker is measured at the M time points $T^{ms}(\tau )={\left(T_1^{ms},\cdots ,T_M^{ms}\right)}^T$ with $0=T_1^{ms}<T_2^{ms}<\cdots <T_M^{ms}\le \tau$, with observed marker values W = (W₁,···,W_M)^T , where $W_m=S\left(T_m^{ms}\right)$. Note that M may vary over individuals. Lastly, let Z^post denote any post-baseline covariate information collected from all participants before infection diagnosis other than T^inf(τ), and let V be information collected at and after HIV infection diagnosis such as HIV diagnostic test results, HIV viral loads, and HIV-1 amino acid sequences, which may be useful for predicting T.

The observed phase-one data (i.e., measured from everyone) are Ω¹ = (Z,X^dx,Δ^dx, Z^post; T^inf (τ), ϵ) and the observed phase-two data (i.e., only measured in the case-control sample with ϵ = 1) are Ω² = (T^ms(τ),W,Δ^dxV). We assume $\left({\Omega }_i^1,{ϵ}_i{\Omega }_i^2\right)$ are an iid sample, i = 1, ⋯ , n, for the n participants assigned to receive VRC01. The sampling indicator ϵ may depend on a discrete phase-one baseline covariate as well as outcome status, constituting a two-phase sampling design.⁵

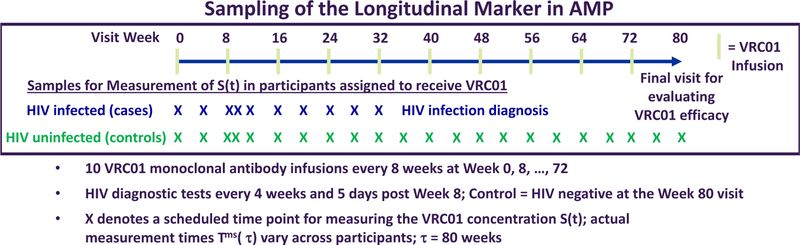
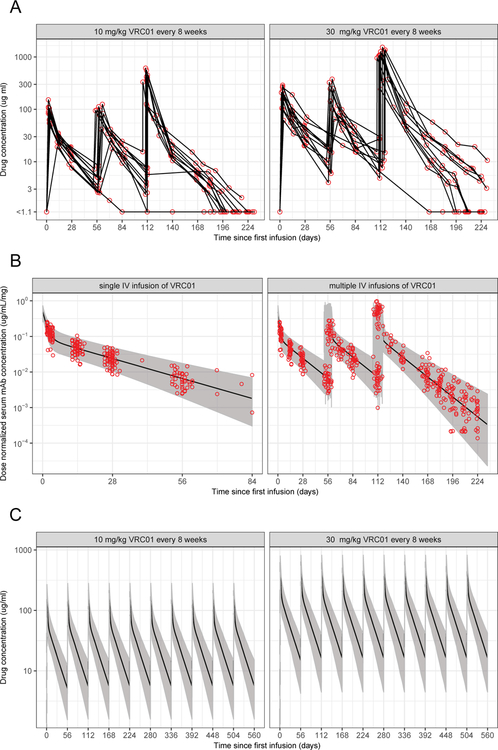
Figure 1 shows the AMP schedules of infusions, HIV diagnostic tests, and sampling of VRC01 concentrations, and Figure 2 shows data on measured VRC01 concentrations, PK model fits to the data, and simulated concentration data for randomly selected VRC01 recipients in the HVTN 104 Phase 1 trial⁸ based on the PK model summarized in Section 3. Figure 2 shows a sawtooth pattern of concentrations that peak within hours of each infusion, drop rapidly in the next few days followed by a slower decline until the lower detection limit of the assay or the next infusion.

Figure 1:

AMP study schedules of infusions, HIV diagnostics, and marker measurements.

Figure 2:

(A) Observed VRC01 concentrations W at 0, 3 days and 2, 4, 8 weeks after each of the three infusions, and at one hour and 10–16 weeks after the last infusion for the 10 mg/Kg (left) and 30 mg/Kg (right) VRC01 dose arms in HVTN 104. (B) Predicted and observed dose-normalized VRC01 concentrations in HVTN 104 after a single (left) and multiple (right) intravenous infusion(s) based on the final popPK model described in Huang et al.¹⁰ (C) Simulated time-concentration data under perfect study adherence. Solid lines are medians; shaded areas are 2.5^th and 97.5^th percentiles over 500 simulated data sets. A body weight of 74.5 Kg is used.

2.2. Target Parameters and Hypothesis Tests of Interest

We define the true target parameters of interest in terms of underlying events of interest, such as the actual infection indicator Y and infection time T. For VRC01 group individuals, the “Times Method” compares two parameters, the first for infected individuals (Y = 1) – the mean time between the last pre-infection infusion date and the infection date, and the second for uninfected individuals (Y = 0) – one-half the mean of the participant-specific average time interval between infusions. These two mean parameters of interest are:

$${\mu }^{Tcase}\equiv E\left[T^{diff}|Y=1\right]\text{\hspace{1em} and \hspace{1em}}{\mu }^{Tctrl}\equiv E\left[{\overline{T}}^{inf\cdot int}|Y=0\right].$$ (1)

Assuming that participant exposures to HIV are uniformly distributed across the follow-up period, μ^Tcase > μ^Tctrl/2 would support that higher concentrations are associated with a lower rate of HIV infection, based on the known sawtooth pattern of S(t) illustrated in Figure 2. For example, with infusions administered every 8 weeks as in AMP, we know that μ^Tctrl/2 is approximately 4 weeks, and a result where infections occur on average 7 weeks after the last infusion (μ^Tcase = 7 weeks) would imply that S(t) tends to be low at infection. As we will see in the Simulations and Application, for data analysis, a result of the estimate of μ^Tcase exceeding the estimate of μ^Tctrl/2 does not necessarily support higher concentrations are associated with a lower rate of HIV infection, if a large proportion of cases have $T<T_N^{inf}<T^{dx}$. Thus a critical objective of the Times Method is design of a good enough estimator of μ^Tcase to make valid such an implication.

The second approach, the “Marker Method,” compares the mean VRC01 concentration at the time of infection for VRC01 group cases, with the mean participant-specific average VRC01 concentration over follow-up time, where the former mean being smaller would again support that higher concentrations are associated with a lower rate of HIV infection. The participant-specific average VRC01 concentration over follow-up time is intended to reflect the expected concentration at the time of a random HIV exposure, where, as for the Times Method, we assume that HIV exposures are uniformly distributed across the follow-up period. (Supplement C considers an extension relaxing this assumption.) For the Marker Method, the mean parameters of interest are:

$${\mu }^{Scase}\equiv E[S(T)\left|Y=1]\text{\hspace{1em} and \hspace{1em}}{\mu }^{Sctrl}\equiv E[\overline{S}(\tau )\right|Y=0].$$ (2)

The null hypotheses of interest are:

$$H_0^T:{\mu }^{Tcase}=\frac{1}{2}{\mu }^{Tctrl}\text{\hspace{1em} and \hspace{1em}}{H}_0^S:{\mu }^{Scase}={\mu }^{Sctrl}.$$ (3)

Interest centers on the 1-sided alternatives $H_1:{\mu }^{Tcase}>\frac{1}{2}{\mu }^{Tctrl}$ and $H_1^S:{\mu }^{Scase}<{\mu }^{Tctrl}$, and below we develop Wald tests of $H_0^T$ and $H_0^S$.

2.4. The Marker Method Approximately has the Desirable Forward Interpretation

As noted in the Introduction, a direct approach to assessing correlates would study the hazard of T conditional on S(t), λ(t|S(t) = s) ≡ lim_h→0 P(T ∈ [t,t + h)|T ≥ t,S(t) = s)/h, where a detected association would have clear interpretation as subgroups with higher S(t) have lower hazard of infection. However, while there are methods implementing this approach with interval-censored failure times (e.g., see work by Sun⁹), they have not accounted for covariate sub-sampling designs, and turn out to have relatively low power for our motivating AMP application as shown in Section 5. Moreover, examining the null hypothesis shows that reversing the order of S(t) and T yields an interpretable test, especially if the failure outcome is rare as in our application. In particular, with λ(t) ≡ lim_h→0 P(T ∈ [t,t+h)|T ≥ t)/h, straightforward calculation (see Supplement A) shows that the null hypothesis $H_0^{Shaz}:\lambda (t|S(t)=s)=\lambda (t)$ for all t ∈ (0,τ] and all s, has implication that E[S(t)|T = t] = E[S(t)|T > t], and moreover E[S(t)|T > t] approximately equals E[S(t)|T > τ], as long as (i) P(T ∈ (t,τ]) or (ii) |E[S(t)|T > τ]−E[S(t)|T ∈ (t,τ]]| is small. Term (i) is small in the rare event setting, and term (ii) is small under the null hypothesis $H_0^{Shaz}$, justifying this approximation (see Supplement B for more details). Now, E[S(t)|T = t] = E[S(t)|T > τ] for all t ∈ (0,τ] implies $E[S(T)\left|Y=1]=E[\overline{S}(\tau )\right|Y=0]$, which is the null hypothesis $H_0^S$ of the Marker Method (Supplement A), showing that the Marker Method provides a way to reject $H_0^{Shaz}$.

Under a random censoring assumption T ⫫ C, simple calculation shows that the approximate equation E[S(t)|T = t] = E[S(t)|T > τ] for all t ∈ (0,τ] may be rewritten as E[S(t)|T = t,Δ^dx = 1] = E[S(t)|Y^obs = 0] for all t ∈ (0,τ]. Next, we add a missing at random assumption for measuring W, P(ϵ = 1|Ω¹, Ω²) = P(ϵ = 1|Ω¹)), which yields the result that $H_0^{Shaz}$ approximately implies the directly testable null hypothesis

$$H_0^{Sobs}:E\left[S(t)|T=t,ϵ{\Delta }^{dx}=1\right]=E\left[S(t)|ϵ\left(1-Y^{obs}\right)=1\right]$$ (4)

for all t ∈ (0,τ]. Therefore, for a test designed to reject $H_0^{Sobs}$, when it rejects $H_0^{Sobs}$ it will also reject $H_0^{Shaz}$ with its desirable forward association interpretation. In the simulations we also include a direct forward association method for comparison – a Cox model with a time-dependent covariate.

2.5. Remarks on Causality

Our forward parameter of interest, λ(t|S(t) = s), is a statistical parameter, not a causal parameter, such that an association between S(t) and T ∈ [t,t + h) could be partly due to covariates associated with both T ∈ [t,t + h) and with S(t) and/or I(T > t). While an alternative causal parameter could be defined for a hypothetical world where all participants were assigned S(t) = s, in this article we restrict attention to the statistical parameter. Nevertheless, in a Cox model analysis of λ(t|S(t) = s), it is useful to control for baseline covariates that capture information on the amount of HIV-1 exposure, because if S(t) varies with an unaccounted for exposure variable then the regression parameter for S(t) measures a gradient in infection risk across subgroups defined by S(t) that vary in both biological and exposure/behavioral factors. Controlling for exposure variables increases the ability of the regression parameter to capture only biological variability, which makes it most useful for applications.

3. PK Model of Antibody Concentration S(t)

As a component of the Marker Method and the Cox model method described in the next section, we specify a two-compartment PK model for S(t), t ∈ (0,τ], after k ∈ {1, ⋯, N} doses of VRC01 with dose amount D_j (j = 1, …, k) administered at times $T_j^{inf}\left(t\ge T_k^{inf}\right)$:

$$S(t)=\sum _{j=1}^k{D}_j\left(A{e}^{-\alpha \left(t-T_j^{inf}\right)}+B{e}^{-\beta \left(t-T_j^{inf}\right)}\right),$$ (5)

where α and β are slopes for the distribution (rapid decline) and elimination (slower decline) phases, and A and B are intercepts on the y-axis for each exponential segment of the time-concentration curve. This PK model assumes that the IV infusion administration time (about 20–30 minutes) is brief relative to the half-life of the mAb and that the PK of the mAb after a single dose is not altered by multiple doses, although cumulations of drug concentrations over multiple doses are accommodated. Both assumptions are reasonable based on the robust fit it provided to repeated-dose PK data from recent Phase 1 studies of VRC01.^8,10

As described in more detail in Huang et al.,¹⁰ the population PK (popPK) model (that includes (1)) of the set of observed concentrations W considers both interindividual variabilities (IIVs) of the PK parameters (A, B, α, and β) for S(t) and a combination proportional + additive residual error via non-linear mixed effects (NLME) modeling. For IIV, an exponential inter-individual random effects model is considered with PK parameters log-normally distributed and random effects normally distributed. Specifically, we consider ${\theta }_i={\text{TV}}_{{\theta }_i}*\text{exp}\left({\eta }_{{\theta }_i}\right)$, where θ_i denotes individual i’s PK parameter value that is log-normally distributed, ${\text{TV}}_{{\theta }_i}$ is her/his population PK parameter value included as a fixed effect in the NLME model, and ${\eta }_{{\theta }_i}$ is her/his inter-individual random effect that is normally distributed. Regarding the residual error, let W_ij and Ŵ_ij denote the j^th measured and model-predicted concentrations, respectively, for individual i. The combination proportional + additive error model is expressed as $W_{ij}={\widehat{W}}_{ij}\left(1+{ϵ}_{1ij}\right)+{ϵ}_{2_{ij}}$, where ϵ₁ and ϵ₂ are the proportional and additive error terms, respectively.

The NLME modeling also accounts for covariates Z (e.g., body weight) that are predictive of the PK variability between individuals in the modeling of the fixed effect ${\text{TV}}_{{\theta }_i}$ via, for example, an exponential or a power covariate model. The former model is expressed as ${\text{TV}}_{{\theta }_i}={\beta }_{\theta }*\text{\hspace{0.17em}exp}\left({\beta }_{BW(\theta )}*B{W}_i\right)$, and the latter model as ${\text{TV}}_{{\theta }_i}={\beta }_{\theta }*{\left(B{W}_i\right)}^{{\beta }_{B}W(\theta )}$, where β_θ denotes the intercept term, BW_i the mean-centered body weight of individual i, and β_BW(θ) the regression coefficient for the association between body weight and the PK parameter θ. After all parameters characterizing the fixed and random effects of the NLME model are estimated, the fitted NLME model is then used to compute an estimate Ŝ(t) for each individual’s S(t) and the variance of Ŝ(t) for every t ∈ (0,τ], accounting for the individual’s infusion information, covariate information and the inter-individual variability of the PK parameters (See Supplement D).

4. Estimation and Testing Procedures

The parameters of interest condition on Y = 1 or Y = 0; by random censoring these conditioning events can be replaced by the observable events Δ^dxY^dx = 1 (observed case) or Y^obs = 0 (eligible control). We describe the estimators for parameters conditioning on Δ^dxY^dx = 1 or Y^obs = 0.

4.1. Times Method

The mean ${\mu }^{Tctrl}=E\left[{\overline{T}}^{inf.int}|Y^{obs}=0\right]$ is estimated using any preferred consistent estimator of a mean, based on all eligible controls (Y^obs = 0). If the sample mean is used, then the variance of ${\widehat{\mu }}^{Tctrl}$ may be estimated simply as the sample variance of the observations ${\overline{T}}_i^{inf.int}|Y_i^{obs}=0$. If a more efficient estimator is used that accounts for baseline covariates Z (e.g., see work by Rose and van der Laan¹¹),then the average of squared influence curve contributions may be used.

For cases, in the idealized situation where true infection times T are observable (i.e., P(T = T^dx) = 1), then it is straightforward to estimate μ^Tcase = E[T^diff|Δ^dxY^dx = 1], equivalent to the problem of estimating μ^Tctrl. In the real situation, where T and hence T^diff is not observable, estimation of μ^Tcase is harder than estimation of μ^Tctrl. Suppose a model is used to predict T for each case based on all available observed data (Ω¹, ϵΩ²); let $T_i^{*}$ be the predicted value of T_i for each case i. We then estimate μ^Tcase by using the predicted values $T_i^{*diff}$ as the observations, where $T_i^{*diff}=T_i^{*}-T_N^{inf}$. Again the simplest estimator is the sample mean of the values $T_i^{*diff}|{\Delta }_i^{dx}{Y}_i^{dx}=1$, and a more efficient estimator could be used that leverages information in (Δ^dxY^dx = 1,X,Z,T^inf(τ),Z^post,V). As for controls, the variance of ${\widehat{\mu }}^{Tcase}$ may be estimated simply as the sample variance or as the average of squared influence curve contributions.

It is easy to construct a consistent estimator of E[T^*diff|Δ^dxY^dx = 1], for example the sample mean of $T_i^{*diff}$ values from all ${\Delta }_i^{dx}{Y}_i^{dx}=1$ individuals, or the stratified sample mean defined as the sum of the two VRC01 dose-group specific sample means weighted by the fractions of ${\Delta }_i^{dx}{Y}_i^{dx}=1$ individuals in each dose-group (because of the AMP study design we use the latter estimator in the Simulations and Application). Under the two assumptions that the utilized estimator for T is (A1) unbiased and (A2) has homoscedastic errors, a consistent estimator of E[T^*diff|Δ^dxY^dx = 1] is also a consistent estimator of E[T^diff|Δ^dxY^dx = 1], and a consistent variance estimator of Ê[T*^diff|Δ^dxY^dx = 1] is also a consistent variance estimator of Ê[T^diff|Δ^dxY^dx = 1] (Section 15.1 in Carroll et al.¹²). Therefore, under (A1) and (A2), one can use “ordinary” statistical methods that treat the predicted values $T_i^{*diff}$‘s as observed values, and is an important reason we tackled the problem by reversing the time ordering. However, the precision of the estimates $T_i^{*diff}$ affects how much precision is lost in estimation of E[T^diff|Δ^dxY^dx = 1] compared to using true values $T_i^{diff}$ measured without error. This discussion highlights that our estimation approach handles the interval-censored outcomes in two modular steps– first develop the best possible estimator of the infection time and second use any consistent estimator of a mean; this modularity allows statisticians to use preferred methods for each step.

In the Simulations and Application we use simple sample average estimators (within VRC01 dose group strata):

$${\widehat{\mu }}^{Tctrl}=\sum _{i=1}^n{\overline{T}}_i^{inf.int}\left(1-Y_i^{obs}\right)/\sum _{i=1}^n\left(1-Y_i^{obs}\right),$$

$${\widehat{\mu }}^{Tcase}=\sum _{i=1}^n{T}_i^{*diff}{\Delta }_i^{dx}/\sum _{i=1}^n{\Delta }_i^{dx}.$$

4.2. Marker Method

For any fixed t, let $\widehat{S}(t)$ be the value Ŝ(t) in equation (1) using the estimates of the popPK parameters A,B,α,β. For estimation of μ^Scase ≡ E [S(T)|Δ^dxY^dx = 1], note that even in the idealized situation with P(T = T^dx) = 1, the outcomes S(T_i) are not observable, because the process S(·) is measured on a discrete visit schedule that generally does not include the infection time T_i. Given an T_i, the popPK model (1) is used to estimate S(T_i). Then, using a similar two-step modular process as for the Times Method, μ^Scase ≡ E [S(T)|Δ^dxY^dx = 1] may be estimated by sample averages of the $\widehat{S}\left(T_i\right)|{\Delta }_i^{dx}{Y}_i^{dx}=1$ values. To aid adherence to the homoscedastic variance assumption (A2), the analysis is done with values Ŝ(t) on the natural log transformed scale that minimizes heteroscedasticity of errors. If substantial variance variability remained, each observation could be weighted by its estimated inverse variance (Sections 15.2.2, A.7 in Carroll et al.¹²). This results in the weighted estimator ${\widehat{\mu }}^{Scase}={\sum }_{i=1}^n{\Delta }_i^{dx}{Y}_i^{dx}{\widehat{w}}_i^{case}\widehat{S}\left(T_i\right)$ with ${\widehat{w}}_i^{case}={\left[\widehat{Var}\left(\widehat{S}\left(T_i\right)\right)\right]}^{-1}/{\sum }_{j=1}^n{\Delta }_j^{dx}{Y}_j^{dx}{\left[\widehat{Var}\left(\widehat{S}\left(T_j\right)\right)\right]}^{-1}$. Here each $\widehat{Var}\left(\widehat{S}\left(T_i\right)\right)$, as well as co-variance terms for different participants with T_i and T_i′, can be calculated analytically by the propagation of error, following a first-order linearization of the nonlinear mixed effects model of the observed concentrations (Supplement D). The variance of ${\widehat{\mu }}^{Scase}$ may then be estimated by $\widehat{Var}\left({\widehat{\mu }}^{Scase}\right)={\sum }_{i=1}^n{\Delta }_i^{dx}{Y}_i^{dx}{\left({\widehat{w}}_i^{case}\right)}^2\widehat{Var}\left(\widehat{S}\left(T_i\right)\right)+{\sum }_{i=1}^n{\sum }_{i^{\prime }=1}^n{\Delta }_i^{dx}{Y}_i^{dx}{\Delta }_{i^{\prime }}^{dx}{Y}_{i^{\prime }}^{dx}{\widehat{w}}_i^{case}{\widehat{w}}_{i^{\prime }}^{case}\widehat{Cov}\left(\widehat{S}\left(T_i\right),\widehat{S}\left(T_{i^{\prime }}\right)\right)$.

In a previous simulation study, we found that this weighted estimator performed worse (in bias and type I error rate control) than the unweighted approach, which uses a dose-group stratified sample-mean estimator of μ^Scase and a dose-group stratified sample-variance estimator of ${\widehat{\mu }}^{Scase}$, not using the analytic variance estimates from the popPK model. We conjecture that those results are due to imprecision in the popPK model variance estimation. Thus, we used the unweighted estimator of μ^Scase in this study. To help understand why the weighted estimator does not confer improvements, literature suggests that the weighted estimator may be recommended if two conditions hold: 1) severe heteroscedasticity still remains for the transformed Ŝ(t), e.g., the maximum variance is greater than 3 times the minimum variance as suggested by Deaton, Reynolds and Myers¹³ and 2) the variance of the transformed Ŝ(t) can be stably estimated. Otherwise, an unweighted analysis may be preferable [e.g., see work by Williams¹⁴].

In the real situation, where T is not observable, the estimation proceeds in the same way, except Ŝ(t_i) is replaced with $\widehat{S}\left(T_i^{*}\right)$. However, the variance terms $\widehat{V}ar\left(\widehat{S}\left(T_i^{*}\right)\right)$ and related covariance terms calculated analytically by the propagation of error do not account for uncertainty in $T_i^{*}$, which is another reason why our analysis in the Simulations and Application does not use these analytic variance-covariance estimates and instead simply uses the sample variance of the $\widehat{S}\left(T_i^{*}\right)|{\Delta }_i^{dx}{Y}_i^{dx}=1$ values. This choice is also supported by our evaluation in the simulation study of how the variance of S(T*) varied over 12 subgroups defined by VRC01 dose group, the diagnostic pattern of first positive (FP) HIV-1 test result, and whether the FP visit was at an infusion visit or a mid-infusion visit (Web Figure 1 in Supplement F – all subsequent Web Figures are in Supplement F). Because the sample variances are approximately uniform over the subgroups, we used the unweighted estimator.

For estimation of μ^Sctrl, we first consider the idealized situation where all eligible control participants have markers measured. For a given control study participant with Y^obs = 0, based on his/her data (X^dx, Δ^dx, Z, T^inf (τ), W), the popPK model described above is used to estimate S(t) at every time point t between 0 and X^dx (e.g., computed on a daily grid), yielding {Ŝ(t) : t ∈ (0, X^dx]}, and then the average $\overline{S}(\tau )$ is estimated numerically by $\widehat{\overline{S}(\tau )}=\frac{1}{X^{dx}}\underset{0}{\overset{X^{dx}}{\int }}\widehat{S}(t)dt$. The concentrations Ŝ(t) are analyzed on the natural log scale so that the averaging is over an approximately symmetrical distribution. Here the assumption of homoscedastic errors for the $\widehat{{\overline{S}}_i(\tau )}$ variables is reasonable, given the averaging of Ŝ(t) over the same daily grid and span of times for all control participants. Next, we consider the real situation, where case-control or two-phase sampling is used that measures the longitudinal markers in a random sample of eligible controls. If Bernoulli simple random sampling is used, then ${\mu }^{Sctrl}\equiv E\left[\overline{S}(\tau )|Y^{obs}=0\right]$ may be estimated by a sample average of the $\widehat{{\overline{S}}_i(\tau )}$ values of participants i with ${ϵ}_i\left(1-Y_i^{obs}\right)=1$. However, if the probabilities of sampling control participants for marker measurement, ${\pi }_i=P\left({ϵ}_i=1|Z_i,T_i^{inf}(\tau ),Y_i^{obs}=0\right)$, are not all equal, then these estimators may be biased. In this situation an estimator is needed that adjusts for the biased sampling. A simple approach weights each participant i in the analysis (with ${ϵ}_i\left(1-Y_i^{obs}\right)=1$) by $1/{\widehat{\pi }}_i$, where ${\widehat{\pi }}_i$ is an unbiased estimate of π_i. Alternatively, more efficient estimators of μ^Sctrl could be used, such as augmented inverse probability weighting (IPW)¹⁵ or IPW targeted minimum loss-based estimation (TMLE).¹¹

In the Simulations and Application we use simple sample average or IPW-weighted sample average estimators:

$${\widehat{\mu }}^{Sctrl}=\sum _{i=1}^n{\widehat{w}}_i{\overline{S}}_i(\tau )\text{ with }{\widehat{w}}_i=\left[{ϵ}_i\left(1-Y_i^{obs}\right)/{\widehat{\pi }}_i\right]/\sum _{j=1}^n\left[{ϵ}_j\left(1-Y_j^{obs}\right)/{\widehat{\pi }}_j\right],$$

$${\widehat{\mu }}^{Scase}=\sum _{i=1}^n\widehat{S}\left(T_i^{*}\right){\Delta }_i^{dx}/\sum _{i=1}^n{\Delta }_i^{dx}.$$

The variance of ${\widehat{\mu }}^{Sctrl}$ may be estimated by $\widehat{Var}\left({\widehat{\mu }}^{Sctrl}\right)={\sum }_{i=1}^n{\left(w_i\right)}^2\widehat{Var}\left(\widehat{{\overline{S}}_i(\tau )}\right)$.

Supplement A consolidates all of the assumptions needed for consistent estimation of μ^Tcase, μ^Tctrl, μ^Scase, and μ^Sctrl.

5. Simulation Study of the AMP Studies for Comparing the Methods

5.1. Evaluated Methods

We study size and power of 1-sided 0.025-level Wald tests to reject $H_0^T$ and $H_0^S$, as well as coverage of 95% Wald confidence intervals for ${\mu }^T\equiv {\mu }^{Tctrl}-\frac{1}{2}{\mu }^{Tcase}$ and μ^S ≡ μ^Sctrl − μ^Scase. Values μ^T = μ^S = 0 reflect the null hypotheses and μ^T < 0,μ^S > 0 reflect the alternative hypotheses of interest. We also study the Cox model with coefficient β for Ŝ(t), and include a baseline behavioral risk score Z_br in an effort to adjust for the amount of HIV-1 exposure. Thus the Cox model fit to data sets is λ(t|Ŝ(t) = s,Z_br = l) = λ₀(t)exp{βs + ηl}. We use Lin’s method⁷ because it applies for the two-phase sampling design used in AMP; this method is coded in the svycoxph function of the survey R package. A limitation of the existing sub-sampling Cox model methods is that they do not accommodate interval censoring of the failure time; for that extensions of other methods such as Zeng, Mao and Lin’s¹⁶ would be needed; we do not pursue those here. Note that our Cox model analysis should be interpreted as studying the association of the estimated time-dependent covariate Ŝ(t) with outcome; to interpret it in terms of the “true marker” S(t), this approach is a regression calibration method, which is well known to suffer from bias, albeit in a limited fashion in rare event settings such as ours.

If the investigator seeks a Cox modeling analysis with regression parameter closer to a causal assocation parameter, then the analysis could control for an estimate of the baseline propensity score (PS); if Ŝ(t) is dichotomized the PS is the probability that Ŝ(t) = 1 conditional on measured baseline variables and if Ŝ(t) is continuous then the PS may be taken to be the conditional expectation of Ŝ(t). Covariate-adjustment via propensity scores faces additional complications in case-cohort/case-control sampled studies compared to studies with full sampling. For example, as studied in Mänsson et al.,¹⁷ there can be artifactual effect modification of the causal association parameter by the estimated PS, and there can be residual confounding due to bias in the estimation of the PS. For our application, if an estimated PS were included in the Cox regression analysis of λ(t|Ŝ(t) = s), then the first issue should be considered if effect modification by the estimated PS is studied. The second issue is not expected to cause serious bias in our setting because the bias is small for rare event studies.

5.2. Simulation Design

We study the methods under a variety of data generation schemes fitting to AMP.

Throughout we use the combined AMP studies sample size of n = 1533 in each of the 10 mg/Kg and 30 mg/kg dose groups. Our first step generates visit times. Following Figure 1, we consider centers of visit windows at Week 0, 4, 8, 8.5, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, where the planned infusion visits are bolded. We study the perfect infusion adherence scenario where all participants attend every visit (except those who drop out as noted below), and we use the target date + random Uniform(−7, 7) draws to set actual visit dates of the scheduled 4-weekly visits with a 7-day upper and lower visit window, except for the Week 8.5 visit that is set to 5 days after the Week 8 infusion plus date + random Uniform(−2, 2) draws. We also study two imperfect adherence scenarios (medium and high), with medium defined by 10% of infusion visits missed and 15% of non-infusion visits missed (determined by randomly deleting visits among participants not yet right-censored), 15% permanent discontinuation of infusions per year, and 15% loss to follow-up per year (the latter two simulated by independent exponential failure times). The high adherence scenario is defined by 2%, 3%, 3%, and 5% for these numbers, respectively. Once the visit dates and the censoring time C (defined as the minimum of the Week 80 visit time, the permanent infusion discontinuation time, and the loss to follow-up time) are simulated, the infusion times T^inf(τ) are determined.

Second, we simulate study participants’ body weight according to the estimated distributions for men and women in past efficacy trials,^18,19 and hence the mAb dose amount, D = body weight (kg) multiplied by the mAb dose level (10 or 30 mg/kg), at each attended infusion visit. For each study participant, conditional on D, the visit dates and T^inf(τ) set in the first step, we then simulate the observed values W of Ŝ(t) at the M attended study visits according to the popPK model.

Third, conditional on the visit dates, the true infection time T is generated according to a Cox model with time-dependent covariate z(t): h(t|x, z(t)) = h₀(t)exp(β₀z(t)). Here h₀(t) is the baseline hazard function, z(t) is the time since the latest infusion prior to t when t ≤ t_s and equals t_s when t > t_s, where t_s is the time since the prior infusion to reach a serum concentration of 5 mcg/mL. This value 5 is near the lower quantification limit of the assay and may be thought of as a “zero-protection threshold,” where we assume that at times when the serum concentration is below 5 mcg/mL, a VRC01 recipient has the same instantaneous risk of infection as a placebo recipient; this allows us to choose β₀ and a constant baseline hazard h₀(t) to yield for all simulation settings the AMP protocol assumption of average annual incidence in placebo recipients of 4.0% (although our analyses do not use any data from placebo recipients). See Huang et al.²⁰ for details on this Cox model simulation technique, which was designed as a proxy model for how VRC01 concentration at time t links to the infection hazard based on the expectation that log-transformed drug concentration changes non-decreasingly and linearly with time after the first few days post infusion during the elimination phase. Once T is simulated, the participant’s last negative test visit and first positive test visit and corresponding first positive test results are also determined, based on the properties of the HIV diagnostic tests described in Supplement E.

The parameter β₀ governs the association of z(t) with the hazard rate, equal to the log hazard ratio per 1-day increase in z(t). We study five different effect size 28-day hazard ratios exp(28 * β₀) = 1.0, 1.32, 1.75, 2.32 and 3.06 per 28 days, which approximately translate to an overall dose-pooled prevention efficacy vs. placebo of 0%, 30%, 50%, 60% and 75% under perfect study adherence, assuming that Ŝ(t) is a perfect surrogate endpoint that fully explains all variabilities in an individual’s risk of HIV infection (Prentice’s “full mediation” condition for a valid surrogate endpoint). Setting β₀ = 0 induces all three null hypotheses of interest μ^T = 0, μ^S = 0, β = 0, whereas setting β₀ < 0 induces the three alternative hypotheses of interest μ^T < 0, μ^S > 0, and β < 0. The values of β,μ^T , and μ^S are not known analytically for alternatives set by β₀ < 0.

Fourth, following the AMP trial design, we use a two-phase sampling design for determining the sampling indicator ϵ, where for observed cases (with Δ^dxY^dx = 1), we set ϵ = 1. For observed controls (with Y^obs = 0), within each of four strata k = 1,2,3,4 defined by VRC01 dose group cross-classified with AMP study, ϵ is generated as Bernoulli(γ_k) with success probability γ_k selected such that the expected number of controls Y^obs = 0 with ϵ = 1 equals $N_k^{case}$, $2N_k^{case}$, or $\text{939547}$, where $N_k^{case}$ is the number of observed cases in stratum k. Fifth, T^ms(τ) is determined by the set of observed visits. Then, W is set to the values of Ŝ(t) at the time points $t=T_1^{ms},\cdots ,T_M^{ms}$. Lastly, we generate Z_br as expit(Y^obsN(1,1) + (1 − Y^obs)N(0,1)) where N(a,b) is a normal variate with mean a and variance b.

For each of 500 simulated data sets, μ^Tcase,μ^Tctrl,μ^Scase,μ^Sctrl, and β are estimated, together with their variances. For the Marker Method, the non-variance weighted implementation is used except where noted. For the Times and Marker Methods, to estimate each of the four mean parameters of interest (and hence the two mean differences μ^T and μ^S), we use sample mean estimators with stratification by dose group, where for estimation of μ^Sctrl a constant IPW sampling weight $1/\widehat{P}\left(ϵ=1|Y^{obs}=\text{0 ,\hspace{0.17em}}{L}_{str}=k\right)$ is used within each of the 4 strata k = 1,2,3,4, where the denominators are empirical fractions. Under the data generating distribution in our simulations, the stratified sample mean estimators are efficient, and thus it was not surprising that swapping these estimators for TMLEs did not improve efficiency (results not shown).

The methods are implemented using an estimator T* of the true infection event time T that is based on the three HIV-1 diagnostic assays that are performed on blood samples at all study visits in AMP. The fact that these tests register positive (+) or negative (−) during different time intervals post-infection constitutes the basis for timing estimation, where cases have FP test results of one of three patterns +−, ++−, +++. Supplement E describes the diagnostic assays and how they are used to define T* and lower and upper bounds for possible infection times. For the Times Method and case-only sign-test method, we excluded cases who missed the infusion prior to infection diagnosis because of the low precision of T*. We also apply the methods using the true infection times T– a gold-standard not fully achievable in practice. Power is computed as the proportion of the 500 Wald Z-statistics exceeding the 0.025-level normal critical value, and coverage is computed as the proportion of the 500 Wald 95% 2-sided confidence intervals that include the true parameter value. Coverage is only studied under the null hypothesis because in that case the exact values of μ^T , μ^S, and β are all known (to be zero). We also compare the three methods to a simple case-only sign test applied to observed cases, with positive sign if a participant has a negative HIV test result at an in-between infusion visit and is diagnosed at the subsequent infusion visit, and a negative sign if a participant has a negative test result at an infusion visit and is diagnosed at the subsequent in-between infusion visit. Participants with neither result are excluded from the analysis. A one-sample binomial proportion Wald test is used comparing the fraction of cases with positive sign to 0.5, with binomial variance estimated under the null hypothesis.

5.3. Simulation Results

We report results for the stratified sample mean procedures unless otherwise noted. We first found that all methods had elevated type I error rates if participants who permanently discontinued infusions prior to infection diagnosis were included, and therefore we report on the methods excluding these cases, which for the Cox model means right-censoring the failure time at the discontinuation date. For the perfect adherence scenario, Web Figures 2–6 show the Monte Carlo distributions of ${\widehat{\mu }}^T$, ${\widehat{\mu }}^{Tcase}$, $\frac{1}{2}{\widehat{\mu }}^{Tctrl}$, ${\widehat{\mu }}^S$, ${\widehat{\mu }}^{Scase}$, ${\widehat{\mu }}^{Sctrl}$and $\widehat{\beta }$ for the 1:2 case:control ratio setting across the five hazard ratio scenarios. The estimators with true infection times are known to be unbiased and thus their distributions depict the effect sizes being studied; moreover they provide a benchmark for the estimators with estimated infection times. The figures show uniform lack of bias of all estimators under the null hypothesis, but that ${\widehat{\mu }}^{Tcase}$ and ${\widehat{\mu }}^{Scase}$ are downward biased under alternative hypotheses, thus attenuating the difference estimates ${\widehat{\mu }}^T$ and ${\widehat{\mu }}^S$ toward the nulls. These biases are caused by the fact that the diagnostic-based infection timing estimator T* yields values $T_i^{*diff}$ that are sometimes too close to the middle of infusion intervals under alternative hypotheses. Similarly $\widehat{\beta }$ in the Cox model has some bias toward the null under alternative hypotheses. Web Figure 7 and 8 repeat Web Figures 3 and 5 for cases stratifying cases by FP test pattern +−, ++−-, +++. They reveal that under alternative hypotheses the estimators ${\widehat{\mu }}^{Tcase}$ and ${\widehat{\mu }}^{Scase}$ are unbiased for the first two patterns and biased for the +++ FP pattern. This occurs because +++ FP participants have least precision in estimation of T^*diff, with Web Figure 9 demonstrating tight correlations of estimated and true infection times for the first two patterns and close to zero correlation for the +++ FP pattern. Moreover, for +++ FP cases there is major uncertainty as to whether the infection date occurred before or after the last negative visit, whereas for +− − and ++− FP cases the true infection date is known to occur after the last negative visit with high probability (Supplement E, especially the HIV-1 Diagnostics Diagram). Therefore it is important to consider variants of the methods that exclude or downweight the +++ FP cases, and we report simulation results for such variant methods below.

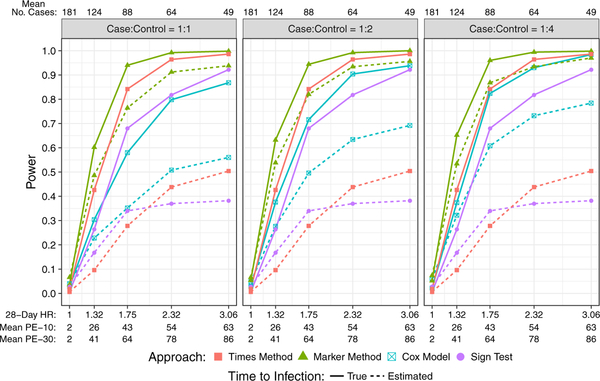
Figure 3 shows size and power of the testing procedures. Under the null hypothesis β₀ = 0, all approaches with true infection times accurately preserve the size of the tests at 2.5%, except a slight inflation 3.6% – 5.4% for the Marker Method; with estimated infection times, the Times Method and sign-test control the size but the Marker Method and Cox model have inflated size 6.6% – 7.4% and 4.0%–6.0%, respectively. As expected, power is always higher when the true infection event times are used, massively so for the Times Method and case-only sign test, a large difference also for the Cox model, and a lesser difference for the Marker Method. Overall, the Marker Method has the highest power, followed by the Cox model, the Times Method, and the case-only sign test. The higher power of the Marker Method and Cox model compared to the Times method and the sign test is partly due to the higher inter-individual variability in Ŝ(t) than in Ť^*diff. We conjecture that the lower power of the Cox model compared to the Marker Method is due to the fact that the difference in covariate values (i.e. Ŝ(t)) between cases and controls at each event time t is rather small because the majority of variability in Ŝ(t) comes from intra-individual time-swings and not from inter-individual variability. In fact, if participants attended study visits with identical intervals between visits, then the Cox analysis would measure an association of Ŝ(t) with infection purely due to inter-individual variability in Ŝ(t), whereas variability in visit schedules allows intra-individual variability to also contribute to the association. We also see that the case-control ratio impacts power of the Cox model method and slightly for the Marker Method, which occurs because precision for estimation of S(t) increases with more data used to fit the popPK model.

Figure 3:

Power to detect VRC01 concentration over time as a correlate of HIV infection for the perfect study adherence scenarios with case:control ratios 1:1, 1:2, 1:4. The effect sizes parametrized by β₀ are shown as 28-day hazard ratios (exp(28*β₀)). Solid lines are based on true (estimated) infection event times. Mean PE-10 (Mean PE-30) is average empirical prevention efficacy over the 500 simulated trials for the 10 (30) mg/Kg VRC01 dose group. Mean No. Cases is the total number of VRC01 recipient cases averaged over the 500 simulated trials.

Web Figure 10 shows 95% confidence interval coverage probabilities of the target parameters under the null hypothesis, which are close to the nominal level for the Cox model and sign test, but are too low (about 87%) for the Times Method and Marker Method. Figure 4 illustrates how study adherence affects power of the testing approaches for the 1:2 case:control ratio scenario. As expected, overall prevention efficacy decreases as study adherence decreases, and so does the power for the Times Method and the case-only sign test due to higher variability in the estimated effects as a result of more missing infusions and study dropouts. In contrast, power of the Cox model increases as study adherence decreases due to the increased inter-individual variability in Ŝ(t) when there are more missing infusions. Power of the Marker Method is less impacted by study adherence because the gain in power due to larger effect sizes with more missing infusions is offset by the loss in power due to a decreased number of cases (and hence controls) to more accurately and precisely estimate S(t).

Figure 4:

Power to detect VRC01 concentration as a correlate of HIV infection for the medium, high, and perfect study adherence scenarios with a 1:2 case:control ratio.

To better understand the Cox model method, for the same simulated data sets we also evaluated the Lin⁷ Cox model for the time-dependent covariate defined as the observed concentrations at study visits, not using the popPK model. Interestingly, the result is that this standard method has power < 0.05 for all effect sizes, demonstrating the necessity of employing the PK model to estimate S(t) on a frequent time grid such as daily, especially at estimated failure times.

5.4. Simulation Results Repeated Excluding the +++ First Positive Cases

When the simulations are repeated with no alterations to the methods except excluding +++ FP cases, the testing procedures have elevated type I error rates, because +− − and ++− FP cases have infection time estimates T* that tend to be closer to the FP visit than expected under the null hypothesis $H_0^T$ (Web Figure 7). To correct for this, for the Times Method we estimate the control mean μ^Tctrl using modified infusion intervals $\left\{f_{+--}{K}_{+--}+\left(1-f_{++-}\right)K_{++-}\right\}\left\{T_j^{inf}-T_{j-1}^{inf}\right\}$, where f₊₋₋ is the fraction of +− − and ++− FP cases that are +− − FP and K₊₋₋ = 1.26 and K₊₊₋ = 0.993 are two fixed constants chosen accounting for the operating characteristics of the diagnostic assays (Supplement E) to create an appropriate comparison to ${\widehat{\mu }}^{Tcase}$ under the null hypothesis $H_0^T$. Using a similar procedure, constants K₊₋₋ = 0.89 and K₊₊₋ = 0.99 are used for the Marker Method. No adjustment was made for the sign test. For the Cox model we right-censor by a +++ FP visit and change the null hypothesis from H₀ : β ≥ β* with β* = 0 to β* = −0.137 (Supplement E).

Web Figures 11–15 show the Monte Carlo distributions of ${\widehat{\mu }}^T$, ${\widehat{\mu }}^{Tcase}$, $\frac{1}{2}{\widehat{\mu }}^{Tctrl}$, ${\widehat{\mu }}^S$, ${\widehat{\mu }}^{Scase}$, ${\widehat{\mu }}^{Sctrl}$ and $\widehat{\beta }$ for the perfect study adherence and 1:2 case:control ratio setting across the five hazard ratio scenarios, using the versions of the methods that exclude +++ FP cases. The results verify unbiased estimation even under strong alternative hypotheses when +++ FP cases are excluded. The methods control the type I error and have approximately nominal coverage probabilities (Web Figures 16–18), except for slight type I error inflation and under-coverage for the Marker Method. In addition, these versions of the methods have decreased power compared to the methods that include all cases (Web Figures 17 and 19, in comparison to Figures 3 and 4, respectively), which occurs due to the reduced number of cases.

6. Pseudo-Example (Planned Analysis of the AMP Studies)

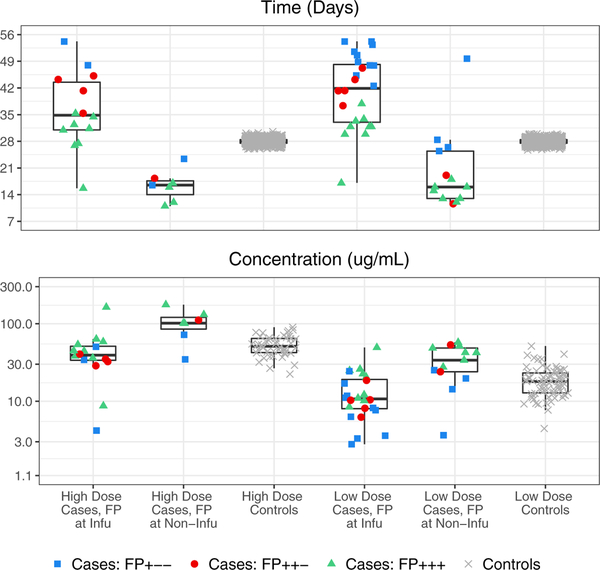
To illustrate the planned real data analysis of AMP, all of the methods studied in the simulations (with stratified sample means for the Times and Marker Methods) were applied to a single simulated AMP data set, which had n = 4600 participants and was simulated under true overall prevention efficacy of 52% and 71% for the low and high dose VRC01 groups. Web Figure 19 shows cumulative incidences of HIV infection over time for the two VRC01 dose groups and the placebo group, detecting this prevention efficacy. Figure 5 shows boxplots of the outcomes $T_i^{*diff}$ and ${\overline{T}}_i^{inf.int}$ of HIV infected cases and uninfected controls used for the Times Method, as well as the corresponding outcomes $\widehat{S}\left(T_i^{*}\right)$ and $\widehat{{\overline{S}}_i\left(\tau \right)}$ used for the Marker Method. The vastly wider boxplots for cases than controls for the Times Method suggests that this method would perform similarly to a case-only one-sample method based on the $T_i^{*diff}$ values. Web Figure 20 shows the $\widehat{S}\left(T_i^{*}\right)$ values for all individual HIV infected cases, as well as the measured concentrations at HIV infection diagnosis dates at the two previous visit dates.

Figure 5.

For the pseudo-AMP trial data set by VRC01 dose group and FP visit type, boxplots of $T_i^{*diff}$ and $\frac{1}{2}{\overline{T}}_i^{inf.int}$ of HIV infected cases and uninfected controls (Times Method, top panel), and of $\widehat{S}\left(T_i^{*}\right)$ and $\widehat{{\overline{S}}_i\left(\tau \right)}$ (Marker Method, bottom panel). The outlier in the fifth boxplots from the left has FP visit at the Day 5 post second-infusion visit, with estimated infection time T* just before the second-infusion visit.

Table 1 shows the results. There is consistent evidence for a VRC01 concentration correlate of risk across the four methods (p-values 0.018–0.071 for the method versions including all cases and p-values 0.001–0.061 for the method versions excluding +++ FP cases). Whether +++ FP cases are excluded makes a substantial difference, with estimated effects ${\widehat{\mu }}^T$ of 4.2 vs. 7.6 days; ${\widehat{\mu }}^S$ of 0.23 vs. 0.43 log₁₀ concentration; and $\widehat{\beta }$ = 0.81 vs. 0.61 when including vs. excluding +++ FP cases, respectively. Interestingly, the versions excluding +++ FP cases gave lower p-values despite the reduced number of cases included in the analysis.

Table 1:

Application of the Times Method, Marker Method, Lin (2000) Cox model, and Case-Only Sign Test to the Pseudo-AMP Trial Data Set^a.

Approach (95% CI)	No. Cases in Analysis (n = 64)	Target Parameter	Estimate of the Parameter (95% CI)	Two-sided P-value
Times	58 (91%)	$\frac{1}{2}{\widehat{\mu }}^{Tctrl}$	27.98 (27.96, 28.01)
Method		${\widehat{\mu }}^{Tcase}$	32.17 (28.69, 35.65)
		${\widehat{\mu }}^T$	4.19 (0.70, 7.67)	0.018
Repeat	30 (47%)	$\frac{1}{2}{\widehat{\mu }}^{Tctrl}$	32.27 (32.24, 32.30)
Excluding		${\widehat{\mu }}^{Tcase}$	39.83 (35.29, 44.37)
+++ FP		${\widehat{\mu }}^T$	7.56 (3.03, 12.10)	0.001
Marker	60 (94%)	${\widehat{\mu }}^{Sctrl}$	3.40 (3.33, 3.47)
Method		${\widehat{\mu }}^{Scase}$	3.17 (2.96, 3.39)
		${\widehat{\mu }}^S$	0.23 (0.003, 0.45)	0.047
Repeat	31 (48%)	${\widehat{\mu }}^{Sctrl}$	3.16 (3.10, 3.23)
Excluding		${\widehat{\mu }}^{Scase}$	2.73 (2.45, 3.02)
+++ FP		${\widehat{\mu }}^S$	0.43 (0.14, 0.72)	0.004
Cox Model	60 (94%)	Hazard Ratio	0.82 (0.66, 1.02)	0.071
		Per Incr. Conc.
Repeat	31 (48%)	Hazard Ratio	0.61 (0.48, 0.77)	0.002
Excluding		Per Incr. Conc.
+++ FP
Case-Only	55 (86%)	Prob. Infected	0.64 (0.496, 0.76)	0.058
Sign Test		Second-Half
Repeat	29 (45%)	Prob. Infected	0.69 (0.49, 0.85)	0.061
Excluding		Second-Half
+++ FP

^aThe four methods are implemented as described for the simulation study. Target parameters for controls are modified for the Times and Marker methods, and the null value for the Cox model was modified as described in Section 5.4.

7. Discussion

Motivated by planning the correlates of risk study in the ongoing AMP studies, we proposed two new approaches to testing the association of VRC01 serum concentration over time, modeled by a two-compartment population PK model, with the instantaneous incidence of HIV infection. In simulation studies of AMP we compared the performance of these approaches to a regression calibration implementation of the Lin⁷ Cox model with a time-dependent covariate measured via two-phase sampling, as well as to a case-only sign test. While the Times Method and sign test have potential resource advantage of not needing marker measurements, they had lowest power in simulations. The Marker Method had greatest power, exceeding that of the Cox model for all scenarios studied, which may stem from the limited inter-individual variability in VRC01 concentration compared to its large intra-individual variability over time resulting from repeated infusions and VRC01’s short half-life. We also found that power of the Cox model improves with the number of sampled event-free controls compared to cases, whereas power of the other three methods does not.

To assure consistent estimation of μ^Tcase and μ^Scase and valid hypothesis tests of $H_0^T$ and $H_0^S$, both the Times and Marker Methods require a model of HIV infection event times T that yield an estimator T* that is (A1) unbiased and (A2) has homoscedastic errors. By studying the methods with true infection times as benchmarks, we found that the methods using a best available estimator T* based solely on the HIV-1 diagnostic testing data collected in AMP violates (A1) under alternative hypotheses, leading to biased-toward-the-null estimation of μ^Tcase and μ^Scase, and of β in the Cox model. This bias is caused by the HIV-1 infected cases with first positive HIV-1 test result +++, given their poor estimation of infection times. In contrast +− − and ++− first positive cases had much better infection time estimates, indicating that if diagnostic testing were frequent enough to always catch infections in these early periods then the methods would be expected to perform well. However, because the AMP testing schedule does not achieve frequent enough diagnostic testing to meet this goal, our conclusion for AMP is that a purely diagnostic-based timing estimator would be insufficient for meeting the correlates scientific objective. Hence, further research is needed to develop an improved timing estimator for +++ first positive cases. Fortunately, longitudinal HIV-1 sequence data are being collected from HIV-1 infected cases in the AMP trials, enabling insight into HIV-1 sequence diversification, and viral load data are also being collected. It is promising to develop an improved infection timing estimator based on these additional data, which, once available, could easily be incorporated into the proposed methods. Not only would the use of an optimized estimator improve unbiasedness, it would also majorly improve power, given our simulations showed that use of true vs. estimated infection times dramatically impacted power.

Moreover, for validity the Marker Method and the Cox model method require a population PK model of monoclonal antibody concentration over time that provides unbiased estimates of the concentration at any study time, where the use of a PK model was necessary for the Cox model to have any power even against large alternative hypotheses. Therefore, an optimal PK sampling design is needed that samples time points within a few days after at least one of the infusions to characterize the distribution phase of the monoclonal antibody, as well as time points in the elimination phase. The Marker Method based on modeled concentrations could also be applied including the entire placebo group in the analysis, with S_i(t) set to zero for all participants i and all t ∈ (0,τ]. The increase in the number of events– and the widened inter-individual variability of S_i(t)– would increase power.