Division plane placement in pleomorphic archaea is dynamically coupled to cell shape

Summary

One mechanism for achieving accurate placement of the cell division machinery is via Turing patterns, where non-linear molecular interactions spontaneously produce spatiotemporal concentration gradients. The resulting patterns are dictated by cell shape. For example, the Min system of Escherichia coli shows spatiotemporal oscillation between cell poles, leaving a mid-cell zone for division. The universality of pattern-forming mechanisms in divisome placement is currently unclear. We examined the location of the division plane in two pleomorphic archaea, Haloferax volcanii and Haloarcula japonica, and show that it correlates with the predictions of Turing patterning. Time-lapse analysis of H. volcanii shows that divisome locations after successive rounds of division are dynamically determined by daughter cell shape. For H. volcanii, we show that the location of DNA does not influence division plane location, ruling out nucleoid occlusion. Triangular cells provide a stringent test for Turing patterning, where there is a bifurcation in division plane orientation. For the two archaea examined, most triangular cells divide as predicted by a Turing mechanism, however, in some cases multiple division planes are observed resulting in cells dividing into three viable progeny. Our results suggest that the division site placement is consistent with a Turing patterning system in these archaea.

Abbreviated Summary

In many organisms, there appears to be an intimate link between cell shape and division plane location. By studying division plane placement in live cells of haloarchaea, which show a wide variety of cell shapes, the results show that the division plane dynamically responds to cell shape, consistent with regulation by an underlying Turing patterning system.

Graphical Abstract

Introduction

During growth and proliferation, cells tightly control the location and orientation of the division plane to ensure viable progeny. In most cells, the location and orientation of the division plane appears to be related to the cell shape (Minc & Piel, 2012). This decision is thought to occur during the assembly of the division machinery, where, in most prokaryotes, the tubulin superfamily protein FtsZ assembles to form a contractile ring effecting cytokinesis. In the archaeal TACK superphylum (Zaremba-Niedzwiedzka et al., 2017), the Cdv/ESCRT-III system mediates cytokinesis, and is homologous to the eukaryotic system involved in vesicle formation (Lindas & Bernander, 2013, Samson & Bell, 2009) and abscission during the late stages of cytokinesis (Addi et al., 2018). In eukaryotic cells, division is effected on the placement of an actin-based contractile ring whose position is determined by a microtubule-based system sensing the cell shape (Minc et al., 2011).

The key question is: how does a cell determine the location of the appropriate division plane? This requires the existence of robust molecular mechanisms for generating intracellular spatial information. Several localization mechanisms that are capable of generating spatial information at a cellular scale have been characterized. These include: membrane curvature sensing (Antonny, 2011, McMahon & Gallop, 2005), geometry-induced protein patterning (Thalmeier et al., 2016), membrane energy minimization (Boss et al., 2012), placement of “ruler” proteins along a cell (Xu et al., 2013) and dynamic Turing patterning systems (Walsh et al., 2017, Wu et al., 2015, Loose et al., 2011, Turing, 1952). Some of these mechanisms have components that sense the cell shape (curvature sensing or ruler proteins) to maintain cell geometry. Other mechanisms can respond more dynamically to the cell shape (Turing patterns and energy minimization) and should be more suitable for pleomorphic or dynamic cells.

The best characterized dynamic system for generating intracellular spatial information is the Escherichia coli Min protein system (Yu & Margolin, 1999, Rowlett & Margolin, 2015). The Min proteins oscillate from pole to pole in the rod-shaped cells, restricting FtsZ-ring formation to the center of the cell (Oliferenko et al., 2009, Bi & Lutkenhaus, 1993, Rowlett & Margolin, 2015, Raskin & de Boer, 1999). Deletion or inhibition of the Min system reduces the accuracy of division (Yu & Margolin, 1999), resulting in frequent asymmetric division and mini-cell formation (de Boer et al., 1989). In some aberrant-shaped E. coli cells, MinD local maxima oscillate in complex patterns that do not appear to provide a well-defined pattern for cell division (Mannik et al., 2012). However, in other irregular morphologies such as almost-spheroid (Corbin et al., 2002) or Y-shaped cells (Varma et al., 2008), the Min system has been shown to provide a robust mid-cell signal. In vitro, MinD and MinE can spontaneously form spatiotemporal patterns on a lipid bilayer when supplied with ATP (Loose et al., 2008). In artificial membrane-lined chambers, Min patterning displays rich dynamics that are determined by the geometry of the confining chamber (Kretschmer & Schwille, 2016, Caspi & Dekker, 2016, Zieske & Schwille, 2014).

Cell division in E. coli is complicated as the division ring and nucleoid are intricately coupled to multiple systems including the Ter-linkage (Bailey et al., 2014), FtsK translocase (Stouf et al., 2013) and nucleoid occlusion (Mannik & Bailey, 2015). Nucleoid occlusion inhibits the onset of Z-ring constriction over the bulk of nucleoid (excluding the terminus region) (Mannik & Bailey, 2015). The replicated nucleoids separate before division ring maturation occurs between the nucleoids.

Despite the complexity of coupled systems, we have shown that in the case of dynamic Turing patterning systems the division plane location can be predicted from the cell shape and the natural wavelength of the underlying Turing system for arbitrary cell morphologies (Walsh et al., 2016). The predicted division plane corresponds to the nodal plane of the lowest order harmonic mode determined by the cell shape, which approximately divides the cell in half. This plane is the most resilient to division plane switching induced by minor shape fluctuations (Woolley et al., 2011). We have recently shown (Walsh et al., 2017) that this holds for our mathematical model of the E. coli Min system (Walsh et al., 2015) and experimental data (Fischer-Friedrich et al., 2010).

Studying the coupling between cell shape and division plane orientation in E. coli is challenging (Ivanov & Mizuuchi, 2010). Whatever coupling between the cell shape and division plane orientation exists, it is likely to be distorted by the interactions of the division plane with the nucleoid. As such, the coupling between the nucleoids and the division plane increases the complexity of the positioning system. Furthermore, when cell shapes are distorted, 3-dimensional characterization becomes important, limiting the accuracy of data and its analysis.

The archaeon Haloferax volcanii is an excellent model organism for studying the relationship between cell shape and division plane location and orientation. The majority of cells are described as relatively flat, plate-shaped cells that vary in shape, and have at least one FtsZ homolog, FtsZ1, that functions in division. FtsZ1 localizes as a mid-cell band throughout most of the cell division cycle apart from some cells, where FtsZ signal remains diffuse immediately after division (Duggin et al., 2015). Depending on conditions, H. volcanii cells can also exist as distinct elongated rod or filamentous forms of regular width, which are associated with motility and biofilm formation, respectively (Duggin et al., 2015, Chimileski et al., 2014). In some media. both plate- and rod-shaped sub-populations coexist and are capable of division (Duggin et al., 2015, Delmas et al., 2013), thus, the division localization machinery has to function robustly in these distinct cell types. H. volcanii is polyploid, normally containing more than ten copies of its genome (Breuert et al., 2006), with the DNA generally appearing throughout the cell (Delmas et al., 2013), making strong coupling between any single, localized nucleoid and the division ring less probable.

Here we show that division plane location in H. volcanii and a second archaeon, Haloarcula japonica, can be predicted from the cell shape via harmonic analysis, suggesting the existence of an underlying Turing patterning mechanism. Analysis of triangular-shaped cells, which are occasionally observed in these species—particularly H. japonica (Hamamoto et al., 1988), showed that the lowest harmonic of the cell shape reasonably predicts the division plane orientation, despite their non-intuitive division plane orientations resulting in two daughter cells of different shape. Time-lapse microscopy of dividing H. volcanii cells showed that each division plane is dictated by the geometry of the cell and not the orientation of the previous division plane. This suggests that the machinery for defining the division plane is dynamically responsive to cell shape, as per a Turing pattern mechanism.

Results

DNA within H. volcanii cells is uniformly distributed

In E. coli, a strong spatial anti-correlation between the division ring and nucleoid distributions in both wild-type and deformed cells has been observed, with the division ring having essentially the same width as the gap between the separated nucleoids (Mannik et al., 2012). From these observations, it has been concluded that positioning of the nucleoids is strongly coupled to the localization of the divisome in E. coli, especially in deformed cells (Mannik et al., 2012). Previous observations of fluorescently stained DNA in H. volcanii have shown that DNA occupies space throughout the cells (Delmas et al., 2013). We have analyzed the distribution of DNA in H. volcanii cells expressing green fluorescent protein (GFP), as a marker for the cell cytoplasm (see SI). By examining 2,286 cells, the cross-correlation between GFP fluorescence and fluorescently-stained DNA peaked at 0.89, demonstrating that the DNA is linearly correlated to the uniform GFP distribution (Fig. S1). There were no large-scale deviations in the DNA distribution (when compared to the uniform GFP distribution) with the largest fluctuations within 0.28 μm of the cell perimeter. On average, there was 2.6% less DNA signal occurring within 0.5 μm of the cell edge in comparison to the GFP (See SI for details). The high degree of uniformity of DNA concentration throughout the cells indicates that DNA is not responsible for positioning the Z-ring in H. volcanii, which assembles very early in the cell cycle (Duggin et al., 2015).

The orientation of the division plane can be predicted from the shape of the cell

To test whether the orientation of the H. volcanii cell division plane is consistent with an underlying Turing mechanism, the experimentally measured orientation of the division plane was compared to the theoretical prediction for division plane orientation based on cell shape. The primary division ring protein FtsZ1 was fluorescently labeled so that phase-contrast and fluorescence images could be recorded (Duggin et al., 2015). Automated image analysis was used to detect the outline of cells in the phase-contrast images, from which the division plane position and orientation were predicted.

Fig. 1 shows a field of cells with FtsZ1-GFP fluorescence (green) and division plane predictions (magenta). Surface plots provide a better representation of both how the FtsZ1 distribution varies across a cell and the division plane prediction (Fig. 2B). Numbers adjacent to each cell in Fig. 1A correspond to the aspect ratio of the cell outlines that are color coded to reflect the aspect ratio (red - quasi-circular cells, aspect ratio > 0.9; yellow - moderately elongated cells, aspect ratio between 0.75 and 0.9: and blue - elongated cells, aspect ratio < 0.75). The quality of the fit for each prediction was measured using a cross-correlation between the FtsZ1-GFP distribution and the division plane prediction for each cell (see Experimental Procedures). The numbers adjacent to each cell in Fig. 1D correspond to this cross-correlation value. Identical distributions, i.e. a perfect fit, would have a value of one. Uncorrelated distributions, where the two are independent of each other would have a value of zero. Perfectly anti-correlated distributions, where a high value in one corresponds to a low value in the other and vice versa, have a cross-correlation value of −1.

Fig. 1. An example of division plane prediction.

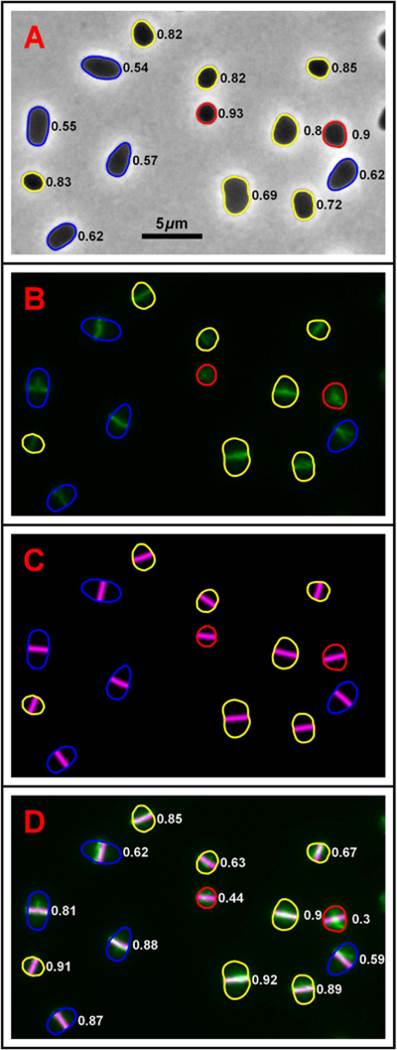
(A) A sample phase-contrast image of H. volcanii (H98 + pIDJL40-FtsZ1) overlaid with the cell shape outlines generated by automated image analysis. Numbers adjacent to each cell correspond to the aspect ratio of the outline: the closer the value is to 1 the higher the degree of rotational (>2-fold) symmetry (for example a circle, equilateral triangle or square). Conversely, the lower the value, the closer the cell outline resembles a one-dimensional line. Outlines are color coded to reflect this aspect ratio, with quasi-circular cells (> 0.9) in red– moderately elongated cells (0.65–0.9) in yellow and elongated cells (<0.75) in blue. (B) The corresponding FtsZ1-GFP fluorescence image showing the future division plane orientation of each cell. This image has been overlaid with the cell outlines calculated using the phase-contrast image shown in (A) with the same aspect ratio color coding. (C) Theoretically calculated predictions for the division plane in each cell. These are given by the nodal line of the lowest harmonic of the cell outlines from (A) which are overlaid with the same aspect ratio color coding. The panel is shown on a black background to match the positions of the actual cells. (D) A false colored overlay of (B) and (C), the experimental FtsZ1-GFP distribution is show in green, the predicted division plane distribution in magenta. The intersection of the two creates white. Numbers adjacent to each cell correspond to the cross-correlation between experimental and predicted division plane distributions. Identical distributions would have a value of one while uncorrelated distributions would have a value of zero.

Fig. 2. Analysis of division plane prediction.

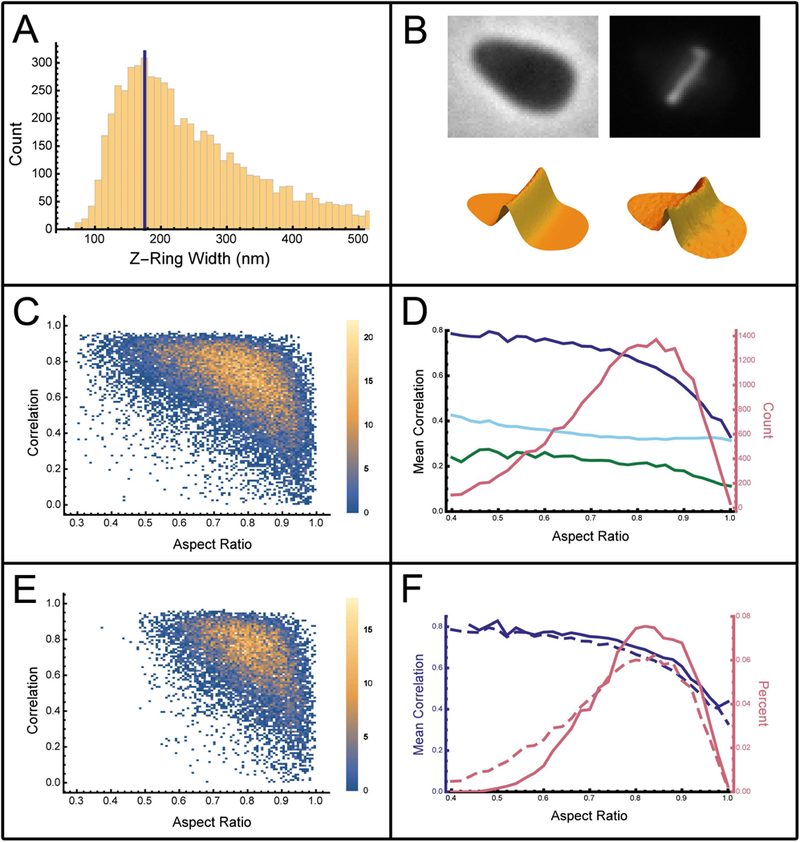
(A) The division ring width as measured by selecting for elongated cells and fitting a Gaussian to the profile along the major axis of the cells. This histogram shows all of the standard deviations for the best fit Gaussian of each cell. (B) Surface plots for a typical cell isolated from Fig. 1 are shown below each of the respective microscopy images used to generate them. Top left is the phase-contrast image, bottom left shows the resulting theoretically predicted division plane distribution for the FtsZ1 in the cell. The right-hand column shows the FtsZ1-GFP fluorescence distribution as an image (top) and surface plot representation (bottom). (C) Scatter plot with point density (color scale on right) showing the cross-correlation between the predicted division plane and the experimental FtsZ1-GFP distribution as a function of cell aspect ratio for 22,217 analyzed cells of H. volcanii (H98 + pIDJL40-FtsZ1). (D) The mean cross-correlation between the predicted and observed division plane orientation for wild type cells (solid blue line) as a function of aspect ratio. The light blue line shows the mean cross-correlation between randomly rotated division planes and the FtsZ-GFP distribution. The green line shows the mean cross-correlation between a randomly offset division plane and the FtsZ-GFP distribution.(E) Scatter plot with point density (color scale on right) showing the cross-correlation between the predicted division plane and the experimental FtsZ1 distribution for cetZ1 gene deletion strain. (F) The mean cross-correlation for predictions using the cetZ1 gene deletion strain (solid blue line) versus the wild type strain (dashed blue line) as a function of aspect ratio. The frequency (probability density) of cells as a function of aspect ratio is shown for wild type cells (dashed pink line) and cetZ1 gene deletion strain (solid pink line).

From the representative field (Fig. 1), one can see that for cells with a low aspect ratio (blue outline), the predicted division plane corresponds to the FtsZ1-GFP fluorescence. Exceptions occur when the FtsZ1-GFP plane is not well-formed (blue outlined cell in the bottom right corner, Fig. 1). Cells with moderate aspect ratios, 0.75–0.9 (yellow outlines), also show close correspondence between predicted division planes and FtsZ1 fluorescence (Fig. 1). For cells that are quasi-circular or approximate regular polygons (aspect ratio ~1, red outlines, Fig. 1), the predictions are poorly correlated to the FtsZ1-GFP fluorescence suggesting that shape alone is not sufficient to determine the division plane orientation in these cells.

To determine whether the orientation of the division plane is determined by the cell shape, a large number of cells (22,217) were analyzed and their individual division planes were predicted using the nodal line of the lowest harmonic of the cell shape. To directly compare the predicted division plane to the FtsZ-GFP fluorescence image, the nodal line was convolved by a Gaussian of fixed width that was perpendicular to the nodal line. To determine the appropriate value for the Gaussian width, the FtsZ-GFP division ring width was measured for a subset of cells where the division plane was likely to be perpendicular to the major axis of the cell. For this, elongated cells were selected and a Gaussian was fit to the FtsZ-GFP fluorescence profile along the major axis of the cells. All measured Gaussian fit widths are shown as a histogram in Fig. 2A. The mode of the division plane width (175 nm) is consistent with the division ring being diffraction limited. The width of 175 nm (2.7 pixels) was then used for all predictions of all cells for this work.

The scatter plot (Fig. 2C) shows that the cross-correlation between the predicted division plane orientation and the observed FtsZ1-GFP distribution is dependent on the aspect ratio of the cell. The mean cross-correlation as a function of aspect ratio is shown in Fig. 2D (solid blue line). For low aspect ratios (less than 0.5), the majority of scatter points are located between cross-correlation values of 0.8 and 1, with a mean cross-correlation of approximately 0.8. As cells approach circular symmetry (aspect ratio close to 1), the cross-correlation scatter plot (Fig 2C) becomes effectively homogeneously distributed between 0 and 1, with a mean value of approximately 0.4 for an aspect ratio of 1. So in rotationally (> 2-fold) symmetric cells, the model fails to predict the orientation of the FtsZ1-GFP division plane.

To ascertain the significance of the cross-correlation values, two alternative models were constructed. For the first, the division plane was modeled by a line passing through the centroid of the cell shape but randomly oriented while for the second, the division plane was modeled as a line parallel to the minor axis of the cell but randomly positioned within the cell. The cross-correlation between the randomly rotated division plane prediction and the FtsZ-GFP distribution (Fig. 2D light blue line) is approximately 0.4, while the cross-correlation between a randomly offset division plane prediction and the FtsZ-GFP distribution is approximately 0.2 (Fig. 2D green line). Comparing our model to these controls shows that the model has a strong predictive power for low aspect ratio cells. In cells which are circular or approximate regular polygons (aspect ratio equal to 1), the mean correlation between the predicted and observed division planes (Fig. 2D solid blue line) converges to mean cross-correlation between the predicted division plane and the randomly rotated predicted division plane and the FtsZ-GFP distribution (Fig. 2D light blue line) at a value of approximately 0.4, suggesting that in these cells the prediction is no better than random.

To estimate the significance of the cross-correlation between the predictions and the data, the standard deviation of the cross-correlation was calculated as a function of aspect ratio (Fig. S2). The plot displays a reasonably constant standard deviation with values of approximately ~0.15 for low aspect ratios increasing to ~0.2 for high aspect ratios. Overall, the standard deviation is 0.18. The mean correlation for all predictions is 0.66. With such a large number of analyzed cells, the probability that the mean is less than 0.4 (corresponding to a randomly oriented division plane prediction) is approximately $3\times {10}^{-9358}$ . Note that cells have preferred values of aspect ratio as shown in the histogram (Fig. 2D solid pink line).

Cell division positioning is unaffected by the deletion of the cytoskeletal protein CetZ1.

In eukaryotes, the division plane orientation is indirectly coupled to the cytoskeleton: broadly speaking, the cytoskeleton dynamically positions the nucleus and mitotic spindle, which determines the orientation of the division plane (Minc et al., 2011). H. volcanii possess a cytoskeleton involving the tubulin-like CetZ proteins, which control cell shape changes. For example, deletion of CetZ1 inhibits rod-cell formation seen in the development of motility (Duggin et al., 2015). To test whether the CetZ cytoskeleton plays a role in positioning the division plane, the above image analysis was applied to cells where cetZ1 was deleted.

The scatter plot showing the cross-correlation between the model and experimental FtsZ1 distributions in cells with CetZ1 deleted is shown in Fig. 2E. Comparing this to the wild type cells (Fig. 2C), we see a significant reduction in the density of cells with low aspect ratios (values less than 0.5). This results from the lack of rod-shaped cells from the population (Duggin et al., 2015). This is reflected in the histogram (Fig. 2F), which compares the density of WT cells (dashed pink curve) and CetZ1 knockout cells (solid pink curve) as a function of aspect ratio. The mean correlation between the predicted division plane and the observed FtsZ1 fluorescence is plotted against aspect ratio (Fig. 2F, solid blue line). The observed relationship is indistinguishable from that observed for wild-type cells (Fig. 2F, dashed blue curve), indicating that CetZ1 does not directly influence the positioning of FtsZ1-GFP in H. volcanii.

Cell division in triangular-shaped H. volcanii cells

Triangular-shaped cells provide a sensitive test for models predicting the orientation and position of cell-division planes. There is a bifurcation in the orientation of the nodal line of the lowest harmonic of an isosceles triangle depending on whether it is sub-equilateral (vertex angle less than 60 degrees) or super-equilateral (vertex angle greater than 60 degrees). In sub-equilateral isosceles triangles, the nodal line of the lowest harmonic predicts that the division plane should cut off the corner of the triangle containing the sub-equilateral angle (Fig. S3A). Whereas in a super-equilateral isosceles triangle (vertex angle greater than 60 degrees), it is predicted that the division plane should run from the vertex of the triangle through the center of the cell, bisecting the cell (Fig. S3B).

To test this, we assayed cells with CetZ1 knocked out, as this deletion inhibits rod-cell formation, thus increasing the proportion of plate-shaped cells (Duggin et al., 2015). The 47 most triangular cells from the H. volcanii CetZ1 knock out cells were identified automatically using constraints on our image analysis algorithm (Fig. 3; see Experimental Procedures for details). The cells isolated are approximately triangular, with rounded corners and both types of division orientation are observed. An example of a sub-equilateral cell dividing by cutting off one corner is seen in the first example (Fig. 3, top row, second column). An example of a super-equilateral cell being cut in half is seen in the second example (Fig. 3 top row third column). However, the cells are not perfect isosceles triangles – they approximate scalene triangles, so rather than the division either cutting through the middle or one corner, there is a continuum transition between these two extreme cases rather than a simple bifurcation. This is illustrated by the second example on the second row. Here, the division plane nearly cuts the cell in half, but is slightly off center so it does not pass through the vertex of the triangle.

Fig. 3. Experimental cell division orientation in triangular H. volcanii cells.

An array showing the division plane orientation in the cells of the CetZ1 knockout of H. volcanii (ID59 + pIDJL40-FtsZ1) that have formed triangular shapes. The left-hand number of each panel is the aspect ratio of the cell outline, while the right-hand number is the resulting cross-correlation between prediction and observation. The left most image is the phase-contrast micrograph, the middle image is the experimental FtsZ1 fluorescence distribution and the right most image is the predicted division plane. The cells have been ordered by the cross-correlation between the predicted and observed division.

Visual inspection suggests that cells often struggle to settle on a division orientation in the triangular shapes. The division ring can appear poorly formed, only extending part of the way across the cell. More startling are the examples where it appears that division rings may have started to form in multiple directions. The example on the right hand side of the third row shows a cell that appears to have proto-division planes that could cut off each of the three corners. The example on the right hand side of the fourth row shows a cell where there is a proto division plane that is almost perpendicular to what appears to be the final division plane.

Despite the high rate of anomalies in the experimentally measured division planes of triangular cells, the Turing pattern correctly predicts the majority of division plane orientations. Of the 47 triangular cells, 27 cells (approximately 60% of the total) show a reasonable match between the prediction and the observation, 8 cells (17% of the total) have a division plane that clearly does not match the prediction and 12 cells (25% of the total) do not have a clear or unique FtsZ1 division plane. Of the cells that have a unique FtsZ1 division planes (35 cells), 77% (27 cells) are accurately predicted.

Although this accuracy of placement of division rings may not look impressive compared to the highly accurate division placement in rod-shaped E. coli cells (Yu & Margolin, 1999), we note that: 1) Rod-shapes do not have the bifurcation in harmonics that occurs in near equilateral triangles, making the triangles extremely sensitive to inaccuracies and fluctuations in cell shape. Thus, prediction of division planes within triangular cells is a much more stringent test, albeit susceptible to inaccuracies in experimental cell shape measurement and actual fluctuation in cell shape. 2) The accuracy of division plane positioning in E. coli is much higher than that observed in rod-shaped archaea, such as Halobacterium salinarum (Eun et al., 2018).

Similar analysis was performed on quadrilateral shaped cells, where the division plane matches the prediction in 2/3 of all cases (Fig. S4). Where predictions fail, the division plane is often not well formed or the cell shape deviates from a regular quadrilateral.

Cell division in triangular-shaped Haloarcula japonica cells

Asymmetric cell division in triangular archaea has previously been reported for the halophilic Haloarcula japonica (Hamamoto et al., 1988). The reported division planes appear to conform with the patterns predicted by our model and demonstrated for H. volcanii. To quantify these observations, we collected 2,672 images of H. japonica and compared the predicted division plane based on cell shape versus the localization of fluorescently labeled FtsZ-GFP (Fig. S5). The mean correlation as a function of aspect ratio showed a similar distribution to that observed for H. volcanii, albeit with a slightly lower mean correlation.

From this set of H. japonica images, we extracted the 47 most triangular cells. As per the triangular H. volcanii cells, we predicted the division plane based on the nodal line of the lowest order harmonic of the cell shape. These were compared to the FtsZ-GFP fluorescence via cross-correlation. The images show reasonable correlation between the predictions and FtsZ localization (Fig. S6). The images show examples of both sub-equilateral and super-equilateral division planes. Of the 47 H. japonica triangular cells analyzed (Fig. S6), 22 cells (approximately 47% of the total) show a reasonable match between the prediction and the observation, 2 cells (4% of the total) have a division plane that clearly does not match the prediction and 23 cells (49% of the total) do not have a clear or unique FtsZ1 division plane. Of the cells that have a unique FtsZ1 division planes (24 cells), 92% (22 cells) are accurately predicted.

Prediction of consecutive cell division planes for H. volcanii

The shape of the cell changes radically during cell division. When the parent cell is only slightly elongated in one direction the daughter cells are likely to be elongated in a perpendicular direction. If the division plane is determined by the nodal line of the lowest order harmonic of the cell shape, then the division planes of the daughter cells should be perpendicular to the original division plane.

To investigate this, we examined movies of multiple rounds of cell division (Movie S1). Both phase-contrast and FtsZ1-GFP epifluorescence movies were collected simultaneously. The cell outlines were calculated automatically and the nodal lines of the first harmonic calculated for each frame. The movie follows four rounds of cell division starting with a single slightly elongated cell. Fig. 4 shows the first two division events. In the first row, the single cell is about to divide. The second row (two frames later, i.e. 20 minutes) shows the two daughter cells that have already established FtsZ1 division planes that are approximately perpendicular to the original division plane, matching the prediction.

Fig. 4. Two rounds of cell division.

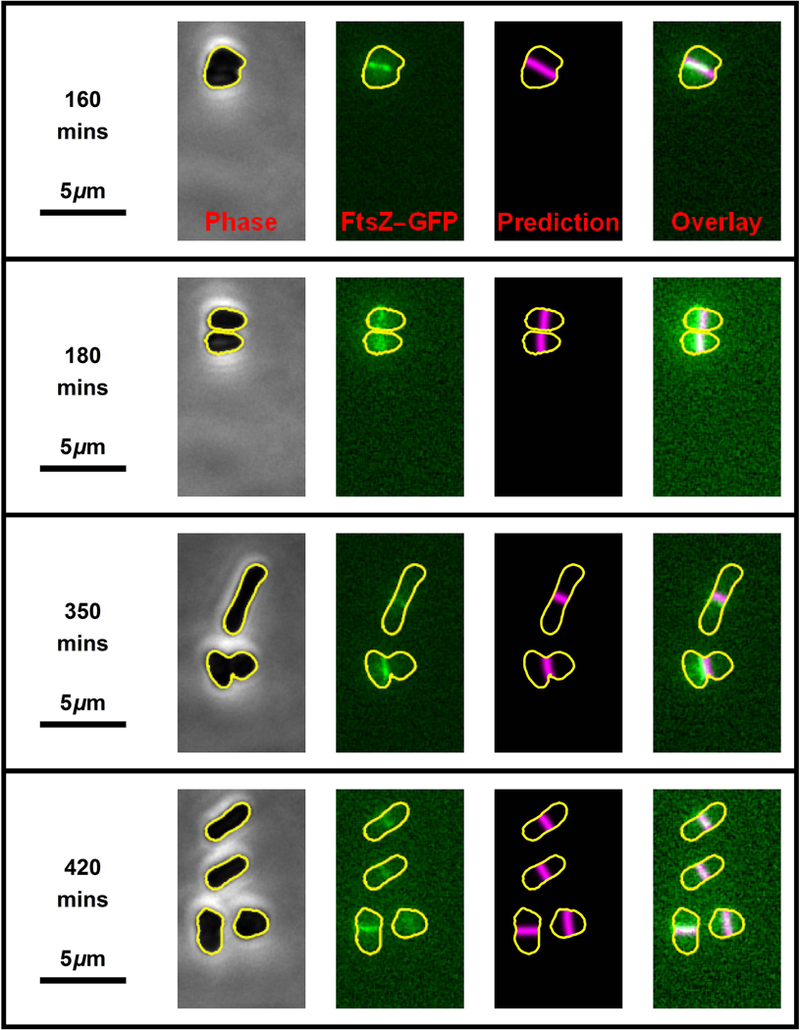
Four still frames (one per row) from the time-lapse movie (Movie S1) showing two consecutive rounds of H. volcanii (H98 + pIDJL40-FtsZ1) cell division. The left-hand images show the phase-contrast micrographs which were used to automatically generate cell outline (shown in yellow). The second column of images shows the FtsZ1 fluorescence with the cell outline superposed (yellow). The third column of images shows the predicted division planes (magenta lines) based on the cell shape. The far right column of images are the overlay of the FtsZ1 fluorescence and the predicted division plane. The first round of cell division (top two rows) correspond to movie frames 17 and 19, while the second round of cell division (bottom two rows) correspond to movie frames 36 and 43. Successive frames are separated by 10 minutes.

The second round of division is more complex (third and fourth rows, Fig. 4). The upper cell becomes very elongated and when it divides, each daughter cell establishes an FtsZ1 division ring that is parallel to the original division plane as predicted by the cell geometry. In contrast, the lower cell produces two daughters whose division planes differ in their relationship to the division plane of the progenitor cell. The daughter cell on the left is elongated in a direction perpendicular to the progenitor cell, hence, its division plane is perpendicular to the parent division plane. However, the daughter cell on the right is elongated in the same direction as the parent cell, hence their division planes are parallel. This can be seen more clearly by following this cell division event in Movie S1. The movie shows that after each division event, the new division plane is established in a manner that is predicted by the nodal line of the lowest order harmonic of the cell geometry.

Complex division for H. volcanii with near equilateral triangular morphology

Many triangular cells display two or more FtsZ rings with different orientations (H. volcanii - Fig. 3; H. japonica - Fig. S6). This is particularly evident in the right-hand column of Fig. 3, rows 3,4, 6 and 7. This suggests that division plane orientation may be determined dynamically and the underlying patterning system may switch drastically if the cell shape changes in a way to make a different orientation preferable. Multiple FtsZ division planes may persist due to the kinetics of ring formation.

While collecting time-lapse data, a particularly symmetric, near equilateral triangular cell was observed. The complete time-lapse of this cell and its progeny are shown in Movie S2 with the critical frames from the time-lapse shown in Fig. 5. The cell is so symmetric that very small variation in the shape over time or small error in the cell outline process cause the predicted division plane to shift dramatically. This is shown in the top two rows of Fig. 5 where the cell is essentially the same shape (left hand column) but the predicted division plane varies between dividing through the right- or left-hand side of the cell (third column). The instability in the prediction is not mirrored in the FtsZ-GFP fluorescence image (Fig. 5, second column), which is stable. However, there always appear to be at least two FtsZ structures present that are nearly orthogonal to each other. When the cell finally divides, it produces three daughter cells (Fig. 5, compare 400 to 405 minutes). We cannot determine whether the three cells separate simultaneously or sequentially due to limitations of optical and temporal resolution, however, the process is complete within two 5-minute frames (Fig. 5, rows 3, 4 and 5). Each of the three daughter cells establishes a new FtsZ division plane dictated by the geometry.

Fig. 5. Time-lapse of a dividing equilateral triangular-shaped cell.

Key frames from the time-lapse of an H. volcanii (H26 + pIDJL40-FtsZ1) cell that is dividing, as shown in Movie S2. The left-hand column shows the phase-contrast image, the second image shows the fluorescent signal superimposed with the cell outline in yellow. The third column shows the predicted division plane and the far right column shows the overlay of the FtsZ1 fluorescence on the predicted plane.

Discussion

Our results show that the location and orientation of the division plane can be predicted from the shape of the cell for the archaea, H. volcanii and H. japonica. The underlying model assumes that a mechanism exists to direct division ring proteins to the nodal line of the lowest order harmonic produced by the cell shape. Such a patterning mechanism is consistent with a Turing pattern generated by a currently uncharacterized protein system (Walsh et al., 2016). Non-linear dynamic patterning systems producing similar patterning include the Min protein system in E. coli, which is involved in the positioning of the cell division FtsZ ring (Bi & Lutkenhaus, 1993).

Our analysis of cell division in triangular-shaped cells provides a strong test for an underlying mechanism that senses cell shape. Isosceles triangles have a bifurcation in their harmonic modes where an equilateral triangle represents the degenerate case, with sub- and super-equilateral triangles exhibiting distinct nodal planes (Fig. S3). This bifurcation makes triangular cells a particularly difficult case to predict and also appears to create instabilities for the placement of the cell division machinery, attested by the cells in Figure 3 showing multiple or ill-formed FtsZ1-GFP planes. Our analysis of Movie S2 makes it clear that the predicted plane is very sensitive to our ability to accurately trace the cell shape. The first two rows of Figure 5 show what appear to be identical cell shapes and yet our algorithm swings from one plane to another. This sensitivity also appears to affect the placement of the cell division machinery, as supported by the fact that two FtsZ1-GFP planes are observed. Given this sensitivity, triangles provide a very stringent test for any model predicting division planes. From our data, the majority (77%) of division planes in triangular cells are accurately predicted by the nodal line of the lowest harmonic of the shape of the cell (Fig. 3). Thus, the underlying mechanism appears to be dynamically sensing cell shape.

The division plane predictions based on cell shape are particularly good for elongated cells (aspect ratios < 0.8), but they fail when the aspect ratio of the cell shape approaches one. This is to be expected for a shape-based mechanism. As the aspect ratio approaches one, the cell shape is likely to adopt approximate rotational symmetry. Under these circumstances, the lowest order harmonic will be degenerate and, as a result, multiple nodal lines will be consistent with the shape. When this occurs, other mechanisms may influence the orientation of the nodal line and consequently the division plane. We note that multiple FtsZ division planes are observed for triangular cells (Fig. 3 and S6), particularly when the cell displays near equilateral symmetry (e.g. the approximately equilateral cell in Fig. 5). Multiple division planes resulting from degeneracy due to near symmetry in cell shape can effect non-binary cell division as seen for a near equilateral triangular cell that produces three viable progeny (Fig. 5 and Movie S2). Similar effects have been observed in spheroidal E. coli cells (Corbin et al., 2002).

Our analysis of movies showing several rounds of cell division shows that cell shape dictates maintenance of the position and orientation of the division plane over time in H. volcanii. The orientation of the division plane in progeny cells does not appear to be biased by the orientation of division in the parent cell; we observed cells where the division plane of one daughter is parallel to that of the parent, while in the other, it is perpendicular (Fig. 4, Movie S1). In all cases we have examined, the geometry of the daughter cell determines the orientation of the division plane. Thus, the patterning system appears to be dynamic, and continuously maintained in response to cell shape. This observation will require the acquisition of a larger data set to determine its generality.

It is clear that there is still much to be learnt about cell division localization mechanisms. In some bacteria, cell division appears to be intricately linked to the position of the nucleoid, however the mechanism by which the nucleoid is positioned is unknown. One of the main difficulties in identifying localization mechanisms is differentiating the primary localization protein systems from the large assortment of other proteins that co-localize. One way to aid in differentiating primary localization proteins is by identifying the type of localization mechanism being utilized, as this in turn dictates a range of characteristics that the underlying protein system is likely to possess.

In the case of Turing patterns, the mechanism requires a system that is far from equilibrium with non-linear interactions and a large difference in diffusion constants. Thus, such a protein system requires an energy source, so one of the proteins in the system is likely to either be an ATPase or GTPase. Furthermore, to produce a large change in diffusion rate, at least one protein in the system is likely to dynamically bind to the membrane, the nucleoid or some other large structure. In the case of H. volcanii, the ATPase/GTPase responsible for patterning could be one of many that have been identified in the genome with no assigned function.

In E. coli, the Min protein system contributes to positioning the division plane (Yu & Margolin, 1999). The Min proteins produce Turing patterning via the ATPase activity of the MinD protein and its non-linear reactions involving the membrane and the MinE regulator of MinD’s ATPase activity (Walsh et al., 2015). This effectively positions the MinC division inhibitor on the polar membranes to inhibit division there and then allow division in the mid-cell region. Many other bacteria and archaea possess MinD homologues, most of which have unconfirmed functions (Lindas & Bernander, 2013). In the genome of H. volcanii, at least 13 NTPases of the broader MinD/ParA superfamily have been identified (Hartman et al., 2010). Given the great diversity of spatial-regulatory functions carried out by members of this superfamily (Lutkenhaus, 2012), substantial further research is needed in order to delineate the functions of these candidate spatial regulators in archaea.

Understanding how cell division is positioned in the cell is complicated by the existence of multiple, redundant mechanisms. In E. coli, at least 3 separate systems appear to operate: the Min, nucleoid occlusion, and Ter-linkage systems (Mannik & Bailey, 2015). Studying organisms where fewer localization mechanisms appear to be present, such as H. volcanii, where there appears to be no nucleoid occlusion, simplifies this problem.

Consistent with a previous report (Delmas et al., 2013), the DNA of H. volcanii was seen to occupy the majority of the cytosol. We have shown that this distribution has no correlation to the division plane orientation (Fig. S1). This suggests that nucleoid occlusion plays little or no role in determining the division plane orientation in H. volcanii. Furthermore, mechanisms associated with the position and timing of chromosome replication and segregation, such as the Ter-linkage system of E. coli, are unlikely to participate in division site placement in H. volcanii because they are highly polyploid and thrive with highly asynchronous chromosome replication (Hawkins et al., 2013, Breuert et al., 2006).

In eukaryotes, the division plane orientation is indirectly coupled to the cytoskeleton by active transport processes positioning the nucleus and mitotic spindle, which determines the orientation of the division plane (Minc et al., 2011). In H. volcanii, the CetZ proteins form a major component of the cytoskeleton. Deletion of CetZ proteins has no effect on cell viability (Duggin et al., 2015). In this work, we have shown that deletion of the CetZ protein known to affect cell shape, CetZ1, had no impact on division site placement, suggesting that it is improbable that a CetZ1-based mechanism similar to that of eukaryotes is present.

Given these features of pleomorphic archaea, and the strength of the cell-shape based prediction of division site placement we have observed here, we speculate that a Turing mechanism may be primarily responsible for wild-type division site placement in H. volcanii and possibly other pleomorphic polyploid archaea.

Experimental procedures

H. volcanii media and culture conditions

Cultures were grown with a variant of Hv-Ca medium (Allers et al., 2004), with additional trace elements (+TE), containing: casamino acids (5 g/l), 18% buffered salt water (BSW) (30% BSW stock contains 240 g NaCl, 30 g MgCl₂.6H₂O, 35 g MgSO₄.7H₂O, 7 g KCl, 5 ml 1 M CaCl₂ and 20 ml 1 M Tris-Cl, pH 7.5, per liter), vitamins solution (1000x stock contained sterile-filtered 1 mg/ml thiamine and 0.1 mg/ml biotin), and trace-elements (100x stock prepared by dissolving 5 g ethylenediaminetetraacetic acid (EDTA), 0.8 g FeCl₃, 0.05 g ZnCl₂, 0.01 g CuCl₂, 0.01 g CoCl₂, 0.01 g H₃BO₃, 1.6 g MnCl₂, 0.01 g Ni₂SO₄, and 0.01 g H₂MoO₄ per liter, adjusting the pH 7 with NaOH, and sterile-filtering the solution, removing the precipitate) (Duggin et al., 2015). Cultures were incubated at 45 °C with rotary shaking (200 rpm), and were maintained in log growth (O.D. 600 < 0.8) for at least 2 days before sampling at O.D. 600 = 0.2–0.8.

H. japonica media and culture conditions

Cultures were grown with Hj-Ca medium consisting of 23 % BSW, and casamino acids (5 g/l) and trace-elements as per the Hv-Ca (+TE) medium described above (Duggin et al., 2015). Cultures were incubated at 45 °C with rotary shaking.

Plasmids and strains for microscopy

For whole-cell fluorescence labeling for still-image microscopy, the plasmid pIDJL40 (Duggin et al., 2015), containing GFP in the pTA962 expression vector (Allers et al., 2010), was used to transform H. volcanii H98 as previously described (Allers et al., 2004). Strains for visualization of the division plane (ring) were constructed by transformation of H98 or H26 with pIDJL40-FtsZ1 (containing FtsZ1-GFP) (Duggin et al., 2015). For experiments conducted in the cetZ1 deletion background, pIDJL40-FtsZ1 (i.e. for expression of FtsZ1-GFP) was used for transformation of H. volcanii ID59 (Duggin et al., 2015).

H. japonica TR-1 was obtained from DSMZ (DSM6131). H. japonica ftsZ1 DNA (including the promoter region) was amplified from H. japonica genomic DNA using primers: HJZ1gene_F (CCCGGGCCCAAGTTCGGGAAACTCGCCTCAGG), and HJZ1_RnoS (CCCGGATCCGTCGACGTAGTCGATGTCTTCGCC). The PCR product was digested with ApaI and BamHI and cloned at these sites in pJWID1 (Liao et al., 2016), replacing the p.tnaA promoter and generating pJWID2 (i.e. containing H. japonica ftsZ1-GFP under the control of the ftsZ1 native promoter). pJWID2 was demethylated by transformation and purification from E. coli C2925 (NEB), and then this DNA was used to transform H. japonica TR-1, with selection on agar medium including 5 μg/ml Pravastatin (Sigma). This concentration was maintained during culturing for microscopy experiments, to maintain the plasmid.

DNA staining

For DNA staining, Hoechst 33342 nucleic acid stain (Life Technologies) was used. A 1 ml culture sample was centrifuged at 6000 g for 5 min at room temperature. The supernatant was discarded, and the pellet was resuspended in 18% BSW (Allers et al., 2004) plus 1 µg/ml Hoechst 33342 and incubated at room temperature for 5 minutes, before spotting ~1 Δl onto an agarose pad for microscopy, as described below.

Light microscopy

For recording still-images by microscopy, H. volcanii (H98 + pIDJL40-FtsZ1) cells in mid-log growth were induced with 200 μM L-tryptophan (Sigma) and incubation was continued for 12 hours before a 1 Δl sample of culture was withdrawn and placed directly onto the surface of a 1% agarose pad containing 18% BSW made using a GeneFrame (ABgene) on a slide. A number 1.5 coverslip was then placed on top. Phase-contrast, Hoechst and GFP epifluorescence images were acquired with a Zeiss AxioPlan2 microscope with a 100× 1.4 NA phase-contrast objective (Carl Zeiss, Germany). For time-lapse microscopy, a submerged soft-agarose media pad [31] (Fig. 4, Movie S1), or a CellASIC ONIX2 microfluidics system was used to immobilize live cells for recording the time-lapse movies. In the microfluidics experiments (Fig. 5, Movie S2), CellASIC B04A plates (EMD Millipore) were equilibrated with Hv-YPC media, including 250 ΔM L-tryptophan, for 1 hour at constant flow pressure of l psi prior to cell loading. After cell loading, cells were maintained at 40°C under constant flow pressure of 0.25 psi for 2 hours. Time-lapse movies were then recorded for 24 hours, at 5-minute frame-intervals, in both phase-contrast and GFP-fluorescence channels (100 milliseconds exposure times). The data were collected on a Nikon Ti2 inverted 25 mm epifluorescence microscope equipped with a FLASH4 sCMOS camera and a 100X, 1.45 NA objective lens.

Automated cell shape detection and analysis

Microscope images were analysed using Mathematica 10.2 software (Wolfram Research). Phase-contrast images were first preprocessed using a bottom-hat transform with a 30-pixel disk matrix for the kernel. Individual cells were then identified using the ‘Morphological Components’ function. Background objects and touching/dividing cells were excluded by the following conditions: cells had to contain at least 150 pixels (1 pixel = 60 nm) with a bounding disk radius of 5 pixels, they had to be dense with a pixel count to area ratio between 0.9 and 1.1, and they had to be essentially convex, with a convex coverage above 0.95. A curve was parametrically fitted to the outline of each cell by two Fourier expansions up to the 10th order mode to smooth the outline. A filled shape of the cell was then generated from this curve using the ‘MeshRegion’ function. This region was used to construct a structured rectangular mesh with grid point separation equal to one pixel. A discrete finite-difference five-point stencil Laplacian matrix was then calculated for this mesh. The lowest harmonic of each shape was calculated using the ‘Eigensystem’ function on the Laplacian matrix.

The nodal line of the lowest order harmonic of the cell shape was used as the basis for a model of the cell division plane. Nodal points were found by linearly interpolating the lowest harmonic (eigenfunction of the Laplace operator) along mesh edges. The distance from the nodal line to each mesh point was then calculated by finding the two closest nodal points, generating a straight line between them, then calculating the distance from the mesh point to that line.

In order to compare the nodal line model with experimental data, the line was convolved with a Gaussian function perpendicular to the nodal line. To determine the appropriate width for the Gaussian, the width of the FtsZ1 fluorescence z-ring image was measured for all dividing cells (Fig. 2A). The mode of the distribution corresponded to a width of 175.5 nm (2.7 pixels). Based on this, a Gaussian with a standard deviation of 2.7 pixels (175.5 nm) was used for cell division orientation predictions. This corresponds to a full-width at half-maximum of approximately 9 pixels (585 nm).

To aid in reproducing the analysis, we have made the analysis code publically available on Github at: https://github.com/lilbutsa/Archaea_Division_Analysis

Control models with random orientation or displacement

Cell division planes with random orientations were generated by taking lines through the centroid of the cell shape with orientations from 0 to 180 degrees in steps of 9 degrees. Randomly shifted planes were generated by taking lines that are parallel to the minor axis of the cell with 20 lines evenly spaced along the major axis of the cell. Each of these lines were then individually convoluted with the same Gaussian width (2.7 pixels) as the harmonic prediction and compared to the FtsZ fluorescence distribution.

Cross-correlation

To compare the quality of predictions to observations, cross-correlations were calculated. The following procedure was used. Pixels lying within the smooth mesh outline of the cell were isolated for the two data sets being compared. These pixels were then flattened into two lists with corresponding pixels from each set in the same position in their respective lists. If we let x be the list of one of the experimental data sets and y the other, the cross-correlation was given by:

$$\mathit{\text{cross}}-\mathit{\text{correlation}}(x,y)=\sum _{x,y}\frac{(x-\overline{x})\cdot (y-\overline{y})}{{\sigma }_x{\sigma }_{y}n}$$

Where $\overline{x}$ and $\overline{y}$ are the means of x and y respectively, ${\sigma }_x$ and ${\sigma }_y$are the standard deviations of x and y respectively, and n is the number of pixels within the cell.

The cross-correlation value ranges from −1 to 1. A value of 1 represents perfect correlation, that is, the two distributions are the same, bar a scaling factor. A value of zero means that the two sets are not linearly correlated. A value of −1 corresponds to two data sets being perfectly anti-correlated, that is, one has low values where the other has high values and vice versa.

Aspect ratio

The aspect ratio of each cell was calculated by taking the ratio of the width to length of the best fit ellipse to the cell. This was calculated using the ‘Component Measurements’ function in Mathematica.

The aspect ratio of a cell varies between 0 and 1. For values close to one, the cell approximates a shape that can be inscribed within a circle. Thus, it may approximate a two-dimensional object with rotational symmetry greater than 3-fold such as a circle, an equilateral triangle or a square. At the other limit, an aspect ratio approaching zero indicates that the shape is elongated in two-dimensions, approximating a one-dimensional line.

Detecting triangular and rectangular cells

To detect triangular and rectangular cells, additional selection criteria (on top of the automated cell shape detection algorithm) were added. Firstly, the curvature of each cell outline was calculated from the parametric cell outline in Cartesian coordinates $\gamma (t)=(x(t),y(t))$ using the equation:

$$\kappa \left(t\right)=\frac{\mid x^{{}^{\prime }}\left(t\right)y^{″}\left(t\right)-y^{{}^{\prime }}\left(t\right)x^{″}\left(t\right)\mid }{{({\left(x^{{}^{\prime }}\left(t\right)\right)}^2+{\left(y^{{}^{\prime }}\left(t\right)\right)}^2)}^{\frac{3}{2}}}$$

where the primes refer to differentiation with respect to the parameter, t. To select for cells with three corners, a Fourier Power Spectrum of the curvature was calculated by taking the absolute value of the ‘Fourier’ function in Mathematica. Cells where the ratio of the third term to the maximum of all other terms was greater than 1.5 were selected as triangular. Similarly, rectangular cells were selected using the fourth term.