Full-Dose PET Image Estimation from Low-Dose PET Image Using Deep Learning: a Pilot Study

Abstract

Positron emission tomography (PET) imaging is an effective tool used in determining disease stage and lesion malignancy; however, radiation exposure to patients and technicians during PET scans continues to draw concern. One way to minimize radiation exposure is to reduce the dose of radioactive tracer administered in order to obtain the scan. Yet, low-dose images are inherently noisy and have poor image quality making them difficult to read. This paper proposes the use of a deep learning model that takes specific image features into account in the loss function to denoise low-dose PET image slices and estimate their full-dose image quality equivalent. Testing on low-dose image slices indicates a significant improvement in image quality that is comparable to the ground truth full–dose image slices. Additionally, this approach can lower the cost of conducting a PET scan since less radioactive material is required per scan, which may promote the usage of PET scans for medical diagnosis.

Introduction

PET images are used in oncology for evaluating lesion malignancy, disease stage, and treatment monitoring [1–3]. In order to obtain PET images, patients are injected with a standard dose of radioactive tracer prior to scanning. The concentration of radioactive uptake is measured and reconstructed by the scanner, which is then used to produce images. The primary method for diagnosis is visual inspection of the images, though radiologists often use the standard uptake value (SUV) of a lesion to supplement their findings [4]. PET imaging, however, uses radioactive tracers for lesion detection, and there is a growing concern over the amount of radiation patients and technicians are exposed to during these scans [5]. Exposure to high levels of radiation can result in an increased risk of cancer developing. Thus, there is a desire to reduce the dose of radioactive tracer with which the patients are injected to minimize radiation exposure. Unfortunately, lower doses of radioactive tracer result in a significant image quality degradation, so higher doses are generally administered in clinical practice.

While low-dose computed tomography (CT) reconstruction and denoising has seen tremendous success in CT imaging, the work on low-dose PET for any given instrumentation is scarce. Some preliminary efforts have been made toward medical imaging dose reduction, specifically toward denoising low-dose medical images using deep learning [6–12]. The relationship between the low-dose images and the full-dose images is learned by the model. Xiang et al. proposed using a convolutional neural network (CNN) to predict full-dose PET images from PET/MR images taken at 1/4th of a full dose [6]. Yang et al. addressed the over-smoothing effect of CNNs by using a different loss function than the mean squared error (MSE) during training [7]. Similarly, Wolterink et al. reduced smoothing by implementing a convolutional generative adversarial network (GAN) using low-dose (1/5th of a full dose) CT images to predict full-dose CT images [8]. While the methods mentioned were relatively effective in reducing the noise in low-dose medical images, the resultant images fell short in edge and structure preservation, as well as under or incorrectly textured the images.

In this paper, we propose a residual CNN to estimate full-dose PET images from 1/10th dose PET images that preserves edge and structural details by specifically accounting for them in the loss function during training, and maintains the appropriate natural texture through the features specified in the loss function and by introducing an adversarial discriminator network partway through training. The main contributions of our work include the following:

1. Applying a low-pass filter to the low-dose image before inputting it into the model to aid training by removing some noise without compromising key structural details.

2. Using a loss function that combines specific features, namely the gradient and total variation, with the MSE and an adversarial network to ensure the estimated full-dose images preserve edge, structure, and texture details. This becomes particularly important when the training data is scarce.

3. Sectioning the body into different regions and training a model for each region to account for the vastly different structures and textures that occur between regions.

Methods

Network Architecture

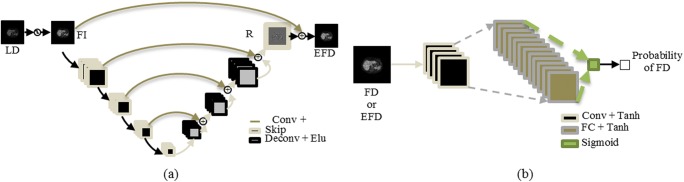
Shown in Fig. 1, the deep learning model consists of an estimator network and an adversarial discriminator network. The estimator network has 4 hidden convolutional layers (conv), which compute the 2D convolution of the previous layer with learned kernels to extract features from the input. These are followed by 4 hidden deconvolutional layers (deconv), which compute the 2D transposed convolution of the previous layer output with learned kernels. Layer 1 uses a 3 × 3 × 1 × 128 kernel, layers 2–7 use 3 × 3 × 128 × 128 kernels, and layer 8 uses a 3 × 3 × 128 × 1 kernel. All kernels use a stride of 2, and all hidden layers are followed by ELU activation. Skip connections, shown as + in Fig. 1, are utilized between layers of the same dimension, where the features from a previous layer are added to the features of a later layer. In the final layer, the skip connection is between a residual image patch R, and the input image patch X, which can be defined as

$$\widehat{Y}=X+R$$ 1

where $\widehat{Y}$ is the estimated full-dose image patch.

Fig. 1.

The deep learning model architecture used for estimating full-dose PET images from low-dose (LD) ones. The filtered image (FI) is inputted to the estimator network (a), which tries to estimate the true full-dose (EFD) by predicting the residual image (R) from the true full-dose image (FD). The network also tries to trick the discriminator network (b) which tries to determine the ground truth full-dose images from the estimated ones

The discriminator network has 1 hidden convolutional layer followed by 1 fully connected layer. Layer 1 uses a 3 × 3 × 1 × 64 kernel with a stride of 1, and layer 2 uses 16,384 hidden units. Both layers are followed by tanh activation. The fully connected layer outputs the logits of the patches, which are then passed through a final sigmoid activation yielding the probability that the patch comes from a ground truth image.

Training

The estimator network is first pre-trained alone so that the generated images are relatively close to the true ones. This is done so that when the adversarial discriminator network is introduced, it learns features beyond the structure and pixel value, such as the texture, that distinguish the true images from the generated ones. The loss function to be minimized prior to introduction of the adversarial network is the weighted sum of the MSE between the estimated full-dose and true full-dose image patches, and various image features that are expected in the final estimation. It can be realized as

$$L\left(\theta \right)=w_1\left(\frac{1}{N}{\sum }_{i=1}^N{\left(Y_i-{\widehat{Y}}_i\left(\theta \right)\right)}^2\right)-w_2\left(\frac{1}{N}{\sum }_{i=1}^N\sum _j\left(\nabla {\widehat{Y}}_{\mathit{ix}}{\left(\theta \right)}^2+\nabla {\widehat{Y}}_{\mathit{iy}}{\left(\theta \right)}^2\right)\right)$$

$$+w_3\left(\frac{1}{N}{\sum }_{i=1}^N{\left(\nabla Y_i-\nabla {\widehat{Y}}_i\left(\theta \right)\right)}^2\right)$$ 2

where N represents the number of patches, θ represents the learned parameters (i.e., the kernel and bias values), $\widehat{Y_i}\left(\theta \right)$ represents the estimated full-dose patch, Y_i represents the true full-dose patch, j represents a pixel for a given patch, and $\nabla {\widehat{Y}}_{\mathit{ix}}\left(\theta \right)$ and $\nabla {\widehat{Y}}_{\mathit{iy}}\left(\theta \right)$ represent the gradients of the estimated patch in the horizontal and vertical directions respectively.

The first term is the MSE, which is minimized to ensure the estimated and true full-dose image patches are as similar in values as possible. Some image smoothing occurs in the process. The second term is a texture-preserving feature, which is the total variation of the estimated patches. This term is maximized (subtracted) in the loss function to reduce the smoothing effect caused by averaging in the MSE. This ensures that the estimated image maintains texture and edge details found in the low-dose image. The third term known as total variation is an edge-preserving feature, which is the MSE of the gradients between the estimated and true full-dose image patches. This term is minimized so that the structural components of the estimated image are as similar as possible to those of the true full-dose images.

The ADAM optimizer is used for training the network with a learning rate equal to 0.001, and L₁ regularization was applied to the kernels. Hyperparameters w₁, w₂, and w₃ were empirically chosen, and w₁ = 1, w₂ = 0.00005, and w₃ = 0.075. Since the magnitude of each term is different, these weights have different scales.

After 100 epochs of training, the estimator network converges, and the adversarial network is introduced and trained alongside it. At this time, the adversarial loss due to the estimated images is incorporated and the loss becomes

$$L^{\ast }\left(\theta \right)=L\left(\theta \right)-w_4\left(\frac{1}{N}{\sum }_{i=1}^N-z_{i}log\left({\widehat{z}}_i\right)-\left(1-z_i\right)log\left(1-{\widehat{z}}_i\right)\right).$$ 3

where ${\widehat{z}}_i$ represents the probability, predicted by the discriminator network, that the patch was from a real image, z_i represents the true labels of the patches (1 = real image, 0 = generated image), and w₄ = 0.1. This term is the cross entropy loss due to the estimated images. We maximize this term in the estimator network loss function so that the network learns how to trick the discriminator network (i.e. increase the error rate of correctly distinguishing between true and generated images). The learning rate is reduced by a factor of 10 when the adversarial loss is included so that the estimator network learns finer details, such as texture, without altering the already learned structural and edge details.

Data

Whole body PET image slices of two patients given a full-dose of ¹⁸F-2-deoxyglucose (¹⁸FDG) acquired on an investigational Philips Vereos PET/CT system were used. The low-dose images (1/10th counts) were reconstructed from the subset events of list-mode files. Full-dose and low-dose images are spatially aligned by default. Since the PET images have a large range in pixel values (either counts or activity concentration), we convert the PET images to their SUV scale which aids in the CNN training. The low-dose images are first passed through a Gaussian filter with σ = 1.5 to reduce some noise without losing too much structural detail. The value of σ was chosen empirically. All images have a large portion of background which contains no relevant information for diagnosis. Only the foreground image containing relevant information is used for estimating the denoised full-dose images. In order to reduce the computational costs and augment data for training, the cropped portions of the images are then split into 16 × 16 pixel patches that overlap by 2 pixels. The number of patches used for training is also increased by flipping the values along the longitudinal axis. The patches are extracted from the low-dose and full-dose images at the same locations and are ultimately fed through the deep learning model. There are 482 slices per patient and all images are 288 × 288 pixels with an isotropic voxel size of 2 mm in each dimension. Each patient data was split into four regions—the brain, chest, abdomen, and pelvis—where a model was trained for each region. This was done to aid training since different regions of the body have vastly different textures and structures.

These patients were chosen in order to simulate a patient follow-up study since they were similar in size and structure. Follow-up studies are used in clinical practice to monitor treatment efficacy and changes in lesions [2]. A similar patient was used to simulate the changes that may occur between follow-up studies since the Vereos system has just been released and there have not yet been follow-up patient studies acquired on the same scanner. The model was trained on one patient using 435 slices (96,692 patches) and tested on the second patient using 440 slices (53,360 patches). Slices from the brain to the legs with edge slices removed were used.

We also conducted an experiment on a single-patient study reserving separate slices for training and testing, which shows similar results but due to space limitations, it will not be discussed here.

Experimental Results

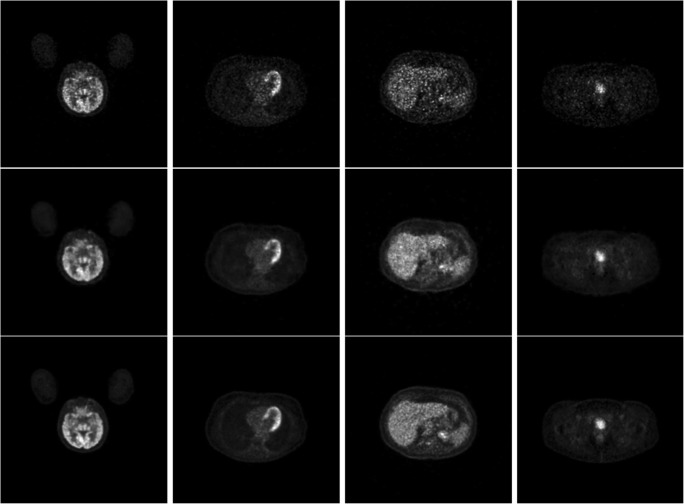
We used the root mean square error (RMSE), mean structural similarity (MSSIM) index, and peak signal-to-noise ratio (PSNR) between the estimated full-dose image and the true full-dose image as metrics for image quality. Resultant images for visual comparison are shown in Fig. 2. Comparing the top row (1/10th dose) and the middle row (estimated full-dose) of Fig. 2, the improvement of image quality is apparent. Notice also the visual similarity between the middle row and the bottom row (true full-dose).

Fig. 2.

PET images from various portions of the body from (top row) 1/10th of a full-dose, (middle row) the estimated full-dose from the deep learning model, and (bottom row) the ground truth full-dose. Column 1 is in the brain, column 2 is in the heart, column 3 is in the liver, and column 4 is in the pelvis

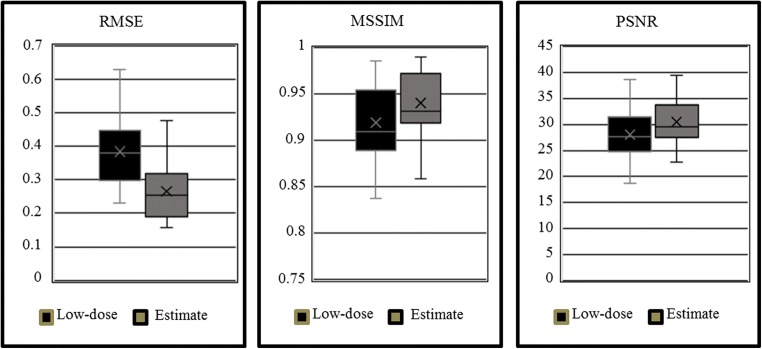
We computed the RMSE, MSSIM, and PSNR between the estimated full-dose and the true full-dose image foregrounds, and between the low-dose and the true full-dose image foregrounds. Due to limited data, we analyzed the data collectively instead of analyzing each network by body section. With more patient data, the body part-based analysis can provide insights to understand and optimize individual networks. The results are shown in Table 1. From the table, it is clear that the estimated full-dose images are more similar to the true full-dose images than the low-dose ones. Additionally, the high values of the MSSIM and PSNR, and the low RMSE of the estimated full-dose images show that the image quality produced by the learned model is more comparable to that of the true full-dose images.

Table 1.

The average values and standard deviation of the RMSE, MSSIM, and PSNR for both 1/10th of a full-dose and the estimated full-dose images using our deep learning model relative to the ground truth full-dose images

	RMSE	MSSIM	PSNR
1/10th dose	0.384 ± 0.096	0.919 ± 0.038	28.075 ± 4.253
Estimated full-dose	0.265 ± 0.078	0.940 ± 0.030	30.557 ± 3.801

We compared the distributions of the three metrics for low-dose and estimated full-dose images. The results are shown in Fig. 3. To determine if these distributions were indeed statistically different, we conducted a paired two-sample t test on the distributions of the RMSE, MSSIM, and PSNR for the 1/10th dose and estimated full-dose image slices. The null hypothesis was that the distribution means are identical and we used significance value of α = 0.05. Each of the three tests resulted in p ≪ 0.001. The extremely small p values for each of the three metrics show that the mean values for 1/10th dose and estimated full-dose image qualities are indeed statistically different.

Fig. 3.

The distributions of the RMSE, MSSIM, and PSNR for both the low-dose and the estimated full-dose images using our deep learning model relative to the ground truth full-dose images

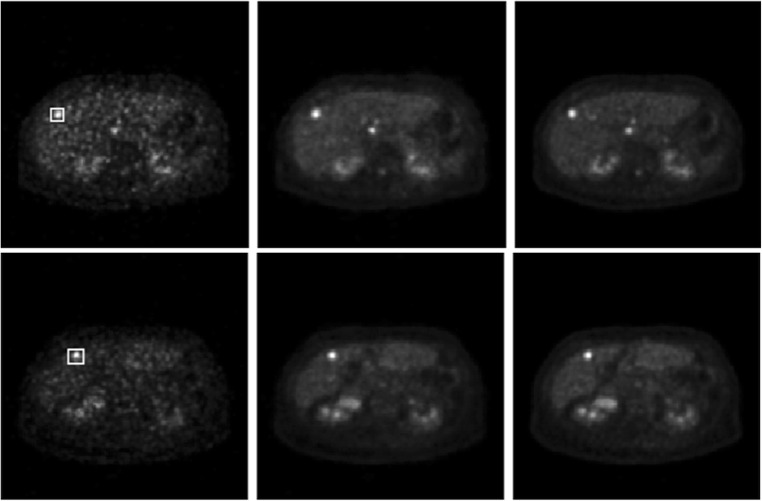
We also examined whether or not the image quality in the estimated images from low-dose images is comparable to the true full-dose images in regions of interests (ROIs) such as tumors or lesions. Some typical results are shown in Fig. 4. On the top row are, from left to right, the low-dose image, estimated full-dose image, and true full-dose image on one slice. On the bottom row are the similar images on a different slice. The ROIs in both cases are delineated with the white boxes on the low-dose images. All images are scaled to their respective SUV ranges for display. 2D ROI analysis was performed for simplicity. The mean and standard deviation of pixels in the ROI for each of the three images on the top row from left to right are 3.99 ± 2.64, 3.94 ± 2.20, and 3.95 ± 2.52, respectively. The associated pixel ranges (i.e., minimum and maximum) are (0.56, 10.22), (0.84, 8.93), and (0.60, 10.37), respectively. The mean and standard deviation of the ROI in the bottom row from left to right are 4.34 ± 3.06, 3.72 ± 2.29, and 3.39 ± 2.10, respectively, and the associated pixel ranges are (0.77, 13.62), (0.96, 10.04), and (0.91, 9.36), respectively. Overall, the ROI statistics in the estimated images are comparable to those in the true full-dose images. Since the low-dose images have a high noise content, which can strongly impact the estimated images, it will limit how much the dose can be reduced for clinical use.

Fig. 4.

From left to right are PET low-dose, estimated full-dose, and true full-dose images. Top and bottom rows show different slices. The lesions analyzed are delineated with the white boxes on the low-dose images (see text for details)

Discussion and Conclusion

We have presented a deep learning algorithm to estimate full-dose PET images from 1/10th dose PET images while preserving edge, structural, and textural details. Unlike existing methods, our method specifically accounts for different features in the loss function during training, as well as by introducing an adversarial discriminator network partway through training. Since we only had access to limited data for training, as is usually the case for medical imaging, the explicit features considered are necessary. Future work will focus on adapting the model for use on a patient-by-patient basis or for a general population. The other possible extension is to handle 3D data directly by using different channels for neighboring slices.

For example, the same patient may have multiple scans taken to monitor the effectiveness of treatment. In this case, the study is more controlled and it is appropriate to train the model on a single patient to estimate the progress of treatment. The scarcity of the training data must be carefully considered. During the initial scan, both low-dose PET and full-dose PET are reconstructed, which are used to train the model. When the patient comes back for a follow-up study, only low-dose PET is prescribed and acquired. The low-dose PET is then fed into the model to predict a full-dose equivalent PET. It should be noted that the model does not warp the previous full-dose image into the space of the current low-dose image, instead the trained network synthesizes the full-dose estimate based on the current low-dose image as input and the learned relationship between the low-dose and true full-dose image data. This work could be thought of as a simulated follow-up study for the training patient where the testing patient represents the changes that may occur between studies. For an actual patient follow-up study, the changes in structure and uptake that occur between scans will not be as drastic as it is between patients. Thus, we argue that the image quality presented in our experiment will improve even more for a real patient follow-up study since the data will be more similar to that of the training set.

To be applied to the general population, the model must be trained using many more patients to acquire large amounts of data that is representative of the population. In the case of surplus data, one extremely complex model could be trained for the entire body. In the case of less, but still large data, it may still be appropriate to section the body into different regions and develop a robust model for each region. Detailed analysis of the model performances can shed more light in this area.

We recently became aware of the work conducted at Stanford University where researchers were able to achieve 200× dose reduction using neuro images [13]. While the brain has much higher activity than the majority of the body which make is easier for dose reduction, 200× dose reduction is still remarkable. It would be interesting to see how far we can reduce the dose for PET imaging while still maintaining clinical relevance.