Toward Automatic Detection of Radiation-Induced Cerebral Microbleeds Using a 3D Deep Residual Network

Abstract

Cerebral microbleeds, which are small focal hemorrhages in the brain that are prevalent in many diseases, are gaining increasing attention due to their potential as surrogate markers of disease burden, clinical outcomes, and delayed effects of therapy. Manual detection is laborious and automatic detection and labeling of these lesions is challenging using traditional algorithms. Inspired by recent successes of deep convolutional neural networks in computer vision, we developed a 3D deep residual network that can distinguish true microbleeds from false positive mimics of a previously developed technique based on traditional algorithms. A dataset of 73 patients with radiation-induced cerebral microbleeds scanned at 7 T with susceptibility-weighted imaging was used to train and evaluate our model. With the resulting network, we maintained 95% of the true microbleeds in 12 test patients and the average number of false positives was reduced by 89%, achieving a detection precision of 71.9%, higher than existing published methods. The likelihood score predicted by the network was also evaluated by comparing to a neuroradiologist’s rating, and good correlation was observed.

Introduction

Cerebral microbleeds (CMBs) are small chronic brain hemorrhages that are prevalent in various diseases such as cerebral amyloid angiopathy [1], stroke [2], neurodegenerative disorders [3], traumatic brain injury [4], as well as following radiation therapy for brain and head and neck tumors [5]. CMBs have been found to serve as biomarkers of complications in these various pathologies. As understanding the role of CMBs is critical, new methods to rapidly detect and quantify CMBs could help shed light on their evolution and correlation with disease status.

The most commonly used medical imaging modality to detect CMBs is susceptibility-weighted magnetic resonance imaging (SWI). SWI is highly sensitive to paramagnetic tissues such as hemosiderin, which is abundant in most CMBs, and therefore can provide high contrast between normal brain parenchyma and veins or vascular injury such as CMBs [6]. To understand the impact of CMBs in various diseases, large-scale detection, segmentation, and quantification of CMB burden is necessary [7], the most challenging aspect of which is the efficient and accurate detection of CMBs on SWI. Typically, CMB detection requires not only intense human labor but also domain-related expertise, making the job time-consuming and laborious, which inevitably affects the detection accuracy and performance. As a result, much effort has been devoted to developing computer vision algorithms to automatically aid in the detection of CMBs [8–11]. Although these recent advances have improved automatic or semi-automatic detection of CMBs, all existing methods suffer from low specificity with a large number of false positives (FPs) that ultimately reduces their value and widespread adoption in both the clinical and research settings.

Since AlexNet [12] won the ImageNet Large Scale Visual Recognition Challenge [13] in 2012 by achieving a 40% lower image classification error rate than traditional computer vision methods, deep convolutional neural networks (DCNNs) have demonstrated their superiority in a wide range of computer vision tasks such as semantic segmentation, object detection, and natural image classification. Although the idea of DCNNs was first proposed more than 30 years ago, they have only recently achieved huge successes due to the availability of parallel computing hardware such as GPUs and large datasets. With the emergence of advanced network structures and techniques such as residual unit [14], DenseNet [15], batch normalization [16], and dropout [12], DCNNs can reach performance superior to humans in some tasks [13].

The goal of this study was to develop a fully automatic pipeline for the identification and labeling of CMBs by combining our previously developed base detection method [17] that used a series of traditional computer vision algorithms with a novel 3D deep residual neural network [14] architecture to reduce the FPs that remain after initial CMB detection and improve specificity. This pipeline uses 3D SWI images as the input to the initial detection algorithm in order to identify the position of potential CMB candidates. These candidates are then passed to a trained 3D deep residual network to both remove definitive CMB mimics and assign a likelihood score for each CMB included in the final detection result. Although this pipeline was trained on 7-T SWI images from patients diagnosed with radiation-induced CMBs after receiving treatment for glioma, our framework is flexible for other imaging acquisitions and readily generalizable to other diseases that result in the formation of CMBs.

Methods

Subjects and Image Acquisition

Seventy-three patients with gliomas were recruited for the study. All patients had previously undergone radiation therapy with a maximum dose ranging from 50 to 60 Gy and had confirmed radiation-induced CMBs. Thirty-one patients were scanned with a 4-echo 3D TOF-SWI sequence (TE = 2.4/12/14.3/20.3 ms, TR = 40 ms, FA = 25°, image resolution = 0.5 × 0.5x1mm, axial plane matrix size = 512 × 512) [18], while 49 patients were scanned with a standard SWI sequence (3D-SPGR sequence with flow compensation along the readout direction, TE/TR = 16/50 ms, FA = 20°, image resolution = 0.5 × 0.5 × 2 mm, axial matrix size = 512 × 512). Serial imaging was performed on 12 patients, resulting in a total of 91 scans. Patients were scanned using either an 8- or 32-channel phased-array coil on a 7-T scanner (GE Healthcare Technologies, Milwaukee, WI, USA). A GRAPPA-based parallel image acquisition was implemented with an acceleration factor of 3 and 16 auto-calibration lines [19].

SWI Processing

The raw k-space data were transferred to a Linux workstation and all image processing was performed using in-house software developed using Matlab 2015b (MathWorks Inc., Natick, MA, USA). The following steps were performed to obtain SWI images from the multi-echo sequence. (1) Auto-calibrating Reconstruction for Cartesian sampling (ARC) algorithm was applied to restore the missing k-space lines of each channel [19]. (2) Magnitude images from each individual channel were combined using the root sum of squares and the skull was stripped using FMRIB Software Library (FSL) Brain Extraction Tool (BET) [20]. (3) The complex data of each coil of echoes 2–4 were homodyne filtered with Hanning filter sizes of 72, 88, and 104 for the 2nd, 3rd, and 4th echoes respectively [18]. (4) The resulting high-pass filtered phase images from echoes 2–4 were averaged to produce a mean phase image and used to construct a negative phase mask by scaling the phase values to between 0 and 1. (5) The final composite SWI image was calculated by multiplying the mean magnitude image of three echoes with the phase mask four times. SWI images were reconstructed from the single-echo scans using the same pipeline but without the multi-echo averaging and the filter size of 96 was selected empirically [5].

Identification of Candidate CMBs and Labeling of False Positives

An example of multiple CMBs is shown in Fig. 1. A computer-aided detection method based on traditional image processing techniques previously developed in our group [17] was adopted to propose candidates for the following neural networks. The method first performs a 2D fast radial symmetry transform on the entire input SWI image volume slice by slice. Candidate voxels will then go through a series of processing and filtering such as vessel mask screening, 3D region growing, and 2D geometric feature extraction (area, circularity, number of spanned slices, centroid shift distance). The output is a set of voxels that satisfy the predetermined thresholds as CMB candidates. Although this initial algorithm has been shown to detect 86% of all CMBs, many structural mimics or FPs are also incorrectly identified as CMBs. In order to achieve a higher sensitivity, we reduced the number of missing CMBs by lowering the threshold in this algorithm and subsequently applied an interactive graphical user interface (GUI) where the user was asked a series of questions surrounding potential CMBs in order to individually label all FPs identified by the original automated approach. The coordinates of the candidates were then used to extract 3D patches of size 16 × 16 × 8 to use as the input of the deep neural networks. An experienced research scientist with several years of experience in identifying microbleeds was asked to use this system to examine all candidates and generate labels used as ground truth after prior guidance by a neuroradiologist. The entire dataset contained 19,762 candidates, 2835 of which were true CMBs, as detailed in Table 1.

Fig. 1.

a An example SWI slice showing multiple cerebral microbleeds (red arrows). b Serial slices in the axial direction demonstrating the difference in 3D structure between a CMB (green box) and a vertical vein (red box) with CMB-like appearance on one slice (color figure online)

Table 1.

Number of patches used in all dataset splits. Numbers in parentheses are the number of subjects in each dataset

	CMB	FP	Total
Train (54)	2243	14,669	16,912
Validation (7)	215	1023	1238
Test (12)	377	1235	1612
Total	2835	16,927	19,762

3D Deep Residual Network

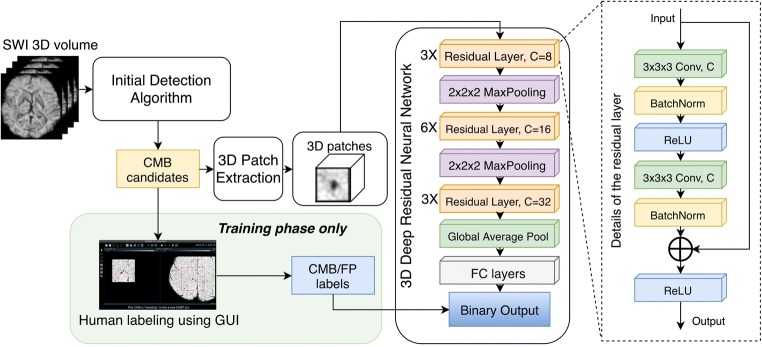
The network we proposed to refine the detection result is the patch-based 3D deep residual network described in Fig. 2. The network takes a three-dimensional patch of the SWI image centered at the coordinate of the candidate discovered by the CMB candidate identification step as input and outputs a likelihood score of the candidate being real CMBs. The network contains a total of 12 3D residual blocks [14] at three different resolution levels connected by 2 × 2 × 2 max pooling layers. After the residual blocks, a global average pooling layer was used to integrate the global information of each channel and the output was fed to a series of fully connected layers for binary classification. ReLU [21] was used as an activation function for all layers except for the last one, where a sigmoid was used to generate a likelihood score that ranged from 0 to 1. Binary cross entropy was selected as loss function of the network. For final classification of candidate patches, we selected a relatively low threshold of 0.1 for CMB/FP decision as a tradeoff for high detection sensitivity. The total number of parameters of the network is about 244,000. Figure 2 shows the data pipeline of the CMB candidate labeler and the detailed architecture of the 3D deep residual network.

Fig. 2.

Data pipeline and architecture of the 3D deep residual convolutional neural network. Human labeling of CMB candidates was performed during the training phase to obtain the input and output pairs for this supervised network. During the test phase, all candidates were fed into the network for false positive reduction

Implementation

Our CNN was implemented using Keras 2.1 [22] with Tensorflow 1.3 [23] backend. The computation was accelerated using an Nvidia Titan Xp GPU with 12 GB memory. The “Adam” algorithm [24] with a learning rate of 1e−4, beta1 = 0.9, and beta2 = 0.999 was used for parameter updating. The network was trained for 200,000 iterations with a batch size of 16. Among the 49 patients with a single-echo acquisition, 7 were randomly selected as a validation set, 12 as a test set, while the remaining were used for training. The multi-echo scans were all included in the training set to enlarge the dataset. In the validation and test sets, only the most recent scan was used if the patient had multiple scans. Because our dataset was relatively small compared to modern deep learning tasks, we improved the generalizability of the network by implementing the following data augmentation techniques during training: (A) rotating the input patch around the axial axis by a random degree, (B) shifting the input patch by 1 voxel in the axial plane, and (C) flipping the patch. This greatly extended the capacity of the training set. Imbalance between classes during training was accounted for by weighting the network loss by the proportion of CMBs to FPs. The model with lowest validation loss was selected as the model for testing.

Results

The benefits of using a 3D patch-based deep residual network with data augmentation over a simple CNN for our application are shown in Fig. 3a, b. The performance of the network as characterized by the AUC score of the validation set improved with each of the three proposed data augmentation strategies. Although random rotation of patches had the most significant effect the combination all augmentation techniques significantly outperformed applying each separately. The addition of Gaussian noise or random constant patches as forms of data augmentation did not affect the network performance.

Fig. 3.

a AUC scores of a simple CNN model compared to our proposed 3D deep residual model, both trained with the same configuration and data augmentations. b AUC scores of the 3D deep residual model trained with different data augmentation schemes. Combining all augmentation schemes provided the best performance

In the 12 test patients, the 3D deep residual network successfully classified 90.1% of the candidate patches. Three hundred fifty-seven out of 377 candidate patches or 94.7% of true CMBs were correctly identified by the network, while the number of FPs were reduced by 89.1% (1096 out of 1235) compared to prior studies. The average precision of the network on test patients was 72%, substantially higher than all previously published methods. Table 2 shows the confusion matrix of the classification by the network. On average, the number of FPs per patient were reduced significantly from 103 to only 11.6, and only 1.7 true CMBs per patient were missed by the network. The entire detection pipeline successfully detected 90% of CMBs with only an average of 11.6 remaining FPs per scan with in 2 min (Intel i7-6700K CPU with 16GB RAM and 12 GB GPU installed), providing a practical automatic detection algorithm for clinical and research applications.

Table 2.

Confusion matrix of the classification results of the test set. The network removed over 88% of FPs and only missed 5% of CMBs. The numbers in parentheses refer to the average number of candidates per test subject

	Predicted CMB	Predicted FP
Actual CMB	TP = 357 (29.8)	FN = 20 (1.7)
Actual FP	FP = 139 (11.6)	TN = 1096 (91.3)

Since we used a sigmoid function in the last fully connected layer in the network as the activation function, the prediction of the network for each candidate CMB is a number between 0 and 1 and can be regarded as the likelihood of the candidate being a true CMB. Figure 4 shows likelihood values for representative true CMBs (Fig. 4a) and the difference between a true and FP CMB (Fig. 4b), overlaid on the corresponding SWI images. In this example, the FP CMB was mis-classified as a true CMB due to its likelihood score of 0.4 even though it is a FP. This is because we set our classification threshold to be .1 in order to maximize sensitivity. If the classification threshold was set to 0.5 as in common classification tasks, it would have been correctly classified; however, the overall sensitivity of our network would have been reduced. The advantage of this approach over binary classification is that it could be used as a soft detection algorithm that guides the users to quickly locate the potential CMBs in patients and distinct thresholds can easily be applied for different populations and applications.

Fig. 4.

Likelihood scores of representative candidates from the test set overlaid on SWI slices. a shows the three correctly identified CMBs by the network with high likelihood scores close to one, while b demonstrates two remaining FPs with lower likelihood scores. Since the classification threshold was empirically selected to be 0.1 instead of 0.5 as in most tasks to maintain high sensitivity, the candidate with likelihood score of 0.4, which would have been correctly classified if we use the usual 0.5 threshold, was mistakenly classified as CMB by the network

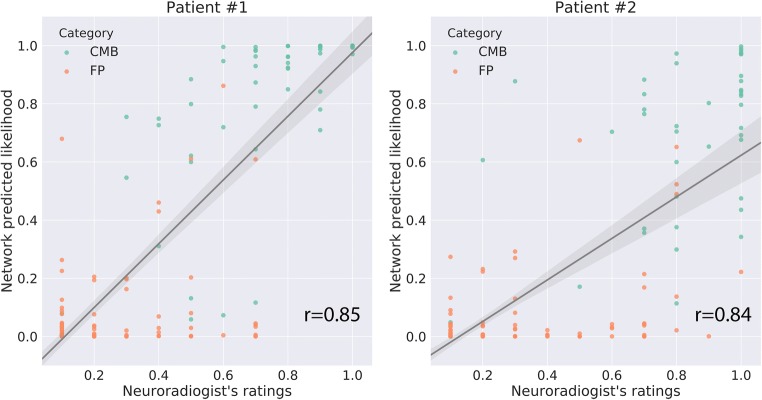
Figure 5 demonstrates the network classification results on some representative CMB candidates from the test patients. The missing CMBs (false negatives of the network) were less clear visually than the correctly identified ones and had more complex structure that likely interfered with the classification. In general, the false negatives tended to be located on the upper or lower edges of the entire image volume (examples 4, 5 and 8 in Fig. 5 “Failed-CMB”), resulting in incomplete patches that likely negatively affect the decision process. We also observed that the remaining FPs (“Failed FP” set: nos. 1, 4, and 8 in Fig. 5) might actually be CMBs but were mistakenly labeled as FPs by the human rater, and the network correctly labels them as CMBs. To further verify this hypothesis, we compared the likelihood scores predicted by the network with a neuroradiologist’s (J.E.V.) scoring of the candidates from two randomly chosen patients. Figure 6 shows the scatter plot of likelihood scores vs. neuroradiologist’s ratings (normalized to 0~1 range) for the two patients, with higher scores representing a higher likelihood of the candidate being a true CMB. For both patients, the neuroradiologist score was significantly correlated with the network likelihood score (r = .85,.84 for patient 1,2; p < 0.0001). These results demonstrate the potential of our network to correct minor errors in the dataset labeled by raters.

Fig. 5.

Classification results for representative CMBs in the test subjects. Each small square shows a slice of a patch centered on a candidate CMB, and each row contains eight consecutive slices in the z-direction for a given 3D patch. Red rectangles highlighted the centered candidates of each patch. (a) Examples that were correctly classified as CMBs and false positives. (b) Examples illustrating errors made by the network. ‘Failed-CMBs’ are true CMBs classified as FPs, while ‘Failed-FP’ are false positives that were incorrectly identified as CMBs by the network

Fig. 6.

The likelihood score predicted by the network compared to a neuroradiologist’s scoring of all candidates. Two panels show all of the candidate CMBs from two randomly selected patients with > 20 and < 60 CMBs

Discussion

We have demonstrated the capability of using a deep residual CNN architecture for the detection and classification of CMBs, small chronic brain hemorrhages, from their mimics on SWI images. The network was designed to both remove FPs and refine CMB detection by adopting several modern features of CNNs in addition to special designs in order to achieve significantly improved performance. The 3D patch input facilitated the learning of 3D features necessary to classify CMBs and structural mimics as demonstrated in Fig. 1b, where 2D information from a single slice was not enough to distinguish true CMB and veins vertical to the image plane. A deep residual network architecture was selected for this task because of its superior performance in classification, detection tasks, and patch-based image segmentation by enabling training of deeper architectures where the layers learn residual functions with reference to the layer inputs rather than learning unreferenced functions. This framework eases the training of CNNs by simplifying a network’s optimization while requiring a similar number of parameters or weights. By building a deeper network with the help of residual connections, we were able to observe significant improvements in classification performance. To demonstrate the strength of incorporating residual units in our network, the 3D patch classification network used in Dou et al. [11] was also implemented for comparison. Both networks were trained using the same dataset and configuration. Figure 3a demonstrates that in the validation dataset, we observed a 0.029 increase in AUC score with our 3D residual network. In order to balance the size of the dataset with the task complexity, we limited the capacity of our network to 244,000 trainable parameters to avoid overfitting. Although this number is considered small in comparison to modern architectures based on large-scale image datasets such as VGG16 [25], Inception [26], and ResNet101 [14], we believed that it is sufficient for the task of distinguishing true CMBs and FPs because good convergence on training set was observed.

Although the proposed 3D residual DCNN model has the potential to largely refine the detection of CMBs, approximately 10 FPs still remained for each patient. While this number is well within the range of human counting error and less relevant clinically for patients with over 100 CMBs, patients with only a handful of CMBs would still require manual removal of FPs, though at a considerable time savings. Although adding Gaussian noise as a form of data augmentation during training did not help improve the performance of our network, one approach to further reduce the number of FPs would be to apply a denoising filter or other image pre-processing steps to improve SWI image quality before inputting these images into the network. While the individual layers of our network were carefully optimized, new CNN model architectures that have since come to fruition might be able to further reduce the remaining FPs. Our current network was constructed based on data from 73 patients with radiation-induced CMBs that resulted in less than 20,000 candidate patches. Compared to other modern deep learning-based computer vision tasks, the size of our dataset is still relatively small. Including additional patients with more CMBs that are caused by other diseases might also facilitate the learning of additional features that the network can use to distinguish CMBs and FPs, as well as improve its generalizability.

Although the goal of this study was to use DCNNs to focus on the most challenging part of CMB detection and segmentation, ultimately, we want to implement an end-to-end learning-based approach for complete detection and segmentation that do not rely on a base detection algorithm whose parameters were empirically defined or further image processing for automatic segmentation once the CMB centers are identified by our network. Incorporating these more advanced approaches [27] that have recently achieved success in other applications into our pipeline holds promise for full automation of the entire detection and segmentation process. As in many applications of DCNNs, our 3D deep residual network approach can accurately detect CMBs, but the network itself lacks transparency. In order for DCNNs to be routinely adopted by clinicians, future exploration of their interpretation is necessary in order to provide a more concrete explanation for the rationale behind different network design strategies and increase confidence in their results.

Conclusions

In conclusion, we have successfully implemented a 3D patch-based deep residual network that was specifically tailored to differentiate true CMBs from their mimics on 7-T SWI images. The 3D residual network was able to achieve 90% sensitivity overall on the 12 patients and reduced the number of FPs to only 11.6 per scan, suggesting that this new approach could greatly facilitate research of various diseases that present with CMBs and potentially increase the benefit of their evaluation in the clinic.

Funding Information

This work was supported by the National Institute for Child Health and Human Development of the National Institutes of Health grant R01HD079568 and GE Healthcare.

Compliance with Ethical Standards

Conflict of Interest

The authors declare that they have no conflict of interest with regard to the content of this manuscript.