Abstract
The goal of this study is to develop an integrated, mathematical–experimental approach for understanding the interactions between the immune system and the effects of trastuzumab on breast cancer that overexpresses the human epidermal growth factor receptor 2 (HER2+). A system of coupled, ordinary differential equations was constructed to describe the temporal changes in tumour growth, along with intratumoural changes in the immune response, vascularity, necrosis and hypoxia. The mathematical model is calibrated with serially acquired experimental data of tumour volume, vascularity, necrosis and hypoxia obtained from either imaging or histology from a murine model of HER2+ breast cancer. Sensitivity analysis shows that model components are sensitive for 12 of 13 parameters, but accounting for uncertainty in the parameter values, model simulations still agree with the experimental data. Given theinitial conditions, the mathematical model predicts an increase in the immune infiltrates over time in the treated animals. Immunofluorescent staining results are presented that validate this prediction by showing an increased co-staining of CD11c and F4/80 (proteins expressed by dendritic cells and/or macrophages) in the total tissue for the treated tumours compared to the controls (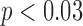 ). We posit that the proposed mathematical–experimental approach can be used to elucidate driving interactions between the trastuzumab-induced responses in the tumour and the immune system that drive the stabilization of vasculature while simultaneously decreasing tumour growth—conclusions revealed by the mathematical model that were not deducible from the experimental data alone.
). We posit that the proposed mathematical–experimental approach can be used to elucidate driving interactions between the trastuzumab-induced responses in the tumour and the immune system that drive the stabilization of vasculature while simultaneously decreasing tumour growth—conclusions revealed by the mathematical model that were not deducible from the experimental data alone.
Keywords: anti-HER2, Herceptin, ordinary differential equations, DCE-MRI, FMISO-PET, immunofluorescence
1. Introduction
An estimated 25–30% of all breast cancer cases overexpress the human epidermal growth factor receptor 2 (HER2+), which indicates an amplification of the HER2 protein (Mitri et al., 2012, American Cancer Society, 2016). HER2+ breast cancer is associated with poorer overall prognoses and a higher incidence of metastases, with five times the rate of recurrences compared to HER2− patients (Gonzalez-Angulo et al., 2009). The current standard-of-care therapy for primary HER2+ breast cancer is cytotoxic therapy in combination with the anti-HER2 therapy, trastuzumab, which has been shown to increase overall survival rates, however nearly 26% of patients have recurring disease within 10 years (Perez et al., 2014).
Trastuzumab is a monoclonal antibody that interferes and blocks the HER2/neu receptor. The antibody binds to the HER2/neu receptor, preventing receptor dimerization and interfering with intracellular signalling, inducing cell cycle arrest and inhibiting cell proliferation and migration (Cho et al., 2003; Ménard et al., 2003; Nahta et al., 2006). It also causes HER2 internalization and subsequent degradation (Klapper et al., 2000; Vu & Claret, 2012). Recent preclinical evidence has shown that trastuzumab can also increase vascular maturation and decrease vessel permeability, similar to anti-angiogenic therapy (Izumi et al., 2002; Klos et al., 2003; Heyerdahl et al., 2013; Sorace et al., 2016). Furthermore, vascular normalization after trastuzumab treatment has been shown to improve tumour perfusion and intratumoural delivery of therapeutics (Sorace et al., 2016) as well as reduce hypoxia in HER2+ breast cancer through improved oxygen delivery (Hardee et al., 2009; McCormack et al., 2014; Walsh et al., 2014a; Sorace et al., 2017).
Anti-angiogenic agents, which block pathways associated with new vascular growth, are used in cancer therapeutics to regulate the tumour vasculature and are used in conjunction with chemotherapies, with the first FDA-approved anti-angiogenic therapy available in 2004 (Ferrara et al., 2005). The primary mechanism for vascular altering agents is inhibition of the vascular endothelial growth factor (VEGF), thereby reducing blood vessel growth and development; however, modulation of the immune response also has been shown to alter vascular characteristics (Huang et al., 2012). HER2+ breast tumours are known to be immunogenic, and tumour associated immune cells (i.e. tumour-infiltrating lymphocytes and myeloid cells) can impact alterations in tumour vasculature, hypoxia and necrosis (Leek et al., 1996; de Visser & Coussens, 2006; de Visser et al., 2006). These observations have led to numerous studies into the role of the immune response in the tumour microenvironment and recent development of successful cancer immunotherapies (Hanahan & Weinberg, 2011; Bertucci & Gonçalves, 2017; Emens, 2017; Huang et al., 2017). Trastuzumab has also been shown to alter macrophage and T-cell behaviour (De Palma and Lewis, 2013); however, the connection between the immune response and trastuzumab therapy has yet to be fully characterized.
The goal of this study is to develop an integrated, mathematical-experimental approach for understanding the interactions between the immune system and the effects of trastuzumab on HER2 overexpressing breast cancer in a mouse model system. The proposed mathematical model incorporates data for tumour size, hypoxia, necrosis and vasculature status to predict the infiltration of immune cells into the tumour. Then, those predictions are qualitatively compared with new results for immunofluorescent staining for myeloid infiltrates obtained from tumours with or without trastuzumab treatment as a preliminary validation of the model results. This investigation also aims to generate experimentally testable hypotheses for potential unknown mechanisms that drive the stabilization of vasculature and decrease tumour growth connected to anti-HER2 therapy, such as cross talk between the immune response and the vasculature as a mechanism for trastuzumab’s success. As few as 30% of HER2+ breast cancer patients effectively respond to current treatment regimens (Bartsch et al., 2006), therefore alternative therapeutic strategies are needed to improve patient care. This may be achieved by developing different therapeutic targets or by optimizing combinations or timings of current standard-of-care therapies. As the present experimental evidence suggests a connection between trastuzumab treatment and tumour-associated host responses, a better understanding of the interplay between these components will elucidate connections that may be useful to improve therapeutic regimens for HER2+ breast cancer.
The manuscript is organized as follows. First, we describe the biological factors pertinent to this study, which are commonly measured in experimental studies. Then, we provide a brief background on previous mathematical studies of tumour growth and describe how our approach fits within the literature. Next, the details for the collection of the experimental data for tumour size, vasculature, hypoxia and necrosis in control and treated tumours with trastuzumab are summarized. Following this are the protocols for acquiring and analysing the new immunofluorescent data characterizing myeloid immune cell infiltrates in the treated versus control tumours. The mathematical model system is then introduced, as well as the methodology for model calibration using the measurements of tumour size, vasculature, hypoxia and necrosis in the control and treated tumours. The calibration method performance is quantified using in silico data, and the model demonstrates consistent results when tested against a separate, independent set of tumour volume data. Further, sensitivity of the model’s outputs on the parameters and uncertainty in the model simulation results is reported. Finally, we qualitatively compare the model’s prediction for the immune response to the immunofluorescence results as a preliminary validation for its predictions and then discuss the model’s differing calibrated parameter values between controls and treated tumours to identify potential unknown dynamics induced by trastuzumab treatment. Please see Fig. 1 for a graphical depiction of the steps in the methodology for integrating the experimental data and mathematical modelling results.
Fig. 1.
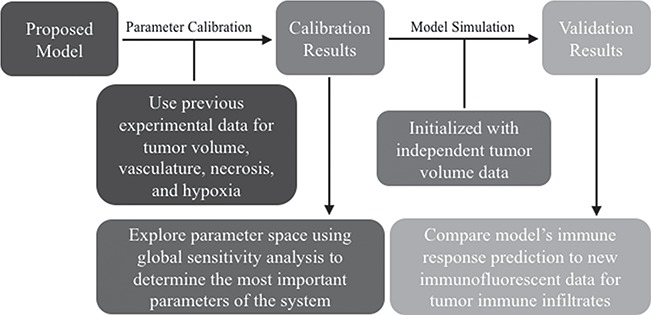
Flow chart to visualize the methodology for combing the data and the model: the proposed model is calibrated using experimental data and the resulting parameter space defined by the calibration is explored globally to identify important parameters; separate tumour volume data is used to validate the model along with immunofluorescence data for the immune response.
2. Biological background
Our model incorporates several of the hallmarks of cancer, as defined by Hanahan & Weinberg (2011), including proliferation, angiogenesis and immune evasion. While there are a variety of experimental approaches to understand these phenomena, below we describe the measures from in vivo and ex vivo experiments of key tumour characteristics used in the present study and how these characteristics play important roles in tumour development—tumour vasculature, hypoxia, necrosis and the immune response.
2.1 Vasculature
For a tumour to grow beyond 1–2 cubic millimeters, cancer cells must recruit vasculature to deliver nutrients and remove waste (Folkman, 1995). Tumour-associated vasculature develops many structural abnormalities, including a leaky, tortuous, and non-hierarchical architecture (Hanahan & Weinberg, 2011; Jain & Carmeliet, 2012). These irregularities lead to heterogeneous blood flow, pressure and insufficient delivery of oxygen, thereby producing regions of necrosis and hypoxia throughout the tumour (Brown, 2000; Goel et al., 2012; Jain, 2013). Therefore, many experimental methods have been developed to measure the quality or extent of vasculature within a tumour. Common methods include histological staining techniques to determine microvessel density, calculations of vessel maturation indices (Kakolyris et al., 2000), and assays for chemical signals such as VEGF (Raleigh et al., 1998). While these techniques are well developed, they typically only assess a portion of the tumour and do not allow for the collection of longitudinal data within the same mouse over time.
One non-invasive, imaging technique used to longitudinally study 3D tumour vasculature is dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) (Gore et al., 2011). In DCE-MRI, a paramagnetic contrast agent is injected into the bloodstream and can extravasate into the tumour, causing an enhancement in the measured signal intensity. By collecting MRI data before, during and after the injection of the contrast agent, physiological parameters related to vessel perfusion and permeability (termed 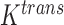 ) can be estimated throughout the tumour tissue (Yankeelov and Gore, 2009; Yankeelov et al., 2012). Therefore, low values of
) can be estimated throughout the tumour tissue (Yankeelov and Gore, 2009; Yankeelov et al., 2012). Therefore, low values of 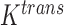 indicate areas with decreased delivery of the contrast agent.
indicate areas with decreased delivery of the contrast agent.
2.2 Hypoxia
A phenomenon that can result from inadequately vascularized tissue is hypoxia, which is defined as the reduction of oxygen in tissues below physiological levels (i.e. 38 mmHg; Helmlinger et al., 1997: Hammond et al., 2014; Kumar & Gabrilovich, 2014; McKeown, 2014). Hypoxia is an important prognostic factor for cancer resistance/aggressiveness, as hypoxic cells have been shown to be less susceptible to chemo- and radiation therapy (Gruber et al., 2004; Liu et al., 2017). Furthermore, reduction of hypoxia has been shown to be a potential measure of treatment response (Sorace et al., 2017; Walsh et al., 2014b; Lee & Scott, 2007). Low levels of oxygen result in increased production of transcription factors that upregulate glycolysis in tumour cells (Kroemer & Pouyssegur, 2008), which has been associated with increased aggressiveness via accelerated tumour growth and higher capabilities of metastatic potential (Gruber et al., 2004; Kumar & Gabrilovich, 2014).
Histological staining is the most common method for measuring and identifying hypoxia in tumour tissues through measures of hypoxia-inducible factor 1 alpha (HIF1-alpha; Rademakers et al., 2011), pimonidazole (a compound that is activated in hypoxic cells to form measurable adducts with cellular proteins; Raleigh et al., 1998) or carbonic anhydrase 9 (CAIX, hypoxia-related protein involved in pH regulation Rademakers et al., 2011). An experimental imaging method, which can report on hypoxia in vivo, is 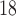 F-fluoromisonidazole positron emission tomography (FMISO-PET). FMISO-PET is a non-invasive method where tumours can be imaged over time to provide a 3D description of the oxygenation within the tumour—unlike histology studies that only look at one to a few central slices of a tumour. FMISO binds covalently to cellular molecules at rates that are inversely proportional to oxygen concentration. In normal, well-oxygenated tissues FMISO will freely enter and exit the tissue. Conversely, in hypoxic conditions, FMISO is retained by irreversible binding to the thiol-rich metabolic proteins due to absence of oxygen. The hydroxylamine products bind stably in cells, but in the presence of oxygen, a futile cycle re-oxidizes to the parent nitroimidazole. Standardized uptake values (SUV; i.e. the ratio of the image derived concentration of the injected radiotracer to the whole body concentration) are calculated for the amount of FMISO in the tumour, generating a map of hypoxia throughout the entire neoplasm (Rajendran et al., 2004; Lee & Scott, 2007).
F-fluoromisonidazole positron emission tomography (FMISO-PET). FMISO-PET is a non-invasive method where tumours can be imaged over time to provide a 3D description of the oxygenation within the tumour—unlike histology studies that only look at one to a few central slices of a tumour. FMISO binds covalently to cellular molecules at rates that are inversely proportional to oxygen concentration. In normal, well-oxygenated tissues FMISO will freely enter and exit the tissue. Conversely, in hypoxic conditions, FMISO is retained by irreversible binding to the thiol-rich metabolic proteins due to absence of oxygen. The hydroxylamine products bind stably in cells, but in the presence of oxygen, a futile cycle re-oxidizes to the parent nitroimidazole. Standardized uptake values (SUV; i.e. the ratio of the image derived concentration of the injected radiotracer to the whole body concentration) are calculated for the amount of FMISO in the tumour, generating a map of hypoxia throughout the entire neoplasm (Rajendran et al., 2004; Lee & Scott, 2007).
2.3 Necrosis
Cell death due to necrosis is when cells burst and release their contents into the surrounding environment (Hanahan & Weinberg, 2011; whereas apoptosis, programmed cell death, is a systematic breakdown of a cell’s organelles and contraction into a digestible corpse for immune cells to consume). Typically, necrosis is considered a measure of cell death due to inadequate nutrient delivery, and some therapeutic strategies using anti-angiogenic drugs aim to decrease blood flow to the tumour thereby increasing necrosis. Moreover, necrotic cell death releases pro-inflammatory signals, activating local myeloid cells and recruiting additional myeloid cells, such as monocytes and neutrophils, all of which can modulate angiogenesis and vascular maturation (De Palma et al., 2007; Murdoch et al., 2008).
Necrosis is most commonly quantified using histological analysis of haematoxylin and eosin (H&E) staining (Titford, 2005). The stain allows for the identification of cellular nuclei (via haematoxylin) as well as the cytoplasm of these cells (via eosin; Alturkistani et al., 2015). Therefore, regions of low nucleic staining are identified as necrotic areas in tissue samples.
2.4 Immune response
The phrase ‘immune response’ is a generic term for the process by which haematopoietic cells and cytokines (chemical signals) become activated in response to pathogens or tissue damage, removing pathogens and damaged tissue and initiating wound healing (Grivennikov et al., 2010). In general, immune responses can be divided into innate and adaptive components, which act coordinately to rapidly respond to pathogens, while generating long-lived immunological memory to protect against re-encounter with the same pathogen or tumour. Innate immune responses are initiated rapidly by myeloid cells, including tissue-resident macrophages and dendritic cells, which have the capacity to recognize signals commonly associated with broad classes of pathogens, such as viruses, as well as stress-associated signals that occur with tissue damage. When these myeloid cells are activated, they release cytokines and chemokines that induce inflammation, and recruit neutrophils and other effector cells to help clear infected or damaged tissue. At the same time, activated dendritic cells travel to the draining lymph nodes where they present antigens (pathogen or tumour derived) to T cells to initiate an adaptive immune response that is specific for the particular pathogen or tumour. The adaptive immune response also generates long-lived memory through differentiation of both memory T cells and B cells, which provide cellular and humoral immunity, respectively. The immune surveillance theory poses that the immune system continuously monitors host tissues to identify and eliminate cancer cells. However, tumours have numerous mechanisms by which they avoid immune detection (Hanahan & Weinberg, 2011; Chimal-Ramirez et al., 2013). Production of immune-suppressive cytokines by the tumour is one mechanism by which tumours can evade the immune response (Coussens & Werb, 2002; Noy & Pollard, 2014; Xu et al., 2015) In addition, myeloid cells in the tumour often differentiate towards a pro-tumour growth, anti-inflammatory signalling pathway (Gabrilovich et al., 2012). Furthermore, tumour-associated myeloid cells can produce factors, such as VEGF, that promote neovascularization, potentially aiding in tumour growth (Noy & Pollard, 2014). Thus, myeloid cell infiltrates in the tumour can be considered pro- or anti-tumourigenic (Chimal-Ramirez et al., 2013).
Immunofluorescent imaging of histological slices can be used to quantify myeloid cell infiltrates. Immunofluorescence is a technique that uses antibodies tagged with fluorescent dyes to bind specific molecules within a cell or receptors on the cell membrane. After staining with appropriate antibodies, imaging the tissue will indicate the presence of the targeted molecules, which can be quantified from the amount of fluorescence detected. Nude mice (the mouse model used for all experimental and mathematical results presented in this work) are athymic, thus, they do not have T cells but do have an intact myeloid compartment, including dendritic cells, monocytes, neutrophils and macrophages (Sharkey & Fogh, 1984). Therefore, myeloid infiltration into implanted tumours can be determined through immunofluorescent staining to detect myeloid markers, such as CD11c and F4/80, which predominantly stain dendritic cells and macrophages, respectively. Co-staining of CD11c and F4/80 on the same cells is indicative of an activated macrophage (Pucci et al., 2009).
3. Mathematical background
Since the immune surveillance hypothesis first questioned the role that the immune system plays in tumour suppression, investigators have attempted to mathematically model the tumour-induced immune responses with varying degrees of complexity (Burnet, 1957; Eftimie et al., 2011; Walker & Enderling, 2016). The dynamic relationships between various immune cells (such as macrophages, T cells and natural killer cells) with stimulation from cytokines have been studied with ordinary differential equations (ODEs), agent based models and even delay differential equations (Stepanova, 1980; Nani & Freedman, 2000; Szymanska, 2003; Villasana and Radunskaya, 2003; d’Onofrio, 2005; Forys et al., 2006; Berner et al., 2007; Knútsdóttir et al., 2014). However, the characterization of the interactions of the tumour-induced immune responses can result in large systems equations with many parameters that are difficult to acquire at multiple time points or in an intact specimen (Kim et al., 2007). Though such approaches are able to provide insights into the interactions between tumours and the immune system, most are not formulated in such a manner that allows them to be directly compared to experimental data.
In addition to the immune response, hypoxia and necrosis also play central roles in the mathematical characterization of tumour growth in conjunction with angiogenesis. These features of the biological system are often described by systems of partial differential equations (PDEs) to provide spatial and mechanical details of tumour growth (Saidel et al., 1976; Mallet & De Pillis, 2006; Macklin & Lowengrub, 2007). For example, the use of PDEs allows a model to describe a pathway to inhibition of tumour growth by suppressing angiogenesis (Chen et al., 2012), and spatially defined mathematical models can capture the role of vessel occlusion in tumour suppression (Jackson & Byrne, 2002; Stamper et al., 2010; Hubbard & Byrne, 2013). Apart from spatially resolved models for tumour growth incorporating vasculature, other models also include features of the tumour microenvironment (e.g. necrosis and hypoxia; Mantzaris et al., 2004; Chen et al., 2012; Hubbard & Byrne, 2013). However, these systems of PDEs require spatial/physical assumptions that are often difficult to validate with data and additional parameters that are generally difficult to estimate using presently available experimental methodology (Altrock et al., 2015).
Models that can be initialized and constrained with experimental data to make predictions that can then be directly compared to other experimental results are important for validation and future clinical translation of results Yankeelov et al., 2013, 2015; Weis et al., 2015; Hormuth et al., 2017; McKenna et al., 2017. Therefore, the aim of this work is to construct and calibrate a representative model for tumour growth that utilizes and reflects specific data of an experimental mouse system. While this data does contain spatial information, the various data types are collected from independent tumour samples, and only certain methods collect 3D data for tumours. The experimental data is quantified in a spatially homogeneous manner (percentages of a total), therefore a model is defined using ODEs. Here, we also elect to compartmentalize the immune components for a simpler, more easily analysed model, which is not only amenable to experimental application, but also may reveal general trends of the immune interaction with tumour cells (Sachs et al., 2001). This is not dissimilar to other investigations looking at the immune response in various disease contexts that revealed interesting and experimentally testable immune behaviours/interactions (Day et al., 2006; Reynolds et al., 2006; Jarrett et al., 2015a,b). Furthermore, a novelty of this work is that the model’s predictions are validated by independent data for both the tumour volume and immune infiltrates.
4. Experimental methods
4.1 Experimental data for tumour volume, vasculature, necrosis and hypoxia
As the data employed in this investigation was acquired as a part of previous efforts, we present only the salient details of those experimental studies. For more information, the interested reader is referred to (Sorace et al., 2016, 2017).
Nude athymic mice (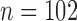 ) were subcutaneously implanted with BT474 HER2+ human breast cancer cells in the flank and allowed to grow for 4–6 weeks until tumours reached approximately 0.22
) were subcutaneously implanted with BT474 HER2+ human breast cancer cells in the flank and allowed to grow for 4–6 weeks until tumours reached approximately 0.22 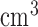 ; at which point, the mice were enrolled into the experiment (defined as Day 0). Treated mice were injected on Days 0 and 3 (this timing, and all those listed below, are relative to when they were enrolled into the study) with trastuzumab (10 mg/kg, Genentech, San Francisco, CA), while control mice were treated with saline. DCE-MRI data to evaluate changes in vascularity was collected in control and treated mice (
; at which point, the mice were enrolled into the experiment (defined as Day 0). Treated mice were injected on Days 0 and 3 (this timing, and all those listed below, are relative to when they were enrolled into the study) with trastuzumab (10 mg/kg, Genentech, San Francisco, CA), while control mice were treated with saline. DCE-MRI data to evaluate changes in vascularity was collected in control and treated mice (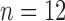 and
and 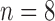 , respectively) on Days 0, 1 and 4 (Sorace et al., 2016). The values of the DCE-MRI parameter,
, respectively) on Days 0, 1 and 4 (Sorace et al., 2016). The values of the DCE-MRI parameter, 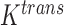 , in the tumour are compared to the normal muscle tissue. Well-vascularized voxels of the tumour are defined as those for which the
, in the tumour are compared to the normal muscle tissue. Well-vascularized voxels of the tumour are defined as those for which the 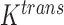 value exceeded the mean plus two times the standard deviation of contralateral muscle tissue. Another subset of mice (
value exceeded the mean plus two times the standard deviation of contralateral muscle tissue. Another subset of mice (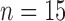 control,
control, 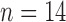 treated) were sacrificed on Days 0, 1, 3, 4 and 7 (
treated) were sacrificed on Days 0, 1, 3, 4 and 7 (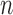 = 3–4 per day) to harvest tumours for immunohistochemistry to assess necrosis (Sorace et al., 2016). To determine percent necrosis, H&E stained histology data was processed with automated histology software Apiro Versa 200 platform (Leica Microsystems Inc., Buffalo Grove, IL). FMISO-PET data (
= 3–4 per day) to harvest tumours for immunohistochemistry to assess necrosis (Sorace et al., 2016). To determine percent necrosis, H&E stained histology data was processed with automated histology software Apiro Versa 200 platform (Leica Microsystems Inc., Buffalo Grove, IL). FMISO-PET data (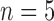 control,
control, 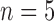 treated) was collected on Days 0, 1, 3, 4 and 7 to determine which voxels of the tumour were hypoxic (Sorace et al., 2017). Hypoxic voxels of the tumour are defined as those for which the SUV is greater than the mean plus two standard deviations of contralateral muscle tissue. Along with these studies, two separate tumour volume data sets were acquired by calliper measurements (Sorace et al., 2016, 2017). The first set of data was collected from a longitudinal study where tumours were measured on Days 0, 1, 3, 4 and 7 using the same set of mice for treated and control over time (
treated) was collected on Days 0, 1, 3, 4 and 7 to determine which voxels of the tumour were hypoxic (Sorace et al., 2017). Hypoxic voxels of the tumour are defined as those for which the SUV is greater than the mean plus two standard deviations of contralateral muscle tissue. Along with these studies, two separate tumour volume data sets were acquired by calliper measurements (Sorace et al., 2016, 2017). The first set of data was collected from a longitudinal study where tumours were measured on Days 0, 1, 3, 4 and 7 using the same set of mice for treated and control over time (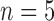 each), whereas the second data set was obtained from a larger takedown study for Days 0, 1, 3, 4, 6 and 7 (
each), whereas the second data set was obtained from a larger takedown study for Days 0, 1, 3, 4, 6 and 7 (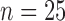 each). For a summary of the data and their sources, please see Table 1. For examples of results from the DCE-MRI and FMISO-PET imaging experiments, please see Fig. 2.
each). For a summary of the data and their sources, please see Table 1. For examples of results from the DCE-MRI and FMISO-PET imaging experiments, please see Fig. 2.
Table 1.
Summary of data types, descriptions and sources (treated and control)
| Data type | Description | Sources |
|---|---|---|
| Tumour volume | Two separate sets recorded using caliper measurements | (Sorace et al., 2016, 2017) |
| Fraction of well-vascularized tumour | DCE-MRI data | (Sorace et al., 2016) |
| Fraction of necrosis in tumour | H&E stained histology data | (Sorace et al., 2016) |
| Fraction of hypoxia in tumour | FMISO-PET imaging data | (Sorace et al., 2017) |
Fig. 2.
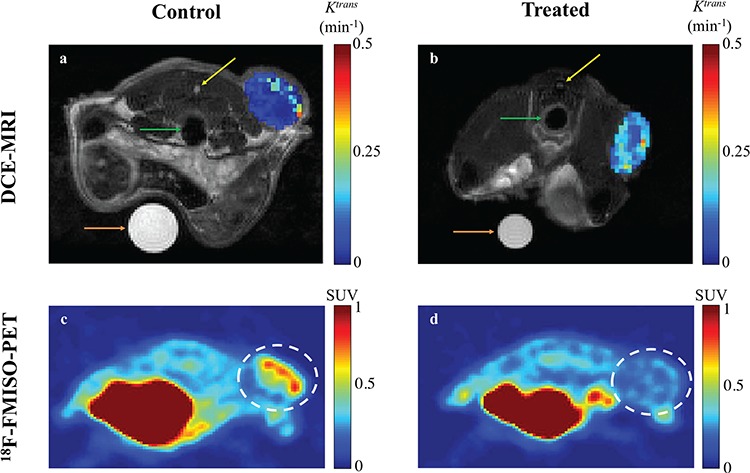
Representative example images from DCE-MRI and FMISO-PET results at Day 4 post trastuzumab (or saline control) treatment (Sorace et al., 2016, 2017). All imaging views are of the cross section through the abdomen from posterior to anterior (i.e. back to front) with tumours located on the flank. Panels a and b display high resolution anatomical MRI scans overlaid with a parametric map of 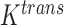 values over the tumour, extracted from the DCE-MRI data. In the anatomical images, the colon (green, middle arrows), the spinal cord (yellow, top arrows) and a water phantom for quality control (orange, bottom arrows) are visible in both panels. Note that for the control mouse (a) the tumour has lower
values over the tumour, extracted from the DCE-MRI data. In the anatomical images, the colon (green, middle arrows), the spinal cord (yellow, top arrows) and a water phantom for quality control (orange, bottom arrows) are visible in both panels. Note that for the control mouse (a) the tumour has lower 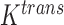 measurements compared to the treated mouse (b). The FMISO-PET images displayed (panels c and d) report the SUVs for each mouse cross section, and the tumour is identified with a dashed white circle. Note that the SUVs in the control mouse’s tumour (c) is larger than the treated mouse (d). The large sections in both mice with high SUVs (in red) is the bladder.
measurements compared to the treated mouse (b). The FMISO-PET images displayed (panels c and d) report the SUVs for each mouse cross section, and the tumour is identified with a dashed white circle. Note that the SUVs in the control mouse’s tumour (c) is larger than the treated mouse (d). The large sections in both mice with high SUVs (in red) is the bladder.
4.2 Immunofluorescent staining for immune infiltrates
Tumours were extracted on Day 4 and flash frozen in optimum cutting temperature (OCT) (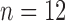 treated,
treated, 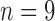 control). A Microm HM550 Cryostat (ThermoFisher, Waltham, MA) was used to slice tissue into 8
control). A Microm HM550 Cryostat (ThermoFisher, Waltham, MA) was used to slice tissue into 8 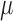 m cryosections. Tissue sections were then fixed in 100% acetone at −20
m cryosections. Tissue sections were then fixed in 100% acetone at −20 C for 20 min, washed 3
C for 20 min, washed 3 in PBS
in PBS 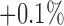 Tween 20 and blocked with TNB (Tris-NaCl blocking) buffer (PerkinElmer, Waltham, MA) for 15 min at room temperature. Immunostaining was performed overnight at 4
Tween 20 and blocked with TNB (Tris-NaCl blocking) buffer (PerkinElmer, Waltham, MA) for 15 min at room temperature. Immunostaining was performed overnight at 4 C in the dark in TNB blocking buffer with the following antibodies: anti-CD11c-biotin (N418, Biolegend, San Diego, CA), anti-F4/80-AF 594 (BM8, Biolegend) and anti-CD31-APC (390, ThermoFisher). The CD11c signal was amplified using the TSA Signal Amplification Kit (PerkinElmer) according to manufacturer’s protocol, then stained with the secondary reagent Streptavidin-AF 488 (Life Technologies (ThermoFisher)) for 1 hr in the dark at room temperature. After washing 3
C in the dark in TNB blocking buffer with the following antibodies: anti-CD11c-biotin (N418, Biolegend, San Diego, CA), anti-F4/80-AF 594 (BM8, Biolegend) and anti-CD31-APC (390, ThermoFisher). The CD11c signal was amplified using the TSA Signal Amplification Kit (PerkinElmer) according to manufacturer’s protocol, then stained with the secondary reagent Streptavidin-AF 488 (Life Technologies (ThermoFisher)) for 1 hr in the dark at room temperature. After washing 3 in PBS + 0.1% Tween 20, nuclei were detected with 0.125
in PBS + 0.1% Tween 20, nuclei were detected with 0.125  g/mL 4’,6-diamidino-2-phenylindole (DAPI; Life Technologies). Tissues were mounted in ProLong Antifade (Life Technologies), then imaged with a DMi8 (Leica, Buffalo Grove, IL) microscope with 10x/0.4 NA (numerical aperture) objectives and uniformly processed with LasX (Leica) software, with pixel size 0.422
g/mL 4’,6-diamidino-2-phenylindole (DAPI; Life Technologies). Tissues were mounted in ProLong Antifade (Life Technologies), then imaged with a DMi8 (Leica, Buffalo Grove, IL) microscope with 10x/0.4 NA (numerical aperture) objectives and uniformly processed with LasX (Leica) software, with pixel size 0.422 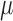 m
m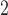 . Prior to segmentation, Fiji was used to convert from proprietary Leica file to tag image file format and the contrast in each colour channel was standardized using histogram equalization (Schindelin et al., 2012). Please see supplementary Figure S1 for negative controls for immunofluorescent stains.
. Prior to segmentation, Fiji was used to convert from proprietary Leica file to tag image file format and the contrast in each colour channel was standardized using histogram equalization (Schindelin et al., 2012). Please see supplementary Figure S1 for negative controls for immunofluorescent stains.
4.3 Tumour image segmentation for immunofluorescence data
Immunofluorescence images are quantitatively processed via an automated MATLAB (Mathworks, Natick, MA) script to calculate the amount of immune infiltration in treated and control tumour sections (all MATLAB code is available upon request). This script utilizes functions from MATLAB’s image processing toolbox (e.g. bwareaopen, imclose, imfill, imcomplement), where all thresholds and disc sizes for dilation, erosion and removal of noise are empirically chosen to best fit the data set following manual training on known positive samples and then automated to be applied uniformly to all histological images.
The four color channels (DAPI, a nuclear stain (blue), the myeloid cell stains indicated by CD11c (green) and F4/80 (red), and CD31, an endothelial cell stain (violet)) are identified; color thresholds are applied using the mean plus two standard deviations of the signal intensity for each channel individually, and masks are defined for each stain. The total area of the tumour is calculated as the union of the masks of all four colour channels. Noise for the total tumour is defined as regions of connected pixels smaller than 5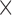 10
10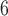 and is removed (please note that the size of the tumours ranges from 1.1
and is removed (please note that the size of the tumours ranges from 1.1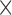 10
10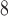 to 4.5
to 4.5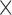 10
10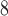 total pixels), and the total region is morphologically closed to preserve the image shape and filled. Necrotic regions are defined as areas with low and sparse DAPI staining, where regions smaller than 10
total pixels), and the total region is morphologically closed to preserve the image shape and filled. Necrotic regions are defined as areas with low and sparse DAPI staining, where regions smaller than 10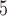 pixels in the DAPI mask are removed and the complement of the DAPI mask within the total tumour is defined as necrotic. Viable regions are defined as the difference between the total tumour mask and the necrotic areas. Following identification of the total tumour, viable areas and necrotic areas, each of these three regions is processed to identify their corresponding pixel counts, and the number of pixels stained for CD11c, F4/80 and co-staining (pixels that are in both the CD11c and F4/80 masks) are counted for each of the regions. The physical areas occupied by each region are calculated by multiplying the number of pixels in each region times the area of each pixel. As the histology sections vary in total area from approximately 4.6
pixels in the DAPI mask are removed and the complement of the DAPI mask within the total tumour is defined as necrotic. Viable regions are defined as the difference between the total tumour mask and the necrotic areas. Following identification of the total tumour, viable areas and necrotic areas, each of these three regions is processed to identify their corresponding pixel counts, and the number of pixels stained for CD11c, F4/80 and co-staining (pixels that are in both the CD11c and F4/80 masks) are counted for each of the regions. The physical areas occupied by each region are calculated by multiplying the number of pixels in each region times the area of each pixel. As the histology sections vary in total area from approximately 4.6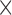 10
10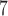
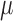 m
m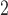 to 1.9
to 1.9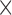 10
10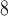
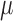 m
m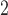 , the results of the immunofluorescence staining are summarized as percentages of the total tumour area for consistency. Please see supplementary Figure S2 e.g. results of the image segmentation process for each individual colour channel.
, the results of the immunofluorescence staining are summarized as percentages of the total tumour area for consistency. Please see supplementary Figure S2 e.g. results of the image segmentation process for each individual colour channel.
Statistical analysis was completed with non-parametric Wilcoxon rank sum test using the statistical package in MATLAB, where median values for pixel staining of the control and treated data sets are compared to determine if they represent significantly different distributions of data.
5. Theoretical and computational methods
5.1 Mathematical model
We propose a coupled system of five ODEs, describing tumour growth (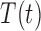 ), immune response (
), immune response (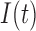 ), vascularity (
), vascularity (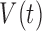 ), necrosis (
), necrosis (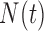 ) and hypoxia (
) and hypoxia (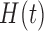 ). The system of ODEs describes the interplay between these four tumour characteristics and the effect they have on the tumour volume; please see Fig. 3 for a diagram of the interactions between five components. The tumour growth component represents the change in tumour volume over time, while the remaining ODEs describe the temporal variations in the fractions of the total tumour occupied by
). The system of ODEs describes the interplay between these four tumour characteristics and the effect they have on the tumour volume; please see Fig. 3 for a diagram of the interactions between five components. The tumour growth component represents the change in tumour volume over time, while the remaining ODEs describe the temporal variations in the fractions of the total tumour occupied by 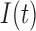 ,
, 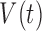 ,
, 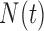 and
and 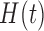 . For example, the vasculature component (
. For example, the vasculature component (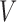 ) represents the fraction of the tumour that is well-vascularized, and the necrosis component (
) represents the fraction of the tumour that is well-vascularized, and the necrosis component (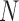 ) is the fraction of the tumour that is necrotic. However, these component fractions do not sum to one because certain characteristics are not mutually exclusive. For example, there is potential overlap in regions of necrosis and hypoxia, and if a tumour is completely well-vascularized, a fraction of that tumour can still display immune infiltration. Therefore, all the components except the tumour volume are maximally limited to one because each component represents a fraction of the total tumour. The system of equations is defined as
) is the fraction of the tumour that is necrotic. However, these component fractions do not sum to one because certain characteristics are not mutually exclusive. For example, there is potential overlap in regions of necrosis and hypoxia, and if a tumour is completely well-vascularized, a fraction of that tumour can still display immune infiltration. Therefore, all the components except the tumour volume are maximally limited to one because each component represents a fraction of the total tumour. The system of equations is defined as
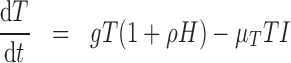 |
(5.1) |
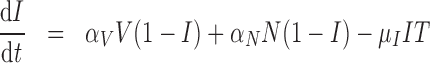 |
(5.2) |
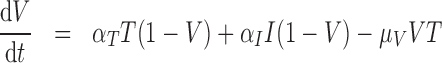 |
(5.3) |
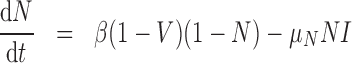 |
(5.4) |
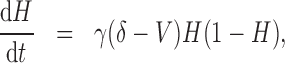 |
(5.5) |
where the 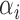 and
and 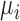 represent rates of stimulation and removal, respectively, and
represent rates of stimulation and removal, respectively, and 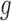 ,
, 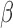 ,
, 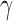 and
and 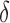 represent the tumour growth rate, necrosis production rate, rate of change in hypoxia and the threshold for hypoxia increase/decrease, respectively. Table 2 summarizes the descriptions of each of the model components and parameters.
represent the tumour growth rate, necrosis production rate, rate of change in hypoxia and the threshold for hypoxia increase/decrease, respectively. Table 2 summarizes the descriptions of each of the model components and parameters.
Fig. 3.
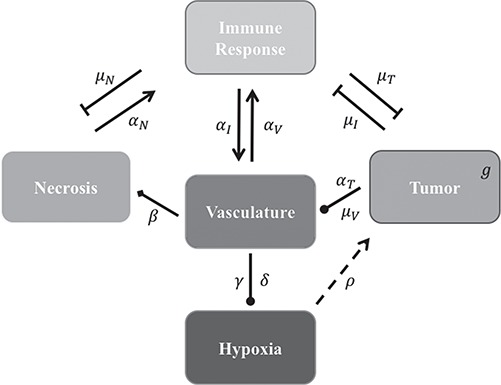
Diagram of the model system in which lines ending in pointed arrows represent an increase/recruitment of one component from another and blunted arrows represent a decrease/blockage of one component from another. The dashed line from hypoxia to the tumour represents an enhancement effect on growth (i.e. not recruitment), arrows with a circular end represent mixed effects from one compartment to the next (i.e. positive or negative) and finally the diamond ended arrow from vasculature to necrosis represents the inverse relationship for necrosis production with suboptimal vasculature. Please see Table 2 for a summary of all model variables and parameters.
Table 2.
Descriptions of model variables and parameters with units. *Immune response corresponds to myeloid infiltration
| Output | Description | Units |
|---|---|---|
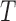
|
Tumour volume | cm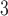
|
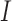
|
Fraction of immune response* in tumour | unitless |
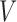
|
Fraction of vascular delivery in tumour | unitless |
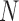
|
Fraction of necrosis in tumour | unitless |
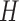
|
Fraction of hypoxia in tumour | unitless |
| Parameter Symbol | Description | Units |
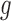
|
Tumour volume growth rate | 1/day |
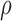
|
Ability of hypoxia to promote tumour growth | unitless |
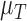
|
Rate tumour volume decreases due to immune response | 1/day |
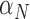
|
Rate immune response increases due to necrosis | 1/day |
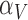
|
Rate immune response increases due to vascular delivery | 1/day |
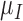
|
Rate immune response decreases per tumour volume | 1/(cm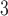 day) day) |
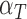
|
Rate vascular delivery increases per tumour volume | 1/(cm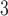 day) day) |
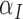
|
Rate vascular delivery increases due to immune response | 1/day |
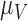
|
Rate vascular delivery decreases per tumour volume | 1/(cm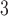 day) day) |
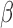
|
Rate of increased necrosis due to decreased vascular delivery | 1/day |
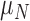
|
Rate necrosis decreases due to immune response | 1/day |
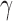
|
Rate of hypoxia increases/decreases due to vascular delivery | 1/day |
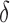
|
Hypoxia increase/decrease threshold due to vascular delivery | unitless |
The tumour growth equation, (5.1), represents exponential growth of the tumour with growth rate, 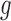 in the absence of hypoxia, that can be increased by the presence of hypoxia with contribution,
in the absence of hypoxia, that can be increased by the presence of hypoxia with contribution, 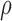 . The maximum rate at which the tumour is removed by the immune response is
. The maximum rate at which the tumour is removed by the immune response is 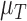 , in accordance with the immune surveillance theory and the apoptotic triggering mechanisms of some immune cells (Bianchini & Gianni, 2014; Hanahan & Weinberg, 2011). Exponential growth is chosen due to the time scale of the experimental results for the mouse model (Walsh et al., 2014a); corresponding to the phase in tumour development for the experimental results (4–6 weeks after implantation) after vasculature has been initially recruited and established.
, in accordance with the immune surveillance theory and the apoptotic triggering mechanisms of some immune cells (Bianchini & Gianni, 2014; Hanahan & Weinberg, 2011). Exponential growth is chosen due to the time scale of the experimental results for the mouse model (Walsh et al., 2014a); corresponding to the phase in tumour development for the experimental results (4–6 weeks after implantation) after vasculature has been initially recruited and established.
The immune response, (5.2), is maximally stimulated by the vasculature at a rate 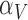 and necrosis at a rate
and necrosis at a rate 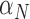 . The immune response at most decreases with rate
. The immune response at most decreases with rate 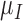 per tumour volume, representing the anti-inflammatory signalling tumour cells produce to prevent immune interactions (Coussens & Werb, 2002; Xu et al., 2015). The vasculature component, (5.3), also has two sources of production: maximal stimulation from the tumour by signalling for angiogenesis at the rate
per tumour volume, representing the anti-inflammatory signalling tumour cells produce to prevent immune interactions (Coussens & Werb, 2002; Xu et al., 2015). The vasculature component, (5.3), also has two sources of production: maximal stimulation from the tumour by signalling for angiogenesis at the rate 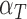 and from the immune response with rate
and from the immune response with rate 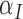 . Vasculature at most decreases with increased tumour volume with rate
. Vasculature at most decreases with increased tumour volume with rate 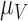 because the vasculature component represents the fraction of the tumour that is well-vascularized. Note that the immune response component is defined in the context of the nude mouse model system, which is T cell deficient; therefore, we make a simplifying assumption that the immune response can only exhibit anti-tumour activity and pro-angiogenesis activity—specifically, the immune response does not exhibit pro-tumour activities such as anti-inflammatory signalling.
because the vasculature component represents the fraction of the tumour that is well-vascularized. Note that the immune response component is defined in the context of the nude mouse model system, which is T cell deficient; therefore, we make a simplifying assumption that the immune response can only exhibit anti-tumour activity and pro-angiogenesis activity—specifically, the immune response does not exhibit pro-tumour activities such as anti-inflammatory signalling.
Necrosis, (5.4), results from suboptimal vasculature (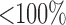 well-vascularized tumour; i.e.
well-vascularized tumour; i.e. 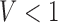 ) with maximum necrosis production rate
) with maximum necrosis production rate 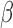 , and is removed by the immune response with rate
, and is removed by the immune response with rate 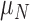 —as one of the primary functions of the immune response is to assess tissue damage and remove necrotic or pathogenic debris (Grivennikov et al., 2010). Finally, hypoxia, (5.5), depends on a threshold
—as one of the primary functions of the immune response is to assess tissue damage and remove necrotic or pathogenic debris (Grivennikov et al., 2010). Finally, hypoxia, (5.5), depends on a threshold 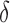 , where the percentage of hypoxia will increase or decrease inversely with the changes in the percentage of the tumour that is well-vascularized at the rate
, where the percentage of hypoxia will increase or decrease inversely with the changes in the percentage of the tumour that is well-vascularized at the rate 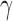 .
.
5.2 Steady state analysis
To help place this new model in the literature and investigate the long-time behaviour of the system, the steady states are found to provide information about the convergence or divergence of the model’s results in the system space (phase space) for the elimination of the tumour. Setting the derivatives on the left-hand sides of (5.1–5.5) to zero, steady states can be defined as the solutions to this algebraic system of equations. Using MATLAB’s symbolic package, the model system is found to have 15 steady state solutions, but only two are biologically relevant (i.e. non-negative and real)—achieved using the parameter values listed in Table 4. One state represents an elimination of the tumour, where the tumour volume, hypoxia, and necrosis are all zero, and the immune response and vasculature are positive (i.e. 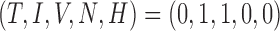 ). The second state is similar to the first with the addition of hypoxia as positive, while necrosis and the tumour are still zero, yielding
). The second state is similar to the first with the addition of hypoxia as positive, while necrosis and the tumour are still zero, yielding 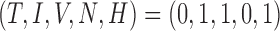 . By defining the Jacobian of the system, eigenvalues are calculated, indicating the stability of these two, biologically relevant steady states. Stability of steady states reveals the local behaviour of the model trajectory in the phase space—indicating whether the model results should converge to or diverge from a particular solution in the phase space. The first state is a stable node (with all real, negative eigenvalues), whereas the second state is an unstable node (with one positive eigenvalue). The first steady state would be the ‘cured’ or normal tissue state. The second state is never stable and therefore is not a viable state. However, this second state’s instability induces the unmitigated growth of the tumour.
. By defining the Jacobian of the system, eigenvalues are calculated, indicating the stability of these two, biologically relevant steady states. Stability of steady states reveals the local behaviour of the model trajectory in the phase space—indicating whether the model results should converge to or diverge from a particular solution in the phase space. The first state is a stable node (with all real, negative eigenvalues), whereas the second state is an unstable node (with one positive eigenvalue). The first steady state would be the ‘cured’ or normal tissue state. The second state is never stable and therefore is not a viable state. However, this second state’s instability induces the unmitigated growth of the tumour.
However, depending on the parameter values of the model, the basin of attraction for the stable node (i.e. a region of the phase space for which the model results will converge to an attractor) can change, resulting in simulation trajectories that converge to the healthy state or diverge to exponential growth of the tumour. As an example, considering a section of the phase space for the 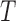 and
and 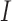 model components, and using the derivatives for
model components, and using the derivatives for 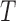 and
and 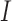 from (5.1) and (5.2), respectively, a phase field can be defined—indicating changes in
from (5.1) and (5.2), respectively, a phase field can be defined—indicating changes in 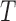 and
and 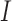 in the positive or negative directions. With the derivative set to zero, we use the resulting nullcline (satisfying the equation) to delineate the areas of the phase space for which the phase field changes direction. Thus, for (5.1) set equal to zero, we have two nullclines
in the positive or negative directions. With the derivative set to zero, we use the resulting nullcline (satisfying the equation) to delineate the areas of the phase space for which the phase field changes direction. Thus, for (5.1) set equal to zero, we have two nullclines
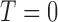 |
(5.6) |
and
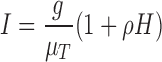 |
(5.7) |
and for (5.2), we have one nullcline
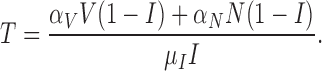 |
(5.8) |
For simplicity in this example, the variables 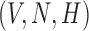 were fixed to non-zero, positive values. Figure 4 depicts two different scenarios where changes in the system’s parameter values cause trajectories to converge to the stable state or are redirected away due to the change in the basin of attraction.
were fixed to non-zero, positive values. Figure 4 depicts two different scenarios where changes in the system’s parameter values cause trajectories to converge to the stable state or are redirected away due to the change in the basin of attraction.
Fig. 4.
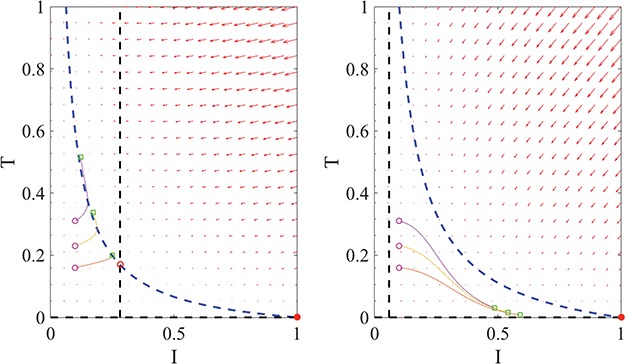
Example phase portraits of the system are depicted for two different parameter sets, showing the potential divergence of trajectories (left) or convergence to the steady state (right). Phase field vectors indicate the directionality of trajectories in the field calculated using the defined derivatives for  (tumour) and
(tumour) and  (immune system) ((5.1) and (5.2), respectively). Nullclines from the
(immune system) ((5.1) and (5.2), respectively). Nullclines from the 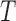 -associated equation ((5.6) and (5.7)), are the vertical and horizontal lines (in black) and for the
-associated equation ((5.6) and (5.7)), are the vertical and horizontal lines (in black) and for the 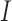 -associated equation ((5.8)), is the remaining dashed curve (in blue). Please see figure online for color. The stable state is represented by a closed red circle and the unstable state with an open red circle. Three trajectories resulting from the model are plotted for each example, where connected with a solid line a pink circle indicates the initial position and a green square the final position. For both examples, the variables
-associated equation ((5.8)), is the remaining dashed curve (in blue). Please see figure online for color. The stable state is represented by a closed red circle and the unstable state with an open red circle. Three trajectories resulting from the model are plotted for each example, where connected with a solid line a pink circle indicates the initial position and a green square the final position. For both examples, the variables 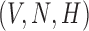 are fixed at
are fixed at 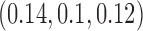 and the initial conditions are
and the initial conditions are 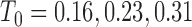 and
and 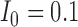 . Note that the only difference between the two panels is changes in the parameter values. Further notice that, depending on the parameter values of the system, the nullclines shift location, expanding or shrinking the area of the phase space for which model trajectories go to zero for the tumour volume. Parameter values used listed in Table 4: left panel,control values, right panel, treated values.
. Note that the only difference between the two panels is changes in the parameter values. Further notice that, depending on the parameter values of the system, the nullclines shift location, expanding or shrinking the area of the phase space for which model trajectories go to zero for the tumour volume. Parameter values used listed in Table 4: left panel,control values, right panel, treated values.
5.3 Parameter calibration
To calibrate the model parameters to the experimental data, the Levenberg–Marquardt method is employed. The Levenberg–Marquardt method is a standard technique used to solve non-linear least squares problems using the combination of the gradient descent method and the Gauss–Newton Method, which we implemented in MATLAB (functions such as lsqnonlin are available for this method but were not used for these results). The sum of squared of errors (SSEs) between the mean values of the data to the corresponding simulation values are minimized at the experimental time points, weighted by dividing the SSEs by the 95% confidence calculated for each data point. For the calibration, only the first set of tumour volume data was utilized. In addition to the 13 model variables, the initial condition for the immune response component is also calibrated, as it is unknown. All numerical simulations were generated by solving the system of equations using MATLAB’s built-in ODE solver ode45.
To verify that the Levenberg–Marquardt method is capable of recovering parameter values for this system and determine potential errors for those parameter values, the method was tested using in silico data generated by randomized parameter values with the following algorithm:
100 parameter sets are randomly generated and stored.
The model is simulated forward using the control data’s Day 0 means for initial conditions for each of the parameter sets, and all 100 simulation results are recorded for all outputs (each component’s time course results), (5.1–5.5).
In silico data is defined from each of the 100 model simulations for four of the five outputs by determining the corresponding component values at the time points for the experimental data (note that immune response data is not available for the calibration; therefore, it is also not included here).
The calibration method is run for each of the 100 in silico data sets, weighted using the control data confidences and the resulting parameter sets are recorded.
For each recovered parameter set, parameter values are compared to the known parameter values that generated the in silico data.
This algorithm is repeated using the treated data. The concordance correlation coefficient (CCC) is used to compare the resulting parameter values from the calibrations to the known parameter sets. The CCC is also used to compare the corresponding simulation result using the calibrated parameters to the corresponding in silico data points. Average error per parameter, average overall error across parameter sets, and 95% confidences are also calculated.
5.4 Model validation
To validate the model’s predictions, initial conditions for the model are defined using the second set of tumour volume data (which has one additional data point for comparison for Day 6). Note, the only data that is different between the calibration and validation steps is the tumour volume data. This type of validation assumes the characteristic components of the tumour and their behaviours over time are similar for tumour data from separate but the same type of experiments. The 95% confidence intervals are calculated for the model’s results from variation in the initial conditions defined by the standard deviation of the experimental data. Randomized initial conditions are defined by taking each component’s Day 0 data and defining a range using mean plus/minus one standard deviation and dividing it into 50 initial values. For the immune response model component, the calibrated initial value plus or minus the calibration error is used to define its 50 initial conditions. Then by randomly pairing all the input values, 50 simulations are run to calculate the 95% confidence intervals for the model prediction.
5.5 Sensitivity analysis
After the calibration of the model to each of the data sets, a global sensitivity analysis is performed on the parameter ranges derived from the calibrated parameters for both data sets and their associated errors. The results of this sensitivity analysis will reveal the most important parameters of the system, causing the greatest variations in outputs, for the area of the parameter space for which the model is able to replicate the experimental data and the area of uncertainty. These important parameters have been shown to be drivers in changing the stability of steady states in mathematical models and may drive future experimental investigations and/or provide support to theories about the biological phenomenon (Marino et al., 2008). Additionally, by identifying parameters that the model is insensitive to, the results may present potential simplified versions of the model that can reliably match future experimental data and can capture the same dynamics while reducing uncertainty by eliminating parameters.
To assess the model’s sensitivity to the parameters of the system, the Sobol’ global sensitivity method is applied. The Sobol’ method is a popular variance-based method that utilizes the analysis of variance (ANOVA) decomposition to define its sensitivity indices (Sobol’, 1993; Saltelli, 2002). As a global method, random sampling is performed over the entire parameter space to calculate the indices. Large sensitivity indices between parameters and model output characteristics indicate that small changes in the parameter values will result in large variations in the output behaviour. For this investigation, to ensure convergences of the indices, a base simulation size of 5000 is chosen, resulting in 70,000 random simulations to generate the following results. For this study, only the total effects of the output values at the final time from the parameters are reported. Specifically, the value of each component of the model at the final time is recorded for each of the random simulations, and per the Sobol’ method, the total effects indices derived from the variances of these outputs is calculated, which account for variations in individual parameters as well as additional effects resulting from the combined variation of parameters. A sensitivity cut-off of 0.05 is used, indicating parameters that cause less than 5% of the total variation of that output.
5.6 Parameter uncertainty
To assess the uncertainty attributable to each parameter based on the calculated calibration error, graphical comparisons are made between the potential model results and the experimental data when parameter values are varied globally. For both the control and treated groups, 1000 model simulations are run using randomized parameter values where each parameter is varied within the parameter’s calibrated value plus/minus its error attributable to the calibration method. The values of all the outputs for all the simulations are recorded for the whole simulation period. From these randomized simulation results, the values of each output at each corresponding experimental time point, are grouped and are converted to histograms—identifying the most and least likely values for each individual output at each experimental time point. For the immune response output, the experimental time points corresponding to the tumour volume data are used. Then these histograms are converted to heat plots overlaid with the 95% confidence intervals of the experimental data for comparison.
6. Results
6.1 Parameter calibration verification
The resulting model simulations calibrated to the in silico results match to the in silico data points with a CCC = 0.99 for both data sets (where the 95% data confidences are used to weigh calibration for the control and treated sets). For the fitted parameters (compared to their known values for these simulations), the calibration method can recover the values with an average parameter error of 16% for the control data confidences and 15% for the treated data confidences—with CCC values of 0.81 and 0.86, respectively (see Table 3).
Table 3.
Calibration CCC values and corresponding errors with 95% confidence for data and parameter fits
| CCC Values | Control | Treated |
|---|---|---|
| Parameters | 0.81 | 0.86 |
| Outputs | 0.99 | 0.99 |
| Average parameter error | 16.48% 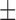 0.01% 0.01% |
14.69% 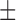 0.01% 0.01% |
6.2 Calibration using first set of tumour volume data
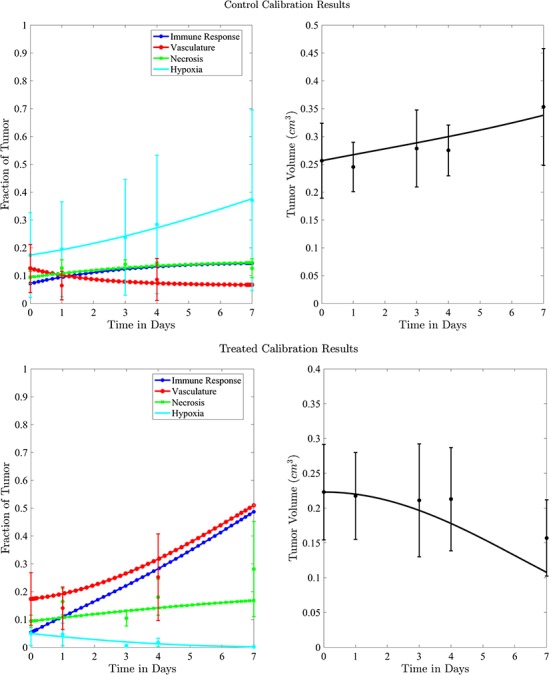
The experimental data used for the calibration of control and treated tumours is presented in Fig. 5 as means with error bars indicating 95% confidence intervals.To calibrate the model parameters to the experimental data, the first set of tumour volume data is utilized for fitting (indicated in black solid lines); necrosis is indicated in green line with symbol  ; percent hypoxia is indicated in cyan line with symbol
; percent hypoxia is indicated in cyan line with symbol  and the percentage of the tumour determined to be well vascularized is indicated in the red line with symbol
and the percentage of the tumour determined to be well vascularized is indicated in the red line with symbol  . Using the data means as initial conditions and the calibrated parameter values, Fig. 5 shows the corresponding model simulations for the control and treated sets. The simulation results agree with the general trends of the data, with CCC = 0.98 and CCC = 0.89 when data points are compared to the corresponding simulation values for the control and treated sets, respectively. Also, the value for the immune response component at the final time for the treated set is more than triple that of the control set’s results (
. Using the data means as initial conditions and the calibrated parameter values, Fig. 5 shows the corresponding model simulations for the control and treated sets. The simulation results agree with the general trends of the data, with CCC = 0.98 and CCC = 0.89 when data points are compared to the corresponding simulation values for the control and treated sets, respectively. Also, the value for the immune response component at the final time for the treated set is more than triple that of the control set’s results ( and
and  , respectively). See Table 4 for the resulting calibrated parameter values for both the control and treated data.
, respectively). See Table 4 for the resulting calibrated parameter values for both the control and treated data.
Fig. 5.
Control versus treated model simulations with experimental data (top panels for control and bottom panels for treated tumours). Data means are shown with 95% confidence intervals (error bars), where tumour volume data and model calibration are shown on the right and the tumour biological data are shown in left panels.
Table 4.
Calibrated parameter values for control and treated sets
| Parameter symbol | Control | Treated |
|---|---|---|
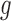
|
0.044 | 0.027 |
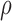
|
1.523 | 0.865 |
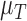
|
0.187 | 0.509 |
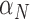
|
0.200 | 0.075 |
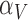
|
0.199 | 0.354 |
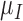
|
0.722 | 0.513 |
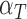
|
0.101 | 0.0007 |
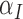
|
0.045 | 0.294 |
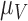
|
1.723 | 0.020 |
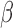
|
0.027 | 0.017 |
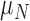
|
0.911 | 0.00004 |
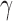
|
0.743 | 1.555 |
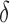
|
0.284 | 0.0002 |
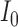
|
0.071 | 0.053 |
6.3 Calibration validation using second set of tumour volume data
Figure 6 displays the model simulation results for both the control and treated data sets using the second set of tumour volume data for initial conditions and the calibrated parameters values. The simulations along with their 95% confidence intervals (derived from varying initial conditions) are in good agreement with the data in both the control and treated groups (CCC = 0.98 and CCC = 0.90, respectively). Note that for Day 4, the immune response component value for the treated group is almost double the value for the control group ( and
and 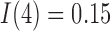 , respectively).
, respectively).
Fig. 6.
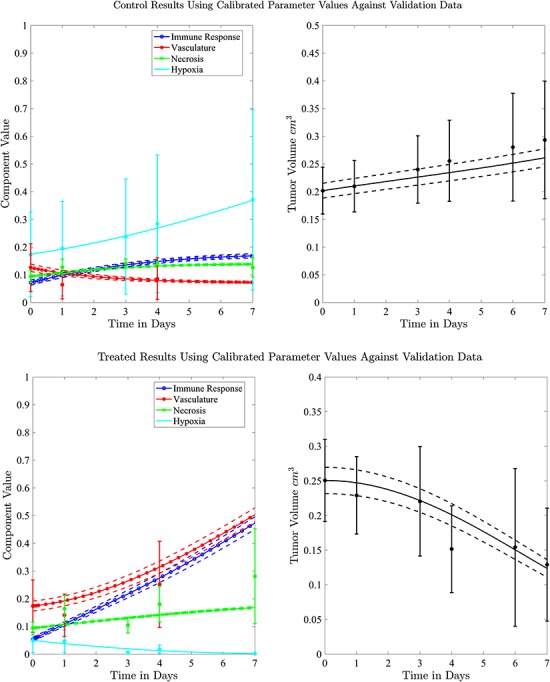
Model simulations for the control and treated sets (top panels for control and bottom panels for treated tumours) with 95% confidence intervals indicated with dashed lines are derived from varying initial conditions based on the experimental data using the second set of tumour data. Tumour volume data and model calibration are shown on the right and the tumour biological data are shown in left panels.
6.4 Results of sensitivity analysis
The Sobol’ sensitivity indices for the total effects of the parameters on the output variables for the final time (Day 7) are illustrated as a bar graph in Fig. 7. All but one (12 of 13) of the parameters have at least one index value > 0.05 within the parameter ranges defined by the parameter calibration. In particular, 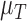 ,
, 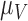 ,
, 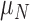 and
and 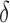 are the most important parameters for the tumour, vasculature, necrosis and hypoxia, respectively, having the highest indices. For the tumour volume,
are the most important parameters for the tumour, vasculature, necrosis and hypoxia, respectively, having the highest indices. For the tumour volume, 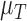 and
and 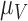 are the first and second most influential parameters. The immune response is sensitive to
are the first and second most influential parameters. The immune response is sensitive to 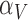 ,
, 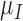 and
and 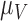 (
(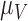 having the highest index). The parameter
having the highest index). The parameter 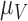 is the most important for the vasculature, and
is the most important for the vasculature, and 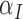 is vasculature’s the second most important. For necrosis,
is vasculature’s the second most important. For necrosis, 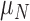 is the dominant parameter for output variations, and similarly for hypoxia
is the dominant parameter for output variations, and similarly for hypoxia 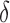 has the highest index. Note that
has the highest index. Note that 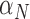 ,
, 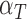 and
and 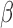 are marginally larger than the cut-off for output sensitivity; whereas all outputs are sensitive to parameter
are marginally larger than the cut-off for output sensitivity; whereas all outputs are sensitive to parameter 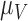 . Additionally,
. Additionally, 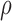 is the only parameter with effects <0.05 for all five components, and the other hypoxia-related parameters (
is the only parameter with effects <0.05 for all five components, and the other hypoxia-related parameters (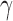 and
and 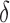 ) only have effect on hypoxia—no other model components are sensitive to these parameters.
) only have effect on hypoxia—no other model components are sensitive to these parameters.
Fig. 7.
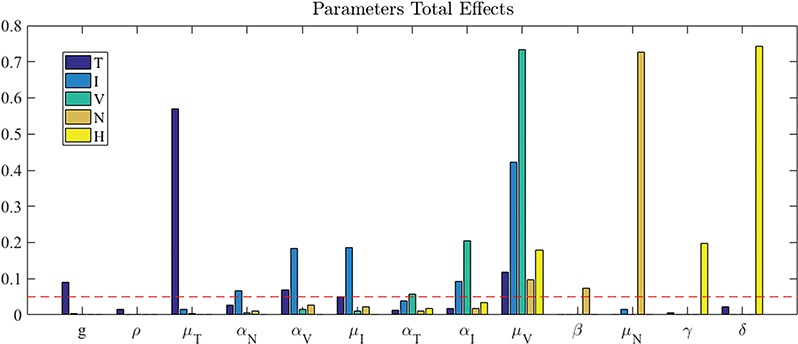
Sobol’ total effects indices for all five outputs and all the system parameters. Sensitivity cut-off indicated by dashed line (0.05); with this threshold, the outputs are sensitive to the majority of the parameters all but one, 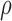 .
.
6.5 Parameter uncertainty
To assess the uncertainty in the parameter values attributable to calibration error, uncertainty distributions are generated for each model component at each of their corresponding experimental time points. Figure 8 shows the resulting normalized distributions for the control and treated groups as heat maps, where black represents zero results of that value and white represents values with maximum probability for that output. Overlaid are the corresponding confidence intervals of the experimental data at each time point (in red). The immune response component is shown for the experimental time points corresponding to the tumour volume data. There is only one instance of non-overlap between the experimental range and the uncertainty distribution in the results—necrosis at its second time point (Day 1) for the treated data set.
Fig. 8.
Model output uncertainty depicted as normalized probability heat maps per experimental time (Days) compared to data (where the 95% data confidence interval is overlaid) from variable parameter values using error intervals from the parameter calibration. The immune response component is shown for the experimental time points corresponding to the tumour volume data. Results reveal general agreement between the probable model simulations and the data confidences for both control and treated results.
6.6 Immunofluorescence staining
CD11c and F4/80 staining is greater in the total tissue of treated tumours compared to controls but not significantly (p  and p
and p 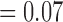 , respectively, with F4/80 staining trending towards significance). While not significant, CD11c staining in viable tissue was larger in treated tumours compared to controls, and average CD11c staining in necrotic tissue was less in treated tumours compared to controls (p
, respectively, with F4/80 staining trending towards significance). While not significant, CD11c staining in viable tissue was larger in treated tumours compared to controls, and average CD11c staining in necrotic tissue was less in treated tumours compared to controls (p 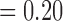 , p
, p 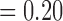 , respectively). F4/80 staining in viable tissue was significantly larger in treated tumours compared to controls, and average F4/80 staining in necrotic tissue was significantly less in treated tumours compared to controls (p
, respectively). F4/80 staining in viable tissue was significantly larger in treated tumours compared to controls, and average F4/80 staining in necrotic tissue was significantly less in treated tumours compared to controls (p 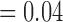 and p
and p 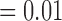 , respectively). There are significantly greater percentages for co-staining of CD11c and F4/80 in both the total tumour tissue for the treated tumours compared to the controls (p
, respectively). There are significantly greater percentages for co-staining of CD11c and F4/80 in both the total tumour tissue for the treated tumours compared to the controls (p 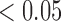 ). For co-staining in viable tissues, average treated co-staining is 4.40% compared to control co-staining of 2.97% (p
). For co-staining in viable tissues, average treated co-staining is 4.40% compared to control co-staining of 2.97% (p 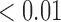 ). Furthermore, the co-staining of CD11c and F4/80 is lower in the necrotic regions for the treated compared to the control (0.93% compared to 2.28%, p
). Furthermore, the co-staining of CD11c and F4/80 is lower in the necrotic regions for the treated compared to the control (0.93% compared to 2.28%, p 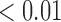 ). Figure 9 shows an example of a control tumour slice versus a treated tumour slice staining and their corresponding segmentation results for CD11c and F4/80 staining as well as bar graphs depicting mean viable tissue staining for treated versus control tumours.
). Figure 9 shows an example of a control tumour slice versus a treated tumour slice staining and their corresponding segmentation results for CD11c and F4/80 staining as well as bar graphs depicting mean viable tissue staining for treated versus control tumours.
Fig. 9.
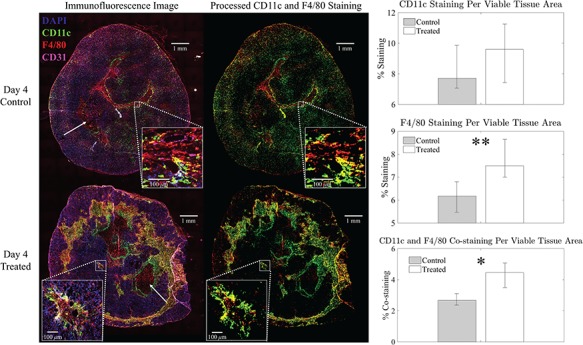
Left panel: example representative immunofluorescent images of control (top) versus treated (bottom) with all stains (left) and corresponding immune (myeloid) segmentation results for CD11c and F4/80 staining only (right). DAPI staining is shown in blue, CD31 staining in violet, CD11c staining in green, F4/80 staining in red and CD11c and F4/80 co-staining in yellow. Example necrotic areas indicated with white arrows. Percent staining of total tumour area for the control slice is: 8% CD11c, 6% F4/80 and 3% co-staining and for the treated slice is: 10% CD11c, 8% F4/80, and 5% co-staining. Right panel: Bar plots for group average viable tissue staining for CD11c, F4/80 and CD11c-F4/80 co-staining for Day 4 control and treated tumours with 95% confidence intervals. F4/80 individual staining and CD11c-F4/80 co-staining is significantly greater in viable tissue of treated tumours compared to controls (**p 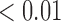 and *p
and *p 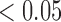 , respectively).
, respectively).
7. Discussion
The model simulates distinct differences in the immune response behaviour when comparing control and trastuzumab-treated tumours. For the control tumours, the immune response gradually increases and begins to plateau after Day 3; whereas for the treated group, the immune response steadily increases, almost linearly with time. Also presented are newly acquired immunofluorescent results for the purpose of supporting or refuting the model’s predictions for the immune infiltrate dynamics and were not considered prior to the model’s construction, analysis and simulation of results. These experimental results agree with the model’s prediction for immune infiltration, showing significantly increased myeloid cell infiltration for the treated tumour specimens compared to the controls. This is also supported by other studies that investigated the roles of macrophages and antibody therapy interacting with tumour cells (Gul et al., 2014; Xu et al., 2015). For example, Gul et al. (2014) revealed that macrophages will more rapidly phagocytose cancer cells following anti-tumour antibody therapy. Xu et al. (2015) showed that switching the phenotype of tumour associated macrophages from anti-inflammatory to pro-inflammatory following anti-HER2 therapy dramatically increasing the therapeutic effect of trastuzumab.
Between the two sets of calibrated parameters (i.e. those obtained from the controls and treated groups, respectively), all of the values differ and all except one of the parameters influence the sensitivity of the outputs. Note that one of the primary aims of this study is to generate experimentally testable hypotheses about the effects of trastuzumab treatment in this system. For this reason, all the parameters of the model were permitted to vary for calibration. Some of these differences are expected, such as the differences in 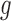 ,
, 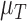 ,
, 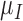 and
and 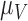 . For example, increased kill rate by the immune response to reduce the tumour size (
. For example, increased kill rate by the immune response to reduce the tumour size (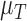 ) and/or a reduced growth rate (
) and/or a reduced growth rate (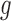 ) for treated tumours are common results across all types of mathematical models for immune and cancer cell dynamics (Walker & Enderling, 2016). Other reasonable variations between the two data sets, such as the lower threshold for hypoxia to decay in treated tumours (
) for treated tumours are common results across all types of mathematical models for immune and cancer cell dynamics (Walker & Enderling, 2016). Other reasonable variations between the two data sets, such as the lower threshold for hypoxia to decay in treated tumours (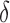 ) or the lower production of necrosis in the treated tumour (
) or the lower production of necrosis in the treated tumour (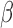 ) are within the expected biological variations. The only parameter by which hypoxia interacts with the system,
) are within the expected biological variations. The only parameter by which hypoxia interacts with the system, 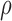 , has a low sensitivity index, and no outputs are sensitive to parameters
, has a low sensitivity index, and no outputs are sensitive to parameters 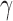 and
and 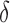 other than hypoxia (the parameters governing that specific ODE). Therefore, future iterations of the model should explore a possible reduction in the system where hypoxia is removed. Although the outputs are sensitive to the majority of the parameters, when parameter variation due to calibration error is considered, the distributions of the model outputs agree with the observed experimental spread at each time point, and the distinct behaviour in the immune response for the control and treated results is also maintained.
other than hypoxia (the parameters governing that specific ODE). Therefore, future iterations of the model should explore a possible reduction in the system where hypoxia is removed. Although the outputs are sensitive to the majority of the parameters, when parameter variation due to calibration error is considered, the distributions of the model outputs agree with the observed experimental spread at each time point, and the distinct behaviour in the immune response for the control and treated results is also maintained.
Differences in the values of other parameters generate several new, distinct hypotheses, as these parameters are not related to known mechanisms of the therapy or downstream effects. For example, the calibrated parameters that generate these differing simulations suggest greater cross-talk in the immune response and the vasculature for the treated tumour—indicated by larger parameter rates (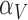 and
and 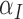 ). Furthermore, the sensitivity analysis results indicate that the immune response and vasculature components are sensitive to those two parameters; therefore, the values of these rates are important to understand and to define for the biological system. Also, the large parameter difference between data sets and the fact that the immune response and vasculature are most sensitive to parameter
). Furthermore, the sensitivity analysis results indicate that the immune response and vasculature components are sensitive to those two parameters; therefore, the values of these rates are important to understand and to define for the biological system. Also, the large parameter difference between data sets and the fact that the immune response and vasculature are most sensitive to parameter 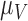 suggest a protective mechanism for the vasculature against the detrimental effects of tumour cell signalling and growth in treated tumours compared to controls. Another phenomenon suggested by the model that should also be investigated experimentally is the distinct change in the myeloid cells’ focus to remove necrosis in the treated tumours (smaller
suggest a protective mechanism for the vasculature against the detrimental effects of tumour cell signalling and growth in treated tumours compared to controls. Another phenomenon suggested by the model that should also be investigated experimentally is the distinct change in the myeloid cells’ focus to remove necrosis in the treated tumours (smaller 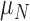 , a sensitive parameter for necrosis). This points to a redirection of the immune response from necrosis to the tumour cells and vasculature, such as the specific reprogramming of macrophages for pro- and anti-inflammatory phenotypes. This difference in calibration is preliminarily supported by the presented immunofluorescence results, showing significantly smaller amounts of immune infiltration in the necrotic areas of the tumour for treated specimens.
, a sensitive parameter for necrosis). This points to a redirection of the immune response from necrosis to the tumour cells and vasculature, such as the specific reprogramming of macrophages for pro- and anti-inflammatory phenotypes. This difference in calibration is preliminarily supported by the presented immunofluorescence results, showing significantly smaller amounts of immune infiltration in the necrotic areas of the tumour for treated specimens.
Experimental data is limited in that it is only capable of indirectly correlating measurable quantities to phenomena of interest, such as hypoxia, necrosis, vasculature and immune infiltrates from the same tumour. These limitations simply can be due to lack of tissue specimens, undeveloped experimental methodologies or (using the example of immunofluorescent staining) having a limited number of colour channels to distinctly identify different cells. Often it is difficult to collect data from all the underlying components of a system in the same experimental paradigm. However, a mathematical model can be exploited for its ability to connect separate but related preclinical experiments. Predictions resulting from the mathematical model, despite the lack of the corresponding data, is a strength where the model can indicate fruitful avenues for future investigation. Therefore, a mathematical framework built upon the major assumptions of the biological phenomenon and directly translatable to the collected data, allows researchers to test theories based on a series of experimental results.
The mathematical model presented in this contribution has the potential to identify dynamic changes in immune infiltrates during trastuzumab therapy in a murine model of HER2+ breast cancer and correlate them with changes in vasculature and hypoxia to identify optimal timing to guide subsequent therapies. As all anti-cancer strategies use a combination of treatments (e.g. chemotherapy, radiation therapy, targeted agents and surgery), understanding and predicting the sensitized states and associations of tumour cells, vascular delivery, oxygenation and immune response, has potential to help guide combination therapies, and thereby improve treatment outcomes. As it is impossible to test in preclinical animal models and clinical trials the numerous therapeutic combinations that might be available to treat HER2+ breast cancer, this mathematical model provides an initial framework for testing out combination therapies.
Limitations of the study include the lack of temporal data for the different tumour components for validation of the model. As more data becomes available for necrosis, hypoxia and vasculature, the model should be simulated and validated on this independent data in addition to the tumour volume. Additionally, specific input values for the most sensitive parameters should be investigated experimentally, if possible, to reduce uncertainty in the model’s predictions for the dynamics of the tumour tissue characteristics. The current formulation of the model does not include the effect of the drug therapy explicitly into the equations. We discuss trastuzumab’s effect implicitly through the differences in calibrated input values, but in future work, to potentially identify optimal dosing strategies for single and combination therapies, the model will need to be expanded. Further experimentation evaluating prospective longitudinal data comparing the immune infiltration to the other biological characteristics of the tumour is warranted, including pro- versus anti-tumour activity and information on additional immune infiltrates (i.e. T cells). Future work could also explore spatial heterogeneity in these parameters by employing PDEs, but some of the methods of data collection presented here, such as histology, preclude the ability to collect spatially and temporally resolved data for these tumours—for which alternative experimental methods must be applied and developed to collect both spatially and temporally defined data. Without time course data to calibrate the immune component, the accuracy of the exact values from the calibrations is arguable and over fitting may be an issue. However, our calibration verification, sensitivity and uncertainty results give confidence in the model’s calibrations. The relationships between the values when comparing parameter sets is likely representative of the biological system and the greatest differences between the sets can at least provide guidance for future experimental investigations. We reiterate that one of these parameter differences (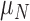 ) is already supported by the new immunofluorescence results.
) is already supported by the new immunofluorescence results.
8. Conclusion
The goal of this study is to develop an integrated, mathematical-experimental approach for understanding the interactions between the immune system and the effects of trastuzumab on breast cancer that overexpresses HER2. An ODE model is developed representing tumour volume change and tumour tissue characteristics, including hypoxia, necrosis, immune infiltration and vasculature. The parameters of the model are calibrated using experimental data from control and trastuzumab-treated tumours resulting in distinct behaviours predicted for the temporal dynamics of the immune response for the two experimental cases. These results agree with the presented immunofluorescent experimental data indicating an increase in myeloid infiltration for treated tumours compared to control tumours. Comparing the values of the calibrated parameters, several interesting differences were found, including the interactions between the immune response and vasculature. These parameter differences illuminate potential future investigations into additional, unknown mechanisms of trastuzumab treatment or downstream effects induced by anti-HER2 therapy—conclusions revealed by the mathematical model that were not deducible from the experimental data alone.
Supplementary Material
Acknowledgements
We thank the National Cancer Institute for support through U01CA174706 and R01CA186193. We thank the Cancer Prevention and Research Institute of Texas (CPRIT) for funding through RR160005. We thank the American Cancer Society for funding for L.I.R.E. through 128265-RSG-158-01-CSM and funding for A.G.S through RSG-18-006-01-CCE. T.E.Y. is a CPRIT Scholar of Cancer Research.
References
- American Cancer Society. Breast cancer facts & figures 2017–2018. Report, American Cancer Society (2017). [Google Scholar]
- Altrock P. M., Liu L. L. & Michor F. (2015) The mathematics of cancer: integrating quantitative models. Nat. Rev. Cancer, 15, 730–745. DOI 10.1038/nrc4029. [DOI] [PubMed] [Google Scholar]
- Alturkistani H. A., Tashkandi F. M. & Mohammedsaleh Z. M. (2015) Histological stains: a literature review and case study. Glob. J. Health Sci., 8, 72–79. DOI 10.5539/gjhs.v8n3p72;https://www.ncbi.nlm.nih.gov/pubmed/26493433 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartsch R., Wenzel C., Hussian D., Pluschnig U., Sevelda U., Koestler W., Altorjai G., Locker G. J., Mader R., Zielinski C. C. & Steger G. G. (2006) Analysis of trastuzumab and chemotherapy in advanced breast cancer after the failure of at least one earlier combination: an observational study. BMC Cancer, 6, 63 DOI 10.1186/1471-2407-6-63;https://www.ncbi.nlm.nih.gov/pubmed/16539726 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berner V., Liu H., Zhou Q., Alderson K. L., Sun K., Weiss J. M., Back T. C., Longo D. L., Blazar B. R., Wiltrout R. H., Welniak L. A., Redelman D. & Murphy W. J. (2007) IFN-gamma mediates CD4+ t-cell loss and impairs secondary antitumor responses after successful initial immunotherapy. Nat. Med., 13, 354–360. DOI 10.1038/nm1554;https://www.ncbi.nlm.nih.gov/pubmed/17334371 [DOI] [PubMed] [Google Scholar]
- Bertucci F. & Gonçalves A. (2017) Immunotherapy in breast cancer: the emerging role of PD-1 and PD-L1. Curr. Oncol. Rep., 19, 64 DOI 10.1007/s11912-017-0627-0; https://www.ncbi.nlm.nih.gov/pubmed/28799073 [DOI] [PubMed] [Google Scholar]
- Bianchini G. & Gianni L. (2014) The immune system and response to HER2-targeted treatment in breast cancer. Lancet Oncol., 15, E58–E68. [DOI] [PubMed] [Google Scholar]
- Brown J. M. (2000) Exploiting the hypoxic cancer cell: mechanisms and therapeutic strategies. Mol. Med. Today, 6, 157–162. https://www.ncbi.nlm.nih.gov/pubmed/10740254 [DOI] [PubMed] [Google Scholar]
- Burnet M. (1957) Cancer; a biological approach. I. The processes of control. Br. Med. J., 1, 779–786. https://www.ncbi.nlm.nih.gov/pubmed/13404306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen D., Roda J. M., Marsh C. B., Eubank T. D. & Friedman A. (2012) Hypoxia inducible factors-mediated inhibition of cancer by GM-CSF: a mathematical model. Bull. Math. Biol., 74, 2752–2777. DOI 10.1007/s11538-012-9776-3;https://www.ncbi.nlm.nih.gov/pubmed/23073704 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chimal-Ramirez G. K., Espinoza-Sánchez N. A. & Fuentes-Pananá E. M. (2013) Protumor activities of the immune response: insights in the mechanisms of immunological shift, oncotraining, and oncopromotion. J. Oncol., 2013, 83595660 DOI 10.1155/2013/835956;https://www.ncbi.nlm.nih.gov/pubmed/23577028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho H. S., Mason K., Ramyar K. X., Stanley A. M., Gabelli S. B., Denney D. W. & Leahy D. J. (2003) Structure of the extracellular region of HER2 alone and in complex with the herceptin fab. Nature, 421, 756–760. DOI 10.1038/nature01392;https://www.ncbi.nlm.nih.gov/pubmed/12610629 [DOI] [PubMed] [Google Scholar]
- Coussens L. M. & Werb Z. (2002) Inflammation and cancer. Nature, 420, 860–867. DOI 10.1038/nature01322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day J., Rubin J., Vodovotz Y., Chow C., Reynolds A. & Clermont G. (2006) A reduced mathematical model of the acute inflammatory response II. Capturing scenarios of repeated endotoxin administration. J. Theor. Biol., 242, 237–256. DOI 10.1016/j.jtbi.2006.02.015. [DOI] [PubMed] [Google Scholar]
- De Palma M. & Lewis C. E. (2013) Macrophage regulation of tumor responses to anticancer therapies. Cancer Cell, 23, 277–286. DOI 10.1016/j.ccr.2013.02.013;https://www.ncbi.nlm.nih.gov/pubmed/23518347 [DOI] [PubMed] [Google Scholar]
- De Palma M., Murdoch C., Venneri M. A., Naldini L. & Lewis C. E. (2007) Tie2-expressing monocytes: regulation of tumor angiogenesis and therapeutic implications. Trends Immunol., 28, 519–524. DOI 10.1016/j.it.2007.09.004;https://www.ncbi.nlm.nih.gov/pubmed/17981504 [DOI] [PubMed] [Google Scholar]
- d’Onofrio A. (2005) A general framework for modeling tumor-immune system competition and immunotherapy: Mathematical analysis and biomedical inferences. Physica D., 208, 220–235. DOI 10.1016/j.physd.2005.06.032. [Google Scholar]
- Eftimie R., Bramson J. L. & Earn D. J. D. (2011) Interactions between the immune system and cancer: a brief review of non-spatial mathematical models. Bull. Math. Biol., 73, 2–32. DOI 10.1007/s11538-010-9526-3. [DOI] [PubMed] [Google Scholar]
- Emens L. A. (2017) Breast cancer immunotherapy: facts and hopes. Clin. Cancer. Res., 3, 511–520. DOI 10.1158/1078-0432.CCR-16-3001.https://www.ncbi.nlm.nih.gov/pubmed/28801472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrara N., Hillan K. J. & Novotny W. A. (2005) Bevacizumab (Avastin), a humanized anti-VEGF monoclonal antibody for cancer therapy. Biochem. Biophys. Res. Commun., 333, 328–335. [DOI] [PubMed] [Google Scholar]
- Folkman J. (1995) The influence of angiogenesis research on management of patients with breast cancer. Breast Cancer Res. Treat., 36, 109–118. https://www.ncbi.nlm.nih.gov/pubmed/8534860 [DOI] [PubMed] [Google Scholar]
- Forys U., Waniewski J. & Zhivkov P. (2006) Anti-tumor immunity and tumor anti-immunity in a mathematical model of tumor immunotherapy. J. Biol. Syst., 14, 13–30. DOI 10.1142/s0218339006001702. [Google Scholar]
- Gabrilovich D. I., Ostrand-Rosenberg S. & Bronte V. (2012) Coordinated regulation of myeloid cells by tumours. Nat. Rev. Immunol., 12, 253–268. DOI 10.1038/nri3175;https://www.ncbi.nlm.nih.gov/pubmed/22437938 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goel S., Wong A. H. & Jain R. K. (2012) Vascular normalization as a therapeutic strategy for malignant and nonmalignant disease. Cold Spring Harb. Perspect. Med., 2, a006486 DOI 10.1101/cshperspect.a006486;https://www.ncbi.nlm.nih.gov/pubmed/22393532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez-Angulo A. M., Litton J. K., Broglio K. R., Meric-Bernstam F., Rakkhit R., Cardoso F., Peintinger F., Hanrahan E. O., Sahin A., Guray M., Larsimont D., Feoli F., Stranzl H., Buchholz T. A., Valero V., Theriault R., Piccart-Gebhart M., Ravdin P. M., Berry D. A. & Hortobagyi G. N. (2009) High risk of recurrence for patients with breast cancer who have human epidermal growth factor receptor 2-positive, node-negative tumors 1 cm or smaller. J. Clin. Oncol., 27, 5700–5706. DOI 10.1200/JCO.2009.23.2025;https://www.ncbi.nlm.nih.gov/pubmed/19884543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gore J. C., Manning H. C., Quarles C. C., Waddell K. W. & Yankeelov T. E. (2011) Magnetic resonance in the era of molecular imaging of cancer. Magn. Reson. Imaging, 29, 587–600. DOI 10.1016/j.mri.2011.02.003;https://www.ncbi.nlm.nih.gov/pubmed/21524870 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grivennikov S. I., Greten F. R. & Karin M. (2010) Immunity, inflammation, and cancer. Cell, 140, 883–899. DOI 10.1016/j.cell.2010.01.025;https://www.ncbi.nlm.nih.gov/pubmed/20303878 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruber G., Greiner R. H., Hlushchuk R., Aebersold D. M., Altermatt H. J., Berclaz G. & Djonov V. (2004) Hypoxia-inducible factor 1 alpha in high-risk breast cancer: an independent prognostic parameter? Breast Cancer Res., 6, R191–R198. DOI 10.1186/bcr775;https://www.ncbi.nlm.nih.gov/pubmed/15084243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gul N., Babes L., Siegmund K., Korthouwer R., Bogels M., Braster R., Vidarsson G., ten Hagen T. L. M., Kubes P. & van Egmond M. (2014) Macrophages eliminate circulating tumor cells after monoclonal antibody therapy. J. Clin. Invest., 124, 812–823. DOI 10.1172/jci66776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammond E. M., Asselin M. C., Forster D., O’Connor J. P., Senra J. M. & Williams K. J. (2014) The meaning, measurement and modification of hypoxia in the laboratory and the clinic. Clin. Oncol. (R. Coll. Radiol.), 26, 277–288. DOI 10.1016/j.clon.2014.02.002;https://www.ncbi.nlm.nih.gov/pubmed/24602562 [DOI] [PubMed] [Google Scholar]
- Hanahan D. & Weinberg R. A. (2011) Hallmarks of cancer: the next generation. Cell, 144, 646–674. DOI 10.1016/j.cell.2011.02.013;https://www.ncbi.nlm.nih.gov/pubmed/21376230 [DOI] [PubMed] [Google Scholar]
- Hardee M. E., Eapen R. J., Rabbani Z. N., Dreher M. R., Marks J., Blackwell K. L. & Dewhirst M. W. (2009) HER2/neu signaling blockade improves tumor oxygenation in a multifactorial fashion in HER2/neu+ tumors. Cancer Chemother. Pharmacol., 63, 219–228. DOI 10.1007/s00280-008-0729-3;https://www.ncbi.nlm.nih.gov/pubmed/18365198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helmlinger G., Yuan F., Dellian M. & Jain R. K. (1997) Interstitial ph and pO2 gradients in solid tumors in vivo: high-resolution measurements reveal a lack of correlation. Nat. Med., 3, 177–182. https://www.ncbi.nlm.nih.gov/pubmed/9018236 [DOI] [PubMed] [Google Scholar]
-
Heyerdahl H., Røe K., Brevik E. M. & Dahle J. (2013) Modifications in dynamic contrast-enhanced magnetic resonance imaging parameters after
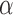 -particle-emitting
-particle-emitting 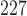 Th-trastuzumab therapy of HER2-expressing ovarian cancer xenografts. Int. J. Radiat. Oncol. Biol. Phys., 87, 153–159. DOI 10.1016/j.ijrobp.2013.04.052;https://www.ncbi.nlm.nih.gov/pubmed/23790511 [DOI] [PubMed] [Google Scholar]
Th-trastuzumab therapy of HER2-expressing ovarian cancer xenografts. Int. J. Radiat. Oncol. Biol. Phys., 87, 153–159. DOI 10.1016/j.ijrobp.2013.04.052;https://www.ncbi.nlm.nih.gov/pubmed/23790511 [DOI] [PubMed] [Google Scholar] - Hormuth D. A., Weis J. A., Barnes S. L., Miga M. I., Rericha E. C., Quaranta V. & Yankeelov T. E. (2017) A mechanically coupled reaction-diffusion model that incorporates intra-tumoural heterogeneity to predict in vivo glioma growth. J. R. Soc. Interface, 14, 20161010 DOI 10.1098/rsif.2016.1010;https://www.ncbi.nlm.nih.gov/pubmed/28330985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang A., Cao S. & Tang L. (2017) The tumor microenvironment and inflammatory breast cancer. J. Cancer, 8, 1884–1891. DOI 10.7150/jca.17595;https://www.ncbi.nlm.nih.gov/pubmed/28819386 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y., Yuan J., Righi E., Kamoun W. S., Ancukiewicz M., Nezivar J., Santosuosso M., Martin J. D., Martin M. R., Vianello F., Leblanc P., Munn L. L., Huang P., Duda D. G., Fukumura D., Jain R. K. & Poznansky M. C. (2012) Vascular normalizing doses of antiangiogenic treatment reprogram the immunosuppressive tumor microenvironment and enhance immunotherapy. Proc. Natl. Acad. Sci. USA, 109, 17.5616. DOI 10.1073/pnas.1215397109;https://www.ncbi.nlm.nih.gov/pubmed/23045683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubbard M. E. & Byrne H. M. (2013) Multiphase modelling of vascular tumour growth in two spatial dimensions. J. Theor. Biol., 316, 70–89. DOI 10.1016/j.jtbi.2012.09.031;https://www.ncbi.nlm.nih.gov/pubmed/23032218 [DOI] [PubMed] [Google Scholar]
- Izumi Y., Xu L., di Tomaso E., Fukumura D. & Jain R. K. (2002) Tumour biology: herceptin acts as an anti-angiogenic cocktail. Nature, 416, 279–280. DOI 10.1038/416279b;https://www.ncbi.nlm.nih.gov/pubmed/11907566 [DOI] [PubMed] [Google Scholar]
- Jackson T. L. & Byrne H. M. (2002) A mechanical model of tumor encapsulation and transcapsular spread. Math. Biosci., 180, 307–328. https://www.ncbi.nlm.nih.gov/pubmed/12387930 [DOI] [PubMed] [Google Scholar]
- Jain R. K. (2013) Normalizing tumor microenvironment to treat cancer: bench to bedside to biomarkers. J. Clin. Oncol., 31, 2205–2218. DOI 10.1200/JCO.2012.46.3653;https://www.ncbi.nlm.nih.gov/pubmed/23669226 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain R. K. & Carmeliet P. (2012) Snapshot: tumor angiogenesis. Cell, 149, 1408–1408.e1. DOI 10.1016/j.cell.2012.05.025;https://www.ncbi.nlm.nih.gov/pubmed/22682256 [DOI] [PubMed] [Google Scholar]
- Jarrett A. M., Cogan N. G. & Hussaini M. Y. (2015. a) Mathematical model for MRSA nasal carriage. Bull. Math. Biol., 77, 1787–1812. DOI 10.1007/s11538-015-0104-6. [DOI] [PubMed] [Google Scholar]
- Jarrett A. M., Cogan N. G. & Shirtliff M. E. (2015b) Modelling the interaction between the host immune response, bacterial dynamics and inflammatory damage in comparison with immunomodulation and vaccination experiments. Math. Med. Biol., 32, 285–306. DOI 10.1093/imammb/dqu008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kakolyris S., Fox S. B., Koukourakis M., Giatromanolaki A., Brown N., Leek R. D., Taylor M., Leigh I. M., Gatter K. C. & Harris A. L. (2000) Relationship of vascular maturation in breast cancer blood vessels to vascular density and metastasis, assessed by expression of a novel basement membrane component, lh39. Br. J. Cancer., 82, 844–851. DOI 10.1054/bjoc.1999.1010;https://www.ncbi.nlm.nih.gov/pubmed/10732757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim P. S., Lee P. P. & Levy D. (2007) Modeling regulation mechanisms in the immune system. J. Theor. Biol., 246, 33–69. DOI 10.1016/j.jtbi.2006.12.012;https://www.ncbi.nlm.nih.gov/pubmed/17270220 [DOI] [PubMed] [Google Scholar]
- Klapper L. N., Kirschbaum M. H., Sela M. & Yarden Y. (2000) Biochemical and clinical implications of the ErbB/HER signaling network of growth factor receptors. Adv. Cancer Res., 77, 25–79. https://www.ncbi.nlm.nih.gov/pubmed/10549355 [PubMed] [Google Scholar]
- Klos K. S., Zhou X., Lee S., Zhang L., Yang W., Nagata Y. & Yu D. (2003) Combined trastuzumab and paclitaxel treatment better inhibits ErbB-2-mediated angiogenesis in breast carcinoma through a more effective inhibition of Akt than either treatment alone. Cancer, 98, 1377–1385. DOI 10.1002/cncr.11656;https://www.ncbi.nlm.nih.gov/pubmed/14508823 [DOI] [PubMed] [Google Scholar]
- Knútsdóttir H., Plsson E. & Edelstein-Keshet L. (2014) Mathematical model of macrophage-facilitated breast cancer cells invasion. J. Theor. Biol., 357, 184–99. DOI 10.1016/j.jtbi.2014.04.031;https://www.ncbi.nlm.nih.gov/pubmed/24810842 [DOI] [PubMed] [Google Scholar]
- Kroemer G. & Pouyssegur J. (2008) Tumor cell metabolism: cancer’s Achilles’ heel. Cancer Cell, 13, 472–482. DOI 10.1016/j.ccr.2008.05.005;https://www.ncbi.nlm.nih.gov/pubmed/18538731 [DOI] [PubMed] [Google Scholar]
- Kumar V. & Gabrilovich D. I. (2014) Hypoxia-inducible factors in regulation of immune responses in tumour microenvironment. Immunology, 143, 512–519. DOI 10.1111/imm.12380;https://www.ncbi.nlm.nih.gov/pubmed/25196648 [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Lee S. T. & Scott A. M. (2007) Hypoxia positron emission tomography imaging with
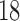 F-fluoromisonidazole. Semin. Nucl. Med., 37, 451–461. DOI 10.1053/j.semnuclmed.2007.07.001;https://www.ncbi.nlm.nih.gov/pubmed/17920352 [DOI] [PubMed] [Google Scholar]
F-fluoromisonidazole. Semin. Nucl. Med., 37, 451–461. DOI 10.1053/j.semnuclmed.2007.07.001;https://www.ncbi.nlm.nih.gov/pubmed/17920352 [DOI] [PubMed] [Google Scholar] - Leek R. D., Lewis C. E., Whitehouse R., Greenall M., Clarke J. & Harris A. L. (1996) Association of macrophage infiltration with angiogenesis and prognosis in invasive breast carcinoma. Cancer Res., 56, 4625–4629. https://www.ncbi.nlm.nih.gov/pubmed/8840975 [PubMed] [Google Scholar]
-
Liu L., Liang Z., Guo K. & Wang H. (2017) Relationship between the expression of CD133, HIF-1
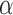 , VEGF and the proliferation and apoptosis in hypoxic human prostate cancer cells. Oncol. Lett., 14, 4065–4068. DOI 10.3892/ol.2017.6726;https://www.ncbi.nlm.nih.gov/pubmed/28943913 [DOI] [PMC free article] [PubMed] [Google Scholar]
, VEGF and the proliferation and apoptosis in hypoxic human prostate cancer cells. Oncol. Lett., 14, 4065–4068. DOI 10.3892/ol.2017.6726;https://www.ncbi.nlm.nih.gov/pubmed/28943913 [DOI] [PMC free article] [PubMed] [Google Scholar] - Macklin P. & Lowengrub J. (2007) Nonlinear simulation of the effect of microenvironment on tumor growth. J. Theor. Biol., 245, 677–704. DOI 10.1016/j.jtbi.2006.12.004;https://www.ncbi.nlm.nih.gov/pubmed/17239903 [DOI] [PubMed] [Google Scholar]
- Mallet D. G. & De Pillis L. G. (2006) A cellular automata model of tumor-immune system interactions. J. Theor. Biol., 239, 334–350. DOI 10.1016/j.jtbi.2005.08.002;https://www.ncbi.nlm.nih.gov/pubmed/16169016 [DOI] [PubMed] [Google Scholar]
- Mantzaris N. V., Webb S. & Othmer H. G. (2004) Mathematical modeling of tumor-induced angiogenesis. J. Math. Biol., 49, 111–187. DOI 10.1007/s00285-003-0262-2;https://www.ncbi.nlm.nih.gov/pubmed/15293017 [DOI] [PubMed] [Google Scholar]
- Marino S., Hogue I. B., Ray C. J. & Kirschner D. E. (2008) A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol., 254, 178–196. DOI 10.1016/j.jtbi.2008.04.011;https://www.ncbi.nlm.nih.gov/pubmed/18572196 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormack D. R., Walsh A. J., Sit W., Arteaga C. L., Chen J., Cook R. S. & Skala M. C. (2014) In vivo hyperspectral imaging of microvessel response to trastuzumab treatment in breast cancer xenografts. Biomed. Opt. Express, 5, 2247–2261. DOI 10.1364/BOE.5.002247;https://www.ncbi.nlm.nih.gov/pubmed/25071962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKenna M. T., Weis J. A., Barnes S. L., Tyson D. R., Miga M. I., Quaranta V. & Yankeelov T. E. (2017) A predictive mathematical modeling approach for the study of doxorubicin treatment in triple negative breast cancer. Sci. Rep., 7, 5725 DOI 10.1038/s41598-017-05902-z;https://www.ncbi.nlm.nih.gov/pubmed/28720897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeown S. R. (2014) Defining normoxia, physoxia and hypoxia in tumours-implications for treatment response. Br. J. Radiol., 87, 20130676 DOI 10.1259/bjr.20130676;https://www.ncbi.nlm.nih.gov/pubmed/24588669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ménard S., Pupa S. M., Campiglio M. & Tagliabue E. (2003) Biologic and therapeutic role of HER2 in cancer. Oncogene, 22, 6570–6578. DOI 10.1038/sj.onc.1206779;https://www.ncbi.nlm.nih.gov/pubmed/14528282 [DOI] [PubMed] [Google Scholar]
- Mitri Z., Constantine T. & O’Regan R. (2012) The HER2 receptor in breast cancer: pathophysiology, clinical use, and new advances in therapy. Chemother. Res. Pract. 2012, 743,193 DOI 10.1155/2012/743193;https://www.ncbi.nlm.nih.gov/pubmed/23320171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murdoch C., Muthana M., Coffelt S. B. & Lewis C. E. (2008) The role of myeloid cells in the promotion of tumour angiogenesis. Nat. Rev. Cancer, 8, 618–631. DOI 10.1038/nrc2444;https://www.ncbi.nlm.nih.gov/pubmed/18633355 [DOI] [PubMed] [Google Scholar]
- Nahta R., Yu D., Hung M. C., Hortobagyi G. N. & Esteva F. J. (2006) Mechanisms of disease: understanding resistance to HER2-targeted therapy in human breast cancer. Nat. Clin. Pract. Oncol., 3, 269–280. DOI 10.1038/ncponc0509;https://www.ncbi.nlm.nih.gov/pubmed/16683005 [DOI] [PubMed] [Google Scholar]
- Nani F. & Freedman H. I. (2000) A mathematical model of cancer treatment by immunotherapy. Math Biosci, 163, 159–199. https://www.ncbi.nlm.nih.gov/pubmed/10701303 [DOI] [PubMed] [Google Scholar]
- Noy R. & Pollard J. W. (2014) Tumor-associated macrophages: from mechanisms to therapy. Immunity, 41, 49–61. DOI 10.1016/j.immuni.2014.06.010;https://www.ncbi.nlm.nih.gov/pubmed/25035953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez E. A., Romond E. H., Suman V. J., Jeong J. H., Sledge G., Geyer C. E., Martino S., Rastogi P., Gralow J., Swain S. M., Winer E. P., Colon-Otero G., Davidson N. E., Mamounas E., Zujewski J. A. & Wolmark N. (2014) Trastuzumab plus adjuvant chemotherapy for human epidermal growth factor receptor 2-positive breast cancer: planned joint analysis of overall survival from nsabp b-31 and ncctg n9831. J. Clin. Oncol., 32, 3744–3752. DOI 10.1200/JCO.2014.55.5730; https://www.ncbi.nlm.nih.gov/pubmed/25332249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pucci F., Venneri M. A., Biziato D., Nonis A., Moi D., Sica A., Di Serio C., Naldini L. & De Palma M. (2009) A distinguishing gene signature shared by tumor-infiltrating Tie2-expressing monocytes, blood “resident” monocytes, and embryonic macrophages suggests common functions and developmental relationships. Blood, 114, 901–914. DOI 10.1182/blood-2009-01-200931;https://www.ncbi.nlm.nih.gov/pubmed/19383967 [DOI] [PubMed] [Google Scholar]
-
Rademakers S. E., Lok J., van der Kogel A. J., Bussink J. & Kaanders J. H. (2011) Metabolic markers in relation to hypoxia; staining patterns and colocalization of pimonidazole, HIF-1
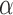 , CAIX, LDH-5, GLUT-1, MCT1 and MCT4. BMC Cancer, 11, 167 DOI 10.1186/1471-2407-11-167;https://www.ncbi.nlm.nih.gov/pubmed/21569415 [DOI] [PMC free article] [PubMed] [Google Scholar]
, CAIX, LDH-5, GLUT-1, MCT1 and MCT4. BMC Cancer, 11, 167 DOI 10.1186/1471-2407-11-167;https://www.ncbi.nlm.nih.gov/pubmed/21569415 [DOI] [PMC free article] [PubMed] [Google Scholar] -
Rajendran J. G., Mankoff D. A., O’Sullivan F., Peterson L. M., Schwartz D. L., Conrad E. U., Spence A. M., Muzi M., Farwell D. G. & Krohn K. A. (2004) Hypoxia and glucose metabolism in malignant tumors: evaluation by
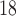 [F]-fluoromisonidazole and
[F]-fluoromisonidazole and 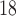 [F]-fluorodeoxyglucose positron emission tomography imaging. Clin. Cancer Res., 10, 2245–2252. https://www.ncbi.nlm.nih.gov/pubmed/15073099 [DOI] [PubMed] [Google Scholar]
[F]-fluorodeoxyglucose positron emission tomography imaging. Clin. Cancer Res., 10, 2245–2252. https://www.ncbi.nlm.nih.gov/pubmed/15073099 [DOI] [PubMed] [Google Scholar] - Raleigh J. A., Calkins-Adams D. P., Rinker L. H., Ballenger C. A., Weissler M. C., Fowler W. C., Novotny D. B. & Varia M. A. (1998) Hypoxia and vascular endothelial growth factor expression in human squamous cell carcinomas using pimonidazole as a hypoxia marker. Cancer Res., 58, 3765–3768. https://www.ncbi.nlm.nih.gov/pubmed/9731480 [PubMed] [Google Scholar]
- Reynolds A., Rubin J., Clermont G., Day J., Vodovotz Y. & Ermentrout G. B. (2006) A reduced mathematical model of the acute inflammatory response: I. Derivation of model and analysis of anti-inflammation. J. Theor. Biol., 242, 220–236. DOI 10.1016/j.jtbi.2006.02.016. [DOI] [PubMed] [Google Scholar]
- Sachs R. K., Hlatky L. R. & Hahnfeldt P. (2001) Simple ODE models of tumor growth and anti-angiogenic or radiation treatment. Math. Comput. Model., 33, 1297–1305. DOI 10.1016/s0895-7177(00)00316-2. [Google Scholar]
- Saidel G. M., Liotta L. A. & Kleinerman J. (1976) System of dynamics of a metastatic process from an implanted tumor. J. Theor. Biol., 56, 417–434. DOI 10.1016/s0022-5193(76)80083-5. [DOI] [PubMed] [Google Scholar]
- Saltelli A. (2002) Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun., 145, 280–297. DOI 10.1016/s0010-4655(02)00280-1. [Google Scholar]
- Schindelin J., Arganda-Carreras I., Frise E., Kaynig V., Longair M., Pietzsch T., Preibisch S., Rueden C., Saalfeld S., Schmid B., Tinevez J. Y., White D. J., Hartenstein V., Eliceiri K., Tomancak P. & Cardona A. (2012) Fiji: an open-source platform for biological-image analysis. Nat. Methods, 9, 676–682. DOI 10.1038/nmeth.2019.https://www.ncbi.nlm.nih.gov/pubmed/22743772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharkey F. E. & Fogh J. (1984) Considerations in the use of nude mice for cancer research. Cancer Metastasis Rev, 3, 341–360. https://www.ncbi.nlm.nih.gov/pubmed/6394126 [DOI] [PubMed] [Google Scholar]
- Sobol’ I.M. (1993) Sensitivity estimates for non-linear mathematical models. Math. Model. Comput. Exp., 1, 407–414. [Google Scholar]
- Sorace A. G., Quarles C. C., Whisenant J. G., Hanker A. B., McIntyre J. O., Sanchez V. M. & Yankeelov T. E. (2016) Trastuzumab improves tumor perfusion and vascular delivery of cytotoxic therapy in a murine model of HER2+ breast cancer: preliminary results. Breast Cancer Res. Treat., 155, 273–284. DOI 10.1007/s10549-016-3680-8;https://www.ncbi.nlm.nih.gov/pubmed/26791520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorace A. G., Syed A. K., Barnes S. L., Quarles C. C., Sanchez V., Kang H. & Yankeelov T. E. (2017) Quantitative [(18)F]FMISO PET imaging shows reduction of hypoxia following trastuzumab in a murine model of HER2+ breast cancer. Mol. Imaging Biol., 19, 130–137. DOI 10.1007/s11307-016-0994-1;https://www.ncbi.nlm.nih.gov/pubmed/27506906 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stamper I. J., Owen M. R., Maini P. K. & Byrne H. M. (2010) Oscillatory dynamics in a model of vascular tumour growth - implications for chemotherapy. Biol. Direct, 5, 1–17. DOI 10.1186/1745-6150-5-27;http://www.biology-direct.com/content/5/1/27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stepanova N.V. (1980) Course of the immune reaction during the development of a malignant tumor. Biophysics, 24, 917–23. [Google Scholar]
- Szymanska Z. (2003) Analysis of immunotherapy models in the context of cancer dynamics. International Journal of Applied Mathematics and Computer Science, 13, 407–418. [Google Scholar]
- Titford M. (2005) The long history of hematoxylin. Biotech. Histochem., 80, 73–78. DOI 10.1080/10520290500138372;https://www.ncbi.nlm.nih.gov/pubmed/16195172 [DOI] [PubMed] [Google Scholar]
- Villasana M. & Radunskaya A. (2003) A delay differential equation model for tumor growth. J. Math. Biol., 47, 270–94. DOI 10.1007/s00285-003-0211-0;https://www.ncbi.nlm.nih.gov/pubmed/12955460 [DOI] [PubMed] [Google Scholar]
- de Visser K. E. & Coussens L. M. (2006) The inflammatory tumor microenvironment and its impact on cancer development. Contrib. Microbiol., 13, 118–137. DOI 10.1159/000092969;https://www.ncbi.nlm.nih.gov/pubmed/16627962 [DOI] [PubMed] [Google Scholar]
- de Visser K. E., Eichten A. & Coussens L. M. (2006) Paradoxical roles of the immune system during cancer development. Nat. Rev. Cancer, 6, 24–37. DOI 10.1038/nrc1782;https://www.ncbi.nlm.nih.gov/pubmed/16397525 [DOI] [PubMed] [Google Scholar]
- Vu T. & Claret F. X. (2012) Trastuzumab: updated mechanisms of action and resistance in breast cancer. Front Oncol., 2, 62 DOI 10.3389/fonc.2012.00062;https://www.ncbi.nlm.nih.gov/pubmed/22720269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker R. & Enderling H. (2016) From concept to clinic: mathematically informed immunotherapy. Curr. Probl. Cancer, 40, 68–83. DOI 10.1016/j.currproblcancer.2015.10.004;https://www.ncbi.nlm.nih.gov/pubmed/26645497 [DOI] [PubMed] [Google Scholar]
- Walsh A. J., Cook R. S., Sanders M. E., Aurisicchio L., Ciliberto G., Arteaga C. L. & Skala M. C. (2014a) Quantitative optical imaging of primary tumor organoid metabolism predicts drug response in breast cancer. Cancer Res., 74, 5184–5194. DOI 10.1158/0008-5472.CAN-14-0663;https://www.ncbi.nlm.nih.gov/pubmed/25100563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh J. C., Lebedev A., Aten E., Madsen K., Marciano L. & Kolb H. C. (2014b) The clinical importance of assessing tumor hypoxia: relationship of tumor hypoxia to prognosis and therapeutic opportunities. Antioxid. Redox Signal., 21, 1516–1554. DOI 10.1089/ars.2013.5378;https://www.ncbi.nlm.nih.gov/pubmed/24512032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weis J. A., Miga M. I., Arlinghaus L. R., Li X., Abramson V., Chakravarthy A. B., Pendyala P. & Yankeelov T. E. (2015) Predicting the response of breast cancer to neoadjuvant therapy using a mechanically coupled reaction-diffusion model. Cancer Res., 75, 4697–4707. DOI 10.1158/0008-5472.can-14-2945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu M., Liu M. Y., Du X. X., Li S. R., Li H., Li X. Z., Li Y., Wang Y., Qin Z. H., Fu Y. X. & Wang S. D. (2015) Instratumoral delivery of IL-21 overcomes anti-HER2/neu resistance through shifting tumor-associated macrophages from M2 to M1 phenotype. J. Immunol., 194, 4997–5006. DOI 10.4049/jimmunol.1402603. [DOI] [PubMed] [Google Scholar]
- Yankeelov T. E., Atuegwu N., Hormuth D., Weis J. A., Barnes S. L., Miga M. I., Rericha E. C. & Quaranta V. (2013) Clinically relevant modeling of tumor growth and treatment response. Sci. Transl. Med., 5 DOI 10.1126/scitranslmed.3005686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yankeelov T. E. & Gore J. C. (2009) Dynamic contrast enhanced magnetic resonance imaging in oncology: theory, data acquisition, analysis, and examples. Curr. Med. Imaging Rev., 3, 91–107. DOI 10.2174/157340507780619179;https://www.ncbi.nlm.nih.gov/pubmed/19829742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yankeelov T. E., Pickens D. R. & Price R. R.. Quantitative MRI in Cancer. Boca Raton, FL: CRC Press, Taylor & Francis Group; (2012). [Google Scholar]
- Yankeelov T. E., Quaranta V., Evans K. J. & Rericha E. C. (2015) Toward a science of tumor forecasting for clinical oncology. Cancer Res., 75, 918–923. DOI 10.1158/0008-5472.can-14-2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


