Improved deep learning-based macromolecules structure classification from electron cryo-tomograms

Abstract

Cellular processes are governed by macromolecular complexes inside the cell. Study of the native structures of macromolecular complexes has been extremely difficult due to lack of data. With recent breakthroughs in Cellular Electron Cryo-Tomography (CECT) 3D imaging technology, it is now possible for researchers to gain accesses to fully study and understand the macro-molecular structures single cells. However, systematic recovery of macromolecular structures from CECT is very difficult due to high degree of structural complexity and practical imaging limitations. Specifically, we proposed a deep learning-based image classification approach for large-scale systematic macromolecular structure separation from CECT data. However, our previous work was only a very initial step toward exploration of the full potential of deep learning-based macromolecule separation. In this paper, we focus on improving classification performance by proposing three newly designed individual CNN models: an extended version of (Deep Small Receptive Field) DSRF3D, donated as DSRF3D-v2, a 3D residual block-based neural network, named as RB3D, and a convolutional 3D (C3D)-based model, CB3D. We compare them with our previously developed model (DSRF3D) on 12 datasets with different SNRs and tilt angle ranges. The experiments show that our new models achieved significantly higher classification accuracies. The accuracies are not only higher than 0.9 on normal datasets, but also demonstrate potentials to operate on datasets with high levels of noises and missing wedge effects presented.

1. Introduction

As the basic unit of life, cell has always been a fundamental focus of biomedical research. Governed by macromolecules, cellular processes occur over a large length scale. To fully understand the biological processes at different levels, it is essential to gain knowledge of native structures and spatial organizations of macromolecular complexes inside single cells. Due to the lack of data acquisition techniques, little has been known about such knowledge due to lack of suitable data acquisition techniques. Recent breakthroughs in Cellular Electron Cryo-Tomography (CECT) imaging technique enables the 3D visualization of macromolecular complex structures and their spatial organizations inside single cells at submolecular resolution and close to their native state [15,19,23,49]. CECT has made possible the discovery of numerous important structural features in prokaryotic cells, eukaryotic cells and viruses [3,11,18,21]. Therefore, CECT emerges as a very promising tool for systematically studying macromolecular complexes with unprecedented coverage, precision and fatality. In principle, a CECT image contains structural information of all macromolecular complexes inside the field of view. However, the systematic recovery of macromolecular structures from CECT is very difficult due to high degree of structural complexity and practical imaging limitations. Specifically, the densely populated cytoplasm makes a very crowded cellular environment for macromolecules. Also, macromolecules are dynamically interacting each other, forming more complex and heterogeneous structures [28]. On the other hand, current technical limitations inherent to the process of structure determination via single-particle cryo-EM require collecting very large datasets often images of several thousands of macromolecules. It would likely require separating and averaging millions of macromolecules represented by subtomograms, potentially containing hundreds of highly heterogeneous structural classes (a subtomogram is a cubic subimage that contains only one macromolecule). Although advances in data acquisition automation make it no longer difficult to acquire CECT images containing such amount of macromolecules, existing computational approaches have very limited scalability and discrimination ability, making them incapable of automatic processing such large amount of data.

Given this challenging task, a number of previous works have been done for analyzing macromolecules from CECT data. In [4,26], template searching-based algorithms were proposed to localize macromolecules of known structures from CECT data. In 2013, Briggs et al. reviewed a number of subtomogram averaging methods to resolve structure of macromolecular complexes in situ [7]. In addition, unsupervised classification-based approaches were also developed (e.g., [2,6,9,32,39]). Even though these methods showed promising macromolecule structure separation and recovery results, the scalability is strictly limited by the intensive computations. Other approaches such as rotation invariant feature [40] and pose normalization [46] were proposed to address the task while reducing the computational complexity. However, these approaches are limited by anisotropic resolution from missing wedge effect, and high level of noise in CECT data.

In order to overcome the limitations mentioned above, recently, we were the first to propose deep learning-based approach [44] for separating particles into structurally homogeneous subgroups through supervised feature extraction using Convolutional Neural Network (CNN). Such approach achieved significantly better separation performance in terms of both accuracy and scalability compared with our previous approaches, showing that deep learning-based approach is potentially a very powerful tool for large-scale particle separation. However, our previous proof-of-principle work is only an initial step toward exploring the full power of deep learning-based large-scale particle separation. The accuracy of classification needs to be substantially improved for better structural reconstruction performance.

In this paper, we focus on improving deep learning-based separation of particles of macromolecular complexes extracted from CECT images by designing new CNN models. The three CNN models we are proposing include: an extended version of (Deep Small Receptive Field) DSRF3D [44], donated as DSRF3D-v2, a 3D residual block-based neural network [20], named as RB3D, and a convolutional 3D (C3D) [36]-based model, CB3D. Our experiment shows that new proposed models can achieve significantly better classification performances than our previous best CNN model proposed in [44]. Among them, CB3D has the best performances and yield accuracy close to 0.9 for normal datasets. Our models also show promising classification performance over datasets of extremely low SNR (0.01).

2. Method

2.1. Convolutional neural networks

Serving as a powerful tool, convolutional deep neural networks have been widely used by researchers to resolve challenging tasks in computer vision especially for image classification. Inspired by biological processes, CNN models are composed of stacked layers including an input, an output and multiple hidden layers, which include convolutional, pooling or fully connected layers. By stacking multiple processing layers, more and more image features are learned and extracted as the training proceeds. More specifically, each convolutional layer contains numerous of filters, considered as neurons with different weights. Neurons in this layer are connected to regions of neighboring neurons in the previous layer, donated as receptive field. For instance, a 1D convolution input x with filter size of 2m + 1 will yield an output $y_i={\sum }_{j=-m}^m{w}_i{x}_{i-j}$, where w_j is the jth weight of the convolutional filter. An activation function is applied after the convolution layer. Some common activation layers include sigmoid, tanh, the rectified linear unit (ReLU) [16], Leaky ReLU [20] and Maxout [17]. These activation functions take the input and perform certain fixed mathematical operations on it. They are used to accelerate the convergence of the optimization process. For example, ReLU is defined as o^ReLU(x) = max(0, x). Next, pooling layers are utilized to reduce the computational costs during the training process by down sampling the data. Two common ways of pooling are calculating the local maximum and average values of the pooling windows. After series of stacked convolutional and pooling layers, a fully connected layer is used to extract more global features. Each unit in fully connected layers, as name suggested, is connected to all units from the previous layer. For instance, given an ith input x_i, the jth output yj is defined as$y_j={\sum }_{i=0}^{n-1}{w}_{ji}{x}_i$, where n is the total number of inputs and wji is the weight between ith input x and jth output y. Sometimes, special techniques such as Dropout [34] and L2 regularization are used to prevent overfitting. Dropout works by simply only keeping a neuron active with some probability p or setting it to zero otherwise during the training process. Lastly, in order to perform the multi-class classification, a softmax activation function is connected to the last fully connected layer to compute a probability of a sample being assigned each class. The softmax function is defined in 1, where $f_j(x)=x^{\text{T}}{w}_j\cdot w_j$ are the weights with jth classand P (j|x) is the probability of the subtomogram is assigned to j class.

$$o_j^{\text{softmax}}(x)=P(j|x)=\frac{{\text{e}}^{f_j}(x)}{{{\sum }_{l=1}^L\text{e}}^{fl}(x)}$$ (1)

The input of this classification problem is a subtomogram X, (i.e., 3D gray scale image of size n₁ × n₂ ×n₃), represented as a 3D array of Rⁿ₁^×n₂^×n₃, and the output label vector L, represented as a 1D array of R^l, where l denotes the number of classes in the dataset. The algorithm aims at classifying subtomograms into the correct class, that is, mapping X to l correctly.

Designing CNN architectures and tuning parameters are essential for the performance of networks. In 2012, Krizhevsky et al. proposed a novel CNN architecture AlexNet [22], which was the first to show a significant improvement of image classification results on a historically difficult dataset, ImageNet [31]. From that on, CNNs have become a household name in computer vision computer community. In recent years, more advanced CNN architectures were proposed and developed such as GoogleNet [35], ResNet [20] and VGGNet [33]. These networks gradually pushed the classification error rate on ImageNet down to 3.6% [20].

In this paper, we propose three different CNN models and comparing them with our previously proposed approaches in [44].

All the models are trained using stochastic gradient descent (SGD) optimizer. We minimize the categorical cross-entropy cost function by adding Nesterov momentum of 0.9. Momentum update [30] is an update approach that often has better converge rates while using gradient descent on deep network optimization. With momentum update, the parameter vector will build up velocity in any direction that has consistent gradient. Nesterov momentum [24] is a slightly different version of the momentum update that enjoys stronger theoretical converge guarantees for convex functions and in practice it also consistently works slightly better than standard momentum. The main difference is in classical momentum it first corrects the velocity and then makes a big step according to that velocity, but in Nesterov momentum it first makes a step into velocity direction and then is corrected to a velocity vector based on new location. Previous work [24] mathematically proves that Nesterov momentum has a better convergence rate in optimization. In addition, the initial learning rate is set at 0.005 with a decay factor of 1e ‒7. The training processes are performed with a batch size of64 for 20 epochs. However, for each dataset, if the classification performance shows no improvement over 5 consecutive epochs based on the loss function, the training process will end early.

2.1.1. DSRF3D-v2 model

In this section, we propose a 3D variant VGGNet [33]-based CNN architecture called Deep Small Receptive Field (DSRF3D). This model is an extended version of our previously proposed model [44], and we donate this model as DSRF3D-v2. Just like a VGGNet, DSRF3D-v2 is featured with sequentially deep stacked layers and small 3D convolution filters with size of 3 × 3×3. As shown in Fig. 1, the input layer is sequentially connected three sets of stacked layers, with each set consisting of 2 3 × 3 × 3 3D convolutional layers and one 2 × 2 × 2 3D pooling layer. Then, it is followed by two fully connected layers with 70% dropout after each layer. The final fully connected output layer has the same number of units as the structure class number. The activation layers are ReLU for all hidden layers and softmax for fully connected layers. Compared to previously designed DSRF3D model, adding more stacked layers with appropriate dropouts should improve the classification performance intuitively.

Fig. 1.

DSRF3D-v2 model: Each box provides configurations for each layer. ‘32−3×3×3−1 Conv’ represents a 3D convolutional layer with 32 5×5×5 filters and stride of 1. ‘ReLU’ and ‘Softmax’ are activation layers. ‘2×2 2–1 MaxPool’ means that max operation is implemented over 2×2×2 regions with stride of 2’. ‘FC-1024’ and ‘FC-L’ represents fully connected layers with 1024 and L(total number of the classes) neurons, respectively

2.1.2. RB3D model

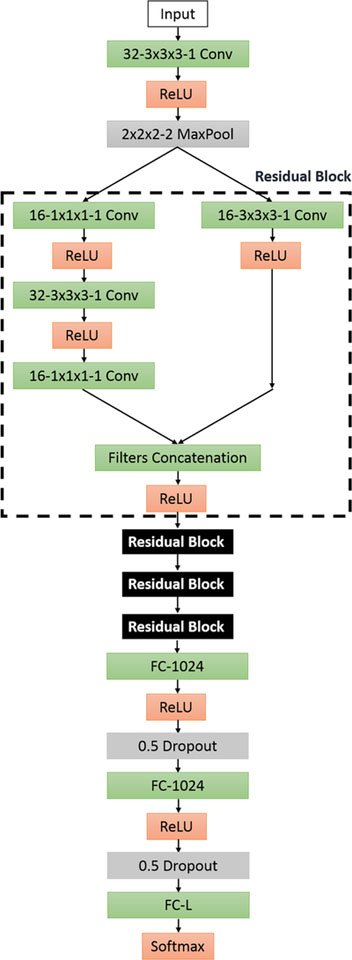
In this section, a 3-D variant residual block-based [20] CNN model is proposed, donated as RB3D. One big advantage for ResNet-based model is that it avoids negative outcomes while increasing the network overall depth. As shown in Fig. 2, this model feeds the input layer to a convolutional layer, a ReLU activation layer and a 2 × 2×2 3D max-polling layer. Then, four bottleneck [20] residual blocks are connected sequentially. For each block, there are two paths that merge together at the end of the block. One path contains one 1×1 layer to reduce dimension, a 3×3 layer and a 1 × 1 layer for restoring dimension. The other path, considered as a “shortcut”, only contains a 3×3 convolutional layer. Lastly, two fully connected layers are constructed with dropout of 50% to prevent overfitting. The usage of residual blocks might lead to higher classification accuracy.

Fig. 2.

RB3D model: each box provides configurations for each layer. The definition of the boxes follows Fig. 1. Four residual blocks are connected, represented by the black boxes. The specific design for a single residual block is shown in the dashlined box

2.1.3. CB3D model

In this section, we propose a 3D convolutional (C3D)-based model, named as CB3D. C3D [36] was originally proposed to be trained on large-scale supervised video datasets. We can think of the 3D structures of macromolecules as multiple slices of 2D images. If we look from the first slice to the last slice, we can interpret it as a continuously changing object just like a video dataset. In our model shown in Fig. 3, we concatenate eight 3D 3 × 3 × 3 convolutional layers and each layer is activated by ReLU. Five max pooling layers are mixed among the convolutional layers. At end, two fully connected layers with 50% dropout are added and a softmax activation is appended.

Fig. 3.

CB3D model: each box provides configurations for each layer. The definition of the boxes follows Fig. 1. Note that ‘1×2 2− (1)2 MaxPool’ means that the max operation is implemented over region of 1×2×2. The stride is 1 for the first dimension and 2 for the others

2.2. Generation of simulated subtomograms from experimental structures

Similar to previous works [4,12,25,29,39,39,42–45,48], we use known structures of macromolecular complexes to generate simulated subtomograms by simulating actual tomographic image reconstruction processes in order to have a reliable assessment of our proposed approaches. There are three significant aspects we focus on when simulating the subtomograms: missing wedge effects, noises and electron optical factors such as modulation transfer function (MTF) and contrast transfer function (CTF).

The contrast transfer function (CTF) mathematically describes how aberrations in a transmission electron microscope (TEM) modify the image of a sample. By considering the recorded image as a CTF-degraded true object, describing the CTF allows the true object to be reverse engineered. This is typically denoted CTF-correction, and is vital to obtain high resolution structures in three-dimensional electron microscopy, especially cryo-electron microscopy. Its equivalent in light-based optics is the optical transfer function (OTF). A typical CTF is of the following form (Eq.2.20 of [13]):

$$\text{CTF}(\widehat{k};\mathrm{\Delta }\widehat{z})=\text{sin}\left[-\pi \mathrm{\Delta }\widehat{z}\mathrm{\Delta }{\widehat{k}}^2+\frac{\pi }{2}{\widehat{k}}^4\right]$$ (2)

where ẑ and $\widehat{k}$ are generalized defocus and spatial frequency, respectively.

The modulation transfer function (MTF) is a variant of the optical transfer function (OTF), neglecting phase effects. The resolution and performance of an optical microscope can be characterized by a MTF, which is a measurement of the microscope’s ability to transfer contrast from the specimen to the intermediate image plane at a specific resolution. Computation of the modulation transfer function is a mechanism that is often utilized by optical manufacturers to incorporate resolution and contrast data into a single specification.

More specifically, we first generate density map volumes of 40³ voxels with a resolution of 0.92 nm using the PDB2VOL program from the Situs [38] package. The density map volumes are generated by convoluting the atomic structures with a Gaussian kernel, whose standard deviation is assumed to be half the target resolution. We then randomly rotate and translate the volumes. Next, we generate projection images of the density maps with different tilt angles to simulate missing wedge effects. The specific tilt angle ranges are ± 60°,± 50° and ±40°. We then convolute the projection images CTF and MTF [13,25] to reproduce the electron optical effects to generate simulated electron micrographic images. Then, the simulated noises are added to electron micrographic images [12] with desired signal-to-noise ratio (SNR) levels so that the SNR of reconstructed subtomograms are of 0.1, 0.05, 0.03 and 0.01. The acquisition parameters are set similar to [47], with spherical aberration of 2 mm, defocus of −5μm and voltage of 300kV. Finally, with all gathered information, we construct the simulated subtomogram datasets using a direct Fourier inversion reconstruction algorithm implemented in the EMAN2 library [14]. Figure4 shows an example of center slices of simulated subtomograms with different SNRs and tilt angle ranges.

Fig. 4.

Left: Isosurface of Yeast 20S proteasome (PDB ID: 3DY4); Right: Center slices of subtomograms with different levels of SNRs(0.5, 0.1, 0.05 and 0.01) and tilt angle ranges(± 60°, ± 50° and ± 40°)

We construct a simulated dataset for each pair of SNRs(4) and tilt angle ranges(3), which yields 12 sets of data in total. Within a single dataset, for each macromolecular complex, we generate 1000 simulated subtomograms that contain randomly rotated and translated particle of that complex. There are 22 macromolecular complexes collected from the Protein Databank (PDB) [5] shown in Fig. 5. Furthermore, we simulate 1000 subtomograms that contain no macromolecule. As an outcome, each dataset contains 23,000 simulated subtomograms of 23 structural classes.

Fig. 5.

Isosurfaces of all 22 types of macromolecular complexes collected from the Protein Databank (PDB), denoted with PDB ID

To fully evaluate classification performances, we first split each dataset into two parts: 80% are used as training data, and 20% are used as testing data. Then, we take 20% of the training data and use it as validation data for parameter tuning during training process, and the rest 80% for training weights. Therefore, we end up with 14,720 training samples, 3680 validation samples and 4600 testing samples. We use the same partitioned datasets across all models to have a fair comparison on their classification performance.

2.3. Implementation details

This work is implemented using Keras [10] with Tensorflow [1] as back-end. Keras is a python-based, high-level neural networks API for fast deep learning experimentation. The experiments are performed on a computer with three Nvidia GTX 1080 GPUs, one Intel Core i7–6800K CPU and 128GB memory. The new proposed models are implemented with the same system as our previously proposed model [44]. For the baseline methods, the rotation invariant features is computed based on SHTools [37]. K-means clustering and support vector machine (SVM)-based supervised multi-class classification are implemented using the Sklearn toolbox [27].

3. Experiment results

3.1. Classification performance

In this section, we compare the classification performance of new CNN models (DSRF3D-v2, RB3D and CB3D) with our previously proposed best model DSRF3D [44], as well as a baseline method on datasets with different SNRs and tilt angles ranges. The baseline method uses spherical harmonics rotation invariant feature [41,43] with SVM using Radial Basis function kernel, denoted as RIF-SVM. The results are shown in Table1. The best performances for each pair of imaging conditions are highlighted in bold. In general, our new proposed CNN models demonstrate significant improvements in classification performance. As shown, the best performance is achieved by newly designed models in all 11 out of 12 situations. The only exception that new models perform worse than previous models (DSRF3D and RIFSVM) is with tilt angle ranges of ± 50° and SNR of 0.001. Given such poor qualities of images, the “best” performance is only around 0.2, which is still considered as bad performance.

Table 1.

The classification accuracy using four CNN models under different SNR and tilt angles

SNR/tilt angle range	±60°					±50°					±40°
	RIF-SVM	DSRF3D	DSRF3D-v2	RB3D	CB3D	RIF-SVM	DSRF3D	DSRF3D-v2	RB3D	CB3D	RIF-SVM	DSRF3D	DSRF3D-v2	RB3D	CB3D
0.1	0.790	0.911	0.977	0.950	0.973	0.672	0.896	0.963	0.925	0.971	0.670	0.868	0.954	0.899	0.970
0.05	0.620	0.844	0.925	0.852	0.933	0.493	0.753	0.910	0.750	0.899	0.495	0.735	0.876	0.671	0.877
0.03	0.479	0.706	0.841	0.711	0.849	0.350	0.581	0.746	0.548	0.747	0.360	0.537	0.038	0.502	0.717
0.01	0.218	0.040	0.407	0.041	0.445	0.153	0.200	0.041	0.042	0.041	0.162	0.043	0.043	0.171	0.041

When comparing among the three new models, we can observe that RB3D often ends up with lower accuracy than DSRF3D-v2 and CB3D. In fact, RB3D establishes obvious improvements (greater than 0.3) only with SNR of 0.1. In situations with low SNRs, RB3D does not show apparent improvement and it performs even worse than DSRF3D. Therefore, the RB3D model is not robust to image noises. In general, residual block structures are proposed and proved to work the best with very deep neural network structures [20]. We also tested increasing the depth of RB3D model by adding one more residual block and train the new structure on three datasets with SNR of 0.01. The accuracies using 5 residual blocks structures are 0.247, 0.042 and 0.171, compared to0.041, 0.042 and 0.171 when using 4 residual blocks. This exploration shows that there is not clear pattern of classification performance improvement when increasing the depth of RB3D. Thus, further study on improving classification performance through increasing depth or modifying residual block internal structure remains open.

In contrast, both DSRF3D-v2 and CB3D show essential accuracy increases in most cases. With SNR of 0.01 and tilt angles of ± 60°, both models can remarkably achieve accuracy greater than 0.4. Even though 0.4 is still not considered as high classification accuracy in Table 1, it at least shows the capability of deep learning to classify a large amount of subtomograms with extremely poor image quality.

DSRF3D-v2 and CB3D generate very similar results, usually with differences less than 0.1. It is proved that both model can accurately classify subtomograms even with much noises and missing wedge effects presented. CB3D is slightly better than DSRF3D-v2 because it achieves the best performance in 8 out of 12 datasets. With SNR of 0.03 and tilt angle ranges of ± 40°, CB3D can still obtain classification accuracy higher than 0.7, which is a very good performance if we consider the poor image qualities.

In addition, we also evaluate the computation time. On average, it takes 0.0056, 0.0083, 0.0141 and 0.0136s for DSRF3D, DSRF3D-v2, RB3D and CB3D, respectively, to process one subtomogram for each epoch during training process. In testing process, it takes 0.0019, 0.0027, 0.0026 and 0.0040s for DSRF3D, DSRF3D-v2, RB3D and CB3D, respectively, to process one subtomogram. Thus, compared to previous model (DSRF3D), our new proposed models cost48.21–151.79% more time for training and 36.84–110.53% more time for testing. Further work can be done to speed up our new deep learning models.

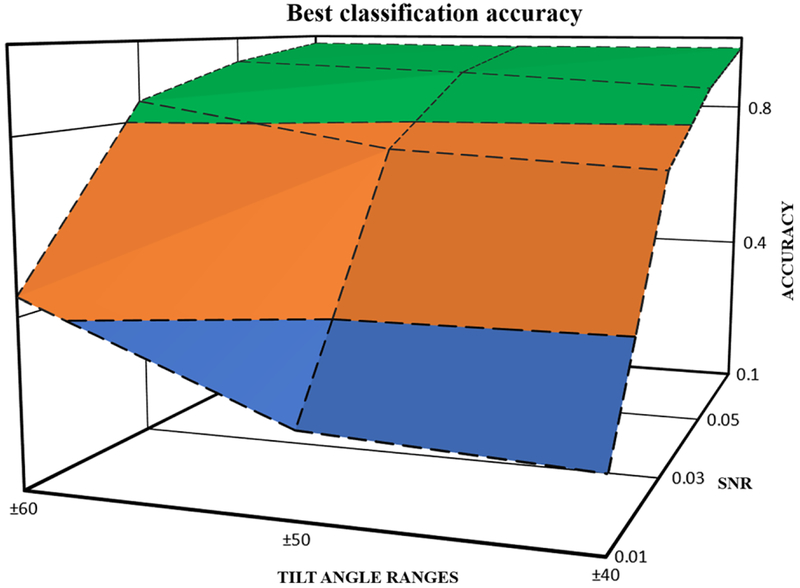
3.2. Classification capability

In this section, we examine the capability of deep learning to classify large-scale datasets of subtomograms. We first extract the the best performance for each of the 12 datasets and then plot the highest accuracy with respect to both SNRs and tilt angle ranges. The 3D surface is plotted in Fig. 6. As shown, the classification accuracy decreases as more noises are added to the dataset for all tilt angles. Similarly, for all SNRs, the accuracy will reduce if tilt angle ranges decrease from ± 60° to ± 40°. Based on the plot, we can observe that for datasets whose SNRs are above or equal to 0.05, our best model can achieve classification accuracy no lower than 0.877. For datasets with poor image qualities, as long as SNR is kept above 0.03, classification can achieve higher than0.7 for all 3 tilt angle ranges. It is proven that our proposed approach has strong abilities to accurately classify macro-molecular structures from CECT images and even greater potentials to process datasets with extremely high level of noises and missing wedge effects.

Fig. 6.

The highest classification accuracy with respect to different SNRs and tilt angle ranges

4. Conclusions

In this paper, three novel CNN models are proposed to significantly improve deep learning-based separation of macromolecules extracted from CECT images. We compare them with our previously proposed model and our best model CB3D ends up with classification accuracy of approximately 0.85 for image datasets with relatively low noise level. More importantly, it demonstrates good potentials to operate on datasets with extremely poor image qualities. After successfully and efficiently subdividing the subtomograms, the computationally intensive reference-free approaches can be applied to selected subsets separately in order to recover the structure of macromolecular complexes. The overall computational cost can be greatly reduced through such divide and conquer approach. This proof-of-principle work represents a useful step toward full systematic structural separation and recovery of millions of macromolecules extracted from CECT images.

Recently, deep learning has also been used for analyzing CECT by other groups, for example [8]. There are several major differences between our approaches and the approach in [8]. (1) We focus on the recovery of macromolecular complexes captured by CECT, instead of supervised segmentation of ultrastructures as in [8]. (2) Because the macromolecules can have arbitrary orientation in a CECT image, our models aim at learning the rotational invariant features. We used 3D filters instead of 2D filters as in [8], so that our CNN models can isotropically capture the inherent 3D spatial structure in such 3D images.

Biography

Chengqian Che received an M.Sc. degree in Biomedical Engineering from Carnegie Mellon University (CMU) and a B.S. degree in Biomedical Engineering from University of Connecticut. He is currently pursuing his Ph.D. in Robotics at CMU. His current research focus is on differentiable rendering and computational imaging.

Ruogu Lin received B.E. degree in Automation from Tsinghua University, China, in 2018. He is pursuing his Ph.D. degree at Department of Computational Biology, Carnegie Mellon University, USA. His research focus is on computer vision and data-driven methods in computational analysis of cellular electron cryotomography.

Xiangrui Zeng received B.S. degree in Neuroscience from University of Pittsburgh, USA, in 2017. He is currently pursuing his Ph.D. degree at Department of Computational Biology, Carnegie Mellon University, USA. His research focus is on computational analysis of cellular electron cryotomography using computer vision techniques.

Karim Elmaaroufi received a B.S. and M.S. in Electrical and Computer Engineering from Carnegie Mellon University (CMU). His academic focus is on the design of embedded systems.

Dr. John Galeotti is a Systems Scientist and Adjunct Assistant Professor at Carnegie Mellon University (CMU), directing the Biomedical Image Guidance Laboratory. He received a Ph.D. in Robotics at CMU and a B.S. and M.S. in Computer Engineering at North Carolina State University. Dr. Galeotti’s research focus is on applying novel, real-time computer-controlled optics, image analysis, and visualization approaches to build and control unique experimental systems for image-guided interventions, diagnosis, and biomedical research.

Dr. Min Xu is an Assistant Research Professor at the Computational Biology Department in the School of Computer Science at Carnegie Mellon University. He received a B.E. in Computer Science from the Beihang University, M.Sc. from School of Computing at the National University of Singapore, M.A. in Applied Mathematics from the University of Southern California (USC), and Ph.D. in Computational Biology and Bioinformatics from USC. He was a postdoctoral researcher at USC. Dr. Xu’s career has centered on developing computational methods for the study of cellular systems using imaging and omics data.