Automated 4π radiotherapy treatment planning with evolving knowledge‐base

Abstract

Purpose

Non‐coplanar 4π radiotherapy generalizes intensity modulated radiation therapy (IMRT) to automate beam geometry selection but requires complicated hyperparameter tuning to attain superior plan quality, which can be tedious and inconsistent. In this study, a fully automated 4π treatment planning was developed using evolving knowledge‐base (EKB) planning guided by dose prediction.

Methods

Twenty 4π lung and twenty 4π head and neck (HN) cases were included. A statistical voxel dose learning model was initially trained on low‐quality plans created using generic hyperparameter templates without manual tuning. To improve the automated plan quality without being limited by the training data quality, a new 4π optimization problem was formulated to include a one‐sided penalty on the organ‐at‐risk (OAR) dose deviation from the predicted dose. This directional OAR penalty encourages superior OAR sparing. The fast iterative shrinkage‐thresholding algorithm (FISTA) was used to solve the large‐scale beam orientation optimization problem. With the improved plans, new predictions were created to guide the next loop of EKB planning for a total of 10 loops. Plan quality was evaluated using a plan quality metric (PQM) points system based on clinical dose constraints and compared with automated planning approaches guided by manual high‐quality plans using all non‐coplanar beams, automated plans using individually evolved targeted dose, and manually created 4π plans.

Results

For the lung cases, the final EKB plans had significantly higher PQM than manually created 4π (+2.60%). The improvements plateaued after the third loop. The final HN EKB plans and manually created 4π plans had comparable PQMs, but had lower PQM compared to automated plans using a high‐quality training set (−3.00% and −4.44%, respectively). The PQM consistently increased up to the sixth loop. Individually evolved plans were able to improve the plan quality from initial condition due to the one‐sided cost function but the 60% of them were trapped in undesired local minima that were substantially worse than their corresponding EKB plans.

Conclusion

Evolving knowledge‐base planning is a novel automated planning technique guided by the predicted three‐dimensional dose distribution, which can evolve from low‐quality plans. EKB allows new beams to be used in the automated planning workflow for superior plan quality.

1. Introduction

Intensity modulated radiation therapy (IMRT) treatment planning involves complex optimizations that not only require numerous hours of tedious work, but can also potentially create suboptimal and inconsistent plans.^{1, 2, 3, 4} Delivering the prescription dose to the tumor while minimizing dose to all normal tissue is not a simple problem. Critical structures have different radiobiological properties and priorities that each need to be considered when creating a treatment plan. Furthermore, anatomical geometry limits the possible extent of dose sparing when prioritizing delivery of the full prescription dose to the tumor. Because of these factors, the treatment planning process involves laborious tuning of parameters to satisfy clinical constraints, often taking hours or longer to plan each case. Moreover, manual treatment plan quality is dependent on the planner experience and the oncologist’s expectation, leading to inconsistent planning quality.

To address this problem, researchers developed knowledge‐based planning (KBP) dose prediction to provide patient‐specific guidance for treatment planning.^{5, 6, 7, 8, 9, 10, 11} Typical KBP methods use geometrical features of prior cases to create a model that can predict dose using the geometrical features of a new patient. Therefore, it not only individualizes the prediction but also propagates the implicit planning priorities from previously accepted plans to the new plan. Reported implementations of KBP have successfully used dose–volume constraints taken from predicted dose–volume histograms to create plans.^{12, 13} Automated planning is also actively being developed that utilize KBP dose predictions to reduce the need for tedious manual planning.^{12, 13, 14, 15} To maximize the efficacy of KBP, accurate dose predictions require numerous plans of high‐quality for training.

As an advanced type of IMRT, 4π radiotherapy utilizes optimized non‐coplanar beam orientations to improve dose conformity and organ‐at‐risk (OAR) sparing.^{16, 17, 18, 19, 20, 21} However, to achieve the dosimetric benefit, 4π planning still requires the tedious and inconsistent process of manually tuning hyperparameters, hampering its wide clinical adoption. The unconventional planning process also precludes the availability of a large dataset of high‐quality 4π plans. Therefore, there is a clear benefit to fully automate 4π planning guided by KBP. To further reduce the dependence on a set of high‐quality manually created plans, the fully automated method should be able to evolve a knowledge base that initially consists of lower quality plans.

4π radiotherapy is still in the early stages of clinical adoption, with the majority of 4π plans planned retrospectively for dosimetric studies of limited treatment sites as opposed to clinical plans. The purpose of this study is to automate 4π planning using KBP dose prediction methods while overcoming the lack of large, high‐quality training sets for many sites.

Although automated planning methods have been reported to result in plans at least equivalent in quality to manual planning, the process of mimicking dose‐volume‐histogram (DVH) parameter tuning limits the search space, which leaves room for improvement.²² In this study, to overcome this challenge, our approach utilizes predicted three‐dimensional (3D) voxel doses to guide the automated planning optimization with a novel objective function free of the structure DVH optimization parameters. This study aims to demonstrate the feasibility of not only automated 4π treatment planning but also KBP‐based automated planning when high‐quality training sets are available.

2. Materials and Methods

In total, 20 patients with lung cancer and 20 patients with head and neck (HN) patients were enrolled for the automated planning study under an Institutional Review Board approved protocol. Centrally located lung plans and oropharyngeal HN cases were selected for more consistent OAR constraints in each cohort. The cohort size was chosen based on the practical consideration of computational time to demonstrate feasibility. Evolving knowledge‐base (EKB) planning requires automated plan generation of each case before proceeding to the next loop, so cohorts that are too large would be computationally difficult. Although larger datasets can improve the prediction accuracy, and subsequently plan quality, the current training size is shown adequate for achieving acceptable prediction quality to guide the treatment planning.¹¹

The EKB planning workflow is shown in Fig. 1. The process begins with an initial set of 20 plans generated from a generic template where all OAR weightings are set equally, with a desired dose of zero for all OAR voxels. For each of the 20 cases, training sets are made on a leave‐one‐out basis that is training set size of 19 patients for prediction of each patient, for predictions generated using statistical voxel dose learning (SVDL), a KBP method¹¹ (Section 2.A.). The predictions are used in one loop of the automated 4π planning process (Section 21.C.). After automatically creating plans for the 20 patients, they are evaluated using a plan quality metric (Section 22.D.) to determine if there is any improvement on the initial set of plans. The next loop’s training set is then comprised of the plans with highest plan quality metric for each of the 20 patients. This method requires that the automated plans for the whole cohort be completed before beginning the next loop. A total of 10 loops were performed.

Figure 1.

Flowchart of the evolving knowledge‐base framework for automated planning. The initial plans use a generic hyperparameter template to jump‐start the EKB planning. In this study, this process was performed for 10 loops (shown in blue). FISTA iterations within each automated planning optimization are shown in orange. FISTA, fast iterative shrinkage‐thresholding algorithm. [Color figure can be viewed at wileyonlinelibrary.com]

2.A. Knowledge‐based dose prediction

In each loop of this EKB framework, a leave‐one‐out scheme was used to predict the dose of each of the 20 lung or HN patients, resulting in training set sizes of 19 patients. Predictions were performed using SVDL, a KBP method that has been demonstrated to be fast and accurate with small training sets.^{7, 11} SVDL sorts each OAR voxel from the training set into bins according to their Euclidean distance to the planning target volume (PTV). The median for each distance bin is taken as the predicted value for new OAR voxels of the same PTV distance.

SVDL was chosen after a 3D dose prediction accuracy comparison study with supervised machine learning regressions, spectral regression (SR), and support vector regression (SVR). The lung and HN patients used in Landers et al use the same patient data.¹¹ For predictions using the lung and HN cohorts in k‐fold cross‐validation, with k = 4, the root mean squared error for voxel dose prediction was lowest with SVDL (2.49 Gy lung and 3.91 Gy HN).

2.B. Manual 4π planning

Manual 4π planning is performed by tuning the OAR weighting hyperparameter $\beta$ and solving.

$$\begin{array}{c}\underset{x}{\text{minimize}}\underset{\text{PTV}}{\underbrace{\frac{1}{2}|{\left(l-A_{0}x\right)}_{+}{|}_2^2+\frac{1}{2}{|{\left(A_{0}x-d\right)}_{+}|}_2^2}}\\ +\underset{\text{OARs}}{\underbrace{\sum _{i=1}^N\frac{{\beta }_i}{2}{|A_{i}x|}_2^2}}+\underset{\text{smoothness}}{\underbrace{{\gamma |\mathit{Dx}|}_1^{\left(\mu \right)}}}+\underset{\text{group sparsity}}{\underbrace{\sum _{b=1}^B{\omega }_b{|x_b|}_2^{1/2}}}\\ \text{subject to}x\ge 0,\\ \end{array}$$ (1)

where:

• ‐The vector $x_b$ contains the beamlet intensity values for candidate beam $b$. The optimization variable $x$ is the concatenation of the vectors $x_b$ for the candidate pool of $B$ beams.
• ‐The matrices $A_i$ are the dose calculation matrices for the PTV ($i=0$) and OARs ($i=1,\dots ,N$) at 2.5 × 2.5 × 2.5 mm³ resolution. The 5‐mm beamlet dose is calculated with convolution/superposition using a 6‐MV kernel.²³
• ‐ $l$ is the prescription dose vector, with an element for each PTV voxel.
• ‐The vector $d$ stores the maximum dose for each voxel in the PTV.
• ‐The matrix $D$ is a discrete gradient operator, such that $\mathit{Dx}$ represents the intensity differences between adjacent beamlets.
• ‐ $\gamma$ and ${\omega }_b$ weight the respective smoothness and group sparsity terms.
• ‐ ${|·|}_2$ represents the $l_2$‐norm.
• ‐The function ${|·|}_1^{\left(\mu \right)}$ is the Huber penalty, and $\mu$ controls the level of smoothing on the $l_1$‐norm.

The PTV and OAR terms encourage sufficient PTV coverage while minimizing OAR dose. The smoothness term promotes smooth fluence maps to reinforce deliverability by multileaf collimators. The group sparsity term performs the actual beam angle selection by encouraging most candidate beams to be zero. The group sparsity weighting parameter ${\omega }_b$ was set to allow approximately 20 remaining beams to be selected. The optimization can converge before the number of beams is reduced to 20. If there are over 20 selected beams, k‐means clustering of the gantry and couch angles is used to identify 20 clusters of beams. If a cluster has more than one beam, we select the beam that is closest to the mean of the cluster, breaking ties arbitrarily. This ensures that each plan results in 20 beams. The deliverability of 4π plans using 20 non‐coplanar beams has been demonstrated in a prospective clinical study.²⁴

The 4π optimization problem is solved using the fast iterative shrinkage‐thresholding algorithm (FISTA), which can handle nondifferentiable penalty terms and nonnegativity constraints efficiently.²⁵ FISTA is an accelerated proximal gradient method, which utilizes proximal operators (prox‐operators) to solve the optimization problem as described by Beck and Teboulle.²⁵

2.C. Automated 4π planning

To remove the need for hyperparameter tuning, the vectors of predicted voxel dose for the $i^{\text{th}}$ OAR, ${\widehat{d}}_i$, are used in one loop of automated 4π planning, which is performed by using FISTA to solve.

$$\begin{array}{c}\underset{x}{\text{minimize}}\underset{\text{PTV}}{\underbrace{\frac{1}{2}|{\left(l-A_{0}x\right)}_{+}{|}_2^2+\frac{1}{2}{|{\left(A_{0}x-1.05l\right)}_{+}|}_2^2}}\\ +\underset{\text{OARs}}{\underbrace{\sum _{i=1}^N\frac{1}{2}{|{\left(A_{i}x-{\widehat{d}}_i\right)}_{+}|}_2^2}}+\underset{\text{smoothness}}{\underbrace{{\gamma |\mathit{Dx}|}_1^{\left(\mu \right)}}}+\underset{\text{group sparsity}}{\underbrace{\sum _{b=1}^B{\omega }_b{|x_b|}_2^{1/2}}}\\ \text{subject to}x\ge 0.\\ \end{array}$$ (2)

This objective automatically encourages the PTV voxel dose to be within 100%–105% of the prescription dose, $l$, rather than a user‐defined maximum dose, $d$. The OAR term in equation (1) penalized OAR voxels based on their entire received dose and weighed them based on the user‐defined hyperparameter $\beta$. For the revised automated planning objective, $\beta$ was set to 1 for all OARs so that there is no dependence on manually tuned hyperparameters. The new one‐sided OAR penalty only penalizes voxels if the dose is over the predicted voxel dose, which allows OARs to neutrally weigh themselves based on their proximity to the predicted dose. This enables automated plans to systematically attain better or equivalent dosimetry compared to the training set. The superior plans will be used to provide predictions in the next loop to evolve the knowledge base. $\gamma$ was set to 1 and ${\omega }_b$ was set to 16 and 30 for lung and HN, respectively. These values were chosen empirically when manually planning but fixed for all EKB plans to attain similar fluence map smoothness and number of beams.

2.D. Plan quality metric

For EKB planning to automatically select a superior plan, it is necessary to quickly quantify the plan quality. The plan quality metric, introduced by Nelms et al,³ scores the plan quality based on a list of dosimetric criteria. The scoring criteria for our lung and HN PQM are shown in Table 1, using the clinical dose constraints from our institution as well as additional PTV and conformity constraints. Scores are linearly interpolated between the minimum and maximum dosimetric value of each criterion, while zero and the maximum are given to scores that are below and above the range, respectively. Minimum and maximum dosimetric values were chosen such that a realistic plan would not attain 100% in all criteria, allowing for a larger dynamic range and plan quality differentiation. PQM is unitless, not normalized, and only meant to compare plans of the same disease site. It is important to note that PQM itself is non‐convex and incompatible with the FISTA optimization framework that makes fast automated 4π planning possible. Directly using PQM in the cost function will require the structure weight tuning that we aim to eliminate in automated planning. In this way, PQM is only used as an evaluation tool to select the highest quality plans at each loop.

Table 1.

Plan quality metric (PQM) criteria for HN and lung plans.

Head and Neck	0 score	Perfect score	Points	Lung	0 score	Perfect score	Points
D95/ presDose	0.95	1	15	D98	42.5	50	10
D98/ presDose	0.925	0.975		HI (D95/D5)	0.85	0.95	3
D99/ presDose	0.9	0.95		Esophagus V10	10	0	3
HI (D95/D5)	0.85	0.95	5	Esophagus V5	13	0	3
Cord max	45	10	3	Trachea V10	13	0	3
Cord V40	20	0	3	Trachea V5	18	0	3
Brainstem max	50	5	3	Bronchus V20	10	0	3
Brainstem mean	20	1	3	Bronchus V15	15	0	3
Parotids mean	26	1	3	Heart V20	18	0	3
Parotids V30	50	0	3	Heart V15	33	0	3
Pharynx mean	54	5	3	Lung V20	20	0	3
Pharynx V45	33	0	3	Lung V10	30	0	3
Larynx mean	35	1	3	Lung V5	40	0	3
Larynx V66%	50	0	3	Skin V20	30	0	3
Oral cavity mean	40	5	3	Skin V15	20	0	3
SMG max	50	15	3	Cord V10	1	0	3
SMG mean	35	1	3	Cord V5	8	0	3
Mandible max	70	40	3	R50	3.5	1.8	10
Mandible V66	1	0	3	R10	50	20	5
Lips mean	30	1	3	D0.1cc	60	53	5
CPI mean	45	1	3
TMJ max	70	5	3
Cochleas mean	35	1	3
Esophagus mean	35	1	3
Orbits mean	25	1	3
Lens max	10	1	3
Opap max	52	1	3
R50	2	1.4	4
R10	10	4	4
D0.1cc/ presDose	1.2	1.05	3

The second and third columns specify the min or max dosimetric value required to get a zero or perfect score. The full points allowed for each criterion is listed in the fourth column. SMG: submandibular glands, CPI: cricoid pharyngeal inlet, TMJ: temporomandibular joints, Opap: optical apparatus; HN, head and neck.

2.E. Plan quality comparison

A final plan quality comparison was performed between:

1. EKB — Final EKB 4π plans after 10 loops.

2. autHQ — Automated 20‐beam 4π plans created with a single loop of automated 4π planning using a training set of unrealistic “ultimate” plans. This training set consisted of high‐quality, individually tuned 4π plans with manual parameter tuning using all non‐colliding non‐coplanar beams, which can range from 300 to 700 beams, depending on the treatment site. The “ultimate” plans were only used as training sets and not in the final analysis.

3. Individually Evolving (IE) — Automated 20‐beam 4π plans created by performing the EKB process for a single patient at a time, where the desired dose, ${\widehat{d}}_i$ in equation (2), is simply the patient’s dose from whichever previous loop scored the highest PQM. In this approach, knowledge‐based dose prediction is completely bypassed so that a 20‐patient cohort is not required and a single IE plan can be created without the need for data from other patients.

4. Manual 4π — Manually created 4π plans using the method described in Section 2.B. It is important to note that these plans are different from the manually created plans used for the training set in autHQ plans. These plans select 20 non‐coplanar beams, whereas the autHQ training set plans unrealistically use hundreds of non‐coplanar beams.

All plans in the comparison used 20 non‐coplanar beams and were normalized to deliver 100% of the prescription dose to 95% of the PTV volume. For HN cases with multiple prescription dose levels, the normalization used the PTV with the highest prescription dose. The PQM and the actual clinical dosimetric constraint values were evaluated to compare the four plan types. Wilcoxon signed‐rank tests were performed between the plans for the PQM and also each of the dosimetric values in Table 1.

3. Results

The PQM results for the 10 loops of EKB planning for 20 lung and 20 HN patients are shown in [Fig. 2(a) and 2(c)]. The lung PQM typically had negligible PQM improvements after the third loop (<0.2%). EKB planning for the HN cases took around six loops to plateau. The average PQM improvement from the initial plan with a generic template to the final EKB plan were 5.2% and 11.1% for lung and HN, respectively. A DVH comparison of the initial and final EKB plans of an example patient is shown in Fig. 3. While the initial plan has better OAR sparing in some cases (esophagus, larynx, pharynx, oral cavity, and mandible), it has substantial cold and hot spots for the PTVs. The final EKB plan was able to find a balance between PTV coverage and OAR sparing to create a high‐quality plan.

Figure 2.

(a,b) Lung and (c,d) head and neck plan quality metric (PQM) results. (a,c) PQM for each evolving knowledge‐base (EKB) planning loop for 20 patients. (b,d) Boxplots of the PQM of 20 patients for the final EKB plans, automated planning using high‐quality plans in the training set (autHQ), the final individually evolving (IE) plans, and manually created 4π plans. Significant (P < 0.05) differences between pairs of plans are labeled by the horizontal black lines. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 3.

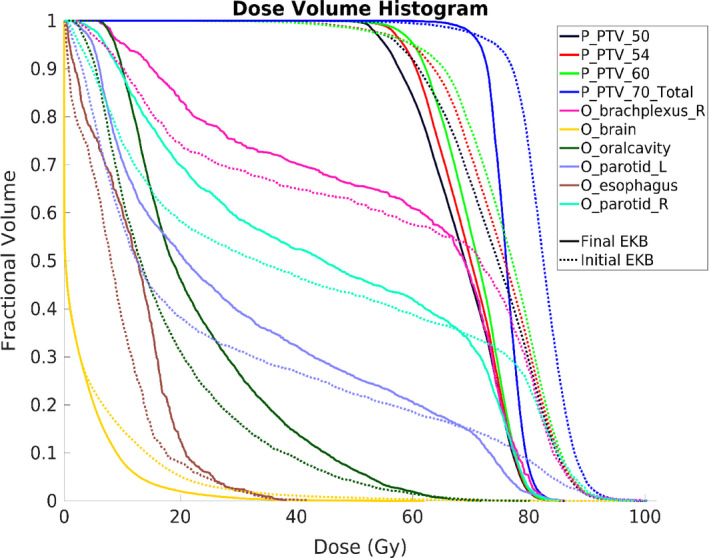
Dose–volume histogram comparison between the initial EKB plan, made with a generic template, and the final EKB plan for an example HN case. Only representative OARs are shown to reduce clutter. EKB, evolving knowledge‐base. [Color figure can be viewed at wileyonlinelibrary.com]

The IE PQMs reached within 3% of the PQM of the final EKB plans for 16 of the 40 lung and HN patients. However, for the other 24 plans, the PQM stagnated after 3 or less loops at quality substantially lower than their EKB counterparts, a 13.4% PQM difference on average. This was an average of 4.51 HN PQM points and 6.94 lung PQM points.

Figures 2(b) and 2(d) shows the boxplot comparison of the PQM between the four planning methods. Their average values are shown in Table 2, which includes the PQM data for the clinically treated VMAT plans for reference. Not surprisingly, all 4π plans were superior to the VMAT plans due mainly to the non‐coplanar beam angles, consistent with previous observation and the greater planning geometrical freedom. Differences between plans that were found significant (P < 0.05) by the Wilcoxon signed‐rank test are marked on boxplots by the horizontal black lines on top. Among the 4π plans, for the lung cases, both automated planning methods had significantly higher lung PQM score compared with the manually created 4π plans, 2.7% (EKB) and 2.3% (autHQ). The overall highest PQM for HN planning was achieved with the autHQ 4π plans, which was significantly higher than all other plans. The EKB and manually created 4π plans were found statistically comparable, with PQM scores just slightly less than autHQ, by 2.8% and 4.4%, respectively.

Table 2.

Mean PQM scores for the final EKB plans, automated planning using high‐quality plans in the training set (autHQ), the final IE plans, and the manually created 4π plans. The manually created clinical VMAT plans are provided as a reference. Significant differences between these groups are shown in [Fig. 2(b) and 2(d)].

	Final EKB	autHQ	Final IE	Manual	Cln VMAT
Lung	59.48	59.08	52.91	57.72	41.22
HN	64.50	66.31	62.10	63.49	53.78

EKB, evolving knowledge‐base; HN, head and neck; PQM, plan quality metric.

The evolution of the 20 optimized non‐coplanar beam orientation through 10 loops is shown for an example case in Fig. 4. The beams are plotted based on their couch and gantry angles. AutHQ and manual 4π beam orientations are also included for comparison. For this case, the highest PQM was achieved at loop 8. Although the selected beams are from the same quadrants, the flexibility of the 4π beam orientation optimization resulted in slight differences between the beam angles for loop 1, loop 8, autHQ, and manual plans.

Figure 4.

Beam orientation evolution for representative EKB loops, autHQ, and manual 4π for an example HN case. EKB, evolving knowledge‐base; HN, head and neck. [Color figure can be viewed at wileyonlinelibrary.com]

Each lung 4π plan took around 6 min on average. This includes SVDL training and prediction, loading the dose calculation matrix, beam angle selection, fluence map optimization, final dose calculation, and PQM calculation. Running 10 loops of lung EKB planning with 20 cases, took just over 17 h. HN planning can take considerably longer, averaging 17 min for each plan, resulting in just under 2.5 days to run 10 EKB loops. The longer computational time for HN planning is due to the considerably larger dose matrix.

Representative examples of the DVH comparison between the four plans are shown in Figs. 5 and 6 for lung and HN, respectively. Boxplot comparisons between plans of the dosimetric values used for lung PQM calculation are shown in Fig. 7. EKB plans had significantly better high‐ and low‐dose spillage compared with the other plans as indicated by the lower R50 and R10 values. The EKB and IE plans have slightly worse D98 than the other 4π planning methods.

Figure 5.

Dose–volume histogram comparison between final EKB, autHQ, final IE, and manual plans of an example lung case. EKB, evolving knowledge‐base; IE, individually evolving. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 6.

Dose–volume histogram comparison between final EKB, autHQ, final IE, and manual plans of an example head and neck case. Only representative OARs are shown to reduce clutter. EKB, evolving knowledge‐base; IE, individually evolving. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 7.

Dosimetric results for 20 lung plans each of (in order from left to right) the final EKB, autHQ, final IE, and manual plans. Significant (P < 0.05) differences between pairs of plans are labeled by the horizontal black lines. EKB, evolving knowledge‐base; IE, individually evolving.

The HN dosimetric comparisons are shown in Fig. 8. Again, there were significant differences in PTV coverage between the 4π plans. For the D98 and D99, EKB was generally outperformed in PTV coverage by the other 4π plans. IE plans were significantly more homogeneous, but at the cost of higher OAR doses and high dose spillage. The EKB plans yielded the lowest R50 and R10, indicating superior high and low dose spillage. Using unrealistically high‐quality training sets for dose prediction, the autHQ plans were superior in most PTV and OAR metrics except at the PTV hot spot as indicated by the higher D0.1cc.

Figure 8.

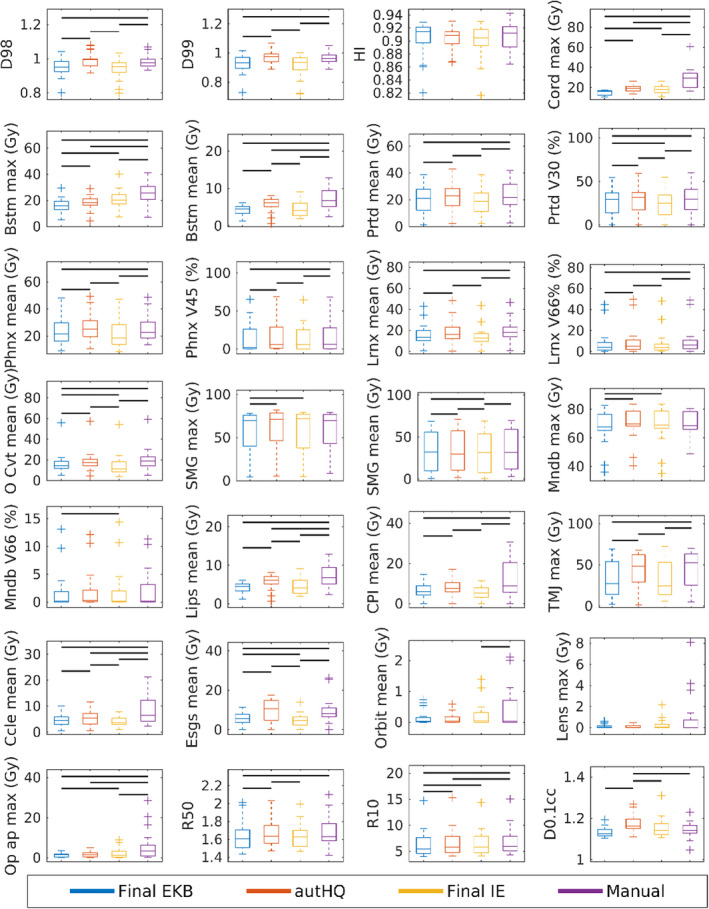
Dosimetric results for 20 head and neck plans each of (in order from left to right) the final EKB, autHQ, final IE, and manual 4π plans. Significant (P < 0.05) differences between pairs of plans are labeled by the horizontal black lines. EKB, evolving knowledge‐base; IE, individually evolving. [Color figure can be viewed at wileyonlinelibrary.com]

Both Figs. 7 and 8 display the small range in OAR metrics for the 4π plans. For the lung OAR metrics, average standard deviations were 1.22 (EKB), 1.70 (autHQ), 1.74 (IE), and 1.63 (manual 4π). For the HN OAR metrics, average standard deviations were 7.14 (EKB), 7.42 (autHQ), 7.31 (IE) and 8.75 (manual 4π).

4. Discussion

Advances in hyperparameter tuning for machine learning could be applied to automate DVH and OAR constraints.^{26, 27, 28, 29} However, these methods have limited search space and are unable to control 3D voxel dose distribution, which often requires additional tuning structures to achieve and inevitably complicates the automated treatment planning workflow. As the first innovation of this study, we removed the hyperparameters from our problem and directly applied predicted doses in the optimization objective. This allows a treatment plan to be automatically created based on the predicted 3D dose distribution. The simple SVDL dose prediction tool used in this study only depends on the Euclidian distance, resulting in dose predictions that can be collapsed into a 1D representation, similar to DVH. We selected this method because it has been to be shown more robust on small training sets than methods relying on more geometrical features.¹¹ However, the EKB framework is compatible with any tool that is capable of predicting 3D voxel dose distributions when additional geometrical features can be more robustly incorporated. The autHQ plans generated with unrealistically high‐quality plans also highlight the benefit of using accurate predictions of high‐quality plans, if available.

The value of the one‐sided cost function was separately studied in the IE plans, where the targeted dose is derived from the individual plan alone. The results show that the majority (60%) of the IE plans stopped improving prematurely without the predicted dose guidance. The study highlights the necessity of collectively updating the predicted dose based on KBP in automated treatment planning.

The second innovation of this study is the incorporation of fast beam orientation optimization in automated treatment planning. Previous automated treatment planning studies used fixed beam or arc selections. The higher degree of freedom by including beam angle selection ensures that the automated plan quality is not restricted due to predefined beam orientations. A previous obstacle for this approach was the relatively slow 4π optimization speed using a greedy optimizer. Breedveld et al implemented a similar greedy algorithm for noncoplanar beam angle selection for Pareto optimal planning, which they reported to take several hours for each optimization. To overcome the challenges of greedy optimizers, we adopted a group sparsity algorithm for beam orientation optimization that reduced the 4π planning time to a few minutes,³⁰ making EKB 4π planning feasible. With the two innovations, we have demonstrated not only automated treatment planning, but also retrospective interrogation of previous plans for continuously improving the plan quality.

This study successfully created high‐quality complex IMRT plans without user supervision or prior plans for training. Starting from an initial training set of plans created using a generic template, EKB planning created high‐quality plans by iteratively improving the plans and training set. This is valuable for initiation of a new treatment technique where there is a scarcity of existing high‐quality plans for training. EKB provides a means to automatically generate high‐quality plans by iteratively improving the plan quality, resulting in a set of clinically viable plans without requiring a large high‐quality training dataset. In contrast, this automated planning framework also allows the inclusion of existing high‐quality plans to warm start the training for faster convergence. DVH analysis of the EKB loops showed that initial plans favored OAR sparing too heavily, whereas the final plans struck the proper balance between PTV coverage and OAR sparing. The final EKB plans were found to be of similar or higher quality compared to manually created 4π plans. The plan quality improvement is quantitatively evaluated by PQM, whose improvement plateaus after three and six loops for the lung and HN EKB plans, respectively. Although HN EKB required more loops to converge, we observed larger total PQM improvement with these cases due to the higher plan complexity.

Among the lung 4π plans, both EKB and autHQ automated plans scored higher PQM than manual 4π. OAR sparing was generally similar between the 4π plans, but R50, R10, and D0.1cc were lowest with EKB planning. R50 is especially important in lung SBRT cases as it has been linked to toxicities to central organs,^{31, 32} so it is promising that the EKB plans can succeed in this aspect given no planner influence. Aside from the PTV cold spots, it is compelling that EKB planning for lung cases surpasses the plan quality of 4π plans.

Among the HN plans, despite similar OAR sparing, autHQ produced better PTV coverage than the final EKB plans. The D98 and D99 were highest with autHQ planning. This highlights the details on how autHQ outperformed all other plans in PQM. PTV coverage can be challenging in HN planning due to multiple dose prescription levels. The manually influenced training set combined with the automated planning process allowed autHQ plans to achieve higher quality than either fully and independently automated planning (EKB) or manual planning.

An important motivation for automated planning is to create more consistent plans by removing any inter‐ and intra‐planner variabilities. Among the 4π plans, EKB plans showed the smallest standard deviation in OAR metrics between the 20 plans in both the lung and HN cohorts. AutHQ had more consistent OAR dosimetry in HN cases compared to the manually created 4π plans, but not in the lung cases. This is also likely due to the vastly different planning challenges in lung and HN planning. There is an abundance of considerations in HN planning that planners must keep track of, and relatively fewer in lung planning leading to greater variabilities when manually planning HN cases. Automated planning excels in cases where the complexity can lead to greater variability in manually created plans.

EKB planning takes 5 h for 20 lung plans while the HN EKB takes 1.5 days. The time may appear to be long but is still substantially more efficient than the sum of individual planning times. More importantly, the process is unsupervised and can be run overnight. It may be possible to only perform beam orientation in the first one or two loops to reduce the total planning time by order of magnitude. Furthermore, with increasing size and stabilization of the knowledge base, it is possible that the evolution needs to happen less frequently and the time to create a new plan for a new patient would decrease to a few minutes, which is the time to optimize a plan using FISTA.

5. Conclusion

EKB planning is a novel automated planning technique that creates plans of equivalent or superior quality compared to manually created plans by iteratively and collectively evolving the quality of the training set, which is then used to improve the individual plan quality. With the capability to automatically select optimal non‐coplanar beam orientations and create competitive plans without being hindered by the initial training set quality, EKB planning facilitates the adoption of 4π into the clinic. At the same time, the automated planning framework can be more specifically guided where a high‐quality training set already exists. This guidance can steer the automated plans for a site’s specific preference.

Conflicts of interest

The authors have no relevant conflicts of interest to disclose.