Alkaline and Alkaline-earth Cyanoacetylides: A Combined Theoretical and Rotational Spectroscopic Investigation

Abstract

The metallic cyanoacetylides LiC₃N, NaC₃N, MgC₃N and CaC₃N have been investigated by combined spectroscopy measurements and theoretical calculations. The theoretical calculations predict for the four species that the linear isomer with formula MCCCN (M= Li, Na, Mg and Ca) is the most stable one. We used the laser ablation molecular beam Fourier transform microwave spectroscopy to synthesize these species by the reaction of metal vapors, produced by laser ablation, and the 3-bromo-2-propynenitrile (BrCCCN). The pure rotational spectra were observed by Fourier transform microwave spectroscopy in the 2–18 GHz frequency region only for LiCCCN and NaCCCN, while no spectral signatures for MgCCCN and CaCCCN could be detected. Finally, we have searched for LiCCCN and NaCCCN species towards the carbon-rich evolved star IRC + 10216 but only upper limits to their abundances have been obtained.

Introduction

Several metallic cyanoacetylides have been synthesized in the gas phase in recent years. Endo and coworkers¹ obtained SiCCCN in a supersonic jet by a pulsed electric discharge in a gas mixture containing SiCl₄ and HC₃N diluted in Ar. They carried out a subsequent structural characterization through Fourier transform microwave spectroscopy (FTMW). On the other hand, AlCCCN,² CuCCCN, AgCCCN and AuCCCN³ were generated and structurally characterized in our laboratory through laser ablation molecular beam FTMW. These metal cyanoacetylides were obtained using the 3-bromo-2-propynenitrile (BrCCCN) as precursor. In all cases only the MCCCN connectivity (M denoting the corresponding metal) was observed. The assignment was supported by theoretical studies, which predict that MCCCN is the most stable isomer in all cases.

Metallic cyanoacetylides are interesting compounds from different points of view. They offer the possibility of studying the metal-carbon interaction and comparing it with the metal-carbon bonding in related compounds. Of paramount relevance is the metal-carbon bonding in the analogue cyanides, MCN, and their competition with the corresponding isocyanides, MNC. The MCN connectivity has been shown experimentally to be preferred for different transition metals,^4–9 such as Cr, Co, Ni, Cu, and Zn. This observation is in agreement with the theoretical predictions,^10,11 for these metals. A peculiar case is iron, for which both isomers, FeCN and FeNC, have been experimentally observed,^12–14 the cyanide form being more stable. Theoretical studies predict a different ground state depending on the level of theory employed, and the iron cyanide/isocyanide competition still remains a challenge for theoretical methods.¹⁵ Concerning main-group metals, Mg and Al favor the isocyanide isomer^15,16, whereas for silicon the SiCN isomer is found to be lower in energy.¹⁷ Theoretical predictions are also in agreement with these observations.^18,19 The quasi-isotropic charge distribution of the cyanide ligand leads to a polytopic behavior for alkaline metals,²⁰ giving rise to T-shape structures.^21–23 It would be interesting to analyze the nature of the interaction of alkaline and alkaline-earth metals with more complex carbon-nitrogen compounds.

Several related molecules, containing different metals, have been already identified in the interstellar medium. Of particular importance is the family of cyanides/isocyanides. So far the list of interstellar molecules includes NaCN,²⁴ KCN,²⁵ MgNC,¹⁵ MgCN,²⁶ HMgNC,²⁷ AlNC,¹⁶ SiCN,¹⁷ SiNC,²⁸ and FeCN.²⁹ In addition, several cyanopolyynes, ranging from HC₃N to HC₉N, have also been detected in space.³⁰ It is then feasible that, in analogy with the HCN parent molecule, substitution of the hydrogen atom by a metal could give rise to a family of carbon chains containing a nitrogen atom and a metal. The compounds with the general formula MC₃N would be the simplest among them.

Building on the success of our previous studies on metal cyanoacetylides,^2,3 we have applied the same experimental approach to generate and characterize the metallic cyanoacetylides with the general formula MC₃N (M = Li, Na, Mg and Ca). In addition to the experimental spectroscopic characterization work we have carried out high-level ab initio quantum chemical calculations to investigate the geometries, stabilities and spectroscopic properties of these molecules. As shown below, Li- and Na-cyanoacetylides could be generated and assigned through their rotational spectra but several experiments to observe Mg- and Ca- species were fruitless. This abnormal spectroscopic behavior for Mg- and Ca-cyanoacetylides will be discussed.

Methods

A. Computational methods

We have carried out explorations of the potential energy surfaces for MC₃N compounds to characterize the relevant species for an experimental search. We consider the cyanoacetylides of Li and Na, as representative alkaline metals while explorations for MgC₃N and CaC₃N were carried out, as well.

Geometry optimizations were performed at the second-order MØller-Plesset (MP2) level of theory with Dunning’s correlated consistent triple-zeta basis sets augmented with diffuse and polarization functions, usually denoted as aug-cc-pVTZ.^31,32 Subsequent harmonic vibrational calculations at the MP2/aug-cc-pVTZ level were carried out for all stationary points obtained in the explorations in order to confirm that they correspond to true minima. The electronic energy was further refined carrying out CCSD(T) calculations³³ (coupled cluster with singles and doubles and a perturbative inclusion of triple excitations) with the aug-cc-pVTZ basis set on the MP2 geometries. In all correlated calculations (MP2, CCSD(T)) the 1s orbitals of carbon and nitrogen were kept frozen. However, for alkaline and alkaline-earth metals it could be necessary to maintain the n-1 orbitals active (n being the largest principal quantum number of the occupied orbitals in the ground state). Thus for alkaline and alkaline-earth metals only the n-2 orbitals were excluded from the active space in correlated calculations. This means that for Li all electrons were included in the calculations, whereas for Na and Mg just the 1s orbital was kept frozen. In the case of Ca 1s, 2s and 2p orbitals were considered as inactive orbitals in the correlated calculations.

Coupled cluster (CC) theory provides a systematic approach for the treatment of the electron-correlation in molecular systems. However, CC calculations are, in general, extremely costly and cannot be used together with a sufficiently large basis set. Thus, to reach accurate predictions of molecular properties it is necessary to introduce additional approximations that are based on the additivity of electron correlation and basis-set effects. In order to aid in the assignment of the rotational spectra, reliable predictions for the rotational constants are required. For this purpose a composite procedure has been applied. Gauss et al. ^34,35 have developed composite schemes at the coupled-cluster level, whereas Barone et al.³⁶ employed a more affordable version of the method, in terms of computational demands, involving geometry optimizations at the MP2 level. Basically, the method of Barone et al.³⁶ is based on the extrapolation to the CBS limit of MP2 geometrical parameters, including corrections for core-valence correlation, inclusion of diffuse functions, and the effect of CCSD(T) corrections. In order to obtain an estimate of B₀ rotational constants, vibration-rotation interaction constants were estimated using second-order perturbation theory at the MP2/aug-cc-pVTZ level. Quadrupole coupling constants were also estimated suing the CCSD/aug-cc-pVTZ electronic density. In order to aid in a possible experimental detection by IR spectroscopy, anharmonic vibrational frequencies and IR intensities have been predicted for the most stable isomer in each case. It should be noted in this point, that the composite approach used in the present work allows the calculation of spectroscopic properties with an overall accuracy of about, 20 MHz, for rotational constants. Both Gaussian 09³⁷ and CFOUR³⁸ program packages were employed in this study.

B. LA-MB-FTMW Spectroscopy

All the experiments to observe the rotational spectra of Li-, Na-, Mg- and Ca-cyanoacetylides were performed using a LA-MB-FTMW spectrometer³⁹ constructed at the University of Valladolid operating in the 2-18 GHz frequency range. The instrument has been described in detail elsewhere.³⁹ Briefly, this Balle−Flygare type Fourier-transform cavity microwave spectrometer⁴⁰ consists of a cylindrical stainless-steel high vacuum chamber, which contains a Fabry-Pérot resonator formed by two spherical aluminum mirrors. As previously reported,^2,3 for this kind of studies the pulsed nozzle system has been modified by the addition of a home-made heatable reservoir extension, placed to hold liquid and/or solid compounds which can be used as precursors of metal bearing species. Metallic cyanoacetylides are generated using this device by laser ablation of pure metal rods in the throat of a pulsed supersonic expansion of Ne and BrCCCN (prepared as previously reported)^2,3 as described below.

Producing a rod of an alkali metal is problematic, so we employed a different method than that used in previous studies. In a 40 mm stainless steel rod with a diameter of 6 mm we machined a 30 mm notch, with a diameter 1.5 mm smaller than the rod itself. Since Li and Na are malleable metals a piece of the solid metal was press into the notch and for better adhesion the rod was then introduced into an in-house designed cast and pressed with a standard hydraulic bench press. Before being inserted in the ablation housing, the alkali metal-coated portion of the rod was submerged in kerosene to avoid the oxidation or inflammation of the alkali metal. In contrast, for Mg and Ca, standard rods of pure metals were used.

The MC₃N species were produced by the chemical reaction between vapor metal, which was ablated using a picosecond Nd:YAG-laser pulse (λ = 355 nm and 10 mJ pulse⁻¹), and the precursor BrCCCN (heated at ca. 65 °C). A motorized micrometer is used to simultaneously rotate and translate the sample rod at each laser pulse, so the laser hits a different point of the sample surface in successive pulses, minimizing the problem of shot-to-shot fluctuation in the amount of the desorbed material. All the resulting products generated in the reaction are supersonically expanded and rapidly cooled to a rotational temperature of ~2 K between the two mirrors of the Fabry–Pérot resonator and then probed by Fourier-transform microwave spectroscopy. Typically 100-200 pulses were accumulated to achieve an adequate signal-to-noise ratio.

Results

A. Alkaline metals

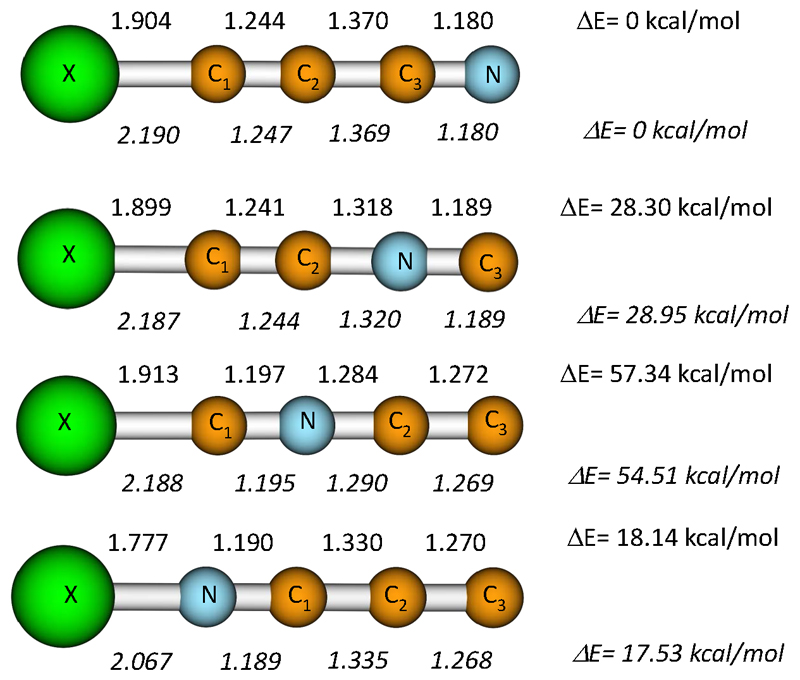
We searched for different possible minima on the XC₃N potential surface (X=Li, Na). We consider cyclic or T-shape structures, resulting from π interactions, but in all cases they eventually evolve to linear structures. We characterized four different linear isomers, differing in the position of the nitrogen atom in the chain. Their optimized structures at the MP2/aug-cc-pVTZ level are shown in Figure 1, whereas the corresponding relative energies at MP2 and CCSD(T) levels of theory, rotational constants and dipole moments are given in Table 1.

Figure 1.

Equilibrium geometries and relative energies (ZPE corrections are included) of the equilibrium structures for the different MC₃N (M=Li,Na) isomers obtained at the MP2/aug-cc-pVTZ and the CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ levels respectively. Distances are given in Ångstroms. Upper values are for LiC₃N species, whereas lower values (in Italics) correspond to NaC₃N isomers.

Table 1.

Relative energies (kcal/mol) of the different LiC₃N and NaC₃N species obtained at the MP2 and CCSD(T) levels with the aug-cc-pVTZ basis set. Zero-point vibrational energy (ZPVE) corrections are taken into account at the MP2/aug-cc-pVTZ level. Equilibrium rotational constants (MHz) and dipole moments (Debye) are estimated at the MP2/aug-cc-pVTZ level.

	ΔE(MP2)	ΔE(CCSD(T))	B	μ
LiCCCN	0.0	0.0	2556.7	11.57
LiCCNC	32.18	28.30	2731.2	9.49
LiCNCC	58.04	57.34	2784.7	16.28
LiNCCC	20.07	18.14	2772.6	13.86
NaCCCN	0.0	0.0	1330.9	13.60
NaCCNC	32.60	28.95	1399.8	11.52
NaCNCC	55.65	54.51	1444.2	18.61
NaNCCC	19.11	17.53	1489.1	16.34

It can be seen in Figure 1 that the C-C and C-N bond distances for the analog lithium and sodium isomers are quite similar, suggesting that no essential changes in the carbon-nitrogen chain are produced upon substitution of lithium by sodium. Only the metal-carbon/nitrogen distances are significantly different. As expected, the optimized Li-C and Li-N distances are considerably shorter than the corresponding Na-C and Na-N distances (by around 0.27-0.29 Å), reflecting both the strength of the bonds as well as the size of the involved alkaline atom. It is remarkable that the predicted dipole moments are very high for all isomers (from 9.49 D to 18.61 D), reflecting the expected high ionic character of the metal-C₃N bonding. The high values of the dipole moments should favor the experimental detection of these species by rotational spectroscopy, since intense lines in the rotational spectra should be expected.

According to the energy values shown in Table 1 the most stable isomer is linear MCCCN. Relative energies for the other isomers are very similar for both LiC₃N and NaC₃N. The second most stable isomer is MNCCC, with the metal bonded to the nitrogen atom but keeping the CCCN chain. The other two isomers, with the nitrogen atom in a middle position of the carbon-nitrogen chain, are less stable. We confirm that all species are true minima on the corresponding potential energy surface through computation of the vibrational frequencies. All of the studied isomers have all their frequencies real. In Table 2 we provide the anharmonic vibrational frequencies at the MP2/aug-cc-pVTZ level for the most stable species, LiCCCN and NaCCCN. Most fundamental frequencies are rather close for both systems. The main difference concerns the M-C₁ stretching frequency, which is much higher for LiCCCN (586 cm^-1) than for NaCCCN (292 cm^-1), in accordance with the expected stronger metal-carbon bond for lithium. In both cases it should give rise to a relatively strong line in the IR spectrum.

Table 2.

Anharmonic vibrational frequencies (ω, cm^-1) and IR intensities (I, km/mol) for LiCCCN and NaCCCNevaluated at the MP2/aug-cc-pVTZ level.

	LiCCCN		NaCCCN
Symmetry / Mode	ω	I	ω	I
π MC1C2bend	104	58.00	71	23.14
π C1C2C3bend	264	38.53	263	28.29
π C2C3N bend	534	3.09	555	3.54
σ M-C1 stretch	586	34.18	292	20.84
σ C2-C3stretch	919	62.53	894	26.32
σ C1-C2stretch	1956	9.54	1945	0.82
σ C3-N stretch	2137	18.14	2134	51.01

More accurate predictions of the rotational constants, employing the previously mentioned composite method and vibration-rotation interactions, were carried out for the predicted global minima, LiCCCN and NaCCCN. These predictions include as well other parameters necessary to interpret the rotational spectrum such as the dipole moments and the nuclear quadrupole coupling constants. The results obtained are collected in Table 3.

Table 3.

Theoretical and experimental spectroscopic constants for the LiCCCN and NaCCCN isomers.

Parameter	LiCCCN		NaCCCN
	Theoretical	Experimental	Theoretical	Experimental
B /MHz	2581.6a	2579.348998(74)f	1343.3a	1321.094334 (28)
D / kHz	0.1931b	0.2350 (49)	0.0922b	0.1011(7)
eQq(Li/Na) / MHz	0.462c	0.3603 (11)	-6.808c	-7.0497 (7)
eQq(N) / MHz	-4.064c	-3.9695(4)	-3.9748c	-3.8761 (5)
Rmsd / kHz		0.7		0.9
Ne		58		122

^aComposite method including vibration-rotation interaction atMP2/aug-cc-pVTZ level

^bMP2/aug-cc-pVTZ level

^cCCSD/aug-cc-pVTZ level

^eNumber of hyperfine components included in the fit.

^fValues in parentheses denote 1σ errors, applied to the last digit.

^dRoot mean square of the fit.

With the help of the predicted molecular parameters, initial experiments were devoted to search for the rotational transitions of Li-cyanoacetylides, in particular lines owing to the predicted global minima, LiCCCN. In this way, frequency scans around 5.0 GHz were directed to detect spectral signatures corresponding to the J = 1–0 rotational transition of LiCCCN, according to the transition frequencies calculated from the estimated rotational constants of Table 3. A group of lines centered around 5157 MHz, showing hyperfine structure, was finally observed. The corresponding rotational transitions J = 2–1 and J = 3–2 were then predicted and observed. The roughly estimated value of the rotational constants for the observed species is B ≈ 2560 MHz in good agreement with the predicted value for LiCCCN isomer, indicating that this species is generated in the supersonic expansion of our experiment. Additional wide frequency scans around 5.4 GHz were done to find rotational signatures of LiC₃N isomers but they were fruitless.

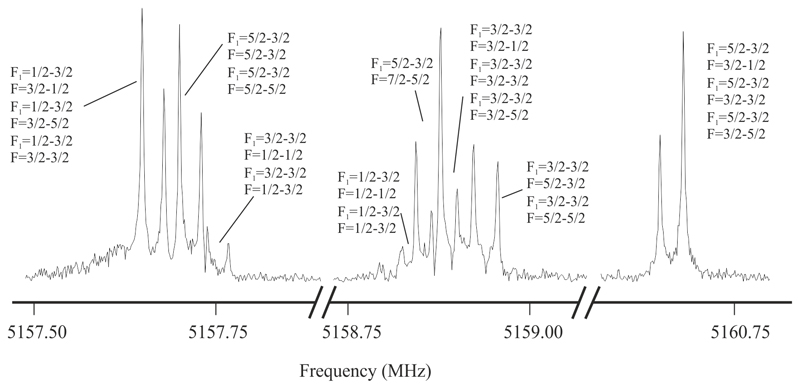
LiCCCN possesses two nuclei with quadrupole moment, ¹⁴N (I = 1) and ⁷Li (I = 3/2). The interaction at the nuclei of these quadrupole moments with the electric field gradient created by the rest of the molecular charges causes the coupling of the nuclear spin moments to the overall rotational momentum. Hence, each rotational transition of LiCCCN carried the nuclear quadrupole hyperfine pattern expected for the presence of ⁷Li nucleus and the additional quadrupolar effect of the ¹⁴N nucleus giving rise to a hyperfine pattern like the one shown in Figure 2 for the J = 1–0 rotational transition. A total of 58 hyperfine components (Table S1 of the Supplementary Material) were analyzed⁴¹ using a ¹Σ Hamiltonian of the following form:⁴² H = H_R + H_Q(Li) + H_Q(N) where H_R contains rotational and centrifugal distortion parameters while H_Q(Li) and H_Q(N) the quadrupole coupling interactions for ⁷Li and ¹⁴N nuclei respectively. The energy levels involved in each transition are labeled with the quantum numbers J, F₁ and F where F₁ = J + I_Li and F = F₁ + I_N. The experimental values for the rotational parameters B and D, and the electric quadrupole coupling constant eQq for the ⁷Li and ¹⁴N nuclei were derived from the analysis and are listed in Table 3, along with the theoretical ones. The standard deviation obtained for the fit is 0.7 kHz. As can be seen, confirmation of the observed species as the linear LiCCCN isomer resides in the excellent agreement between the experimental and theoretical values of the rotational and ⁷Li and ¹⁴N nuclear quadrupole coupling constants.

Figure 2.

Spectrum of a section of the J = 1–0 rotational transition of LiCCCN near 5.2 GHz showing the multiple hyperfine components arising from both ⁷Li (I=3/2) and ¹⁴N (I=1) nuclei. The coaxial arrangement of the adiabatic expansion and the resonator axis produces an instrumental Doppler doubling. The resonances frequencies are calculated as the average of the two Doppler components. Each hyperfine component is labeled with the corresponding values of F₁´, F´←F₁´´, F´´ quantum numbers.

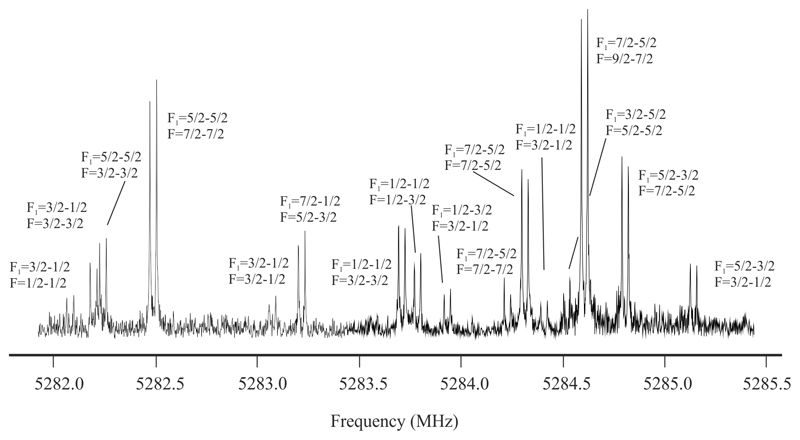
In the case of NaC₃N, frequency scans were conducted to search for the J = 2–1 transition of the global minimum NaCCCN in the frequency region around 5.2 GHz. One cluster of lines showing a very congested hyperfine structure was detected centered in 5284 MHz (see Figure 3). In addition, another five rotational transitions at 2.6, 7.9, 10.5, 13.2 and 15.8 GHz corresponding to J = 1–0, J = 3–2, J = 4–3, J = 5–4 and J = 6–5 respectively were measured. As in the case of LiCCCN the experimental value of the rotational constant for the observed isomer (B ≈ 1320 MHz) clearly points to the observation of the NaCCCN isomer.

Figure 3.

Central section of the J = 2–1 rotational transition of NaCCCN. The nuclear quadrupole coupling hyperfine structure arising from both from both ²³Na (I=3/2) and ¹⁴N (I=1) nuclei is clearly resolved. Each hyperfine component is labeled with the corresponding values of F₁´, F´← F₁´´, F´´ quantum numbers.

NaCCCN as LiCCCN possesses two nuclei with quadrupole moment. With ²³Na (I=3/2) and ¹⁴N (I = 1) nuclei, each rotational transition of NaCCCN presents a very complex hyperfine pattern as shown in Figure 3 for the J = 2–1 rotational transition. A ¹Σ Hamiltonian with this form:⁴² H = H_R + H_Q(Na) + H_Q(N) was used to fit 122 hyperfine components and the analysis rendered the rotational parameters B and D and the electric nuclear quadrupole coupling constants for the ²³Na and ¹⁴N nuclei, which are listed in Table 3. Again the good agreement between the experimental and predicted values confirms the observation of NaCCCN isomer. No other lines attributable to further isomers were observed in spite of the wide frequency regions scanned.

B. Alkaline-earth metals

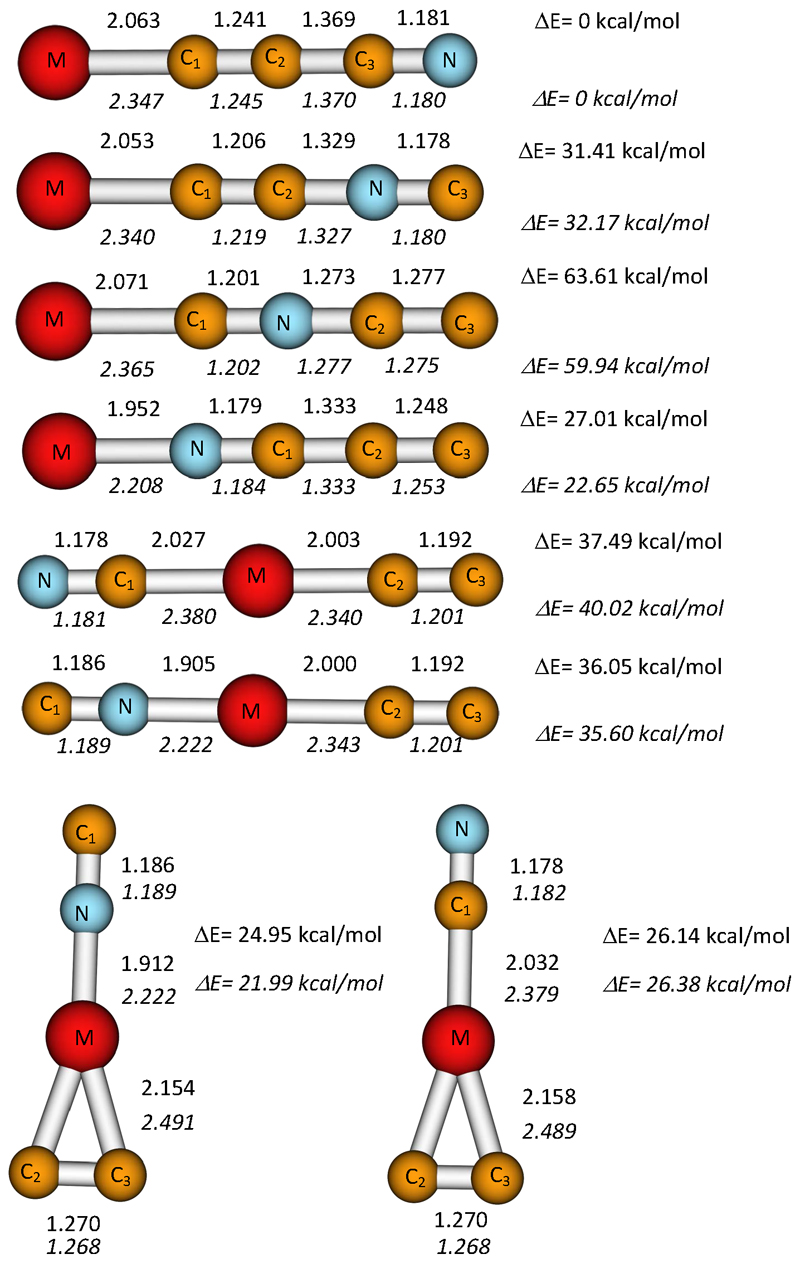
In the same way done for Li and Na, we searched for different possible minima on the Mg- and CaC₃N potential surface, considering cyclic or T-shape structures as well as linear structures. In this case we found two three-member-cyclic structures with Mg/Ca in the middle of the chain. Thus, the optimization ended up with either CN-M(C₂) or NC-M(C₂), being M= Mg, Ca. These two structures have an MC₂ triangle subunit bonded to CN either through the nitrogen or the carbon atom, respectively. All the optimized structures at the MP2/aug-cc-pVTZ level are shown in Figure 4, whereas the corresponding relative energies at MP2 and CCSD(T) levels of theory, rotational constants and dipole moments are given in Table 4. We confirm that all species are true minima on the corresponding potential energy surface through the computation of the vibrational frequencies. All of the studied isomers have all their frequencies real. In Table 5 we provide the anharmonic vibrational frequencies at the MP2/aug-cc-pVTZ level for the most stable species, MgCCCN and CaCCCN.

Figure 4.

Equilibrium geometries and relative energies (ZPE corrections are included) for the different MC₃N (M=Mg,Ca) isomers obtained at the MP2/aug-cc-pVTZ and the CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ levels respectively. Distances are given in Ångstroms. Upper values are for MgC₃N species, whereas lower values (in Italics) correspond to CaC₃N isomers.

Table 4.

Relative energies (kcal/mol) of the different MgC₃N and CaC₃N species obtained at the MP2 and CCSD(T) levels with the aug-cc-pVTZ basis set. Zero-point vibrational energy (ZPVE) corrections are taken into account at the MP2/aug-cc-pVTZ level. Equilibrium rotational constants (MHz) and dipole moments (Debye) are estimated at the MP2/aug-cc-pVTZ level.

	ΔE(MP2)	ΔE(CCSD(T))	A	B	C	μ
MgCCCN	0.0	0.0		1366.0		6.26
MgCCNC	36.98	31.41		1469.1		5.20
MgCNCC	63.48	63.61		1479.2		10.36
MgNCCC	30.01	27.01		1536.1		10.17
CCMgCN	54.41	37.49		1391.7		2.53
CCMgNC	55.46	36.05		1505.4		2.68
CNMg(C2)	42.65	24.95	52185.3	1905.9	1838.7	3.25
NCMg(C2)	41.39	26.14	52200.6	1739.1	1683.0	3.08
CaCCCN	0.0	0.0		967.9		7.78
CaCCNC	37.09	32.17		1023.2		6.73
CaCNCC	60.11	59.94		1038.7		12.29
CaNCCC	25.25	22.65		1102.8		11.65
CCCaCNa	57.47	40.02		1096.4		2.43
CCCaNCa	55.12	35.60		1188.4		2.15
CNCa(C2)	40.85	21.99	52405.3	1461.4	1421.7	3.14
NCCa(C2)	43.09	26.38	52401.4	1330.8	1297.9	3.38

^aStructures with two degenerate Π vibrational frequencies.

Table 5.

Anharmonic vibrational frequencies (ω, cm^-1) and IR intensities (I, km/mol) for MgCCCN and CaCCCN evaluated at the MP2/aug-cc-pVTZ level.

	MgCCCN		CaCCCN
Symmetry / Mode	ω	I	ω	I
π MC1CM2 bend	79	0.16	62	0.47
π C1C2C3 bend	262	5.69	243	6.62
σ M-C1 stretch	401	70.53	296	55.72
π C2C3N bend	515	2.68	486	3.30
σ C2-C3stretch	928	54.22	906	54.24
σ C1-C2stretch	1936	9.42	1940	11.11
σ C3-N stretch	2389	37.29	2177	24.34

As can be seen in the Figure 4, Mg- and Ca-C₃N follow the same trends found for lithium and sodium isomers and the C-C and C-N bond distances for the analog isomers are quite similar, suggesting that no essential changes in the carbon-nitrogen chain are produced upon substitution of Mg by Ca. Only the metal-carbon/nitrogen distances are significantly different.

The rotational transition frequencies of the global minima MgCCCN and CaCCCN species were predicted using the rotational and quadrupole coupling constants of Table 6. It has to be noted that both isomers are paramagnetic species (²Σ⁺ ground electronic state) and thus, their rotational spectrum would show fine and hyperfine splitting. The total coupling scheme for them is that: the rotational angular momentum N couples with the total electron spin angular momentum S to give the fine structure, J = N + S, which further couples with the nuclear spin angular momentum I to give the hyperfine structure, F = J + I(¹⁴N). Due to the total electron spin (S=1/2) in the doublet state, every N state is split into two J levels, which are further split into hyperfine levels by ¹⁴N nuclear spin (I=1). In addition each transition for MgCCCN and CaCCCN would show first-order Zeeman splitting due to the Earth's magnetic field. To avoid this effect, a set of three mutually perpendicular Helmholtz coils are used to collapse the Zeeman pattern down to the expected Doppler components.

Table 6.

Theoretical spectroscopic constants for the MgCCCN and CaCCCN isomers.

Parameter	MgCCCN	CaCCCN
	Theoretical	Theoretical
B /MHz	1391.3a	982.4a
D / kHz	0.0622b	0.0922b
eQq(N) / MHz	-4.1106c	-0.2992c

^aComposite method including vibration-rotation interaction at MP2/aug-cc-pVTZ level

^bMP2/aug-cc-pVTZ level

^cCCSD/aug-cc-pVTZ level

First, we searched for the N = 2-1 transition predicted around 5.5 GHz using the same experimental conditions than those used for Li- and Na-cyanoacetylides. We scanned large frequency regions (wider than 2 GHz) for several times increasing the number of shots per point, but we could not observe any lines attributable to MgCCCN species. We searched for the N = 1-0 and 3-2 transitions around 2.7 and 8.2 GHz regions but signals were not found either. In light of this result, we predicted the rotational transition frequencies for the higher energy isomers and then searched for their plausible rotational signatures but with the same result, no rotational transitions could be found.

A similar search was carried out for Ca to observe the N = 1-0, 2.1 and 3-2 transitions for CaCCCN predicted around 1.9, 3.8 and 5.7 GHz respectively. No lines for this species or for any other higher energy isomers were found.

Discussion

A reasonable agreement between experimental and theoretically predicted spectroscopic parameters is generally observed in Table 3. In the case of LiCCCN, the predicted rotational constant is within 2.3 MHz of the experimental value. This remarkable agreement slightly deteriorates when moving to NaCCCN, with a discrepancy of around 22 MHz. It should be noted that the trend in the centrifugal distortion constants is well reproduced by theory in both cases. The electronic nuclear quadrupole coupling constants for the ¹⁴N nucleus in LiCCCN and NaCCCN agree well with the predicted values. The LiCCCN and NaCCCN determined eQq constants are very similar, -3.9695 (4) MHz and -3.8761 (5) MHz, respectively, indicating that the electronic environment around the ¹⁴N nucleus is very similar in both species. On the other hand, the Li and Na eQq values are well described by our calculations and they are similar to those found experimentally for analogous molecules, such as the lithium and sodium acetylides.⁴³ Thus, the eQq values for Li and Na in the LiCCH and NaCCH systems, 0.375 MHz and -7.264 MHz, respectively,⁴³ are very close to our values of 0.3603 and -7.0497 MHz, respectively. Thus, Li-C and Na-C bond character in the LiCCCN and NaCCCN molecules are almost the same than those for LiCCH and NaCCH, which present a high degree of ionic metal–ligand bonding character similar to the halides or hydroxides while the covalent character of the metal–ligand bond is minimal, as it has been shown by Sheridan et al.⁴³

Since we widely explored the predicted frequency regions for the rotational transitions for MgCCCN and CaCCCN we can conclude that the formation of both species does not take place using the current experimental conditions of laser ablation and the BrCCCN precursor. Different attempts were carried out using different experimental conditions with other laser wavelengths, focal distances or laser fluencies as well different precursors such as HCCCN and ICCCN but all our trials resulted unfruitful. In fact, the production rates for LiCCCN and NaCCCN were very poor when HCCCN and ICCCN were employed instead of BrCCCN.

We wonder if MgCCCN and CaCCCN species have a very different behavior from LiCCCN and NaCCCN, in terms of their thermochemical properties. To get some insights we calculated the reaction enthalpies for processes M + BrCCCN, (M =Li, Na, K, Cu, Al, Mg and Ca). We considered Cu and Al in addition to Li, Na, Mg and Ca because we have previously investigated their gas phase generation and rotational spectra using the same method related in this work. For the reaction process M + BrCCCN → Br + MCCCN we found (See Table 7) that all the reaction enthalpies were negative except those for Mg and Ca, which indicates that the formation of the Mg- and Ca-cyanoacetylides is much less favorable than the formation of the analogs with Li, Na, Al or Cu. In addition, we theoretically explored the thermochemistry on the formation of other species instead of the Mg- and CaCCCN and we found (at B3LYP/aug-cc-pVTZ level of theory) that the production of symmetric species with general formula NCCCMCCCN from MCCCN+CCCN is very favorable for M=Mg and Ca, being the formation enthalpies -114.5 and -52.14 kcal/mol respectively. These facts indicate that Mg, Ca and BrCCCN can be involved in other reaction processes that preclude the formation of MgCCCN and CaCCCN in an enough proportion to be detected through rotational spectroscopy.

Table 7.

Reaction enthalpies (kcal/mol) for the production of MCCCN species from M + BrCCCN. The level of calculation is CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ, including ZPE corrections at the MP2 level.

Reaction	Li	Na	Mg	Ca	Al	Cu
M+ BrCCCN → Br + MCCCN	-17.14	-7.37	16.46	0.73	-12.49	-14.48

Finally, the rotational constants derived from the observed laboratory spectra of LiCCCN and NaCCCN allow performing a search in the millimeter domain using the 3 mm line survey of IRC + 10216 taken with the 30-m IRAM radiotelescope.^44,45 The values of the experimental constants obtained in the present investigation have been used to predict its transitions in the 3 mm domain with uncertainties of 0.15–0.4 MHz. We have searched for possible lines within ±20 MHz around the predicted frequencies which is enough to search for features with a total linewidth ~29 km/s. Unfortunately, we have not detected plausible candidates for the transitions J = 27–26 up to J = 44–43. From the most sensitive spectra, and assuming that NaCCCN could arise from the same region than NaCN,⁴⁶ we obtain an upper limit (3σ) to the column density of NaCCCN in front of IRC + 10216 of < 8 × 10¹⁰ cm⁻². The upper limit obtained for the column density of NaCCCN is around 100 times lower than that for NaCN. The chemical paths leading to the formation of NaCN and NaCCCN have been discussed previously by Petrie.⁴⁷ The chemical models, performed by Cabezas et al.²⁷ and Quintana-Lacaci et al.⁴⁶, show that the main formation path for these species involves HCN, HCCCN and Na ions. The derived abundance ratio NaCN/NaCCCN is compatible with an abundance ratio the HCN/HCCCN>100.

A similar search was dome for LiCCCN and an upper limit similar to that for NaCCCN was obtained. The non-observation is expected due to the probable low abundance of lithium in the ISM, and the lack of emission from species such as LiCl, LiF or LiCN, which could be more abundant than LiCCCN.

Conclusions

The cyanoacetylides LiCCCN and NaCCCN, have been synthesized and characterized in the laboratory using a combination of laser ablation techniques and Fourier transform microwave spectroscopy. This method is not suitable for MgCCCN and CaCCCN, which could not be detected using the same experimental procedure than that for LiCCCN and NaCCCN. Additionally, we have carried out high-level ab initio quantum chemical calculations for Li, Na, Mg and Ca cyanoacetylides to investigate the geometries, stabilities of these molecules and to provide accurate rotational transition frequencies that allow its spectroscopic characterization. The analysis of the rotational spectra rendered the experimental rotational parameters that are in reasonable good agreement with those predicted theoretically.

The non-observation of MgCCCN and CaCCCN has been interpreted in terms of a different thermochemical behavior of Mg and Ca with respect to that of Li and Na. From our results, it seems that, probably Mg, Ca and BrCCCN can undergo different reaction processes under our experimental conditions.

Supplementary Material

See supplementary material for all the measured transition frequencies for LiCCCN and NaCCCN species.