Skip to main content
PMC home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2019 Oct 16.
Published in final edited form as: Ann Intern Med. 2019 Mar 26;170(8):538–546. doi: 10.7326/M18-3542

Threshold Analysis as an Alternative to GRADE for Assessing Confidence in Guideline Recommendations Based on Network Meta-Analyses

David M Phillippo 1, Sofia Dias 1,2, Nicky J Welton 1, Deborah M Caldwell 1, Nichole Taske 3, A E Ades 1
PMCID: PMC6739230  EMSID: EMS82751  PMID: 30909295

Abstract

Guideline development requires synthesising evidence on multiple treatments of interest, typically using Network Meta-Analysis (NMA). Because treatment effect estimates may be imprecisely estimated or based on evidence which may lack internal or external validity, guideline developers need to assess the robustness of recommendations made based on the NMA to potential limitations in the evidence. Such limitations arise because the observed estimates differ from the true effects of interest, for example due to study biases, sampling variation, or issues of relevance. The widely-used GRADE framework aims to assess the quality of evidence supporting a recommendation using a structured series of qualitative judgements. We argue that GRADE approaches proposed for NMA are insufficient for the purposes of guideline development, as the influence of the evidence on the final recommendation is not accounted for. We outline threshold analysis as an alternative approach, demonstrating the method with two examples of clinical guidelines from the UK National Institute for Health and Care Excellence. Threshold analysis quantifies precisely how much the evidence could change (for any reason, such as potential biases or simply sampling variation) before the recommendation changes, and what the revised recommendation would be. If it is judged that the evidence could not plausibly change by more than this amount then the recommendation is considered robust, otherwise the recommendation is sensitive to plausible changes in the evidence. In this manner, threshold analysis directly informs decision makers and guideline developers of the robustness of treatment recommendations.

Introduction

Health technology assessments and guidelines require evidence on multiple treatments of interest from several studies to be synthesised. Typically, such analyses are performed using Network Meta-Analysis (NMA), which provides a consistent set of treatment effect estimates so that coherent recommendations may be made (1–3). However, if the NMA estimates are imprecise, if studies included in the analysis have flaws in their conduct or reporting, or there are concerns over relevance, the reliability of results from the NMA can be in doubt. Therefore, analysts and decision makers need to assess the robustness of any conclusions based on the NMA to potential limitations in the included evidence.

The framework developed by the Grading of Recommendations Assessment, Development and Evaluation (GRADE) Working Group, known as GRADE NMA (4, 5) has been proposed to assess this.

A GRADE assessment rates the quality of evidence contributing to the treatment effect estimates for each pair of treatments as high, moderate, low or very low across five domains—study limitations, imprecision, indirectness, inconsistency (heterogeneity), and publication bias—and a qualitative summary judgement is formed (6). The GRADE Handbook (7) states two different aims for this quality assessment, depending on whether the intended users are systematic reviewers or guideline developers.

  1. For systematic reviewers, “the quality of evidence reflects the extent to which we are confident that an estimate of the effect is correct.”

  2. For guideline developers, “the quality of evidence reflects the extent to which our confidence in an estimate of the effect is adequate to support a particular recommendation.”

GRADE NMA reaches a judgement for each treatment comparison by considering the individual GRADE judgements for the direct and indirect evidence between each pair of treatments. However, this approach does not deliver an assessment of the credibility of recommendations based on the NMA for guideline developers. Instead, it delivers a set of independent assessments of the confidence in the estimates for individual pairwise comparisons. Moreover, GRADE NMA suggests replacing the NMA estimates with the direct or indirect estimates if they have a higher quality rating, leading to a set of final estimates which are not consistent with each other and therefore cannot be used for rational decision making (4). For example, it would be possible to obtain estimates where intervention A is better than B, B is better than C, but C is better than A. Not only is it possible for GRADE NMA to reach a set of conclusions that are logically incoherent, it also fails to indicate how evidence quality might affect the final recommendation. As such, whilst GRADE NMA may achieve the prescribed aim for systematic reviewers, it is inadequate for guideline developers. The GRADE NMA ratings describe how likely each comparison estimate is to differ from the “truth”, but the influence of evidence on the recommendation is not considered. For example, low quality evidence that has negligible influence on the treatment recommendation should be of little concern, but more influential evidence should be scrutinised carefully and confidence in the robustness of the recommendation may be diminished. Recent advances in GRADE guidance (5) acknowledge that the influence of evidence is important, suggesting that “there is no need to rate the indirect evidence when the [quality] of the direct evidence is high, and the contribution of the direct evidence to the network estimate is as least as great as that of the indirect evidence.” However, this reasoning is only applied to each pairwise comparison, and influence on the overall decision is not considered. Furthermore, GRADE NMA quickly becomes infeasible as the number of treatments in the network increases, since the number of loops of evidence that must be assessed grows very large (such as the social anxiety disorder example discussed later).

An alternative, statistically rigorous, extension of GRADE to NMA proposed by Salanti et al. (8) formally evaluates the influence of the direct evidence on each estimate and uses this to combine quality judgements from each piece of direct evidence into an overall quality assessment. This approach avoids the possibility of incoherent conclusions. Salanti GRADE has been implemented in the CINeMA web application (9) which automates the statistical operations and facilitates the required judgement steps, making it feasible even in large networks with many evidence loops since the quality and contribution of indirect evidence is accounted for automatically. Salanti GRADE clearly meets the aim of quality assessment for systematic reviews and does so in a much more rigorous manner than GRADE NMA. However, it still does not fully meet the aim of GRADE for guideline developers because the quality assessments reflect the confidence in the NMA estimates, which does not necessarily translate into robustness of treatment recommendations: evidence may be influential for an NMA result but may not actually change a decision (10). In addition, it does not detail how potential bias would change a recommendation and is therefore less useful to decision makers and guideline developers than the approach described in this paper, which directly assesses the robustness of the recommendations based on an NMA.

Network meta-analyses are based on data from studies of relative treatment effects. Both the study estimates and resulting NMA estimates may differ from the “true effects” of interest in the decision setting for two basic reasons: bias (systematic error) and/or sampling variation (random error). In the most general statistical sense, bias is any systematic departure from the truth. This may be due to issues of internal validity (i.e. study limitations) or external validity (affecting the generalisability of results into the decision setting). Sampling variation is captured by the confidence interval, representing the uncertainty in the estimate, and is typically reduced as sample size increases. The issues addressed by the five GRADE domains all concern either bias (study limitations, inconsistency, indirectness, publication bias) or sampling variation (imprecision). From here onwards we use the phrase “change in the evidence” to refer to any difference between an estimate and the true effect of interest, whether due to bias or sampling variation.

Treatment recommendations can be made using a variety of decision criteria. The simplest is to choose the treatment with the “best” estimate on a particular outcome, for example the treatment with the highest mean reduction in pain, or on a composite outcome, such as a weighted average of outcomes (as in multi-criteria decision making (11)) or net monetary benefit (12). Other formats include recommending: the top few treatments with the highest mean estimates; treatments achieving a benefit above a certain cut-point; the top treatments within a minimally clinical important difference; or a “do not do” recommendation against using the treatments with the worst outcomes. To determine the robustness of a treatment recommendation, we are concerned with whether there are plausible changes to the evidence that would translate into NMA estimates that lead to a different recommendation being reached.

Threshold analysis is a standard form of sensitivity analysis used in health economics which answers the question, “how much would the evidence have to change before the recommendation changes?” (13). In its basic form we can simply re-run the NMA, iteratively changing the data until a new recommendation is reached (10). These changes to the data can be made at one of two levels: either changing an estimate from a single study (which we refer to as a study level threshold analysis), or changing the combined evidence on a contrast (relative effect) between two treatments (a contrast level threshold analysis). The result is a set of thresholds which describe how much each (study or contrast) data point could change before the recommendation changes, and what the revised recommendation would be. Investigators can then judge whether the evidence could plausibly change by more than the threshold amount in each direction to determine the robustness of the recommendation. For potential changes due to sampling variation one can refer to the confidence interval (or credible interval if a Bayesian analysis was used) and whether this overlaps the threshold. For potential changes due to bias a judgement of the plausible magnitude and direction of potential bias is required. If it is judged that the evidence could not plausibly change beyond the thresholds then the recommendation is considered robust, otherwise the recommendation is sensitive to plausible changes in the evidence.

A more sophisticated algebraic approach that does not require multiple re-runs of the NMA has recently been proposed (14), which only requires the user to supply the NMA estimates and the decision criteria. This is computationally much faster and offers additional flexibility: we can consider potential changes to individual study estimates or to a set of estimates on a treatment comparison, and examine the impact of specific potential biases. The analysis is not limited to greatest efficacy decisions: we can consider how changes in the evidence affect any treatment rankings, for example to determine the robustness of a “do not do” decision for the worst treatment, and we can consider complex decision rules such as those based on a minimal clinically important difference, and simple net benefit functions. An R (15) package is available (https://cran.r-project.org/package=nmathresh)(14), making it quick and easy to conduct.

Threshold analysis in practice

We illustrate threshold analysis in two practical examples taken from Clinical Guidelines produced by the National Institute for Health and Care Excellence (NICE). In the first, we demonstrate that the method can be used with large networks with complex modelling, and in the second we demonstrate an application with different formats for the recommendations. All R code is given in the Supplementary Material, and a brief guide to performing threshold analysis with the R package nmathresh is given in the Appendix.

Example: social anxiety

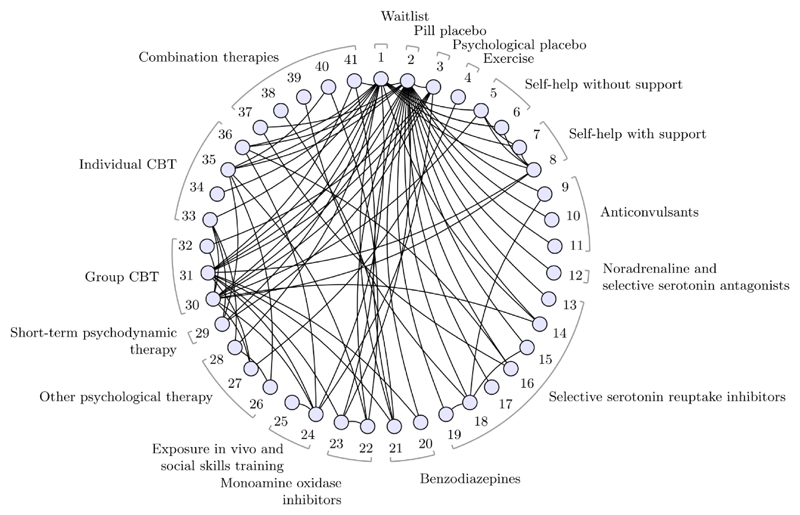
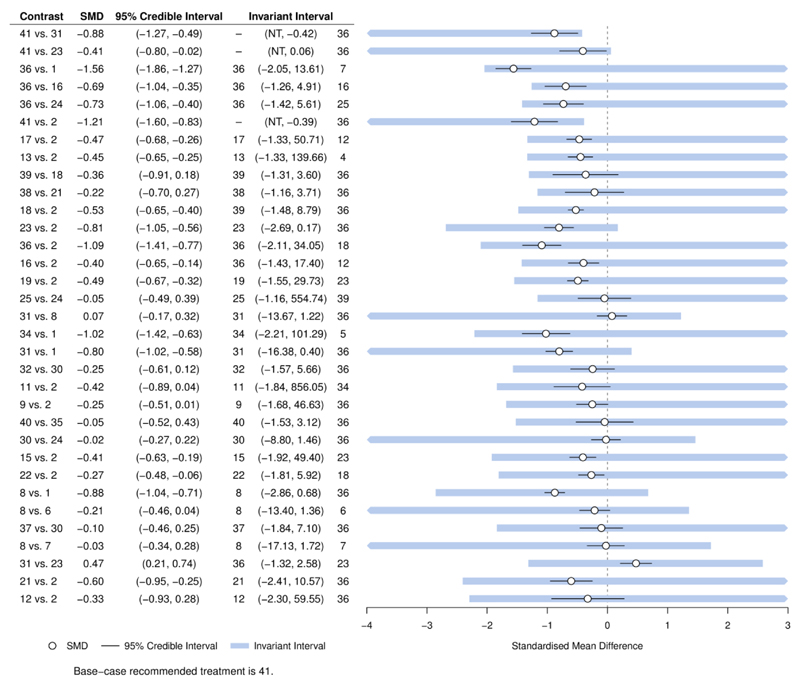
Large networks with many treatments are common in guideline development. A NICE guideline (CG159) for social anxiety disorder included evidence on 41 treatments in 17 different classes from 100 studies, forming the evidence network in (Figure 1) (16)(17). Based on greatest efficacy, the base case treatment recommendation is group cognitive behavioural therapy with phenelzine (treatment 41), with the largest estimated reduction in symptoms of social anxiety (most negative standardised mean difference (SMD)) of −1.68 and 95% credible interval (−2.10, −1.27) compared to placebo. GRADE NMA is simply not practicable in this scenario: there are 820 possible pairwise comparisons, of which 84 are directly informed by studies, and the number of indirect evidence loops is very large. However, we can easily perform a threshold analysis to assess the robustness of the recommendation; the results are shown in Figure 2. Each row of the figure corresponds to a comparison between two treatments for which direct study evidence was available, sorted to show comparisons with smallest thresholds first. We visualise the positive and negative thresholds for each comparison by creating invariant intervals, plotted as shaded lines. These are formed by adding the positive and negative thresholds (listed in Supplementary Table 1) to the point estimate, to show how much the combined evidence on each comparison would have to change before a new treatment decision is reached. Changes to the evidence within the invariant interval do not alter the treatment recommendation. If evidence were to change beyond the thresholds at either end of the invariant interval, then new treatment decisions would be reached; these are presented in the table (using treatment codes) at the corresponding side of the invariant interval. For some comparisons there is no threshold in one direction (indicated by “NT”), so no amount of change to the evidence in this direction would alter the recommendation. The smallest threshold (see Supplementary Table 1) is a positive change of 0.46 in the estimate of −0.88 SMD for the 41 vs. 31 comparison (i.e. the upper limit of the invariant interval is −0.88+0.46=−0.42), at which point cognitive therapy (treatment 36) would be recommended. At the negative side of the invariant interval for the 41 vs. 31 comparison, there is no threshold—no amount of change in the negative direction to the evidence on this comparison (i.e. becoming even more favourable to treatment 41) could ever result in a new recommendation. In total, only 5 comparisons have thresholds smaller than 0.8 SMD—a value considered to be large (18)—and for each of these, the new treatment recommendation would be cognitive therapy, which was ranked second in the original NMA. For the remaining 79 comparisons, we judge that the magnitude of change required to alter the treatment decision is unrealistically large and the treatment recommendation is therefore robust to plausible changes to these comparisons. As this example shows, with such large networks typically only a few contrasts are decision-sensitive and require further scrutiny, whereas GRADE NMA may be infeasible.

Figure 1.

Figure 1

Open in a new tab

Social Anxiety treatment network. Circles (nodes) represent treatments and connecting lines (edges) show study comparisons. Numbers around the edge are the treatment codings. Treatment classes are indicated by the braces, some classes contain a single treatment. See (17) for full details; figure modified from (14).

Figure 2.

Figure 2

Open in a new tab

Forest plot for the Social Anxiety example showing results of the threshold analysis, sorted with smallest thresholds first. Only contrasts with a threshold less than 2 standardised mean differences (SMD) are shown here for brevity. The first 5 comparisons have thresholds less than 0.8 SMD. The base-case optimal treatment is 41 (cognitive behavioural therapy with phenelzine).

NT – no threshold: no amount of change in this direction would change the recommendation. At either side of the invariant interval are shown the new optimal treatment if threshold exceeded in this direction.

Figure modified from (14).

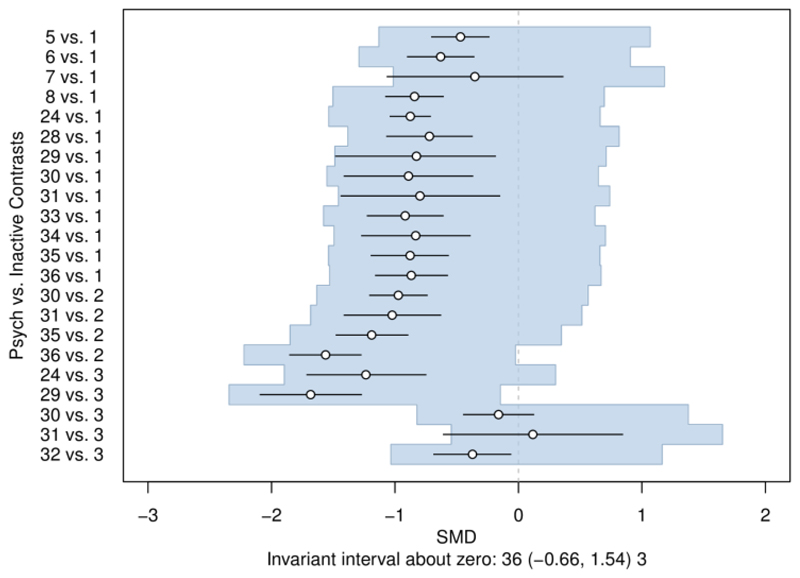
We also use threshold analysis to examine the potential impact of more complex biases, exploring concerns in sets of treatment comparisons or studies. For example, it is plausible that the effects of psychological interventions are overestimated compared to inactive control, perhaps due to difficulties of blinding. Threshold analysis (Figure 3) reveals that adjusting for such bias (if present) would change the treatment recommendation only if the effects were overestimated by at least 1.54 SMD. This threshold is implausibly large and would require most psychological treatments to in fact be harmful. The recommendation is therefore considered robust to plausible overestimation of the psychological treatment effects.

Figure 3.

Figure 3

Open in a new tab

The invariant interval for all psychological treatments against an inactive control, considered to be bias adjusted by the same amount on the standardised mean difference (SMD) scale. The base-case optimal treatment is 41. At either side of the invariant interval are shown the new optimal treatment if threshold exceeded in this direction. Figure reproduced from (14).

Example: headaches

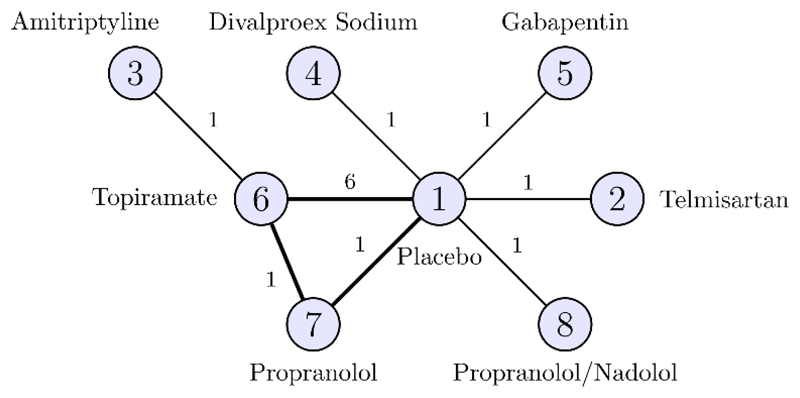
Threshold analysis may also be applied to more complex decision rules. A NICE clinical guideline (CG150) examined eight prophylactic treatment regimens for chronic or episodic migraine (19); a NMA was performed on a treatment network formed of 11 studies comparing 8 treatments (Figure 4). A minimal clinically important difference of 0.5 headache days per month was defined, with which we form a decision rule: recommend any treatment which shows a reduction of 0.5 days or more compared to Placebo, and is within 0.5 days of the most effective treatment. Based on this decision rule, propranolol with an expected change in headache days (and 95% credible interval) of –1.19 (−2.20, −0.20), topiramate with −1.04 (−1.52, −0.58), and amitriptyline with −1.14 (−2.45, 0.16) were recommended.

Figure 4.

Figure 4

Open in a new tab

Headaches treatment network. Circles (nodes) represent treatments and connecting lines (edges) show study comparisons, with numbers on the edges show the number of studies making the comparison. Numbers inside the nodes are the treatment codings. The bold loop is formed by a single three-arm study.

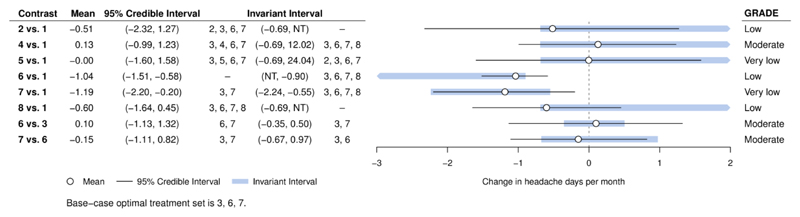
Applying threshold analysis to the body of evidence on each comparison (Figure 5), we see that the credible intervals for the evidence on each comparison extend beyond the limits of the invariant intervals; the recommendation is therefore sensitive to the level of uncertainty in the data (which is also reflected in the credible intervals for the treatment effects). The smallest threshold (see also Supplementary Table 2) is −0.09 days (just over 2 hours per month) for the propranolol/nadolol vs. placebo (8 vs. 1) comparison, at which point propranolol/nadolol joins the recommended set of treatments. As propranolol/nadolol was very close to within 0.5 days of propranolol (the most effective treatment) in the original analysis, this is not surprising. We might expect bias to exaggerate the effect of treatment compared to placebo, but the small thresholds for comparisons of treatments 2, 4, 5, and 8 vs. placebo are for changes in the opposite direction. Any bias in the evidence on these comparisons is therefore unlikely to change the decision; the decision is still sensitive to the level of uncertainty in the evidence however. Notably, the GRADE assessments shown in Figure 5 do not show any relationship with the magnitude of the thresholds. As observed previously (10), evidence quality is unrelated to the influence of evidence on the results of the NMA.

Figure 5.

Figure 5

Open in a new tab

Forest plot for headaches example, showing results of the threshold analysis applied to the combined evidence on each comparison and the GRADE quality ratings. The base-case optimal set of treatments is 3, 6, 7 (amitriptyline, topiramate, propranolol).

NT – no threshold: no amount of change in this direction would change the recommendation. At either side of the invariant interval are shown the new set of optimal treatments if threshold exceeded in this direction.

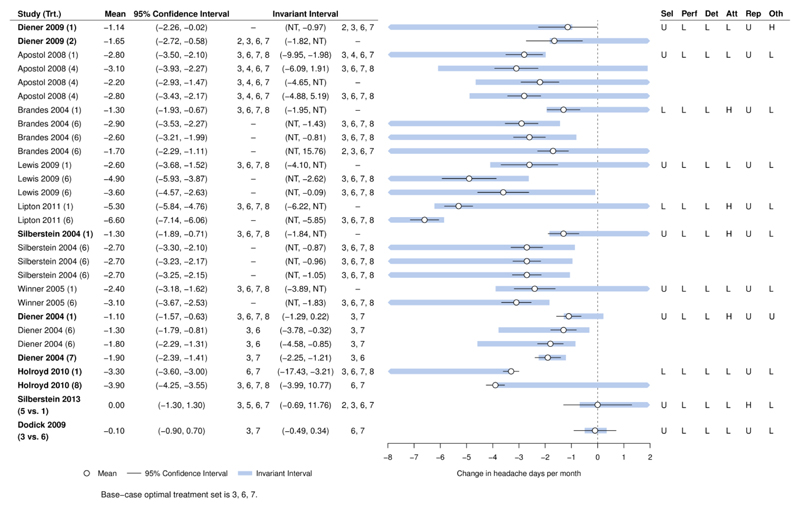
The combined body of evidence on a contrast often involves more than one study, and these are likely to have different characteristics, assessments of risk of bias, and to have greater or lesser influence on the treatment recommendation. Threshold analysis can also be applied to the individual study estimates, to determine sensitivity at the study level. Figure 6 gives the results of a study level threshold analysis, showing that the recommendation is sensitive to the level of imprecision in 6 out of 11 studies. The thresholds for the remaining five studies are larger, and a judgement is required as to whether changes of plausible magnitude and direction could surpass these thresholds (see also Supplementary Table 3). Thresholds which might plausibly result in a treatment dropping out of the recommended set are found for only two studies (Diener 2004 and Dodick 2009), so these studies may be prioritised for further scrutiny. Risk of Bias assessments (shown in Figure 6) are low or unknown in all domains for Dodick 2009, but there is a high risk of attrition bias for Diener 2004 which should be investigated further. For six studies, there are no thresholds in one direction, so no amount of change in this direction could alter the recommendation.

Figure 6.

Figure 6

Open in a new tab

Forest plot for headaches example, showing results of the threshold analysis applied to each study estimate. The base-case optimal set of treatments is 3, 6, 7 (amitriptyline, topiramate, propranolol). Bold study labels indicate studies with thresholds that lie within the 95% confidence interval. The Risk of Bias table is displayed to the right of the plot.

NT – no threshold: no amount of change in this direction would change the recommendation. At either side of the invariant interval are shown the new set of optimal treatments if threshold exceeded in this direction. Risk of bias is judged as low (L), high (H), or unknown (U) in six domains (selection, performance, detection, attrition, reporting, other).

The results of the threshold analysis should lead to further scrutiny of the study evidence to which the recommendation is sensitive and may placate any concerns raised about studies to which the treatment recommendation is not so sensitive.

Discussion

Threshold analysis is a powerful tool for analysts and decision makers to examine sensitivity of decisions to potential changes in the evidence. Conducting a threshold analysis requires a basic ability to prepare data in R and to call the R package. Interpretation of the results does not require technical knowledge and is best performed by clinical/content experts in a guideline development group with some statistical guidance. Frameworks such as GRADE cannot by themselves evaluate the robustness of a treatment recommendation because the influence of each piece of evidence on the recommendation is not accounted for. The thresholds and invariant intervals produced by a threshold analysis directly indicate how sensitive a decision is to each piece of evidence, which should then be combined with judgements of the plausible magnitude and direction of bias, informed by assessments such as the Cochrane Risk of Bias tool (20). The meta-epidemiological literature on the empirical evidence for bias is likely to be helpful in this regard, once potential biases in the evidence have been identified (21, 22). It is also possible to consider the effects of several potential changes simultaneously (14). The resulting multi-dimensional thresholds are straightforward to compute, but visualisation is challenging; some suggestions are discussed in (14).

Recently the GRADE Evidence to Decision (EtD) framework (23, 24) has been proposed to support the development of healthcare guidelines and policy. One of the criteria presented in EtD tables is the “certainty” of the evidence. The EtD framework proposes using GRADE to assess certainty. However, threshold analysis is arguably more relevant to the assessment of evidence certainty in the EtD context because it directly evaluates the sensitivity of treatment recommendations to changes in the evidence.

GRADE NMA, Salanti GRADE, and threshold analysis all require subjective judgement in their application or interpretation. However, the level of subjectivity differs between the three approaches. GRADE NMA and Salanti GRADE both make structured but subjective judgements of the quality of each piece of evidence. GRADE NMA then combines these judgements in a subjective manner to reach an overall judgement, whereas Salanti GRADE uses an objective statistical rationale to reach an overall judgement. Further subjectivity in interpreting the GRADE judgement is one of the challenges raised in a previous commentary (25), along with reproducibility and predictive validity. In comparison, threshold analysis is objective in deriving thresholds and determining the respective changes in treatment recommendation—these both follow from the mathematical structure of the NMA. Interpretation of these thresholds then requires subjective judgements of the plausible magnitude and direction of changes in the evidence, which can be informed by risk of bias assessments and the meta-epidemiological literature on bias (21, 22). This is not a trivial task and is a potential limitation, however the authors have piloted the method in a live guideline development scenario and found the required judgements to be feasible (26).

For simplicity, the two examples in this paper focussed on decisions based on efficacy; in reality, both guidelines ultimately made treatment recommendations based on cost-effectiveness (along with other considerations such as licensing arrangements in the UK), as is usual in guidelines produced by NICE. Threshold analysis is applicable within a cost-effectiveness framework and algebraic solutions may be found for simple economic models (14), however this is not possible in general. Alternative approaches to applying threshold analysis for cost-effectiveness decisions are therefore an area for further research. For decision rules based on statistical “significance” rather than on expected treatment effects, numerical methods are required to determine the thresholds. The current algebraic approach only determines the influence of the evidence on the point estimates and not on the uncertainty.

Threshold analysis is just one of several sensitivity analyses that may be used to assess the robustness of a NMA and the resulting recommendations. One common approach is to remove from the analysis all studies at high risk of bias. However, this may lead to issues such as disconnected networks or removing treatments of interest. Threshold analysis allows a more informative assessment of the potential impact of high-risk studies, whilst avoiding such problems. Meta-regression offers the possibility of adjusting for biases that are suspected to be present, but typically requires external evidence on bias (27–30). Threshold analysis is always possible, regardless of the number of studies in the analysis, since no bias-estimation is performed.

Whilst we have demonstrated the use of threshold analysis for NMA, the ideas and processes apply equally to pairwise meta-analysis as a special case. We suggest that threshold analysis is integrated into the guideline development process in the following manner. Prior to analysis, the included studies should be assessed for risk of bias (20, 31) and a decision rule formulated, as is current best practice. Once the (network) meta-analysis has been performed, undertake threshold analysis to determine the sensitivity to the evidence on individual comparisons (for NMA) and to each study. Further threshold analyses may then be used to address more specific concerns, such as biases in sets of treatment comparisons or studies. If sensitivities are identified, the plausible magnitude and direction of potential changes in the evidence should be investigated. The impact (if any) of plausible changes in the evidence is then easily determined, and decision makers can incorporate knowledge of robustness or sensitivity into their recommendations.

Supplementary Material

Supplementary Tables
Threshold analysis code
Appendices

Acknowledgements

Part of this work was carried out with funding from the Centre for Guidelines (CfG), NICE, through the NICE Guidelines Technical Support Unit, University of Bristol. SD was also part-funded by the UK Medical Research Council (MRC Grant MR/M005232/1). NJW was part funded by the MRC ConDuCT-II Hub for Trials Methodology Research (MR/K025643/1). Any views expressed in this work are those of the authors and not the funders.

The authors would like to acknowledge Dr Kathryn Hopkins, Technical Adviser at NICE CfG, for providing the Risk of Bias assessments for the headaches example, members of the UK GRADE Network Steering Group and the NICE NMA Working Group, and all NICE developers who commented on earlier versions of this work.

Footnotes

This is the prepublication, author-produced version of a manuscript accepted for publication in Annals of Internal Medicine. This version does not include post-acceptance editing and formatting. The American College of Physicians, the publisher of Annals of Internal Medicine, is not responsible for the content or presentation of the author-produced accepted version of the manuscript or any version that a third party derives from it. Readers who wish to access the definitive published version of this manuscript and any ancillary material related to this manuscript (e.g., correspondence, corrections, editorials, linked articles) should go to Annals.org or to the print issue in which the article appears. Those who cite this manuscript should cite the published version, as it is the official version of record.

References

  • 1.Lumley T. Network meta-analysis for indirect treatment comparisons. Statistics in Medicine. 2002;21(16):2313–24. doi: 10.1002/sim.1201. [DOI] [PubMed] [Google Scholar]
  • 2.Caldwell DM, Ades AE, Higgins JPT. Simultaneous comparison of multiple treatments: combining direct and indirect evidence. British Medical Journal. 2005;331(7521):897–900. doi: 10.1136/bmj.331.7521.897. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Lu GB, Ades AE. Assessing evidence inconsistency in mixed treatment comparisons. Journal of the American Statistical Association. 2006;101(474):447–59. [Google Scholar]
  • 4.Puhan MA, Schunemann HJ, Murad MH, Li T, Brignardello-Petersen R, Singh JA, et al. A GRADE Working Group approach for rating the quality of treatment effect estimates from network meta-analysis. Br Med J. 2014;349 doi: 10.1136/bmj.g5630. g5360. [DOI] [PubMed] [Google Scholar]
  • 5.Brignardello-Petersen R, Bonner A, Alexander PE, Siemieniuk RA, Furukawa TA, Rochwerg B, et al. Advances in the GRADE approach to rate the certainty in estimates from a network meta-analysis. J Clin Epidemiol. 2018;93:36–44. doi: 10.1016/j.jclinepi.2017.10.005. [DOI] [PubMed] [Google Scholar]
  • 6.Balshem H, Helfand M, Schunemann HJ, Oxman AD, Kunz R, Brozek J, et al. GRADE guidelines: 3. Rating the quality of evidence. J Clin Epidemiol. 2011;64(4):401–6. doi: 10.1016/j.jclinepi.2010.07.015. [DOI] [PubMed] [Google Scholar]
  • 7.GRADE Working Group. GRADE handbook for grading quality of evidence and strength of recommendations. [accessed 2018/09/03];2013 Available from: https://gdt.gradepro.org/app/handbook/handbook.html.
  • 8.Salanti G, Del Giovane C, Chaimani A, Caldwell DM, Higgins JP. Evaluating the quality of evidence from a network meta-analysis. PLoS One. 2014;9(7):e99682. doi: 10.1371/journal.pone.0099682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.CINeMA: Confidence in Network Meta-Analysis [Software] Institute of Social and Preventive Medicine, University of Bern; 2017. Available from: cinema.ispm.ch. [Google Scholar]
  • 10.Caldwell DM, Ades AE, Dias S, Watkins S, Li T, Taske N, et al. A threshold analysis assessed the credibility of conclusions from network meta-analysis. Journal of Clinical Epidemiology. 2016;7(15):68–7. doi: 10.1016/j.jclinepi.2016.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Thokala P, Duenas A. Multiple Criteria Decision Analysis for Health Technology Assessment. Value Health. 2012;15(8):1172–81. doi: 10.1016/j.jval.2012.06.015. [DOI] [PubMed] [Google Scholar]
  • 12.Stinnett AA, Mullahy J. Net health benefits: A new framework for the analysis of uncertainty in cost-effectiveness analysis. Medical Decision Making. 1998;18(2):S68–S80. doi: 10.1177/0272989X98018002S09. [DOI] [PubMed] [Google Scholar]
  • 13.Gray AM, Clarke PM, Wolstenholme JL, Wordsworth S. Applied methods of cost-effectiveness analysis in health care. Oxford ; New York: Oxford University Press; 2011. p. 313. [Google Scholar]
  • 14.Phillippo DM, Welton NJ, Dias S, Didelez V, Ades AE. Sensitivity of treatment recommendations to bias in network meta-analysis. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2018;181(3):843–67. doi: 10.1111/rssa.12341. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2018. [Google Scholar]
  • 16.National Collaborating Centre for Mental Health. Social Anxiety Disorder: Recognition, Assessment and Treatment [Full Guideline] Leicester and London: The British Psychological Society and the Royal College of Psychiatrists; 2013. [accessed 2018/01/16]. Available from: www.nice.org.uk/guidance/cg159. [Google Scholar]
  • 17.Mayo-Wilson E, Dias S, Mavranezouli I, Kew K, Clark DM, Ades AE, et al. Psychological and pharmacological interventions for social anxiety disorder in adults: a systematic review and network meta-analysis. Lancet Psychiatry. 2014;1:368–76. doi: 10.1016/S2215-0366(14)70329-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Cohen J. Statistical Power Analysis for the Behavioral-Sciences. Second edition. Hillsdale, New Jersey: Lawrence Erlbaum Associates; 1988. [Google Scholar]
  • 19.National Institute for Health and Care Excellence. Addendum to Clinical Guideline 150, Headaches in over 12s: diagnosis and management. [accessed 2018/01/16];2015 Available from: www.nice.org.uk/guidance/cg150. [PubMed]
  • 20.Higgins JPT, Altman DG, Gotzsche PC, Juni P, Moher D, Oxman AD, et al. The Cochrane Collaboration's tool for assessing risk of bias in randomised trials. British Medical Journal. 2011;343 doi: 10.1136/bmj.d5928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Savovic J, Jones HE, Altman DG, Harris RJ, Juni P, Pildal J, et al. Influence of Reported Study Design Characteristics on Intervention Effect Estimates From Randomized, Controlled Trials. Annals of Internal Medicine. 2012;157(6):429–38. doi: 10.7326/0003-4819-157-6-201209180-00537. [DOI] [PubMed] [Google Scholar]
  • 22.Chaimani A, Vasiliadis HS, Pandis N, Schmid CH, Welton NJ, Salanti G. Effects of study precision and risk of bias in networks of interventions: a network meta-epidemiological study. Int J Epidemiol. 2013;42(4):1120–31. doi: 10.1093/ije/dyt074. [DOI] [PubMed] [Google Scholar]
  • 23.Alonso-Coello P, Oxman AD, Moberg J, Brignardello-Petersen R, Akl EA, Davoli M, et al. GRADE Evidence to Decision (EtD) frameworks: a systematic and transparent approach to making well informed healthcare choices. 2: Clinical practice guidelines. Br Med J. 2016;353:i2089. doi: 10.1136/bmj.i2089. [DOI] [PubMed] [Google Scholar]
  • 24.Alonso-Coello P, Schunemann HJ, Moberg J, Brignardello-Petersen R, Akl EA, Davoli M, et al. GRADE Evidence to Decision (EtD) frameworks: a systematic and transparent approach to making well informed healthcare choices. 1: Introduction. Br Med J. 2016;353:i2016. doi: 10.1136/bmj.i2016. [DOI] [PubMed] [Google Scholar]
  • 25.Norris SL, Bero L. GRADE Methods for Guideline Development: Time to Evolve? Ann Intern Med. 2016;165(11):810–1. doi: 10.7326/M16-1254. [DOI] [PubMed] [Google Scholar]
  • 26.National Guideline Alliance. Specialist neonatal respiratory care for babies born preterm [GID-NG10039] [accessed 2018/10/24];2018 (In development). Available from: https://www.nice.org.uk/guidance/gid-ng10039/documents/evidence-review-2.
  • 27.Dias S, Welton NJ, Marinho VCC, Salanti G, Higgins JPT, Ades AE. Estimation and adjustment of bias in randomized evidence by using mixed treatment comparison meta-analysis. Journal of the Royal Statistical Society Series a-Statistics in Society. 2010;173:613–29. [Google Scholar]
  • 28.Moreno SG, Sutton AJ, Turner EH, Abrams KR, Cooper NJ, Palmer TM, et al. Novel methods to deal with publication biases: secondary analysis of antidepressant trials in the FDA trial registry database and related journal publications. Br Med J. 2009;339:b2981. doi: 10.1136/bmj.b2981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Turner RM, Spiegelhalter DJ, Smith GCS, Thompson SG. Bias modelling in evidence synthesis. Journal of the Royal Statistical Society Series a-Statistics in Society. 2009;172:21–47. doi: 10.1111/j.1467-985X.2008.00547.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Welton NJ, Ades AE, Carlin JB, Altman DG, Sterne JAC. Models for potentially biased evidence in meta-analysis using empirically based priors. Journal of the Royal Statistical Society Series a-Statistics in Society. 2009;172:119–36. [Google Scholar]
  • 31.Higgins J, Sterne J, Savović J, Page M, Hróbjartsson A, Boutron I, et al. A revised tool for assessing risk of bias in randomized trials. Cochrane Database of Systematic Reviews. 2016 doi: 10.1186/s13643-016-0259-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Tables
EMS82751-supplement-Supplementary_Tables.pdf (161.1KB, pdf)
Threshold analysis code
EMS82751-supplement-Threshold_analysis_code.zip (20.8KB, zip)
Appendices
EMS82751-supplement-Appendices.pdf (149.9KB, pdf)

RESOURCES