Abstract
We compile a large data set designed for the efficient benchmarking of exchange–correlation functionals for the calculation of electronic band gaps. The data set comprises information on the experimental structure and band gap of 472 nonmagnetic materials and includes a diverse group of covalent-, ionic-, and van der Waals-bonded solids. We used it to benchmark 12 functionals, ranging from standard local and semilocal functionals, passing through meta-generalized-gradient approximations, and several hybrids. We included both general purpose functionals, like the Perdew–Burke–Ernzerhof approximation, and functionals specifically crafted for the determination of band gaps. The comparison of experimental and theoretical band gaps shows that the modified Becke–Johnson is at the moment the best available density functional, closely followed by the Heyd–Scuseria–Ernzerhof screened hybrid from 2006 and the high-local-exchange generalized-gradient approximation.
1. Introduction
Since its first appearance more than 50 years ago, Kohn–Sham density-functional theory (DFT)1,2 has become pivotal in modern solid state physics.3 Coupled to the evolution of computational capabilities, it is no longer a mere companion to experimental work but stands on its own as a tool with predictive ability. Although the formulation of the theory is exact, all complexities of the many-body problem are cast into an unknown object, famously referred to as the exchange–correlation (xc) functional Exc. This is a crucial term, which has to be approximated in every numerical application of the theory. As a consequence, success or failure of DFT calculations rests solely on the validity of the chosen approximation to the xc functional.
Currently more than 400 xc functionals exist in the literature.4 Some of these are widely used and known, but most functionals do not find widespread use. Two striking examples are PBE5 and B3LYP,6 which have become the de facto standards within the physics and chemistry communities, respectively. Beyond these “Swiss-army knife” functionals, there exists a series of more specialized ones for particular uses. For example, PBEsol7,8 has been shown to improve the description of lattice parameters of solids, and HSE069 is the preferred functional for the calculation of band gaps of semiconductors.
There are several paths used to develop xc functionals. Some rely on exact limits and sum rules, and a deep understanding of the physics of correlated electron gases (e.g, the PBE,5 the AK13,10 or the SCAN11 functionals). Others use a more pragmatic and practical approach and rely on fitting experimental or high-quality theoretical results for atoms, molecules, or solids (e.g., the HCTH12−14 family, or the Minnesota family of functionals15). In any case, there is a lot of ingenuity and imagination involved in the creation of a functional, but these, of course, can never guarantee the quality of the final results. Therefore, benchmarking functionals in large data sets is perhaps as important as developing them. As such, in this Article, we are concerned with benchmarking a selection of approximations to the xc functionals for electronic band gaps of solids.
Band gaps are without doubt one of the most important quantities for electronic and optoelectronics applications. For example, the size of the band gap determines the absorption threshold and limits the maximum open circuit voltage of photovoltaic modules, and it is therefore a crucial factor in their efficiency. Also the frequency of the light emitted by a diode depends directly on the band gap, as does the transparency, or the lack thereof, of a given crystal. It is such a basic attribute that it is often the second property measured (or calculated) for any semiconductor, following the crystal structure of course.
In standard DFT the fundamental band gap is not directly given by the difference between the conduction band minima and valence band maxima. In fact, there is a contribution missing due to the discontinuity of the derivative of the xc functional with respect to the number of particles.16−18 Unfortunately, standard local density approximations (LDA) and generalized gradient approximations (GGA) lack this discontinuity, leading to band gaps that are approximately half of their experimental value. In the case of the meta-GGA and hybrid functionals, the orbital dependence renders the implementation of the Kohn–Sham scheme (through the optimized effective potential method19,20) very complicated. Therefore, these functionals are typically used through the minimization of the energy with respect to the Kohn–Sham orbitals, in what is called the generalized Kohn–Sham scheme.21,22 In this scheme, the Kohn–Sham band gap of a solid equals the fundamental gap for the approximate functional if the potential operator that enters the generalized Kohn–Sham equations is continuous and the density change is delocalized when an electron or hole is added.23 This helps explaining why band-gaps calculated with meta-GGAs and hybrid functionals are typically closer to experimental values than the ones obtained with the multiplicative potential that stems from a LDA or a GGA functional.24
Of course, several benchmarks of band gaps of semiconductors and insulators already appeared in the literature. However, such benchmarks typically contain somewhere from 10 to around 10025−30 systems. Reference (31) is a notable exception to this observation, containing a set of 270 inorganic compounds. These numbers are nevertheless small, in view of the diversity of crystalline semiconductors that one can find in nature. Not only may they contain any of the ∼100 chemical elements that constitute the periodic table, but they also exhibit different kinds of chemical bondings. In fact, we have semiconductors and insulators that are purely covalent (e.g., silicon, diamond), strongly ionic (e.g., NaCl), or even van der Waals bonded (such as the elemental solids made of rare gases). Ideally, to test functionals against any bias, and to assess them for the different situations one requires large and varied benchmark sets.
As such, our goals are 2-fold. First to compile a large data set of experimental band gaps (together with the corresponding experimental crystal structures). Second, to use it as an effective large-scale benchmark of some of the most used xc functionals for the determination of electronic gaps.
The rest of this Article is structured as follows. In secion 2 we give a brief overview of the properties of our selection of functionals, followed by a description of the construction of the benchmark data set and the details of the numerical methods. Results are then presented in section 5, and finally our conclusions are drawn in section 6.
2. Functionals
At the
lowest rung of Jacob’s Ladder,32 we find the LDA which, as its name well indicates, approximates
the xc energy at any given point in space r, by that
of a homogeneous electron gas with density n(r). This leads to a simple expression for the exchange energy
density33,34 in terms of the Wigner–Seitz radius 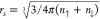 and the magnetization
density ζ =
(n↑ – n↓)/(n↑ + n↓), where n↑ and n↓ are the spin-up and spin-down
electronic densities. Correlation is more problematic, as no exact
analytic form is available. Because of this, several different fits
to Monte Carlo results are used, giving rise to the different correlation
functionals in the literature. In the current work we make use of
the Perdew–Zunger35 (PZ81) approximation,
which captures the spin dependency by interpolating between the para-
and ferromagnetic electron gases, as suggested by ref (36).
and the magnetization
density ζ =
(n↑ – n↓)/(n↑ + n↓), where n↑ and n↓ are the spin-up and spin-down
electronic densities. Correlation is more problematic, as no exact
analytic form is available. Because of this, several different fits
to Monte Carlo results are used, giving rise to the different correlation
functionals in the literature. In the current work we make use of
the Perdew–Zunger35 (PZ81) approximation,
which captures the spin dependency by interpolating between the para-
and ferromagnetic electron gases, as suggested by ref (36).
At the GGA level we first consider the functional of Perdew–Burke–Ernzerhof5 (PBE), the de facto standard functional in the physics community. By design, each part of PBE obeys some exact conditions. The exchange part must (i) scale correctly under the uniform density scaling and be exact for uniform densities, (ii) obey the exact spin-scaling relationship, (iii) recover the linear response of the LDA for small gradients, and (iv) satisfy the local Lieb–Oxford bound.37 The correlation has to (i) recover the exact second-order gradient expansion in the slowly varying limit, (ii) vanish in the rapidly varying limit, and (iii) scale correctly under an uniform scaling in the high-density limit. The explicit form of the PBE functional depends on four parameters (μ, κ, β, γ), whose values are fixed from theoretical considerations using the aforementioned set of conditions, making PBE a fully ab initio functional.
Another very popular GGA for the study of solids is PBEsol.8 It shares the same functional form as the PBE but sets μ = 10/81 (restoring the density-gradient expansion for the exchange) and β = 0.046. Compared to the PBE, this reparametrization yields improved results for the lattice constants of solids7 and for formation energies.38
The high-local exchange functional39 (HLE16) is a member of the Hamprecht–Cohen–Tozer–Handy (HCTH)12−14 family, and more specifically, it can be obtained with a rebalancing of the weights of the exchange and correlation components of HCTH/407.12 HLE16 neglects the constraints for the homogeneous electron gas and the limit of slowly varying densities but still obeys the exchange scaling condition. Furthermore, it has been shown to give band gaps comparable with those calculated with more expensive methods (except for systems with localized d states),25 at the expense of a rather poor performance for the relaxation of lattice parameters.39
Climbing to the meta-GGA rung of the Jacob’s ladder, we consider the Becke–Johnson40 (BJ) functional. This is a potential-only approximation to the exchange contribution of vxc, built to resemble the exact-exchange potential by using the Slater potential41 augmented by an additional term:
| 1 |
where the kinetic energy density is defined as
| 2 |
Besides correctly describing the homogeneous electron gas, it is exact for the hydrogen atom and reproduces the step-like structure of the exchange potential for atoms. Unfortunately, this functional is not gauge invariant nor exact for all one-electron systems42 and it asymptotically approaches a (spin-dependent) constant whose value depends on the eigenvalue of the highest occupied orbital. To build the BJ functional, we follow the common recipe in the literature to approximate the Slater potential with the Becke–Roussel (BR) formula43 and we add correlation at the level of the LDA.
The modified Becke–Johnson44 (mBJ) is an adaptation of the BJ potential, where each term is scaled by means of a new (density-dependent) parameter c:
| 3 |
with
| 4 |
The parameters α and β were originally obtained by fitting band gaps of all-electron calculations to experimental ones. The size of the band gap increases monotonically with c which, being larger than 1, somewhat corrects the underestimation of gaps by BJ.
We close the selection of meta-GGA’s with the strongly constrained and appropriately normed11 (SCAN) functional. This was designed to obey 17 exact constrains, essentially using a function α as a measure of electron localization (α ≈ 0 for single covalent bonds, α ≈ 1 for metallic bonds, α ≫ 1 for weak bonds), and using it to interpolate between well-approximated regimes. This machinery leads to a functional that is exact, or very close to it, for a diverse range of model systems. In terms of results, it represents a remarkable improvement for the calculation of formation energies with respect to PBE,45,46 although it tends to overestimate them for magnetic alloys by a factor of 2–3.47
The first hybrid functional we take into account is PBE0.48,49 This global hybrid uses a simple mixture of Hartree–Fock (HF) and PBE exchange,
| 5 |
A series of arguments exists to justify the use of a α = 1/4 mixing, and this is generally understood as an adequate value for a wide range of materials. However, we know that this functional tends to overestimate band gaps of semiconductors due to its constant mixing and to the lack of screening.50,51
The Heyd–Scuseria–Ernzerhof (HSE)9,52,53 functional improves upon the performance of global hybrids for solids by splitting the Coulomb interaction into short and long-range. The two ranges are determined by the function erfc(μr), where μ is a parameter. This separation opens the door to a continuum of possible parametrizations, among which we find HSE06,9 with μ = 0.11 and α = 0.25. This is possibly the most famous HSE member, and it is the state-of-the-art method used in the physics community for the determination of accurate band gaps.25,27
We consider an additional member of the hybrid family, namely, the HSE reparametrization from ref (54). The resulting functional, which we henceforth refer to as HSE14, uses μ = 0.5 and α = 0.6. This allows us to obtain a diagonal part of the dielectric tensor closer to that of Thomas–Fermi or of the random-phase approximation.54 The HSE14 choice of parameters was observed by its authors to improve the description of band gaps, at the cost of a worsening of thermochemistry results.
Lastly, we also consider two hybrids with density-dependent mixing parameters proposed by Marques et al.,50 namely, PBE0mix and HSEmix. These two hybrids make use of the correlation between the optimal mixing parameter of a material and the inverse of its low-frequency dielectric constant,50,55,56 approximating α ∼ 1/ϵ∞ via a simple global function g̅,
| 6 |
where the integral is taken over the unit cell. Similarly to the case of the mBJ functional, the resulting potential is not the derivative of the energy due to neglecting the functional derivative of the mixing parameter. Calculations with density-dependent mixing parameters showed improved results with respect to the use of the parent functionals for a set mostly composed of sp materials.50 As already observed by Marques et al.,50 it is not immediate to generalize this approach to non-sp materials.55
3. Data Set
For the creation of the band gap data set, we inspected the available literature for experimental data on band gaps. Given the huge volume of the literature available, this task is rather tedious but, fortunately, it was eased by some existing compilations.57,58 Besides these, several individual entries from the available literature were also used. The complete list of references is available as Supporting Information.
Unfortunately, the compilation of the experimental values suffered from a series of unavoidable issues. For example, it is very rare to find an indication of the experimental uncertainties in the measurement. This uncertainty is, of course, fundamental to have an idea of the accuracy of the experimental measurement and could certainly be used to weight the data points. Moreover, for several systems, different articles report very different estimates for the band gap, and often these discrepancies are not discussed. On the other extreme, materials that fail to attract mainstream interest have sometimes been measured only once, and the experiment can date back more than 50 years. We examined all sources and removed the data points that suffered severely from these problems.
Then, reported values of gaps often come from optical measurements (e.g., photoluminescence), as these experiments are relatively straightforward when compared to other methods. Optical absorption measures, of course, the optical gap, and this differs from the fundamental (photoemission) gap by the excitonic binding energy. It is true that the exciton binding energy can be of the order of several electronvolts for systems of reduced dimensionality.59,60 However, for bulk systems, this quantity is much smaller, usually of the order of tens of millielectronvolts. Additionally, the experimental determination of band gaps done via Tauc plots61 or reflectivity studies often passes by the analysis of low-intensity tails. These studies can provide quantitative information on band gaps, but inferences regarding their qualitative nature (direct vs indirect, allowed vs forbidden, etc.) are not trivial.
Temperature effects are another ubiquitous problem in the literature. Comparatively few gap measurements are performed at low temperature and many are reported at unspecified temperature. Since for most materials the optical band gap decreases with increasing temperature, this will naturally introduce a systematic error in comparison to the theoretical results. Moreover, we note that our calculations (as most other reported calculations) do not include zero-point effects. This can again lead to corrections of the order of tens of millielectronvolts (see, for example, Table 5 of ref (62)).
Another big issue that we encountered is the fact that experimental papers sometimes present insufficient information on the material beyond its composition. This problem can be particularly serious for materials that exhibit polymorphism. For the sake of reproducibility, we decided therefore to use only crystal structures that were present in both the inorganic crystal structure database63,64 (ICSD) and the materials project database.65 Furthermore, we only kept materials if enough crystallographic data (space group, Wyckoff positions, etc.) were available in the literature to index them to their respective entries in the materials databases: primary references were consulted to the best of our capacity and cases of inconclusive or contradictory data were discarded.
It is true that, on an individual basis, these issues are almost unavoidable. We estimate that this can lead all in all to uncertainties of the order of tenths of an electronvolt. However, we can greatly alleviate the problem thanks to statistics, by using a sufficiently large data set of materials.
In the definition of the benchmark data set we included also a few constraints coming from the computational side. First, hybrid functionals are rather expensive; therefore, few structures with more than 24 atoms in the unit cell (and none with more than 32) were considered. Second, materials with atoms for which no pseudopotential is available in the VASP distribution were discarded. Third, failure to converge calculations leads to discarding the material (this problem was met for several compounds containing cerium, for example).
As a last remark, we only included nonmagnetic materials. Magnetic systems are often found to be antiferromagnetic, with the band gap sometimes strongly dependent on the magnetic configuration. As the correct identification of the ground state magnetic configuration requires the construction of supercells, we estimated that the inclusion of magnetic materials goes beyond the scope of this Article.
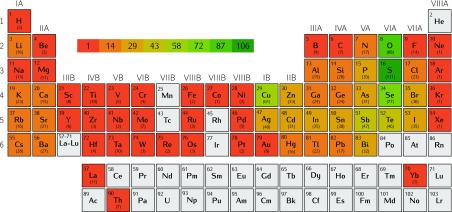
In the end, this selection process resulted in a final data set of 472 materials for which we can define an experimental band gap and experimental crystal structure. The complete data set is presented as Supporting Information and is openly available online.66Figure 1 gives an overview on the data set, showing the frequency of chemical elements in all considered materials. We can observe that the whole periodic table is represented. The most represented elements are, of course, the nonmetals, which are constituents of almost all semiconductors and insulators. This is particularly true for oxides, sulfides, and selenides that are rather common and thoroughly studied. The most underrepresented set of elements are the lanthanides and the actinides, due to a combination of lack of experiments, lack of pseudopotentials, and difficulties in converging the calculations.
Figure 1.
Frequency of elements in our data set. Gray boxes indicate elements not present in the data set.
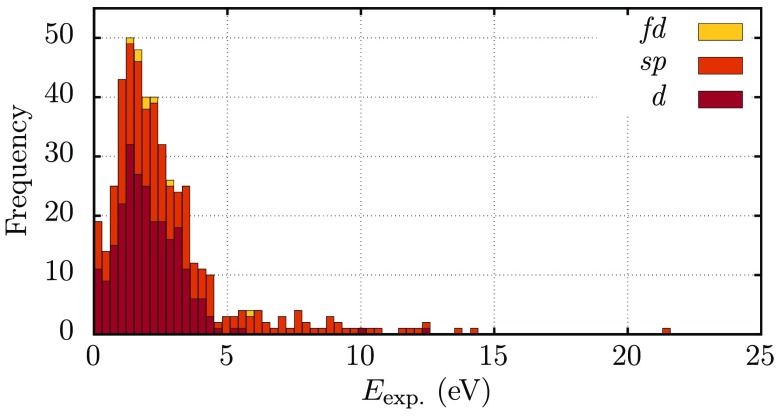
The distribution of experimental band gaps is displayed in Figure 2. Note that we separate our list in categories, differing by the type of elements in the chemical composition of the materials: set sp, containing only elements of groups Ia, IIa, and IIIa–VIIIa; set d, containing at least one transition metal; set f, containing at least one lanthanide or actinide. As our complete data set is rather large, the sp and d subsets are still statistically significant, and separating the data set in different families allows for more insight into the results.
Figure 2.
Histogram of experimental gaps in the data set. Boxes have a width of 0.3 eV. Colors represent the amount of each data set in the corresponding box. Description of the partial data sets is done in the main text.
The majority of the gaps clearly lies around the 2 eV region, with a noticeable fat tail extending from around 5 eV to more than 20 eV. The insulators with largest gaps are either van der Waals bonded (like Ne, Ar, or Kr) or are strongly ionic fluorides (such as LiF, YF3, MgF2, etc.). The oxide with largest gap is BeO, with a gap of 10.6 eV, and the chloride is LiCl, with a gap of 9.4 eV. On the opposite side of the scale one finds small-gap antimonides, selenides, and tellurides, such as PtSb2 (0.11 eV), ScNiSb (0.11 eV), PbSe (0.145 eV), Ag2Se (1.5 eV), etc. The elemental substance with the smallest gap in our data set is black phosphorus with a gap of 0.31 eV.
4. Methods
All calculations were performed using the Vienna ab initio simulation package (VASP; version 5.4)67 within the projector augmented wave formalism (PAW).68 A custom version of VASP, linked to Libxc,4,69 was also used to access xc functionals not implemented in the standard distribution, such as HLE16. We used the pseudopotentials distributed with the version 3.3.5 of VASP, as recommended by the materials project database.65 All calculations were performed at the experimental geometries, as provided by the ICSD database. We used geometries marked as high-quality data when available. Otherwise, we chose low-temperature data or the most recent experiment.
We calculated all band gaps as the difference of Kohn–Sham eigenvalues obtained from self-consistent calculations. To ensure a reliable value of the gap, the k-point grids were chosen so that the computed band gaps were converged within 50 meV for both PBE and HLE16 calculations. This resulted in grids with densities ranging from 500 to 4000 k-points per atom. Finally, all meta-GGA and hybrid calculations were performed by accounting for nonspherical contributions of the density gradient inside the PAW spheres.
To quantify the effect of spin–orbit coupling (SOC) on the band gap size, we also performed calculations with this term for the semilocal functionals (LDA, PBE, and HLE16).
5. Results
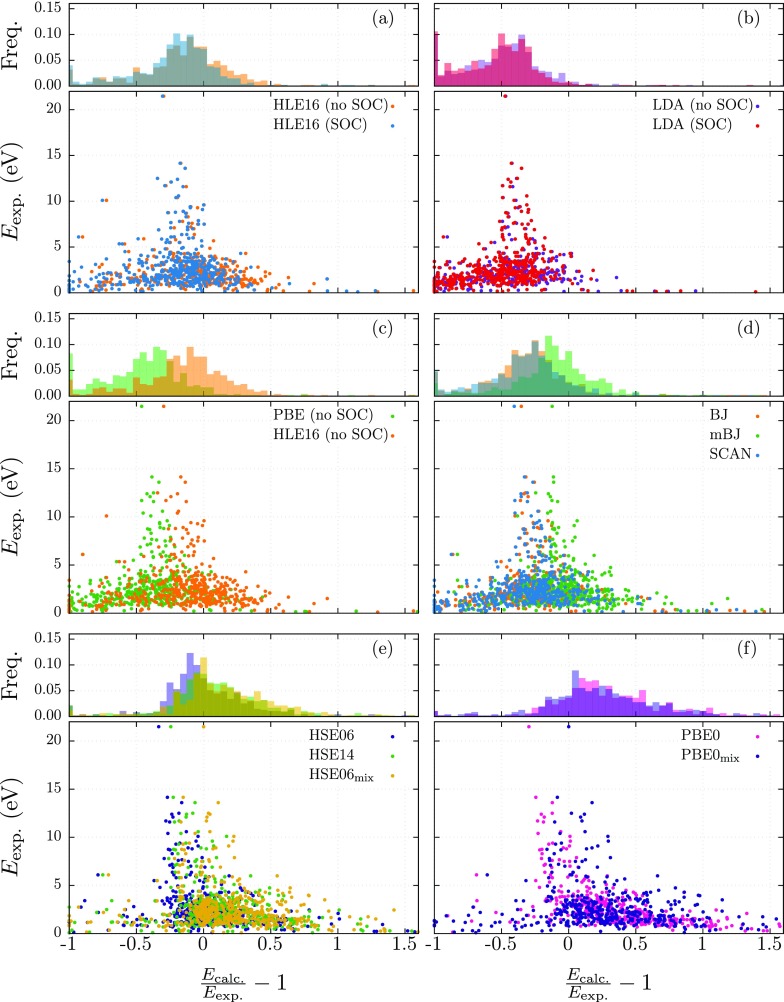
The comparison between calculated and experimental band gaps is presented graphically in Figure 3, while the tabulated list of results can be found as Supporting Information. To evaluate the performance of the functionals, we calculated several relevant statistical quantities70 (see Table 1), namely, Kendall’s71,72 rank correlation and Pearson’s correlation coefficients (τ and r, respectively); the coefficients of the linear fit (y = ax + b) to the calculated versus the experimental gaps; the mean absolute error, MAE = ∑in|yi – yi,exp|/n; the mean error, ME = ∑i(yi – yi,exp)/n; the variance, σ2 = ∑in(yi – yi,exp – ME)2/n; the median error (MnE); the interquartile range (IQR); the median of the absolute deviations from the median (MADM); the mean absolute percentage error, MAPE = 100 × ∑i|yi – yi,exp|/(n yi,exp); and the mean percentage error, MPE = 100 × ∑in(yi – yi,exp)/(nyi,exp). These quantities were obtained for the complete data set and for the different subsets of materials defined in the previous section. We also present in the Supporting Information a detailed analysis of the errors for the subsets containing any given element.
Figure 3.
Relative frequency and experimental band gap as a function of the ratio between theoretical and experimental band gaps for the different xc functionals: (a) comparison of HLE16 with and without spin–orbit coupling effect; (b) LDA with and without spin–orbit coupling; (c) comparison of GGA functionals; (d) comparison of mGGA functionals; (e) comparison of screened hybrid functionals; (f) comparison of PBE0 with PBE0mix. For representation purposes the x-axis of these plots was truncated at 1.6.
Table 1. Dataset Sizes, Number of Calculated False Metals, Mean Absolute Errors (MAE, in eV), Mean Absolute Percentage Errors (MAPE), Mean Percentage Errors (MPE), Mean Errors (ME, in eV), Variance (σ2, in eV2), Median Error (MnE, in eV), Median Absolute Deviation from the Median (MADM, in eV), Interquartile Range (IQR, in eV), Linear Fit (y = ax + b) Coefficients, Pearson’s Correlation Coefficient (r), and Kendall’s Rank Correlation Coefficient (τ) for Calculations of the Kohn–Sham Band Gap for All Considered Functionalsa.
| LDA | LDA (SOC) | PBE | PBE (SOC) | PBEsol | HLE16 | HLE16 (SOC) | BJ | mBJ | SCAN | HSE06 | HSE14 | HSEmix | PBE0 | PBE0mix | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sp | set size | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 |
| false metals | 13 | 14 | 11 | 13 | 11 | 6 | 8 | 9 | 4 | 8 | 4 | 4 | 2 | 2 | 2 | |
| Kendall τ | 0.76 | 0.77 | 0.76 | 0.78 | 0.76 | 0.77 | 0.80 | 0.78 | 0.79 | 0.79 | 0.79 | 0.79 | 0.79 | 0.79 | 0.77 | |
| Pearson r | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.96 | 0.96 | 0.97 | 0.95 | 0.95 | 0.95 | 0.96 | 0.95 | 0.95 | |
| a | 0.59 | 0.60 | 0.62 | 0.62 | 0.61 | 0.78 | 0.80 | 0.70 | 0.88 | 0.68 | 0.75 | 0.84 | 0.97 | 0.76 | 1.01 | |
| b (eV) | 0.06 | –0.05 | 0.13 | 0.01 | 0.07 | 0.37 | 0.13 | 0.20 | 0.21 | 0.24 | 0.55 | 0.47 | 0.30 | 1.09 | 0.39 | |
| MAE (eV) | 1.3 | 1.4 | 1.2 | 1.3 | 1.3 | 0.7 | 0.6 | 0.9 | 0.6 | 0.9 | 0.7 | 0.6 | 0.7 | 0.8 | 0.8 | |
| ME (eV) | –1.3 | –1.4 | –1.2 | –1.3 | –1.2 | –0.4 | –0.5 | –0.8 | –0.2 | –0.8 | –0.3 | –0.1 | 0.2 | 0.3 | 0.4 | |
| σ2 (eV2) | 1.9 | 1.8 | 1.7 | 1.7 | 1.8 | 1.0 | 0.8 | 1.2 | 0.6 | 1.4 | 1.1 | 0.9 | 0.8 | 1.1 | 1.0 | |
| MnE (eV) | –0.9 | –1.0 | –0.8 | –0.9 | –0.9 | –0.1 | –0.3 | –0.5 | –0.1 | –0.5 | –0.1 | 0.0 | 0.2 | 0.5 | 0.4 | |
| IQR (eV) | 1.3 | 1.2 | 1.2 | 1.1 | 1.2 | 0.9 | 0.8 | 1.1 | 0.8 | 1.0 | 0.8 | 0.8 | 0.8 | 0.8 | 1.2 | |
| MADM (eV) | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.4 | 0.3 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.6 | |
| MAPE (%) | 43.8 | 47.4 | 40.0 | 43.0 | 42.1 | 33.8 | 25.5 | 32.9 | 29.0 | 33.0 | 28.9 | 30.4 | 32.9 | 52.6 | 42.2 | |
| MPE (%) | –40.8 | –45.7 | –34.7 | 41.8 | –38.5 | 4.4 | –14.1 | –19.6 | 3.4 | –22.2 | 4.1 | 9.0 | 16.1 | 42.4 | 25.5 | |
| d | set size | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 |
| false metals | 22 | 20 | 19 | 17 | 24 | 8 | 7 | 11 | 7 | 10 | 5 | 4 | 2 | 3 | 2 | |
| Kendall τ | 0.61 | 0.62 | 0.63 | 0.64 | 0.62 | 0.67 | 0.68 | 0.72 | 0.71 | 0.66 | 0.72 | 0.73 | 0.73 | 0.72 | 0.73 | |
| Pearson r | 0.87 | 0.87 | 0.88 | 0.88 | 0.87 | 0.81 | 0.81 | 0.91 | 0.90 | 0.89 | 0.91 | 0.91 | 0.90 | 0.90 | 0.88 | |
| a | 0.66 | 0.65 | 0.67 | 0.67 | 0.67 | 0.65 | 0.65 | 0.73 | 0.82 | 0.75 | 0.90 | 1.02 | 1.14 | 0.92 | 1.20 | |
| b (eV) | –0.31 | –0.36 | –0.24 | –0.29 | –0.28 | 0.34 | 0.27 | –0.10 | 0.14 | –0.14 | 0.28 | 0.35 | 0.24 | 0.80 | 0.33 | |
| MAE (ev) | 1.0 | 1.1 | 0.9 | 1.0 | 1.0 | 0.5 | 0.6 | 0.7 | 0.4 | 0.7 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
| ME (ev) | –1.0 | –1.1 | –0.9 | –1.0 | –1.0 | –0.4 | –0.5 | –0.6 | –0.2 | –0.7 | 0.1 | 0.4 | 0.5 | 0.6 | 0.8 | |
| σ2 (eV2) | 0.5 | 0.5 | 0.4 | 0.4 | 0.5 | 0.6 | 0.6 | 0.3 | 0.4 | 0.4 | 0.3 | 0.4 | 0.6 | 0.4 | 0.8 | |
| MnE (eV) | –0.9 | –1.0 | –0.9 | –0.9 | –0.9 | –0.2 | –0.3 | –0.6 | –0.2 | –0.6 | 0.0 | 0.3 | 0.4 | 0.6 | 0.6 | |
| IQR (eV) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.6 | 0.6 | 0.6 | 0.6 | 0.7 | 0.5 | 0.6 | 0.7 | 0.6 | 0.8 | |
| MADM (eV) | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 | 0.4 | |
| MAPE (%) | 56.7 | 59.1 | 51.7 | 54.1 | 54.6 | 30.3 | 31.3 | 39.8 | 30.2 | 42.2 | 32.6 | 41.4 | 46.4 | 69.6 | 58.2 | |
| MPE (%) | –52.6 | –56.3 | –46.2 | –50.4 | –49.8 | –15.1 | –20.4 | –32.9 | –6.4 | –31.5 | 15.8 | 32.7 | 39.5 | 64.1 | 52.0 | |
| f | set size | 7 | 7 | 8 | 8 | 8 | 8 | 8 | 7 | 7 | 8 | 8 | 8 | 8 | 8 | 8 |
| false metals | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |
| Kendall τ | 0.90 | 0.90 | 0.71 | 0.71 | 0.64 | 0.71 | 0.71 | 0.90 | 0.81 | 0.64 | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | |
| Pearson r | 0.99 | 0.99 | 0.97 | 0.98 | 0.98 | 0.92 | 0.93 | 0.99 | 0.99 | 0.96 | 0.95 | 0.96 | 0.96 | 0.93 | 0.97 | |
| a | 0.92 | 0.91 | 0.95 | 0.94 | 0.96 | 0.63 | 0.63 | 0.97 | 1.04 | 1.00 | 1.22 | 1.37 | 1.44 | 1.23 | 1.53 | |
| b (eV) | –1.02 | –1.05 | –1.11 | –1.14 | –1.18 | –0.33 | –0.53 | –0.77 | –0.62 | –0.93 | –0.94 | –1.14 | –1.23 | –0.45 | –1.33 | |
| MAE (eV) | 1.2 | 1.3 | 1.2 | 1.3 | 1.3 | 1.2 | 1.5 | 0.9 | 0.5 | 0.9 | 0.5 | 0.5 | 0.6 | 0.6 | 0.6 | |
| ME (eV) | –1.2 | –1.3 | –1.2 | –1.3 | –1.3 | –1.2 | –1.5 | –0.9 | –0.5 | –0.9 | –0.4 | –0.2 | –0.2 | 0.1 | –0.0 | |
| σ2 (eV2) | 0.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.4 | 0.4 | 0.0 | 0.0 | 0.1 | 0.4 | 0.6 | 0.7 | 0.5 | 0.8 | |
| MnE (eV) | –1.2 | –1.2 | –1.2 | –1.2 | –1.3 | –1.0 | –1.3 | –0.9 | –0.6 | –0.8 | –0.3 | –0.1 | –0.1 | 0.3 | –0.0 | |
| IQR (eV) | 0.3 | 0.2 | 0.3 | 0.3 | 0.3 | 0.5 | 0.3 | 0.3 | 0.2 | 0.2 | 0.4 | 0.5 | 0.5 | 0.4 | 0.6 | |
| MADM (eV) | 0.2 | 0.0 | 0.2 | 0.1 | 0.2 | 0.2 | 0.1 | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 | 0.3 | 0.2 | 0.4 | |
| MAPE (%) | 57.3 | 59.8 | 59.0 | 61.6 | 62.2 | 53.7 | 64.2 | 40.4 | 25.4 | 44.9 | 25.9 | 25.8 | 25.6 | 25.3 | 26.7 | |
| MPE (%) | –57.3 | –59.8 | –59.0 | –61.6 | –62.2 | –53.7 | –64.2 | –40.4 | –25.4 | –44.9 | –24.1 | –18.9 | –16.1 | 1.4 | –12.0 | |
| all | set size | 471 | 471 | 472 | 472 | 472 | 472 | 472 | 471 | 471 | 472 | 472 | 472 | 472 | 472 | 472 |
| false metals | 35 | 34 | 31 | 31 | 36 | 15 | 16 | 20 | 11 | 19 | 10 | 9 | 5 | 5 | 4 | |
| Kendall τ | 0.68 | 0.69 | 0.69 | 0.70 | 0.68 | 0.71 | 0.73 | 0.74 | 0.75 | 0.72 | 0.75 | 0.75 | 0.75 | 0.75 | 0.74 | |
| Pearson r | 0.93 | 0.94 | 0.94 | 0.94 | 0.94 | 0.93 | 0.94 | 0.95 | 0.96 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.93 | |
| a | 0.62 | 0.62 | 0.64 | 0.64 | 0.63 | 0.78 | 0.78 | 0.72 | 0.88 | 0.70 | 0.78 | 0.86 | 0.98 | 0.78 | 1.03 | |
| b (eV) | –0.14 | –0.21 | –0.07 | –0.16 | –0.12 | 0.21 | 0.07 | 0.03 | 0.10 | 0.05 | 0.49 | 0.55 | 0.41 | 1.04 | 0.51 | |
| MAE (eV) | 1.2 | 1.2 | 1.1 | 1.1 | 1.1 | 0.6 | 0.6 | 0.8 | 0.5 | 0.8 | 0.5 | 0.6 | 0.6 | 0.8 | 0.8 | |
| ME (eV) | –1.2 | –1.2 | –1.0 | –1.1 | –1.1 | –0.4 | –0.5 | –0.7 | –0.2 | –0.7 | –0.1 | 0.2 | 0.4 | 0.5 | 0.6 | |
| σ2 (eV2) | 1.1 | 1.1 | 1.0 | 1.0 | 1.1 | 0.8 | 0.7 | 0.8 | 0.5 | 0.8 | 0.7 | 0.7 | 0.7 | 0.8 | 0.9 | |
| MnE (eV) | –0.9 | –1.0 | –0.8 | –0.9 | –0.9 | –0.2 | –0.3 | –0.5 | –0.1 | –0.6 | –0.0 | 0.2 | 0.3 | 0.6 | 0.5 | |
| IQR (eV) | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.8 | 0.7 | 0.8 | 0.7 | 0.8 | 0.7 | 0.7 | 0.8 | 0.6 | 0.9 | |
| MADM (eV) | 0.5 | 0.5 | 0.4 | 0.4 | 0.5 | 0.4 | 0.3 | 0.4 | 0.4 | 0.4 | 0.3 | 0.3 | 0.4 | 0.3 | 0.4 | |
| MAPE (%) | 50.7 | 53.7 | 46.4 | 49.0 | 48.9 | 32.4 | 29.1 | 36.6 | 29.6 | 38.0 | 30.8 | 36.0 | 39.7 | 60.9 | 50.2 | |
| MPE (%) | –47.2 | –51.4 | –41.1 | –46.6 | –44.8 | –6.7 | –18.2 | –26.8 | –2.1 | –27.4 | 9.6 | 20.8 | 27.7 | 52.9 | 38.6 |
Averages are done over the total dataset (all) and over the partial sets sp, d, and f, defined in the main text. A material is classified as a false metal if the calculated band gap is smaller than 0.01 eV.
We start our analysis by looking at the mean errors. As expected, LDA, PBE, and PBEsol present the highest errors among the tested (semi-) local functionals. The results in Table 1 show that LDA underestimates band gaps by 50%, while PBE follows closely with an underestimation of about 40%. They also yield a rather large number of false metals, namely, 35 (7.4%) for LDA and 31 (6.6%) for PBE. Finally, it is clear that sp materials are described much better than compounds including d or f electrons. However, a per-element analysis shows that the largest errors come from materials containing Ni, Pd, and Pt (for a total of 9 compounds) and are not uniformly distributed among the periodic table. Because of the gross underestimation of the band gap, spin–orbit coupling (which tends to close gaps; see Figure S1 of the Supporting Information) generally worsens these results, as seen by the increase of around 0.1 eV of the MAE.
Results obtained with PBEsol are very close to the ones from PBE. In fact, PBEsol almost constantly underestimates the gap of PBE by about 0.05 eV (see Figure S2 of the Supporting Information). This downshift can be understood from the reduction in the μ parameter that leads to a reduction of the exchange contribution to the energy, and thus to a lower estimate of the band gaps.
HLE16 clearly stands as the best functional of the GGA rung, with mean absolute and mean absolute percentage errors of 0.60 eV and 32%, respectively. This is perhaps not surprising as this functional was crafted to yield good band gaps. There is still, however, a small systematic error, with an overall tendency to underestimate band gaps (although much smaller than the LDA or the PBE). This can be seen from its mean (percentage) error of −0.37 eV (−6.7%). This underestimation is due to results for the d subset, as for the sp subset this functional actually overestimates gaps below 3 eV. Many of the largest errors come from compounds with Pb, Bi, Se, and Te. These errors are greatly reduced by the inclusion of spin–orbit coupling. From Table 1 we see that this term improves the HLE16 band gaps by an average of 3%. This improvement is nevertheless rather concentrated in a few materials containing heavy chemical elements. The largest corrections can be found for BiI3 (1.36 eV), CsPbBr3 (1.31 eV), PbI2 (1.24 eV), BiF3 (1.12 eV), PbTe (1.09 eV), Cs3Bi2Br9 (1.03 eV), TlI (1.03 eV), and PbCl2 (1.02 eV). Interestingly, this correction depends considerably on the xc functional used, and we can find systems where the spin–orbit correction is twice as large using HLE16 as using PBE (for example, for PbI2). This speaks against the common practice of calculating the SOC correction with LDA or PBE and adding it as a perturbative correction to a higher quality calculation of the band gap. Finally, we note that even if for specific systems the SOC correction can be rather large, on average the error introduced by neglecting SOC is still considerably smaller than the total average error in the band gap. Therefore, it is still meaningful to compare the quality of the functionals without SOC.
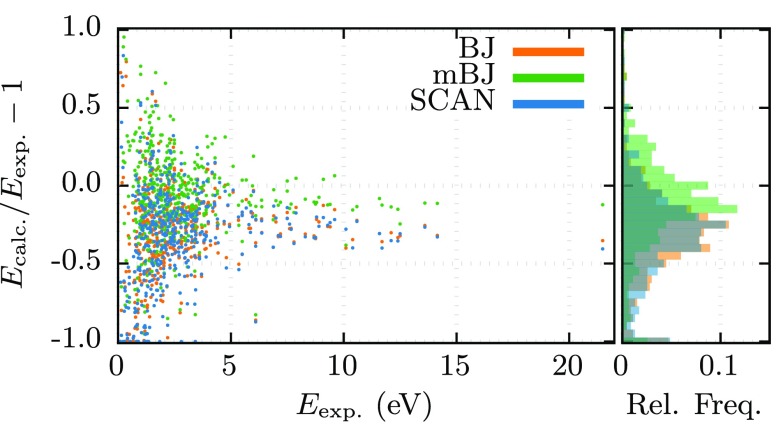
We move now to the meta-GGA rung, where all the functionals tested outperform both the LDA and the PBE. BJ and SCAN show quite a similar behavior, as they both tend to underestimate gaps by the same amount (∼0.8 eV, corresponding to 37–38%), and exhibit similar error dispersions (see Figure 3). As expected, mBJ corrects part of the underestimation of the band gaps (this fact is clearly visible in Figure 2). With a mean (percentage) error of just −0.22 eV (−2.1%), in addition to an (percentage) absolute error of about 0.5 eV (30%), mBJ ranks first among meta-GGA functionals (and, as we will see, among the entire selection of functionals). Curiously, it presents errors very similar to those of HLE16, showing the same tendency to overestimate gaps lower than 1 eV. It also performs badly for lead compounds, although this can certainly be improved by including spin–orbit coupling.
Among hybrid functionals, PBE0 shows the worst performance, as it grossly overestimates gaps smaller than 5 eV. For larger gaps the effect of the unscreened exact-exchange term is somewhat beneficial for PBE0, as the overestimation almost balances the systematic underestimation of PBE. Unfortunately, this compensation is not enough and PBE0 turns out to be the functional with the largest MAPE (61%) among all tested functionals.
Accounting for electron screening allows us to considerably improve upon the performance of PBE0. HSE06 has absolute errors (MAE of 0.53 eV; MAPE of 31%) comparable with those of mBJ. Its performance on the sp subset is slightly better than on the d subset (see Supporting Information). This improvement is largely due to the better description of gaps smaller than 5 eV. For larger values, HSE06 underestimates band gaps more than PBE0. Curiously, the MAPE for sp materials is not significantly smaller than for d materials, and it is actually larger than the MAPE for f-electron materials (although this may be an artifact due to the small size of the f subset). These results go against the conviction that standard density-functionals work much better for an sp system with respect to the more problematic d or f materials, which often exhibit very localized states.
Concerning the LDA, PBE, HLE16, mBJ, HSE06, and PBE0, our global error analysis is in qualitative agreement with that of ref (25). Quantitatively, our errors for HLE16, HSE06, and mBJ are larger (as expected, given the increased size of our data set), while those for LDA and PBE are smaller. This result could be explained by the absence in our data set of antiferromagnetic systems, which are particularly badly described by these functionals (and also by HLE1625).
HSE14 deteriorates the results with respect to HSE06, especially in the subset of d materials. As a result of the reparametrization, the error on band gaps larger than 5 eV is reduced, but at the same time smaller band gaps become less accurate. Apart from that, there is no qualitative difference between the two functionals with regards to their behavior across the periodic table.
We conclude this discussion with the analysis of the performance of the two hybrid functionals with a density-dependent mixing parameter of ref (50). HSEmix does not improve over HSE06 in the subset of d materials, exhibiting noticeably larger absolute errors and a tendency to overestimate band gaps. This is not a surprise, as the necessity to find a better functional form for the mixing in the case of localized electronic states has already been discussed in ref (50). The situation is different if one considers the subset of sp materials. Below 6 eV HSE06 is still better than HSEmix, presenting lower errors (both absolute and percentage). The situation is inverted for band gaps larger than 6 eV, where HSEmix takes the lead. The reason HSEmix does not yield results of similar quality over the entire range of gaps is not clear, as the global estimator of ref (50) was fitted to a set of sp materials with a wide range of band gaps (from Ge to Ne). Overall, both functionals end up to have very similar MAEs, even if HSE06 slightly underestimates band gaps and HSEmix slightly overestimates them. In view of the present results, the fitting of the density-dependent mixing functional should be re-evaluated, and possibly the functional form should be adapted to describe the screening due to more localized d and f electrons.
Similar observations can be done also for PBE0mix. The density-dependent mixing improves the description of some materials, notably noble gases, as well as Pb, Sb, and Bi. This improvement is visually represented in Figure 3f as a peak around 0 for the quantity Ecalc/Eexp – 1. Unfortunately, this trend is not maintained on a larger material range, and not even for all sp elements. With respect to PBE0, PBE0mix improves the MAPE (50% instead of 61%) and the MPE (39% instead of 53%) but its absolute errors are worse, with a ME of 0.59 eV and a MAE of 0.82 eV. This counterintuitive result comes from the better description of only the small band gaps by PBE0mix.
We can now verify whether the errors come from statistically different distributions by performing the Wilcoxon sign-ranked test.72,73 For two general paired data sets {xi} and {yi}, this test checks if the difference between pairs of values (xi – yi) is symmetric around zero, i.e., if both sets come from populations with the same distribution (null hypotheses). This is performed by comparing the obtained p-value to a certain significance level (α), which is usually taken as 0.05. If p > α, then the differences are symmetric around zero and both sets are assumed to come from the same distribution (at the given level of confidence).
We performed this test for the absolute errors and absolute percentage errors of each pair of functionals. The respective values of p are presented in Tables SI and SII of the Supporting Information. For the absolute errors (disregarding spin–orbit coupling), we expect all studied functionals to produce statistically different distributions with the exception of HLE16 and HSE06 (p = 0.14), HLE16 and HSE14 (p = 0.89), BJ and PBE0 (p = 0.89), BJ and PBE0mix (p = 0.88), mBJ and HSE06 (p = 0.36), SCAN and PBE0 (p = 0.66), and SCAN and PBE0mix (p = 0.60).
For the absolute percentage errors the statistically similar distributions are PBE and PBE0 (p = 0.19), HLE16 and mBJ (p = 0.21), HLE16 and HSE06 (p = 0.13), HLE16 and HSE14 (p = 0.32), BJ and SCAN (p = 0.10), mBJ and HSE06 (p = 0.86), and SCAN and PBE0mix (p = 0.19).
Still within the analysis of errors we see that although mBJ does not simultaneously present the best performance for the IQR, MADM and MnE, its values are consistently among the smallest. Within the total data set, the best performer for the IQR is PBE0 (IQR = 0.6 eV), for the MADM are HLE16 (with SOC), HSE06, HSE14, and PBE0 (with 0.3 eV), and for the absolute value of MnE is HSE06 (|MnE| = 0.01 eV). Notice, however, that the differences in these quantities among the best performing functionals are small, typically 0.1–0.2 eV.
We turn now to the linear fit (y = ax + b) to the calculated versus experimental data points. This is a traditional quantity used in this type of analysis because the ideal case (y = x) is immediately perceived in the respective plots. The values of the slope (a) and y-intercept (b) reflect the trend of the functional and eventual systematic errors. Ideally, a = 1 and b = 0 eV, but as expected, this is not the case for any functional. Instead, we must look at these two variables more as points on a Pareto curve.
The overall winner in this sense is mBJ, with a = 0.88 (close to the ideal value) and a small, but non-negligible, b = 0.10 eV. For HLE16, the inclusion of spin–orbit coupling greatly benefits this measure, by shifting b from 0.22 to 0.07 eV. Coupled with a slope of 0.78, HLE16 (with SOC) is also a good contender in this front. Curiously, HSE06mix and PBE0mix have the best slope (with a = 0.98 and 1.03, respectively) but their values for b (b = 0.41 and 0.51 eV) and variances (0.7 eV2 and 0.9 eV2) translate into a poor overall performance (as previously discussed). For the b parameter, the best performance in seen for BJ, with b = 0.03 eV.
Lastly we turn to the correlation coefficients. As it turns out, these two quantities are not particularly useful in the current context, as differences between functionals are small (lying in a 0.07 interval).
6. Conclusion
In conclusion, we compiled a data set of 472 experimental band gaps of semiconductors and insulators. Structural information on all materials presented can be easily obtained via well established crystal structure databases. This provides a data set for high-throughput exchange–correlation functional testing, which is the basis for true, large scale performance analysis of exchange–correlation functionals. This data set will be useful for perform further benchmark studies or to design improved functionals for band gap calculations.
Here we tested several functionals that are commonly used for band structure calculations. The selected functionals belong to different rungs of Jacob’s Ladder. Among these, the modified Becke–Johnson meta-GGA showed the best performance. This functional is closely followed by the HSE06 hybrid (which excels for semiconductors with band gaps in the range of 1–5 eV) and the HLE16 generalized gradient approximation. These results must nonetheless be weighted with consideration for the pros and cons of each functional. For example, from a computational perspective, HSE06 is by far the most demanding functional due to the effort required to evaluate the screened Fock term. The functional mBJ is considerably better in this front since it is of the semilocal type. However, it is generally observed that a large number of iterations is necessary to achieve self-consistent field convergence with mBJ (whatever the computer code used), while this is not the case with HLE16, which is basically as fast as PBE. Unfortunately, in spite of its good overall performance and speed, HLE16 is worse than mBJ for antiferromagnetic solids. In essence, we have three very good options, each with their own trade-offs that must be taken into consideration when choosing one from among them.
Lastly, we turn to the question of whether these functionals could be further improved. It is indeed difficult to improve HSE06 and mBJ, as they both already yield small systematic errors. Furthermore, these latter functionals depend solely on two parameters that are already well optimized. HLE16, however, has a large number of parameters that may provide enough flexibility for further improvement. Sadly, any further improvement in the band gaps will likely lead to a further deterioration of other properties, such as thermochemistry, geometries, or mechanical properties. In any case, we strongly believe that the existence of specialized functionals for the calculation of band gaps is fully justified in view of the practical importance of such calculations for optoelectronic applications.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.9b00322.
Figure S1, difference between the band gap with and without spin–orbit coupling for LDA, PBE, and HLE16 as a function of the experimental band gap for the entire data set; Figure S2, dispersion of band gaps with the PBE versus PBEsol functionals; Figures S3−S7, mean absolute percentage error for each element of the periodic table for the most relevant functionals; Figure S8, mean average percentage error and mean absolute percentage error for the different functionals as a function of the experimental band gap; Table SI, results for the p value obtained with the Wilcoxon signed-rank test for the absolute errors of each pair of functionals; Table SII, results for the p value obtained with the Wilcoxon signed-rank test for the absolute percentage errors of each pair of functionals (PDF)
Spreadsheet containing the data set and the calculated gaps (XLSX)
S.B. acknowledges partial support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the project BO 4280/8-1. Computational resources were provided by the Leibniz Supercomputing Centre through the projects pr62ja. M.A.L.M. acknowledges partial support from the German DFG through the project MA6787/6-1. F.T. acknowledges support from the Austrian Science Fund (FWF) through project F41 (SFB ViCoM) and P27738-N28.
The authors declare no competing financial interest.
Supplementary Material
References
- Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
- Burke K. Perspective on Density Functional Theory. J. Chem. Phys. 2012, 136, 150901. 10.1063/1.4704546. [DOI] [PubMed] [Google Scholar]
- Lehtola S.; Steigemann C.; Oliveira M. J.; Marques M. A. Recent Developments in Libxc – A Comprehensive Library of Functionals for Density Functional Theory. SoftwareX 2018, 7, 1–5. 10.1016/j.softx.2017.11.002. [DOI] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
- Csonka G. I.; Perdew J. P.; Ruzsinszky A.; Philipsen P. H. T.; Lebègue S.; Paier J.; Vydrov O. A.; Ángyán J. G. Assessing the Performance of Recent Density Functionals for Bulk Solids. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 155107. 10.1103/PhysRevB.79.155107. [DOI] [Google Scholar]
- Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
- Krukau A. V.; Vydrov O. A.; Izmaylov A. F.; Scuseria G. E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 2006, 125, 224106. 10.1063/1.2404663. [DOI] [PubMed] [Google Scholar]
- Armiento R.; Kümmel S. Orbital Localization, Charge Transfer, and Band Gaps in Semilocal Density-Functional Theory. Phys. Rev. Lett. 2013, 111, 036402. 10.1103/PhysRevLett.111.036402. [DOI] [PubMed] [Google Scholar]
- Sun J.; Ruzsinszky A.; Perdew J. P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. 10.1103/PhysRevLett.115.036402. [DOI] [PubMed] [Google Scholar]
- Boese A. D.; Handy N. C. A New Parametrization of Exchange–Correlation Generalized Gradient Approximation Functionals. J. Chem. Phys. 2001, 114, 5497–5503. 10.1063/1.1347371. [DOI] [Google Scholar]
- Boese A. D.; Doltsinis N. L.; Handy N. C.; Sprik M. New Generalized Gradient Approximation Functionals. J. Chem. Phys. 2000, 112, 1670–1678. 10.1063/1.480732. [DOI] [Google Scholar]
- Hamprecht F. A.; Cohen A. J.; Tozer D. J.; Handy N. C. Development and Assessment of New Exchange-Correlation Functionals. J. Chem. Phys. 1998, 109, 6264–6271. 10.1063/1.477267. [DOI] [Google Scholar]
- Peverati R.; Truhlar D. G. Quest for a Universal Density Functional: The Accuracy of Density Functionals across a Broad Spectrum of Databases in Chemistry and Physics. Philos. Trans. R. Soc., A 2014, 372, 20120476–20120476. 10.1098/rsta.2012.0476. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Density Functional Theory and the Band Gap Problem. Int. J. Quantum Chem. 1985, 28, 497–523. 10.1002/qua.560280846. [DOI] [Google Scholar]
- Perdew J. P.; Levy M. Physical Content of the Exact Kohn-Sham Orbital Energies: Band Gaps and Derivative Discontinuities. Phys. Rev. Lett. 1983, 51, 1884–1887. 10.1103/PhysRevLett.51.1884. [DOI] [Google Scholar]
- Sham L. J.; Schlüter M. Density-Functional Theory of the Energy Gap. Phys. Rev. Lett. 1983, 51, 1888–1891. 10.1103/PhysRevLett.51.1888. [DOI] [Google Scholar]
- Sharp R. T.; Horton G. K. A Variational Approach to the Unipotential Many-Electron Problem. Phys. Rev. 1953, 90, 317–317. 10.1103/PhysRev.90.317. [DOI] [Google Scholar]
- Talman J. D.; Shadwick W. F. Optimized Effective Atomic Central Potential. Phys. Rev. A: At., Mol., Opt. Phys. 1976, 14, 36–40. 10.1103/PhysRevA.14.36. [DOI] [Google Scholar]
- Seidl A.; Görling A.; Vogl P.; Majewski J. A.; Levy M. Generalized Kohn-Sham Schemes and the Band-Gap Problem. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 53, 3764–3774. 10.1103/PhysRevB.53.3764. [DOI] [PubMed] [Google Scholar]
- Neumann R.; Nobes R. H.; Handy N. C. Exchange Functionals and Potentials. Mol. Phys. 1996, 87, 1–36. 10.1080/00268979600100011. [DOI] [Google Scholar]
- Perdew J. P.; Yang W.; Burke K.; Yang Z.; Gross E. K. U.; Scheffler M.; Scuseria G. E.; Henderson T. M.; Zhang I. Y.; Ruzsinszky A.; Peng H.; Sun J.; Trushin E.; Görling A. Understanding Band Gaps of Solids in Generalized Kohn–Sham Theory. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 2801–2806. 10.1073/pnas.1621352114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z.-h.; Peng H.; Sun J.; Perdew J. P. More Realistic Band Gaps from Meta-Generalized Gradient Approximations: Only in a Generalized Kohn-Sham Scheme. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 205205. 10.1103/PhysRevB.93.205205. [DOI] [Google Scholar]
- Tran F.; Blaha P. Importance of the Kinetic Energy Density for Band Gap Calculations in Solids with Density Functional Theory. J. Phys. Chem. A 2017, 121, 3318–3325. 10.1021/acs.jpca.7b02882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coskun D.; Jerome S. V.; Friesner R. A. Evaluation of the Performance of the B3LYP, PBE0, and M06 DFT Functionals, and DBLOC-Corrected Versions, in the Calculation of Redox Potentials and Spin Splittings for Transition Metal Containing Systems. J. Chem. Theory Comput. 2016, 12, 1121–1128. 10.1021/acs.jctc.5b00782. [DOI] [PubMed] [Google Scholar]
- Garza A. J.; Scuseria G. E. Predicting Band Gaps with Hybrid Density Functionals. J. Phys. Chem. Lett. 2016, 7, 4165–4170. 10.1021/acs.jpclett.6b01807. [DOI] [PubMed] [Google Scholar]
- Peverati R.; Truhlar D. G. Performance of the M11-L Density Functional for Bandgaps and Lattice Constants of Unary and Binary Semiconductors. J. Chem. Phys. 2012, 136, 134704. 10.1063/1.3698285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crowley J. M.; Tahir-Kheli J.; Goddard W. A. Resolution of the Band Gap Prediction Problem for Materials Design. J. Phys. Chem. Lett. 2016, 7, 1198–1203. 10.1021/acs.jpclett.5b02870. [DOI] [PubMed] [Google Scholar]
- Tran F.; Ehsan S.; Blaha P. Assessment of the GLLB-SC Potential for Solid-State Properties and Attempts for Improvement. Phys. Rev. Mater. 2018, 2, 023802. 10.1103/PhysRevMaterials.2.023802. [DOI] [Google Scholar]
- Lee J.; Seko A.; Shitara K.; Nakayama K.; Tanaka I. Prediction Model of Band Gap for Inorganic Compounds by Combination of Density Functional Theory Calculations and Machine Learning Techniques. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 115104. 10.1103/PhysRevB.93.115104. [DOI] [Google Scholar]
- Perdew J. P. Jacob’s Ladder of Density Functional Approximations for the Exchange-Correlation Energy. AIP Conf. Proc. 2000, 1–20. 10.1063/1.1390175. [DOI] [Google Scholar]
- Dirac P. A. M. Note on Exchange Phenomena in the Thomas Atom. Math. Proc. Cambridge Philos. Soc. 1930, 26, 376. 10.1017/S0305004100016108. [DOI] [Google Scholar]
- Bloch F. Bemerkung zur Elektronentheorie des Ferromagnetismus und der elektrischen Leitfähigkeit. Eur. Phys. J. A 1929, 57, 545–555. 10.1007/BF01340281. [DOI] [Google Scholar]
- Perdew J. P.; Zunger A. Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B: Condens. Matter Mater. Phys. 1981, 23, 5048–5079. 10.1103/PhysRevB.23.5048. [DOI] [Google Scholar]
- Barth U v.; Hedin L A Local Exchange-Correlation Potential for the Spin Polarized Case. i. J. Phys. C: Solid State Phys. 1972, 5, 1629–1642. 10.1088/0022-3719/5/13/012. [DOI] [Google Scholar]
- Lieb E. H.; Oxford S. Improved Lower Bound on the Indirect Coulomb Energy. Int. J. Quantum Chem. 1981, 19, 427–439. 10.1002/qua.560190306. [DOI] [Google Scholar]
- Sarmiento-Pérez R.; Botti S.; Marques M. A. L. Optimized Exchange and Correlation Semilocal Functional for the Calculation of Energies of Formation. J. Chem. Theory Comput. 2015, 11, 3844–3850. 10.1021/acs.jctc.5b00529. [DOI] [PubMed] [Google Scholar]
- Verma P.; Truhlar D. G. HLE16: A Local Kohn–Sham Gradient Approximation with Good Performance for Semiconductor Band Gaps and Molecular Excitation Energies. J. Phys. Chem. Lett. 2017, 8, 380–387. 10.1021/acs.jpclett.6b02757. [DOI] [PubMed] [Google Scholar]
- Becke A. D.; Johnson E. R. A Simple Effective Potential for Exchange. J. Chem. Phys. 2006, 124, 221101. 10.1063/1.2213970. [DOI] [PubMed] [Google Scholar]
- Slater J. C. A Simplification of the Hartree-Fock Method. Phys. Rev. 1951, 81, 385–390. 10.1103/PhysRev.81.385. [DOI] [Google Scholar]
- Räsänen E.; Pittalis S.; Proetto C. R. Universal Correction for the Becke–Johnson Exchange Potential. J. Chem. Phys. 2010, 132, 044112 10.1063/1.3300063. [DOI] [PubMed] [Google Scholar]
- Becke A. D.; Roussel M. R. Exchange Holes in Inhomogeneous Systems: A Coordinate-Space Model. Phys. Rev. A: At., Mol., Opt. Phys. 1989, 39, 3761–3767. 10.1103/PhysRevA.39.3761. [DOI] [PubMed] [Google Scholar]
- Tran F.; Blaha P. Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Phys. Rev. Lett. 2009, 102, 116401. 10.1103/PhysRevLett.102.226401. [DOI] [PubMed] [Google Scholar]
- Isaacs E. B.; Wolverton C. Performance of the Strongly Constrained and Appropriately Normed Density Functional for Solid-State Materials. Phys. Rev. Mater. 2018, 2, 063801. 10.1103/PhysRevMaterials.2.063801. [DOI] [Google Scholar]
- Zhang Y.; Kitchaev D. A.; Yang J.; Chen T.; Dacek S. T.; Sarmiento-Pérez R. A.; Marques M. A. L.; Peng H.; Ceder G.; Perdew J. P.; Sun J. Efficient First-Principles Prediction of Solid Stability: Towards Chemical Accuracy. Npj Comput. Mater. 2018, 4, 9. 10.1038/s41524-018-0065-z. [DOI] [Google Scholar]
- Romero A. H.; Verstraete M. J. From One to Three, Exploring the Rungs of Jacob’s Ladder in Magnetic Alloys. Eur. Phys. J. B 2018, 91, 193. 10.1140/epjb/e2018-90275-5. [DOI] [Google Scholar]
- Adamo C.; Barone V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0Model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
- Perdew J. P.; Ernzerhof M.; Burke K. Rationale for Mixing Exact Exchange with Density Functional Approximations. J. Chem. Phys. 1996, 105, 9982–9985. 10.1063/1.472933. [DOI] [Google Scholar]
- Marques M. A. L.; Vidal J.; Oliveira M. J. T.; Reining L.; Botti S. Density-Based Mixing Parameter for Hybrid Functionals. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 035119. 10.1103/PhysRevB.83.035119. [DOI] [Google Scholar]
- Engel E.; Dreizler R. M.. Density Functional Theory - An Advanced Course; Springer-Verlag: Berlin, Heidelberg, 2013; OCLC 922647081. [Google Scholar]
- Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 2003, 118, 8207–8215. 10.1063/1.1564060. [DOI] [Google Scholar]
- Heyd J.; Scuseria G. E.; Ernzerhof M. Erratum: “Hybrid Functionals Based on a Screened Coulomb Potential” [J. Chem. Phys. 118, 8207 (2003)]. J. Chem. Phys. 2006, 124, 219906. 10.1063/1.2204597. [DOI] [Google Scholar]
- Freysoldt C.; Grabowski B.; Hickel T.; Neugebauer J.; Kresse G.; Janotti A.; Van de Walle C. G. First-Principles Calculations for Point Defects in Solids. Rev. Mod. Phys. 2014, 86, 253–305. 10.1103/RevModPhys.86.253. [DOI] [Google Scholar]
- Koller D.; Blaha P.; Tran F. Hybrid Functionals for Solids with an Optimized Hartree–Fock Mixing Parameter. J. Phys.: Condens. Matter 2013, 25, 435503. 10.1088/0953-8984/25/43/435503. [DOI] [PubMed] [Google Scholar]
- Skone J. H.; Govoni M.; Galli G. Self-Consistent Hybrid Functional for Condensed Systems. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 195112. 10.1103/PhysRevB.89.195112. [DOI] [Google Scholar]
- Madelung O.Semiconductors: Data Handbook; Springer: Berlin, Heidelberg, 2004. [Google Scholar]
- Kiselyova N. N.; Dudarev V. A.; Korzhuyev M. A. Database on the Bandgap of Inorganic Substances and Materials. Inorg. Mater. Appl. Res. 2016, 7, 34–39. 10.1134/S2075113316010093. [DOI] [Google Scholar]
- Vilhena J. G.; Botti S.; Marques M. A. L. Excitonic Effects in the Optical Properties of CdSe Nanowires. Appl. Phys. Lett. 2010, 96, 123106. 10.1063/1.3368126. [DOI] [Google Scholar]
- Wirtz L.; Marini A.; Rubio A. Excitons in Boron Nitride Nanotubes: Dimensionality Effects. Phys. Rev. Lett. 2006, 96, 126104. 10.1103/PhysRevLett.96.126104. [DOI] [PubMed] [Google Scholar]
- Viezbicke B. D.; Patel S.; Davis B. E.; Birnie D. P. Evaluation of the Tauc Method for Optical Absorption Edge Determination: ZnO Thin Films as a Model System: Tauc Method for Optical Absorption Edge Determination. Phys. Status Solidi B 2015, 252, 1700–1710. 10.1002/pssb.201552007. [DOI] [Google Scholar]
- Chen W.; Miceli G.; Rignanese G.-M.; Pasquarello A. Nonempirical Dielectric-Dependent Hybrid Functional with Range Separation for Semiconductors and Insulators. Phys. Rev. Mater. 2018, 2, 073803. 10.1103/PhysRevMaterials.2.073803. [DOI] [Google Scholar]
- Bergerhoff G.; Hundt R.; Sievers R.; Brown I. D. The Inorganic Crystal Structure Data Base. J. Chem. Inf. Model. 1983, 23, 66–69. 10.1021/ci00038a003. [DOI] [Google Scholar]
- Belsky A.; Hellenbrandt M.; Karen V. L.; Luksch P. New Developments in the Inorganic Crystal Structure Database (ICSD): Accessibility in Support of Materials Research and Design. Acta Crystallogr., Sect. B: Struct. Sci. 2002, 58, 364–369. 10.1107/S0108768102006948. [DOI] [PubMed] [Google Scholar]
- Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G.; Persson K. A. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 2013, 1, 011002 10.1063/1.4812323. [DOI] [Google Scholar]
- https://docs.google.com/spreadsheets/d/e/2PACX-1vTTXWmdw86kBsJ8kVD8m_VegaVez62W4tvm4-BXcY6F_O7zGyOVmfp6IbOsgzc7kzK_KXGF4V1Xu6Yd/pubhtml?gid=0&single=true.
- Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Marques M. A.; Oliveira M. J.; Burnus T. Libxc: A Library of Exchange and Correlation Functionals for Density Functional Theory. Comput. Phys. Commun. 2012, 183, 2272–2281. 10.1016/j.cpc.2012.05.007. [DOI] [Google Scholar]
- Civalleri B.; Presti D.; Dovesi R.; Savin A. In Chemical Modelling; Springborg M., Ed.; Royal Society of Chemistry: Cambridge, 2012; Vol. 9; pp 168–185. [Google Scholar]
- Kendall M. G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. 10.1093/biomet/30.1-2.81. [DOI] [Google Scholar]
- Jones E.; Oliphant T.; Peterson P.. SciPy: Open source scientific tools for Python. 2001; http://www.scipy.org/, accessed 2019.
- Wilcoxon F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80. 10.2307/3001968. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.