Abstract

Molecular mechanics force field parameters for macromolecules, such as proteins, are traditionally fit to reproduce experimental properties of small molecules, and thus, they neglect system-specific polarization. In this paper, we introduce a complete protein force field that is designed to be compatible with the quantum mechanical bespoke (QUBE) force field by deriving nonbonded parameters directly from the electron density of the specific protein under study. The main backbone and sidechain protein torsional parameters are rederived in this work by fitting to quantum mechanical dihedral scans for compatibility with QUBE nonbonded parameters. Software is provided for the preparation of QUBE input files. The accuracy of the new force field, and the derived torsional parameters, is tested by comparing the conformational preferences of a range of peptides and proteins with experimental measurements. Accurate backbone and sidechain conformations are obtained in molecular dynamics simulations of dipeptides, with NMR J coupling errors comparable to the widely used OPLS force field. In simulations of five folded proteins, the secondary structure is generally retained, and the NMR J coupling errors are similar to standard transferable force fields, although some loss of the experimental structure is observed in certain regions of the proteins. With several avenues for further development, the use of system-specific nonbonded force field parameters is a promising approach for next-generation simulations of biological molecules.
1. Introduction
Molecular mechanics (MM) force fields for biomolecular simulations have been under continuous development for many years.1−5 In traditional transferable force fields, every atom in a molecule is assigned a type based on its atomic number, bonding, and local chemical environment. The atom type then dictates the parameters that are used to model that atom’s interactions.3 The force field parameters for each atom type are stored as a library, which is built by carefully reproducing the experimental or quantum mechanical properties of a benchmark set of small molecules.2−7 Due to the infeasibility of accurately parameterizing all of chemical space, a balance must be made between the size of the library and potential inaccuracy due to transferring parameters to molecules outside the fitting set. In many cases, it is acknowledged that transferable force fields are not sufficiently accurate.8 When building force fields for small molecules, the atomic charges are usually assigned in a system-specific or “bespoke” manner, using methods such as RESP, CM1, or AM1-BCC.9−13 This is because it is well-known that atomic charges polarize in response to their chemical environment (for example, the presence of electron-donating or electron-withdrawing groups).8 Bespoke charges are usually assumed to be compatible with the fixed Lennard-Jones parameters of the force field, although these have also been shown to be dependent on the local environment of the atom.14 Although proteins must also experience polarization effects in both the charges and Lennard-Jones parameters, protein force field parameters have always, to date, been assigned from a transferable library.1−3,15 This leads to an inconsistency in the parametrization strategy used for protein force fields and bespoke small-molecule force fields. This is potentially problematic when studying properties that depend on the electrostatic potentials of proteins, such as their interactions with small molecules, and there is no clear way around this using traditional force field fitting methods.
To improve the consistency between charge and Lennard-Jones parameters and also reduce the reliance on fitting to experimental data, one could either directly fit nonbonded MM parameters to reproduce quantum mechanical (QM) energies and forces16−19 or derive the nonbonded parameters of the force field directly from QM. In the latter approach, the QM interaction energy may be broken down into physically motivated components using intermolecular perturbation theory,20−22 although these methods are limited to quite small system sizes. Encouragingly, Grimme’s quantum mechanically derived force field (QMDFF) method is capable of outputting bespoke nonbonded force field parameters for molecules comprising more than 100 atoms.23 Despite using fixed point charges, with no explicit polarization term, the bespoke force field reproduces both QM inter- and intramolecular energies to an accuracy of around 1 kcal/mol for small-molecule benchmarks.
In recent years, we have been following a similar strategy to Grimme’s QMDFF, focusing more on condensed phase properties and heterogeneous systems.24,25 The basis of this approach is the density derived electrostatic and chemical (DDEC) atoms-in-molecule (AIM) scheme,26,27 which partitions the total electron density into approximately spherical atom-centered basins. Atomic charges are derived by integrating the atomic electron density over all space, and in contrast to direct fitting of the QM electrostatic potential (ESP charges), it is possible to derive chemically meaningful DDEC atomic electron densities and charges for both surface and buried atoms.28 A further advantage of this approach is that the Lennard-Jones parameters may also be computed directly from the atomic electron densities, using methods based on the Tkatchenko–Scheffler relations that are commonly used to incorporate dispersion effects into density functional theory (DFT) calculations.14,24 Similar to the Grimme approach, these nonbonded parameters are derived from a single QM optimized structure, which would be problematic if the charges show strong conformation dependence. However, Manz and Sholl have demonstrated that DDEC charges are transferable between different conformations of a molecule (as measured by their ability to recreate the QM electrostatic potential), and they concluded that the charges are suitable for the construction of flexible force fields.27 Furthermore, it should be noted that AIM electron density partitioning lends itself naturally to the derivation of both off-site charges to model electron anisotropy (such as lone pairs and σ-holes)25 and atomic polarizabilities,29 although we have not yet investigated a fully polarizable force field.
In keeping with our goal of deriving force field parameters directly from QM, rather than fitting to experiment, we have supplemented the AIM nonbonded parameters with harmonic bond and angle parameters derived directly from the QM Hessian matrix.30 There are a number of methods available for deriving bonded parameters from the QM Hessian matrix,23,31 but our recent adaptation of the Seminario method32 (which we named the modified Seminario method) is conceptually quite straightforward while yielding parameters that reproduce QM vibrational frequencies with a mean unsigned error (MUE) of 49 cm–1, below that of OPLS (59 cm–1). Collectively, we have named this method as the quantum mechanical bespoke (QUBE) force field. This name reflects the fact that force field parameters are derived by the user specifically for the small molecule under study, directly from QM calculations. We have released a software toolkit (QUBEKit) that facilitates the derivation of small organic molecule force field parameters and also allows the user to derive the positions of off-site charges to model anisotropic electron density and to fit dihedral parameters to QM torsion scans.25 QUBE force fields have been derived for 109 small organic molecules and yield mean unsigned errors of 0.024 g/cm3, 0.79 kcal/mol, and 1.17 kcal/mol in computed liquid density, heat of vaporization, and free energy of hydration, respectively.25 These results are competitive with standard transferable force fields, which have been extensively fit to properties such as these.
To achieve our goal of employing the QUBE force field in computer-aided drug design applications, we require a compatible protein force field. Since the nonbonded parametrization strategy employed in QUBE is very different to that used in the standard biomolecular force fields (e.g., AMBER, OPLS, and CHARMM), there is no reason to believe that they are compatible. However, by implementing the AIM nonbonded parameter derivation methods in the ONETEP linear-scaling density functional theory (DFT) software,33 we have shown that it is feasible to derive these charges and Lennard-Jones parameters for entire proteins.24 In this way, the number of fitting parameters is substantially reduced, and we have a consistent parametrization approach that can be applied to both small and large molecules, including entire biomolecular assemblies. Since, in this approach, all nonbonded parameters are derived from a single QM calculation, both the charge and Lennard-Jones parameters naturally include the native state polarization effects of the environment. Importantly, we have shown that protein charges derived using DDEC electron density partitioning recreate the underlying QM electrostatic potential with high accuracy, and that charges derived for an NMR ensemble of BPTI protein structures are not too conformation-dependent (standard deviations per residue less than 0.04 e).34 This is in contrast to the performance of RESP charges, which have been shown to be significantly more conformation-dependent for an ensemble of polypeptide structures.35 Additional simulations demonstrated the feasibility and advantages of deriving bespoke parameters for a protein–ligand complex. The computed relative binding free energy of indole and benzofuran to the lysozyme protein using the environment-specific force fields (−0.4 kcal/mol) was in excellent agreement with experiment (−0.6 kcal/mol) and was substantially more accurate than standard force fields (−2.4 kcal/mol). However, the force field was in need of further development as the bespoke nonbonded terms were used in combination with standard OPLS-AA bonded parameters. The use of these parameters potentially limits the accuracy of the force field due to interdependency between the bonded terms, particularly the torsional parameters, and the nonbonded components of the force field. This issue is the subject of the current paper.
In standard transferable force fields, the torsional component is typically parameterized using QM dihedral energy scans, with the difference between analogous MM and QM energy scans minimized by fitting the torsional parameters.1 Reparameterization of the torsional terms has been shown to be a crucial step in improving the accuracy of force fields, and this has recently been demonstrated for AMBER ff15ipq, CHARMM36, and OPLS-AA/M.1,2,15 Bond and angle reparameterization has also been shown to be an essential stage in improving the accuracy of biomolecular force fields,2,36 although it is not so frequently carried out. Since it is not currently feasible to derive accurate QM Hessian matrices for entire proteins, we have used the modified Seminario method to compute a complete set of bond and angle parameters for the 20 naturally occurring amino acids.30 This work focuses on the remaining component of the force field, namely, the refitting of key torsional parameters that describe the backbone and sidechain dynamics of an amino acid. The methods and validation tests broadly follow the approaches employed in the development of OPLS-AA/M, the latest OPLS force field.1 Torsional parameters are fit by minimizing the differences between multiple QM and MM potential energy scans of dipeptide backbone and sidechain dihedral angles. Our overall goal is to test the extent to which bespoke nonbonded parameters may be combined with libraries of bonded parameters to produce a protein force field that is compatible with our QUBE small-molecule force field for use in computer-aided drug design applications.
The performance of the QUBE protein force field is tested through comparisons between experiment and molecular dynamics (MD) simulations for a set of 20 dipeptides, the glycine tripeptide and alanine pentapeptide, and a range of small folded proteins. This benchmark test set is similar to those used in the development of protein force fields such as AMBER ff15ipq, AMOEBA, CHARMM36, and OPLS-AA/M.1,2,5,15 As we shall show, the QUBE protein force field is competitive with standard transferable force fields for the dipeptide set and alanine pentapeptide while retaining the experimental structures of small folded proteins reasonably well. To encourage further testing of the QUBE protein force field, MD input files for the molecules studied and the necessary scripts to convert the QM electron density to QUBE force field format have been made available (https://github.com/cole-group/QUBEMAKER). Finally, in Discussion and Conclusions, we outline a roadmap for future improvements to QUBE.
2. Theory
The functional form of the standard biomolecular force field has five components. Covalent interactions between atoms are modeled using harmonic bond stretching and angle bending parameters, while rotations about a bond are described by anharmonic four-body torsional terms. Nonbonded interactions are described by a sum of Coulombic interactions between (usually) atom-centered point charges and a physically motivated Lennard-Jones interaction, which combines a short-range repulsive r–12 potential with a longer-range attractive r–6 interaction. We now provide an overview of how these various components are parameterized in the QUBE protein force field and contrast the approaches to those used in standard transferable force fields. Since the methods used to parameterize the nonbonded and bond and angle terms have been extensively described elsewhere,24,25,28,30 we focus here on the derivation of the torsional parameters.
2.1. Nonbonded Parameters
The nonbonded components of a molecular mechanics force field aim to describe the quantum mechanical electrostatic, dispersion, and exchange–repulsion interactions in a computationally efficient manner.37 The charge parameters are generally fit to the quantum mechanical electrostatic potential of small molecules. The Lennard-Jones parameters are then fit to reproduce experimental data, such as liquid densities and heats of vaporization.2,6,38
The aim of QUBE is to move away from the requirement for transferable force field parameters and instead to derive bespoke parameters for molecules directly from QM calculations. First, a QM simulation of the molecule under study is performed. From the output of the QM calculation, the total electron density of the molecule is partitioned onto individual atoms using an AIM weighting scheme. There is no unique method to perform this partitioning, but we favor the DDEC scheme,26,27 which is a weighted combination of the iterative stockholder atoms and iterative Hirshfeld approaches.39,40 With the electron density partitioned to individual atoms, the atom-centered charges can be simply found by integrating the electron density over all space (and adding the nuclear charge). We have implemented the DDEC approach in the ONETEP software package, which allows us to perform QM calculations of, and assign parameters to, systems comprising thousands of atoms. The derived charges have been shown to be suitable for use in flexible force field design in multiple works because they are able to reproduce the underlying QM electrostatic dependence while exhibiting low conformation dependence.24,27,34 The charges are specific to the system under study, and by performing the QM calculation in the presence of an implicit solvent model, polarization of the charges in the condensed phase can be included in the model.24
The dispersion and exchange–repulsion interactions are described using a Lennard-Jones potential with a form:
| 1 |
The dispersion coefficient, Bij, is
calculated from the partitioned electron density by using the Tkatchenko–Scheffler
relationship to rescale the free atom dispersion coefficient by the
computed volume of the atom in the molecule.14,24 The standard combination rule, 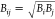 , can then be
used to determine heteroatomic
dispersion coefficients. The Aij parameter,
which describes the short-range repulsion between overlapping electron
clouds, cannot be readily calculated directly from the electron density.
Instead, it is computed by requiring that the minimum in the interatomic
Lennard-Jones potential coincides with the estimated van der Waals
radius of the atom in the molecule.24 This
nonbonded parameter derivation scheme requires just one fitting parameter
per element (corresponding to the van der Waals radius of the free
atom in vacuum).
, can then be
used to determine heteroatomic
dispersion coefficients. The Aij parameter,
which describes the short-range repulsion between overlapping electron
clouds, cannot be readily calculated directly from the electron density.
Instead, it is computed by requiring that the minimum in the interatomic
Lennard-Jones potential coincides with the estimated van der Waals
radius of the atom in the molecule.24 This
nonbonded parameter derivation scheme requires just one fitting parameter
per element (corresponding to the van der Waals radius of the free
atom in vacuum).
2.2. Bond and Angle Parameters
The parameterization approach used to determine bond and angle harmonic force constants in traditional force fields, such as OPLS and AMBER, is to fit them to reproduce QM data or experimental normal mode frequencies. This creates interdependencies in the force field parameters. That is, bond and angle parameters depend on the nonbonded and torsional parameters used during the fitting process, and therefore, they cannot be easily transferred to the QUBE force field. Instead, we derive bond and angle force constants directly from the QM Hessian matrix of the molecule under study, while equilibrium bond lengths and angles are taken from the optimized geometry of the molecule.30 This method is a modification of the Seminario method32 and is based on the computation of the eigenvalues and eigenvectors of the partial Hessian matrix, kAB:
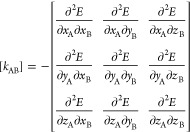 |
2 |
The harmonic bond force constants are given by
| 3 |
where ûAB is a vector in the direction of the bond AB, and νiAB (λiAB) is an eigenvector (eigenvalue) of the kAB matrix.
Similar methods may be used to derive the angle force constants, and we introduce a correction to the standard Seminario method, which takes into account the geometry of the molecule under study.30 Consistent improvements in the computed normal modes were demonstrated using this modified Seminario method for a range of molecules. In particular, QM vibrational frequencies for a set of dipeptides were reproduced with an accuracy of 40 cm–1, which compares favorably with the OPLS force field (47 cm–1) and the original Seminario method (104 cm–1). Since the derived bond and angle parameters do not depend on the choice of nonbonded and torsional parameters, the derived parameters are suitable for use in the QUBE protein force field. Since large-scale polarization effects are expected to be significantly less important for bond and angle parameters than for charges, we use the library of bonded parameters provided previously30 (and the same atom types as those used for OPLS-AA/M1).
While preparing the protein simulations, it was found that our library had missing parameters for the disulfide bridge between pairs of cysteine residues. These bond and angle parameters were therefore derived using the QM Hessian matrix of dimethyl disulfide and are supplied in Section S2.3 of the Supporting Information.
2.3. Torsional Parameters
With new bond, angle and nonbonded parameters derived, all that remains to complete the QUBE protein force field is to obtain the torsional parameters. Unfortunately, it is infeasible to derive torsional parameters from QM simulations that are specific to each protein. Therefore, we make the assumption that the derived parameters for dipeptides are transferable to proteins, and in Section 4, we test the limitations of this assumption by validating the force field against experimental peptide and protein dynamical observables.
The torsional terms in a force field are a function of the dihedral angles (ϕ) in a molecule. Here, we use the same functional form as the OPLS force field
| 4 |
where the sum runs over all dihedrals (k) in the molecule and V1–4kare parameters to be fit. We focus on reparameterizing the backbone (ϕ, ϕ′, ψ, and ψ′) and sidechain (χ1, χ1, χ2, and χ2′) torsional parameters (Figure 1). Refitting of the remaining torsional and improper parameters are beyond the scope of the current work, and these parameters are instead taken from the OPLS-AA/M force field.1 However, parallel efforts are being made to develop a toolkit for automated parameterization of small molecules using the QUBE force field, which will facilitate derivation of the remaining parameters in future.25
Figure 1.
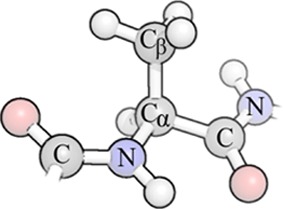
Alanine residue showing the atom naming convention for dihedral angles. The main dihedral angles reparameterized are ϕ (C–N–Cα–C), ϕ′ (C–N–Cα–Cβ), ψ (N–Cα–C–N), ψ′ (Cβ–Cα–C–N), χ1 (N–Cα–Cβ–Xγ), χ1′ (C–Cα–Cβ–Xγ), and χ2 (Cα–Cβ–Xγ–Yδ). Xγ and Yδ (not shown) are the neighboring heavy atoms in the sidechains (if present).
When fitting torsional parameters, the main objective is to minimize the difference between MM and QM gas phase dihedral energy scans. However, weighting schemes and regularization can also be used to change the form of the error function that is minimized. Regularization is a technique generally used to prevent overfitting to data. There are multiple forms of regularization that can be applied to improve fitting.2,25 In this work, we use a harmonic restraint that is added to the error function.2 This penalty term ensures that torsional parameters do not deviate significantly from their initial value unless a significant improvement in the agreement with the QM energy surface is observed. As we will show, even with low levels of regularization (a small λ value), a sizeable increase in performance is observed for the QUBE force field. The general form of the error function used in this study is given by
| 5 |
where kB is the Boltzmann constant, T is a weighting temperature, n is the number of points at which the energy is evaluated, Wj is the contribution from the weighting scheme, λ is the regularization coefficient (this term is independent of n and can take any positive value), Vi is the torsional parameter being optimized, and Vi0 is an initial estimate of the torsional parameter. Where we have used a harmonic restraint, we have used Vi = 0 as the initial guess as previously suggested.41 The V4 term was set to zero throughout the fitting procedure to avoid overfitting.1EQMjand EMMare the QM and MM optimized energies at each sampled dihedral angle relative to the lowest QM or MM energy, respectively. MM scans allow all other degrees of freedom to optimize, and so, the structures are similar, but not identical, to the QM structures. Weighting schemes are used to prioritize accuracy in particular regions of the dihedral scan, for example, in the β-sheet region of the Ramachandran plot. A range of weighting schemes has been previously used, including schemes that prioritize the lowest QM energies1 or that prioritize regions that have been shown experimentally to be most populated by proteins.5,15
3. Methods
3.1. Torsional Parameter Fitting
Torsional parameter fitting followed the general strategy employed in the development of the OPLS-AA/M force field,1 among others, in which parameters are fit to reproduce QM gas-phase potential energy surfaces. Fitting and validation were performed using dipeptides of the form (Ace-X-NMe), where X is the amino acid, Ace is an acetyl group, and NMe is the N-methyl group.
3.1.1. QUBE Parameter Derivation
The ground-state electron densities of the dipeptides were computed using the ONETEP linear-scaling DFT code33 with the PBE exchange-correlation functional and standard parameter settings (Supporting Information, Section S2.2).24 Since the reference QM potential energy scans are performed in the gas phase, we have decided to derive QUBE force field charges and Lennard-Jones parameters from the vacuum electron density (rather than in an implicit solvent). The assumption here is that the required correction to the MM potential energy surface is approximately the same in the gas and condensed phases.
Charge and Lennard-Jones parameters were derived from the QM ground-state electron density using the DDEC scheme26,27 as implemented in the ONETEP code28,34 (Section 2.1). As discussed previously, DDEC charges show low, but nonzero, conformational dependence.28 To account for this, the nonbonded parameters were derived for multiple conformations of each dipeptide and averaged. Input files for the full set of dipeptide structures are provided in the Supporting Information. Nonbonded parameters on identical atoms (for example, hydrogen atoms in a methyl group) were symmetrized. It should be noted that only atom-centered charges were used in this work, although off-site charges to model anisotropic electron density distributions, particularly on sulfur atoms,42 may lead to improvements in future work.25 Bonded parameters were assigned to the dipeptides from the library developed using the modified Seminario method using OPLS-AA/M atom typing rules.30
3.1.2. Potential Energy Scans
The torsional potential energy scans of alanine, glycine, and all sidechains are the same as those used in the development of the OPLS-AA/M force field, as described previously.1 In brief, structures were relaxed in the gas phase using Gaussian 09 with a ωB97X-D functional and a 6-311++G(d,p) basis set. Dihedral angles were scanned in 15° increments from −180 to 180°. A single-point energy calculation was then performed on the optimized structure using the double-hybrid functional B2PLYP-D3(BJ) and the Dunning basis set aug-cc-pVTZ. A 2D scan of ϕ (C–N–Cα–C) and ψ (N–Cα–C–N) was carried out for alanine and glycine.
The sidechain energy scans follow the same methods as the backbone scans, except that the single-point B2PLYP calculation was not performed for all χ2 scans, as ωB97X-D was shown to give sufficiently accurate results.1 These 1D scans give the energy as a function of the χ1 dihedral angle (N–Cα–Cβ–Xγ) or the χ2 dihedral angle (Cα–Cβ–Xγ–Yδ). The ψ and ϕ angles were constrained to an α-helical (ϕ = – 60 ° , ψ = – 45°) or a β-sheet (ϕ = – 135 ° , ψ = 135°) conformation. All scans used in this work can be found in the Supporting Information of ref (1).
In this work, an additional 2D scan of the ϕ and ψ dihedral angles of serine was found to be necessary for accurate torsional parameters for serine and threonine, which both have a polar oxygen atom at the Xγ position. This followed similar protocols to those previously described; however, the sidechain χ1 angle now had to be taken into account. Scans were performed at 30° increments of ϕ/ψ, for χ1 initially set to −60, 60, and 180°. These gave three 2D energy scans for the main rotamers of serine. The minimum energy structure for each ϕ/ψ angle was then used to construct the overall minimum ϕ/ψ potential energy surface (Section S3.1).
3.1.3. Fitting Dipeptide Torsional Parameters
Torsional parameters were optimized by minimizing the error function shown in eq 5 using a steepest descent algorithm. MM potential energy surfaces were computed by scanning dihedral angles in 15° increments using the BOSS software.43 The backbone torsional parameters for all dipeptides tested, excluding serine and threonine, were fit to the alanine and glycine scans previously described. The total error for the two scans was given by
| 6 |
with the prefactors corresponding to the relative frequency of each amino acid in the human proteome. Preliminary testing (Section S1.1) showed that a weighting function and regularization did not significantly improve the conformations sampled during the dipeptide MD simulations and so were not used (λ = 0, W = 0).
The remaining dipeptides, threonine and serine (both of which contain aliphatic hydroxyl groups in their sidechain), were assigned identical backbone parameters that were fit to reproduce the QM scans of serine. For these scans, regularization and weighting were shown to be necessary to produce dipeptide dynamics, which were in agreement with experiment. An investigation of how the simulation error changes with regularization is given in Section S1.2. The harmonic restraint parameter was set to λ = 0.05.
The sidechain scans for all dipeptides followed the same fitting process as the alanine/glycine backbone with no weighting or regularization used. As atom typing is not used for the nonbonded parameter assignment in the QUBE force field, each set of sidechain torsional parameters is also residue-specific. This differs from the approach used in OPLS-AA/M in which sidechain torsional parameters with the same set of atom types are generally assigned the same parameters.
In a number of cases, it was necessary to make manual changes to the fitting process. This was restricted to setting a number of torsional parameters to zero (that is, λ = ∞) and reducing the number of scans used in the fitting process. In particular, the aspartic acid ψ/ϕ distribution was improved by setting the χ2 torsional parameters to zero. Additionally, using only the QM energy scan with the lowest minimum energy in the fitting process was shown to result in an improvement in the MD simulations of the dipeptides for the χ1 torsional parameters of cysteine, methionine, serine, and threonine. The need for manual input in the fitting process was also required for developing OPLS-AA/M and is likely due to the restrictive functional form of the torsional potential and the conformational dependence of the energy scans.1 The full set of manual changes involved is listed, along with the final torsional parameters, in Section S3.3.
3.1.4. Alanine Pentapeptide and Glycine Tripeptide
As the nonbonded parameters used are specific to the system under study, they are not the same for an alanine dipeptide molecule as for the alanine pentapeptide (Ala5). The alanine residue in the dipeptide is blocked by acetyl and N-methyl groups, whereas the central three alanine residues in Ala5 have neighboring alanine residues on both sides. Therefore, varying environments exist for alanine residues in the different molecules. Consequently, the parameters found for the alanine dipeptide were found to be unsuitable for MD simulations of Ala5 (Table S5). However, the use of a harmonic restraint in the fitting process resulted in torsional parameters that were sufficiently accurate for the alanine and glycine peptide simulations. Alanine and glycine backbone torsional parameters were refit to the QM energy scans with λ = 0.50, and no weighting was used. The optimal value used for the regularization parameter was found by minimizing the differences between simulated and experimental NMR observables for Ala5 (Table S5). We note that the J coupling error is not too sensitive to the strength of the harmonic restraint. Separate torsional parameters are used for the alanine pentapeptide and glycine tripeptide (Gly3), as residue-specific parameters should result in a more accurate force field.
3.1.5. Protein Torsional Parameters
It is expected that optimal backbone torsional parameters for protein simulations are more similar to those developed for Ala5 and Gly3 than for the set of dipeptides. We therefore use a regularization λ = 0.50 for all protein backbone torsional parameter derivation. Alanine, glycine, serine, and proline torsional parameters are fit to available QM potential energy surfaces and are therefore residue-specific. Threonine uses torsional parameters fit to the serine torsional scan, and all other amino acid use torsional parameters fit to joint alanine/glycine energy scans. These backbone parameters are combined with the dipeptide sidechain torsional parameters to give the full QUBE protein force field parameter set.
3.2. Molecular Dynamics Simulations
3.2.1. Simulation Details
Following a number of previous force field studies,1,2,5,15 the QUBE force field was validated through molecular dynamics (MD) simulations of a benchmark test set of five proteins. The structures chosen (with the PDB codes shown in parentheses) were ubiquitin (1UBQ), GB3 (1P7E), BPTI (5PTI), binase (1BUJ), and a villin headpiece subdomain (2F4K).
Figure 2 shows the steps required to set up a QUBE protein force field for an MD simulation. In Section 2.1, the ONETEP linear-scaling DFT software is used to compute the ground-state electron density of the five proteins and assign the charge and Lennard-Jones parameters from the partitioned atomic electron densities. Consistent with the QUBE small-molecule approach, every atom in the protein is assigned bespoke nonbonded parameters derived from the quantum mechanical electron density. To model polarization effects in the condensed phase, the electron density is computed first in vacuum and then using an implicit solvent model44,45 with a dielectric constant of 80. The iPol approach used in AMBER ff15ipq is then employed, with all nonbonded parameters set halfway between their vacuum and condensed phase values.2 The purpose of this approach, as well as overcoming issues associated with closing of the electronic band gap in large system sizes,46 is to account for electrostatics and induction in the condensed phase in an effective manner using a fixed point charge force field.47 Typical computational requirements for a QM calculation on a small protein (≈1000 atoms) are approximately 2000 cpu-h. In order to provide a consistent and computationally efficient approach to assigning the nonbonded parameters, we recommend minimizing the experimental structure using a standard transferable force field in explicit water prior to the DFT calculation. In this study, we used the OPLS-AA/M force field for the initial minimization.
Figure 2.
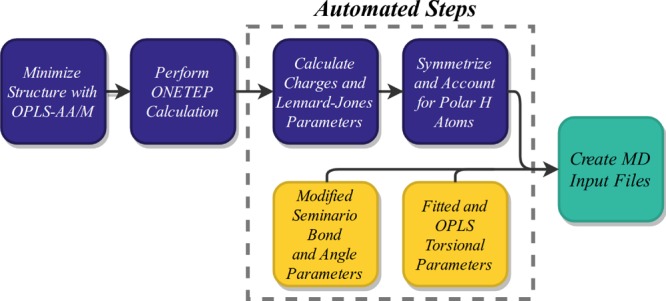
Flowchart illustrating the steps required to assign the QUBE protein force field. Blue is used for nonbonded terms, and yellow is used for bonded terms.
Following nonbonded parameter assignment, bond, angle, and torsional parameters were assigned as described in Section 2 based on the OPLS-AA/M atom types. For torsion and improper types not reparameterized in this study, OPLS-AA/M parameters are retained.1,7Table 1 summarizes the number of bespoke nonbonded parameters for each protein studied, along with the bonded parameters that are parametrized using the dipeptide molecules as described above. All parameters, including atom-specific nonbonded parameters, are written to a CHARMM-style parameter file. The psf, pdb, and inp files are provided in the Supporting Information. We note that preparation of the parameter files is fully automated, and scripts and step-by-step tutorials are available from https://github.com/cole-group/QUBEMAKER. MD simulations were performed using the NAMD software, using input parameters detailed elsewhere (Section S2.1).1 Statistics were collected over a period of 200 ns for dipeptides, Ala5, and Gly3 and 0.5 μs for the proteins. All MD simulations were performed in triplicate.
Table 1. Number of Atoms of the Proteins Tested in This Work along with a Breakdown of the Parameters Employed in the Force Fielda.
| PDB ID | system size | bespoke parameters | refit dihedrals | OPLS-AA/M dihedrals | bonds and angles |
|---|---|---|---|---|---|
| 1P7E | 862 | 2586 | 1224 | 2141 | 4282 |
| 1UBQ | 1231 | 3693 | 1167 | 2292 | 4584 |
| 1BUJ | 1712 | 5136 | 1161 | 2402 | 4804 |
| 5PTI | 576 | 1728 | 1065 | 2362 | 4724 |
| 2F4K | 892 | 2676 | 711 | 1509 | 3018 |
3.2.2. Simulation Analysis
All backbone and sidechain dihedral angles sampled during the dipeptide simulations were analyzed and compared with experimental data (Section S2.4). The simulated J coupling was calculated using the Karplus equation
| 7 |
where ϕ is the relevant dihedral angle, and A, B, and C are the Karplus parameters, which can be derived from experimental measurements or QM calculations.48 For the alanine pentapeptide, the J coupling error is calculated as
| 8 |
where ⟨Jj⟩sim is the time-averaged simulated J coupling, Jj,exp is the experimental J coupling, σ is the estimated systematic error,48 and N is the number of J coupling measurements considered.
The backbone J coupling term 3J(HN, Hα) was calculated from the dipeptide simulations using the Karplus parameters proposed in ref (49) and the ϕ dihedral angles sampled, with the experimental J coupling values taken from ref (49). The sidechains sampled were separated into P(+60°), T(180°), and M(−60°) rotamers, and the populations of each were then compared to protein coil library data.1
The J coupling values computed from the alanine and glycine peptide simulations could be compared to multiple experimental values given in ref (51). Three separate Karplus parameter sets were used as given in ref (48).
The Karplus parameters used for the protein simulations came from multiple sources, with both refs (49) and (52) used for backbone parameters. Methyl sidechain Karplus parameters are also supplied in ref (52), and ref (53) was used for all other sidechain Karplus parameters.
4. Results
4.1. Torsional Parameter Fitting
The final backbone torsional parameters and associated errors in the recreation of the QM energy scans are given in Section S3.2 of the Supporting Information. For the alanine and glycine scans, the error for the QUBE force field evaluated using eq 5 is 1.25 kcal/mol compared to 0.93 kcal/mol for OPLS-AA/M, which is a reasonable level of agreement. For proline and serine, the errors remain comparable to OPLS-AA/M.
For the sidechain torsional parameters (Section S3.3), the mean error in the recreation of the QM potential energy scans for the QUBE force field is 1.29 kcal/mol compared to 1.12 kcal/mol for OPLS-AA/M. Particularly high errors occur for both the χ1 and χ2 glutamic acid scans and the glutamine χ2 scan. For glutamic acid, the error is also high for the OPLS-AA/M force field parameters, but the rotamer populations remained close to the experimental data, and this may be due to a problem with the functional form used in classical force fields.1 The OPLS-AA/M error in the potential energy scan for glutamine is roughly half that of the QUBE force field. However, as we will show, the accuracy of the glutamine dipeptide MD simulations is good, and so, no further refinement was made to the sidechain torsional parameters in this work.
Although a low error in the reproduction of the QM potential energy surface is clearly the desired result, this does not necessarily correspond to accurate nonbonded force field parameters. The degree to which torsional parameters can improve the fit between MM and QM scans depends not only on the accuracy of the nonbonded and bond and angle parameters but also on the shape of the energy difference between the QM and MM scans. The functional form used in classical MM force fields is very restrictive. However, the energy difference between the QM and MM energy scans must be corrected by the functional form for low errors to be achieved. Therefore, although we use errors in potential energy scans as a guide to performance, they cannot be relied upon as a measure of the accuracy of a force field. Therefore, we now investigate the performance of the QUBE force field in MD simulations.
4.2. Dipeptide Simulations
Extensive MD simulations were performed for each of the dipeptides. Computed NMR J couplings provide a quantative measure of the accuracy of the backbone ϕ torsion angle distribution sampled during the MD simulations. The full results are shown in Table S8. The QUBE force field achieves a root mean square error (RMSE) of 0.42 Hz, which can be compared to 0.35 Hz for OPLS-AA/M.1 Encouragingly, the error in the J couplings simulated using the QUBE force field is much lower than that of OPLS-AA (0.97 Hz) and OPLS-AA/L (0.79 Hz).1 With the arginine dipeptide excluded from the QUBE data, the error drops further to 0.33 Hz. Residue-specific arginine backbone torsional parameters could be computed, however, given that the ϕ/ψ distribution of arginine occupies the main conformations expected, this is not investigated in this work.
Figure 3 shows the collective ϕ/ψ distributions from the dipeptide MD simulations, along with the main expected protein conformational propensities.54 As discussed in Section S9 of the Supporting Information, it is important to consider the dihedral distributions present as well as the J coupling data. Encouragingly, the ϕ/ψ distribution for the dipeptides shows that the major conformations present in protein structures are sampled in the QUBE MD simulations. The ζ conformation does have a slightly lower ψ angle than suggested, and there is an additional region with very low occupancy to the right of the γ conformation. However, these are very small discrepancies.
Figure 3.
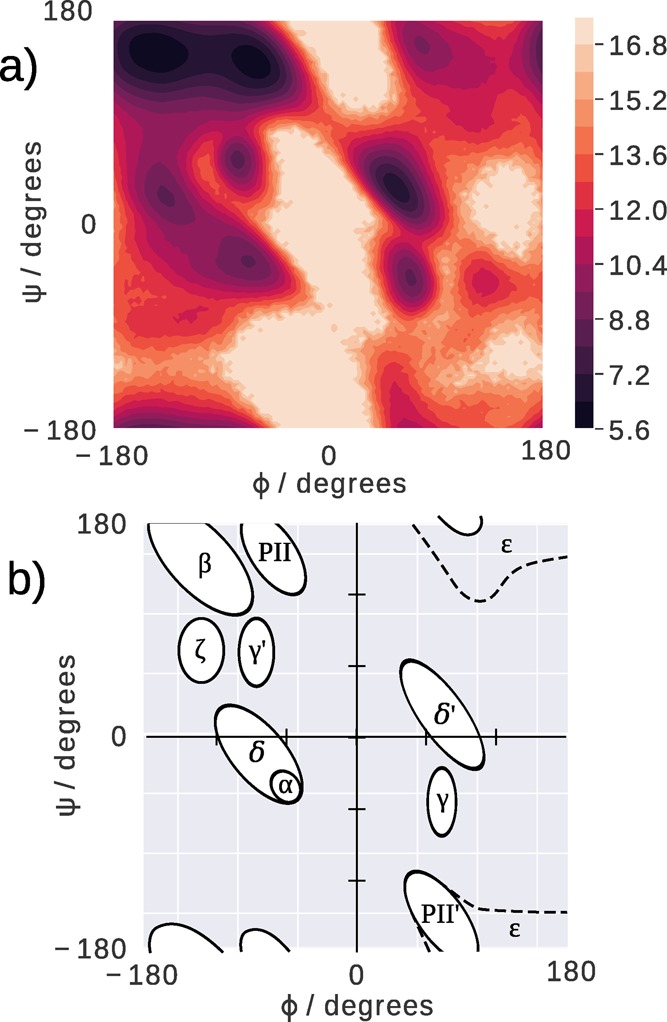
(a) ϕ/ψ distribution extracted from the dipeptide MD simulations, plotted in the form – log (pψ, ϕ) (where pψ, ϕ is the probability of a region being occupied). The lighter regions correspond to low probability areas including conformations that are not sampled during the simulation. (b) Major conformations observed in protein structures.54 The right-handed α-helical region is labeled as δ and the left-handed α-helical region as δ′.
The ϕ/ψ distributions for each individual dipeptide are shown in Section S4.2 of the Supporting Information. Generally, similar areas of the ϕ/ψ distribution are occupied by all the dipeptides. The serine and threonine dipeptides do not sample identical regions to the other dipeptides, which is expected given that they have a separate set of backbone torsional parameters. There are several dipeptides that show populations of left-handed α-helical conformation. High left-handed helical populations have previously caused problems for other force fields.55 However, since the occupancy of PPII and β regions always remain higher than the populations of the left-handed α-helical region, reducing the left-handed helical population was not considered a priority in this work. The right-handed α-helical populations are small for all the dipeptides. This is in agreement with experimental results.50
As well as the backbone conformations sampled, the sidechain rotamer populations were also analyzed. In Figure 4, the simulated rotamer populations are compared to experimental data taken from protein coil libraries (the data are given in the Supporting Information of ref (1)). Given that the experimental data are not specific to dipeptides, perfect agreement is not expected. However, populations at extreme values would cause concern, and a correlation between the experimental and simulated values is favorable. Figure 4 shows that no dipeptides have populations consisting of just one type of rotamer and there are no extremely high values (as was observed for OPLS-AA and OPLS-AA/L1). The rotamer M populations are occasionally slightly lower than expected. However, given the issues previously mentioned with the experimental data used, further changes were not made to adjust the outliers.
Figure 4.
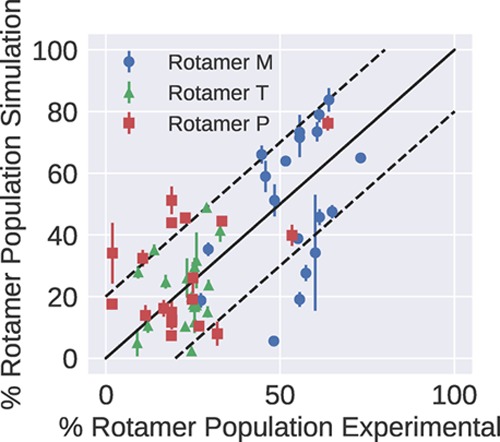
Comparison of the rotamer populations for the dipeptide MD simulations and experimental values from the protein coil library. The dashed lines show the populations that fall within ±20% of the experimental values.
The rotamer data, which were used to construct Figure 4, are reproduced in Table S9. With an MUE of 14%, QUBE performs better than both OPLS-AA and OPLS-AA/L, which have errors of 23 and 21%, respectively.1 The error is not as low as OPLS-AA/M, which has an error of 10%, however with further empirical changes to the torsional parameters, the error could likely be further reduced. Examining individual dipeptide errors, protonated histidine and aspartic acid are found to have the highest errors. The protonated histidine experimental data includes all ionization states of histidine and therefore may not be accurate, which would explain the high error. The higher error in the simulated dynamics of the aspartic acid dipeptide is more problematic, and in future versions of the QUBE force field, further changes to these sidechain torsional parameters may be considered.
4.3. Peptide Simulations
The J coupling errors extracted from MD simulations of the alanine pentapeptide are shown in Table 2, with the ϕ/ψ distribution shown in Figure 5, and further results given in Section S5.1 of the Supporting Information. Three sets of Karplus parameters are used to evaluate the error, and the values in parentheses exclude the 2J(N, Cα) coupling term. Issues with the 2J(N, Cα) coupling Karplus parameters are discussed in Section S9 of the Supporting Information and elsewhere.1,2 The J coupling error for set 1 is very encouraging and is lower than both the OPLS-AA/M (1.16 ± 0.02) and AMOEBA force field errors (0.99).1,5 The errors for sets 2 and 3 with the excluded 2J(N, Cα) term are similar in value. In the simulations carried out in this work, as well as the work of Amber ff15ipq and OPLS-AA/M, the low β backbone populations present result in a high 2J(N, Cα) error for the second and third set of Karplus parameters.1,2 The pentapeptide conformation with the largest population is PPII with 62 ± 2% of the simulation spent in this conformation (Table S11). This is similar to the conformational propensity observed for OPLS-AA/M (53.5 ± 0.2%). Both force fields also result in a low α-helical population, which is consistent with experimental data.15
Table 2. J Coupling Error for the Alanine Pentapeptide Simulationa.
|
J coupling error | ||
|---|---|---|
| set 1 | set 2 | set 3 |
| 0.90 ± 0.03 | 4.16 ± 0.01 | 1.51 ± 0.02 |
| (0.86 ± 0.03) | (0.81 ± 0.03) | (0.87 ± 0.03) |
The Karplus parameter sets are the same as those used previously.1 The values shown in parentheses correspond to the J coupling errors excluding 2J(N, Cα).
Figure 5.
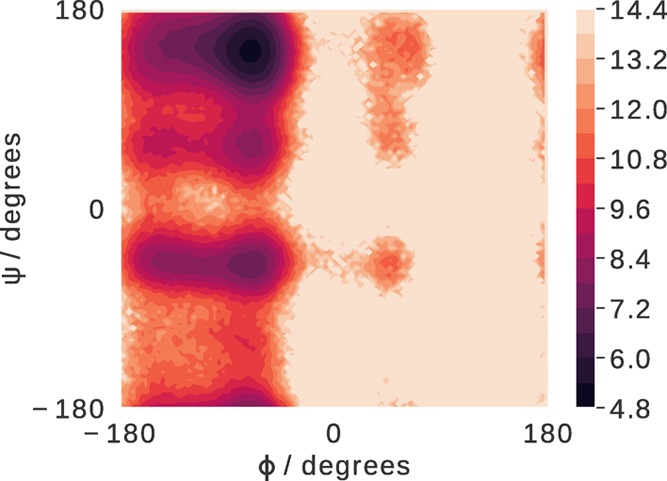
ψ and ϕ distributions of the central residues of the alanine pentapeptide, plotted in the form – log (pψ, ϕ) (where pψ, ϕ is the probability of a region being occupied). The lighter regions correspond to low probability areas including conformations that are not sampled during the simulation.
The problems associated with using the Karplus parameters for Gly3 are discussed in Section S9 of the Supporting Information and elsewhere.1,51,56 Therefore, we evaluate the backbone conformations of Gly3 through its ϕ/ψ distribution alone. In Figure 6, the OPLS-AA/M backbone conformational distribution is compared to that obtained using the QUBE force field. A lower α-helical population is occupied by the QUBE force field, but otherwise both distributions are very similar.
Figure 6.
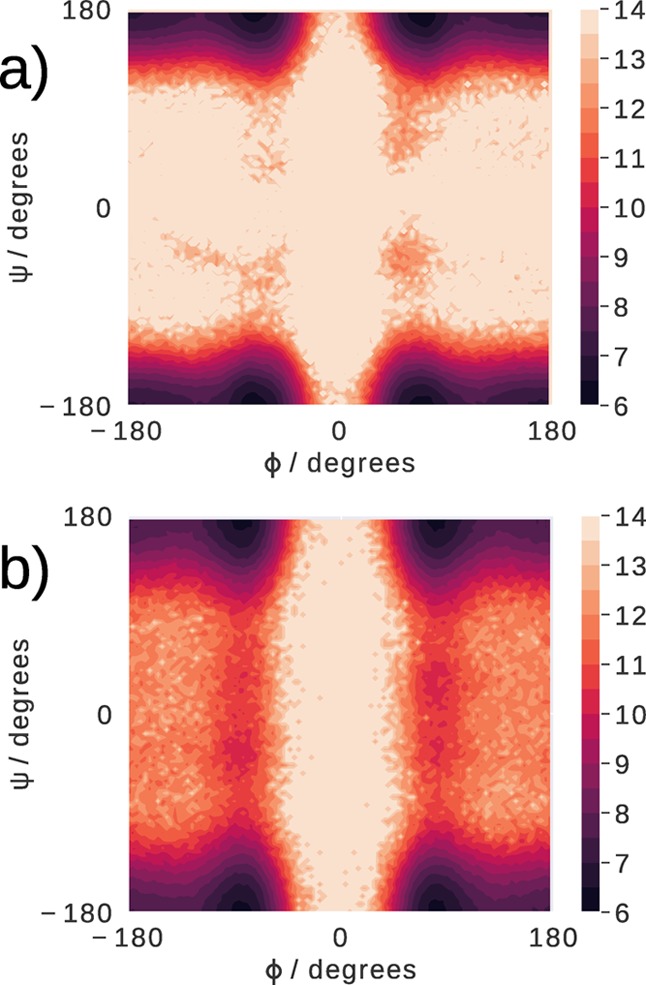
ψ and ϕ distribution for the glycine tripeptide (all residues are included) using (a) QUBE force field and (b) OPLS-AA/M, plotted in the form – log (pψ, ϕ) (where pψ, ϕ is the probability of a region being occupied). The lighter regions correspond to low probability areas including conformations that are not sampled during the simulation.
The MD simulations presented here have demonstrated that the QUBE force field and the parameterization methods used to create it are sufficiently accurate to recreate conformational propensities of short, flexible peptides. The errors in the simulated dynamics of these molecules are comparable to OPLS-AA/M, and the ϕ/ψ distributions demonstrate that the major conformations observed in protein structures are populated. Issues with the transferability of torsional parameters have already been identified from the longer peptide simulations and are solved by applying regularization. In the following subsection, the performance of QUBE for entire proteins is evaluated to demonstrate the feasibility of applying the methodology to macromolecules and to further understand the intricacies of fitting torsional parameters to a system-specific force field.
4.4. Protein Dynamics
The use of system-specific nonbonded parameters for biomolecular force fields allows for long-ranged polarization effects to be included, which is expected to improve the accuracy of the force field, particularly for measurements such as protein–ligand binding affinity that are sensitive to the electrostatic potential at the protein surface. A comparison of the QUBE and OPLS nonbonded parameters for ubiquitin is shown in Figure 7. Figures for the other proteins tested follow similar trends. As we have described, QUBE nonbonded parameters are derived directly from the QM partitioned electron density, and so, each atom has a unique charge and set of Lennard-Jones coefficients, which depend on its environment. In contrast, the OPLS parameters are read from a library of atom types. The QUBE and OPLS charges correlate well with no clear outliers. As has previously been observed,24 the QUBE Lennard-Jones parameters show a far greater level of variation than OPLS (and most other force fields).
Figure 7.
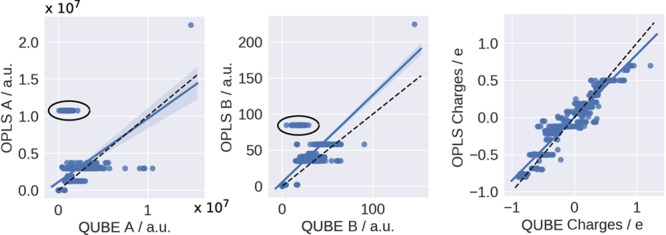
Comparison of the QUBE and OPLS nonbonded parameters for ubiquitin. The regions circled corresponding to carbonyl carbon atoms, which are expected to be electron deficient and therefore require small A and B Lennard-Jones coefficients.24 Blue and dashed black lines represent lines of best fit and y = x, respectively.
One assumption employed in the use of system-specific charges for proteins (and small molecules) is that the derived parameter set is not too dependent on the molecular conformation. To investigate this assumption, the sensitivity of the nonbonded parameters, for the GB3 protein, to the choice of the input structure is investigated in Section S6.2. Ten structures were extracted from an MD simulation employing the OPLS-AA/M force field, and QUBE nonbonded parameters were computed for each snapshot. The standard deviation of the charge distribution across the ensemble is just 0.02 e, supporting previous observations that the underlying DDEC AIM charges are relatively independent of conformation.27,34
It is important to test whether these system-specific force field parameters translate into more accurate protein interactions and dynamics. In this regard, although the conformational preferences of the peptides tested in the previous section are promising, it is not known whether the torsional parameters will continue to be appropriate for use with proteins. As the nonbonded parameters vary with the system studied, the transferability of torsional parameters cannot be readily assumed. To assess this, we begin by studying MD simulations of the proteins ubiquitin and GB3.
The J coupling errors for ubiquitin and GB3 are summarized in Table 3. With an overall RMSE of 1.54 Hz, the error using the QUBE force field for ubiquitin is higher than that of OPLS-AA/M, which has an RMSE of 1.12 Hz, but lower than OPLS-AA and OPLS-AA/L with errors of 1.84 and 1.70 Hz, respectively.1 GB3 follows the same trend with an RMSE of 1.10 Hz for the QUBE force field, compared to the error for OPLS-AA/M of 0.90 Hz, while OPLS-AA and OPLS-AA/L both have an error of 1.46 Hz.1
Table 3. J Coupling Errors for the Proteins Ubiquitin and GB3.
| backbone couplings (Hz) | sidechain coupling (Hz) | overall | ||||
|---|---|---|---|---|---|---|
| protein | 1997 values | 2007 values | 3J(Hα, Hβ) | 3J(C′, Cγ) | methyl Cγ | RMSE (Hz) |
| ubiquitin | 0.94 ± 0.07 | 1.15 ± 0.05 | 2.40 ± 0.11 | 1.16 ± 0.20 | 1.20 ± 0.05 | 1.54 ± 0.07 |
| GB3 | 0.93 ± 0.05 | 1.03 ± 0.05 | 1.80 ± 0.05 | 0.84 ± 0.02 | 1.10 ± 0.04 | |
The J coupling results suggest that while the transfer of torsional parameters from dipeptides to proteins may cause some issues, the QUBE force field remains more accurate than OPLS-AA and OPLS-AA/L. This is promising when we consider that OPLS has been in development for many years with multiple iterations and parameter adjustments performed. The 3J(Hα, Hβ) coupling term is the main contributor to the J coupling error. For GB3, the 3J(Hα, Hβ) error for the QUBE force field is 1.80 Hz, this is well below the errors for OPLS-AA and OPLS-AA/L of 3.71 and 3.38 Hz, respectively.
However, as discussed in Section S9 of the Supporting Information, the J coupling error should not be used as the only measure of force field accuracy. To further test the performance of the QUBE force field, we compared the ϕ/ψ torsion angle distributions and root mean square deviation (RMSD) of the backbone Cα atoms of each residue from the experimental crystal structure for five proteins (Section S7 of the Supporting Information). The dihedral angles of the experimental structure are shown on each ϕ/ψ plot and these experimental points, along with the previous data for AMBER ff15ipq (the ϕ/ψ plots are given in the Supporting Information of ref (2)), are used to evaluate the performance of the force field. Figure 8 shows the five proteins tested, with the residue labels indicating the main regions that deviated from the crystal structure during simulation.
Figure 8.
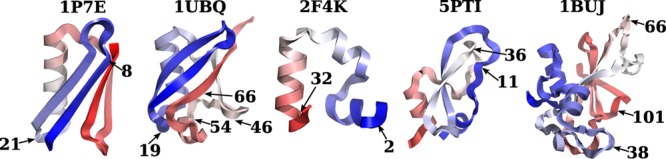
Experimental structures of the proteins tested. Regions that showed the most significant deviation from the experimental structure in the simulations are labeled. The red-white-blue color gradient represents the residue number.
Figure 9 shows the average RMSD of the Cα atoms of the five proteins from the experimental crystal structures over the course of the simulation. Each line represents an average over three separate MD trajectories. Both GB3 (PDB: 1P7E) and ubiquitin (PDB: 1UBQ) remain close to the experimental structure for the first 100 ns of the simulation, although there is some increase in RMSD to around 2–3 Å over the second half of the simulation.
Figure 9.
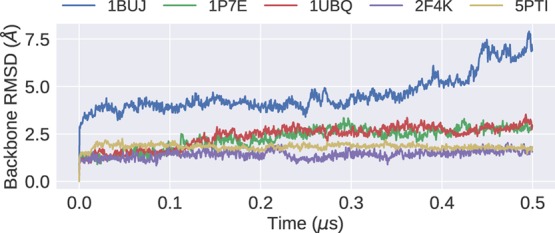
Mean RMSD, relative to the experimental structures, from the MD simulations of the five proteins tested.
The ϕ/ψ distributions of GB3 (Figure S8) and the RMSD per residue (Figure S7) help us to further analyze the results. Residues, which deviate from the experimental structure, and the results from the AMBER ff15ipq force field also tend to have high J coupling errors. For example, residues 8–21 have a large deviation from the experimental structure, and this is reflected by high J coupling errors in this region. The backbone J coupling error, using the 2007 Karplus parameters, for residues 8–21 is 2.00 Hz, which is almost double the total backbone error. This region corresponds to a β-sheet, which separates over the second half of the MD trajectory and contributes to the increased backbone RMSD. Aside from this region, the only other residues, which show noticeable deviation from the crystal structure, are Val39, Asp40, Gly41, and Thr55. However, the small deviations that are present in these four residues are also observed in simulations using the AMBER ff15ipq force field.2
Deviations between the simulated ubiquitin dynamics and experiment tend to be confined to regions without clear secondary structures. Often this is of little concern since both experimental NMR measurements and simulations with the AMBER force field also indicate flexibility in these regions (e.g., residues 7–11 and 72–74). However, deviations from the crystal structure in the disordered region between residues 54–66 are more of a concern and contribute to the high J coupling and rising RMSD of the protein backbone over the second half of the simulation.
In contrast, Figure 9 shows that both the villin headpiece (PDB: 2F4K) and BPTI (PDB: 5PTI) retain their experimental structures extremely well (average RMSD in the range of 1–2 Å). The three α-helices present in the villin headpiece are retained throughout the simulations, and the ϕ/ψ distributions are in excellent agreement with experiment and the AMBER force field (Figure S10). Similarly, in BPTI, regions with helical or β-sheet structures retain their structure. Some small changes in the structure are observed (for example, residues 10–12 in villin and 36–40 in BPTI), although these correspond to regions with no fixed secondary structure or a bend.
We have also included in Figure 9 the protein binase (PDB: 1BUJ). This is an interesting test case as the experimental NMR structural ensemble reveals a high degree of residue flexibility, with loops that adopt multiple conformations (Figure S12), but it is also challenging. The two α-helices present in 1BUJ, around residues 10 and 30, are generally well represented with the QUBE force field. However, in regions with no structure, a bend, or a turn, significant deviations from experiment are observed, and the RMSD reaches extremely high values. By way of comparison, the backbone RMSD using the AMBER ff15ipq force field was 3.4 Å after 10 μs of simulation and, after 0.5 μs, was approximately 3 Å. In the AMBER ff15ipq work, the high RMSD was attributed to variability in the loop regions, which had also been observed in experimental structures.2 Closer examination of the ϕ/ψ distributions of each residue reveals the difficulty of capturing accurate conformational preferences. For example, the NMR ensemble for Lys38 shows the presence of both β-sheet and α-helical conformations. These are also observed in MD simulations using both AMBER ff15ipq and the QUBE force field, but the proportion of each conformation is different. The ensemble of Ser66 is not well represented with AMBER ff15ipq, but with the QUBE force field, all structures in the ensemble are captured to some degree, although an additional α-helical conformation is also observed.
Table 4 summarizes the performance of the QUBE protein force field across the peptide and protein data sets presented in this study and compares it with analogous assessments of the OPLS force fields studied previously.1 Overall, QUBE outperforms legacy OPLS-AA and OPLS-AA/L force fields but is less accurate (with the exception of alanine pentapeptide simulations) than the latest OPLS-AA/M force field. This is an encouraging result for this first generation protein-specific force field but also indicates that there is room for improvement of QUBE within the fixed functional form of the biomolecular force field. The next section summarizes our roadmap for future development and application of the QUBE force field.
Table 4. Summary of Averaged Simulation Errors Compared to Experiment for QUBE (This Work) and OPLS Force Fields1a.
| data set | QUBE | OPLS-AA/M | OPLS-AA | OPLS-AA/L |
|---|---|---|---|---|
| dipeptide rotamer populations | 14% | 10% | 23% | 21% |
| dipeptide 3J (HN,Hα) (Hz) | 0.42 | 0.35 | 0.97 | 0.79 |
| Ala5J coupling (set 1) | 0.90 | 1.16 | 2.31 | 2.35 |
| ubiquitin J coupling RMSE (Hz) | 1.54 | 1.12 | 1.84 | 1.70 |
| GB3 J coupling RMSE/Hz | 1.10 | 0.90 | 1.46 | 1.46 |
See the main text for details of the simulations.
5. Discussion and Conclusions
The assumption that biomolecular force fields must be parametrized against the experimental properties of small molecules has persisted since MM simulations began and remains in all force fields under widespread use.6,57,58 In this work, we look to challenge this assumption by deriving system-specific nonbonded parameters, from linear-scaling QM simulations, for consistency with the QUBE small-molecule force field. These nonbonded terms were used here alongside libraries of (nonbespoke) bond and angle parameters, derived using the modified Seminario method,30 and newly reparametrized torsional terms.
We have shown here that using system-specific nonbonded force field parameters can result in accurate conformational preferences for short peptides. Rotamer populations and simulated J couplings for the dipeptide molecules are in good agreement with experimental data and compare favorably with the latest OPLS force field. For longer peptide molecules, the problems associated with fitting torsional parameters to a system-specific force field became more apparent. Using regularization in the fitting process was shown to overcome these issues and resulted in a J coupling error of just 0.90 ± 0.03 for the alanine pentapeptide. Further work investigating disordered peptides will ascertain how general this fix is. The accuracy of the peptide simulations supports the use of our nonbonded and modified Seminario bonded parametrization strategies. In protein MD simulations, the RMSD of the backbone atoms relative to experimental structures remained low, below 2 Å, for two of the five proteins tested. The α-helices present in all of the proteins generally remained close to the experimental structures, but the β-sheets exhibited greater loss of structure, and regions with no clear structure or exhibiting a turn regularly deviated from the starting structure. These regions also contributed greatest to J coupling errors. Despite this, the majority of the regions in the proteins retained their experimental structure, and the J coupling errors for GB3 and ubiquitin were below those of OPLS-AA and OPLS-AA/L, two force fields regularly used in biomolecular modeling studies.
While developing QUBE, manual adjustments to some torsional parameters were required. This was also required in the development of OPLS-AA/M, and we can infer from this that automatically fitting backbone and sidechain torsional parameters using dihedral energy scans is still challenging. The most obvious failure of dihedral energy scan fitting was that for a number of sidechains it was more accurate to set the torsional parameters to zero than to use the originally derived terms. This is in part due to the functional form used, with potential improvements to this discussed below, but is also due to the poor sampling of relevant structures by scanning one or two dihedral angles at a time. This problem is reduced by the iterative fitting methods used in AMBER ff14ipq and ff15ipq,2,38 which sample the structures used for torsional parameter fitting by performing MD simulations with the current iteration of the force field. This approach will be considered in future versions of the force field.
Another potential source of error is the choice of the modified Seminario method for derivation of bond and angle force constants. However, this method has been shown to accurately reproduce QM vibrational frequencies30 and, importantly, also reproduce QM intramolecular potential energy surfaces of drug-like molecules when combined with the QUBE nonbonded and torsional parameters.25
There are also additional considerations involved in using a library of torsional parameters alongside system-specific nonbonded parameters. The torsional parameters are fit using one set of nonbonded parameters but are then used for a range of environment-dependent nonbonded terms. This is likely the reason for the importance of regularization in this study. During the sidechain torsional parameter fitting process, it was observed that the optimal torsional parameters for α-helical and β-sheet backbone conformations can vary greatly. It may be possible to address this issue by changing the functional form of the torsional component of the force field. The functional form currently used is inaccurate due to the parameter dependency on only a single dihedral angle. The coupling between torsional terms has been addressed in a number of different ways.59−62 These include the use of the CMAP term in CHARMM22, a grid-based correction used to improve the backbone torsional energetics.61 Extending the CMAP correction so it is dependent on the χ1 sidechain dihedral angle has also recently been investigated.62 The functional form could also be improved by adding a torsion–torsion coupling term as employed in previous studies.60
Importantly, the flexibility of the QUBE parametrization process means that changes to the torsional parameters are not the only alterations that could be made to improve the accuracy of the benchmark validation tests studied here. It is not just protein–protein interactions that determine the structure but also interactions with the water model. In particular, the balance between electrostatic and dispersive interactions has been shown to be crucial.63,64 Interactions between the QUBE force field and the TIP3P water model may be responsible for some of the instabilities in the structure that we have observed, and development of a QUBE water model may lead to improved dynamics and computed free energies of hydration.25 An advantage of using a parametrization scheme that depends almost entirely on QM data is that alterations to the parametrization strategy or functional form can be readily inserted into the existing workflow. There is future scope for improvement in the choice of exchange-correlation functional used to derive nonbonded parameters, for example, through the use of hybrid functionals,65 the choice of electron density partitioning methods,66 or the addition of off-center charges to model electron anisotropy effects.25 More fundamentally, we have the opportunity to investigate improvements to the functional form of the force field itself, for example, by adding higher order dispersion terms beyond the dipole–dipole interaction37,66,67 or by altering the short-range repulsion term.37 A future QUBE polarizable force field is also envisaged, and toward this goal, the derivation of accurate AIM atomic polarizabilities is under investigation.68
As presented in the Results section, the general picture that emerges is that this first generation quantum mechanical bespoke force field is an improvement over legacy OPLS-AA and OPLS-AA/L force fields but is outperformed by the most recent OPLS-AA/M force field for simulated dynamics of folded proteins in their native state. While we have previously shown that DDEC charges are not too dependent on small conformation changes,28 further investigation is needed to establish the utility of QUBE for protein folding simulations. Hence, although we have outlined our roadmap to future improvements, a natural question is where can the QUBE protein force field be used now (especially given the higher cost of parameterization compared to transferable force fields)? Importantly, it has been shown previously that the use of system-specific force field charges leads to improvements in binding energetics of small molecules8 and reproduction of the QM electrostatic potential for both small molecules27 and proteins.34 Therefore, although simulated protein backbone dynamics is an important test, we envisage the QUBE small-molecule and protein force field being particularly important for the study of intermolecular interactions in the condensed phase. Indeed, QUBE was originally developed to provide, by construction, a compatible protein and small-molecule force field for computer-aided drug design where an accurate surface electrostatic potential of the protein is crucial. In this regard, the absolute binding free energies between the L99A mutant of T4 lysozyme and six benzene analogs have been recently computed using QUBE with a mean unsigned error of 0.85 kcal/mol, which compares very favorably with OPLS-AA/M (1.26 kcal/mol).69 Although further work is required to establish this accuracy across a significantly wider range of protein–ligand complexes, the promise of these initial biomolecular simulation results indicate a viable pathway toward improved protein dynamics and interactions using quantum mechanical bespoke force fields.
Acknowledgments
This research made use of the Rocket High Performance Computing service at Newcastle University and the Darwin/CSD3 Supercomputer of the University of Cambridge High Performance Computing Service (EPSRC grant EP/J017639/1 and EP/P020259/1). The authors acknowledge the financial support from EPSRC grant EP/R010153/1 (DJC) and the EPSRC Centre for Doctoral Training in Computational Methods for Materials Science under grant EP/L015552/1 (AEAA).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b01769.
Results of preliminary parametrization work, details of the parametrization methods used, QM backbone energy scans, torsional parameters employed, dipeptide and peptide J coupling and ϕ/ψ results, protein nonbonded parameters, protein MD results, Ramachandran plots for alanine and glycine, and discussion of the J Coupling analysis (PDF)
J coupling data, MD and ONETEP input files, and torsion parameterization data (ZIP)
The authors declare no competing financial interest.
Supplementary Material
References
- Robertson M. J.; Tirado-Rives J.; Jorgensen W. L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509. 10.1021/acs.jctc.5b00356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Debiec K. T.; Cerutti D. S.; Baker L. R.; Gronenborn A. M.; Case D. A.; Chong L. T. Further along the Road Less Traveled: AMBER ff15ipq, an Original Protein Force Field Built on a Self-Consistent Physical Model. J. Chem. Theory Comput. 2016, 12, 3926–3947. 10.1021/acs.jctc.6b00567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; Mackerell A.D. Jr. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2009, 31, 671–690. 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L.-P.; Martinez T. J.; Pande V. S. Building Force Fields: An Automatic, Systematic, and Reproducible Approach. J. Phys. Chem. Lett. 2014, 5, 1885–1891. 10.1021/jz500737m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y.; Xia Z.; Zhang J.; Best R.; Wu C.; Ponder J. W.; Ren P. Polarizable Atomic Multipole-Based AMOEBA Force Field for Proteins. J. Chem. Theory Comput. 2013, 9, 4046–4063. 10.1021/ct4003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Tirado-Rives J. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. 10.1021/ja00214a001. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
- Jorgensen W. L.; Jensen K. P.; Alexandrova A. N. Polarization Effects for Hydrogen-Bonded Complexes of Substituted Phenols with Water and Chloride Ion. J. Chem. Theory Comput. 2007, 3, 1987–1992. 10.1021/ct7001754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
- Vanommeslaeghe K.; Guvench O.; MacKerell A. D. Jr. Molecular Mechanics. Curr. Pharm. Des. 2014, 20, 3281–3292. 10.2174/13816128113199990600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storer J. W.; Giesen D. J.; Cramer C. J.; Truhlar D. G. Class IV charge models: A new semiempirical approach in quantum chemistry. J. Comput.-Aided Mol. Des. 1995, 9, 87–110. 10.1007/BF00117280. [DOI] [PubMed] [Google Scholar]
- Udier-Blagović M.; Morales De Tirado P.; Pearlman S. A.; Jorgensen W. L. Accuracy of free energies of hydration using CM1 and CM3 atomic charges. J. Comput. Chem. 2004, 25, 1322–1332. 10.1002/jcc.20059. [DOI] [PubMed] [Google Scholar]
- Jakalian A.; Jack D. B.; Bayly C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1632–1641. 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- Tkatchenko A.; Scheffler M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005–073009. 10.1103/PhysRevLett.102.073005. [DOI] [PubMed] [Google Scholar]
- Best R. B.; Zhu X.; Shim J.; Lopes P. E. M.; Mittal J.; Feig M.; MacKerell A. D. Jr. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cacelli I.; Cinacchi G.; Prampolini G.; Tani A. Computer Simulation of Solid and Liquid Benzene with an Atomistic Interaction Potential Derived from ab Initio Calculations. J. Am. Chem. Soc. 2004, 126, 14278–14286. 10.1021/ja046642u. [DOI] [PubMed] [Google Scholar]
- Prampolini G.; Livotto P. R.; Cacelli I. Accuracy of Quantum Mechanically Derived Force-Fields Parameterized from Dispersion-Corrected DFT data: The Benzene Dimer as a Prototype for Aromatic Interactions. J. Chem. Theory Comput. 2015, 11, 5182–5196. 10.1021/acs.jctc.5b00642. [DOI] [PubMed] [Google Scholar]
- Greff da Silveira L.; Jacobs M.; Prampolini G.; Livotto P. R.; Cacelli I. Development and Validation of Quantum Mechanically Derived Force-Fields: Thermodynamic, Structural, and Vibrational Properties of Aromatic Heterocycles. J. Chem. Theory Comput. 2018, 14, 4884–4900. 10.1021/acs.jctc.8b00218. [DOI] [PubMed] [Google Scholar]
- Waldher B.; Kuta J.; Chen S.; Henson N.; Clark A. E. ForceFit: A Code to Fit Classical Force Fields to Quantum Mechanical Potential Energy Surfaces. J. Comput. Chem. 2010, 31, 2307–2316. 10.1002/jcc.21523. [DOI] [PubMed] [Google Scholar]
- Xu P.; Guidez E. B.; Bertoni C.; Gordon M. S. Perspective: Ab Initio Force Field Methods Derived from Quantum Mechanics. J. Chem. Phys. 2018, 148, 090901 10.1063/1.5009551. [DOI] [Google Scholar]
- McDaniel J. G.; Schmidt J. R. Physically-Motivated Force Fields from Symmetry-Adapted Perturbation Theory. J. Phys. Chem. A. 2013, 117, 2053–2066. 10.1021/jp3108182. [DOI] [PubMed] [Google Scholar]
- Van Vleet M. J.; Misquitta A. J.; Stone A. J.; Schmidt J. R. Beyond Born-Mayer: Improved Models for Short-Range Repulsion in ab Initio Force Fields. J. Chem. Theory Comput. 2016, 12, 3851–3870. 10.1021/acs.jctc.6b00209. [DOI] [PubMed] [Google Scholar]
- Grimme S. A General Quantum Mechanically Derived Force Field (QMDFF) for Molecules and Condensed Phase Simulations. J. Chem. Theory Comput. 2014, 10, 4497–4514. 10.1021/ct500573f. [DOI] [PubMed] [Google Scholar]
- Cole D. J.; Vilseck J. Z.; Tirado-Rives J.; Payne M. C.; Jorgensen W. L. Biomolecular Force Field Parameterization via Atoms-in-Molecule Electron Density Partitioning. J. Chem. Theory Comput. 2016, 12, 2312–2323. 10.1021/acs.jctc.6b00027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horton J. T.; Allen A. E. A.; Dodda L. S.; Cole D. J. QUBEKit: Automating the Derivation of Force Field Parameters from Quantum Mechanics. J. Chem. Inf. Model. 2019, 59, 1366–1381. 10.1021/acs.jcim.8b00767. [DOI] [PubMed] [Google Scholar]
- Manz T. A.; Sholl D. S. Chemically Meaningful Atomic Charges That Reproduce the Electrostatic Potential in Periodic and Nonperiodic Materials. J. Chem. Theory Comput. 2010, 6, 2455–2468. 10.1021/ct100125x. [DOI] [PubMed] [Google Scholar]
- Manz T. A.; Sholl D. S. Improved Atoms-in-Molecule Charge Partitioning Functional for Simultaneously Reproducing the Electrostatic Potential and Chemical States in Periodic and Nonperiodic Materials. J. Chem. Theory Comput. 2012, 8, 2844–2867. 10.1021/ct3002199. [DOI] [PubMed] [Google Scholar]
- Lee L. P.; Cole D. J.; Skylaris C.-K.; Jorgensen W. L.; Payne M. C. Polarized Protein-Specific Charges from Atoms-in-Molecule Electron Density Partitioning. J. Chem. Theory Comput. 2013, 9, 2981–2991. 10.1021/ct400279d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher K. M.; Geerke D. P. Deriving Force-Field Parameters from First Principles Using a Polarizable and Higher Order Dispersion Model. J. Chem. Theory Comput. 2019, 15, 1875–1883. 10.1021/acs.jctc.8b01105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen A. E. A.; Payne M. C.; Cole D. J. Harmonic Force Constants for Molecular Mechanics Force Fields via Hessian Matrix Projection. J. Chem. Theory Comput. 2018, 14, 274–281. [DOI] [PubMed] [Google Scholar]
- Barone V.; Cacelli I.; De Mitri N.; Licari D.; Monti S.; Prampolini G. Joyce and Ulysses: Integrated and User-Friendly Tools for the Parameterization of Intramolecular Force Fields from Quantum Mechanical data. Phys. Chem. Chem. Phys. 2013, 15, 3736–3751. 10.1039/c3cp44179b. [DOI] [PubMed] [Google Scholar]
- Seminario J. M. Calculation of intramolecular force fields from second-derivative tensors. Int. J. Quantum Chem. 1996, 60, 1271–1277. . [DOI] [Google Scholar]
- Skylaris C.-K.; Haynes P. D.; Mostofi A. A.; Payne M. C. Introducing ONETEP: Linear-scaling density functional simulations on parallel computers. J. Chem. Phys. 2005, 122, 084119 10.1063/1.1839852. [DOI] [PubMed] [Google Scholar]
- Lee L. P.; Limas N. G.; Cole D. J.; Payne M. C.; Skylaris C.-K.; Manz T. A. Expanding the Scope of Density Derived Electrostatic and Chemical Charge Partitioning to Thousands of Atoms. J. Chem. Theory Comput. 2014, 10, 5377–5390. 10.1021/ct500766v. [DOI] [PubMed] [Google Scholar]
- Verstraelen T.; Pauwels E.; De Proft F.; Van Speybroeck V.; Geerlings P.; Waroquier M. Assessment of Atomic Charge Models for Gas-Phase Computations on Polypeptides. J. Chem. Theory Comput. 2012, 8, 661–676. 10.1021/ct200512e. [DOI] [PubMed] [Google Scholar]
- Robertson M. J.; Tirado-Rives J.; Jorgensen W. L. Improved Treatment of Nucleosides and Nucleotides in the OPLS-AA Force Field. Chem. Phys. Lett. 2017, 683, 276–280. 10.1016/j.cplett.2017.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone A. J. Intermolecular Potentials. Science 2008, 321, 787–789. 10.1126/science.1158006. [DOI] [PubMed] [Google Scholar]
- Cerutti D. S.; Swope W. C.; Rice J. E.; Case D. A. ff14ipq: A Self-Consistent Force Field for Condensed-Phase Simulations of Proteins. J. Chem. Theory Comput. 2014, 10, 4515–4534. 10.1021/ct500643c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lillestolen T. C.; Wheatley R. J. Atomic charge densities generated using an iterative stockholder procedure. J. Chem. Phys. 2009, 131, 144101. 10.1063/1.3243863. [DOI] [PubMed] [Google Scholar]
- Bultinck P.; Van Alsenoy C.; Ayers P. W.; Carbó-Dorca R. Critical analysis and extension of the Hirshfeld atoms in molecules. J. Chem. Phys. 2007, 126, 144111. 10.1063/1.2715563. [DOI] [PubMed] [Google Scholar]
- Vanommeslaeghe K.; Yang M.; MacKerell A. D. Jr Robustness in the fitting of molecular mechanics parameters. J. Comput. Chem. 2015, 36, 1083–1101. 10.1002/jcc.23897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan X. C.; Robertson M. J.; Tirado-Rives J.; Jorgensen W. L. Improved Description of Sulfur Charge Anisotropy in OPLS Force Fields: Model Development and Parameterization. J. Phys. Chem. B 2017, 121, 6626–6636. 10.1021/acs.jpcb.7b04233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Tirado-Rives J. Molecular modeling of organic and biomolecular systems using BOSS and MCPRO. J. Comput. Chem. 2005, 26, 1689–1700. 10.1002/jcc.20297. [DOI] [PubMed] [Google Scholar]
- Dziedzic J.; Helal H. H.; Skylaris C.-K.; Mostofi A. A.; Payne M. C. Minimal parameter implicit solvent model for ab initio electronic-structure calculations. EPL 2011, 95, 43001. 10.1209/0295-5075/95/43001. [DOI] [Google Scholar]
- Dziedzic J.; Fox S. J.; Fox T.; Tautermann C. S.; Skylaris C.-K. Large-scale DFT calculations in implicit solvent—A case study on the T4 lysozyme L99A/M102Q protein. Int. J. Quantum Chem. 2013, 113, 771–785. 10.1002/qua.24075. [DOI] [Google Scholar]
- Lever G.; Cole D. J.; Hine N. D. M.; Haynes P. D.; Payne M. C. Electrostatic considerations affecting the calculated HOMO–LUMO gap in protein molecules. J. Phys.: Condens. Matter 2013, 25, 152101. 10.1088/0953-8984/25/15/152101. [DOI] [PubMed] [Google Scholar]
- Karamertzanis P. G.; Raiteri P.; Galindo A. The Use of Anisotropic Potentials in Modeling Water and Free Energies of Hydration. J. Chem. Theory Comput. 2010, 6, 1590–1607. 10.1021/ct900693q. [DOI] [PubMed] [Google Scholar]
- Best R.; Buchete N.-V.; Hummer G. Are Current Molecular Dynamics Force Fields too Helical?. Biophys. J. 2008, 95, L07–L09. 10.1529/biophysj.108.132696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J.-S.; Bax A. Determination of ϕ and χ1 Angles in Proteins from 13C-13C Three-Bond J Couplings Measured by Three-Dimensional Heteronuclear NMR. How Planar Is the Peptide Bond?. J. Am. Chem. Soc. 1997, 119, 6360–6368. 10.1021/ja970067v. [DOI] [Google Scholar]
- Avbelj F.; Grdadolnik S. G.; Grdadolnik J.; Baldwin R. L. Intrinsic backbone preferences are fully present in blocked amino acids. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 1272–1277. 10.1073/pnas.0510420103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graf J.; Nguyen P. H.; Stock G.; Schwalbe H. Structure and Dynamics of the Homologous Series of Alanine Peptides: A Joint Molecular Dynamics/NMR Study. J. Am. Chem. Soc. 2007, 129, 1179–1189. 10.1021/ja0660406. [DOI] [PubMed] [Google Scholar]
- Vögeli B.; Ying J.; Grishaev A.; Bax A. Limits on Variations in Protein Backbone Dynamics from Precise Measurements of Scalar Couplings. J. Am. Chem. Soc. 2007, 129, 9377–9385. 10.1021/ja070324o. [DOI] [PubMed] [Google Scholar]
- Pérez C.; Löhr F.; Rüterjans H.; Schmidt J. M. Self-Consistent Karplus Parametrization of 3J Couplings Depending on the Polypeptide Side-Chain Torsion χ1. J. Am. Chem. Soc. 2001, 123, 7081–7093. 10.1021/ja003724j. [DOI] [PubMed] [Google Scholar]
- Hollingsworth S. A.; Karplus P. A. A fresh look at the Ramachandran plot and the occurrence of standard structures in proteins. Biomol. Concepts 2010, 1, 271–283. 10.1515/BMC.2010.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J.; Rauscher S.; Nawrocki G.; Ran T.; Feig M.; de Groot B. L.; Grubmüller H.; MacKerell A. D. Jr. CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2016, 14, 71–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nerenberg P. S.; Head-Gordon T. Optimizing Protein-Solvent Force Fields to Reproduce Intrinsic Conformational Preferences of Model Peptides. J. Chem. Theory Comput. 2011, 7, 1220–1230. 10.1021/ct2000183. [DOI] [PubMed] [Google Scholar]
- Weiner S. J.; Kollman P. A.; Case D. A.; Singh U. C.; Ghio C.; Alagona G.; Profeta S.; Weiner P. A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc. 1984, 106, 765–784. 10.1021/ja00315a051. [DOI] [Google Scholar]
- Ponder J. W.; Case D. A. Force fields for protein simulations. Adv. Protein Chem. 2003, 66, 27–85. 10.1016/S0065-3233(03)66002-X. [DOI] [PubMed] [Google Scholar]
- Friederich P.; Konrad M.; Strunk T.; Wenzel W. Machine learning of correlated dihedral potentials for atomistic molecular force fields. Sci. Rep. 2018, 8, 2559. 10.1038/s41598-018-21070-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmo K.; Mannfors B.; Mirkin N. G.; Krimm S. Potential energy functions: From consistent force fields to spectroscopically determined polarizable force fields. Biopolymers 2003, 68, 383–394. 10.1002/bip.10254. [DOI] [PubMed] [Google Scholar]
- Buck M.; Bouguet-Bonnet S.; Pastor R. W.; MacKerell A. D. Jr. Importance of the CMAP Correction to the CHARMM22 Protein Force Field: Dynamics of Hen Lysozyme. Biophys. J. 2006, 90, L36–L38. 10.1529/biophysj.105.078154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang W.; Jiang F.; Wu Y.-D. Universal Implementation of a Residue-Specific Force Field Based on CMAP Potentials and Free Energy Decomposition. J. Chem. Theory Comput. 2018, 14, 4474–4486. 10.1021/acs.jctc.8b00285. [DOI] [PubMed] [Google Scholar]
- Piana S.; Donchev A. G.; Robustelli P.; Shaw D. E. Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States. J. Phys. Chem. B 2015, 119, 5113–5123. 10.1021/jp508971m. [DOI] [PubMed] [Google Scholar]
- Robustelli P.; Piana S.; Shaw D. E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, E4758–E4766. 10.1073/pnas.1800690115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dziedzic J.; Hill Q.; Skylaris C.-K. Linear-scaling calculation of Hartree-Fock exchange energy with non-orthogonal generalised Wannier functions. J. Chem. Phys. 2013, 139, 214103. 10.1063/1.4832338. [DOI] [PubMed] [Google Scholar]
- Manz T. A.; Limas N. G. Introducing DDEC6 atomic population analysis: part 1. Charge partitioning theory and methodology. RSC Adv. 2016, 6, 47771–47801. 10.1039/C6RA04656H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone A. J.; Misquitta A. J. Atom–atom potentials from ab initio calculations. Int. Rev. Phys. Chem. 2007, 26, 193–222. 10.1080/01442350601081931. [DOI] [Google Scholar]
- Manz T. A.; Chen T.; Cole D. J.; Limas N. G.; Fiszbein B. New scaling relations to compute atom-in-material polarizabilities and dispersion coefficients: part 1. Theory and accuracy. RSC Adv. 2019, 9, 19297–19324. 10.1039/C9RA03003D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole D. J.; de Vaca I. C.; Jorgensen W. L. Computation of protein-ligand binding free energies using quantum mechanical bespoke force fields. Med. Chem. Commun. 2019, 10, 1116–1120. 10.1039/C9MD00017H. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


