Resolution of Sensory Ambiguities for Gaze Stabilization Requires a Second Neural Integrator

Abstract

The ability to simultaneously move in the world and maintain stable visual perception depends critically on the contribution of vestibulo-ocular reflexes (VORs) to gaze stabilization. It is traditionally believed that semicircular canal signals drive compensatory responses to rotational head disturbances (rotational VOR), whereas otolith signals compensate for translational movements [translational VOR (TVOR)]. However, a sensory ambiguity exists because otolith afferents are activated similarly during head translations and reorientations relative to gravity (i.e., tilts). Extra-otolith cues are, therefore, necessary to ensure that dynamic head tilts do not elicit a TVOR. To investigate how extra-otolith signals contribute, we characterized the temporal and viewing distance-dependent properties of a TVOR elicited in the absence of a lateral acceleration stimulus to the otoliths during combined translational/rotational motion. We show that, in addition to otolith signals, angular head position signals derived by integrating sensory canal information drive the TVOR. A physiological basis for these results is proposed in a model with two distinct integration steps. Upstream of the well known oculomotor velocity-to-position neural integrator, the model incorporates a separate integration element that could represent the “velocity storage integrator,” whose functional role in the oculomotor system has so far remained controversial. We propose that a key functional purpose of the velocity storage network is to temporally integrate semicircular canal signals, so that they may be used to extract translation information from ambiguous otolith afferent signals in the natural and functionally relevant bandwidth of head movements.

Introduction

In many sensory systems, the information provided by a given peripheral sensor or local detector is inadequate to resolve the true nature of the physical stimulus (Mazer, 1998; Pack and Born, 2001). Such sensory ambiguities are often eliminated by the CNS by integrating information from multiple sources. An example of such a situation arises in the vestibular system. Everyday activities such as walking and running typically involve both rotational and translational head movements. It is traditionally believed that behavioral responses to rotational motion are driven by sensory signals from the semicircular canals, whereas those associated with translational movements are derived from the otolith organs. However, because linear accelerometers cannot distinguish between inertial versus gravitational accelerations (Einstein, 1908) a “tilt/translation sensory ambiguity” exists in the interpretation of otolith signals. Specifically, the linear acceleration sensed by primary otolith afferents could have been generated during either translation or head reorientation relative to gravity (Fernández and Goldberg, 1976a; Angelaki and Dickman, 2000). Yet, behavioral responses to tilts and translation are different.

In the oculomotor system, for example, lateral head translation elicits horizontal compensatory eye movements [translational vestibulo-ocular reflex (TVOR)] (Paige and Tomko, 1991a, 1991b; Schwarz and Miles, 1991; Telford et al., 1997; Angelaki, 1998), whereas dynamic roll tilt generates mainly ocular torsion [rotational VOR (RVOR)] (Crawford and Vilis, 1991; Seidman et al., 1995). Given the equivalence of primary otolith afferent responses to these motions, why isn't an inappropriate TVOR generated whenever our head changes orientation relative to gravity?

Early on, this question motivated several theoretical studies that explored potential roles for head movement frequency and multisensory contributions (Guedry, 1974; Mayne, 1974; Young, 1984). Recently, a role for semicircular canal signals in generating the TVOR was proposed based on the hypothesis that they are used to explicitly construct internal neural estimates of gravity and translational acceleration (Merfeld and Young, 1995; Merfeld et al., 1999; Zupan et al., 2000; Merfeld and Zupan, 2002). However, experimental support for this proposal was provided primarily by observations at very low frequencies, below those relevant for the VORs. The contribution of canal-borne sensory cues to the TVOR was more directly demonstrated by showing that after canal inactivation both head tilt and translation elicited similar horizontal eye movement responses (Angelaki et al., 1999).

Thus, substantial evidence suggests that the canals provide important extra-otolith cues to ensure that otolith signals, appropriately routed to generate the TVOR during pure head translations, are somehow eliminated from driving this reflex during high-frequency roll head movements. However, how this is actually accomplished by the brain remains unknown; so far, only abstract models that incorporate the necessary physical laws to solve the problem but remain physiologically intangible have been proposed (Merfeld, 1995; Glasauer and Merfeld, 1997; Mergner and Glasauer, 1999; Angelaki et al., 1999; Merfeld and Zupan, 2002; Zupan et al., 2002). The goal of the current study was to quantitatively address how this problem is resolved within a physiologically relevant context. These results have been presented in abstract form (Green and Angelaki, 2003).

Materials and Methods

Animal preparation and eye movement recordings. Three rhesus monkeys (Macaca mulatta) were used in this investigation. Each animal was chronically implanted with a delrin head-restraint ring imbedded in dental acrylic that was secured to the skull with six stainless steel T-bolts (Angelaki, 1998). In separate surgical procedures, eye coils were implanted under the conjunctiva of each eye. All surgeries were performed under sterile conditions in accordance with the Institutional Animal Care and Use Committee and National Institutes of Health guidelines. Binocular eye movements were recorded using the magnetic search coil technique (Robinson, 1963) (CNC Engineering). One eye in each of two animals (A and B) was implanted with dual search coils to allow recording of three-dimensional eye positions (Hess, 1990). The second eye in each of animals A and B and both eyes in animal C were implanted with traditional two-dimensional coils. Eye movements in the three dimensions were calibrated according to both preimplantation and daily calibration procedures, as described previously (Hess, 1992; Angelaki, 1998).

Ocular and stimulus motions were expressed in a right-handed coordinate system with forward, leftward, and upward vector components along the naso-occipital, interaural (IA) and vertical [dorsoventral (DV)] head axes considered positive. Accordingly, positive angular deviations were clockwise, downward, and leftward (as viewed from the animal). Three-dimensional eye positions were expressed as rotation vectors (Haustein, 1989) using straight ahead as the reference position. Angular eye velocity was subsequently calculated from these rotation vectors (Angelaki and Hess, 1996a; Angelaki, 1998). For the eyes in which two-dimensional eye position was recorded, horizontal and vertical eye movements were expressed in Fick angles. Although eye positions in Fick coordinates differ from those expressed in a head-fixed coordinate frame (Van Opstal, 1993; Haslwanter, 1995), the difference in horizontal eye velocity between these two coordinates systems was measured to be less than 5% in the current experiments. Thus, all data were considered similarly in the analyses.

Experimental set-up and protocols. Animals, seated upright in a primate chair, were secured inside the inner frame of a three-dimensional rotator mounted on a linear sled (Acutronics USA) (Angelaki et al., 1999). The magnetic field coil system was rigidly mounted on the rotator such that it moved with the animal's head during all motion stimuli. Eye movements were, therefore, always measured in a head-fixed reference frame. The experimental protocols consisted of either lateral (IA) translation (translation only), roll tilt (roll tilt only), or combined lateral translation and roll tilt transient motion stimuli (translation + roll tilt motion and translation - roll tilt motion; Fig. 1). The roll stimulus consisted of a 15° tilt (angular velocity, 60°/sec; angular acceleration, 220°/sec²) to elicit a maximum IA acceleration of ≈0.2 × g. The translation stimulus was adjusted such that the IA acceleration profile generated during the first 600 msec of translation closely matched that induced by the head reorientation relative to gravity during the roll tilt. Hence, with the chosen stimulus profiles, the IA acceleration that would be sensed by the otoliths along the IA axis during either pure head roll or during a pure translation was approximately the same. Spectral analysis of the translational acceleration profile showed most (92%) of the energy in the signal below 2 Hz with a 3 dB cut off at ≈1 Hz. The high-frequency content of the transient translational acceleration stimulus was limited because of the requirement for these experiments that it closely match the gravitational acceleration induced by head roll along the IA axis (see below).

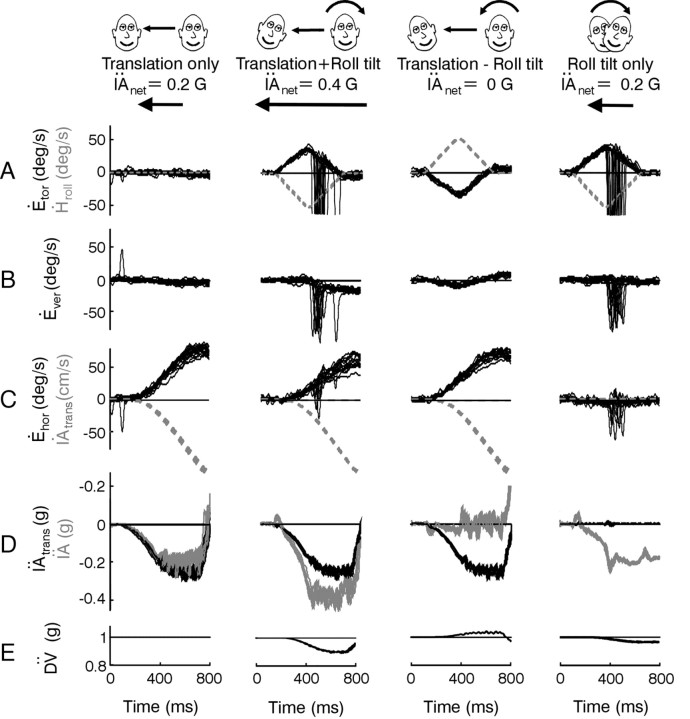
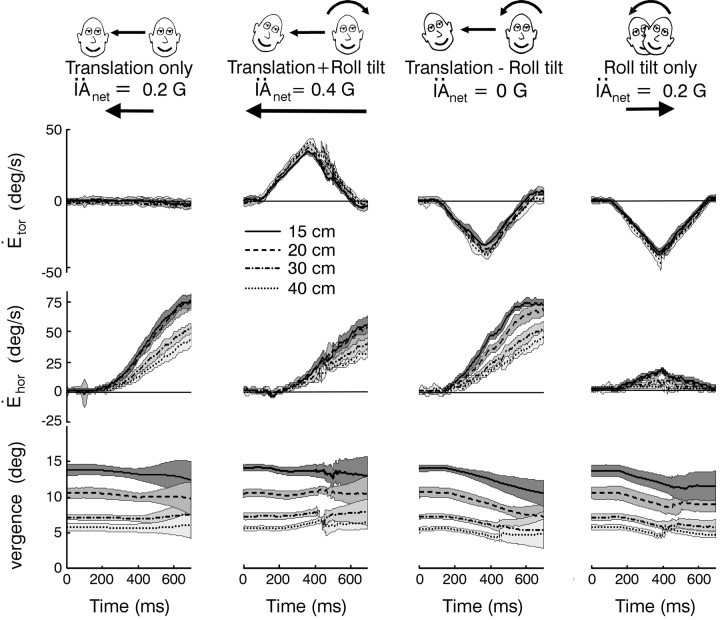
Figure 1.

Examples of eye movements and sensory stimuli. A-C, Torsional, vertical, and horizontal right eye velocities (Ė_tor, Ė_ver, and Ė_hor) are superimposed for several successful trials. Large deviations in eye velocity represent fast phases. Dashed gray traces represent the head roll velocity stimulus (Ḣ_roll) or the translational velocity of the sled (IȦ_trans). Positive directions are leftward, downward, and clockwise (from the subjective viewpoint). Data are from animal A at a viewing distance of 20 cm. D, The translational acceleration of the sled (IÄ_trans, black traces) is superimposed on the net IA acceleration (IÄ, gray traces; measured by a linear accelerometer mounted on the animal's head). E, The DV acceleration (DV̈; calculated from the angular head position and translational acceleration stimuli) also changes during roll.

The net IA acceleration (IÄ) sensed by the otoliths is the vectorial sum of gravitational and translational components (IÄ_G and IÄ_trans) along the IA head axis. Specifically, IÄ (5) = IÄ_G (t) + IÄ_trans (t) = g sin(H_roll (t)) + IÄ_trans (t) cos(H_roll (t)), where H_roll is roll head position and g = 981 cm/sec² is a constant representing the acceleration caused by gravity (Angelaki et al., 1999). Because the linear acceleration component profiles along the animal's IA axis were matched for the roll tilt and translation only stimuli [i.e.,|IÄ_G (t)| =|IÄ_trans (t)|], the combined tilt/translation protocols elicited either zero (translation - roll tilt) or double (translation + roll tilt) the IA acceleration during head translation or roll tilt alone, depending on the relative directions of the translational and roll motions. This was verified by a three-dimensional accelerometer (NeuwGhent Technology) mounted on the animal's head. Translation + roll tilt protocols included rightward translation and counter-clockwise roll or leftward translation and clockwise roll. Translation - roll tilt transients comprised rightward translation and clockwise roll or leftward translation and counter-clockwise roll. In general, all stimuli were applied with the animal in the upright orientation such that roll rotation activated both the otolith organs and the semicircular canals. However, one of the animals was also tested during roll in the supine position (supine roll), a stimulus that dynamically activated only the semicircular canals.

Responses were recorded in complete darkness. Binocular fixation was controlled by initializing each trial only when the animal had satisfactorily fixated on a target LED (paired with an auditory cue) centered between the two eyes (above the roll rotation axis) at a distance of 15, 20, 30, or 40 cm. Adequate fixation was defined when both eyes were within ±2° behavioral windows, computed separately for each eye (Angelaki et al., 2000). The target was extinguished before the onset of motion and remained off until the animal came to a complete stop at the initial starting position. In the absence of movement, trained animals maintained binocular fixation of the remembered target location as well as vergence angle within ±1-2° for 400-1000 msec in the presence of an auditory tone. During movement trials, only a vergence window was imposed for the first 400-500 msec after motion onset. Because of the large translational distances traveled during the experimental protocol (≈70 cm), geometrical requirements predict that binocular eye movements should be increasingly disconjugate as viewing distance decreases; a significant decay in vergence can, therefore, be shown to be geometrically appropriate and part of the compensatory response. The size of the imposed vergence window was accordingly systematically increased for closer viewing distances (40 cm, 1-1.5°; 30 cm, 1.5-2°; 20 cm, 2-2.5°; 15 cm, 3-4°). Data were also collected in one animal without a reinforced vergence window, and results were similar. Motion protocols were chosen randomly and interleaved with nonmovement trials such that the animal could not predict whether a movement would occur or what the movement would be.

Data analysis. Data analysis was performed off-line using MATLAB (Mathworks, Inc.). The horizontal, vertical, and torsional components of the calibrated eye position and velocity were smoothed and differentiated with a Savitzky-Golay quadratic polynomial filter using a 15-point forward and backward window (Savitzky and Golay, 1964; Press et al., 1988). Successful runs were aligned on stimulus onset. Means and SDs of the aligned and desaccaded responses were computed for each animal, stimulus type (i.e., translation only, roll tilt only, translation + roll tilt, and translation - roll tilt), stimulus direction (left/right translation or roll), viewing distance, and left/right eye. Horizontal eye velocity sensitivities to viewing distance for the different stimuli were computed by plotting eye velocity as a function of instantaneous vergence angle at different times after motion onset and quantifying this relationship using linear regressions.

A key goal of the study was to quantify the sensory stimuli and associated central processing that could predict the dynamics of the observed responses. Thus, a series of different linear regression models were fitted to individual and mean horizontal eye velocity, Ė_hor, response profiles. These models consisted of all possible combinations of angular as well as IA and DV linear position, velocity, and acceleration signals. In its most general form, the equation used was of the form:

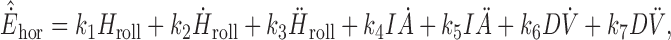1

where H_roll, Ḣ_roll, Ḧ_roll represent angular roll position, velocity, and acceleration, IȦ, IÄ denote IA linear velocity and acceleration and DV̇, DV̈ represent DV linear velocity and acceleration stimuli, respectively. Ė_hordenotes the model estimate of the actual Ė_hor response. IA and DV position terms were not included in this analysis because their temporal profiles were very similar to those of the corresponding velocities (IȦ and DV̇). However, models where H_roll was replaced with its integral (∫ H_roll) were also evaluated (see Results).

The fitting procedure was applied simultaneously to data from 0 to 600 msec after motion onset for all runs for the translation only and translation - roll tilt stimulus combinations. This approach allowed estimation of coefficients k₁ through k₇ for each viewing distance, left/right eye, and stimulus direction (when DV terms were not included) in each animal. The obtained models were subsequently cross-checked by examining their abilities to fit mean translation + roll tilt and roll tilt only responses (i.e., validated on data not used to obtain the fit parameters). To compare the ability of each model to describe the transient response profiles, three measures were used. First, variance-accounted-for (VAF) coefficients were computed as VAF = {1- [var (Ė_hor - &̂˙E_hor)/var (Ė_hor)] × 100} and provided a normalized measure of the goodness of fit. Second, the mean square error (MSE) was computed as MSE = Σ_i [Ė_hor (i) - &̂˙E_hor (i)]², where Ė_hor (i) represents the actual horizontal eye velocity responses and &̂˙E_hor (i) the corresponding values estimated from the model fit. Third, the Bayesian information criteria (BIC) measure was computed as BIC = log(1/N Σ_i [Ė_hor (i) - &̂˙E_hor (i)]²) + P/2 logN/N with P the number of model parameters and N the number of data points (Caines, 1988). Whereas the VAF measure provides a goodness of fit criterion, it does not take the number of model parameters into account. In contrast, the BIC takes into account the cost of adding additional parameters. For a larger parameter model to be more appropriate to describe the temporal response profiles over a fewer parameter model, the former should be characterized by a larger VAF and smaller BIC than the latter.

Model simulations. A simple model structure was explored as a means of interpreting the experimental data and delineating a possible physiological correlate for the contribution of semicircular canal signals to compensatory responses to translation. The model structure is based on classical feedforward realizations for two well known dynamic processing stages in the VOR: (1) “velocity storage” (Robinson, 1977; Raphan et al., 1979) and (2) oculomotor neural integration and eye plant compensation (Skavenski and Robinson, 1973; Robinson, 1981). First-order approximations to the dynamics of the sensors [semicircular canals, C(s) = T_cs/(T_cs + 1); otolith organs, O(s) = 1/(T_os + 1)] and the eye plant [P(s) = 1/(T_ps + 1)] were implemented with T_c = 6 sec, T_o = 0.016 sec, and T_p = 0.25 sec (Fernández and Goldberg, 1976b; Robinson, 1981). Model parameters associated with the gains of different pathways (see Fig. 6 A) were chosen to satisfy the following criteria: (1) to ensure compensation for the dynamic characteristics of the eye plant in the traditional RVOR pathways, weight c was chosen such that 1/c = T_p (Robinson, 1981). Projection weight p_dh was then chosen to reproduce a high-frequency horizontal VOR gain (Ė_hor/Ḣ_yaw), for close to zero vergence, of 0.88; (2) weight q_z was chosen to reproduce experimentally observed high-frequency TVOR characteristics (Telford et al., 1997; Angelaki, 1998); (3) weight p_vsh was chosen to compensate approximately for the dynamic properties of the canals in the RVOR response (Robinson, 1977; Raphan et al., 1979); (4) the remaining pathway strengths (p_dv, p_vsv, and q) as well as a TVOR reflex delay, τ_TVOR = 44 msec, were chosen to fit recorded data using a constrained optimization routine in MATLAB. The delay, τ_RVOR, associated with canal inputs to the RVOR pathway, was set to 14 msec (Lisberger, 1984).

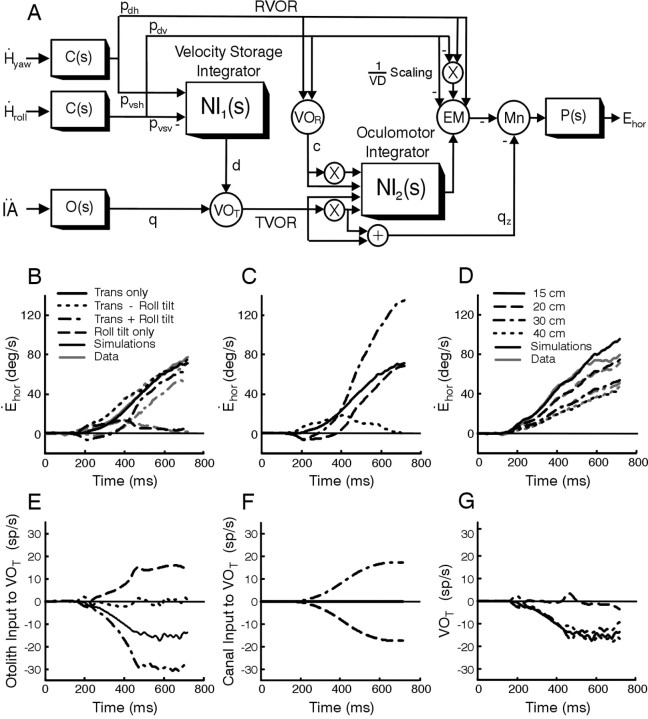
Figure 6.

A, Proposed model for the VOR during rotations and translations. Circles are summing junctions used to represent particular cell populations including vestibular-only (VO) cells, VO_R and VO_T, that mediate signal flow in the RVOR and TVOR pathways, respectively, premotor eye movement-sensitive (EM) neurons, and motoneurons (Mn). Boxes are dynamic elements that represent either a sensor [C(s) and O(s)], the motor plant [P(s)] or a neural filtering process [NI₁(s) = 1/(T_VORs + 1), NI₂(s) = 1/s]. The two filtering processes include the velocity storage integrator (low-pass filter with a long time constant, T_VOR = 20 sec) and the oculomotor integrator (assumed for simplicity to be a perfect integrator). Inputs to the model are roll and yaw head velocities, Ḣ_roll and Ḣ_yaw, sensed by the vertical and horizontal semicircular canals, respectively, and IA acceleration, IÄ, sensed by the otolith organs. The output of the model is conjugate horizontal eye position, E_hor. Xs in the schematic indicate scaling by inverse viewing distance (i.e., multiplication by 1/VD). Model parameters have been adjusted for the upright orientation (in general, weights p_vsh, p_vsv, and d depend on head orientation relative to gravity) (Green et al., 2002). B, Comparison between model predictions and mean horizontal eye velocity responses from animal A for all stimulus combinations at a single viewing distance (20 cm). C, Predicted horizontal eye velocity responses when the contribution of semicircular canal signals to the TVOR is eliminated (i.e., projection weight d = 0). D, Comparison between simulated and mean horizontal eye velocity responses from animal A at all viewing distances during translation-roll tilt motion. Otolith (E) and semicircular (F) canal signal contributions to the responses of cell VO_T (G) during the four stimulus combinations. The legend in B also applies to C and E-G. Dashed and dotted traces are superimposed in F. The simulated response to head roll in C (dashed trace) was inverted for display purposes. Model parameters used in all simulations are: c = 4; d = 1; p_dh = 0.22; p_dv = 0.0092; p_vsh = 2.05; p_vsv = 24.6; q = 0.0772; q_z = 0.03.

The model was implemented with the MATLAB dynamic simulation environment SIMULINK (Mathworks). Model simulations were performed using a Runge-Kutta integration routine with time steps of 1.2 msec.

Results

Four unique combinations of translational and rotational motion stimuli were used to compare the otolith and extra-otolith sensory contributions to the TVOR. These included lateral translation (translation only), roll tilt (roll tilt only), or combined lateral translation and roll tilt transient motion stimuli (translation + roll tilt motion and translation - roll tilt motion; Fig. 1). The translation stimulus was adjusted such that the IA acceleration profile generated during the first 600 msec of translation closely matched that induced by the head reorientation relative to gravity during the roll tilt (see Materials and Methods). Hence, either pure translation or head roll resulted in a similar stimulus to the otoliths along the IA axis (Fig. 1D, gray traces in columns 1 and 4). During simultaneous rotational and translational stimulation, the gravitational acceleration elicited by head roll and the inertial acceleration elicited by head translation summed along the IA axis in either an additive or subtractive fashion, depending on the relative directions of the stimuli. Hence, during combined rotation and translation, the net IA linear acceleration activating the otolith receptors either doubled (translation + roll tilt; e.g., simultaneous rightward translation and left-ear-down roll; Fig. 1, column 2) or was nearly zero (translation - roll tilt; e.g., rightward translation and right-ear-down roll; Fig. 1, column 3), even though the actual translation of the animal was the same (Fig. 1D, compare gray lines with black lines).

Superimposed response profiles for the translation only, translation + roll tilt motion, translation - roll tilt motion, and roll tilt only stimulus combinations are shown in Figure 1A-C. As expected for movements that included a roll tilt component, a robust torsional RVOR was generated that followed the profile of roll head velocity (Fig. 1A, compare solid black lines with dashed gray lines). Small disconjugate vertical (Fig. 1B) and conjugate horizontal responses (Fig. 1C, right) were also present during roll (Seidman et al., 1995; Angelaki and Hess, 1996b; Angelaki et al., 1999; Bergamin and Straumann, 2001; Jauregui-Renaud et al., 2001; Kori et al., 2001). Large horizontal eye movements that followed the profile of translational head velocity were elicited in all cases in which the motion included a translational component (Fig. 1C, compare solid black traces with dashed gray traces). This was true, even though the IA head acceleration that would have been encoded as a population average of otolith afferent responses, varied considerably for the different motion stimuli (Fig. 1D, gray traces). Notably, a robust compensatory horizontal eye velocity response was elicited even for the translation - roll tilt motion combination when the net linear acceleration along the IA axis was nearly zero (Fig. 1D, column 3, gray IÄ traces).

Thus, horizontal eye velocity was similar during the translation only, translation + roll tilt, and translation - roll tilt motion combinations, although the IA acceleration that was sensed by the otolith organs would have been different. Accordingly, the otolith IÄ signal, sensed mainly by the utricles, does not appear to be the only stimulus that drives the TVOR. Because motion in this study was passive and the animal's head was fixed to the body, additional dynamic information could only be provided by two other sources. First, the angular (rotational) velocity during roll is sensed by the semicircular canals. Second, the reorientation of the head relative to gravity is sensed, mainly by saccular otolith afferents, as a change in linear acceleration along the DV axis (Fig. 1E DV̈). However, although the net DV̈ stimulus differs for the various motion profiles, the change in DV̈ is the same for both directions of stimulation during a given protocol. Specifically, for both clockwise and counterclockwise roll head movements, DV̈ always decreases from 1 × g as the cosine of roll head position, cos(H_roll). Similarly, during combined rotation and translation stimuli, the net DV̈ stimulus (including both gravitational and inertial components) is the same for both directions of either translation + roll tilt or translation - roll tilt motion. Thus, it is unlikely that the DV̈ signal by itself could be responsible for driving bidirectional horizontal eye movements in the absence of an IA acceleration stimulus during the translation - roll tilt combinations.

In the following analyses, we provide quantitative evidence that dynamically processed (integrated) semicircular canal signals are responsible for “driving” the TVOR in the absence of utricular afferent activation and for “eliminating” the TVOR during roll rotations. These experimental results are then summarized into a conceptual model that formulates a quantitative hypothesis as to the nature of otolith/canal interactions necessary to account for these observations.

General properties and dependence on viewing distance

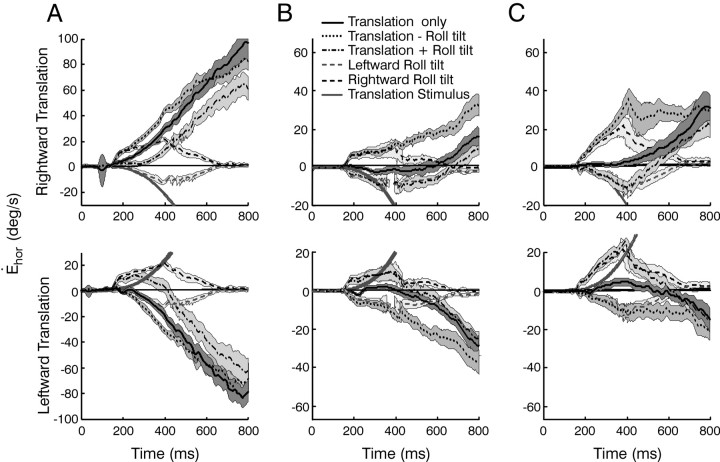
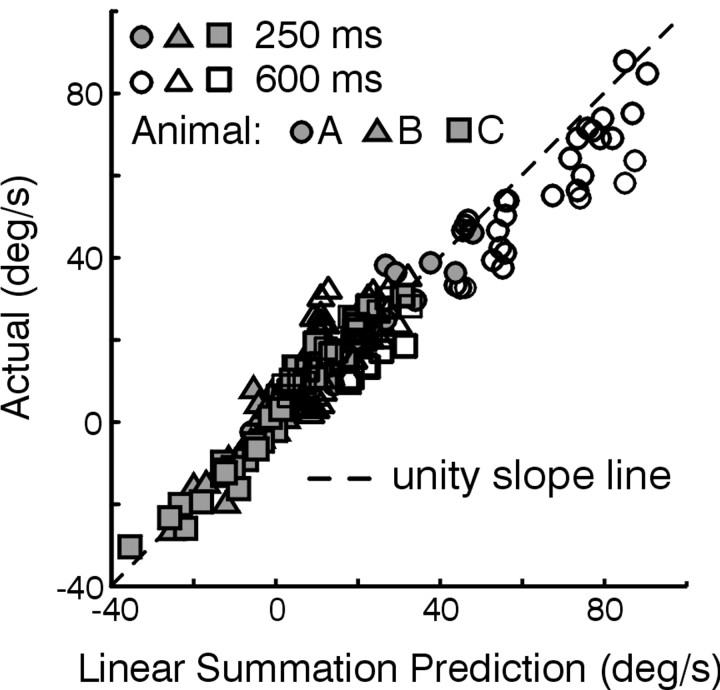
Mean (±SD) horizontal eye velocity responses to the four stimulus combinations for a viewing distance of 20 cm are superimposed for each of three animals (Fig. 2A-C). Despite variability in the amplitudes of the responses elicited by individual animals that is typical for the transient TVOR (Schwarz and Miles, 1991; Angelaki, 2002), the general observations for each animal were the same. Horizontal responses elicited during roll tilt only followed the profile of angular head velocity and were similar during supine roll when there was no dynamic reorientation relative to gravity (data not shown). These RVOR responses can be attributed both to the geometrical requirements for near target stabilization (Seidman et al., 1995; Bergamin and Straumann, 2001; Jauregui-Renaud et al., 2001) and the misalignment of the roll RVOR (Angelaki and Hess, 1996b). Because of these horizontal RVOR responses to head roll, eye velocity tended to be larger, at least initially, for the subtractive translation - roll tilt combination, as compared with the translation only condition (Fig. 2, compare dotted lines with solid lines). The converse was true for translation + roll tilt stimulation, in which the RVOR horizontal component was directed opposite to that of the TVOR (Fig. 2, dash-dot traces). Thus, ocular responses during the combined protocols appeared to reflect a linear combination of the horizontal eye movements elicited during translation only and roll tilt only motions (i.e., the sum of RVOR and TVOR response components). This observation was investigated by comparing mean horizontal eye velocities during the combined motion stimuli (translation - roll tilt and translation + roll tilt motion) with the sums of the respective mean velocities during roll tilt only and translation only stimulation at different times (250 and 600 msec) after motion onset. The plotted data falls close to the unity-slope line, particularly early in the response profile (Fig. 3, solid symbols; linear regression slope of 1.02 ± 0.05 for all animals together). The same observation held when the responses for each animal were considered individually (Fig. 3).

Figure 2.

Comparison of responses for different stimulus profiles. A-C, Mean ± SD horizontal eye velocities for a viewing distance of 20 cm in the three animals. Each column shows the responses of a different animal (i.e., animals A-C). Responses to rightward (top) and leftward (bottom) translations are superimposed on the bidirectional roll tilt stimuli (solid line, translation only; dash-dot line, translation + roll tilt; dotted line, translation - roll tilt; dashed gray line, leftward roll tilt; dashed black line rightward roll tilt). The solid gray lines illustrate the head velocity stimulus.

Figure 3.

Investigation of linear superposition. Actual responses during translation + roll tilt and translation - roll tilt are plotted versus the values computed by linear superposition of the respective roll tilt only and translation only responses. Illustrated data are means over a ±20 msec interval centered at 250 msec (solid symbols) and 600 msec (open symbols) after motion onset, calculated separately for each eye, stimulus direction, and viewing distance. Data are from animals A-C (circles, triangles, and squares, respectively). The black dashed line is the unity-slope line. Linear regressions of the data from all three animals yielded slopes and 95% confidence intervals of 1.02 ± 0.05 (slope ± 95% confidence interval) early in the response and 0.87 ± 0.04 late in the response. Regressions for each animal considered individually yielded slopes of 0.99 ± 0.06, 1.01 ± 0.06, and 1.07 ± 0.09 early in the response and 0.85 ± 0.04, 1.01 ± 0.16, and 0.88 ± 0.11 late in the response for animals A-C, respectively (regression lines not shown).

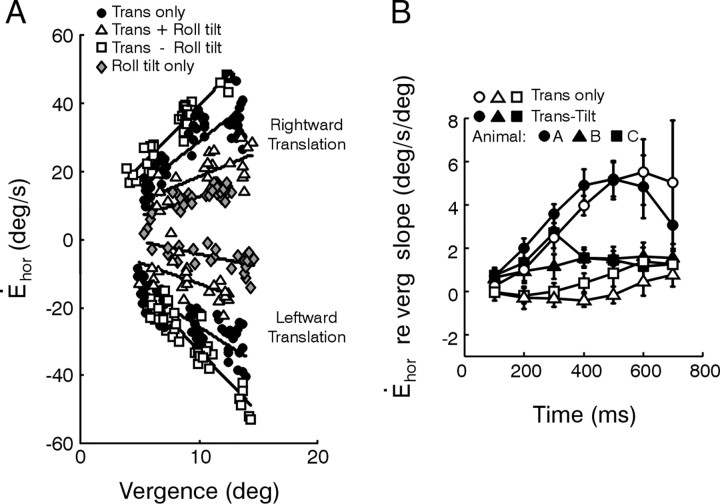
A key feature of compensatory responses to head translation is their required dependency on viewing distance that has been well characterized during pure translational motion (Paige and Tomko, 1991b; Schwarz and Miles, 1991; Telford et al., 1997; Angelaki et al., 2000). If a TVOR driven by extra-otolithic signals provides a true functional complement to the purely otolith-driven reflex, then responses in the absence of an IA acceleration stimulus (translation - roll tilt motion) should also exhibit viewing distance scaling. Indeed, horizontal (but not torsional) eye velocity depended on viewing distance for all four stimulus combinations (Fig. 4). This dependence was quantified using linear regressions (Fig. 5A). Results for the translation - roll tilt stimulus combination were compared with those during translation only motion by plotting the eye velocity dependence on instantaneous vergence angle for each stimulus at different times after stimulus onset (Fig. 5B). Viewing distance sensitivity varied considerably among the animals and was quite small in both animals B and C as compared with animal A during purely translational motion. We attribute the small sensitivity to viewing distance in two animals during pure head translation to the relatively low-frequency bandwidth of the linear acceleration stimulus profile (below 2 Hz; see Materials and Methods). The viewing distance dependence of the TVOR has been shown previously to decrease inversely with frequency (Schwarz and Miles, 1991; Telford et al., 1997; Angelaki, 2002). Nonetheless, the general qualitative trends were the same in all cases. Importantly, eye velocity demonstrated a dependence on viewing distance during translation - roll tilt motion (i.e., in the absence of an IA acceleration stimulus) that was comparable with (late in the response) or even larger than (early in the response) that of the purely otolith-driven TVOR (translation only motion; Fig. 5B, compare solid symbols vs open symbols).

Figure 4.

Dependence of horizontal eye velocity on viewing distance. Mean ± SD torsional (Ė_tor, top) and horizontal (Ė_hor, middle) eye velocities for each of the stimulus combinations at different target distances (dotted line, 40 cm; dash-dot line, 30 cm; dashed line, 20 cm; solid line, 15 cm). Only rightward translation and right-ear-down roll tilt (for roll tilt only stimulus) profiles are shown. The bottom row shows corresponding mean ± SD vergence angles. Data are from animal A.

Figure 5.

Quantification of viewing distance sensitivity. A, Horizontal velocity 300 msec after stimulus onset plotted as a function of vergence angle for each of the translation only, translation + roll tilt, translation - roll tilt, and roll tilt only stimuli (solid circles, open triangles, open squares, and gray diamonds, respectively). Solid lines are linear regressions. Data are from animal A during rightward (top) and leftward (bottom) translation. B, Comparison of the dependence of horizontal eye velocity on instantaneous vergence angle during translation only and translation - roll tilt motions (open and solid symbols, respectively) at different times after stimulus onset. Data shown are means for both eyes and both directions of translation for animals A (circles), B (triangles), and C (squares). Error bars represent SDs.

Quantitative investigation of sensory signal contributions

To quantify which stimuli contributed to the observed horizontal response profiles and to determine how a given sensory stimulus was dynamically processed centrally, we compared the fits of several different linear regression models of increasing complexity to the response profiles from 0 to 600 msec after motion onset for all successful runs during translation only and translation - roll tilt motions. The models summarized here represent a subset of those described in Equation 1 (see Materials and Methods) that involved one or more of the following parameters: H_roll, Ḣ_roll, Ḧ_roll, IȦ, and IÄ representing angular roll position, velocity, and acceleration, as well as IA linear velocity and acceleration, respectively.

Only 8 of 31 models gave mean VAF values larger than 75% (Table 1). The lowest-parameter model in this category consisted of head roll position and IA velocity (H_roll, IȦ). All other higher-order models with large VAF values included these two terms. Although the VAF and BIC improved as the complexity of the model increased further, this improvement was small and did not allow a clear further distinction between the different models (Table 1). Cross-validation of the fits using the obtained parameters to predict mean translation + roll tilt and roll tilt only responses, however, revealed both qualitatively (i.e., by inspection) and quantitatively (as described by the mean square errors in Table 2) that the ability to fit the data was significantly improved by the additional contribution of a roll head velocity component, Ḣ_roll. In fact, this term is necessary to fit horizontal responses to roll tilt only, in line with the observation that horizontal eye velocity during roll followed the profile of head roll velocity (Figs. 2, 4). In addition, the contribution of an IÄ term was important in improving the fits for movements that included translational motion in animals B and C. The observed sensitivity to viewing distance (Figs. 4, 5) was reflected in all of the H_roll (or ∫H_roll), Ḣ_roll, IȦ, and IÄ coefficients.

Table 1.

Mean goodness-of-fit parameters for the eight models with the best fits

Model	VAF (%)	BIC	MSE
VAF>75%
Hroll, IȦ	81.0	2.7	17.4
Hroll, Ḧroll, IȦ	83.3	2.5	15.5
Hroll, Ḣroll, IȦ	83.7	2.5	14.7
Hroll, IȦ, IÄ	84.9	2.5	14.6
Hroll, Ḣroll, Ḧroll, IȦ	84.8	2.4	13.8
Hroll, Ḧroll, IȦ, IÄ	87.8	2.3	12.5
Hroll, Ḣroll, IȦ, IÄ	88.0	2.3	11.8
Hroll, Ḣroll, Ḧroll, IȦ, IÄ	89.4	2.2	10.8
VAF >75% using ∫ Hroll in place of Hroll
∫ Hroll, IȦ	77.7	3.0	27.8
∫ Hroll, Ḧroll, IȦ	79.8	2.9	26.0
∫ Hroll, Ḣroll, IȦ	84.1	2.5	15.4
∫ Hroll, IȦ, IÄ	81.5	2.8	25.3
∫ Hroll, Ḣroll, Ḧroll, IȦ	84.8	2.4	14.1
∫ Hroll, Ḧroll, IȦ, IÄ	84.0	2.7	23.2
∫ Hroll, Ḣroll, IȦ, IÄ	88.5	2.3	12.6
∫ Hroll, Ḣroll, Ḧroll, IȦ, IÄ	89.4	2.2	11.1

Values represent means for all animals, both eyes, both directions of translation only and roll tilt - translation motions and all viewing distances.

Table 2.

MSEs associated with predictions of the mean response profiles for the translation + roll tilt (Trans + roll) and roll tilt only (Roll only) motion conditions using the parameters obtained from the fits described inTable 1

Model	Trans + roll	Roll only
Hroll, IȦ	87.8	47.8
Hroll, Ḧroll, IȦ	82.0	42.2
Hroll, Ḣroll, IȦ	67.4	36.0
Hroll, IȦ, IÄ	74.6	45.7
Hroll, Ḣroll, Ḧroll, IȦ	65.2	33.4
Hroll, Ḧroll, IȦ, IÄ	70.0	39.9
Hroll, Ḣroll, IȦ, IÄ	67.8	40.2
Hroll, Ḣroll, Ḧroll, IȦ, IÄ	63.3	36.0

Data represent averages for all conditions in all animals.

More complicated models that included DV acceleration and velocity terms (DV̈ and DV̇; see Eq. 1 in Materials and Methods) were also investigated. These models either did not fit the data (if the H_roll and IȦ terms were not included) or provided little improvement in the fits. This quantitative result is consistent with the qualitative observation that the vertical linear acceleration stimulus (DV̈) could not account for the horizontal TVOR in the absence of an IA acceleration stimulus, because it was the same for both movement directions for a given stimulus paradigm. Finally, it should be added that equally good fits were obtained if the integral of H_roll (i.e., ∫H_roll) was used instead of H_roll (Table 1).

Development and simulations of a dynamic VOR model

Evidence has been presented that integrated semicircular canal signals functionally complement otolith signals to ensure that ambiguous sensory otolith information results in appropriate gaze stabilization behavior during head motions that include reorientation relative to gravity. We now incorporate our experimental observations into a simple model (Fig. 6A) that is based on well known dynamic processing stages in the VOR, to delineate a potential physiological correlate for the contribution of this integrated canal signal to the TVOR.

The schematic in Figure 6A shows the classical RVOR model proposed by Skavenski and Robinson (1973) (cf. Robinson, 1981) that consists of a parallel set of pathways that convey angular head velocity signals (Ḣ_roll, Ḣ_yaw) sensed by the semicircular canals, C(s), to extraocular motoneurons (Fig. 6A, top pathways labeled RVOR). These include a “direct” pathway via eye movement-sensitive neurons in the vestibular nuclei and an “indirect” pathway via the well known oculomotor integrator (e.g., Cannon and Robinson, 1987). Signals in both pathways include a component that scales with viewing distance, denoted by Xs representing multiplication by inverse viewing distance, 1/VD (Viirre et al., 1986; Snyder and King, 1992; Viirre and Demer, 1996; Crane and Demer, 1998; Telford et al., 1998). The bottom pathway (Fig. 6A, labeled TVOR) shows a previously proposed extension of the parallel pathway structure to account for the dynamic processing of IA linear acceleration signals, IÄ, sensed by the otolith organs, O(s), in the TVOR. Briefly, otolith signals were proposed to project through a vestibular interneuron (VO_T) mainly to the neural integrator (NI₂) (i.e., into the indirect RVOR pathway) without a strong complementary projection into the direct pathway (Green and Galiana, 1998; Musallum and Tomlinson, 1999; Green, 2000; Angelaki et al., 2001). The proposed projection into NI₂ is also shown to include scaling by inverse viewing distance to explain the strong dependence of the TVOR on vergence angle (Paige and Tomko, 1991b; Schwarz and Miles, 1991; Telford et al., 1997; Angelaki et al., 2000).

What is novel in the model and of particular relevance to the investigation here is the postulated additional neural integrator, NI₁, and its projection (Fig. 6A, labeled with weight d) to the vestibular interneuron (VO_T)of the TVOR pathway. This additional pathway has been included to account for our present observations that integrated semicircular canal signals also contribute to generating an appropriate TVOR when head translation is accompanied by a reorientation relative to gravity. We further hypothesize that NI₁ could represent the so-called velocity storage integrator, an integrative network proposed previously to account for the observation that the RVOR extends to lower frequencies than those predicted based on the dynamic characteristics of the canals (Raphan et al., 1977, 1979; Robinson, 1977). However, the functional role of this network has remained controversial because the observed improvement in RVOR performance exists only at very low frequencies (<0.05) where it has little behavioral relevance and where visual tracking mechanisms are sufficient to generate compensatory ocular responses to head movement (e.g., Lisberger et al., 1987; Barnes, 1993). Here, we propose that the most important functional contribution of this network to gaze stability may instead be at mid-high frequencies, at which a temporally integrated semicircular canal signal (i.e., at the output of NI₁) could be combined with otolith signals (on cell VO_T) to eliminate an inappropriate otolith-driven TVOR during high-frequency roll head movements. As shown in the present study, during translation in the absence of an IA otolith stimulus (i.e., when IÄ = 0 during translation - roll tilt), it is this integrated canal signal that drives compensatory responses to translation.

The basic dynamic behavior of this structure can be understood by considering the general Laplace domain expression for horizontal eye velocity, Ė_hor, predicted by the model in response to IA acceleration, IÄ, and roll velocity, Ḣ_roll, stimuli sensed by the otoliths and semicircular canals, respectively. For ease of description (although not in the model simulations), both NI₁ and NI₂ are assumed to represent perfect neural integrators, and the high-frequency dynamic characteristics of the TVOR are ignored (i.e., O(s) = 1 and q_z = 0). As an additional simplification, we consider an approximation valid at frequencies well above those associated with the dominant time constant of the canal (i.e., at frequencies f ≫ 1/T_c). Thus, the following equations apply only at mid-high frequencies (e.g., >0.1 Hz) at which a contribution of semicircular canal cues has been illustrated (Angelaki et al., 1999). At low frequencies (<1/T_c), the semicircular canals do not provide an accurate estimate of head velocity and the resolution of ambiguous otolith sensory information must rely on different strategies, such as frequency segregation (Paige and Tomko, 1991a; Telford et al., 1997) or the use of otolith-derived estimates of head rotation (Mergner and Glasauer, 1999). Ocular responses are then described as:

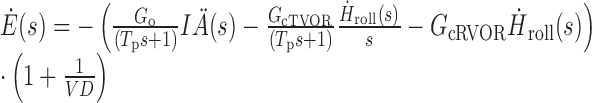2

where gains, G, can be written in terms of model parameters as G_o = q, G_cTVOR = p_vsvd and G_cTVOR = p_dvc, s is the Laplace operator representing complex frequency, T_p is the dominant time constant of the eye plant (see Materials and Methods), and VD is the viewing distance.

The first term in Equation 2 describes ocular responses to IA acceleration stimuli, IÄ, sensed by the otoliths. Hence, this is the only term that contributes to the TVOR during translation only motion. Otolith-derived IÄ information is integrated and appropriate to produce compensatory deviations in horizontal eye velocity (i.e., Ė_hor proportional to IȦ) at frequencies above the eye plant pole [f > 1/(2πT_p) ≈ 0.6 Hz], as observed experimentally (Telford et al., 1997; Angelaki, 1998).

In the absence of a net IA otolith stimulus (translation - roll tilt condition), only the last two terms of Equation 2 contribute to horizontal eye movements. In the second term, roll head velocity, Ḣ_roll, sensed by the semicircular canals, appears integrated (i.e., appears as Ḣ_roll/s). Hence, in agreement with our experimental observations, the model predicts a TVOR in the absence of an IA acceleration stimulus driven mainly by an angular head position signal. Furthermore, based on Equation 2, at frequencies above the eye plant pole [f > 1/(2πT_p) ≈ 0.6 Hz], the contribution to horizontal eye velocity from term 2 should, in fact, be proportional to the integral of angular head position. In line with these predictions, both angular head position (H_roll) and the integral of H_roll (∫ H_roll) provided equally good fits to the data (Table 1). The third term in Equation 2 contributes a signal proportional to head velocity, Ḣ_roll, that accounts for the observed small horizontal RVOR elicited by head roll.

During pure roll rotation, all three terms in Equation 2 contribute to the generation of horizontal eye velocity. However, in this case, the angular position signal (term 2) effectively eliminates an inappropriate otolith drive (term 1) to the TVOR. This occurs because for small roll head deviations from upright (as would typically be the case during natural high-frequency head movements), the IA gravitoinertial acceleration is approximately proportional to angular head position [i.e., IÄ = IÄ_G = gsin(H_roll) ≈ gH_roll]. Thus, if G_og ≈ G_cTVOR, then the effects of the first two terms in Equation 2 cancel out. Horizontal ocular responses during roll then simply reflect the contribution of the third term, representing the small RVOR response component.

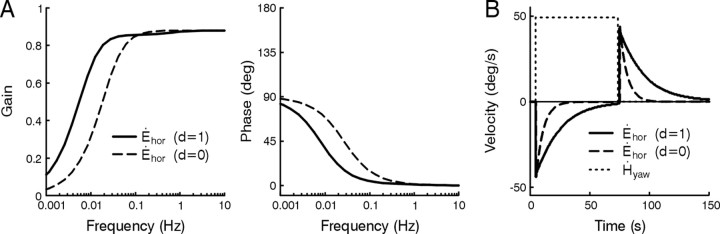
Simulations of the model using the parameters indicated in the legend of Figure 6 are shown in Figure 6B-G. As expected from Equation 2, the model can predict the general characteristics of the observed responses for all four stimulus combinations (Fig. 6B; 20 cm viewing distance) when integrated semicircular canal signals contribute to the TVOR pathway (Fig. 6A, d = 1). In contrast, when the contribution of this pathway is eliminated (Fig. 6A,d = 0), the predicted responses instead reflect the net IÄ stimulus acting on the otoliths (and the small component of the response related to Ḣ_roll mediated by the direct RVOR pathway; Fig. 6C). Model predictions (d = 1) for different viewing distances are compared with observed responses during translation - roll tilt motion in Figure 6D. Notice that in the model the net drive to the TVOR is provided by vestibular-only cell VO_T. To provide insight as to how otolith and canal signals combine in the model, the contributions of each sensor to the response of cell VO_T are shown in Figure 6E, F. For each of the four motion stimuli used in the current study, the otolith input to cell VO_T (Fig. 6E) simply represents a scaled estimate of the net IA acceleration stimulus, IÄ. The semicircular canal contribution (Fig. 6F) appears as an integrated head velocity signal proportional to roll head position, H_roll. The combination of these signals results in a net response on cell VO_T (Fig. 6G) that in all cases reflects the translational component of the acceleration along the IA axis. It is this signal that provides the drive to the TVOR. In particular, notice that for all stimulus combinations that include a translational component (i.e., translation only, translation + roll tilt, translation - roll tilt) the responses of cell VO_T are similar (Fig. 6G, solid, dash-dot, and dotted traces are superimposed) and are nearly identical to the otolith sensory stimulus elicited during a pure head translation (Fig. 6E, compare with solid curve). In contrast, during simulated roll tilt motion, the canal and otolith contributions cancel one another out, ensuring that cell VO_T does not respond (Fig. 6G, dashed trace), so that a TVOR is not elicited. A key prediction of the model is, therefore, that there should exist populations of vestibular-only neurons that selectively encode for the translational component of linear acceleration. Indeed, such neurons have recently been described in the vestibular nuclei (Angelaki et al., 2003).

We have postulated here that NI₁ could represent the dynamic network known as the velocity storage integrator, traditionally used to explain the observed low-frequency improvement in RVOR behavior when the axis of rotation is aligned with gravity (Raphan et al., 1977, 1979). The fact that the model can account for this effect on horizontal eye movements during upright yaw rotations is shown in Fig. 7. The model predicts improved low-frequency gain and phase (Fig. 7A, solid lines) and a lengthening of the RVOR decay time constant during constant velocity rotation (Fig. 7B, solid lines) when a small horizontal canal signal (weight p_vsh) is conveyed via NI₁ and the TVOR pathways to the eye (i.e., when d = 1). When the contribution of this signal is eliminated (d = 0), the low-frequency RVOR reflects the dynamic characteristics of the canals (Fig. 7A, B, dashed lines).

Figure 7.

Predictions of the model in Figure 6A during upright yaw rotation. A, Predicted gain (Ė_hor/Ḣ_yaw) and phase of the horizontal RVOR plotted as a function of frequency. B, Simulated responses to constant velocity rotation. Without the contribution of the output from NI₁ (i.e., if d = 0), the dynamics of the RVOR at low frequencies reflect those of semicircular canal afferents (A, B, dashed lines). When the pathway via NI₁ is intact (i.e., when d = 1; A, B, solid lines), an extended low-frequency RVOR bandwidth is predicted (A) as illustrated in a lengthened decay of simulated per- and post-rotatory responses to constant velocity rotation (B) (Raphan et al., 1977, 1979). Dotted lines in B illustrate the head velocity input to the model, Ḣ_yaw.

Discussion

Natural roll movements of the head from upright activate both semicircular canal and otolith afferents (Fernández and Goldberg, 1976a; Angelaki and Dickman, 2000). Ocular torsion (an RVOR) is required to compensate for the dynamic head rotation. However, if all high-frequency otolith stimuli were interpreted as translations (Paige and Tomko, 1991a; Telford et al., 1997), then head roll at such frequencies would also generate large horizontal eye movements (a TVOR), particularly during near target viewing. As clearly demonstrated here, this is not the case. Although a small horizontal eye velocity was present during roll tilt only motion, it was temporally related to the rotational (angular) velocity, rather than the translational stimulus. How then are otolith signals that are appropriately routed to generate the TVOR during pure head translations eliminated from driving this reflex during roll head movements? Although this problem is fundamental for gaze stabilization, a quantitative solution that is physiologically plausible (i.e., not based simply on abstract nonlinear vector algebra) has so far been missing.

Here, novel stimulus combinations have been used to address this question directly by quantitatively investigating, for the first time, the temporal properties of extra-otolith signals necessary to generate compensatory responses during motions that include both rotations and translations. Experimental evidence has been presented that integrated angular velocity signals from the semicircular canals combine centrally with otolith information to elicit functionally appropriate VORs. Such integrated canal signals, necessary to eliminate the otolith drive to horizontal eye movements during head reorientations relative to gravity, are salient but typically hidden during pure head rotation. Yet, they become unmasked and appear as a canal-driven TVOR during combined translation and rotation in the absence of an IA otolith stimulus. This canal-driven response to translation exhibits the dynamic properties and scaling with viewing distance required to provide a fully functional complement to the otolith-driven TVOR.

These experimental results have been complemented with the development of a simple model that exploits central processing known to exist in the VORs, to delineate a potential neural pathway for the canal-driven component of the TVOR. The model of Figure 6A, although restricted to horizontal eye movements for simplicity, can be simulated to predict the basic characteristics of our experimental results, including the generation of a viewing distance-dependent TVOR in the absence of a net lateral acceleration acting on the otoliths. This was achieved through the incorporation of a neural filter, which we postulate could be the so-called velocity storage integrator (Raphan et al., 1977, 1979). In addition to explaining the experimental data, this proposal has important consequences for the long-debatable and controversial functional role of this integrative network.

A novel function for the velocity storage integrator?

Early attempts to understand the functional significance of the velocity storage integrator focused on its role in providing an improved internal estimate of head velocity at very low frequencies (i.e., <0.03 Hz), resulting in a low-frequency RVOR that is better than would be predicted based on the dynamic properties of the semicircular canals (Raphan et al., 1977, 1979; Robinson, 1977). Subsequent investigations of velocity storage in three dimensions revealed intriguing gravity-dependent properties that suggested that the network is used to compute an estimate of inertial head velocity (i.e., absolute head velocity in space) (Angelaki and Hess, 1994, 1995). However, a functional oculomotor purpose for the network has remained unclear, because observed properties were associated with RVOR performance below 0.05 Hz (Angelaki et al., 1995), a frequency range that has little relevance for natural head movements.

Here, we propose a novel role for the velocity storage integrator in generating functional oculomotor responses that centers on the extra-otolith processing necessary to discriminate dynamic gravitational versus inertial linear accelerations. We suggest that the real functional purpose of the velocity storage network is not to provide low-frequency estimates of head velocity. Rather, the goal of this network is to perform a temporal integration of canal-borne angular velocity signals at mid-high frequencies such that it is the integrative properties of the network itself that generate a dynamic estimate of head position relative to gravity. As shown here (Fig. 7), the observed lengthening of the RVOR time constant (i.e., the traditional effect known as “velocity storage”) simply becomes a consequence of the coupling of semicircular canal signals to eye movement pathways, via an integrative network that exists for a different and functionally very important purpose.

Other low-frequency observations typically associated with velocity storage in the RVOR, such as the head-tilt-induced shortening of the VOR time constant (Raphan et al., 1981; Merfeld et al., 1993; Angelaki and Hess, 1994) and reorientation of the three-dimensional eye velocity vector along the direction of gravity (Harris, 1987; Raphan et al., 1992; Merfeld et al., 1993; Angelaki and Hess, 1994) may also merely arise as a consequence of combining otolith and integrated canal signals in three dimensions. Specifically, the extent to which canal and otolith signals must combine to elicit appropriate compensatory responses depends critically on head orientation. For example, in the supine position (i.e., nose-up orientation), head roll elicits no dynamic activation of the otoliths. Instead, it is during yaw rotation in the supine position that the otoliths are dynamically stimulated along the IA head axis. The simple model presented here would clearly function inappropriately for different head orientations unless parametric weights in the model (e.g., p_vsh, p_vsv, and d) scale as a function of head orientation (Green et al., 2002). Generally, the implication is that the semicircular canal signals that must be integrated to combine with an IA otolith signal should be spatially referenced. Previous experimental observations that the velocity storage network apparently computes low-frequency estimates of head velocity in spatial as opposed to head-fixed coordinates (Merfeld et al., 1993; Angelaki and Hess, 1994; Angelaki et al., 1995), thus, lend support to our hypothesis. Here, however, we suggest that the real functional purpose of the network is to integrate spatially referenced semicircular canal signals to ensure an appropriate TVOR at mid-high frequencies during combined translational and tilt movements.

Although the present study does not illustrate these three-dimensional aspects of the proposed hypothesis explicitly, preliminary modeling results show that the observation of velocity storage itself (i.e., lengthening of the RVOR time constant; Fig. 7) as well as the deterioration in this effect with changes in head orientation relative to gravity are predicted consequences of the proposed role of this integrator in mid-high frequency canal/otolith functional convergence (Green et al., 2002). If true, the proposed hypothesis not only provides for the first time a realistic rationale for the usefulness of the velocity storage integrator in oculomotor function, but also further attests to the rich and computationally intriguing central processing of vestibular signals.