Vibrissa Resonance as a Transduction Mechanism for Tactile Encoding

Abstract

We present evidence that resonance properties of rat vibrissae differentially amplify high-frequency and complex tactile signals. Consistent with a model of vibrissa mechanics, optical measurements of vibrissae revealed that their first mechanical resonance frequencies systematically varied from low (60-100 Hz) in longer, posterior vibrissae to high (∼750 Hz) in shorter, anterior vibrissae. Resonance amplification of tactile input was observed in vivo and ex vivo, and in a variety of boundary conditions that are likely to occur during perception, including stimulation of the vibrissa with moving complex natural stimuli such as sandpaper. Vibrissae were underdamped, allowing for sharp tuning to resonance frequencies. Vibrissa resonance constitutes a potentially useful mechanism for perception of high-frequency and complex tactile signals. Amplification of small amplitude signals by resonance could facilitate detection of stimuli that would otherwise fail to drive neural activity. The systematic map of frequency sensitivity across the face could facilitate texture discrimination through somatotopic encoding of frequency content. These findings suggest strong parallels between vibrissa tactile processing and auditory encoding, in which the cochlea also uses resonance to amplify low-amplitude signals and to generate a spatial map of frequency sensitivity.

Introduction

Rats can use their posterior vibrissae (whiskers) as high-acuity sensors for detection and discrimination (Guic-Robles et al., 1989; Carvell and Simons, 1990, 1995). In a forced-choice task, blindfold rats, using a single vibrissa, can select between smooth and fine grooved surfaces (depth, 30 μm; interval, 90 μm) (Carvell and Simons, 1990). Rats are also capable of differentiating surfaces milled with 1.00 or 1.06 mm groove width in a rough-rough discrimination task (Carvell and Simons, 1990). These spatial frequencies should correspond to temporal frequencies of ∼205 and ∼220 Hz at the vibrissa contact point, assuming known whisking velocities (Carvell and Simons, 1990, 1995). The capacity of the rat to make these high-acuity distinctions suggests that the vibrissa-barrel system is optimized for the transformation of high-frequency information.

In many sensory systems, mechanical properties of peripheral sensors play an essential role in filtering information. Mechanical resonance, the propensity of a structure to demonstrate greater amplitude of vibration when stimulated at a specific frequency, is one key property used. Resonance is used in biological (e.g., the inner ear) and human-made (e.g., functional magnetic resonance imaging) sensing systems to enhance both detection and discrimination of signals. In detection, the tendency of a structure to vibrate at a larger amplitude when stimulated at a specific frequency facilitates the probability that the structure will be detected by a nervous system or sensing device. In discrimination, the variation in the specificity of resonance tuning of the sensors allows a sensing system to distinguish between the different frequencies that characterize distinct objects. In complex stimulus processing, a gradient in resonance tuning properties over an array of receptors enables the system to prepare the information for parallel processing, decomposing the signal into an ensemble of components at different frequencies. The cochlea is the primary example of a biological sensing system that employs the principle of resonance in these three contexts (Kiang et al., 1965; Merzenich and Brugge, 1973; Geisler, 1998).

Here, we show that vibrisse resonance amplifies and bandpass filters tactile stimuli. In agreement with a biomechanical model of the vibrissa, optical recording of vibrissae revealed that they resonate across a range of biologically relevant stimulus conditions and demonstrate strong frequency tuning, and that resonance frequencies correlate with vibrissa length. As such, the anterior-posterior gradient of increasing vibrisse length on the rat face provides a systematic map of frequency sensitivity. These observations suggest that vibrissa resonance is optimally positioned to increase the range of detection and the specificity of discrimination, and may provide the ability to represent complex stimuli through a compact, somatotopically distributed code. The relevance of these biomechanical observations is highlighted by ongoing studies in our laboratory showing that vibrissa resonance is translated into neural activity (Andermann et al., 2002). Furthermore, Hartmann et al. (2003) have recently observed vibrissa resonance in the behaving animal. The findings reported here have been presented in preliminary form previously (Neimark, 2001; Neimark et al., 2001; Andermann et al., 2002; Neimark et al., 2002).

Materials and Methods

All of the experiments were performed in compliance with research protocol guidelines approved by the Massachusetts General Hospital. Rats (n = 11) were anesthetized with urethane (1.4 gm/kg, i.p.) and placed in a stereotaxic frame (Kopf Instruments, Tujunga, CA) on a floating table (TMC) to minimize external vibrations and ensure maximal stability. All of the ex vivo vibrissa experiments were conducted on vibrissae carefully removed from the rat face after termination of the experiment.

Vibrissa stimulation in PZ mode. Vibrissa measurements were performed under two conditions: (1) in vivo: vibrissa motion was measured while vibrissae were left intact on the face of a head-fixed, anesthetized rat, and (2) ex vivo: vibrissae were clamped to a stiff metal beam at 2 mm from their base. We used high-performance piezoelectric (PZ) bimorphs (Q234-H4CL-303X; Piezo Systems) that were customized to have a high fundamental resonance (≥850 Hz; achieved by reducing piezoelectric length), calibrated with optoelectronics and compensating output voltage adjustment to <3% amplitude deviation from 5 to 600 Hz (Andermann et al., 2002). The frequency tuning curve was obtained by presentation of a continuous chirp stimulus or by presentation of 500 msec sinusoidal bursts every second (5 Hz intervals from 5 to 600 Hz or from 5 to 750 Hz, randomized, resulting in ∼80 μm deflections of the PZ tip). Voltage commands were generated in Matlab, sent through an input-output (I-O) board (National Instruments, Austin, TX), amplified (MDT-693; Thorlabs) and sent to the piezoelectric. The vibrissa was attached at 1-2 mm from its tip to a light, wooden 2 cm bimorph extension with bone wax, and deflections were typically made along the rostral-caudal axis. In fixed-fixed experiments, the relative tension on the vibrissa was adjusted as needed to optimize imaging of resonance peaks. To measure vibrissa motion, an infrared (IR) slotted optical switch (QVA series; Fairchild Semiconductor) with nearly linear responses to small (<3 mm) static changes in position (<10 μm resolution) was positioned at 50% of the vibrissa length. The motion signals were high-pass filtered above 10 Hz and amplified (100×) with a differential amplifier (Warner Instruments, Hamden, CT), and then command and motion signals were digitized at 20 kHz using the I-O board. Relative response amplitude to stimulation at each frequency in PZ mode was calculated from 250 to 500 msec poststimulus onset (spanning ∼25-300 cycles at frequencies from 100 to 600 Hz). Measurements were made using the total root-mean-square (rms) power, a robust measurement that is linearly proportional to sinusoidal amplitude: calculations of oscillation amplitude using peak-to-trough estimates averaged over each cycle provided nearly identical results. The fundamental resonance frequency (FRF) of the vibrissa in PZ mode was defined as the lowest frequency peak in resonance amplification that exceeded six SDs above the mean amplitude, compared with the 50 Hz region of the spectrum that showed the lowest deviation in values (see Fig. 2). The amplitude of vibrissa motion was reported as relative motion, because absolute motion amplitude was difficult to calculate for shorter vibrissae, typically from arc 4, where the precise sensor position along the vibrissae was difficult to determine. At a position of 50% of the vibrissa length, 80 μm deflections at the vibrissa tip should drive 40 μm amplitude nonresonant motion (independent of the length of the vibrissa). In Figure 2, the 10-fold resonance amplification in the 37 mm long C2 vibrissa measured at 50% of vibrissa length should result in a ∼400 μm motion at the vibrissa midpoint at peak resonance amplitude, generating a 1.23° deflection and a maximal angular velocity of 495°/sec. The coefficient of correlation between in vivo and ex vivo data sets was determined using Matlab.

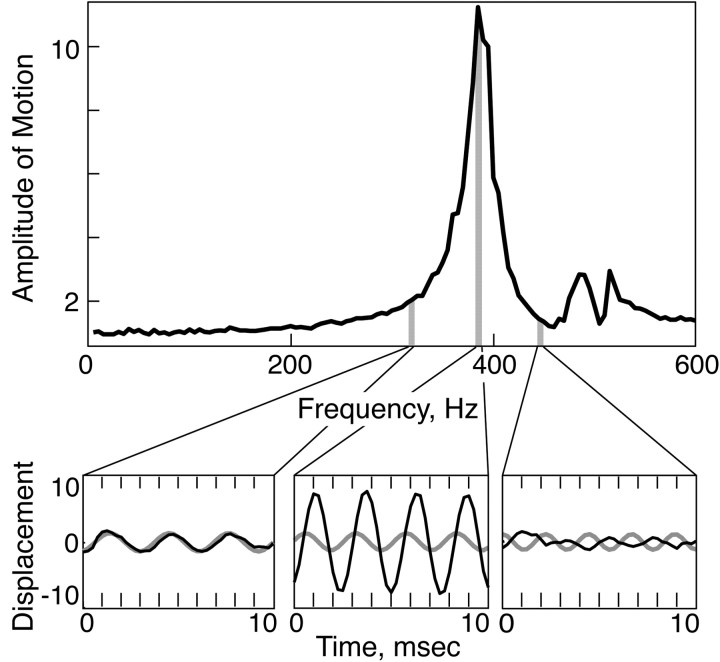
Figure 2.

Vibrissae resonate. The average amplitude of vibrissa motion in response to a periodic ex vivo PZ stimulation of a C3 vibrissa from the left side of the rat face at 5 Hz intervals, 5-600 Hz. C3 displays an 11-fold amplification when driven at its FRF of 385 Hz (gray bar). The vibrissa motion and the PZ motion, when driven by a periodic input at 320, 385, and 450 Hz, are shown in the insets. Note the increase in the amplitude and the 90° phase shift at the FRF. A similar phase shift (≥25°) was observed within 10 Hz of the FRF in the majority of cases (n = 17 of 20 measurements of 10 vibrissae, in vivo and ex vivo). Gray, Stimulus wave form. Black, Vibrissa motion.

Vibrissa stimulation in pulse mode. In in vivo and ex vivo conditions, the vibrissa was deflected manually with a solid rod and allowed to relax freely to rest. The vibrissa motion signal from the IR switch was acquired as described above, and local maxima and minima were located. Midpoints between these extrema were least-squares fit to the two-parameter function Be^-t/τ2, which was then subtracted from the data. The absolute values of the adjusted extrema were then fit to the two-parameter function Ae^-t/τ1. The FRF was determined as the inverse of the average time interval between extrema.

Measurement of vibrissa sweep past a complex texture. Periodic grating (50 pin cable; spatial frequency, 0.78/mm) or sandpaper (40 or 80 grit; Norton, Akron, OH; rms amplitudes of ∼30 and 60 μm, respectively) textures were mounted on a 32 mm diameter wheel whose rotation speed was controlled via a direct-current motor (RadioShack) driven at various speeds by the computer-controlled voltage output (National Instruments; Matlab). The rough texture covered one-half of the outer circumference of the wheel. The other one-half was left smooth to monitor the response to the smooth stimulus and to the onset of the response to the rough texture (see Fig. 7D). The in vivo vibrissa was positioned such that it rested against the rotating wheel at ∼5 mm from its tip, along the plane of the texture, with vibrissa tip pointing in the direction of surface motion (see Fig. 7A). Vibrissa motion was monitored as described above. The average temporal rms frequency spectrum of the vibrissa motion was calculated for each velocity in Matlab.

Figure 7.

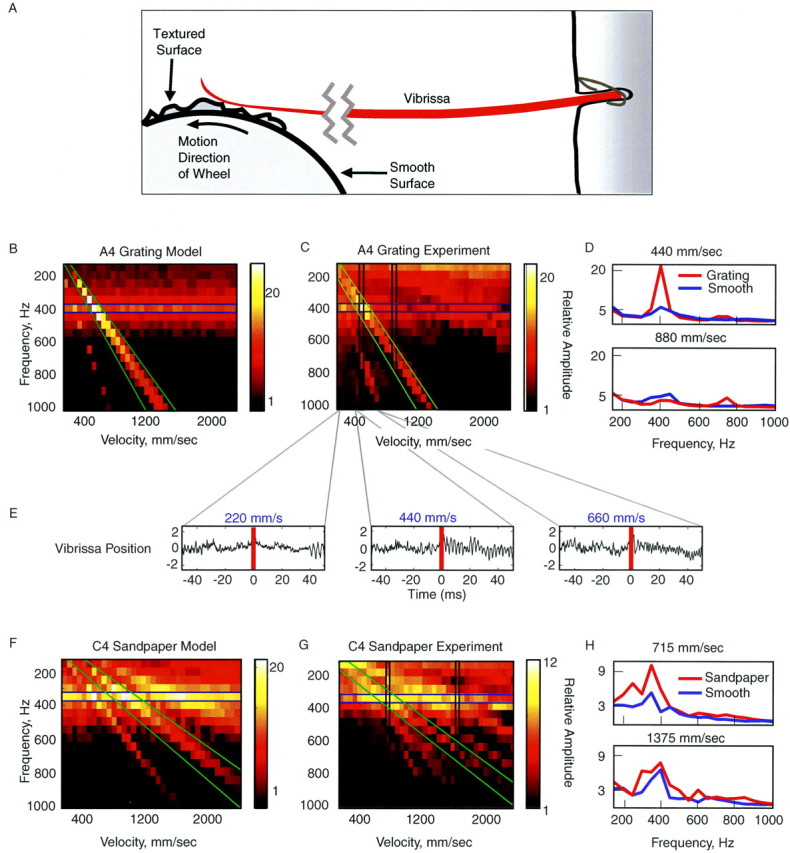
Complex textures evoke resonance in vibrissae. A, Experimental setup of the texture wheel driving vibrissa motion. Under natural conditions, rats may contact the stimulus at the tip, in the middle, or close to the base of the vibrissa (Brecht et al., 1997; Hartmann, 2001) and frequently sample textures with the vibrissae pressed against the sensory surface (one study observed typical contact points at ∼15 mm from the face) (Carvell and Simons, 1990, 1995). This stimulation emulates features of this configuration, because the vibrissae were pinned against the complex surface with a contact point on the wheel at ∼15 mm from face. B, C, The model (B) and experimental (C) measurements of the rms temporal spectra of the motion of an A4 vibrissa driven by a periodic grating at different velocities. The texture was presented at velocities from 155 to 2200 mm/sec. The brightness of the color scale represents the predicted amplitude of the motion of the vibrissa, given the texture presented at a specific velocity. C, Corresponding measurements were made with a grating mounted on a wheel and spun past an in vivo A4 vibrissa. The velocities ranged from 200 to 2000 mm/sec. Note the presence of a horizontal band (resonant motion) and diagonal bands (prominent driving frequencies of sandpaper texture) (see Materials and Methods for details). D, Amplitude temporal spectrum of the A4 vibrissa in response to the periodic grating (same as in C) and in response to a smooth texture presented by the wheel at 440 and 880 mm/sec (the measured regions are marked with vertical bands in C). E, Trace of vibrissa motion when presented with the periodic grating at 220, 440, and 660 mm/msec. Note the prominent increase in vibrissa motion at the FRF during contact with the textured stimulus (red line marks texture onset) at 440 mm/msec, at which the velocity of the grating applied the FRF to the vibrissa. F, G, The model and experimental measurements of the temporal spectra of the motion of the C4 vibrissa when presented with sandpaper (40 grit) at different velocities. Same axes as in B and C. H, Power spectra of the C4 vibrissa in response to the sandpaper and in response to a smooth texture presented (similar to D) at 715 and 1375 mm/sec (vertical bands in G).

Model of the vibrissa as a thin elastic beam. To establish specific predictions regarding vibrissa behavior, the following biomechanical model was developed. The thin elastic beam (TEB) was described with a single partial differential equation, by equating the shear and the bending moments (Den Hartog, 1952). In the presence of linear damping, the motion of the beam was described as follows:

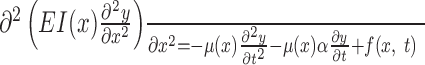1

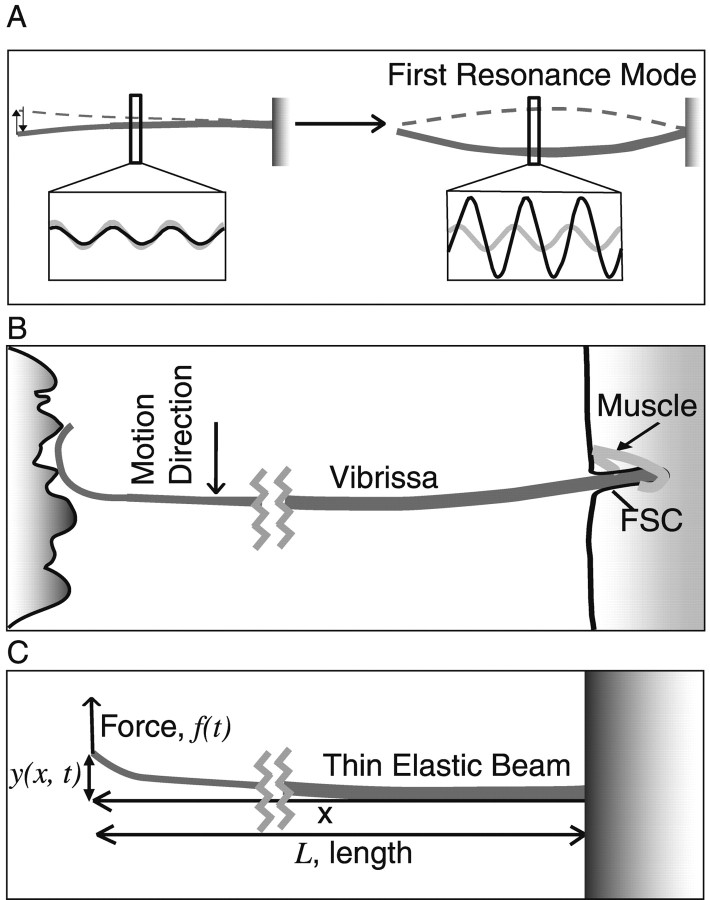
where y(x) is the displacement of the vibrissa from its principal axis caused by bending, E is the bending modulus, I(x) is the moment of inertia, μ(x) is the linear density, α is the damping coefficient, and f(x,t) is an external force applied to the tip of the vibrissa (f = 0 away from x = L) (see Fig. 1C) (Den Hartog, 1952; Landau and Lifshitz, 1970).

Figure 1.

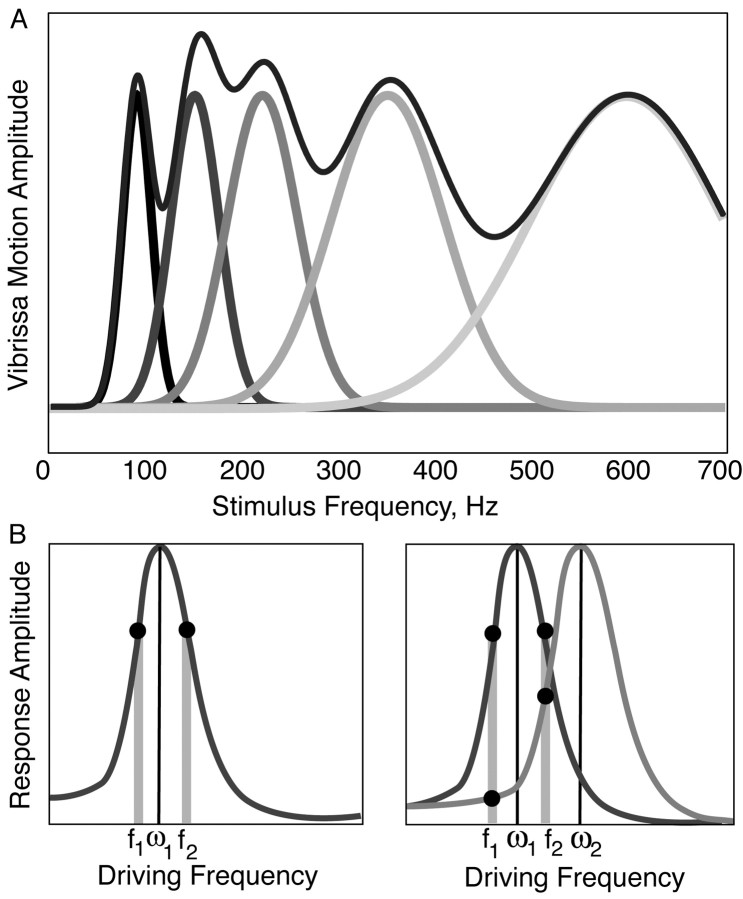
A diagram of a TEB expressing resonance and the vibrissa sweeping past a surface. A, Left, When stimulated at frequencies lower than the FRF, TEB motion reflects the amplitude of displacement. Right, When driven at its FRF, a TEB demonstrates a significantly larger amplitude motion at its resonance mode. The increase in motion amplitude at this mode is accompanied by a 90° phase shift. Insets: gray, stimulus wave form; black, TEB motion. B, As the vibrissa sweeps past a surface, spatial frequency components in the surface exert a time-varying force on the vibrissa, causing it to deflect at specific temporal frequencies. As with the TEB motion in A, this action should induce resonance in the vibrissa. The vibrissa base is secured in the FSC. C, A diagram of the axes and directions of motion used in the model.

By the method of separation of variables (Weaver et al., 1990), solutions to Equation 1, in the absence of forcing (f = 0 for all x, t), can be decomposed into a sum of spatial modes, χ_n(x), which oscillate with corresponding characteristic frequencies, ω_n. The characteristic frequencies for a conical beam (the model that best approximates the shape and resonance behavior of vibrissae) (see Table 2) are given by:

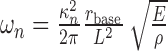2

where r_base is the radius at the base, L is the length, ρ is the density of the vibrissae, and κ_n are constants encapsulating boundary conditions (see below) and the geometry of the vibrissa (Weaver et al., 1990).

Table 2.

Vibrissa measurements

Whisker	L (mm)	Diameter base (mm)	Diameter tip (mm)	Volume (mm3)	Mass (mg)	Density (mg/mm3)	Slope of radius
α	39	0.12	0.015	0.168	0.166	0.99	0.0013
β	29	0.09	0.001	0.062	0.102	1.64	0.0015
δ	58	0.17	0.005	0.452	0.623	1.38	0.0014
γ	42	0.15	0.03	0.31	0.166	0.54	0.0014
A1	47	0.12	0.012	0.20	0.29	1.48	0.0011
B1	34	0.145	0.03	0.23	0.292	1.25	0.0017
C1	26	0.09	0.025	0.075	0.118	1.58	0.0013
D1	35	0.145	0.035	0.25	0.356	1.42	0.0015
E1	36	0.155	0.025	0.27	0.358	1.33	0.0018
A2	34	0.13	0.006	0.16	0.197	1.25	0.0018
B2	24	0.085	0.035	0.071	0.118	1.64	0.0010
C2	37	0.14	0.001	0.19	0.291	1.52	0.0019
E2	38	0.18	0.005	0.33	0.411	1.24	0.0023
A3	24	0.098	0.002	0.062	0.0875	1.42	0.0020
B3	26	0.115	0.005	0.094	0.135	1.44	0.0021
C3	28	0.125	0.005	0.12	0.201	1.69	0.0021
D3	28	0.14	0.005	0.15	0.26	1.75	0.0024
E3	28	0.155	0.005	0.18	0.241	1.33	0.0027
Mean						1.4	0.0017
SD						0.6	.0004

L, Length.

We considered the effect on the system when forcing was temporally periodic with frequency σ. Decomposing over the spatial modes, the steady-state solution to the forced equation can be represented as follows:

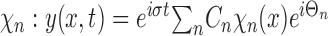3

The amplitude (C_n) of the oscillation of spatial mode (χ_n) and the phase (Θ_n) of the oscillation with respect to the driving force are given by the following (Weaver et al., 1990):

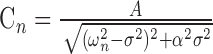4

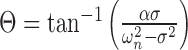5

where A is the forcing amplitude. From Equation 4, the oscillation amplitude of a particular mode is greatest when the driving frequency is near the characteristic frequency (ω_n) and in general, the modes corresponding to the smallest ω_n have the largest response. For this reason (see also Discussion), we focused on the fundamental mode corresponding to the FRF ω₁. The sharpness of the tuning increases as the absolute value of the damping coefficient α decreases. From Equation 5, when the driving frequency is equal to the FRF, the predicted phase angle between the stimulus and the response is 90°.

Boundary conditions describe the configuration in which external forces drive vibrissa motion and are critical to defining resonance behavior. We assumed for the purpose of this initial description that the vibrissa was clamped rigidly in the follicle at the base [y(0) = y′(0) = 0]. Vibrissa motion typically occurs in one of three boundary conditions. In a fixed-free boundary condition, the vibrissa is not in contact at the tip, as in whisking in air [y″(L) = y‴(L) = 0]. In a fixed-pinned boundary condition, the vibrissa tip is pushed against an object but not held rigidly, similar to the scanning behavior during texture perception [y(L) = y″(L) = 0]. In a fixed-fixed boundary condition, the vibrissa is rigidly attached at the tip [y(L) = y′(L) = 0] (Weaver et al., 1990). For a conical beam, under the three different boundary conditions, κ₁ is as follows: κ₁ (fixed-free) = 2.1, κ₁ (fixed-pinned) = 4.4, κ₁ (fixed-fixed) = 5.3 (Thomson, 1972; Weaver et al., 1990). Therefore, the model FRFs scale as r_base/L² and are greatest for the fixed-fixed condition and smallest for the fixed-free condition.

Fitting of the bending modulus. From the solution to Equation 2 for the fixed-free condition, the model predicted that the coefficient for the resonance frequency was κ₁ = 2.08 (Weaver et al., 1990). We used the measurement of the FRF from the in vivo pulse measurements in the 10 vibrissae from the C row on each side of the rat face (Table 1) and our measurements of the density (Table 2) to fit by a least-squares method the bending modulus (E), using the relationship of Equation 2 (see Fig. 3B). We found the bending modulus to be 7.8 GPa (R² = 0.97). The parameter κ₁ for the in vivo PZ measurement was fit by least squares on the same 10 vibrissae to the relationship of Equation 2, using the fitted value of E. We found κ₁ = 2.6 for PZ measurement (R² = 0.96).

Table 1.

Vibrissa FRFs measured in four conditions from the left and right Crows

Vibrissa	Left in vivo	Left ex vivo	Right in vivo	Right ex vivo
Pulse mode, FRF in Hz
β	34	38	75	33
C1	50	55	50	43
C2	62	72	59	76
C3	140	152	128	168
C4	276	244	310	360
PZ mode, FRF in Hz (Q factor)a
β	115 (12)	105 (5.5)	120 (8)	140 (9.3)
C1	165 (11)	165 (7)	145 (9.7)	205 (11)
C2	160 (10.5)	150 (6.4)	120 (6)	350 (17.8)
C3	275 (7.9)	385 (13.3)	310 (7.8)	295 (14.7)
C4	480 (12)	565 (12.8)	585 (4.6)	510 (8.6)

Summary of the FRFs and Qvalues from in vivo and ex vivo pulse mode and PZ measurements from 10 row-Cvibrissas from the two sides of the face of the same rat. FF, Fixed-fixed.

^aValues are given for left FF in vivo, left FF ex vivo, right FF in vivo, and right FF ex vivo.

Figure 3.

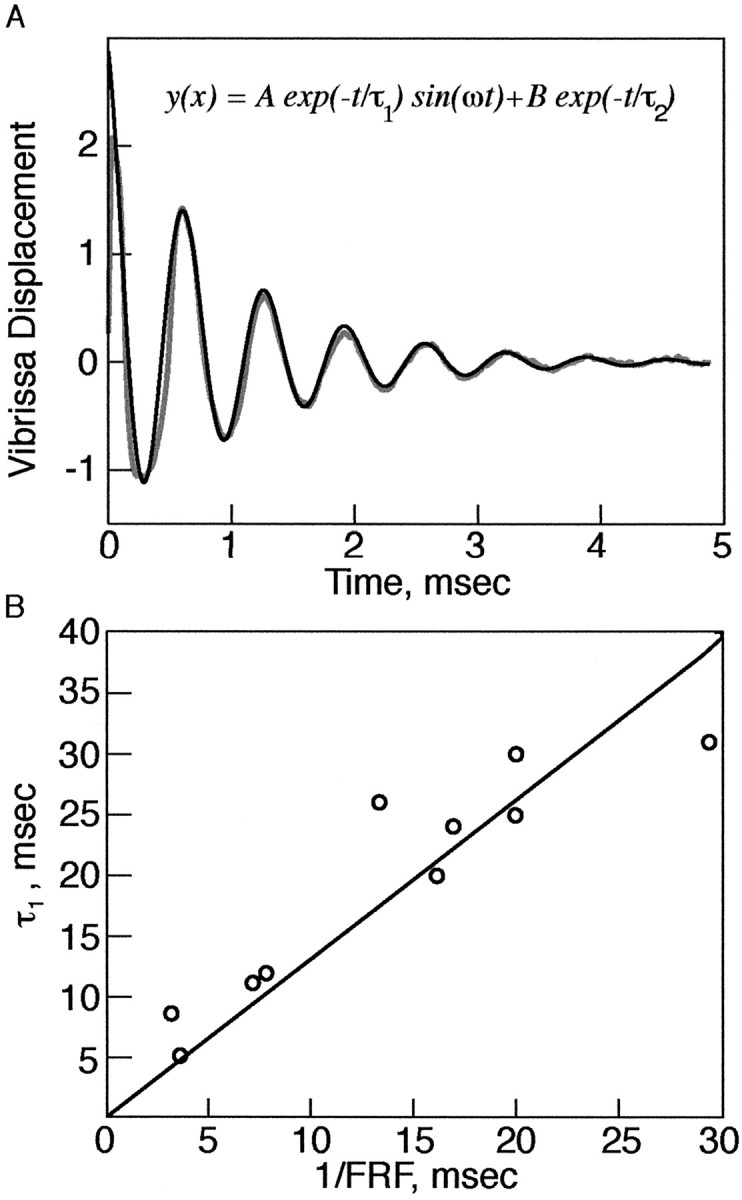
Vibrissae are underdamped. A, Motion trace of a C3 vibrissae from the right side of the face after a pulse deflection ex vivo. The vibrissa undergoes several oscillations before relaxing to the original position. Gray, Vibrissa. Black, Fit to model. Inset, Equation to fit (see Materials and Methods). B, A plot of the damping coefficients versus 1/FRF of vibrissae as measured in pulse mode, in vivo and ex vivo. Circles, Experimental results. Line, Least-squares fit. Slope of line (C) = 1.3; R² = 0.93.

Prediction of FRF by the model. The radius of the vibrissa was measured at the base, in the middle, and at the tip of the vibrissa using a stage micrometer at 40× magnification. We confirmed that the vibrissa could be described as conical in shape (Table 2), an approximation we used for the model. Equation 2 was used (see Fig. 6) to predict the resonance frequencies from geometrical measurements across all of the macrovibrissae on a second rat's face, using the E and κ₁ values for PZ mode determined by the fit described above. The average value of ρ = 1.4 mg/mm² was determined by measurements of the mass (Cahn Microbalance 2000) and the geometric parameters of the vibrissae listed in Table 2 (Neimark et al., 2002).

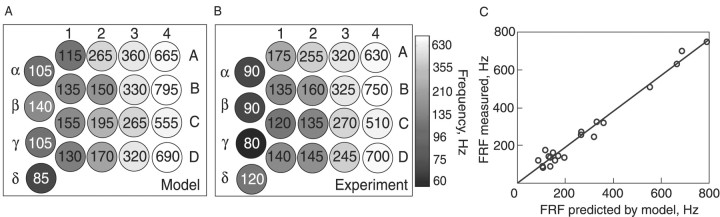
Figure 6.

The biomechanical model of the vibrissae reliably predicts their FRF across animals. A, Color map of the PZ-mode FRFs predicted by the model for vibrissae from one rat mystacial pad, using the measurements of their r_base and L. The FRFs (in Hz) are displayed in gray scale and in inset text. Each circle represents a single vibrissa. Arcs are denoted by numerals and rows by letters. Values used for κ₁ and E were extrapolated from measurements presented in Figure 5 in a different animal. B, A gray-scale map of the measured FRFs corresponding to the predictions in A (responses for in vivo PZ mode). C, Plot of the predicted versus measured FRFs from A and B (C = 0.95; R² = 0.98).

Model of vibrissa sweep past a complex texture. The effect of the complex texture on the vibrissa was modeled by defining the force exerted on the vibrissa by the texture at varying velocities. A complex texture was defined, whose spatial amplitude spectrum is represented by P(u), the amplitude coefficient at spatial frequency u. When the vibrissa sweeps past this simulated texture at constant velocity v, the temporal frequency spectrum of the force exerted on the vibrissa can be represented as follows:

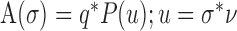6

Equation 6 allows for a one-to-one conversion between the spatial frequency spectra of textures and the temporal frequency spectrum of the force exerted on the vibrissa as a result of its motion. The force of the vibrissa can be discretized over the frequencies σ_k. The steady-state motion of the vibrissa can again be decomposed:

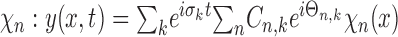7

where C_n,k and Θ_n.k are given by Equations 4 and 5 with σ_k as the driving frequency, respectively. A stationary amplitude spatial spectrum was generated for the sample textures. The grating was defined by a spatial spectrum containing a prominent peak at 0.8 mm^-1 at 15 relative amplitude units (RAU), and at 1.5 mm^-1 at 5 RAU. At all of the other spatial frequencies, the relative amplitude was randomly distributed around 0.3 RAU with an SD of 0.2 RAU. The spectrum of the sandpaper was defined by a spatial spectrum containing three peaks at 0.25, 0.42, and 0.71 mm^-1 at 2, 3, and 5 RAU, respectively. At all of the other spatial frequencies, the relative amplitude was randomly distributed around 0.5 RAU with an SD of 0.5 RAU. To model the vibrissa, the FRFs were taken to be 400 and 350 Hz, and the damping coefficients (α) were set to 70 and 50, respectively, for the A4 and B4 vibrissae. The temporal spectrum of the force was calculated by using Equation 7 for different velocities.

Results

We first describe the vibrissa model used to develop a set of quantitative predictions for vibrissa behavior and then discuss the testing of these predictions by optical monitoring of vibrissa motion.

Description of the vibrissa as a TEB

The vibrissa is a thin, long, pliable hair, attached underneath the skin in a follicle-sinus complex (FSC) (Fig. 1B). As such, a reasonable first-order approximation of the vibrissa is a thin elastic beam—an object whose length is significantly greater than its width, that is of a uniform shape (conical or cylindrical), and that has intermediate boundary conditions. Elasticity theory shows that a TEB possesses characteristic spatial modes (patterns) of motion at progressively higher temporal frequencies (Landau and Lifshitz, 1970). When a TEB is driven by a periodic force at or close to its characteristic frequency, the amplitude of the corresponding spatial mode is increased, exhibiting the phenomenon of resonance. In steady state, the first mode, driven at the fundamental resonance frequency, occurs at a point at which vibrissa motion and stimulus motion (e.g., motion of a stimulator at a vibrissa tip) move out of phase, and exhibits the largest resonant amplification of motion of all of the modes (Fig. 1A) (Weaver et al., 1990). When a vibrissa moves over a spatial texture (e.g., a grating) at a given velocity, the spatial texture should generate oscillations in the vibrissae at a temporal frequency that depends on the velocity of the sweep (Fig. 1B). Applied to the vibrissae, the properties of the TEB suggest that, when this temporal frequency matches the FRF, a significantly greater increase in the motion of the vibrissa should be observed.

Model predictions and experimental verification

As described in Materials and Methods, we developed a biomechanical model of the vibrissa as a TEB and derived specific analytical predictions about its resonance behavior under a set of different boundary conditions. To experimentally test a set of five resonance-related predictions derived from Equations 2, 4, and 5, we drove the vibrissae at the two extremes of boundary conditions they are likely to encounter while contacting an object. At one end of the continuum, emulating a fixed-free condition, we provided transient sharp deflections of the vibrissa and measured its relaxation dynamics (the pulse mode). At the other end of possible boundary conditions, we fixed the vibrissa tip to a calibrated, high-resonance frequency piezoelectric bimorph (piezoelectric FRF, >850 Hz) (see Materials and Methods) and drove it across a range of frequencies from 0 to 600 or 750 Hz (the PZ mode) at tip deflections of ∼80 μm in amplitude. To evaluate the contribution of the FSC to resonance behavior, we performed our measurements in two conditions: in vivo, on intact vibrissae on the face of a head-fixed, anesthetized rat, and ex vivo, in plucked vibrissae rigidly clamped at the base.

Prediction 1: vibrissae resonate

When stimulated at their FRFs, vibrissae should demonstrate significantly larger oscillations than at other stimulus frequencies, as in Equation 4. In PZ-driven oscillations, the amplitude of vibrissa motion often increased >10-fold as the driving frequency approached the FRF. Figure 2 depicts the relative amplitude of the frequency response of a C3 vibrissa to constant amplitude periodic PZ stimulation. The vibrissa demonstrated sharp tuning to within 20 Hz of the FRF of 375 Hz, resulting in up to an order of magnitude increase in its motion amplitude. The insets in Figure 2 display the relative amplitude of motion of the vibrissa and of the driving frequencies and the phase shift from the input oscillation at frequencies below the FRF, at the FRF, and above the FRF. Resonance amplification was observed in all of the vibrissae measured, spanning the first five arcs on the rat face (Greek arc - arc 4, n = 61 of 61 vibrissae; n = 8 rats).

To fit the parameters of the model for various boundary conditions, we measured the resonance behavior in 10 vibrissae within a row in vivo (the β and C1-C4 from both sides of the face in one rat) with PZ and pulse stimulation and then plucked the vibrissae (postmortem) and repeated these measurements ex vivo (Table 1).

Prediction 2: vibrissae are underdamped and demonstrate sharp tuning curves

For resonance amplification to occur, vibrissae must be under-damped. Furthermore, the degree of tuning of the vibrissa resonance response (the sharpness of the peak) should be dependent on the degree of damping (Gelfand, 1998). In pulse measurements, all of the vibrissae (n = 10 in vivo and 35 ex vivo) demonstrated several oscillations before relaxation to rest (i.e., all of the vibrissae were underdamped) (Fig. 3). We fit a linear damping curve to the relaxation kinetics and found that the damping time constant (τ₁) (see Materials and Methods) scaled inversely in magnitude with the FRF of the vibrissae (C = 1.3, R² = 0.93) (Fig. 3), suggesting that, independent of the FRF, vibrissae undergo a similar number of cycles before relaxation to rest upon a single deflection. To quantify the tuning expressed by the FRF peaks, we calculated the Q factor (the resonance frequency divided by the width of the curve, measured here at 1/√2, of the peak amplitude) from PZ measurement. The Q values observed (mean = 9.8; SD = 3.6) (Table 1) were comparable with similar measurements made in bandpass-tuned neurons in the auditory pathway (Geisler, 1998; Gelfand, 1998).

Prediction 3: a posterior-to-anterior gradient of frequency tuning exists across vibrissae

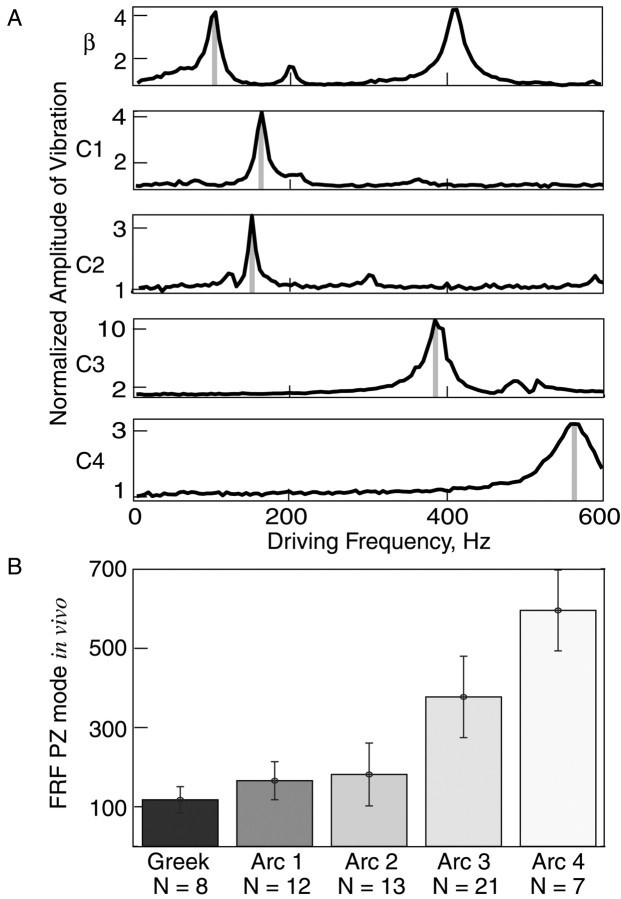
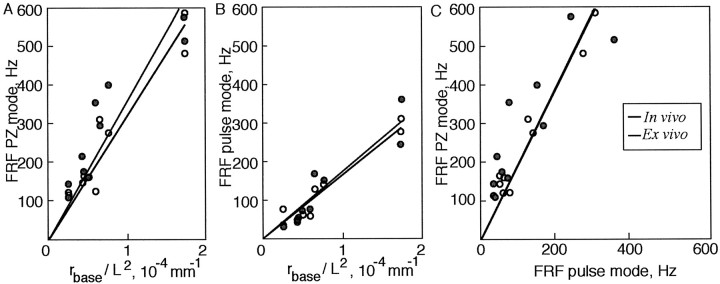
From the model, vibrissa FRFs were predicted to scale as the ratio of the radius at the base over length squared (Eq. 2). As vibrissae increase in length along the anterior-to-posterior axis, they should exhibit a systematic decrease in their FRFs along a row. For 10 C-row vibrissae measured in all four stimulation conditions (in vivo and ex vivo; PZ and pulse stimulation), this gradient in FRFs was present (Table 1). Figure 4A depicts the posterior-anterior shift in FRFs along a C row of vibrissae recorded during PZ stimulation. This systematic frequency gradient was subsequently confirmed by in vivo PZ measurements in 61 vibrissae. Within a row, FRFs increased from posterior to anterior vibrissae, whereas vibrissae within a single arc possessed similar FRFs (consistent with the similarity in vibrissa lengths within an arc) (Table 2, Fig. 4B). Figure 4 highlights a finding that was consistent across measurements—the similarity in expressed FRFs of the 1 and 2 arcs, resulting from their typically similar lengths (in Fig. 4A, the C1 and C2 vibrissa were both 41 mm long) (for sample vibrissa parameters from another animal, see also Fig. 6 and Table 2). The FRFs of the vibrissae presented in Table 1 scaled linearly with r_base/L² (R² = 0.95, 0.97) (Fig. 5A,B), allowing us to fit the values for E and κ₁ for PZ mode. To compare measured and modeled resonance frequencies across animals, these estimates were then used to predict the FRFs obtained from in vivo PZ measurements of an entire set of posterior vibrissae (Greek arc and arcs 1-4) (see Materials and Methods) from another animal. Figure 6 depicts the predicted and measured results, which match closely (C = 0.95; R² = 0.98). Similar to the gradient in FRFs in Figure 4B, a posterior-anterior increase in FRFs was again observed along each row, and the FRFs were similar within each arc. In this data set, the average coefficient of variation (CV) was smaller within an arc (CV = 0.19) than within a row (CV = 0.69).

Figure 4.

A systematic anterior-posterior gradient of FRFs on the rat face. A, The average amplitude of vibrissa motion in response to bursts of PZ stimulation of the ex vivo β and C1-C4 vibrissae from the left side of a rat face (Table 1). B, Mean vibrissa FRFs plotted as a function of arc location (sampled from n = 8 rats, n = 61 vibrissae). Number of vibrissae per arc is shown in parentheses. Gray bars in A mark the FRF of each vibrissa. Error bars indicate SD.

Figure 5.

Vibrissa FRF scales linearly as a function of its radius and length in PZ and pulse mode, in vivo and ex vivo. A, Plot of the FRFs measured in PZ mode from 10 C-row vibrissae in vivo (black circumference lines, open circles) and ex vivo (gray circumference lines, closed circles) versus the ratio of r_base/L², as measured for the same vibrissae. Circles, Experimental values. Lines, Least-square fit. In vivo, C = 3.2 × 10 ⁶ Hz · mm; R² = 0.96. Ex vivo, C = 3.5 × 10 ⁶ Hz · mm; R² = 0.93. B, Plot of the FRFs measured in pulse mode from the same 10 vibrissae versus the ratio of r_base /L². In vivo, C = 1.7 × 10 ⁶ Hz · mm; R² = 0.97. Ex vivo, C = 1.7 × 10 ⁶ Hz · mm; R² = 0.94. C, Plot of the FRFs measured in PZ mode from 10 vibrissae versus FRFs measured in pulse mode (data from parts A and B combined). In vivo, C = 1.9, R² = 0.98. Ex vivo, C = 1.9; R² = 0.87.

Prediction 4: resonance behavior is observed across varied boundary conditions

As predicted by the model, across all of the boundary conditions measured, FRFs were correlated with the length of the vibrissae (R² = 0.97 and 0.96 in vivo and R² = 0.94 and 0.93 ex vivo for pulse and PZ measurements, respectively) (Fig. 5), and the gradient of FRFs along a row was preserved for in vivo and ex vivo experimental conditions. Our various experimental configurations also confirmed the predicted importance of boundary conditions for resonance behavior. In pulse mode, the tip of the vibrissa was free, whereas the base was secured in the FSC, corresponding to the fixed-free boundary condition. In comparison, the tip of the vibrissa was more constrained in PZ mode, approximating the fixed-pinned or the fixed-fixed boundary condition. As predicted from Equation 2, the FRFs in PZ mode were higher than in pulse mode for the same vibrissae. To compare the dependence of FRF on the boundary conditions, we performed a least-square fit between the PZ- and the pulse-mode FRFs. We found that the ratio of κ₁ values (√C), which determines the dependence of the FRF on the boundary condition, was 1:1.4 for the pulse versus the PZ modes (both in vivo, R² = 0.98, and ex vivo, R² = 0.87) (Fig. 5C) (see Eq. 2). This ratio was lower than the analytically calculated ratio of 1:2.5 for the predicted values of κ₁ in the fixed-free versus fixed-fixed conditions, and of 1:2.1 for fixed-free versus fixed-pinned (Thomson, 1972). This finding suggests that, in practice, the boundary conditions for the tip of the vibrissa created by our experimental setup fell between the free and pinned predictions.

Prediction 5: vibrissa resonance is evoked by complex textures

Having studied resonance amplification under controlled conditions, we next sought to examine the contributions of resonance to vibrissa motion under more natural conditions, emulating realistic texture contact at typical whisking velocities. To develop predictions regarding the behavior of the vibrissa in this context, we modeled a vibrissa sweeping across a grating or a complex texture (e.g., sandpaper) at varying velocities (see Materials and Methods). For this simulation, the spatial frequency spectrum of the grating was chosen to have a single peak, whereas the complex texture was chosen to have three prominent peaks at three spatial frequencies and significantly smaller amplitudes at all of the other frequencies. In Figure 7, B and F, we plotted the predicted temporal frequency spectrum of vibrissa motion in response to stimulation by these textures at varying velocities. The temporal frequency of the vibrissa response is depicted on the y-axis, and the sweep velocity is depicted on the x-axis. The color code denotes the amplitude of the Fourier component of the response of the model vibrissa at a particular frequency. Three central predictions for the response of the vibrissa were generated by the model. At all of the velocities, horizontal bands of increased amplitude at the FRF of the vibrissa were apparent. This finding suggested that the vibrissa should be driven to vibrate at its FRF by any rough textured stimulus that contains some power at its FRF. The brighter diagonal bands corresponded to the effect of the spatial frequency peaks in the texture stimulus: with increased contact velocity, the same spatial frequency should drive the vibrissa at a higher temporal frequency (see Materials and Methods). The largest model vibrissa motions during stimulus contact occurred at the intersection of the horizontal and the diagonal bands. Here, the distinct spatial component was presented to the vibrissa at its FRF (v = u/w₁). The model predicted that the greatest absolute amplification of vibrissa motion driven by a complex texture occurs if the texture possesses a prominent spatial frequency component that, for a given sweep velocity, drives the vibrissa at the FRF. It is important to note that, at natural whisking speeds (∼200-2000 mm/sec) (Carvell and Simons, 1990), a subset of the vibrissa resonances from 50 to 750 Hz will be excited by any rough stimulus containing power at spatial frequencies smaller than 4 mm^-1.

To test these predictions for vibrissa responses to complex stimuli, we presented a moving textured stimulus to in vivo vibrissae by leaning them against a rotating wheel covered with a periodic grating or sandpaper, and monitoring vibrissa motion while spinning the computer-controlled wheel at different velocities (Fig. 7A). The texture covered one-half of the circumference of the smooth, plastic wheel, enabling us to measure the response of the vibrissa to rough and smooth textures. As predicted by the model (Fig. 7B,F), the frequency spectrum of vibrissa motion during texture contact demonstrated a prominent peak at the FRF, independent of the velocity of the wheel (horizontal band of signal highlighted with a blue bar in C and G). This effect was less prominent for the periodic grating, which had less frequency content outside of its dominant periodic spatial frequency (Fig. 7C,D). As expected from the model, the spectrum of the vibrissa sweep past a periodic grating displayed a single prominent diagonal band of amplification (Fig. 7C, diagonal band in green). The ratio of the temporal frequency to velocity within that band (0.8 mm^-1) corresponded to the measured spatial frequency of the grating (0.78 mm^-1). Figure 7E shows the trace of vibrissa motion past the grating, in which the amplification of the fundamental mode at the FRF of the vibrissa is apparent. This amplification was 10 times greater when the velocity of the grating motion created a temporal driving frequency that coincided with the FRF of the vibrissa.

The spectrum of motion of the vibrissa during sandpaper contact also revealed several peaks corresponding to the peaks in the spatial spectrum of the sandpaper (Fig. 7F,G, diagonal band highlighted in green). When the wheel rotated at the velocity at which the dominant spatial frequency of sandpaper is encountered at the FRF of the vibrissa, the amplitude at the resonance frequency of vibrissa motion again was increased by a factor of 3-5 (Fig. 7G,H). Figure 7, D and H, demonstrates that the vibrissae responded to the rough stimuli by increasing their amplitude of motion in response to the spatial components in the texture, compared with the response to a smooth stimulus. The amplification of vibrissa motion at the FRF (at frequencies between ∼50 and 400 Hz) was observed in all of the vibrissae (n = 11 of 11) during experiments using sandpaper (n = 7) or grating (n = 4) stimuli. The vibrissae as an ensemble should thus be able to differentially filter the complex signal into separate channels at their resonance frequencies. These findings, together with the results of Hartmann et al. (2003) showing that oscillation at the base of the vibrissa demonstrates similar properties, suggest that across the range of possible boundary conditions, vibrissa resonance is a consistent and important feature of signal transduction.

Utility of resonance for detection and discrimination

Resonance behavior allows for up to an order of magnitude amplification of motion in the vibrissa with respect to the amplitude of the driving oscillations. Because vibrissae, as an ensemble, span a large range of frequencies, resonance endows the vibrissa system with an ability to amplify a wide range of textures, thus increasing the detection capabilities of the system (Fig. 8A). Rats are known to vary their whisk velocity during texture-grating exploration (Carvell and Simons, 1990, 1995; Berg and Kleinfeld, 2003). One explanation of this behavior is that the animal may be searching out speeds that optimize resonance of different vibrissae during surface contact. Although we measured vibrissa amplification as a function of increased amplitude of motion, many neural elements in the vibrissa-to-barrel pathway are more sensitive to increased velocity or, potentially, acceleration (Pinto et al., 2000; Shoykhet et al., 2000; Minnery and Simons, 2003). These aspects of vibrissa motion are also increased during resonance amplification, and robust amplification of neural activity is observed in the periphery and cortex, correlated with resonance amplification of vibrissa motion (Andermann et al., 2002; M. L. Andermann, M. A. Neimark, and C. I. Moore, unpublished observations).

Figure 8.

Models of vibrissae resonance in detection and discrimination. A, An idealized diagram of the spectra of vibrissae within a single row. As an ensemble, vibrissae should amplify all of the high-frequency stimuli from 50 to 700 Hz. As such, they may improve the detection of small-amplitude, high-frequency stimuli that otherwise would not drive sufficient vibrissa motion to recruit significant changes in neural activity. B, A diagram of the response of a single versus a pair of vibrissae with overlapping frequency spectra to two sinusoidal stimuli. The two stimuli are presented at frequencies f₁ and f₂, which are equidistant from the FRF (ω₁) of vibrissa 1. The two stimuli will evoke similar responses in vibrissa 1. However, when compared across two vibrissae, the two stimuli will evoke different responses. Relatively greater neural activity should be evoked in the neural representation of both vibrissae when presented with the higher frequency (f₂), whereas relatively greater neural activity should be evoked in the neural representation of vibrissae 1 in response to the lower frequency input (f₁). The prediction from this schema that multiple vibrissae within the same row are required for high-frequency discrimination is well met in the psychophysical literature (Carvell and Simons, 1990) and supported by neural recordings in the periphery and barrel cortex of the vibrissae-to-barrel pathways (Andermann et al., 2002; Andermann, Neimark, and Moore, et al., unpublished observations). Gray bars mark the input frequencies f₁ and f₂, and filled circles indicate the evoked response amplitude for each vibrissa at these frequencies. Thin black vertical lines indicate the FRF.

Vibrissa resonance may also facilitate discrimination of different spatial textures. The neural code for discrimination of the spatial frequency of a given surface could consist of a relative comparison of the mean firing rates between arcs of vibrissae, where the more posterior arc vibrissae will amplify signals with lower spatial frequency components (Fig. 8). In our experiments, a significant peak was detected in the power spectrum of a vibrissa at its FRF when it was driven by sandpaper presented at differing velocities. This result demonstrated that even complex, natural stimuli excite the fundamental resonance mode of a vibrissa, and thus texture identification could be facilitated by the vibrissae resonance properties. Figure 8B shows a diagram of the proposed discrimination mechanism. A single vibrissa tuned to the frequency w₁ can experience similar resonance amplification when driven at two different frequencies, f₁ and f₂ (f₁ < w₁ < f₂). However, the addition of another vibrissa with an elevated resonance frequency w₂ will result in a differential response motion in the two vibrissae. Subsequently, the relative neural response in a given somatotopic vibrissa location can be assayed, and the two surfaces can be discriminated from each other (Fig. 8B).

Discussion

In this study, we provide evidence for a novel mechanism of tactile sensory encoding, in which vibrissa resonance properties selectively amplify high-frequency signals. We found that vibrissae exhibit resonance amplification under conditions that span those generated during surface exploration. Such natural stimuli include free vibrissa oscillations after punctate contact and vibrissa resonance during continuous high-frequency interactions with complex surfaces. The range of FRFs spanned 50-750 Hz for the macrovibrissae, and was organized in a systematic posterior-anterior gradient along vibrissa rows. Within vibrissa arcs, FRFs were similar because of the consistency in their geometry. These findings suggest that, as the name “vibrissa” implies, mechanical resonance driven by vibration is important to the neural representation of surface textures in the vibrissa-to-barrel pathway. This suggestion is supported by trigeminal and cortical recordings using identical stimuli in our laboratory (Andermann et al., 2002; Andermann, Neimark, and Moore, unpublished observations). Specifically, resonance amplification of signals by the vibrissae may facilitate detection, and the bandpass filter properties may enhance texture discrimination. Furthermore, the fine-tuning of each vibrissa and the wide range of FRFs spanned by the vibrissae may allow for a decomposition of the signal into periodic components, encoded in a set of parallel somatotopic channels.

Vibrissa resonance and psychophysical capabilities of rats

The proposed roles of vibrissa resonance in detection and discrimination (Fig. 8) are consistent with the known psychophysical capabilities in rats. Detecting differences between smooth and rough surfaces is possible with a single vibrissa (Carvell and Simons, 1990), where comparisons between the specific components of high-frequency inputs are not paramount, but where the detection of a surface amplitude difference is essential. By varying vibrissa sweep velocity, a rat could use a single vibrissa to determine, over a range of spatial frequencies, whether a surface contains significantly greater power at spatial frequencies greater than ∼50 Hz (is rougher) (Fig. 8A). In contrast, two vibrissae within the same row were required to judge the relative spatial frequency of different textures (Carvell and Simons, 1990). This finding is consistent with the predicted need to compare the resonance amplification of multiple vibrissae of different lengths to disambiguate differences in spatial frequency components between textures (Fig. 8B).

We emphasize that, in the proposed framework, texture discriminations made with the vibrissa system can be represented as relative neural activity comparisons between arc signals. These relative judgements do not require that the rat know the temporal frequency generated by a given velocity convolved with a spatial frequency—a difficult decoding problem for a variety of reasons, including continued vibrissa growth (Ibrahim and Wright, 1982). Rather, this scheme requires only that the rat determine the relative shift in signal strength between arcs of vibrissae in response to different textures. The redundancy in resonance properties along an arc of vibrissae could provide statistical robustness to the estimation of the power at different frequencies, sustaining this capability in case of vibrissa loss or damage. The representation of similar resonance properties along an arc is also consistent with the suggestion that arcs are distinct units for temporal information processing (Ahissar and Zacksenhouse, 2001).

Vibrissa resonance and the representation of complex surfaces

We showed that vibrissae can amplify the periodic components in a complex texture. This finding suggests that, when the vibrissae, as an ensemble, sweep past a complex texture, the amplitude of motion of each vibrissa will be proportional to the coefficient of the frequency component in the force exerted on the vibrissae at its resonance frequency. The spectral content of surface features of many natural textures, such as concrete and sandpaper, is known to have maximal power between 0.01 and 0.5 mm (Costa, 2000). These surface features should generate temporal frequencies that fall within the observed range of vibrissa FRF values, presuming known whisking velocities (Carvell and Simons, 1990, 1995). This model of encoding of complex textures allows for an efficient, spatially distributed representation. Furthermore, as the central representations of the vibrissae preserve somatotopy (Woolsey and Van der Loos, 1970; Woolsey et al., 1975), the code can be transmitted as a spatial map to downstream neural processing areas.

Parallels with the auditory system and neural implications

The system we described for tactile sensory amplification is similar to known mechanisms in the auditory system. In auditory processing, several resonance properties of the cochlea create a spatial gradient of temporal frequency responses, much like the spatial gradient observed here across the rat face (Geisler, 1998). These mechanisms of auditory transduction may facilitate detection (through amplification of changes in pressure level) and discrimination (through spatial segregation) of sound pressure waves (von Bekesy, 1947; Freeman and Weiss, 1990; Geisler, 1998; Gelfand, 1998). Central auditory maps preserve the tono-topic spatial gradient established in the cochlea, with horizontally elongated isofrequency columns, a key organizing feature of the primary auditory cortex map (Kiang et al., 1965; Merzenich and Brugge, 1973; Geisler, 1998). In parallel with the auditory system, our findings in vibrissa transduction clearly predict bandpass tuning of peripheral and central neurons, and an organized system of somatotopically maintained isofrequency columns, in which horizontal bands of neurons, representing arcs of vibrissae, are most sensitive to the same frequencies. Preliminary data from electrophysiological recordings suggest that these predictions are well met (Andermann et al., 2002; Andermann, Neimark, and Moore, unpublished observations).

The parallels between the model proposed here and the auditory system suggest that vibrissa resonance may also act to amplify signals that are carried in media other than hard surfaces (e.g., sound pressure waves in air). In support of this view, cercal hairs of invertebrates show distinct sensitivity to the frequency composition of air currents, potentially using similar mechanisms (Levin and Miller, 1996; Roddey and Jacons, 1996; Paydar et al., 1999). Preliminary observations suggest that rat vibrissae may oscillate at their resonant frequencies in response to persistent air currents (Andermann and Moore, unpublished observation). Furthermore, seals show a remarkable ability to trace vortices generated by objects moving through the water, a skill that is vibrissa dependent and may employ the resonance of the vibrissae to promote amplification (Bleckmann, 1994; Dehnhardt et al., 2002).

Future directions

An important future direction for studies of resonance will be to elucidate the effects that vibrissa bending and contact point have on resonance amplification. The effective boundary condition at the end of a vibrissa sweeping across a rough surface depends on the details of contact. For strong contact forces and rough surfaces, the vibrissa may jump (in a stick-slip manner) between pinning points representing a pinned-end condition. For weak contacts, texture probably provides a spatially varying coefficient of sliding friction, and the motion of the whisker should reflect the spatial Fourier coefficients of texture. Although no studies have examined resonance behavior in the awake behaving rat whisking over a texture, Hartmann et al. (2003) have recently extended the findings reported here to demonstrate that, in the awake behaving rat, vibrissae resonate when released from contact with a bar.

Under the currently examined conditions, higher resonance frequencies, above the FRF, were observed in many vibrissae (e.g., the second amplification region at 410 Hz in the β vibrissa in Fig. 4). If these higher harmonics are expressed in behaviorally relevant stimulation conditions, they should prove important: these peaks may further enhance detection by providing a broader range of possible driving frequencies but may also complicate the application of vibrissa resonance for discrimination of spatial frequencies. The relative impact of these higher resonance frequencies could be diminished by the geometry of the vibrissae, because the conical shape should result in a smaller amplification of motion at the base at higher modes.

A caveat regarding the model proposed here is that the predictions generated from it are constrained to the linear regime, valid for vibrissa deflections of up to 1 mm. Preliminary experiments suggest that this assumption is well met (Andermann and Moore, unpublished observations). The principle of resonance amplification should be preserved by larger deflections that may be used in other whisking contexts, although this assumption needs to be tested empirically.

Vibrissa damping could also significantly influence the expression of resonance effects, as was evident from our model and measurements. As suggested by Yohro (1977) (Rice et al., 1986), the anatomical organization of the FSC is well positioned to modulate the expression of characteristic frequencies of the vibrissa through changes in blood pressure and by muscular contraction. Because increasing damping should broaden the tuning curve of the vibrissa, it is possible that a relaxation of sinus pressure would be valuable in a general detection task, in which a response to a broad range of frequencies is optimal. Stiffening the vibrissa follicle could create sharper tuning curves, which would be advantageous for discrimination or complex texture encoding tasks. Recent work (Hartmann et al., 2003) suggests that these damping effects are robust in a behaving rat. Additional studies of resonance in the awake preparation will be essential to determine whether and how resonance may be expressed during behavioral tasks and, more generally, to assess the behavioral relevance of the resonance properties described here.