Presynaptic Capacitance Measurements and Ca²⁺ Uncaging Reveal Submillisecond Exocytosis Kinetics and Characterize the Ca²⁺ Sensitivity of Vesicle Pool Depletion at a Fast CNS Synapse

Abstract

The intracellular Ca²⁺ sensitivity of synaptic vesicle fusion is an important determinant of transmitter release probability, but it is unknown for most CNS synapses. We combined whole-cell membrane capacitance measurements and Ca²⁺ uncaging at the large calyx of Held nerve terminals to determine the Ca²⁺ sensitivity of synaptic vesicle fusion at a glutamatergic CNS synapse, independent of recording EPSCs. Capacitance increases measured 30-50 msec after elevating the intracellular Ca²⁺ concentration ([Ca²⁺]_i) by Ca²⁺ uncaging were half-maximal at ∼5 μm [Ca²⁺]_i. At 10 μm [Ca²⁺]_i, capacitance increases reached maximal values (256 ± 125 fF; mean ± SD), indicating the depletion of an average pool of ∼4000 readily releasable vesicles. Vesicle pool depletion was confirmed in cross-depletion experiments, in which capacitance responses were measured after Ca²⁺ uncaging, or after combined stimuli of prolonged presynaptic depolarizations and Ca²⁺ uncaging. To analyze the Ca²⁺-dependent rates of vesicle pool depletion, the capacitance rise after Ca²⁺ uncaging was fitted with single- or double-exponential functions. The fast time constants of double-exponential fits, and the time constants of single-exponential fits were 2-3 msec at 10-15 μm [Ca²⁺]_i and reached submillisecond values at 30 μm [Ca²⁺]_i. These results suggest that three to five readily releasable vesicles can fuse within <1 msec at each active zone of a calyx of Held, given that [Ca²⁺]_i rises sufficiently high. Submillisecond kinetics of exocytosis are reached at significantly lower [Ca²⁺]_i than at ribbon-type sensory synapses previously investigated by capacitance measurements.

Introduction

At most CNS synapses, as well as at neuromuscular junctions, transmitter release is triggered by brief presynaptic action potentials that admit Ca²⁺ influx into the nerve terminal (Katz, 1969). The intracellular Ca²⁺ concentration, [Ca²⁺]_i, relevant for vesicle fusion builds up in local microdomains near the open Ca²⁺ channels (Simon and Llinás, 1985; Yamada and Zucker, 1992; Roberts, 1994), and binding of several Ca²⁺ ions to a Ca²⁺ sensor, probably represented by the vesicle protein Synaptotagmin (Brose et al., 1992; Geppert et al., 1994; Fernández-Chacón et al., 2001), initiates vesicle fusion. In this process, the Ca²⁺ sensitivity of vesicle fusion is a major determinant for the transmitter release probability at synapses, besides the exact distance and geometrical arrangement between vesicles and Ca²⁺ channels (Neher, 1998; Meinrenken et al., 2002). The intracellular Ca²⁺ sensitivity of vesicle fusion is, however, not known for most CNS synapses, because the microdomain Ca²⁺ signal relevant for vesicle fusion cannot be quantified directly with current imaging techniques.

By using Ca²⁺ uncaging to produce a spatially homogenous cytosolic [Ca²⁺]_i signal, the Ca²⁺ sensitivity of transmitter release has recently been estimated at the large calyx of Held nerve terminals (Forsythe, 1994; Borst et al., 1995), which form excitatory, glutamatergic synaptic connections in the auditory brainstem circuitry. By combining presynaptic Ca²⁺ uncaging with measurements of EPSCs, it was found that notable transmitter release was triggered by Ca²⁺ elevations to ∼1 μm, and large and rapidly rising EPSCs were observed at 10-20 μm [Ca²⁺]_i (Bollmann et al., 2000; Schneggenburger and Neher, 2000; Felmy et al., 2003). These estimates of the intracellular Ca²⁺ requirement for rapid transmitter release are significantly lower than the previous ones of ∼100 μm [Ca²⁺]_i, which were inferred from theoretical analyses of the microdomain [Ca²⁺]_i signal (Simon and Llinás, 1985; Yamada and Zucker, 1992) and from experiments at the squid giant synapse (Adler et al., 1991; Llinás et al., 1992; Hsu et al., 1996). Also, membrane capacitance measurements combined with Ca²⁺ uncaging at the ribbon-type synapses of retinal bipolar cells (Heidelberger et al., 1994) and inner hair cells of the cochlea (Beutner et al., 2001) have indicated higher Ca²⁺ requirements for rapid vesicle fusion than the ones estimated at the calyx of Held.

With capacitance measurements, the Ca²⁺-dependent rate of vesicle fusion can be analyzed from the kinetics of the depletion of a limited pool of readily releasable vesicles (Thomas et al., 1993; Heinemann et al., 1994). This analysis relates to the question of how fast a pool, or subpool, of readily releasable vesicles can be released at saturating Ca²⁺ concentration (Almers, 1994). This exocytotic time is probably well below 1 msec for rapidly releasing synapses; it is, however, not known which fraction of the readily releasable pool of vesicles can, in principle, be released at such high rates. At active zones of CNS synapses, the readily releasable pool consists of ∼3-10 docked vesicles (Schikorski and Stevens, 2001; Xu-Friedman et al., 2001; Sätzler et al., 2002; Taschenberger et al., 2002). With very strong Ca²⁺ stimuli, the resulting multivesicular release at individual active zones will lead to saturation of postsynaptic AMPA receptors (Meyer et al., 2001; Sun and Wu, 2001; Wadiche and Jahr, 2001). If AMPA receptors saturate, or desensitize before a sizeable fraction of the readily releasable pool has been released, then the time course of vesicle pool depletion would be underestimated. We were therefore interested to measure the kinetics of vesicle pool depletion with a method that does not depend on measurements of EPSCs. Here, we apply presynaptic membrane capacitance measurements (Sun and Wu, 2001) combined with Ca²⁺ uncaging to quantify the Ca²⁺ sensitivity of synaptic vesicle pool depletion at the calyx of Held.

Materials and Methods

Slice preparation and solutions. Slices containing the medial nucleus of the trapezoid body were prepared from 8- to 10-d-old Wistar rats. In an attempt to cut the axon close to the calyx of Held nerve terminals (Borst and Sakmann, 1998; Sun and Wu, 2001), we prepared transverse slices at an angle of 30-40° with respect to the sagittal plane. The extracellular solution contained (in mm): 125 NaCl, 25 NaHCO₃, 2.5 KCl, 1.25 NaH₂PO₄, 1 MgCl₂, 2 CaCl₂, 25 glucose, 0.4 ascorbic acid, 3 myoinositol, and 2 Na-pyruvate, pH 7.4 when bubbled with 95% O₂-5% CO₂. During recording under standard conditions, the extracellular solution also contained 50 μm d-(-)-2-amino-5-phosphonopentanoic acid, 10 μm 2,3-dioxo-6-nitro-1,2,3,4-tetrahydrobenzo[f]quinoxaline-7-sulfonamide (NBQX), 1 μm TTX, and 10 mm TEA⁺, to block the generation of EPSPs in the postsynaptic cell, as well as to block presynaptic K⁺ and Na⁺ conductances. The standard intracellular solution contained (in mm): 130 Cs-gluconate, 20 TEA-Cl, 20 HEPES, 5 Na₂ATP, 0.3 Na₂GTP, 0.1 fura-2FF, 1.5 (3) DM-nitrophen, 1.3 (2.4) CaCl₂, and 0.5 (1.0) MgCl₂. In this solution, most of the Mg²⁺ will be bound to ATP. In some experiments, CsCl was used instead of Cs-gluconate (see Fig. 2C, filled circles). In yet another set of experiments, 140 mm KCl was used instead of Cs-gluconate and TEA-Cl in the intracellular solution, and TEA⁺ was omitted from the extracellular solution (see Fig. 2 B). Experiments were done at room temperature (21-24°C).

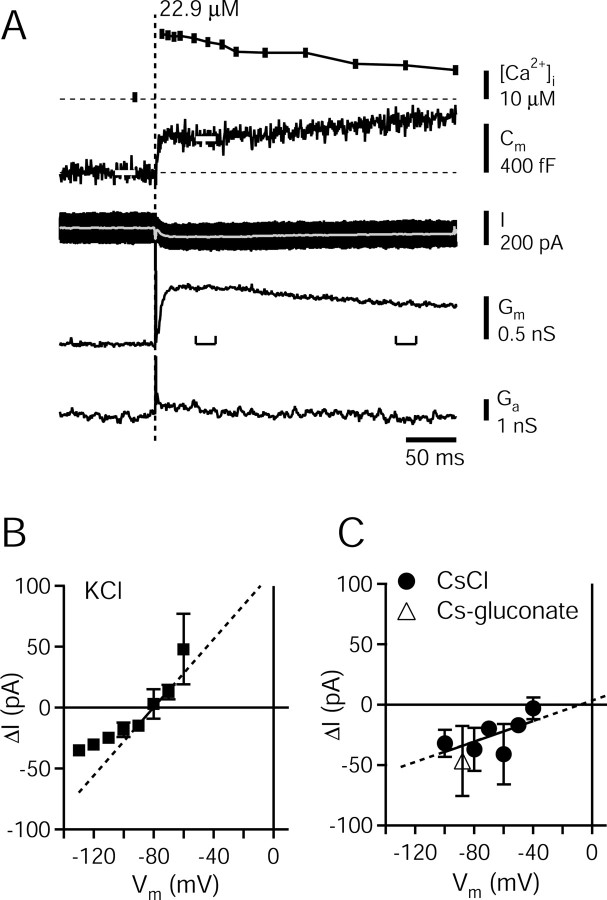
Figure 2.

Changes in membrane capacitance and membrane conductance induced by Ca²⁺ uncaging at the calyx of Held. A, Example of a typical flash-photolysis experiment made with the Cs-gluconate intracellular solution. The traces, from top to bottom, represent presynaptic [Ca²⁺]_i (measured by ratiometric imaging of the Ca²⁺ indicator fura-2FF), membrane capacitance (C_m), membrane current (I), membrane conductance (G_m), and access conductance (G_a). The amplitude of the C_m increase was analyzed as the difference between the basal C_m and the temporal average of C_m in a window of 30-50 msec after the flash (see white bars in C_m trace). The amplitudes of the Ca²⁺-induced changes in C_m and G_m were also compared for times early and late after flashes (see brackets near G_m trace). B, Ca²⁺-activated currents (ΔI) were measured at varying holding potentials (V_m), with a KCl intracellular solution, and without TEA⁺ in the extracellular solution (n = 4 cells). Each data point represents the average of two to six independent measurements. The linear fit in a range of -70 to -90 mV indicates a slope conductance of 1.4 nS. C, Current-voltage relationship with Cs⁺-containing intracellular solutions and with 10 mm TEA⁺ present in the extracellular solution. Closed circles represent the averages of two to six independent measurements with intracellular CsCl solution (n = 12 cells). In this and all subsequent Figures, average data points with error bars represent mean ± SD values. The linear fit to these average data points indicated a slope conductance of 0.42 nS and an extrapolated reversal potential of -10 mV. The average Ca²⁺-activated current measured with the standard Cs-gluconate intracellular solution at -80 mV is also shown (open triangle; n = 20 cells). This symbol is slightly left-shifted on the x-axis for clarity. V_m, XXX.

Data analysis. For fitting the time course of current relaxations after hyperpolarizing steps (Fig. 1 A), as well as for fitting the time course of capacitance changes after Ca²⁺ uncaging (see Fig. 5), single- and double-exponential fits were made in IgorPro (WaveMetrics, Lake Oswego, OR). Double-exponential fits were accepted if the time constants for the fast and the slow component differed by more than threefold and if the amplitude of each component contributed at least 10%. If one of the two criteria was not met, a single-exponential function was regarded as the better fit. Results are expressed as mean ± SD values.

Figure 1.

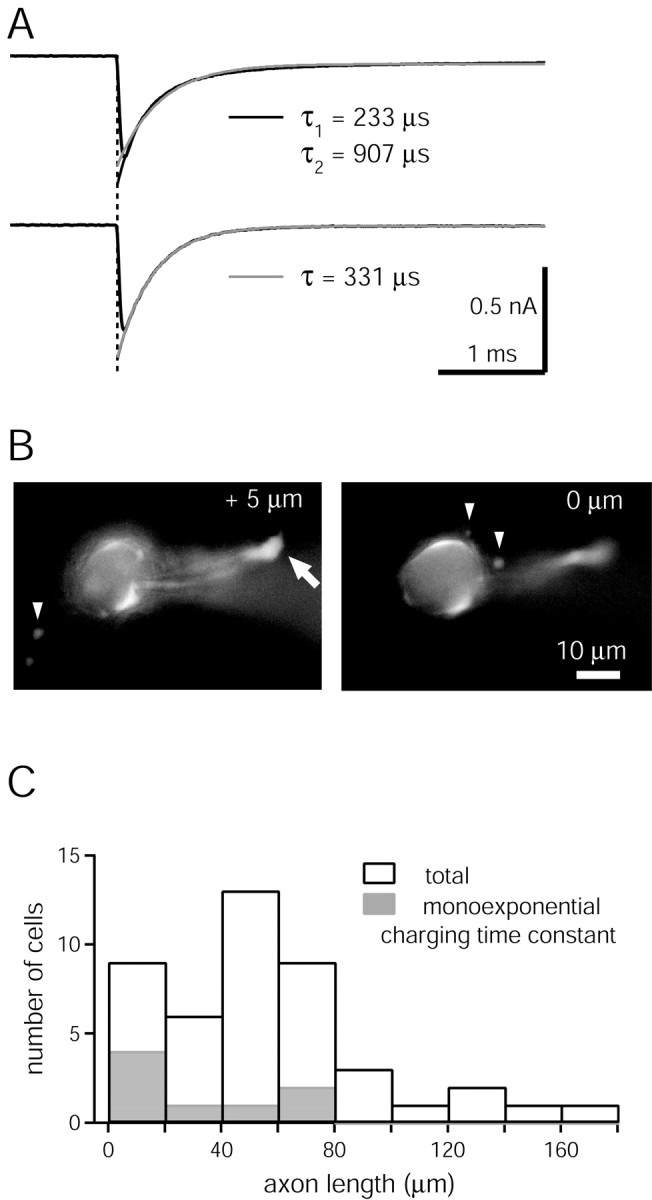
Electrotonic properties of calyx of Held nerve terminals. A, The charging currents in response to 10 mV hyperpolarizing voltage steps were fitted with exponential functions. For the cell shown at the top, a double-exponential fit (black trace) was found necessary, whereas the charging currents of the cell shown at the bottom could be fitted by a single exponential (gray trace). The acceptance criteria for single- and double-exponential fits are given in Materials and Methods. B, Fluorescence images of a calyx of Held filled with 100 μm fura-2FF, taken at two focal depths. In the left image, the cut axon close to the slice surface can be identified (arrow). Filopodial extensions are also visible (arrowheads). This cell had an axon length of 48 μm and a monoexponential membrane charging time constant. C, Histogram of the axon lengths for the calyces used in this study (n = 45; open bars). A histogram for the calyces with monoexponential charging time constant is superimposed (n = 8; gray bars). Note that the cut axon at the slice surface could be identified only in 9 of 45 calyces (see B for an example); in all of the other calyces, the axon length must be regarded as a minimal estimate. In the group of calyces with axon lengths <20 μm, a cut axon was identified in seven of nine calyces.

Figure 5.

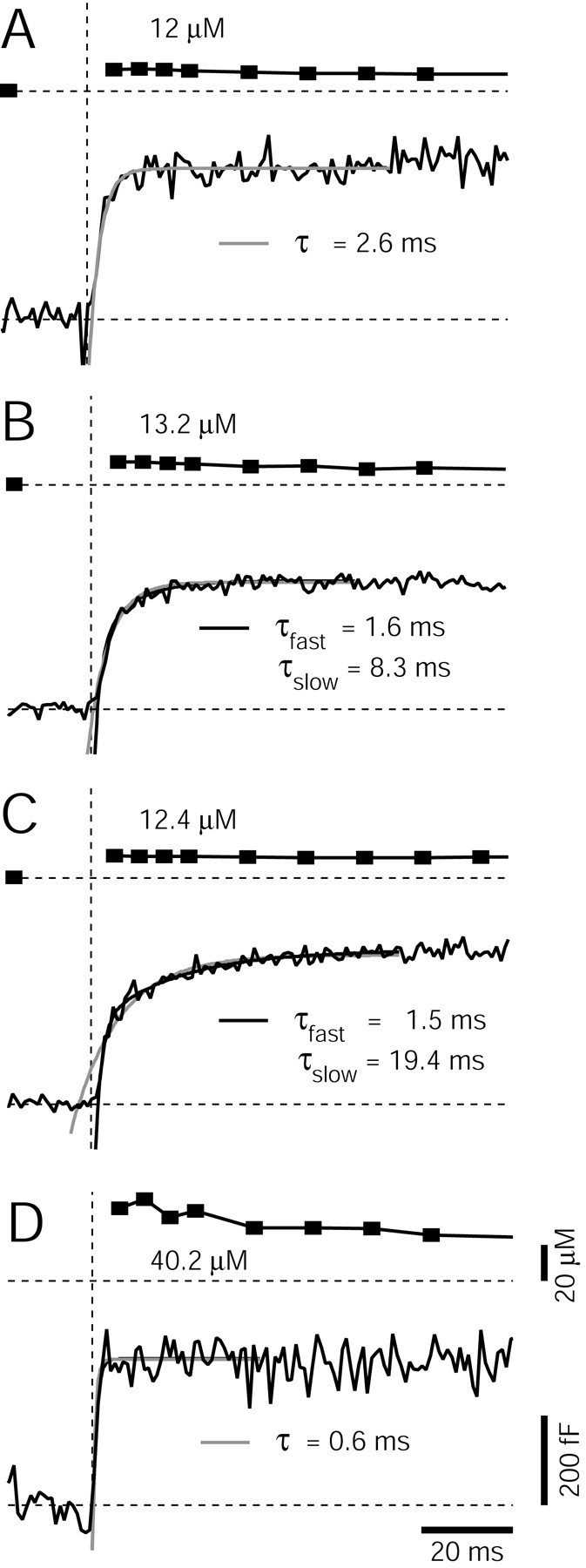
Analyzing the time course of C_m increase as an indicator of the rate of vesicle pool depletion. A-C, C_m increases in response to flashes that elevated [Ca²⁺]_i in a range of 10-15 μm are shown for three different calyces. Each C_m trace was fitted by single- and double-exponential functions (gray and black lines, respectively). In A, a single-exponential fit was found sufficient, whereas in B and C, double exponentials were necessary to fit the rise in C_m, according to the criteria outlined in Materials and Methods. D, The C_m increase in response to a flash that elevated [Ca²⁺]_i to 40 μm. A single exponential with time constant of 0.6 msec fitted the C_m increase. The scale bars also apply to the traces shown in A-C.

Membrane capacitance measurements. Whole-cell recordings of calyx of Held nerve terminals were made with an EPC-9/2 patch-clamp amplifier (HEKA Elektronik, Lambrecht, Germany). Membrane capacitance (C_m) was measured with the software lock-in extension of the Pulse software (HEKA Elektronik), using the sine plus DC technique (Gillis, 2000) with a 70 mV peak-to-peak sine wave at 2 kHz, or 1 kHz in some experiments. The holding potential was -80 mV. Basal C_m and the series resistance at the time of the first flash were 22.4 ± 7.0 pF and 13.5 ± 3.9 MΩ, respectively (n = 45 cells). During recordings, the capacitance cancellation circuit of the EPC9/2 was active, but the series resistance compensation was off. The reversal potential in the lock-in software was set to 0 mV, close to the estimated reversal potential of a Ca²⁺-activated conductance measured with the standard Cs⁺- and TEA⁺-containing solutions (see Fig. 2C). However, the C_m changes calculated by the lock-in software did not change significantly (<1% change of ΔC_m) when the reversal potential was arbitrarily set to values in the range of -40 to +40 mV.

Electrotonic properties of calyx of Held nerve terminals. Most available methods for rapid lock-in measurements of C_m, such as the sine plus DC technique used here, assume that the cell under study can be described by a single-compartment resistance-capacitance network (Gillis, 2000). We therefore assessed the electrotonic parameters of each calyx, by recording the voltage-clamp charging currents in response to 10 mV hyperpolarizing steps at the beginning of each recording (Fig. 1). In each case, charging transients were fitted with a single- and a double-exponential function (Fig. 1 A). In most cells (37 of 45), double exponentials were necessary to accurately describe the relaxation of the charging currents, with average fast and slow decay time constants of 153 ± 91 and 731 ± 337 μsec, respectively (n = 37 cells) (Fig. 1 A, top panel). In 8 of 45 cells, single exponentials were sufficient (Fig. 1 A, bottom panel).

To correlate the electrotonic properties of calyces with their morphology, we measured the axon length from fluorescence images taken at the end of each experiment, by exciting fura-2FF at 380 nm wavelength (Fig. 1 B). We found that the chance of observing a monoexponential charging time constant was higher in calyces with short axons (Fig. 1C) (Borst and Sakmann, 1998; Sun and Wu, 2001). Nevertheless, we also found calyces with double-exponential charging time-constants for axon lengths <20 μm (n = 5 of 9 calyces) (Fig. 1C).

These findings indicate that most calyces studied here could not be approximated with a single-compartment electrotonic model, maybe because of the filopodial extensions close to the calyx (Fig. 1 B, arrowheads) and/or because of the presence of an axon of >20 μm length. We therefore asked how a second, slowly charging membrane compartment, in combination with a Ca²⁺-activated conductance increase (see Results and Fig. 2) would influence C_m changes obtained from lock-in measurements. Model calculations for an electrotonic two-compartment model (not shown), with realistic values of C_m and membrane conductance (G_m) for both compartments, showed that a conductance increase localized in the second (slowly charging) electrotonic compartment can lead to an apparent reduction of C_m from lock-in measurements at the first compartment. The effect was moderate, however: Assuming that a Ca²⁺-activated conductance of 0.5 nS (see Fig. 2C) was localized exclusively in the second (axonal) compartment, a reduction in C_m of 23 fF was calculated for a sine-wave frequency of 2 kHz. This error is small, but not negligible, when compared with the C_m increases typically observed (∼100-600 fF) (see Figs. 2, 3, 4, 5). To further verify the validity of our C_m measurements, we grouped the data according to cells with single- or double-exponential decays in their charging transients. Both groups of cells had C_m changes with similar amplitudes and time courses after Ca²⁺ uncaging (see Figs. 3D and 6 A; gray symbols are data obtained from cells with single-exponential charging currents).

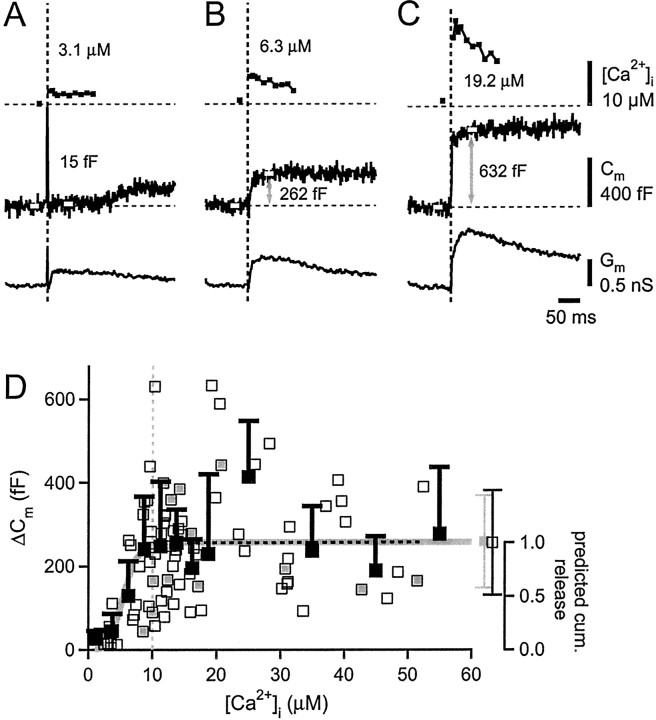
Figure 3.

The amplitudes of C_m increases are maximal for [Ca²⁺]_i steps higher than 10 μm. A-C, [Ca²⁺]_i traces (top panels), C_m traces (middle panels), and G_m traces (bottom panels) are shown for a calyx in which flashes with increasing intensity were given. White bars superimposed onto C_m traces indicate 20 msec time intervals used for the analysis of C_m amplitudes. D, Amplitude of C_m increase as a function of [Ca²⁺]_i for n = 77 flash responses (open squares) obtained in 45 calyces. The amplitudes were analyzed in a time window of 30-50 msec after the flash, as shown in A-C. The data points marked by additional gray squares were obtained from n = 8 calyces with single-exponential charging currents (Fig. 1). The average C_m increase for [Ca²⁺]_i steps to >10 μm was similar for cells with single- and double-exponential charging currents (gray average square and open average square, respectively). The horizontal dotted line is a linear regression analysis for [Ca²⁺]_i of >10 μm. Filled black squares represent binned and averaged data points. A prediction of the model of cooperative Ca²⁺ binding and vesicle fusion (Fig. 7E) is shown by the gray line plotted on the right axis. For the model calculations, the cumulative amount of vesicle fusion in a time interval of 30-50 msec was calculated from simulations like the ones shown in Figure 7B, with the parameters of the model set to the values reported in Schneggenburger and Neher (2000). Cum., Cumulative.

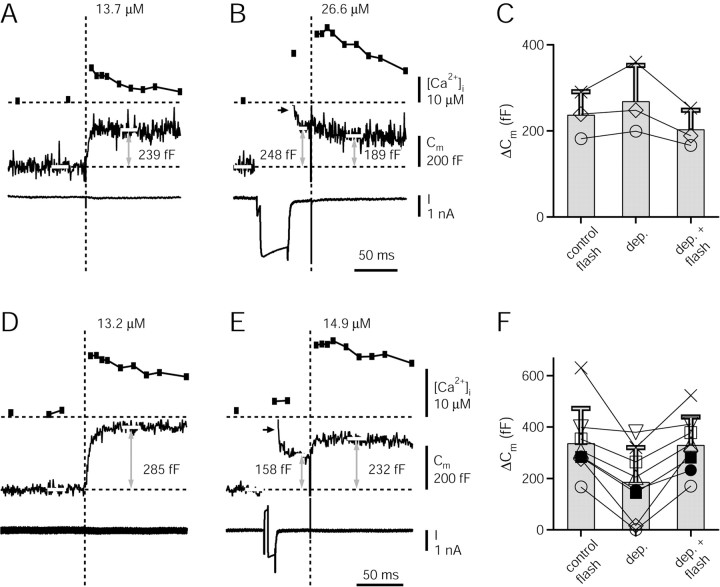
Figure 4.

Cross-depletion experiments indicate that a pool of readily releasable vesicles is depleted by [Ca²⁺]_i steps >10 μm. A, [Ca²⁺]_i, C_m, and current trace for a control flash. In this and all subsequent panels, white bars superimposed onto C_m traces indicate the time intervals used for the analysis of C_m amplitudes. B, A 32 msec depolarization to 0 mV, preceded by a 4 msec interval at +80 mV to open Ca²⁺ channels more quickly, was followed by a flash with the same intensity as in A. The Ca²⁺ current caused a C_m jump of 248 fF as analyzed in a 15 msec interval preceding the flash. Note the rapid, partial decay of the C_m trace at times shortly after repolarization (<5 msec; see arrows in B and E), which we attribute to the relaxation of voltage-gated conductances. The flash-evoked Ca²⁺ increase did not induce any additional rise in C_m. C, Amplitudes of C_m increases attained after control flashes (left bar), after depolarizations to 0 mV for 32 msec (middle bar), and in a 30-50 msec analysis window after the depolarization and the flash (B). Data points for the individual calyces (n = 3) are also shown. D-F, Similar experiment as in A-C, but using shorter depolarizations of 8 msec. The depolarization-induced C_m increase was approximately one-half of the one induced by control flashes. Note that the C_m response to control flashes agreed well with the C_m response to combined stimuli across individual calyces (compare left and right bar in F).dep., Depolarization.

Figure 6.

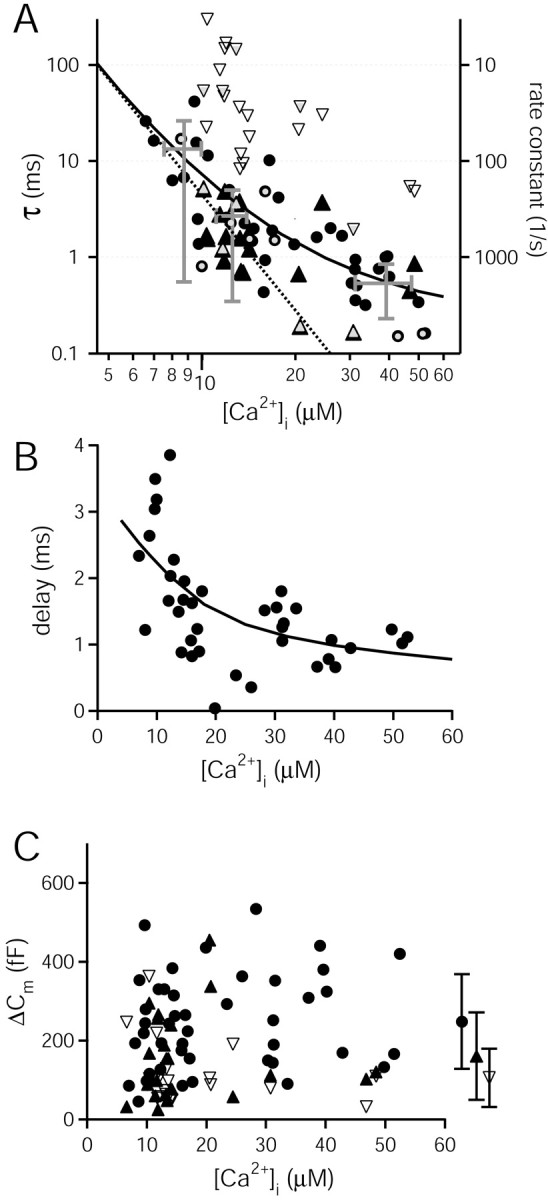
Ca²⁺ dependence of the rate of vesicle pool depletion at the calyx of Held. A, Plot of the time constants of vesicle pool depletion as a function of [Ca²⁺]_i attained after flashes. C_m responses that were fitted by single exponentials are shown by filled black circles (n = 44 responses). The fast and the slow components of C_m responses with double-exponential rise (n = 21) are represented by filled and open triangles, respectively. The solid line is the prediction of the kinetic scheme shown in Figure 7E, with the following parameters: k_on, 9 × 10⁷m^-1 · sec^-1; k_off, 9500 sec^-1, γ, 6000 sec^-1, and b, 0.25, as in Schneggenburger and Neher (2000). Data points marked by additional gray symbols were obtained from calyces with single-exponential voltage-clamp charging currents (Fig. 1). The dotted line indicates a slope of 4 in the double-logarithmic plot. B, Delay of the C_m response as a function of [Ca²⁺]_i. Delays were taken as the x-axis intercept of the extrapolated single-exponential fits to C_m increases. The line is the prediction of the model shown in Figure 7E, with the same parameter set as in A. C, Plot of the amplitude of C_m increases as estimated from single-exponential fits (circles), or from the fast and the slow component of double-exponential fits (filled and open triangles, respectively). Average symbols represent the corresponding mean ± SD values averaged over all of the [Ca²⁺]_i values.

Calculations for a model of cooperative Ca²⁺ binding and vesicle fusion. The kinetic scheme of Figure 7E was solved by numerical integration with the Euler method. For the model predictions of Figures 3D and 6, the kinetic scheme was driven by the [Ca²⁺]_i waveform shown in Figure 7A (continuous line), calculated from the measured time course of the flash lamp as described previously (Felmy et al., 2003). For the predictions in Figure 7, the kinetic scheme was driven by a simple step-like increase of [Ca²⁺] (A, dotted line). In both cases, the simulations for each final [Ca²⁺] yielded the accumulation of vesicles in the fused state, like those shown in Figure 7B. These traces were fitted by single-exponential functions (see Fig. 7B, dotted lines), starting at the point of the steepest rise, to predict the time course of vesicle pool depletion. The x-axis intercept of the exponentials were taken as the delay of the C_m response. The occupancy of the Ca²⁺ sensor (see Fig. 7C) was simulated after omitting the final, irreversible fusion step from the kinetic scheme in E. Steady-state Ca²⁺ binding (see Fig. 7D, open circles) was taken from the occupancy reached at the end of 400 msec simulation traces. For the prediction in Figure 3D, the cumulative vesicle fusion normalized to the pool size was calculated for a time window of 30-50 msec after the flash.

Figure 7.

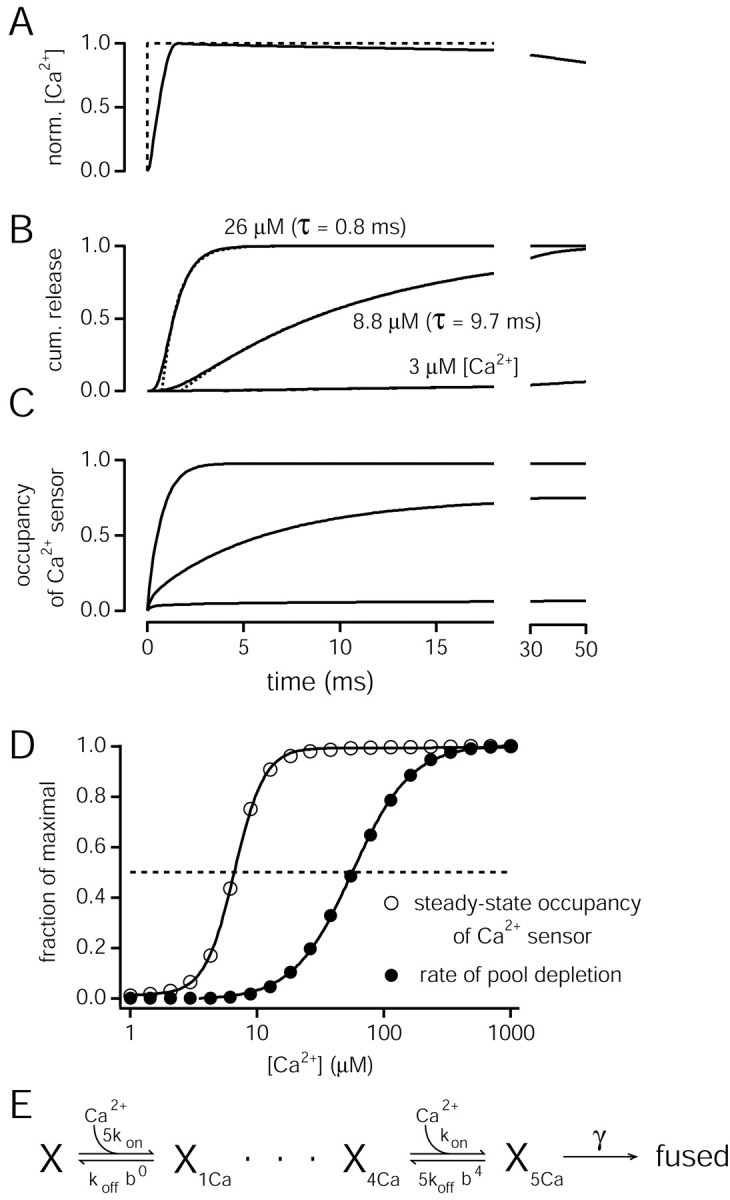
Simulations of the kinetic and equilibrium properties of Ca²⁺ binding and vesicle fusion. A, An ideal [Ca²⁺]_i step (dashed line) and the calculated time course of the rise in [Ca²⁺]_i produced by Ca²⁺ uncaging (solid line) (see Material and Methods). norm., Normalized. B, Simulated accumulation of vesicles in the fused state for three [Ca²⁺]_i steps to the indicated amplitude. cum., Cumulative. C, Occupancy of the Ca²⁺ sensor for vesicle fusion for the same [Ca²⁺]_i steps as in B. The occupancy was calculated after omitting the irreversible fusion step from the scheme in E. Note that a [Ca²⁺]_i step to 8.8 μm leads to a steady-state occupancy of >50%. In contrast, the kinetics of vesicle fusion for the same [Ca²⁺]_i step has a time constant of pool depletion of 9.7 msec (B, middle trace), much slower than the expected half-maximal value of (1/γ) × 2, which corresponds to ∼350 μsec. D, Ca²⁺ dependence of the steady-state occupancy of the Ca²⁺ sensor (open circles) and of the rate of vesicle pool depletion (closed circles), both normalized to maximal values. Note the leftward shift of the steady-state Ca²⁺ occupancy with respect to the Ca²⁺ dependence of the rates of vesicle pool depletion. The simulation results were obtained with the model parameters given in Figure 6 and were fitted by Hill equations (lines). E, Kinetic scheme of cooperative Ca²⁺ binding and vesicle fusion used for the model predictions. Note that, with b < 1, the off-rates of higher bound states will be increasingly reduced, thus introducing positive cooperativity of Ca²⁺ binding (Heidelberger et al., 1994).

The simple model of Figure 7E with the parameters used here applies to a fast component of vesicle fusion (see Fig. 6 A, filled symbols). If a slow release component at the calyx of Held (Sakaba and Neher, 2001) is caused by vesicles with intrinsically lower Ca²⁺ sensitivity or lower final fusion rate, then a more complex model with at least two sets of parameters would be necessary.

Ca²⁺ uncaging and Ca²⁺ imaging. Ca²⁺-loaded DM-nitrophen was photolyzed by a light pulse from a flash lamp (1.1 msec half-width; Rapp Optoelektronik, Hamburg, Germany), limited to a wavelength of <390 nm by a Schott UG 1 filter (Itos, Mainz, Germany). The fluorescence of the Ca²⁺ indicator, fura-2FF, was excited by light of 350 and 380 nm wavelengths, produced by a monochromator (T.I.L.L. Photonics, Gräfelfing, Germany). The excitation light from the flash lamp and the monochromator were fed via quartz lightguides into the upright microscope (Axioskop; Zeiss, Oberkochen, Germany) and were combined by a sapphire window (Linos Photonics, Göttingen, Germany) in the two-port epifluorescence condenser (T.I.L.L. Photonics) of the microscope. An area of 50 × 50 μm in the image plane was illuminated by the flash lamp, set by a field stop in the flash-light illumination pathway. In some experiments, the intensity of the flash light was attenuated by neutral density filters (transmittance of 10, 32, or 50%).

For Ca²⁺ imaging, an interline-transfer CCD chip (480 × 640 pixel; T.I.L.L. Photonics) was used with pixel binning of 8 × 15, allowing for short exposure times of 5 msec. Fura-2FF images were taken at alternating excitation wavelengths of 380 and 350 nm, except for a period immediately after the flash, during which four consecutive images at 380 nm were taken. Off-line analysis of [Ca²⁺]_i was done by extracting fluorescence values from single superpixels or from small regions of interest, corresponding to calyx regions or to a background region in the slice devoid of calyceal processes. The fluorescence values were transferred to a data analysis program (IgorPro), and the fluorescence ratio R was calculated as F₃₅₀/F₃₈₀ after background subtraction. [Ca²⁺]_i was calculated from the fluorescence ratio R according to the equation derived by Grynkiewicz et al. (1985). The calibration was a modified three-point calibration (Felmy et al., 2003). In brief, the fluorescence of fura-2FF was measured in buffered Ca²⁺ solutions with defined Ca²⁺ concentrations, in the presence of 1.5 mm DM-nitrophen. The limiting ratios at low Ca²⁺ (R_min; 10 mm EGTA) and at an intermediate Ca²⁺ concentration (R_int; 10 μm) were confirmed by in vivo calibration measurements, during which strongly buffered Ca²⁺ calibration solutions were loaded via a patch pipette into a calyx of Held. The calibration constants were corrected for the effects of photolysis of DM-nitrophen (Zucker, 1992), as described by Heinemann et al. (1994). This gave a slightly decreased R_max, a slightly increased K_eff, and an unchanged value for R_min [for the meaning of these calibration parameters, see Felmy et al. (2003), their Eq. 1].

Results

Capacitance increases and Ca²⁺-activated conductances after Ca²⁺ uncaging

We made whole-cell patch-clamp recordings from calyx of Held nerve terminals in slices from 8- to 10-d-old rats, and recorded membrane capacitance (C_m) after step-like elevations of [Ca²⁺]_i, produced by flash-photolysis of the Ca²⁺-loaded photolyzable chelator, DM-nitrophen. Figure 2 shows a typical C_m change triggered by Ca²⁺ uncaging in a calyx of Held nerve terminal, using the standard Cs-gluconate intracellular solution. The flash elevated [Ca²⁺]_i to 22.9 μm, as measured by the ratiometric fluorescent Ca²⁺ indicator fura-2FF (Fig. 2A, top panel). Membrane capacitance increased by 276 fF in a time window of 30-50 msec after the flash, and showed a slow, sustained increase up to the end of the observation interval of 300 msec (Fig. 2A). On average, at 250 msec after the flash, the increase in C_m was 111 ± 17.2% (n = 17) of the value measured at 50 msec. In parallel to the increase in C_m, there was an inward current with a peak amplitude of -55 pA at 14 msec after the flash, corresponding to a membrane conductance increase of 0.7 nS (Fig. 2A). The amplitude of these conductance changes depended on the level of [Ca²⁺]_i attained after the flash (Fig. 3A-C). The conductance decreased to 79.6 ± 11.3% of its peak value at 250 msec after the flash. Thus, the time course of the conductance change was not strictly correlated with the time course of C_m.

We attempted to suppress the Ca²⁺-activated conductance, to minimize the possible influence of a conductance change on the quantification of membrane capacitance from lock-in measurements (see Materials and Methods). For this purpose, we first investigated the ionic mechanism(s) of the Ca²⁺-activated conductance. We repeated measurements similar to the ones shown in Figure 2A, now using a K⁺-based intracellular solution, in the absence of extracellular TEA⁺ (see Materials and Methods). Under these ionic conditions, the Ca²⁺-activated currents reversed close to -80 mV, with an average slope conductance of 1.4 nS in a range of -70 to -90 mV (Fig. 2B). With a CsCl-based intracellular solution and 10 mm TEA⁺ in the extracellular solution, the Ca²⁺-activated currents were inward up to a membrane potential of -40 mV, with a reduced average conductance of 0.42 nS, and a reversal potential of -10 mV as estimated by linear extrapolation (Fig. 2C, filled circles). Replacing Cl^- with gluconate in the intracellular solution did not lead to a reduction of the Ca²⁺-activated current at -80 mV (Fig. 2C, average triangle), indicating that the current was not carried by Cl^-. It is possible that the inward current was mediated by small conductance (sK-type) Ca²⁺-activated K⁺ channels (Tucker and Fettiplace, 1996). However, addition of apamine (0.2 μm) and bicuculline (10 μm), which block sK-type Ca²⁺-activated K⁺ channels (Hugues et al., 1982; Johnson and Seutin, 1997), did not reduce the residual Ca²⁺-activated conductance. Specifically, with the Cs-gluconate containing intracellular solution at -80 mV, the Ca²⁺-activated inward currents were -45.3 ± 18 pA (n = 10 cells) with 0.2 μm apamine, -39.2 ± 12.8 pA (n = 6 cells) with 0.2 μm apamine and 10 μm bicuculline, and -47 ± 29 pA under control conditions (n = 20 cells) (Fig. 2C, triangle).

These experiments indicate that a Ca²⁺-activated K⁺ current is present in calyx of Held nerve terminals (Fig. 2B), and this current can be blocked by Cs⁺ and TEA⁺ (Fig. 2C). The residual current in the presence of Cs⁺ and TEA⁺ is not carried by Cl^- (Fig. 2C), and it is not mediated by apamine-sensitive sK channels. Its estimated reversal potential of -10 mV or higher is compatible with a contribution by Ca²⁺-activated, nonselective cation channels, and/or by an electrogenic exchanger such as the Na⁺-Ca²⁺ exchanger. Indeed, when we replaced the standard extracellular solution with a Na⁺-free solution containing 150 mmN-methyl-d-glucamine, the Ca²⁺-activated currents were reduced from the control value of -37 ± 18 pA (n = 12 cells with CsCl) to -4.2 ± 5.5 pA (n = 5 cells). However, under these conditions, the basal [Ca²⁺]_i values were strongly increased, a condition that was not suitable for making C_m measurements. In all of the experiments shown subsequently, we used the Cs-gluconate internal solution with the standard, Na⁺-containing extracellular solution supplemented with 10 mm TEA⁺ (see Materials and Methods).

Vesicle pool depletion occurs with [Ca²⁺]_i steps >10 μm

We next studied the amplitude of C_m changes as a function of step-like increases in [Ca²⁺]_i produced by Ca²⁺ uncaging (Fig. 3). In the example of Figure 3A, a flash with attenuated intensity elevated [Ca²⁺]_i to 3.1 μm, but no significant change in C_m was observed up to 100 msec after the flash. There was, however, a Ca²⁺-activated inward current (not shown), which, in this example, corresponded to a peak increase in G_m of 0.26 nS (Fig. 3A, bottom panel). Subsequent flashes in the same calyx elevated [Ca²⁺]_i to 6.3 and 19.2 μm, and induced increases in C_m of 262 and 632 fF, as analyzed in a time window of 30-50 msec after the flash (Fig. 3B,C). The membrane conductance also increased with flashes to higher [Ca²⁺]_i (Fig. 3B,C; bottom panels). Note, however, that in Figure 3A, a significant increase in G_m was not accompanied by a change in C_m, indicating that the occurrence of changes in G_m and C_m were not strictly correlated.

Figure 3D shows the C_m increases as a function of postflash [Ca²⁺]_i for n = 45 calyces. Below 5 μm [Ca²⁺]_i, the rises in C_m were small or, in some cases, absent. However, a line fit to the data points >10 μm gave a slope close to 0 (0.04 fF/μm) (Fig. 3D, dotted line), indicating that the amplitude of the C_m increases reached maximal values at a [Ca²⁺]_i of >10 μm. This is expected for models that assume a series of Ca²⁺ binding steps, followed by an irreversible fusion reaction (Thomas et al., 1993; Heinemann et al., 1994; Voets, 2000). Below a critical [Ca²⁺]_i, the rate of vesicle fusion is slow, and thus depletion of the entire pool of readily releasable vesicles is not expected within the time of analysis, giving rise to submaximal C_m responses. Indeed, the model of cooperative Ca²⁺ binding and vesicle fusion (see Fig. 7E) predicts a saturating behavior of the cumulative amount of vesicle fusion (Fig. 3D, gray line), with submaximal responses <10 μm. The model parameters for this prediction were as described by Schneggenburger and Neher (2000).

The Ca²⁺ dependence of the C_m changes shown in Figure 3D suggest that these capacitance signals resulted from vesicle fusion in the nerve terminal, and furthermore, that step-like elevations of [Ca²⁺]_i >10 μm exhausted a pool of readily releasable vesicles. The average value of C_m increases for [Ca²⁺]_i steps in the range of 10-55 μm was 256 ± 125 fF (n = 55 flash responses). When only flashes from cells with monoexponential charging transients were averaged (Fig. 3D, gray data points), the C_m increase for [Ca²⁺]_i of >10 μm was virtually identical (258 ± 110 fF; n = 12 flash responses). Considering the estimated C_m change for a single small synaptic vesicle (65 aF) (Sun et al., 2002), the average C_m increase between cells corresponds to the fusion of ∼4000 vesicles.

Cross-depletion between Ca²⁺ uncaging and presynaptic depolarization

We sought to confirm in independent experiments that [Ca²⁺]_i steps >10 μm depleted the pool of readily releasable vesicles. We therefore made cross-depletion experiments, in which the response to control flashes that elevated [Ca²⁺]_i to 10-15 μm were compared with combined stimuli consisting of strong, pool-depleting presynaptic depolarizations and flashes (Fig. 4A-C). In Figure 4A, a control flash elevated [Ca²⁺]_i to 13.7 μm, and induced an increase in C_m of 239 fF. After a waiting time of 120 sec, a combined stimulus, consisting of a depolarization to 0 mV for 32 msec, followed by a flash, was applied. The depolarization activated a Ca²⁺ current of 2.3 nA, which elevated C_m by 248 fF, as measured in a short time window (15 msec) between the end of the depolarization, and the flash (Fig. 4B). A flash with the same intensity as the control flash, given 28 msec after the depolarization, did not further increase C_m. On the contrary, the C_m trace decayed slightly during the first tens of milliseconds after the flash (Fig. 4B), an effect that might be caused by the relaxation of conductances after the prolonged (32 msec) presynaptic depolarization to 0 mV. In general, the C_m increases measured in a time window of 30-50 msec after the combined stimuli of a depolarization and a flash agreed well with the responses to the control flashes (Fig. 4C, compare left and right bars and data points for individual cells). This indicates that a pool of readily releasable vesicles was exhausted by flashes that elevated [Ca²⁺]_i to 10-15 μm.

To further confirm this conclusion, we performed experiments with shorter depolarizations, which are expected to release a smaller fraction of the pool of readily releasable vesicles (Sakaba and Neher, 2001; Sun and Wu, 2001). We used 8 msec depolarizations to 0 mV, preceded by a short (4 msec) period at +80 mV (Fig. 4E). These depolarizations increased C_m to an average percentage of 50 ± 32% of the corresponding control response (Fig. 4D-F). The responses to the combined stimuli were again similar to the ones of the corresponding control flashes (Fig. 4D-F). This was observed in all of the cells in which partial pool depletion was investigated (Fig. 4F, individual data points). Note, however, that the absolute values of C_m changes showed a considerable scatter between cells (Fig. 4F, left bar) (range, 167-630 fF; 338 ± 136 fF; mean ± SD). This suggests that the size of the readily releasable vesicle pool is variable between nerve terminals (see Discussion).

Ca²⁺ dependence of the rate of vesicle pool depletion

Having established that step-like [Ca²⁺]_i elevations to 10-15 μm depleted a pool of readily releasable vesicles, we next analyzed the time course of cumulative vesicle fusion and its Ca²⁺ dependence, by fitting the rise of C_m changes after Ca²⁺ uncaging with exponential functions (Fig. 5). In 44 of 65 flash responses, the rise of C_m was well fitted by single-exponential functions. An example trace is shown in Figure 5A, with the superimposed single-exponential fit (gray line) with time constant of 2.6 msec. In other flash responses (21 of 65), double-exponential fits better described the rise of C_m after Ca²⁺ uncaging. In the example of Figure 5B, the difference between single- and double-exponential fits was not large, however. The example shown in Figure 5C shows a better separation between a putative fast and slow component of vesicle fusion. In this case, the back-extrapolated monoexponential fit gave an x-axis intercept at a time before the flash was given (Fig. 5C, gray line), clear evidence that the rise in C_m was not adequately described by a single exponential. In this example, a double-exponential function with fast and slow time constants of 1.5 and 19.4 msec fitted the rise in C_m well (Fig. 5C, black line). However, such a clear indication of a fast and a slow component of vesicle fusion was observed in only 7 of 65 flash responses.

Figure 5D shows a C_m response to a flash that elevated [Ca²⁺]_i to 40 μm. At these higher [Ca²⁺]_i, the time course of C_m changes were faster than the ones observed at 10-15 μm [Ca²⁺]_i. In the example of Figure 5D, a single-exponential fit indicated a time constant of 0.6 msec; note, however, that this time constant is at the limit of the resolution of C_m measurements, which used a 2 kHz sine wave.

We plotted the time constants of cumulative vesicle fusion, derived from exponential fits to the rise in C_m (Fig. 5) as a function of the measured [Ca²⁺]_i after flashes (Fig. 6A). This was done separately for responses with single-exponential rise (Fig. 6A, circles) and for responses in which double-exponential fits were found adequate (triangles). In this plot, the time constants for the single-exponential fits and for the fast component of the double-exponential fits overlapped (Fig. 6A, circles and filled triangles), suggesting that they represent the kinetics of the same pool of readily releasable vesicles. These time constants showed a steep Ca²⁺ dependence: in a range of 6-10 μm [Ca²⁺]_i, the average value was 13.4 ± 12.8 msec; at 10-15 μm [Ca²⁺]_i, the time constant was 2.7 ± 2.3 msec. Finally, in a range of 30-55 μm [Ca²⁺]_i, the pool was depleted with a time constant of 0.5 ± 0.3 msec (Fig. 6A, average symbols). The dotted line in the double-logarithmic plot of Figure 6A indicates a slope of 4.

The delays of the C_m responses as a function of [Ca²⁺]_i are shown in Figure 6B. Delays were analyzed as the difference between the time at which the flash was triggered and the x-axis intercept of monoexponential fits to the C_m increase. Ca²⁺-dependent delays in the range of 0.5-4 msec were found. The delays and the time constants shown in Figure 6, A and B, were analyzed with a model that assumed the cooperative binding of five Ca²⁺ ions, followed by an irreversible fusion step (Fig. 7E) (Schneggenburger and Neher, 2000). Note that this model, which was previously derived to describe the relationship between transmitter release rates estimated by EPSC deconvolution and [Ca²⁺]_i, gave a good prediction for the time course of vesicle pool depletion as measured by membrane capacitance (Fig. 6A, solid line). Also, the Ca²⁺ dependence of delays was compatible with the predictions of the five-site Ca²⁺ binding model (Fig. 6B), using the same parameter set as estimated previously (Schneggenburger and Neher, 2000).

Figure 6C plots the amplitude of the C_m changes, analyzed from the amplitude values obtained from exponential fits (Fig. 5). For 44 of 65 C_m responses that were adequately described by a single-exponential function, an amplitude of 248 ± 120 fF was found (Fig. 6C, average symbol with circle), in good agreement with the analysis of C_m increases in a time window of 30-50 msec after the flash (Fig. 3). The amplitude of the fast component in responses with a double-exponential rise (21 of 65 flashes) was 160 ± 111 fF (Fig. 6C, filled triangles and average data point with filled triangle). It is possible that many of the single-exponential fits had resulted from an insufficient separation between a fast and a slow component of vesicle fusion (see Discussion). In that case, a genuine fast component of transmitter release might have an average pool size of <200 fF, or <3000 vesicles.

Discussion

We used whole-cell capacitance measurements at the calyx of Held nerve terminals, combined with Ca²⁺ uncaging and Ca²⁺ imaging, to estimate the Ca²⁺-dependent kinetics of synaptic vesicle fusion. We find half-maximal C_m increases for step-like elevations of [Ca²⁺]_i to 5 μm, and the Ca²⁺ dependence of the amplitude of C_m increases followed the prediction of a model of cooperative Ca²⁺ binding and vesicle fusion (Fig. 3D). The time course of cumulative vesicle fusion, analyzed by fitting exponential functions to the rise in C_m, showed a steep dependence on [Ca²⁺]_i, with an average time constant of 2-3 msec in a range of 10-15 μm [Ca²⁺]_i (Fig. 6A). Our estimate of the Ca²⁺ sensitivity of vesicle fusion on the basis of capacitance measurements agrees well with previous studies in which transmitter release was estimated from measurements of EPSCs (Bollmann et al., 2000; Schneggenburger and Neher, 2000). Together, these findings allow us to make inferences on the Ca²⁺-dependent kinetics of vesicle fusion at a CNS nerve terminal, as well as on the kinetic and equilibrium properties of Ca²⁺ binding to the Ca²⁺ sensor for vesicle fusion.

Comparison with previous estimates of release kinetics at the calyx of Held

At the calyx of Held, pool-depleting Ca²⁺ stimuli have previously been applied by prolonged presynaptic voltage-clamp depolarization (Sakaba and Neher, 2001; Sun and Wu, 2001; Taschenberger et al., 2002) or by Ca²⁺ uncaging (Bollmann et al., 2000; Schneggenburger and Neher, 2000; Felmy et al., 2003). Sun and Wu (2001) have measured C_m steps after presynaptic depolarizations of varying duration. They found maximal C_m increases of ∼400 fF, and an exponential function with time constant of 3 msec fitted the relationship between C_m amplitude and step length well. We observed somewhat smaller maximal C_m increases after Ca²⁺ steps >10 μm (256 ± 125 fF, mean ± SD) (Fig. 3D). With a conversion factor of 65 aF/vesicle (Sun et al., 2002), and assuming that the C_m signals resulted exclusively from the fusion of small synaptic vesicles, a C_m increase of 256 fF corresponds to ∼4000 vesicles, in good agreement with the average pool size from EPSC deconvolution analysis [3500 ± 1131 quanta; mean ± SD value from Sakaba and Neher (2001)]. We found, however, that the cell-to-cell variability of the maximal C_m increase was large, with a range of 100-600 fF between cells (Fig. 4F). This suggests that the readily releasable pool size is variable among calyces, with a coefficient of variation of ∼0.4-0.5. A similarly large variability of pool sizes was found by EPSC deconvolution analysis, with a range of 2040 to 5800 quanta (Sakaba and Neher, 2001).

Sakaba and Neher (2001) have used EPSC deconvolution analysis to measure transmitter release rates after prolonged presynaptic depolarization. They found a clearly biphasic release, with time constants of 2-3 msec and 10-30 msec estimated from biexponential fits to cumulative release rates. By fitting the rise of C_m increases after Ca²⁺ uncaging, we observed a time constant of 2-3 msec at 10-15 μm [Ca²⁺]_i (Fig. 6A), indicating that the [Ca²⁺]_i at the release sites must be in the range of 10-15 μm during voltage-clamp steps close to 0 mV (Sakaba and Neher, 2001; Sun and Wu, 2001). We also found evidence, in 21 of 65 responses, for a second component of vesicle fusion with a slower time constant (Figs. 5B,C, and 6A, open symbols). Thus, it is possible that a rapidly and a slowly releasable subpool of vesicles (Sakaba and Neher, 2001) are caused by different Ca²⁺ sensitivities and fusion rates between vesicles, as in chromaffin cells (Voets, 2000). However, the low rate of occurrence of C_m responses with a clearly biphasic rise precluded a more detailed analysis of the slow component. At present, we cannot entirely rule out that the Ca²⁺-activated conductance after Ca²⁺ uncaging (Fig. 2) affected the detection of a slow component of vesicle fusion in C_m measurements. Also, rapid endocytosis might partially mask a slow exocytotic component, although rapid endocytosis more likely takes place under conditions of weak stimulation (Sun et al., 2002).

Schneggenburger and Neher (2000) measured rates of transmitter release by EPSC deconvolution after presynaptic Ca²⁺ uncaging. They analyzed peak transmitter release rates, but restricted their analysis to the first 10 msec after a flash. They described the intracellular Ca²⁺ dependence of peak transmitter release rates by a model of cooperative Ca²⁺ binding, using their pool size estimate of 1800 ± 870 quanta. In the present approach, we measured the time course of vesicle pool depletion (Fig. 5). The Ca²⁺ dependence of the single-exponential time constants, and the one of the fast time constants in case of double-exponential fits agreed well with the prediction of the previous model (Fig. 6A, filled black data points and solid line). How many vesicles can be released rapidly after Ca²⁺ uncaging? If we assume that release after Ca²⁺ uncaging normally occurs in two kinetically distinct phases, but that the separation between a fast and a slow component was often hampered by the relatively poor resolution of C_m measurements (see above), then it would be appropriate to use the amplitude of the fast component of C_m increases (160 ± 111 fF; n = 21) (Fig. 6C, average data point with filled triangle). This indicates that a mean number of ∼2500 vesicles can fuse with submillisecond kinetics, in reasonable agreement with the previous estimate from EPSC deconvolution (1800 ± 700) (Schneggenburger and Neher, 2000). Considering the mean number of ∼600 active zones for rat calyces of Held at this developmental stage (Meyer et al., 2001; Sätzler et al., 2002; Taschenberger et al., 2002), it is seen that approximately three to five vesicles can fuse within <1 msec at a given active zone, provided that [Ca²⁺]_i is sufficiently high.

Comparison with ribbon-type synapses

The rate of vesicle pool depletion at the calyx of Held has a higher Ca²⁺ sensitivity than the one measured previously at ribbon-type synapses. Rates of pool depletion >1000 sec^-1 were observed in retinal bipolar cells and in cochlear inner hair cells at [Ca²⁺]_i of ∼150 and 100 μm, respectively (Heidelberger et al., 1994; Beutner et al., 2001), whereas at the calyx of Held, this rate is reached at 30 μm (Fig. 6A). The functional consequences of this differential Ca²⁺ sensitivity of vesicle fusion between synapses are not fully understood at present. It is possible that CNS synapses with conventional active zones generally have a higher Ca²⁺ sensitivity than cochlear and retinal sensory synapses with ribbon-like ultrastructure. To test this hypothesis, the Ca²⁺ sensitivity of vesicle fusion at other CNS synapses needs to be evaluated. Another possibility is that the Ca²⁺ sensitivity of vesicle fusion is higher in synapses with high release probability (p) than in low p synapses. However, other factors, like the exact colocalization of vesicles and Ca²⁺ channels also have a large influence on p (Neher, 1998; Rozov et al., 2001; Meinrenken et al., 2002).

Inferences on the equilibrium properties of the Ca²⁺ sensor for vesicle fusion

Because Synaptotagmin-1 or related isoforms are likely candidates for the Ca²⁺ sensor for phasic transmitter release (Geppert et al., 1994; Fernández-Chacón et al., 2001), it is desirable to correlate the intracellular Ca²⁺ sensitivity of synaptic vesicle fusion with the known steady-state Ca²⁺ binding parameters of Synaptotagmin (Brose et al., 1992; Davis et al., 1999; Fernández-Chacón et al., 2001; Sugita et al., 2002). To allow for such a comparison, we simulated the Ca²⁺-dependent rates of pool depletion, as well as the steady-state Ca²⁺ binding (Fig. 7), for the model of cooperative Ca²⁺ binding and vesicle fusion used here (E). Figure 7B shows traces of cumulative vesicle fusion, simulated with the parameters given in the legend to Figure 6. A time constant of vesicle pool depletion of ∼10 msec fitted the trace of cumulative vesicle fusion for a [Ca²⁺] step to 8.8 μm (Fig. 7B, middle trace). This time constant indicates a rate of pool depletion of only ∼100 sec^-1; a small fraction of the estimated maximal value (γ) of 6000 sec^-1. However, simulation of the amount of Ca²⁺ binding for the kinetic scheme in Figure 7E, made in the absence of the irreversible fusion step (see Materials and Methods), indicates that at 8.8 μm [Ca²⁺], >70% of the Ca²⁺ binding sites are occupied at steady state (Fig. 7C, middle trace). Thus, the occupancy of the Ca²⁺-binding sites shows a ∼10-fold leftward shift on the Ca²⁺ concentration axis with respect to the rate of vesicle pool depletion, with half-maximal values of 6.6 and 56 μm [Ca²⁺], respectively (Fig. 7D). If this shift, predicted here by a simple kinetic model of cooperative Ca²⁺ binding and vesicle fusion, is a general property of the Ca²⁺ sensor for vesicle fusion, then it must be considered when functional data measuring the rates of vesicle pool depletion are compared with steady-state Ca²⁺-binding characteristics of C2-domain proteins.

The calculated steady-state Ca²⁺ binding showed a steep cooperativity (Fig. 7D, open circles) (Hill coefficient of 3.7), as expected from the cooperativity implemented in the model shown in Figure 7E. Interestingly, Ca²⁺ binding to Synaptotagmins in the presence of phospholipids also shows a steep cooperativity (Fernández-Chacón et al., 2001). We also calculated the half-maximal Ca²⁺ occupancies for models of cooperative Ca²⁺ binding and vesicle fusion, using the published model parameters for inner hair cells (Beutner et al., 2001) and bipolar cells (Heidelberger et al., 1994). The resulting half-maximal values were 12.6 μm for the inner hair cells and 36 μm for the retinal bipolar cells, comparing with a value of 6.6 μm for this study (Fig. 7D, open circles). Thus, the deduced steady-state Ca²⁺ binding affinity is highest for the calyx of Held, as expected from the comparison of the kinetics of vesicle pool depletion among the three types of synapses (see above). In general, the calculated steady-state Ca²⁺ binding affinities for the three types of synapses are within the range of previously reported Ca²⁺-binding affinities of Synaptotagmin-1 in the presence of different phospholipids (∼5 to >30 μm) (Brose et al., 1992; Davis et al., 1999; Fernández-Chacón et al., 2001).

What are the molecular mechanisms for “tuning” the Ca²⁺ sensitivity of vesicle fusion in different synapses? One possibility is that Synaptotagmin isoforms are differentially expressed between synapses (Chapman, 2002; Südhof, 2002), given that Synaptotagmin isoforms have different Ca²⁺ sensitivities (Sugita et al., 2002). Next, it is possible that posttranslational modifications of Synaptotagmins lead to differences in the function of these proteins. Another possibility is that proteins associated with the core complex of SNARE (soluble N-ethylmaleimide-sensitive factor attachment protein receptor) proteins like Complexins modulate the Ca²⁺ sensitivity of vesicle fusion (Reim et al., 2001). Last but not least, the in vitro affinity of Ca²⁺ binding to Synaptogamins depends on the phospholipid composition of the membrane (Brose et al., 1992; Fernández-Chacón et al., 2001), which in turn might differ between cells, or in specialized membrane regions (Simons and Ikonen, 1997). It will be interesting to find out about the molecular mechanisms that determine the differential Ca²⁺ sensitivity of vesicle fusion between synapses and to explore the functional consequences of differential Ca²⁺ sensitivity for the short-term modulation of transmitter release.