The Statistical Structure of Human Speech Sounds Predicts Musical Universals

Abstract

The similarity of musical scales and consonance judgments across human populations has no generally accepted explanation. Here we present evidence that these aspects of auditory perception arise from the statistical structure of naturally occurring periodic sound stimuli. An analysis of speech sounds, the principal source of periodic sound stimuli in the human acoustical environment, shows that the probability distribution of amplitude-frequency combinations in human utterances predicts both the structure of the chromatic scale and consonance ordering. These observations suggest that what we hear is determined by the statistical relationship between acoustical stimuli and their naturally occurring sources, rather than by the physical parameters of the stimulus per se.

Introduction

All human listeners perceive tones in the presence of regularly repeating patterns of sound pressure fluctuation over a wide range of frequencies. This quality of audition forms the basis of tonal music, a behavioral product characteristic of most if not all human populations. The widely shared features of tonal music that are deemed to be “musical universals” include: (1) a division of the continuous dimension of pitch into iterated sets of 12 intervals that define the chromatic scale (Nettl, 1956; Deutsch, 1973; Kallman and Massaro, 1979; Krumhansl and Shepard, 1979); (2) the preferential use in musical composition and performance of particular subsets of these 12 intervals [e.g., the intervals of the diatonic or (anhemitonic) pentatonic scales] (Budge, 1943; Youngblood, 1958; Knopoff and Hutchinson, 1983); and (3) the similar consonance ordering of chromatic scale tone combinations reported by most listeners (Malmberg, 1918; Krumhansl, 1990). Although the response properties of some auditory neurons to musical tone combinations (Tramo et al., 2001) and other complex time-varying signals (Escabi and Schreiner, 2002) are now known, as are some neuroanatomical correlates of music perception (Peretz et al., 2001; Janata et al., 2002), these perceptual phenomena have no generally accepted explanation in either physiological or psychological terms. Thus, the basis for tonal music, one of the most fascinating and widely appreciated aspects of human audition, remains obscure.

Here we explore a conceptual framework for understanding musical universals suggested by recent work on human vision (for review, see Knill and Richards, 1996; Purves et al., 2001; Rao et al., 2002; Purves and Lotto, 2003). A fundamental challenge in understanding what we see is that the physical source of a retinal image cannot be derived directly from the information in the stimulus (a quandary referred to as the “inverse optics” problem). In audition as well, the physical characteristics of the stimulus at the ear cannot uniquely specify the generative source to which the listener must respond (Gordon et al., 1992; Hogden et al., 1996; Driscoll, 1997), presenting a similar “inverse acoustics” problem. Acoustical stimuli are inherently ambiguous because a given variation in sound pressure can arise from many different combinations of initiating mechanical force, resonant properties of the body or bodies acted on, and qualities of the medium and structural environment intervening between the source and the listener. Even though the physical sources of sound stimuli are not specified by the sound pressure variations at the receptor surface, it is these sources that the auditory brain must decipher to generate successful behavior. This fundamental problem suggests that the auditory system, like the visual system, may generate percepts statistically (i.e., based on the relative number of times different possible sources have been associated with a particular stimulus in the history of the species and the individual).

The hypothesis examined here is therefore that tonal percepts and the musical universals that characterize this aspect of auditory perception are determined by the statistical relationship between periodic sound stimuli at the ear and their possible sources. Because this statistical linkage derives from the structure of naturally occurring periodic sound stimuli, the widely shared aspects of music perception such as musical scale intervals and consonance ordering should be predicted by the statistical structure of the periodic stimuli to which human beings have always been exposed. Although periodic sound energy derives from many different natural sources, including nonhuman animal calls (Fletcher, 1992) and circumstances in which mechanical forces generate periodic stimuli (e.g., “blowholes” or other resonant structures that occasionally produce periodic sounds from the action of wind or water), human vocalization is a principal source of periodic sound energy to which human beings have been chronically exposed over both evolutionary and individual time. Accordingly, speech sounds provide a first approximation of the universe of tone-evoking stimuli for humans. We therefore examined a database of recorded human speech to ask whether the relative likelihood of different amplitude-frequency combinations in these utterances predicts the phenomenology of musical scale structure and consonance ordering.

Materials and Methods

The primary source of speech sounds we analyzed was the Texas Instruments/Massachusetts Institute of Technology (TIMIT) Acoustic-Phonetic Continuous Speech Corpus (Garofolo et al., 1990). This corpus, created for linguistics and telecommunications research, comprises 6300 utterances of brief sentences by native English speakers. The corpus was generated by having 441 male and 189 female speakers representing eight major dialect regions of the United States each utter the same set of 10 sentences (Garofolo et al., 1990). Technical specifications regarding the selection of speakers, construction of the sentence list, recording conditions, and signal processing can be found in Fisher et al. (1986) and Lamel et al. (1986) or obtained from the Linguistic Data Consortium at the University of Pennsylvania (http://www.ldc.upenn.edu/). To ensure that any conclusions reached on the basis of the TIMIT analysis were not dependent on the specific features of English or any particular language, we also analyzed the Oregon Graduate Institute of Science and Technology (OGI) Multi-language Telephone Speech Corpus (Muthusamy et al., 1992). This second corpus comprises ∼1000 utterances in Farsi, French, German, Hindi, Japanese, Korean, Mandarin Chinese, Spanish, Tamil, and Vietnamese, respectively.

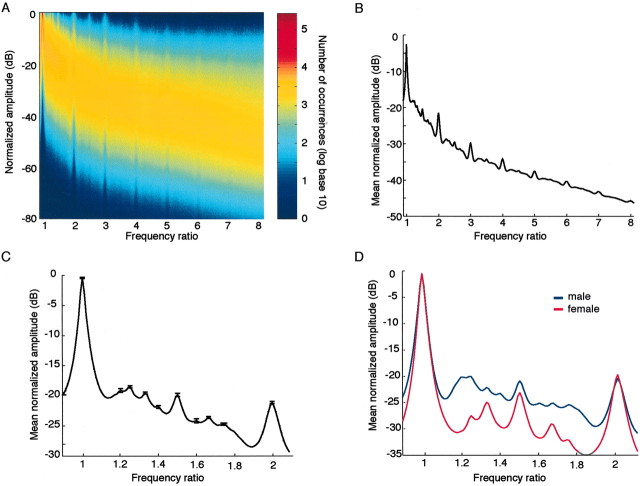
Figure 1 A shows the change in sound pressure over time for a representative spoken sentence in the TIMIT corpus. For each speaker, we randomly sampled 40, 0.1 sec speech sounds from each of the 10 utterances. To avoid silent intervals, segments in which the maximum amplitude was <5% of the maximum amplitude in the utterance as a whole were excluded, eliminating ∼8% of the initial sample. A discrete fast Fourier transform (Nyquist frequency, 8000) was applied to each of the remaining segments. To identify patterns of spectral energy common to the large number of individual spectra in the corpus, these data were normalized by expressing all amplitude and frequency values in a given spectrum as ratios with respect to the amplitude maximum of the spectrum and the frequency at that maximum. Thus, the abscissa and ordinate in Figures 2 and 4 are, respectively, F_n = F/F_m and A_n = A/A_m, where A_m and F_m are the maximum amplitude and its associated frequency. A and F are any given amplitude and frequency values in the spectrum, and A_n and F_n are the normalized values. This method of normalization avoids any assumptions about the structure of human speech sounds, e.g., that such sounds should be conceptualized in terms of ideal harmonic series.

Figure 1.

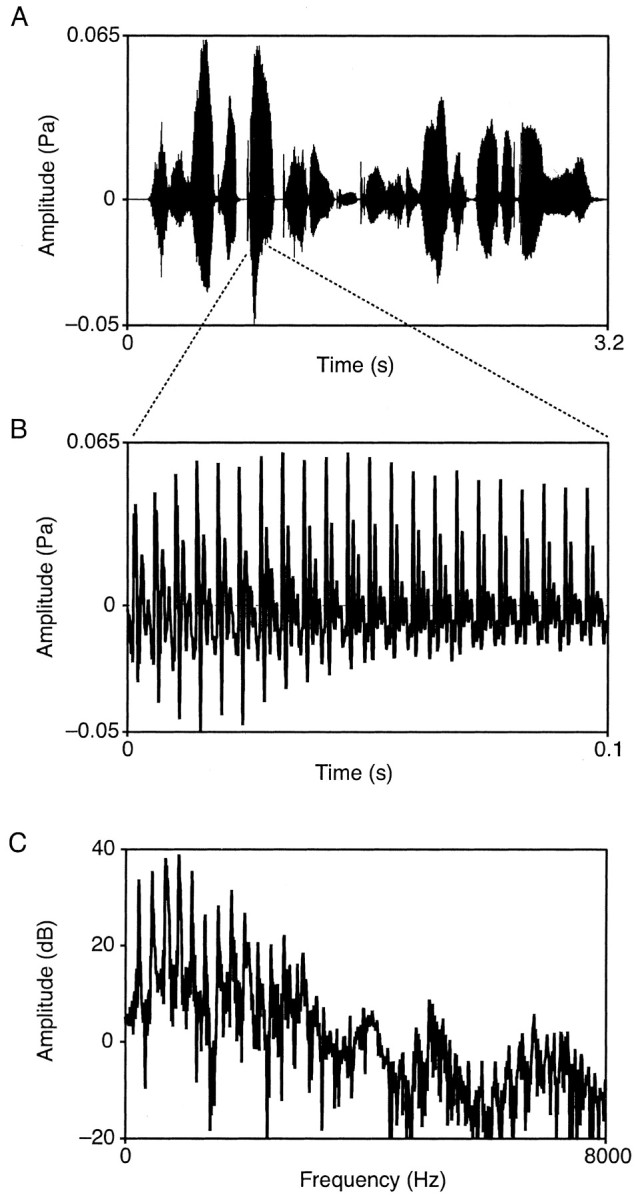
Analysis of speech segments. A, Variation of sound pressure level over time for a representative utterance from the TIMIT corpus (the sentence in this example is “She had your dark suit in greasy wash water all year”). B, Blowup of a 0.1 sec segment extracted from the utterance(in this example the vowel sound in“dark”). C, The spectrum of the extracted segment in B, generated by application of a fast Fourier transform.

Figure 2.

Statistical characteristics of spoken American English based on an analysis of the spectra extracted from the >100,000 segments (200 per speaker) in the TIMIT corpus. Mean normalized amplitude is plotted as a function of normalized frequency, the maxima indicating the normalized frequencies at which power tends to be concentrated. A, The normalized probability distribution of amplitude-frequency combinations for the frequency ratio range 1-8. B, Mean normalized amplitude plotted as a function of normalized frequency over the same range. C, Blowup of the plot in B for the octave interval bounded by the frequency ratios 1 and 2. Error bars show the 95% confidence interval of the mean at each local maximum. D, The plot in C shown separately for male (blue) and female (red) speakers.

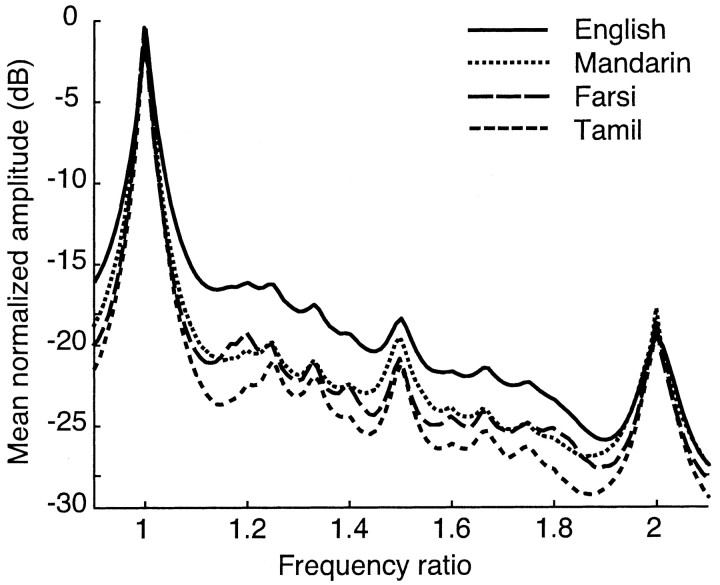
Figure 4.

Statistical structure of speech sounds in Farsi, Mandarin Chinese, and Tamil, plotted as in Figure 2 (American English is included for comparison). The functions differ somewhat in average amplitude, but are remarkably similar both in the frequency ratios at which amplitude peaks occur, and the relative heights of these peaks.

For each speaker, a probability distribution of amplitude-frequency pairs was generated by summing the number of occurrences of all possible amplitude-frequency combinations in the randomly sampled speech sounds; a normalized spectrum for the speaker was then obtained by taking the average amplitude at a given frequency ratio. The normalized spectrum for the corpus as a whole was generated by plotting the group mean amplitude values for all 630 individual speakers at each frequency ratio value. The functions in Figure 2 thus represent the relative concentration of sound energy at different frequency ratios relative to the maximum amplitude of a spectrum in the stimuli generated by spoken American English. The same procedure was used to generate normalized spectra for the other languages studied, except that the OGI data were not analyzed by individual speaker. File conversion and acoustic analyses were performed using Praat (Boersma and Weenink, 2001) and Matlab (Mathworks, 1996) software running on a Macintosh G4 computer.

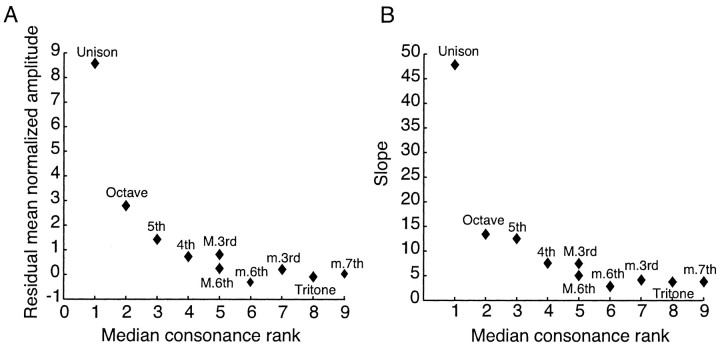
The robustness of the relative consonance rankings across the seven different empirical studies reviewed in Malmberg (1918) was assessed by reliability analysis, in which we treated each musical interval as an item and each of the studies as a measure (see Fig. 7). To quantify the relative concentration of power at each of the maxima in the normalized spectrum, we performed regression analysis and obtained the residual mean normalized amplitude values at each maximum from a logarithmic function fit to the data (r² = 0.97). A second measure of power concentration was obtained by calculating the slope of each local maximum.

Figure 7.

Consonance rankings predicted from the normalized spectrum of speech sounds. A, Median consonance rank of musical intervals (from Fig. 6) plotted against the residual mean normalized amplitude at different frequency ratios. B, Median consonance rank plotted against the average slope of each local maximum. By either index, consonance rank decreases progressively as the relative concentration of power at the corresponding maxima in the normalized speech sound spectrum decreases.

Results

The statistical structure of American English speech sounds

Figure 2A shows the probability distribution of amplitude-frequency pairs in the speech sounds sampled from the TIMIT corpus over three octaves; the mean amplitude values over this same range are shown in Figure 2B. The blowup of the normalized spectrum over the single octave range 1-2 in Figure 2C shows statistical concentrations of power not only at integer multiples of the global maximum, as would be expected for any set of periodic stimuli, but also at frequency ratios that are not simply integer multiples of the maximum. Figure 2D shows this portion of the spectrum separately for male and female speakers. The variation in the normalized amplitude values is least at frequency ratios where power is concentrated for both male and female utterances (e.g., 2.0, 1.5) and greatest at frequency ratios where only male utterances show concentrations of power (e.g., 1.4, 1.6; see below).

The structure of the normalized data in Figure 2 is a direct consequence of the acoustics of human vocalization. In physical terms, the human vocal apparatus has been modeled as a source and filter (Lieberman and Blumstein, 1988; Stevens, 1999). During voiced speech, air expelled from the lungs drives the laryngeal folds into sustained harmonic oscillation, which generates a roughly triangular sound pressure wave that is approximately periodic over short time intervals (Ladefoged, 1962). This complex waveform has maximum power at the fundamental frequency of the laryngeal oscillation, and a rich set of overtones at frequency values approximating integer multiples (i.e., harmonics) of the fundamental. The power in the spectrum of the waveform decreases exponentially with increasing frequency, such that the power at harmonic number n is equal to 1/n² the power at the fundamental, accounting for the exponential decrease in mean amplitude as a function of frequency apparent in Figure 2.

As the sound pressure wave generated at the larynx propagates through the vocal tract, it is modified (filtered) by the natural resonances of the tract. The frequency values of these resonances are determined by both the length and shape of the vocal tract, and it is at these resonance frequencies (called formants) that the power of the laryngeal pressure wave will be least attenuated. Whereas the shape of the vocal tract varies for differeent speech sounds, the length of the vocal tract for a given speaker is relatively fixed. Consequently, the resonance related to tract length is the most influential feature of the vocal tract in determining the statistical spectrum of speech sounds.

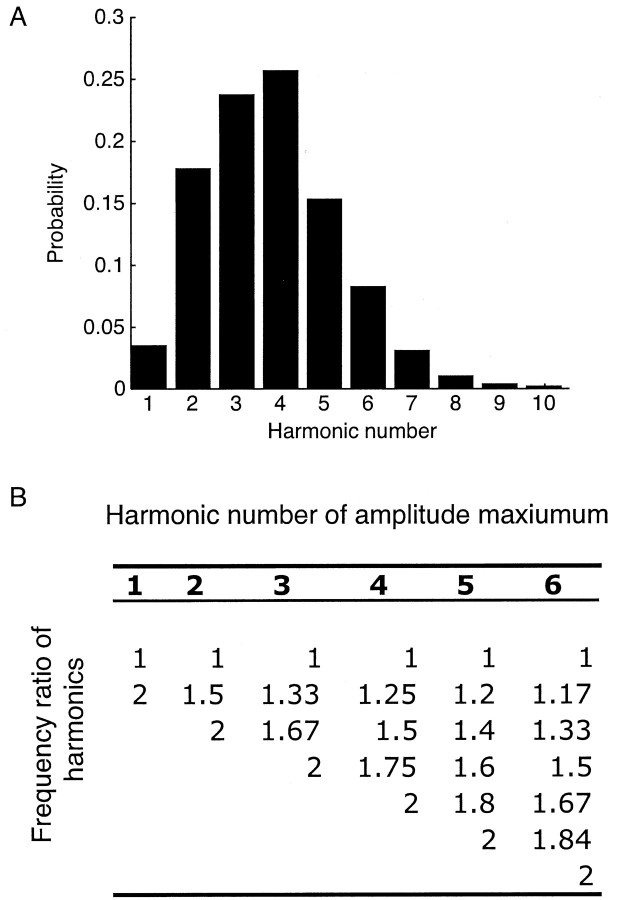
For an ideal pipe closed at one end and measuring 17 cm (the approximate length of the vocal tract in adult human males), resonances occur at 500 Hz, and its odd harmonics (e.g., 1500 Hz, 2500 Hz, etc.). The human vocal tract is not, of course, an ideal pipe of this length, and the frequencies of the primary resonance in voiced speech sounds range from ∼340 -1000 Hz (Hillenbrand et al., 1995). Considering the vocal tract as an ideal pipe, however, is a useful simplification here: given that the power of the complex sound signal generated by the laryngeal source decreases with increasing frequency, the spectral component of the waveform having frequency in this neighborhood (or somewhat higher for female and juvenile speakers) will typically be the frequency associated with much of the power in any speech sound. Thus, for a male utterance having a fundamental frequency of 100 Hz, for example, the fifth harmonic is likely to be the frequency at which power is concentrated in the spectrum of that utterance (because the harmonics at or near 500 Hz are likely to be least attenuated). Similarly, for a female utterance having a fundamental frequency of 250 Hz, the second harmonic will tend to be the frequency at which the amplitude in the vocal spectrum is greatest. Because the fundamental frequency of most adult human utterances lies between 100 and 250 Hz (Stevens, 1999), the frequency of the third or fourth harmonic should most often be the frequency at which the power is maximal in adult human utterances; conversely, power maxima at harmonic numbers less than two or greater than five will be relatively rare. The empirical distribution of amplitude maxima plotted according to harmonic number for the speech sound spectra in the TIMIT corpus accords with this general analysis (Fig. 3A).

Figure 3.

Probability distribution of the harmonic number at which the maximum amplitude occurs in speech sound spectra derived from the TIMIT corpus. A, The distribution for the first 10 harmonics of the fundamental frequency of each spectrum. More than 75% of the amplitude maxima occur at harmonic numbers 2-5. B, The frequency ratio values at which power concentrations are expected within the frequency ratio range 1-2 (Fig. 2C) when the maximum amplitude in the spectrum of a periodic signal occurs at different harmonic numbers. There are no peaks in Figure 2 at intervals corresponding to the reciprocals of integers >6, reflecting the paucity of amplitude maxima at harmonic numbers >6 (A). See Materials and Methods for further explanation.

Figure 3B shows why the distribution of amplitude maxima in Figure 3A produces the statistical concentrations of power observed in Figure 2. If the maximum power in a given utterance were to occur at the fundamental frequency of the spectrum in question, additional peaks of power would be present at frequency ratios of 2, 3, 4,... n with respect to the maximum. Note that “peaks” refer to concentrations of power at integer multiples of the fundamental frequency of a speech sound, and not to the formants of the vocal tract (see above). If, however, the maximum amplitude were to be at the second harmonic, additional amplitude peaks would occur at frequency ratios of 1.5, 2, 2.5, etc., with respect to the fundamental. And, if the maximum amplitude were to occur at the third harmonic, additional amplitude peaks would be apparent at ratios of 1.33, 1.67, 2, etc. Therefore, in any normalized speech sound spectrum where frequency values are indexed to the value at the amplitude maximum, sound energy will tend to be concentrated at intervals equal to the reciprocal of the harmonic number of the amplitude maximum.

The distribution of amplitude maxima in speech sound spectra thus explains why power in human utterances analyzed in this way tends to be concentrated at frequency ratios that correspond to the reciprocals of 2, 3, 4, and 5, and not simply at integer multiples of the frequency at the maximum amplitude (as would be the case for complex periodic stimuli that have maximum power at the fundamental frequency). The important corollary for the present analysis is that the occurrence of amplitude maxima at the positions evident in Figure 2 follows directly from the empirically determined probability distribution of the harmonic numbers at which the maximum power tends to be concentrated in speech sounds (Fig. 3) and cannot be derived from any a priori analysis of an idealized harmonic series.

The statistical structure of speech sounds in other languages

Figure 4 shows the normalized spectrum for English together with corresponding analyses for speech sounds in Farsi, Mandarin Chinese, and Tamil (see Materials and Methods). Although the average amplitude differs somewhat across languages, the frequency ratio values at which amplitude maxima occur, as well as the relative prominence of these maxima, are remarkably consistent.

Thus, the relative concentration of power at different frequency ratios in the normalized spectrum of speech sounds is largely independent of the language spoken, as expected if these data are determined primarily by the physical acoustics of the larynx and vocal tract. It is reasonable to suppose, therefore, that the statistical structure of speech sounds shown in Figures 2 and 4 is a universal feature of the human acoustical environment. By the same token, musical perceptions predicted by the normalized spectrum of the speech sounds in any particular language should apply to all human populations.

Rationalizing musical universals on the basis of speech sound statistics

The widely shared phenomena in musical perception that require explanation in terms of the probabilistic relationship of auditory stimuli and their sources are: (1) the partitioning of the continuous dimension of pitch into the iterated sets of 12 intervals that define the chromatic scale; (2) the preferential use of particular subsets of these intervals in musical composition and performance; and (3) similar consonance ordering of chromatic scale tone combinations across human populations.

The chromatic scale

All musical traditions employ a relatively small set of tonal intervals for composition and performance, each interval being defined by its relationship to the lowest tone of the set. Such sets are called musical scales. Despite some interesting variations such as the pélog scale used by Gamelan orchestras in Indonesia whose metallophone instruments generate nonharmonic overtones, the scales predominantly used in all cultures over the centuries have used some (or occasionally all) of the 12 tonal intervals that in Western musical terminology are referred to as the chromatic scale (Nettl, 1956; Carterette and Kendall, 1999). There is at present no explanation for this widely shared tendency to use these particular tones for the composition and performance of music from among all the possible intervals within any given octave.

Figure 5A shows the frequency ratio values of the nine peaks that are apparent in the spectra of all four languages illustrated in Figures 2 and 4. As indicated, the local amplitude maxima within any octave in the normalized spectrum of speech sounds occur at frequency ratios corresponding to intervals of the chromatic scale. For any of the three tuning systems that have been used over the centuries, the frequency ratios that define the octave, fifth, fourth, major third, major sixth, minor third, minor seventh, minor sixth, and tritone fall on or very close to the relative frequency values of the mean amplitude maxima in the normalized spectrum of human speech sounds (Fig. 5B). The remaining intervals of the chromatic scale, the major second, the major seventh, and the minor second, are not apparent as peaks within frequency ratio range 1-2. Within the octave interval defined by the normalized frequency ratio range of 2-4, however, the spectral peaks at frequency intervals of 2.25 and 3.75 correspond in this higher octave to the frequency ratios that define the major second (1.125) and the major seventh (1.875) in the lower octave. Only the frequency ratio of the minor second (1.067) has no apparent peak in the statistical analysis we have done. Recall that these concentrations of power cannot be derived from an ideal vibrating source, but are specific empirical attributes of sound stimuli generated by the human vocal tract.

Figure 5.

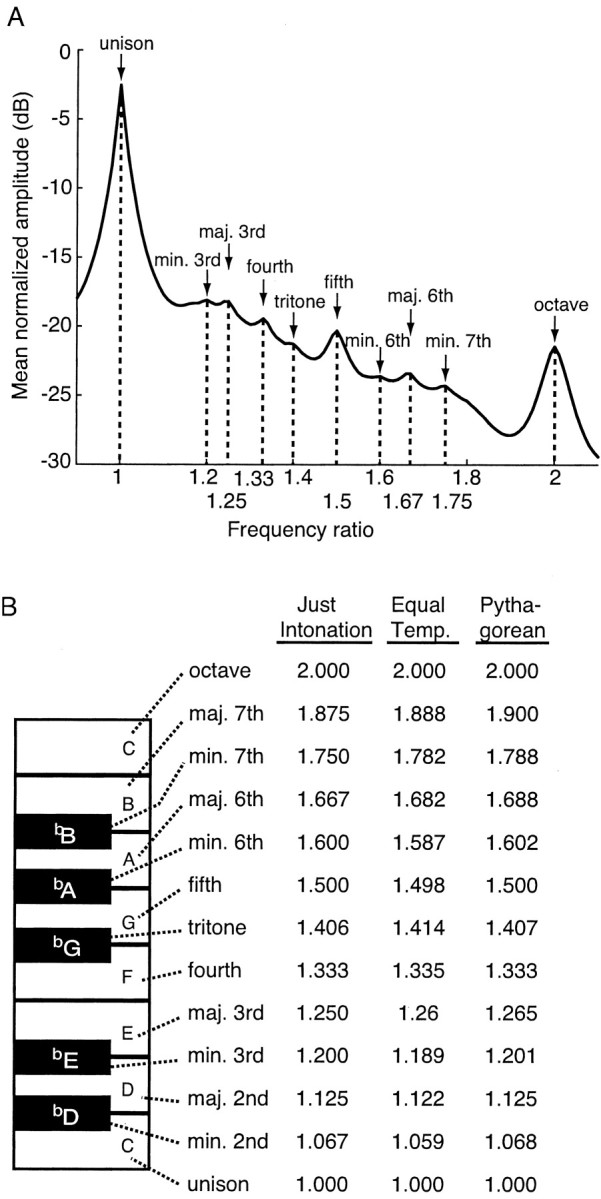
Comparison of the normalized spectrum of human speech sounds and the intervals of the chromatic scale. A, The majority of the musical intervals of the chromatic scale (arrows) correspond to the mean amplitude peaks in the normalized spectrum of human speech sounds, shown here over a single octave (Fig. 2C). The names of the musical intervals and the frequency ratios corresponding to each peak are indicated. B, A portion of a piano keyboard indicating the chromatic scale tones over one octave, their names, and their frequency ratios with respect to the tonic in the three major tuning systems that have been used in Western music. The frequency ratios at the local maxima in A closely match the frequency ratios that define the chromatic scale intervals.

The fact that the frequency ratios that define most of the 12 intervals of the chromatic scale correspond to the empirical concentrations of power in human speech sounds supports the hypothesis that the chromatic scale arises from the statistical structure of tone-evoking stimuli for human listeners.

The preferred use of particular intervals in the chromatic scale

Some intervals of the chromatic scale, such as the octave, the fifth, the fourth, the major third, and the major sixth, are more often used in composition and performance than others (Budge, 1943; Youngblood, 1958; Knopoff and Hutchinson, 1983). These, along with the major second, form the intervals used in the pentatonic scale, and the majority of the seven intervals in a diatonic major scale, the two most frequently used scales in music worldwide (Carterette and Kendall, 1999).

The preference for these particular intervals among all the possible intervals in the chromatic scale is also predicted by the normalized spectrum of human speech sounds illustrated in Figures 2 and 4. As is apparent in Figure 5, the frequency ratios that define the octave, fifth, fourth, major third, and major sixth are those that, among the ratios that define the 12 chromatic scale tones within an octave, correspond to the five greatest statistical concentrations of power in the signals generated by human utterances (see also next section).

The fact that the most frequently used musical intervals correspond to the greatest concentrations of power in the normalized spectrum of human speech sounds again supports the hypothesis that musical percepts reflect a statistical process by which the human auditory system links ambiguous sound stimuli to their physical sources.

Consonance and dissonance

Perhaps the most fundamental question in music perception, and arguably the common denominator of all the musical phenomena considered here, is why certain combinations of tones are perceived as relatively consonant or “harmonious” and others as relatively dissonant or “inharmonious”. These perceived differences among the possible combinations of tones making up the chromatic scale are the basis for harmony in music composition. The more compatible of these combinations are typically used to convey “resolution” at the end of a musical phrase or piece, whereas less compatible combinations are used to indicate a transition, a lack of resolution, or to introduce a sense of tension in a chord or melodic sequence.

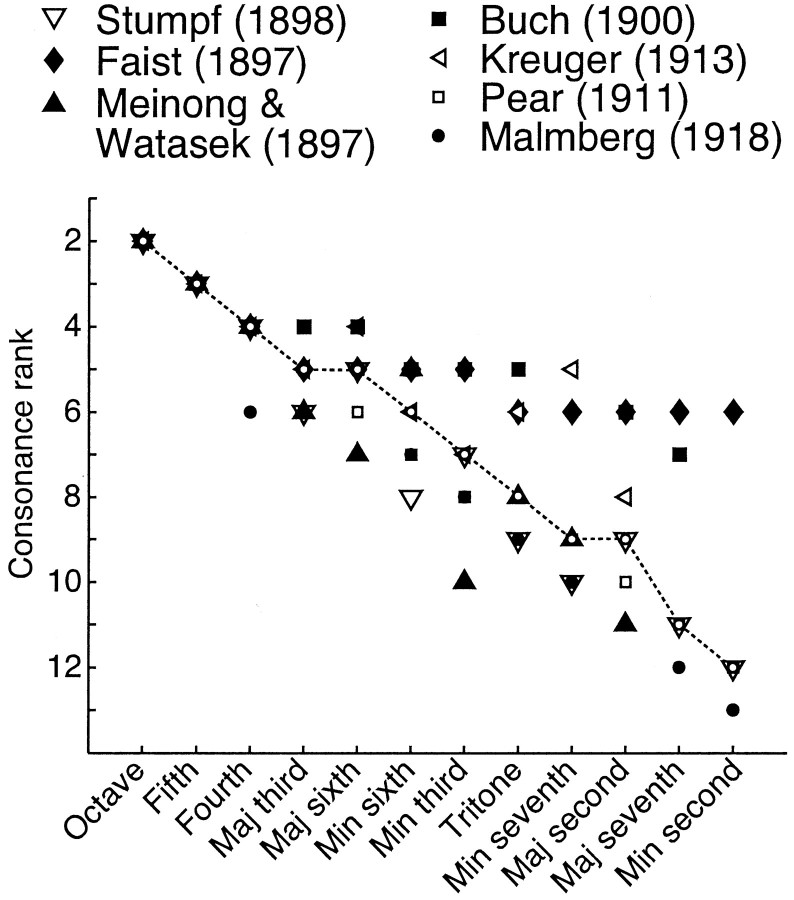
Malmberg (1918) has provided the most complete data about this perceptual ordering, based on seven psychophysical studies of some or all of the 12 combinations of simultaneously sounded chromatic scale tones (Fig. 6) (Kameoka and Kuriyagawa, 1969; Hutchinson and Knopoff, 1978; Krumhansl, 1990; Huron, 1994). Although 72 combinations of the tones in the chromatic scale are possible, others are redundant with the 12 combinations tested. There is a broad agreement across these studies about the relative consonance of a given tone combination, the concordance being greater for combinations rated high in consonance than for the combinations rated low. The coefficient of reliability of the several rankings shown in Figure 6 (Cronbach's α) is 0.97.

Figure 6.

Consonance ranking of chromatic scale tone combinations (dyads) in the seven psychophysical studies reported by Malmberg (1918), Faist (1897), Meinong and Witasek (1897), Stumpf (1898), Buch (1900), Pear (1911), and Kreuger (1913). Graph shows the consonance rank assigned each of the 12 chromatic dyads in the various studies reported. The median values are indicated by open circles connected by a dashed line.

To examine whether consonance ordering is also predicted by the statistical relationship between tone-evoking stimuli and their generative vocal sources, we compared the consonance ranking of chromatic scale tone combinations to the relative concentrations of power in human speech sounds at the frequency ratios that define the respective chromatic scale tone combinations (i.e., musical dyads) (Fig. 7). The two measures of power concentration used were the residual amplitude at each local maximum in Figure 2C (Fig. 7A) and the slopes of these local peaks (Fig. 7B). The Spearman rank-order correlation coefficient for the data plotted in Figure 7A is r_s =-0.91 (t [8] =-6.05; p < 0.001); for the data plotted in Figure 7B, r_s = -0.89 (t[8] = -5.45; p < .001). For the nine maxima evident in the octave range 1-2, both metrics show that the relative concentration of power in human speech sounds at a particular frequency ratio matches the relative consonance of musical dyads. The absence of maxima corresponding to the major second, major seventh, and minor second in Figure 5A predicts that these intervals should be judged the least consonant of the 12 possible chromatic scale tone combinations, as indeed they are (Fig. 6).

This evidence that consonance ordering is also predicted by the statistical structure of human speech sounds further supports the hypothesis that musical universals reflect a probabilistic process underlying the perception of periodic auditory stimuli.

Discussion

The results of these analyses show that the statistical acoustics of human speech sounds successfully predict several widely shared aspects of music and tone perception. Here we consider earlier explanations of these phenomena in relation to the evidence in the present report and the implications of our results for further studies of auditory processing.

Earlier explanations of these musical phenomena

Explanations of consonance and related aspects of scale structure put forward by previous investigators fall into two general categories: psychoacoustical theories and pattern recognition theories (Burns, 1999). The inspiration for both lines of thought can be traced back to Pythagoras, who, according to ancient sources, demonstrated that the musical intervals corresponding to octaves, fifths, and fourths in modern musical terminology are produced by physical sources whose relative proportions (e.g., the relative lengths of two plucked strings) have ratios of 2:1, 3:2, or 4:3, respectively (Gorman, 1979; Iamblichus, c.300/1989). This coincidence of numerical simplicity and perceptual effect is so impressive that attempts to rationalize phenomena such as consonance and scale structure solely in terms of mathematical or geometrical relationships have continued to the present day (Balzano, 1980; Janata et al., 2002).

These long recognized mathematical relationships are explicitly the foundation for modern psychoacoustical theories of consonance. Hemholtz (1877/1954), the most vigorous exponent of this approach to the problem in the nineteenth century, attempted to provide a physical basis for Pythagoras's observation by explaining consonance in terms of the ratio between the periods of two complex acoustical stimuli. In his view, consonance was simply the absence of the low frequency amplitude modulations that occur when the spectral components of two musical tones are close enough in frequency to generate destructive interference (i.e., when the two tones are within each other's “critical band”). When such interference occurs, listeners perceive “beating” or “roughness”, which Helmholtz (1877/1954) took to be the signature of dissonance. More recent investigators have refined this general idea (Plomp and Levelt, 1965; Pierce, 1966, 1983; Kameoka and Kuriyagawa, 1969), and have explored how such effects might arise from the mechanics of the cochlea (von Bekesy, 1962).

Pattern recognition theories (Goldstein, 1973; Terhardt, 1974) were proposed primarily to explain observations inconsistent with psychoacoustical models. These discrepancies include the perception of dissonance in the absence of physical beating (recognized by Preyer as early as 1879) and the persistence of dissonance when the two tones of a dyad are presented dichotically (i.e., one tone to each ear) (Houtsma and Goldstein, 1972). Pattern recognition theories, however, like the psychoacoustical models they sought to improve on, also focus on the numerical relationships among the frequency values of idealized tone combinations. Terhardt (1974), for instance, proposed that the perception of musical intervals derives from the familiarity of the auditory system with the “specific pitch relations” among the frequencies of the lower harmonics of complex tones.

A few authors working within this general framework have noted that amplitude relationships among the frequency components of tone-evoking stimuli might also have some influence in determining consonance. For example, Kameoka and Kuriyagawa (1969) reported that the relative consonance of tone combinations depends in part on the degree and direction of the sound pressure level difference between the tones in a dyad. More recently, Sethares (1998) also suggested that consonance depends in part on the amplitudes of the frequency components of a complex tone (“timbre” in his usage), and that the relative consonance of almost any musical interval varies as a function of these relationships. An awareness that consonance depends on the distribution of power as well as on frequency relationships in the stimulus did not, however, lead these authors to suggest a fundamental revision of the traditional approaches to explaining music perception. Both Kameoka and Kuriyagawa (1969) and Sethares (1998), for example, explicitly espouse the psychoacoustical theory that the overall consonance of a musical interval is a function of the physical interaction or “local consonance” among the sinusoidal components of the complex tones defining the interval.

Musical universals and the statistical structure of speech sounds

A different approach to understanding these musical phenomena, and perhaps audition in general, is suggested by the inevitably uncertain nature of the stimulus-source relationship. Auditory stimuli, like visual stimuli, are inherently ambiguous: the physical characteristics of the stimulus at the ear do not, and cannot, specify the physical properties of the generative source (Gordon et al., 1992; Hogden et al., 1996). Nevertheless it is toward the stimulus sources that behavior must be directed if auditory, or indeed any, percepts are to be biologically useful. Thus, the physical similarities and differences among the sources of stimuli must somehow be preserved in a corresponding “perceptual space”.

A wide range of recent work in vision is consistent with the hypothesis that the visual system meets the challenge of stimulus ambiguity by relating stimuli to their possible sources and constructing the corresponding perceptual spaces for lightness, color, form, and motion probabilistically (Knill and Richards, 1996; Purves et al., 2001; Rao et al., 2002; Purves and Lotto, 2003). By generating percepts determined according to the statistical distribution of possible stimulus sources previously encountered rather than by the physical properties of the stimuli as such, the perceiver brings the lessons derived from the success or failure of individual and ancestral behavior to bear on the quandary of stimulus ambiguity. The fact that musical scale structure, the preferred subsets of chromatic scale intervals, and consonance ordering all can be predicted from the distribution of amplitude-frequency pairings in speech sounds suggests this same probabilistic process underlies the tonal aspects of music.

The biological rationale for generating auditory percepts probabilistically is thus the same as the rationale for this sort of process in vision, namely, to guide biologically successful behavior in response to inherently ambiguous stimuli. In the case of tone-evoking stimuli, this way of generating percepts would enable listeners to respond appropriately to the biologically significant sources of the information embedded in human vocalization. This information includes not only the distinctions among different speech sounds that are important for understanding spoken language, but also indexical information such as the probable sex, age, and emotional state of the speaker. Indeed, the hedonic aspects of musical percepts may also be rooted in probabilities. Unlike pitch, which is more or less affectively neutral, tone combinations judged to be consonant are “preferred” over dissonant combinations (Butler and Daston, 1968). Such preferences may reflect the relative probability of different amplitude-frequency combinations in the human acoustical environment (Zajonc, 1968, 2001).

Neural correlates

How the statistical structure of acoustic stimuli is instantiated in the auditory nervous system to achieve these biological advantages is, of course, an entirely open question. Perhaps the most relevant physiological observation is a recent study of the responses of cat auditory neurons to dyads that human listeners rank as consonant (a perfect fifth or a perfect fourth) compared with dyads that listeners deem relatively dissonant (a tritone or a minor second) (Tramo et al., 2001). Autocorrelation of the spike trains elicited by such stimuli mirrors the autocorrelation of the acoustic stimulus itself; moreover, the characteristics of the population interspike interval correctly predict the relative consonance of these four musical intervals.

Another pertinent observation is that the cat inferior colliculus is tonotopically organized into laminas exhibiting constant frequency ratios between corresponding locations in adjacent layers (Schreiner and Langner, 1997). The authors suggest that reciprocal lateral inhibition between neighboring laminas might be the anatomical basis of the “critical band” phenomenon apparent in psychoacoustical studies (Moore, 1995). It has also been suggested that the architecture of the inferior colliculus in the cat is an adaptation for the extraction of the fundamental frequency of complex naturally occurring sounds and that perceptions of consonance and dissonance might be a consequence of this functional organization (Braun, 1999).

To the extent that these physiological findings can be generalized to the organization of the human auditory system, the dynamical representation of neuronal firing patterns and/or the laminar structure of the colliculus could embody some aspects of the statistical structure of acoustic stimuli, but this remains a matter of speculation. The implication of the present results is that one important aspect of the enormously complex neuronal circuitry underlying the appreciation of music by human beings may be best rationalized in terms of the statistical link between periodic stimuli and their physical sources.

The evidence presented here is consistent with the hypothesis that musical scale structure and consonance ordering derive from the necessarily statistical relationship between sensory stimuli and their physical sources. Generating perceptual responses to ambiguous periodic stimuli on this statistical basis takes the full complement of the stimulus characteristics into account, thus facilitating a listener's ability to glean biologically significant information about the sources of periodic sound energy, human speakers in particular. Finally, this conceptual framework for understanding the major features of tonal music allows audition and vision to be considered in the same general terms.