Abstract
During ischemia, the transport of molecules in the extracellular space (ECS) is obstructed in comparison with healthy brain tissue, but the cause is unknown. Extracellular tortuosity (λ), normally 1.6, increases to 1.9 in ischemic thick brain slices (1000 μm), but drops to 1.5 when 70,000 Mr dextran (dex70) is added to the tissue as a background macromolecule. We hypothesized that the ischemic increase in λ arises from diffusion delays in newly formed dead-space microdomains of the ECS. Accordingly, λ decreases when dead-space diffusion is eliminated by trapping dex70 in these microdomains. We tested our hypothesis by analyzing the diffusion of several molecules in neocortical slices. First we showed that diffusion of fluorescent dex70 in thick slices declined over time, indicating the entrapment of background macromolecules. Next, we measured diffusion of tetramethylammonium (TMA+) (74 Mr) to show that the reduction of λ depended on the size of the background macromolecule. The synthetic polymer, 40,000 Mr polyvinylpyrrolidone, reduced λ in thick slices, whereas 10,000 Mr dextran did not. The dex70 was also effective in normoxic slices (400 μm) after hypoosmotic stress altered the ECS to mimic ischemia. Finally, the dex70 effect was confirmed independently of TMA+ using fluorescent 3000 Mr dextran as a diffusion marker in thick slices: λ decreased from 3.29 to 2.44. Taken together, these data support our hypothesis and offer a novel explanation for the origin of the large λ observed in ischemic brain. A semiquantitative model of dead-space diffusion corroborates this new interpretation of λ
Keywords: extracellular space, diffusion, tortuosity, volume fraction, background macromolecules, ischemia, dwell-time diffusion model
Introduction
Brain extracellular space (ECS) is essential for intercellular communication (Nicholson, 1979), nutrient and metabolite trafficking (Fellows et al., 1992), and delivery of drugs (Ulbrich et al., 1997; Saltzman, 2001). The distribution of many molecules is governed by the diffusion properties of the ECS. These properties are well characterized on the macroscopic level (Nicholson and Syková, 1998; Nicholson, 2001), where a representative elementary volume may include hundreds or thousands of cells. It remains unknown whether ECS properties vary locally, on a scale comparable with the size of a few cells. This question is important because microscopic heterogeneity could imply existence of microdomains in the ECS with distinct physiological characteristics. Here we used a novel experimental approach to alter ECS structure by adding extrinsic macromolecules to the tissue to form an artificial background. Diffusion of small markers was then exploited to measure the ECS parameters. We found that dead-space microdomains are formed in the brain during ischemia and that they retard extracellular diffusion.
Two structural parameters, tortuosity (λ) and volume fraction (α), determine the macroscopic diffusion properties of the ECS. Tortuosity quantifies the hindrance imposed on the diffusion process by the tissue in comparison with an obstacle-free medium. Tortuosity is defined as (D/D*)1/2, where D is the free diffusion coefficient and D* is the effective diffusion coefficient in brain (Nicholson and Phillips, 1981; Nicholson, 2001). The volume fraction is simply the proportion of tissue volume occupied by the ECS. In a healthy brain, λ ≈ 1.6 and α ≈ 0.2, but during ischemia λ increases to ≈2.0 and α decreases to 0.05-0.10 (Lehmenkühler et al., 1993; Pérez-Pinzón et al., 1995; Vor̆ís̆ek and Syková, 1997; Hrabětová et al., 2002). This well established behavior was challenged by Patlak et al. (1998), who used radiotracers to measure λ values as low as 1.2 in a thick slice (1000 μm) model of ischemia. These paradoxical results were reconciled when we found that 70,000 Mr dextran (dex70), routinely added as a background macromolecule by Patlak et al. (1998), caused λ, measured with tetramethylammonium (TMA+), to drop from 2.0 to 1.5 and reduced α from 0.12 to 0.10 (Hrabětová and Nicholson, 2000); however, the mechanism of the reduction remained unclear.
Two interrelated questions arise that have fundamental implications for our understanding of brain dysfunction in ischemia. How is λ increased in ischemia, and how do the background macromolecules lower it? Our hypothesis is shown schematically in Figure 1. During ischemia, swelling cells form blockages in the intercellular gaps, and some dead-end pores might be created. Diffusing markers become delayed after entering such dead-space microdomains and this increases λ, but when bulky macromolecules are selectively trapped in the dead spaces, these spaces are effectively eliminated, causing both λ and α to decrease.
Figure 1.
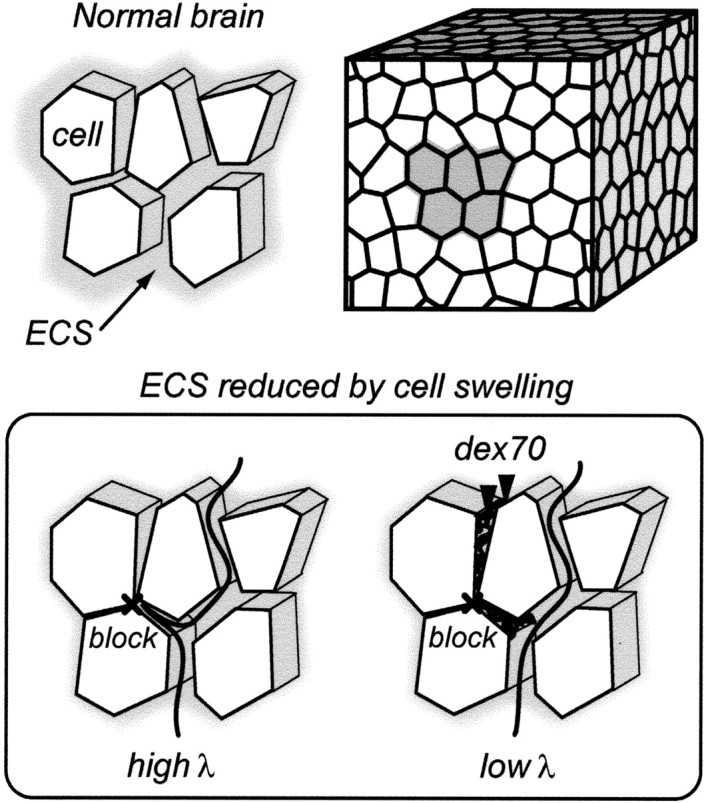
Background macromolecules exclude dead-space diffusion: a hypothesis. Brain tissue is composed of cells surrounded by a thin layer of the ECS. Because the interstitial spaces are interconnected, they form a system of channels where signaling molecules and substances diffuse (top). During ischemia and other pathological conditions, cellular elements expand their volume as water moves from the extracellular to the cellular compartment, and blockages are formed in some interstitial planes. Diffusing molecules that enter these pocket-like regions are delayed and tortuosity increases (bottom left). When background macromolecules, such as dex70, are added to this tissue, they become trapped in the dead spaces. By excluding the dead-space volume, dex70 prevents marker molecules from being delayed there, and tortuosity decreases (bottom right). See the mathematical model in Materials and Methods for more detail.
This hypothesis was supported by experiments that demonstrated the following: (1) dex70 did become trapped in ischemic tissue, (2) the reduction of λ and α depended on size of background macromolecule, (3) dex70 was effective even in normoxic tissue when hypoosmotic stress elevated λ and diminished α, and (4) effects of dex70 were independent of the diffusion marker and method of measurement. The interpretation of the results was further supported by a simple model of tortuosity on the basis of diffusion dwell-times.
Materials and Methods
Rat brain slices. All experiments were conducted at New York University School of Medicine in accordance with National Institutes of Health guidelines and local Institutional Animal Care and Use Committee regulations. Neocortical brain slices were prepared from adult Sprague Dawley female rats (200-250 gm) as described previously (Rice and Nicholson, 1991; Pérez-Pinzón et al., 1995). The animals were anesthetized with sodium pentobarbital (65 mg/kg, i.p.) and then decapitated with a guillotine. The brain was extracted from the skull and cooled with ice-cold artificial CSF (ACSF). Coronal sections of 1000 and 400 μm thickness were cut using a vibrating blade microtome (VT 1000 S; Leica Instrument GmbH, Nuβloch, Germany). The slices were submerged in ACSF and incubated at room temperature. The composition of normal ACSF was as follows (in mm): 115 NaCl, 5 KCl, 35 NaHCO3, 1.25 NaH2PO4,10 d-glucose, 1.3 MgCl2, 1.5 CaCl2. The ACSF was gassed with 95% O2/5% CO2 to buffer pH at 7.4. For TMA+ diffusion measurements, 0.5 mm TMA+ chloride was added to the ACSF to provide a calibration standard. The macromolecules [dex70 (catalog #D-1390, Sigma, St. Louis, MO), 40,000 Mr polyvinylpyrrolidone (pvp40) (catalog #P-0930, Sigma), and 10,000 Mr dextran (dex10) (catalog # D-9260, Sigma)] were added to the ACSF to form an artificial background in the ECS. The background macromolecules were used at a concentration of 0.44 mm, which corresponds to 3.1% (w/v) of dex70, as used in previous studies (Patlak et al., 1998; Hrabětová and Nicholson, 2000).
For diffusion measurements, a brain slice was transferred to a submersion tissue chamber (model RC-27L; Warner Instruments, Hamden, CT) and superfused with ACSF at a flow rate of 2.0 ml/min. The temperature of the ACSF was maintained at 34 ± 1°C using an in-line heater (model SH-27A; Warner Instrument) in combination with a chamber heating system connected to a dual automatic temperature controller (model TC-344B; Warner Instrument). All recordings were made in neocortical layers III-VI.
Osmolality of ACSF. The osmolality of the ACSF was determined with a freezing point-depression osmometer (Osmette A #5002; Precision Systems, Natick, MA). A typical value of normal ACSF was 300 mOsm/kg. In experiments that involved hypoosmotic treatment of the tissue, the amount of NaCl was reduced to bring the osmolality of ACSF to 150 mOsm/kg.
When the background macromolecules were added to the ACSF, the average osmolalities were 306, 306, and 303 mOsm/kg in the presence of dex10, pvp40, and dex70, respectively. Because the freezing point-depression osmometer is not an optimal instrument to measure the osmotic pressure generated by macromolecules, we compared our values with the membrane osmometer measurements published at http:/aqueous.labs.brocu.ca/osfile.html (Parsegian et al., 1995). The published values for media containing 0.44 mm of 40,000 and 110,000 Mr dextrans were ≈1 and 2 mOsm/kg, respectively. It was similarly low for pvp40: ≈1 mOsm/kg (Parsegian et al., 1986). On the basis of these data and our own measurements of osmolality, we concluded that the addition of background macromolecules had only a negligible effect on the osmolality of ACSF.
Real-time iontophoretic method. In the real-time iontophoretic (RTI) method, charged marker is iontophoretically delivered from a microelectrode and detected by an ion-selective microelectrode (ISM) positioned ≈100 μm away from the source (Nicholson and Phillips, 1981). Because TMA+ (74 Mr) is most commonly used, this method is sometimes called the TMA method. Iontophoretic source microelectrodes and TMA+-ISMs were prepared from double-barreled theta glass (Warner Instruments) as described previously (Nicholson, 1993). Iontophoretic microelectrodes were filled with 150 mm TMA+ chloride, and a continuous positive bias current of 20 nA was applied from a constant-current, high-impedance source (model Axoprobe-A1 Amplifier; Axon Instruments, Union City, CA) to maintain a steady transport number (nt) (Nicholson and Phillips, 1981). For diffusion measurements, this current was stepped up to 40-100 nA for 50 sec.
The ion-detecting barrel of the TMA+-ISM was filled with 150 mm TMA+-chloride, and a tetraphenylborate-based exchanger (Corning exchanger 477317, currently available as IE 190 from WPI, Sarasota, FL) was used in the tip. The reference barrel, which detected the local DC potential, was filled with 150 mm NaCl. To extract the TMA+ signal, the potential of the reference barrel was subtracted continuously from the potential of the ion-detecting barrel using a dual-channel microelectrode preamplifier (model IX2-700; Dagan Corp., Minneapolis, MN). Each TMA+-ISM was calibrated in a set of standard solutions (0.5, 1, 2, 4, and 8 mm TMA+ in 150 mm NaCl). Calibration voltages were used to obtain the slope and the interference of the microelectrode by fitting the data to the Nikolsky equation (Nicholson, 1993).
The iontophoretic microelectrode and the TMA+-ISM were held in two separate robotic micromanipulators (MP 285; Sutter Instrument Co., Novato, CA), each microelectrode at an angle of 31° from the horizontal plane. The precision and stability of the micromanipulators ensured positioning accuracy over several hours of recording (Hrabětová et al., 2002). The recorded TMA+ signal and DC potential were amplified, low-pass filtered (6 Hz) using a CyberAmp 320 (Axon Instruments), and monitored continuously on a chart recorder. The TMA+ diffusion curves were digitized using an analog-to-digital converter (model PCIMIO-16E-4; National Instruments, Austin, TX) installed in a personal computer and saved using a LabView (National Instruments)-based program. An appropriate solution to the diffusion equation (Nicholson, 1993) was fitted to the diffusion curves using a Matlab (MathWorks, Natick, MA)-based program developed in-house. The free diffusion coefficient D cm2/sec, and the transport number nt of the iontophoretic micropipette were extracted from data obtained in dilute agarose gel (0.3% in 150 mm NaCl; NuSieve GTG, FMC BioProducts, Rockland, ME). Curve-fitting to recordings in the brain provided the effective diffusion coefficient D* cm2/sec and an amplitude value that were combined with D and nt to extract the tortuosity λ, volume fraction α, and a nonspecific clearance k′ sec-1. Nonspecific clearance quantifies loss of the TMA+ marker from the ECS (Nicholson, 1992, 2001).
Integrative optical imaging method. In the integrative optical imaging (IOI) method, a fluorophore-labeled marker molecule is pressure injected into the brain from a glass micropipette, and its distribution is measured using a compound microscope with a charge-couple device (CCD) camera (Nicholson and Tao, 1993; Tao and Nicholson, 1995). We used two fluorescent molecules: 3000 Mr dextran (fdex3) labeled with Texas Red (catalog #D-3329, Molecular Probes, Eugene, OR) and 70,000 Mr dextran (fdex70) labeled with fluorescein (catalog #FD-70S, Sigma). Each was dissolved in 150 mm NaCl to give a final concentration of 0.1-1 mm. Fluorescent dextran was injected into 0.3% (w/v) agarose gel or brain slice from a glass micropipette pulled from thin-wall glass tubing (catalog #6170, A-M System, Carlsborg, WA). The excitation light from a 75 W xenon source mounted on the epifluorescent port of an Olympus BX50WI compound microscope (Olympus America, Melville, NY) was directed to the slice using a dichroic mirror with either Texas Red or fluorescein filter set. The microscope was equipped with a water-immersion objective (Olympus, UMPlanFl; 10×, numerical aperture 0.3). The light emitted by diffusing fluorescent molecules was imaged at preset time intervals using a CCD camera (model CH350, Photometrics, Tucson, AZ) attached to the microscope. Both the injections and the image acquisition were controlled by V-Pascal-based software for Windows (Digital Optics, Auckland, New Zealand) installed on a personal computer.
The diffusion analysis of the acquired sets of images was performed using a Matlab-based program developed in-house. The details of the algorithm have been described previously (Nicholson and Tao, 1993; Prokopová-Kubinová et al., 2001). The program fits an appropriate solution of the diffusion equation to intensity curves obtained along the horizontal, vertical, and two diagonal lines running through the center of each image within a set. The resulting diffusion coefficient is based on linear regression using several time points over the entire acquisition period. This analysis was modified slightly for those IOI experiments designed to verify that the background molecules of dex70 became trapped in the ECS. Because D* was expected to change over time, the total acquisition period was subdivided into intervals of 4 min that were analyzed individually under the assumption that D* remained constant within each interval. To increase the data points available to estimate D* in each time interval, we fitted symmetrical Gaussian distributions to the entire two-dimensional (2D) data set instead of using one-dimensional profiles. The modification was implemented using an IDL (Research Systems, Bolder, CO)-based program.
The influence of background macromolecules on calculations of D and λ. We reported previously that addition of dex70 to a dilute agarose lowered D of TMA+ from 1.24 × 10-5 to 1.13 × 10-5 cm2/sec (Hrabětová and Nicholson, 2000). Here we measured a reduction in D for the fdex3 marker caused by the dex70 background macromolecule from 2.42 ± 0.02 × 10-6 cm2/sec (mean ± SEM, n = 32) to 1.93 ± 0.03 × 10-6 cm2/sec (n = 31) at 34°C. The choice of an appropriate D is critical for the calculation of λ. We estimated previously (Hrabětová and Nicholson, 2000) that a 4 hr preincubation period is sufficient to equilibrate [dex70]ECS with [dex70]bath in a 400 μm slice. In such slices, λ was calculated using the value of D measured in agarose gel with dex70 present. In a thick slice, however, the distribution of dex70 in the ECS may be nonuniform because of trapping (see Results). Therefore, the value of D measured in dex70-free agarose gel was used. This approach may underestimate the effect of background macromolecules on λ.
A simple tortuosity model based on diffusion dwell-time. As an aid to understanding the data, we developed a simple semiquantitative tortuosity model on the basis of a concept of the average dwell-time that the molecule spends in an ECS microdomain. The model predicts a relationship between λ and α in isotropic media that is consistent with the experimental data (see Results).
We neglect the contribution of extracellular matrix viscosity and consider diffusion in the narrow planar gaps between the cells, where the local diffusion is essentially 2D and can be described by (Einstein, 1956):
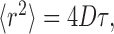 |
1 |
which implies that the mean square distance
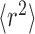 of a diffusing molecule from its initial position is proportional to the elapsed time τ. Equation 1 does not include any averaging process, and D is therefore a free diffusion coefficient.
of a diffusing molecule from its initial position is proportional to the elapsed time τ. Equation 1 does not include any averaging process, and D is therefore a free diffusion coefficient.
The microscopic averaging process in a complex medium introduces two macroscopic variables: the extracellular volume fraction α and the tortuosity λ measured in our experiments. The square of tortuosity, λ2, can be interpreted as a time scaling factor. This means that the macroscopic diffusion in a complex environment looks exactly the same as the diffusion in an obstacle-free environment played out in slow motion. The molecules are delayed by spending certain dwell-times in the ECS microdomains, in agreement with Equation 1. We first analyze an assembly of closely packed cubic cells, the simplest three-dimensional (3D) arrangement. The unit environmental element of this medium is formed by a single cube of side length l, together with the thin layer of ECS adjacent to three of its faces. The ECS adjacent to the remaining three faces is included with neighboring cubical elements. The ECS layer has thickness d, representing the gap between the cubes, and we assume d << l. Consider macroscopic diffusion along one coordinate axis through this medium. If all of the pathways perpendicular to this direction were eliminated, the diffusion would not differ from free diffusion because all of the obstacle boundaries would be aligned with the direction of the diffusion flow so we would measure a free diffusion coefficient. With the perpendicular pathways open, the situation changes. When the molecule arrives at the intersection of two pathways, it has an equal probability of entering either one, and so it spends additional dwell-time in the pathways perpendicular to the macroscopic diffusion flow, causing delay. The delay can be estimated from Equation 1 applied to the ECS of a unit environmental element. The dwell time τ0 corresponding to the free diffusion is proportional to the surface area of the two faces aligned along the macroscopic diffusion flow. With the perpendicular gap open as well, the dwell time will increase by τd, proportional to the surface area of this cubical face. We thus arrive at an estimate for the tortuosity:
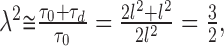 |
2 |
in agreement with other analyses (Mathias, 1983; El-Kareh et al., 1993; Tao et al., 2002).
If the environmental element is represented by a convex polyhedron, the dwell-time for any of its faces can be decomposed into dwell-times corresponding to two independent face projections parallel to the macroscopic diffusion flow and one perpendicular to it. Providing that the polyhedral elements can be tightly packed and form an isotropic environment, the approximation given by Equation 2 remains valid. This has been shown by Monte Carlo simulation in a 3D medium composed of packed truncated octahedra (Tao et al., 2002). A more randomized arrangement, such as the one depicted in Figure 1, is characterized by changing sizes and directions of the polyhedral faces. Nevertheless, if the gaps are all well connected (that is, if there are no dead spaces), we get the same average result. The exact size and shape of the polyhedral elements does not matter as long as the gaps are uniformly small and interconnected and the environment remains macroscopically homogeneous and isotropic.
The tortuosity in the brain is typically significantly higher than the geometrical limit, obtained from Equation 2, of 1.225; however, Equation 2 assumed that all of the gaps are well connected. If there are partial closures, akin to “pockets” that form dead-space microdomains (see Fig. 1, bottom left), the situation changes. Any molecule that enters the dead space will spend extra dwell-time there (τe on the average) before it is able to leave it and continue diffusing in the well connected spaces. To take account of the extra time, we assume that the ECS in every environmental element contains an average dead space with characteristic dimension L (and gap width d). Equation 2 becomes:
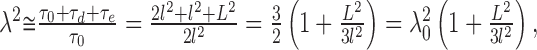 |
3 |
and the ECS α can be estimated as:
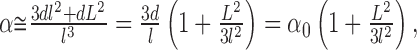 |
4 |
and consequently the dependence of tortuosity on a volume fraction is:
 |
5 |
The volume fraction α0 = 3d/l is that part of the total volume fraction that would remain after elimination of all dead spaces (the volume fraction associated with a well connected medium). If the volume fraction is changed by altering only the gap width d or element size l, the tortuosity λ remains approximately equal to λ0 = 1.225. If, on the other hand, the ECS volume changes exclusively by dead-space addition or elimination (so that α0 is kept constant), Equation 5 predicts that the tortuosity will be proportional to the square root of the volume fraction. This holds even when the dead space is modeled as a collection of several smaller spaces with characteristic dimensions L1, L2, L3,..., which corresponds to the situation depicted in the bottom right panel of Figure 1.
Results
Background macromolecules are trapped in the ECS of thick slices
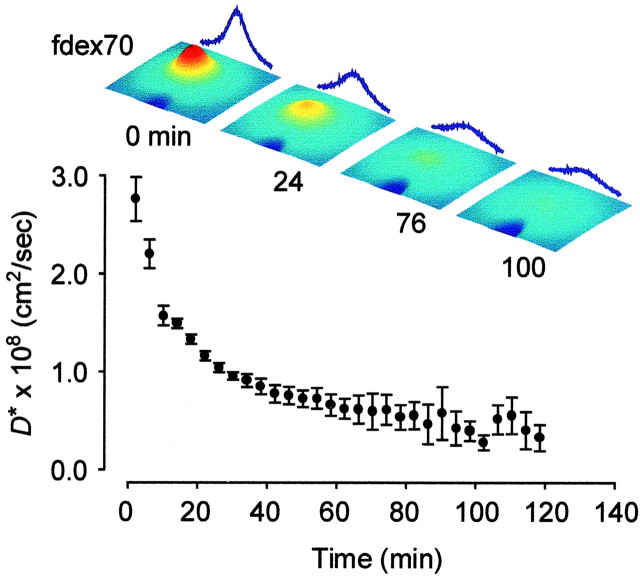
We first examined the behavior of dex70, which had been used previously as a background macromolecule in thick slices (Hrabětová and Nicholson, 2000). We used dex70 tagged with a fluorescent label (fdex70) and observed its movement in thick slices using IOI (Nicholson and Tao, 1993; Tao and Nicholson, 1995). The fdex70 molecules were pressure injected 300 μm below the slice surface rather than at the center (500 μm) to reduce the influence of light scattering on the fluorescent signal. This was justified because ischemic conditions persist into the superficial layers of thick slices (Hrabětová et al., 2002). The distribution of the diffusing fdex70 was imaged every 4 min over a period of 2 hr. The movement of fdex70 gradually declined, suggesting that a substantial proportion of the macromolecules had become immobile. This behavior of fdex70 manifests itself as an apparent decrease in the D* because both mobile and immobile fluorescent molecules contribute to the signal. Results from five experiments are summarized in Figure 2.
Figure 2.
Trapping of dex70 in thick slices. The diffusion of fdex70 in a thick slice of neocortex was measured for 2 hr using the IOI method. Over time, an increasing number of macromolecules became immobile, which was detected as an apparent decrease in D*. Three-dimensional representations of concentration of fdex70 shown in pseudocolor (red highest, blue lowest) taken immediately after the injection (0 min) and 24, 76, and 100 min later are shown above the graph. The time course of D* was estimated by evaluating the diffusion process over 4 min intervals between any two successive image acquisitions (see Methods and Materials for details).
The fdex70 molecules could become immobile through several mechanisms, such as trapping in the constricted microdomains of the ECS, binding to the membranes, or even endocytosis. We favor the first scenario because membrane binding would have had no effect on small diffusing molecules such as TMA+,or it would have led to increased ECS tortuosity by homogeneous scattering of additional obstacles into the path of diffusing marker. Endocytosis of dex70 presumably would have had no effect on TMA+ diffusion through the ECS.
The size of background macromolecules is critical for ECS alteration
We next established that the size, but not the chemical structure, of the background macromolecules was important for the reduction of λ and α in thick slices. Two macromolecules, pvp40 and dex10, were used as a background, and the RTI method with TMA+ was used to determine their effect on λ, α, and k′. The pvp40 molecules are coils (Molyneux, 1987) of lower molecular weight than dex70, but polyvinylpyrrolidone is a synthetic polymer composed of vinyl pyrrolidone monomers whereas dextran is a biopolymer composed of D-glucose. The dex10 molecule is substantially smaller than dex70. Stokes radii are 23 and 81 Å for dex10 and dex70, respectively (Nicholson and Tao, 1993). The background macromolecules were added to the tissue at least 4 hr before the diffusion measurements. Several thick slices were incubated without any background macromolecules to serve as a control group.
Representative records measured in the center of the thick slices containing pvp40 and dex10 are shown in Figure 3A. The TMA+ signal rose and declined faster when pvp40 was added to the tissue compared with slices with dex10 molecules. This reflected a greater drop in the extracellular tortuosity in the presence of larger background macromolecules. All data are summarized in Figure 3, B and C, and compared with λ and α measured in control thick slices and thick slices containing dex70 (Hrabě-tová and Nicholson, 2000). There was no significant difference in ECS parameters between the control group and the thick slices containing dex10. With dex10 in the tissue, the tortuosity remained high (λ = 1.90 ± 0.03; n = 8). Tortuosity decreased, however, in the presence of pvp40, where λ = 1.68 ± 0.01 (n = 18), and the tortuosity was reduced even further, to 1.54 ± 0.06 (n = 24), when dex70 was in the bath (p < 0.01; ANOVA followed by Tukey test). The ECS volume fraction was 0.140 ± 0.003 in the presence of dex10, 0.123 ± 0.003 in tissue incubated with pvp40, and 0.100 ± 0.002 when dex70 was included (p < 0.01; ANOVA followed by Tukey test). Nonspecfic clearances (k′) were 0.15 ± 0.1 × 10-3, 1.64 ± 0.39 × 10-3, and 1.74 ± 0.25 × 10-3sec-1 in the presence of dex10, pvp40, and dex70, respectively (p < 0.05; Kruskal-Wallis ANOVA followed by Dunn's test). We conclude that only larger background macromolecules reduce λ and α and that the effect does not depend on their chemical structure.
Figure 3.
Size of background macromolecules is critical for the decrease in λ in the thick slice. A, Representative examples of TMA+ diffusion curves recorded in neocortical thick slices incubated in ACSF containing pvp40 or dex10. A pulse of TMA+ (+60 nA iontophoretic current) was applied for 50 sec (horizontal bar), and its concentration was measured with a TMA+-ISM positioned 100 μm away. Recorded curves (solid line) are superimposed with the appropriate theoretical curves (dotted line). Measurements were done at 34°C at which temperature D for TMA+ is 1.24 × 10-5 cm2/sec. The parameters of the ECS in the thick slice incubated with dex10 were λ = 1.88, α = 0.148, and k′ = 1.3 × 10-6 sec-1 for an iontophoretic microelectrode transport number nt = 0.44. The parameters of the ECS in the thick slice incubated with pvp40 were λ = 1.63, α = 0.111, and k′ = 4.4 × 10-3 sec-1 with nt = 0.48. B, C, Summary of tortuosity (B) and volume fraction (C) measured in the thick slices without background macromolecules (empty bars) and in the presence of dex10, pvp40, and dex70 (hatched and filled bars). The decrease in both parameters observed in the presence of pvp40 and dex70 was statistically significant (asterisks). [Data measured in the presence of dex70 are from Hrabětová and Nicholson (2000)].
Background macromolecules alter ECS under hypoosmotic stress
The effect of background macromolecules on the ECS parameters measured with the RTI method was observed previously in ischemic tissue but not in normoxic 400 μm slices (Hrabětová and Nicholson, 2000). The effect of background macromolecules on λ and α therefore could be unique to the ischemic condition. Alternatively, it may be a general phenomenon that occurs whenever the ECS is significantly reduced. To decide between these alternatives, we evaluated the effect of background macromolecules in 400 μm slices under hypoosmotic stress (150 mOsm/kg). Such stress causes a reduction of the ECS similar to that occurring in thick ischemic slices (Kriz̆aj et al., 1996; Kume-Kick et al., 2002). Although severe, this magnitude of hypoosmotic stress does not cause irreversible changes in the tissue. Field potentials evoked by local electrical stimulation, representing excitatory postsynaptic events, are sustained throughout the challenge. The amplitudes of the potentials are elevated during the challenge, which is consistent with an increase in extracellular impedance caused by a reduction of α. The amplitude returns to the pre-stimulus level when isoosmotic conditions are restored (Kume-Kick et al., 2002).
Neocortical 400 μm slices were incubated in ACSF containing dex70 for at least 4 hr before the diffusion measurements, and dex70 was also included in the ACSF perfusing the recording chamber. A group of control slices was kept in normal ACSF. After the slice was placed in the chamber, several TMA+ diffusion curves were recorded in normal ACSF, which was then replaced by ACSF with osmolality reduced to 150 mOsm/kg. Frequently, the hypoosmotic stress triggered a spreading depression, a massive depolarization lasting ≈2 min that was detected as a large amplitude negative potential on the reference barrel of the TMA+-ISM. This was not surprising because hypoosmotic media is known to facilitate the induction of spreading depression (Leão, 1963). Because spreading depression itself profoundly but reversibly affects the parameters of the ECS (Hansen and Olsen, 1980; Nicholson et al., 1981), slices were allowed to recover from the episode of spreading depression for ≈20 min before diffusion measurements. No differences were observed between slices that underwent spontaneous spreading depression and slices in which spreading depression was absent; therefore all measurements were pooled.
Figure 4A shows representative records obtained during hypoosmotic stress from the center of a slice, both with and without background macromolecules. The rise and fall of the TMA+ signal is steeper in the presence of dex70, indicating a reduced λ. The data are summarized in Figures 4, B and C. During hypoosmotic stress without background macromolecules, λ rose to 1.86 ± 0.01 (n = 8) as expected but remained as low as 1.63 ± 0.01 in the presence of dex70 (n = 8; p < 0.001; Student's t test). The volume fraction, reduced to 0.136 ± 0.007 by hypoosmotic stress without background macromolecules, was further diminished to 0.114 ± 0.003 by dex70 (p < 0.05; Student's t test). There was no significant difference in the nonspecific clearance between these two groups (k′ was 4.6 ± 1.0 × 10-3 and 6.2 ± 0.4 × 10-3 sec-1 in the absence and presence of dex70, respectively). We conclude that the reduction of tortuosity observed with large background molecules is not unique to ischemic conditions but also occurs when the ECS is reduced to a similar extent by hypoosmotic stress.
Figure 4.
Background macromolecule dex70 reduces λ during hypoosmotic stress. A, Representative examples of TMA+ diffusion curves recorded in the neocortex of 400 μm slices. TMA+ pulse (+60 nA iontophoretic current) was applied for 50 sec (horizontal bar), and the concentration was measured with a TMA+-ISM positioned 120 μm away. Recorded curves (solid line) are superimposed with the appropriate theoretical curves (dotted line). The measurements were done at 34°C at which temperature the free diffusion coefficients are 1.24 × 10-5 and 1.13 × 10-5 cm2/sec in the absence and presence, respectively, of background macromolecule dex70. The iontophoretic transport number for all three records was nt = 0.4. During hypoosmotic stress in dex70-free ACSF (no macro.), λ = 1.86, α = 0.139, and k′ = 2.3 × 10-3 sec-1. In the presence of dex70 (dex70), λ = 1.62,α = 0.112, and k′= 5.1 × 10-3 sec-1. The ECS parameters of the same slice before the challenge were λ = 1.65, α = 0.216, and k′ = 7.6 × 10-3 sec-1. B, C, Summary of tortuosity (B) and volume fraction (C) measured in 400 μm slices during hypoosmotic stress without background macromolecules (empty bars) and in their presence (hatched and filled bars). During hypoosmotic stress, both λ and α were significantly lower (asterisks) in the presence of dex70.
Small background macromolecules at elevated concentration restore α in thick slices
For all experiments presented, except those described in this section, background macromolecules were used at 0.44 mM to keep the number of added molecules constant. In one set of supplementary experiments we used the RTI method to test whether an increased number of the small background macromolecules, dex10, would alter λ and α of thick slices in the same way as did 0.44 mM of the large background macromolecules, dex70 and pvp40. For these experiments dex10 was added to the ACSF at the concentration 3.1 mM, but this increased the osmolality of the ACSF to ≈325 mOsm/kg. In thick slices bathed in the ACSF containing 3.1 mM dex10, α increased to 0.20 ± 0.02 (n = 13), whereas λ dropped to 1.67 ± 0.08. The nonspecific clearance was 0.60 ± 0.85 × 10-3 sec-1. Thus it appears that applying these small background macromolecules at higher concentration led to significant osmotic forces causing water to move from the cells to the ECS. Consequently, the size of the ECS increased and dead space was eliminated.
Use of another marker and method confirms that background macromolecules decrease tissue hindrance
To confirm the findings obtained by the RTI method and to test the effect of background macromolecules on diffusion of a larger marker, we used the IOI method to image diffusion of fdex3 in thick slices in the absence and presence of background dex70. The measurements were also done in normoxic 400 μm slices.
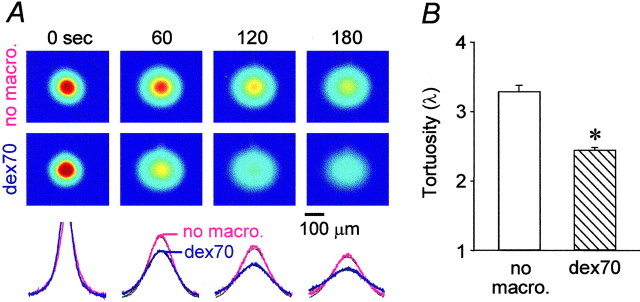
Representative records obtained by focusing the microscope at a depth of 300 μm below the surface of a thick slice are shown in Figure 5A. The first sequence of images (Fig. 5A, top) shows the diffusion of fdex3 in the thick slice with no added background molecule. The second sequence (Fig. 5A, bottom) shows that, in the presence of dex70, the fluorescent signal dissipated faster, indicating lower tortuosity. Data were obtained from depths 200, 300, and 500 μm below the surface of the thick slice. Because there were no differences among these records, all data were pooled and summarized in Figure 5B. In thick slices, λ was 3.29 ± 0.09 (n = 27), and it decreased to 2.44 ± 0.04 (n = 20; p < 0.001; Student's t test) when dex70 was present.
Figure 5.
Background macromolecule dex70 enhances the diffusion of fdex3 in the thick slices. A, Images (top) of fdex3 taken immediately after the pressure injection (labeled as 0 sec) and at 60, 120, and 180 sec later in neocortical thick slices at 34°C. The intensity shown in pseudocolor (red highest, blue lowest) represents the concentration of the fdex3 in the tissue. The images in the top row were taken in the absence of background macromolecules (no macro.). The images in the bottom row were in the presence of dex70 (dex70). The intensity profiles of data (bottom), obtained along the horizontal line running through the center of the image, are superimposed with theoretical curves (black dotted lines). In the presence of dex70, the image intensity dissipated faster, and therefore the collapse of the intensity curve (blue) is more pronounced. Tortuosities were 3.66 and 2.37 in the absence and presence of dex70, respectively. B, Summary of tortuosity measurements in the thick slices without background macromolecules (empty bar) and in the presence of dex70 (hatched bar). The tortuosity was significantly lower (asterisk) in the presence of dex70.
In normoxic 400 μm slices, dex70 had no effect on the diffusion of fdex3, as expected. The tortuosities were 2.01 ± 0.06 (n = 18) and 2.09 ± 0.03 (n = 13) in the absence and presence of dex70, respectively.
Dwell-time diffusion model supports the interpretation of λ
Table 1 compares the experimental data with the theoretical predictions of Equation 5 (see Materials and Methods). Using the measured values of volume fraction before and after addition of dex70, and tortuosities before the addition, the model predicts the tortuosity values after the dex70 addition. The model assumes that the entire change in the volume fraction is caused by the applied macromolecules blocking the dead-space microdomains and becoming stationary. The model prediction is somewhat smaller than the observed effect, and this discrepancy probably can be explained by a slight change in the well connected volume fraction, α0, that had been assumed constant.
Table 1.
Comparison of λ obtained experimentally with values predicted by the dwell-time diffusion model
|
|
Experiment |
Model |
||||||
|---|---|---|---|---|---|---|---|---|
| α
|
λ
|
λ
|
||||||
| Experimental conditions
|
No macro.
|
dex70
|
No macro.
|
dex70
|
dex70
|
|||
| Ischemia | 0.140 | 0.100 | 1.90 | 1.54 | 1.61 | |||
| Hypoosmotic stress
|
0.136
|
0.114
|
1.86
|
1.63
|
1.70
|
|||
No macro., No macromolecules; dex70, 70,000 Mr dextran.
The model (Eq. 5; see Materials and Methods) also estimates the percentage ratio of the dead space volume fraction to well connected volume fraction in the total ECS, assuming that λo = 1.225 (Eq. 2). This ratio, in both the thick and osmotically challenged slices, is ≈58:42; addition of background macromolecules alters the ratio to ≈40:60. From typical measurements in normal healthy brain tissue in vivo (α = 0.2, λ = 1.6), we obtain α0 = 0.12, which means that the corresponding ratio of dead space to well connected volume is again 40:60. In terminal ischemia, where α = 0.06, λ = 2.0 (Vor̆ís̆ek and Syková, 1997), the ratio would rise to ≈62:38. These estimates neglect any viscosity contribution from the extracellular matrix. Increased viscosity would lead to a value of λ0 higher than 1.225 and thus produce lower dead-space percentages in all cases.
Discussion
The main goal of this study was to test the hypothesis that the increase in tortuosity observed in ischemia (and possibly other brain disorders accompanied by cellular swelling) arises from delays in diffusion caused by formation of dead-space microdomains. Selectively occluding the dead spaces with background macromolecules then restores the measured tortuosity to normal values. The hypothesis predicts that tortuosity is affected mostly by the dead-space formation or elimination rather than changes in the gaps between the cells. Consequently, a remarkably small proportion of the change in ECS volume fraction is responsible for most of the change in tortuosity. The background macromolecules introduced into the ECS prevent marker molecules entering dead spaces and thus reveal the previous effect of those microdomains on diffusion. A semiquantitative model of how dead-space diffusion affects tortuosity further supports the hypothesis.
We note that brain pathologies other than ischemia may be accompanied by a larger tortuosity (Nicholson and Syková, 1998; Syková et al., 2000). Factors other than dead-space microdomains, such as rearrangement of tissue geometry or accumulation of extracellular matrix, then may be operative. This study only addresses the mechanism of ischemia.
Effect of background macromolecules on diffusion of small markers in normal brain ECS
We showed previously that dex70 added to normoxic 400 μm slices had no effect on λ measured with the RTI method (Hrabě-tová and Nicholson, 2000). In this study, we found that dex70 also did not change λ measured with a larger marker (fdex3) using the IOI method. This does not mean that addition of dex70 did not change some slice properties. Certainly, interstitial viscosity slightly increased and diffusion therefore slowed, however, because both the free and effective diffusion coefficients would be affected similarly; no increase would occur in λ.
Effect of background macromolecules on tortuosity results from interplay between the ECS volume reduction and macromolecule size
We established that two conditions are necessary for the background macromolecules to reduce ECS tortuosity. The macromolecules must be sufficiently large and the ECS volume has to be reduced sufficiently by ischemia or osmotic challenge. We also observed that large macromolecules become trapped in the ECS of ischemic tissue but small molecules do not. Therefore the ECS diffusion environment should be thought of as a microscopically heterogeneous ensemble of local microdomains with distinct properties. Diffusion will be enhanced through the elimination of some delays of the randomly walking markers by the background macromolecules, and the likely sites of the delays are microscopic dead spaces. Blockage of dead spaces can happen only when their interstitial gaps become comparable in size to the macromolecules.
The largest of the background macromolecules, dex70, had the most effect on λ and α. The slightly smaller molecule, pvp40, caused a smaller reduction in both λ and α, whereas the substantially smaller molecule, dex10, had no effect. Thus size of background macromolecules is critical for lowering tortuosity.
We measured λ ≈ 1.5 in the thick slices in the presence of dex70, whereas Patlak et al. (1998) reported λ ≈ 1.2. Both studies agree on surprisingly low extracellular tortuosity in ischemic tissue when dex70 is present, but the reason for the difference in values of λ is unclear. The experimental protocol of Patlak et al. (1998) differed from ours: they used a radiotracer diffusion method, hippocampal slices, and an industrial grade of dextran with high polydispersity.
The background macromolecules tested in this study were effective in thick slices only when ECS had been reduced. Similarly, the low values of λ reported by Patlak et al. (1998) were obtained in ischemic thick slices containing dex70 where α ≈ 0.17, measured as a distribution space for 14C-polyethylene glycol (PEG, 3000 Mr). In contrast, in hypoxic 450 μm slices containing dex70 where α ≈ 0.25, i.e., comparable with control values in a normoxic slice, Patlak et al. (1998) measured λ ≈ 2.1 with 45Ca2+ and 14C-PEG. These studies, and our previous measurements (Hrabětová and Nicholson, 2000), confirm that macromolecules decrease tortuosity only when ECS volume fraction is small.
Further support was obtained in normoxic 400 μm slices after altering the ECS by hypoosmotic stress. Such stress lowers α and elevates λ (Kriz̆aj et al., 1996) in turtle cerebellum and in rat neocortical slices (Kume-Kick et al., 2002), mimicking the ECS parameters found in thick slices. Using the RTI method, Kume-Kick et al. (2002) observed λ to rise from 1.69 in normal ACSF to 1.86 in 150 mOsm/kg ACSF, whereas α fell from 0.24 to 0.12. We obtained similar results and then showed that when dex70 was present, λ decreased from 1.86 to 1.63. Thus, the effect of background macromolecules is not unique to ischemia but occurs under other conditions of reduced volume fraction.
How do background macromolecules alter the ECS? It is usually assumed that a spherical macromolecule can only enter a space considerably larger than its Stokes radius (Ogston, 1958). It appears, however, that dextran, a flexible coiled polymer with considerable conformational freedom, can enter small pores equal to its Stokes radius (Basedow and Ebert, 1979; Schultz et al., 1979; Burton and Brant, 1983; Bohrer et al., 1984). These properties may allow dextran to enter constricted interstitial spaces of the ECS and become lodged there.
In thick slices, nonspecific clearance (k′) was altered by large background macromolecules. As proposed previously (Hrabě-tová and Nicholson, 2000), increased clearance in slices may reflect greater loss of marker to the superfusing ACSF because of smaller tissue hindrance.
Background macromolecules do not significantly alter osmotic pressure but they exclude part of the ECS
Both dextran and polyvinylpyrrolidone are water-soluble macromolecules known to prevent cell swelling and water gain in brain tissue (Pappius and Elliot, 1956; Banay-Schwartz et al., 1974;Newman et al., 1995). So an alternative explanation of our data might be that macromolecules trapped in dead-space microdomains cause local osmotic redistribution of water to the interstitial spaces, which would widen, removing blockages in the interstitial spaces and restoring ECS connectivity and ultimately decreasing λ. Our data negate this argument. First, addition of background macromolecules to the ACSF at the concentration 0.44 mM did not significantly increase osmolality (see Materials and Methods). Second, macromolecules at this concentration did not increase the measured tissue α, showing that water did not move into the ECS; actually, α decreased from 0.14 to 0.10 in the thick slices and from 0.14 to 0.11 in slices under hypoosmotic stress. The dex70 occupied <4% of medium volume, as confirmed by measurements of volume fraction in agarose gel containing [dex70] = 3.1% (w/v). Despite this, dex70 excluded as much as 20 and 16% of α in ischemia and hypoosmotic stress, respectively. Third, when the concentration of the background macromolecule dex10 was increased from 0.44 to 3.1 mM, osmolarity of the ACSF did increase, and under these conditions, α increased and λ decreased.
Diffusion of the fdex3 marker measured with IOI confirms RTI results
Most of our results were obtained using TMA+ with the RTI method. We confirmed some of them independently, using fdex3 and the IOI method. This fluorescent molecule is larger than TMA+ and consequently gave λ = 3.29 in ischemic tissue. Remarkably, when dex70 was added to the thick slices, λ fell to 2.44. This result also implies that diffusion of comparably large molecules (such as cytokines or growth factors, 5000-30,000 Mr) will be predominantly hindered by the dead-space microdomains under appropriate pathological conditions.
In normoxic 400 μm slices, dex70 had no effect on the diffusion of fdex3. Both in the absence and presence of background macromolecules, λ ≈ 2.0. Previously, λ ≈ 1.7 was reported in neocortical slices with the IOI method and fdex3 (Nicholson and Tao, 1993), but another study with fdex3 (Tao, 1999) reported D* = 6.8 × 10-6 cm2/sec in the same preparation, which translates into λ ≈ 1.9 (using D = 2.42 × 10-6 cm2/sec). The variations in λ among studies probably reflects polydispersity in fdex3. According to the manufacturer, the 3000 Mr dextran preparation actually contains polymers between 1500 and 3000 Mr.
Concluding remarks
The tortuosity-reducing effect of the background macromolecules provides new insights into the microstructure of the ECS and a novel experimental tool with which to explore it. A substantial microscopic heterogeneity exists in the ECS. Elimination of only a small proportion of the ECS using macromolecules substantially reduces overall tortuosity. This suggests that increased tortuosity associated with ischemia, and other conditions involving cellular swelling, is caused by formation of dead-space microdomains within the ECS. A study by Van Harreveld and Malhotra (1967) shows many tight junctions between cellular elements in electron micrographs of ischemic neocortex that might create dead-end pores in the ECS by occluding the gaps between cells. Identifying these microdomains will be a challenging task, but we speculate that astrocytic expansions are likely candidates because of their complex morphology and tight appositions (Špac̆ek, 1985; Kosaka and Hama, 1986; Grosche et al., 1999). Moreover, astrocytes readily swell under many pathological conditions (for review, see Aschner et al., 1999). We do not know whether dead-space microdomains exist in normal tissue. Using background macromolecules larger than dex70 may answer this important question. Finally, this study has complex implications for diffusion of endogenous signaling molecules within the ECS as well as for nutrient and drug delivery in brain tissue compromised by ischemia or stroke. On the one hand, the movement of large macromolecules declines over time, implying reduced penetration for macromolecular drug carriers in challenged brain. On the other hand, large macromolecules can block dead spaces, facilitating the movement of small molecules with therapeutic potential.
Footnotes
This work was supported by National Institutes of Health Grants NS 28642 and NS 34115 from National Institute of Neurological Disorders and Stroke. We thank Dr. Robert Thorne for critical comments on this manuscript.
Correspondence should be addressed to Dr. Sabina Hrabětová, Department of Physiology and Neuroscience, New York University School of Medicine, 550 First Avenue, New York, NY 10016. E-mail: sh36@nyu.edu.
Copyright © 2003 Society for Neuroscience 0270-6474/03/238351-09$15.00/0
References
- Aschner M, Allen JW, Kimelberg HK, LoPachin RM, Streit WJ ( 1999) Glial cells in neurotoxicity development. Annu Rev Pharmacol Toxicol 39 : 151-173. [DOI] [PubMed] [Google Scholar]
- Banay-Schwartz M, Gergely A, Lajtha A ( 1974) Independence of amino acid uptake from tissue swelling in incubated slices of brain. Brain Res 65 : 265-276. [DOI] [PubMed] [Google Scholar]
- Basedow AM, Ebert KH ( 1979) Production, characterization, and solution properties of dextran tractions of narrow molecular weight distributions. J Polym Sci Pol Sym 66 : 101-115. [Google Scholar]
- Bohrer MP, Patterson GD, Carroll PJ ( 1984) Hindered diffusion of dextran and Ficoll in microporous membranes. Macromolecules 17 : 1170-1173. [Google Scholar]
- Burton BA, Brant DA ( 1983) Comparative flexibility, extension, and conformation of some simple polysaccharide chains. Biopolymers 22 : 1769-1792. [Google Scholar]
- Einstein A ( 1956) Investigation on the theory of the Brownian movement. New York: Dover.
- El-Kareh AW, Braunstein SL, Secomb TW ( 1993) Effect of cell arrangement and interstitial volume fraction on the diffusivity of monoclonal antibodies in tissue. Biophys J 64 : 1638-1646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fellows LK, Boutelle MG, Fillenz M ( 1992) Extracellular brain glucose levels reflect local neuronal activity—a microdialysis study in awake, freely moving rats. J Neurochem 59 : 2141-2147. [DOI] [PubMed] [Google Scholar]
- Grosche J, Matyash V, Möller T, Verkhartsky A, Reichenbach A, Kettenmann H ( 1999) Microdomains for neuron-glia interaction: parallel fiber signaling to Bergmann glial cells. Nat Neurosci 2 : 139-143. [DOI] [PubMed] [Google Scholar]
- Hansen AJ, Olsen CE ( 1980) Brain extracellular space during spreading depression and ischemia. Acta Physiol Scand 108 : 355-365. [DOI] [PubMed] [Google Scholar]
- Hrabětová S, Nicholson C ( 2000) Dextran decreases extracellular tortuosity in thick-slice ischemia model. J Cereb Blood Flow Metab 20 : 1306-1310. [DOI] [PubMed] [Google Scholar]
- Hrabětová S, Chen KC, Masri D, Nicholson C ( 2002) Water compartmentalization and spread of ischemic injury in thick-slice ischemia model. J Cereb Blood Flow Metab 22 : 80-88. [DOI] [PubMed] [Google Scholar]
- Kosaka T, Hama K ( 1986) Three-dimensional structure of astrocytes in the rat dentate gyrus. J Comp Neurol 249 : 242-260. [DOI] [PubMed] [Google Scholar]
- Kriz̆aj D, Rice ME, Wardle RA, Nicholson C ( 1996) Water compartmentalization and extracellular tortuosity after osmotic changes in cerebellum of Trachemys scripta. J Physiol (Lond) 492 : 887-896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kume-Kick J, Mazel T, Vor̆ís̆ek I, Hrabětová S, Tao L, Nicholson C ( 2002) Independence of extracellular tortuosity and volume fraction during osmotic challenge in rat cortex. J Physiol (Lond) 542 : 515-527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leão AAP ( 1963) On the spread of spreading depression. In: Brain function, Vol 1, Cortical excitability and steady potentials, relations of basic research to space biology (Brazier MAB, ed), pp 73-85. Berkeley, CA: University of California.
- Lehmenkühler A, Syková E, Svoboda J, Zilles K, Nicholson C ( 1993) Extracellular space parameters in the rat neocortex and subcortical white matter during postnatal development determined by diffusion analysis. Neuroscience 55 : 339-351. [DOI] [PubMed] [Google Scholar]
- Mathias RT ( 1983) Effect of tortuous extracellular pathways on resistance measurements. Biophys J 42 : 55-59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molyneux P ( 1987) Water-soluble synthetic polymers: properties and behavior. Boca Raton, FL: CRC.
- Newman GC, Hospod FE, Qi H, Patel H ( 1995) Effects of dextran on hippocampal brain slice water, extracellular space, calcium kinetics and histology. J Neurosci Methods 61 : 33-46. [DOI] [PubMed] [Google Scholar]
- Nicholson C ( 1979) Brain cell microenvironment as a communication channel. In: The neurosciences fourth study program (Schmitt FO, Worden FG, eds), pp 457-476. Cambridge, MA: MIT.
- Nicholson C ( 1992) Quantitative analysis of extracellular space using the method of TMA+ iontophoresis and the issue of TMA+ uptake. Can J Physiol Pharmacol 70 : S314-S322. [DOI] [PubMed] [Google Scholar]
- Nicholson C ( 1993) Ion-selective microelectrodes and diffusion measurements as tools to explore the brain cell microenvironment. J Neurosci Methods 48 : 199-213. [DOI] [PubMed] [Google Scholar]
- Nicholson C ( 2001) Diffusion and related transport mechanisms in brain tissue. Rep Prog Phys 64 : 815-884. [Google Scholar]
- Nicholson C, Phillips JM ( 1981) Ion diffusion modified by tortuosity and volume fraction in the extracellular microenvironment of the rat cerebellum. J Physiol (Lond) 321 : 225-257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson C, Syková E ( 1998) Extracellular space structure revealed by diffusion analysis. Trends Neurosci 21 : 207-215. [DOI] [PubMed] [Google Scholar]
- Nicholson C, Tao L ( 1993) Hindered diffusion of high molecular weight compounds in brain extracellular microenvironment measured with integrative optical imaging. Biophys J 65 : 2277-2290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson C, Phillips JM, Tobias C, Kraig RP ( 1981) Extracellular potassium, calcium and volume profiles during spreading depression. In: Ion-selective microelectrodes and their use in excitable tissues (Syková E, ed), pp 211-223.New York: Plenum.
- Ogston AG ( 1958) The spaces in a uniform random suspension of fibers. T Faraday Soc 54 : 1754-1757. [Google Scholar]
- Pappius HM, Elliot AC ( 1956) Water distribution in incubated slices of brain and other tissues. Can J Biochem Physiol 34 : 1007-1022. [PubMed] [Google Scholar]
- Parsegian VA, Rand RP, Fuller NL, Rau DC ( 1986) Osmotic stress for the direct measurements of intermolecular spaces. Methods Enzymol 127 : 400- 416. [DOI] [PubMed] [Google Scholar]
- Parsegian VA, Rand RP, Rau DC ( 1995) Macromolecules and water: probing with osmotic stress. Methods Enzymol 259 : 43-94. [DOI] [PubMed] [Google Scholar]
- Patlak CS, Hospod FE, Trowbridge SD, Newman GC ( 1998) Diffusion of radiotracers in normal and ischemic brain slices. J Cereb Blood Flow Metab 18 : 776- 802. [DOI] [PubMed] [Google Scholar]
- Pérez-Pinzón MA, Tao L, Nicholson C ( 1995) Extracellular potassium, volume fraction, and tortuosity in rat hippocampal CA1, CA3, and cortical slices during ischemia. J Neurophysiol 74 : 565-573. [DOI] [PubMed] [Google Scholar]
- Prokopová-Kubinová S, Vargová L, Tao L, Ulbrich K, s̆ubr V, Syková E, Nicholson C ( 2001) Poly[N-(2-hydroxypropyl)methacrylamide] polymers diffuse in brain extracellular space with the same tortuosity as small molecules. Biophys J 80 : 542-548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice ME, Nicholson C ( 1991) Diffusion characteristics and extracellular volume fraction during normoxia and hypoxia in slices of rat neostriatum. J Neurophysiol 65 : 264-272. [DOI] [PubMed] [Google Scholar]
- Saltzman WM ( 2001) Drug delivery: engineering principles for drug therapy. New York: Oxford UP.
- Schultz JS, Valentine R, Choi CY ( 1979) Reflection coefficients of homopore membranes: effect of molecular size and configuration. J Gen Physiol 73 : 49- 60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Špac̆ek J ( 1985) Three-dimensional analysis of dendritic spines. Anat Em- bryol (Berl) 171 : 245-252. [DOI] [PubMed] [Google Scholar]
- Syková E, Mazel T, Vargová L, Vor̆ís̆ek I, Prokopová-Kubinová S̆ ( 2000) Extracellular space diffusion and pathological states. In: Progress in brain research, Vol 125. Volume transmission revisited (Agnati LF, Fuxe K, Nicholson C, Syková E, eds), pp 155-158. Amsterdam: Elsevier. [DOI] [PubMed]
- Tao L ( 1999) Effects of osmotic stress on dextran diffusion in rat neocortex studied with integrative optical imaging. J Neurophysiol 81 : 2501-2507. [DOI] [PubMed] [Google Scholar]
- Tao L, Nicholson C ( 1995) The three-dimensional point spread functions of a microscope objective in image and object space. J Microsc 178 : 267-271. [DOI] [PubMed] [Google Scholar]
- Tao L, Hrabětová S, Nicholson C ( 2002) Effect of brain extracellular space geometry on molecular diffusion revealed by Monte Carlo simulation. Soc Neurosci Abstr 28 . 763.1. [Google Scholar]
- Ulbrich K, Pechar M, Strohalm J, S̆ubr V, R̆íhová B ( 1997) Synthesis of biodegradable polymers for controlled drug release. Ann NY Acad Sci 15 : 137-141. [DOI] [PubMed] [Google Scholar]
- Van Harreveld A, Malhotra SK ( 1967) Extracellular space in the cerebral cortex of the mouse. J Anat 101 : 197-207. [PMC free article] [PubMed] [Google Scholar]
- Vor̆ís̆ek I, Syková E ( 1997) Ischemia-induced changes in the extracellular space diffusion parameters, K+, and pH in the developing rat cortex and corpus callosum. J Cereb Blood Flow Metab 17 : 191-203. [DOI] [PubMed] [Google Scholar]