Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2003 Jul 30;23(17):6798–6809. doi: 10.1523/JNEUROSCI.23-17-06798.2003

Coherent Oscillations in Neuronal Activity of the Supplementary Motor Area during a Visuomotor Task

Daeyeol Lee 1
PMCID: PMC6740733  PMID: 12890774

Abstract

Neural activity recorded in behaving animals is nonstationary, making it difficult to determine factors influencing its temporal patterns. In the present study, rhesus monkeys were trained to produce a series of visually guided hand movements according to the changes in target locations, and multichannel single-neuron activity was recorded from the caudal supplementary motor area. Coherent oscillations in neural activity were analyzed using the wavelet cross-spectrum, and its statistical significance was evaluated using various methods based on surrogate spike trains and trial shuffling. A population-averaged wavelet cross-spectrum displayed a strong tendency for oscillatory activity in the γ frequency range (30∼50 Hz) to synchronize immediately before and after the onset of movement target. The duration of synchronized oscillations in the γ frequency range increased when the onset of the next target was delayed. In addition, analysis of individual neuron pairs revealed that many neuron pairs also displayed coherent oscillations in the β frequency range (15-30 Hz). Coherent β frequency oscillations were less likely to be synchronized than γ frequency oscillations, consistent with the fact that coherent β frequency oscillations were not clearly seen in the population-averaged cross-spectrum. For a given neuron pair, the time course and phase of coherent oscillations were often similar across different movements. These results are consistent with the proposal that synchronized oscillations in the γ frequency range might be related to the anticipation of behaviorally relevant events and the contextual control of cortical information flow.

Keywords: neuron assemblies, monkey, SMA, spike synchrony, wavelet cross-spectrum, sequence learning

Introduction

Cortical information processing relies on a massive number of connections within a large population of neurons. The number of neurons contributing synaptic inputs to a given cortical neuron is large, and many such inputs arise locally or from neighboring cortical columns with similar functional properties (Breitenberg and Schüz, 1998). In addition, long-distance corticocortical projections are mostly reciprocal, providing additional opportunities for nearby cortical neurons to receive correlated inputs. Consistent with these anatomical patterns, cortical neurons often display correlation in their spike trains. For example, spike synchrony has been observed in many different cortical areas (Gray, 1999), and synchronous activity of individual neurons often displays oscillations at various frequencies (Eckhorn et al., 1988; Gray et al., 1989). However, the role of correlated activity in cortical information processing is not well understood. On the one hand, correlated activity might be merely a consequence of anatomical and biophysical means to achieve reliable information transmission (Shadlen and Newsome, 1998). On the other hand, correlated activity might play a more active role in cortical information processing. For example, effects of synaptic inputs on the activity of a given neuron can be influenced by the pattern of correlation in the inputs (Murthy and Fetz, 1994; Salinas and Sejnowski, 2000; Svirskis and Rinzel, 2000). In addition, the relationship between correlated activity and the information-coding capacity of a neuronal ensemble depends on how different variables are coded in neural activity (Oram et al., 1998; Panzeri et al., 1999). Finally, it has been proposed that synchronization of oscillatory activity across different neuronal populations enhances transmission of information among them (Roelfsema et al., 1997; Llinás et al., 1998; Rodriguez et al., 1999; von Stein et al., 2000; Engel et al., 2001; Varela et al., 2001).

Flow of information through a population of neurons is reflected in temporal changes in their activity. If coherent oscillations play an important role in the control of cortical information flow, they must also display dynamic patterns systematically related to the requirements of behavioral tasks. However, nonstationarity in the spike trains often makes it difficult to evaluate the statistical significance of coherent oscillations. In the present study, coherent oscillations in the activity of neurons in the supplementary motor area proper (SMA) were analyzed using the wavelet cross-spectrum (Lee, 2002). Although oscillatory activity has been found in other motor cortical areas (Murthy and Fetz, 1996a,b; MacKay, 1997; Crone et al., 1998a,b; Donoghue et al., 1998; Aoki et al., 1999; Lebedev and Wise, 2000; Baker et al., 2001), coherent oscillations in activity of individual SMA neurons had not been examined. It was found in the present study that SMA neurons displayed coherent oscillations in the β (15-30 Hz) and γ (30-50 Hz) frequency bands. In addition, coherent oscillations in the γ frequency range became strongly synchronized during the hold period, suggesting that synchronized γ frequency oscillations might play a role in anticipation or preparation of upcoming movements.

Materials and Methods

Animal preparation and neural recording

Two male adult rhesus monkeys (Macaca mulatta; body weight, 6-8 kg) were used. Four titanium posts were attached to the skull, and an eye coil was placed around the orbit of one eye by sterile surgery. In a second surgery, a titanium chamber (inner diameter, 18 mm) was implanted above the supplementary motor area for the purpose of neurophysiological recording. Neuronal activity was recorded using an Eckhorn 16-channel mictroelectrode manipulator (Thomas Recording, Giessen, Germany) and a Plexon (Dallas, TX) multichannel acquisition processor. Electrodes were arranged in a four-by-four grid, and the distance between neighboring electrodes was 350 μm. A detailed description of the methods used to collect behavioral and single-unit data has been published (Lee and Quessy, 2003). All the procedures used in the current study were approved by the University of Rochester Committee on Animal Research and conformed to the principles outlined in the Guide for the Care and Use of Laboratory Animals (National Institutes of Health publication 85-23, revised 1985).

Behavioral task

The animal was seated in a primate chair and faced a 17-inch computer monitor on which visual stimuli were presented. The monitor was located ∼57 inches from the animal's eyes and subtended 30 and 22° visual angles horizontally and vertically, respectively. The neural data described in this report were collected from two different behavioral paradigms. In both cases, the animal was required to capture a series of targets (red disk) presented on the monitor by moving its right hand on a touch screen, which was installed horizontally in front of the animal at its waist level. The location of the touch was indicated to the animal by a feedback cursor (white disk; radius, 0.5°) on the computer screen. The touch screen was calibrated so that a 1 cm displacement on the touch screen corresponded to the same distance (1° visual angle) on the computer monitor. In each trial, the animal was required to acquire 10 successive targets to receive a drop of apple juice.

In the first paradigm, targets were presented in a four-by-four grid. The center-to-center distance between the neighboring target locations was 4.2°, and the radius of the target was 1.4°. The interval between the acquisition of a target and the onset of the next target [response-stimulus interval (RSI)] was always 250 msec. Within a block of eight trials, target locations were determined randomly in one pseudorandomly selected trial, whereas for the remaining trials, they followed three different deterministic sequences. These sequences were generated with five locations that were selected randomly for each daily session. Denoting them A-E, the sequence ABC-ABC-ABC-A was used in five trials selected randomly in each block (primary trials). For the remaining two trials in each block, the sequences were DEC-DEC-DEC-D (secondary trials) and DEC-DEC-ABC-A (switch trials), respectively. This particular combination of target sequences was designed to evaluate the nature of changes in neural activity related to the learning of visuomotor sequences (Lee and Quessy, 2003). In the present report, only the data from the primary trials were used because they provided a large amount of data with a consistent pattern of visual stimuli and behavioral responses.

In the second paradigm, two different values of the RSI (250 and 650 msec) were used to determine how the time course of coherent oscillations in the activity of SMA neurons was affected by the temporal parameters of the task. Targets were presented in a three-by-three grid, and the center-to-center distance between the neighboring target locations was 5.6°. The radius of the target was the same as in the first paradigm. Within a block of 10 trials, target locations were determined randomly in two trials. In one of these two trials, the long and short RSIs were selected randomly for each target, whereas for the other trial, they alternated. For the remaining eight trials, the target locations followed a predetermined sequence of nine targets, which was selected pseudorandomly for each recording session, but the pattern of RSI varied across different trial types. For six of these (referred to as primary trials), either the even- or odd-numbered (determined randomly for each sequence) targets in the sequence were associated with the short RSI, whereas the long RSI was used for the remaining targets. For another trial, this RSI-target mapping was reversed. For the remaining one trial in a block, the RSI was selected randomly for each target. The order of these different trial types was randomized for each block. These different types of trials were designed to examine the interaction between the temporal and spatial dimensions of sequence learning (Lee, 2000). In the present study, only the data from the primary trials with consistent mapping between the targets and the RSI were analyzed.

Data analysis

Time-resolved cross-correlation function. For the quantitative analyses of single-unit activity, the spike train from a neuron j was represented as:

graphic file with name jneuro23_17_6798.1.jpg

where t indicates time from target onset; n is the index for the analysis window for each target (n = 1, 2,..., N); and Δt = 1 msec. For most analyses in the present study, the analysis window covered the period beginning 200 msec before and ending 500 msec after target onset. Because 10 targets were presented in a given trial, each successful trial provided 10 analysis windows. The first window in each trial was excluded from the analysis because the initial hand position was not controlled for the first target. Although temporal correlation in spike trains has been commonly analyzed with cross-correlation function (CCF; Perkel et al., 1967), the utility of CCF is primarily limited to stationary processes. Spike trains are nonstationary, however, when they are influenced by sensory stimuli or behavioral responses. In such cases, the joint perievent time histogram (JPTH) can be used (Aertsen et al., 1989). This is defined as:

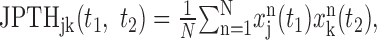graphic file with name M1.gif

where t1 and t2 denote time for spikes in neurons 1 and 2, respectively. For visualization of synchronous spikes, it is convenient to use the time-resolved cross-correlation function (TrCCF; Baker et al., 2001), which is related to the JPTH according to the following equation:

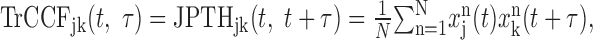graphic file with name M2.gif

where t denotes time from target onset, and τ is the time lag. For neuron pairs with independent, rate-modulated spike trains, the expected TrCCF can be estimated as the product of spike density functions of individual neurons (Aertsen et al., 1989; Baker et al., 2001; Lee, 2002). Denoting the spike density function for neuron j in trial n as Fjn(t), the expected TrCCF can be defined as:

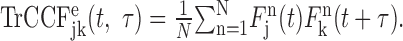graphic file with name M3.gif

In the present analysis, the spike density function was calculated with a Gaussian kernel (σ = 40 msec).

Wavelet cross-spectrum. Whereas the TrCCH provides a tool to examine temporal changes in the amount of synchronous spikes, analyses in the frequency domain can provide more concise descriptions for temporal correlation in the oscillatory patterns of spike trains. However, the need to examine time-dependent changes in the frequency characteristics of neural activity faces a problem known as the uncertainty principle because there is a tradeoff between temporal and spectral resolutions. In the wavelet analysis, this problem is resolved by adjusting the width of the kernel as a function of frequency (Torrence and Compo, 1998; Lee, 2002). The wavelet transform of a spike train from neuron j in the nth analysis window can be defined as:

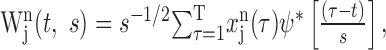graphic file with name M4.gif

where ψ[] denotes a wavelet function, and * is the complex conjugate. The variables t and s indicate the time and scale of the wavelet function, and T is the duration of the analysis window. In practice, this was calculated using the fast Fourier transform implemented in MATLAB (The MathWorks, Natick, MA). To avoid edge effects, the original spike trains during the additional 150 msec intervals surrounding the analysis window were included before the Fourier transform and removed after the inverse Fourier transform. The mean spike rate of each analysis window was subtracted from the spike train. In the present study, the Morlet wavelet function was used (Fig. 1 B), which is defined as:

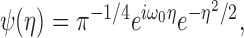graphic file with name M5.gif

where

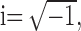graphic file with name M6.gif

η is the nondimensional time parameter; and ω0 is taken to be 6 to make this function localized in both time and frequency space (Torrence and Compo, 1998). The frequency of the Morlet wavelet function is approximately the inverse of the scale parameter. In the present study, the frequency range between 10 and 82.5 Hz was examined at a 2.5 Hz resolution. The wavelet cross-spectrum for the two spike trains from neurons j and k in the nth analysis window can be defined as Wjn(t, s)Wkn*(t, s) (Fig. 1 D). To determine whether a pair of neurons displays any consistent phase relationship in their oscillatory activity, the cross-spectrum was averaged across all trials to compute the average wavelet cross-spectrum (AWCS) according to the following:

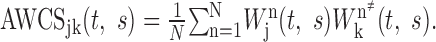graphic file with name M7.gif

The summation in the above equation is performed in the complex plane, and as a result, the amplitude of the resulting cross-spectrum would be relatively small if there were no consistent phase relationship (Fig. 1 E). Accordingly, a significantly large amplitude in the average wavelet cross-spectrum is referred to as coherent (i.e., phase-locked) oscillation. Coherent oscillations with a small phase difference (e.g., <90°) are referred to as synchronized or synchronous coherent oscillations. In the present study, cross-spectrum was used instead of coherence because the latter could not be computed for many neuron pairs when the spike rates became close to zero.

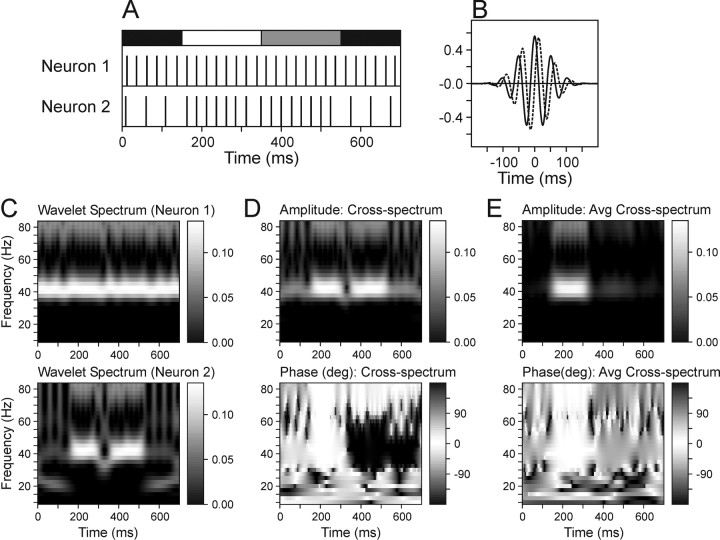
Figure 1.

Figure 1.

Open in a new tab

The wavelet cross-spectrum can detect coherent oscillations in simultaneously recorded spike trains. A, Examples of two separate simulated spike trains. Spikes in Neuron 1 were generated at the constant frequency of 40 Hz, whereas the frequency of spikes in Neuron 2 changed from 20 Hz during the first 150 msec (black bar at top), to 40 Hz during the next 400 msec (white, gray bars), and back to 20 Hz during the last 150 msec (black bar). During the period indicated by the white bar, the spikes of the two neurons were synchronized, whereas the gray bar indicates the period in which the spikes of the two neurons were counterphased. The exact timing of spikes was jittered according to a normal distribution with the SD of 1 msec. B, Example of the Morlet wavelet function with the frequency of 20 Hz (scale, 50 msec) centered at 0 msec. Real and imaginary components are indicated by solid and dotted lines, respectively. C, Wavelet spectra calculated for the spike trains of Neurons 1 (top) and 2 (bottom). D, Amplitude (top) and relative phase (bottom) of the wavelet cross-spectrum computed for the same spike trains. E, Amplitude (top) and relative phase (bottom) of the average wavelet cross-spectrum. This was calculated over 10 different pairs of simulated spike trains like those in A. The spikes during the interval indicated by the white bar were always synchronized, whereas the relative phase of the spikes during the interval indicated by the gray bar was randomly varied.

Phase-locking index. The average wavelet cross-spectra of individual neuron pairs were averaged across the entire population of simultaneously recorded neuron pairs to yield the population average wavelet cross-spectrum. To quantify the extent to which the oscillatory activity of neuron pairs in the SMA display consistent phase locking across the population, the phase-locking index (PLI) was defined as the following:

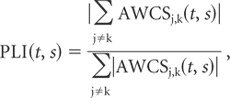graphic file with name jneuro23_17_6798.2.jpg

where the summation was performed for all neuron pairs recorded simultaneously, and ∥ indicates the amplitude of the cross-spectrum. The value of PLI would be 1 if the AWCS for all neuron pairs displayed the same phase difference, whereas it would be close to zero if the phase difference is randomly distributed.

Statistical significance of the wavelet cross-spectrum. Although a large amplitude in the cross-spectrum could indicate a consistent phase relationship for a given pair of neurons, the possibility that this might be the result of random variations in spike trains must be evaluated. In practice, however, this task is not trivial because the statistical significance of any observation can be evaluated only relative to a specific null hypothesis. In the present study, the statistical significance of coherent oscillations in each neuron pair was evaluated using three different methods.

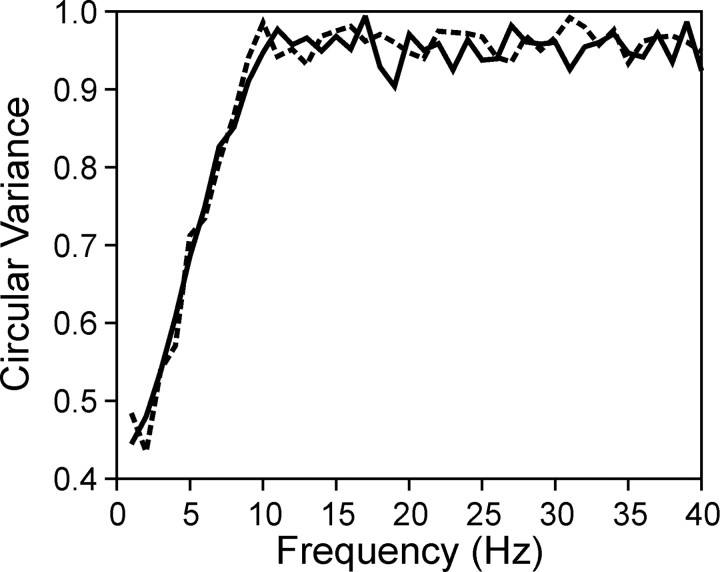
The first method was based on a set of surrogate spike trains (Oram et al., 1999). In this method, the spike density function was calculated for each analysis window with a Gaussian kernel (σ = 40 msec). Next, the amplitude of the average wavelet cross-spectrum was recalculated from the Poisson surrogate spike trains generated according to the same spike density functions on a trial-by-trial basis. This process was repeated 10 times to estimate the mean and SD for the amplitude of the surrogate average cross-spectrum. A p value for the amplitude of the original average cross-spectrum was then calculated for each combination of time and frequency, according to a normal distribution with the mean and SD of the surrogate average cross-spectrum amplitude after square root transformation (Lee, 2002). The result is a map of p values indicating for each point in the cross-spectrum how likely it would be for the amplitude value of the original average cross-spectrum to have occurred by chance in surrogate spike trains. For the Gaussian kernel used in the present study with the SD of 40 msec, simulations showed that this method effectively randomized the phase for high-frequency components of >10 Hz (Fig. 2). The phase of lower-frequency components was still preserved because the surrogate spike trains shared the same spike density functions with the original spike trains. Accordingly, this procedure tested the null hypothesis that the observed level of coherent oscillation resulted by chance from two spike trains in which spike rates were modulated by the same spike density functions and the phase difference for frequency components of >10 Hz was random. Because the surrogate spike trains included the same number of spikes in each data window as the original spike trains, the results obtained with this method would not be biased by correlated changes in spike counts (Lee et al., 1998; Brody, 1999). However, a potential problem with the use of Poisson surrogate spike trains is that it destroys all of the temporal structures in the original spike trains. This would increase the variance of the wavelet cross-spectrum, raising the possibility that the estimates obtained with this method might be too conservative. For example, the Poisson process is not an ideal model for real spike trains, which display a refractor period. Therefore, a separate analysis was performed with γ surrogate spike trains. In this analysis, a relative refractory period was introduced to the surrogate spike trains by initially generating a Poisson spike train with twice as many spikes as in the original spike train and then decimating every other spike. This procedure produces the distribution of an interspike interval histogram that follows the γ distribution with the shape parameter of 2 (Baker and Lemon, 2000).

Figure 2.

Figure 2.

Open in a new tab
Circular variance for the phase difference between the two simulated Poisson spike trains generated with the same spike density functions. Spike density functions were computed using a Gaussian kernel with the same SD used in the analysis of the present study (σ = 40 msec). The circular variance is defined as:
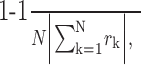graphic file with name M8.gif
where rk = sinϕk + icosϕk; ϕk is the phase difference for a given frequency between the two spike trains in trial k; and N is the number of trials (N = 500). If the phase difference is completely randomized across different trials, the circular variance would be close to 1. For this simulation, the phase was calculated from the Fourier transform of the spike train. The simulation was performed for two different spike rates (5, 10 Hz; dotted, solid lines, respectively).

The second method used the shift predictor (Perkel et al., 1967). This method tests the null hypothesis that the spike trains of different trials are independent and drawn from the same distributions. Accordingly, the significance of coherent oscillations could be potentially inflated when there are correlated changes in spike counts or the latency of neural activity (Brody, 1999). This method, however, has the advantage that it preserves all the temporal structures within the spike trains of individual neurons (e.g., autocorrelation function). For comparison with the methods based on surrogate spike trains, the statistical significance of coherent oscillation for each neuron pair was also evaluated using the resampled wavelet cross-spectrum calculated after shuffling the order of trials (Lee, 2002). Similar to the method based on surrogate spike trains, the p value was evaluated for each combination of time and frequency by fitting a normal distribution to a set of 10 resampled average wavelet cross-spectra.

As shown in Results, the proportion of neuron pairs with significant coherent oscillations differed for the above two methods, especially for coherent oscillations in the β frequency range. To understand the cause of this discrepancy better, statistical significance of coherent oscillations was also tested with surrogate spike trains generated after trial shuffling. This method was identical to the methods based on surrogate spike trains, except that the spike density functions were calculated after randomizing the order of trials for one of the neurons in the pair. This analysis was performed for Poisson and γ surrogate spike trains separately.

Results

Neuronal database

A total of 191 neurons were recorded in the left SMA proper of two animals during 33 daily recording sessions. Of these, 60 neurons were excluded from the analysis either because they were recorded individually, or because they were lost without sufficient amount of data (120 trials in the primary condition, or 1080 movements). The remaining 131 neurons provided 270 neuron pairs analyzed in the present study. Among them, 217 pairs were examined with a single RSI (250 msec), and 53 pairs were examined with two different RSIs (250 and 650 msec). The mean numbers of trials ± SD for neuron pairs examined with these two paradigms were 263.7 ± 69.0 and 269.2 ± 61.7, respectively. These values corresponded to ∼2373 and 2422 movements. Among the neuron pairs tested with a 250 msec RSI, 10 were isolated from the same electrode.

Coherent oscillations in individual SMA neuron pairs

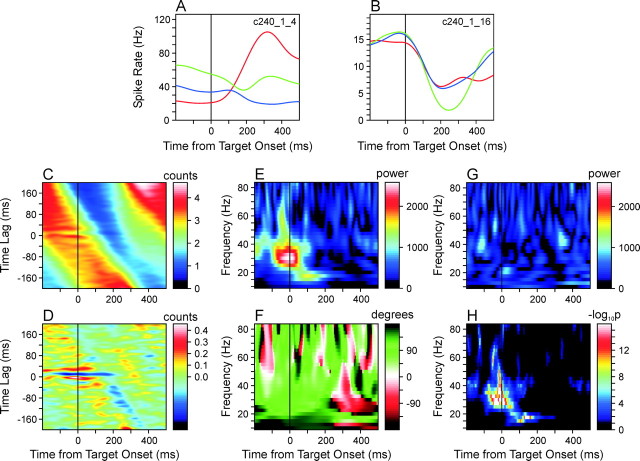
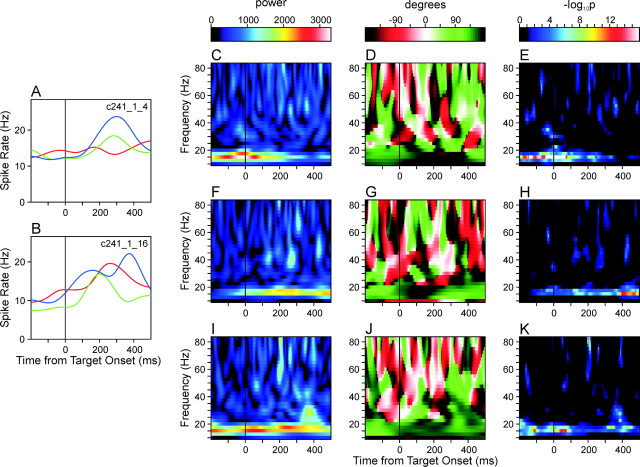
Individual neuron pairs in the SMA displayed substantial variability in their phase-locked (coherent) oscillatory activity in terms of the frequency and phase of oscillations and their time course. For example, the neuron pair shown in Figure 3 displayed coherent oscillations in both the β and γ frequency ranges. One of the neurons in this pair displayed substantial modulation in its activity throughout the task period according to the changes in target locations (Fig. 3A), whereas the modulation in the second neuron was similar across different targets (Fig. 3B). There was a robust tendency for these two neurons to display phase-locked oscillatory activity during a period of several hundred milliseconds around the time of target onset. This can be seen from the time-resolved cross-correlation function (Fig. 3C,D), but the wavelet cross-spectrum revealed more clearly how the frequency of this coherent oscillation and its phase changed over time. In the wavelet cross-spectrum averaged across three different target positions used in the primary trials, the peak amplitude was found precisely at the time of target onset at the frequency of 30 Hz (Fig. 3E). The corresponding phase difference was 74.7° (Fig. 3F), which is equivalent to the time lag of 6.9 msec at 30 Hz. This coherent oscillation in the γ frequency range was highly significant statistically. For the phase-locked oscillations around the time of target onset in the frequencies ranging from 27.5 to 35 Hz, the p values calculated on the basis of Poisson surrogate spike trains (see Materials and Methods) were <10-16 (Fig 3H), and the results were similar for shuffled wavelet cross-spectra. The maximum power in the wavelet cross-spectrum computed from the Poisson surrogate spike trains was only 41.2% compared with the original cross-spectrum (Fig. 3G). For this particular neuron pair, the frequency of coherent oscillation decreased to the β range within the first 100 msec period after target onset (Fig. 3E). The power in the wavelet cross-spectrum at <20 Hz peaked 100 msec from target onset at 17.5 Hz and the corresponding phase difference was 148.8°, equivalent to the time lag of 23.6 msec. This coherent oscillation in the β frequency range was also highly significant regardless of the methods used to evaluate the statistical significance (p < 10-16; Fig 3H).

Figure 3.

Figure 3.

Open in a new tab

Coherent oscillations in an example neuron pair recorded from two separate electrodes in the supplementary motor area during the task with a constant RSI (250 msec). A, B, Spike density functions of the two neurons, averaged separately for three movements directed to the target triplet used in the primary trials. C, TrCCF calculated for the same neuron pair. This was smoothed with a two-dimensional Gaussian kernel withσx = 40 msec andσy = 4 msec. D, Difference between the smoothed TrCCF (C) and the TrCCF expected for independent spike trains. The latter was calculated on the basis of the spike density functions of the individual neurons (see Materials and Methods). E, F, Amplitude (or power; E) and relative phase (F) of the AWCS computed for the same neuron pair. G, Amplitude of the AWCS computed for the Poisson surrogate spike trains generated according to the spike density functions of the same neuron pair. H, Map of statistical significance (p values) calculated from a set of 10 surrogate AWCSs as shown in G (see Materials and Methods).

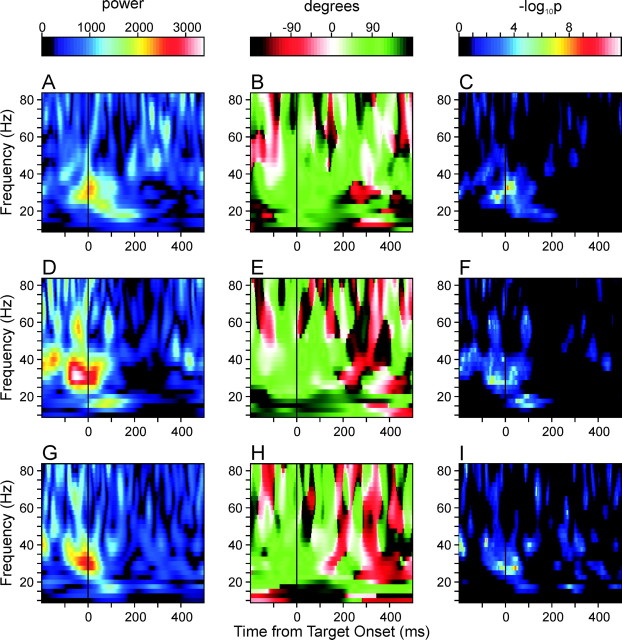
For many neuron pairs in the SMA, the pattern of coherent oscillation was consistent across individual target locations. For example, in the neuron pair illustrated in Figure 3, the strong coherent oscillations at the γ frequency range at the time of target onset and the β-frequency oscillation after target onset were consistently observed in all of the three different movements examined in the primary trials (Fig. 4). The peak amplitude at 30 Hz occurred 6 and 2 msec after target onset for the first and third movements (Fig. 4A,G), respectively, and 49 msec before target onset for the second movement (Fig. 4D). The corresponding phase differences were 82.7, 62.9, and 72.8°, respectively. The peak amplitudes at 17.5 Hz occurred 159, 89, and 95 msec from target onset, and again displayed similar phase differences (135.4, 153.9, and 163.7°).

Figure 4.

Figure 4.

Open in a new tab

Amplitude (A, D, G), relative phase (B, E, H), and the map of p values (C, F, I) of the average wavelet cross-spectra of the same neuron pair illustrated in Figure 3, computed separately for three different movements directed toward the triplet of targets used in the primary trials. The average spike density functions for these three different movements are indicated by different colors in Figure 3,A and B (A-C, red; D-F, green; G-I, blue).

In some neuron pairs, coherent oscillations were predominantly observed in the β frequency band. For example, in the neuron pair illustrated in Figure 5, the peak amplitude in the average wavelet cross-spectrum collapsed across different targets was found 15 msec after target onset at the frequency of 15 Hz, and the phase difference for this peak was 142°, which corresponds to 26.3 msec. Therefore, although the oscillatory activity was phase-locked for these two neurons, there was a relatively large difference in their phases. For this neuron pair, the time course of coherent oscillation in the β frequency varied somewhat across different target locations, although robust oscillations with similar phase differences were found in all cases (Fig. 5C-K).

Figure 5.

Figure 5.

Open in a new tab

Coherent oscillation in the β frequency range found in a pair of SMA neurons. A, B, Spike density functions of individual neurons, same format as in Figure 3. C-K, Amplitude (C, F, I), relative phase (D, G, J), and the map of p values (E, H, K) of the average wavelet cross-spectra calculated separately for the movements directed to three different targets, same format as in Figure 4.

Population analysis of coherent oscillation in the SMA

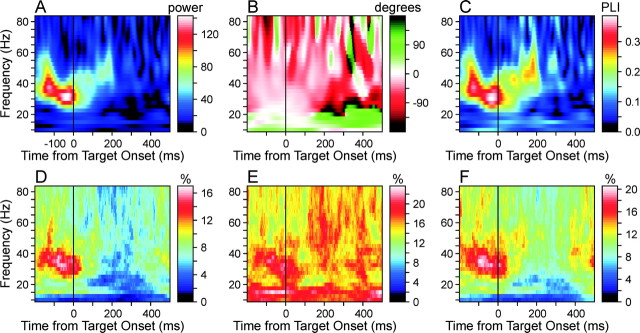
To determine whether there was any systematic pattern in the frequency and relative phase of coherent oscillations across SMA neurons, the average wavelet cross-spectra obtained for individual neuron pairs were averaged in the complex plane across all the neuron pairs examined in this study. In this averaging process, coherent oscillations in different neuron pairs would be canceled if their phase differences were opposite. The resulting population-averaged wavelet cross-spectrum would therefore emphasize coherent oscillations with consistent phase differences, particularly those with small phase differences. This population-averaged cross-spectrum displayed a salient peak in the γ frequency range, and its amplitude reached the maximum value 33 msec before target onset at the frequency of 32.5 Hz (Fig. 6A). The phase difference for this peak amplitude was 21.5°, which corresponds to 1.8 msec (Fig. 6B). Therefore, there was a tendency for γ frequency oscillations in the SMA neurons to become synchronized shortly before target onset. In addition, relatively large power in the γ frequency range was clearly seen throughout the 200 msec period before target onset. During this period, the frequency of oscillation decreased somewhat from 37.5 to 32.5 Hz before target onset and increased to ∼50 Hz during the following 200 msec interval after target onset. Beginning ∼200 msec from target onset, the amplitude of the averaged cross-spectrum decreased substantially. The average reaction time for this task was 242 msec (Lee and Quessy, 2003); therefore, this decrease in the cross-spectrum amplitude began on average ∼40 msec before movement onset.

Figure 6.

Figure 6.

Open in a new tab

Coherent oscillations in the population of SMA neurons. A, B, Amplitude (A) and phase (B) of the population AWCS. C, Phase-locking index for the population AWCS (see Materials and Methods). D-F, Percentage of neuron pairs (N = 217 neuron pairs × 3 movements = 651) with coherent oscillations that were judged to be statistically significant (p < 0.05), according to the methods based on Poisson surrogate spike trains (D), trial shuffling (E), and their combination (F).

The phase in this population-averaged cross-spectrum was relatively close to zero when its amplitude was large (Fig. 6B), and this is expected because oscillations in any neuron pair with nonzero phase lags are likely to be canceled by similar oscillations in another neuron pair with opposite phase differences. However, the population-averaged cross-spectrum provides little information regarding the extent to which the phase difference varies across the population. To examine this issue, a phase-locking index (see Materials Methods) was calculated for the entire population of simultaneously recorded neuron pairs (Fig. 6C). Essentially, the phase-locking index reflects the amount of coherent oscillations that display consistent phase differences across the entire population, normalized by the total amount of coherent oscillations found for individual neuron pairs regardless of their phase differences. This index displayed a pattern similar to that of the population-averaged wavelet cross-spectrum amplitude, suggesting that the latter reflected mostly the result of phase locking that takes place consistently across a large number of neurons. Similar to the amplitude of the population-averaged cross-spectrum, the phase locking index reached its peak 33 msec before target onset at the frequency of 30 Hz. This maximum value was 0.39, suggesting that a substantial number of neuron pairs tended to display similar phase differences. Combined with the observation that the population-averaged cross-spectrum displayed phase differences close to zero at the γ frequency range during the target hold period, these results indicate that there was a robust tendency for synchronous oscillations in the γ frequency range.

Phase difference in coherent oscillations

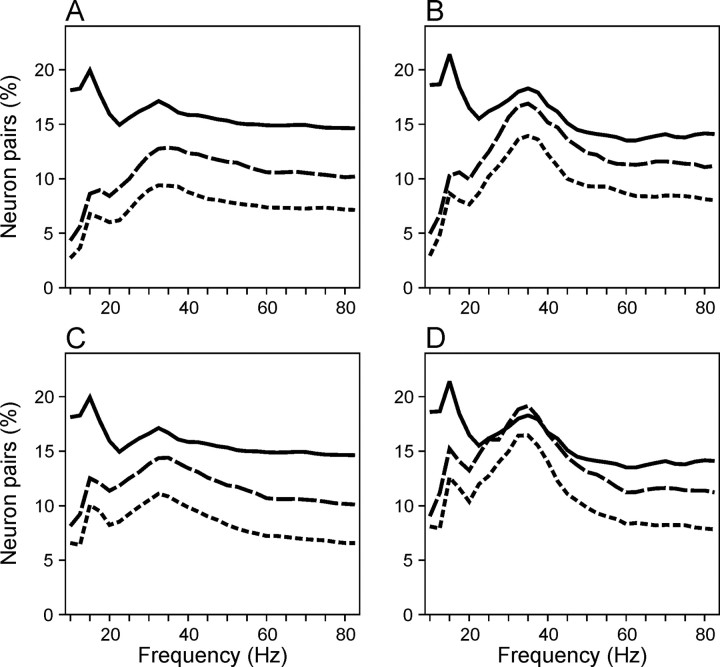
To determine how often neuron pairs in the SMA displayed coherent oscillations with relatively large phase differences, the percentage of cases with statistically significant powers in the average cross-spectra for individual neuron pairs was calculated for each combination of frequency and time. A total of 651 cases were examined in this analysis because each of 217 neuron pairs contributed three different average wavelet cross-spectra, corresponding to the three movements included in the primary trials. As described in Materials and Methods, statistical significance was evaluated using three different methods. Overall, the method based on surrogate spike trains generated consistently lower percentages of neuron pairs with significant coherent oscillations compared with the method based on trial shuffling for the entire range of time and frequency range examined (Figs. 6D,E, 7). The difference was most pronounced in the β frequency range but was also found in the γ frequency range after movement onset.

Figure 7.

Figure 7.

Open in a new tab

A, Average percentage of neuron pairs with statistically significant coherent oscillations collapsed across the entire duration of the analysis window shown in Figure 6. The results obtained with the method of Poisson surrogate spike trains (solid line), trial shuffling (dotted line), and their combination (dashed line) are shown separately. B, Average percentage of neuron pairs with significant coherent oscillations estimated using the same methods as in A during the 200 msec interval before target onset. C, D, Same as in A and B, except that surrogate spike trains were generated as aγ process with a shape parameter of 2 to incorporate a refractory period.

As described in Materials and Methods, these two methods are somewhat complementary because they test different null hypotheses. As a result, each method has a weakness. The results obtained with the method of trial shuffling might have been inflated by correlated changes in spike counts and spike density functions, whereas those with the Poisson surrogate spike trains could have underestimated the amount of coherent oscillations attributable to the increased variance in the cross-spectrum. To resolve these issues, statistical significance of coherent oscillations was also evaluated with γ surrogate spike trains that incorporated a relative refractor period (see Materials and Methods). If the discrepancy between the methods based on Poisson surrogate spike trains and trial shuffling were at least in part attributable to the increased variance in the Poisson spike trains, one would expect that the inclusion of refractory periods in γ surrogate spike trains would increase the estimate of neuron pairs with coherent oscillations in the β frequency. The results were consistent with this prediction (Fig. 7C,D). In addition, a method that combined trial shuffling and Poisson surrogate spike trains was also tested. If the trial-to-trial variation in the spike counts and spike density function inflated the estimates obtained with the method of trial shuffling, the results obtained by this combined approach should be similar to those of trial shuffling because both of these methods used the same spike counts and spike density functions. In contrast, if the destruction of temporal structures in the original spike trains was responsible for the difference between the method based on surrogate spike trains and that of trial shuffling, the results from this third approach should be similar to those of surrogate spike trains. The results from this third method were intermediate between the other two methods (Figs. 6F, 7), indicating that at least a part of the discrepancy was attributable to the increased variance of the cross-spectrum in the surrogate spike trains.

Despite these differences related to the statistical methods, however, the percentage of neuron pairs with significant coherent oscillations revealed two additional features (Fig. 6D-F) not obvious in the population-averaged cross-spectrum (Fig. 6A) or phase-locking index (Fig. 6C). First, coherent oscillations in the β frequency range were found in a significant number of neuron pairs. According to the method based on Poisson surrogate spike trains, the percentage of significant coherent oscillations averaged across the entire duration of the 700 msec analysis window was 6.8% for the frequency of 15 Hz, and this was significantly higher than the used criterion (p < 0.05) of statistical significance (binomial test, p = 0.019). During the last 200 msec of the hold period, this percentage was 8.7% (binomial test, p < 0.001). The corresponding percentages for the method of trial shuffling were 20.0 and 21.4%, respectively, and they were 8.6 and 10.3% when Poisson surrogate spike trains with shuffled spike density functions were used. When γ processes were used to generate surrogate spike trains, the percentage of neuron pairs with significant coherent oscillations in the β frequency range increased somewhat. The averages for the entire analysis window and the last 200 msec of the hold period were 10.1 and 12.6%, respectively (Fig. 7). Second, the method based on Poisson surrogate spike trains showed a modest increase in the percentage of neuron pairs with significant coherent oscillations in the γ frequency range after movement onset (Fig. 6D,F), whereas the method based on shuffling produced much higher estimates throughout the analysis window (Fig. 6E). A large reduction in the amount of coherent oscillations before movement onset was found for both the original Poisson surrogate spike trains and those combined with trial shuffling. Therefore, this discrepancy is probably related to the intertrial variability in the movement-related activity in the SMA.

These results raise the possibility that some neuron pairs displayed coherent oscillations with large phase differences, although they were canceled out in the population-averaged cross-spectrum. To examine this further, the percentages of neuron pairs with significant coherent oscillations were calculated separately for neuron pairs with small (<90°, in-phase) and large (>90°, out-of-phase) phase differences. As expected, the percentage of neuron pairs with significant coherent oscillation in the γ frequency range was substantially higher for in-phase oscillations than for out-of-phase oscillations until ∼100 msec after target onset, regardless of the methods used to evaluate statistical significance (Fig. 8). In contrast, coherent oscillations in the β frequency displayed a much weaker tendency for synchronization (Fig. 8). The method of trial shuffling revealed some bias for synchronization in the β frequency range, but this was still much weaker than in the γ frequency oscillations. The methods based on Poisson surrogate spike trains did not reveal any bias for synchronization in the β frequency range. Overall, these results are consistent with the observation that the population-averaged cross-spectrum and phase-locking index did not reveal clear signs of coherent oscillations in the β frequency range.

Figure 8.

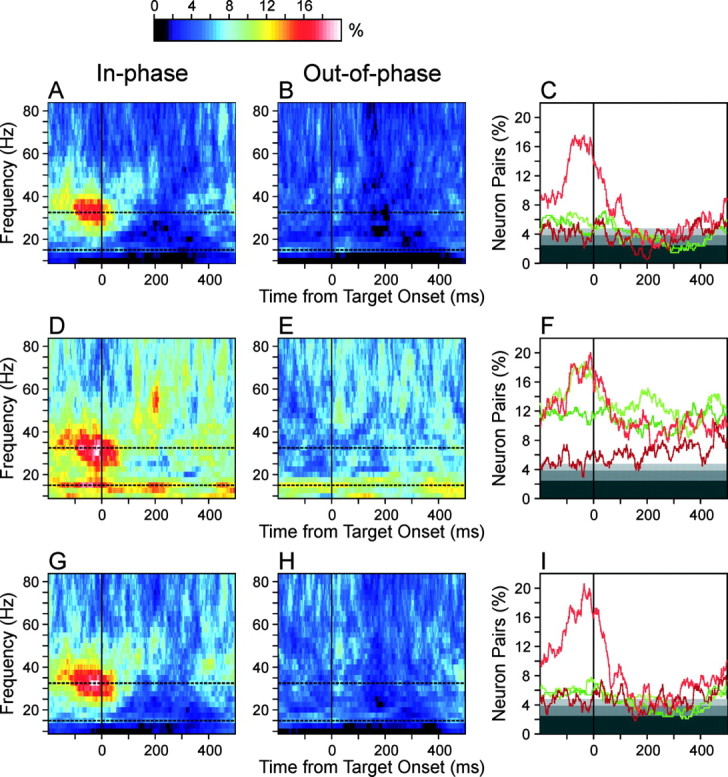
Figure 8.

Open in a new tab

Percentage of neuron pairs that displayed significant coherent oscillations with small (<90°; A, D, G) and large (≥90°; B, E, H) phase differences among neuron pairs in which the average activity was ≥5 spikes/sec for both neurons (N = 335). C, F, I, Percentage of neuron pairs with significant coherent oscillations with small (light) and large (dark) phase differences calculated for the two frequency values selected at the peaks ofβ andγ frequency bands (green, 15 Hz; red, 32.5 Hz) as indicated by the dotted lines in the other panels. Given the level of statistical significance used for testing individual neuron pairs (5%), the expected percentage of neuron pairs with significant coherent oscillations for each of the in-phase and out-of-phase groups is 2.5%, as indicated by the border between the dark and intermediate levels of gray. Light gray and white backgrounds correspond to p < 0.05 and 0.01, respectively. The results obtained with the method of Poisson surrogate spike trains (A-C), trial shuffling (D-F), and their combination (G-I) are shown separately.

Time course of synchronous oscillations

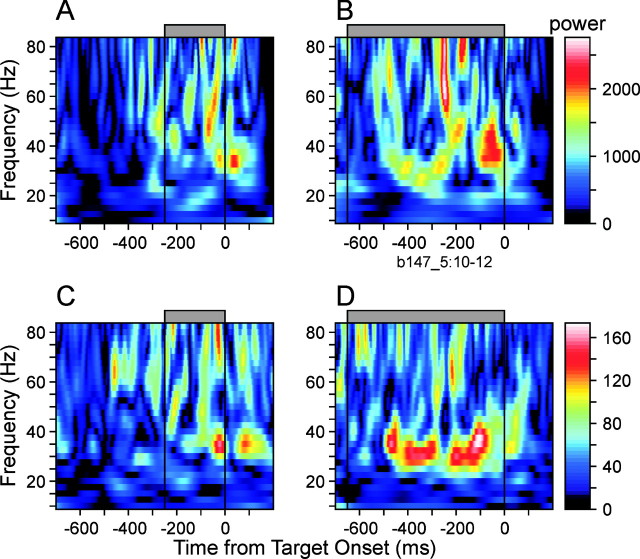
To determine whether synchronization of oscillatory activity was more closely related to the offset of the preceding movement or the onset of the next target, the interval between these two events was systematically varied in 53 neuron pairs (see Materials and Methods). As shown for an example neuron pair (Fig. 9A,B) and for the population average (Fig. 9C,D), synchronous oscillations in the γ frequency range were prolonged as the RSI was increased from 250 to 650 msec, suggesting that such oscillatory activity might reflect the anticipation of upcoming targets. The results in the β-frequency range were not clear, presumably because of the small size of samples examined with this paradigm. This is not surprising because the tendency for synchronous oscillatory activity before target onset was weaker for β frequency oscillations (Fig. 8).

Figure 9.

Figure 9.

Open in a new tab

Effect of the RSI on coherent oscillations in the SMA. A, B, Amplitude of the average wavelet cross-spectrum in an example pair of SMA neurons during a short (250 msec; A) and long (650 msec; B) RSI. C, D, Amplitude of population-averaged wavelet cross-spectrum. RSI is indicated by the gray bar at the top.

Discussion

Coherent oscillations in the SMA

A tendency for individual neurons to synchronize their spikes has been demonstrated in a large number of cortical areas, including the primary sensory cortical areas in visual (Eckhorn et al., 1988; Gray et al., 1989), auditory (Barth and MacDonald, 1996), and somatosensory (Nicolelis et al., 1995; Steinmetz et al., 2000) modalities. Similar findings were also obtained for the posterior parietal cortex and frontal cortex (Vaadia et al., 1995; Murthy and Fetz, 1996a,b; Riehle et al., 1997; Lee et al., 1998; Funahashi and Inoue, 2000; Baker et al., 2001; Constantinidis et al., 2001). Nevertheless, it is not yet clear what role, if any, synchronous spikes play. Theoretical studies showed that synchronous spikes can be more effective in driving a postsynaptic neuron compared with when they are randomly distributed in time (Murthy and Fetz, 1994; Salinas and Sejnowski, 2000; Svirskis and Rinzel, 2000). In addition, recent in vitro physiological studies have uncovered many cellular and network properties necessary for individual cortical neurons to act as coincidence detectors (Larkum et al., 1999; Galarreta and Hestrin, 2001; Pouille and Scaziani, 2001). These findings are consistent with the proposal that cortical neurons synchronize their spikes as a means to combine (or “bind”) different types of information they carry. However, it remains difficult to demonstrate that synchronization or coherent oscillation in the activity of cortical neurons in behaving animals plays a special role in the integration of locally processed information. One common methodological problem stems from the fact that spike trains recorded in behaving animal are not stationary. Previous studies have demonstrated that the presence of synchronous spikes or oscillatory activity may last only for brief periods related to various behavioral events (Murthy and Fetz, 1996a; Riehle et al., 1997), suggesting that spike synchronization is a dynamic process. Similarly, many SMA neurons examined in the present study displayed coherent oscillations in their activity, but they were relatively brief. This was analyzed with the wavelet cross-spectrum, because traditional methods, such as cross-correlation functions or the Fourier spectrum, are not adequate for the analysis of nonstationary spike trains. The results showed that coherent oscillations occurred throughout the task mostly in the β and γ frequency bands. Interestingly, the pattern of phase difference in coherent oscillation changed during the task. For both β and γ frequency oscillations, there was a tendency for oscillatory activity to be synchronized during the hold period before target onset. This tendency was stronger for the γ frequency band. The duration of synchronized oscillations in the γ frequency range increased when the duration of the hold period was lengthened. For the β frequency band, a weak tendency for synchronization was found only with the method of trial shuffling. For both frequency bands, the proportion of neuron pairs with synchronized oscillation decreased after target onset.

Functions of coherent oscillations in the motor cortex

Although a large number of studies have reported synchronous spikes in many different brain regions, coherent oscillations have been found less consistently in the recordings of single-neuron activity. This discrepancy might be related to the fact that coherent oscillations tend to occur briefly and that their frequencies might change over time, as demonstrated in the present study. In addition, a large number of trials may be required to detect a statistically significant level of coherent oscillation for neurons with low levels of activity. Recordings of local field potentials (LFP) or electroencephalographic (EEG) activities have commonly revealed oscillatory activity (Niedermeyer and Lopes da Silva, 1999). This is likely the result of the averaging process intrinsic to the recording of field potentials because many neuron pairs examined in the present study show little or no sign of coherent oscillations. However, averaging is also a weakness in field potential recording studies because coherent oscillations in single-neuron activity with large phase differences may not be detected. For example, many neuron pairs examined in the present study displayed coherent oscillations in the β frequency range with phase differences of ≥90°. In some neuron pairs, oscillations with such large phase differences were also found in the γ frequency range. These oscillations with large phase differences were cancelled in the population-averaged wavelet cross-spectrum, as would happen in the recordings of field potentials.

With these caveats, the fact that synchronous oscillations in the γ frequency range dominated the pattern in the population-averaged cross-spectrum is consistent with the results from previous EEG and electrocorticographic (ECoG) recording studies in human subjects. For example, the power of the EEG activity recorded over the SMA in human subjects decreased (referred to as event-related desynchronization) for the α frequency range but increased (event-related synchronization) for the γ frequency range during an interval of several seconds before movement onset (Andrew and Pfurtscheller, 1996). Similar results have been observed in ECoG activity (Ohara et al., 2000, 2001). Although EEG or ECoG activity in the human SMA has been examined only in a small number of studies, the results from these studies are also similar to the patterns found in the regions around the primary motor and somatosensory cortex (Pfurtscheller et al., 1993; Andrew and Pfurtscheller, 1996; Crone et al., 1998a,b; Aoki et al., 1999; Pfurtscheller and Lopes da Silva, 1999; Ohara et al., 2001). LFP recordings obtained from the primary motor cortex also display an increase in the γ frequency oscillation in association with preparation of upcoming movements (Donoghue et al., 1998).

There are also some differences between the results from the present study and previous EEG and ECoG recording studies. Most noticeably, previous studies have commonly observed opposite changes in the β and γ frequency bands (Crone et al., 1998a,b; Aoki et al., 1999; Ohara et al., 2001), whereas in the present study, the increase in the percentages of neuron pairs with synchronous oscillatory activity in the γ frequency range was found without the corresponding decrease in the β frequency band. For the method of trial shuffling, synchronized oscillation in the β and γ frequency bands displayed a similar time course. This discrepancy might be related to the differences in recording methods, but it is also possible that the discrepancy was attributable to the differences in behavioral tasks. For the majority of the neuron pairs examined in the present study, a target for the next movement was presented only 250 msec after the completion of the previous movement. It is possible that desynchronization in the β frequency range might develop more slowly.

Despite the large number of studies demonstrating oscillatory activity in distinct frequency bands, functions of these rhythmic brain activities are not yet completely understood. A few studies have provided evidence that synchronous spikes or an oscillatory pattern in spike trains might carry behaviorally relevant information independent of other measures of neural activity such as spike rates (Vaadia et al., 1995; Riehle et al., 1997). Other studies found that synchronization of oscillatory activity might occur more frequently during the periods in which the animal anticipates the delivery of a stimulus and prepares for required behavioral responses (Cardoso de Oliveira et al., 1997; Donoghue et al., 1998). In addition, it has been shown that synchronous spikes and synchronization of oscillatory activity in the γ frequency band occur more frequently for neurons activated by attended stimuli (Steinmetz et al., 2000; Fries et al., 2001). These results have been interpreted according to the proposal that coherent oscillation in the activity of cortical neurons contributes to the establishment of the behavioral context or task set (Llinás et al., 1998; Engel et al., 2001).

Many studies have also shown that field potential recordings from multiple brain regions display task-dependent changes in their coherence (Bressler et al., 1993; Sarnthein et al., 1998; Rodriguez et al., 1999; Srinivasan et al., 1999; von Stein et al., 1999; Fries et al., 2001). Activity throughout the cortical network involved in the preparation of movements might be integrated through the same mechanism. For example, the oscillatory field potentials recorded in the SMA and the primary motor cortex become synchronized before movement onset (Ohara et al., 2001). Coherent oscillations in the activity of individual SMA neurons might provide a substrate for such interareal synchronization of oscillatory activity. In future studies, this possibility needs to be tested directly with simultaneous single-unit recordings in multiple cortical regions.

Footnotes

This work was supported by National Institutes of Health Grants R01-MH59216 and P30-EY01319. I am grateful to Rita Farrell, Ryan Murray, and Stephan Quessy for help with the experiment and Bruno Averbeck, Michelle Conroy, and Jeong-woo Sohn for comments on this manuscript.

Correspondence should be addressed to Dr. Daeyeol Lee at the above address. E-mail: dlee@cvs.rochester.edu.

Copyright © 2003 Society for Neuroscience 0270-6474/03/236798-12$15.00/0

References

  1. Aertsen AMHJ, Gerstein GL, Habib MK, Palm G ( 1989) Dynamics of neuronal firing correlation: modulation of “effective connectivity.” J Neurophysiol 61: 900-917. [DOI] [PubMed] [Google Scholar]
  2. Andrew C, Pfurtscheller G ( 1996) Event-related coherence as a tool for studying dynamic interaction of brain regions. Electroencephalogr Clin Neurophysiol 98: 144-148. [DOI] [PubMed] [Google Scholar]
  3. Aoki F, Fetz EE, Shupe L, Lettich E, Ojemann GA ( 1999) Increased gamma-range activity in human sensorimotor cortex during performance of visuomotor task. Clin Neurophysiol 110: 524-537. [DOI] [PubMed] [Google Scholar]
  4. Baker SN, Lemon RN ( 2000) Precise spatiotemporal repeating patterns in monkey primary and supplementary motor areas occur at chance levels. J Neurophysiol 84: 1770-1780. [DOI] [PubMed] [Google Scholar]
  5. Baker SN, Spinks R, Jackson A, Lemon RN ( 2001) Synchronization in monkey motor cortex during a precision grip task. I. Task-dependent modulation in single-unit synchrony. J Neurophysiol 85: 869-885. [DOI] [PubMed] [Google Scholar]
  6. Barth DS, MacDonald KD ( 1996) Thalamic modulation of high-frequency oscillating potentials in auditory cortex. Nature 383: 78-81. [DOI] [PubMed] [Google Scholar]
  7. Breitenberg V, Schüz A ( 1998) Cortex: statistics and geometry of neuronal connectivity. Berlin: Springer.
  8. Bressler SL, Coppola R, Nakamura R ( 1993) Episodic multiregional cortical coherence at multiple frequencies during visual task performance. Nature 366: 153-156. [DOI] [PubMed] [Google Scholar]
  9. Brody CD ( 1999) Correlations without synchrony. Neural Comput 11: 1537-1551. [DOI] [PubMed] [Google Scholar]
  10. Cardoso de Oliveira S, Thiele A, Hoffmann K-P ( 1997) Synchronization of neuronal activity during stimulus expectation in a direction discrimination task. J Neurosci 17: 9248-9260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Constantinidis C, Franowicz MN, Goldman-Rakic PS ( 2001) Coding specificity in cortical microcircuits: a multiple-electrode analysis of primate prefrontal cortex. J Neurosci 21: 3646-3655. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Crone NE, Miglioretti DL, Gordon B, Sieracki JM, Wilson MT, Uematsu S, Lesser RP ( 1998a) Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. I. Alpha and beta event-related desynchronization. Brain 121: 2271-2299. [DOI] [PubMed] [Google Scholar]
  13. Crone NE, Miglioretti DL, Gordon B, Lesser RP ( 1998b) Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. Brain 121: 2301-2315. [DOI] [PubMed] [Google Scholar]
  14. Donoghue JP, Sanes JN, Hatsopoulos NG, Gaál G ( 1998) Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. J Neurophysiol 79: 157-173. [DOI] [PubMed] [Google Scholar]
  15. Eckhorn R, Bauer R, Jordan W, Brosch M, Kruse W, Munk M, Reitboeck HJ ( 1988) Coherent oscillations: a mechanism of feature linking in the visual cortex? Biol Cybern 60: 121-130. [DOI] [PubMed] [Google Scholar]
  16. Engel AK, Fries P, Singer W ( 2001) Dynamic predictions: oscillations and synchrony in top-down processing. Nat Rev Neurosci 2: 704-716. [DOI] [PubMed] [Google Scholar]
  17. Fries P, Reynolds JH, Rorie AE, Desimone R ( 2001) Modulation of oscillatory neuronal synchronization by selective visual attention. Science 291: 1560-1563. [DOI] [PubMed] [Google Scholar]
  18. Funahashi S, Inoue M ( 2000) Neuronal interactions related to working memory processes in the primate prefrontal cortex revealed by cross-correlation analysis. Cereb Cortex 10: 535-551. [DOI] [PubMed] [Google Scholar]
  19. Galarreta M, Hestrin S ( 2001) Spike transmission and synchrony detection in networks of GABAergic interneurons. Science 292: 2295-2299. [DOI] [PubMed] [Google Scholar]
  20. Gray CM ( 1999) The temporal correlation hypothesis of visual feature integrations: still alive and well. Neuron 24: 31-47. [DOI] [PubMed] [Google Scholar]
  21. Gray CM, König P, Engel AK, Singer W ( 1989) Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature 338: 334-337. [DOI] [PubMed] [Google Scholar]
  22. Larkum ME, Zhu JJ, Sakmann B ( 1999) A new cellular mechanism for coupling inputs arriving at different cortical layers. Nature 398: 338-341. [DOI] [PubMed] [Google Scholar]
  23. Lebedev MA, Wise SP ( 2000) Oscillations in the premotor cortex: single-unit activity from awake, behaving monkeys. Exp Brain Res 130: 195-215. [DOI] [PubMed] [Google Scholar]
  24. Lee D ( 2000) Learning of spatial and temporal patterns in sequential hand movements. Cognit Brain Res 9: 35-39. [DOI] [PubMed] [Google Scholar]
  25. Lee D ( 2002) Analysis of phase-locked oscillations in multi-channel single-unit spike activity with wavelet cross-spectrum. J Neurosci Methods 115: 67-75. [DOI] [PubMed] [Google Scholar]
  26. Lee D, Quessy S ( 2003) Activity in the supplementary motor area related to learning and performance during a sequential visuomotor task. J Neurophysiol 89: 1039-1056. [DOI] [PubMed] [Google Scholar]
  27. Lee D, Port NL, Kruse W, Georgopoulos AP ( 1998) Variability and correlated noise in the discharge of neurons in motor and parietal areas of the primate cortex. J Neurosci 18: 1161-1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Llinás R, Ribary U, Contreras D, Pedroarena C ( 1998) The neuronal basis for consciousness. Philos Trans R Soc Lond B Biol Sci 353: 1841-1849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. MacKay WA ( 1997) Synchronized neuronal oscillations and their role in motor process. Trends Cogn Sci 1: 176-183. [DOI] [PubMed] [Google Scholar]
  30. Murthy VN, Fetz EE ( 1994) Effects of input synchrony on the firing rate of a three-conductance cortical neuron model. Neural Comput 6: 1111-1126. [Google Scholar]
  31. Murthy VN, Fetz EE ( 1996a) Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behavior. J Neurophysiol 76: 3949-3967. [DOI] [PubMed] [Google Scholar]
  32. Murthy VN, Fetz EE ( 1996b) Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys. J Neurophysiol 76: 3968-3982. [DOI] [PubMed] [Google Scholar]
  33. Nicolelis MAL, Baccala LA, Lin RCS, Chapin JK ( 1995) Sensorimotor encoding by synchronous neural ensemble activity at multiple levels of the somatosensory system. Science 268: 1353-1358. [DOI] [PubMed] [Google Scholar]
  34. Niedermeyer E, Lopes da Silva F ( 1999) Electroencephalography: basic principles, clinical applications, and related fields, Ed 4. Baltimore: Williams & Wilkins.
  35. Ohara S, Ikega A, Kunieda T, Yazawa S, Baba K, Nagamine T, Taki W, Hashimoto N, Mihara T, Shibasaki H ( 2000) Movement-related changes of electrocorticographic activity in human supplementary motor area proper. Brain 123: 1203-1215. [DOI] [PubMed] [Google Scholar]
  36. Ohara S, Mima T, Baba K, Ikeda A, Kunieda T, Matsumoto R, Yamamoto J, Matsuhashi M, Nagamine T, Hirasawa K, Hori T, Mihara T, Hashimoto N, Salenius S, Shibasaki H ( 2001) Increased synchronization of cortical oscillatory activities between human supplementary motor and primary sensorimotor areas during voluntary movements. J Neurosci 21: 9377-9386. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Oram MW, Földiák P, Perrett DI, Sengpiel F ( 1998) The “ideal homunculus”: decoding neural population signals. Trends Neurosci 21: 259-265. [DOI] [PubMed] [Google Scholar]
  38. Oram MW, Wiener MC, Lestienne R, Richmond BJ ( 1999) Stochastic nature of precisely timed spike patterns in visual system neuronal responses. J Neurophysiol 81: 3021-3033. [DOI] [PubMed] [Google Scholar]
  39. Panzeri S, Schultz SR, Treves A, Rolls ET ( 1999) Correlations and the encoding of information in the nervous system. Proc R Soc Lond B Biol Sci 266: 1001-1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Perkel DH, Gerstein GL, Moore GP ( 1967) Neuronal spike trains and stochastic point processes. II. Simultaneous spike trains. Biophys J 7: 419-440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Pfurtscheller G, Lopes da Silva FH ( 1999) Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol 110: 1842-1857. [DOI] [PubMed] [Google Scholar]
  42. Pfurtscheller G, Neuper C, Kalcher J ( 1993) 40-Hz oscillations during motor behavior in man. Neurosci Lett 164: 179-182. [DOI] [PubMed] [Google Scholar]
  43. Pouille F, Scaziani M ( 2001) Enforcement of temporal fidelity in pyramidal cells by somatic feed-forward inhibition. Science 293: 1159-1163. [DOI] [PubMed] [Google Scholar]
  44. Riehle A, Grün S, Diesmann M, Aertsen A ( 1997) Spike synchronization and rate modulation differentially involved in motor cortical function. Science 278: 1950-1953. [DOI] [PubMed] [Google Scholar]
  45. Rodriguez E, George N, Lachaux J-P, Martinerie J, Renault B, Varela FJ ( 1999) Perception's shadow: long-distance synchronization of human brain activity. Nature 397: 430-433. [DOI] [PubMed] [Google Scholar]
  46. Roelfsema PR, Engel AK, König P, Singer W ( 1997) Visuomotor integration is associated with zero time-lag synchronization among cortical areas. Nature 385: 157-161. [DOI] [PubMed] [Google Scholar]
  47. Salinas E, Sejnowski T ( 2000) Impact of correlated synaptic input on output firing rate and variability in simple neuronal models. J Neurosci 20: 6193-6209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Sarnthein J, Petsche H, Rappelsberger P, Shaw GL, von Stein A ( 1998) Synchronization between prefrontal and posterior association cortex during human working memory. Proc Natl Acad Sci USA 95: 7092-7096. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Shadlen MN, Newsome WT ( 1998) The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci 18: 3870-3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Srinivasan R, Russell DP, Edelman GM, Tononi G ( 1999) Increased synchronization of neuromagnetic responses during conscious perception. J Neurosci 19: 5435-5448. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Steinmetz PN, Roy A, Fitzgerald PJ, Hsiao SS, Johnson KO, Neibur E ( 2000) Attention modulates synchronized neuronal firing in primate somatosensory cortex. Nature 404: 187-190. [DOI] [PubMed] [Google Scholar]
  52. Svirskis G, Rinzel J ( 2000) Influence of temporal correlation of synaptic input on the rate and variability of firing in neurons. Biophys J 79: 629-637. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Torrence C, Compo GP ( 1998) A practical guide to wavelet analysis. Bull Am Meteorol Soc 79: 61-78. [Google Scholar]
  54. Vaadia E, Haalman I, Abeles M, Bergman H, Prut Y, Slovin H, Aertsen A ( 1995) Dynamics of neuronal interactions in monkey cortex in relation to behavioral events. Nature 373: 515-518. [DOI] [PubMed] [Google Scholar]
  55. Varela F, Lachaux J-P, Rodriguez E, Marinerie J ( 2001) The brainweb: phase synchronization and large-scale integration. Nat Rev Neurosci 2: 229-239. [DOI] [PubMed] [Google Scholar]
  56. von Stein A, Rappelsberger P, Sarnthein J, Petsche H ( 1999) Synchronization between temporal and parietal cortex during multimodal object processing in man. Cereb Cortex 9: 137-150. [DOI] [PubMed] [Google Scholar]
  57. von Stein A, Chiang C, König P ( 2000) Top-down processing mediated by interareal synchronization. Proc Natl Acad Sci USA 97: 14748-14753. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES