Neural Noise and Movement-Related Codes in the Macaque Supplementary Motor Area

Abstract

We analyzed the variability of spike counts and the coding capacity of simultaneously recorded pairs of neurons in the macaque supplementary motor area (SMA). We analyzed the mean-variance functions for single neurons, as well as signal and noise correlations between pairs of neurons. All three statistics showed a strong dependence on the bin width chosen for analysis. Changes in the correlation structure of single neuron spike trains over different bin sizes affected the mean-variance function, and signal and noise correlations between pairs of neurons were much smaller at small bin widths, increasing monotonically with the width of the bin. Analyses in the frequency domain showed that the noise between pairs of neurons, on average, was most strongly correlated at low frequencies, which explained the increase in noise correlation with increasing bin width.

The coding performance was analyzed to determine whether the temporal precision of spike arrival times and the interactions within and between neurons could improve the prediction of the upcoming movement. We found that in ∼62% of neuron pairs, the arrival times of spikes at a resolution between 66 and 40 msec carried more information than spike counts in a 200 msec bin. In addition, in 19% of neuron pairs, inclusion of within (11%)- or between-neuron (8%) correlations in spike trains improved decoding accuracy. These results suggest that in some SMA neurons elements of the spatiotemporal pattern of activity may be relevant for neural coding.

Introduction

Behavioral performance is constrained by the information processing capacity of the nervous system. For many tasks, this processing capacity can be understood by studying the coding properties of cortical neural networks. A first step in the study of these networks is to understand the way in which individual neurons or ensembles of neurons encode information. The number of possible codes that neurons may be using, independently or as ensembles, is immense (Perkel and Bullock, 1969), and therefore a systematic approach to the investigation of putative neural codes is important. One can approach this question by assessing whether patterns in neural responses within or between neurons are correlated with behavioral variables. After having identified a potential code, one can then ask whether the code is behaviorally relevant. The total information in the code can be considered an upper limit with respect to behavior, because the networks mediating the behavior may extract only a portion of the information available.

The question of which parameters of the neuronal signal carry information has an extensive theoretical and empirical history. Early theoretical papers often considered the limit of the information content of various neural codes (MacKay and McCulloch, 1952; Barlow, 1963), whereas early empirical work by Mountcastle and colleagues (Mountcastle et al., 1968; Talbot et al., 1968) initiated the study of the neuronal basis of psychophysical performance and explicitly explored the question of which parameter of the neural signal accounted for sensory detection thresholds (Mountcastle et al., 1968, 1990). Other empirical studies have estimated the amount of information that neurons can carry about stimulus or behavioral parameters (Heggelund and Albus, 1978; Parker and Hawken, 1985; Bradley et al., 1987; Hernandez et al., 2000) and compared the coding performance of single neurons with the psychophysical performance of behaving animals (Newsome et al., 1989; Vogels and Orban, 1990).

Our main goal in this paper was to explore the information content of several related neural codes, as well as the statistical structure of the neural signal. The mean-variance function as well as the correlation in the signal and the correlation in the noise were found to depend strongly on the bin width chosen for analysis. The results of the decoding analyses suggest that information about upcoming movements is coded in the arrival times of spikes on a time scale as small as ∼40 msec and that using some form of correlation between pairs of neurons or between different time points within a given neuron improved the prediction of the movement for 19% of the pairs of neurons in our sample.

Materials and Methods

Neurons analyzed in the present study were recorded from the left caudal supplementary motor area (SMA-proper or F3) in two rhesus macaques performing a series of visually guided reaching movements. The detailed methods of recording as well as the behavioral task have been published previously (Lee and Quessy, 2003). All of the procedures used in this study were approved by the University of Rochester Committee on Animal Research and conformed to the principles outlined in the NIH Guide for the Care and Use of Laboratory Animals (publication no. 85-23, revised 1985).

Behavioral task

Two animals were trained on a serial reaction time (SRT) task. They sat facing a computer monitor on which a series of targets was presented. There were 16 possible target locations defined by a 4 × 4 grid. A touch screen placed horizontally in front of the animal was used for behavioral input. The animals indicated acquisition of each target by contacting the corresponding location on the touch screen. Each subsequent target in the sequence appeared 250 msec after the previous target had been acquired. A trial consisted of a sequence of 10 target acquisitions. If the 10 targets were acquired successfully, a juice reward was given. Within the task, four different types of sequences were presented (Lee and Quessy, 2003). In the random condition, the sequence of target locations was selected pseudorandomly for every trial. In the primary condition, the monkey executed a repeating sequencing of three targets (i.e., a single trial was three repeats of the three target sequence), with the first target of the sequence repeated at the end of the sequence, (for example, ABCABCABCA). In the secondary condition, the monkey executed a different repeating sequence of three targets. In the final condition, the monkey began executing the primary sequence and then switched to the secondary sequence from seventh target onward. New primary and secondary sequences were selected pseudorandomly for each day's session. A block of trials consisted of five sequences from the primary condition, and one sequence from each of the remaining conditions. Trial types were presented in a randomized block design. In this paper, we analyzed only the data from the primary condition, because trials in this condition provided a large amount of data with consistent visual stimuli and behavioral responses.

Data analysis

Analysis of neuronal variability. The data for each behavioral trial were split into epochs corresponding to each of the 10 movements, 1 for each target in the movement. Data from the first movement were not considered because they followed the intertrial interval and varied from trial to trial. For the analysis of variability in the neural activity, spikes occurring during a 600 msec interval from 300 msec before to 300 msec after target presentation were binned using bin sizes of 5, 10, 20, 25, 33, 40, 50, 66, 100, and 200 msec.

We calculated the mean and variance of the neural activity for each neuron in different time bins relative to stimulus onset. We also calculated the correlation in the mean response and the correlation in the residual response between pairs of neurons. The correlation in the mean response, or signal correlation (Gawne and Richmond, 1993; Lee et al., 1998), was calculated by first concatenating the poststimulus time histogram (PSTH) for each movement for each pair of neurons. This resulted in a vector with 3n elements for each neuron, where n was the number of bins into which the 600 msec epoch was divided, and there were three different movements in the primary condition. Correlations were calculated between these vectors. Correlation in the residual response, or noise correlation, was calculated by first subtracting the mean response from each trial, giving the residual response. The correlation in these vectors between neurons was calculated separately for each movement as an estimate of the correlation in the noise (Gawne and Richmond, 1993; Zohary et al., 1994; Lee et al., 1998).

We also performed three analyses in the frequency domain. Because a large quantity of data were available, no smoothing in the frequency domain was necessary (Jarvis and Mitra, 2001). Also, the rectangular window was used in the time domain, because it has the smallest main lobe and therefore gives the best frequency resolution, although at the expense of larger side lobes (Oppenheim and Schafer, 1989). Using other windowing functions would lead to a broadening of the peaks in the power and coherence plots. All frequency domain values presented in this paper were calculated across the 600 msec window beginning 300 msec before target onset, at a 1 msec resolution. Analyses were implemented in C ⁺⁺, using compiled versions of the fft and cohere functions from Matlab (The Mathworks, Inc., Natick, MA).

Estimates of the population periodogram of the mean response (signal) were calculated by averaging across the individual periodograms of each neuron. The periodogram, P_xx(k), of the mean response for each neuron was calculated by taking the fast Fourier transform (FFT) of the PSTH and normalizing by the length of the signal (Papoulis, 1991):

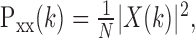1

where X(k) is the FFT of the signal, in this case the PSTH, and N is its length, equal to 600. We also estimated the periodogram of the noise, by calculating the periodogram of the residual of each trial, with the residual calculated as defined above, and then averaging across trials for individual neurons and finally across neurons. In the final frequency domain analysis, we analyzed the coherence between residuals of neuron pairs. The coherence is defined as:

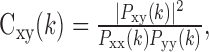2

where P_xy(k) is the cross spectrum (Papoulis, 1991). Each trial was treated as a data segment. These estimates were also averaged across the entire population to produce the population coherence plots. Because the rectangular window used in the time domain can result in power bleeding between frequencies (Oppenheim and Schafer, 1989), we also examined periodograms and coherence functions calculated with the mean removed. There was little difference in the non-DC components, so we show the plots with the DC information intact, because it is informative. In Results, we will make comparisons between the frequency domain analyses and the binned analyses in the time domain. Because calculating histograms in the time domain leads to aliasing in the frequency domain, the time domain analyses could have been performed by first low-pass filtering the spike trains and then subsampling at the corresponding bin width; however, binning is a much more common practice in the analysis of neurophysiological data. Furthermore, we performed many of the decoding and noise analyses by filtering and then subsampling, and the main results of the paper were not changed. Therefore, we present the results from the binning analyses to make comparisons between studies easier.

Decoding analyses. After we examined the statistical structure of the neural activity, we developed decoding algorithms that used the neural activity of pairs of simultaneously recorded neurons to estimate the target to which the monkey reached. We performed the decoding analyses using a 200 msec window that began at target onset. We restricted our decoding analyses to this window so that we could explore relatively small bin sizes without generating too many degrees of freedom in our model.

We will discuss our analysis in terms of a Bayesian framework (Oram et al., 1998; Zhang et al., 1998). Within our task, however, the prior probability of each movement was the same, and therefore Bayesian and maximum likelihood decoding frameworks are equivalent. In the decoding analysis, the target (or corresponding movement) was predicted by selecting the target with the maximum probability over the joint distribution of neural activity and possible targets. This can be formalized as:

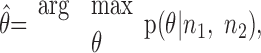3

where 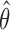is the estimated target for the subsequent movement, and p(θ|n₁,n₂) is the conditional distribution of θ given the response of two neurons across several bins. The conditional probability of θ is given by Bayes rule:

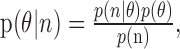4

where p(θ) is the prior probability of a given target, n is the vector of neural responses, and p(n) is a normalizing constant, calculated as:

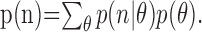5

In pilot studies we explored both Poisson and Gaussian distribution for the data. We will only discuss results from the Gaussian distribution, because it generally provided better decoding performance. The multivariate Gaussian distribution is given by:

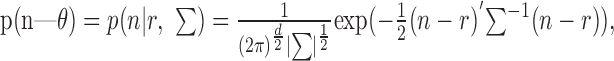6

where n is a vector of spike counts for each bin and each neuron for a given trial, r is the corresponding vector of mean spike counts for a given target, ∑ is the covariance matrix of the spike counts for each bin and each neuron, ∥ indicates the determinant of the matrix, and d is the dimensionality of the firing rate vector being considered. In the analyses, we manipulated r by changing the number of bins into which the 200 msec epoch was divided. Thus, r was always a vector of the response across two neurons, but in the case of 50 msec bins, r had eight elements, four for each bin for each neuron, whereas in the case of 200 msec bins, r had only two elements. The covariance matrix was calculated accordingly. A separate version of Equation 6 was estimated for each target. Thus the decoding procedure was as follows. For a given neural response, n, the probability of each target was assessed using Equation 6, with the mean, r, and covariance, ∑, which corresponded to each target. The target with the maximum probability was then selected as the estimate.

Some neurons failed to fire spikes in one or more of their response bins. This resulted in a column of zeros in the data matrix, which leads to a noninvertible covariance matrix. We corrected the problem by eliminating those columns from the data matrix and still treating the model as if it had all of its parameters.

We assessed the ability of specific interaction terms to improve the prediction of the subsequent target. We restricted our analyses to a set of specific hypotheses. This was done by setting all or a subset of the off-diagonal terms of the covariance matrix, ∑, in Equation 6 to zero, and, in the case of the variance equals mean (VEM) model, by restricting the diagonal terms of the matrix to be equal to the mean. A matrix with all but the diagonal matrix entries set to zero will be referred to as a diagonal matrix. For the main analyses, only one covariance matrix was estimated for each pair of neurons, for all targets. The VEM model had a diagonal covariance matrix, with the diagonal elements set equal to the mean, similar to a Poisson distribution. The “independent” model had a diagonal covariance matrix, with each variance along the diagonal estimated from the data. The “between” model included off-diagonal elements corresponding to interactions between identical time bins between the neurons in the pair. The “within” model included the off-diagonal elements of the covariance matrix corresponding to interactions between adjacent time bins of the neural spike train. Finally, the “full” model included all off-diagonal elements of the covariance matrix. We also examined models that had separate covariance matrices for each movement direction. We did this by first selecting the best model from among the models with a pooled covariance matrix and then testing whether a model that had a separate covariance matrix for each movement but the same off-diagonal elements set to zero in each of the separate matrices performed better. For example, if the model selection procedure chose the between model as best, we compared the between model that had a single covariance matrix calculated from the neural response pooled across movements with a between model that had a separate covariance matrix for each movement.

Model selection. We used two techniques to decide which of the various models described above provided the best explanation of the data: Akaike's information criterion (AIC) and K-fold cross validation (CV). AIC uses the likelihood of the model parameters, conditioned on the data and the model to discriminate between models. The likelihood f(X, P_m) is the product of the likelihood of all data points, as predicted by the model,

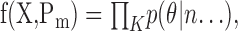7

where X is the data set, with K samples, the likelihood p(θ|n...) is the probability of sample k, i.e., the probability of the actual target for a given trial, and P_m indicates that the likelihood is calculated using the maximum likelihood parameters. AIC is then calculated as follows:

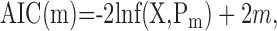8

where m is the number of free parameters of the model under consideration. The model within the family of models that had the minimum AIC was selected as the best model.

We also used K-fold CV (Efron and Tibshirani, 1998) to assess model performance. CV has been shown to be asymptotically equivalent to AIC (Stone, 1977); however, the small sample properties of the two approaches are less well understood. In CV, the data are split repeatedly into two non-overlapping sets. The model is estimated with one set, and its performance is assessed on the other. In our implementation, the data were split 10 times (we also tried splits of 3, 5, and 20, but the results were similar). For each split, 1 of every 10 trials was placed in the test data set, and the other 9 trials were placed in the data set used for estimating the model. The model was then estimated, and its performance was evaluated using the test data set. This was repeated 10 times, such that all trials were included in one of the test data sets. Results were compiled across the 10 runs. The model with the highest percentage correct performance was selected as the best model.

Finally, the finite impulse response high-pass filter, discussed near the end of Results, had an order of 2000. The high filter order was necessary to confine the stop band to a rather small set of frequencies. The cutoff frequency was 0.5 Hz, and the filter had an almost linear roll-off from 1 Hz to DC, achieving an amplitude response of 0.15 at DC. Thus low frequencies were strongly suppressed.

Results

Database

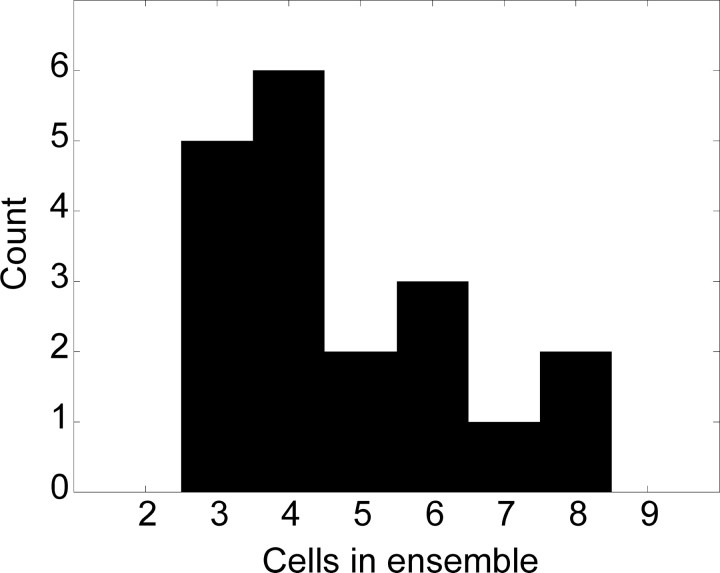
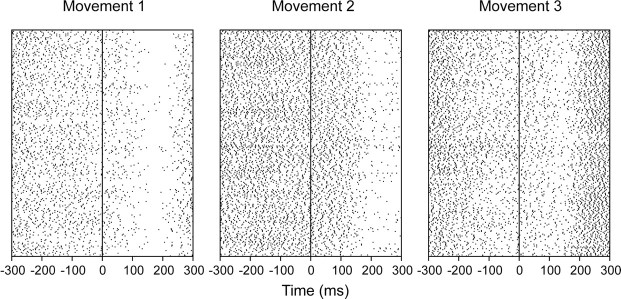
The analyses were performed on 19 ensembles of simultaneously recorded neurons containing a total of 90 single neurons from the SMA of two monkeys (12 ensembles from monkey 1, 7 ensembles from monkey 2). The distribution of the number of neurons in each ensemble is shown in Figure 1. A total of 193 pairs of neurons were available for the analyses. All ensembles were recorded for at least 152 trials in the task condition that we analyzed (average number of trials per ensemble = 267). The SRT task made it possible to collect a large number of examples of each movement, because the animal repeated each movement three times in every trial. Therefore at least 456 movements were available for each of the 3 movements, which resulted in at least 1368 total movements (average number of movements = 2402). Figure 2 shows 249 trials, of each of the three movements, for an example neuron. The rasters are aligned to target onset. The neural response to movements one and two shows a reduction in activity before movement onset, which may be a return to baseline or an inhibition. For the noise analyses, we analyzed the neural activity from 300 msec before target onset to 300 msec after target onset. For the decoding analyses we restricted the time window to the period from 0 to 200 msec after target onset. The time window was divided into bins of 5, 10, 20, 25, 33, 40, 50, 66, 100, and 200 msec, which approximately divided the epoch into an integer number of bins. Individual time bins at a specific time relative to target onset from a single neuron for a single movement were considered as separate random variables.

Figure 1.

Distribution of number of neurons in each ensemble.

Figure 2.

Single-cell raster for 249 trials of each of the three movements. These example movements were the first three of each behavioral trial. Rasters are aligned to target onset (0 msec).

Noise analyses

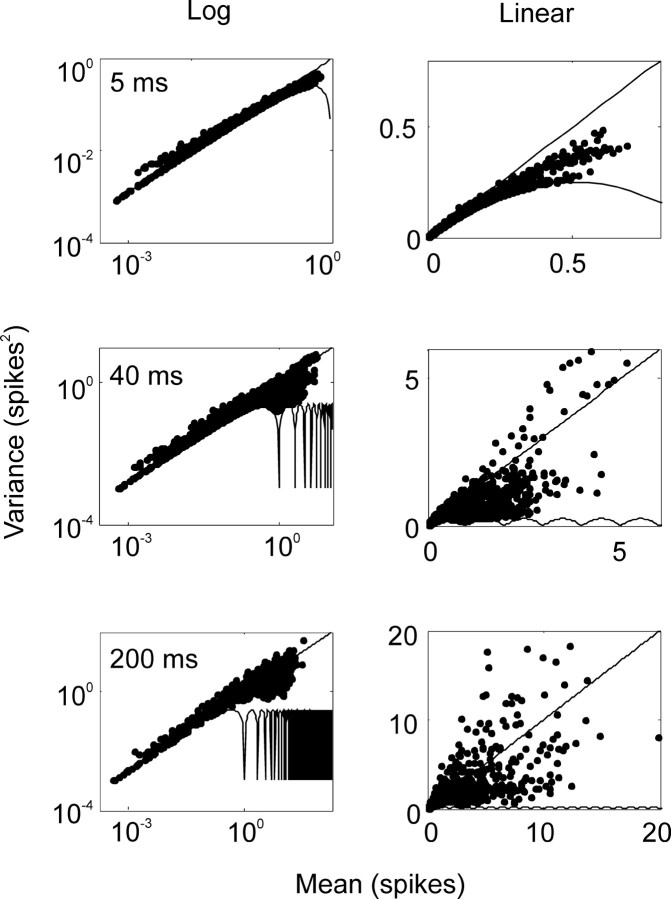
We began by exploring the variance of the spike count in a bin, as a function of the mean, for different bin sizes. In Figure 3, the mean spike count is plotted against the variance of the spike count for several different bin sizes for the entire population. The minimum variance possible, given that spikes are discrete events, is given by f(1-f) (de Ruyter van Steveninck et al., 1997), where f is the fraction of the firing rate over the largest integer smaller than the firing rate. This lower bound is indicated by the “scalloped” lines along the bottom of the plots in Figure 3. A line with a slope of 1 is also plotted. For the small and intermediate bin sizes it can be seen that some of the data fell near the line given by the minimum obtainable variance. For large bin sizes, the data were scattered broadly around the line indicating a linear relation between mean and variance.

Figure 3.

Mean-variance relation for spike counts across the population for several bin widths. The left column shows the relation in log-log coordinates; the right column shows the relation in linear coordinates. Bin widths of 5, 40, and 200 msec are shown, as indicated by the number in each panel of the left column. The mean for each bin is plotted on the abscissa, and the variance is plotted on the ordinate. The scalloped line that defines the bottom of each distribution is the minimum obtainable variance, given that spikes are discrete events. The line with a slope of 1 defines the mean-variance function expected of a Poisson process, in which the mean equals the variance. For small bin sizes, most data fell below the unity line, and many data points actually had the minimum variance obtainable. For larger bin sizes, the mean-variance relation was distributed about unity. The data plotted included all bins, before and after target onset. When the analysis was restricted to the period after target onset, the results were similar. The slope of the best fit line (data not shown) was assessed using the following equation: log(var) = a + b^*log(mean). The coefficients a and b were as follows: a = -0.21, b = 0.96; a = -0.58, b = 0.83; a = -0.05, b = 0.87 for the 5, 40, and 200 msec bin sizes, respectively.

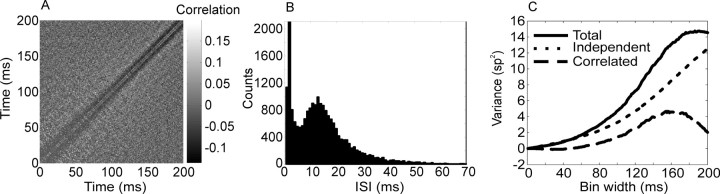
In Figure 4A we plot the matrix of correlation coefficients among 1 msec time bins for an example cell from our population, for the period from 0 to 200 msec after stimulus onset. This cell shows strong negative correlation near the main diagonal and positive correlation over larger intervals, violating the independence assumption of a Poisson process. This structure in the correlation matrix can also be seen in the interspike interval histogram, which is plotted in Figure 4B. We can see how correlations affect the measured variance for a large bin of neural activity, by separating the variance into terms attributable to the mean of a time bin and correlations between events within a bin. To do this we divide a large bin into 1 msec bins and calculate the means of and correlations among the 1 msec bins. The total variance of the large bin is given by:

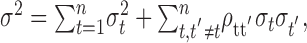9

where ρ_tt' is the correlation coefficient between the 1 msec time bins and σ_t² is the variance of the 1 msec bin at time t. From this, it can be seen that if a large bin of neural activity covers an interval over which the correlation coefficients are negative, the variance of the bin will decrease below the mean, attributable to the second sum in Equation 9, and if the bin extends over an interval during which the balance of the correlation is positive, the variance of the bin will increase. The plot in Figure 4C shows the variance caused by each component of Equation 9, as a function of bin width, for the cell with its correlation matrix plotted in Figure 4A. The line labeled “Total” (Fig. 4C) corresponds to σ ² on the left-hand side of Equation 9. The line labeled “Independent” is the variance attributable to the first sum of Equation 9, which is the sum of the variances of each separate 1 msec bin, and the line labeled “Correlated” is the variance attributable to the correlation between bins, given by the second sum in Equation 9. For this example the effect of the correlations between bins increased the variance for bin widths >60 msec. Therefore, the scatter in the mean-variance plots shown in Figure 3 can be accounted for by correlations between 1 msec bins that make up a larger bin. This implies that if there are correlations in the spike trains, the size of the bin chosen to estimate the variance will affect the estimate of the variance, a fact that has been shown previously (Oram et al., 2001). This is important for measures of neuronal variability and models that try to account for variability in neuronal responses (Salinas and Sejnowski, 2000), because these measures may depend strongly on correlations in the neuronal response within the large time bin being considered.

Figure 4.

Effect of positive correlation between spikes within a bin on variance of spike counts. A, Correlation matrix from a sample neuron for a 200 msec period at a 1 msec resolution. Time 0 corresponds to stimulus onset. The peak equal to 1 along the main diagonal has been removed. The refractory period, which is the dark region paralleling the diagonal from the bottom left to the top right becomes smaller late in the epoch. Either a decrease in the refractory period or an increase in the positive correlation in the flanks contributes to the increase in the variance, after ∼60 msec. B, Interspike interval histogram for the same neuron. This neuron showed a large peak at short latencies, attributable to bursting. C, Variance plotted as a function of bin size for the correlation matrix shown in A, per Equation 9. All bins start at time 0. The line labeled “Independent” represents the variance that would be obtained if the spikes within the bin were independent. This variance is given by Equation 9 when ρ_tt' is zero between all bins. The line labeled “Correlated” shows the variance component attributable to the correlation, which is given by the second sum in Equation 9. The total variance is given by the line labeled “Total.”

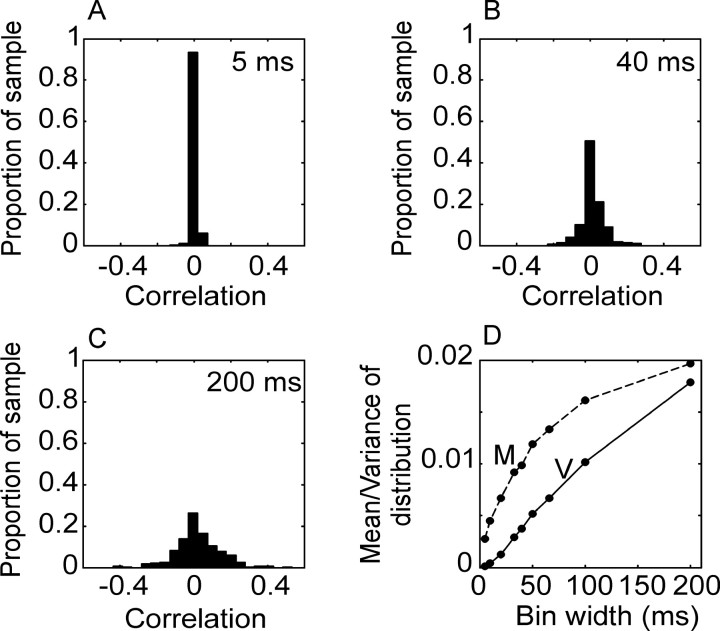
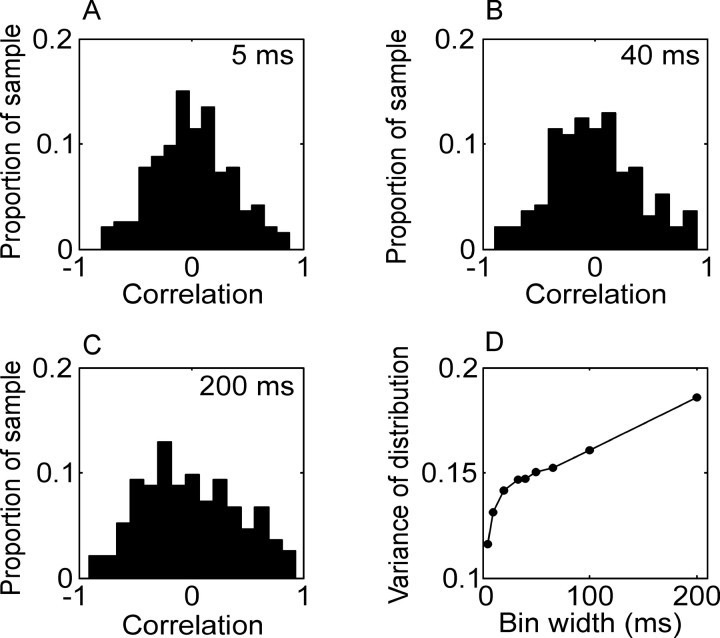
We also explored the covariance structure of the noise between pairs of neurons in our data set. The question of correlated responses has been approached from two perspectives. If the total response of the neurons is considered, the total correlation in their responses can be calculated (Kruger and Aiple, 1988). If the mean response of the neurons to a behavioral event is estimated, however, the correlation can be split into a signal and a noise component, with the correlation in the mean response taken as the correlation in the signal, and the correlation in the trial to trial residual taken as the correlation in the noise (Gawne and Richmond, 1993; Zohary et al., 1994; Lee et al., 1998). Subtracting the mean response removes the effect of first-order nonstationarity on the correlation between neurons. Residual correlation, therefore, cannot be accounted for by the interval histogram or correlations in the mean responses of the two neurons. In our case, the correlation in the mean was calculated as the correlation in the PSTHs across neurons, and the correlation in the noise was calculated as the correlation in the residual after the PSTH was subtracted, with both measures being pooled across bins (see Materials and Methods). The correlation in the residual was calculated separately for each movement. In Figure 5 we show the distribution of the correlation in the noise (residual) as a function of bin size, and in Figure 6 we show the distribution of the correlation in the signal (PSTH) as a function of bin size for the population. The width of the distribution of correlations at each bin size was measured and plotted as the variance of the distribution (Figs. 5D, 6D). This measures the amount of correlation in the population, because wider distributions imply larger absolute values of correlation. It can be seen that the correlation in the noise changed considerably as a function of bin size. The correlation in the signal changed as well, although less. This suggests that the noise correlation among the neurons was not broadband but was stronger at low frequencies (see below).

Figure 5.

Correlation in residual (noise correlation) as a function of bin size. A-C show the distribution of correlation coefficients for the population of pairs of neurons analyzed for three different bin widths: 5, 40, and 200 msec. D, Mean and the variance of the distribution of correlation coefficients as a function of bin size. Dashed line is mean (M); solid line is variance (V).

Figure 6.

Correlation in PSTH (signal correlation). Conventions are as in Figure 5. There was little systematic effect of bin size on the mean of the distribution of correlations in the mean response (data not shown). The variance of the distribution of correlations in the mean is plotted in D. As with the correlation in the noise, increasing the bin size increases the variance of the signal correlation.

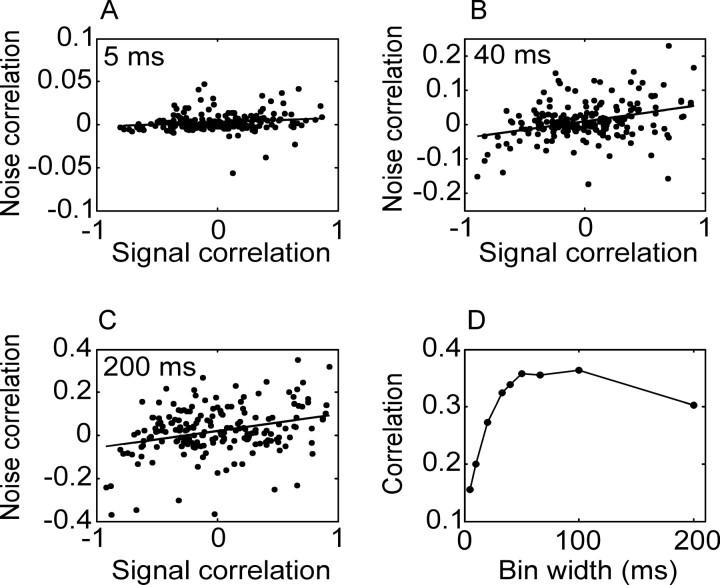
In Figure 7, we plot the function that relates the correlation in the noise to the correlation in the signal. There was a positive correlation between these two measures, such that neurons with a more strongly correlated mean response also tended to have a more strongly correlated noise response. Thus there was some tendency for correlations to be stronger locally (in tuning function space, not in the space of the cortical surface), which in general is deleterious to information coding (see Discussion); however, it was not a strong relationship. The strength of this correlation also tended to increase as a function of bin width as shown in Figure 7D.

Figure 7.

Correlation between signal correlation and noise correlation for pairs of neurons. Conventions are as in Figure 5. The signal and noise correlation were positively correlated. Furthermore, the correlation increased as a function of bin size. Note the difference in the scale for the vertical axes in A-C, reflecting the narrower distribution of correlated noise for smaller bin sizes.

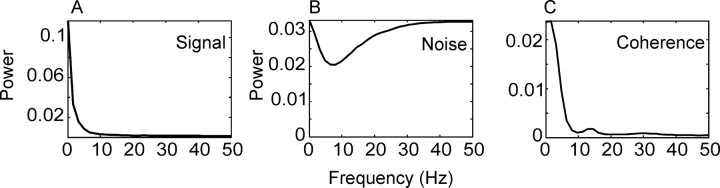
In Figure 8, we plot the population average periodograms for the signal, the noise, and the coherence between the residuals for pairs of neurons. It can be seen that the signal power and coherence were strongest at low frequencies. The noise power displayed a dip at low frequencies, which has been described previously (Bair et al., 1994). This dip may be the result of the neural refractory period or a network level inhibitory mechanism (Mar et al., 1999). The fact that the coherence was strongest at low frequencies accounts for the change in correlation between neurons as a function of bin width. Larger bins filter more of the high-frequency variability in the neural response, leaving only the low-frequency variability, which is more strongly correlated.

Figure 8.

Frequency domain representation of the neural signal in single and pairs of neurons. A, Population averaged periodogram of the PSTH. B, Population averaged periodogram of residual neural activity after the subtraction of the PSTH. C, Population averaged coherence plot between the residuals of neuron pairs. There is a bump at ∼12 Hz, which corresponds to β frequency oscillation, and a smaller bump centered around 30 Hz, which corresponds to γ frequency oscillation (Lee, 2003).

Spike count distributions

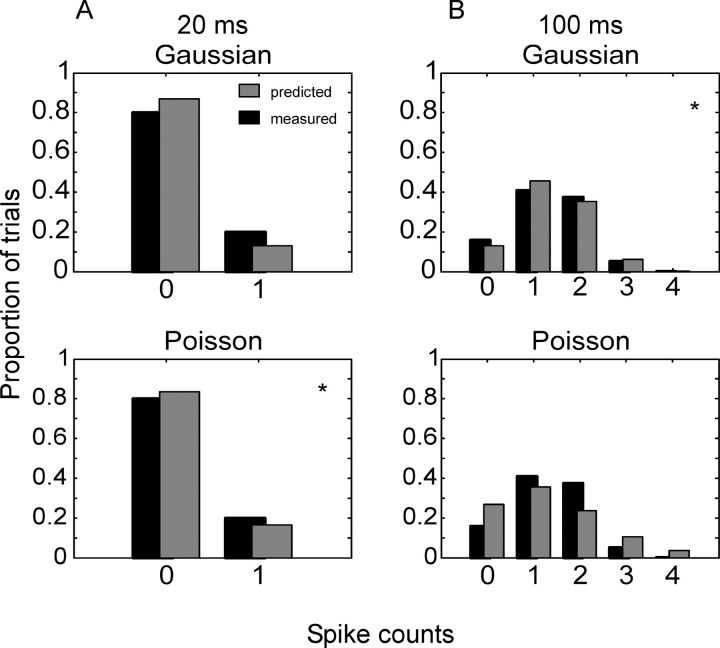
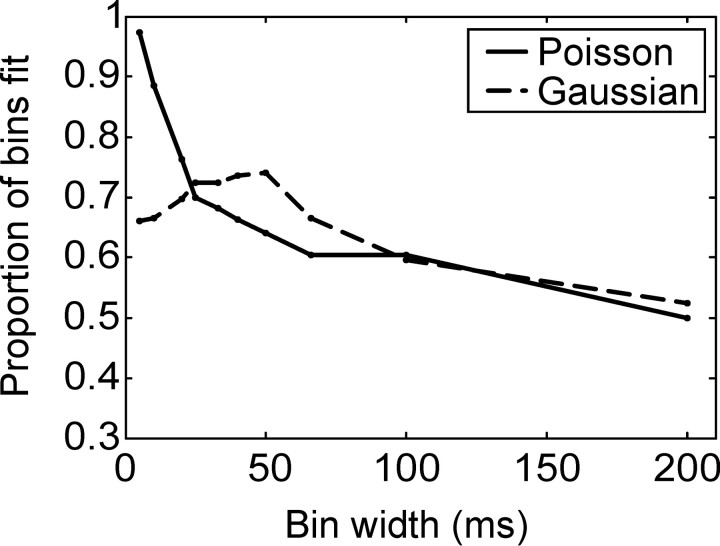
In the decoding analyses we assumed a multivariate Gaussian distribution as an approximation to the distribution of spike counts (Oram et al., 1998). Other studies have assumed a Poisson distribution (Zhang et al., 1998). We characterized the empirical distributions by assessing the fit of Gaussian and Poisson distributions to all samples in our data set. An example is shown in Figure 9. Figure 9A shows the distributions fit to the data for a 20 msec bin, and Figure 9B shows the distributions fit to the data for a 100 msec bin. In the example shown in Figure 9A, the Poisson distribution could not be rejected [Kolmogorov-Smirnor (KS) test; p > 0.05], whereas for the example shown in Figure 9B, the Gaussian distribution could not be rejected (KS test; p > 0.05). Figure 10 shows the proportion of individual bins (each cell contributed multiple bins to this plot) as a function of bin size, which was fit by each parametric distribution. For small bin sizes the Poisson distribution fit most bins; however, for larger bin sizes, the ability of the Poisson distribution to fit the data decreased to the level of the Gaussian distribution. The Gaussian distribution fit the data better for intermediate bin sizes. For the largest bin sizes the distributions did about equally well.

Figure 9.

Examples of parametric distributions fit to empirical spike count distributions. The asterisk in the corner of a plot in each column indicates the distribution that fit the data, i.e., could not be rejected at a p value of 0.05 with the KS test. A, Normal and Poisson distributions fit to the data from a single 20 msec bin. B, Same distributions fit to the data from a single 100 msec bin.

Figure 10.

Proportion of times that a Gaussian or Poisson distribution successfully fit the empirical distribution of spike counts as a function of bin size. Each neuron contributed several bins. For example, for a single neuron at a bin width of 10 msec there were 60 bins (600 msec, 10 msec bins) for each of three movements. Thus the parametric distributions considered were fit to 180 separate empirical distributions for each neuron, at the 10 msec bin width. Bins with a mean spike rate of 0 were not considered.

Decoding models

The noise analyses suggested that most of the mean responses, as well as the correlation between neurons, were concentrated at low frequencies. Conversely, the noise was stronger at high frequencies. The next question that we addressed was whether any of this variability carried information about the target for movement. We approached this problem directly, by comparing models that decoded information using different parameters of the neural signal. For these analyses, we used data in the 200 msec window beginning at target onset to predict the subsequent target toward which the monkey would move. The sequence of movements was deterministic; therefore, increasing the data window backward or forward in time would have allowed us to achieve better decoding performance, because the previous and subsequent targets were perfectly correlated with the current target. We were not directly interested in the absolute performance of the models, however, but rather in the relative performance of different models. We chose the 200 msec window for several reasons. First, pilot analyses showed that many of the pairs of neurons reached their peak predictive capacity at the end of this window. Second, the reaction time in the task was on average ∼240 msec (Lee and Quessy, 2003), so the neural activity during this window is preparatory. Third, the 200 msec window allowed us to construct a series of models of increasing complexity yet limited the number of model parameters (NMPs).

We characterized the models using two heuristic dimensions. The first dimension was the size of the bin used in the analysis. The bin widths considered were the same as those used in the noise analyses, except we did not consider the 5 or 10 msec bin size, because the models became too complex (i.e., too many free parameters for our data set size), and pilot analyses had shown that there was little information to be gained by using bin widths this small. By increasing the bin width we reduced the temporal precision of the neural signal. If information was not lost by eliminating the temporal information, one would conclude that the temporal structure of the spike arrival times was not important.

The second dimension was the structure of the covariance within and between neurons. We constructed several model structures, all on the basis of the multivariate Gaussian distribution. We used the multivariate Gaussian for two reasons: (1) the univariate Gaussian distribution provided a reasonable fit to the data over a range of relevant bin sizes, and (2) it was straightforward to test the hypotheses that we were interested in by manipulating the covariance matrix. The VEM model had a diagonal covariance matrix (i.e., all off-diagonal elements were set to zero), with the variance equal to the mean as in an independent Poisson model. The independent model had a diagonal covariance matrix with the variance estimated from the data instead of being set equal to the mean. The between model included only off-diagonal elements of the covariance matrix that corresponded to interactions between neurons at the same time point. The within model included only off-diagonal elements that corresponded to interactions between adjacent time bins within neurons, and the full model used a full covariance matrix.

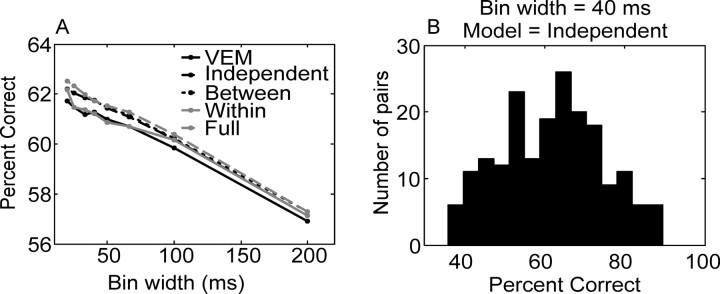
In Figure 11A, we plot the average decoding performance of the models, as a function of bin width, for all pairs of neurons. It can be seen that the performance of the models decreased relatively linearly as a function of the bin width (decreasing number of bins). Of the various models considered, the model with a full covariance matrix gave the best prediction, although it was only marginally better than the other models. There was a wide distribution of performance across pairs of neurons, as can be seen from Figure 11B, which shows the distribution of percentage correct performance across the population at a bin width of 40 msec for the independent model. Although the raw performance of the models is a useful benchmark, we would like to know the generalization performance of the models, that is, how they would perform on an unseen data set. We approached this problem using two model selection procedures: K-fold CV and AIC. We performed CV by splitting the data set 10 times, in each case using 1 of every 10 trials for the test set and the other trials for estimating the model.

Figure 11.

Percentage correct for all analyzed pairs of neurons. A, Mean percentage correct as a function of bin width and covariance model considered. VEM (solid black line) indicates the model with the variance set equal to mean, independent (dashed black line) is the model with the variance estimated from the data, between (dotted black line) considers interaction between neurons, within (solid gray line) considers interactions between time bins for a single neuron, and full (dashed gray line) is the full covariance matrix. B, An example distribution of percentage correct across the population at a bin width of 40 msec for the independent model.

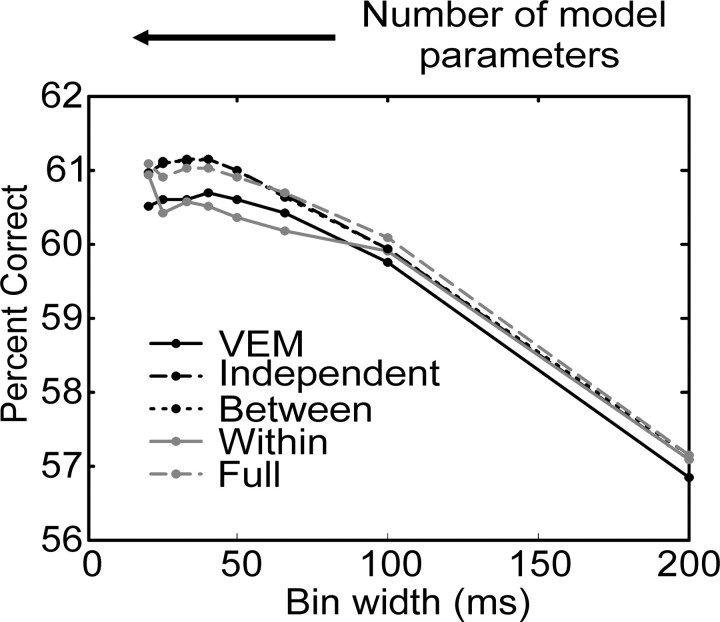
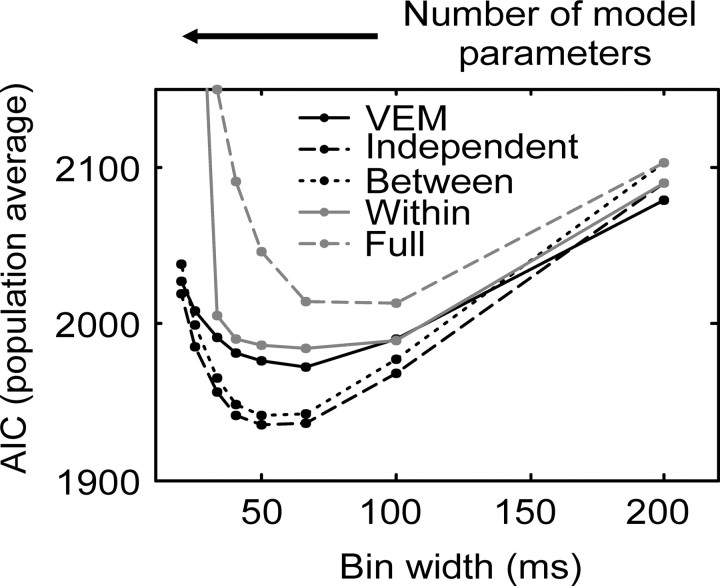
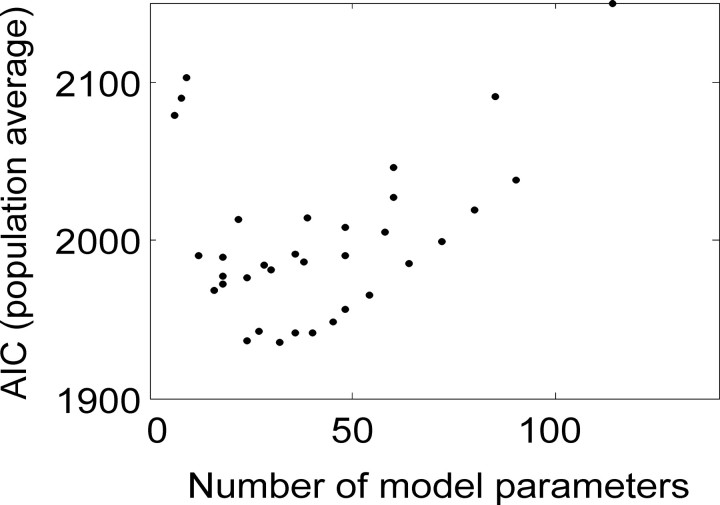
In Figure 12 we plot the population average percentage correct performance of the models, assessed by CV. This population average was compiled by computing the percentage correct for each pair of neurons, then averaging across all pairs, for each model. It can be seen that cross validation corrects for model complexity, because the most complex model no longer has the best performance (compare with Fig. 11A). At the population level, using the percentage correct as a measure of model performance, the CV analysis suggests that either the independent or between model, at a bin width of 33-40 msec, has the best performance. In Figure 13, we plot the population average of AIC, as a function of bin width for each covariance structure. The AIC measure is a composite of the likelihood of the data under the model and the model complexity (see Eq. 8). The model that has the minimum AIC is selected as the best model within this framework. From the population data, the independent model would be selected as the best at a bin width of 50 msec. The between model, which considered interactions between neurons, did almost as well. On the other hand, the full model did rather poorly, which is in contrast to its raw percentage correct performance (Fig. 11A). In Figure 14, the population average AIC is plotted as a function of the NMPs. It can be seen that the AIC first decreased quickly as a function of NMPs and then increased more slowly with model complexity. If the AIC decreased and then increased again before finally decreasing, we would have been within a regimen of the criteria within which we were ineffectively penalizing overly complex models. Furthermore, the AIC decreased quickly and then increased with a more gradual slope. In general terms, this indicates that the model family is reasonably well matched to the data.

Figure 12.

Proportion correct in K-fold cross validation analysis. Different models are indicated using the same conventions as in Figure 11 A.

Figure 13.

Population mean AIC as a function of bin width and model considered. Different models are indicated using the same conventions as in Figure 11 A.

Figure 14.

Relation between the population average of AIC and the number of model parameters. The AIC first dropped quickly to a minimum at ∼40 model parameters and then increased again slowly. The shape of this function is characteristic of a model that is not poorly matched to the structure of the data. Furthermore the AIC value did not begin to decrease again for large numbers of parameters, and thus we did not inadvertently select overly complex models.

The AIC and CV methods make slightly different predictions about the optimal model at the population level. We compared the performance of these two criteria by testing them on a surrogate data set. The surrogate data set was generated by independently shuffling individual bins across trials. This preserved the mean and variance of each bin of the original data set but destroyed all real correlations. We selected the best model, for each pair of neurons, using the surrogate data set. A conservative model selection criterion should not select between, within, or full models because the correlations have been destroyed in the surrogate data set. In Tables 1 and 2, we show the performance of AIC and CV. It can be seen that AIC selected no spurious models, whereas CV selected spurious models 98 of 193 (51%) times. We obtained similar results when the likelihood, instead of the percentage correct, was used as a selection statistic for the CV analysis. These results are consistent with the fact that CV can select overly complex models (Larsen and Goutte, 1999). Furthermore, the performance of CV is always limited by the fact that the sample sizes used to estimate and test the models are smaller than those available to other model selection procedures (Kearns et al., 1995). Because AIC seems to be a more conservative criterion, the remaining results will be on the basis of model selection using AIC.

Table 1.

Best model selected from entire parameter space using AIC on surrogate data

Cov/Bin	200	100	66	50	40
VEM	3	16	10	24	30
Independent	8	3	20	36	43
Between	0	0	0	0	0
Within	0	0	0	0	0
Full	0	0	0	0	0

Cov/Bin, Covariance/bin.

Table 2.

Best model selected from entire parameter space using maximum percentage correct and CV, on surrogate dataset

Cov/Bin	200	100	66	50	40
VEM	1	4	12	19	15
Independent	0	4	9	9	22
Between	1	2	4	15	30
Within	0	3	6	3	9
Full	0	2	6	9	8

Cov/Bin, Covariance/bin.

We performed the AIC model selection analysis on all pairs of neurons, selecting the best model for each pair. Table 3 shows the number of times each model was selected as best for all neuron pairs. There are several relevant points. (1) The simplest model (bin width = 200 msec; VEM) was selected in only 22 cases (11%). (2) Many pairs of neurons (62%) had their best performance at bin sizes between 40 and 66 msec. (3) Many pairs of neurons (19%) also preferred covariance structures more complex than the independent model, including interactions between neurons (between, 8%) or between time bins for a single neuron (within, 11%). (4) Overall, 92% of the neuron pairs could be treated as independent without a loss of information.

Table 3.

Best model selected from entire parameter space using AIC test

Cov/Bin	200	100	66	50	40	33	25	20	Total
VEM	22	9	24	3	6	3	0	0	67/0.35
Independent	9	9	21	29	18	0	2	0	88/0.46
Between	1	3	4	7	1	0	0	0	16/0.08
Within	0	14	6	1	1	0	0	0	22/0.11
Full	0	0	0	0	0	0	0	0	0/0
Total	32/0.17	35/0.18	55/0.28	40/0.21	26/0.13	3/0.02	2/0.01	0/0.00	193

Cov/Bin, Covariance/bin.

We also considered which model was best, within one dimension of the analysis, while holding the other dimension constant. For example, at a bin width of 200 msec, what was the best covariance structure for each neuron? Table 4, which shows the best bin size for each covariance structure, shows that for many neuron pairs temporal precision down to 40 msec improved the decoding performance, for all models except for the full model. Furthermore, the within model showed a slightly greater preference for the 20 msec bin size (eight pairs) than the other models, consistent with the fact that the noise power was stronger at higher frequencies. Table 5 shows that when the best covariance structure for a given bin size was considered, the between and within models were often significant (93 and 108 neuron pairs, respectively), but the full model was almost never significant. The profile of the within model, in Table 5, followed the profile of the noise power relatively well: there was a tendency for the within model to be selected for large bins, which dropped off for the intermediate-sized bins (40-66 msec) but then became strong again for smaller bins. Analyses of the between model in Table 5 also followed the profile of the coherence curve (Fig. 8) to a certain extent, because it was selected more often for large bin sizes but then less often for small bin sizes. Overall the simplest models (VEM and independent) were preferred most often.

Table 4.

Best bin size for each covariance structure using AIC test

Cov/Bin	200	100	66	50	40	33	25	20	Total
VEM	44	26	65	29	26	3	0	0	193
Independent	19	39	51	42	30	7	3	2	193
Between	22	38	54	42	26	6	5	0	193
Within	38	35	43	30	27	6	6	8	193
Full	49	64	76	4	0	0	0	0	193
Total	172	202	289	147	109	22	14	10

Cov/Bin, Covariance/bin.

Table 5.

Best covariance structure for each bin size using AIC test

Cov/Bin	200	100	66	50	40	33	25	20	Total
VEM	103	67	74	77	81	85	105	121	713
Independent	75	83	87	90	89	84	69	51	628
Between	15	13	20	17	10	10	4	4	93
Within	0	28	12	9	13	14	15	17	108
Full	0	2	0	0	0	0	0	0	2
Total	193	193	193	193	193	193	193	193

Cov/Bin, Covariance/bin.

All of the models that we have considered thus far have assumed that the neuronal variability and interneuronal correlation are constant across different targets. It is possible, however, that either the variability or the correlation may have changed across different targets, and taking this change into account could improve our results. We assessed this possibility by performing an analysis in which we compared, for each pair of neurons, the performance of the model selected as best above (i.e., with a pooled covariance matrix) with the performance of a model that used the same interactions, but estimated them separately for each movement. We found that these more complex models were selected as best only four times. Thus, for our data set, the model with a pooled covariance matrix performed better than the models that used separate covariance matrices for each target, a result that has been shown previously (Averbeck et al., 2003).

Neural activity shows variation across multiple time scales (Bair et al., 2001). We have also shown this with our coherence analysis (Fig. 8) because the coherence values at different frequencies imply correlation at different time scales; low-frequency coherence is long time scale correlation. We repeated the decoding analysis on neural signals that had their low-frequency components removed, because these are the components that are assumed to be unimportant for the purposes of neural information transmission and are probably more related to slow changes in neuronal responsiveness (Bair et al., 2001; Lee and Quessy, 2003). We performed the analysis by high-pass filtering the spike trains (see Materials and Methods) before the binning process. Interestingly, the decoding performance averaged over all models (compared with Fig. 11A) improved by ∼3% for bin sizes <200 msec (e.g., from ∼0.60 to ∼0.63 at a bin size of 100 msec). The VEM model did poorly; because most of the mean response was removed by the filter, the variance would be set to a very small value. Thus the lowest frequencies were carrying more noise than signal.

In the final analysis, we considered whether the presence of correlation between neurons would be related to the best model selected for pairs of neurons. If the AIC criterion is selecting models properly, it should select the between model for neurons that are correlated more strongly. The absolute value of the correlation, calculated as the integral of the coherence curve, is 0.085 (SEM = 0.016; n = 67), 0.085 (SEM = 0.009; n = 88), 0.257 (SEM = 0.048; n = 16), and 0.108 (SEM = 0.032; n = 22) for the VEM, independent, between, and within models, respectively. The difference in the correlation between neurons as a function of the covariance model selected was highly significant (ANOVA; F = 10.276; n = 192; p < 0.0005). Post hoc tests confirmed that pairs of neurons that had a best model structure of between had significantly more correlation than neurons that had a best model structure of VEM (Tukey's HSD; p < 0.0005) or independent (Tukey's HSD; p < 0.0005). Thus, the model selected as best used the covariance structure between the neurons.

Discussion

Noise analyses

The function relating the mean spike count to its trial-to-trial variance has been investigated in the visual (Schiller et al., 1976; Tolhurst et al., 1983; Gur et al., 1997; Wiener et al., 2001), somatosensory (Werner and Mountcastle, 1963), auditory (Teich and Khanna, 1985), and motor (Lee et al., 1998) systems. Most of these studies used static stimuli and relatively large bin sizes. These studies found a roughly linear mean-variance relation in log-log coordinates with a slope near 1, which would be expected of a Poisson process. In our data, the variance was often less than the mean for small bin sizes, likely because of negative correlations over small time scales. Several authors have recently reported very small variances in the visual system of various species (Bair and Koch, 1996; Berry et al., 1997; de Ruyter van Steveninck et al., 1997). Our results do not show the extreme consistency demonstrated in these studies, perhaps because of the fact that the movements in our task are less consistent than the stimuli used in studies of the visual system.

Our analyses of correlation in the mean and variability of neuronal responses in pairs of neurons have shown that their estimates are affected by the time scale over which they are measured, a finding that has also been reported in V1 (Reich et al., 2001a). Because most of the coherence between neurons is at low frequencies, correlations are higher between neural responses for larger bin widths. Thus, it is important when considering neural coding in ensembles of neurons to explicitly consider the time scale at which the information is being represented, because the noise characteristics of the ensemble will be dependent on the time scale.

There is an important difference between the question of whether a model (or a downstream neuron) that takes into account covariance can outperform a model that does not (Nirenberg et al., 2001; Wu et al., 2001), a question that we addressed with the decoding analyses and the question of which covariance structures can carry the most information, (Johnson, 1980; Zohary et al., 1994; Abbott and Dayan, 1999; Wilke and Eurich, 2002; Pola et al., 2003). Uniform noise correlation improves the ability of a population of neurons to carry information, if there is an inverse relation between the correlated signal and the correlated noise. Conversely, if the correlation in the signal and noise are both either positive or negative, the correlation will be deleterious. Local noise correlation, in tuning function space, is deleterious in general. We found that noise correlation tended to be stronger locally, which suggests that the correlations in our data affect information encoding deleteriously. This analysis has limitations, however, because variations in the kinematics of the movement from trial to trial may cause neurons that have similar tuning functions to have more strongly correlated noise. A similar problem in the visual system is caused by small eye movements; however, it has been shown previously that there was no difference in noise correlation between a center hold epoch and a movement epoch (Lee et al., 1998). Also, the data that we analyzed came mostly from a time period when the monkey's hand was stationary, which should have minimized the effect of correlation attributable to kinematic variability. Similarly, correlated noise in the prefrontal cortex has been shown to be relatively independent of small eye movements (Constantinidis and Goldman-Rakic, 2002).

Decoding analyses

We explored a hierarchy of decoding models with respect to two questions. First, did the times at which spikes occurred within a 200 msec window matter? Second, which interactions between bins within a neuron or across neurons should be accounted for to optimize decoding? At the population level, we found that spike arrival times at a resolution of ∼50 msec were optimal. The findings for individual pairs of neurons were similar, except that the best model for the largest number of pairs was 66 msec. There was little evidence for signal in bin sizes below 40 msec. The preferred bin size of 50 msec corresponds to an upper cutoff frequency of 10 Hz. Including frequencies above 10 Hz did not add significant information about the subsequent movement. This is consistent with the results of the noise analysis, given that the signal-to-noise ratio was highest at low frequencies, and the coherence was also strongest below 10 Hz (Fig. 8). Thus, the model that used a bin size of 50 msec might represent a useful tradeoff between signal and noise, because at >10 Hz there was little signal power but the noise power remained larger.

We found evidence that some form of correlation was important for 19% of the pairs of neurons; however, correlations between neurons in our study improved decoding performance in only 8% of the individual pairs of neurons. Previous results have been split on the question of whether there is information in correlations between neurons. Some studies have found that interactions can improve decoding performance (Dan et al., 1998; Maynard et al., 1999), whereas others have found that neurons could be treated independently without losing much information (Nirenberg et al., 2001; Petersen et al., 2001; Averbeck et al., 2003; Rolls et al., 2003). Our results support the claim that ignoring correlation between neurons, in some systems, does not dramatically affect the information extracted from the neural code.

The question of whether spike arrival times can carry information has been approached with several analytical techniques. One approach is to assume that the cross-correlation between a pair of neurons carries information (Vaadia et al., 1995; Riehle et al., 1997). It is important, however, to control for the effect of spike rate when looking for information in cross-correlations (Oram et al., 2001), which our analytical approach has done. Many other studies in the visual system (Buracas et al., 1998; Reinagel and Reid, 2000; Reich et al., 2001b) and the somatosensory system (Panzeri et al., 2001; Petersen et al., 2001) have shown that the arrival times of spikes within single neurons can carry information. Studies using static visual stimuli have shown that the arrival times of spikes add additional information, down to a temporal resolution on the order of 30-50 msec (Heller et al., 1995; Victor and Purpura, 1998), whereas other studies, using dynamic visual stimuli, have shown that spike arrival times in the submillisecond range can carry information (Dan et al., 1998; Strong et al., 1998; Reinagel and Reid, 2000).

An additional question is whether we have modeled the behavior appropriately, because we have treated the movement as a categorical variable. It seems likely that the underlying behavioral process is dynamic, in which case the temporal properties of the code that we have identified could be linear representations of a dynamically evolving behavior (Golomb et al., 1994). This consideration effectively places a limit on studies of the neural coding of cognitive factors or decisions, because one cannot directly measure the dynamics of cognitive processes.

An important question is whether the cortex is decoding neural responses optimally. Theoretical work has shown that biologically plausible networks can optimally decode neural responses, when the noise is uncorrelated across neurons (Deneve et al., 1999). As stated in Introduction, the information present in the neural response is an upper bound on the information actually used by the cortical networks mediating behavior. The decoding approach cannot address the question of whether downstream neurons are capable of extracting the same patterns as the decoding algorithm, but the analysis does set a lower limit on the sophistication of a downstream neuron if it is to extract all the information in the neural response.