Frequency-Specific Interaural Level Difference Tuning Predicts Spatial Response Patterns of Space-Specific Neurons in the Barn Owl Inferior Colliculus

Abstract

Space-specific neurons in the barn owl's inferior colliculus have spatial receptive fields (RFs) because of sensitivity to interaural time difference and frequency-specific interaural level difference (ILD). These neurons are assumed to be tuned to the frequency-specific ILDs occurring at their spatial RFs, but attempts to assess this tuning with traditional narrowband stimuli have had limited success. Indeed, tuning assessed in this manner, when processed via a linear model of spectral integration, typically explains only approximately half the variance in spatial response patterns. Here we report our findings that frequency-specific ILD tuning of space-specific neurons, when assessed from responses to broadband stimuli, predicted nearly 75% of the variance in spatial responses, using a linear model of spectral integration (p < 0.0001; n = 97 neurons). Furthermore, when we tested neurons using only those frequencies we found to be spatially relevant, we saw that their responses were similar to those elicited by broadband stimuli. When we used frequencies not identified as spatially relevant, such similarity was lacking. Furthermore, spectral components that elicited high firing rates when presented as narrowband stimuli were found in several cases to be irrelevant for or detrimental to the definition of spatial RFs. Thus, neurons achieved sharp spatial tuning by selecting for ILDs of a subset of spectral components in noise, some of which were not identified using narrowband stimuli.

Introduction

Sound localization cues, such as the average binaural sound level (ABL) or the interaural time difference (ITD) and frequency-specific interaural level difference (ILD), vary by frequency because of the directional filtering of the head and external ears. Individual frequency components can only be localized to wide regions of space. To localize sounds precisely, the auditory system must integrate these cues across frequency.

Studies of the neural mechanisms of sound localization have often assumed that neuronal tuning to spatial cues could be measured accurately by presenting narrowband stimuli (Kuwada and Yin, 1983; Yin and Kuwada, 1983; Yin et al., 1984; Takahashi and Konishi, 1986; Brainard et al., 1992; Arthur, 2001; Fitzpatrick and Kuwada, 2001). Although this approach is useful, neurons underlying spatial hearing may be specialized to take advantage of spectral breadth (Xu et al., 1999). For such neurons, responses to narrowband stimuli may not indicate the most spatially relevant components used by individual neurons to encode auditory space.

The space-specific neurons of the auditory space map in the barn owl's inferior colliculus (IC) are a case in point. These neurons integrate ITD and ILD across frequency to compute their spatial receptive fields (RFs) (Knudsen and Konishi, 1978a, 1978b, 1978c; Moiseff and Konishi, 1981; Takahashi and Konishi, 1986; Wagner et al., 1987; Takahashi, 1989). Studies have shown that they are tuned to the ITDs that occur at their spatial RFs (Gold and Knudsen, 2000b). It has been thought that a space-specific neuron is likewise selective for the spectrum of ILDs associated with its RF (Brainard et al., 1992; Knudsen, 1999). Euston and Takahashi (2002) recently tested this hypothesis by first measuring the “ILD-alone” response of a neuron. ILD-alone responses are measured using broadband noises filtered to have the ILD spectrum of each location in space but with a fixed ITD. Euston and Takahashi (2002) then measured ILD tuning with tones of varying frequencies and asked whether these responses could be summed across frequency to account for the ILD-alone responses measured with noise. The ILD-alone response thus predicted accounted for only 56% of the variance in the ILD-alone responses measured with noise.

One possible explanation for this modest predictivity is that responses of space-specific neurons to tones are not good estimates of the frequency-specific ILD tuning that is operative in forming responses to broadband stimuli. Indeed, space-specific neurons respond poorly to tone pips. To achieve reliable firing, Euston and Takahashi (2002) presented tones at intensity levels considerably higher than those of the corresponding bands in noise, and they suggested that this may have affected responses in more peripheral nuclei.

In the present study, we measured ILD-alone responses using broadband noise and identified the frequency-specific ILD tuning directly from these responses. This tuning yielded better predictions of the ILD-alone response pattern of the neuron than did the tuning measured with tones. Moreover, presentation of only those frequencies identified from the response to noise produced ILD-alone responses that resembled those obtained with broadband noise. This suggests that our approach effectively identified the spatially relevant spectral components in the noise, and that these relevant components were not in fact as reliably identified using narrowband stimuli.

Materials and Methods

Subjects. Eight adult barn owls (Tyto alba) weighing 390–500 gm were used in this study. All procedures were approved by the Institutional Animal Care and Use Committee at the University of Oregon.

Stimuli in virtual auditory space. All stimuli were presented in virtual auditory space (VAS). The stimulus waveforms were filtered with each bird's own head-related transfer functions (HRTFs) measured and processed as described by Keller et al. (1998). The individualized HRTFs were sampled to afford a 5° resolution in double polar coordinates (Knudsen, 1982) in azimuth (±90°) and elevation (±90°) in the frontal hemisphere. Negative azimuths and elevations denote loci to the left of midline and below eye level, respectively.

Terminology. Fully-cued refers to stimuli that simulate free-field conditions in all respects and to the neuronal responses to such stimuli. In fully-cued stimuli, spatial cues, including ITD, ILD, and ABL, vary in the frequency-specific manner characteristic of each location in the frontal hemisphere.

ILD-alone refers to stimuli in which only ILD was available as a spatial cue and to the neuronal responses to such stimuli. The ABL and ITD were held constant across space.

ILD-frequency tuning refers to the selectivity of a neuron for combinations of frequency and ILD.

Neurophysiology and stimuli. Surgery and neurophysiological recordings in the IC proceeded according to the methods of Keller and Takahashi (1996, 2000) and Euston and Takahashi (2002). Owls were initially anesthetized with intramuscular injections of ketamine (0.5 mg) and diazepam (0.25–0.5 mg), given subcutaneous saline injections (5–10 ml), and maintained on either intramuscular anesthesia with ketamine and diazepam or on vaporous anesthesia using oxygen (1–1.5 l/min), nitrous oxide (0.5–0.7 l/min), and occasionally isoflurane (0.5–1%). Vaporous anesthesia was administered using an anesthesia unit (Summit Medical, Bend, OR) via a mask placed over the beak and sealed with Parafilm (3M, St. Paul, MN). Blunt-tip, platinum-coated tungsten microelectrodes (Fredrick Haer Co.; 10–12 MΩ) were inserted into the IC at known stereotaxic coordinates. Responses were recorded from isolated units in the IC, typically between 14 and 17 mm below the telencephalic surface. Once isolated, neurons were selected for further analysis on the basis of quantitative criteria for spatial specificity. All of the neurons included in this study exhibited a clear single response peak in the frontal hemisphere that was spatially restricted in both azimuth and elevation. Units that did not meet space-specific requirements were not included for further analysis. That such neurons were indeed in the IC was verified in one owl by inserting an electrode coated with the fluorescent marker DiI (Molecular Probes, Eugene, OR; owl 897) and recovering the electrode track histologically (Euston, 2001).

Stimuli consisted of fixed-amplitude, random-phase broadband noise (2–11 kHz) and one-third octave narrowband noise, tone pips, and gamma tones. Noise stimuli had a uniformly distributed amplitude spectrum that deviated by <0.5 dB from the mean amplitude between specified frequencies and rolled off at 0.5 dB/Hz outside this range. Gamma tone filters were fourth-order and 100 Hz wide at half-height. All stimuli were synthesized de novo for each stimulus presentation and used in 3–10 repetitions per trial type.

On isolation, the responses of a unit to ABL, ITD, and ILD were initially characterized using broadband noise. A rate–ITD curve was measured at 5 μsec intervals using broadband noise set to the initial ILD preference. A rate–ILD curve was then determined at 5 dB intervals using broadband noise set to the ITD of the peak in the rate–ITD curve. A rate–ABL curve subsequently was measured at 5 dB intervals using broadband noise set to the ITD and ILD indicated by the previous two tests. All other tests, including those with tones and gamma tones, were done at 10–20 dB above the threshold of the neuron, as determined in the ABL test [30–60 dB sound pressure level (SPL), peak A-weighted]. In all but a few cases, tones, gamma tones, or both were presented at the same overall level as noise stimuli. All stimuli had 5 msec on–off ramps and were 100 msec in duration, with 200 or 300 msec interstimulus intervals. Spontaneous activity was determined during a 100 msec period without stimulation before the onset of each stimulus.

After the initial characterization, the spatial RF of the neuron was measured using fully cued stimuli at 359 locations in the frontal hemisphere. An ILD-alone response was measured using individualized ILD-alone filters, sampling the same locations that were sampled with fully cued stimuli. ITD cues were removed in the frequency domain first. We replaced measured phases for the left-and right-ear filters at all locations with one linear set of phases. This set ITD = 0 for each location. The optimal ITD of a neuron was then imposed in the time domain during unit recording via delay impulse responses. To correct for ABL, it was necessary to perform calculations in the frequency domain (i.e., on the HRTFs). This is because ABL varies in a frequency-dependent manner. Therefore, for each frequency value (e.g., 2–11 kHz, 1024 points in all), we calculated the average ABL across all locations. For each frequency value along the spectrum of each location, we imposed this average ABL so that the spectra maintained the original ILD value at that frequency. Thus, we modified the left and right HRTF spectra for each location so that (1) at each frequency value, the average of the left and right levels was the average ABL across all locations for that frequency; and (2) at each frequency value, subtracting the left level from the right level yielded the correct ILD value for that location and that frequency.

The ILD–frequency response of a neuron was recorded using tone pips, narrow gamma tones, or one-third octave noise at 4–5 dB ILD intervals between ±30 dB in ILD and at 450 Hz frequency intervals between 2 and 11 kHz. Finally, additional ILD-alone tests were performed for validation of the spatially relevant ILD cues (see below).

Identification of frequency-specific ILD tuning from responses to noise. Our approach is based on the idea that if the activity of a neuron is influenced by a particular frequency band in a broadband ILD-alone stimulus, the firing rate at each location would be related to the frequency-specific ILD value that occurs at that location. More precisely, the firing rate at a given location should be proportional to the difference between the ILD for that frequency at that location and the ILD for that frequency at the location that elicited the maximal response, i.e., the “optimal” location of the neuron.

The approach is illustrated in Figure 1. The diamond in Figure 1 A represents the frontal hemisphere in VAS, and the colors represent the firing evoked (red, high; blue, low) by ILD-alone stimuli in one cell. The optimal location of this neuron was at -25° elevation and 15° azimuth. The ILD spectrum giving rise to the activity at this location was defined as the optimal ILD spectrum and is shown as the solid gray line in Figure 1 B. For each of 15 one-sixth octave frequency bands (2–11 kHz), we computed the root mean square difference between the ILD spectrum at the optimal location and that of each of the remaining spatial locations. We appended a negative sign to this difference, if, overall, the ILD spectrum for the location in question was less than that of the optimal location and a positive sign otherwise. The resulting signed quantity is the “ILD distance” (d_ILD). Had we used the ordinary mean difference instead of d_ILD, we would have underestimated the true difference in ILD spectra, because the negative and positive differences within a frequency band would have canceled out. In Figure 1 B, the ILD spectra of the optimal location and locations that elicited low (Fig 1 A, white circle, B, blue dotted line) and high (Fig. 1A, black circle, B, magenta dashed line) firing rates are superimposed. The thickened segments of each ILD spectra in Figure 1 B indicate 3 of the 15 one-sixth octave bands (f4, f12, f14) for which we calculated the d_ILD.

Figure 1.

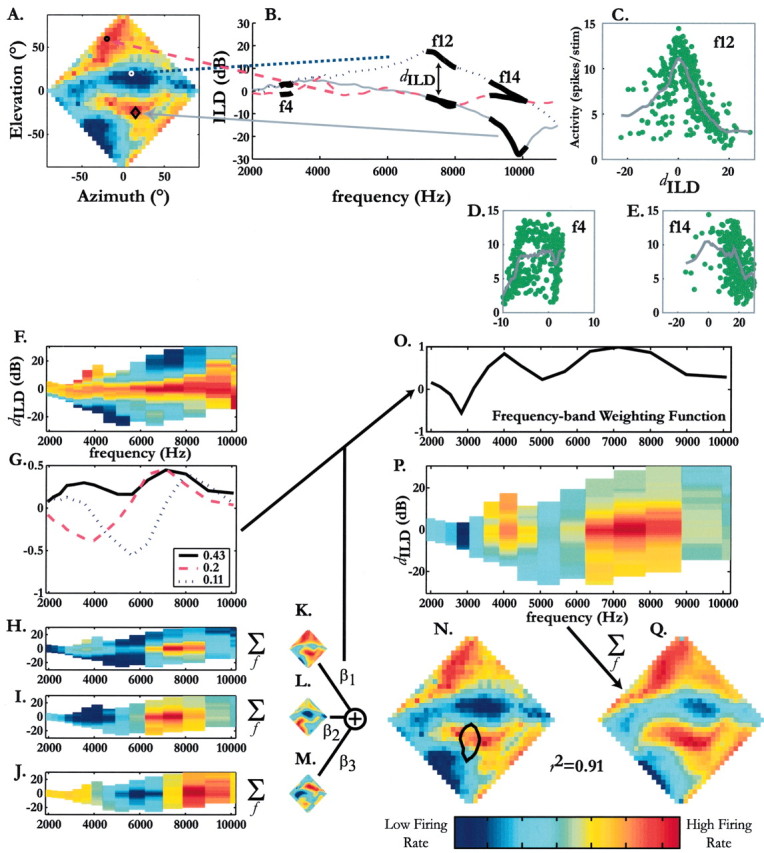
Identification of frequency-specific ILD tuning from ILD-alone response surfaces measured using broadband noise. ILD-alone responses using broadband stimuli were measured (A) and decomposed by frequency band according to d_ILD, calculated from the location-dependent ILD spectra. B, Location-dependent ILD spectra are shown for 3 of the 359 locations from which responses were obtained: gray, spectrum for optimal location; magenta, spectrum for another location that elicits a high spike rate; blue, spectrum for a location that elicits a low spike rate. For each frequency band, the firing rate at a given spatial location was plotted against the d_ILD occurring at that location. Such plots are shown for three representative one-sixth octave bands in C–E. Local regression (C–E, gray lines) yielded a curve that estimated the relationship between firing rate and ILD distance for each frequency band. F, Surface showing the local regression functions for all frequency bands. G, Principal frequency components of the surface shown in F. For clarity, only three principal components are shown. The proportion of variance that each principal component explains is shown in the inset. H–J, Plot shown in F weighted by the three highest principal components. K–M, Principal components regression. The d_ILD–frequency surfaces weighted by the principal components were transformed into spatial plots via linear spectral integration, and multiple regression was used to compute the weight (β_i) for each principal component. This is shown by the weighted summation of K–M, compared against the measured ILD-alone response surface, shown in A and reproduced in N. The principal component matrix (represented in G) was then multiplied by the vector of β_i values, and the result was normalized to form a frequency–band weighting function (O; this process is represented by the joined lines pointing to Frequency-band Weighting Function). This weighting function (O) was then used to weight the initial d_ILD–frequency surface, shown in F, thereby yielding the putative tuning for d_ILD at each frequency (P). The predicted ILD-alone response surface (Q) was determined from P via linear spectral integration. For the neuron used in this example (N10), the predicted surface (Q) explained 91% of the variance in the measured surface, which is shown in both A and N. The scale bar shows the normalized firing rate and applies to all color surfaces in this article.

Thus, for each frequency band, we computed a set of d_ILD values that were associated with the locations on the measured ILD-alone surface, resulting in a frequency decomposition in which frequencies were assumed to be independent. At low frequencies, at which the head and facial ruff imposed little sound shadowing, the range of ILDs was limited, whereas at higher frequencies, the range was wider (Keller et al., 1998).

If a neuron is responsive to a particular frequency band, its location-dependent firing rate should be correlated with the d_ILD values of that band. We therefore plotted, for each frequency, the firing rate measured at the various locations in the ILD-alone surface against the associated d_ILD values. Figure 1C–E shows the plots for bands f4, f12, and f14. The gray lines are the estimated activity versus d_ILD curves obtained from zero-order local regression, using 15% of the data around each point (i.e., α = 0.15; Loader, 1999). Clearly, f12 showed the most structure, suggesting that frequencies within this band contributed strongly to the spatial response of this neuron. The resulting curves for each of the 15 frequency bands are shown in Figure 1F, forming a d_ILD versus frequency surface in which neural activity is denoted according to the accompanying scale bar.

The contribution of each frequency band (i.e., the frequency band weighting) was determined using principal-component regression (MATLAB princomp and regress functions) as illustrated in Figure 1 F–O. First, the principal frequency components were calculated using the covariance matrix of the activity versus d_ILD curves (Fig. 1 F). Figure 1G shows the first three principal frequency components, which accounted for 41, 20, and 11% of the variance in the covariance matrix, respectively (inset). All components that uniquely accounted for at least 1% of the total variance in the covariance matrix of the broadband d_ILD–frequency surface were kept for further processing. For the neuron whose results are shown in Figure 1, the first six principal components met this criterion (although only the first three are shown for clarity). The frequency weights thus derived are closely related to the goodness of fit between spike rate and d_ILD (Fig. 1C–E). Weighting with the goodness of fit itself, although possible, poses the problem of multicollinearity, in which d_ILD tuning curves of neighboring frequency bands are correlated. Principal-component regression circumvents this problem.

The unweighted d_ILD–frequency response surface (Fig. 1 F) was then multiplied by each of the retained principal components to yield a set of component-weighted response surfaces (Fig. 1 H–J) as follows:

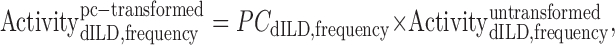1

where Activity_{dILD,frequency}^{untransformed} is an element in a matrix whose columns are the frequency-specific activity–d_ILD curves, and PC_{dILD,frequency} is an element in a matrix of identical columns whose rows are the frequency weights of a given principal component. The three principal component-transformed surfaces for neuron N10 are shown in Figure 1 H–J.

Each response surface in Figure 1 H–J was transformed into space using the method described by Euston and Takahashi (2002). Briefly, the ILD spectrum for each location in space, obtained from the HRTFs, was overlaid on top of the weighted ILD–frequency surface. The firing rate obtained at each frequency–ILD combination underneath the ILD–spectrum line was summed, normalized, and assigned to the location from which the spectrum came. Note that this method assumed that each frequency band contributes independently to the response of the neuron. Transformation of the response surfaces shown in Figure 1 H–J yielded principal-component estimates of the broadband ILD-alone response surface, which are shown in Figures 1 K–M.

Finally, multiple regression analysis was performed:

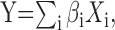2

in which the dependent variable was the measured ILD-alone response surface (Fig. 1 N) and the independent variables were the principal-component estimates of the ILD-alone response surface (Fig. 1 K–M). Only those components that yielded regression coefficients (β_i) significantly different from 0 at the 95% confidence limit were retained. The final frequency weight vector, shown in Figure 1O, was obtained by multiplying the matrix of retained principal components by the vector of regression coefficients:

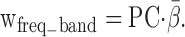3

Each frequency-specific activity–d_ILD curve (Fig. 1 F) was multiplied by the appropriate frequency band weight to yield the final d_ILD–frequency response surface (Fig. 1 P). This surface was transformed into an ILD-alone response surface (Fig. 1Q), which, in essence, was a prediction of the ILD-alone surface measured with noise under the assumption that the space-specific neuron integrated the contribution of each frequency band independently and linearly (Euston and Takahashi, 2002). The measured ILD-alone response surface shown in Figure 1 A is reproduced next to the predicted version for comparison.

In Figure 1, the ILD–frequency surface was obtained using the responses from all the locations of the measured ILD-alone response. The ILD–frequency surface may be thought of as a filter that transforms responses in the frequency domain into the spatial domain. The standard method of evaluating the quality of such a filter is to build it with a random subset of the measured locations and to test its output on the locations that were not selected for filter estimation. We took this approach to assess how well the modeled responses predicted the measured data. The square of the Pearson product–moment correlation coefficient (r) between the measured ILD-alone surface and that predicted using the method described above were computed. Mean r² values were calculated for 20 repetitions. For each repetition, we randomly selected n% of the locations and tested the predictivity on the remaining (1 n)%. It is important to note that this random procedure is a more robust test of the identified ILD–frequency tuning than, say, always selecting the same locations for parameterization and testing.

Neurophysiological validations. We evaluated the extent to which the frequency bands identified from the response of a neuron to noise were necessary and sufficient to account for the ILD-alone response surface measured with the broadband noise. We therefore constructed “minimal” stimuli consisting only of those spectral components identified from the noise response as being spatially relevant. These bands were defined as those that showed at least half the maximum frequency weight in the ILD–frequency response surface. Complementary stimuli, termed “negative” stimuli, consisted of only those frequency bands between 2 and 11 kHz that were not identified as spatially relevant. Minimal and negative stimuli were used to record ILD-alone response surfaces that were compared with the ILD-alone response surfaced obtained with the full-spectrum stimuli. ILD-alone response surfaces using the minimal and negative stimuli were measured using the same overall ABL level used to record responses to broadband stimuli. When comparing two measured ILD-alone response surfaces, we included all 359 measured locations.

We also compared the effectiveness with which the ILD tuning identified from the tonal stimuli and noise could account for the measured ILD-alone response surface. To this end, we constructed “tone-indicated” stimuli, comprising only those frequencies that elicited more than half-maximal firing in the ILD–frequency response surfaces assessed with the tone pips and gamma tones. Tone-indicated stimuli were analogous to the minimal stimuli just described, except that their spectral components were identified using the more standard method of presenting tone pips and gamma tones of differing center frequencies and ILDs. ILD-alone surfaces were measured using the tone-indicated stimuli, and r² values were computed to compare them with those generated by broadband noise and by the minimal stimuli.

Comparison of frequency-specific ILD tuning assessed with tones and noise. We compared the ILD–frequency tuning estimated from responses to noise and tones. When using tones, we measured responses at a broad range of ILDs (±30 dB) and frequencies (2–11 kHz), and some ILD values were outside the ILD range encountered naturally. By contrast, when inferring the tuning from responses to noise, response estimates were necessarily restricted to the ethological range. To make the comparisons, therefore, we only considered frequency-specific ILD values common to the two surfaces. The ILD–frequency response surface estimated from the noise response was linearly interpolated in both the frequency and ILD dimensions to match the shared frequency and ILD values. The Pearson r between the two ILD-frequency surfaces was then computed.

We also compared the frequency tuning curves identified with noises and tones in terms of their shape, bandwidth, and peak location. To assess the similarity between simple tuning curves, we first generated rate versus frequency tuning curves by selecting, for each frequency, the maximal firing rate across ILD values. This was done for both the tone-and noise-based ILD–frequency surfaces. The correlation between these curves was then computed. To compare bandwidths, we measured the widths of each curve at half-height, after the curves were linearly interpolated to 1000 samples. To compare the peak positions of the interpolated curves, we calculated a “peak shift ratio,” which is the absolute value of the difference in peak frequencies divided by the difference in peak bandwidths:

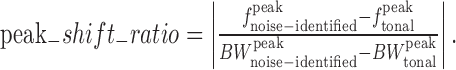4

Results

Spatial properties of space-specific neurons tested

We analyzed 135 single units, but only 103 were categorized as space-specific neurons and included in the data set analyzed here. Twenty-nine of these were also included in a previous study (Euston and Takahashi, 2002). The fully cued RFs of neurons in the present study had sizes and shapes consistent with those reported in earlier studies making use of virtual and free-field stimuli (Knudsen and Konishi, 1978b; Keller et al., 1998; Euston and Takahashi, 2002). The RFs were located within the frontal 80° in azimuth and 80° elevation.

ILD–frequency tuning identified from responses to broadband stimuli

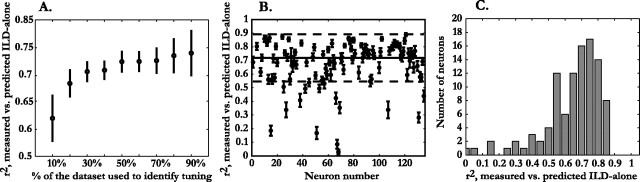
We sought to identify the ILD selectivity at each frequency that could best explain the features of the ILD-alone response surface of a neuron measured with broadband noise. We first determined the fraction of locations of the ILD-alone response surface that was required for robust identification of spatially relevant frequency-specific ILD tuning. Figure 2A plots the fractional variance (r²) between measured and predicted ILD-alone responses against the percentage of loci used to derive the predicted values. The reported r² values do not include the loci used to derive the prediction. When 30% of the data were used, the prediction accounted for 72% of the variance in the remaining locations. Incorporating up to 90% of the data yielded only a 5% increase.

Figure 2.

Predictive capacity of the frequency-specific ILD tuning identified by responses to noise. All reported r² values are calculated using only those locations not included in the parameterization data set. A, Variance in the measured ILD-alone response surface accounted for by the frequency-specific ILD tuning extracted from noise responses plotted against the percent of the total data set (359 locations) used to calculate that tuning. Each point is the median r² value across all 102 neurons, calculated from mean values for each neuron obtained using 10 randomly selected fractional data sets. Error bars estimate the variance in the median values and are the SDs around the mean r² values obtained across the 10 randomly selected data sets for the 102 neurons. B, Mean ± SD of 20 randomly selected fractional data sets, using 30% of the total number of data points to predict the remaining 70%, plotted versus neuron number. C, Distribution of the mean r² values obtained using 30% of the data across 102 neurons.

Figure 2B assesses the robustness of our method of identifying frequency-specific ILD tuning for 102 cells. Each point represents the r² value of a neuron averaged over the 20 iterations, randomly selecting 30% of the loci each time. The error bars represent the SDs. The SDs are quite restricted, suggesting that the tuning inferred from any set of 108 locations will yield consistent values of r².

Figure 2C shows the distribution of r² values for our population of neurons. The value of r² was ≥0.75 (r ≥ 0.87) for 39% of the neurons analyzed here, and 69% of the neurons had r² values ≥0.64 (r ≥ 0.8).

Comparison of the predictive capacities of ILD tuning identified from responses to broadband and tonal stimuli

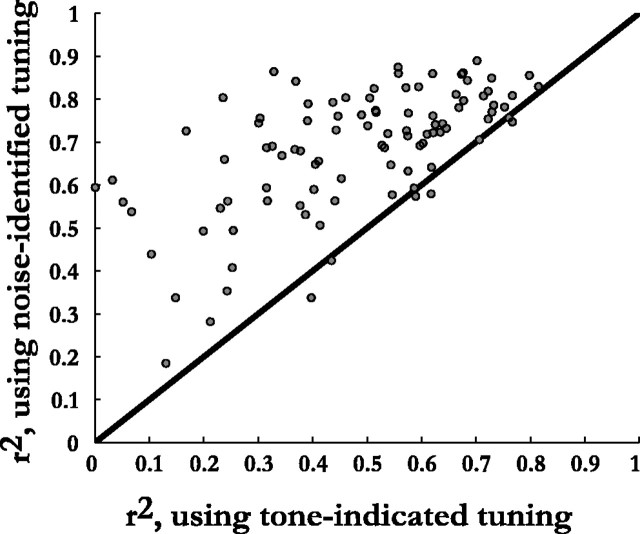
We compared the degree to which the frequency-specific ILD tuning derived from responses to tones and noise could predict the measure ILD-alone response in 97 neurons.

For each neuron, we used the tuning estimated from 30% of the responses to broadband ILD-alone stimuli to predict the ILD-alone responses at the remaining 70% of locations. This yielded a median r² of 0.72 ± 0.14. Sixty-seven percent of these 97 neurons had r² values ≥0.64. The same integration algorithm using the tuning obtained from responses to tonal stimuli produced a median r² of 0.51 ± 0.19, consistent with the results of Euston and Takahashi (2002). Only 22% of the neurons had r² values ≥0.64. This difference between the predictive capacities of the two methods of identifying frequency-specific ILD tuning was highly significant (Fig. 3; p < 0.0001, Wilcoxon signed rank test). This suggests that tuning obtained from responses to broadband stimuli better estimated the frequency-specific ILDs used by individual neurons to encode auditory space.

Figure 3.

Proportion of variance, r², in the measured ILD-alone response surfaces explained by frequency-specific ILD tuning inferred from broadband responses compared with r² values obtained from tuning measured with tones. The bootstrapping procedure used to infer the tuning from broadband responses was based on 30% of the locations picked at random, with replacement, and averaged over 20 repetitions.

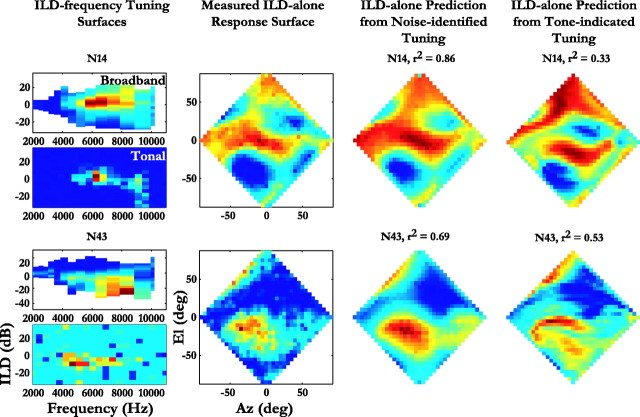
A more detailed comparison of the predictive capacities of ILD–frequency tuning identified from responses to broadband and tonal stimuli is shown in Figure 4 for two representative neurons. The top row depicts results from neuron N14, showing a high level of agreement between the measured ILD-alone response surface and the prediction using noise-indicated ILD tuning (r² = 0.86). Peaks in the ILD–frequency surfaces obtained from responses to noises and tones matched well (Fig. 4, top, first column). However, the tonal ILD–frequency surface indicated that the neuron was driven by a narrower range of frequencies (6–7 kHz) than was shown by the ILD–frequency tuning identified from responses to noise (5–8 kHz). As a result, there was poor overall agreement (r² = 0.33) between measured ILD-alone responses and predicted responses using the ILD–frequency tuning based on responses to tones.

Figure 4.

Predictive capacities of frequency-specific ILD tuning obtained from noise and tonal responses of two representative neurons. First column, Frequency-specific ILD tuning obtained from responses to broadband noise (top) and the tuning measured using tone or gamma tone pips (bottom). The neuron number is shown above the ILD–frequency tuning surface determined from responses to noise. Second column, Measured ILD-alone response surfaces to broadband noise. Third column, ILD-alone response surface predicted from the frequency-specific ILD tuning identified from responses to noise, shown in the first column. The reported r² above each surface is the mean variance accounted for in the 70% of locations that were not used to infer the frequency-specific ILD tuning. Fourth column, ILD-alone response surface predicted from the tonal response shown in the first column. The r² above each of these surfaces is the variance accounted for using the tone-indicated inputs.

Figure 4, bottom row, shows results from neuron N43, for which the ILD–frequency tuning obtained using noise stimuli accounted for 69% of the variance. In the case of N43, both the tonal and broadband ILD–frequency tuning indicated that this neuron relied on a broad frequency range for its spatial specificity. However, the ILD–frequency tuning identified using noise was shifted to higher frequencies and was broader in the ILD dimension than was the tuning estimated with tones. Because the ILD range of the tone-indicated tuning was so restricted, the corresponding predicted ILD-alone surface was actually more restricted than the measured surface (Fig. 4, row 3, compare second, fourth columns). The two estimates predicted more activity in the right hemisphere than seen in the measured ILD-alone surface, yet the noise-indicated ILD–frequency tuning was better at predicting the spatial response pattern of the neuron.

For both neurons N14 and N43, the ILD–frequency surfaces estimated by the two methods showed clear differences in identified spectral components. This suggests that spectral components that elicited maximal spike rates under narrowband conditions were not necessarily the most important in defining the spatial response of a neuron to complex stimuli.

Comparison of ILD–frequency tuning surfaces identified from responses to broadband and tonal stimuli

The ILD–frequency response surfaces that were obtained from responses to broadband and tonal stimuli differed in several key aspects. We grouped these differences into four general classes. For many neurons, examples of more than one class were observed. Thus, it was often impossible to classify neurons as belonging to only one class.

In the first class, responses to noise identified a wider frequency bandwidth in the ILD–frequency surface than did responses to tonal stimuli. Overall, the median peak bandwidth of noise-identified tuning was 3410 Hz, whereas the median peak bandwidth of tone-indicated tuning was 2007 Hz, yielding a median difference of 1058 ± 1863 Hz (p < 0.0001, Wilcoxon signed rank test; n = 97). A total of 62 of 97 neurons showed noise-identified tuning that was at least 500 Hz wider than their tonal tuning curves. However, only 37 of 97 neurons showed peak bandwidths in their noise-identified tuning curves that were at least 1 SD wider than the peak bandwidths in their tone-indicated tuning curves. Examples of these, N13 and N14, are shown in Figure 5, A and B, respectively.

Figure 5.

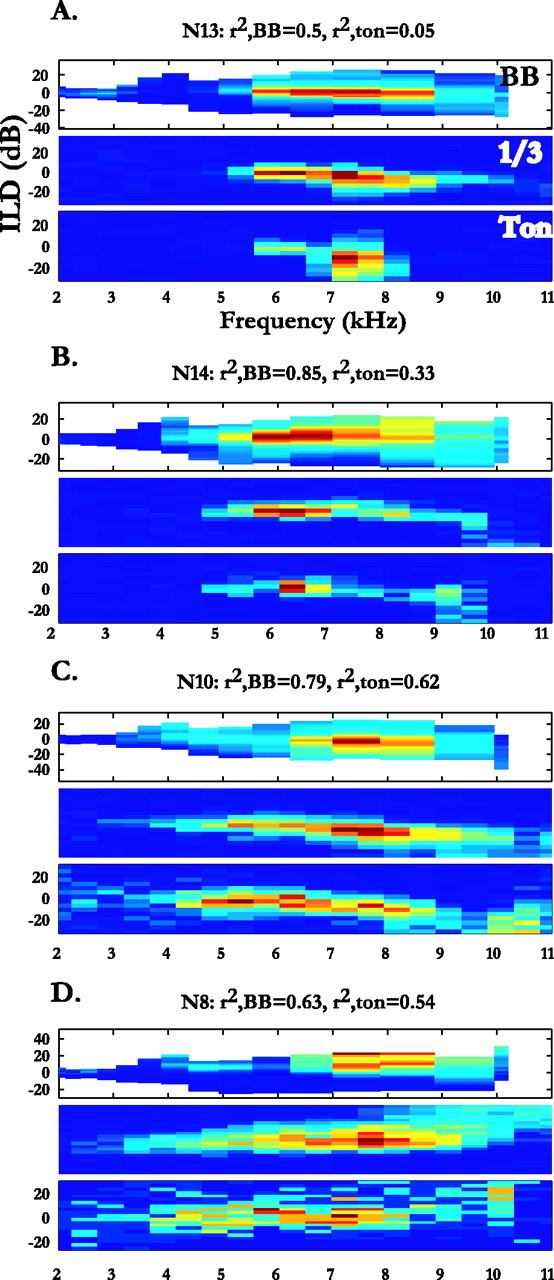
A–D, Comparisons of the frequency-specific ILD tuning obtained with tones (Ton; bottom), one-third octave noises (1/3; middle), or broadband noise (BB; top). The r² values quantifying the similarity of the measured ILD alone surfaces and those predicted using the noise and tonal responses are shown above each set of plots.

Some neurons (24 of 97) showed a narrower frequency range in their noise-identified tuning curves compared with their tone-indicated curves (median difference, 510 ± 1167 Hz; p < 0.0001, Wilcoxon signed rank test). This was somewhat surprising, given that space-specific neurons are generally characterized as broadband (Knudsen and Konishi, 1978a). However, only 12 of these 24 showed tonal tuning curves at least 1 SD wider than their noise-identified tuning curves. One example of such a case, N10, is shown in Figure 5C.

A third class of difference was a noticeable frequency shift in the peaks of the ILD–frequency tuning surfaces. Of our 97 neurons, 56 exhibited peak frequency shifts that were at least as great as 50% of the difference in peak bandwidths in their tuning curves (peak shift ratio, ≥0.5; see Materials and Methods, Eq. 4). Of these, 30 shifted to a higher frequency in the noise-identified tuning curve, and 26 shifted to a lower frequency. One such case is seen with N10 in Figure 5C (peak shift ratio, 1.03).

Finally, for many neurons (68 of 97), tonal stimuli elicited stronger activity at frequencies of >9.5 kHz than did broadband noise (p < 0.0001, Wilcoxon signed rank test; n = 68). Only 21 of 97 neurons showed stronger high-frequency activity with noise. In neuron N8 (Fig. 5D), for example, tonal stimuli at ∼10 kHz elicited strong responses, producing a “high-frequency tail” not indicated by responses to noise. Note that in Figure 5, C and D, the high-frequency tails obtained using tonal stimuli were markedly reduced when one-third octave noises were used instead of tonal stimuli.

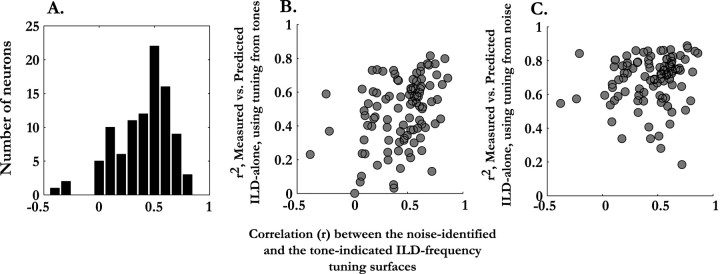
Despite these four classes of difference between the tonal and broadband ILD–frequency surfaces, the surfaces did correspond, often overlapping considerably in frequency even when they differed in ILD. The median correlation between the tonal frequency tuning curves and the frequency tuning obtained from responses to broadband stimuli was 0.59 ± 0.38. The median correlation between the two types of ILD–frequency surfaces was 0.52 ± 0.24. The distribution of correlation coefficients between surfaces is shown in Figure 6A. Of the 97 neurons for which both tonal- and noise-identified ILD–frequency surfaces were available, only 28% showed correlations between ILD–frequency surfaces of >0.60.

Figure 6.

Comparisons of the frequency-specific ILD tuning obtained from responses to tones and broadband stimuli. A, Distribution of correlation coefficients between the ILD–frequency surfaces obtained by the two methods. B, Scatter plot showing that the predictive capacity of tone-indicated ILD–frequency tuning is better when it is more similar to the tuning obtained with broadband stimuli. C, Scatter plot showing that there is no relationship between the predictive capacity of the noise-identified ILD-frequency tuning and its similarity to the tone-indicated tuning.

As another test of whether the estimate of ILD tuning identified using the noise method more accurately estimated the response of a neuron as stimulus bandwidth increased, we also measured frequency-specific ILD tuning from 13 neurons using one-third octave noise. For most of the neurons tested in this manner (n = 13), the response pattern using one-third octave noise resembled the tuning identified from responses to broadband noise more closely than did the tuning identified using tonal stimuli. Correlations between tuning curves identified using broadband noise and those obtained with tones or one-third octave noise increased from a median r = 0.55 (tones) to a median r = 0.83 (one-third octave noise; p = 0.0012, Wilcoxon signed rank test). Correlations between ILD–frequency tuning surfaces increased from a median r = 0.47 (broadband noise vs tones) to a median r = 0.67 (broadband noise vs one-third octave noise; p < 0.0001, Wilcoxon signed rank test).

An important question was whether the ability of tonal ILD–frequency tuning surfaces to predict the measured ILD-alone response surfaces was related to their similarity to the tuning identified with noise. If the ILD–frequency tuning identified from responses to noise accurately reflected the tuning contributing to the measured ILD-alone responses of a neuron, then the closer a tonal ILD–frequency surface came to the tuning obtained from broadband stimuli, the better the tonal result should have predicted the measured ILD-alone surface. Thus, we expected a correlation between the quality of the tonal ILD-alone prediction and the agreement between the ILD–frequency tuning surfaces identified using tonal and broadband stimuli. However, we did not expect an association between the predictivity of ILD–frequency tuning surfaces obtained using noise and how closely these surfaces resembled the tonal ILD–frequency tuning surfaces.

This was, in fact, observed (Fig. 6B,C). In Figure 6B, the r² value of the ILD-alone prediction obtained using tonal tuning is plotted for each neuron (n = 97) against the correlation between the tonal and noise-identified ILD–frequency surfaces. There was a clear correlation (r = 0.34; p = 0.0006), suggesting that the more the tonal ILD–frequency surface resembled the tuning obtained from responses to noise, the better the tonal tuning was at predicting the broadband ILD-alone response surface. There was no correlation seen between the predictive capacity of the noise-identified ILD–frequency tuning and the agreement between the ILD–frequency surfaces (Fig. 6C; r = 0.12; p > 0.1).

Direct neurophysiological assessment of frequency tuning obtained from responses to broadband noise

Tests with minimal, negative, and tone-indicated stimuli were used to assess the degree to which the spatially relevant frequency bands identified for a neuron could elicit ILD-alone responses similar to those obtained with broadband stimuli.

ILD-alone response surfaces using minimal stimuli were recorded from 13 neurons. The median r² value, calculated using all 359 locations, between the measured broadband and measured minimal ILD-alone response surfaces was 0.50 ± 0.15. This indicates good agreement with responses to broadband stimuli, keeping in mind that the trial-to-trial variance in firing can diminish the apparent agreement between the two measured ILD-alone surfaces.

Of these 13 neurons, 10 also were tested using negative stimuli, which yielded a median r² value of 0.086 ± 0.20. Direct comparison of the r² values obtained using the minimal and negative stimuli revealed that the former showed significantly higher predictive capacity than the latter (p = 0.002, Wilcoxon signed rank test). Thus, those frequency bands identified as spatially relevant were necessary and sufficient to produce ILD-alone responses similar to those obtained with broadband stimuli, whereas the remaining frequency bands, when presented alone, did not elicit such similar responses.

For 9 of 13 neurons, we compared the effects of minimal and tone-indicated stimuli. In these 9 cases, the ILD-frequency tuning surfaces obtained with tonal and broadband stimuli overlapped considerably, with a correlation coefficient of 0.75, a value significantly higher than the median value of 0.59 across all 97 neurons. Because of this significant overlap in frequencies and the subsequent similarity in the minimal and tone-indicated narrowband stimuli, we did not expect the minimal stimuli to be significantly better than tonal stimuli in eliciting ILD-alone surfaces similar to broadband ILD-alone surfaces. In fact, the median r² value for the minimal stimuli was 0.50, whereas that for the tonal stimuli was 0.42, but this difference did not reach statistical significance (p > 0.1, Wilcoxon signed rank test). However, the ILD-frequency tuning identified from responses to broadband noise yielded better predictions of the measured minimal ILD-alone response surfaces than did the tone-indicated tuning. The median r² value between minimal ILD-alone surface and that predicted using the ILD–frequency tuning identified from responses to broadband noise was 0.66, whereas that between the measured minimal and tonally predicted surfaces was 0.52 (p = 0.033; Wilcoxon signed rank test). Thus, even when there was significant overlap between tone- and noise-identified frequency bands, the noise-identified ILD–frequency tuning was better at predicting the ILD-alone response surface measured with minimal stimuli than was the tone-indicated ILD–frequency tuning. There was no difference between noise- and tone-indicated tuning in predicting measured tone-indicated ILD-alone response surfaces (r² = 0.54 for each; p > 0.1). This crossvalidation test showed that the ILD–frequency tuning surfaces identified from responses to broadband stimuli yielded the tuning that most strongly determined the spatial response of a neuron.

In three of the nine neurons for which ILD-alone responses were obtained with both minimal and tone-indicated stimuli, the ILD–frequency tuning differed considerably, each showing a correlation coefficient ≤0.59 (N69, N72, and N135). In these neurons, the noise-identified frequency bands were better than the tone-indicated bands at eliciting ILD-alone response surfaces similar to those measured with broadband stimuli.

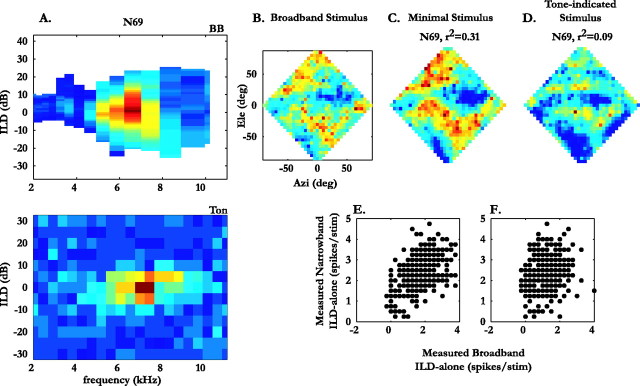
Results from one of these neurons, N69, are shown in Figure 7. Here, the ILD–frequency tuning surfaces obtained from responses to noise (Fig. 7A, top) and tonal (Fig. 7A, bottom) stimuli exhibited a marked lack of overlap (r = 0.59), attributable to a peak shift along the frequency axis. The ILD-alone response surface obtained using the minimal stimulus showed a better overall match to the broadband ILD-alone surface (Fig. 7C; r² = 0.31) compared with the ILD-alone response surface obtained using the tone-indicated stimulus (Fig. 7D; r² = 0.09).

Figure 7.

Contribution of frequency bands identified by tonal and broadband stimuli, shown for neuron N69.A, Tuning for ILD and frequency obtained with broadband stimuli (BB; top) and tonal stimuli (Ton; bottom). B, ILD-alone response surface measured with broadband stimuli. C, ILD-alone surface measured using the minimal stimulus (see Materials and Methods for details). D, ILD-alone surface measured using a tone-indicated stimulus (see Materials and Methods for details). E, Firing elicited at each location by the minimal stimulus plotted against the firing at each corresponding location in the ILD alone surface obtained with the broadband stimulus (B). F, Firing elicited at each location by the tone-indicated stimulus plotted against the firing at each corresponding location in the ILD-alone surface obtained with the broadband stimulus (B). The variances, r², obtained from the scatter plots in E and F are shown above the ILD-alone surfaces in C and D, respectively.

Similar results were obtained for the other two neurons. Both N135 and N72 exhibited significant disagreement between tone-indicated and noise-identified ILD–frequency tuning surfaces (r =-0.41 and 0.31, respectively) although nonetheless sharing a major frequency band. In neuron N135, the frequency bands identified with noise elicited an ILD-alone response surface more similar to that observed with broadband stimuli (r² = 0.51) compared with those identified with tonal stimuli (r² = 0.39). In neuron N72, the minimal stimulus also gave a response pattern (r² = 0.29) more similar than did the tone-indicated stimulus (r² = 0.23).

Discussion

The spatial RFs of auditory neurons are determined by the cues and frequencies to which neurons are tuned and the distribution of the cues in space. We showed that a linear model for the integration of ILD across frequency works well for most neurons but only if the frequency-specific ILD tuning is correctly estimated. We also showed that this tuning can be reliably identified from the neuronal responses to noise. Our approach was robust for noises 10–20 dB above threshold, in that only 30% of the measured responses picked at random were sufficient to explain much of the ILD-alone response surface of a neuron.

We also presented data suggesting that narrowband stimuli, such as tones, are not optimal in assessing the frequency-specific ILD tuning of space-specific neurons in the barn owl (Euston and Takahashi, 2002). The method of presenting tones can identify the frequency that elicits the highest spike rate and is thus typically used to delineate the frequency response of a neuron. The method introduced here, on the other hand, used low-SPL naturalistic stimuli and estimated spectral components that were most relevant for defining a spatial RF. Specifically, in the cases of N135 and N72, when both noise-identified and tone-indicated ILD-frequency tuning surfaces shared a major frequency band (i.e., neurons N135 and N72), the addition of frequency bands suggested by responses to tones actually decreased the similarity of the neuronal response to that obtained with broadband noise. This result suggests that responses to tonal stimuli by these space-specific neurons can be detrimental to understanding the frequency-specific encoding of auditory space. One possible reason for our observations is that the stimulus levels applied to drive these neurons with tone pips may have been beyond the dynamic range of more peripheral neurons.

Saturation effects occur because of processing within the effective bandwidth of auditory nerve fibers (Greenwood, 1991). In the majority of sampled auditory nerve fibers of the barn owl, for example, Köppl and Yates (1999) found that rate–level functions at characteristic frequencies were linear at <25–30 dB SPL. At higher sound pressure levels, auditory nerve fibers grew rapidly less sensitive to changes in level. Furthermore, Köppl (1997) found that the center frequency (CF) divided by the bandwidth of the curve at 10 dB above threshold at the CF in auditory nerve fibers, which can be used to estimate the effective bandwidths in these fibers, yielded bandwidths of ∼530 Hz for a CF of 2 kHz to ∼1000 Hz for a CF of 6 kHz to ∼1240 Hz for a CF of 9 kHz. Given these values, it is clear that the broadband stimuli used in the present study avoided the saturation in the rate–level functions of the owl's auditory nerve fibers. It is important to note that, were broadband stimulus levels high enough to cause saturation in specific frequency bands, the approach outlined here would not yield useful estimates of frequency-specific ILD tuning.

Comparisons with earlier studies

A number of recent studies have manipulated HRTFs to study the individual contributions of sound localization cues. Delgutte et al. (1999) measured the contribution of monaural and binaural cues to the spatial RFs of neurons in the cat's IC by presenting stimuli filtered with HRTFs corresponding to locations along the horizon to one or both ears. In addition, they were able to assess the contribution of the shape of the monaural and binaural spectra by comparing RFs sampled with HRTF-filtered noises and unfiltered noise. More recently, Tollin and Yin (2002a,b) tested the hypothesis that ILD determines the azimuthal RF in the cat's lateral superior olive (LSO). By manipulating the HRTFs to vary one spatial cue at a time, they successfully demonstrated the salience of ILD to spatial coding in LSO neurons (Tollin and Yin, 2002b). This method resembles that used by Delgutte et al. (1999) and Euston and Takahashi (2002) in its attempt to measure the contribution of each cue individually.

In the owl's space map, Euston and Takahashi (2002), like Tollin and Yin (2002b), derived the contributions of ITD and ILD separately and demonstrated how these ITD and ILD-alone response surfaces could be combined to generate the fully cued RF (Pena and Konishi, 2001). Unlike the case of the cat LSO, however, neurons in the owl's space map receive inputs from a wide range of frequencies. ILD tuning therefore had to be assessed at each frequency, and to determine the contribution of ILD, this frequency-specific tuning was transformed into spatial coordinates using an additive model of cross-frequency integration. The predicted ILD-alone response surface was then compared with the measured version. This approach is essentially that of Fuzessery et al. (1985), who showed that the free-field RF of bat IC neurons could be predicted from the directionality of the ears and the rate–level functions measured with components of the biosonar pulse.

The spatial transformation used here and by Euston and Takahashi (2002) provides a somewhat more direct way to determine the role of ILD than comparing individual features, such as positions, slopes, and modulation indices of ILD functions and azimuthal RFs, as was done in the cat LSO (Tollin and Yin, 2002a) and IC (Delgutte et al., 1999). It also provides a method of assessing the degree to which the neurons summed the contributions from each frequency channel independently and the adequacy of tones as probe stimuli. Our results speak directly to both of these issues and raise questions about estimating spatially relevant ILD tuning from responses to tonal stimuli. The degree to which the ILD-alone response surfaces measured with noise agreed with those predicted from responses to tones is modest (Euston and Takahashi, 2002). It was suggested that the space-specific requirement of neurons for spectral breadth made tonal stimuli less effective at probing the ILD tuning. This is consistent with work in the cat. There is evidence in the cat IC that ILD tuning probed with tonal stimuli can be quite different from that probed with noise (Irvine and Gago, 1990; Delgutte et al., 1999). The possible cause for this difference may be that ILD functions are sensitive to spectral density (Irvine and Gago, 1990; Delgutte et al., 1999; Tollin and Yin, 2002b), which is much higher for tones than for the corresponding band in noise.

Analogies to other input–output models of neural coding

The current method of extracting frequency-specific spatial information from responses to broadband stimuli is reminiscent of reverse correlation, in which spectral properties of auditory neurons are estimated from responses to broadband stimuli on the basis of the timing of individual spikes (deBoer and Kuyper, 1968; Marmarelis and Naka, 1972; Marmarelis and Naka, 1973a, 1973b, 1973c; Carney and Friedman, 1998) or average spike rates (Calhoun et al., 1998; Young et al., 1998). These neuronal filtering properties, or spectrotemporal RFs (STRFs), are often used to predict, with varying levels of accuracy, the response of neurons to arbitrary inputs that were not part of the stimulus set from which the STRFs were initially estimated (Eggermont et al., 1983a, 1983b, 1983c; Wickesberg et al., 1984; Knipschild et al., 1992; Schafer et al., 1992; Carney and Friedman, 1998; Yamada and Lewis, 1999; Keller and Takahashi, 2000; Theunissen et al., 2000, 2001). Analogously, in the present study, we found that the frequency-specific ILD tuning inferred from 30% of loci, randomly chosen from the measured ILD-alone response surface, could be used to effectively predict the responses at the remaining loci, which were not used for the initial estimate of ILD tuning.

Schnupp et al. (2001) recently determined the degree to which the spatial response of neurons in the ferret's primary auditory cortex (A1) could be accounted for by assuming that the response of a neuron is proportional to the energy within its STRF, measured with combinations of tone pips (deCharms et al., 1998). The spectrum at the ears would vary as a result of the locationspecific filtering of the ferret's head. No binaural interactions were assumed to be operating. In a significant number of the neurons, this simple model accounted for approximately half the variance of the spatial response of a neuron measured directly using VAS stimuli. Although this kind of linearity might be expected of more peripheral neurons, it is surprising at the cortical level. The approach used by Schnupp et al. (2001) would be difficult to apply to the owl's space-specific neurons, however, because they typically require binaural stimuli having the right ILD spectrum and right ITD value. Tests of linear models of frequency integration are thus complicated by the fact that the frequency tuning curve of a space-specific neuron is highly dependent on ILD (Figs. 4, 5) (Brainard et al., 1992; Arthur, 2001; Euston and Takahashi, 2002), and it is therefore necessary to first estimate this ILD-dependent frequency tuning. We found that once the tuning is assessed in a manner that avoids putative saturation at auditory centers before the IC, an additive model accounts for a considerably higher fraction of the variance of responses from neurons in the barn owl's IC than that reported in the ferret's A1 (r² ∼ 0.49; Schnupp et al., 2001).

Implications for developmental plasticity of neural mechanisms for sound localization

Studies of developmental plasticity in the neural coding of sound localization rely on altering frequency-dependent cues during an animal's critical developmental period and assessing the subsequent effects on neural activity (Szczepaniak and Moller, 1996; Wang et al., 1996; Jiang et al., 1997; Gold and Knudsen, 1999, 2000a,b, 2001; Knudsen, 1999; Gao and Suga, 2000; Knudsen et al., 2000; Shinn-Cunningham, 2001). Gold and Knudsen (1999) sutured an acoustic device that attenuated sound levels in a specific frequency range into the right ears of 35-d-old barn owls and measured responses from space-specific neurons 60 d after the implantation. They found good agreement between the frequency-specific effects of the device and the effect on frequency-specific ITD tuning measured using narrowband stimuli. However, no such correspondence was found when they measured ILD tuning. There are a number of possible reasons for this result. First, their analysis assumed that the optimal ILD spectrum corresponded to that at the center of the spatial RF. Furthermore, they measured frequency-specific ILD tuning with narrowband stimuli (1 kHz bandwidth). Finally, they did not identify spatially relevant features of the frequency-specific ILD tuning of a neuron. Euston and Takahashi (2002) pointed out the frequent lack of correspondence between the optimal ILD spectrum of a space-specific neuron and the ILD spectrum at the center of the spatial RF. This was confirmed in our study (data not shown). Perhaps more significant is that the frequency-specific ILD tuning of a neuron to narrowband stimuli measured under free-field conditions could differ significantly from the ILD cues used by the neuron to generate its spatial response.

Therefore, it is still possible that responses to broadband noise from space-specific neurons of device-reared owls would yield a correspondence between the frequency-specific ILD effects of the acoustic device and spatially relevant ILD–frequency response surfaces. This could help advance studies of the mechanisms of plasticity in ILD tuning responsible for neural encoding of auditory space.