Cochlear Phase and Amplitude Retrieved from the Auditory Nerve at Arbitrary Frequencies

Abstract

It is currently impossible to mechanically measure the overall vibration pattern of the intact mammalian cochlea because of its inaccessibility and vulnerability. At first sight, data from the auditory nerve are a poor substitute because of their limited temporal resolution. The nonlinear character of neural coding, however, causes low-frequency interactions among the components of multitone stimuli. We designed a novel stimulus for which these interactions take a particularly systematic form, and we recorded the response of the auditory nerve to this stimulus. A careful analysis of interactions in the data allowed us to reconstruct frequency transfer functions (both their amplitude and their phase) at multiple points spanning the entire length of the cochlea. The generic character of our stimuli and analysis suggests its wider use in nonlinear system analysis, particularly in those instances in which limitations in temporal resolution restrict the use of customary methods.

Introduction

The mammalian cochlea serves as a spectrum analyzer. Low- and high-frequency components cause maximal excitation at its apical and basal portions, respectively. Different stimulus frequencies are mapped to different cochlear locations, and this map is reflected in the tonotopy of the auditory nerve (AN), which innervates sensory cells along the entire cochlear helix. Cochlear transfer characteristics have been studied through mechanical measurements of the basilar membrane (BM) (for review, see Robles and Ruggero, 2001). These delicate measurements have yielded many important insights into the mechanics of the cochlea, but they have their limitations: the opening of the cochlea easily leads to physiological damage (Rhode, 1971; Robles et al., 1986) as well as functional artifacts (Cooper and Rhode, 1992, 1996); it is difficult to cover a broad range of characteristic frequencies (CFs) within a single cochlea without severely damaging it; the mid-frequency region is exceedingly hard to reach, and identical anatomical structures cannot be accessed in different cochlear regions (Robles and Ruggero, 2001). Recordings from the AN do not suffer the same disadvantages, but the AN cannot follow the fine structure of high-frequency stimuli. This decline of phase-locking frustrates a straightforward evaluation of cochlear vibrations through neural data. Furthermore, the small dynamic range of single nerve fibers restricts the reach of customary techniques like Wiener-kernel analysis; the resulting dynamic range is usually in the order of only 20 dB (de Boer, 1967; Recio et al., 1997).

We present a novel method that enabled us to overcome the temporal limitations of AN coding and to measure cochlear amplitude and phase transfer characteristics at arbitrary CFs with an effective dynamic range of >70 dB. The approach is not based on any physiological intricacies but on the use of a particular stimulus and an appropriate analysis of the response.

Materials and Methods

Theory. The basic idea is to reconstruct the cochlear transfer characteristics from the low-frequency interactions among the components of a multitone stimulus. These interactions, which constitute the envelope of the stimulus, are coded by the nerve regardless of whether the individual primary frequencies exceed the phase-locking limit. For a pair of tones with angular frequencies ω₁ and ω₂, the dominant frequency in the envelope is the beat frequency Δ = (ω₂ - ω₁). This elementary fact generalizes to multitone stimuli as follows. The analytical waveform of a tone complex is:

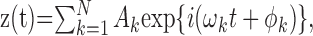1

where the ω_k are the primary angular frequencies, and A_k and ϕ_k are the primary amplitudes and phases, respectively. The squared envelope of z(t) equals:

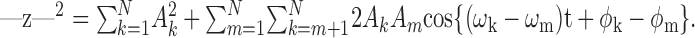2

The first term is a time-independent constant; the second is literally a sum of beats, in which each possible pair of primaries interacts to produce a contribution at a frequency Δ_km = ω_k - ω_m.

In an arbitrary tone complex, several pairs of primaries may have the same frequency spacing and thus contribute to one and the same envelope component so that the contributions of the individual primaries cannot be disentangled. The situation is greatly simplified by choosing a set of primary frequencies for which each pair (k,m) has a unique distance Δ_km. We have named tone complexes with this property “zwuis” stimuli (a contraction of the Dutch words for “beat” and “noise”). For zwuis stimuli, each envelope component at a frequency Δ_km stems from the interaction of two known primaries, and the primary amplitudes and phases determine the amplitude A_km and phase ϕ_km of the envelope component via Equation 2:

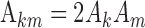3a

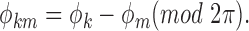3b

In this study, the interaction components (“beats”) are extracted from the response of individual AN fibers to acoustic zwuis stimuli containing five or more primaries, and Equation 3 is used to reconstruct the primary components from the beats. Because there are at least twice as many pairs of primaries as there are primaries, the measurement of all interaction components yields an overdetermined (redundant) set of equations in the unknown primary amplitudes and phases. This set is solved numerically, i.e., those values of A_k and ϕ_k are computed for which the beat components given by Equation 3 are optimally consistent, in a least-squares sense, with the measured beat components. Because of the redundancy, the primary amplitudes and phases can still be estimated accurately when only a subset of the beat components can be extracted from the neural response.

Robustness against nonlinear transduction. Naturally, AN fibers do not code the squared envelope of cochlear vibration, but rather a deformed representation of it caused by nonlinear transduction properties. Provided there are enough primaries, however, the constant term of Equation 2 will be sufficiently dominant to justify a linearization and the continued use of Equation 3. Thus, the validity of Equation 3 will hardly be affected by instantaneous nonlinear mappings. The following numerical test provides an illustration of this robustness in the context of the compression known to occur in the transduction stage. We compressed the envelope of our stimuli using an x^0.2 power function and computed its complex spectrum. We found that the beat components were 8 dB above any other non-DC components. Next, we reconstructed the original stimulus from the beats using the same algorithm that we apply to our data. Mismatches in the reconstructed relative primary amplitudes never exceeded 0.6 dB; relative phases were reconstructed with an accuracy of 0.02 cycle. Thus, the method is robust against a considerable degree of nonlinearity.

Animal physiology. We recorded from several hundred nerve fibers in four cats, using standard techniques (Joris and Yin, 1992). Animals were placed on a heating pad in a sound-attenuated chamber; surgical preparation and recording were done under pentobarbital anesthesia. Micropipettes (3 m KCl) were inserted under visual control into the nerve trunk, exposed through a posterior fossa craniotomy. All procedures were approved by the K.U. Leuven Ethics Committee for Animal Experiments and were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Sound was delivered with a dynamic speaker coupled to an earbar that was tightly inserted into the cut ear canal. Stimuli were generated with commercial hardware controlled with custom software and compensated for the acoustic transfer function measured with a probe tube near the eardrum and a 12.7 mm condenser microphone. The neural signal was amplified, filtered, timed (1 μsec resolution), and displayed. For each fiber encountered, we measured spontaneous rate (SR) and the threshold tuning curve with an automated tracking algorithm. The fiber was then studied with zwuis stimuli.

Results

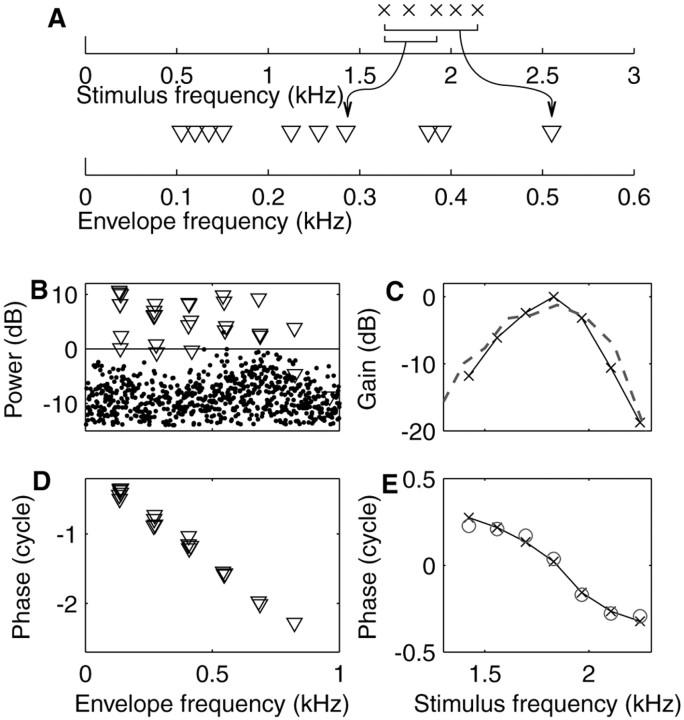
Figure 1 shows responses of a nerve fiber to a zwuis stimulus. For illustrative purposes, the top panel shows a diagram of a zwuis stimulus with five irregularly spaced primaries (top axis) resulting in 10 unique beat components in the spectrum of the envelope of the stimulus (bottom axis). The equality of the primary amplitudes results in equal-amplitude beat components. The remaining panels illustrate the data analysis. A seven component, 1 Hz periodic, zwuis stimulus was presented during 45 sec at a level of 5 dB SPL per primary. The action potentials recorded from an AN fiber served to compile a 1 Hz cycle histogram from which a Fourier transform was computed. In the discrete power spectrum (Fig. 1B), two types of components are distinguished: those at the stimulus beat frequencies are plotted as triangles; dots are used for the remaining components. The horizontal line demarcates a confidence level of 0.001 according to Rayleigh statistics (Mardia, 1972). Clearly the beats dominate the AN response, whereas almost all non-beat components are insignificant. Thus, the response resembles the “sum of beats” of Equation 2, confirming that the envelope of the filtered stimulus is coded.

Figure 1.

Zwuis stimulus and data analysis. A, Diagram showing how a tone complex with five primaries (top axis) results in an envelope spectrum (bottom axis) whose dominant components occur at 10 unique beat frequencies between the primaries, two of which are illustrated with brackets and arrows. B, Power spectrum of the 1 Hz cycle histogram of the response of a low-CF fiber (1850 Hz; SR = 60 spikes/sec; driven rate = 93 spikes/sec) to a seven component zwuis stimulus. Components at the 21 beat frequencies are plotted as triangles, and remaining components as dots. The horizontal line demarcates a p = 0.001 Rayleigh significance of the components, corresponding to 0 dB by convention. C, Amplitude transfer function reconstructed from the power spectrum of B. Peak amplitude is arbitrarily set to 0 dB. Dashed line is the inverted tuning curve from the same fiber. D, Phases of the significant beat components of the response expressed relative to the corresponding phases in the stimulus. E, Phase transfer function (crosses, solid line) reconstructed from the data of D. Its vertical position was adjusted to match phases determined directly from phase locking to the primaries (circles).

Although the beat components in the stimulus envelope have equal amplitudes, their counterparts in the response are unequal because of cochlear filtering of the primaries. From the beat amplitudes, the primary amplitudes were estimated using Equation 3a. The resulting amplitude curve (Fig. 1C) has a bandpass character and peaks at ∼1830 Hz, in agreement with the CF of the fiber of 1850 Hz obtained from the threshold curve (dashed line).

The phases of the primaries of the stimulus were given random values. The phases of the measured beats are therefore only informative after subtraction of the corresponding phases in the stimulus. These phase differences would all vanish if the AN fiber would code the stimulus envelope without any delay or dispersion. A uniform, frequency-independent delay would result in a phase lag that grows linearly with beat frequency. Frequency-dependent delays caused by cochlear dispersion would result in deviations from linearity in a complex pattern because the phase of a single primary affects the phases of multiple beat components. The measured phase differences of the beats (Fig. 1D) reveal a phase lag that accumulates with beat frequency; the slope indicates a delay of ∼3.31 msec. The seemingly erratic deviations from a straight line are unraveled at the next stage of analysis, viz., the reconstruction of the cochlear phase transfer of the individual primaries using Equation 3b. This phase function (Fig. 1E, crosses, solid line) has an average downward slope of 3.30 msec, consistent with the 3.31 msec delay of the beat components. This delay is not uniform: the phase function deviates from a straight line and reveals a type of dispersion familiar from BM measurements (Robles and Ruggero, 2001).

At <5 kHz, AN fibers of the cat can phase-lock to the primaries themselves in addition to the beats (Johnson, 1980). The phase transfer derived from beats may then be compared directly with that derived from synchronization to the primaries, by reprocessing the same raw data (Fig. 1E, open circles). After equalizing their means, the two curves match very well: the RMS of their difference is <0.03 cycle.

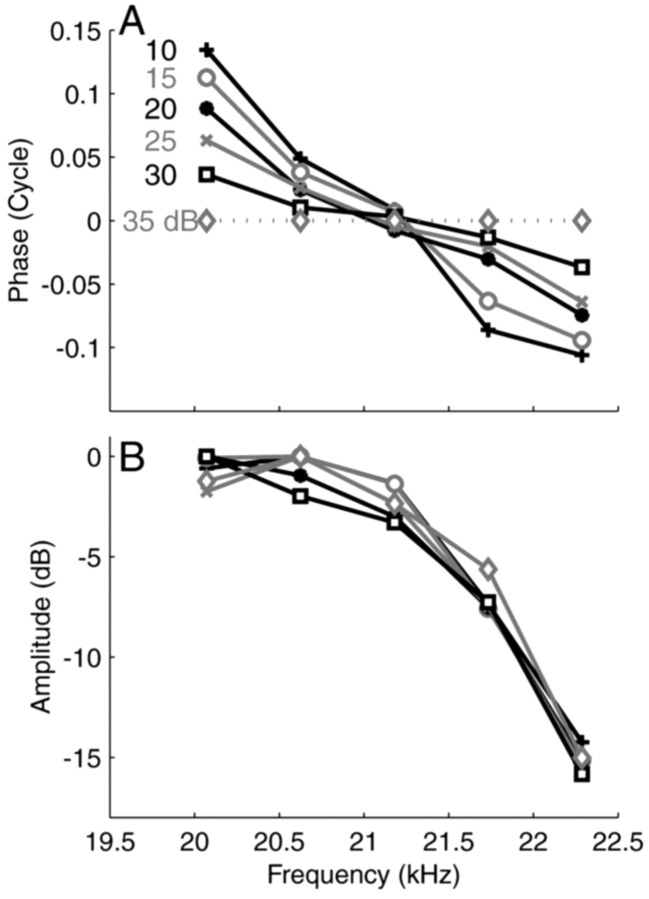
Effective temporal acuity of 20 μsec

To illustrate the effect of stimulus intensity on cochlear phase, Figure 2 shows data from an AN fiber with a CF of 20.5 kHz, far above the limit for phase-locking to the primaries. Intensity was varied from 10 to 35 dB SPL per primary in 5 dB steps. To bring out the small phase differences, we took the 35 dB curve as a reference and plotted the other curves relative to it (Fig. 2A). Note that the lack of absolute phase information renders the vertical position of the curves arbitrary; that all curves intersect at ∼21.2 kHz is but a consequence of our choice to position the phase curves at a zero-mean phase. The slopes of the curves, however, have true content.

Figure 2.

Phase and amplitude curves of a high-CF fiber (20.6 kHz; SR, 57 spikes/sec; driven rates between 82 and 130 spikes/sec) obtained at stimulus levels varying from 10 to 35 dB per primary. A, Phases are plotted as differences relative to the 35 dB reference condition. The vertical offset of the curves is arbitrary. B, Amplitude curves.

Despite the small steps, intensity had a perfectly systematic effect on the steepness of the phase curves; group delay decreased from 1.48 to 1.37 msec over the 25 dB range used. The average difference in group delay between successive curves is therefore only 22 μsec! The effect of sound level on group delay agrees with BM data (Ruggero et al., 1997). The amplitude curves (Fig. 2B) showed little variation with stimulus level, consistent with typical high-frequency BM isointensity curves obtained at low sound levels. We found similar effects of stimulus level on phase for fibers with CFs between 1.5 and 40 kHz. At higher sound levels, many of these showed the broadening and shift toward low frequencies of tuning at higher stimulus levels also found in BM measurements.

Increasing the spectral range

The frequency span of our measurements is limited in two ways. First, if the distance between primaries is too large, the beat frequencies are too high to evoke significant phase locking (Joris and Yin, 1992). Second, if the number of primaries is too large, a subset of primaries often dominates the response at the expense of others. This limited ability to code simultaneous components reflects the small dynamic range of AN fibers. Sometimes one can compensate such imbalance by attenuating the dominant primaries. In our experiments, a single zwuis stimulus typically covered a 1- to 3-kHz-wide range. To enlarge the effective range, we obtained responses from the same fiber to successive stimuli with partially overlapping spectra; all stimuli were presented at a level of ∼15 dB above threshold. We then aligned the individual curves by optimizing the mutual consistency of overlapping data with a least-squares technique.

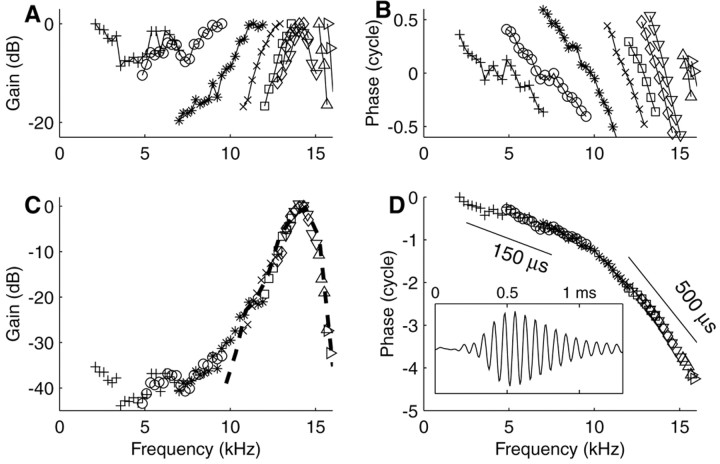
The construction of composite transfer functions is illustrated in Figure 3 for a high-CF (14.4 kHz) fiber. The top panels show the individual curves determined from the responses to stimuli with different but overlapping spectra. For easier comparison with BM data, phases were uniformly advanced by 1 msec, the estimated synaptic and neural delay (Ruggero and Rich, 1987). Alignment results in composite curves (bottom panels). These show several well known features of BM data: a low-frequency tail, a steep high-frequency slope (Fig. 3C), and an increase in group delay with frequency, starting well below CF (Fig. 3D). The inverted tuning curve is superimposed on the composite amplitude curve (Fig. 3C). These two independent estimates of auditory filter shape match closely over a range of about half an octave around CF. The composite curve has a larger range of amplitudes (∼40 dB in Fig. 3C) than the individual amplitude curves. We refer to the former as the “the effective dynamic range.” From the phase curve, we inferred cochlear group delays of 500 μsec around CF and 150 μsec well below CF (Fig. 3D, bars). The inset of Figure 3D shows the impulse response obtained from the composite curves via Fourier transformation. It shows the main features of BM click responses in the base of the cochlea: oscillations reflecting CF, an asymmetric envelope, and an upward FM glide (de Boer and Nutall, 1997).

Figure 3.

Construction of composite amplitude and phase curves for a high-CF fiber (14.4 kHz; SR, 52 spikes/sec; driven rates between 77 and 126 spikes/sec). A, Multiple amplitude curves obtained successively with tone complexes that partially overlap. B, Corresponding multiple phase curves, advanced by 1 msec. C, Composite amplitude curve obtained by aligning the individual curves of A. The dashed line is the inverted tuning curve from the same fiber. D, Composite phase function, advanced by 1 msec. Tilted bar and values indicate group delays. Inset, Impulse response reconstructed from composite curves.

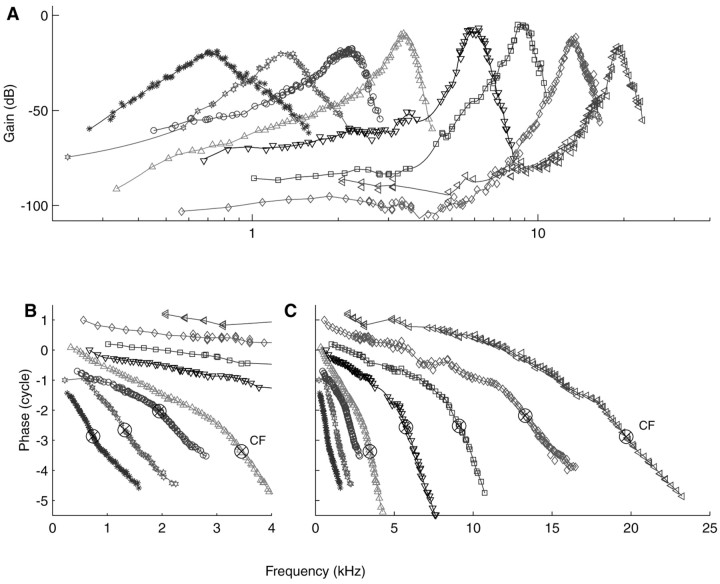
Covering many CFs

An overview of cochlear vibration can be obtained by measuring composite curves for fibers of different CFs. Figure 4 shows a sample of eight curves, selected from 81 fibers for which zwuis data were obtained from a single ear. The eight fibers span a CF range of 740 Hz to 19.7 kHz and include both low and high-SR fibers. Figure 4C shows the phase data in their entirety; Figure 4B shows an expanded view at low frequencies. There is clearly no limitation to the CF range (and, by extension, to cochlear position) that can be studied, other than the availability of experimental data.

Figure 4.

Family of composite curves from a single AN of a cat. A, Amplitude curves. CFs range from 740 Hz to 19.7 kHz. Individual curves have been vertically offset according to the respective thresholds of the fibers. B, Blow-up of the low-frequency portions of the phase curves. The ⊗ indicates the CFs of the fibers. Note the transition from a concave shape to a convex shape with increasing CF. C, Entire phase curves, advanced by 1 msec. Relative vertical positions were adjusted to avoid overlap.

The amplitude curves (Fig. 4A) have effective dynamic ranges that exceed 70 dB in several cases, much larger than customary neural analysis techniques (Carney and Yin, 1988). Their shape gradually changes with CF: low-CF fibers have shallow, symmetric, tuning; high-CF fibers show sharp tuning at CF and extended low-frequency tails. These observations are consistent with neural tuning curves (Kiang et al., 1965) and with BM data (Robles and Ruggero, 2001).

The phase curves (Fig. 4B,C) show a systematic transition from a concave shape for CFs of <1 kHz to a convex shape at >1 kHz. A similar trend was first noticed by Pfeiffer and Molnar (1970) in neural phase-locking to pure tones. The contrast between low-CF and high-CF phase curves is also visible in many mechanical data. We never observed high-frequency amplitude or phase plateaus sometimes encountered in cochlear mechanics. In passing we note that the reconstructed impulse response of the 740 Hz fiber (data not shown) exhibits a downward FM glide; most of our low-CF (<1 kHz) fibers share this feature.

Discussion

We retrieved cochlear amplitude and phase characteristics for a wide range of CFs and stimulus frequencies, using a new stimulus and analysis technique. The effective dynamic range was at least 70 dB, and the effective temporal resolution at least as good as 20 μsec. In many aspects, our results agree with data from mechanical and neural measurements, but our method has significant advantages over previous measurement techniques. Compared with BM measurements, our method has the advantages of an intact cochlea, easy access to all frequency regions, and the examination of many different CFs within a single cochlea. Compared with analyses conventionally applied to neural data, our method has the advantages of the continued applicability beyond the limit of phase-locking and a much larger frequency span and, by implication, effective dynamic range.

Limitations and ways to overcome them

The zwuis method only yields relative amplitudes and phases of simultaneously presented primaries; absolute values remain unknown. Hence, without supplementary data or assumptions, no absolute relations can be established across recordings. The construction of composite curves (Fig. 3) shows that, in practice, this limitation need not be a severe one: the consistency of data on overlapping frequency regions allowed their mutual alignment.

Because each of the multitone stimuli used for the construction of the composite curves was presented at a level of 15 dB above threshold, composite curves are more akin to iso-response data on tuning (such as threshold curves) than to the iso-input curves usually reported in BM studies. This distinction may complicate their interpretation in terms of transfer functions but, as pointed out by de Boer and Nutall (1999), it should not be exaggerated. These authors combined BM responses across stimulus frequencies in a manner comparable to ours and, maintaining that mechanical nonlinearities are restricted to a narrow band around CF, interpreted their composite spectrum as if it was obtained “in one experiment with a constant-amplitude weak stimulus over the entire frequency range.”

The collection of individual curves in Figure 4 seems far removed from a “panoramic view” of cochlear vibration, i.e., a description of the envelope and phase of traveling waves. In fact, an across-fiber analysis of such population data does allow an elaborate quantitative analysis of the cochlear traveling wave, but that is outside the scope of this paper.

Envelope coding in the AN depends on stimulus level (Joris and Yin, 1992). This imposes another limitation on our methods. For most fibers, sound levels between 10 and 50 dB above threshold cause no problems. At higher levels, saturation of the fibers often renders our methods increasingly inefficient so that more repetitions are needed. Near threshold, low driven rates also necessitate longer stimulation. We have not systematically explored these limits but we estimate that for most fibers, the method works over an intensity range of at least 50 dB. The upper limit might well be extended by optimizing the number and spacing of primaries as well as their relative amplitudes. Note that these dynamic range restrictions are primarily relevant for frequencies near a the CF of a fiber.

How mechanical is the reconstructed tuning?

Given the fairly indirect derivation of transfer characteristics, it is important to examine the validity of our interpretation in terms of cochlear mechanics. We assume that the vibration at a given cochlear site is dominated by the primary components comprising the stimulus. Their relative strengths and latencies constitute what we call the “cochlear transfer characteristics.” The subsequent transduction stage involves a process of rectification that results in envelope coding and the necessary occurrence of second-order interactions on stimulation with tone complexes.

Could the beat frequencies of Equation 2 be physically present in the spectrum of cochlear vibration rather than be a reflection of envelope coding? In that case the beats would correspond to quadratic difference tones (QDTs) on the BM. However, at the base of the cochlea, QDTs are insignificant, and at the apex they are at least 20 dB below the response to the primaries (Cooper and Rhode, 1997). Our beat frequencies are always further away from CF than the primaries themselves. Thus QDTs, even if physically present on the BM, will not contribute significantly to the AN responses.

Higher-order distortions such as cubic difference tones, however, may play a role. Indeed, in a minority of our measurements (<5%), we found evidence for the occurrence of higher-order distortions. Unlike the power spectrum of Figure 1B, the spectra of such data were “contaminated” by significant non-beat frequencies. On close inspection, the anomalous components occurred at frequencies corresponding to higher-order interactions. Any data showing these anomalies were excluded from our analyses.

What effect do details of the transduction process have on the beat components? It was shown above that it is immaterial how the envelope is coded exactly; the only crucial condition is that the instantaneous firing rate of the fiber is positively correlated with fluctuations in stimulus power. To this theoretical argument we can add the observation that the spontaneous rate classification of AN fibers did not have an effect on the reconstructed amplitude or phase curves: regardless of their respective SRs, fibers from the same cochlea yielded very similar transfer functions for matched CFs.

Finally, dynamic aspects of the transduction might affect the beat components. Adaptation, for example, would enhance the faster envelope components. Such biasing, however, does not have a sizable systematic effect on the reconstruction of primary amplitude and phase because there is no monotonic relation between beat frequencies and underlying primary frequencies (Fig. 1A). Any biases in the beat-frequency domain do not translate to similar biases in the primary-frequency domain. Moreover, the redundancy discussed above tends to protect the estimates from such biases.

Last but not least, the detailed consistency of our data with many facts known from cochlear mechanics cannot be ignored.

Closing statement

In this paper, we have emphasized the ability to retrieve amplitude and phase information for single auditory nerve fibers at all CFs and the consistency of such curves with BM measurements at single cochlear locations. The scope of the zwuis method can be significantly extended by combining data across nerve fibers, allowing a reconstruction of BM motion for individual stimulus components. Outside the field of cochlear mechanics, zwuis-like methods may be applied to the more central parts of the auditory pathway, which are known to show a progressive loss of phase locking to the stimulus. From a more general point of view, this study presents a novel “black box” approach to the analysis of nonlinear systems. Its successful application to the neural coding of sound suggests its wider use in nonlinear system analysis, particularly in those instances in which limitations in temporal resolution restrict the use of customary methods.