Cerebellar Signatures of Vestibulo-Ocular Reflex Motor Learning

Abstract

The vestibulo-ocular reflex (VOR) comprises an outstanding system to perform studies that probe possible cerebellar roles in motor learning. Novel VOR gains can be induced (learned) by the wearing of minifying or magnifying lenses, and learning requires the presence of the cerebellum. Previously, it was shown that Purkinje cells change their head velocity sensitivities with learning and that this change was thought to be inappropriate to be causal for the changed behavior. We now demonstrate that Purkinje cells also change their eye position, eye velocity, and head velocity sensitivities after learning. These combined changes at the Purkinje cell level contribute to a net modulation that is appropriate to support the new VOR gains. Importantly, the changes in the eye position parameter, reported for the first time, suggest the involvement of the neuronal integrator pathways in VOR learning. We provide evidence that all of these changes are necessary for VOR behavior and can explain learning deficits after cerebellar removal.

Introduction

The vestibulo-ocular reflex (VOR) has been used as a model system to probe the role of the cerebellum in motor learning. The cerebellum is necessary for motor learning to proceed, because new learned responses are precluded after cerebellar removal (Zee et al., 1981; De Zeeuw et al., 1998; Rambold et al., 2002). The VOR counterrotates the eyes during head movement to stabilize a visual target on the retina, thus improving visual clarity. VOR gain is defined as eye velocity divided by head velocity (gain = eye velocity/head velocity) and is normally one in the light for frequencies between 0.01 and 5 Hz (Paige, 1983a). If a change in gain is required, the brain is recalibrated by a teaching or error signal provided by the visual system. In this scenario, visually driven eye movement commands take precedence over vestibular commands, causing the eyes to accurately fixate or follow a visual target in the light. If visual–vestibular mismatch continues, then learning prevails and the VOR gain changes. To evaluate this new reflex gain, the VOR is tested in the dark without vision by measuring the amplitude of eye velocity during angular head velocity.

VOR gain depends on the estimate of angular head velocity by the brain. Because the behavior changes monotonically (increasing the gain from low to high), a focus of the search for the neural loci supporting VOR motor learning has been centered on the demonstration of a monotonic change in head velocity sensitivity of candidate neurons. Each of three possibilities has its proponents: (1) the flocculus (FL) is the exclusive site of learning (Marr, 1969; Albus, 1971; Ito, 1982); (2) the brainstem is exclusively responsible (Miles and Lisberger, 1981); and (3) the multisite hypothesis, presently most accepted, suggests roles for both the FL and brainstem (Lisberger and Sejnowski, 1992; Lisberger et al., 1994a,b; Hirata and Highstein, 2001). In support of the latter hypothesis, during training toward novel gains, Partsalis et al. (1995a) showed evolving changes in brainstem FL target neuron (FTN) responses, and once novel gains were firmly established after several weeks of training, FTNs and FL Purkinje cells demonstrated remembered changes (Miles et al., 1980; Lisberger et al., 1994a,b; Partsalis et al., 1995a,b; Hirata and Highstein, 2001). Also relevant, in FTNs only a part of the remembered changes remained after chemical inactivation of the FL, suggesting the necessity of an intact FL pathway for the expression of the complete memory of the novel gain.

Presently, we show that changes in head velocity sensitivity are not monotonic and are accompanied by changes in eye velocity and eye position sensitivity. We propose that changes in these additional parameters may reflect the requirement that brainstem changes in sensitivity to head velocity be accompanied by parallel changes in eye movement-related parameters. Furthermore, changes in eye position parameters suggest modifications in the strength of signal flow through the integrator pathways that may be necessary to maintain appropriate broadband reflex performance.

Materials and Methods

A total of nine male squirrel monkeys were used for behavioral and recording experiments. Three monkeys (062, 066, and 70F) were used for behavioral studies (see Fig. 7), and seven monkeys (70F, 2H, C15, M146, 3Y, O63, and 1F) for electrophysiological recordings in all lobules of the left FL and ventral paraflocculus. An eye coil for monitoring eye movements (Robinson, 1963) and a head post for head fixation were surgically implanted. After a recovery period of 3 weeks, a recording chamber was implanted aimed at the left FL (7.5 mm lateral, 1 mm posterior, and tilted 0° mediolateral and 0° anteroposterior). During both behavioral and electrophysiological studies, amphetamine sulfate (0.15 cc/kg, oral) was given to maintain constant alertness. Experimental protocols were approved by the Washington University Committee on Animal Care and performed in accordance with National Institutes of Health guidelines.

Figure 7.

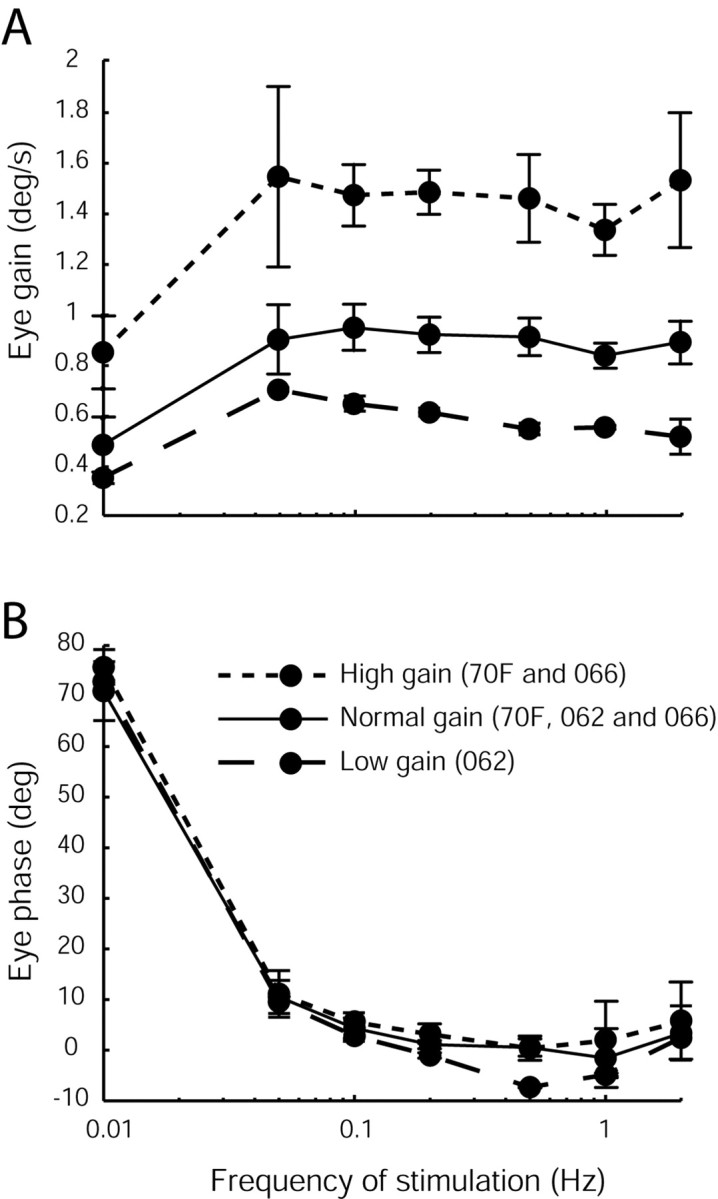
Experimental data showing the bode plots obtained in three monkeys in the naive gain state (70F, 062, and 066), after chronic low-gain (062) and chronic high-gain (70F and 066) adaptation to show that the dynamics of the reflex are maintained across the entire broadband spectrum of head movement. VOR gain (A) and phase (B) were measured during sinusoidal rotations in the dark (±40°/sec). Animals were adapted for 3 weeks before the start of sessions for the low- or high-gain data. Note that the dynamics of the reflex (phase) are relatively unchanged and that the gain changes span the entire frequency spectrum tested.

For vertical vestibular stimulation, the animal was placed on its right side atop a turntable, with the axes of rotation coincident with the interaural axes. Optokinetic visual stimulation (OKS) was produced by an optokinetic system projecting vertical lines onto a cylindrical white screen at 45 cm from the animal's eyes. For enhancement (e) and cancellation (c) of the VOR, the optokinetic stimulus was rotated either out of phase or in phase with respect to the chair. The gain of the eye was calibrated during passive head rotations in the light (0.5 Hz and 40°/sec) in the normal VOR gain state (Paige, 1983a,b; Partsalis et al., 1995b).

Behavioral training. Chronic adaptation of the VOR was used to study behavioral and neuronal changes during motor learning. Animals wore magnifying (2.2×) or minifying (0.45×) goggles for several weeks or months while in their home cages. Goggles were constructed to fit each animal's face using a dental acrylic frame.

Recording procedures. A Power 1401 data acquisition system (Cambridge Electronic Design) and Spike2 software were used to record the vertical and horizontal eye position, head velocity, drum velocity, and neuronal activity. Neural activity was recorded in two ways, as an analog 40 KHz signal and as an event marker occurring every time the signal exceeded a threshold set manually using a time-amplitude window discriminator.

Purkinje cells were selected when they showed a clear modulation for vertical eye velocity during optokinetic responses (OKR) and little or no modulation for horizontal OKR. If we found a clear modulation during vertical OKR, then we rotated the animal in the dark (d) for at least 1 min (30 cycles at 0.5 Hz). After VORd, we tested VORc and VORe in the light by rotating the OKS drum either in phase or out of phase of the chair for at least 1 min (30 cycles at 0.5 Hz). Spontaneous eye movements were recorded in the light (just before VORd, VORe, and VORc) and in the dark before and after VORd. The order of the tasks was chosen to correspond with the order used for analysis (compare below). In many cases, it was possible to distinguish complex spikes (CS) from simple spikes (SS) in a single recording (see Results). CS could be extracted from the SS recording by setting a second threshold (CS are larger than SS). These cells were then identified as Purkinje cells by their CS–SS interaction. All of the Purkinje cells identified by their response to OKS and with clear difference between their CS and SS showed a pause in their SS after the occurrence of a CS.

Analysis methods. At the end of each recording session, the data collected were exported into Matlab format for off-line analysis. All subsequent analyses were performed using Matlab 6.1 (The MathWorks). Only smooth eye movements and neuronal response during smooth eye movements were considered in this study. Saccades were removed by setting an acceleration threshold (set automatically to 200–400°/sec²) and later double-checking the eye data for additional manual desaccading, if needed. As a first analysis, we averaged the desaccaded data over cycles of sinusoidal stimulation and fit a sinusoidal curve to the resultant averaged traces. Amplitude and phase of each neuronal modulation was compared with the corresponding behavioral output (average eye movement) and stimulus input (chair or OKS). The phase of the neuronal modulation was referred to as the difference, in degrees, between the peak head velocity (eye velocity during visual following paradigm) and the peak neuronal firing rate.

To extract the component corresponding to the eye, head, and retinal slip parameters, we used a multiple linear regression technique. A detailed description has been reported previously (Hirata and Highstein, 2001). In brief, we first used the data obtained during OKR to extract the retinal slip and eye component of the firing rate by using a multiple linear regression model consisting of retinal slip velocity and acceleration, eye position, eye velocity, eye acceleration, and a DC term (Eq. 1). Delay between retinal slip and firing rate and that between eye movement and firing rate were globally searched to minimize the squared sum of residuals. Before this procedure, retinal slip was linearized by using a sigmoidal function, because there usually exists a strong nonlinear (saturation) relationship between retinal slip and Purkinje cell firing pattern. Head parameters (head velocity and head acceleration) were subsequently obtained by fitting another multiple linear regression model (Eq. 2) to a modified firing rate (resulting from the original firing rate minus the estimated firing rate caused by the eye contribution) during VORd. To verify the model fits, data during VORe and VORc were predicted by using the combined multiple linear regression model described in Equation 3:

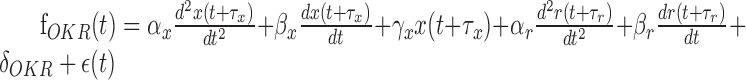(1)

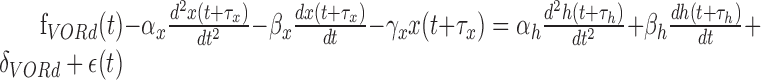(2)

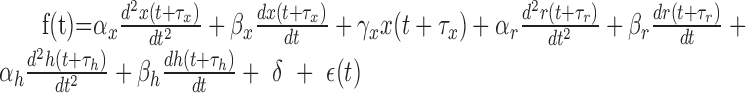(3)

Parameters f, x, r, and h denote the Purkinje cell firing pattern, eye, retinal slip, and head position, respectively, whereas α, β, and γ denote sensitivities to acceleration, velocity, and position, respectively. δ and τ are DC firing rate and delay in firing rate with respect to eye, head, or retinal slip movement. ϵ denotes an error term or a residual component.

In addition to the analysis described previously, we correlated the neuronal firing rate to the vertical eye position data recorded during spontaneous eye movements in the light (at least 60 sec). This analysis was also performed on desaccaded data. Our animals were not required to fixate any particular target. They did that spontaneously as part of exploring their visual surroundings. We used the eye position trace and firing rate in the time between saccades to estimate the Purkinje cell sensitivity to static eye position. A table that contains the corresponding eye position for each spike (as firing rate) was constructed. The firing rate was then plotted against eye position, and a corresponding line was fit to the data. That gave us the Purkinje cell sensitivity to static eye position (see Fig. 3D), whereas in the previous analysis we obtained the Purkinje cell sensitivity to a dynamic eye position (see Fig. 3C).

Figure 3.

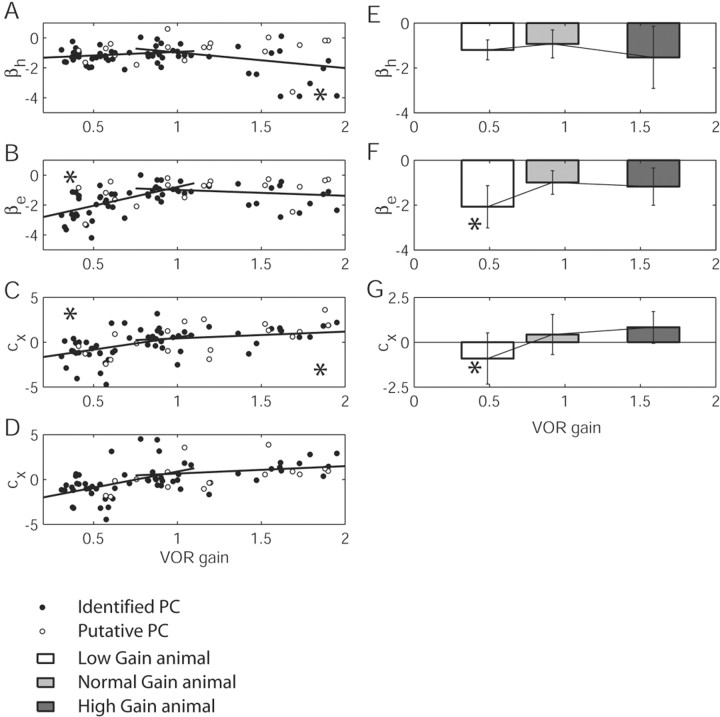
Plots displaying the changes in Purkinje cell sensitivities to eye and head parameters with respect to changes in the VOR gain. A–D (ordinate) plot head velocity sensitivity (β_h), eye velocity sensitivity (β_e), eye position sensitivity (C_x) (dynamic), and eye position sensitivity (C_x) (static) with respect to VOR gain (abscissa). Filled circles, Identified Purkinje cells; empty circles, putative Purkinje cells. The significance of the slope is indicated by an asterisk in the corresponding corner of the plot. In E–G, the data were separated into three populations, corresponding to the low-, normal-, and high-gain-adapted animal. Statistical significance of a one-way ANOVA (high or low versus normal population) is indicated with an asterisk.

All parameters extracted from the Purkinje cell firing rate were plotted against the VOR gain of the animal. To account for possible changes in the Purkinje cell parameters with respect to the VOR gain, we calculated a linear fitting of each parameter with respect to the VOR gain. These analyses were performed for the normal and low-gain and normal and high-gain populations. Statistical significance of the slope was calculated by means of a Pearson correlation (p < 0.05). Additionally, we divided the Purkinje cell population into three separate groups (low, normal, and high gain) and looked for any statistical significance between groups using a one-way ANOVA (p < 0.05). These statistical comparisons were performed using Analyze-it software for Microsoft Excel.

Results

Behavioral studies

Animals were trained to high or low VOR gains by the chronic wearing of minifying (0.45×) or magnifying (2.2×) spectacles. Three animals wore magnifying or minifying glasses for a maximum period of 4 months. After a period of 3 weeks of wearing magnifying lenses, the VOR gain reached values >1.5 (mean ± SD, 1.59 ± 0.26; minimum, 1.16; maximum, 1.95). Similarly, when animals were adapted to low gain, a gain decrease (mean ± SD, 0.47 ± 0.1; maximum, 0.63; minimum, 0.31) was observed. Chronically trained rhesus monkeys remember their novel gains for long periods after training (Miles and Eighmy, 1980). The asymptotic levels for the chronically adapted squirrel monkeys were 82.8 ± 10.0% of the net acquired gain for low-gain training and 78.4 ± 12.0% for high-gain chronic training. Just as in rhesus monkeys (Miles and Eighmy, 1980), our results in squirrel monkeys (data not shown) suggest that at least 1 week of continuous training is required to firmly establish the memory of this new behavior in squirrel monkeys. Four additional animals were also used to collect data in the naive state. Naive and normal-gain animals showed VOR gains close to 1 (mean ± SD, 0.9 ± 0.1; maximum, 1.08; minimum, 0.685).

Our experiments were performed with animals lying on their right side. Previous work (Baker et al., 1984, 1987; Rude and Baker, 1988; Brettler et al., 2000; Brettler and Baker, 2001, 2003) has shown the influence of the utricular otolith on the low-frequency vertical VOR when an upright animal is rotated in the pitch plane. By placing animals side down, the otolithic influence on the reflex is minimized, resulting in relatively isolated vertical canal stimulation and rendering the vertical VOR comparable with its horizontal counterpart.

Neuronal recordings

Ninety-five Purkinje cells throughout all lobules of the FL and ventral paraflocculus were recorded in seven chronically trained animals. Cells were classified as vertical zone Purkinje cells by their modulation during visual following of an optokinetic drum in the vertical plane (Fig. 1A,E,I) and by a CS recorded in the vicinity of the SS. In 65 Purkinje cells (68%), the SS and CS were recorded simultaneously. Those cells were additionally identified as Purkinje cells by their typical CS–SS pause (Fig. 1D,H,L). All of the Purkinje cells recorded showed an increasing discharge with downward eye velocity during OKS at 0.5 Hz and a decreasing discharge for upward eye velocity (Fig. 1A,E,I,M). Thus, the excitatory or on-direction for all vertical Purkinje cells was a downward slow eye movement. The neuronal gain defined as spikes per second per degrees per second of eye movement was dependent on the VOR gain (compare Fig. 3, as discussed below).

Figure 1.

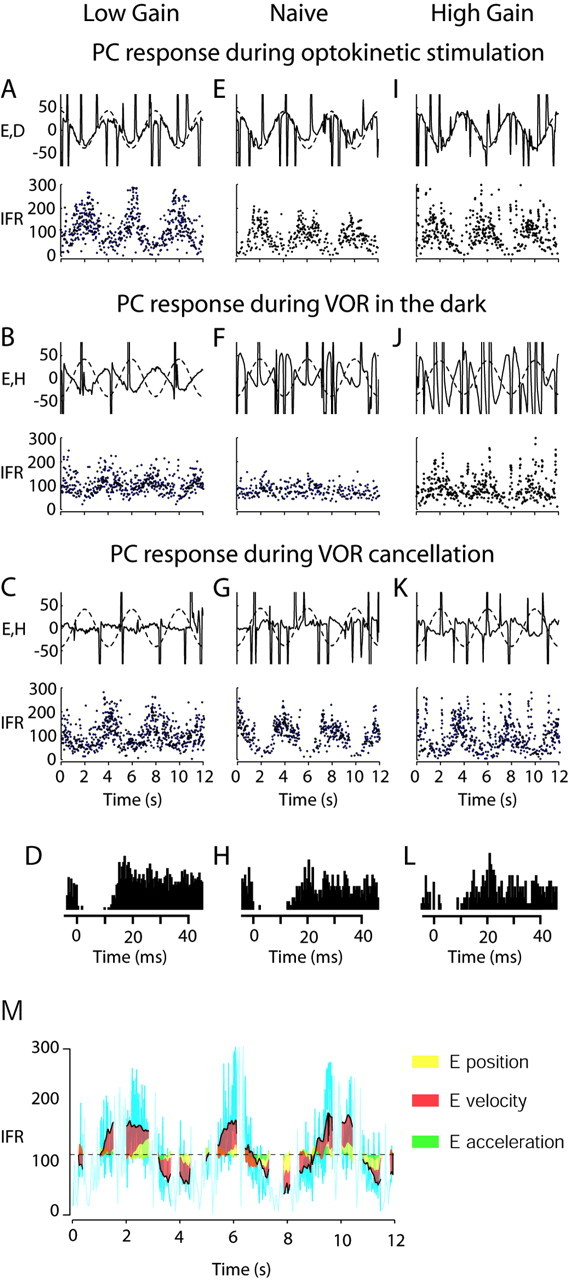
Examples of FL Purkinje cell (PC) responses during OKS (A,E,I), VORd (B,F,J), and VORc (C,G,K) before and after VOR adaptation, to show that cells change their response to VORd and the OKR after motor learning. Each panel shows: Top, solid lines, Eye velocity in degrees per second; dashed lines, the OKS velocity (first row) or head velocity (second row) or both (third row) in degrees per second; bottom, instantaneous firing rate in spikes per second. The first column (A–D) corresponds to a PC recorded after chronic low-gain adaptation in monkey 2H, the second column (E–H) corresponds to a PC recorded in the naive state in monkey 063, and the third column (I–L) corresponds to a PC recorded after chronic high-gain adaptation in monkey 2H. At the bottom of each column, we show CS and SS interaction for each of the three cells. SS responses were aligned around the occurrence of a CS at time 0 on the abscissa. Note the pause in SS activity for > 10 msec after a CS. This provides positive identification that the recorded element was a Purkinje cell. In M, we present as an example the amount of firing rate caused by any of the eye parameters during OKR for the cell presented in A. The cyan lines represent the original firing rate of the cell. In yellow, red, and green, we show the amount of firing rate contributed by the eye position, velocity, and acceleration components. The dashed line indicates the DC firing rate in light. The portions of the data that correspond to a saccade are indicated by a lighter cyan line (these portions corresponding to saccades are not used for analysis).

Twenty-nine Purkinje cells were recorded in the naive state, 26 Purkinje cells after >3 weeks of chronic adaptation to high gain, and 40 cells after >3 weeks of chronic adaptation to low gain. Cells were analyzed first as performed traditionally by averaging over cycles of neural responses to sinusoidal visual or vestibular stimulation and fitting a sinusoidal curve to their average firing rate (Lisberger and Fuchs, 1978; Hirata and Highstein, 2001). Cells were analyzed further using a multiple linear regression technique (Hirata and Highstein, 2001) to obtain coefficient values relating their responses to eye movement, head movement, and retinal slip parameters. The original firing rate was then compared with the reconstructed firing rate obtained from a model of the responses and tested for the goodness of fit (see Materials and Methods). Seventeen Purkinje cells (18%) were discarded from the analysis for one or more of the following reasons: (1) the cell was lost before all paradigms were completed (2 cells); (2) SS firing was unstable (12 cells); and (3) our model was not able to reliably predict the original firing rate (15). The latter cells include mostly examples that clearly saturated during the visual following paradigm (5) and those with an unstable SS firing rate. In these cases, our model could not extract the eye component parameters properly because of the linearity and time invariance assumption made when constructing the model (Hirata and Highstein, 2001). No saturation was found in any of the cells during VORd. The data presented below correspond to the remaining 78 Purkinje cells (18 putative and 60 identified) that were analyzed successfully (Table 1).

Table 1.

Purkinje cells recorded in the naive and adapted animal that passed the tests and were used for further analysis

Animal	Low gain	High gain	Normal gain	Total
2H	11	12		23
70F	20	10		30
1F	1			1
C15			9	9
063			7	7
3Y			3	3
146			5	5
Total	32	22	24	78

Purkinje cell responses during VORd

In the normal-gain animal, Purkinje cells showed a very small modulation during head rotation in the dark [(Fig. 1F) mean ± SD neuronal amplitude × cos (neuronal phase) = –3.9 ± 8.7 spikes/sec/degrees/sec]. After chronic high-gain adaptation, Purkinje cell responses showed an in-phase modulation with respect to upward head velocity [(Fig. 1J) mean ± SD neuronal amplitude × cos (neuronal phase) = 15.1 ± 10.9 spikes/sec/degrees/sec]. In contrast, after chronic low-gain adaptation, responses showed an out-of-phase modulation with respect to upward head velocity [(Fig. 1B) i.e., modulation closely in phase with downward velocity; mean ± SD neuronal amplitude × cos (neuronal phase) = –10.8 ± 11 spikes/sec/degrees/sec]. These vertical VOR results are similar to those demonstrated when the gain of the horizontal VOR was chronically adapted (Lisberger et al., 1994b).

As reported for the horizontal system (Miles et al., 1980; Lisberger et al., 1994b), Purkinje cells in the low- and high-gain states seem to be clearly segregated into two distinct populations (one-way ANOVA; comparison of low-gain vs high-gain population; p < 0.0001). We used a three-dimensional plot in Figure 2A to show differences in cell firing in high and low VOR gains. Green spheres are data recorded in naive animals, blue spheres in high-gain animals, and red spheres in low-gain animals. The gain of the reflex is plotted on the ordinate. The length of the line in the plane of the circular plot indicates the depth of modulation. The angle of the line in the plane of the circle indicates the phase. Zero degrees phase equates to increasing discharge when the head moves up, whereas 180° indicates increasing modulation when the head moves down. We also decomposed this three-dimensional plot into a top view (Fig. 2B) and a two-dimensional plot of Purkinje cell modulation versus VOR gain (Fig. 2C) for additional clarity. In Figure 2B, the blue arrow indicates the average neuronal phase for the high-gain state, whereas the red arrow is the representation for the low-gain condition. In Figure 2C, it can be seen that there is little Purkinje cell modulation in the naive VORd (green), whereas modulation increases in one direction for high gain (blue) and in the other direction for low gain (red). It is notable that, in the chronic condition, the phases associated with high- and low-gain conditions are almost all clustered into two distinct groups ∼180° apart and that the depth of modulation is similar among examples in each group. The data plotted in Figure 2 are detailed in Table 2. Purkinje cell responses during VORd are consistent with previous results in the horizontal system and demonstrate that Purkinje modulation should help to move the eyes appropriately after adaptation. Below, we decompose Purkinje cell modulation into component responses related to head and eye movement.

Figure 2.

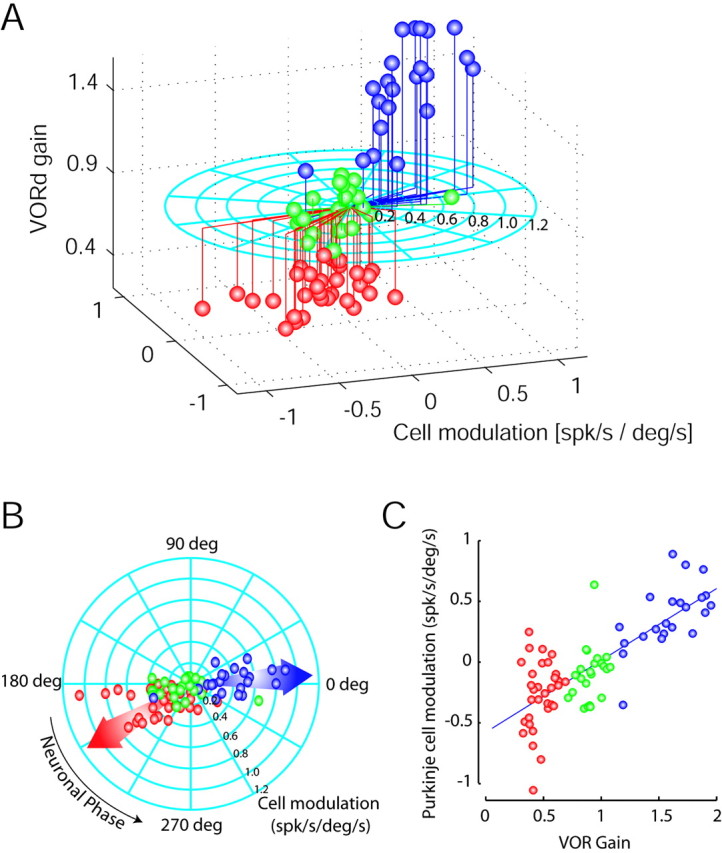
Polar plots representing differential Purkinje cell responses during VORd in low-, normal-, and high-gain-adapted animals. A, Three-dimensional representation in which the modulation amplitude for each cell is indicated as the length of the line running on the flat circle, and the phase of the modulation is indicated by the angle of that line. Zero degrees indicates modulation in phase with upward head movement, and 180° is modulation out of phase with upward head movement (modulation increases with downward head movement). The gain of the reflex is plotted on the ordinate. B and C decompose the three-dimensional plot into two-dimensional plots. B is a top view of the graph in A. Arrows indicate the average phase for the high-gain (blue arrow) and low-gain (red arrow) populations. C, The Purkinje cell modulation versus VORd gain in a Cartesian plot. The x-axis represents VOR gain, whereas the y-axis represents the normalized PC modulation (cosine function of the neuronal phase multiplied by the total modulation). Cells recorded in the low-, normal-, and high-gain animal are plotted as red, green, and blue spheres, respectively.

Table 2.

Purkinje cell sensitivities and modulation during VORd in the naive and adapted animal

Gain state	Eye velocity sensitivity (spks/sec/deg/sec)	Eye position sensitivity (spks/sec/deg)	Eye acceleration sensitivity (spks/sec/deg/sec2)	Head velocity sensitivity (spks/sec/deg/sec)	Head acceleration sensitivity (spks/sec/deg/sec2)	Retinal slip velocity sensitivity (spks/sec/deg/sec)	Retinal slip acceleration sensitivity (spks/sec/deg/sec2)	VORd modulation amplitude (spks/sec/deg/sec)	VORd modulation phase (deg)
High gain	-1.1759 ± 0.8302	0.8196 ± 0.8906	-0.0616 ± 0.0685	-1.5310 ± 1.3841*	-0.0495 ± 0.0773	-1.4880 ± 2.5032	0.0315 ± 0.0628**	0.42 ± 0.21	4.02
Normal gain	-1.0785 ± 0.6344	0.4941 ± 1.1206	-0.0712 ± 0.0690	-0.9845 ± 0.6435	-0.0519 ± 0.0370	-0.6408 ± 0.9782	-0.0155 ± 0.0885	0.2016 ± 0.1522	202.3
Low gain	-2.0781 ± 0.9498**	-1.0548 ± 1.3452**	-0.1129 ± 0.0821**	-1.1783 ± 0.4299	-0.0516 ± 0.0481	-0.3431 ± 0.7234	-0.0349 ± 0.0987	0.37 ± 0.23	211.6565

Purkinje cells were separated in groups based on the state of the animal (low, naive, or high gain). Statistical significance of the comparison between groups was performed by using an ANOVA single factor (**p < 0.05 and *p < 0.1 when compared with the naive population). spks/sec/deg/sec, Spikes per second per degrees per second.

Purkinje cell sensitivities to eye and head velocity after VOR adaptation

Additional analysis of the signals contributing to Purkinje cell responses after motor learning revealed significant changes in sensitivities to both eye and head velocity. Both increased when the VOR was adapted chronically either to lower or to higher values (Fig. 3A,B,E,F; Table 2). Of particular note is the change in eye velocity sensitivity that was observed between the normal-gain population and the low-gain population in both the slope of the line (Fig. 3B) and in the comparison between groups (Fig. 3F; Table 2) (slope, p < 0.0001; ANOVA, p < 0.0001; mean ± SD: –2.0781 ± 0.95 spikes/sec/degrees/sec for low gain, –1.0785 ± 0.63 spikes/sec/degrees/sec for normal gain). A smaller increase was observed for high gain when compared with the normal gain (Fig. 3B) (slope, p < 0.17; ANOVA, p > 0.6; mean ± SD, –1.1759 ± 0.83 spikes/sec/degrees/sec for high gain). When looking at the Purkinje cell head velocity component (Fig. 3A,E), neurons in both high- and low-gain-adapted animals increased their sensitivities to head velocity, on average, with a larger increase for the high-gain population (mean ± SD: –1.18 ± 0.43 spikes/sec/degrees/sec for low-gain animals; –0.98 ± 0.64 spikes/sec/degrees/sec for normal-gain animals; –1.53 ± 1.38 spikes/sec/degrees/sec for high-gain animals). The slope of the line fitting normal to low gain was not significant (Fig. 3A; p > 0.12), although the change in this parameter from normal to high gain was significant (Fig. 3A; p < 0.015). These increases are not statistically significant when dividing the population into groups and applying a one-way ANOVA (p > 0.18 for low vs normal; p > 0.08 for high vs normal; Table 2). In Figure 3, changes in the parameters versus VOR gain showed the same tendency when considering the entire Purkinje cell population (data shown above) or exclusively the identified Purkinje cell population.

Although changes in the head velocity sensitivities of Purkinje cells after both acute and chronic VOR adaptation have been observed previously (Watanabe, 1984; Lisberger et al., 1994b; Hirata and Highstein, 2001), we now report significant changes in the eye velocity and position sensitivities of these neurons as well. In an attempt to compare our results with previous reports, we normalized head velocity relative to eye velocity for each cell (Fig. 4). This analysis showed very similar results to those found in the horizontal system (Lisberger et al., 1994b). Head velocity sensitivity seems to increase for the high-gain animal and decrease for the low-gain animal (Fig. 4A–C) (slope values: 1.6, 0.81, and 0.35 for the high-gain, normal-gain, and low-gain animals, respectively). The r² value obtained after fitting the line to our data also showed a high correspondence between the eye velocity and head velocity components (r² = 0.97, 0.87, and 0.61 for the high-gain, normal-gain, and low-gain animal, respectively). Miles et al. (1980) also reported significant increases in eye velocity sensitivity with low-gain adaptation. But, in contrast to our results, a decrease in head velocity sensitivity for low-gain adaptation was seen by Miles et al. (1980). We caution that Miles et al. (1980) used prisms to train to low gain instead of miniaturizing lenses. Prisms caused unusually large phase lags in ocular responses, as noted by Miles and Eighmy (1980), and this needs to be taken into account when comparing the differences between results.

Figure 4.

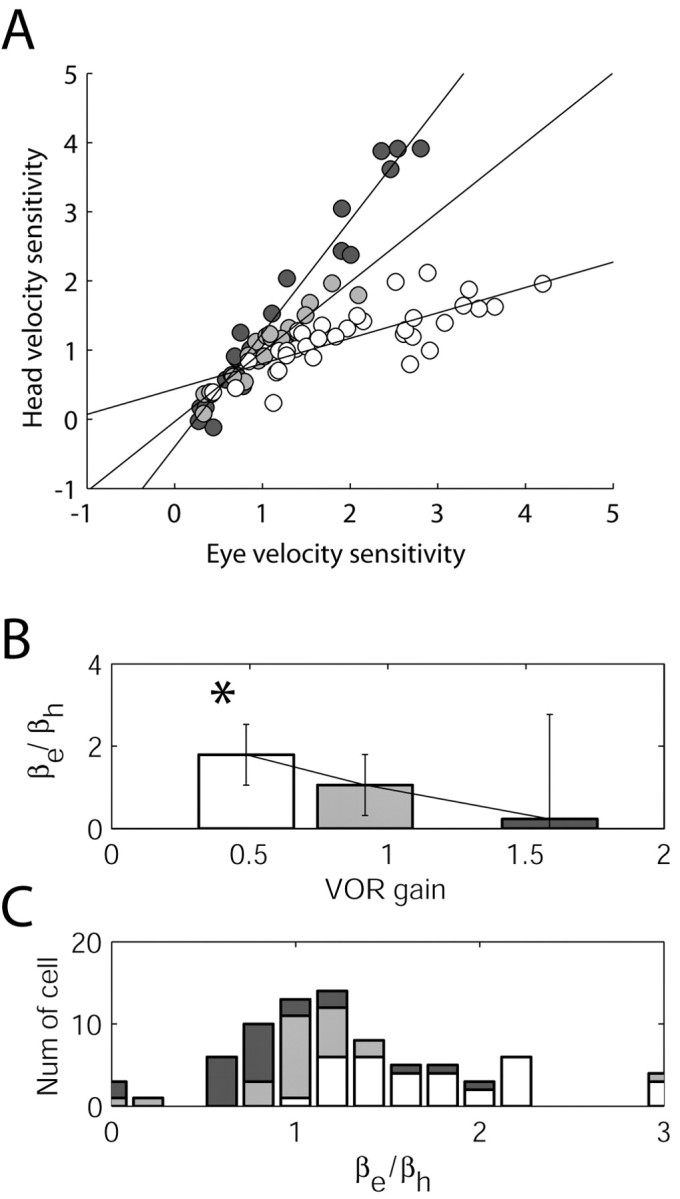
Normalized plots of head velocity sensitivity in Purkinje cells with respect to eye velocity sensitivity. This form of normalization could mistakenly be interpreted as monotonic changes in head velocity. In all panels, Purkinje cells were separated into groups corresponding to the low-gain (white), normal-gain (gray) and high-gain (black)-adapted animals. A, Data from individual cells in which head velocity sensitivity was normalized with respect to eye velocity sensitivity (from Fig. 3A,B). The lines represent the result of linear fitting of the data. In B, β_e/β_h is plotted as the average and SD for the low, normal, and high populations. Note the monotonic change in the ratio of these parameters with VORd gain. In C, a density histogram is plotted as stacked bars graphically showing the most common values for each subpopulation (low, normal, and high).

The previous analyses (Lisberger et al., 1994a,b) were based on the assumption that the eye velocity sensitivity does not change after VOR adaptation. The present results show that eye velocity sensitivity increases, on average, for both high- and low-gain adaptation, with a significant change for the low-gain-adapted animal (Fig. 3B,F). Thus, analyses that used eye velocity sensitivity as a control to determine changes in head velocity sensitivity might need reevaluation and reinterpretation (see below).

Head and eye velocity contributions to Purkinje cell firing rate

In an additional analysis, we quantified the eye velocity and head velocity information in the FL in terms of the net strength of the head velocity signal contribution (i.e., in spikes per second instead of sensitivity measurements in spikes per second per degrees per second) versus the net contribution of the eye velocity signal (Fig. 5A). This analysis was performed to account for the behavioral differences between normal-, low-, and high-gain conditions and the fact that eye velocity changes after VOR adaptation. To simplify the presentation, because the stimulus used to evoke head rotation in the dark was always a sinusoidal rotation at 0.5 Hz (±40°/sec), we normalized to a 1°/sec head rotation (equivalent to head velocity sensitivity). In addition, we considered only those cells with eye velocity or head velocity sensitivities >0.5, because the ratio of error in parameter estimation versus parameter value (eye or head velocity sensitivity) becomes larger for low values of eye or head velocity sensitivity and, therefore, may produce misleading results. Consideration of only those cells with either eye or head velocity sensitivity >0.5 may also be justified by the realization that cells with such a low level of sensitivity do not contribute to the VOR behavior. This analysis (Fig. 5A,B) shows that in low-gain animals, the strength of the vestibular pathway is increased compared with that in high-gain animals (one-way ANOVA; p < 0.0001).

Figure 5.

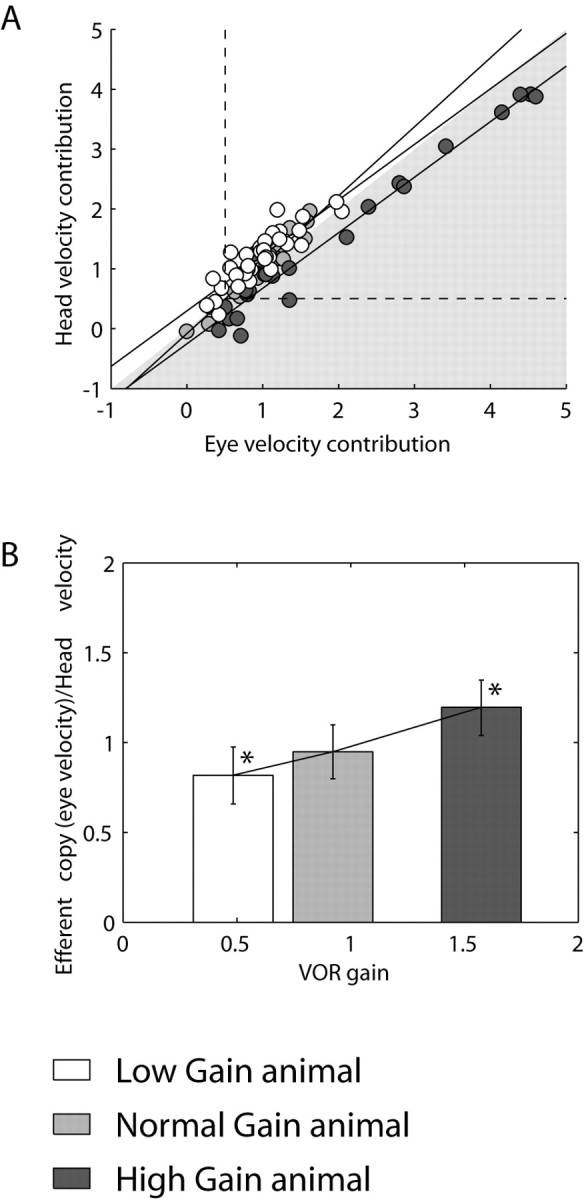
Normalized plot of head velocity input in Purkinje cells with respect to eye velocity input indicates lower head velocity contribution to Purkinje cell firing after high-gain adaptation. As in Figure 4, Purkinje cells were separated into three groups corresponding to the low-gain (white), normal-gain (gray), and high-gain (black)-adapted animals. A, The same data presented in Figure 3A are normalized versus the eye velocity contribution (eye velocity sensitivity × VOR gain) during the three VOR gain states. The shaded area divides the graph into a zone dominated by eye velocity contribution (inside the shaded area) and a zone dominated by head velocity contribution (outside the shaded area). High-gain data are preferentially dominated by the eye component whereas low-gain data are dominated by the head component. The dotted lines delineate values of eye or head velocity contribution larger or smaller than 0.5. B, Bar plot representing the average ± SD from the data in A above and to the right of the dotted lines (see Results for additional explanation). Asterisks indicate the statistical significance between the high- or low-gain Purkinje cell population.

Thus, changes in the net modulation of Purkinje cells after chronic gain adaptation are appropriate to support the new gain state. A significant portion of this change can simply be attributed to the eye velocity signal that makes a larger overall contribution after high gain and a smaller net contribution after low-gain training. Namely, in high gain, the eye movements are more than three times as large as in low gain: thus, the Purkinje cell eye velocity contribution to the reflex is magnified even though eye velocity sensitivity is larger in low gain than in high gain. In contrast to previous studies (Lisberger et al., 1994b), we demonstrate an actual plasticity in the strengths of both eye and head movement signal components of the response of the cell. Interestingly, however, changes in these signal components are not a monotonic function of VOR gain. Sensitivities to these parameters changed in the same direction and increased for both low-gain and high-gain VOR conditions (Fig. 3A,B). Hence, it seems that it is the net modulation of the cell after motor learning, rather than plastic changes in the strengths of either of these signal components taken individually that is most relevant.

Changes in other parameters including eye position sensitivity

Purkinje cells in the chronically adapted animal showed a significant increase in retinal slip acceleration with increasing VOR gain (p < 0.0027) (Table 2). Also, coinciding with previous studies (Partsalis et al., 1995a; Hirata and Highstein, 2001) in the chronic animal, the DC firing rate in light was larger than the DC firing rate in darkness (mean ± SD, 97.2 ± 27 spikes/sec and 79 ± 23.9 spikes/sec for light and dark, respectively), and both of these rates tended to decrease for larger VOR gains with a significant change for DC firing rate in the dark (p < 0.0135). A significant increase in sensitivity to eye acceleration was also found when comparing the low-gain and normal-gain populations.

Purkinje cells exhibit sensitivities to eye position under normal-gain conditions that are weak and highly variable (Fig. 3C,G). Significant sensitivities to eye position in these cells were, however, observed after motor learning, particularly for the low-gain condition. Furthermore, eye position sensitivity changed in direction from downward to upward as VORd gain increased (Fig. 3C,G). A similar change in eye position sensitivity during spontaneous eye movements in the light was also observed (Fig. 3D). The cells exhibited, on average, downward eye position sensitivity in the low-gain animal (mean ± SD, –1.06 ± 1.35 spikes/sec/degrees). For the high-gain animal, the eye position sensitivity reversed its directional tuning to upward eye position (mean ± SD, 0.89 ± 0.89 spikes/sec/degrees). The slope of the line-fitting eye position versus VOR gain was significant at p < 0.0001; a one-way ANOVA also showed a significant difference between the eye position sensitivity in the low- and high-gain populations (p < 0.0001) (Table 2). Hence, not only did a clear sensitivity to eye position become apparent after chronic VOR gain adaptation, but also the changes showed a monotonic trend in relation to VOR gain. Below, we address one possible explanation for the observed change in eye position sensitivity that points to the requirement for changes in parameters other than those strictly related to head velocity, to ensure that the reflex maintains the same broadband performance before and after motor learning.

A proposal for the monotonic changes in Purkinje cell sensitivity to eye position

In the classical feedforward realization of the VOR (Skavenski and Robinson, 1973), sensory signals from the semicircular canals are conveyed to the extraocular motor neurons via a set of parallel pathways. Vestibular signals are conveyed directly to the motor nuclei via eye movement-sensitive vestibular neurons (EM; i.e., the shortest latency brainstem VOR pathways associated with weights a and b in Fig. 6A). In a second, “indirect” pathway (associated with weights c and d), sensory signals are prefiltered by a leaky “neural integrator” [1/(T_Is+1), where T_I ≈20 sec and s is the Laplace operator representing complex frequency]. At the output of this integrator, semicircular canal signals appear transformed into an internal estimate of desired eye position, E* (i.e., negative of head position in the case of the VOR). The basic goal of this network is to ensure that sensory head velocity signals, Ḣ, sensed by the semicircular canals, C(s), are transformed into appropriate compensatory deviations in eye position, E, over a broad frequency range (Fig. 6B, solid traces). This occurs in the simple model of Figure 6A when weights in the “direct” and neural integrator pathways are appropriately balanced to “cancel out” or compensate for the dynamic characteristics of the eye plant EP(s) (Robinson, 1981).

Figure 6.

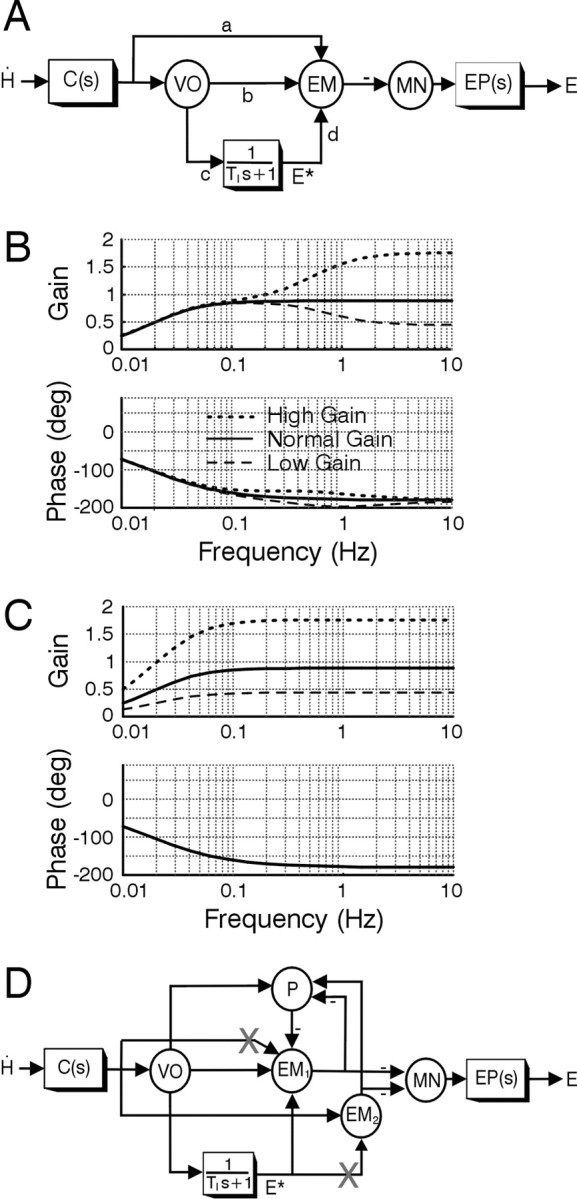
Feedforward model of the VOR. A, Schematic of the classical feedforward realization for the VOR adapted from the original proposal of Skavenski and Robinson (1973). The circles denote summing junctions that are used to represent particular cell populations, whereas the boxes are dynamic elements. Parameters associated with signal projections (a–d) are gain elements that indicate the strength or weight of the projection. Angular head velocity, Ḣ, sensed by the semicircular canals, C(s) = T_cs/(T_cs + 1), is conveyed to motor neurons (MN) that drive the eye plant, EP(s)=1/(T_ps+1), via two parallel pathways: (1) a direct pathway via vestibular neurons (VO and EM); and (2) an indirect pathway via a leaky neural integrator [1/(T_Is + 1), where T_I is a very long time constant of ≈20 sec] (Robinson, 1981). Vestibular neurons include vestibular-only cells (VO) and EM, including FTN cells that are key interneurons in the shortest-latency disynaptic pathways. EM cells sum both sensory head velocity signal inputs and an internal estimate of eye position, E*, provided at the output of the neural integrator. Under normal-gain conditions, the model parameters are: a = 0.12; b = 0.1; c = 17.38; d = 1; T_I = 20; T_p = 0.25; T_c = 6. The bode plots in B show VOR gain and phase as a function of frequency for the normal-gain condition (solid curves) and for simulated adapted gain states when the only site for plasticity was assumed to be associated with the sensitivity of cell EM to primary afferent inputs (i.e., weight a). The dotted and dashed traces show the reflex frequency response when weight a was modified to achieve either a doubling (a = 0.34) or halving (a = 0.01) of the high-frequency VOR gain. C, Modifications of both a and c to simulate plasticity in both the direct and indirect pathways give rise to a doubling (a = 0.34; c = 34.76) or halving (a = 0.01; c = 8.69) of the VOR gain over a broad frequency range. D, Feedforward model schematic extended to incorporate interconnections between eye-movement-sensitive brainstem neurons (EM₁, EM₂) and cerebellar neurons, represented by Purkinje cells (P). Downward head and eye deviations are considered positive. X, Postulated sites for plasticity (see Results).

To date, investigations of the neural correlates for motor learning have focused mainly on localizing plastic sites associated with changes in head velocity sensitivity (i.e., equivalent to changes in the parameter strengths a and b). Changes in these direct pathways will give rise to changes in the high-frequency VOR gain. However, if motor learning is associated with modifications in these direct reflex pathways only, gain changes will be much smaller or even negligible at low frequencies (Fig. 6B, dashed and dotted traces). This occurs because the dynamic characteristics of the eye plant are no longer compensated for after selective changes only in the direct pathway. Notably, however, this is inconsistent with experimental observations. Chronic adaptation with telescopic lenses typically gives rise to broadband changes in reflex gain (Miles and Eighmy, 1980). Presently, we confirmed that the lens training used in our study also provided broadband changes in the VOR (Fig. 7A,B)

To ensure the same broadband reflex characteristics before and after motor learning requires that changes in the direct VOR pathways be matched by complementary changes in the indirect pathways. Specifically, in the model of Figure 6A, changes in a or b must be accompanied by parallel changes in c or d (i.e., in the net strength of the projections through the neural integrator pathway) to maintain broadband reflex performance (Fig. 6C). Depending on where such changes occur, one may expect to observe changes in the eye position sensitivity of individual cells.

In Figure 6D, the feedforward structure shown in Figure 6A has been extended to incorporate known VOR pathway side loops through the cerebellum (P, Purkinje cells). Sites for plasticity in brainstem EM populations are proposed to exist both on synapses associated with sensory head velocity signals (projection labeled with an X onto brainstem cell population EM₁) and on those associated with efference copy of eye position, E*, signal inputs (projection labeled with an X onto brainstem cell population EM₂) to produce broadband changes in reflex performance. As a result of the interconnectivity between the brainstem EM cell populations and the cerebellum, the changes in sensitivity to eye position are also observed in Purkinje cell activities.

Discussion

Vertical Purkinje cells change their eye velocity and head velocity sensitivity after VOR adaptation

In previous studies (Miles et al., 1980; Lisberger et al., 1994b), it was assumed that changes in VOR gain would happen as a consequence of changes in the head velocity sensitivity in one or more nodes of information relay. The FL was initially identified as a candidate site to convey these changes in head velocity. Eye velocity sensitivity was overlooked, assuming that changes in this parameter were not significant. Thus, eye velocity sensitivity was used as a control to evaluate changes in the ratio of head velocity to eye velocity. Any differences in the ratio with varying VOR gains were assigned to changes of the head velocity component (Lisberger et al., 1994b).

Changes in pursuit signals after VOR learning have actually been documented previously but not emphasized (Miles et al., 1980; Lisberger et al., 1994b). Our results indicate that visual and vestibular pathways are strongly interrelated in the chronically adapted animal. Changes occur in both pathways, and, therefore, it is inaccurate to use eye velocity as a control or reference element to account for changes in head velocity. Eye velocity sensitivity increases (becomes more negative) for both high- and low-gain conditions, but this change is more profound for low gain than for high gain. Using eye velocity as a control will, therefore, underestimate the head velocity component in the low-gain animal and will overestimate it in the high-gain animal. In fact, when we look at the head velocity sensitivity changes after chronic adaptation, we see that, on average, head velocity sensitivity also increases for both the low- and high-gain-adapted animal, but the increase for the high-gain animal is larger than that for the low-gain animal. This result also emphasizes that there are possibly different mechanisms and neural sites for high- and low-gain adaptation.

Changes in vertical Purkinje cell eye position sensitivity

A significant difference in eye position sensitivity after adaptation to high and low VOR gain is reported for the first time. We have shown one possible explanation for this observation that is suggested by the predictions of the classical feedforward model for the VOR (Skavenski and Robinson, 1973; Robinson, 1981). To date, investigations of the neural correlates for motor learning have focused mainly on localizing plastic sites associated with changes in head velocity sensitivity. So far, changes in this parameter have been identified only in populations of eye movement-sensitive cells in the vestibular nuclei and cerebellar flocculus. However, if such a feedforward model structure is indeed correct (for alternatives, see Green et al., 2003), then observed changes in the head velocity sensitivities of these cells can account only for changes in the high-frequency VOR gain. To achieve the broadband reflex adaptation that is observed experimentally implies that plasticity in the most direct VOR pathways must be complemented by changes somewhere within the indirect pathway through the neural integrator. Depending on where modifications in this latter pathway occur, changes in neural sensitivities to eye position might be observed at the output of the integrator and throughout the network that intervenes in conveying eye position signals to the motor neurons. The FL is a part of this circuitry and, therefore, it is not surprising to find changes in the eye position sensitivity of its output element, the Purkinje cell.

The requirement for a site of plasticity involving the integrator pathways has been discussed extensively and proposed in previous models of frequency-specific adaptation or of VOR phase adaptation when there are clear changes in the dynamic characteristics of the reflex (Lisberger et al., 1983; Powell et al., 1991; Tiliket et al., 1994; Kramer et al., 1995). Here, however, we show that changes in the strength of signal flow through the integrator pathways may also be required to maintain the same dynamic reflex characteristics before and after motor learning (Quinn et al., 1992a,b; Green et al., 2003). The observation of changes in sensitivity to eye position on at least one cell type provides support for this possibility. Hence, despite a wealth of information that has now been collected with respect to the neural correlates for motor learning in the VOR, our present observations show that the story is far from complete. Potential sites for plasticity, other than those strictly related to changes in head velocity sensitivity, have yet to be investigated at the brainstem level, and the complex role that the cerebellum plays in modifications of both sensory- and motor-related parameters associated with learning in the VOR has yet to be elucidated.

A new viewpoint to interpret changes in Purkinje cells accompanying VOR memory

It is generally agreed that Purkinje cell responses during VORd after chronic VOR learning are in the correct direction to support the new behavior. However, understanding the mechanisms underlying these changes has proven controversial. After VOR adaptation, it was hypothesized (Lisberger et al., 1994b) that the changes observed in the net modulation of Purkinje cells are in the “correct” direction to support the adapted gain state because of the feedback of eye movement-related signals conveyed from the brainstem. However, the local changes in head velocity sensitivity observed at the Purkinje cell level were in the “incorrect” direction to be causal for the new behavior. The rationale behind this view was that (1) eye velocity and head velocity components in Purkinje cell firing are nearly equal in individual Purkinje cells in the naive animal, (2) changes occur only in the head velocity information, and (3) based on points 1 and 2, the eye velocity sensitivity of a Purkinje cell in the chronically adapted animal can be used as an estimation of its head velocity sensitivity in the naive state. Our experimental results are in agreement with point 1 but suggest that the observed changes in eye velocity sensitivity (Fig. 3B) invalidate the assumption that eye velocity can be used as a normalizing factor for head velocity (3). Nonetheless, our results confirm that the changes in the net modulation of the Purkinje cell response are in the correct direction to contribute to the adapted behavior. These results, therefore, are also consistent with the observations that the removal of the FL causes a partial loss of the remembered behavior (Partsalis et al., 1995b).

Our data, together with previous studies, favor the hypothesis that combined changes in the brainstem and cerebellum are causal for the new behavior. The FL hypothesis championed by Ito (1972) proposed that changes in the response of FL Purkinje cells after VOR adaptation produced appropriate signals in brainstem target neurons and were, thus, fully responsible for VOR adaptation. This hypothesis was later reinterpreted to incorporate changes in brainstem neurons (Lisberger et al., 1994a; Partsalis et al., 1995b). A previous analysis of the signal components at the Purkinje cell level concluded that the changes causal for the new behavior originated as changes in the head velocity estimation in the brainstem pathway and argued that the head velocity change at the FL Purkinje cells was not appropriate (incorrect direction) for the new behavior (Miles et al., 1980; Lisberger et al., 1994b). However, our results show that changes in Purkinje cell sensitivities to head and eye velocity are not monotonic. We, therefore, propose a revision of the concept of “wrong directional change.” We suggest that considerations of sensitivity alone at a single node in the pathway might be misleading. In light of the present results, we suggest that the mechanisms involved in VOR adaptation require changes in head-related and oculomotor-related signals and propose that these are necessary for maintenance of VOR performance over the natural range of frequencies (full range of head movement). Purkinje cells in FL show changes in both eye and head signals, indicating that FL is an essential node for reflex performance after VOR adaptation.