Impact of Photon Noise on the Reliability of a Motion-Sensitive Neuron in the Fly's Visual System

Abstract

Variable behavioral responses to identical visual stimuli can, in part, be traced back to variable neuronal signals that provide unreliable information about the outside world. This unreliability in encoding of visual information is caused by several noise sources such as photon noise, synaptic noise, or the stochastic nature of ion channels. Neurons of the fly's visual motion pathway have been claimed to represent perfect encoders, with photon noise as the main noise source limiting their performance. Other studies on the fly's visual system suggest, however, that internal noise emerging within the nervous system also affects the reliability of motion vision. To resolve these contradictory interpretations, we performed an electrophysiological investigation, inspired by the “equivalent noise” paradigm applied in psychophysics, on the fly's motion-sensitive H1 neuron. Noise-like brightness fluctuations of different strength were superimposed on the motion stimuli. Because the noise level found to affect the temporal properties of the spike responses is much larger than the estimate of photon noise under the experimental conditions, our results indicate that motion vision is more likely to be limited by internal sources of variability than by photon noise.

Introduction

Animals, including humans, respond to sensory stimuli with limited reliability. In the brain, this behavioral or perceptual variability is reflected in variable neuronal responses providing unreliable information about the outside world. For instance, neurons in the visual cortex of cats and monkeys respond to stimuli with a spike count variance in the range of the mean activity (Tolhurst et al.,1983; Vogels et al.,1989; Britten et al.,1993; Barberini et al.,2000). Although neuronal variability of insect visual interneurons (Warzecha and Egelhaaf, 1999, 2001; Warzecha et al., 2000; de Ruyter van Steveninck et al., 2001; Borst and Haag, 2002) and of vertebrate retinal ganglion cells is somewhat smaller (Levine et al., 1988; Berry et al., 1997; Kara et al., 2000), it still limits the reliability of behavioral reactions.

Various noise sources within the nervous system constrain the reliability of neuronal responses, such as the phototransduction process (Rodieck, 1998), the stochastic nature of ion channels, as well as synaptic transmission (Johnston and Wu, 1995). In addition, the incoming visual signal is inherently noisy because of the quantum nature of light (Rodieck, 1998). Especially at extremely low light levels, the absorption of single photons triggers prominent membrane potential changes in the photoreceptor [insects (Hardie, 1979); vertebrates (Rodieck,1998)]. In flies, single-photon effects could then be detected in spike patterns of the motion-sensitive H1 neuron that is several synapses away from the photoreceptors (Lillywhite and Dvorak, 1981) and in behavioral responses (Reichardt, 1965). In humans, single-photon absorptions were found to affect perception (Bouman et al., 1985). Thus, at the sensitivity threshold, the reliability of motion vision is limited by photon noise.

Although individual photons contribute much less to the overall photoreceptor response at higher light levels, it was concluded that, even in daylight, photon noise is the major source of variability in the fly motion-sensitive H1 neuron (de Ruyter van Steveninck and Bialek, 1995; Borst and Haag, 2001; Lewen et al., 2001). The H1 neuron is a well established system for analyzing the reliability of neural coding (for review, see Egelhaaf and Warzecha, 1999; de Ruyter van Steveninck, et al., 2001; Warzecha and Egelhaaf, 2001; Egelhaaf et al., 2002; Haag and Borst, 2002). All internal sources of variability were claimed to be of minor relevance, implying that neuronal information processing is virtually perfect (de Ruyter van Steveninck and Bialek, 1995; Borst and Haag, 2001; Lewen et al., 2001). However, at least for the light-adapted eye, noise sources inherent in synaptic transmission between photoreceptors and second-order neurons were shown to significantly affect the reliability with which visual information is signaled to higher-order processing stages (Laughlin et al., 1987; de Ruyter van Steveninck and Laughlin, 1996).

Is response reliability of H1 limited by photon noise or also shaped by noise sources inherent in the nervous system? In an experimental design adapted from psychophysics, external noise was introduced into the system. Random brightness modulations, which corrupt the input signal similar to photon noise, were superimposed on random dots, moving in the preferred direction of H1. We examined how much noise could be added before the motion response was affected noticeably and how this noise level relates to photon noise under the experimental conditions.

Materials and Methods

Electrophysiology. Experiments were performed on 21 female blowflies (Lucilia species), 2-8 d old, at temperatures between 22° and 26°C. The animals were obtained from laboratory stocks. Dissection was performed as described previously (Warzecha et al., 1993). After dissection, the flies were adjusted in the experimental setup with respect to the symmetry of the deep pseudopupil (Franceschini, 1975).

The spike activity of the H1 cell, a directionally selective motion-sensitive neuron (Hausen, 1976) was recorded extracellulary at its output region in the left half of the fly's visual system. This H1 cell has its input region in the right visual field and conveys visual motion information to the contralateral visual system. To reduce background noise resulting from the activity of neurons that receive input from the left visual field, the left eye was covered with black varnish. Insulated tungsten electrodes were used for recording. As reference electrode, a glass capillary filled with Ringer's solution (Hausen, 1982) was used. The recorded signals were amplified (factor 3000) and bandpass filtered (corner frequencies, 300 Hz and 3 kHz). Recorded action potentials were transformed into pulses of fixed height and duration, fed into a personal computer, and stored onto hard disk for off-line analysis. Data acquisition was performed at a sampling frequency of 1200 Hz using the analog input of a visual stimulus generator (VSG) 2/3 card (Cambridge Research Systems, Cambridge, UK). Data were analyzed using Matlab (version 6.5, release 13; The Mathworks Inc.), and some routines were written in ANSI-C.

Visual stimulation. Visual stimuli were presented to the fly at 300 Hz with a Joyce Scope DM5 monochrome (P-31 phosphor; decay to 10% in ∼40 μsec) computer monitor (Joyce Electronics, Cambridge, UK). The brightness range of the monitor was resolved with eight bits. The monitor was controlled using the VSG 2/3 graphics card (Cambridge Research Systems). The card was programmed using Borland Delphi 3.0 and VSG Software Library version 6.0.

As seen by the fly, the monitor screen (464 × 375 pixel resolution) had a horizontal and vertical extent of 127° and 120°, respectively. The screen center was positioned at 0° elevation and 20° azimuth. At this point, one pixel had a vertical and horizontal extent of ∼0.5°.

Although the frame rate was 300 Hz, the update rate of the presented motion stimulus was 150 Hz. Cross-correlation of 200 response traces of H1 revealed no time locking to either of these frequencies.

Random dot stimuli. Random dot kinematograms were used as visual stimuli. They consisted of 10 bright dots with a vertical and horizontal extent of ∼1.5°, as seen by the fly. In the first frame of the stimulus sequence, the dots were positioned randomly in front of a dark background. In subsequent frames, these dots were moved in the preferred direction of the H1 cell [i.e., from back to front, by steps of three pixels (corresponding to 1.5°) per frame]. The position of the dots was updated at a rate of 150 Hz, which results in a velocity of ∼450°/sec in the screen center. The same dot pattern was used in every stimulus presentation. The stimulation sequence consisted of a 3 sec motion and 7 sec interstimulus interval, during which the monitor showed the starting image of the motion sequence. At mean brightness, all dots had a radiance of 2.7 × 10^-1W × m^-2 × sr^-1 and a background of 3.0 ×10^-5 W × m^-2 × sr^-1 (corresponding to 130 cd/m² and 0.001 cd/m², respectively). We indicate light intensities and intensity changes in relative units. Because the brightness range of our stimulus was resolved with eight bits (i.e., 256 intensity levels), an intensity level of 127 corresponds to the mean brightness of the dots and 0 to the background brightness. The gamma correction of the video screen was approved to result in a virtually linear relationship between intensity level and real brightness.

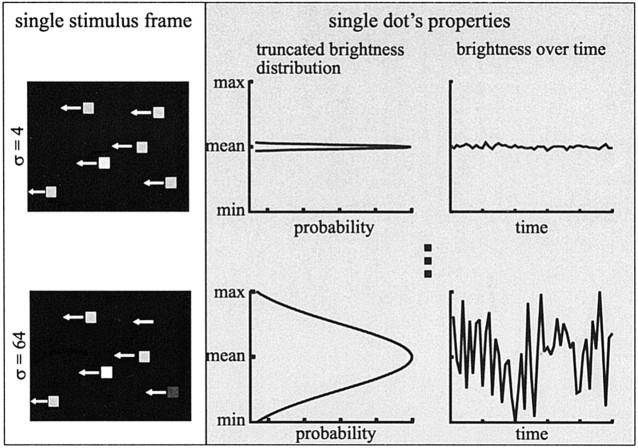
To introduce external noise into the fly's visual system, random brightness modulations were superimposed on the dots (i.e., the brightness of each dot was varied between subsequent frames). As shown in Figure 1, the brightness values were taken randomly from Gaussian distributions with the same mean but different SDs. The distributions were truncated at mean level ±2σ. We define the noise level as the SD of the original Gaussian. Five noise levels were used in the experiments (σ = 4, 8, 16, 32, and 64 brightness levels on the eight-bit scale). Thus, at the maximum noise level, brightness modulations covered the available brightness range entirely (Fig. 1, compare bottom).

Figure 1.

Visual stimuli for the smallest (σ = 4; top) and the largest (σ = 64; bottom) noise level. On the left, the same frame of the motion sequence is shown. For the first frame, a number of dots are placed randomly on the screen, and in subsequent frames the dots are shifted in the preferred direction of the H1 cell (indicated by the arrows). As shown, each dot has its own brightness. Properties of a sample dot are shown on the right. The noise sequence applied to this dot during presentation was made up of randomly drawn brightness values drawn from a Gaussian distribution centered at the mean brightness (127 on the eight-bit scale) and a SD of σ = 4, 8, 16, 32, or 64, defining the noise level (shown for σ = 4 and 64). This distribution was truncated at mean ± 2σ. Although the brightness variations over time are quite small (top), modulations covering the full brightness range are possible at the largest noise level (σ = 64).

In a first set of experiments, the time-dependent noise sequences added to all 10 dots were statistically independent. In a second set of experiments, the noise added on fractions of the dots was correlated. We used six correlation levels (0, 20, 40, 60, 80, and 100%) at two different noise levels (σ = 16 and σ = 64).

In both sets of experiments, the noise was added in two different ways: (1) the same brightness noise sequence was superimposed on the dots in each stimulus presentation (“reference stimulus”); and (2) different brightness noise sequences, yet with the same statistical properties, were used in each presentation (“test stimulus”).

Experimental protocol. Before data acquisition, the fly was adapted to the stimulus and laboratory conditions. For this purpose, the stimulus with a randomly chosen noise level was presented 40 times in a row, which lasted ∼7 min.

After this adaptation period, the experiments were performed blockwise for each noise level (σ = 4, 8, 16, 32, and 64) or each correlation level (0, 20, 40, 60, 80, or 100%). The interstimulus interval, during which the monitor showed the starting image of the motion sequence with all dots at mean brightness, was used for data storage and for providing Ringer's solution to the fly, if necessary. Both reference and test stimuli were presented 30 times in random order within each noise level/correlation block. The blocks were also shuffled in experiments performed on different H1 cells in different animals.

For additional analysis, 25 of the 30 responses to each stimulus type were used. We selected those 25 spike trains that deviate least with respect to their mean activity from the mean response averaged over all reference and test responses.

Data analysis and comparison of spike trains. The aim of the experiments was to find the level of external noise that leads to a major change in the responses of the cell to the test stimuli, compared with the responses to the reference stimulus. Because reference and test stimuli have the same statistical properties, we expected them to lead to the same spike rate but possibly to different spike patterns. We applied two approaches to detect differences in the temporal properties of the spike trains.

The first approach compares spike trains by calculating the minimal costs of transforming one spike train into another (Victor and Purpura, 1997). The transformation is performed by deleting, inserting, or temporally shifting the single spikes. Each of these procedures is linked to defined costs. Deleting or inserting the single spikes has the cost of “1.” The costs for a temporal shift (“q” per second) is variable and determines the temporal resolution of the measure. For example, a q value of 200 equals a temporal resolution of 10 msec: for this time scale, spikes in two response traces are considered “nearly coincident” if a given spike in one of the spike trains is shifted by less than ±10 msec, with respect to the corresponding spike in the other spike train. As long as this condition is met, it is “cheaper” to temporally adjust the spikes in the two spike trains by shifting than by deleting and inserting one of them. In our analysis, we used a set of nine different values for q (q = 2, 4, 8, 16, 32, 64, 128, 256, and 512) that correspond to temporal resolutions of 1000, 500, 250, 125, 62.5, 31.25, 15.625, 7.8125, and 3.90625 msec. Moreover, we calculated the similarity between test and reference responses on the basis of the mean spike rate over the entire stimulation interval (see Figs. 4b, 5b,e, rightmost data points).

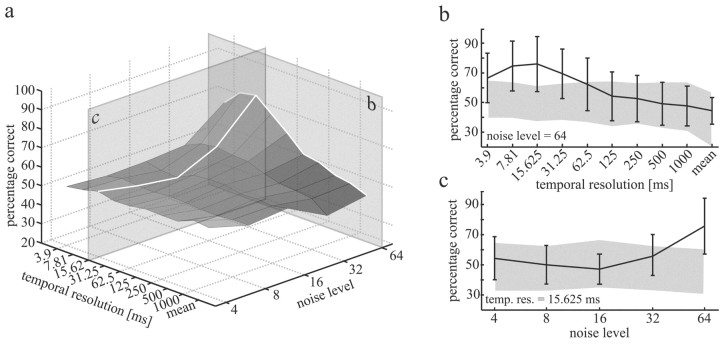
Figure 4.

Averaged discrimination of reference and test responses as a function of the noise level added to the stimuli and the temporal resolution of the measure of discrimination as developed by Victor and Purpura (1997). Data are based on a set of 11 H1 neurons recorded in 11 different flies. Transects b and c are shown in more detail in b and c. b, Mean discrimination of reference and test responses at the maximum noise level (σ = 64) in dependence of the temporal resolution was used for data analysis. The error bars show the SD of percentage correct decisions across the 11 cells. The shaded area represents the domain of uncertainty (see Materials and Methods). c, As in b, but the noise amplitude was varied at the “best” temporal resolution (15.625 msec).

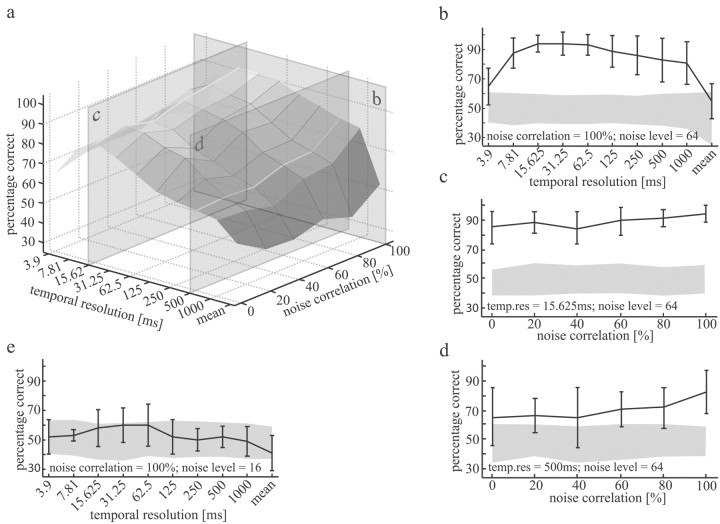
Figure 5.

Mean discrimination performance as a function of the noise correlation and the temporal resolution of the measure of discrimination as developed by Victor and Purpura (1997). The experiments were performed at the maximum noise level (σ = 64). The average performance is based on 10 H1 recordings in another set of 10 different flies than those on which the data shown in Fig. 4 are based. The transections refer to sections shown in b-d. b, The average discrimination performance at 100% noise correlation expressed in percentage correct decisions as a function of the temporal resolution was used for data analysis. Error bars show the SD across the 10 H1 recordings. The shaded area shows the domain of uncertainty (see Materials and Methods). c, Same data as in b but the noise correlation was varied at the “best” temporal resolution. The temporal resolution was 15.625 msec. d, Same data as in c but at a temporal resolution used for data analysis of 500 msec. e, Mean discrimination performance at 100% noise correlation and a noise level of σ = 16 as a function of the temporal resolution for four H1 recordings of four different flies. The error bars represent the SD of performance levels. Shown in gray is the domain of uncertainty, which represents the performance levels that are likely to be the result of internal noise and photon noise but not of the added external noise.

The second approach calculates the distance between two spike trains by determining spike-count differences between the smoothed spike trains (Kretzberg et al., 2001):

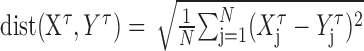1

with N as the number of time steps, τ as filter width (milliseconds), and X^τ, Y^τ as the smoothed spike trains that are to be compared. A rectangular filter of variable width was used for smoothing. We calculated the distances using six different filter widths (500, 200, 100, 50, 20, and 10 msec).

Classification of responses. To determine the similarity of the spike trains, we took each single reference response (e.g., the highlighted spike train in Fig. 2a) and computed the mean similarity (see above) to the other reference responses and to the test responses. We can assume the reference responses to be more similar to each other than to the test responses if the external noise affects the responses. Thus, a reference response is subsequently classified correctly as a reference response when its similarity within the reference responses is higher than between reference and test responses. This procedure was performed for all 25 reference responses. The percentage of correct classifications represents a measure of the discriminability of reference and test responses. If the test responses do not differ more from the reference responses than the reference responses do from each other, the percentage of correct assignments is 50%. In this case, the added noise does not affect detectably the temporal structure of the spike trains, and their variability is dominated by noise sources intrinsic to the nervous system, by photon noise, or by both noise sources. If both types of responses can be discriminated perfectly, the percentage of correct classifications is 100%. In this case, the responses are affected heavily by the external noise that was added to the stimuli. We assume a major influence of the external noise on the responses when the discrimination performance exceeds 75%, a threshold value often used in psychophysics.

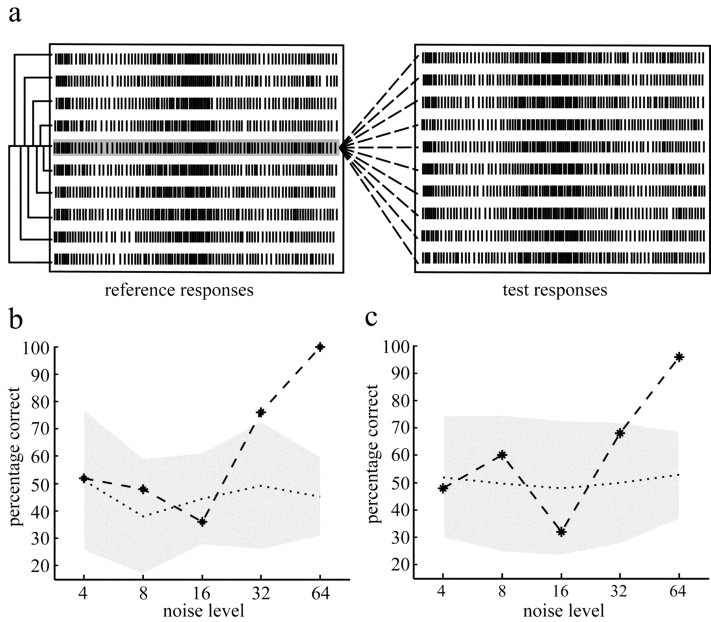
Figure 2.

Data analysis for a single cell example. a, The raster plots show 750 msec sections of 10 responses to reference (left) and test (right) stimulus at the maximum noise level (σ = 64). A common spike pattern can be seen in all responses despite differences in timing of individual spikes. Although all reference responses were elicited by the same stimulus, they do not seem to be more similar to each other compared with the test responses that were evoked by stimuli, which were statistically equivalent but differed in the noise sequence added on the stimuli. The way of analyzing more subtle changes in the temporal structure of the responses is sketched by the lines drawn between the highlighted reference response and all other reference and test responses: (1) each reference response is compared with all other reference responses (solid lines) with two different measures of similarity (see Materials and Methods), and the average similarity within the reference responses is calculated; (2) the mean similarity of each reference response to all test responses is determined (dashed lines), and the average similarity between reference and test responses is calculated. b, If the external noise affects the responses, the reference responses should be more similar to each other compared with the test responses. With this assumption, we tried to classify the individual reference responses on the basis of the similarity values estimated with the measure developed by Victor and Purpura (1997) (see Materials and Methods). The percentage of correct classifications is plotted as a function of added noise level for this single cell example. The shaded area represents the domain of uncertainty (see Materials and Methods). Discrimination performances falling into this range are likely to be a consequence of chance. A significant effect of the added noise on the responses can be assumed if the actual percentage correct value is outside the domain of uncertainty. c, Same data as in b but the responses were compared using the measure developed by Kretzberg et al. (2001).

Domain of uncertainty. To assess whether deviations of the discrimination performance from chance level (Fig. 2, compare b, c) are attributable to the external noise, we calculated the percentage of correct decisions for 10 different sets of shuffled responses [i.e., we replaced half of the reference responses (selected by chance) with the same number of test responses chosen randomly]. For each shuffle, the classification performance was calculated as described above. A 50% performance is expected, because the shuffle consists of responses of either type mixed in equal shares. A deviation from chance level can, thus, be understood as a measure of variability caused by any kind of noise. The shaded area in Figure 2, b and c, shows the “domain of uncertainty” that is defined by the mean (dotted line) and twice the SD of the classification performances obtained by comparing the 10 different sets of shuffled responses. Classification performances that fall into the domain of uncertainty are likely to be a result of the noise in the system (including photon noise) and not of the added external noise.

Estimation of photon noise. Following the approach of de Ruyter van Steveninck (1986), the number of photons impinging per second on a single photoreceptor can be estimated according to:

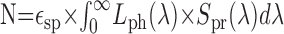2

with λ as the wavelength, ϵ_sp (m² × sr) as the spatial efficiency factor, L_ph(λ) (photons × m^-2 × sr^-1 × sec^-1 × nm^-1) as the spectral density of the photon flux, and S_pr(λ) as the relative spectral sensitivity of fly photoreceptors (type R1-6). The spatial efficiency factor is given by the product of lens surface and photoreceptor solid angle, which results in:

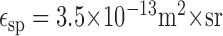3

assuming a circular lens (van Hateren, 1984) with a point spread function approximation as a circular symmetric Gaussian (Götz, 1965). The lens diameter and the acceptance angle are assumed as D = 30 μm and Δρ = 1.2°, respectively (Smakman et al., 1984). The integral in formula 2 is the spectral overlap L_so, which can be calculated for the mean radiance of the dots of 2.7 × 10^-1 W × m^-2 × sr^-1 to (de Ruyter van Steveninck, 1986):

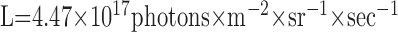4

Inserting formulas 3 and 4 in formula 2 we get:

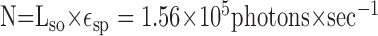5

Thus, ∼1034 photons impinge on a photoreceptor while a dot is in its receptive field (1/150 sec).

Because the number of photon arrivals is a statistical event following the Poisson distribution, the variance of which is equal to the mean, the SD and, thus, the signal-to-noise ratio (SNR) amounts to ∼32. To mimic an SNR matching photon noise in our stimulation paradigm, brightness noise with a SD of σ = 4 [with a mean brightness of 127 on the eight-bit scale (0... 255)] would have to be added to the moving dots (i.e., 128/4 = 32).

Persistence of the P-31 phosphor increases the time a dot stimulates a photoreceptor and, thus, slightly increases the number of photons impinging on the receptors. Consequently, photon noise is slightly overestimated by the above approximation.

Results

To find out whether the reliability of H1 responses to motion stimuli is limited by photon noise or noise sources intrinsic to the nervous system, the consequences of external brightness noise superimposed on a random dot kinematogram were analyzed. The brightness of the 10 dots moving coherently in the preferred direction of the H1 cell was modulated in two ways. The time-dependent brightness noise was either exactly the same in each stimulus presentation (reference stimulus) or it was different but had the same statistical properties in each presentation (test stimulus). We examined for a wide range of time scales to what extent the temporal structure of spike responses was affected by the added noise.

In case of photon noise being the dominant noise source limiting motion vision, the added noise, as soon as it is larger than photon noise itself, should affect the responses. Thus, the reference responses should be more similar to each other than to the test responses. This is because the reference stimulus is, apart from photon noise, the same for each trial, and the variability in the reference responses reflects the consequences of noise sources in the nervous system and of photon noise. In contrast, the variability of the test responses is also affected by the external noise introduced by using a different stimulus for every presentation, unless the external noise level is negligible in the presence of the other noise sources that cannot be controlled by the experimenter. The larger the brightness noise level needed to have a major impact on the responses, the less important is photon noise for the reliability of motion vision in H1.

Impact of uncorrelated noise

Because the statistical properties of reference and test stimuli were identical, we expected them to elicit the same average responses. Comparing the mean response amplitudes for all noise levels using a Wilcoxon's test for paired samples confirmed this expectation (Fig. 3). Thus, if there were differences in the responses to reference and test stimuli, they existed only on a finer time scale (i.e., in the temporal spike pattern). The raster plots shown in Figure 2a reveal some variability in the spike trains, even if the responses were elicited by repeated presentation of the same stimulus (Fig. 2a; reference responses at maximum noise level). In case of different noise sequences superimposed on the moving dots at each presentation (Fig. 2a; test responses at maximum noise level), the responses appear not to be more variable than the reference responses. Under both stimulus conditions, a common time structure is visible despite differences in the timing of individual spikes. Based on the raster plots, it is hard to tell whether the individual spike trains obtained under the reference condition are more similar to each other than to spike trains obtained with the test stimulus. Therefore, we scrutinized the responses by quantitative measures.

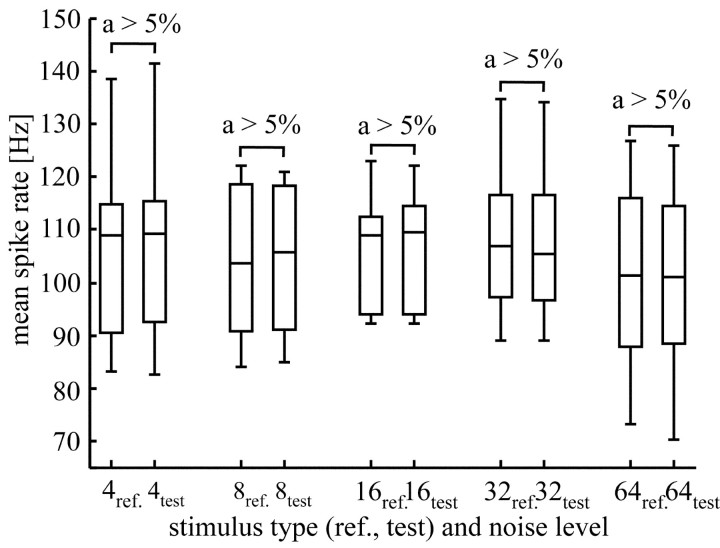
Figure 3.

Mean firing rate of H1 in response to reference and test stimuli at the five noise levels (σ = 4, 8, 16, 32, and 64) used in the experiments. The box and whisker diagrams represent the distribution of mean firing rates, averaged over all presentations of each stimulus type. All diagrams are based on the same 11 H1 neurons recorded in 11 different flies. The horizontal lines in the boxes represent the lower, median, and upper quartile of the data. The whiskers extending vertically from the boxes show the extent of the rest of the data. The distributions were tested for significant differences using a Wilcoxon's test for paired samples. An α value, shown above each pair of distributions, larger than 5% denotes a nonsignificant difference.

Two different measures were applied to quantify the similarity of individual spike trains (see Materials and Methods). As shown for the single cell example in Figure 2, b and Figure c [measures developed by Victor and Purpura (1997) (Fig. 2b) and Kretzberg et al. (2001) (Fig. 2c) were used], the classification performance varies ∼50% for small noise levels; it increases with increasing noise level to almost perfect discrimination. The responses of this H1 cell to reference and test stimulus can be distinguished reliably at noise levels larger than σ = 32 if the 75% criterion is satisfied and the data value is outside the domain of uncertainty. At maximum noise level, the responses can be distinguished perfectly. Because both measures of similarity lead to qualitatively the same results for all analyzed cells, only results obtained with the measure of Victor and Purpura (1997) will be shown below.

The average discrimination performance (n = 11 H1 cells recorded in 11 different flies) is shown in Figure 4a as a function of both the temporal resolution and the noise level. In some flies, the 75% criterion, as shown in Fig. 2b, was reached for high noise levels whereas other recordings revealed discrimination performances below this threshold, even at the highest noise levels used in the experiments. The averaged discrimination performance peaks at large noise levels and at temporal resolutions between 5 and 20 msec. Finer resolutions yield performances, even at the highest noise level, below threshold and only weakly above the domain of uncertainty (Fig. 4b). On average, temporal resolutions coarser than 62.5 msec also result in no significant discrimination. Even for the temporal resolution at which the discrimination performance is best (15.625 msec), the performance is significantly better than chance level only at noise levels above σ = 32 (Fig. 4c). Hence, the temporal structure of the neuronal responses is affected systematically only at noise levels exceeding this value. However, even at the highest noise level the 75% threshold is not reached, on average. In none of the recordings was the discrimination threshold reached with noise levels lower than σ = 32. As is common in psychophysical experiments, this value may be understood as an estimate of the overall noise in the system, including internal sources of variability as well as photon noise (Pelli, 1990). In our stimulus paradigm, photon noise is estimated to equal a brightness modulation of approximately σ = 4 (see Materials and Methods). As can be concluded from the experiments, this level of added noise has no major impact on the mean response amplitude and the temporal fine structure of the cell.

Impact of correlated noise

In the experiments described so far, the noise added to the different moving dots was uncorrelated. The effect of external noise on a neuron can be expected to increase if the noise carried by the different inputs of the neuron is correlated to some extent (Zohary et al., 1994). Because photon noise is uncorrelated at the different photoreceptors, the degree of correlation needed to affect the neuronal response pattern can be used as another way to assess the role of photon noise versus noise intrinsic to the nervous system for the reliability of visual motion computation. In a second set of experiments (n = 10 recorded H1 cells in another set of 10 different flies), the noise superimposed on a fraction of the dots was correlated. The number of dots with correlated noise was 0, 2, 4, 6, 8, or 10 of 10 dots. When the correlation at maximum noise level was increased, the H1 responses were affected not only on a relatively fine time scale, as is the case for uncorrelated noise, but also on a coarser time scale. When the noise was 100% correlated (i.e., the brightness fluctuations of all 10 dots are identical), reference and test responses could be discriminated with temporal resolutions of up to 1000 msec (Fig. 5a, transection b, b). With the finest temporal resolution, the discrimination performance is significantly different from chance level but does not reach the 75% threshold. However, even with 100% noise correlation at the maximum noise level (σ = 64), no effect on the mean spike rate could be observed (only 1 of the 10 cells showed a significant difference in the mean spike rate; α < 5%, Wilcoxon's rank sum test; the mean spike frequency of the corresponding reference responses was 78.6 Hz with a SD of 1.55 Hz; the test responses had a mean and SD of 80.7 and 2.3 Hz, respectively). At the temporal resolution, which led to the best discrimination performance (15.625 msec) with uncorrelated external noise (compare Fig. 4), we found a weak increase in performance with increasing noise correlation (Fig. 5a, transection c, c). At this temporal resolution, the performance was above threshold for all correlation levels. Again, the responses of some cells could not be distinguished with >75% performance. With a coarser temporal resolution (500 msec; Fig. 5a, transection d, d), a more obvious increase in performance could be observed. Although it was below threshold and not clearly different from chance level without noise correlation, a major impact of the external noise was obtained at 100% noise correlation.

When adding noise to the moving dots with a noise level of σ = 16 and 100% correlation, the responses to reference and test stimuli are nearly indistinguishable for all temporal resolutions (n = 4 recorded in four different flies; Fig. 5e). Hence, even for absolutely correlated noise, a noise level, more than four times larger than photon noise, is needed to affect the responses significantly.

Conclusion

The temporal structure of the H1 responses to motion stimuli is affected by superimposed noise only if the noise fluctuations cover most of the available brightness range of the monitor screen and, thus, is much larger than photon noise under our experimental conditions. Then, the temporal structure of the responses is affected on a time scale in the range of ∼15 msec. If the noise added to different dots of the motion stimulus is correlated, the range of temporal resolutions at which changes in the response can be detected is extended. Nevertheless, a high noise level is needed to affect the responses, even when the noise in the input signal is 100% correlated. Thus, both sets of experiments, using uncorrelated as well as correlated noise superimposed on the input signal, support the conclusion of photon noise being of only minor importance for the reliability of motion vision in H1.

Discussion

Comparison with photon noise

Is the neuronal variability a consequence of the noisy visual input (i.e., photon noise), as has been proposed recently (Borst and Haag, 2001; Lewen et al., 2001), or does it emerge within the nervous system? Whereas these studies applied more indirect methods to tackle this question, with our approach we directly manipulated the input signal. The brightness modulations superimposed on the dots mimicked photon noise and, by varying the strength of the modulations, allowed us to assess the impact of photon noise on the reliability of the H1 responses.

The overall system noise is approximately equivalent to a noise level of σ > 32 in our stimulus paradigm (compare Fig. 4). How much of the overall noise can be attributed to photon noise, and to noise emerging within the visual system? As estimated in Materials and Methods, photon noise under the conditions of our experiments corresponds to a noise of approximately σ = 4 in our paradigm. Thus, neuronal unreliability, rather than photon noise, seems to be the major noise source that limits the reliability of visual motion computation.

This conclusion needs to be qualified in two respects. First, the estimation of the relevant photon noise is based on the implicit assumption that noise in only those photoreceptors that are stimulated by the moving dots contribute to the response variability of H1. This assumption seems to be justified, in a first approximation, because the stationary background was much darker than the dots and the variability found in fly motion-sensitive neurons during stimulation with stationary dark patterns was much smaller than during motion stimulation (Hengstenberg, 1982; Warzecha, 1994). Second, it was assumed that each motion dot perfectly covers the receptive field of just a single photoreceptor and does not affect neighboring receptors. Because this may frequently not be the case, the photons emitted by a dot may be shared, as a consequence of the hexagonal lattice of ommatidia, by three adjacent photoreceptors. As a consequence, the amount of photons reaching a single receptor and, thus, the SNR of the input signal may be reduced. In the worst case, a single dot is centered above the corner of three neighboring ommatidia. This would reduce the number of photons reaching a single photoreceptor by two-thirds. To meet the worsened SNR caused by light reduction, an added noise with a SD of approximately σ = 6.8 would be needed. Even this noise level is much smaller than the noise level found to influence the H1 responses. In contrast, in the fly retina, the signals of six photoreceptors sampling the same point in space are averaged by electric coupling of their axons (Laughlin, 1994). This coupling would reduce the variance in the averaged signal by the square root of 6, because photon noise is independent for each of them.

Moreover, at noise levels of more than twice this noise level, the responses to the reference and to the test stimulus are indistinguishable even when the noise added to all moving dots is completely correlated (Fig. 5e). Because photon noise affecting different photoreceptors is statistically independent, this finding further corroborates our conclusion that under the conditions of our experimental analysis photon noise does not limit the reliability of neural coding. Rather, we can conclude that the variability in the timing of spikes in H1 is mainly a consequence of noise sources intrinsic to the nervous system. This conclusion is likely to extend to most light levels when the diurnal flies fly around, because our stimulus was much darker than daylight. Under behaviorally relevant light conditions, the number of photon arrivals and, thus, the SNR is much higher.

The conclusion that noise intrinsic to the nervous system limits the reliability of motion information processing is in accordance with experimental data on the peripheral visual system of the fly. Although in completely dark-adapted eyes single photons could be inferred to affect the signal of the H1 neuron (Lillywhite and Dvorak, 1981), even at moderate light levels that are still much lower than daylight, individual photons only have a small effect on the overall photoreceptor potential, and the synapse between photoreceptor and second-order neurons contribute significantly to the response variability at this processing stage (Laughlin et al., 1987; Juusola et al., 1995; de Ruyter van Steveninck and Laughlin, 1996). Thus, our results are in line with previous findings that suggest that, at least for light levels as used in our experiments and for larger ones, internal noise sources are of more importance than the noise in the visual input (Laughlin et al., 1987; de Ruyter van Steveninck and Laughlin, 1996) but are in contrast with other interpretations (Borst and Haag, 2001; Lewen et al., 2001).

Comparison with contradictory interpretations

Lewen et al. (2001) performed methodologically challenging outdoor recordings of H1 while rotating the whole fly about its vertical body axis in a naturalistic manner. Experiments were performed with the same fly at different times of the day and, thus, at different mean light levels. From noon to half an hour after sunset, the H1 cell responded to the same motion sequence with a decreasing mean spike rate. The conclusion of photon noise being the limiting factor is based on the finding that the information rate increases with an increasing light level and, thus, with an increasing SNR of the stimulus. However, in other studies, the information rate was shown to be linked approximately linearly to the mean number of spikes, even if spike activity was increased at the same mean light level by changes in stimulus parameters such as velocity or contrast (Schneidman et al., 2000; Borst and Haag, 2001). Hence, the changes in the information rate observed during the course of the day may be interpreted as a consequence of an increasing spike rate rather than SNR of the incoming signals. This suggestion is corroborated by the finding that during the course of the day changes in spike rate are more likely linked to changes in ambient temperature than to changes in light level (Warzecha et al.,1999; Egelhaaf et al., 2001). On this basis, we conclude that the experimental results of Lewen et al. (2001) do not necessarily disagree with our finding that the performance of the H1-neuron is mainly limited by noise sources intrinsic to the nervous system rather than by photon noise.

Borst and Haag (2001) analyzed the amount of information transmitted by H1 in dependence of the activity level that was altered by visual motion stimulation. The experimental results were compared with predictions that were drawn from a model H1 that receives input from eight correlation type motion detectors and transforms the resulting graded membrane potential changes into spike trains using a Hodgkin-Huxley-type spike generator. The input signal of the model was additionally corrupted by brightness modulations mimicking photon noise that were adjusted to match experimentally found response variability. Because the performance of both real and model H1 were similar and no other noise but photon noise was introduced into the system, it was concluded that photon noise is the dominant noise source of the fly's visual motion pathway. Given that the model H1 cell was driven by only eight motion detectors, their gain had to be sufficiently high to drive the cell to a realistic activity level. However, under the stimulus conditions of the experiments of Borst and Haag (2001), the H1 cell receives input from hundreds of motion-sensitive elements that contribute to the overall response. Hence, the individual input channels are likely to have contributed much less to the variability of the H1 neuron than was assumed in the corresponding model simulations. Thus, these results do not seem to contradict our conclusion that the noise level found in H1 is mainly determined by sources intrinsic to the nervous system rather than by photon noise.