Competition between Retinal Ganglion Axons for Targets under the Servomechanism Model Explains Abnormal Retinocollicular Projection of Eph Receptor-Overexpressing or Ephrin-Lacking Mice

Abstract

Topographic mapping of retinal ganglion axons to the midbrain is computed by the servomechanism model, which is based on the experimental result of cell attachment. Cells expressing a certain level of Eph proteins (receptors for ephrin ligands) optimally attach to a surface that expresses a specific level of ephrin ligand density. The retina has an increasing nasal-to-temporal gradient of Eph receptor density, and the optic tectum/superior colliculus has an increasing rostral-to-caudal gradient of membrane-bound ephrin ligand. An axon from the retina has an identification tag of a certain level of Eph receptor density depending on its retinal position and adheres to the site on the tectum/superior colliculus expressing ephrin ligands at a critical ligand density level. Quantitatively, a retinal axon has a receptor density (R) that is determined by its retinal position, and the axon terminal is induced to adhere to the tectal site of ligand density (L = S/R), where S is a constant. Consequently, the servomechanism model defines positions of axon terminals on the midbrain. Abnormal topographic maps are reported in a knock-in experiment with elevated density of Eph receptors and a knock-out experiment lacking ephrin ligands using gene-targeting technology. By adding competition between axon terminals for target sites to the servomechanism model, the abnormal maps became easy to understand. Furthermore, the servomechanism-competition model allowed conjecture of the gradient shapes of receptor and ligand densities and estimation of the capacity of the midbrain surface to accept retinal axon terminals.

Introduction

Images on the retina are transferred to the midbrain by spatially ordered sets of neural axons. In the early stages of development, axons of retinal ganglion cells find their target sites on the midbrain [the optical tectum of amphibians, fish, and birds or the superior colliculus (SC) in mammals]. In an attempt to explain how retinal axons recognize their targets, Sperry (1963) proposed the chemoaffinity theory, in which individual neurons are assumed to have distinct chemical labels for identification in gradients of topographic labeling. Since then, many studies have been published on topographic mapping. A mathematical formula of a gradient was developed for conceptual understanding of mapping (Gierer, 1981, 1983, 1987; Bonhoeffer and Gierer, 1984), although the gradients are not based on actual substances. Recently, such gradients have materialized by the discovery of a gradient of Eph receptor molecules in the retina, and a gradient of the membrane-bound ligand molecules, ephrins, in the tectum (Cheng et al., 1995; Drescher et al., 1995). Topographic projection of retinal axons to the midbrain is modeled on the basis of these molecules (Honda, 1998; Goodhill and Richards, 1999; Loschinger et al., 2000). A model is named the servomechanism model (Honda, 1998). An important assumption used in the servomechanism model is the bilateral threshold control, which is supported by the finding that cells expressing Eph receptors adhere to the surface expressing a specific density of ephrin ligands (Huynh-Do et al., 1999).

According to the servomechanism model, sites on which retinal axons are projected are rigidly defined (Honda, 1998). However, the topographic maps generated in some experiments on surgically or genetically manipulated animals do not match those defined by the servomechanism model. Optic nerve regeneration experiments in goldfish showed not rigid but plastic or flexible mapping (Yoon, 1971, 1972, 1976; Schmidt, 1978; Schmidt et al., 1978). Experiments of knock-in mice with elevated Eph receptor expression (Brown et al., 2000) and knock-out mice lacking ephrin ligands (Frisén et al., 1998; Feldheim et al., 2000) showed abnormal mapping. I tried to understand the abnormal mapping. Computer simulations by the servomechanism model enable us to estimate a population distribution of retinal axon terminals on the midbrain. I found irregular population distributions of axon terminals in the results of simulations for the experiments with manipulated animals. Axon terminals of high population density may compete between them for target sites. Then competitive interaction was introduced to the servomechanism model. Computer simulations under the servomechanism-competition model were performed. I succeeded in explaining plastic mapping of nerve regeneration experiments (my unpublished results). In the present study, the topographic maps by the knock-in experiment with elevated Eph receptor expression were closely simulated. Shapes of graded receptor and ligand densities were not exactly observed in experiments. I present a method for conjecturing gradient shapes with a clue of the elevated level of ectopic Eph receptors. Furthermore, the servomechanism-competition model simulated topographic maps of the knock-out experiment lacking ephrins. The simulated maps explained abnormal shifts of axonal projections on the midbrain. Competition between axon terminals for target sites was assumed to take place when the population density of the axon terminals was higher than a critical level. The critical level of population density for competition was reasonably estimated.

Model

The servomechanism model including competitive interaction

The servomechanism model (Honda, 1998) is based on two processes: (1) Eph receptors bound by ephrin ligands act in a signal transduction pathway involving tyrosine kinase activity (Flanagan and Vanderhaeghen, 1998); and (2) cells expressing Eph receptors at a certain level respond when they make contact with a critical level of ephrin density, which is called the bilateral threshold control (Honda and Mochizuki, 2002). Cells contact a surface expressing ephrin ligands. When the level of ephrin ligands increases, cells receiving the signal of the ephrin ligands do not respond until the ligand level becomes close to a critical level. When the ligand level is around the critical level, the cells respond, i.e., adhere to the surface expressing the ligands, and do not respond again when the ligand level is above the critical level.

In the system of the topographic projection of retinal ganglion cells to the midbrain, the retina has an increasing nasal-to-temporal gradient of Eph receptor molecules, and the midbrain optic tectum/SC has an increasing rostral-to-caudal gradient of ephrin ligand molecules (Cheng et al., 1995; Drescher et al., 1995; Nakamoto et al., 1996). (In the present paper, only one-dimensional projection along the nasotemporal axis on the retina to the rostrocaudal axis on the midbrain is considered; projection of the dorsoventral axis on the retina to the mediolateral axis on the midbrain was not considered.) When retinal ganglion cells expressing Eph receptors are assumed to be in the bilateral threshold control, the topographic mapping of the retinal axons on the midbrain becomes comprehensible as follows (Honda, 1998). An axon expresses Eph receptors [receptor density (R)] according to the position of its ganglion cell body on the retina from which the axon extends. The axon terminal crawls on the midbrain, and the receptors on the axon terminal collide with the ligands [ligand density (L)] on the surface of the midbrain. The axon terminal is assumed to receive signal strength of R · L through the receptors, and the signal strength varies depending on a position of the axon terminal on the midbrain, because the ligand density of the midbrain is graded along the rostrocaudal axis. The retinal ganglion axon is assumed to have a reference value S for the signal strength. When the signal strength R · L that the axon terminal receives is around the reference value S (|R · L - S| = 0), the axon terminal is induced to adhere to the site of ligand density L on the midbrain; otherwise (|R · L - S| ≠ 0), the axon terminal does not adhere and is repelled from the site. Consequently, the axon terminal migrates so that|R · L - S| becomes zero. This is called servomechanism for the topographic mapping of retinal ganglion cells to the midbrain (Honda, 1998). The amount of|R · L - S| is called repulsiveness. The axon expressing high receptor density (R_H) adheres to the site of low ligand density (L = S/R_H), whereas the axon that expresses low receptor density (R_L) adheres to the site of high ligand density (L = S/R_L). Thus, topographic mapping takes place on the midbrain.

In the present study, I introduced competition between axon terminals to the servomechanism. Axon terminals have been considered to avoid overlapping each other. Recently, neighboring neural cells were confirmed to show mutual exclusion, constructing minimally overlapping territories (Sugimura et al., 2003). When sites being crowded with axon terminals are adjacent to sites not crowded, some of the axon terminals at the crowded sites move to less crowded sites, forming uniform distribution of population densities of the axon terminals. I will call the movement of some of the axon terminals at crowded sites toward less crowded sites competition between axon terminals.

Algorithm of the servomechanism

An array of sites exists on the rostrocaudal axis of the midbrain. An axon terminal at a particular site tries to migrate to one of the two neighboring sites. The direction of migration (right or left) is determined using random numbers. The ligand densities of the present and the new sites are L and L′, respectively. The axon terminal has repulsiveness|R · L - S| at the present site and|R · L′ - S| at the new site. If|R · L ′ - S| is less than|R · L - S|, the axon terminal migrates to the new site; otherwise, it remains at the same site. The procedure of servomechanism is applied on every axon terminal. After repetition of the procedure the axon terminals migrate so that|R · L - S| becomes small.

Algorithm of competition for target sites

A pair of neighboring sites (i and i + 1) on the midbrain is picked up at random, and if any population density of the two sites is larger than the critical population density (n_C) the following procedure is performed (otherwise, the picked-up pair is discarded, and a new pair is picked up at random). Migration of one axon terminal from the site of higher population density (crowded site) to the site of lower population density is considered. For example, I considered a case in which site i + 1 has higher population density, and its density is greater than n_C. For all the axon terminals k at site i + 1, assuming movement of axon terminal k to site i, repulsiveness|R_k · L_i - S| at site i is estimated, where R_k is the receptor density of axon terminal k, and L_i is the ligand density of site i. Then the axon terminal whose|R_k · L_i - S| is the minimum actually moves to site i. This is one step of the procedure of competition. The procedure of competition is repeated. Therefore, the axon terminal migrates to a less crowded site even though the site is not the best for the axon terminal with respect to its repulsiveness. Thus, the population distribution of the axon terminals on the midbrain has a tendency to become homogeneous.

Topographic map generated by the servomechanism model

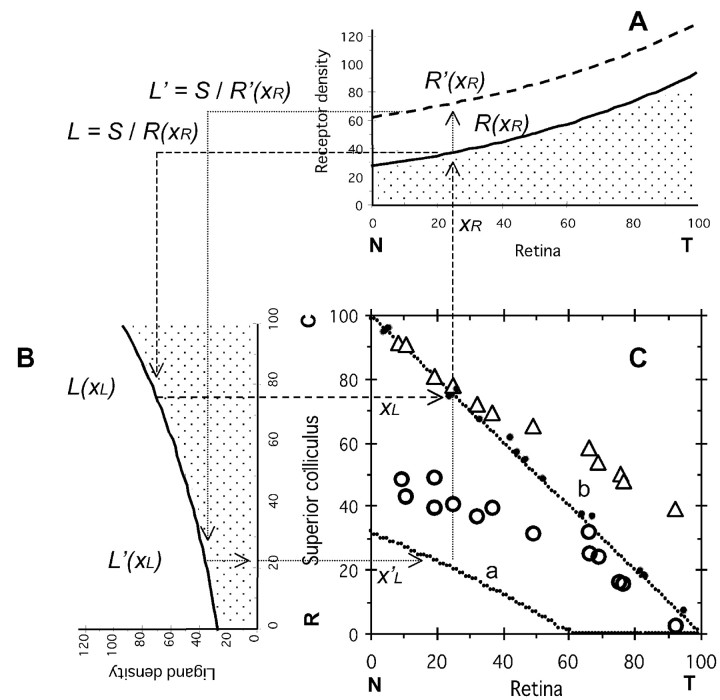
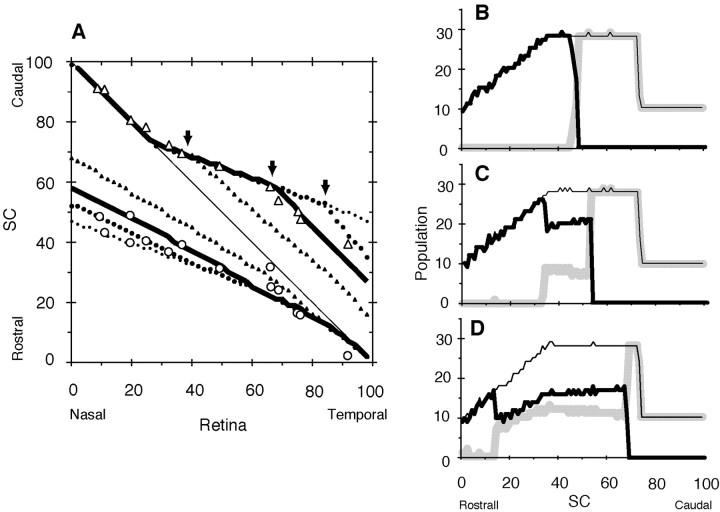
According to the servomechanism model, we can obtain a topographic map of retinal ganglion axons to the SC in the midbrain as shown in Figure 1. Gradients of receptor density of the retina [R(x_R)] and ligand density of the SC [L(x_L)] are shown in Figure 1, A and B. A retinal ganglion cell at x_R of the nasotemporal axis on the retina extends its axon to the SC, and the axon terminal is projected at x_L of the rostrocaudal axis on the SC. I will describe a method to obtain x_L from x_R. An axon terminal from a retinal ganglion cell at x_R on the retina has the receptor density R(x_R) as shown in Figure 1A. The receptors collide with ligands on the SC. According to the servomechanism model (|R · L - S| = 0), the axon terminal is projected at the site where ligand density is L = S/R(x_R). In Figure 1B, the site x_L on the SC can be obtained using L(x_L) = L. Then the point (x_R, x_L) is plotted on Figure 1C.

Figure 1.

Topographic mapping of the retinocollicular projection in wild-type mice and mice with increased EphA3. S = 2500; a = 1/80; and R_E = 36. C, R, Caudal and rostral superior colliculus (SC), respectively; N, T, nasal and temporal retina, respectively. A, Eph receptor density of the normal retinal ganglion cells (EphA3^-; thick line R(x_R) = S^1/2 exp[a (x_R - 50)]) and the retinal ganglion cells with increased EphA3 receptor (EphA3⁺; broken line; R(x_R) = S^1/2 exp[a (x_R - 50)] + R_E) on the retina. B, Ligand ephrin density in the SC. L(x_L) = S^1/2 exp[a (x_L - 50)]. C, Topographic maps of the elevated retinal ganglion cells EphA3⁺ (a) and normal retinal ganglion cells EphA3^- (b). x_R (percent nasotemporal axis of retina) is the starting point of axonal projection, and x_L (percent rostrocaudal axis of the SC) is the arrival point. Topographic map of the retinal ganglion cells (b) is on the line x_R + x_L = 100. Solid circles, Actual data of the retinocollicular projection of wild-type mice by Brown et al. (2000); open circles, open triangles, actual data of the retinocollicular projection of knock-in mice with EphA3⁺ and EphA3^- retinal axons (Brown et al., 2000), respectively.

Materials and Methods

In total, 2000 or 1000 retinal ganglion cells are evenly distributed on the retina and express Eph receptor density according to their position on the retina. They extend axons to the midbrain. There are 100 sites (x_L = 1,..., 100) along the rostrocaudal axis of the midbrain. Initially, all axon terminals are at site x_L = 1, the rostral extreme. For the experiment with increasing EphA3 receptor, the numbers of axon terminals with increasing EphA3 (EphA3⁺) and normal axon terminals (EphA3^-) are 1000, respectively. For the experiment lacking ephrin, the number of axon terminals is 1000. An axon terminal is picked up in random sequence, and the procedure of the servomechanism takes place. When the selected axon terminal is at the terminal end (x_L = 1 or 100), it only tries to migrate to one possible site (x_L = 2 or 99, respectively). The procedure of the servomechanism is applied on every axon terminal in one step. Because the computer simulation continues over 500 steps, the axon terminals are moved 10⁵ or 2 × 10⁵ times in total. This process is called initial mapping. After the initial mapping, the procedure of competition takes place until the distribution of the axon terminals on the midbrain remains unchanged.

Computer simulations were performed with parameter values that determine the shapes of gradients of the retina and midbrain (S^1/2 exp[a(x - 50)], see Fig. 1 legend), were set at S = 2500 and a = 1/80, unless indicated otherwise. Population density was computed by (population of axon terminals in a site)/(area of the site). The area of the site was 1 when the effective area was not considered. Effective area is shown in Figure 3D. Increased receptor density R_E = 36 unless indicated otherwise. Computer programs were written in Fortran 77, and calculations were performed by workstation computers (Toshiba AS7000 U1E/170 and Silicon Graphics Octane-R12000). Results were displayed and analyzed by a personal computer (Apple Power Macintosh G4 and Power Macintosh 7500/100) using Mathematica, version 2.2 (Wolfram Research Inc).

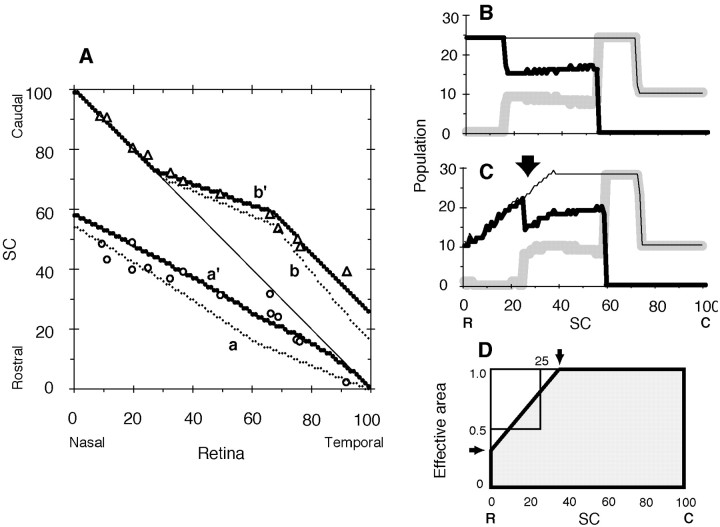
Figure 3.

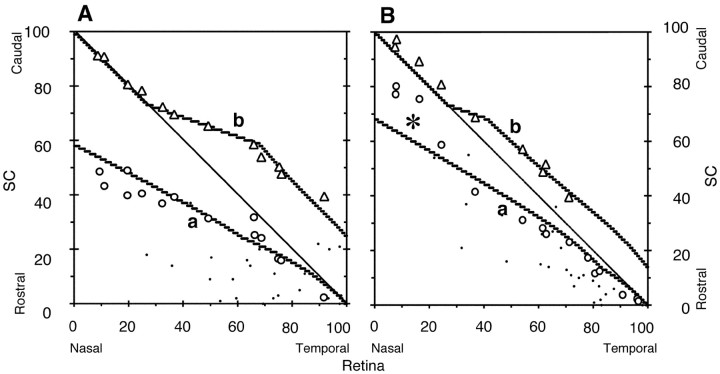
Influence of effective area of the rostral SC. Critical population density n_C = 24, and R_E = 36. C, R, Caudal and rostral SC, respectively; N, T, nasal and temporal retina, respectively. A, Topographic map. a, a′, Projection maps of EphA3⁺ axons; b, b′, projection maps of EphA3^- axons. Projection maps on the truncated SC at the rostral side (see D) are indicated a′, b′; a and b are for comparison and the same as a′ and b′ in Figure 2 A. Open circles, open triangles, Experimental results of EphA3⁺ and EphA3^- retinal axons by Brown et al. (2000), respectively. B, C, Population distributions of retinal axon terminals on the rectangular SC and the rostrally truncated SC, respectively. Thick, gray, thin lines, EphA3⁺ axons, EphA3^- retinal axons, and their sum, respectively. D, Effective area of the SC. Shapes of the rectangular and truncated SCs (thick line) are shown. The rostrally truncated SC has a smaller area by one-eighth in comparison with the rectangular SC. Arrows indicate corner positions (horizontal arrow, 0.293; vertical arrow, 35.4).

Results

Experiments with knock-in mice overexpressing the EphA receptor

Knock-in mice are engineered using a gene-targeting technique that increases EphA receptor expression in a subset of mouse ganglion cells, producing two intermingled ganglion cell populations. A population expresses a wild-type level of EphA5 and EphA6 receptors (EphA3^-), whereas another population expresses ectopic EphA3 receptors (EphA3⁺), being superimposed on the wild-type level of EphA5 and EphA6 (Brown et al., 2000). The topographic map of ganglion cells on the SC of the knock-in mice consists of points that belong to two distinct groups (Fig. 1C, open triangles, open circles). The two groups were discriminated by labeling EphA⁺ cells with retrogradely transported fluorescent latex beads (Brown et al., 2000). The top group (open triangles) in the topographic map corresponds to EphA3^- (wild-type) retinal ganglion cells, and the bottom group (open circles) corresponds to EphA3⁺ retinal ganglion cells.

Topographic mapping in knock-in mice by the servomechanism model

Ligand density on the SC was assumed as shown in Figure 1B. When the wild-type level of receptor density on the retina (EphA3^-) was as shown in Figure 1A (solid line), the topographic map of EphA3^- retinal ganglion cells generated by computer simulation was on the diagonal line of Figure 1C (dotted line b). The experimental results of the retinocollicular projection in normal mice (Brown et al., 2000) appear in Figure 1C as solid circles, which are close to the diagonal line. When ectopic EphA3 receptors were superimposed on the wild-type level of receptor expression (EphA3⁺), the receptor density became as shown in Figure 1A (broken line). An EphA3⁺ retinal ganglion cell at x_R on the retina has a receptor density R′(x_R) as shown in Figure 1A, which was higher than R(x_R). According to the servomechanism model, L′ was obtained as S/R′(x_R), which was smaller than L shown in Figure 1B. Consequently, the topographic map that was localized on the rostral side of the SC (Fig. 1C, dotted line a) was obtained for EphA3⁺ retinal ganglion cells. The result differed from the experimental results (Fig. 1C, open circles). The topographic map of EphA3^- retinal ganglion cells (Fig. 1C, dotted line b) by computer simulation also differed from the experimental results (Fig. 1C, open triangles), especially for temporal (high-x_R) retinal axons.

Time course of computer simulation including competitive interaction

I established a method to estimate the population of axon terminals using the topographic map. When I looked at the map along the y-axis (Fig. 1C, turning the map 90° clockwise) and calculated the slope of curves by differentiation, I obtained the population of axon terminals along the rostrocaudal axis of the SC under consideration of population density along the nasotemporal axis of the retina. The distribution patterns of various axon terminal populations are shown in Figure 2B. EphA3⁺ axon terminals were not even but localized at high density in the rostral part of the SC, especially at the rostral extreme (thick solid line), whereas EphA3^- axon terminals were evenly distributed (gray line). EphA3⁺ axon terminals that accumulated in the rostral SC competed with each other for their target sites, and some of axon terminals were considered to be forced to migrate toward the caudal SC.

Figure 2.

Time course of competition of axon terminals on the SC. Critical population density n_C = 24, and R_E = 36. A, Topographic map. a to a′, Projection maps of EphA3⁺ axons; b to b′, projection maps of EphA3^- axons. Thin line, dotted line, triangles, thick line, Initial mapping, 5 × 10⁴ steps of competition, 10⁵ steps, and 5 × 10⁵ steps, respectively; open circles, open triangles, experimental results of EphA3⁺ and EphA3^- retinal axons by Brown et al. (2000), respectively. B-E, Population distributions of EphA3⁺ and EphA3^- retinal axons on the SC are on the initial map (B), 5 × 10⁴ steps of competition (C), 10⁵ steps (D), and 5 × 10⁵ steps (E). Thick, gray, thin lines, EphA3⁺ axons, EphA3^- retinal axons, and their sum, respectively. Value of the peak truncated in B is 398.

Figure 2A shows the results of computer simulation by the servomechanism-alone model, i.e., without competition (initial mapping; thin solid lines a, b). A computer simulation by the servomechanism-competition model interaction was performed, and the time course of the population distribution of the simulation is shown in Figure 2B-E. The accumulated EphA3⁺ axon terminals at the rostral extreme (Fig. 2B, thick solid line) began to migrate in a caudal direction (Fig. 2C), continued to migrate (Fig. 2D), and took the final distribution (Fig. 2E). The migrating EphA3⁺ axon terminals pushed EphA3^- axon terminals (Fig. 2C,D, gray line) to the caudal SC, and even population distribution of the EphA3^- axon terminals became uneven. Finally, the total population of the axon terminals became evenly distributed except for the caudal SC (Fig. 2E). The SC consisted of three parts, single EphA3⁺ axon terminals, a mixture of EphA3⁺ and EphA3^- axon terminals, and single EphA3^- axon terminals (Fig. 2E, rostral to caudal). Sequential changes in the topographic map are shown in Figure 2A (solid line, dotted line, triangles, thick solid line). The thick solid lines in Figure 2A approximated the experimental results (open circles, open triangles) as a whole but partly differed from the experimental results (asterisk).

Effective area for axon terminals on the SC

Comparison of the topographic maps generated by the experiment and computer simulation showed that the actual population of EphA3⁺ axon terminals on the rostral SC (Fig. 2A, asterisk) was lower than in the computer simulation. Shapes of the retina and the SC differed from each other. The discrepancy was solved by adjustment of the effective area of the SC. When the effective area of the SC was assumed to be as shown in Figure 3D, where the rostral part of the SC was truncated (dotted area), the topographic maps of EphA3⁺ and EphA3^- axon terminals appeared as shown in Figure 3A (dotted lines a′, b′, respectively). The results of the computer simulation became closer to the experimental results. The population distribution on the truncated SC is shown in Figure 3C, where the population on the rostral SC is reduced (arrow) because the competition between axon terminals becomes equal to the population density (not the population itself) between neighboring sites, and the effective areas of the rostral sites are small.

Dependency of critical population density n_C and elevated EphA3⁺ receptor density R_E

The present computer simulation contains two essential parameters, the critical population density n_C and elevated EphA3⁺ receptor density R_E. The values of these parameters in Figure 3 were n_C = 24 and R_E = 36. Next, I examined the effects of changing the parameter values on the results of simulation.

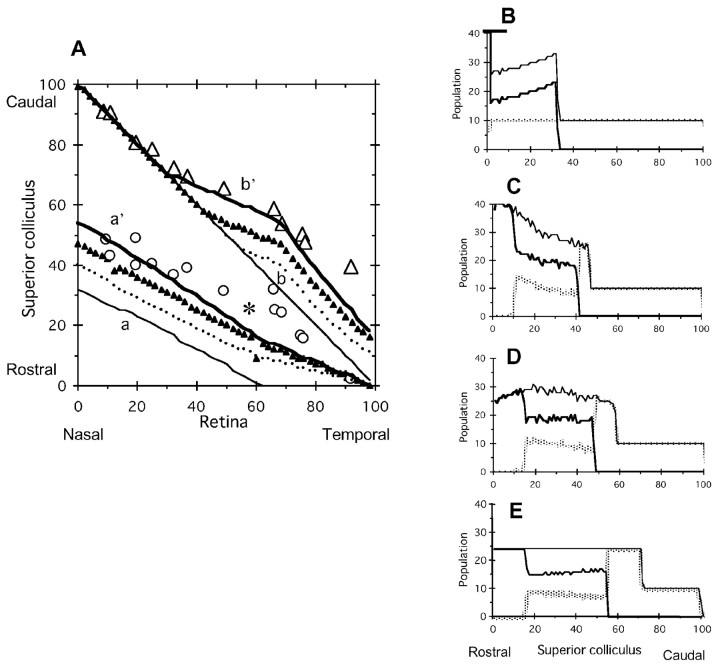
Critical population density is the maximum density of axon terminals that a site of the SC is capable of accepting. Figure 4, A and B, shows the topographic maps and population distributions, respectively, under various critical population densities at high EphA3 receptor density (R_E = 65). As the critical population density increased (n_C = 23, 28, and 33), the total axon terminals (EphA3⁺ and EphA3^- retinal axons) increased onto the rostral side (Fig. 4B, dots, thick solid line, large dots). The deviation point from the diagonal line in the topographic map of EphA3^- axon terminals shifted to the rostral side (Fig. 4A, three arrows). At the critical population density of 28 (Fig. 4A, thick solid line), the topographic map by the computer simulation fitted the experimental results well (open triangles, open circles).

Figure 4.

Variation of topographic maps depending on the critical population density n_C. Increased EphA3 receptor density, R_E = 65. A, Topographic map. Projection maps of n_C = 23 (dot), 28 (thick solid line), and 33 (large dot) are presented. Open circles, open triangles, Experimental results of EphA3⁺ and EphA3^- retinal axons by Brown et al. (2000), respectively. B, Population distributions of retinal axon terminals on the SC. Total populations of EphA3⁺ and EphA3^- retinal axons when n_C = 23 (dot), 28 (thick solid), and 33 (large dot) are presented.

Increased EphA3⁺ receptor density R_E was represented from R(x_R) to R′(x_R) in Figure 1A (solid line to broken line). Topographic maps generated with various R_E values (65, 50, 36, and 18) are shown in Figure 5A (dot, large dot, thick solid line, solid triangles) at a critical population density of n_C = 28. Deviation points between maps of different R_E values are shown by arrows. The population distributions at various R_E values are shown in Figure 5B-D. When the R_E value was large (R_E = 65; Fig. 5B), the EphA3⁺ axon terminal (solid line) and EphA3^- axon terminal (gray line) were separated clearly on the rostral and caudal halves of the SC, respectively. With decreased R_E (50, 36, and 18), EphA3⁺ and EphA3^- axon terminals became intermingled with each other (Figs. 5C, 3C, and 5D, respectively). When R_E = 36 (Fig. 3C), the topographic map by the computer simulation (Fig. 5A, thick solid line) fitted the experimental results well (open triangles).

Figure 5.

Variation of topographic maps depending on increased EphA3 receptor density R_E. Critical population density n_C = 28. A, Topographic map. Projection maps of R_E = 65 (dot), 50 (large dot), 36 (thick line), and 18 (solid triangle) are presented. Open circles, open triangles, Experimental results of EphA3⁺ and EphA3^- retinal axons by Brown et al. (2000), respectively. Population distributions of retinal axon terminals on the SC when R_E = 65 (B), 50 (C), and 18 (D) are presented. For R_E = 36, see Figure 3C. Thick, gray, thin lines, EphA3⁺ axons, EphA3^- axons, and their sum, respectively.

Heterozygotes of knock-in mice with high EphA receptor expression

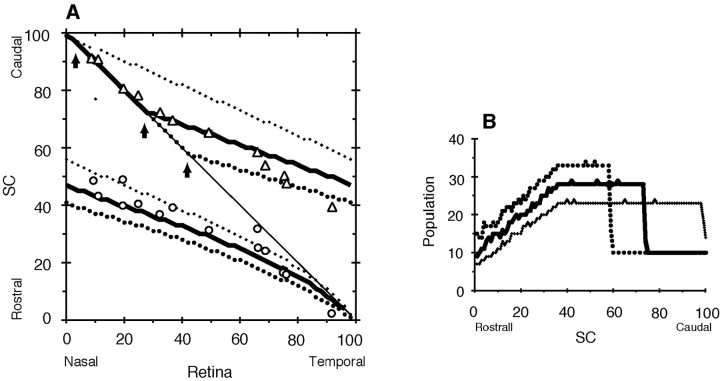
Brown et al. (2000) prepared two types of knock-in mice, homozygotes and heterozygotes, using a gene-targeting technique to increase EphA receptor expression. Homozygous knock-in mice were investigated here. Expression of superimposed EphA3 in heterozygotes is half that of homozygotes. For heterozygotes, a computer simulation with a half-increase of EphA3⁺ receptor density (R_E = 18) was performed. Figure 6 shows the topographic maps of homozygotes (Fig. 6A) and heterozygotes (Fig. 6B). For population distributions of respective zygotes, see Figures 3C and 5D. Although the topographic map of heterozygotes, as a whole, matched the experimental results, the nasal EphA3⁺ retinal axons (Fig. 6B, left side of line a) showed a discrepancy (asterisk) from the experimental result (open circles). The exact reason for this discrepancy cannot be elucidated at present. Axons from the nasal side of the retina in heterozygotes do not regularly express their receptor molecules or are not normally terminated on the SC.

Figure 6.

Computer simulations for topographic maps of homozygous and heterozygous knock-in mice with EphA3 receptor. A, Topographic map of homozygote mice. Simulated projection maps of EphA3⁺ (a) and EphA3^- (b) axons of homozygotes (R_E = 36) are presented. Open circles, open triangles, Experimental results of EphA3⁺ and EphA3^- retinal axons of homozygotes by Brown et al. (2000), respectively. B, Topographic map of heterozygote mice. Simulated projection maps of EphA3⁺ (a) and EphA3^- (b) axons of heterozygotes (R_E = 18) are presented. Open circles, open triangles, Experimental results of EphA3⁺ and EphA3^- retinal axons of heterozygotes by Brown et al. (2000), respectively. For simulated population distributions of homozygotes and heterozygotes, see Figures 3C and 5D, respectively.

Experiments on knock-out mice with disrupted ephrin-A ligand expression

The graded ligand density in the tectum of chick or the SC of mouse consists of two species of ephrins, ephrin-A2 and -A5 (Cheng and Flanagan, 1994; Cheng et al., 1995; Drescher et al., 1995; Frisén et al., 1998; Feldheim et al., 2000). A genetic loss-of-function strategy is adapted, and knock-out mice are generated. Topographic mapping under conditions of the gene disruptions of ephrin-A5 (Frisén et al., 1998) and either or both ephrin-A2 and -A5 (Feldheim et al., 2000) was examined. The experimental results are summarized in Figure 7A-D. In the experiment lacking ephrin-A2 and -A5, retinal axons from the temporal extreme of the retina are projected to a site shifted caudally on the SC, in addition to the normal rostral end (Fig. 7B-D, solid circles). The shifted sites had an average x_L of 20.3 from Feldheim et al. (2000) (their Fig. 1). On the other hand, the retinal axons from the nasal extreme are all projected to the caudal end (Fig. 7B-D, open circles). Furthermore, the nasal axons in ephrin-A5 knock-out homozygotes projected to another site shifted rostrally (Fig. 7C, open circles). The sifted site had an x_L = 71.2 from Feldheim et al. (2000) (their Fig. 1). Unfortunately, the data of each experimental result included only a single point rather than a series of points constituting a map, as were the data of the knock-in experiments (Fig. 1C, open triangles, open circles). I made two computer simulations that allowed understanding of the experimental results of knock-out mice with disrupted ephrin-A ligand expression.

Figure 7.

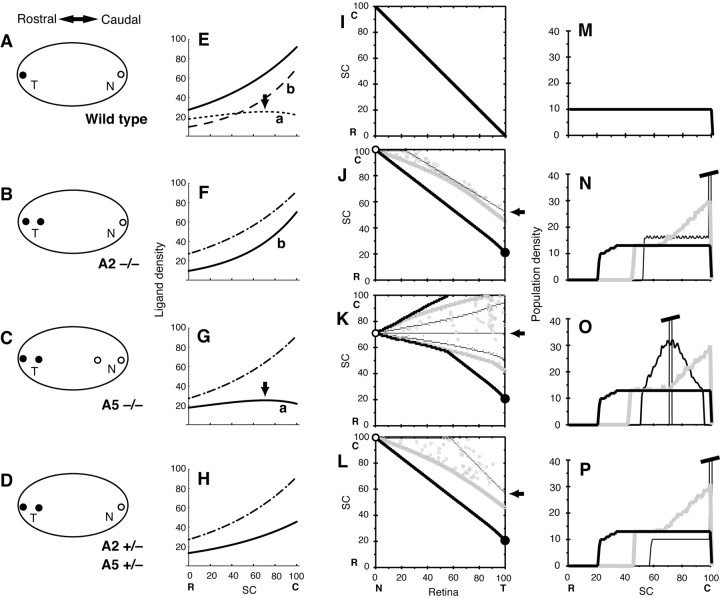
Simulations for knock-out mice with disrupted ephrins. A-D, Schematic illustration of the results of experiments of retinocollicular projections in ephrin-A2 and -A5 knock-out mice (adapted from Feldheim et al., 2000). Oval figures show the SC (left, rostral region; right, caudal region). Terminal positions of temporal and nasal retinal axons are shown by solid circles (T) and open circles (N), respectively. A, Wild-type mouse. B, Homozygotes of A2^-/-). C, Homozygotes of A5^-/-. D, Heterozygotes of A2^+/- and A5^+/-. E-H, Graded ligand densities in the SC used for computer simulations. Dotted-dashed line (for comparison), Total ligand density in E. E, Solid line, Total ligand density of lines a and b. Line a (dotted line), Ligand density of A2^+/+, 27.17(exp[(x_L - 50)/82] - 0.35 exp[(x_L - 50)/50]). Arrow, Position of broad peak. Line b (broken line), Ligand density of A5^+/+, 27.17 × 0.35 exp[(x_L - 50)/50]. F, Solid line (line b), Ligand density of A2^-/-. G, Solid line (line a), ligand density of A5^-/-. Arrow, Position of broad peak. H, Solid line, Total ligand density of A2^+/- and A5^+/-, 27.17 exp[(x_L - 50)/82]/2. I-L, Topographic maps by computer simulations. For the receptor density, the curve similar to that in E (solid line) was used. Thin, gray, thick lines, Initial mapping, 1 × 10⁶ steps of competition, and 3 × 10⁷ steps, respectively; open, solid circles, projected positions of nasal and temporal retinal axon terminals on 3 × 10⁷ steps; arrow, projected position of temporal retinal axon terminal of the initial mapping. I, Map by the ligand density of E (solid line). The map did not change during competition steps. J, Map by the ligand density of F (solid line). Open circles, x_L = 100; arrow, x_L = 52; solid circle, x_L = 21. K, Map by the ligand density of G (solid line). Moderate solid line, Map on 6 × 10⁴ steps; open circles, x_L = 71; arrow, x_L = 71; solid circle, x_L = 21. L, Map by the ligand density of H (solid line). Open circles, x_L = 100; arrow, x_L = 57; solid circles, x_L = 21. M-P, Distribution of population densities of axon terminals on the SC. Thin, gray, thick solid lines, Initial mapping, 1 × 10⁶ steps of competition, and 3 × 10⁷ steps, respectively. M, Distribution did not change during competition steps. N, Value of truncated peak of the distribution of the initial mapping is 245. O, Moderate solid line, Map on 6 × 10⁴ steps. Value of the truncated peak of the distribution was 1000 of the initial mapping. P, Value of the truncated peak of the distribution of the initial mapping was 583. C, R, Caudal and rostral SC, respectively; N, T, nasal and temporal retina, respectively.

The first computer simulation was performed with an assumption that the ligand density of ephrin-A2 on the SC has a broad peak. For the wild-type mouse, the graded density of ligands on the SC was assumed to consist of two species of ligands, ephrin-A2 and -A5. Ephrin-A2 is graded in ligand density but has a broad peak at the caudal side on the SC (see ephrin-A2 in Feldheim et al., 2000, their Fig. 8A). Then, a gradient of ligand density a for ephrin-A2 was constructed so that it had a broad peak as shown in Figure 7E (dotted line). Because ephrin-A5 is simply graded in ligand density on the SC (see ephrin-A5 in Feldheim et al., 2000, their Fig. 8A), a gradient of ligand density b for ephrin-A5 was constructed using an exponential function (Fig. 7E, broken line). The total ligand density of gradients a and b was used to prepare a topographic map of the wild-type mouse. The retina of the wild-type mouse was assumed to have a gradient of receptor density of the same shape as the solid line in Figure 7E (gradient of receptor density not shown). To obtain the following four topographic maps, this gradient of receptor density was used throughout. The constructed topographic map of the wild-type mouse was a diagonal line (Fig. 7I), and the population distribution of axon terminals was flat (Fig. 7M).

Figure 8.

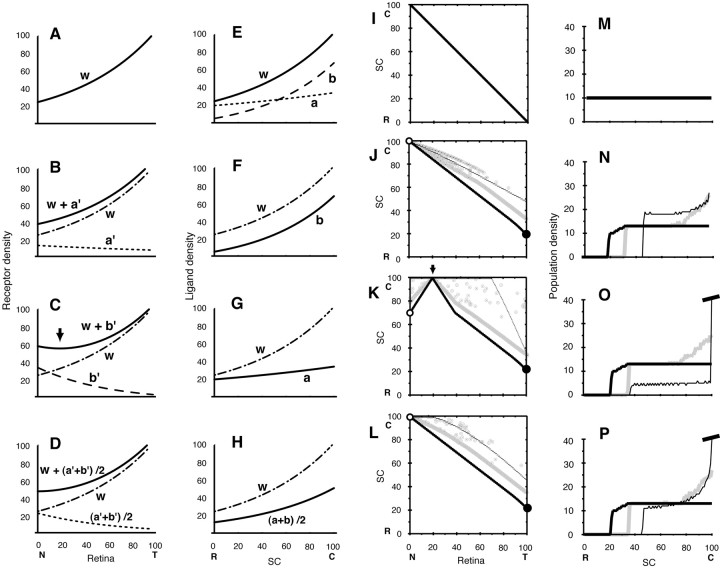
Simulations for knock-out mice with upregulation of Eph in the retina attributable to disrupted ephrins. A-D, Graded receptor densities in the retina used for computer simulations. Dotted-dashed line (line w), 1.224 f(x_R), the same as line w in A (for comparison). A, Receptor density of wild-type mouse (line w), 1.224 f(x_R). B, Solid line, Receptor density of A2^-/- (line w + a′), 1.224 f(x_R) + 0.45 f_a(100 - x_R); dotted line (line a′), 0.45 f_a(100 - x_R). C, Solid line, Receptor density of A5^-/- (line w+b′),1.224f(x_R)+0.6f_b(100-x_R);arrow, position of a trough; dotted line (line b′), 0.6 f_b (100-x_R). D, Solid line, Receptor density of heterozygote A2^+/- and A5^+/-, line w + (a′+ b′)/2, 1.224 f(x_R) + 1/2 [0.6 f_a(100 - x_R) + 0.45 f_b(100 - x_R)]. Dotted line, (a′+ b′)/2, 1/2 [0.6 f_a(100 - x_R) + 0.45 f_b(100 - x_R)]. E-H, Graded ligand densities in the SC used for computer simulations. Dotted-dashed line, 1.224 f(x_L) the same of line w in E (for comparison). E, Solid line (line w), Total ligand density of lines a and b, 1.224 f(x_L); dotted line (line a), 1.224 f_a(x_L); broken line (line b), 1.224 f_b(x_L). F, Ligand density of A2^-/-, 1.224 f_b(x_L). G, Ligand density of A5^-/-, 1.224 f_a(x_L). H, Solid line, Ligand density of heterozygote A2^+/- and A5^+/-, line (a + b)/2, 1/2 [1.224 f_b(x_L) + 1.224 f_a(x_L)]. In the above-mentioned explanation, the following functions are used: f(x) = 20 exp(x/ 70); f_a(x) = 16 exp(x/180); and f_b(x) = f(x) - f_a(x). I-L, Topographic maps by computer simulations. Thin, gray, thick lines, Initial mapping, 5 × 10⁶ steps of competition, and 2 × 10⁷ steps, respectively; open, solid circles, projected positions of nasal and temporal retinal axon terminals on 2 × 10⁷ steps. I, Map by the ligand density of E (line w) and the receptor density of A (line w). The map did not change during competition steps. J, Map by the ligand density of F (line b) and the receptor density of B (line w + a′). Open circles, x_L = 100. K, Map by the ligand density of G (line a) and the receptor density of C (line w + b′). Open circles, x_L = 71; solid circle, x_L = 21; arrow, x_R = 20. L, Map of heterozygote by the ligand density of H [solid line, line (a + b)/2] and the receptor density of figure D [solid line, line w + (a′+ b′)/2]. Open circles, x_L = 100; solid circles, x_L = 21. M-P, Distribution of population densities of axon terminals on the SC. Thin, gray, thick solid lines, Initial mapping, 5 × 10⁶ steps of competition, and 2 × 10⁷ steps, respectively. M, Distribution did not change during competition steps. N, Distribution changed during competition steps. O, Value of the truncated peak of the distribution of the initial mapping was 703. P, Value of the truncated peak of the distribution of the initial mapping was 222. C, R, Caudal and rostral SC, respectively; N, T, Nasal and temporal retina, respectively.

For the homozygous knock-out mouse A2^-/-, the gradient of ligand density was as in Figure 7F (solid line), which was similar to gradient b in Figure 7E. The ligand density was considerably reduced compared with the wild-type mouse. The topographic map was obtained as an initial mapping (Fig. 7J, thin line). The axon terminals interacting with a low level of ligand density on the SC were overshot caudally and accumulated at the caudal extreme. The population distribution of axon terminals of the initial mapping is shown Figure 7N, thin solid line, which had a sharp peak at the caudal extreme. A computer simulation including competition was performed for the population of axon terminals of the initial map. The population distribution changed, through the distribution presented by the gray line finally to the distribution presented by the thick solid line. The sequential changes in the topographic map are represented by the thin, gray, and thick lines (Fig. 7J). The projected points of axon terminals of the nasal and temporal extremes are indicated by the open and solid circles. Although the temporal axon terminals showed a caudal shift too large on the initial map (x_L = 52; Fig. 7J, arrow), the competitive interaction made a reasonable shift as follows. When critical population densities of n_C = 12.5, 13.5, and 14.5 were used for the computer simulation including competition, the positions of the temporal axon terminals were x_L = 10, 21, and 27, respectively. When the critical population density was set at 13.5, the position of the temporal axon terminals was close to the experimental result (x_L = 20.3), as indicated by the solid circle. For the homozygous knock-out mouse A5^-/-, the gradient of ligand density was the solid line in Figure 7G, which was similar to gradient a in Figure 7E. It should be noted that the gradient of the ligand density has a broad peak at the site of the caudal SC (x_L = 71; Fig. 7G, arrow). The topographic map was obtained as an initial map, represented by the horizontal thin solid line in Figure 7K. All axon terminals accumulated at the site of x_L = 71 because their repulsiveness|R · L - S| was the minimum at the site (although repulsiveness is not zero). The population distribution of axon terminals of the initial mapping is shown by the thin solid line in Figure 7O, which had a sharp peak at the site (x_L = 71) where the broad peak of ligand density a stood. The computer simulation including competition was performed, and a change of the population distribution was obtained (Fig. 7O). The sequential changes in the topographic map are shown by the horizontal solid, moderately solid, gray, and thick lines (Fig. 7K). It should be noted that axon terminals from the nasal extreme (open circles) rostrally shifted in comparison with those in Figure 7J, where they are at the caudal extreme. Although the temporal axon terminals stood at the site of x_L = 71 in the initial map (Fig. 7K, arrow), the competitive interaction made a reasonable shift (x_L = 21), as indicated by the solid circle.

For the heterozygous knock-out mouse A2^+/- and A5^+/-, the gradient of ligand density is shown in Figure 7H (solid line), which was at half-density of the total density of gradients a and b in Figure 7E. The topographic map was obtained as an initial mapping, which is shown by the thin line in Figure 7L. The axon terminals were overshot caudally and accumulated at the caudal extreme. The population distribution of axon terminals of the initial mapping is shown by the thin solid line in Figure 7P, which had a sharp peak at the caudal extreme. Computer simulation including competition was performed, and a change of the population distribution was obtained (Fig. 7P). The sequential changes in the topographic map are also shown in Figure 7L. Although the temporal axon terminals showed a large caudal shift on the initial map (x_L = 57; Fig. 7L, arrow), the competitive interaction made a reasonable shift (x_L = 21), as indicated by the solid circle.

For the double homozygous knock-out mouse A2^-/- and A5^-/-, the servomechanism model did not generate a map; the model did not have any solution because L(x_L) is zero everywhere. This is consistent with the experimental results in the A2^-/- and A5^-/- mouse, in which we observed projection spots, but the spot positions are not distinct. The projection system could probably make spots but could not direct their positions.

The second computer simulation was performed with an assumption that receptor density on the retina has a trough when ephrin-A2 is disrupted. A number of investigators showed that ephrins are expressed not only in the tectum/SC but also in the retina (Hornberger et al., 1999; Feldheim et al., 2000). Furthermore, ephrins may downregulate functional receptors in the nasal retina (Hornberger et al., 1999). On the other hand, ephrins are considered to reduce the sensitivity of Eph receptors (desensitization model; Wilkinson, 2000). Therefore, it was assumed that the functional graded receptor density is determined by an overlap of the graded ligand density and the receptor density. Ephrins in the retina form a diminishing nasal-to-temporal gradient (Hornberger et al., 1999). Disruption of one of the ligand genes results in upregulation of receptor density at the nasal extreme.

As shown in Figure 8E, I made a gradient of ligand density on the SC consisting of gradients of ephrin-A2 and -A5 (curves a, b, respectively). Then ligand densities on the SC of the two homozygous knock-out mice (A2^-/- and A5^-/-) and the heterozygous knock-out mouse (A2^+/- and A5^+/-) are in Figure 8F-H, respectively. For receptor density on the retina, disruption of one of the ligand genes results in upregulation at the nasal extreme. Receptor densities on the retina of the two homozygous knock-out mice (A2^-/- and A5^-/-) and the heterozygous knock-out mouse (A2^+/- and A5^+/-) are in Figure 8B-D, respectively. It should be noted that the receptor gradient of mouse A5^-/- has a trough near the nasal extreme (Fig. 8C, arrow), although the overall shape is an increasing nasal-to-temporal gradient of the Eph receptor. The trough of receptor density exhibited an upward, convex pattern in the topographic map by the servomechanism-competition model (Fig. 8K). Other topographic maps (Fig. 8I,J,L) were similar to those of Figure 7, I, J, and L.

The two computer simulations (with the broad peak of ligand density on the SC and the trough of receptor density on the retina) showed the same abnormal shifts at the nasal and temporal extremes in the topographic map that were close to the experimental results of knock-out mice (Figs. 7J-L, 8J-L, open, solid circles). It should be noted that retinal axons from the nasal side of the retina (x_R = 20 - 40) in Figure 7K are projected to two sites on the SC (rostral and caudal, both sides of x_L = 71). We could discriminate between the two models (the broad peak or the trough) by examination of whether the nasal projection site is one or two. In either case, the assumption of competitive interaction between axon terminals seems to be necessary to explain the abnormal topographic shifts in knock-out mice.

The second computer simulation (Fig. 8) was based on the fact of coexpression of ephrin ligands and Eph receptors in the retina, and ephrins reduce the activity of Eph receptors. On the other hand, a model is proposed that the coexpression of these molecules contributes to formation and maintenance of the gradients of ligand and receptor densities (Honda and Mochizuki, 2002).

Discussion

Competitive interaction between axons for their target sites

Competition of neural axons for their targets has been demonstrated in many areas of the nervous systems (Purves and Lichtman, 1985), including muscle fibers, ganglion cells, spinal motor neurons, optic tectum/SC (Schmidt, 1978; Schmidt et al., 1978), and visual cortex (Wiesel et al., 1974; Hubel et al., 1977), and has been discussed with respect to the plastic properties of innervation (Schmidt et al., 1978; Goodhill and Richards, 1999; Brown et al., 2000; Feldheim et al., 2000). Although competition between axon terminals may be a general property of topographic projections of neural axons, it results only in displacement, rearrangement, diffusion, or out-of-focus axonal arborization. Competition itself is a passive behavior and does not actively create any ordered patterns. There is a principle of organization in the first place, and then competition modifies the organization process under the principle. Therefore, competition could be examined in detail only if a principle is established. In the topographic projection of retinal ganglion cells to the midbrain, the servomechanism model is considered a reliable principle of organization.

Before the development of the servomechanism model, the pioneer model by Gierer was known for the retinotectal projection (Gierer, 1981, 1983, 1987; Bonhoeffer and Gierer, 1984). Gierer used the guiding parameter p(x), consisting of two gradients with opposite slopes. The guiding parameter p(x) is given several names, a potential, a metabolic parameter, or a substance of distribution interfering with the intercellular pattern formation system of the axons. A retinal axon has its own p(x) and is positioned at a minimum p(x) within the tectum. Both the one-dimensional case of Gierer's model and the servomechanism model (involving exponential types of receptor and ligand densities) produce the same topographic map. The opposite slopes in Gierer's guiding parameter are not clear, and actual substances of graded distribution on the retina and the tectum were not established at that time. Despite these difficulties, Gierer foresightedly formulated function p(x). In the servomechanism model, the function p(x) can be replaced by|R(x_R) · L(x_L) - S|, which is defined as the level related to signal strength based on the interaction of ephrin ligands and Eph receptors.

By addition of competitive interaction to the servomechanism model, the servomechanism-competition model explained the abnormal topographic projections in knock-in mice with increased EphA3 receptors. Furthermore, the competitive interaction was necessary to explain actual moderate shifts of temporal axon terminals on the SC (Fig. 7J-L, solid circles) in knock-out mice lacking ephrin-A ligands. Without the competitive interaction, the temporal axon terminals had shifted too far to the caudal side in the computer simulation (Fig. 7J-L, arrow). Taken together, it is concluded that competitive interaction between axon terminals is a plausible behavior in neural topographic projections of artificially manipulated animals.

Competition between axon terminals takes place because their target area is limited and crowded with many axon terminals. On the other hand, selection of surviving axons is closely related to the pattern of neural activity (Purves and Lichtman, 1985). Synchronous activity of axons impedes their competitive interaction, whereas asynchronous activity enhances competition between axons that innervate the same target. Here I propose another selection mechanism; axon terminals at sites of high population density are displaced to neighboring sites of low population density depending on a level of repulsiveness|R · L - S|. Rearrangement through the neural activity may refine mapping of axon terminals after the process of servomechanism including competition.

Abnormal topographic map of knock-in mice could be explained without competitive interaction, but several other assumptions are necessary

In another report (my unpublished results), I tried to explain the abnormal topographic mapping of knock-in mice with elevated EphA3 without competitive interaction. Three assumptions were made: (1) retinal ganglion cells have an upper limit of receptor protein synthesis, and the gradient pattern of EphA receptor density on the retina is truncated on the temporal side of the retina; (2) EphA receptors have an oligomeric structure (Thanos et al., 1999), and heteromers consisting of intrinsic EphA and ectopic EphA3 receptors have reduced receptor activity; and (3) ephrin-A ligands on the SC are cleaved by metalloproteases in the presence of ectopic Eph3 receptors of retinal axon terminals (Hattori et al., 2000). Ephrin ligands at sites where many retinal axons are projected are extensively degraded. On the basis of these assumptions, the servomechanism model without competitive interaction constructed a topographic map close to the abnormal topographic map. The assumptions, however, were not simple and contained several arbitrary parameters. In contrast, the servomechanism model including competitive interaction was simple and clear.

Shape of gradients of receptor density on the retina and ligand density on the SC

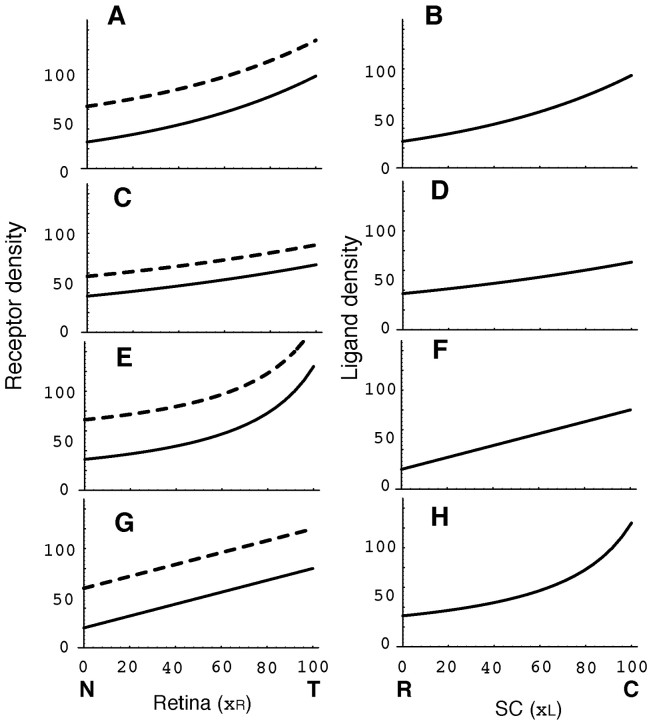
The diagonal line b of the topographic map in Figure 1C could be generated by the gradients of receptor density on the retina (Fig. 1A, solid line) and ligand density on the SC (Fig. 1B). Experimental results of the retinocollicular projection in normal mice (Brown et al., 2000) were plotted as solid circles in Figure 1C, which matched the diagonal line (dotted line b). To obtain the diagonal line in the topographic map, gradients of receptor density R(x_R) and ligand density L(x_L) should have a special relationship. An example of the relationship is a pair of the same type of exponential functions, as shown in Figure 9, A (solid line) and B. Another pair of functions with more moderate slopes (Fig. 9C, solid line, D) generated the same diagonal topographic map. Other pairs of functions, parabola and linear, generated the same diagonal topographic map (Fig. 9E, solid line, F; G, solid line, H). In the present report, a pair of exponential functions of Figure 9, A (solid line) and B, was used. The servomechanism model does not uniquely define the functions of receptor and ligand gradients but constrains the relationship between a pair of functions.

Figure 9.

Various combinations of the ligand density gradient on the SC and receptor density gradient on the retina that produce the topographic maps of Figure 1C (dotted lines a, b). Solid line, Wild-type level of receptors or ligands; broken line, elevated level of receptor gradient by ectopic receptor R_E. R_E was defined so that the simulation result becomes close to the experimental result. C,R, Caudal and rostral SC, respectively; N, T, nasal and temporal retina, respectively. A, Exponential function, R(x_R) = S^1/2 exp[a(x_R-50)] + R_E, where a = 1/80, and R_E = 36 (broken line) or 0 (solid line). B, Exponential function, L(x_L) = S^1/2 exp[a (x_L - 50)], where a = 1/80. C, Exponential function of moderate slope, R(x_R), same as A, but a = 1/160, and R_E = 20 (broken line) or 0 (solid line). D, Exponential function of moderate slope, L(x_L), same as B, but a = 1/160. E, Hyperbola, R(x_R) = S/[0.6(x_R - 50) + 50] + R_E, where R_E = 40 (broken line) or 0 (solid line). F, Linear, L(x_L) = 0.6(50 - x_L) + 50. G, Linear, R(x_R) = 0.6(x_R - 50) + 50 + R_E, where R_E = 40 (broken line) or 0 (solid line). H, Hyperbola, L(x_L) = S/[0.6(50 - x_L) + 50].

I found that simulation of the knock-in experiment was best when R_E = 36 under the assumptions that gradients of receptor density on the retina and ligand density on the SC are the solid lines in Figure 9, A and B. As previously mentioned, we can use various gradients of the receptor and its ligand, as shown in Figure 9. R_E could be defined to produce simulations close to the experimental results (Fig. 5). R_E for close simulation varied depending on the shape of gradients of receptor and ligand densities. Receptor gradients with R_E for close simulations are shown by the broken lines in Figure 9, A, C, E, and G. I further examined gradients of exponential type S^1/2 exp[a(x - 50)], where a is a parameter that defines gradient shape. It was found that R_E for close simulations was approximately proportional to a; i.e., when a value of R_E is known from an experiment, I can conjecture the shape of gradients of receptor and ligand densities. This is noteworthy because the shapes of gradients of receptor and ligand densities are not simultaneously observed in the present experiments. I will introduce a formula that determines the gradient shape of the exponential type as follows. R_E is presented in a relative value, R_E/R₅₀, where R₅₀ is receptor density at the middle retina (x_R = 50). According to the present study, R_E/R₅₀ = 36/50, and a = 1/80. Because R_E/R₅₀ is proportional to a, we can present a by R_E/R₅₀ as a = (50/36) (1/80) R_E/R₅₀ = 0.0174 R_E/R₅₀. If a relative value R_E/R₅₀ is known, I suggest that the shape of gradients of receptor and ligand density is R₅₀ exp[a(x - 50)], where a = 0.0174 R_E/R₅₀.

Capacity of the tectum/SC to accept axon terminals

Competitive interaction between axon terminals for target sites is based on the assumption that there is a limitation of the number of axon terminals for the surface of the SC to accept for synapse formation. The limitation is characterized by a critical population density, n_C. For the knock-in experiment with increased EphA3⁺, the result of computer simulation fitted the experimental result when n_C = 28 (Fig. 4A). Because the total population of axons is 2000 (1000 EphA3⁺ axons and 1000 EphA3⁺ axons), and the effective SC area is 100 × 7/8 = 87.5, as shown in Figure 3D, the average population density is 2000/87.5 = 22.9. Then the relative critical population density is 28/22.9 = 1.22. On the other hand, for the knock-out experiment lacking ephrin, the result of computer simulation fitted the experimental result when n_C = 13.5 as described in Results. In this case, the total population of axons is 1000, and the average population density is 1000/87.5 = 11.4. Then the relative critical population density is 13.5/11.4 = 1.18. The two relative critical population densities are close to each other. The assumption of the critical population density may be reasonable; i.e., the surface of the SC in the mouse midbrain can accept retinal axon terminals at ∼120% of the normal population of accepted axon terminals.