Neuronal Avalanches in Neocortical Circuits

Abstract

Networks of living neurons exhibit diverse patterns of activity, including oscillations, synchrony, and waves. Recent work in physics has shown yet another mode of activity in systems composed of many nonlinear units interacting locally. For example, avalanches, earthquakes, and forest fires all propagate in systems organized into a critical state in which event sizes show no characteristic scale and are described by power laws. We hypothesized that a similar mode of activity with complex emergent properties could exist in networks of cortical neurons. We investigated this issue in mature organotypic cultures and acute slices of rat cortex by recording spontaneous local field potentials continuously using a 60 channel multielectrode array. Here, we show that propagation of spontaneous activity in cortical networks is described by equations that govern avalanches. As predicted by theory for a critical branching process, the propagation obeys a power law with an exponent of -3/2 for event sizes, with a branching parameter close to the critical value of 1. Simulations show that a branching parameter at this value optimizes information transmission in feedforward networks, while preventing runaway network excitation. Our findings suggest that “neuronal avalanches” may be a generic property of cortical networks, and represent a mode of activity that differs profoundly from oscillatory, synchronized, or wave-like network states. In the critical state, the network may satisfy the competing demands of information transmission and network stability.

Introduction

During neuronal processing, individual neurons can integrate inputs from thousands of other neurons and, after reaching threshold, distribute their activity back to the network. This basic process of neuronal integration and redistribution is similar to that seen in many other complex systems in which simple units with thresholds integrate and then dissipate energy back to the system (Paczuski et al., 1996). In such systems, events like earthquakes (Gutenberg and Richter, 1956), forest fires (Malamud et al., 1998), and nuclear chain reactions (Harris, 1989) emerge as one unit exceeds threshold and causes other units to do so in turn, thereby initiating a cascade that propagates through the larger system. The spatial and temporal distributions of such cascades or “avalanches” have been well described by power laws (Paczuski et al., 1996), indicating that the system is in a critical state (Bak et al., 1987) and that the dynamics can be seen at many different scales. This type of avalanche propagation typically occurs in these systems without oscillations, synchrony, or waves. Neuronal activity could similarly be considered as a kind of neuronal avalanche in which activity propagates as individual neurons trigger action potential firing in subsequent neurons. Although just such a process has been suggested by several neuronal network models (Chen et al., 1995; Corral et al., 1995; Herz and Hopfield, 1995; Eurich et al., 2002), it has been unclear so far whether actual neuronal networks display such critical behavior and whether such criticality is a robust feature of neuronal organization. If present, neuronal avalanches would constitute a new mode of network activity, and could have important implications for information processing.

To examine these issues, we studied propagation of spontaneous neuronal activity in cultured and acute slices of rat cortex on 60-channel multielectrode arrays (Plenz and Aertsen, 1996; Plenz and Kitai, 1998; Karpiak and Plenz, 2002). We also used complementary network simulations to examine how propagation like that observed in the cultures would influence information processing in a simple feedforward network. Using these methods, the present study was conducted to examine two issues: (1) Do cortical networks in vitro produce avalanches that comply with physical theories of critical systems? (2) If cortical networks are in the critical state, what consequences does this have for information processing?

Materials and Methods

Organotypic culture experiments. Organotypic cultures from coronal slices of rat somatosensory cortex were prepared in accordance with National Institutes of Health guidelines (Plenz and Kitai, 1998), with the cortical slice placed onto the 8 × 8 multielectrode array (interelectrode distance, 200 μm; electrode diameter, 30 μm; Multichannelsystems, Reutlingen, Germany) (Egert et al., 1998; Karpiak and Plenz, 2002). Acute coronal slices were cut at 350 μm thickness and were ∼1.5 mm deep and ∼2-3 mm wide. The array covered ∼50-70% of the cortical tissue, with the basal row aligned to the white matter and the upper row extending into the supragranular layers (see Fig. 1A). In three of seven cultures, a coronal striatal and nigral slice (500 μm thickness) were cocultured outside the array (Plenz and Kitai, 1998). These areas do not project to cortex, and no differences in cortical activity were found for single or combined cortex cultures. Photographs taken at 1-3 d in vitro (DIV) and after recording sessions confirmed that recording electrodes were located in the cortical culture. Most recordings were performed with cultures submerged in standard culture medium at a flow rate of 1 ml/min.

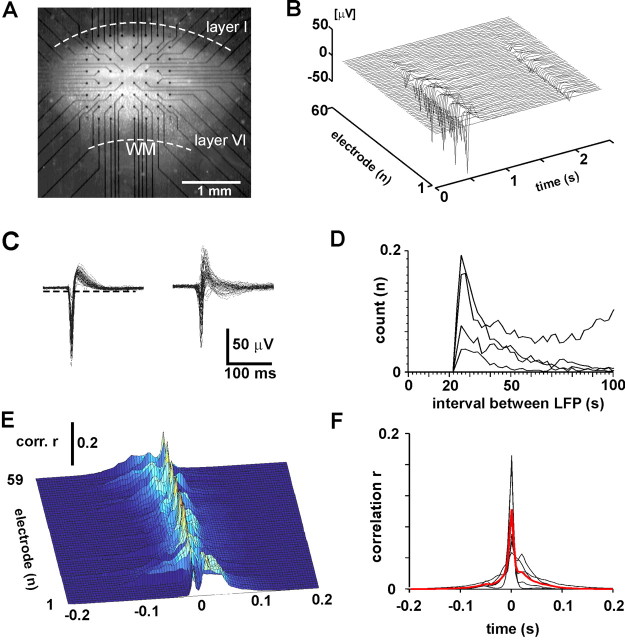
Figure 1.

Spontaneous, correlated neuronal activity in organotypic cortex cultures. A, Organotypic coronal cortex slice culture on 8 × 8 multielectrode array (IED, 200 μm). WM, White matter. B, Spontaneous LFP from 60 electrodes (linear order) with two periods of correlated activity. C, Overplot of LFPs from a single electrode (left, ∼1 min spontaneous activity) and from all electrodes during one correlated period of activity (right, aligned to negative peaks). Note typical negative peaks riding on a longer-lasting depolarization. Broken line, -3 SD. D, Successive LFPs on individual electrodes are >20 msec apart in time. Average time interval distributions for successive LFPs on one electrode for four representative cultures (1 hr spontaneous activity). E, Representative cluster of 59 cross-correlation functions for one electrode in relation to all other electrodes (single culture). F, Population cross-correlogram shows correlation falls to zero within ± 100-200 msec. red, Average; black, individual cultures.

Acute slice experiments. Coronal sections from adult rat brains (6-8 weeks) were cut at 350-400 μm in chilled artificial CSF (ACSF) containing the following (in mm): 124 NaCl, 0.3 NaH₂PO₄, 3.5 KCl, 1.2 CaCl₂, 1 MgSO₄, 26.2 NaHCO₃, 10 d-glucose, and 50 μm d,l-2-amino-5-phosphonovalerate (APV; Sigma, St. Louis, MO), saturated with 95% O₂ and 5% CO₂ (310 ± 5 mOsm). Slices were stored submerged for 1-2 hr in ACSF without APV at room temperature before recording. For recording, slices were gently transferred onto the multielectrode array. The electrode array covered mostly supragranular layers of primary motor and somatosensory cortex. Electrode positions were reconstructed using pictures taken at the end of each recording session (see Fig. 6A). Slices were submerged in ACSF without APV at 35.5 ± 0.5°C saturated with 95% O₂ and 5% CO₂ and recordings were performed at a flow rate of 2 ml/min.

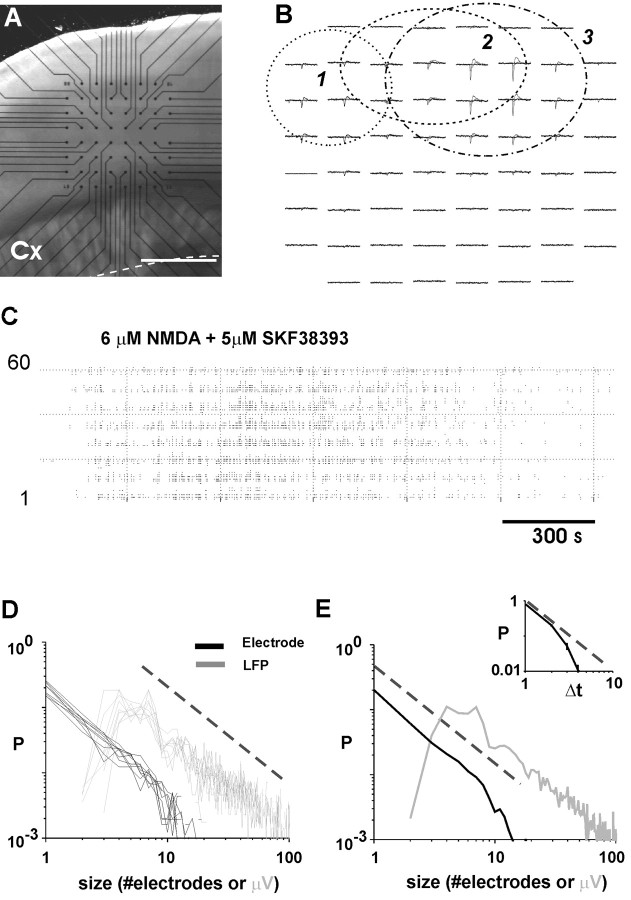
Figure 6.

Neuronal avalanches in acute cortex slices. A, Light microscopic picture of the acute coronal brain slice and position of the microelectrode array. Cx, Cortex. B, Overplot of three different periods in which spontaneous, synchronized LFPs are visible. Three different periods (1-3) are shown (1 sec each) that reveal the occurrence of neuronal avalanches in three different, partially overlapping locations. For spatial location in the slice, see A. C, Raster plot of LFP activity in response to bath application of the NMDA receptor agonist NMDA and the D₁ receptor agonist SKF-38393. Note that synchronized events are visible across the array for ∼2000 sec after which the activity subsides. D, Individual event size distribution at Δt = IEI_avg from each acute slice experiment over plotted (n = 9 acute slices). Black, Number of electrodes; gray, summed LFPs; broken line, power law with α = -3/2). E, Average event size distribution from data shown in D. Inset, Lifetime distributions of avalanches display a power law in initial portion with characteristic slope of -2 and exponential cutoff. Broken line, Power law with exponent of α = -2.

Pharmacology. To study propagation under reduced inhibition, the noncompetitive GABA_A-receptor antagonist picrotoxin (2 μm; Invitrogen, Gaithersburg, MD) was bath-applied. Event size distributions were calculated based on 5 hr spontaneous activity before and during drug application and 24 hr after recovery (see below).

In acute slices, spontaneous activity was induced by bath perfusion with the glutamate-receptor agonist NMDA (6 μm in ACSF; Sigma) in combination with the dopamine D₁-receptor agonist (±)-SKF-38393 (5 μm in ACSF; Sigma). Preliminary experiments revealed that the combination of both drugs at those concentrations robustly induced synchronized local field potentials (LFPs), for an average of ∼0.4 hr in the acute slice.

Signal processing. Extracellular signals were continuously sampled at 1 kHz, low-pass-filtered at 50 Hz, and binned at Δt = 1, 2, 4, 8, or 16 msec. A threshold was used to determine events of interest, and this threshold was given by the receiver operating characteristic curve produced by the filtered data and a Gaussian noise distribution (Gabbiani and Koch, 1998). Noise was not significantly different from a Gaussian distribution (Kolmogorov-Smirnov test; p > 0.05), and produced an average threshold of -2.86 ± 0.23 SD. The filtered voltage traces were searched for times at which they crossed this threshold, and it was found that LFPs typically crossed over the threshold for 20 msec before crossing back. During this 20 msec interval of threshold crossing, the LFPs often displayed a sharp negative peak, indicative of a population spike, that had a distinct point of maximum excursion. Algorithms were used to identify the time of occurrence of this maximum excursion and to record its amplitude. The processed data thus contained both a time point and an amplitude value for every LFP that crossed the threshold (see Fig. 1C). A refractory period of 20 msec was imposed after each maximum to prevent counting large excursions more than once. For control, a refractory period of 2 msec, much shorter than 20 msec, was also used.

Cross-correlation functions and contiguity index. Cross-correlation functions were calculated from 3 hr (cultures) or 0.4 hr (acute slice) of data over a window of -0.2-0.2 sec at a bin width of 1 msec. The contiguity index measured the extent to which propagation in cortical networks was wave-like. The index is given by the fraction of active electrodes whose activity was preceded by activity on at least one nearest-neighbor electrode (n = 8 neighbors/electrode except for border electrodes). Note that active electrodes in the first time bin of an avalanche are counted as not preceding the nearest-neighbor activity.

Average interevent interval calculation. Traditionally, the interevent interval (IEI) has been defined as the interval between events at a single electrode. In the sense used in the current paper, the IEI denotes the interval between LFPs occurring at all electrodes. For example, an LFP might occur on electrode 1 at time t = 0, and the next LFP recorded by the array might occur on electrode 24 at time t = 4 msec. In this case, the IEI would be 4 msec. Thus, the IEI distributions plotted in this report take into account the interval between LFPs recorded over all electrodes. Because activity did not generally propagate directly between nearest-neighbor electrodes, the average IEI (IEI_avg) was obtained by calculating the average value of the IEI distribution over the time from 0 to T_max. T_max was given by the time at which the population cross-correlation function dropped to a constant, near zero baseline. T_max ranged between 150 and 200 msec in cultures and 50 and 80 msec in acute slices (see Fig. 1E).

Rescaling of arrays. Each electrode array was a square 8 by 8 grid without the corners, thus having 60 electrodes. The interelectrode distance (IED) between each electrode and its nearest neighbor was 200 μm. To examine how the spatial scale given by the IED influences the power law distributions, we performed two types of manipulations to the arrays during analysis.

First, rescaling the arrays tested whether or not the slope of the power law found to describe event size distributions (see Results) was dependent on the IED. Rescaling was accomplished by removing some of the intercalated electrodes from the analysis, while still maintaining a square array. This also reduced the number of electrodes considered in the analysis. For example, to create an IED of 400 μm, a regular array of 4 by 4 electrodes was chosen from the 8 by 8 array (see Fig. 4D), which resulted in twice the distance between the electrodes from the original array. This rescaled array could be fit onto the original array in four ways, although each way caused one of the corner electrodes to be missing, leaving only 15 electrodes. The data for this rescaled array was obtained from 15 electrodes for each of the four ways and averaged. A similar rescaling was done to create an IED of 600 μm, leaving only eight electrodes (a 3 by 3 array with one corner missing). As before, this rescaling could be done in four possible ways, so the result reported was from an average of the data obtained from arrays positioned these four ways. Increasing the IED resulted in a longer IEI for the rescaled arrays (see Fig. 4A), and data from the rescaled arrays were always binned at the nearest integer value to the corresponding IEI.

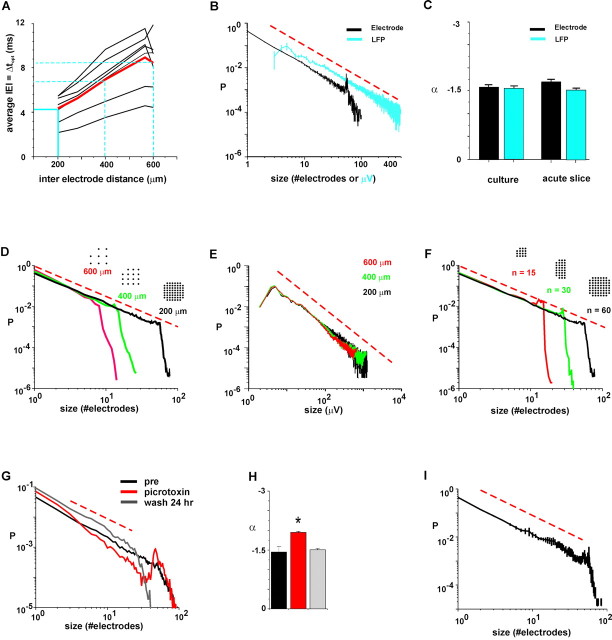
Figure 4.

Characteristic exponent for neuronal avalanche sizes is -3/2. A, IED versus IEI_avg for original and rescaled grid sizes. Red, Average; black, individual cultures. B, Power laws at Δt = IEI_avg for each culture have characteristic exponent α ≈ -1.5. Black, Number of electrodes; blue, LFP; average for all cultures. C, Average slopes for cultures (left) and acute slices (right). D, At Δt = IEI_avg and corresponding IED, the slope α is independent of array size. Icons indicate resampled arrays at IED = 200, 400, and 600 μm. E, Resampled power laws for summed LFP values (same arrays as in D). F, Cutoff point of the power law is determined by the number of electrodes in the array (n = 15, 30, 60; IED = 200 μm). G, Reduction in inhibition in the presence of the GABA_A receptor antagonist picrotoxin destroys the power law and renders the event size distribution bimodal. Note the presence of a large hump at higher values, indicating epileptic discharge. H, The initial slope of the event size distribution is significantly steeper (p < 0.05) in the presence of picrotoxin. Same color code as in G. I, Average event size distribution for refractory period set to 0 msec at Δt = 4 msec (three cultures). Broken line in red indicates slope of -3/2.

Second, reducing the number of electrodes in the arrays tested whether the cutoff point in the power law (the point at which the linear portion of the graph shows a break; see Results and Figs. 3A, 4B,D,F) was dependent on the number of electrodes. To explore this issue, we effectively cut the array into halves and quarters without changing the IED. For example, to create an array with 30 electrodes, only electrodes on the left side of the array would be chosen for analysis. The array was bisected in two ways, producing four half-size arrays (see Fig. 4F). The results from these four arrays were averaged to produce the power law for the half-sized array. In a similar manner, the array could also be divided into quarters, each containing 15 electrodes for analysis. Although quartering could be done in more than four ways, only the four quarters near the corners were used in this study for creating an average power law.

Figure 3.

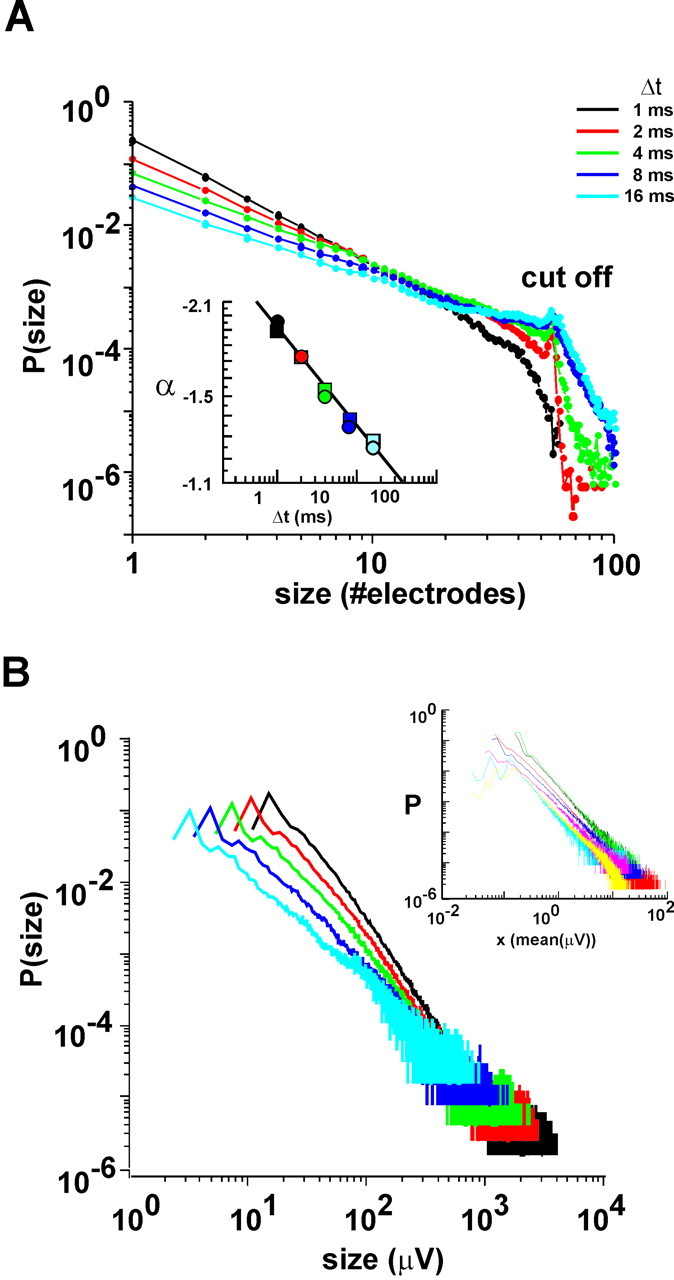
Size distributions for avalanches follow power laws independently of bin width Δt. A, Probability distribution of avalanche sizes (number of electrodes activated) in log-log coordinates at different Δt (average for n = 7 cultures). The linear part of each function indicates power law. Cutoff given by maximal number of electrodes (n = ∼60). Inset, Dependence of slope α on Δt: α(Δt) ∼ Δt^{-0.16 ± 0.01} (R² = 0.99 ± 0.01; averages for all cultures). Circles, Electrodes; squares, LFP. B, Probability distribution of avalanche size distributions based on summed LFPs as a function of bin width Δt. Inset, Single culture; overplot of power laws for all seven cultures at Δt = 1 msec expressed in multiples of average LFP size.

Branching parameter. The branching parameter σ was used to describe activity propagation in the cortical cultures. By definition, σ is the average number of descendants from one ancestor (de Carvalho and Prado, 2000) and, intuitively, was defined in our system as the average number of electrodes activated in the next time bin, given a single electrode being active in the current time bin. Mathematically, the average branching parameter σ for the electrode array in the case of one ancestor electrode is simply given by

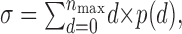1

where d is the number of electrode descendants, p(d) is the probability of observing d descendants, and n_max is the maximal number of active electrodes. Note that formula (1) does not describe a probability density, and theoretically σ can take any value ≥0. Because of refractoriness in activity at single electrodes, σ was estimated only from the first and second time bin of an avalanche. Although strictly speaking, σ is only defined for one ancestor, we also estimated σ when there were multiple ancestors. Under these conditions, d is given by:

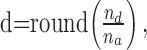2

where n_a is the number of electrode ancestors observed in the first time bin, n_d is the number of active electrodes in the second time bin of an avalanche, and round is the rounding operation to the nearest integer. The likelihood of observing d descendants was approximated by:

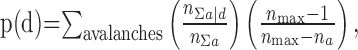3

where n_∑a|d was the total number of electrode ancestors in all avalanches when n_d descendants were observed, n_∑a was the total number of ancestors observed in all avalanches, and

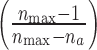was a factor that provided an approximate correction for the reduced number of electrodes available in the next time bin because of refractoriness. Note that the branching parameter is not defined for 0 ancestors and thus does not provide information about the initiation of bursts. In cases in which there was only one ancestor, the formula for σ was mathematically equivalent to (1).

Network simulations. Simulations were used to explore the implications of a critical branching process on information transmission. Feedforward networks had N processing units per layer and L layers. Binary units (on or off) made C randomly assigned connections to units in the next layer. Each connection had a probability p_i of transmitting that was randomly chosen, but the sum of probabilities emanating from a unit was constrained to be equal to

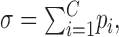4

where 0 ≤ p_i ≤ 1 and 0 ≤ σ ≤ C. Note that this formulation allows the branching parameter σ to be adjusted in the network. A unit in the next layer became active only if a unit in the previous layer was active and the connection between them transmitted. A given network type was determined by the choice of N, L, and C. Results from 20 network types are reported: (N: 6, 8, 10, 12, 14; L: 3, 4; C: 2, 3). Ten networks of each type were constructed, and each was run five times for each value of σ (σ = 0.1-3.0, in increments of 0.1 for 30,000 total simulations). All possible binary input patterns (2^N) were presented to the input layer as a stimulus set S. Binary patterns appeared in the output layer as a response set R. Information I transmitted through the network was given by: I(S; R) = H(R) - H(R/S), where H(R) was the entropy of the response set, and H(R/S) was the entropy of a response, given a stimulus, calculated over all responses and all stimuli (Cover and Thomas, 1991).

All values are expressed as means ± SD unless stated otherwise.

Results

The results are composed of four main sections. First, we derive the power laws that characterize propagation of spontaneous activity in mature organotypic cortex cultures. Second, we demonstrate that these laws also describe propagation of spontaneous activity in acute, mature cortex slices. Third, we demonstrate that the spontaneous activity observed indicates that the cortical network operates in a critical state. Finally, we describe the outputs of feedforward neural network models that were used to explore the consequences of the critical state on information transmission.

General characteristics of spontaneous activity

We analyzed the propagation of neuronal activity in seven organotypic cultures prepared from rat somatosensory cortex and grown on 60-channel multielectrode arrays (Fig. 1A). After 28 ± 3 DIV, spontaneous LFPs were recorded continuously from the cortex for at least 10 hr in each culture at a 1 kHz sampling rate. The present analysis is based on a total of 70 hr of recording. A typical LFP consisted of a negative population spike superimposed on a positive envelope (Fig. 1B), as has been described previously (Jimbo and Robinson, 2000). This general LFP shape was consistent over time at individual electrodes and across electrodes (Fig. 1C). Time interval distributions for successive LFPs on individual electrodes revealed that LFPs were at least 24 msec apart from each other (calculated with refractory period t_ref = 2 msec), which allowed us to reliably extract LFPs with a refractory period set to t_ref = 20 msec (Fig. 1D) (see Materials and Methods). On average, 58.9 ± 0.4 electrodes per culture were active; i.e., they had negative population spikes that crossed an optimum threshold as determined by receiver-operating characteristic curves (see Materials and Methods). The rate of LFPs differed widely between individual cultures and was on average 58,000 ± 55,000 LFPs per hour (mean ± SD; range, 10,000-240,000 LFPs/hr). The total voltage produced by each network when expressed as sum of LFP amplitudes was on average -2 × 10³ mV ± 3 × 10³ per hr (n = 7 cultures).

Synchronized bursting separated by many seconds of quiescence is considered a hallmark of mature cortical networks grown in isolation (Crain, 1966; Calvet, 1974; Gutnick et al., 1989; Maeda et al., 1995; Gopal and Gross, 1996; Kamioka et al., 1996; Plenz and Aertsen, 1996; Corner et al., 2002). In agreement with these previous reports, LFPs appeared on many electrodes almost simultaneously when viewed at low temporal resolution, forming synchronized activity epochs separated by many seconds with no activity (Fig. 1B). Despite this apparent synchrony, cross-correlation functions suggested a different picture. Within a single network, cross-correlation functions between pairs of electrodes were highly variable, but quickly declined within ± 100-200 msec (Fig. 1E), which was found in all networks analyzed (Fig. 1F). The variability in correlation at higher temporal resolution across electrodes suggested that “synchronous” events were composed of more complex spatiotemporal patterns, for which currently no exhaustive description is available. In the following paragraph, we will derive such a statistical description of this activity at high temporal resolution.

The definition of neuronal avalanches

As predicted from cross-correlation analysis, when the LFP data were binned at finer temporal resolution (e.g., bin width Δt = 4 msec), it became clear that LFPs did not appear on all electrodes at exactly the same time (Fig. 2A). Rather, some LFPs occurred before others, forming spatiotemporal patterns on the electrode array. To begin to characterize these patterns, two terms were defined. The spatial pattern of active electrodes on the multielectrode array during one time bin Δt was called a frame and a sequence of consecutively active frames that was preceded by a blank frame and ended by a blank frame was called an avalanche (Fig. 2A). When activity was classified using this definition, the cortical cultures were found to produce numerous avalanches per hour at various lengths (Fig. 2B). The distribution of avalanches ranged from several thousand avalanches with just one frame to a few dozen avalanches at longer duration and was similar for all bin sizes tested (Δt = 1-16). Thus, within the synchronous epochs there existed an entirely different form of activity, avalanches of different durations, in which nonsynchronous activity was spread over space and time.

Figure 2.

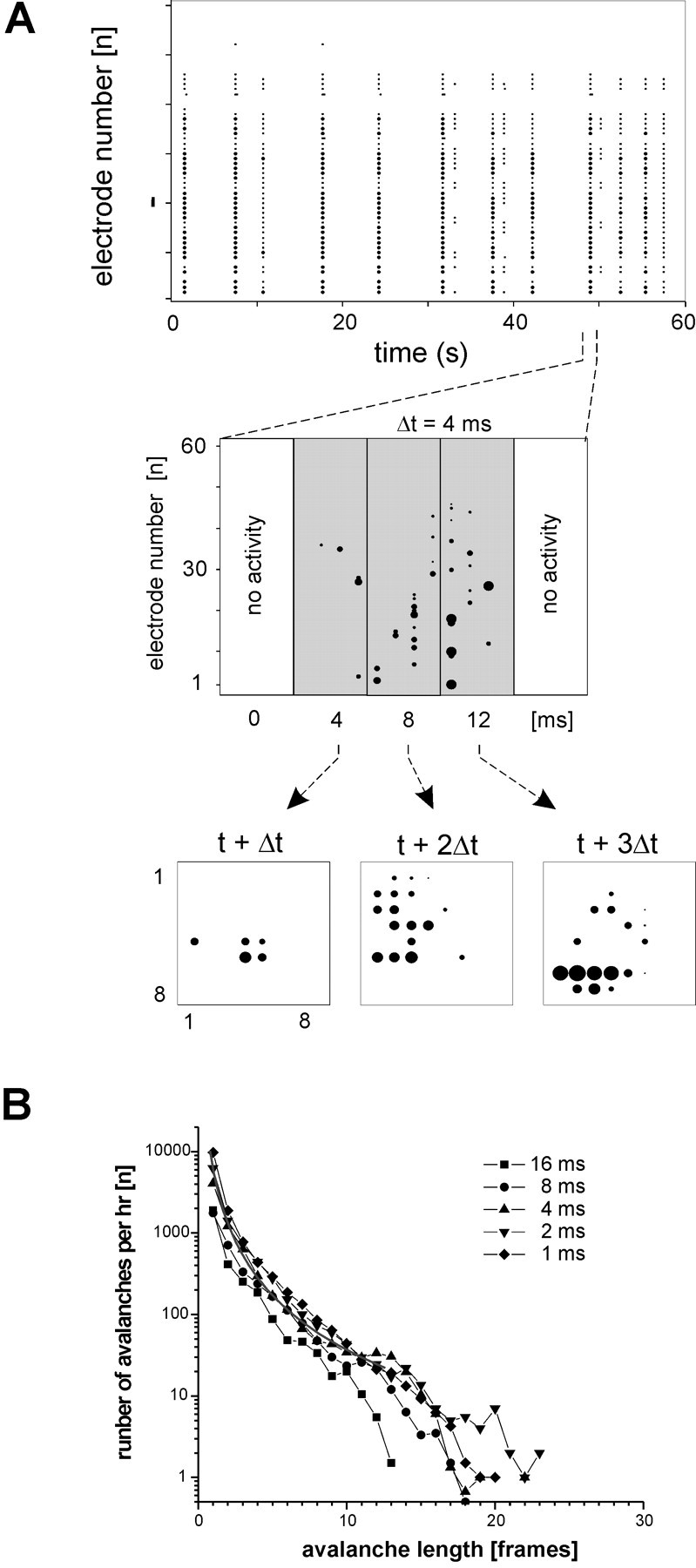
Activity within synchronized periods is composed of avalanches. A, Raster of spontaneous activity (top) shows correlated periods containing spatiotemporal patterns (middle) and an avalanche of three frames in the original coordinates of the multielectrode array (bottom). Avalanches were defined as sequences of continuous activity that were preceded and terminated by a bin width of Δt with no activity. Dots, LFP times (dot sizes proportional to LFP amplitudes); 1 and 8, columns and rows on the grid. B, Cultured cortical networks produce thousands of avalanches of different durations per hour.

The fact that LFPs occurred consecutively within an avalanche suggested that activity initiated at one electrode might spread later to other electrodes. Because activity has been reported to propagate successively, but in a wave-like manner in the developing retina (Meister et al., 1991), in slow cortical oscillations (Sanchez-Vives and McCormick, 2000), and in the epileptic cortical slice (Chervin et al., 1988), it was of interest to test how this activity might differ from a wave-like propagation. An index of contiguity (see Materials and Methods) was developed to measure how often activity spread from a given electrode to its nearest neighbors. In a perfect wave, almost 100% of activity would proceed from the nearest neighbors, but in the cortical cultures only 39.3 ± 8% of the electrodes showed activity that was preceded by activity from nearest neighbors (bin width Δt = 4 msec for all networks). Thus, most of the time, LFPs in the cortical networks did not propagate in a spatially contiguous way.

The power law in neuronal avalanche size

The variability of spatiotemporal patterns within and across cultured networks raised the question of whether or not there was a general law that would provide insight into this variability as well as allow prediction of the features of these patterns. As a first step toward this, we expressed the size of an avalanche as the number of electrodes that were activated during the avalanche. The probability distribution of avalanche sizes revealed a simple, linear relationship in log-log coordinates (Fig. 3A). This linear relationship had a cutoff near 60, the maximal number of active electrodes in the array, indicating that most electrodes were not activated more than once in a given avalanche. More importantly, this linear relationship also demonstrated the existence of a power law P(n) ∼ n^α, where n was the size of an avalanche, P(n) was the probability of observing an avalanche of size n, and α was the exponent of the power law, giving the slope of the relationship. The power law remained linear even when avalanche sizes were measured using different time bins Δt ranging from 1 to 16 msec (mean R² = 0.98 ± 0.04). This demonstrated the robustness of the power law for avalanche sizes at multiple time scales. However, the slope α revealed a clear dependence on bin width Δt (Fig. 3A, inset), to be explained more fully below.

Similar relationships were found when the size of an avalanche took into account different LFP values for each electrode (Fig. 3B). In this case, avalanche size was expressed as the absolute sum of LFP amplitudes over all electrodes with LFPs above threshold and ranged from just a few to several thousands of microvolts, thereby covering several orders of magnitude. Again, a simple power law described the probability of finding avalanches for a given field size, whether expressed in absolute LFP amplitudes or multiples of average LFP amplitude (Fig. 3B, inset). The dependence of the exponent α in these power laws based on LFP amplitudes was identical to that found when measuring avalanche size based on number of active electrodes only (Fig. 3A, inset).

Thus, the power laws captured the distribution of the widely varying spatiotemporal patterns in a simple equation. They also indicated a fundamental scale invariance of network dynamics over many orders of magnitude (in this case, involving either a few neurons or an entire neuronal network); that is, if f(size₀) = (size₀)^a then the ratio f(k × size₀)/f(size₀) = k^a is independent of any chosen unitary event size (size₀; k is an arbitrarily chosen number). In other words, at any given scale, e.g., fixed size, the ratio of patterns with size above or below that scale is constant and the dynamics do not have a critical size threshold.

A unique power law exponent of -3/2 in cortical networks

Many complex systems with power law behavior in event size distributions can be described by a single, characteristic exponent (Paczuski et al., 1996), which raises the question of whether such a characteristic exponent exists for the cultured neuronal networks. To answer this question, we begin by pointing out the inherent relationship that was observed to exist between the IEI_avg for successively active electrodes and the IED of the electrode array. At a fixed IED, a temporal bin width Δt > IEI_avg would group many LFPs into the same bin, thereby concatenating several smaller avalanches together into a longer avalanche. Thus, long bin widths would bias the power law distribution toward fewer short avalanches and more long avalanches (i.e., a decrease in slope). Conversely, at Δt < IEI_avg long avalanches would be preferentially fragmented into several smaller avalanches, resulting in a power law with a steeper slope. When the power law was calculated at the highest spatial resolution (200 μm) and the corresponding IEI_avg for each culture (Fig. 4A), the power law exponent α was observed to be -1.50 ± 0.008 for electrode number and -1.49 ± 0.005 for summed LFP amplitude (Fig. 4B,C) (linear regression ± SE). Thus, despite the large variability in IEI_avg between individual cultures of 2.7-6 msec (equivalent to a “propagation velocity” of ∼74-33 mm/sec), the power law exponent was constant when the data were binned at the corresponding IEI_avg. In addition, it should be noted that work in other laboratories has shown that the average propagation velocity of activity in cultured networks of dissociated neurons grown on multielectrode arrays is ∼50 mm/sec (Maeda et al., 1995). This figure matches exactly with the IED in our arrays of IED = 200 μm divided by the average optimal bin width Δt = 4 msec).

Several findings indicated that the value of -3/2 should be taken as the characteristic exponent for this system. First, the slope of the power law did not significantly change even when the data were sampled using a wide range of different thresholds (3-10 times SD; ANOVA; number of electrodes, p = 0.66; sum of LFP amplitudes, p = 0.442; Tukey test; data not shown). Second, because neuronal activity propagates with limited velocity, the IEI_avg measured in the networks should increase with the IED of the electrode array, whereas the power law exponent α should be truly independent from such external scaling. To demonstrate that α was indeed independent, we effectively rescaled the arrays by removing some of the intermediate electrodes from the analysis, still maintaining a square array (see Materials and Methods). This had the effect of increasing the average distance between electrodes and also increasing the average IEI for the rescaled arrays (Fig. 4A). When the data were binned at the optimal bin widths given by these new IEDs, the avalanche size distributions still followed a power law with slope α ≈ -1.5 (number of electrodes: α = -1.489 to -1.55; summed LFP amplitude: α = -1.489 to -1.55; r = 0.98-0.99), which also suggested that the network behavior was scale-free (Fig. 4D,E). Third, the number of electrodes at which the power law no longer shows a linear relationship gives the cutoff point. To demonstrate that the cutoff point was limited solely by the number of electrodes in the array, during analysis we cut the array into halves and quarters, effectively removing electrodes without changing the IED. As expected, the cutoff point always appeared at the maximum number of electrodes available in the array, suggesting that the power law would continue indefinitely for an infinite array (Fig. 4F). Note that some avalanche sizes are actually larger than 60, the maximum number of electrodes in the array. This unusual occurrence could be caused by an avalanche that spread through the array and returned to its point of origin to reactivate some of the ancestor electrodes again. In that way, some electrodes would participate more than once in the same avalanche, thus allowing the total size of an avalanche to exceed 60 electrodes.

To further understand the network state that is represented by a power law with slope of -1.5, we increased the excitability of the cortical network, which should reduce the power law slope because of an increased incidence of larger avalanches. However, when spontaneous activity in the network was increased by application of the GABA_A-receptor antagonist picrotoxin (2 μm), the power law behavior was destroyed and the distribution of event sizes changed to a bimodal distribution with an initial slope significantly lower than -1.5 (Fig. 4G,H) (α_pre = -1.45 ± 0.08; α_picrotoxin = -1.95 ± 0.02; α_wash = -1.51 ± 0.03; means ± SE; ANOVA; number of electrodes; p < 0.05; Tukey test; n = 3 cultures). Network activity was dominated either by very small or very large, all-inclusive events, typical for epileptic tissue (Chervin et al., 1988). This suggests that a power law of slope -1.5 indicates the optimal excitability of the network at which the power law exists. Finally, to test whether the refractory period of 20 msec, which is larger than any of the bin widths Δt used, might artificially reduce the number of LFPs recorded, we recalculated the event size distributions with a different set of parameters. At a refractory period of 2 msec and bin width Δt = 4 msec, the power law for spontaneous propagation of LFPs was still present with the characteristic exponent of -1.5 (Fig. 4I).

The scale-free lifetime distribution of neuronal avalanches

Although we have only considered avalanche sizes so far, the lifetime distribution of avalanches has also been shown to be an important parameter that characterizes systems dynamics; in the case of neuronal networks, it describes the temporal dimension of propagation. Theoretical considerations (Zapperi et al., 1995) as well as neuronal network simulations (Eurich et al., 2002) predict that the distribution of lifetimes for avalanches should likewise obey a power law, but with an exponential cutoff. We also observed this relationship in the neuronal avalanches in the cultured networks. Here, the shape of lifetime distributions was largely independent of bin width Δt (Fig. 5A) (IED = 200 μm), and the distributions were shown to be scale-free using the transformation t′ = t/Δt (Fig. 5B). As predicted by theory (Zapperi et al., 1995), the scale-invariant life time distribution revealed an initial slope close to α = -2.

Figure 5.

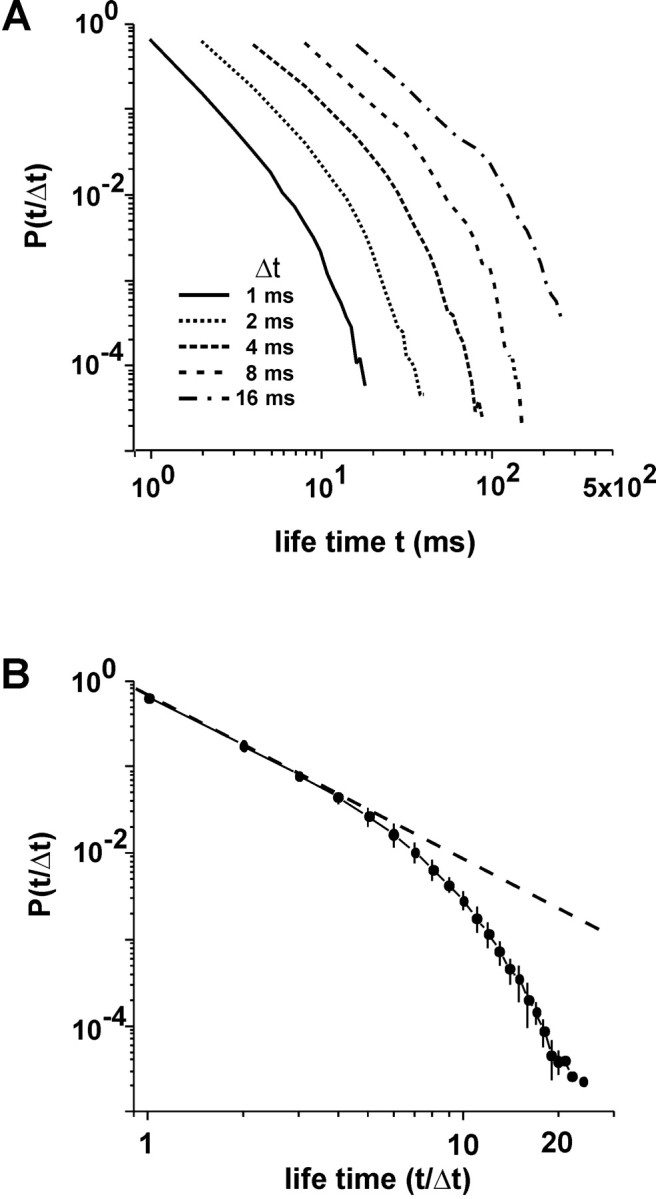
Lifetime distributions of avalanches display a power law in initial portion with characteristic slope of -2 and exponential cutoff. A, Lifetime distributions as a function of bin width Δt. B, Normalized time t/Δt collapsed from inset giving scale-invariant lifetime distributions (average for Δt = 1, 2, 4, 8, and 16 msec for n = 7 cultures). Broken line indicates slope of -2.

Neuronal avalanches in acute cortex slices

Because neuronal propagation as described in the above paragraphs might be affected by the specific culture condition, we further examined propagation of synchronized, negative LFPs in mature, acute slices from rat primary motor and somatosensory cortex. Spontaneous activity was induced pharmacologically by increasing the NMDA-mediated sustained excitation in the cortical networks (Seamans et al., 2001) through bath application of the glutamate receptor agonist NMDA and the dopamine D₁-receptor agonist SKF-38393, which robustly induced spontaneous LFP activity (Fig. 6). Similarly as in the organotypic cortex cultures, LFPs had a typical time course of a negative peak followed by a longer-lasting depolarization. Many electrodes initiated spontaneous LFPs in the acute slices, and neuronal avalanches typically encompassed a spatial extent of up to 10-15 neighboring electrodes (Fig. 6B). Spontaneous activity lasted on average for 1780 ± 448 sec (n = 9 acute slices) and correlation between LFPs declined sharply within ∼50-80 msec, resulting in an IEI_avg = 3.73 ± 0.467. At the closest integer of Δt = 4 msec, this activity had a contiguity index of 28 ± 9% and was composed of on average 505 ± 420 avalanches (rate, 966 ± 590 avalanches/hr) (Fig. 6C). The event size distributions for spontaneous activity in the acute slices clearly revealed the initial signature of the same power law as was described for the cultured networks (Fig. 6D,E). The average initial slope values for acute slices were -1.50 ± 0.08 for LFP (r = 0.95; 10-80 μV) and -1.58 ± 0.04 for electrode data (r = 0.999; 1-8 electrodes). Thus, neuronal avalanches also exist in acute, mature cortex slices and display a characteristic exponent of -3/2. However, neuronal avalanches in acute slices are more compact and spatially restricted to fewer electrodes compared with the neuronal culture. This is indicated by the exponential cutoff of the power law (Fig. 6E) and most likely reflects the severed long-range cortical connectivity in the acute slice.

Finally, the lifetime distribution for neuronal avalanches in acute slices was also characterized by an initial slope close to -2 and an exponential cutoff, as was described for neuronal avalanches in organotypic cortex cultures (Fig. 6E, inset).

A critical branching process in cortical network

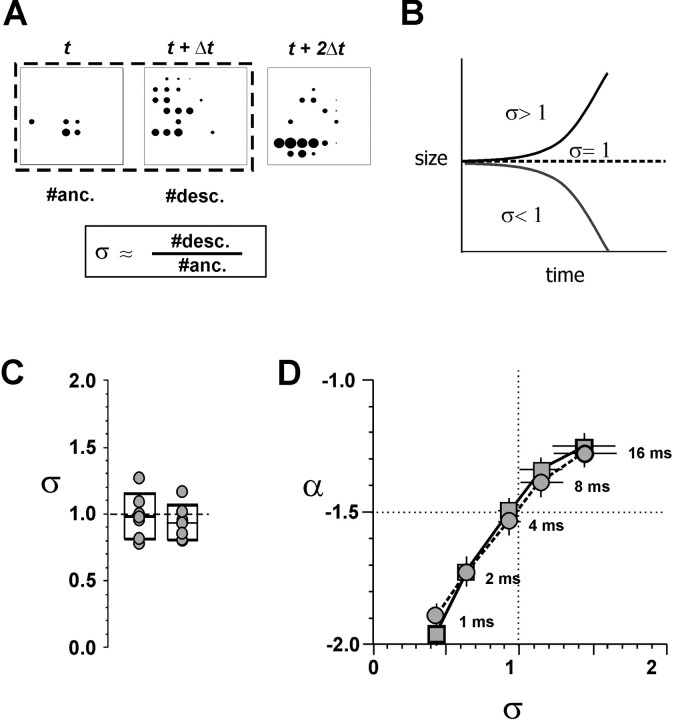
What mechanism could be responsible for a power law of event sizes in a neural network with a slope of -3/2? A particular process is immediately suggested by the data, given that the slopes α = -3/2 for avalanche sizes and α = -2 for avalanche life times have been predicted by theory for a critical branching process (Harris, 1989; Zapperi et al., 1995). To investigate whether such a branching process might adequately describe propagation of activity in the cultured neural networks, we measured the branching parameter sigma (σ) directly (de Carvalho and Prado, 2000). For our system, σ gives the expected number of electrodes that will be active in the next time step after a single active electrode. This average number of descendants can be approximated by the ratio of descendant electrodes to ancestor electrodes for two successive time bins at the beginning of an avalanche (Fig. 7A). According to theory, σ > 1 would represent a supercritical state in which an increasing number of electrodes would be activated at each step, eventually leading to an unstable runaway activation of the network (Fig. 7B). If σ < 1 (subcritical state), activity would decrease over successive steps. If σ = 1 (critical state), activity at one electrode would lead to activity in one other electrode on average, keeping the network at the edge of stability (Harris, 1989). Because σ is estimated only from a small aspect of the avalanches and can vary tremendously for individual avalanches (range, 1/59 to 59/1), reliable calculations of σ require a very large number of avalanches. Nevertheless, direct measurement of σ from avalanches in the cultured networks at Δt = IEI_avg and IED = 200 μm revealed numbers that were remarkably close to the critical value of one: σ = 1.04 ± 0.19 for avalanches starting with a single electrode, and σ = 0.90 ± 0.19 for avalanches starting with more than one electrode (Fig. 7C) (∼90,000 avalanches measured; note that σ calculated from multiple ancestors will be underestimated because of collision effects). To verify that this finding was caused by the temporal pattern of activity in the cultured cortical networks, σ was estimated for 50 control sets of shuffled data whose LFP times were randomly jittered by amounts from 4 to 80 msec. After a jitter of ±4 msec, σ was significantly decreased to 0.7 (ANOVA; p < 0.05; Tukey test; n = 7 networks) and decreased further with increased jittering. These results show that the branching parameter was significantly different from what would be expected by chance.

Figure 7.

Network dynamics in cultured networks are characterized by a critical branching parameter of σ = 1, suggesting a state of optimal information transmission. A, Estimate of branching parameter σ from individual avalanches. σ = the ratio of descendant electrodes to ancestor electrodes. B, Sketch depicting the critical behavior of a branching process over time. If σ > 1, the size of the avalanche will grow over time, taking over the network (epilepsy), whereas at σ < 1, the avalanche will diminish quickly in size. Only at σ = 1 (critical) can avalanches persist at all scales. C, Values of σ for individual cultures (circles) based on single ancestor (left) or multiple ancestor (right) calculations. Boxes, Means ± SD. D, Phase plot of (σ, α) as a function of Δt. Note that the trajectory passes through critical point (1,-1.5) at the average population IEI of 4.2 msec. σ calculated from single ancestor avalanches. Circles, LFPs; squares, number of electrodes; ± SE.

Finally, both, the slope of the power law α and the branching parameter σ were calculated from different aspects of the neuronal avalanches (size and branching parameter over the initial duration) as a function of the freely chosen bin size Δt. This allowed the calculation of a trajectory in (σ, α)-space as a function of Δt. This trajectory (1) crossed through the critical point (σ, α) = (1, -1.5), and (2), this crossing happened at Δt ≈ 4 msec, which was close to the average IEI_avg = 4.2 msec calculated for the population of neuronal cultures (Fig. 7D, Fig. 4A at IED = 200 μm). This analysis independently confirmed our initial results for α using an IEI_avg that was optimized for individual networks. Together, these data strongly imply a critical branching process as the mechanism behind the power law distributions in cortical networks.

Information transmission and criticality

If activity in cortical networks obeys a critical branching process, what implications does this have for information transmission? To explore this issue, we studied the effects of changes in σ on information transmission in artificial neural networks (see Materials and Methods).

To model propagation of activity in the cortical networks we used a feedforward, rather than a recurrent, neural network architecture. This choice was motivated by the following results. The vast majority of runs lasted <20 msec, which was the absolute refractory period observed at each individual electrode, so most electrodes would be activated only once during a run. In fact, the percentage of times that a given electrode was reactivated in a given run was <4.6%. Of the few electrodes that were reactivated, there were at least five intervening frames (when binned at Δt = 4 msec: 5 × 4 msec ≤20 msec absolute refractory period) of no activity before the electrode was activated again. Thus, under no circumstances was an electrode immediately, or even four time bins later, reactivated by a recurrent connection. Under these conditions, the avalanches were propagating through the cortical network in a manner that was functionally equivalent to propagation in a feedforward network. Such feedforward architectures have been used recently by many investigators to model propagation of activity in cortical networks (Diesmann et al., 1999; Cateau and Fukai, 2001; van Rossum et al., 2002; Litvak et al., 2003; Reyes, 2003).

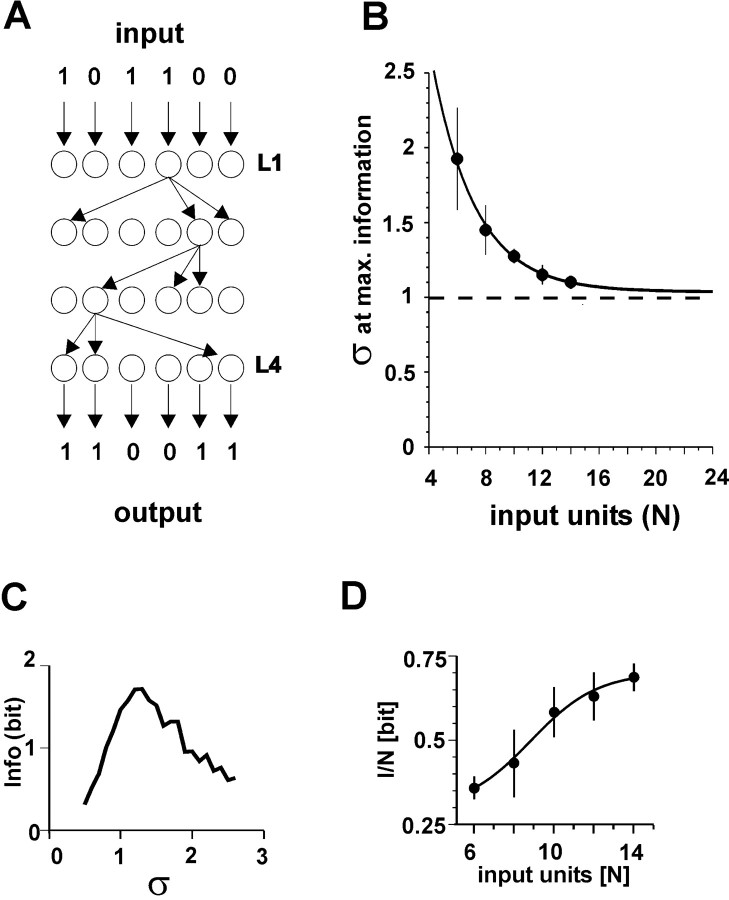
In the feedforward networks that we used, each binary processing unit was connected to C other units in the next layer, and each of these connections was given a probability p_i of successfully transmitting activity from one unit to another (Fig. 8A). Because the branching parameter σ is constrained by the sum of the probabilities (Harris, 1989; de Carvalho and Prado, 2000), it was possible to vary σ in the networks and measure its effect on information transmission (see Materials and Methods). Networks with two and three connections per unit as well as three and four layers were tried. Averaging over all networks, information transmission peaked when σ was tuned to σ = 1.1 ± 0.30, and this peak value asymptotically approached σ = 1.04 ± 0.10 as the number of input units in the network, N, increased (Fig. 8B,C) (R² = 0.99). It is also interesting to note that network performance, measured as the peak information transmitted per input unit, increased as the ratio of input units to connections (N/C) increased (Fig. 8D). This suggests that the critical state would maximize information transmission especially under conditions of sparse network connectivity, as is suggested to be the case in the neocortex (Braitenberg and Schüz, 1991). The fact that the critical state (σ = 1) maximized information transmission in these networks is consistent with an intuitive understanding of how a branching process would work in the context of a highly parallel network. If the network were subcritical, an input signal would attenuate, causing most output units to be inactive, thus leaving little evidence of the input. If the network were supercritical, any input signal would eventually lead to most output units being active, again leaving little information as to what the input was.

Figure 8.

Critical branching parameter of σ = 1 suggests a state of optimal information transmission in feedforward networks. A, Example of feedforward network with connections removed for clarity, except for one neuron/layer. B, Branching parameter σ that optimizes information transmission approaches 1 for increasing network sizes. Exponential fit for all networks tested (L = 3, 4; C = 2, 3; R² = 0.99). C, Transmitted information (Info) peaks near σ = 1 (one network with N = 8, L = 4, C = 3). D, Change in transmitted information with increase in total number of input units.

Discussion

Three distinct modes of correlated population activity have been experimentally identified in cortex in vivo: oscillations, synchrony, and waves (for review, see Singer and Gray, 1995; Engel et al., 2001; Ermentrout and Kleinfeld, 2001). These network modes have also been described in cortical networks in vitro [e.g., γ-oscillations (Plenz and Kitai, 1996), synchrony (Kamioka et al., 1996), and waves (Nakagami et al., 1996)].

In the present study, we identified a new mode of spontaneous activity in cortical networks from organotypic cultures and acute slices: the neuronal avalanche. Neuronal avalanches were characterized by three distinct findings: (1) Propagation of synchronized LFP activity was described by a power law. (2) The slope of this power law, as well as the branching parameter, indicate that the mechanism underlying these avalanches is a critical branching process. (3) Our network simulations and pharmacological experiments suggest that a critical branching process optimizes information transmission while preserving stability in cortical networks.

The analysis presented here focuses exclusively on the propagation of sharp (<20 msec) negative LFP peaks. Such LFPs peaks are commonly observed in slice cultures (Jimbo and Robinson, 2000) or evoked extracellular potentials in acute slices. Current source density analysis in combination with optical recordings has demonstrated that sharp, negative LFPs peaks are indicative of synchronized population spikes (Plenz and Aertsen, 1993). Similarly, cortical LFPs in vivo are closely correlated with single spike cross-correlations of local neuronal populations (Arieli, 1992). Thus, negative LFP peaks in the present study might represent synchronized action potentials from local neuronal populations. This is supported by computer simulations of the neuron-electrode junction of planar microelectrode arrays, which demonstrate that sharp, negative LFPs originate from synchronized action potentials from neurons within the vicinity of the electrode (Bove et al., 1996). Therefore, our results might be specifically applicable to the propagation of synchronized action potentials in the form of neuronal avalanches through the network, and the power law of -3/2 provides the statistical framework for transmitting information through the cortical network in form of locally synchronized action potential volleys.

Other authors who have studied propagation of synchronized action potentials in neural networks have concluded that precise patterns of activity could travel through several synaptic stages without much attenuation (Abeles, 1992; Aertsen et al., 1996; Reyes, 2003). The concept of a critical branching process does not necessarily conflict with this view, but does place constraints on the distance that activity could propagate when it is traveling in avalanche form. Although it is natural to think that a critical branching parameter of 1 will produce a sequence of neural activity in which one neuron activates only one other neuron at every time step, this is not the case. Because the branching parameter reflects a statistical average, it gives only the expected number of descendants after many branching events, not the exact number at every event. Thus, a single neuron might activate more than one other neuron on some occasions, whereas on others it may activate none. In fact, the most common outcome in the critical state will be that no other neurons are activated. The resulting events generated by this system will contain many short avalanches, some medium-sized avalanches, and very few large avalanches.

Neuronal avalanches in the context of self-organized criticality

The spontaneous activity observed in the present study remarkably fulfills several requirements of physical theory developed to describe avalanche propagation. Tremendous attention in physics has been given recently to the concept of self-organized criticality, a phenomenon observed in sandpile models for avalanches (Paczuski et al., 1996), earthquakes (Gutenberg and Richter, 1956), and forest fires (Malamud et al., 1998). In brief, this theory states that many systems of interconnected, nonlinear elements evolve over time into a critical state in which avalanche or event sizes are scale-free and can be characterized by a power law. This process of evolution takes place without any external instructive signal; it is an emergent property of the system. In addition, many of these systems are modeled as branching processes.

The neuronal activity discussed here has numerous points of contact with this body of theory: (1) All cortical networks displayed power law distributions of avalanche sizes. (2) The cortical networks in the cultures arrived at this state without any external instructive signal. (3) The slope of the power law for avalanche sizes and for avalanche life times, as well as the experimentally obtained values of σ all indicate that the avalanches can be accurately modeled as a critical branching process. For these reasons, the activity observed in the cortical networks should be considered as neuronal avalanches.

Neuronal avalanches as a new mode of network activity

Although some power law statistics have been observed before in the temporal domain of neuronal activity [e.g., time series of ion channel fluctuations (Toib et al., 1998), transmitter secretion (Lowen et al., 1997), interevent times of neuronal bursts (Segev et al., 2002), and EEG time series in humans (Linkenkaer-Hansen et al., 2001; Worrell et al., 2002)] our results go beyond the phenomenological description of a power law only. We provide two independent approaches to understanding neuronal propagation in cortical networks (unique exponent of -3/2 and critical branching parameter) that lead to a statistical description of neuronal propagation that can be viewed in the framework of information processing. To our knowledge, no previous evidence has been presented for the existence of a critical branching process operating in the spatiotemporal dynamics of a living neural network.

The power law in the present study basically says that the number of avalanches observed in the data scales with the size of the avalanche, raised to the -1.5 power. This allows for a prediction of very large avalanches. They are a natural consequence of the local rule for optimized propagation, and are expected to occur even in normal (i.e., nonepileptic) networks, and are not particularly rare. For example, in a network with ∼10,000 avalanches/hr that engage just one electrode, at least 21 avalanches will occur every hour that will encompass exactly all 60 electrodes. Thus, on average, activity on every electrode will be correlated with every other electrode in the network at least once every 3 min.

The neuronal avalanches described here are profoundly different from previously observed modes of network operation. As shown by the correlograms, activity in the cortical networks was not periodic or oscillatory within the duration of maximal avalanche lifetimes. In addition, the contiguity index revealed that activity at one electrode most often skipped over the nearest neighbors, indicating that propagation was not wave-like. Finally, although the spontaneous activity did display notable synchrony at relatively long time scales, the avalanches that we describe here actually occurred within such synchronous epochs at a much shorter time scale (<100 msec). At this shorter time scale, the avalanches themselves did not display synchrony, regardless of the threshold level, IED, or number of electrodes used to obtain the data. These are compelling reasons for neuronal avalanches to be considered a new mode of network activity.

Features of the critical state

It should be noted that the branching parameter used to characterize the critical state is a statistical measure and does not say anything about the specific biological processes that could produce a particular value of σ. There are several mechanisms operative in cortical networks that are likely to influence σ: the degree of fan-in or fan-out of excitatory connections, the degree of fan-in or fan-out of inhibitory connections, the ratio of inhibitory synaptic drive to excitatory drive, the timing of inhibitory responses relative to excitatory responses, and the amount of adaptation seen in both excitatory and inhibitory neurons, to name a few. To clearly distinguish the specific role each of these mechanisms would play in the branching process will be the subject of future experiments.

Previous theoretical work has discussed the importance of a balance between excitation and inhibition in network dynamics (Van Vreeswijk and Sompolinsky, 1996; Shadlen and Newsome, 1998). This balance has been implicated in proportional amplification in cortical networks (Douglas et al., 1995) as well as in the maintenance of cortical up states (Shu et al., 2003). Here, we extend the idea of balance by using the branching parameter, a concept that allows us to explore information transmission at the network level. Although a branching parameter well below unity would confer stability on a network, the simulations suggest that this stability would come at the rather severe price of greatly reduced information transmission. In contrast, a branching parameter hovering near unity would optimize information transmission, but at the risk of losing stability every time the network became supercritical. Although these neural network simulations are vastly oversimplified representations of the dynamics that occur in cortical networks in vivo, they may nonetheless offer some insight as to why the cerebral cortex is so often at risk for developing epilepsy. In fact, our experimental results demonstrate that removal of inhibition to increase propagation in the neuronal network to obtain a power law with slope α > -1.5 results in epileptic activity. The competing demands of stability and information transmission may both be satisfied in a network whose branching parameter is at or slightly below the critical value of 1. Thus, calculating the power law exponent and/or branching parameter might offer quantitative means to evaluate the efficacy of cortical networks to transmit information.