Self-Organizing Neural Integrator Predicts Interval Times through Climbing Activity

Abstract

Mammals can reliably predict the time of occurrence of an expected event after a predictive stimulus. Climbing activity is a prominent profile of neural activity observed in prefrontal cortex and other brain areas that is related to the anticipation of forthcoming events. Climbing activity might span intervals from hundreds of milliseconds to tens of seconds and has a number of properties that make it a plausible candidate for representing interval time. A biophysical model is presented that produces climbing, temporal integrator-like activity with variable slopes as observed empirically, through a single-cell positive feedback loop between firing rate, spike-driven Ca²⁺ influx, and Ca²⁺-activated inward currents. It is shown that the fine adjustment of this feedback loop might emerge in a self-organizing manner if the cell can use the variance in intracellular Ca²⁺ fluctuations as a learning signal. This self-organizing process is based on the present observation that the variance of the intracellular Ca²⁺ concentration and the variance of the neural firing rate and of activity-dependent conductances reach a maximum as the biophysical parameters of a cell approach a configuration required for temporal integration. Thus, specific mechanisms are proposed for (1) how neurons might represent interval times of variable length and (2) how neurons could acquire the biophysical properties that enable them to work as timers.

Introduction

The ability to predict forthcoming events on the basis of observed environmental stimuli is essential for goal-directed behavior and planning. Mammals and birds are able to predict not only events to happen but also their time of occurrence relative to the time at which a predicting stimulus appears (Gibbon and Church, 1990; Gallistel and Gibbon, 2000). This ability is fundamental, because behavioral preparation and planning are most useful if actions are time-locked to the anticipated events. However, relatively little is known about the physiological basis for extracting the precise temporal structure within predictive event relationships.

The prefrontal cortex is a brain area involved in working memory, prediction, planning, and also time estimation in humans (Lalonde and Hannequin, 1999; Rainer et al., 1999; Fuster, 2000; Miller and Cohen, 2001; Goldman-Rakic, 2002). In working memory tasks, a cue is briefly presented followed by a choice situation, after a delay of 1-2 sec in which the correct response depends on the previously presented cue, which therefore has to be kept in (working) memory during the delay. In vivo electrophysiological recordings from prefrontal neurons during working memory tasks have shown that activity in prefrontal cortex is often anticipatory (Niki and Watanabe, 1979; Quintana and Fuster, 1999; Rainer et al., 1999; Romo et al., 1999). Many prefrontal neurons exhibit sustained activity during the delay periods of these tasks that is related to the expected target stimulus, not to the presented cue. This predictive activity often takes a particular form: it slowly climbs during the delay and reaches a maximum almost coincident with presentation of the choice stimuli. The slope of this climbing activity is often surprisingly linear and might span intervals from hundreds of milliseconds (Rainer et al., 1999) to tens of seconds (Quintana and Fuster, 1999). Thus, slowly climbing “anticipatory” activity could linearly encode interval time. At any point in time, the instantaneous firing rate contains information about the relative amount of time that will pass until the choice situation occurs. In favor of this interpretation, Komura et al. (2001) found in recordings from thalamic neurons that the slope of climbing activity is adjusted within a few trials to the length of the delay interval between predicting and rewarding stimuli.

It remains, however, unclear how climbing activity might be generated, both in terms of the required system dynamics and with respect to the biophysical mechanisms. Moreover, it is unclear how a neural system might organize itself into a biophysical configuration that can give rise to climbing activity and how the slope of this activity might be adjusted to observed time intervals as found by Komura et al. (2001). Here I show (1) that climbing activity may be generated through a dynamical phenomenon known as a “ghost” of a line attractor; (2) that line attractor ghosts could be achieved on the single-cell level through interactions between firing rate output and Ca²⁺-gated ion channels that have been found in pyramidal neurons; and (3) that single-cell line attractors might emerge in a self-organizing manner using solely fluctuations in intracellular Ca²⁺ or other molecules.

Materials and Methods

Neuron model. All computations were performed using a spiking leaky-integrate-and-fire (LIF) neuron model described by the following membrane potential equation:

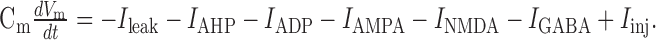1

A spike was elicited whenever V_m > V_th, after which the membrane potential was reset to V_reset = E_leak. A refractory period was ensured by the afterhyperpolarizing current:

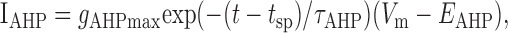2

where g_AHPmax is a constant maximum conductance strength; τ_AHP is the decay time constant (5 msec); E_AHP is the reversal potential; and t_sp is the time of the last spike (i.e., each spike brought g_AHP to its maximum value from where it decayed exponentially). I_ADP modeled a Ca²⁺-dependent afterdepolarizing current, activating on Ca²⁺ influx, that has been described in pyramidal neurons (Andrade, 1991; Haj-Dahmane and Andrade, 1997, 1998, 1999). It was given by the following equations:

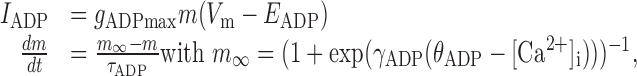3

where m is the Ca²⁺-dependent activation gate. To keep the model simple, an explicit implementation of Ca²⁺ conductances was omitted, and Ca²⁺ influx was simply triggered by spiking according to the double-exponential function:

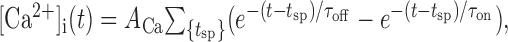4

where the sum is over all spike times t_sp.

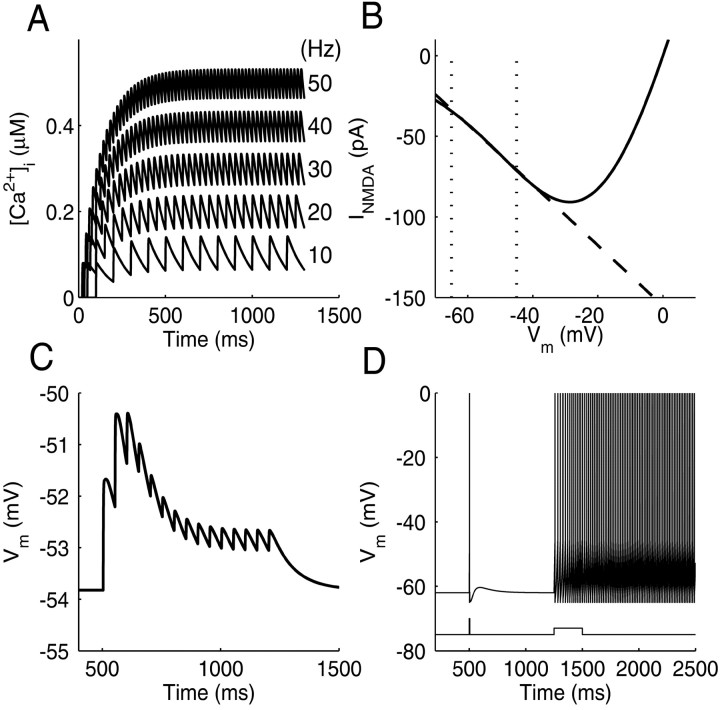
With the parameter settings used here for A_Ca and τ_on/τ_off (Table 1), this yielded a spike frequency-dependent Ca²⁺ influx comparable with the data by Helmchen et al. (1996) (Fig. 1 A). Thus, this simple equation is a phenomenologically adequate description of the Ca²⁺ influx triggered by series of spikes.

Table 1.

Range of model parameters for line attractor configurations

Single-neuron parameters	Minimum/maximum value	Synaptic parameters	Minimum/maximum value
Cm	0.8/1.13	gAMPAmax(recur)	4/5.89
gleak	0.012/0.076	gAMPAmax(backgr)	2.8 × 10−6/2.1 × 10−3
Eleak	−68/−65	EAMPA	0
Vth	−48/−45	τAMPA_on	0.2
		τAMPA_off	1
gAHPmax	2/6	USE	0.2/0.5
τAHP	5	τrec	800
EAHP	Eleak	τfac	800
gADPmax	0.078/0.2	gNMDAmax(recur)	0.05/0.29
EADP	35a	gNMDAmax(backgr)	1.1 × 10−5/6.4 × 10−5
τADP	35a	ENMDA	0
γADP	3.35/5.96	τNMDA_on	2.3
θADP	0.68/1.02	τNMDA_off	94
ACa	0.08/0.133	USE	0.2/0.5
τCa_on	1	τrec	800
τCa_off	120	τfac	800
τx	10000	gGABAmax(recur)	0.2/5.6
τy	10	gGABAmax(backgr)	6.2 × 10−5/1.7 × 10−4
		EGABA	Eleak-5
		τGABA_on	2
		τGABA_off	20
		USE	0.3/0.5
		τrec	800
		τfac	800

Units: capacitance (microfarads per square centimeter), conductances (millisiemens per square centimeter), potentials (millivolts), time constants (milliseconds). A_Ca and all maximum synaptic conductances were multiplied with a constant τ_on × τ_off/(τ_off − τ_on). Note that amplitudes of background (backgr) synaptic inputs are much smaller than those of recurrent (recur) inputs, because they (1) were much higher in frequency and (2) did not involve short-term depression. Note also that although τ_rec and τ_fac are quite slow, they do not contribute to the slowness of climbing activity, because the recursive dynamics defined by Equation 6 reaches its steady state within just a couple of EPSPs; hence, substituting Equation 6 by its steady-state form Equation 9 does not significantly affect the slope of climbing activity (confirmed by simulations).

^a Values are taken from Haj-Dahmane and Andrade (1999).

Figure 1.

Basic model properties. A, Accumulation of internal Ca²⁺ in the model cell at different (output) spiking rates. The average level of [Ca²⁺]_i increases linearly with spike rate, as found by Helmchen et al. (1996). B, I_NMDA as a function of voltage (solid line). Between E_leak (-65 mV) and firing threshold (less than -45 mV), I_NMDA is well described by a linear fit (dashed line). C, Train of EPSPs elicited by presynaptic stimulation at 20 Hz. EPSP amplitude decreases over time as described by the model of Tsodyks and Markram (1997) and Markram et al. (1998). D, Response of the model cell to brief (5 msec) or longer-lasting (250 msec) current injections. A brief current pulse elicits a single spike followed by an after depolarizing potential caused by g_ADP. Longer current pulses drive the cell in to a persistent spiking up state maintained by Ca²⁺-activated g_ADP. (Note that spike generation is not explicitly modeled in an LIF-model, and spikes were therefore added to the figure whenever V_m crossed V_th.)

Synaptic currents (I_AMPA, I_NMDA, and I_GABA) were given by double-exponential functions, multiplied by a synaptic short-term depression/facilitation factor, a(t_sp). I_NMDA in addition contained a voltage-dependent Mg²⁺ gate, s(V_m) (Jahr and Stevens, 1990):

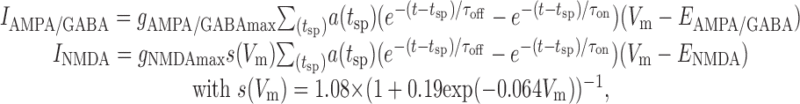5

where τ_on and τ_off are the onset and offset time constants of the conductances. It is important to note that synaptic input was not required for producing climbing activity, which in the present model was generated through a single-neuron feedback loop (consistent with recent data by Egorov et al., 2002). Nevertheless, it was included to simulate the kind of input a single neuron would receive in a cortical environment from a surrounding network and to provide a source of noise required for self-organized adjustment of parameters (see Results). Synaptic input had both a structured component related (phase-locked) to the spike times of the neuron and a Poisson-like unstructured component. The first component represented recurrent feedback triggered by spiking of the neuron or input attributable to synchronized and phase-locked oscillatory activity as it has been observed during delay periods in working memory tasks (Funahashi and Inoue, 2000; Constantinidis et al., 2001, 2002; Pesaran et al., 2002). This component included synaptic short-term depression as described below. The second component represented more asynchronous background activity of the surrounding network and other cortical areas, unrelated to spike times of the neuron. It was modeled for AMPA-, NMDA-, and GABA_A-like input by Poisson processes with rates of 20,000–40,000 Hz (representing, e.g., 4000 presynaptic neurons firing at 5–10 Hz on average). In the noise-free cases (see Fig. 3A–D), this component was substituted by constant synaptic conductances with the same mean as the Poisson-like input.

Figure 3.

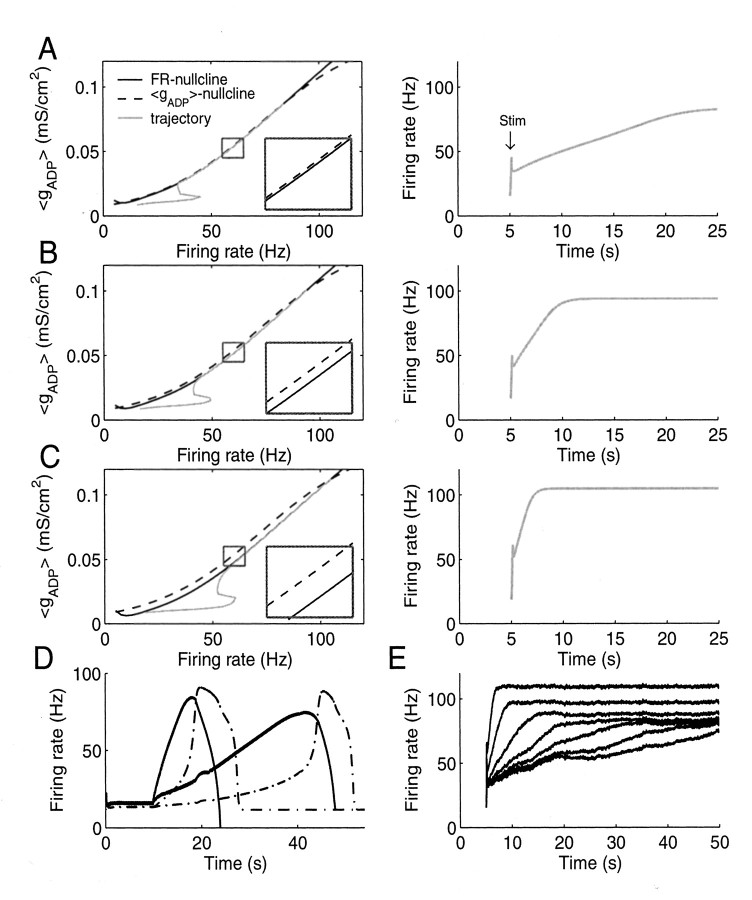
Climbing activity in the LIF model based on the positive feedback loop illustrated in Figure 2. A, Left, State space spanned by the instantaneous FR of the LIF neuron and the g_ADP conductance averaged across interspike intervals (〈g_ADP〉). The 〈g_ADP〉 nullcline (dashed) is the curve that gives for each firing rate the level of 〈g_ADP〉 generated at that rate. The FR nullcline (black, solid) gives for each firing rate the amount of 〈g_ADP〉 that would be required to maintain exactly that rate. Wherever these curves intersect or overlap, the neuron receives exactly what it needs to maintain the corresponding firing rate. Here the FR nullcline is just slightly below the 〈g_ADP〉 nullcline from ∼10 to 75 Hz, such that the neuron over this range receives slightly more ADP current than would be needed to maintain any of these rates. Inset, Magnified area of the graph within the box, to better visualize the distance between nullclines. The gray line is the trajectory that the system takes through 〈g_ADP〉/FR space when briefly excited by afferent inputs. The small bump in the trajectory is caused by the brief stimulus. Right, Time graph corresponding to the left side. After a brief stimulation at 5 sec (Stim), the instantaneous firing rate slowly climbs over tens of seconds. B, C, Same as A for configurations in which the FR nullcline is shifted further downward (left) such that climbing activity rises faster (right). D, Climbing activity in an LIF neuron (solid traces) coupled to a response neuron (dashed traces) from which it receives feedback inhibition. Traces for two different synaptic input weights producing very slow or faster climbing activity are shown. Note that the system was adjusted to maintain a basal firing rate at ∼10–20 Hz, as observed in thalamus (Komura et al., 2001) and some prefrontal cortex neurons (Quintana and Fuster, 1999; Rainer et al., 1999), from which climbing activity smoothly emerges at the time of cue presentation. The slight parallel dislocation of the nullclines such that the line attractor vanishes and the system starts climbing was achieved in this case by injecting a small depolarizing current (or by stimulating excitatory external synapses) with trial onset. In a working memory or prediction task, such a stimulation might originate from neurons with plateau-like delay activity that are turned on by the cue stimulus (Fuster, 1973, 2000; Funahashi et al., 1989; Durstewitz et al., 2000). E, Climbing activity is still preserved in the presence of noise from background synaptic input.

In most model simulations and for derivation of the nullclines (see Appendix, Derivation of nullclines), the NMDA current was linearized by fitting a line to the relevant portion of I_NMDA between V_reset and V_th. As shown in Figure 1 B, this describes I_NMDA reasonably well below the firing threshold (approximately -45 mV), and simulation results with the linear version of I_NMDA and the one given in Equation 5 were in close agreement.

Synaptic short-term depression and facilitation were included in the model according to formulas and parameters suggested by Tsodyks and Markram (1997) (Markram et al., 1998; Tsodyks et al., 2000). In particular, synaptic short-term dynamics were determined by the available synaptic efficacy (R) and a utilization variable (u), which followed the recursive relationship (for details, see Markram et al., 1998):

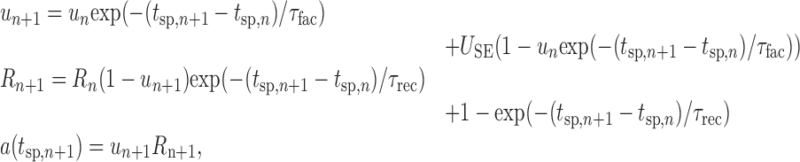6

where a(t_sp) is the amplitude of the synaptic response (as used in Eq. 5 above) at presynaptic spike time t_sp; U_SE is the resting relative amount of synaptic efficacy used per synaptic pulse; and τ_rec and τ_fac are the recovery (from depression) and facilitation time constants for synaptic efficacy. Figure 1C illustrates EPSPs resulting from these equations during trains of synaptic stimulation. With synaptic short-term depression, a rise in the presynaptic firing rate causes a transient of synaptic current, which falls off over time according to the equations given above (Abbott et al., 1997; Tsodyks and Markram, 1997). In part, this mechanism was included to demonstrate that smooth climbing activity can be achieved even in the presence of such transients.

All model parameters were constrained within physiologically reasonable ranges (Table 1). The whole system of equations was implemented both as C-code and in MATLAB (The MathWorks, Inc., Natick, MA) and integrated numerically using a fourth-order Runge–Kutta method or one of the MATLAB ordinary differential equation solvers (mainly ode23s, an implicit solver based on the Rosenbrock method; see Press et al., 1992) using the inbuilt event detection function for spike detection. Relative (error) tolerance was set to 10 ^-6 or 10 ^-5 (using smaller relative errors did not lead to notable differences).

Figure 1 D shows the response of the single model neuron (without synaptic currents) to current pulses of 5 and 250 msec. A brief current pulse elicits a single spike followed by an afterdepolarizing potential attributable to I_ADP. A longer current pulse triggers enough spikes to load the cell with Ca²⁺ sufficient to move the cell into a persistent spiking mode maintained by I_ADP, in accordance with empirical data (Andrade, 1991; Haj-Dahmane and Andrade, 1998; Egorov et al., 2002).

Construction of line attractors. Many of the figures presented here show two-dimensional “state spaces” of the above system, spanned by the instantaneous firing rate (FR) of the LIF model and by the interspike interval-averaged ADP conductance (denoted 〈g_ADP〉). Linearization of the NMDA current allowed writing of self-consistent equations for the FR and 〈g_ADP〉 nullclines of these state spaces. To find line attractor configurations as required for climbing activity, the distance between these nullclines was minimized over some range of firing rates through optimization methods to yield an approximately continuous line of fixed points. The details for derivation of nullclines and optimization are given in Appendix, Derivation of nullclines.

Tracking changes in intracellular Ca²⁺levels. For self-organized adaptation of the nullclines of the system, variables were introduced that represent fluctuations in intracellular Ca²⁺ levels. First, intracellular Ca²⁺ was low-pass-filtered by:

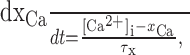7

where τ_x is in the range of seconds (usually 10 sec), and x_Ca approaches the average Ca²⁺ level in the cell, filtering out faster variations (x_Ca might represent the amount of some Ca²⁺-buffering protein with a slow time constant bound to Ca²⁺). Now a dynamical variable was defined that followed the squared temporal derivative of x_Ca:

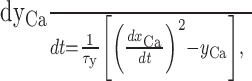8

which approached the variance in intracellular Ca²⁺ levels (τ_y = 10 msec). Such a quantity might be computed through intracellular molecular networks. The temporal derivative of intracellular Ca²⁺ or a related variable might be encoded, for example, by Ca²⁺-dependent proteins such as calmodulin (CaM) (Franks et al., 2001). In turn, any downstream protein, such as calmodulin-dependent protein kinase II (Kubota and Bower, 2001), that requires cooperative binding or whose activation requires some form of cooperativity, such that its activated steady state satisfies an equation of the general form [X] = [CaM] × [CaM] × [Y] might implement a multiplicative operation as assumed in Equation 8 (also see Discussion).

Results

The first part of Results discusses a single-neuron feedback loop for generating climbing activity and predicting interval times. The second part examines how the system might self-organize into a biophysical configuration required for neural integration (climbing activity).

Biophysical model for climbing activity

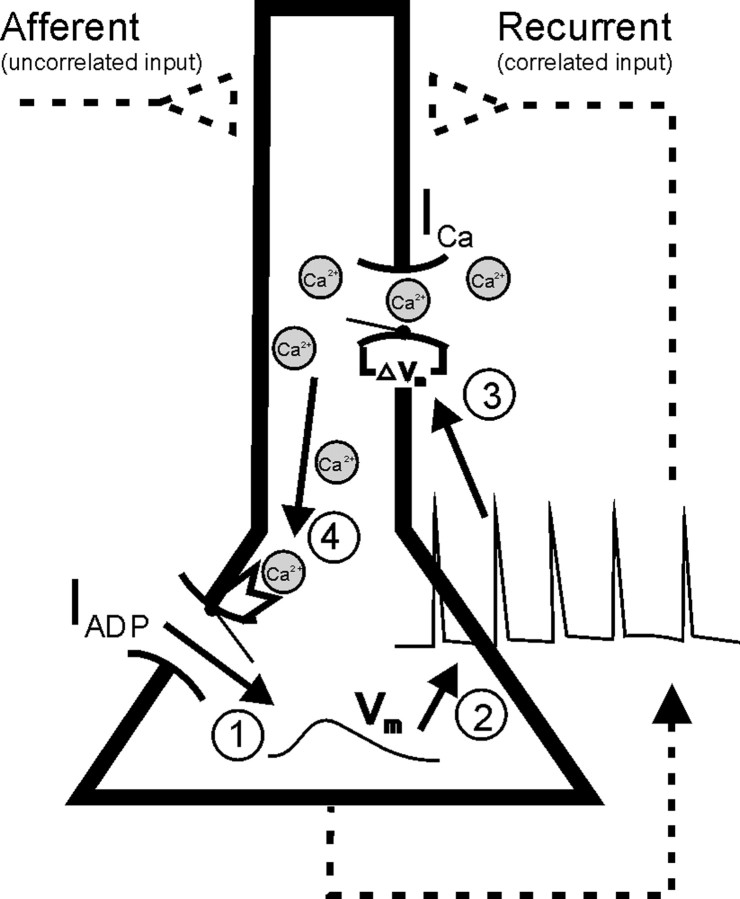
Figure 2 depicts a single-neuron feedback loop that could give rise to climbing activity with variable slopes. This system was modeled by a spiking LIF neuron that includes a Ca²⁺-dependent afterdepolarizing (inward) current (I_ADP) as it has been described in prefrontal and entorhinal pyramidal cells (Andrade, 1991; Haj-Dahmane and Andrade, 1997, 1998, 1999; Egorov et al., 2002). In the presence of ACh, I_ADP in prefrontal neurons in vitro can sustain spiking over many minutes without additional synaptic or current input (Andrade, 1991; Haj-Dahmane and Andrade, 1998; Egorov et al., 2002) (see Fig. 1D). In addition, although not necessary for generating climbing activity, AMPA-, NMDA-, and GABA_A-like synaptic input was included. Synaptic input simulated a cortical network environment for the single neuron by providing (1) recurrent excitation and inhibition (including short-term depression) phase-locked to the spike times of the neuron, as it will occur during oscillatory and synchronized network activity (Funahashi and Inoue, 2000; Constantinidis et al., 2001, 2002; Pesaran et al., 2002), and (2) uncorrelated (Poisson-like) background activity.

Figure 2.

Positive feedback loop generating climbing activity. Membrane depolarization (1) triggers spiking (2), which induces opening of high-voltage-activated Ca²⁺ channels (I_Ca) via dendritic back-propagating spikes (3) leading to Ca²⁺ influx. Inflowing Ca²⁺ in turn activates Ca²⁺-dependent cation currents (I_ADP; 4), which cause further membrane depolarization (1) and spiking. Albeit not necessary for generating climbing activity (Egorov et al., 2002), the model also included recurrent and feedforward synapses as indicated by dashed lines.

The system can produce climbing activity through a finely tuned positive feedback loop between spiking-mediated Ca²⁺ influx and the Ca²⁺-activated I_ADP (Fig. 2). The intracellular Ca²⁺ level rises monotonically with output firing frequency (Fig. 1A) as observed in vitro (Helmchen et al., 1996). Intracellular Ca²⁺, in turn, activates I_ADP, which provides additional depolarizing current and hence increases the firing rate. Figure 3 demonstrates how this feedback loop produces climbing activity. The black solid curves in Figure 3A–C (left, the FR nullcline) gives for each instantaneous firing rate, defined here as the reverse of the current interspike interval of the LIF neuron, the average amount of ADP conductance (g_ADP) that would be required to maintain exactly that rate, where the average is taken across single interspike intervals and denoted 〈g_ADP〉. Conversely, the dashed curve (the 〈g_ADP〉 nullcline) gives for each firing rate the actual amount of average g_ADP produced at that rate. If these two curves precisely overlap for a larger range of firing rates, then, within that range, for any firing rate precisely the amount of 〈g_ADP〉 is produced that is required to maintain that rate; hence the cell has a continuum of (stable) fixed points. This is called a line attractor.

In Figure 3A (left) the FR nullcline is actually shifted from its line attractor position downward just a tiny bit (see Fig. 3A, inset). Thus, for each firing rate, the neuron receives slightly more depolarizing current through g_ADP than would be needed to maintain the current rate; hence the firing rate increases over time. Because the difference in current provided and the one required is very small, however, the firing rate increases very slowly after a brief stimulus (Fig. 3A, right), over tens of seconds (as observed by Quintana and Fuster, 1999), approximately two orders of magnitude slower than the slowest intrinsic time constant determining temporal dynamics of the LIF neuron (∼120 msec). In fact, the increase in firing rate could (ideally) be made arbitrarily slow as the distance between the FR and the 〈g_ADP〉 nullcline is made arbitrarily small (a phenomenon known in nonlinear dynamics as the ghost of a line attractor). The gray line in Figure 3A (left) shows how the firing rate and 〈g_ADP〉 change together over time; i.e., it shows the trajectory of the system in the 〈g_ADP〉/FR state space corresponding to the time graph in Figure 3A (right). As the FR nullcline is further shifted downward (Fig. 3B,C, left), parallel to the 〈g_ADP〉 nullcline, the slope of climbing activity becomes steeper and steeper (Fig. 3B,C, right). In Figure 3A–C, the parallel shift was achieved by increasing the strength of recurrent excitatory synapses, as might be accomplished through synaptic learning (see Discussion), but other parameter changes that provide the neuron with more depolarizing input (which is relatively constant across rates) or increase its general excitability will work as well. Thus, by shifting the FR nullcline in parallel to the 〈g_ADP〉 nullcline through manipulation of synaptic weights, the slope of climbing activity can be varied within an ideally almost unlimited range, largely independent of the intrinsic time constants of the system.

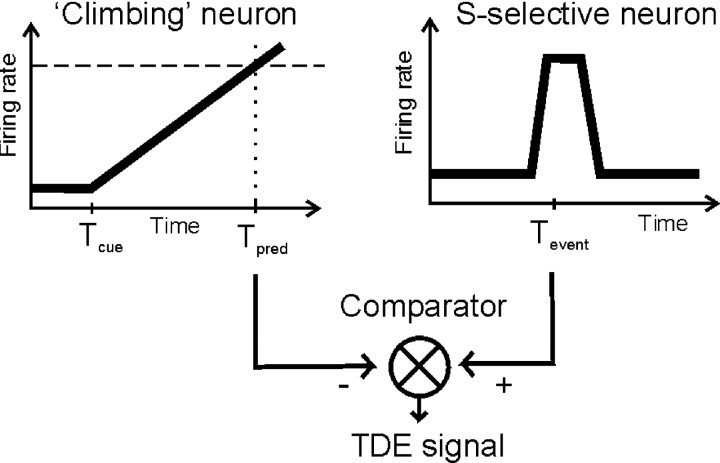
Figure 3D illustrates how this system could predict the time of occurrence of an expected stimulus and could initiate a response aligned to the predicted time. Responses could be initiated through neurons postsynaptic to the climbing neuron that become active whenever the rate of the climbing neuron crosses a certain threshold (e.g., 70 Hz; Hanes et al., 1998; Komura et al., 2001). The response unit (Fig. 3D, dashed curves) was modeled by LIF equations including the same mechanisms as for the climbing neuron (solid curves). It receives excitatory input from the climbing neuron and returns inhibition to it via facilitatory synapses (Markram et al., 1998). The parameters were adjusted such that the response unit experiences a sharp rise in firing rate when the climbing neurons exceed ∼70 Hz (through a saddle node bifurcation mechanism similar to the one causing spike initiation in cortical neurons; Wilson, 1999), and it shuts down activity of the climbing system once fully activated, as observed in vivo (Hanes et al., 1998; Komura et al., 2001). Such a response unit could represent the readout of the climbing unit by signaling the expected time of occurrence. This signal could also be used to compute the temporal difference error between the predicted time of occurrence and the actual time of occurrence, which might promote synaptic learning required to adjust the slope of climbing activity to the actual time of occurrence (see Fig. 8).

Figure 8.

Hypothetical model for using a temporal difference error (TDE) to drive adjustment of the slope of climbing activity. Climbing activity via response neurons (see Fig. 3D) inhibits a population of comparator neurons at the predicted time of occurrence T_pred. Neurons coding for the to-be-predicted stimulus event (at time T_event) in contrast excite the comparator neurons. Thus, if T_pred<T_event, comparator neurons will discharge below baseline, where as they will fire above baseline if T_event < T_pred. Only if the predicted and the actual times of occurrence coincide, the firing rate of the comparator neurons will not change, because incoming signals cancel each other.

Figure 3E demonstrates that climbing activity still works in the presence of moderate noise, induced by Poisson-like synaptic background activity, as necessary for the self-organization process discussed next.

Self-organized adjustment of 〈g_ADP〉/FR space geometry for climbing activity

In the preceding section, it was shown how a cell could represent different interval times by adjusting the slope of climbing activity through parallel shifts of the FR and 〈g_ADP〉 nullclines. How, though, could a cell learn to become a timer, assuming the nullclines are not parallel to begin with? It would have to rotate both or one of its nullclines into a parallel position, because this is the precondition for producing linearly climbing activity. Note that this is a more general question applying to all models based on line attractors (Seung, 1996; Seung et al., 2000).

An answer to this question might be derived from the observation that the rotation angle between the 〈g_ADP〉 and FR nullclines will affect how the system behaves in the vicinity of its steady states (stable fixed points). Suppose the FR nullcline and the 〈g_ADP〉 nullcline are not parallel but intersect at some point (as in Fig. 4A), which therefore is a fixed point. First note that the firing rate of a neuron could only be stable if the FR nullcline were steeper (or at least not flatter) than the 〈g_ADP〉 nullcline at the intersection, because otherwise the LIF neuron would receive less g_ADP-mediated depolarization than required for firing rates slightly lower than within the fixed point and more than required for firing rates slightly higher; hence the firing rate would continue to decrease or to increase if slightly perturbed into the negative or positive direction.

Figure 4.

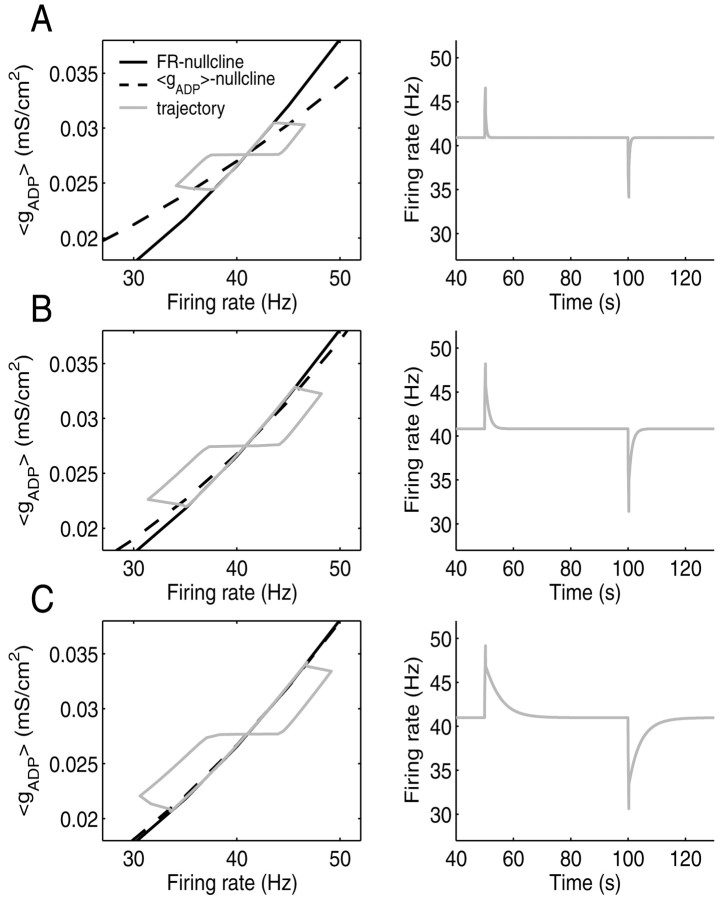
Length and return time of trajectories caused by perturbations increase as the angle between the FR and 〈g_ADP〉 nullcline decreases. A, Left, State space with FR nullcline (black, solid), 〈g_ADP〉 nullcline (dashed), and a trajectory (gray, solid) around the stable fixed point caused by 300 msec depolarizing and hyperpolarizing current pulses (for briefer current steps, the perturbation in instantaneous firing rate would also depend very much on the relative phase of the interspike interval at which the step arrives). Right, Time graph of the instantaneous firing rate corresponding to the trajectory on the left. B,C, Same as A for decreasing angles between nullclines. The closer the system is to a line attractor configuration, the farther perturbations take the system away from the fixed point (left), and the slower the decay back to the steady state firing rate (right).

Now suppose the cell has settled into a stable firing rate from which it is perturbed with current steps as illustrated in Figure 4A–C. Figure 4A–C (left) depicts the FR nullcline (black, solid) together with three different 〈g_ADP〉 nullclines (dashed) intersecting the FR nullcline at different angles. Superimposed are the trajectories (gray, solid) for the three different parameter configurations corresponding to the three 〈g_ADP〉 nullclines, caused by 300 msec depolarizing or hyperpolarizing current steps that perturb the system to the right (increasing firing rate) or to the left (decreasing firing rate), respectively. Notice that with decreasing angles between the nullclines, same-sized current steps take the state of the system further and further away from the steady state. That is, the smaller the mismatch between the 〈g_ADP〉 level required to maintain some rate and the actual amount produced at that rate in the vicinity of the steady state, the larger the conjoint changes in firing rate and 〈g_ADP〉 caused by perturbations. Moreover, the smaller this mismatch, the longer it takes for the firing rate to return to its steady state, as shown in Figure 4A–C (right). Hence, successive perturbations would be integrated more effectively, taking the system potentially even further away from its steady state. Thus, the total length and return time of trajectories in 〈g_ADP〉/FR space caused by perturbations contain information about the alignment of the nullclines, with a maximum being reached when the nullclines are perfectly aligned.

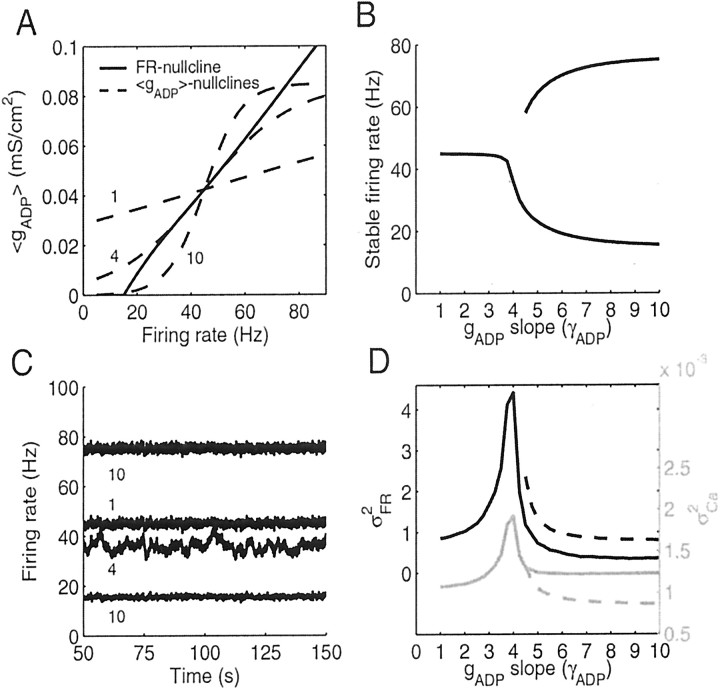
How would a neuron know about the length and return time of its trajectories? In a noisy neural environment, this information is encoded in fluctuations of the firing rate and the ADP conductance caused by the noise. Noisy background synaptic input will cause the system to permanently fluctuate around its stable fixed points where the size and time course of the fluctuations will depend on the alignment of the nullclines. This is shown in Figure 5. In Figure 5A, three representative 〈g_ADP〉 nullclines (dashed) with different slopes (rotation angles) are shown together with the FR nullcline (solid). The slope of the 〈g_ADP〉 nullcline was varied by changing the slope γ_ADP of the Boltzmann function (Eq. 3) that determines the Ca²⁺ dependence of g_ADP. The three cases shown in Figure 5A exemplify a 〈g_ADP〉 nullcline with a very flat slope (γ_ADP = 1, yielding a single steady state), the 〈g_ADP〉 nullcline aligned closest to the FR nullcline over the range of 30–60 Hz (γ_ADP ∼ 4, line attractor), and a 〈g_ADP〉 nullcline steeper than the FR nullcline at the center fixed point (γ_ADP = 10), where the center fixed point therefore is unstable, as explained above, and is replaced by two new stable fixed points given by the lower and upper intersections of the nullclines (i.e., the neuron becomes bistable). Figure 5B shows for a range of different g_ADP slopes (1 ≤ γ_ADP ≤ 10) the average firing rates that are stable in the presence of noise. Beyond the line attractor configuration where the 〈g_ADP〉 slope becomes steeper than that of the FR nullcline (γ_ADP > 4) and the center fixed point becomes unstable, the average firing rate of the neuron settles at either a lower or higher rate, corresponding to the lower and upper intersections of the nullclines for which γ_ADP > 4 (see Fig. 5A, curve for γ_ADP = 10).

Figure 5.

Variance in output firing rate and [Ca²⁺]_i increases as the angle between the FR and 〈g_ADP〉 nullclines decreases. A, Variation of angles between the 〈g_ADP〉 nullcline (dashed) and the FR nullcline (solid). Three representative 〈g_ADP〉 nullclines are shown for whichγ_ADP = 1 (single stable fixed point), 4 (line attractor), and 10 (bistable neuron). B, Stable firing rates of model neurons in the presence of synaptic noise for a range of different g_ADP slopes including the cases illustrated in A. Beyond the line attractor configuration (γ_ADP > 4), neurons exhibit two different stable firing modes corresponding to the top and bottom intersections of the nullclines as for γ_ADP = 10 in A. The gap in the top curve results from the fact that for g_ADP slopes only slightly larger than that of the line attractor configuration, the top fixed points are not stable in the presence of noise (because their basins of attraction might be too small and flat). C, Firing rate as a function of time for the three representative configurations shown in A, labeled by their g_ADP slopes (γ_ADP). For the largest g_ADP slope (10), activity is shown for the system being either in its higher or lower stable activity mode (see B). Note that activity for the line attractor configuration (γ_ADP = 4) is clearly distinguished by its high variance and more prominent slow frequency components. D, Variance in firing rates (σ_FR²; black) and in intracellular Ca²⁺ concentration (σ_Ca²; gray) as a function of the slope of the 〈g_ADP〉 nullcline (γ_ADP). Both signals increase sharply as γ_ADP approaches the line attractor configuration.

Figure 5C shows activity traces for the configurations with the g_ADP slopes shown in Figure 5A. The activity trace for the configuration closest to a line attractor (γ_ADP ∼ 4) sticks out immediately by the higher variance and presence of slower frequency components. Figure 5D summarizes the data for a 10-fold range of g_ADP slopes. The smaller the rotation angle between the 〈g_ADP〉 and FR nullclines, the higher the variance in firing rate (σ_FR²), with a sharply peaked maximum at the line attractor configuration. For g_ADP slopes larger than that of the line attractor configuration, this holds true for whether the system settles in the low state (solid lines) or in the high state (dashed lines). Moreover, the variance in intracellular [Ca²⁺] ([Ca²⁺]_i) fluctuations (Fig. 5D, gray curves) and the variance of the g_ADP conductance (data not shown) also attain a maximum at the line attractor configuration. Hence, by maximizing the variance in these variables, a neuron would approach a line attractor configuration. A neuron might want to achieve a high variance in interspike intervals, because this would also allow the maximum amount of information to be encoded in the spike train (Rieke et al., 1997; Stemmler and Koch, 1999), and the Poisson-like nature of cortical spike trains might reflect this fact (Softky and Koch, 1993). In any case, [Ca²⁺]_i fluctuations and through g_ADP possibly also fluctuations in submembrane levels of other ionic species provide an intracellularly accessible signal that could be used to drive the system toward a line attractor configuration. The amount of noise used for the simulations in Figure 3E, i.e., an amount that is compatible with reasonable climbing performance and variance observed in behavioral data (Gibbon and Church, 1990; Gallistel and Gibbon, 2000), is completely sufficient to bring out this property.

In general, the size of fluctuations does not solely depend on the angle between the 〈g_ADP〉 and FR nullclines. It also depends on where in 〈g_ADP〉/FR space the fixed point is located around which perturbations are measured; for instance, on the local slope of the FR nullcline and on the state and dynamics of other variables of the system (e.g., those determining synaptic short-term depression) within that region of state space. Moreover, the variance in [Ca²⁺]_i depends on the average firing rate to some degree (compare Fig. 1A) which might become a significant factor if noise is smaller than depicted in Figure 3E. On the other hand, if the noise is much larger (in fact, so large that it would corroborate climbing activity), it might switch bistable cells (those for which γ_ADP > 4 in Fig. 5) back and forth between their two stable states, causing large fluctuations in the firing rate.

However, there is evidence that neurons try to maintain some optimal range of average output firing rates through adjusting properties of intrinsic voltage-gated and synaptic ion channels (Desai et al., 1999; Abbott and Nelson, 2000; Nick and Ribera, 2000; Buzsaki et al., 2002). Thus, assuming that in the long run, the average firing rate is quite constant, then for any fixed orientation of the FR nullcline and all other parameters being equal, the maximum firing rate and Ca²⁺ variance will occur for configurations in which the 〈g_ADP〉 nullcline overlaps with the FR nullcline. To show this, six different parameter configurations were generated, which had different stable firing rates (within the range of 25–60 Hz; configurations could differ in all parameters except for time constants and most reversal potentials; see Table 1). For each of these six configurations, 100 different collections of the three g_ADP parameters γ_ADP (see above), θ_ADP, and g_ADPmax were generated at random but with the constraint that all 〈g_ADP〉 and FR nullclines must yield a stable fixed point at the same location in 〈g_ADP〉/FR space. θ_ADP is the half-maximum activation value of the Boltzmann function (Eq. 3) that gives the Ca²⁺ dependence of g_ADP; higher values will shift the 〈g_ADP〉 nullcline to the right. g_ADPmax, the maximum ADP conductance factor (see Eq. 3), scales the 〈g_ADP〉 nullcline along the 〈g_ADP〉 dimension. From these 100 possible g_ADP parameter settings, 6 were then hand-selected to ensure some range of possibilities, and another 13 were drawn at random. Together with the g_ADP configuration that gives the line attractor, this made a total of 20 different g_ADP parameter settings for each of the six basis configurations.

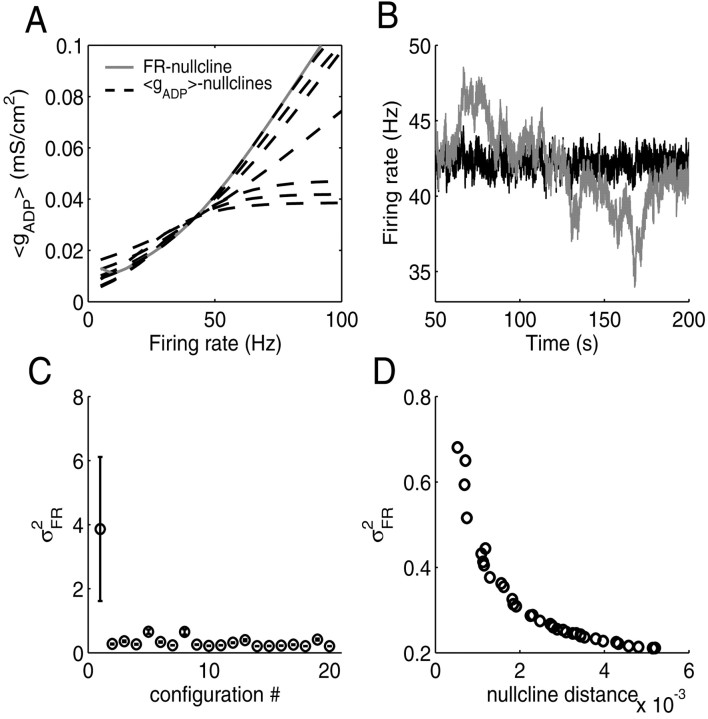
In Figure 6, the results from one of these six basic configurations are shown (the basic results were the same for all six configurations). Figure 6A shows the state space with 〈g_ADP〉 nullclines for the line attractor configuration and for the six hand-selected settings. Figure 6B shows activity traces for the line attractor configuration (gray) and for one other g_ADP parameter setting (black; all settings having approximately the same average rate now, ∼42 Hz). Figure 6C summarizes the data from all 20 g_ADP parameter settings averaged over 12 simulations with different random seeds. The highest variance in firing rate clearly occurs for the line attractor configuration. As another check of the results, Figure 6D depicts for all 19 g_ADP parameter settings drawn at random (i.e., excluding the line attractor configuration) plus another 20 random settings the variance in firing rate as a function of the average (Euclidian) distance between the 〈g_ADP〉 and FR nullclines, averaged across a 20 Hz range around the steady state. Figure 6D reveals that configurations for which the 〈g_ADP〉 and FR nullclines are more closely aligned yield a higher variance in the output firing rate. Thus, for a given average firing rate, the cell would maximize its firing rate variance by bringing the 〈g_ADP〉 and FR nullclines to overlap. Again, the same picture was obtained for the variance in [Ca²⁺]_i and g_ADP (data not shown).

Figure 6.

Variance in firing rates for neurons with the same average rate is maximal if these are in a line attractor configuration. A, State space with FR (gray, solid) and 〈g_ADP〉 (dashed) nullclines, illustrating a representative subset of the different configurations used for simulations. The 〈g_ADP〉 nullcline for the configuration closest to a line attractor almost completely covers the (gray) FR nullcline. B, Firing rate as a function of time for a neuron in the line attractor configuration (gray) compared with a neuron with randomly selected g_ADP parameters and a firing rate variance somewhere within the range shown in D (black). C, Variance in firing rates for 20 randomly selected configurations (see Results), averaged over 12 simulations with different random seeds (error bars indicate SD). Configuration 1 with the highest variance is the line attractor configuration. Note that for the line attractor configuration, also the variance of the variance of the firing rates becomes largest. D, Correlation between the magnitude of the variance in firing rates and the average distance of the 〈g_ADP〉 and FR nullclines in state space for 39 randomly selected configurations (excluding the line attractor). The smaller the average distance between nullclines, the larger the variance in firing rates. Euclidian distance was measured at different, equally spaced points within a ±10 Hz range around the fixed point and averaged across these points.

Therefore, in principle, it should be possible to use the Ca²⁺ or g_ADP variance (σ_gADP²) as a learning signal in a self-organizing process to adjust the slope of g_ADP in a way that yields a line attractor. To show this, variables were introduced into the system that track changes in intracellular Ca²⁺ levels (see Materials and Methods). A dynamical variable (y_Ca) was made to approach the squared temporal derivative of low-pass-filtered [Ca²⁺]_i, a computation that might be performed by intracellular molecular networks (see Materials and Methods and Discussion). Whatever the molecular mechanism that could underlie such a computation, the aim here was just to demonstrate that an intracellular quantity accessible to the computational machinery of the cells could be used to adjust the nullclines of the system. The average level of y_Ca as defined by Equation 8 was in close agreement (except for scaling) with the [Ca²⁺]_i variance.

Learning might now proceed by iteratively adjusting the slope of the g_ADP nullcline (γ_ADP) according to the gradient dy_Ca/dγ_ADP or dσ_gADP²/dγ_ADP (the gradient of the curve in Fig. 5D), a procedure called gradient ascent (or “hill climbing”). However, two potential difficulties arise for a learning procedure using σ_gADP² or y_Ca, because (1) these signals increase exponentially with the g_ADP slope toward the maximum (Fig. 5D), implying the danger of missing the maximum by stepping across it; and (2) these signals are inherently noisy by nature. To accommodate the first problem, changes in slope were made proportional to dγ_ADP/dy_Ca instead of dy_Ca/dγ_ADP; i.e., the relationship was reversed such that the region around the peak flattened out, whereas the biggest changes were now being made for the most extreme slopes. To alleviate the second problem, σ_gADP² or y_Ca, respectively, was averaged (integrated) over some period after a change in g_ADP slope. The learning algorithm (see Appendix, Learning algorithm) proceeded in fixed (discrete) time steps of 5–30 sec in which the maximum change of the g_ADP slope per averaging step was limited to ±2, and the minimum change was limited to ±0.02, assuming that there are natural physiological bounds on resolution and on the maximum change possible per time step. In addition, an annealing factor (Aarts and Korst, 1989) decreased the size of the changes in the g_ADP slope over time (see Appendix, Learning algorithm). It should be pointed out that this learning procedure was not intended as a physiological implementation but just as a simple demonstration that, in principle, cells could use gradient ascent on y_Ca or σ_gADP² to move into a line attractor configuration. [Note, however, that single cells are capable of deriving chemical gradients from temporally consecutive measurements as, e.g., in bacterial chemotaxis (MacNab and Koshland, 1972).]

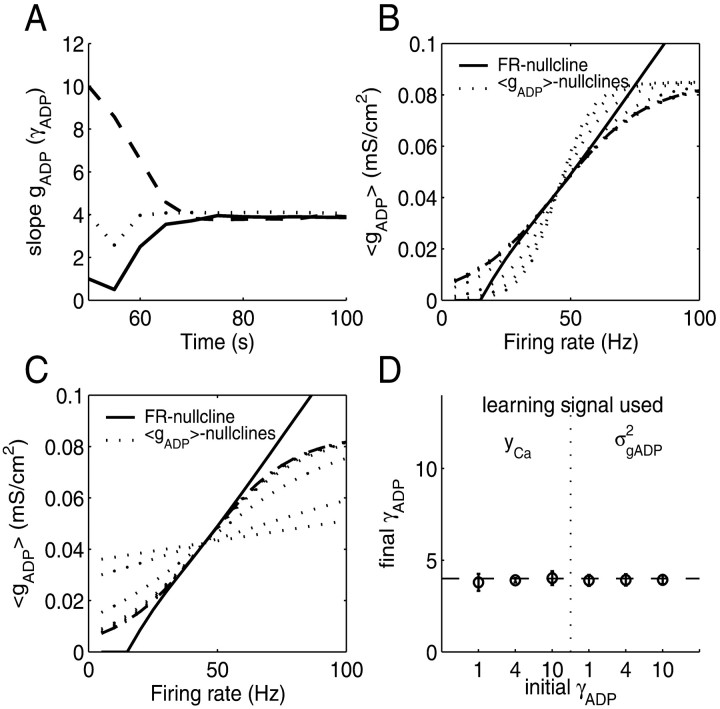
Figure 7 gives the results of this procedure. Figure 7A shows an example for the convergence of the g_ADP slope to its optimal value over time, starting with either a very flat (γ_ADP = 1; solid) or a very steep (γ_ADP = 10; dashed) g_ADP nullcline and, for comparison, starting at the already optimal value of γ_ADP ∼ 4 (dotted). Figure 7, B and C, plots the transition of the g_ADP nullcline in 〈g_ADP〉/FR space (dotted lines) from its initial condition to its final position (dashed line). Figure 7D summarizes the results from 10 simulations with different random seeds and for y_Ca versus σ_gADP² as a learning signal. This confirms that neurons can self-organize into a line attractor configuration solely on the basis of intracellular variables in principle accessible to the cell.

Figure 7.

Self-organization into a line attractor configuration by using the variance in internal Ca²⁺ or g_ADP as a signal (using the same parameters as in Fig. 5). A, The slope of the g_ADP nullcline (γ_ADP) quickly rotates toward the optimal region within a few sampling periods, starting from different initial conditions, although its fine adjustment might take more time. σ_gADP² was used as learning signal (for y_Ca as a signal, learning usually takes longer; for details, see Appendix, Learning algorithm). B, Rotation process of the 〈g_ADP〉 nullcline (dotted lines) toward its final position (dashed line) in state space with the FR nullcline (solid line), starting fromγ_ADP = 10. C, Same as B but starting fromγ_ADP = 1. D, Final slope of the 〈g_ADP〉 nullcline relative to the optimal slope (dashed line) averaged over 10 simulations with different random seeds, starting with a very small initial slope (γ_ADP = 1), with a slope close to the line attractor (γ_ADP = 4), or with a very high initial slope (γ_ADP = 10) and using eitherσ_gADP² or y_CA as the learning signal. Error bars indicate SD.

Discussion

The main findings of the present study are as follows. First, climbing activity can be generated through a single-cell positive feedback loop among the firing rate, Ca²⁺ influx, and a Ca²⁺-activated inward current (I_ADP). Once this feedback loop has been finely adjusted to yield a line attractor, the slope of climbing activity can be adapted to arbitrary time intervals by changing the strength of incoming synapses. Second, the variance of [Ca²⁺]_i or Ca²⁺-dependent molecules provides an intracellular signal for guiding the fine adjustment toward a line attractor configuration, shaping single cells into temporal integrators.

Biophysics of climbing activity and line attractors

The concept of a line attractor has been proposed by Seung et al. (2000) (Seung, 1996) to explain how an oculomotor network can keep stable arbitrary eye positions even in the absence of sensory feedback. In the model of Seung et al. (2000), the term line attractor refers to the fact that the system possesses (ideally) a continuum of stable firing rates corresponding to eye position. To explain climbing activity with arbitrary slow rise times, it is, in addition, important to note that as a neural system is slightly dislocated from its line attractor configuration, the speed of activity changes grows only gradually from zero to higher levels such that the temporal gain of climbing activity can be adjusted almost independently of the intrinsic time constants. Starting from a continuum of fixed points will ensure that the slope of climbing activity will be approximately constant over time as required for a temporal integrator (compare Fig. 3). A recent network model by Wang (2002) makes use of a similar dynamical phenomenon to explain the time course of cortical activity during decision-making tasks. The temporal periods considered by Wang (2002) were, however, relatively brief (≤1 sec) compared with those used here and in many behavioral and in vivo studies (Gibbon and Church, 1990; Quintana and Fuster, 1999) and hence did not require very precise tuning of network parameters.

Here it was furthermore assumed that line attractors are established on the single-neuron level rather than on the network level, involving positive feedback from Ca²⁺-activated inward currents. Ca²⁺-dependent inward currents can, in the presence of ACh, maintain spiking in prefrontal neurons for minutes (Andrade, 1991; Haj-Dahmane and Andrade, 1998). Furthermore, very recently it has been demonstrated in entorhinal cortex slices that the cellular feedback loop described here might indeed establish a line attractor on the single-cell level (Egorov et al., 2002). These authors found that synaptically isolated pyramidal neurons under muscarinergic modulation could (independently) maintain a range of different firing rates between which the cell could be switched by depolarizing or hyperpolarizing current pulses. Moreover, the authors could show that this cellular multistability depended on a Ca²⁺-activated cation current, providing strong support for the existence of cellular mechanisms of the kind described here.

Robustness and self-organized adjustment of line attractors

A potential problem with the line attractor configuration is that it needs very precisely tuned parameters to maintain the continuum of steady states (Seung et al., 2000). Recently, Koulakov et al. (2002) demonstrated that robust line attractors can be constructed by using bistable units as building blocks, ensuring a range within which perturbations will not destroy the line attractor. However, the experimental evidence cited above suggests that a line attractor configuration could also be attained on the single-cell level on the basis of a feedback loop involving I_ADP (Egorov et al., 2002). Hence, the mechanisms described by Koulakov et al. (2002) to achieve robustness on a network level cannot be applied to the present system, because there must be some solution that works for single neurons using the feedback loop described here.

Here it was proposed that neurons might use the variance of g_ADP or [Ca²⁺]_i as a learning signal to drive biophysical parameters toward a line attractor configuration or to maintain it. Fluctuations in [Ca²⁺]_i are a consequence of fluctuations in the firing rate caused for example by synaptic noise present in cortex (Allen and Stevens, 1994). Hence, spontaneous activity and noise were essential ingredients without which the neuron could not detect the appropriate setting of biophysical parameters. This might be a more general principle applying to many behavioral learning problems requiring exploration (Sutton and Barto, 1998) as well as to cortical plasticity (Katz and Shatz, 1996).

The assumption that the variance of [Ca²⁺]_i or Ca²⁺-dependent molecules could be exploited for learning of course ultimately remains to be demonstrated experimentally, but it seems entirely reasonable given our current knowledge about neural plasticity and molecular networks. Intracellular networks possess enormous computational power that includes performing various operations such as filtering, integration, differentiation, complex temporal decoding, and extracting the frequency of [Ca²⁺]_i oscillations (De Koninck and Schulman, 1998; Bhalla and Iyengar, 1999; Katz and Clemens, 2001; Kubota and Bower, 2001; Bhalla, 2002). As outlined in Materials and Methods, something akin to the [Ca²⁺]_i variance might be computed through Ca²⁺-dependent proteins such as calmodulin that capture the temporal derivative of intracellular Ca²⁺ fluctuations (Franks et al., 2001) and proteins further downstream that require some form of cooperativity in calmodulin or related proteins for activation. However, “explicit” computation of a variance might not even be necessary. Any intracellular process that is sensitive to the magnitude of deviations of [Ca²⁺]_i from its average value, e.g., by adapting to the average value, should be sufficient for detecting the line attractor.

Furthermore, there is much evidence that the level of intracellular Ca²⁺ after synaptic stimulation triggers specific synaptic changes (Sjöström and Nelson, 2002). Moreover, there is accumulating evidence that biophysical properties of intrinsic voltage- or Ca²⁺-gated ion channels are also changing with neural experience (Desai et al., 1999; Ganguly et al., 2000; Nick and Ribera, 2000). For example, changes in intrinsic ion channel properties have been shown to underlie activity regulation within single cells, which seem to try to attain an optimal level of mean output activity (Desai et al., 1999; Nick and Ribera, 2000). Likewise, neurons might try to achieve an optimal level of variance in output activity (Stemmler and Koch, 1999), thereby also optimizing discriminability, which could trigger convergence to a line attractor configuration. Thus, single cells seem to be equipped both with the molecular computational machinery required for processing the variance (or related quantities) in [Ca²⁺]_i or other molecules and with the plasticity mechanisms required for converting such a signal into appropriate changes of Ca²⁺-gated ion channels.

Time interval prediction and temporal difference errors

As described, the slope of climbing activity might be adjusted by modifying synaptic weights, but what could drive these parameter changes in the right direction? A possible learning signal is the temporal difference error between the predicted time of occurrence and the actual time of occurrence, as illustrated in Figure 8. A comparator system might receive inhibitory inputs from the prediction system and excitatory inputs from sensory neurons encoding actual stimuli. If the comparator neurons fire above baseline, this could trigger increases in synaptic weights within the prediction system, because it would indicate that the stimulus occurred earlier than predicted, whereas below baseline firing would indicate that the predicted time of occurrence was too early. Note that the response properties of the postulated comparator are exactly the ones exhibited by dopaminergic midbrain neurons (Schultz et al., 1997; Hollerman and Schultz, 1998; Schultz and Dickinson, 2000). It has been pointed out previously that these neurons could therefore signal a prediction error (Montague et al., 1996; Schultz et al., 1997). Because this signal, in addition, seems to be accurately timed (Schultz et al., 1997), it could also be used to adjust the slope of climbing activity to the to-be-predicted interval time. Such a signal alone would, however, not be specific enough to also drive a neuron into a line attractor configuration as a basis for climbing activity.

Experimental predictions

One major prediction of the model that goes beyond the evidence provided by Egorov et al. (2002) is the proposal that the variance in firing rate (and intracellular Ca²⁺ levels) is maximal for pyramidal neurons with an optimized firing rate–[Ca²⁺]_i–I_ADP feedback loop. Because pyramidal cells in entorhinal and possibly also prefrontal cortex seem to be close to a line attractor configuration (Egorov et al., 2002), partially blocking I_ADP or buffering or enhancing intracellular Ca²⁺ should reduce the variance in spike rate when a cell is perturbed in vitro under muscarinergic modulation with noisy current inputs. Moreover, variance might increase again over time as the cell tries to reorganize, such as to achieve a line attractor configuration.

At the behavioral and in vivo electrophysiological level, the present model suggests that interfering with climbing activity, in particular through pharmacological manipulation of I_ADP, should shift the predicted time of occurrence forth or back, depending on whether I_ADP is enhanced or diminished. Such a shift might be reflected in a shift of the time at which climbing activity suddenly drops, as it does if reward does not occur at the time predicted (Komura et al., 2001) (see Fig. 3D), by an offset in the normal time at which dopaminergic midbrain neurons are inhibited (Schultz et al., 1997), or by behavioral measures such as increased operant responding, which is time-locked to the expected event in fixed-interval schedules.

Appendix

Derivation of nullclines

The full single-neuron climbing activity model consists of two coupled nonlinear ordinary differential equations with time-dependent terms (synaptic currents and Ca²⁺ influx) plus two dynamic variables for each synapse describing short-term dynamics (u and R) given by the recursive relationship (Eq. 6). To simplify the system, the NMDA current was linearized [I_NMDA(t,V_m) = -g_NMDA(t) × (0.29 V_m + 24); see Figure 1 B], and u and R were substituted by their steady-state values for interspike interval T_ISI:

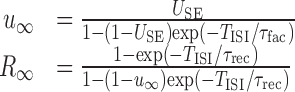9

(Markram et al., 1998). To derive the FR nullcline, for any mean ADP conductance level 〈g_ADP〉, where 〈g_ADP〉 is the average over an interspike interval T_ISI, the following linear differential equation has to be solved in a self-consistent manner:

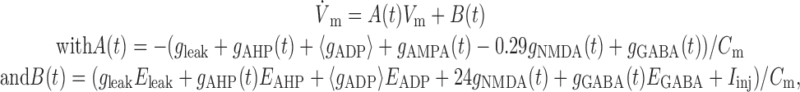10

where it was assumed that E_AMPA = 0, and V_m = V_reset whenever V_m > V_th from below. The interspike-interval T_ISI is the time it takes for the membrane potential V_m to proceed from the initial condition V_m(0) = V_reset to spike threshold V_m(T_ISI) = V_th. The solution to differential Equation 10 is:

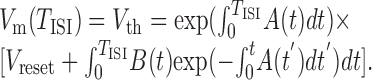11

To make this equation self-consistent, all conductances and [Ca²⁺]_i have to be determined such that they return to their initial values after time T_ISI. Double-exponential functions of the form in Equations 4 and 5 can easily be transformed into a recursive relationship in which g_syn(t) (or, equivalently, [Ca²⁺](t), except for synaptic depression terms) is given for any T_ISI by:

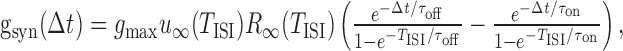12

where Δt is the time from onset of the interspike interval (i.e., Δt/T_ISI is the relative phase). The FR nullcline (FR^*) is then obtained by solving Equation 11 for T_ISI given 〈g_ADP〉 and taking the inverse FR^* = 1/T_ISI(〈g_ADP〉).

Unfortunately, the integrals on the right side of Equation 11 cannot be computed explicitly and were solved by quadrature using the MATLAB quad (or quadl) function. In fact, rather than solving Equation 11 for T_ISI given 〈g_ADP〉, it turned out to be easier to determine the 〈g_ADP〉 that satisfied Equation 11 for fixed T_ISI. This was done through function minimization (MATLAB fzero), minimizing the difference between the right and left sides of Equation 11. This gave the FR nullclines depicted in Figures 3, 4, 5, 6, 7.

The nullcline for the mean conductance level (〈g_ADP〉^*) given firing rates 1/T_ISI is obtained by solving differential Equation 3:

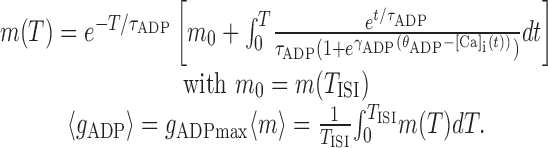13

The condition m₀ = m(T_ISI) ensures the self-consistence of this equation by requiring that m returns to its initial value after time T_ISI. [Ca]_i(t) = [Ca]_i(Δt,T_ISI) is determined as in Equation 12 (omitting synaptic depression terms). Again, the integral on the right side cannot be solved explicitly, because it involves exponentials of exponentials, which arise because the firing rate interacts with the ADP conductance only via Ca²⁺ influx, which has to be integrated over the period T_ISI. Note that by inserting Equation 13 (first line) into Equations 10 and 11, the whole system could be collapsed into a single self-consistent equation, which could be solved exactly.

For finding line attractor configurations, given the nullclines 〈g_ADP〉^* and FR^*, constrained optimization was run on a selection of system parameters [C_m, V_th, A_Ca, γ_ADP, and θ_ADP, as well as all maximum conductances (except g_AHPmax) and utilization variables U_SE] to minimize the following error function over a range r_E = 1/T_ISI of (instantaneous) firing rates:

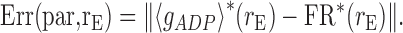14

where par is the current parameter configuration, and ∥·∥ denotes the norm of the vector. The fmincon function from the MATLAB Optimization toolbox was used for minimization. Fmincon performs constrained optimization of multivariate nonlinear functions (all variables were constrained within physiologically reasonable ranges; see Table 1) using sequential quadratic programming combined with line search.

Learning algorithm

The following procedure was taken for learning the slope of the g_ADP nullcline (γ_ADP). The procedure started by changing γ_ADP randomly by a small amount into one or the other direction to obtain an initial estimate of the gradient. For all successive learning steps n, y_Ca (Eq. 8) was averaged over ≥20 sec (during which γ_ADP was held constant), or σ_gADP² was calculated for 5 sec. (Thus, as is the case for long-term synaptic plasticity, adjusting the slope would be a relatively slow process compared with the neural dynamics, extending over at least tens of seconds over which signals such as y_Ca have to be integrated.) γ_ADP was then changed according to:

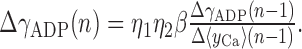15

η₁ is a general constant learning factor whose magnitude depends on the variable used as a learning signal. η₂ is an annealing factor (Aarts and Korst, 1989), which was decreased by η₂(n) = α × η₂(n - 1) with 0 < α ≤ 1 at each step n (usually α > 0.94). The general constant β took account of the difference in magnitudes between changes in γ_ADP and changes in the learning signal used. It was adjusted at the onset of learning during an initialization period according to β = 2^*x/(γ_ADPmax - γ_ADPmin) and then held constant during learning, where γ_ADPmax/γ_ADPmin is the maximum/minimum slope allowed, and x is the learning signal (e.g., x = y_Ca). The maximum and minimum changes Δγ_ADP allowed per time step n were limited to 2.0 and 0.02, respectively, and the total maximum and minimum slopes that could be achieved were limited to 15 and 0.5, respectively, assuming that there are natural physiological constraints on these variables. The first 20% of the signal sampling period of 5–30 sec were eliminated from the averaging, because the discrete change in slope according to Equation 15 caused a significant transient if Δγ_ADP was large (the transient might partly be regarded as an artifact of changing γ_ADP in discrete steps rather than continuously). Parameters used for Figure 7 were η₁ = 70, α = 0.945, and a sampling interval of 5 sec for simulations with σ_gADP² as a learning signal and η₁ = 0.3, α = 0.99, and a sampling interval of 30 sec for simulations with y_Ca as a learning signal. For some reasonable configurations of learning parameters using y_Ca as a signal, in a few cases, the algorithm got stuck at a very high slope (γ_ADP > 10; ∼3% of cases across different parameter configurations). This might be attributable to faster [Ca²⁺]_i fluctuations caused by the mere spiking process (Fig. 1A), which are negatively correlated with mean firing rate and might become a prominent factor at extreme slopes if synaptic noise is not large enough. σ_gADP² seems, in general, to be a better learning signal than y_Ca, because g_ADP filters out these faster fluctuations not caused by variance in the firing rate (in addition, especially low-frequency components increase toward the line attractor configuration). Hence, learning might be further improved by low-pass filtering [Ca²⁺]_i before subjecting it to Equation 7.

As discussed in Results, this learning algorithm was not designed as a physiological implementation; rather, the main goal here was to demonstrate that y_Ca and σ_gADP² could be used as learning signals despite the difficulties arising from the particular form of the learning landscape and the noisy nature of the signal. Note, however, that the general procedure, taking temporally consecutive measurements of a chemical concentration to perform gradient ascent, is quite akin to what bacteria do during chemotaxis (MacNab and Koshland, 1972), although the sensors and effectors are different here. In a more physiological version, one would express Equation 15 as a continuous time differential equation and would add additional dynamical variables that integrate the signal y_Ca or σ_gADP² over some period. The maximum and minimum g_ADP slopes allowed might be substituted by smooth sigmoid functions continuously approaching the limits γ_ADPmax and γ_ADPmin.

In general, the learning procedure would also have to be supplemented by a mechanism that keeps the average firing rate of a neuron within a certain range (see Results; as formalized, e.g., by Van Rossum et al., 2000). A similar learning schema as used for adjusting γ_ADP (Eq. 15) could then also be applied to other parameters of the ADP conductance.