Reversal Frequency in Caenorhabditis elegans Represents an Integrated Response to the State of the Animal and Its Environment

Abstract

The locomotion of Caenorhabditis elegans consists of forward crawling punctuated by spontaneous reversals. To better understand the important variables that affect locomotion, we have described in detail the locomotory behavior of C. elegans and identified a set of parameters that are sufficient to describe the animal's trajectory. A model of locomotion based on these parameters indicates that reversal frequency plays a central role in locomotion. We found that several variables such as humidity, gravidity, and mechanostimulation influence reversal frequency. Specifically, both gentle and harsh touch can transiently suppress reversal frequency. Thus, reversal behavior is a model for the integration of information from numerous modalities reflecting diverse aspects of the state of an organism.

Introduction

A central problem in neurobiology is understanding how competing sensory inputs are weighted and an appropriate behavioral output is chosen. In vertebrates this problem is often expressed in terms of determining the neural correlates of attention or decision making (Corbetta and Shulman, 2002; Platt, 2002). Caenorhabditis elegans is a simple invertebrate model system in which the mechanisms of sensory integration can be addressed at the molecular, circuit, and behavioral levels.

The most obvious behavioral output of C. elegans is its locomotion. C. elegans moves on an agar plate by generating sinusoidal waves along the length of its body (Croll, 1975). When these waves are propagated from head to tail the animal moves forward, and when propagated from tail to head the animal moves backward. The periods of backward movement, generally brief, are referred to as “reversals.” The reversals can occur spontaneously or can be induced as a direct response to a sensory stimulus. C. elegans can also execute “omega” turns wherein, during forward locomotion, the body of the animal bends such that the head touches the tail (causing the animal to trace an Ω-shaped path). The animal then proceeds in its new bearing. Animals may bias their forward locomotion to left or right causing them to trace an arc or spiral. Together, these mechanisms for changing the bearing of the animal allow it to navigate in a complex soil environment.

Locomotion has been used to assay the response of C. elegans to various sensory stimuli. For example, animals reverse in direct response to mechanosensory stimuli such as when the animal's nose bumps into a barrier (Croll, 1975; Kaplan and Horvitz, 1993), when the animal is touched with an eyelash (Chalfie et al., 1985; Way and Chalfie, 1989), or in response to a tap on its Petri dish (Chiba and Rankin, 1990; Rankin, 1991). The sensitivity of C. elegans to volatile compounds and temperature can be assayed by measuring the degree to which animals chemotax or thermotax toward the source of an attractive compound or temperature (Bargmann and Mori, 1997). Chemotaxis combines runs, long periods of forward locomotion, with pirouettes, a rapid series of reversals, and omega turns, which increase the probability that the animal will begin its next run heading up the gradient of an attractive compound (Pierce-Shimomura et al., 1999).

Changes in locomotory behavior can also reflect plasticity in the processing of sensory information. Reversals in response to mechanical stimuli are subject to habituation (Rankin and Broster, 1992). Chemotaxis exhibits odorant-specific adaptation (Colbert and Bargmann, 1995). Thermotaxis constitutes a simple associative learning paradigm because animals thermotax to a temperature that they associate with the presence of food (Bargmann and Mori, 1997). Finally, the speed of locomotion and reversal frequency are affected by the presence of food, and the effect of food on speed is enhanced in starved animals (Zheng et al., 1999; Sawin et al., 2000; Shingai, 2000).

We have defined in detail the locomotory behavior of wild-type C. elegans and have developed a computer model of locomotion. We found that an animal's trajectory is sensitive to only a few locomotory parameters, among them is reversal frequency. We explored the effects of several intrinsic and extrinsic factors on reversal frequency to identify sensory inputs that C. elegans must integrate when deciding to reverse. We have uncovered an interesting example of behavioral plasticity wherein animals suppress their reversal frequency in response to mechanical stimuli.

Materials and Methods

Strains and strain constructions

C. elegans were grown on the Escherichia coli strain HB101 at 20°C under standard conditions that included uncrowded conditions and the presence of ample food. N2 was the reference wild-type strain. Mutant strains used for reversal assays were CB1489 him-8(e1489) IV, MT1082 egl-1 (n487) V, JK1744 glp-3(q145)/sma-3(e491) unc-36(e251) III, and CB1338 mec-3(e1338) IV, che-2(e1033) X, osm-1(ad1307) X. The glp-3; egl-1 double mutant was constructed by crossing N2 males into JK1744 and crossing the male cross-progeny into MT1082. Progeny from this cross were singled, and from those producing sterile progeny, egg-laying defective animals were singled. Those strains producing sterile progeny were saved and propagated by singling 10 animals each generation and saving those that produced sterile, glp-3(q145) progeny. The sterile progeny were used for assays.

Locomotion assay

It was important to ensure that animals were assayed on a food-free plate so that the presence of food would not bias the animals' behavior. To ensure that no food was transferred with the animals from their growth plate to the assay plate, animals were moved using a drop of halocarbon oil to adhere them to the pick. Animals were removed from the bacterial lawn of an agar culture plate to a plate with no food and allowed to crawl away from any food residue that remained with the animal, which usually occurred within 5–10 sec. Then, again using a drop of halocarbon oil on the end of the platinum pick, animals were moved to the 100 mm agar assay plate with the lid off. The time that the tail of the animal left the halocarbon oil marked the beginning of the assay. If the animal did not immediately begin crawling when placed on the assay plate, it was discarded. Animals showed no attraction to the halocarbon oil in standard chemotaxis assays using isoamyl alcohol as a positive control (data not shown). However, worms reverse when they encounter halocarbon oil, so worms that circled back and reentered the oil were discarded (9 of 62 tracking experiments).

To measure the speed and bearing of the animals, a tracking system was constructed. It consisted of an ES110 motorized stage (Prior Scientific Inc., Rockland, MA) mounted on an Olympus SZX-12 microscope set to 15× zoom. A Hitachi KP-M1U CCD camera with 640× 480 resolution was mounted on the microscope and connected to a Matrox Meteor-II frame grabber board (Matrox Electronic Systems, Dorval, QC, Canada). The captured images were transformed into a white silhouette of the animal on a black background. The threshold grayscale value used to transform the image was determined empirically before each experiment using a dead animal. Also, before each experiment, the stage was calibrated using a dead animal to generate separate pixel per micrometer conversion factors for both X and Y coordinates in each diagonal.

While recording, an image was captured every second (0.98 ± 0.01 sec; mean ± SD), and the centroid in pixels of the animal's silhouette was determined. The centroid was converted to micrometers, recorded, and used to command the stage to recenter the animal in the field of view. Because it was not possible to identify perfectly all behavioral events from the coordinates, we also observed the animals during the experiment and recorded the time and duration of reversals and indicated when omega turns occurred. The data from a tracking experiment consisted of the coordinates of the centroid every second for 200 sec and the visual record of reversals and omega turns.

Reversals. The absolute bearing of the animal was determined, and its change in bearing in each successive pair of time points was calculated. Visually recorded reversals were correlated with changes in bearing calculated from the data, and these data were used to determine when the animal was moving forward and when it was moving backward. There was a good correlation between visually recorded reversals and changes of bearing >100°. However, because the centroid of a animal making a deep body bend (especially an omega turn) can move backward even though the animal is moving forward, the correlation was not perfect. Only changes in bearing that correlated with visually scored reversals were used.

Speed. The mean forward speed averaged over all animals was determined for each pair of consecutive time points. Excluded from the forward speed calculations were 1 sec time intervals during which the animal was moving backward or intervals during which the animal was moving forward but was within 1 sec of (before or after) an interval when the animal was moving backward. This was to ensure that time points during which the animal spent part of the 1 sec interval moving forward and the other part moving backward did not bias the forward speed calculation toward lower values. Similarly, the reverse speed calculation included only those intervals that were more than 1 sec away from an interval when the animal was moving forward.

Bearing. The absolute bearing (with right on the x-axis set to 0°) at each successive pair of time points was calculated and found to have no apparent overall bias. From the absolute bearing, the change in bearing or turning rate (degrees per second) was calculated, and a graph of the distribution of turning rates during forward locomotion was generated. We estimated the SD by visually fitting a Gaussian distribution to the data. To determine whether individual animals had a tendency to veer to one side (i.e., a directional bias), we calculated the ANOVA of the turning rate with the null hypothesis that the mean turning rate up to the first reversal for all animals was equal. There was no statistically verifiable bias.

Reversal intervals. A reversal interval was defined as the duration of uninterrupted forward movement. For reversal assays (without tracking), three reversal intervals were recorded. A reversal was operationally defined as the backward translation of the animal for a distance greater than the length of the pharynx (∼150 μm). This definition resulted in <10% of the reversals being discarded. The first reversal interval was defined as the time interval from the point when the animal completely exited the oil drop to the point when the animal began its first reversal. The subsequent reversal times are defined as the time interval from the moment when the animal finished its most recent reversal and resumed forward movement again to the point when it initiated its next reversal. Stimuli (e.g., light touch) were applied to the animals right after the completion of their second reversal, and four reversal intervals (total) were recorded. If any reversal interval lasted >3 min, the assay was terminated and that reversal interval was recorded as being 180 sec long.

Three stimuli were applied. The “gentle body touch” stimulus consisted of drawing an eyelash over the tail of the animal. The third reversal interval was calculated from the point when touch was applied to the next reversal. The “harsh touch” stimulus consisted of prodding the animal with a platinum wire at or posterior to its vulva. The animal responded by either accelerating or reversing. If it accelerated, the third reversal time was recorded from the point when touch was applied, whereas if it reversed, the third reversal time was calculated from the point when it resumed forward movement. The “heat stimulus” consisted of moving a hot platinum wire increasingly close to the animal's head immediately after the animal finished its second reversal until the heat from the wire induced a reversal. Again, the third reversal interval was calculated from the point when the animal resumed forward movement.

Temperature—humidity—texture control. Temperature- and humidity-controlled experiments were performed in PGW36 growth chambers (Conviron, Winnipeg, MT, Canada). The animals and assay plates were introduced into the chamber within 15 min of the beginning of the experiment. The experiments were performed on consecutive days, low humidity first, using the same batch of assay plates. Agar plates dry out at room temperature, losing ∼2% of their water per day. Normal, “wet” assay plates were 3 d old, whereas “dry” agar plates were 2 weeks old. The effect of the texture of the agar on animals' reversal behavior was examined by spreading silica (Sigma, St. Louis, MO) suspended in M9 salts solution (Sulston and Hodgkin, 1988) on food-free agar assay plates. The density of silica particles on the agar plate was approximately five particles per square millimeter. Agar plates covered by M9 from which silica was removed by centrifugation were used as a control. Three-day-old adults were used for this assay.

The C. elegans locomotion model. In this model, speed was determined as a function of time as described by the equation in Figure 3A with the minimum speed parameter, C, chosen from a Gaussian distribution of mean 82 and SD 35. The turning angle at each time point was the sum of two values: the first was chosen for every 1 sec interval from a Gaussian distribution of mean = 0 and SD = 14. The second (referred to as the “bias”) was chosen once for each animal from a distribution of mean = 0 and SD = 2. The probability of reversal per second was based on the estimated lognormal hazard function. This function was different depending on whether it applied to the first reversal interval or a subsequent interval (see Fig. 4A,B). If an animal reversed, the program determined whether the reversal would terminate with an omega turn or not, and the reversal duration was chosen from the appropriate empirically determined distributions (see Fig. 5B). For simplicity, the reversal speed was held constant at the mean averaged over all reversals (140 μm/sec), and the animal was assumed to move backward 180° relative to its last forward bearing for the duration of the reversal. For non-omega-terminated turns, the interval angle was chosen from a Gaussian distribution of mean = 0 and an SD determined as a function of the reversal duration according to the fitted curve in Figure 5D. For omega terminated reversals, the interval angle (x) was chosen from a distribution defined by the linear density function f(x) = ax + b, where a = -0.02175 and b = 10.1 and 0 ≤ x ≤ 180 (determined from a linear regression fit to measured data; data not shown) and the direction (left or right) was chosen randomly. A flow chart of the program and the code are available on request.

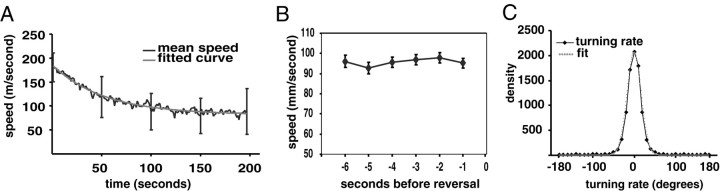
Figure 3.

Speed of locomotion. A, The speed of all animals (n = 53) averaged at each time point from the beginning of the assay is indicated by the black line. Representative error bars indicate SD. The gray line indicates a fitted curve of the form speed = (S/β)^*exp(-t/β) + C, where t = time,β = 53, S = 5500, and the minimum speed C = 82. B, The speed as a function of time before initiation of a reversal. Error bars indicate SEM. C, The black line indicates the distribution of turning rate in degrees per second for all time points during which animals were moving forward. The gray line is the fitted normal curve. Mean = 0; SD = 16; n = 8789.

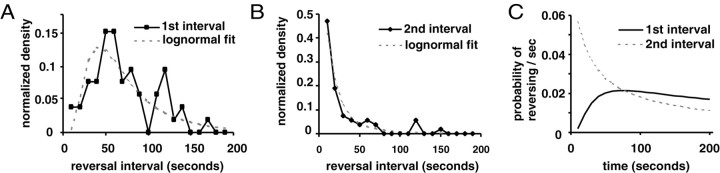
Figure 4.

Reversal intervals. A, Reversal interval histogram for first reversal. Gray line indicates the fitted lognormal distribution. Mean = 4.04; SD = 0.67. B, Reversal interval histogram for subsequent reversals. The gray line indicates a lognormal fit. Mean = 2.55; SD = 1.18. C, Hazard function. The probability of reversal as a function of time from beginning of assay (first reversal interval) or completion of last reversal (second reversal interval) estimated from the lognormal fit.

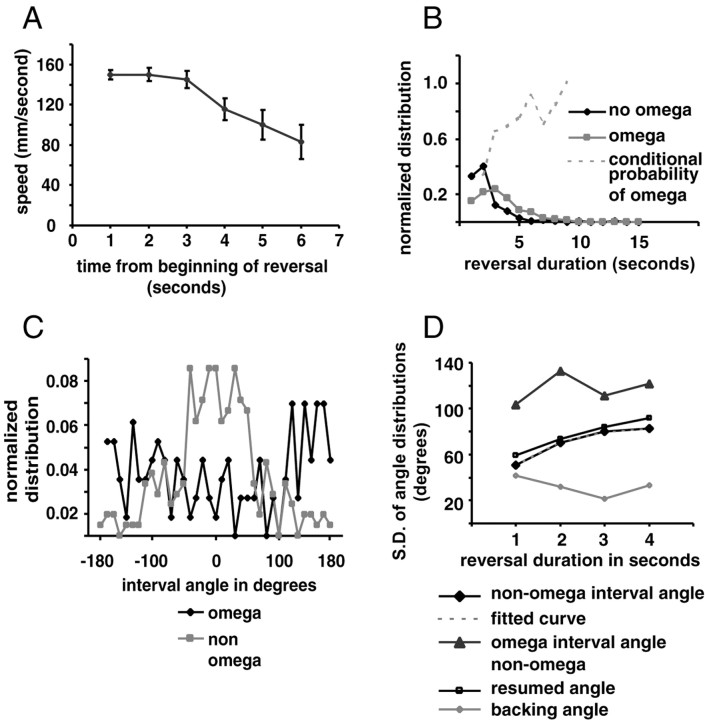
Figure 5.

Reversal parameters. A, Speed of retrograde motion as a function of time from the initiation of reversal. Error bars indicate SEM. n (from 1 to 6) = 160, 95, 52, 28, 16, and 9 for each time point, respectively. B, Plot of normalized reversal duration. n = 249 for non-omega terminated turns and n = 135 for omega terminated turns. Dotted gray line is the conditional probability of an omega turn as a function of reversal duration. C, Distribution of resumption angles according to whether the reversals terminated in an omega turn. D, SD of various angles that make up the reversal expressed as a function of the duration of the reversal. Black diamonds indicate the SD of interval angles of reversals that do not end in omega turns. The gray triangles indicate interval angles of reversals that end with omega turns. Open squares indicate SD of the resumed angles of reversals that do not end in omega turns, and open circles indicate the SD of the backing angle. The fitted curve (gray dashed line) is of the form (1 - exp(d/β))^*C, where d = duration of backward movement, β = 1.1, and C = 85 are constants.

Statistics

Unless indicated otherwise, statistical significance was determined by Mann—Whitney test. Curves were fitted using a maximum likelihood method. Sample SDs were compared using the F test.

Results

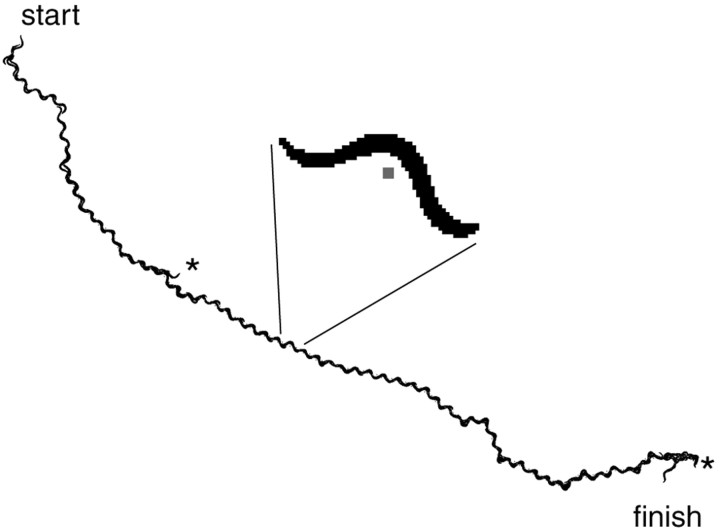
To define parameters that describe the locomotory trajectory of animals that experienced minimal sensory stimulation, we tracked 53 N2 (wild-type) L4 larvae for 200 sec each on agar plates. Our tracking system recorded an image of each animal once per second and calculated how far the animal's centroid had moved (Fig. 1). To verify that the tracking was working properly, we reconstructed the path of the animal by realigning the images based on the calculated position when the image was captured (Fig. 2). The alignment indicates a good correlation between the calculated centroid, the silhouette of the animal, and the movement of the stage.

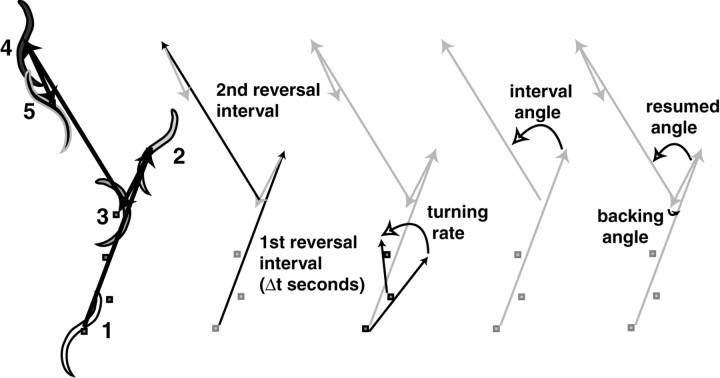
Figure 1.

Parameters that define C. elegans locomotion. The silhouette of the animal is captured, and the centroid (indicated by small gray square) is determined. The centroids trace the trajectory of the animal, which consists of periods of forward motion punctuated by periods of backing up called reversals. The numbers indicate the sequence of the silhouettes, which do not represent evenly spaced time intervals in this diagram. Several of the parameters that we looked at are defined.

Figure 2.

Reconstructed path of a tracked animal. Every second for 200 sec the individual silhouettes were captured, and the X and Y coordinates of centroid were calculated. The coordinates of the centroid associated with each silhouette were used to reassemble the silhouettes into the path followed by the animal. The inset shows a blowup of the image from a single time point from the series. The centroid is indicated by the small gray square. Asterisks indicate reversals that occurred at 47 and 192 sec.

Parameters that define the animal's trajectory: speed

As they leave the point of origin, animals move fast and then slow down (Fig. 3A). The average speed as a function of time can be fitted to a negative exponential that begins at 184 μm/sec and asymptotically approaches 82 μm/sec. It has been reported that C. elegans slow down in the few seconds before a reversal (Pierce-Shimomura et al., 1999). We plotted the speed as a function of the time until reversal and found no change (Fig. 3B). This discrepancy may reflect the already slow speed of the animals before reversal in our assay.

Changes in speed could result from changes in the amplitude of the sinusoidal body bends or from changes in the rate of bend propagation. Greater amplitude (deeper) bends would result in less forward translation per bend. Using reconstructed traces (Fig. 2) to count total body bends during the first reversal interval, we found that the number of body bends correlated nearly perfectly with the distance traveled (r = 0.98) and somewhat less with the time (r = 0.94). Thus, the distance traveled per bend was constant across animals, and speed was determined by the rate of body bend propagation.

Turning rate

Animals often appeared to have a distinct bias toward veering either to the left or right (see Fig. 6A). To explore the presence of bias in our animals, we looked at the distribution of the turning rate, defined as the change in bearing in degrees per second (Fig. 1). The mean of this distribution was not significantly different from zero, indicating that there was no population bias. Individual animals might also have a bias, which would be reflected in individual mean turning angles that were significantly different from the population mean. An ANOVA did not confirm an individual bias. However, we suspect that this negative result reflects our small data set and included an individual bias in our model (see below and Materials and Methods).

Figure 6.

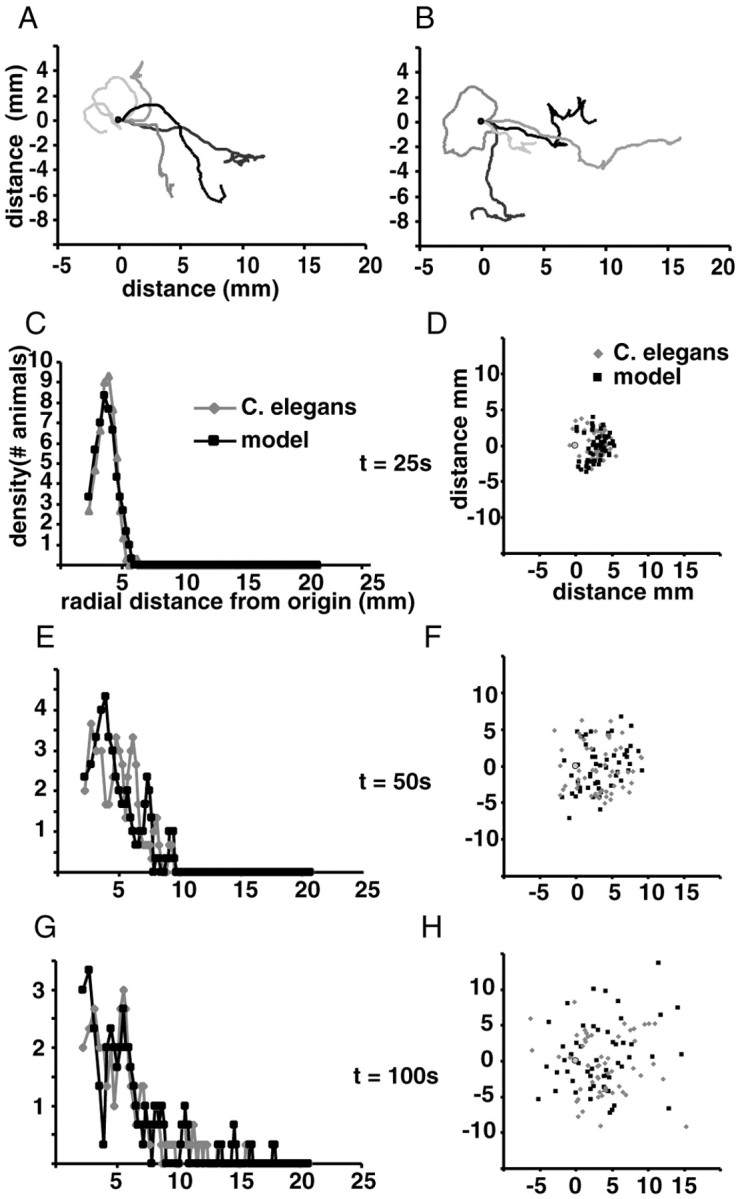
Comparison of the locomotion model with the behavior of real animals. A, B, Traces of real animals and model animals, respectively. Five traces of real animals were chosen at random, and five traces of similar overall form were chosen from a set of 53 model animals. Traces were normalized so animals begin the trace moving to the right from the origin (0,0). C, E, G, Density histogram of radial distance from the origin of real (gray diamonds) and modeled (black squares) animals at 25, 50, and 100 sec into the experiment, respectively. The radii defining bins in the radial dispersion histogram are normalized so that each bin defines a constant area (i.e., the area of the donut whose inner and outer radii are determined by the limits of the bin). The distribution has been smoothed by averaging three consecutive bins. D, F, H, Each animal is plotted according to its X and Y coordinates at 25, 50, and 100 sec, respectively, from the beginning of the experiment. Each real animal is indicated by a gray diamond, and each modeled animal is indicated by a black square. The gray circle indicates the origin.

Reversals

The frequency of spontaneous reversals varies with time. We plotted a histogram of the reversal interval (i.e., the time between reversals) (Fig. 1) for all animals for each reversal (first, second, third, etc.). Longer reversal intervals reflect a lower reversal frequency. There is a clear distinction between the first reversal, which has a more Gaussian reversal interval distribution, and the distributions of subsequent reversals, which all appear to fit a negative exponential distribution (Fig. 4A,B). We fitted Gaussian, lognormal, and gamma distributions and found, in accordance with previous studies (Hardaker et al., 2001), that the lognormal distribution gave the best fit for the distributions of all reversals (Fig. 4A,B). From the fitted lognormal distributions we estimated the hazard function, which in this case estimates the probability that an animal will reverse as a function of time (Fig. 4C). Over time, the probability of reversal increases for the first reversal and decreases for subsequent reversals. For the second and subsequent reversal intervals, the relatively high probability of reversal immediately after a reversal (Fig. 4C) indicates that reversals have a slight tendency to cluster.

We found no significant correlations between other parameters that we examined. For instance, there was no correlation between speed and the first reversal interval. There was a modest negative correlation between the first and second reversal interval (r = -0.26; df = 50; p = 0.07; t test). Thus, a short first reversal interval may be more likely to be followed by a longer second interval.

If C. elegans uses reversals to change bearing, several factors might determine how the bearing changes. We considered four parameters that define a reversal: the speed of backward movement, the duration of backward movement (reversal duration), whether the reversal terminated with an omega turn, and the bearing change when the animal resumed forward motion (interval and resumed angles) (Fig. 1). The speed when backing up is relatively fast (140 μm/sec averaged over all time points) but drops somewhat after 3 sec (Fig. 5A). The percentage of reversals that terminated with omega turns was 35% (n = 384). In addition, nine omega turns were not preceded by backward movement. These omegas were not included in further analysis.

The probability of a reversal terminating with an omega correlated with the duration of the reversal. We plotted the distribution of the reversal duration for reversals ending in omega turns and for non-omega reversals (Fig. 5B). The mean reversal duration for omega reversals (3.4 ± 1.8 SD; n = 135) was longer than for non-omega reversals (2.3 ± 1.6 SD; n = 249; p < 0.001). Thus, the conditional probability of an omega turn after a reversal increases with reversal duration (Fig. 5B).

Reversals that ended with an omega turn generally resulted in a much larger change in bearing. We plotted the distribution of the interval angle, which is the change in bearing from just before each reversal to when the animal resumes forward motion (Fig. 1), for turns that ended with omegas and those that did not. Interval angles for omega turns were nearly random, with a slight bias toward bearings of 180°, whereas the reversals that did not end with an omega turn showed a roughly Gaussian distribution with a mean of -0.7° (Fig. 5C).

Because the probability of a reversal terminating with an omega turn correlates with duration of backward movement, the difference between the interval angle distributions in Figure 5C might reflect the duration of reversals and not the omega turn. If the interval angle depends on the reversal duration, independent of whether the reversal terminates in an omega turn, then the SD of the interval angle of non-omega terminated reversals should also increase (i.e., show a wider distribution) with duration; it does (Fig. 5D, black diamonds). The interval angle was more likely to be larger the longer the animal moved backward (p = 0.005 when comparing SD for 1 sec reversals vs 2 sec reversals; F = 1.89; n.df = 75; d.df = 84). A similar plot of reversals terminated by omega turns showed no clear trend (Fig. 5D, black triangles)

One explanation for the increase in interval angle SD with longer reversal duration is that animals back up with a large constant turning rate (different for each reversal) so that they change bearing in proportion to the reversal duration. If so, then the resumed angle (the difference between the bearing of the animal just after it finishes backing but before it turns and the bearing when it resumes forward motion) (Fig. 1) should be small and constant as a function of reversal duration. On the contrary, the SD of the resumed angle shows the same relation to reversal duration as the SD of the interval angle (Fig. 5D, open squares), whereas the backing angle (the difference in bearing between the beginning and end of the period of backing but before the turn) (Fig. 1), is small and constant (Fig. 5D, open diamonds). Thus, animals move straight back during a reversal, and the biggest change in bearing occurs when the animals turn and resume forward movement. The degree of this turn correlates with the duration of the reversal independent of whether it is an omega turn.

We considered the possibility that omega turns are merely the deepest of a continuum of body bends that terminate every reversal and that the depth of the body bend determines the interval angle. If so, the distribution of interval angles for all reversals that lasted only 1 sec would fit a simple Gaussian distribution better than it would fit a distribution that consists of the combination of a constant distribution for reversals ending in omega turns and a Gaussian distribution for non-omega reversals. Our data better fit the latter model (p < 0.01), indicating that all interval angles are not taken from the same distribution and suggesting that interval angles resulting from omega turns are qualitatively different.

A model of C. elegans locomotion confirms the importance of reversal frequency, speed, and directional bias for wild-type dispersal

To determine how each of the parameters that we identified influences the two-dimensional space explored by C. elegans, we modeled locomotory trajectory using the above-mentioned parameters, distributions, and functions (see Materials and Methods for description of the model). To evaluate the effects of varying each parameter on how animals disperse, we plotted the X and Y coordinates of the real and model animals as well as a histogram of the radial distance from the origin. Comparison with the behavior of real animals shows that the model captures the essential aspects of the animal's trajectory (Fig. 6A,B). Furthermore, the dispersal of real and modeled animals is comparable (Fig. 6C—H), and there was no statistical difference between the mean radial dispersion at any time point (p > 0.2).

Notably, the dispersal of C. elegans occurs in two phases: a first “escape” phase and a second “random walk” phase. In a random walk, the concentration of animals will always be highest at the origin and will fall off exponentially with radial distance. Instead, we found that animals initially vacate the center until ∼100 sec into the trial and then begin to show a distribution that more closely resembles a random walk (Fig. 6C—H).

Three parameters had profound effects on the pattern of dispersal in model animals: the reversal frequency, the speed, and the turning angle. When we removed the suppression of the first reversal by applying the hazard function of the second reversal to all reversals, the result was a radial dispersion that was significantly different from that of real animals (p < 0.001, t = 25 sec; p < 0.03, t = 100 sec) and more closely resembled a random walk (Fig. 7A). A similar result was obtained by setting the speed of the animals to a constant equal to the average speed over the whole assay (111 μm/sec; p < 0.001, t = 25 sec; p < 0.02, t = 100 sec). Finally, increasing the turning rate by increasing the SD of the turning rate bias (see Materials and Methods) from 2 to 6°/sec also keeps the animals near the origin (p < 0.03, t = 25 sec; p < 0.001, t = 100 sec).

Figure 7.

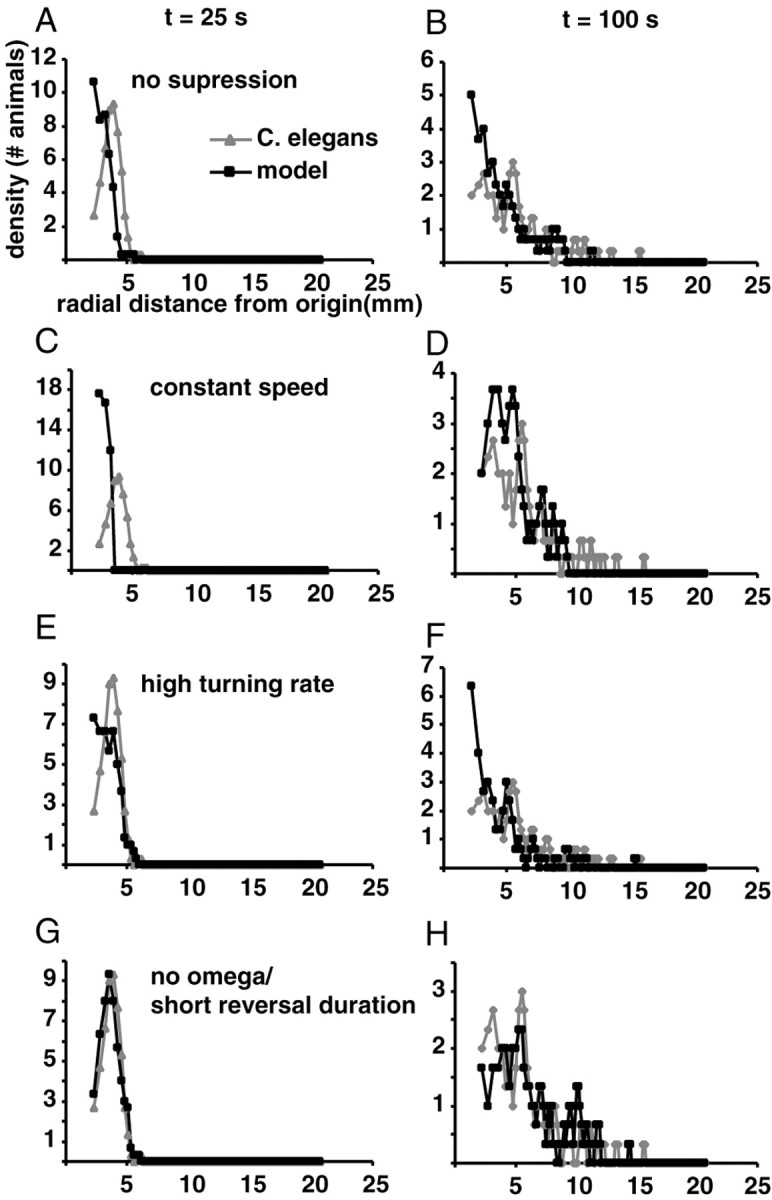
Effects of varying parameters on the locomotory behavior of the model. A, B, Radial dispersion at 25 and 100 sec of modeled animals that use the same hazard function for the first reversal as they do for subsequent reversals. C, D, Radial dispersion of modeled animals that have a constant speed of 111 μm/sec. E, F, Radial dispersion of modeled animals that have a high turning rate bias SD of 6°. G, H, Radial dispersion of modeled animals whose reversal duration = 1 sec and who never terminate their reversals with an omega turn.

No other parameter had a significant effect on dispersal. One might have expected that decreasing the interval angle would cause animals to prolong the escape phase because, even as reversal frequency increases, there would be little change in bearing after each reversal so worms would continue to move away from the origin. Yet, limiting modeled animals to a 1 sec reversal duration and no omega turns had little effect (Fig. 7G,H). The same was true when all turns terminated with omega turns (data not shown).

The intrinsic state of C. elegans influences reversal frequency

The reversal frequency has a substantial effect on dispersal, varies with time and reversal interval, and is easy to assay. Therefore, we determined the effects of various intrinsic and extrinsic factors on reversal frequency. We visually scored the reversal intervals for three reversals for each animal.

We first considered states intrinsic to the animal. To determine the effect of age/developmental stage (Chiba and Rankin, 1990), we examined fourth-staged larvae (L4), 3-d-old gravid adults, and 6-d-old animals that were mostly sterile adults. The mean reversal interval duration increased with age, indicating a decrease in reversal frequency (Table 1) (L4 vs 6-d-old animals: first reversal vs first reversal: p < 0.001; second vs second: p < 0.003; third vs third: p < 0.001). The less frequent reversal of 6-d-old adult animals as compared with 3-d-old animals did not achieve statistical significance in our data set.

Table 1.

Effect of intrinsic variables on mean reversal interval

	Mean reversal interval (seconds)
Variables	First	Second	Third
Age of the worms
Wild-type N2 L4 larvae	45 ± 2.8 (138)	18 ± 1.7 (138)	15 ± 1.6 (138)
3-d-old gravid N2 adult	86 ± 4.8 (124)	44 ± 4.5 (110)	34 ± 3.6 (104)
6-d-old adult	99 ± 7.1 (51)	52 ± 7.7 (45)	42 ± 6.1 (41)
Sex
him-8 Hermaphrodites	63 ± 5.1 (50)	14 ± 2.8 (50)	14 ± 2.2 (50)
him-8 Males	38 ± 3.2 (50)	8 ± 0.9 (50)	7 ± 0.9 (50)
Gravidity
3-d-old gravid N2 adult	57 ± 4.8 (50)	34 ± 4.9 (50)	35 ± 4.8 (50)
egl-1	67 ± 5.9 (50)	41 ± 5.1 (50)	36 ± 5.4 (50)
glp-3	64 ± 5.5 (50)	25 ± 3.7 (50)	22 ± 4.1 (50)
egl-I; glp-3	50 ± 4.6 (50)	32 ± 4.3 (50)	24 ± 4.0 (50)

The data consist of the mean reversal intervals in seconds ± SEM for the first, second, and third intervals. The numbers of worms assayed are in parentheses.

To determine the effect of sex on reversal frequency, we compared L4 males and hermaphrodites of the strain him-8. Hermaphrodites of this strain produce many normal, fertile male XO progeny by X chromosome nondisjunction (Hodgkin, 1979). We found that the males reversed more frequently than hermaphrodites (first vs first: p < 0.001; second vs second: p < 0.02), in agreement with previous results (Mah and Rankin, 1992).

To ask whether the presence of eggs in the uterus had an effect on animals' reversal behavior we examined gravid 3-d-old adult N2 (wild-type), egl-1, glp-3, and egl-1;glp-3 double mutant animals. In egl-1 mutants, the HSN neurons, which stimulate egg-laying, undergo apoptosis (Conradt and Horvitz, 1998). Consequently, egl-1 mutants retain eggs in their uteruses. glp-3 mutants are defective in germline proliferation, so glp-3 mutants and egl-1; glp-3 double mutants produce no eggs (Kadyk et al., 1997). We found no statistically significant difference between wild-type animals and egl-1 mutants (Table 1), nor were glp-3 mutants different from N2 or egl-1;glp-3 double mutants. However, egl-1 mutants reversed less frequently than either glp-3 or egl-1;glp-3 mutants for some reversals (egl-1 vs glp-3: second vs second: p < 0.03; third vs third: p < 0.03; egl-1 vs egl-1;glp-3: first vs first: p < 0.03). Thus, there appears to be a modest but significant effect of gravidity that is most apparent when comparing egg-laying defective animals with sterile animals. The gravidity effect is different from the immediate effect of egg-laying on reversal behavior (Hardaker et al., 2001) because the animals rarely laid eggs during our assay.

Extrinsic (environmental) states also affect reversal frequency

Reversal frequency is sensitive to factors in the environment of C. elegans (summarized in Introduction). We supposed that much of the variability in our data (e.g., compare N2 reversals in gravidity and age experiments) was the result of environmental factors. Identifying some of these extrinsic variables would (1) reveal novel sensory inputs that affect reversal behavior and 2) reduce variability in the assays by allowing us to control extrinsic influences. We performed our subsequent assays with L4 hermaphrodite larvae to control for the effects of age, sex, and gravidity.

Because C. elegans is poikilothermic, ambient temperature is likely to affect its metabolic rate and behavior. Animals at constant 50% humidity reversed less frequently at 16°C than at 26°C (first vs first: p < 0.001; second vs second: p < 0.001) (Table 2). However, the difference between animals assayed at 26°C and those assayed at 21–23°C (above) was not significant.

Table 2.

Effect of extrinsic variables on mean reversal interval

	Mean reversal interval (seconds)
Variables	First	Second	Third
Temperature
Low (16°)	76 ± 3.9 (100)	34 ± 3.5 (100)	29 ± 2.9 (98)
High (26°)	58 ± 3.3 (102)	21 ± 1.8 (100)	17 ± 2.1 (100)
Dryness of the assay plate
Wetter	48 ± 4.1 (75)	20 ± 3.6 (75)	22 ± 3.6 (75)
Drier	63 ± 4.1 (75)	24 ± 3.5 (75)	22 ± 2.7 (75)
Humidity
High (90%)	45 ± 2.0 (50)	11 ± 1.4 (50)	10 ± 0.9 (50)
Low (30%)	64 ± 4.1 (50)	20 ± 2.6 (50)	18 ± 3.4 (50)
Texture of the assay plate
M9	23 ± 4.3 (40)	22 ± 4.4 (40)	16 ± 3.6 (40)
Silica	34 ± 7.2 (40)	18 ± 4.2 (40)	15 ± 2.9 (40)
Food
N2
− food	37 ± 2.1 (112)	17 ± 1.7 (112)	19 ± 2.7 (112)
+ food	150 ± 6.1 (56)	85 ± 16.3 (21)	48 ± 14.6 (16)
− food
N2	37 ± 2.1 (112)	17 ± 1.7 (112)	19 ± 2.7 (112)
che-2	49 ± 7.2 (30)	27 ± 6.7 (30)	13 ± 1.5 (30)
osm-1	43 ± 6.2 (30)	20 ± 3.6 (30)	17 ± 4.2 (30)
+ food
N2	111 ± 10.9 (25)	44 ± 7.4 (25)	33 ± 8.6 (25)
che-2	55 ± 5.3 (30)	17 ± 3.8 (30)	24 ± 6.9 (30)
osm-1	71 ± 6.1 (30)	33 ± 7.0 (30)	18 ± 3.9 (30)
bas-1	161 ± 7.1 (31)	64 ± 16.1 (7)	41 ± 23.2 (5)

The data consist of the mean reversal intervals in seconds ± SEM for the first, second, and third intervals. The numbers of worms assayed are in parentheses.

C. elegans is sensitive to desiccation and must remain on a moist surface. We compared normal wet agar assay plates with dry plates and found that animals reversed less frequently on the dry plates (first vs first: p < 0.003) (Table 2). Because the salts in dryer plates are more concentrated, which might influence our results, we looked at the effect of ambient humidity on reversal frequency. At 22°C, animals at 90% relative ambient humidity reversed more frequently than worms at 30% humidity (first vs first: p < 0.001; second vs second: p < 0.03) (Table 2).

Although reversals appear to be spontaneous, they might be a response to microheterogeneities in the texture of the agar surface. To test this, we spread silica suspended in M9 salts solution on the surface of agar plates to produce a density of approximately five particles per square millimeter. As a control, M9 from which the silica was removed was spread on plates. This should ensure that the animals are not responding to the smell or taste of the silica slurry. We did not see a significant difference (p > 0.2) between the reversal frequency of animals moving on silica and the controls, indicating that the texture of plates has little effect on reversal frequency (Table 2).

Chemosensation appears to mediate the effect of food on reversal frequency

Previous studies showed that the speed of locomotion and the frequency of reversal are both reduced when the animals enter a bacterial lawn (Zheng et al., 1999; Shingai, 2000). We confirmed this result by assaying animals on a bacterial lawn (+food vs -food; first vs first: p < 0.001; second vs second: p < 0.001; third vs third: p < 0.01) (Table 2). Two sensory systems could mediate the effect of food on reversal behavior. C. elegans exhibits chemotaxis to chemoattractants released by bacteria (Bargmann and Mori, 1997). Animals also sense the texture of the bacteria as they crawl over it, which requires the function of mechanosensory dopaminergic neurons (Sawin et al., 2000). To ask whether the reduced reversal frequency is a response to the smell or the texture of the bacteria, we compared mutant strains defective in each of these sensory modalities. The bas-1 mutant lacks dopamine and does not slow when it encounters food. However, its reversal behavior on food was not significantly different than wild type (Table 2). In contrast, che-2 and osm-1 mutants, which are defective in chemosensation (Lewis and Hodgkin, 1977; Culotti and Russell, 1978), had a significantly higher reversal frequency in the presence of food relative to wild type (che-2 vs N2 on food; first vs first: p < 0.001). The reversal frequency of che-2 in the absence of food was no different from its frequency in the presence of food, nor was it different from the frequency of wild type in the absence of food (p > 0.1). Thus, che-2 is not generally more prone to reverse. These results are consistent with the idea that the chemosensory modality mediates the change in reversal frequency in response to food.

Mechanosensory stimuli can suppress reversal frequency

We consistently observed a dramatic difference between the mean reversal interval for the first reversal and subsequent reversals (Table 2), which reflects a suppression of reversals during the first reversal interval (Fig. 4). We hypothesized that this might result from mechanical stimulation when the animal is moved to the assay plate. We therefore modified our assay by applying a mechanical stimulus immediately after the second reversal. If a mechanical stimulus suppresses reversals, then the reversal interval distribution for the third reversal should resemble that of the first. To confirm that the animal recovers from mechanical stimulation, we also measured the fourth reversal, the distribution of which should resemble that of the second reversal.

When animals were touched on the tail with an eyelash (gentle touch), their forward movement rate accelerated (our unpublished observation). Moreover, the third mean reversal interval was longer than the second (Table 3), indicating that gentle tail touch suppressed reversal frequency. The mean fourth reversal interval was not different from the second, indicating that the animal had recovered.

Table 3.

Effect of mechanosensory stimulation on mean reversal interval

	Mean reversal interval (seconds)
Stimulus applied	First	Second	Third	Fourth	Significance (p value) second versus third
Gentle touch (tail)
N2	26±2.7 (50)	14±2.2 (50)	21±3.2 (50)	13±2.8 (50)	0.02
mec-3	22±2.4 (30)	12±1.6 (30)	10±1.3 (30)	10±0.8 (30)	0.32
Harsh touch
N2	45±2.0 (50)	11±1.4 (50)	42±3.8 (50)	10±0.9 (50)	0.01
mec-3	30±3.3 (50)	11±1.7 (50)	14±1.9 (50)	12±1.4 (50)	0.25
Heat stimulus	63±4.5 (60)	21±3.0 (60)	19±2.9 (60)	15±2.1 (60)	0.79

The data consist of the mean reversal intervals in seconds ± SEM for the first, second, third, and fourth intervals. The numbers of worms assayed are in parentheses. In all cases the stimulus was applied after completion of the second reversal.

The second and third reversal intervals were compared using the Mann-Whitney U statistic.

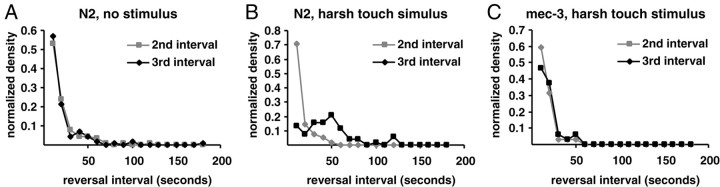
After the worms were prodded with a platinum wire (harsh touch), the animals either accelerated or initiated a reversal. If the animal reversed, then the third reversal interval was measured from completion of this touch-induced reversal. The suppression of the third reversal compared with the second reversal was even greater than that induced by gentle touch (Table 3). The suppression did not depend on whether the animal responded to the stimulus by moving forward or backward. Like the first reversal interval, the distribution of the poststimulus third reversal interval had a more Gaussian distribution (Fig. 8). By the fourth reversal, the animal had recovered from the stimulus. Thus, mechanosensory stimuli could account for the difference between the first and subsequent reversal intervals in our assays.

Figure 8.

Harsh touch suppresses reversals. Reversal interval histogram for second and third reversals of a wild-type unstimulated animal (A), a wild-type animal that has experienced harsh touch between the second and third reversals (B), and a mec-3(e1338), touch-insensitive mutant animal that has experienced harsh touch between the second and third reversals (C).

Suppression of reversal by touch should be mediated by the mechanosensory neurons ALM, AVM, and PLM, which respond to gentle touch stimuli, and/or the neuron PVD, which is thought to mediate the response to harsh touch (Driscoll and Kaplan, 1997). The mec-3 gene encodes a transcription factor that is necessary for the differentiation of ALM, AVM, PLM, and PVD (Way and Chalfie, 1988, 1989). In mec-3 mutants, neither gentle nor harsh touch suppressed the frequency of the poststimulus third reversal (Table 3, Fig. 8). Thus, the suppression of reversals in response to touch is mediated through the mechanosensory neurons affected in the mec-3 mutant and not through some other sensory modality. Interestingly, the mean first reversal interval was still longer in mec-3 mutants, indicating that although mechanostimulation is sufficient to suppress the reversals during the first interval, other factors are also involved.

Do all stimuli that affect locomotion acutely suppress subsequent reversals? Animals reverse in response to a source of intense heat at their head. We moved a hot platinum wire near the animal's head immediately after the second reversal, thus inducing another reversal. We found no significant difference between the reversal intervals of the second, third, and fourth reversals (Table 3). Therefore, merely inducing reversal does not suppress the frequency of subsequent reversals. Rather, reversal suppression depends on the type of sensory input.

Discussion

Our results indicate that the probability of initiating a spontaneous reversal is a critical parameter that determines the locomotory trajectory of C. elegans. Reversal frequency is influenced by multiple inputs that reflect the internal state of the animal and its external environment. As such, reversal behavior is a model for the integration of sensory inputs to generate an appropriate motor output.

A model of the trajectory of C. elegans reveals important parameters

We have defined several parameters that determine the trajectory of C. elegans. Although we have not looked exhaustively at both auto- and cross-correlations among parameters, when incorporated into a model of C. elegans locomotion, our functions resulted in trajectories that appeared to mimic those of the real animal. Thus we feel it is likely that we have incorporated into our model most of the relevant parameters and parameter relationships.

Plotting the dispersal of the C. elegans in our assay shows that locomotion is biphasic: it begins with an escape response when animals vacate the origin, and then, after ∼100 sec, the animals adopt a pattern of locomotion that resembles a random walk. This difference in the first 100 sec is clearly a result of the initial higher velocity and lower probability of reversal during the first reversal interval. If, in the model, we set the reversal probability function and speed of the first reversal to values characteristic of subsequent reversals, then the virtual animals exhibited only the second, random walk phase.

Although our model predicted that the turning rate distribution, and in particular the turning rate bias, should have a strong influence on dispersal, the role of turning rate regulation remains enigmatic. We could not confirm statistically the presence of a bias, but we included a bias in our model on the basis of our impression that the trajectories of some animals exhibit a distinct tendency to veer to one direction. Animals move their head from side to side when crawling, and a tendency toward deeper bends to one side may cause some animals to veer slightly in that direction (Croll, 1975). It may be possible to test this hypothesis by ablating neurons that control the magnitude of the bends on one side.

Interestingly, the frequency with which reversals are terminated by an omega turn affects dispersal relatively little. Because the omega turns nearly randomize the interval angle, it might be expected that increasing the frequency of omega turns would generate a trajectory that more nearly resembles a pure random walk. The lack of an effect of increased omega turns may reflect the fact that even non-omega turns of long duration (>3 sec) showed a significant dispersion (large SD) of the resumed angle distribution. This, in combination with the higher reversal frequency and slower speed after the first reversal, may represent a degree of behavioral redundancy that ensures the switch to a random walk.

Reversal frequency reflects the integration of many sensory inputs

We found that reversal frequency, in addition to being an important determinant of dispersal, is sensitive to many sensory inputs measuring both the internal state of the C. elegans and its environment. Thus, the circuit that determines reversal frequency is a point of integration for many sensory modalities.

Although each of the variables that we looked at reflects some sensory modality, not every variable necessarily reflects a different sensory input. For instance, we found significant effects of larval stage, gravidity, and sex on reversal frequency. Each of these might be conflated into one variable reflecting a single sensory input: whether the animals had eggs in the uterus. Before concluding that these variables reflect distinct sensory modalities, one would have to demonstrate an association between each variable and a specific neuron or signaling pathway.

Another sensory input that could easily be reflected in several variables is the texture of the agar. It has been proposed that microheterogeneities in the surface of the agar are sufficient to induce reversals (Zheng et al., 1999). C. elegans can sense texture because they slow down when crawling on agarose beads (Sawin et al., 2000). However, although it appears that animals slow down when entering bacteria because the bacterial lawn has a different texture, the animals show no increase in reversal frequency on bacteria. Moreover, if reversals are a response to bumps in the agar, animals should reverse more frequently on the plates sprinkled with silica. We saw no evidence of this.

Other types of mechanosensation have a profound effect on reversal frequency. We showed that both gentle tail touch and harsh touch are capable of suppressing spontaneous reversals for up to 1 min after the stimulus, even if the touch induced an immediate reversal. This phenomenon appears to represent a form of nonassociative memory. Touch does not simply induce a general tendency toward forward motion rather than backward motion because when the touch stimulus induced a reversal, the reversal was not of short duration. In fact the touch-induced reversals are of somewhat longer average duration (our unpublished observation). Touch does not simply suppress direction change, because in cases in which the touch stimulus induced a reversal, the animal changed direction normally to resume forward motion. Touch-induced reversal suppression is also not another manifestation of mechanosensory habituation because habituation has no effect on spontaneous reversal frequency (Rankin and Wicks, 2000). Finally, it is not a general response to an acute stimulus, because heat induces reversal but does not result in subsequent reversals being suppressed. Thus, the reversal suppression is a complex change in the state of synapses or cells in the touch circuit that integrate information coming from the mechanosensory neurons.

Because we have ruled out the texture of the agar as a significant factor in reversal frequency, it appears that the effect of humidity on reversal frequency represents a specific sensory input measuring water balance in the animal. Water balance is likely to be an important sensory input for the locomotor circuit because non-dauer animals have a limited ability to resist desiccation and must migrate to areas with sufficient moisture. Our results suggest that reversal frequency plays an important role in seeking moisture. Because C. elegans inhabit the interface between a moist substrate and the air, they might respond to the moisture in either of these environments. Our results suggest that moisture in both the substrate and the air is important.

The rules governing sensory integration are not specifically addressed by our results, but we can draw some preliminary conclusions. Under all conditions that we examined, the mean first reversal interval was longer than subsequent reversal intervals, indicating that no sensory input overrides this effect. Thus, to some extent the effects of various sensory inputs are at least additive.

Finally, two locomotory parameters, speed and reversal frequency, can be varied independently. During the first reversal interval, animals move fast but reverse infrequently. As they slow down, their reversal frequency increases. In contrast, on a bacterial lawn animals move slowly and reverse infrequently.

The purpose of reversals

At first glance, reversals seem to be a means of avoiding undesirable environments. C. elegans reverses in response to a touch to the head, in response to a decreasing gradient of attractive odorant, and in response to moving off of a food-rich bacterial lawn. However, we show that C. elegans combines both high acute reversal frequency (at the moment of harsh touch) with low reversal frequency (after it resumes forward movement) to generate a more sophisticated and effective avoidance behavior. Therefore, if reversals are simply an avoidance behavior, then C. elegans is constantly reassessing its priorities. For example, after it avoids harsh touch by reversing, an animal may try to avoid further touch stimuli by moving forward as long as it does not encounter another touch stimulus. However, food may gradually become the new priority. This switch in priorities would explain the increased probability of first reversal over time as the animal begins to seek, and fails to encounter, food. Of course, if the stimulus that the animal is avoiding depends on a complex and time-varying environmental context, it becomes difficult to predict what the worm is avoiding, and the generalization that reversals are an avoidance behavior becomes less useful and potentially circular.

Of course not all factors affecting reversal frequency necessarily act through a behavioral program. The reduced reversal frequency at low temperature is presumably a direct consequence of lower temperature on metabolic rate. Similarly, the reduced reversal frequency in 6-d-old animals may be a general effect of aging that includes changes in muscle morphology and general sluggishness.

This analysis of the parameters defining locomotion and particularly reversal behavior provides the basis for identifying the neural and molecular basis of the integration of several sensory modalities. Future research can combine the laser ablation of identified neurons and the use of mutants that affect specific aspects of the nervous system to understand the molecular mechanisms underlying a simple multimodel integration circuit.