The Contribution of Resurgent Sodium Current to High-Frequency Firing in Purkinje Neurons: An Experimental and Modeling Study

Abstract

Purkinje neurons generate high-frequency action potentials and express voltage-gated, tetrodotoxin-sensitive sodium channels with distinctive kinetics. Their sodium currents activate and inactivate during depolarization, as well as reactivate during repolarization from positive potentials, producing a “resurgent” current. This reopening of channels not only generates inward current after each action potential, but also permits rapid recovery from inactivation, leading to the hypothesis that resurgent current may facilitate high-frequency firing.

Mutant med mice are ataxic and lack expression of the Scn8a gene, which encodes the Na_V1.6 protein. In med Purkinje cells, transient sodium current inactivates more rapidly than in wild-type cells, and resurgent current is nearly abolished. To investigate how Na_V1.6-specific kinetics influence firing patterns, we recorded action potentials of Purkinje neurons isolated from wild-type and med mice. We also recorded non-sodium currents from Purkinje cells of both genotypes to test whether the Scn8a mutation induced changes in other ion channels. Last, we modeled action potential firing by simulating eight currents directly recorded from Purkinje cells in both wild-type and med mice.

Regular, high-frequency firing was slowed in med Purkinje neurons. In addition to disrupted sodium currents, med neurons had small but significant changes in potassium and leak currents. Simulations indicated that these modified non-sodium currents could not account for the reduced excitability of med cells but instead slightly facilitated spiking. The loss of Na_V1.6-specific kinetics, however, slowed simulated spontaneous activity. Together, the data suggest that across a range of conditions, sodium currents with a resurgent component promote and accelerate firing.

Introduction

Cerebellar Purkinje neurons fire high-frequency action potentials spontaneously, in vivo and in vitro (Granit and Phillips, 1956; Thach, 1968; Latham and Paul, 1971; Llinás and Sugimori, 1980; Häusser and Clark, 1997). These neurons express voltage-gated tetrodotoxin (TTX)-sensitive Na channels with unusual properties, including a “resurgent” sodium current that is elicited by step repolarizations from positive potentials (Raman and Bean, 1997). The resurgent current is associated with a rapid recovery from inactivation of transient (depolarization-evoked) sodium current, leading to the hypothesis that sodium channels that produce both transient and resurgent current may facilitate high-frequency firing of action potentials (Raman and Bean, 1997, 2001).

The characteristic sodium currents of Purkinje neuronal somata are disrupted in ataxic mice that have mutations in Scn8a (Duchen and Searle, 1970; Duchen and Stefani, 1971; Burgess et al., 1995). This gene encodes the Na_V1.6 protein, one of the sodium channel α subunits expressed by mature Purkinje neurons (Burgess et al., 1995; Schaller et al., 1995; Felts et al., 1997). In med mice, which lack Na_V1.6 expression, transient current inactivates more rapidly and resurgent sodium current is reduced by 90% (Kohrman et al., 1996a,b; Raman et al., 1997).

Because of these changes, Purkinje neurons of med mice provide a good preparation for testing the role of resurgent sodium current in facilitating high-frequency firing of action potentials. Regular and burst firing both appear to be disrupted in Purkinje neurons of these mice (Harris et al., 1992; Raman et al., 1997), supporting the idea that the specific sodium current kinetics may be important for normal firing patterns. Mutations of a single gene, however, have been reported to change the expression of other proteins, including ion channels (Brickley et al., 2001; Zhang et al., 2002). Consequently, any changes in firing observed in med cells cannot necessarily be ascribed to alterations in sodium currents.

Conversely, the presence of resurgent sodium current is not sufficient to guarantee a particular mode of firing. Resurgent currents have been documented in at least three other neuronal classes, the patterns of activity of which are clearly distinct from those of Purkinje cells (Mossadeghi and Slater, 1998; Raman et al., 2000; Do and Bean, 2003). Such observations not only illustrate that firing patterns are dictated by multiple ionic currents, but also reopen the question of the extent to which resurgent sodium current promotes high-frequency activity.

To test the contribution of Na_V1.6-dependent currents to firing patterns, we first recorded electrical properties of current-clamped Purkinje neuronal somata isolated from wild-type and med mice. Next, we made comparisons between phenotypes of the ionic currents other than sodium currents that are most likely to participate in high-frequency activity. Finally, we developed a computer model incorporating eight ionic currents recorded directly from Purkinje neurons and simulated action potentials with and without resurgent current. The data suggest that although several types of currents interact to preserve high-frequency firing, resurgent kinetics consistently increase the rate of action potential firing and promote spontaneous activity.

Materials and Methods

Preparation

Heterozygous Scn8a^med breeder mice were obtained from Jackson Laboratories (Bar Harbor, ME). Experiments were performed on both unaffected (Scn8a^med +/+ and +/-) and affected (Scn8a^med -/-) mouse pups, aged postnatal day 14–20. DNA was extracted from tails of mice used for experiments and genotypes were determined by PCR, with forward primer AGG TTC TAG GCA GCT TTA AGT GTG and reverse primer GGA CTT AGA ATG TAC AAG GCA GGA G (Kohrman et al., 1996a). Reactions were performed for 35 cycles of 30 sec at 94°C, 30 sec at 60°C, and 30 sec at 72°C, followed by one cycle at 72°C for 2.5 min, giving a PCR product of 190 base pairs for the wild-type and 370 base pairs for the mutant. Throughout the text, the term “med” refers to the animals that were homozygous for the recessive null mutation.

Cerebellar Purkinje neurons were acutely dissociated as described previously (Regan, 1991; Raman et al., 1997). In accordance with institutional guidelines, mice were deeply anesthetized with halothane and then decapitated. The superficial layers of the cerebellum were removed and minced in ice-cold, oxygenated dissociation solution containing (in mm): 82 Na₂SO₄, 30 K₂SO₄, 5 MgCl₂, 10 HEPES, 10 glucose, and 0.001% phenol red (buffered to pH 7.4 with NaOH). The tissue was incubated for 7 min in 10 ml of dissociation solution containing 3 mg/ml protease XXIII (pH readjusted) with 100% oxygen blown over the surface of the fluid at 31°C. The tissue was then washed in warmed, oxygenated dissociation solution containing 1 mg/ml bovine serum albumin and 1 mg/ml trypsin inhibitor and then transferred to Tyrode's solution containing (in mm): 150 NaCl, 4 KCl, 2 CaCl₂, 2 MgCl₂, 10 HEPES, and 10 glucose (pH readjusted) at room temperature. Tissue was microdissected and triturated with a series of fire-polished Pasteur pipettes to release individual neurons. Purkinje cell bodies were identified by their large size and characteristic tear shape. Cells were used for recording between 1 and 6 hr after trituration.

Electrophysiological recording

Action potential measurements. Cells were bathed in Tyrode's solution. Borosilicate pipettes (3–5 MΩ) were filled with a quasi-physiological intracellular solution containing (in mm): 103.5 KCH₃O₃S (K-methanesulfonate), 1.8 NaCl, 0.9 EGTA, 9 HEPES, 1.8 MgCl₂, 57.6 sucrose, 14 Tris-creatine phosphate, 4 MgATP, 0.3 Tris-GTP, buffered to pH 7.4 with KOH for a final potassium concentration of 128 mm. To test for effects of calcium buffering on firing, we used an alternative pair of intracellular solutions, containing (in mm): 117 K-gluconate, 3.6 Nagluconate, 5.4 NaCl, 1.8 MgCl₂, 9 HEPES, 14 Tris-creatine phosphate, 4 MgATP, 0.3 Tris-GTP, and 0.9 or 9 EGTA, buffered to pH 7.4 with KOH (for 0.9 EGTA) or KOH and TrisOH. In both of these gluconate-based intracellular solutions (low and high EGTA), the total potassium concentration was kept constant at 124 mm. With each solution, recordings were made from equal numbers of wild-type and med cells (K-methanesulfonate, n = 10; K-gluconate, low EGTA, n = 4; K-gluconate, high EGTA, n = 4). Action potential waveforms and rates of firing were not measurably different with the different solutions, and the data have been pooled.

Whole-cell patch recordings were made with a Dagan BVC amplifier (Minneapolis, MN). Data were recorded with an ITC-18 interface (InstruTech, Great Neck, NY) and PULSE software (HEKA Electronik, Lambrecht, Germany). At the beginning of each recording, cells were held at -60 mV in voltage-clamp mode, and a step depolarization to 0 mV was applied. Although the quality of clamp was suboptimal, the peak inward current provided an estimate of the total sodium current in each neuron. Action potentials were subsequently measured in current-clamp (bridge) mode.

Voltage-clamped current measurements. Borosilicate pipettes (1–3 MΩ) were filled with the same K-gluconate-based, high EGTA solution that was used for current-clamp recordings, except as noted. Whole-cell voltage-clamp recordings were made with an Axopatch 200B amplifier and pCLAMP software (Axon Instruments, Foster City, CA). Series resistance was compensated by >90%. After a recording was established, cells were placed in front of an array of gravity-driven flow pipes, through which the desired extracellular solutions were applied. Currents were pharmacologically isolated by subtraction of currents measured with and without blockers.

Voltage-gated, calcium-independent potassium currents were measured first in Tyrode's solution in which 2 mm CoCl₂ replaced the 2 mm CaCl₂ and to which 900 nm TTX was added. A series of increasing concentrations of TEA-Cl (30 μm to 5 mm) was then applied through successive flow pipes. Because gluconate has been reported to reduce some potassium currents (Zhang et al., 1994; Velumian et al., 1997), TEA dose–response curves were measured with methanesulfonate replacing gluconate in the pipette in five control experiments. Although there was a tendency for the currents remaining in 5 mm TEA to be a few percent larger with methanesulfonate in the pipette, the dose–response curves were statistically indistinguishable from the data measured with gluconate. For consistency, only the recordings made with gluconate are reported.

Hyperpolarization-activated cation currents (I_h) were recorded in Tyrode's solution, and currents were evoked by 1 sec step hyperpolarizations from -50 mV. At each potential, I_h was estimated as the difference between the instantaneous and steady-state currents. Iberiotoxin-sensitive K(Ca) currents were recorded in normal Tyrode's solution plus 1 mg/ml cytochrome c with and without 100–300 nm iberiotoxin. These recordings were made with either the low EGTA K-methanesulfonate intracellular solution or the high EGTA K-gluconate solution. Instantaneous leak currents were measured with step hyperpolarizations from -60 mV to potentials from -70 to -90 mV.

Voltage-clamp recordings were made at room temperature to improve the quality of clamp of whole-cell currents. Most current-clamp recordings were made at room temperature so that the simulations of spiking based on models of these currents could be compared with the experimental data. For the experiments testing the effect of temperature on spiking, cells were warmed with a heating plate directly beneath the recording chamber, and recordings were made at temperatures between 22° and 34°C in ∼4°C increments. All drugs were obtained from Sigma (St. Louis, MO) except TTX and iberiotoxin, which were from Alomone Labs (Jerusalem, Israel).

Analysis

Data were analyzed with IGOR software (Wavemetrics, Lake Oswego, OR). Conductance–voltage curves were constructed from peak currents divided by the driving force at each voltage, and data were fit with the Boltzmann equation, G(V) = G_max/(1 + exp(-(V - V_1/2)/k)), where G is conductance, V is voltage, G_max is the maximal conductance, V_1/2 is the voltage at which half the channels are activated, and k is the slope factor. Dose–response curves were fit with the Hill equation I/I_max = (I^{TEA-sensitive}/I_max)^*(1 - ([TEA]/([TEA] + IC₅₀))) + (1 - I^{TEA-sensitive}/I_max), where I is current, I_max is the maximal current, I^{TEA-sensitive} is the TEA-sensitive current, [TEA] is the concentration of TEA, and IC₅₀ is the concentration of TEA that blocks half I^{TEA-sensitive}.

Data are reported as mean ± SE. Statistical significance of differences relative to wild type was assessed with t tests, and p values are reported.

Simulations

Experimentally recorded currents were modeled with NEURON (Hines and Carnevale, 1997). All experimental data used for the model were obtained in this study, with the exception of TTX-sensitive sodium currents (Raman et al., 1997) and P-type calcium currents (Raman and Bean, 1999). Currents were modeled as described below, and action potentials were simulated with a single compartment cylindrical model of length 20 μm and radius 10 μm.

Sodium current

The resurgent sodium current in simulations of wild-type Purkinje cell bodies was modeled using a kinetic scheme based on the model of Raman and Bean (2001). The state model is reproduced here:

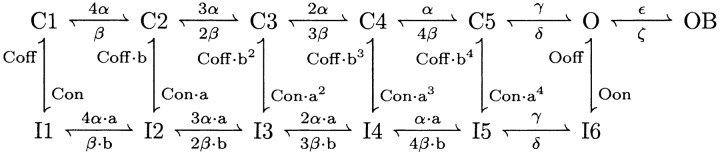1

C, I, O, and OB represent closed, inactivated, open, and blocked states, respectively. The rate constants α, β, γ, δ, ϵ, ζ, Con, Coff, Oon, and Ooff have values identical to those of Raman and Bean (2001). The factor a in Raman and Bean (2001) was replaced by the factors a and b in this model. Here, a = (Oon/Con) ^1/4 and b = (Ooff/Coff) ^1/4. In simulations of med Purkinje cells, in which resurgent current is absent, the rate constant ϵ was reduced to 1 × 10 ^-12/msec to eliminate entry into the blocked state OB. To produce the faster decay of the transient current observed in med cells (Raman et al., 1997), the rate constant Oon was increased from 0.75/msec to 2.3/msec. Current was calculated using Ohm's law, multiplying the occupancy of O by the driving force and G_max (150 pS/cm ²). E_Na was set at +60 mV.

Hodgkin-Huxley simulations

All currents other than the sodium current were modeled using the formalism of Hodgkin and Huxley (1952) (Huguenard and McCormick, 1992; McCormick and Huguenard, 1992). Currents were modeled as populations of identical channels, the activity of which depended on one or more gates (e.g., m), which in turn depended on the empirically determined voltage-dependent factors m_∞ and τ_m (in seconds) according to the equation:

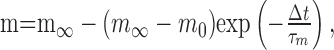2

where t is time, and m₀ is the value of m at t = 0. The steady-state activation and inactivation (m∞) were modeled with the Boltzmann equation:

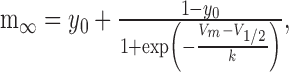3

where V is the membrane potential, V_1/2 is the voltage of half (in)activation, k is the slope factor, and y₀ is the voltage-insensitive fraction of gates. For all activation curves, y₀ was constrained to 0. The parameters of the steady-state activation and inactivation equations for each current are presented in Table 1. Equations used to calculate the values of τ_m (in seconds) are presented in their respective sections.

Table 1.

Model parameters for currents simulated with Hodgkin-Huxley kinetics

			m			h
Current	G	Gmax(pS/cm2)	V½(mV)	k(mV)	y0(pS/cm2)	V½(mV)	k(mV)
Kfast	m3h	40	−24	15.4	0.31	−5.8	−11.2
Kmid	m4	20	−24	20.4
Kslow	m4	40	−16.5	18.4
P-type Ca	m	See Materials and Methods	−19	5.5
BK	m3z2h	70	−28.9	6.2	0.085	−32	−5.8
Ih	m	1	−90.1	−9.9
Leak	1	0.5

The value of G, which ranges from 0 to 1, was then calculated from the values of the gates, as indicated in Table 1. For all ionic currents but calcium, current was calculated from Ohm's law:

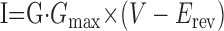4

where E_rev is the reversal potential of the permeant ion. Calcium current was calculated using the Goldman-Hodgkin-Katz current equation:

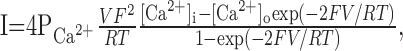5

where P_Ca2+ = 5 × 10 ^-5 cm/sec, [Ca²⁺]_i = 100 nM, [Ca²⁺]_o = 2 mm, and T = 295 K. F and R had their usual values.

Voltage-gated potassium currents

Three separate voltage-gated potassium currents were simulated (see Results), called K_fast, K_mid, and K_slow. E_K was set at -88 mV for all potassium currents. The τ_m and τ_h of K_fast were simulated with the two-part piecewise functions:

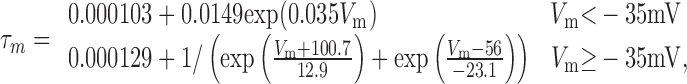6

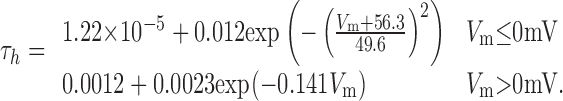7

The τ_m of K_mid was simulated with the two-part piecewise function:

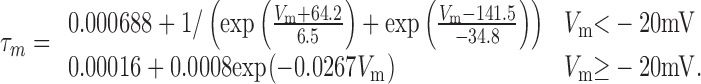8

The τ_m of K_slow was described by the function:

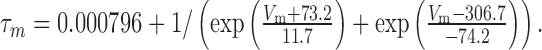9

P-type calcium current

The model of P-type calcium current was based on data from Raman and Bean (1999). The activation of P-type calcium current in Purkinje neurons displays no delay in activation (Regan, 1991) and can be modeled with a single activation gate (De Schutter and Bower, 1994). The τ_m was simulated with a two-part piecewise function:

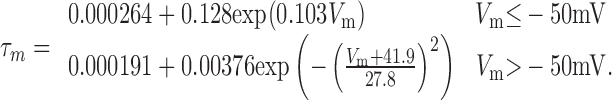10

Calcium-activated potassium current

The τ_m and τ_h of calcium-activated potassium (BK) current were modeled as:

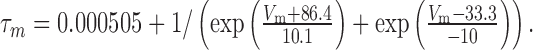11

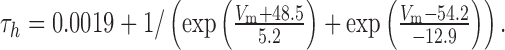12

For the calcium-dependent gate z, the time constant τ_z was set equal to 1 msec, and the steady-state values were described by the equation:

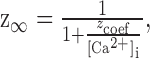13

where z_coef = 0.001 mm and [Ca²⁺]_i is in millimolar concentration. Calcium concentration was simulated in a 100 nm shell underneath the cell membrane (McCormick and Huguenard, 1992). The internal calcium concentration changed according to:

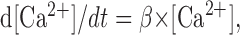14

where the rate constant β was 1/msec (McCormick and Huguenard, 1992). The calcium concentration was calculated as:

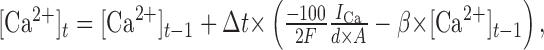15

where [Ca²⁺] is concentration in millimolar, Δt is time in milliseconds, d is depth in micrometers, A is area in square micrometers, and current is in nanoamperes. The calcium concentration was constrained to be ≥100 nm.

Hyperpolarization-activated cation current

Because I_h activates without a delay in activation, it was modeled as a single gate, with τ_m described by the function:

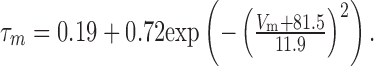16

The E_rev for I_h was set to be -30 mV.

Leak current

The leak current was modeled as a linear voltage-independent conductance following Ohm's law (Eq. 4), with E_leak = -60 mV.

Results

Firing properties of wild-type and med Purkinje neurons

Extracellular recordings from Purkinje cells in vivo have shown that the basal rate of simple spikes is greatly reduced in med relative to wild-type mice (Harris et al., 1992). To quantify these changes and to explore their kinetic basis, we recorded the action potentials produced by Purkinje cell bodies acutely isolated from med mice (referred to as “med neurons”), as well as from wild-type littermate controls.

Because Purkinje cells isolated from normal mice generate regular, spontaneous action potentials (Nam and Hockberger, 1997; Raman and Bean, 1997, 1999) that are similar in frequency to those recorded in more intact preparations, we first tested whether the reduced spontaneous activity, defined as firing rate in the absence of any current injection, of med cells recorded in vivo was retained in vitro. Consistent with previous studies, 15 of 18 wild-type cells produced action potentials spontaneously, with mean firing rates across all cells of 29 ± 5 spikes/sec (Fig. 1A,B). Only 10 of 18 med cells, however, fired spontaneously, and firing was generally more irregular and slower than in wild-type cells, with a mean firing rate of 5 ± 1 spikes/sec (n = 18; p < 0.0001) (Fig. 1A,B). Comparing only the spontaneously active cells, wild-type cells fired at 35 ± 4 Hz and med cells fired at 9 ± 2 Hz (p < 0.0001).

Figure 1.

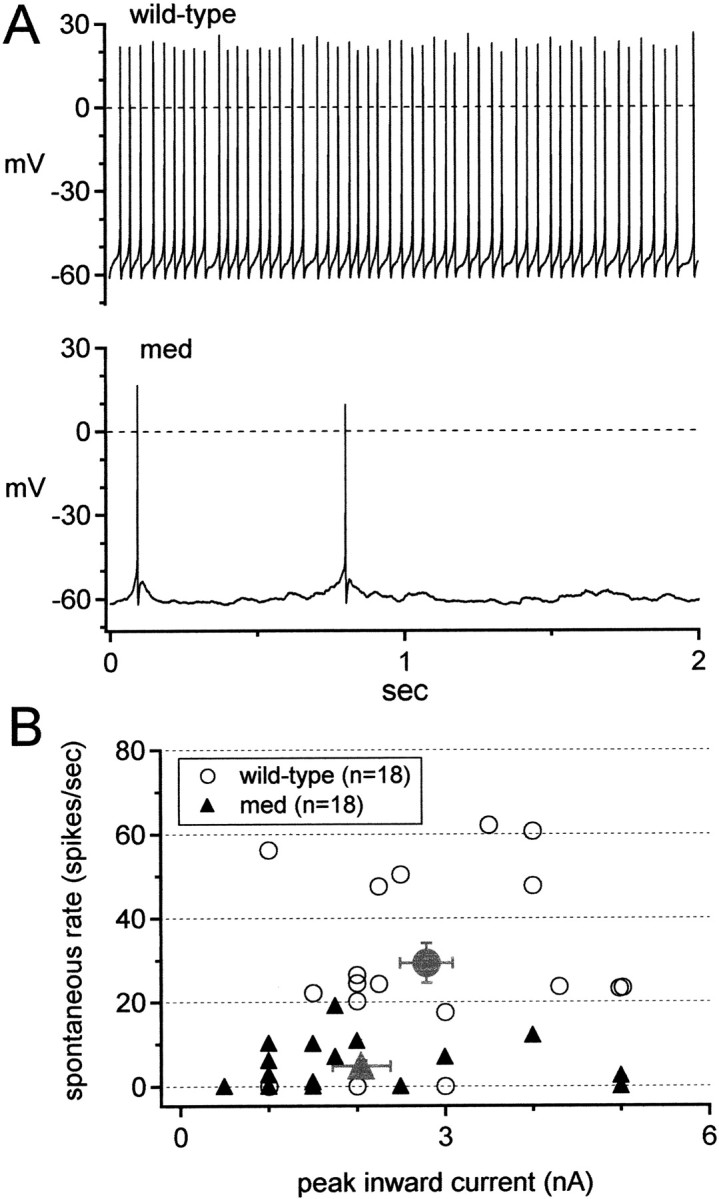
Reduction of spontaneous firing rate in med Purkinje neurons. A, Representative traces of spontaneous firing of a wild-type (top) and med (bottom) neuron; physiological solutions, no injected current. B, Spontaneous firing rates of all cells tested versus peak inward current (as an estimate of sodium current density) evoked by a step from -60 to 0 mV. Gray symbols show mean spontaneous rates for each phenotype.

Next, we tested whether this difference in spontaneous firing rate depended strongly on temperature or intracellular solutions. Raising the recording temperature from 22 to 34°C increased the firing rates by 0.65 ± 0.37 Hz/°C (wild type, n = 8) and 0.65 ± 0.65 Hz/°C (med, n = 4). The effect of increasing temperature, however, varied widely across cells; firing rates of five of eight wild-type cells and three of four med cells did not change, whereas three wild-type cells and one med cell increased their rates by >1.5 Hz/°C. Importantly, however, changing the temperature did not raise med firing rates to normal values, consistent with extracellular recordings made in vivo (Harris et al., 1992). Additionally, in the spontaneously active cells of either genotype, the firing rate was not significantly influenced by the intracellular calcium buffering (low vs high EGTA in each phenotype: wild type, p = 0.6; med, p = 0.11), suggesting that the exogenously applied calcium buffer does not strongly regulate firing in isolated cell bodies.

Because the absolute and relative amplitudes of various currents differ across individual neurons, even from the same genotype, it is possible that the silent cells had larger-than-average potassium currents or smaller-than-average sodium currents, or both, preventing their depolarization to threshold. Consistent with this idea, the 3 of 18 wild-type cells that did not fire spontaneously rested at unusually negative potentials, near -75 mV, which may account for their lack of spontaneous activity. In contrast, silent med cells were not strongly hyperpolarized, resting at -65 ± 3mV(n = 8), a value quite similar to the resting potential in TTX of normal Purkinje cells of -62.5 mV (Raman and Bean, 1999).

A decrease in total sodium current, which might arise from either a smaller cell size or a reduced channel density, might underlie the impaired ability of med cells to fire spontaneously. Regarding cell size, however, isolated med and wild-type cells looked the same under the light microscope, as reported previously (Raman et al., 1997). Moreover, their cell capacitances were statistically indistinguishable (wild type, 17.6 ± 3.5 pF, n = 16; med, 16.0 ± 1.7, n = 17; p = 0.12), suggesting that changes in cell size did not underlie the differences in electrical activity.

Even without a change in cell size, however, a reduction of sodium channel density in med cells might decrease spontaneous firing rates. This scenario seems plausible, given that the med cells lack expression of one of the three voltage-gated sodium channel α subunits that are normally expressed by Purkinje cells. To test whether sodium current amplitude was indeed reduced in med cells and whether it predictably regulated firing rate, we estimated the sodium current amplitude from the peak inward current evoked by a step depolarization from -60 to 0 mV in each cell in which action potentials were recorded. Consistent with direct measurements of TTX-sensitive sodium currents (Raman et al., 1997), med cells had ∼25% smaller average inward currents than wild-type cells, although the distributions overlapped considerably (wild type, 2.8 ± 0.3 nA vs med, 2.1 ± 0.3 nA; p = 0.1) (Fig. 1B, gray symbols). In both phenotypes, however, firing rate failed to correlate with peak inward current (Fig. 1B). Independently of the peak inward current, 14 of 18 wild-type cells fired at rates >20 spikes/sec, whereas all 18 med cells fired at rates <20 spikes/sec. Because the spontaneous firing rates of wild-type and med Purkinje cells differ even at a fixed inward current amplitude, it is possible that sodium channel kinetics play a significant role in regulating activity.

Among the kinetic properties that distinguish Na_V1.6 from other α subunits is a tendency to produce larger steady-state sodium currents (Raman et al., 1997; Smith et al., 1998; Maurice et al., 2001). If med Purkinje cells fire more slowly than wild-type cells primarily because they lack sufficient steady depolarizing sodium current to bring the cells to threshold, then injections of steady depolarizing current injections might compensate for this loss. To study the effects of depolarizing inputs on neurons of the two phenotypes, therefore, we recorded responses of Purkinje cells to 400 msec step current injections. No holding current was applied before the step, and the amplitude of current injected was increased in 10 pA increments up to 50 pA. All cells responded to depolarizing injections with a train of action potentials, a single spike, or a burst. Sustained firing rates were quantified as the inverse of the mean interspike interval during each step; the firing rate for steps eliciting only a single spike or a single burst was scored as 0 spikes/sec. Characteristic responses for wild-type and med cells to 20 and 50 pA injections are illustrated in Figure 2A. These data are quantified in Figure 2B, in which firing rate (including cells scored as zero) is plotted against the amplitude of injected current for steps between -20 and 50 pA. For all depolarizing steps, med neurons fired more slowly than the wild-type neurons. For the 50 pA injection, the firing frequencies for wild-type and med cells were 65 ± 7 spikes/sec (n = 18) and 13 ± 5 spikes/sec (n = 18; p < 0.0001).

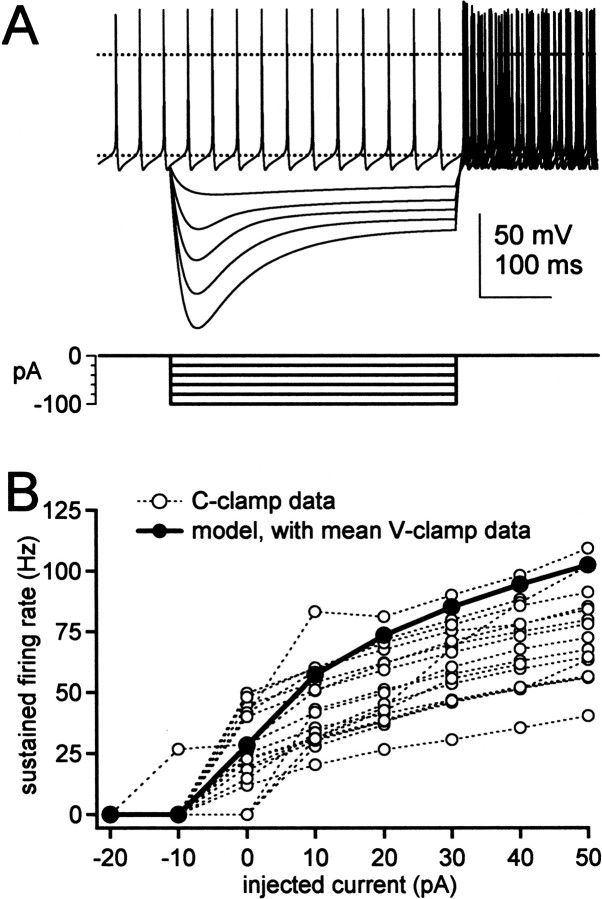
Figure 2.

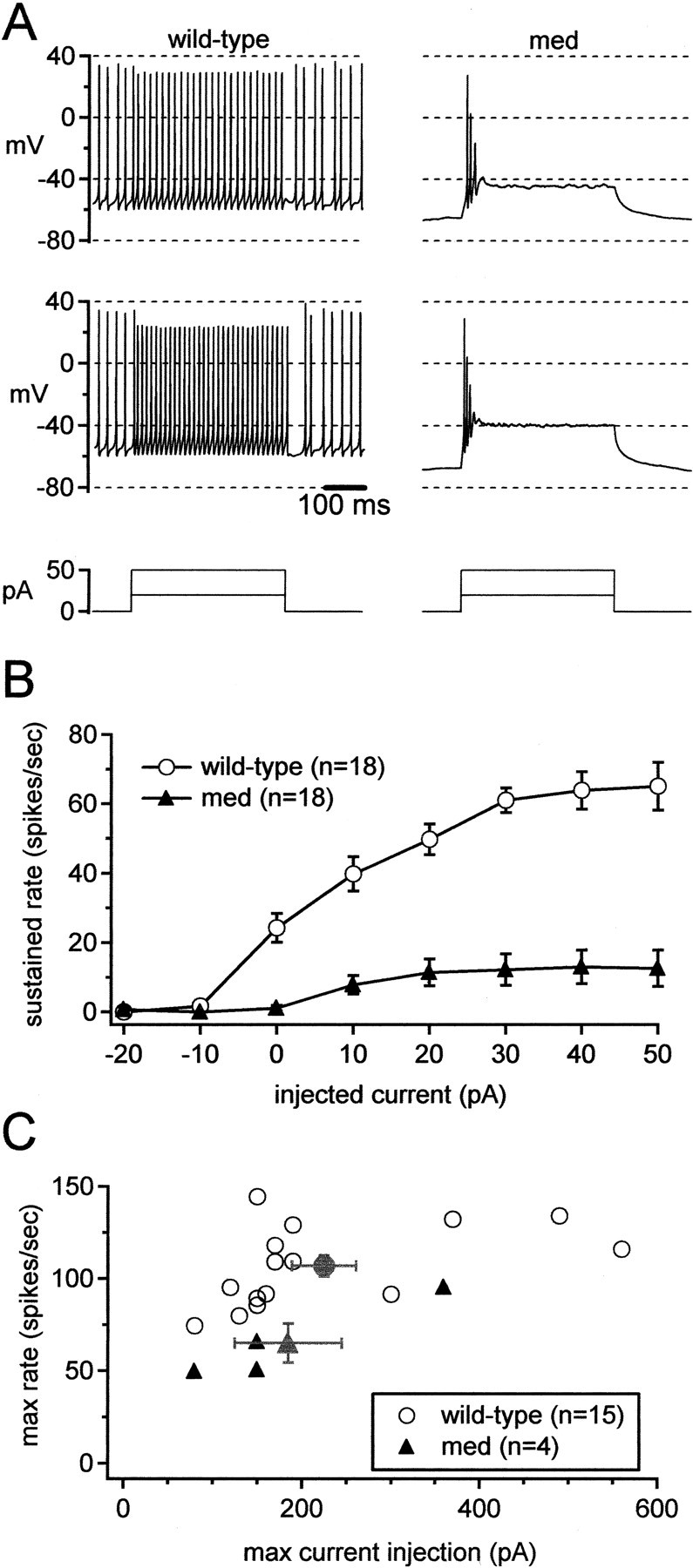
Disruption of sustained high-frequency firing in med Purkinje neurons. A, Representative action potentials evoked by 20 or 50 pA depolarizing current injections (top panels). Bottom panels, Current protocols. B, Mean sustained firing rates versus current injections for all cells tested. Cells that fired only a single spike or burst were scored as zeroes. Same cells as in Figure 1. C, Maximal sustained firing rates (before depolarization block) for only the regularly firing cells in B versus the current injection eliciting the response. Gray symbols indicate mean values.

To test whether this difference was dominated by the fact that failures to fire during the step were included in the averages, we compared excitability of the most reliably firing wild-type and med cells. For only those cells that continued firing throughout a 50 pA step, we increased the amplitude of current injections until the cell failed to fire throughout the step. We then measured the maximal sustained firing rates achieved by wild-type and med cells. Figure 2C plots the maximal firing rates of those regularly firing neurons against the amplitude of current injection eliciting that response. Even with this selection of the most strongly firing mutant cells, wild-type neurons attained significantly higher maximal firing frequencies than med cells (107 ± 6 spikes/sec at 225 ± 36 pA, n = 15 vs 65 ± 10 spikes/sec at 185 ± 60 pA, n = 4; p = 0.02). Thus, steady current injections could not raise firing by the med cells up to wild-type rates, suggesting that the mutant cells lack something more than a persistently depolarizing current.

One possibility is that the slower firing of med results from the loss of more complex components of Na_V1.6-mediated currents, including the resurgent component of sodium current. Alternatively, however, other modifications in intrinsic properties, which may be secondary consequences of the mutation, may also contribute to these changes in excitability. We therefore made direct measurements of currents that were likely to be involved in action potential production in both wild-type and mutant cells. These experiments had two purposes: (1) to test for differences in non-sodium currents between the med and wild-type cells, and (2) to obtain data for development of a computer simulation of action potential firing by Purkinje cells.

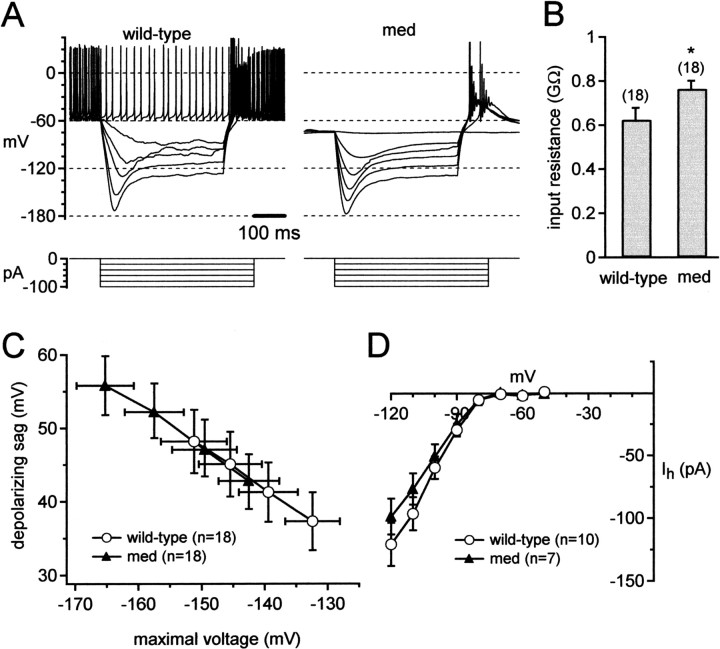
We began testing the med neurons for such changes by recording responses evoked by hyperpolarizing current injections. Representative voltage changes in wild-type and med cells elicited by step hyperpolarizing currents are shown in Figure 3A. For each neuron, we measured the maximal voltage reached during the step plotted against the injected current (between -100 and -70 pA). As shown in Figure 3B, the same current injections evoked larger voltage changes in med cells. The slope of voltage versus current plot gave a coarse estimate of input resistance; this value was significantly higher for med cells (763 ± 38 MΩ; n = 18) than for wild-type cells (624 ± 54 MΩ; n = 18; p = 0.04). Because cell capacitance was the same across cell types, this difference suggests that disruption of Na_V1.6 expression led to measurable changes in other subthreshold currents. Currents that are likely to be active in this voltage range, and therefore may contribute to the observed voltage changes, include hyperpolarization-activated cation currents (I_h) and voltage-independent currents such as inward rectifiers and leak currents.

Figure 3.

Modification of passive properties in med Purkinje neurons. A, Responses to hyperpolarizing current injections (top). Bottom, Current protocols. B, Input resistance, calculated from peak voltages during hyperpolarizing steps (-70 to -100 pA). Asterisk indicates statistical significance. These are the same cells as in Figure 1. C, Depolarizing sags versus maximal voltages during current injections (-70 to -100 pA). D, Current–voltage relation for I_h recorded from wild-type and med cells.

In both cell types, I_h was evident as a “sag” depolarization after hyperpolarization to potentials more negative than approximately -100 mV (Fig. 3A). To test whether changes in I_h led to the increase in apparent input resistance, we plotted the amplitude of the depolarizing sag against the maximal negative voltage reached during current injections between -100 and -70 pA. As illustrated in Figure 3C, at any voltage, the mean sags of med neurons overlaid those of wild-type cells. Linear regression over the data from each cell indicated that the sag amplitudes were indistinguishable (at -120 mV; p = 0.83), suggesting that the increase in apparent input resistance of med cells did not result from a decrease in I_h. To verify this result, we measured I_h directly from wild-type and med neurons. Mean current–voltage relations are plotted in Figure 3D.At -120 mV, I_h was -121 ± 17 pA in wild-type (n = 10) and -99 ± 14 pA in med cells (n = 7; p = 0.34), indicating that I_h was unchanged in med cells. Instead, this result supports the idea that the increased input resistance of med cells may result from decreased amplitudes of voltage-independent or leak-like conductances.

Voltage-gated potassium currents

We next tested whether currents actively involved in action potential production might also have been modified as a consequence of the med mutation. In many cells, high-frequency firing is facilitated by highly TEA-sensitive currents (Rudy et al., 1999; Rudy and McBain, 2001). Consistent with this idea, all of the potassium currents that flow during spontaneous action potentials in isolated Purkinje neurons can be blocked by 1 mm TEA (Raman and Bean, 1999). Therefore, we recorded voltage-gated, calcium-independent potassium currents and compared the TEA sensitivity of these currents in wild-type and med cells.

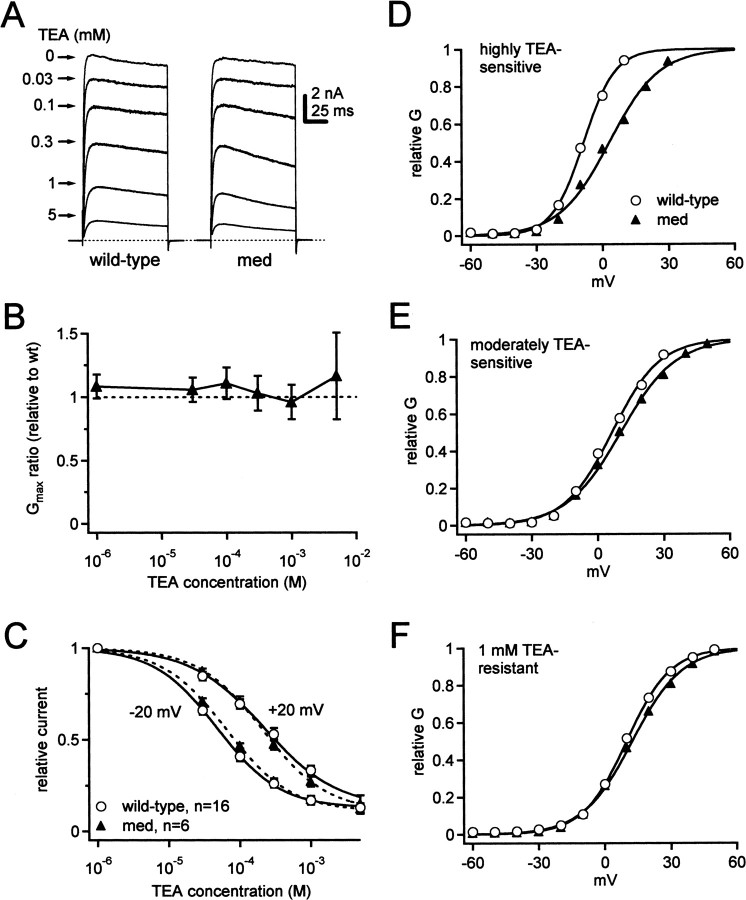
Potassium currents were evoked with step depolarizations from -60 mV. Although this holding potential inactivates some potassium currents, it was chosen because spontaneously firing Purkinje neurons do not hyperpolarize strongly between spikes. Steps from -60 mV therefore provide a reasonable estimate of currents that are available during spontaneous activity. Currents were evoked in control solutions with step depolarizations, and all measurements were repeated in five concentrations of TEA (Fig. 4A). As documented previously, voltage-gated potassium currents in Purkinje neurons were highly TEA sensitive (Gähwiler and Llano, 1989), with ∼90% of the step-evoked current blocked by 5 mm TEA (Southan and Robertson, 2000).

Figure 4.

Distinct TEA-sensitive potassium currents of Purkinje cells. A, Calcium-independent outward currents at +20 mV in different concentrations of TEA (holding potential, -60 mV). Dotted line represents 0 pA. B, Ratio of G_max in mutants relative to wild-type versus TEA concentration. Dotted line represents no change in G_max. C, TEA dose–response curves at -20 and +20 mV for both phenotypes. Data were fit with the Hill equation (Materials and Methods) and are shown as solid lines (wild type) and dashed lines (med). D–F, Representative conductance–voltage curves from one wild-type and one med cell for currents with TEA sensitivity that was high (D), moderate (E), and low (F). The V_1/2 was positively shifted in the med cell for only the most highly sensitive TEA-sensitive currents.

Conductance–voltage curves were constructed for potassium currents recorded in all concentrations of TEA, and maximal conductances (G_max) were estimated from Boltzmann fits to the data. Both cell types had similar maximal potassium conductances (in 0 TEA: wild-type 154 ± 10 nS, n = 16; med, 167 ± 16 nS, n = 6; p = 0.5). The ratio of G_max in mutant to wild-type control stayed near 1 in all TEA concentrations, suggesting little if any upregulation or downregulation of the amplitudes of these potassium currents (Fig. 4B).

Inspection of the dose–response curves showed that the sensitivity to TEA appeared voltage dependent, with a more efficacious block at -20 mV than at +20 mV (Fig. 4C). In wild-type cells, the IC₅₀ was 48 μm at -20 mV and 219 μm at + 20 mV (n = 16 cells). A comparable difference in IC₅₀ values was present in the med cells (65 and 208 μm; n = 6). Because binding of external TEA is voltage independent (Taglialatela et al., 1991; Jarolimek et al., 1995; Hille, 2001), these data suggest the presence of multiple potassium channels that differ in their voltage dependence and TEA sensitivity. The more negatively activating potassium currents appear more highly TEA sensitive, whereas currents with a lower TEA sensitivity may activate substantially only at more depolarized potentials.

This difference is experimentally useful because it allows us to make an approximate discrimination among potassium currents based on their TEA sensitivity. We therefore isolated “highly TEA-sensitive current” by subtracting currents recorded in 100 μm TEA from control currents and “moderately TEA-sensitive current” by subtracting currents recorded in 1 mm TEA from those in 300 μm TEA. We also examined the properties of the remaining currents (“1 mm TEA-resistant current”). The subtracted currents, as well as the residual currents, are likely to yield an aggregate of potassium currents. Nevertheless, because 100 μm TEA blocks a large proportion of the current activated at -20 mV, the highly TEA-sensitive current should reveal the overall properties of the relatively low voltage-activated currents. Additionally, the moderately TEA-sensitive current should exclude the low voltage-activated current while including the rest of the current active during spontaneous firing of isolated Purkinje cells. Finally, the 1 mm TEA-resistant currents should reveal properties of any other potassium currents that are present in the cells and may participate in firing during exogenous depolarizations, such as from current injection or synaptic input.

Representative conductance–voltage curves for the three pharmacologically separated classes of voltage-gated potassium currents in the wild-type and med cells are shown in Figure 4D–F, and the mean parameters of Boltzmann fits are given in Table 2. As predicted by the dose–response curves, the highly TEA-sensitive currents activated at the most negative potentials; in wild-type neurons the V_1/2 was ∼16 mV more negative than the moderately TEA-sensitive currents (Fig. 4D,E, Table 2). Additionally, the highly TEA-sensitive currents activated and inactivated rapidly at positive potentials, whereas the moderately TEA-sensitive currents showed no rapid inactivation phase (Fig. 6A,C). The 1 mm TEA-resistant currents had a voltage dependence similar to the moderately TEA-sensitive currents (Fig. 4F) but activated more slowly (Fig. 6E). These differences in voltage dependence and kinetics support the idea that TEA can be used to obtain, to a first approximation, the parameters of distinct voltage-gated potassium currents in Purkinje neurons.

Table 2.

Activation curve parameters for TEA-sensitive and TEA-resistant currents

	Wild type	med	p value
Control (100 μm TEA)
V½ (mV)	−8.1 ± 1.6	0.3 ± 3.5	0.06
k (mV)	10.5 ± 0.7	12.5 ± 1.4	0.23
Gmax (nS)	55 ± 5	61 ± 5	0.44
300 μm to 1 mm TEA
V½ (mV)	8.7 ± 2.1	11.4 ± 2.2	0.39
k (mV)	12.4 ± 0.6	12.7 ± 0.6	0.73
Gmax (nS)	47 ± 7	51 ± 9	0.69
1 mm TEA-resistant
V½ (mV)	8.3 ± 1.7	7.4 ± 1.9	0.73
k (mV)	11.1 ± 0.4	10.8 ± 0.3	0.57
Gmax (nS)	58 ± 6	56 ± 9	0.84
Iberiotoxin-sensitive
V½ (mV)	−12 ± 3	−11 ± 3	0.70
k (mV)	6.4 ± 0.7	7.9 ± 0.9	0.19

Figure 6.

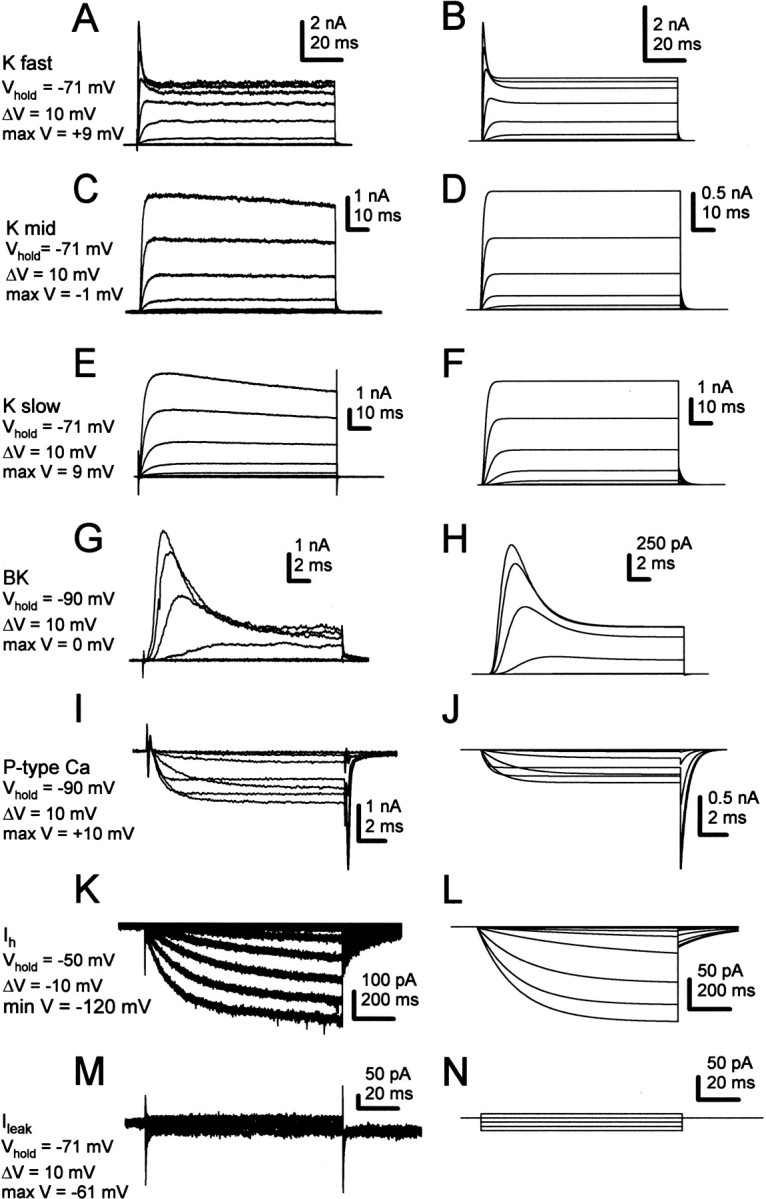
Simulations of non-sodium currents active during spontaneous activity of Purkinje neurons. Left column, Experimental records. Right column, Simulations. Current amplitudes in simulations correspond approximately to the mean experimental data. Voltage protocols are indicated to the left of the traces. A, B, Highly TEA-sensitive potassium current (K_fast). C, D, Moderately TEA-sensitive potassium current (K_mid). E, F, TEA-insensitive (1 mm) potassium current (K_slow). G, H, Iberiotoxin-sensitive K(Ca) current (BK). I, J, P-type calcium current. Data from Raman and Bean (1999). K, L, Hyperpolarization-activated current (I_h). M, N, Leak currents.

The same subtractions of potassium currents recorded from mutant neurons showed moderately TEA-sensitive and 1 mm TEA-resistant currents with mean properties that were indistinguishable from those of wild-type cells (Fig. 4E,F, Table 2). The highly TEA-sensitive currents, however, had an ∼8 mV positive shift in the half-activation voltage (Fig. 4D, Table 2). Thus, in addition to the changes in subthreshold leak-like currents, at least one class of potassium currents appears to change in Purkinje neurons lacking Na_V1.6.

Calcium-activated potassium currents

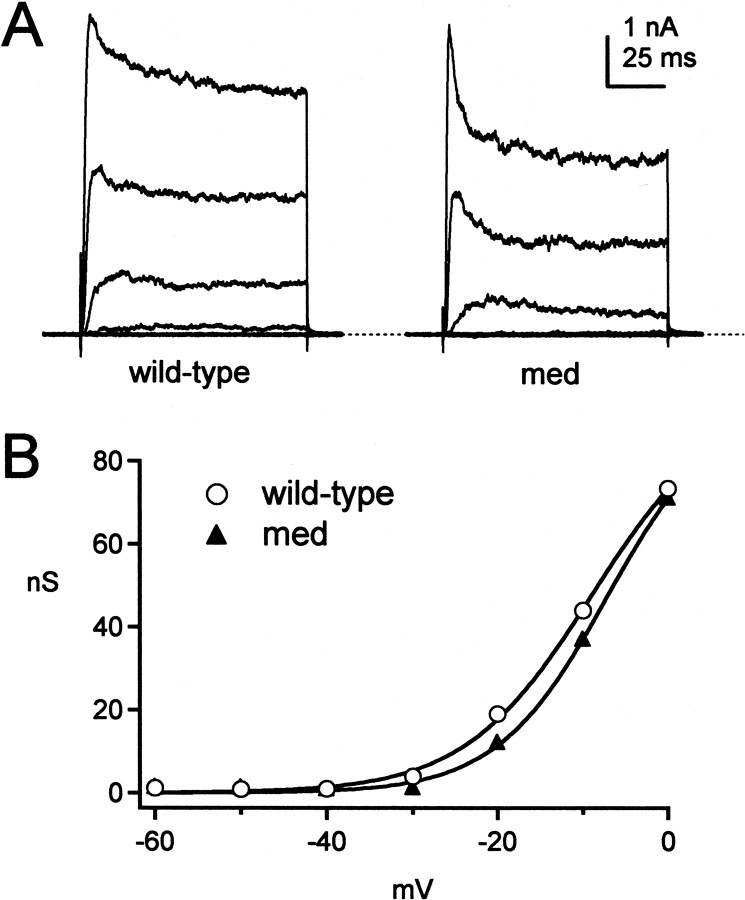
In addition to calcium-independent potassium currents, large, TEA-sensitive calcium-activated potassium currents are activated by voltage changes simulating action potential waveforms (Raman and Bean, 1999). This observation is consistent with changes in spike shape observed when blockers of BK channels, such as iberiotoxin, are applied to Purkinje cells in slices (Womack and Khodakhah, 2002a; Edgerton and Reinhart, 2003). Calcium current density in med neurons has been reported to be the same as in wild-type cells (Garcia et al., 1998). To compare calcium-activated BK channels in wild-type and med cells, we measured iberiotoxin-sensitive currents.

In both phenotypes, iberiotoxin-sensitive currents varied widely in amplitude, voltage dependence, and kinetics, regardless of intracellular solution (see Materials and Methods). Extrapolated maximal conductances ranged from 26 to 113 nS in wild-type cells (n = 6) and from 14 to 94 nS in med cells (n = 9). The inactivation kinetics of iberiotoxin-sensitive currents were also highly variable. In some cells, currents showed no inactivation phase (n = 2 of 6 wild-type and 3 of 9 med) (Womack and Khodakhah 2002a), but in the other cells, the currents inactivated significantly at potentials positive to -10 mV (Fig. 5A) (Raman and Bean, 1999). Despite this variability, the half-activation voltages and slope factors of Boltzmann fits to activation were indistinguishable (Fig. 5B, Table 2). The V_1/2 of both cell types ranged widely, however, from -26 to -1 mV. This wide range may result from variations in the concentration of calcium at BK channels, as suggested by studies of BK channels in inside-out patches from Purkinje cells (Womack and Khodakhah, 2002b). In these studies, the V_1/2 shifts from approximately -45 to +15 mV with a 10-fold decrease in calcium concentration. The range of properties of iberiotoxin-sensitive currents, however, was not measurably different in wild-type and med cells.

Figure 5.

Iberiotoxin-sensitive K(Ca) currents in wild-type and med Purkinje neurons. A, A family of iberiotoxin-sensitive currents evoked from -60 mV in 10 mV increments for a wild-type (left) and a med (right) neuron. Dashed line indicates 0 pA. The extent of inactivation was variable across cells of both phenotypes (see Results). B, Conductance–voltage curves for the currents in A.

Simulations of excitability in Purkinje cells

Although non-sodium currents appeared to be changed only modestly in med cells, these modifications nevertheless might contribute to the excitability of the med neurons. Depending on the effects of these changes, analysis of firing by med cells may lead us either to exaggerate or to underestimate the importance of Na_V1.6-mediated currents in regulating activity. Therefore, to test how firing patterns were shaped by sodium currents with a resurgent component, as well as by the modified non-sodium currents in med neurons, we simulated action potentials produced by Purkinje cell bodies.

We began by simulating the seven non-sodium currents that are likely to participate in high-frequency firing by Purkinje cells (Raman and Bean, 1999). Figure 6 illustrates representative families of each of these currents recorded from wild-type neurons (left column) and the results of Hodgkin-Huxley simulations of each current (right column). These included the highly TEA-sensitive current (Fig. 6A,B, K fast), the moderately TEA sensitive current (Fig. 6C,D, K mid), the 1 mm TEA-resistant current (Fig. 6E,F, K slow), the iberiotoxin-sensitive current (Fig. 6G,H, BK), the P-type calcium current (Fig. 6I,J), I_h (Fig. 6K,L), and the leak current (Fig. 6M,N, I_leak). P-type calcium currents were not directly measured in this study, because they have been described in detail previously (Regan, 1991; Mintz et al., 1992), and calcium currents have been reported to be unchanged in med cells (Garcia et al., 1998). Leak currents were measured in three wild-type cells (see Materials and Methods) and yielded current amplitudes that were consistent with the input resistances measured in Figure 3. All simulated currents were scaled to approximate the mean amplitude observed in wild-type Purkinje neurons. Parameters of the simulations are given in Materials and Methods and Table 1.

Currents expressed by Purkinje neurons but excluded from the model include T-type calcium current (McDonough and Bean, 1998), A-type potassium current (Sacco and Tempia, 2002), and small conductance calcium-activated potassium (SK) current (Cingolani et al., 2002; Womack and Khodakhah, 2003). Because of their voltage dependences of activation and inactivation, T-type and A-type current are unlikely to play a major role in spontaneous and current-evoked firing of isolated cell bodies at room temperature (Raman and Bean, 1999). Apamin- and bicuculline-sensitive current was present only irregularly in our wild-type cells (n = 3 of 25), even measured with K-methanesulfonate-based intracellular solutions with low EGTA (see Materials and Methods), which tend to preserve SK currents. This observation is consistent with the lack of detectable apamin-sensitive current in somatic patches excised from Purkinje cells in slices (Southan and Robertson, 2000). Therefore, because somatic spontaneous firing does not appear to rely heavily on these channels, these three currents were omitted from the simulations.

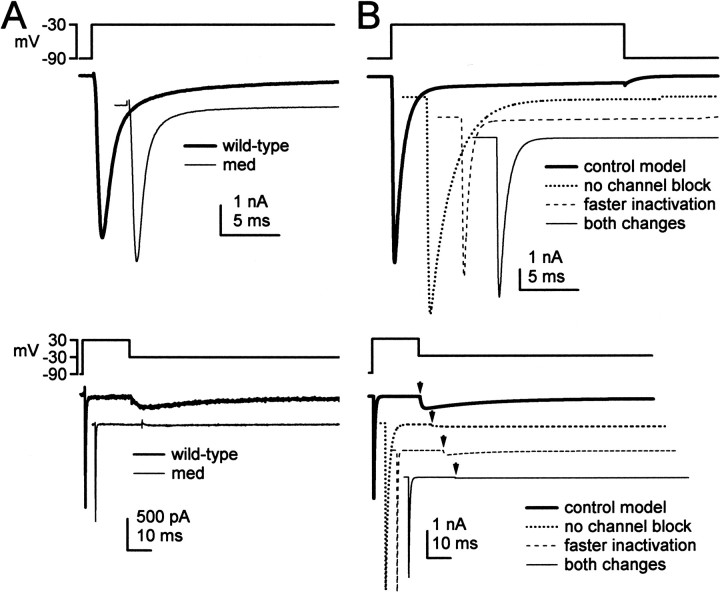
Next, we simulated sodium currents from wild-type and med Purkinje cells. Relative to wild-type currents, sodium currents of Purkinje neurons lacking Na_V1.6 inactivate more rapidly at negative potentials, have a negatively shifted steady-state inactivation curve, and have ∼90% less resurgent sodium current (Raman et al., 1997) (Fig. 7A). Step depolarizations to -30 mV evoked TTX-sensitive transient currents that inactivated more rapidly in med than in wild-type neurons (top traces), and step repolarizations to -30 mV evoked large resurgent sodium currents in wild-type but not med cells (Fig. 7A, bottom traces). To simulate these currents, we started with the kinetic scheme of Raman and Bean (2001), which modeled wild-type Purkinje sodium currents as arising from conventional voltage-gated channels with fast inactivation kinetics, which are also subject to a rapid, voltage-dependent, open channel block (Fig. 7B, thick traces). In this scheme, at positive potentials, the blocking factor competes successfully with the inactivation gate for a binding site that prevents the flow of current. When the blocker unbinds at negative potentials, resurgent current flows until the channel deactivates or inactivates.

Figure 7.

Simulations of sodium currents in wild-type and med Purkinje neurons. In all panels, currents are offset for clarity. A, Experimental records of TTX-sensitive sodium currents elicited by step depolarizations (top traces) and step repolarizations (bottom traces) to -30 mV for wild-type and med cells. Resurgent current is visible in the wild-type trace as a slowly rising, slowly decaying current evoked during repolarization. B, Simulations of sodium currents evoked by voltage protocols as in A. Currents were generated by four variants of the kinetic model of Raman and Bean (2001), as indicated. Arrowheads in bottom panel indicate the time of the repolarizing step.

To simulate the mutant currents, we modified the existing kinetic model for wild-type sodium currents of Purkinje cell bodies. The simplest way to abolish resurgent current was to decrease the transition rate into the blocked state nearly to zero (see Materials and Methods), so that block did not occur (Fig. 7B, bottom). This modification, however, also increased transient current amplitude by 10% and greatly slowed inactivation (Fig. 7B, top); such slow decays are not typical of sodium currents in med cells (Fig. 7A, top). The result that removal of block fails to replicate med currents is not unexpected, because the genetic defect of med Purkinje cells is not the loss of a blocking factor but that the loss of an α subunit. The remaining α subunits in Na_V1.6-lacking Purkinje cells may well have kinetics distinct from Na_V1.6 channels not subject to open-channel block. Specifically, the experimental data suggest that the remaining sodium channels inactivate more quickly.

We therefore tested the effect of increasing the transition rate from the open state to the inactivated state in the model from 0.75/msec to 2.3/msec (Fig. 7B, top panel). This manipulation reduced the peak amplitude of the transient current simulated at -30 mV by 10%, greatly accelerated inactivation of the current, and negatively shifted the steady-state inactivation curve. Moreover, the more rapid transition from the open state to the inactivated state limited the accumulation of channels in the blocked state, consequently decreasing resurgent current by ∼60% (Fig. 7B, bottom panel). This result is qualitatively consistent with the experimental data from the mutants, which indicate that resurgent current in Na_V1.6-lacking Purkinje cells is not abolished but greatly reduced, raising the possibility that the remaining α subunits weakly bind the blocker. To decrease resurgent current as much as in med cells (by 90%), however, it was necessary to increase the inactivation rate even further, which led to an excessively rapid decay of transient current. Therefore, to reduce the resurgent current as well as account for the faster inactivation, we simulated currents with both the faster inactivation rate and the slowed transition to a blocked state. When both changes were applied to the model, the currents closely mimicked those recorded from med cells (Fig. 7B), having faster inactivation kinetics, a negatively shifted steady-state inactivation, and a lack of resurgent current.

Before examining how sodium current kinetics may influence action potential firing, we tested whether the simulated currents, with the mean amplitudes and kinetics recorded from wild-type cells, could successfully replicate wild-type action potentials. We simulated firing in a single compartment model, representing a Purkinje soma with a 19 pF capacitance. With the simulated current amplitudes and kinetics illustrated in Figure 6, the model produced spontaneous firing at 27 spikes/sec, very close to the mean wild-type firing rate of 29 Hz, and accurately replicated passive responses to hyperpolarizing current injections (Fig. 8A). The model with mean currents, however, produced a steeper gain curve (Fig. 8B) than predicted by the mean experimental data. Varying parameters indicated that the slope of the gain curve was highly sensitive to the modeled calcium-dependence of the BK current, the parameter that was least constrained by our data. Nevertheless, the model responses were within the range of experimentally observed responses, suggesting that the mean current amplitudes and kinetics adequately represented the major ionic currents involved in firing in wild-type Purkinje somata.

Figure 8.

Simulations of firing in Purkinje cell bodies. A, Top, Simulations of spontaneous firing and responses to hyperpolarizing current injections in wild-type cells. Horizontal dotted lines indicate -60 and 0 mV. Note that the firing rate does not increase after the hyperpolarization, but that six traces of asynchronous action potentials are overlaid. Bottom, Current protocol. B, Simulations (filled symbols and thick line) of sustained firing rate versus current injection. Raw experimental data points (open symbols and dotted lines) from Figure 2 are superimposed for comparison.

Next, we tested how changing sodium channel kinetics influenced firing rates, by simulating action potentials with each of the four sodium channel models: control, no block, faster inactivation, and both changes (med like). In these simulations it was necessary to control for differences in sodium current amplitude across models, because changing the rates of inactivation and block changed the simulated peak amplitude of transient sodium currents (Fig. 7B, top). Therefore, for each model, we modified the number of channels so that the peak current simulated with a step from -90 to 0 mV had an amplitude identical to that in control. With the mean current amplitudes of Figures 6 and 7, med-like kinetics slowed spontaneous firing by 19%. Varying the total sodium current amplitude above and below the mean control value showed that at all amplitudes at which firing persisted in control, med-like kinetics slowed firing (by 21–31%) or stopped it completely (Fig. 9A). The “no block” model produced a similar reduction in firing rate (by 17 to 38%; data not shown), whereas the “faster inactivation” model also slowed firing, but to a lesser extent (7–17%; data not shown). Thus, across all conditions, the Na_V1.6-specific kinetics of moderate inactivation rates and significant open channel block produced the fastest and most robust firing.

Figure 9.

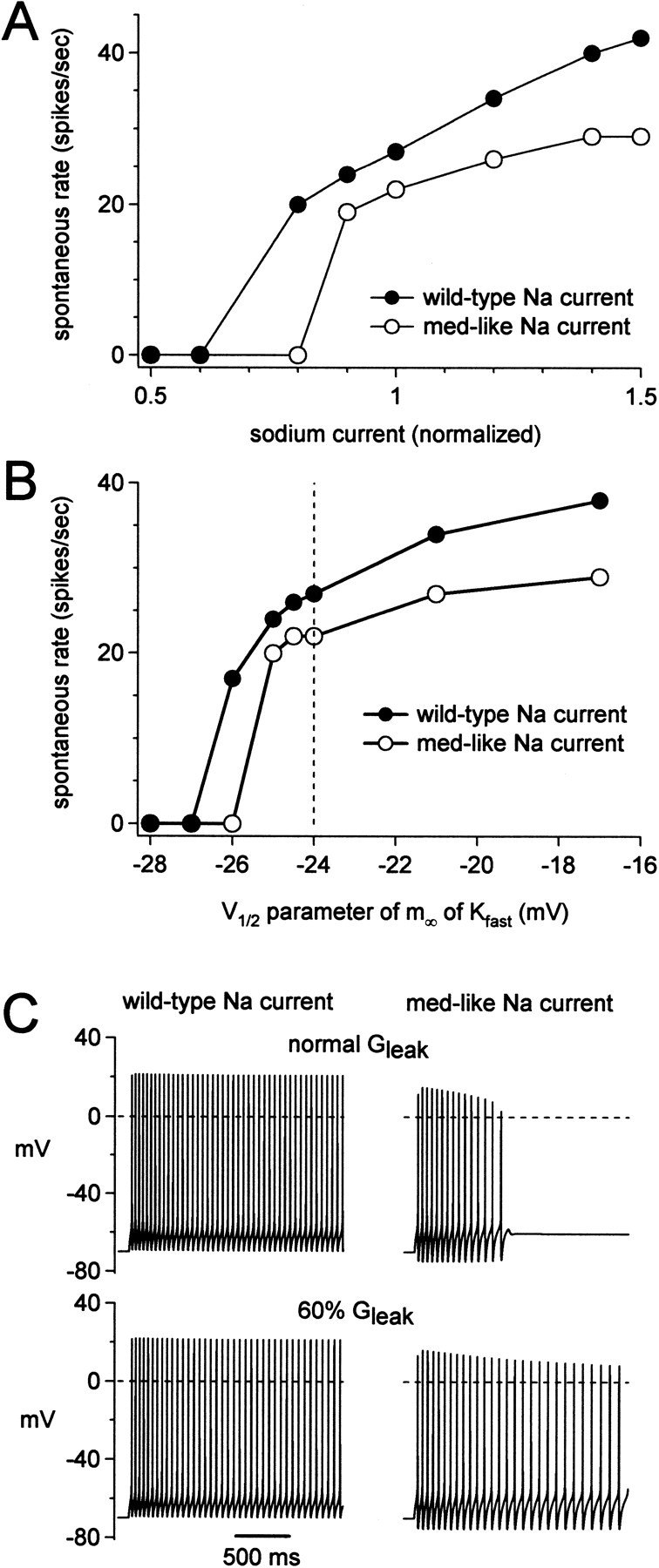
Simulations of the dependence of spontaneous firing on resurgent sodium current kinetics. A, Simulated spontaneous firing rate as a function of sodium current amplitude for the model with wild-type (filled symbols) and med-like (open symbols) sodium current kinetics. The x value of 1 corresponds to the modeled G_Na that replicates the mean current amplitudes recorded from wild-type cells. G_Na was increased in the med-like model to produce a peak transient sodium current during depolarization to 0 mV that was the same as the wild-type model. B, Spontaneous firing rate simulated with the wild-type (filled symbols) and med-like (open symbols) sodium current kinetics, as a function of the parameter controlling the V_1/2 of the highly TEA-sensitive current, K_fast. This parameter does not correspond directly to the experimental V_1/2. The value simulating the wild-type experimental mean V_1/2 is indicated with a vertical dashed line. C, Simulated firing after equilibration at -70 mV with wild-type (left) and med-like sodium currents (right), with input resistances similar to wild-type (top) or med (bottom) cells.

We next used the model to test whether changes in non-sodium currents similar to those observed in the med cells exacerbate or compensate for the loss of Na_V1.6. Not surprisingly, the spontaneous firing rate in the model was highly sensitive to changes in potassium currents, particularly K_fast. With all other currents at their mean values, positively shifting the midpoint of the activation curve of K_fast increased the spontaneous firing rate in all conditions (Fig. 9B). Thus, the tendency for the K_fast current to have a positively shifted activation curve in med cells may increase the safety factor for maintaining some spontaneous activity. Nevertheless, at all but the extreme negative values of V_1/2 at which firing stopped, wild-type kinetics produced a higher rate of spontaneous firing than any of the other sodium current models.

Last, we tested the effects of changing input resistance on the model with med-like sodium current kinetics. All other currents were maintained at their mean values. We mimicked the higher input resistance of med cells by reducing the leak conductance by 30%. With all sodium current models, at all sodium current amplitudes, the increase in membrane time constant resulting from the smaller leak slightly decreased the spontaneous firing rate (Fig. 9C, left). Despite this slowing, it seemed possible that firing might be more robust under some conditions, because the higher input resistance would promote depolarization to small currents. We tested this possibility by reducing the sodium current amplitude to 82% of the mean value, a level that did not produce spontaneous firing in the model with med kinetics. Under these conditions, transient spiking could be initiated by “equilibrating” channels at -70 mV before firing was assessed (Fig. 9C, right). Reducing the leak current permitted this regular firing to last for >2 sec (Fig. 9C, right).

These results provide information about the ways in which currents in Purkinje cell bodies interact to produce firing patterns. First, the relatively high activation voltages of Purkinje potassium currents indeed facilitate spontaneous firing. Second, the reduced excitability of med Purkinje cells cannot be accounted for by changes in non-sodium currents, which instead appear to preserve some level of activity. Finally, across a range of modeling conditions, the kinetics of sodium currents with a resurgent component consistently increase excitability.

Discussion

The role of resurgent sodium current

These experiments help clarify the role of sodium currents with a resurgent component in determining the patterns of neuronal activity. The initial observation of resurgent current (Raman and Bean, 1997) emphasized the TTX-sensitive inward current that might flow on the down stroke of an action potential. Subsequent work related the presence of resurgent current to the robustness of burst firing (Raman et al., 1997) and showed that TTX-sensitive sodium current flowed in the interval between spontaneous action potentials (Raman and Bean, 1999). These results led to the idea that resurgent current might contribute to the distinctive high-frequency firing patterns of Purkinje cells. Recently, however, resurgent current has been identified in other neurons, including unipolar brush cells, some cerebellar nuclear neurons, cerebellar granule cells, and neurons of the subthalamic nuclei (Mossadeghi and Slater, 1998; Raman et al., 2000; D'Angelo et al., 2001; Do and Bean, 2003). All of these cells have firing patterns distinct from those of Purkinje cells, indicating that resurgent current alone is neither necessary nor sufficient for spontaneous (or burst) activity.

The present experiments, however, suggest that channels that produce resurgent current may have consistent effects on excitability. Relative to wild-type neurons, isolated med Purkinje cells are less likely to fire spontaneously and have slower rates of evoked firing. The largest change in intrinsic currents is indeed the loss of a sodium current with a resurgent component. Importantly, the effect of this sodium current is distinct from that of other, tonically depolarizing currents, such as I_h or persistent sodium current. No matter the size of the depolarizing current injections, the med cells did not fire at rates comparable with wild type. This observation emphasizes the idea that repetitive spiking requires not only an initial depolarization but also a sufficient number of available sodium channels to support an action potential; in other words, some sodium channels must recover from inactivation. Biophysical studies indicate that recovery from inactivation is facilitated in sodium channels that can pass resurgent current. During depolarization, instead of inactivating into conventional fast-inactivated states, these channels rapidly enter a state resembling open-channel block. During repolarization, the flow of resurgent current occurs as channels quickly exit the block-like state, leading to a rapid recovery of sodium channels, even in the absence of a strong hyperpolarization (Raman and Bean, 2001; Grieco et al., 2002).

It is this accelerated recovery that may be relevant across preparations. Both real and model cells with wild-type resurgent current had relatively shallow interspike hyperpolarizations and rapid firing rates, consistent with recovery of sodium channels even at moderately negative potentials. Conversely, many of the mutant cells could not maintain firing during current injections. One reason for this behavior may be that the current injection actually limited recovery of sodium channels by reducing after-hyperpolarizations, thereby initiating depolarization block. Thus, by failing to accumulate in inactivated states, sodium channels that produce resurgent current may not only promote high-frequency spontaneous activity in Purkinje neurons but may also increase the rate of firing evoked by excitation in other cells.

Specializations of other intrinsic currents for spontaneous firing

When sodium currents without a resurgent component were incorporated into the model, regular spontaneous firing still sometimes occurred, although at lower rates than normal. This behavior, which was also observed in some med cells, supports the hypothesis that the non-sodium channels in Purkinje cell bodies are also specialized to preserve high-frequency activity. One relevant feature of the non-sodium currents is the relatively positive voltage-dependence of activation of the rapidly activating and deactivating TEA-sensitive potassium currents. This characteristic, which is typical of the K_V3 family of potassium channels, has been noted repeatedly in rapidly firing cells (Rudy and McBain, 2001). In our model, increasing the density of the most negatively activating potassium currents (K_fast or BK) could silence firing, reinforcing the idea that spontaneous generation of action potentials in Purkinje cells depends on minimizing the activity of subthreshold potassium currents. Consequently, the densities of specific potassium currents, as well as the quantitative details of calcium buffering, may have significant effects on regulating basal firing rates in Purkinje cells.

In this context, it is interesting that instead of upregulating other Na_V channels or increasing calcium current density (Garcia et al., 1998; Kearney et al., 2002), the loss of Na_V1.6 changed highly TEA-sensitive currents (K_fast) as well as leak currents. The positive shift in activation of the K_fast, which dominated action potential repolarization in our model, is in a direction that would generally promote excitability. Similarly, the increased input resistance in med cells can facilitate subthreshold depolarization, even while slowing it.

Validity of the model

Recording voltage-clamped currents from dissociated somata allowed us to construct a model of Purkinje cell firing based entirely on currents recorded from the cells of interest. This model thereby complements previous work, which has simulated the structural features of Purkinje neurons as well as their synaptic inputs (De Schutter and Bower, 1994; Jaeger et al., 1997). Our “wild-type” model successfully replicated many aspects of normal activity of isolated Purkinje cells; however, incorporating med-like sodium and non-sodium currents into the model failed to disrupt firing as much as was observed in med cells. Several factors may contribute to this shortcoming of the model. First, in testing the effects of modified currents, we changed only one parameter at a time, while maintaining all other currents constant, with the mean amplitudes and kinetics. This approach would accurately simulate med firing only if all currents are independent, an assumption that is probably not valid. For example, unlike the modeled cells, the firing rate of real cells did not increase monotonically with sodium current amplitude, suggesting that in the real cells, the amount of sodium and non-sodium currents may covary. Consistent with this idea, currents in individual cells can be regulated by the activity or expression of other channels (Golowasch et al. 1999a,b, 2002; MacLean et al., 2003). Second, if a current that we did not measure, such as SK, T-type, or A-type currents, was strongly modified in the med cells, the med simulations could have been distorted. A third possibility is that stochastic channel openings contribute significantly to action potential initiation in isolated Purkinje somata; such a possibility cannot be tested with our model. Despite its limitations, the model was useful in revealing the interactions among different currents, specifically the contribution of resurgent current to firing patterns, as well as the predicted consequence of the modified non-sodium currents of med Purkinje cells.

Implications for intact preparations

Exactly how the intrinsic excitability observed in isolated Purkinje somata relates to that of more intact preparations is still uncertain. In our preparation, both dendrite and axon were cleaved; under more physiological conditions, regular spontaneous somatic spiking, or the lack of it, is undoubtedly modified by dendrites as well as synaptic inputs. In slices held at elevated temperatures and in which synaptic transmission is blocked, regular firing similar to that of isolated somata as well as repetitive bursts of dendritically driven activity have been documented (Häusser and Clark, 1997; Womack and Khodakhah, 2002b). Whatever the intrinsic patterns of activity in vitro, however, the signals transmitted by Purkinje neurons in vivo are likely to depend heavily on the modulation of this activity by synaptic excitation and inhibition. Given the consistent acceleration of firing by sodium current kinetics with a resurgent component in our model, it seems likely that this role for resurgent sodium current may be extrapolated to Purkinje cells in more intact preparations.

Considering the effect of the med mutation on the rest of the nervous system, it is worth noting that Na_V1.6 is widely expressed (Burgess et al., 1995; Schaller et al., 1995; Schaller and Caldwell, 2000), including in cells that produce no resurgent current (Raman and Bean, 1997; Smith et al., 1998; Pan and Beam, 1999). Therefore, the effects of the loss of Na_V1.6 on total brain function are likely to be extensive and are almost certainly not entirely a consequence of the loss of resurgent current. The premature death of med mice on postnatal day 21 (Burgess et al., 1995), for example, seems more likely to result from the loss of nodal sodium channels during postnatal development (Caldwell et al., 2000) than from any changes in cerebellar function. To date, however, the cells expressing resurgent current have all been parts of brain regions involved in motor control, and the salient phenotype of 2- to 3-week-old med mice is a loss of coordinated movement. It is interesting to speculate, therefore, that in the mutant animals, synaptically driven firing rates may be reduced in all the neurons that generally produce resurgent currents, contributing to the overall phenotype of ataxia.