Abstract
The development of accurate potentials for computational simulations has been an active area of research. Our group has been involved in the development of the Gaussian electrostatic model (GEM), a force field based on molecular densities. The philosophy of GEM is based on the pioneering work of N. Gresh and co–workers of the reproduction of individual inter–molecular interaction components obtained from quantum mechanical (QM) energy decomposition analysis (EDA). The molecular densities used in GEM are represented by fitting accurate QM molecular densities using auxiliary basis sets (comprised of Hermite Gaussians). The use of these molecular densities results in the need to evaluate a large number of Gaussian integrals. We have previously shown that the particle–mesh Ewald (PME), and fast Fourier Poison (FFP) methods can be used for efficiently evaluating these types of integrals. Here, we present the latest parametrization of GEM* and its application for an extensive study of PME and FFP for molecular dynamics (MD) simulations using a hybrid version of our potential, GEM*. The temperature dependence of various bulk properties is presented and discussed, as well as the effect of various parameters affecting the performance/accuracy of both methods.
Keywords: Gaussian Electrostatic Model, Particle mesh Ewald, Fast Fourier Poison, Polarizable Force Field
1. Introduction
Force field (FF) development continues to receive significant attention. [1–6]. The need for extensive phase–space sampling results in the need to make various approximations to increase computational efficiency. In particular, many FF separate the calculation of the energy in bonded and non–bonded terms. The non–bonded interactions are usually approximated by Coulomb and Van der Waals (VdW) terms using atom–centered point charges and atom–specific parameters for VdW. The use of these functions provides improved sampling efficiency. However, problems with these approximations give rise to reduced accuracy because of the loss of charge density anisotropy, the failure to account for penetration effects, among others [7].
Some of these issues can be ameliorated by including a better description of the charge density distribution and/or a more detailed description of the intermolecular interactions. For example, force fields like AMOEBA, SIBFA, EFP, X–Pol, and NEMO employ distributed multipoles and use explicit polarization [8–14]. The use of atomic–centered multipoles gives a better results for Coulimb interactions [7,15–19]. However, multipoles cannot reproduce the charge density overlap effect, giving rise to the so–called penetration effect at close range [7,20], although this may be ameliorated by the use of damping functions to correct the electrostatic interactions at close distances [20–26].
The explicit description of the molecular charge density avoids the charge penetration issue. This feature has been exploited by several methods [27–34]. This is a key feature of the Gaussian Electrostatic Model (GEM) [35–39]. GEM uses the density fitting (DF) formalism [40–42] to expand the molecular density using Hermite Gaussian auxiliary basis sets (ABSs). Additionally, following the philosophy promoted by Gresh and co–workers, GEM relies on the reproduction of each individual term from ab initio QM intermolecular interaction results from energy decomposition analysis (EDA) [43–52].
Consequently, GEM includes separate terms for each contribution including Coulomb, exchange–repulsion, polarization, charge–transfer and dispersion [36,37,39]. Additionally, the use of continuous functions provides a more accurate description of molecular properties compared to conventional point charges [37]. We have also shown that GEM results in very accurate energies and forces for a range of systems including homo–dimers, hetero–dimers and molecular clusters, and it can be used in multi–scale implementations. [36,37, 53–56].
The use of Hermite Gaussians results in the need to evaluate a large number of Coulomb and overlap integrals. Various reciprocal space methods have been developed for the efficient evaluation of integrals [57–61]. We have previously shown that Ewald–based methods can be extended for Gaussian distributions for the efficient evaluation of these integrals [37]. In particular, we have extended the smooth particle mesh Ewald (PME) [62] and fast Fourier Poisson (FFP) [63] methods to allow the evaluation of continuous Gaussian functions in periodic boundary conditions (PBC) [37,64].
We previously reported a water potential that included the Coulomb and exchange–repulsion terms from GEM, combined with the polarization and a modified Halgren function from AMOEBA, this hybrid water potential was termed GEM* [65]. This potential employed a molecular electronic density fitted at the MP2/aug–cc–pVTZ level of theory for the water monomer, and was parametrized to reproduce BSSE–corrected MP2/aug-cc-pVTZ intermolecular interaction energies, as well as individual EDA terms calculated at the RVS (HF/aug–cc–pVTZ) level for dimers and selected oligomers.
In this contribution we present an update for GEM* by fitting the molecular electronic density and parametrizing the individual terms to higher levels of theory (vide infra). This new paremetrization is employed to test the latest implementation of the PME and FFP algorithms in pmemd.gem as released in the AMBER18 suite of programs. Thermodynamic, structural and dynamical properties for this new GEM* parametrization are presented and discussed. The remainder of the paper is organized as follows, Section 2 presents the theory and details of the computational simulations, followed by presentation of the performance of the reciprocal space algorithms using various parameters and bulk property calculations in Section 3, followed by concluding remarks.
2. Computational Methods
This section presents the details of the GEM* force field in Subsection 2.1, followed in Subsection 2.2 by a description of the mathematical details for the extension of PME and FFP for Gaussian distributions in PBC. Finally, Subsection 2.3 provides a description of the new parametrization and MD simulations.
2.1. The GEM* force field
The initial implementation of the full GEM potential involved the use of spherical type Hermites only, resulting in what was termed GEM–0 [36]. This version, along with the extension to Hermite Gaussians of arbitrary angular momentum were shown to be highly accurate for the calculation of single energies and forces [37]. The only drawback with these potentials was that MD simulations were not possible in an efficient manner since the analytical form of one of the terms (charge–transfer) was not available. Therefore, a compromise to enable efficient MD simulations was realized by combining terms from GEM with terms from AMOEBA, which resulted in the development of the GEM* force field [65].
In brief, GEM* employs the Electrostatic and exchange terms from GEM, combinded with polarization, modified van der Waals and bonded terms from AMOEBA. The functional form for GEM* is thus:
| (1) |
The Coulomb and exchange–repulsion terms for GEM* are obtained by evaluating the two center Coulomb and overlap integrals involving the fitted densities [65]. The buffered Halgren function from AMOEBA for Van der Waals was modified given the fact that GEM* includes a separate exchange term. To this end, the function (modHalgren) was modified by removing the repulsive term resulting in the following expression:
| (2) |
The polarization and bonded terms employ the same functional forms as AMOEBA [66]. One important difference in GEM* is that the permanent electric fields for the calculation of the induced dipoles are calculated with the distributed multipoles obtained from the fitted Hermites for consistency between the Coulomb and polarization terms [67,68].
The initial implementation of GEM* was tested by developing and testing paramterers for a model water potential [65]. These parameters were compared with reference ab initio values for total intermolecular interactions corrected for basis set superposition error via the counterpoise correction. The reference data was calculated at the MP2(full)/aug–cc–pVTZ level to match the original AMOEBA parametrization [66,69,10,70]. The molecular density used to obtain the fitting coefficients for GEM* was calculated at the same level of theory as above for a water molecule at the AMOEBA equilibrium geometry.
Three parametrizations were investigated, termed models 1–3. The difference among the three models involves the use of different ABSs, A1 or A2 [71,72], and/or the dataset of water oligomers used for the parametrization. Model 1 was fitted using the A2 ABS to reproduce intermolecular interaction energies for the canonical water dimer, several random dimers, and selected water clusters from [73]. Models 2 and 3 were parametrized to reproduce intermolecular energies for the canonical water dimer only using the A2 (model2) and A1 (model 3) ABSs. All calculations for GEM* were performed with a modified pmemd.amoeba version in the AMBER16 suite of programs [1].
2.2. Ewald–based methods for Evaluation of Coulomb Integrals
The use of fitted densities for the Coulomb and exchange terms results in the need to evaluate a large number of Gaussian integrals. As mentioned above, one possibility to efficiently evaluate these integrals is to employ Ewald–based methods. This is achieved by employing periodic boundary conditions and performing part of the calculation in reciprocal space. The reciprocal term for calculations involving Gaussian functions requires special care given that the charge densities need to be gridded. This issue can be a major hurdle for Gaussian functions with large exponents (compact Gaussians) due to the need to employ dense grids for an accurate representation. Alternatively, it is possible to classify the Gaussian functions as compact or diffuse and employ the reciprocal term only for operations involving diffuse functions.
Our initial implementation of GEM introduced a method to enable the use of Ewald–based approaches whereby a single Ewald exponent, β, was used to classify the Gaussian functions in the ABS as compact (αi ≥ β) or diffuse (αi < β) [37]. In this way, all contributions involving diffuse Hermites may be efficiently calculated in reciprocal space. This approach can be employed for systems where the molecular density has been fitted only using spherical Hermite Gaussians l = 0 such as GEM–0, that involve both atomic, and off–atom fitting sites [36], as well as charge densities using higher angular momentum Hermites [37].
This approach was subsequently improved by the realization that the Ewald exponent, β does not need to be the same for all interactions. That is, β may be different for each Gaussian pair ij [64]. Therefore, β can be selected to be ∞ for Gaussian pairs where at least one of the functions has a small exponent (diffuse). Thus, all pairs that involve diffuse Hermites can be calculated exclusively in reciprocal space, with no direct space contribution. In this way, for a specific θ > 0 a charge distribution qiρi is classified as compact (i ∈ c) if αi ≥ 2θ and diffuse (i ∈ d) otherwise. Subsequently, for i, j ∈ {c}, an Ewald exponent is selected such that 1/θ = 1/αi + 1/αj + 1/β, otherwise β = ∞. For GEM* (and GEM), the fitted densities are expanded in a linear combination of Hermite Gaussians Λtuv(r, α, R).
In this way, expressions for spherical (l = 0) and higher order angular momentum charge distributions can be derived as described in Refs. [37,64,39] and several algorithms can be employed for the various terms. In our case, the direct space contributions are calculated using the McMurchie-Davidson (McD) recursion. The use of the McD algorithm allows the efficient evaluation of integrals involving high angular momentum Hermites since only vertical recursions need to be employed [74]. This recursion can be used to calculate the required erfc and higher derivatives for multipoles as well as Hermite interactions [75,37]. Additionally, we have previously shown that the McD recursion is applicable to other types of integrals such as the overlap, required for the exchange term [37].
For the reciprocal terms, three methods were implemented: full Ewald [76], sPME [77] and FFP [78]. The smooth PME (sPME) method is based on the fact that the complex exponential in can be approximated by B–splines, resulting in a O(N(log(N)) method [77]. The FFP algorithm uses a similar method to FFT–based approaches for the acceleratiion of density map calculations in macromolecular structure determinations [78,37,64].
2.3. Parametrization and MD Simulation Details
The original parametrization of GEM* employed a fitted density for the water monomer calculated using a single orientation of a reference water molecule, with a molecular electronic density obtained at the MP2/aug–cc–pVTZ level. The inter–molecular interactions were parametrized using total inter–molecular interaction energies at the MP2/aug–cc–pVTZ level, combined with energy decomposition analysis using the RVS method with the aug–cc–pVTZ as reference [65].
In the present work, we have updated the parameters by fitting single monomer densities for 500 water molecules in random orientations using the A2 ABS only, with reference monomer densities obtained at the CCSD/aug–cc–pVTZ level of theory. The calculated GEM coefficients were optimized and averaged to obtain one single set of average coefficients. These coefficients were used to update the parameters of the different terms of the GEM* potential. The new parametrization has been performed by optimizing the fitting parameters to reproduce the interactions of 500 water dimers selected from the water dimer surface calculated at the CCSD(T)/CBS level reported by Babin et al. [79,80], coupled with EDA results obtained from SAPT2+3/aug–cc–pVTZ as reported in [55] using the SAPT implementation in Psi4 [81]. Additionally, the energies and forces of six hexamers have been employed to ensure accurate reproduction of many–body effects as well as the value of the density and heat of vaporization at 300K to optimize the modified Halgren parameters, similarly to the initial GEM* implementation [65]. The optimized parameters were tested against the 43500 dimers from the water dimer potential energy surface both for total intermolecular energies, as well as individual EDA components (see SI), in addition to various bulk properties (vide infra).
The optimized GEM* parameters were employed to perform MD simulations for water boxes of various sizes in the NVT, NPT and NVE ensembles to test the accuracy and performance of the new parameters and optimized implementation of pmemd.gem. For the constant temperature and pressure simulations, the Berendsen thermostat [82] and Monte Carlo barostat were employed. Simulations for the determination of bulk properties were performed using boxes of 1024 water molecules for at least 1 ns at various temperatures. NVE simulations were performed on water boxes of 512 water molecules. In all cases the polarization tolerance is 10−6, with a non–bonded cutoffff 8 Å and similar cutoffff for the direct space cutoffff for the Ewald–based methods.
For the integral evaluation, the B–spline order is 6, with FFT grids of 643, exchange factor of 6.6899 and exchange cutoff of 6.0 Å. All bulk–property calculations were calculated with a split exponent of 0.15 (i.e. all Hermites assumed as compact). For the Gaussian split performance test, the split exponent was also set to 0.5, which results in one of the Gaussians being diffuse. All MD simulations were carried out using the Beeman integrator with a 1 fs time–step. Radial and structural distribution functions (rdf and sdf) were obtained using the Travis software [83].
3. Results and Discussion
This section presents the results and discussion of the new GEM* parametrization with respect to calculation of bulk properties in Subsection 3.1 as well as the performance of the new GEM* implementation in pmemd.gem and testing of the two Ewald–based methods using two different Gaussian cutoffs in Subsection 3.2.
3.1. Bulk properties
Radial and structural distribution functions were calculated from a 1024 water box at 300 K run under NPT conditions. Figures 1 and 2 show that the new parametrization results in an overall better agreement of the structural features for GEM* compared with experimental data, in particular for the O–O rdf. Interestingly, the new parameters results in slight over–stabilization of the O–H and H–H interactions, in particular for the first solvation shell.
Fig. 1.
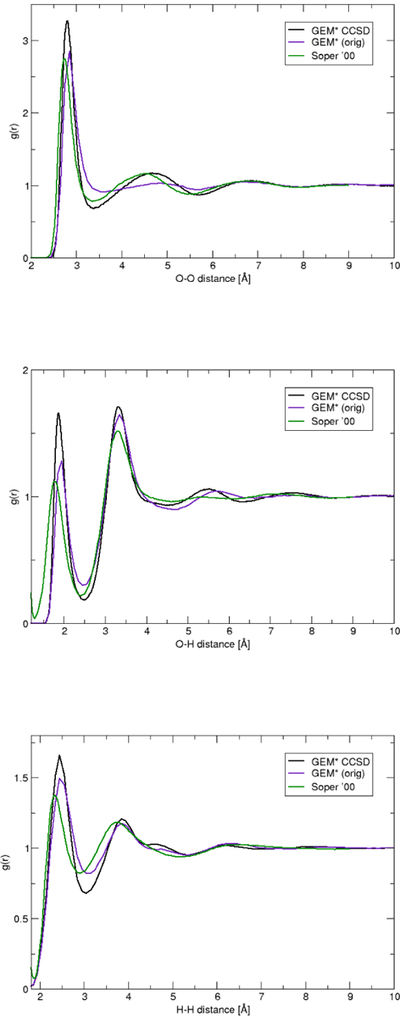
Radial distribution functions (g(r)) for O–O (top), O–H (middle), and H–H (bottom) for GEM* compared with previous GEM* parametrization and experimental data [65,84]
Fig. 2.
Structural distribution functions in three orientations calculated with the new GEM* parameters
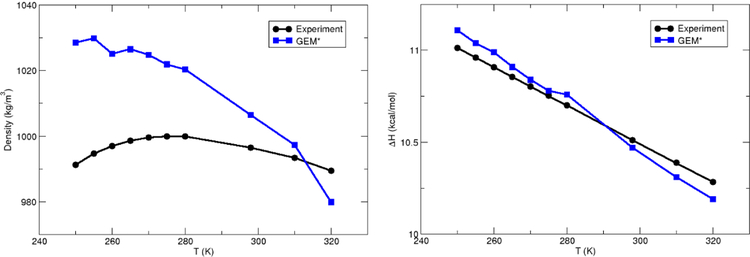
Following the work for the initial GEM* implementation, the new parameters have been evaluated by calculating the density and heat of vaporization for a range of temperatures between 250 and 320 K. The heat of vaporization can be calculated from the difference in potential energies between the liquid and gas phases. The average potential energy of the gas is 0.9 kcal/mol at 300 K as reported previously [65] and follows a similar trend as the bulk. As shown in Figure 3 the new parametrization shows good accuracy for the temperature range close to 300K, especially for the calculated heats of vaporization. However, deviations are exhibited, especially at low temperatures, in particular for the calculated densities, which show errors as large as 4% for the lower temperatures. The observed deviation for the calculated thermodynamic properties is due to the inadequate functional form for the description of the induction and charge transfer terms, as well as other appsoximations such as the lack of nuclear quantum effects (in particular for ΔHvap). One more possible effect that could affect the accuracy of the calculated densities is the relatively short sampling times (1ns).
Fig. 3.
Calculated densities and heats of vaporization for a range of temperatures
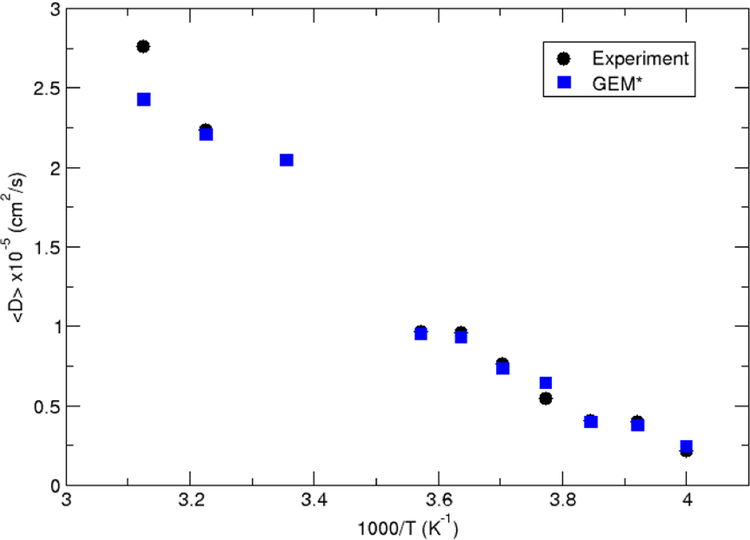
Another liquid property that can be used to validate the quality of the potential is the self–diffusion coefficient, D±. In the present work, the D± have been calculated by means of Einstein’s relation: D± = limt→∞ 〈MSD(t)±〉 (6t)−1, where 〈MSD(t)±〉 is the mean squared displacement of the water molecule’s center of mass and t is the time. The calculated diffusion coefficients for the temperature range under consideration shows very good agreement at both low and high temperatures (Figure 4), and predict faster diffusion at high temperatures and low diffusion rates at low temperatures.
Fig. 4.
Calculated diffusion coefficients for a range of temperatures
3.2. Ewald–based Methods Performance Analysis
The A2 auxiliary basis sets employed for the current version of GEM* comprise 16 Gaussian primitives with exponents ranging from 0.30 to 2566.00. Timings for the single energy and force calculation of the Coulomb energy for various water boxes under PBC showed significant improvement of PME and FFP compared with full Ewald sum results [37,64]. The new implementation in pmemd.gem for improved parallel performance maintains this trend as shown in Table 1. The trends observed in the previous implementation are maintained in pmemd.gem. Additionally, the use of different C–D split exponent (C–D exp), θ, shows the possibility of increased performance. In most cases, it is necessary to use a relatively dense grid for the accurate evaluation of the Coulomb interaction of the entire system if a C–D split exponent is chosen such that some integrals involving diffuse functions are evaluated exclusively in reciprocal space (grid ≥ 100 for this example). The best performance/accuracy is observed for sPME with a C–D split exponent of 0.5, which results in two primitives from the A2 set designated as diffuse, using a grid of 1003. This combination results in the evaluation of the energies and forces for this system in 1.96 s, with an error of 0.007 kcal mol1 (0.01 μH) in the total Coulomb energy. It should also be noted that both PME and FFP are almost 30 times faster than the fastest setup for the full Ewald sum.
Table 1.
Accuracy and performance of Ewald, sPME and FFP for single Coulomb energy/force calculations of a 512 GEM* water box using a B–spline order of 8. All calculations were performed on an i7–5820K@3.3GHz using a single core.
| grid size = 2003 | ||||||
|---|---|---|---|---|---|---|
| C–D exp | PME | FFP | Ewald | |||
| ECoul | t (s) | ECoul | t (s) | ECoul | t (s) | |
| 0.100 | −7761.784660 | 6.72 | −7761.784660 | 156.62 | – | – |
| 0.250 | −7761.784659 | 6.04 | −7761.784659 | 52.52 | – | – |
| 0.500 | −7761.784724 | 6.42 | −7761.784718 | 21.99 | – | – |
| 1.250 | −7761.775239 | 6.51 | −7538.336333 | 12.26 | – | – |
| 2.000 | −7761.760290 | 6.46 | 6817.189360 | 10.17 | – | – |
| grid size = 1503 | ||||||
| PME | FFP | Ewald | ||||
| ECoul | t (s) | ECoul | t (s) | ECoul | t (s) | |
| 0.100 | −7761.784660 | 4.56 | −7761.784660 | 62.55 | – | – |
| 0.250 | −7761.784661 | 4.37 | −7761.784659 | 21.74 | – | – |
| 0.500 | −7761.784238 | 4.24 | −7761.784720 | 10.17 | – | – |
| 1.250 | −7761.658504 | 4.26 | −7619.653416 | 5.71 | – | – |
| 2.000 | −7761.692765 | 4.83 | 2518.484768 | 4.85 | – | – |
| grid size = 1003 | ||||||
| PME | FFP | Ewald | ||||
| ECoul | t (s) | ECoul | t (s) | ECoul | t (s) | |
| 0.100 | −7761.784659 | 2.50 | −7761.784660 | 19.42 | −7761.784660 | 410.56 |
| 0.250 | −7761.784643 | 2.13 | −7761.784659 | 7.59 | −7761.784659 | 408.89 |
| 0.500 | −7761.791994 | 1.96 | −7761.784723 | 3.82 | −7761.784677 | 406.25 |
| 1.250 | −7757.544636 | 1.93 | −7709.917195 | 2.47 | −7758.809650 | 410.10 |
| 2.000 | −7787.095605 | 1.92 | −2837.159878 | 2.53 | −7787.734594 | 387.86 |
| grid size = 503 | ||||||
| PME | FFP | Ewald | ||||
| ECoul | t (s) | ECoul | t (s) | ECoul | t (s) | |
| 0.100 | −7761.784675 | 1.95 | −7761.784660 | 4.22 | −7761.784660 | 64.51 |
| 0.250 | −7761.788669 | 1.46 | −7761.784888 | 2.21 | −7761.784659 | 64.05 |
| 0.500 | −7734.891895 | 1.18 | −7753.682565 | 1.42 | −7747.938468 | 65.00 |
| 1.250 | 57367.505736 | 1.26 | −41549.335491 | 1.22 | 45434.658996 | 64.72 |
| 2.000 | −7761.692765 | 1.16 | −13677.969316 | 1.17 | 9852.239609 | 61.69 |
The stability of the present implementation of these methods was tested by performing a short (200 ps) run of the 512 box under NVE conditions. Figure 5 shows that performing the evaluation of integrals involving diffuse Gaussians exclusively in reciprocal space results in energy conservation for the simulation time. For comparison, an NVE simulation with a C–D exp of 0.15 (all Gaussians considered as compact) is presented to show energy conservation in this regime as well.
Fig. 5.
Total energy vs. time for a 512 water box using the NVE ensemble with two different C–D exp (0.15 and 0.5).
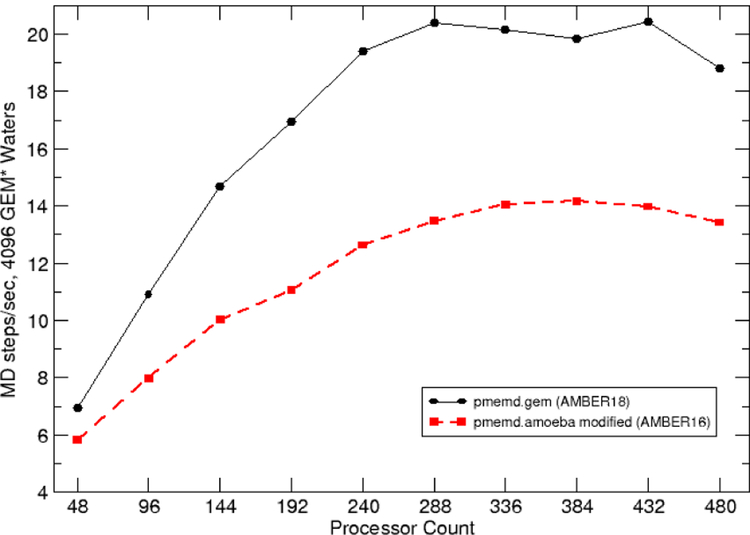
Finally, Figure 6 shows a comparison between the performance of the original implementation of GEM* in the modified pmemd.amoeba implemented in AMBER16, with the new pmemd.gem implementation released in AMBER18. As can be observed, good scaling is found for a water box of 1024 molecules. In particular, the evaluation of 100 MD steps running on Stampede2 shows a 2–fold improvement for the new pmemd.gem implementation, with a top performance of 22 MD steps per second on 432 cores.
Fig. 6.
Performance comparison between the initial and current implementations of GEM*.
4. Conclusions
This contribution presents the implementation and testing of two Ewald–based methods compared with full Ewald sums for the evaluation of integrals involving Gaussian distributions as applied for the GEM* potential. A new parametrization of GEM* employing very high accuracy data for intermolecular interactions for total and EDA contributions is also presented and tested by determining various bulk properties. Our results show that the new GEM* implementation at the higher level of theory provides an accurate reproduction of the water dimer surface and gives accurate results for bulk properties around 300K, although deviations are observed especially at low temperature. These deviations are likely due to the very approximate functional form employed to reproduce the dispersion and charge–transfer contributions, a new version of GEM with a more accurate functional form is currently under development. The use of Ewald–based methods is shown to provide a viable approach for the evaluation of a large number of Gaussian distributions under PBC with high accuracy, in particular when evaluating some of the Gaussian primitives exclusively in reciprocal space.
Supplementary Material
Acknowledgements
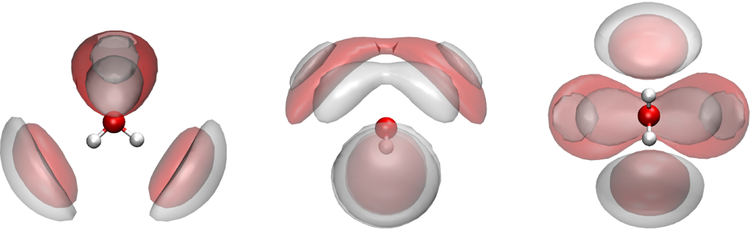
This work was supported by NIH/NIGMS via grant R01GM108583. Computing time from CASCaM, with partial support from NSF Grant No. CHE1531468, and XSEDE (Stampede2) project #CHE160044, is gratefully acknowledged. The authors thank Mr. E.A. Vázquez–Montelongo for assistance with preparing the SDF images.
Footnotes
Supplementary Information
SAPT2+3/aug-cc-pVTZ components compared with individual GEM*, and total intermolecular interaction energies for the full 43500 water dimers are provided as a csv file.
Conflict of interest
The authors declare that they have no conflict of interest.
Contributor Information
Robert E. Duke, Department of Chemistry, University of North Texas, Denton, TX 76202
G. Andrés Cisneros, Department of Chemistry, University of North Texas, Denton, TX 76202.
References
- 1.Case DA, Cheatham III TE, Darden TA, Gohlke H, Luo R, Merz KM Jr., Onufirev A, Simmerling C, Wang B, Woods RJ, J. Comput. Chem 26, 1668 (2005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jorgensen WL, Tirado-Rives J, J. Comput. Chem 26, 1669 (2005) [DOI] [PubMed] [Google Scholar]
- 3.van der Spoel D, Lindahl E, Hess B, Groenho G, Mark AE, Berensen HJC, J. Comput. Chem 26, 1701 (2005) [DOI] [PubMed] [Google Scholar]
- 4.Christen M, Hünenberger PH, Bakowies D, Baron R, Brúgl R, Geerke DP, Heinz TN, Kastenholz MA, Kräutler V, Oostenbrink C, Peter C, Trzesniak D, van Gunsteren WF, J. Comput. Chem 26, 1719 (2005) [DOI] [PubMed] [Google Scholar]
- 5.MacKerrell AD Jr., Brooks B, Brooks CL III, Roux NB, Won Y, Karplus M, “CHARMM: The energy function and its parametrization with an overview of the program” in Encyclopedia of computational Chemistry (John Wiley & Sons Ltd., New York, NY, 1998) [Google Scholar]
- 6.Salomon-Ferrer R, Case DA, Walker RC, Wiley Interdisciplinary Reviews: Computational Molecular Science 3(2), 198 (2013) [Google Scholar]
- 7.Stone AJ, The theory of intermolecular forces (Oxford University Press, Oxford, UK, 2000) [Google Scholar]
- 8.Hermida-Ramón JM, Brdarski S, Karlström G, Berg U, J. Comput. Chem 24(2), 161 (2003) [DOI] [PubMed] [Google Scholar]
- 9.Gresh N, Cisneros GA, Darden TA, Piquemal JP, J. Chem. Theo. Comp 3, 1960 (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ponder JW, Wu C, Ren P, Pande VS, Chodera JD, Schnieders MJ, Haque I, Mobley DL, Lambrecht DS, DiStasio Robert A. Jr., Head-Gordon M, Clark GNI, Johnson ME, Head-Gordon T, J. Phys. Chem. B 114, 2549 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Day PN, Jensen JH, Gordon MS, Webb SP, Stevens WJ, Krauss M, Garmer D,Basch H, Cohen D, J. Chem. Phys 105, 1968 (1996) [Google Scholar]
- 12.Xie W, Gao J, J. Chem. Theo. Comp 3(6), 1890 (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xie W, Orozco M, Truhlar DG, Gao J, J. Chem. Theo. Comp 5(3), 459 (2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shaik MS, Liem SY, t..P.j..j.y…v…n…p… Popelier, Paul L. A”,
- 15.Price S, in Reviews in Computational Chemistry, vol. 14, ed. by Lipkowitz K, Boyd DB (VCH Publishers, New York, NY, 1999) [Google Scholar]
- 16.Popelier P, Atoms in Molecules: An Introduction (Prentice Hall, Harlow, England, 2000) [Google Scholar]
- 17.Kosov DS, Popelier PLA, J. Phys. Chem. A 104, 7339 (2000) [Google Scholar]
- 18.Popelier PLA, Joubert L, Kosov DS, J. Phys. Chem. A 105, 8254 (2001) [Google Scholar]
- 19.Popelier PLA, Kosov DS, J. Chem. Phys 114, 6539 (2001) [Google Scholar]
- 20.Freitag MA, Gordon MS, Jensen JH, Stevens WJ, J. Chem. Phys 112, 7300 (2000) [Google Scholar]
- 21.Kairys V, Jensen JH, Chem. Phys. Lett 315(1–2), 140 (1999) [Google Scholar]
- 22.Piquemal JP, Gresh N, Giessner-Prettre C, J. Phys. Chem. A 107, 10353 (2003) [DOI] [PubMed] [Google Scholar]
- 23.Cisneros GA, Tholander SNI, Parisel O, Darden TA, Elking D, Perera L, Piquemal JP, Int. J. Quantum Chem 108, 1905 (2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang B, Truhlar DG, J. Chem. Theo. Comp 6(11), 3330 (2010) [DOI] [PubMed] [Google Scholar]
- 25.Stone AJ, J. Phys. Chem. A 115(25), 7017 (2011) [DOI] [PubMed] [Google Scholar]
- 26.Liu C, Piquemal JP, Ren P, J. Chem. Theo. Comp 0(0), null (0). DOI 10.1021/acs.jctc.9b00261 [DOI] [Google Scholar]
- 27.Wheatley R, Mol. Phys 7(3), 761 (2011). DOI 10.1021/ct100530r [DOI] [Google Scholar]
- 28.Gavezzotti A, J. Phys. Chem. B 106, 4145 (2002) [Google Scholar]
- 29.Eckhardt CJ, Gavezzotti A, J. Phys. Chem. B 111(13), 3430 (2007) [DOI] [PubMed] [Google Scholar]
- 30.Volkov A, Coppens P, J. Comput. Chem 25, 921 (2004) [DOI] [PubMed] [Google Scholar]
- 31.Coppens P, Volkov A, Acta Cryst. A 60(5), 357 (2004) [DOI] [PubMed] [Google Scholar]
- 32.Paricaud P, Predota M, Chialvo AA, Cummings PT, J. Chem. Phys 122(24), 244511 (2005) [DOI] [PubMed] [Google Scholar]
- 33.Giese TJ, Chen H, Dissanayake T, Giambasu GM, Heldenbrand H, Huang M, Kuechler ER, Lee TS, Panteva MT, Radak BK, York DM, J. Chem. Theo. Comp 9(3), 1417 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hu H, Lu Z, Elstner M, Hermans J, Yang W, J. Phys. Chem. A 111(26), 5685 (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cisneros GA, Piquemal JP, Darden TA, J. Chem. Phys 123, 044109 (2005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Piquemal JP, Cisneros GA, Reinhardt P, Gresh N, Darden TA, J. Chem. Phys 124, 104101 (2006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cisneros GA, Piquemal JP, Darden TA, J. Chem. Phys 125, 184101 (2006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cisneros GA, Elking DM, Piquemal JP, Darden TA, J. Phys. Chem. A 111, 12049 (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cisneros GA, Darden TA, Gresh N, Reinhardt P, Parisel O, Pilmé J, Piquemal JP, ”Design of next generation polarizable force fields from ab initio computations: beyond point charges”, in ”Multi-scale Quantum Models for Biocatalysis: Modern Techniques and Applications”. Challenges and Advances in Computational Chemistry and Physics (Springer–Verlag, 2009) [Google Scholar]
- 40.Boys SF, Shavit I, A Fundamental Calculation of the Energy Surface for the System of Three Hydrogen Atoms (AD212985, NTIS, Springfield, VA, 1959) [Google Scholar]
- 41.Dunlap BI, Connolly JWD, Sabin JR, J. Chem. Phys 71, 4993 (1979) [Google Scholar]
- 42.Köster AM, Calaminici P, Gómez Z, Reveles U, “Density functional theory calculation of transition metal clusters”, in Reviews of Modern Quantum Chemistry, A Celebration of the Contribution of Robert G. Parr (World Scientific, Singapore, 2002) [Google Scholar]
- 43.Kitaura K, Morokuma K, Int. J. Quantum Chem 10, 325 (1976) [Google Scholar]
- 44.Bagus PS, Hermann K, Bauschlicher CW Jr., J. Chem. Phys 80, 4378 (1984) [Google Scholar]
- 45.Stevens WJ, Fink WH, Chem. Phys. Lett 139, 15 (1987) [Google Scholar]
- 46.Jeziorski B, Moszynski R, Szalewicz K, Chem. Rev 94, 1887 (1994) [Google Scholar]
- 47.Glendening ED, J. Am. Chem. Soc 118, 2473 (1994) [Google Scholar]
- 48.Mo Y, Gao J, Peyerimho SD, J. Chem. Phys 112, 5530 (2000) [Google Scholar]
- 49.Heßelmann A, Jansen G, Schütz M, J. Chem. Phys 122, 14103 (2005) [DOI] [PubMed] [Google Scholar]
- 50.Piquemal JP, Marquez A, Parisel O, Giessner-Prettre C, J. Comput. Chem 26, 1052 (2005) [DOI] [PubMed] [Google Scholar]
- 51.Khaliullin RZ, Head-Gordon M, Bell AT, J. Chem. Phys 124(20), 204105 (2006) [DOI] [PubMed] [Google Scholar]
- 52.Lu Z, Zhou N, Wu Q, Zhang Y, J. Chem. Theo. Comp 7(12), 4038 (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cisneros GA, Piquemal JP, Darden TA, J. Phys. Chem. B 110, 11571 (2006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chaudret R, Ulmer S, van Severen MC, Gresh N, Parisel O, Cisneros GA, Darden TA, Piquemal JP, AIP Conf. Proc 1102, 185 (2009) [Google Scholar]
- 55.Gokcan H, Kratz E, Darden TA, Piquemal JP, Cisneros GA, J. Phys. Chem. Lett 9(11), 3062 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gokcan H, Vázquez-Montelongo EA, Cisneros GA, J. Chem. Theo. Comp 15(15), 3056 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Fusti-Molnar L, Pulay P, J. Chem. Phys 116(18), 7795 (2002) [Google Scholar]
- 58.Fü-Molnár L, Kong J, J. Chem. Phys 122(7), 074108 (2005) [DOI] [PubMed] [Google Scholar]
- 59.Kong J, Brown ST, Fusti-Molnar L, J. Chem. Phys 124(9), 094109 (2006) [DOI] [PubMed] [Google Scholar]
- 60.Chang CM, Shao Y, Kong J, J. Chem. Phys 136(11), 114112 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Exl L, Mauser NJ, Zhang Y, J. Comput. Phys 327, 629 (2016) [Google Scholar]
- 62.Essmann U, Perera L, Berkowitz M, Darden TA, Lee H, Pedersen LG, J. Chem. Phys 103, 8577 (1995) [Google Scholar]
- 63.York D, Yang W, J. Chem. Phys 101(4), 3298 (1994) [Google Scholar]
- 64.Darden TA, “Dual bases in crystallographic computing” in International Tables of Chrystallography, vol. B (Kluwer Academic Publishers, Dordrecht, The Netherlands, 2007) [Google Scholar]
- 65.Duke RE, Starovoytov ON, Piquemal JP, Cisneros GA, J. Chem. Theo. Comp 10, 1361 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ren P, Ponder JW, J. Phys. Chem. B 107, 5933 (2003) [Google Scholar]
- 67.Cisneros GA, J. Chem. Theo. Comp 12, 5072 (2012). DOI 10.1021/ct300630u. URL http://pubs.acs.org/doi/abs/10.1021/ct300630u. DOI: 10.1021/ct300630u [DOI] [PubMed] [Google Scholar]
- 68.Cisneros GA, J. Chem. Theo. Comp 12, 5072 (2012) [DOI] [PubMed] [Google Scholar]
- 69.Ren P, Ponder JW, J. Comput. Chem 23, 1497 (2002) [DOI] [PubMed] [Google Scholar]
- 70.Ren P, Wu C, Ponder JW, J. Chem. Theo. Comp 7(10), 3143 (2011). DOI 10.1021/ct200304d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Andzelm J, Wimmer E, J. Chem. Phys 96, 1280 (1992) [Google Scholar]
- 72.Godbout N, Andzelm J, DGauss Version 2.0, 2.1, 2.3, 4.0: the file that contains the A1, A2 and P1 auxiliary basis sets can be obtained from the CCL WWW site at http://www.ccl.net/cca/data/basis-sets/DGauss/basis.v3.html (Computational Chemistry List, Ltd., Ohio, 1999) [Google Scholar]
- 73.Temelso B, Archer KA, Shields GC, J. Phys. Chem. A 115(43), 12034 (2011) [DOI] [PubMed] [Google Scholar]
- 74.McMurchie L, Davidson E, Comput J. Phys 26, 218 (1978) [Google Scholar]
- 75.Sagui C, Pedersen LG, Darden TA, J. Chem. Phys 120, 73 (2004) [DOI] [PubMed] [Google Scholar]
- 76.Ewald P, Ann. Phys 64, 253 (1921) [Google Scholar]
- 77.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG, J. Chem. Phys 103, 8577 (1995) [Google Scholar]
- 78.York D, Yang W, J. Chem. Phys 101, 3298 (1994) [Google Scholar]
- 79.Babin V, Leforestier C, Paesani F, J. Chem. Theo. Comp 9(12), 5395 (2013). DOI 10.1021/ct400863t. URL http://pubs.acs.org/doi/abs/10.1021/ct400863t [DOI] [PubMed] [Google Scholar]
- 80.Babin V, Medders GR, Paesani F, J. Phys. Chem. Lett 3(24), 3765 (2012). DOI 10.1021/jz3017733. URL http://pubs.acs.org/doi/abs/10.1021/jz3017733 [DOI] [PubMed] [Google Scholar]
- 81.Parrish RM, Burns LA, Smith DGA, Simmonett AC, DePrince AE, Hohenstein EG, Bozkaya U, Sokolov AY, Di Remigio R, Richard RM, Gonthier JF, James AM, McAlexander HR, Kumar A, Saitow M, Wang X, Pritchard BP, Verma P, Schaefer HF, Patkowski K, King RA, Valeev EF, Evangelista FA, Turney JM, Crawford TD, Sherrill CD, J. Comput. Chem 13(7), 3185 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Berendsen HJ, Postma J.v., van Gunsteren WF, DiNola A, Haak J, J. Chem. Phys 81(8), 3684 (1984) [Google Scholar]
- 83.Brehm M, Kirchner B, J. Chem. Inf. Model 51(8), 2007 (2011) [DOI] [PubMed] [Google Scholar]
- 84.Soper A, Rossky P, Chem. Phys 258, 107 (2000) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.