How AMPA Receptor Desensitization Depends on Receptor Occupancy

Abstract

AMPA-type glutamate receptors mediate fast excitatory transmission at many central synapses, and rapid desensitization of these receptors can shape the decay of synaptic currents and limit the fidelity of high-frequency synaptic transmission. Here we use a combination of fast glutamate application protocols and kinetic simulations to determine how AMPA receptor desensitization depends on the number of subunits occupied by glutamate. We show that occupancy of a single subunit is sufficient to desensitize AMPA-type channels and that receptors with one to four glutamates bound enter desensitization at similar rates. We find that recovery from desensitization follows a similar sigmoid time course for channels with two to four glutamates bound but is faster and exponential for singly occupied channels. The results suggest that desensitization, at intermediate and high glutamate concentrations, is accompanied by two conformational changes that slow glutamate dissociation. We propose a kinetic scheme that accurately predicts several types of experimental results and differs significantly from previous models in the assignment of affinities for binding to closed and desensitized states. We conclude that desensitization involves a rearrangement that stabilizes the binding domains of one subunit in each dimer in a partially closed conformation. This stabilization likely results from an interaction at the dimer–dimer interface between the binding domains of adjacent subunits.

Introduction

AMPA receptors are tetrameric assemblies (Rosenmund et al., 1998; Chen et al., 1999), probably dimers of dimers (Armstrong and Gouaux, 2000; Ayalon and Stern-Bach, 2001;Mansour et al., 2001; Robert et al., 2001). Because each AMPA receptor subunit can form functional channels, AMPA-type channels can bind up to four glutamate molecules. Occupancy of one or two of the four subunits is sufficient for activation gating, and the unitary conductance of AMPA-type channels increases with receptor occupancy (Rosenmund et al., 1998; Smith and Howe, 2000). AMPA receptors also desensitize within a few milliseconds in the sustained presence of glutamate. It has been suggested that AMPA receptor desensitization requires a concerted conformational change of all four subunits (Partin et al., 1996; Robert et al., 2001), perhaps involving sequential concerted rearrangements of the monomers in each dimer (Bowie and Lange, 2002; Sun et al., 2002).

The structure of the ligand-binding core of glutamate receptor (GluR) subunits shows that glutamate binds at the base of a deep cleft between two globular domains (1 and 2) and induces the translation and rotation of domain 2 such that the cleft closes (Armstrong et al., 1998). The extent of domain closure increases with agonist efficacy, and for strongly desensitizing full agonists like glutamate and AMPA, it is stabilized by the formation of hydrogen bonds between residues in domain 1 and domain 2 at the interdomain interface (Armstrong et al., 1998; Armstrong and Gouaux, 2000; Mayer et al., 2001). The structural results confirm earlier proposals that binding-induced conformational changes trap glutamate in the binding pocket in a “Venus flytrap” mechanism (Mano et al., 1996). Recently it was suggested that binding domain closure results in a short-lived transition state the instability of which can be partially relieved by either channel opening or desensitization (Sun et al., 2002), suggesting a physical interpretation for previous electrophysiological evidence that channel activation and desensitization proceed in parallel from the same closed states (Vyklicky et al., 1991; Raman and Trussell, 1995). Although the binding domains of open channels are likely closed (Benveniste and Mayer, 1995; Armstrong and Gouaux, 2000; Sun et al., 2002), it has been proposed that the initial step during recovery from desensitization corresponds to ligand dissociation and that this contributes to the kinetics of recovery (Patneau and Mayer, 1991; Raman and Trussell, 1995; Partin et al., 1996). If this is so, then some subunits of fully occupied desensitized channels must have binding domains that are at least partially open.

Here we use a combination of fast glutamate application protocols and kinetic modeling to compare desensitization for the flip splice variants of GluR1 and GluR4, recombinant channels that recover from desensitization at substantially different rates. Measurements of desensitization and recovery from desensitization were made over a range of glutamate concentrations to determine how these channel properties depend on receptor occupancy. The results provide insight into the extent of binding domain closure during desensitization and the relative affinity of glutamate for closed and desensitized states.

Materials and Methods

Cell culture and patch-clamp recording. Human embryonic kidney (HEK) 293 or tsA201 cells were plated onto 12 mm glass coverslips that had been coated with poly-l-lysine (100 μg/ml). The culture medium was modified Eagle's medium (MEM-E; Invitrogen), Gaithersburg, MD) containing 10% fetal bovine serum. The cells were transiently transfected using Lipofectamine 2000 (Invitrogen) with 0.2–1 μg of total cDNA per coverslip. The solution used for transfection consisted of 200 μl of Opti-MEM medium (Invitrogen), 3 μl of Lipofectamine 2000, 0.5 μg of a reporter cDNA encoding green fluorescent protein in pCMVsport, and 1–5 μg of GluR1_flip or GluR4_flip (unedited at the R/G site), both in a cytomegalovirus-driven mammalian expression vector. The GluR1 and GluR4 plasmids were kindly provided by Derek Bowie (Emory University) and Michael Tang (Yale University). Patch-clamp recordings were performed 24–72 hr after transfection at room temperature with an EPC 9 amplifier (Heka) as described previously (Robert et al., 2001). Whole-cell recordings were performed to measure steady-state plateau currents during sustained applications of glutamate. All other recordings were from excised outside-out patches. The holding potential was always set to −90 mV, and the series resistance before patch excision was typically 3–5 MΩ. In patches in which the peak glutamate-activated currents were >1 nA, series resistance compensation was used and set to 80%. The external solution was (in mm): 150 NaCl, 3 KCl, 2 CaCl₂, 1 MgCl₂, and 5 glucose, buffered with 10 mm HEPES (pH adjusted to 7.4 with NaOH). Patch pipettes (open tip resistance 2–4 MΩ) were filled with a solution containing (in mm): 120 KF, 33 KOH, 2 MgCl₂, 1 CaCl₂, 0.1 spermine, and 11 EGTA (pH adjusted to 7.4 with CsOH). Glutamate and 2,3-dioxo-6-nitro-1,2,3,4-tetrahydrodenzo[f]quinoxaline-7-sulfonamide (NBQX) were added to the external solution.

Fast perfusion. Concentration–response data for glutamate-induced desensitization and steady-state and peak glutamate-evoked currents were obtained with a rapid perfusion system consisting of a theta-glass pipette in which each barrel contained four small-diameter glass capillaries connected to different solution reservoirs. Solutions were switched with a series of solenoid valves controlled by the acquisition software (Pulse) of the patch-clamp amplifier (Robert et al., 2001). To measure the time course of entry into and recovery from desensitization, glutamate was applied using theta pipettes mounted on a piezoelectric bimorph (Morgan Matroc, part no. 62003/5H-144D) that itself was mounted on a plastic rod held on a micromanipulator. The tips of the pipettes were broken to ∼300 μm, and the width of the septa separating the barrels of the theta glass was reduced by etching with hydrofluoric acid. Both two- and three-barrel theta glass was used. Patches were positioned near the interface of the solutions flowing from adjacent barrels, and the interface was moved by applying voltage across the bimorph with a constant voltage source (HVA-100; ALA Scientific). Voltage pulses were triggered with one of the analog-to-digital outputs on the EPC 9 and were analog low-pass filtered (200 Hz, −3 dB, four-pole Bessel-type) to reduce mechanical oscillations of the piezoelectic device. The rate of solution exchange estimated from open-tip potentials was 100–200 μsec. The rise of currents activated by 5 mm glutamate was consistently slower for GluR4 channels than for GluR1 channels, suggesting that channel activation was not limited by the speed of solution exchange. The bath was superfused constantly with normal external solution flowing at a rate of 1 ml/min.

Glutamate-evoked currents were analog low-pass filtered at 3 kHz (four-pole Bessel-type, −3 dB) and were written directly to the hard-drive of the computer at sampling rates of 10–100 kHz. The digital records were analyzed using Igor software (Wavemetrics). Exponential functions were fitted to the decays of the currents as described previously (Robert et al., 2001). All the records shown are individual responses. Concentration–response data from individual cells and patches were normalized (see Results), and the mean normalized results were fitted with Hill-type functions to obtain IC₅₀ and EC₅₀ values and values for the Hill coefficient (n_H).

Recovery data were obtained from two-pulse protocols. In experiments in which 5 mm glutamate was applied during each pulse of the pair, the peak amplitude of the second pulse was expressed as a fraction of the peak amplitude of the paired first pulse. For GluR1 and GluR4, results were pooled from several patches, and the mean data were fitted with the Hodgkin-Huxley equation:I_t = (I_max^1/m− (I_max^1/m−I₀^1/m)exp(−t/τ))^m, where I_t is the peak current at a given interpulse interval, t,I_max is the peak current at long interpulse intervals, I₀ is the current at zero time (the relative amplitude of the plateau current), τ is the recovery time constant, and m is an exponent the value of which corresponds to the number of kinetically equivalent rate-limiting transitions that contribute to the recovery time course. The larger the value of m, the more sigmoid the recovery. For experiments requiring rapid application of three solutions, the results of individual experiments were fitted with the same Hodgkin-Huxley equation. When mean results from these experiments are shown, the current amplitudes at each interval were normalized to the value of I_max obtained from the fit to each set of results.

Kinetic modeling and the assignment of values for rate constants. Kinetic modeling was done using Monte Carlo simulations with the software package ChannelLab (Synaptosoft Inc.). All the simulations started in zero glutamate and included the effect of any conditioning pulses. Simulated recovery time courses were calculated as 1 − probability of finding the channel in one of the desensitized states, which for the channels studied here was very close (within 1% at all times) to the probability of finding the channel in the unoccupied closed state. At the glutamate concentration used for the test pulses in the recovery experiments (5 mm), the forward rate of binding far exceeds the rate of channel opening or desensitization. It was therefore not necessary to include the effect of the test pulse in the recovery simulations.

Our goal was to find a kinetic scheme (as simple as possible, yet physically plausible) that would allow us to estimate rate constants for binding to closed and desensitized states and for entry into and exit from desensitization. In addition, we sought to determine how these rate constants depend on receptor occupancy. Because AMPA receptors are tetramers and each subunit contains a binding site for glutamate, any physically plausible model must include a large number of physically discrete states, which in principle could be connected in a very large number of ways. The models that we explored were limited by previous evidence that AMPA receptor desensitization occurs from closed rather than open states (Vyklicky et al., 1991; Raman and Trussell, 1995) and by evidence that glutamate does not dissociate from open channels (Benveniste and Mayer, 1995; Armstrong and Gouaux, 2000;Sun et al., 2002). We were also cognizant of previous work showing that recombinant and native AMPA receptors show multiple concentration-dependent open levels, where the unitary conductance of the channels increases in discrete steps with receptor occupancy (Rosenmund et al., 1998; Smith and Howe, 2000). We considered the possibility, however, that some open levels may not be prominent when desensitization is intact, and we tested models in which the number of open states varied from one to four.

Despite the above constraints, the large number of states required for any physically realistic model ensured that there would be many sets of rate constants that were equally good solutions for any particular data set. This is so even for our final mechanism in which the number of free parameters was minimized by making many of the rate constants integer multiples of each other. Ideally, estimates of the rate constants for each data set would have been obtained from least-squares or maximum-likelihood fits, and the values from these fits to the various data sets would have converged. However, the large number of free parameters in the models tested renders this ideal approach unrealistic (especially because any given data set depends strongly on only a subset of these parameters). In a previous study (Smith et al., 2000), we attempted such an approach using hidden Markov modeling (HMM) of single-channel data from one-channel patches. Although the kinetic models explored were simpler than those tested here, repeated HMM runs on the same stretches of data gave values for individual rate constants that varied wildly, although the dwell times obtained for the different states were well defined and reproducible from run to run (Smith et al., 2000). The impracticality of an automated fitting approach also prohibited statistical comparisons of a wide variety of kinetic schemes.

Our approach to these problems was to limit our comparisons to models that differed primarily in the number of open and desensitized states and in the values assigned for binding to closed and desensitized channels. Our goal was not to find exact values for any set of rate constants but to find plausible values of all the rate constants that accounted well for the results from various different experimental protocols. For the most part, the measurements made here did not give direct estimates of the rate constants for channel opening and closing, nor did we measure single-channel currents. We therefore begin by setting values for channel opening and closing rate constants (β and α) on the basis of published values for apparent open times and burst lengths (Swanson et al., 1997; Derkach et al., 1999; Banke et al., 2000), as well as p_open values estimated after reducing desensitization (Smith and Howe, 2000;Irizarry, 2001; Robert et al., 2001). When multiple open levels were included, unitary conductance values were assigned on the basis of previous single-channel data for GluR1 and GluR4 (Swanson et al., 1997;Derkach et al., 1999; Banke et al., 2000; Irizarry, 2001). The values of β and α were assumed to be similar for different open levels, on the basis of observations that at saturating agonist concentrations the competitive antagonist NBQX has little effect on the open probability of AMPA receptors (Rosenmund et al., 1998; Smith and Howe, 2000). We next refined our initial estimates for β and α by obtaining deactivation and desensitization time constants from fitting exponential functions to the decay of currents evoked by brief (1 msec) and sustained (≥20 msec) applications of glutamate. The latter measurements also gave initial values for the rate constants for entry into desensitization (δ). Rate constants for exit from desensitization, γ, were then estimated from measurements of the time-course of recovery from desensitization at different glutamate concentrations. Binding rate constants for association and dissociation to and from closed channels were estimated from the time-course of entry into desensitization at low glutamate concentrations, as well as concentration–response data for desensitization and peak and steady-state glutamate-activated currents. If rate constants were altered during this procedure, simulations of previous data sets were rerun to ensure that the new set of values approximated them well.

We also limited the number of free parameters by interpreting the results in the context of specific physical mechanisms. In the mechanism proposed in Figure 6a, many of the rate constants for sets of similar transitions are integer multiples of each other. The multiples derive from our conclusion that desensitization is correlated with stabilization of binding domain closure for one subunit in each dimer, as well as our proposal that this stabilization is mediated by subunit–subunit interactions across the dimer–dimer interface between loop 1 in one subunit and helices F and G in the adjacent subunit. This interpretation of the data implies that only two equivalent subunits in each tetramer (one pair of those diagonally related to each other across the dimer–dimer interface) can be stabilized in a closed conformation. Our interpretation of the results also implies that occupancy and closure of the binding domain greatly increase the probability of these subunit–subunit interactions (δ₁ ≈ 1 × 10⁶δ₀). In this context, the multiples of δ₁ in Figure6a arise from combinatorial predictions of the likelihood that one or both of the equivalent subunits are occupied by glutamate for channels with one, two, three, or four subunits occupied. Conversely, the rate constants for exit from the first row of occupied desensitized states, γ₁, are not multiples because these rates all correspond to the rate at which the binding domain of one subunit goes from a closed to an open conformation. The multiples for the association and dissociation rate constants change as you descend in a given column through the rows of desensitized states in Figure 6a because we propose that the various states differ in the number of subunits with open and closed binding domains. For example, k_-1 is the rate constant for dissociation from subunits with open binding domains, and the number of such subunits decreases by one for each successive row of desensitized states. The dissociation rate for subunits with partially closed domains, k_-2, is four orders of magnitude smaller. Therefore the dissociation rates as you descend from the closed state in the rightmost column of Figure 6a are ∼4k_-1, 3k_-1, 2k_-1,k_-1, and exactly 4k_-2.

Fig. 6.

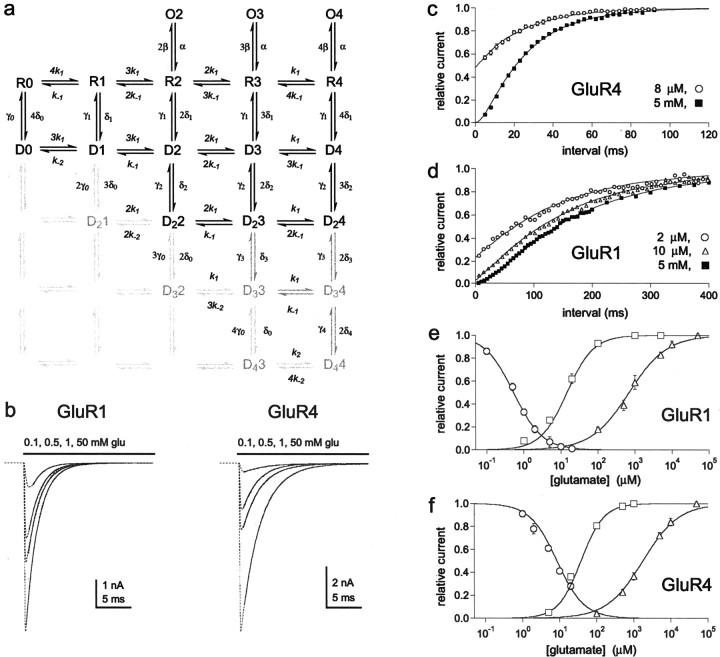
Kinetic model for recombinant AMPA receptors.a, The model in Figure 3a has been modified to include a constitutive desensitized stateD0, as well as additional desensitized states that are progressively further removed from closed states. Each desensitized state differs in the number of subunits occupied by glutamate and the number of subunits with partially closed binding domains. For example, channels in state D₂4 have four glutamates bound and two partially closed binding domains. Desensitized channels with three or four glutamates bound and more than two binding domains closed are rare or unstable, i.e., either the steady-state occupancy of states D₃3, D₃4, and D₄4 is small or occupancy of these states declines rapidly during recovery. The probability of finding channels in any of the light gray states is very low and decreases as channels move toward the bottom left corner. Closed states (R) have subunits with binding domains that are in the open conformation. Glutamate association and dissociation to and from these subunits are rapid and characterized by the rate constantsk₁ and k_-1. For desensitized channels, dissociation from subunits with open binding domains is rapid. Glutamates dissociate approximately four orders of magnitude slower from subunits with partially closed binding domains. This occurs for a small percentage of channels during recovery, “trapping” them in state D0 (and to a lesser extent D₂1) and accounting for our findings thatI_max values were <1.0 for both channel types (Fig. 4). The values for the rate constants estimated for GluR1 and GluR4 are given in Table 1. Movies depicting how occupancy of the various states changes during and after applications of glutamate similar to those investigated here can be found athttp://info.med.yale.edu/pharm/howe/movies.html.b, Simulated currents (dotted lines) during sustained applications of the indicated concentrations of glutamate. The single exponential fits to the decays (solid curves) gave time constants that agreed within 5% of those determined experimentally. c, d, Thelines are the recovery time courses predicted from the model in Figure 6a after equilibration in the indicated concentrations of glutamate. The symbols are the corresponding data points for GluR4 (c) and GluR1 (d) channels (mean ± SEM; 4–6 patches at each concentration). Hodgkin-Huxley fits to the simulated time courses gave values for τ and m that agreed within 5% of experimental values. e, f, Thelines are the simulated concentration–response relationships for glutamate-induced desensitization and for plateau and peak currents for GluR1 (e) and GluR4 (f) channels. The symbolsare the corresponding data points (from Fig.1e,f). The IC₅₀, EC₅₀, andn_H values obtained from fitting the simulated data differed from the experimental values by <10%.

In summary, our goal was to evaluate our results in light of what we currently know about the structure of AMPA-type glutamate receptors and to try to place the results in the context of a physically plausible kinetic model. The advantage of this approach is that it allows predictions that can be directly tested in future studies. Although the necessary complexity of any such model makes it unlikely that a unique set of rate constants will be found that is clearly better than all others, in total we explored thousands of different sets of rate constants. For some sets of experimental data, the predictions of the model were relatively insensitive to the absolute values of individual rate constants. For example, given the parallel nature of activation and desensitization, the desensitization time constants are defined by the ratio, β/δα, rather than the values of any one of these rate constants. However, for each model tested, the various δ values also had major effects on the concentration–response relationships for desensitization and the plateau currents, as well as effects on the predicted time course of recovery from desensitization. Our requirement that there must be good agreement between experimental and simulated data for various experimental protocols ensured that the values for the rate constants were well defined within the constraints imposed by any particular kinetic scheme. For the model in Figure 6a and the rate constants in Table 1, this agreement was within 10% for all parameters investigated.

Table 1.

Rate constants for GluR1 and GluR4 channels

	GluR1	GluR4		GluR1	GluR4
α1-a	3100 sec−1	8000 s−1	δ01-g,1-h	3.3 × 10−3 s−1	3.5 × 10−3
β1-a,1-b,1-j	8000 s−1	20,000 s−1	γ01-g,1-h,1-i	1 s−1	6 s−1
k11-c,1-d	2 × 107m−1/s−1	1 × 107m−1/s−1	δ11-d,1-j	1800 s−1	800 s−1
k−11-c,1-d,1-e,1-f	9000 s−1	10,000 s−1	γ11-d,1-k	7.6 s−1	45 s−1
k21-g	910m−1/s−1	1000m−1/s−1	δ21-d,1-e,1-l,1-m	200 s−1	4000 s−1
k−21-g,1-k	0.41 s−1	1 s−1	γ21-l,1-m	35 s−1	220 s−1

The rate constants above refer to the kinetic model in Figure6a. Rate constants were estimated using ChannelLab by comparing currents or occupancies from Monte Carlo simulations with experimental data (reported here or published previously). The conductance values for the three open states were set to 9, 15, and 21 pS for GluR1 (Derkach et al., 1999; Banke et al., 2000; Irizarry, 2001) and 8, 16, and 24 pS for GluR4 (Swanson et al., 1997). The conductance of all other states was set to zero. All final simulations were performed with the rate constants above using 5000–20,000 channels. The experimental measurements or considerations that were the main constraints on the values of each rate constant are indicated by the superscript letters as follows.

^F1-aDeactivation time constants, open time, and burst length distributions (Swanson et al., 1997; Derkach et al., 1999; Banke et al., 2000).

^F1-bp_openmeasurements (Smith and Howe, 2000; Robert et al., 2001).

^F1-cKinetics of entry into desensitization at low glutamate concentrations and the time-course of activation.

^F1-dConcentration–response data for desensitization.

^F1-eConcentration–response data for plateau currents.

^F1-fConcentration–response data for peak currents.

^F1-gMaximal recoveries from Hodgkin–Huxley fits.

^F1-hMicroscopic reversibility.

^F1-iRate of slow component of recovery.

^F1-jDesensitization time constants.

^F1-kRecovery time constants.

^F1-lRelative amplitude of plateau and peak currents.

^F1-mRecovery time-course at intermediate and high glutamate concentrations.

Results

Concentration–response relationships for glutamate-evoked currents and desensitization

To determine how desensitization and activation depend on receptor occupancy for GluR1 and GluR4 channels, we first compared concentration–response data for glutamate-evoked currents and glutamate-induced desensitization. Figure1 shows concentration–response data for glutamate-induced desensitization and the steady-state plateau currents for GluR1 (Fig. 1a–c) and GluR4 (Fig.1d–f). Because the plateau current measurements did not require rapid solution exchange, we measured these currents using whole-cell recordings so that they would be as large as possible. As illustrated in Figure 1, concentrations of glutamate that produced substantial desensitization produced only minimal plateau current. The IC₅₀ values for glutamate-induced desensitization were 0.56 and 7.49 μm for GluR1 and GluR4 channels compared with respective EC₅₀ values for the plateau currents of 12.5 and 32.3 μm. The concentration–response curves for peak currents measured in patches (see Fig. 3b,c) indicate that even higher glutamate concentrations were required to achieve full receptor occupancy. The EC₅₀ values for the peak currents (717 μm for GluR1 and 1800 μm for GluR4) (Fig.1c,f) were nearly 60 times larger than the corresponding values for the plateau currents. The three sets of data show that full receptor occupancy requires glutamate concentrations that are approximately three orders of magnitude greater than concentrations that produce virtually complete desensitization.

Fig. 1.

GluR1 and GluR4 channels desensitize at glutamate concentrations that produce minimal activation. a,d, Currents evoked by 5 mm glutamate in control solution and after equilibrating patches containing GluR1 (a) and GluR4 (d) channels with the indicated concentrations of glutamate. b,e, Steady-state plateau currents evoked in cells expressing GluR1 (b) and GluR4 (e) channels by the indicated applications of glutamate (bars). c, f, Concentration–response curves for glutamate-induced desensitization (squares), the steady-state plateau current (triangles), and the peak current (circles; from results like those shown in Fig.3b,c) for GluR1 (c) and GluR4 (f) channels. Eachsymbol is the mean value obtained from measurements in four to nine patches or cells. Results from individual patches or cells were normalized to the amplitude of the peak current evoked by 5 mm glutamate in the absence of preincubation (glutamate-induced desensitization), the plateau current evoked by 1 mm glutamate, and the peak current evoked by 50 mm glutamate. Error bars indicate SEM for each set of data. Some of the error bars in this and subsequent figures are less than one-half the symbol size.

Fig. 3.

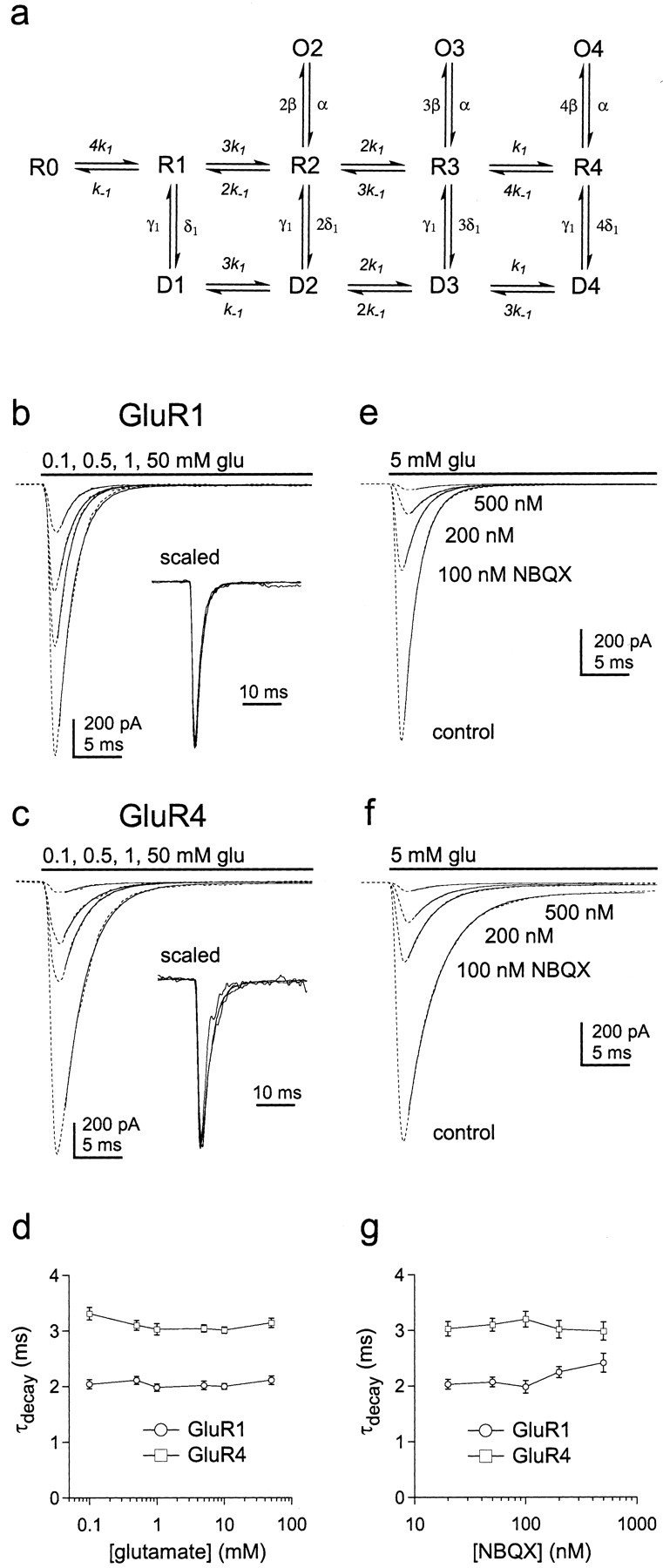
The decay of GluR1 and GluR4 currents varies little with subunit occupancy. a, Hypothetical kinetic model for AMPA receptor gating. Each subunit of the tetrameric channel contains a binding site for glutamate. There are therefore five discrete closed states, which differ in the number of subunits occupied by glutamate (0–4, states R0 toR4). Channels with two, three, or four glutamates bound can open to discrete subconductance levels (O2,O3, O4) where unitary conductance increases with receptor occupancy. Channels with one, two, three, or four subunits occupied by glutamate can desensitize (statesD1 to D4). b,c, Currents (dotted lines) evoked by sustained applications of the indicated concentrations of glutamate in outside-out patches from cells transfected with the cDNAs encoding GluR1 (b) or GluR4 (c). The decays of the currents have been fitted with single exponential functions (smooth curves) that gave time constants of 1.92–2.18 msec for GluR1 and 2.78–3.27 msec for GluR4. The insets show the currents superimposed after they were normalized to their peak amplitudes. d, Plot of the decay time constants for GluR1 (circles) and GluR4 (squares) channels obtained from single exponential fits to the decay of currents evoked by sustained applications of a range of glutamate concentrations (mean ± SEM values from 6 and 7 patches, respectively). e,f, Currents (dotted lines) through GluR1 (e) and GluR4 (f) channels evoked by sustained applications of 5 mm glutamate before (control) and after equilibrating individual patches in solutions containing 100–500 nmNBQX. The decays of the currents have been fitted with single exponential functions (smooth curves) that gave time constants of 1.88–2.21 msec for GluR1 and 2.71–3.35 msec for GluR4.g, Plot of the decay time constants for GluR1 (circles) and GluR4 (squares) channels as a function of NBQX concentration (mean ± SEM values from 4 and 5 patches, respectively).

Occupancy of a single subunit is sufficient to desensitize AMPA receptors

We compared several kinetic schemes to determine which could best reproduce the three types of concentration–response data. Because AMPA receptors are tetramers with four binding sites for glutamate, all of the models tested had five closed states (zero to four glutamates bound). Channel activation and desensitization were assumed to proceed in parallel from the same closed states (Vyklicky et al., 1991; Raman and Trussell, 1995). The models were of the class shown in Figure3a, but differed in the number of desensitized and open states: each desensitized and open state had different numbers of subunits occupied by glutamate. All of the comparisons were done using Monte Carlo simulations of the activity of at least 5000 channels (see Materials and Methods for details).

Although some native AMPA receptors display four concentration-dependent open levels (Smith and Howe, 2000), models with four open states reproduced the concentration–response data only if it was assumed that the open probability was very small for channels with one glutamate bound, i.e., these channels generate negligible current. It was also generally true that models in which the number of desensitized states did not exceed the number of open states failed to reproduce the separation between desensitization and activation. In addition, models with only two open states (three and four glutamates bound) and three desensitized states (two, three, and four glutamates bound) reproduced the concentration–response data only if substantial negative cooperativity of binding to closed states was included. Specifically, by requiring two molecules of glutamate to be bound before the channels desensitize, it was necessary to reduce the dissociation rate constant for the first binding step (relative to subsequent ones) 90-fold for GluR1 and 30-fold for GluR4 (or the rates for the first two steps 10- and 6-fold) to reproduce the IC₅₀ values for desensitization. In contrast, the three sets of concentration–response results were reproduced well without introducing cooperativity of binding if it was assumed that channels with one glutamate bound desensitize, but do not open, and that the binding of two glutamates is sufficient for activation gating. Previous work on AMPA receptors, including GluR1, also indicates that occupancy of two subunits is sufficient to open AMPA-type channels (Clements et al., 1998; Rosenmund et al., 1998; Irizarry, 2001). We therefore tentatively concluded that the binding of one glutamate molecule is sufficient to desensitize AMPA channels and that two glutamate molecules must bind to GluR1 and GluR4 channels before they have significant probability of opening.

To test our conclusion further, we determined the kinetics of entry into desensitization at low glutamate concentrations. If channels with one subunit occupied desensitize, then entry into desensitization should follow a nearly exponential time course and be faster than if occupancy of multiple subunits is required. The protocols for these experiments required rapid switching between three different solutions, which was achieved by mounting pipettes pulled from theta glass with two internal septa on the piezoelectric bimorph (Fig.2a,b). Outside-out patches containing GluR1 or GluR4 channels were first exposed to concentrations of glutamate that produced little channel activation and >50% steady-state desensitization, and the patches were then switched to 5 mm glutamate at increasing intervals to determine how many channels were available for activation. Examples of results obtained for GluR1 and GluR4 are shown in Figure 2c,d. At glutamate concentrations that produce minimal activation but substantial desensitization, the envelope of the peak currents follows a simple exponential time course (Fig. 2e,f). Hodgkin-Huxley fits to the time course data gave values for the exponent, m, that were indistinguishable from 1.0 for both GluR1 and GluR4 (1.02 ± 0.07 and 0.97 ± 0.09; n = 5 and 6 patches, respectively). The mean results obtained for GluR1 and GluR4 channels are plotted in Figure 2, g and h. Superposed on the results are the predicted time courses for entry into desensitization if singly occupied channels desensitize (thick solid lines). The dotted and thin solid lines are the predictions for models in which desensitization requires the binding of two glutamates (see legend to Fig. 2 for details), both of which give onset kinetics substantially slower than those observed. These results strongly suggest that occupancy of a single subunit is sufficient to desensitize AMPA receptors.

Fig. 2.

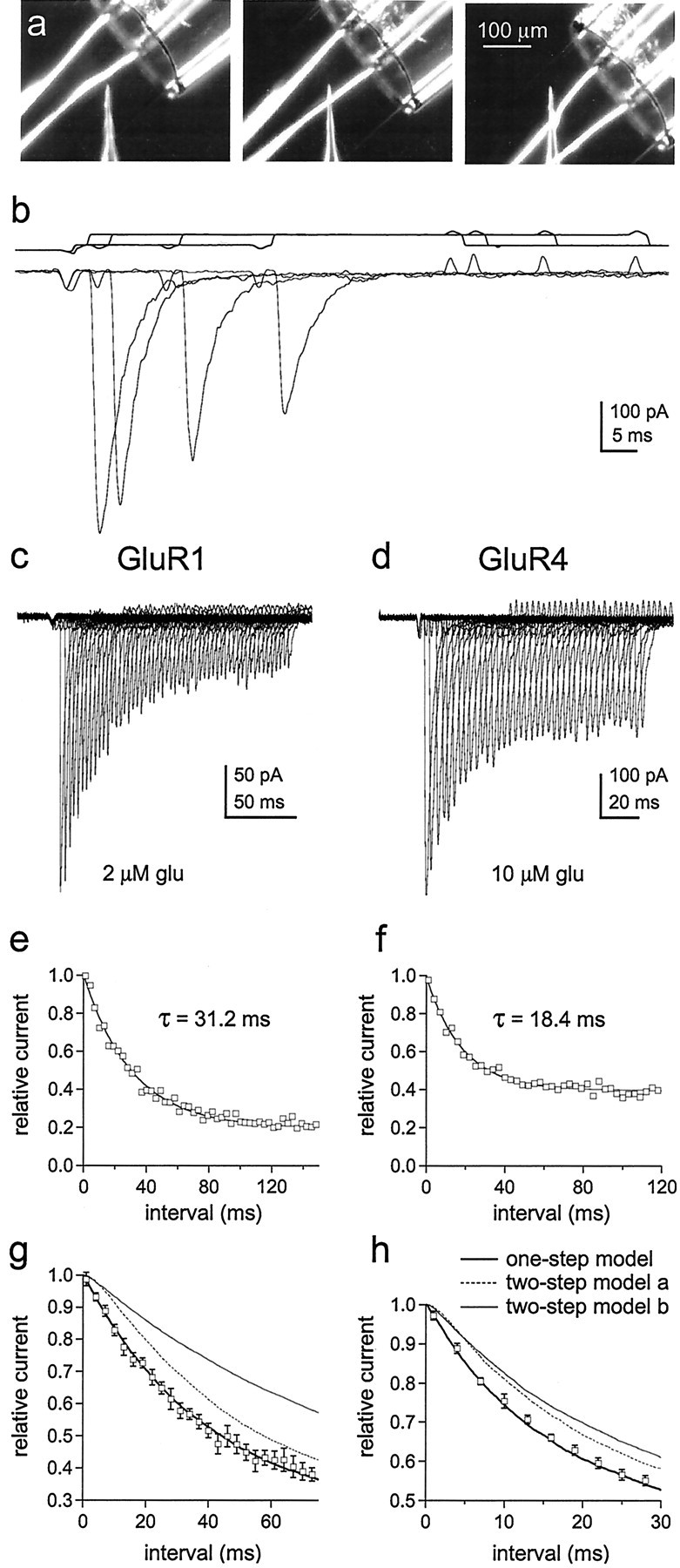
The time course of entry into desensitization shows that occupancy of a single subunit is sufficient to desensitize AMPA receptors. a, Photomicrographs of the two-septa pipettes used for experiments requiring rapid switching between three solutions (interfaces visualized by adding ethanol to the solution in the middle barrel). The interfaces were moved in sequential steps as shown. b, Currents evoked by 5 mm glutamate 1, 4, 16, and 28 msec after exposing a patch containing GluR4 channels to 10 μm glutamate. The open tip responses measured for the same pre-exposure intervals are shown above the currents.c, d, Peak currents evoked by 5 mm glutamate at various times after exposing a patch containing GluR1 channels to 2 μm glutamate (c) and a patch containing GluR4 channels to 10 μm glutamate (d, same patch as inb). The duration of the first conditioning pulse was 1 msec. Subsequent pulses were incremented in 3 msec steps.e, f, The amplitude of the peak currents in c and d plotted as a function of the duration of the conditioning pulse (e, GluR1;f, GluR4). The results were fitted with single exponential functions (smooth curves) that gave the indicated time constants. To allow averaging of results obtained from different patches, the peak current amplitudes measured at each pre-exposure interval were normalized to the amplitude of the peak current at zero time (obtained from the exponential fits to each set of data). g, h, Mean (±SEM) results obtained for GluR1 (n = 5 patches) (g) and GluR4 (n = 6 patches) (h). The curves are the time courses for entry into desensitization predicted with 2 μm(g) and 10 μm(h) glutamate from kinetic schemes in which occupancy of one or two subunits is required to produce substantial desensitization. The thick solid lines show the kinetics predicted with the model in Figure 6a (black states only) and the rate constants in Table 1. The dotted andthin lines were obtained with models identical to Figure6a except that states D0, D1, D₂2, and O₂ were eliminated. The dotted lines are the predictions when the first binding step was higher affinity than subsequent ones (two-step model a), and the thin solid lines are the predictions when the first two binding steps are equivalent and higher affinity than the last two (two-step model b). The dissociation rate constants were altered to give the same steady-state desensitization. For model a, this was achieved by decreasing the dissociation rate constant for the first binding step (to 100 sec⁻¹for GluR1 and 350 sec⁻¹ for GluR4) and decrementing the subsequent dissociation rate constants by one integer multiple of k_-1. For model b, the dissociation rate constants for the first two binding steps were set to k_-3 and 2k_-3 (k_-3 = 800 sec⁻¹ for GluR1 and 1750 sec⁻¹ for GluR4), and the subsequent steps were decremented by two integer multiples ofk_-1. All other rate constants in Table 1were identical in each case. We also tested two-step models in which we shifted all of the values for the rate constants in Figure6a one step to the right and adjusted the values of the dissociation rate constants for the first, and first and second, binding steps to maintain the experimentally observed steady-state desensitization. These models also gave time courses for entry into desensitization that were much slower than those measured experimentally.

Subunit occupancy and the rate and extent of desensitization

The results above suggested to us that the kinetic scheme in Figure 3a might provide a physically plausible model for AMPA receptor gating. The model builds on earlier proposals (Patneau and Mayer, 1991; Vyklicky et al., 1991;Raman and Trussell, 1992, 1995; Jonas et al., 1993; Partin et al., 1996; Hausser and Roth, 1997) but incorporates the tetrameric structure of the channels and concentration-dependent substate gating (Rosenmund et al., 1998; Smith and Howe, 2000). Binding transitions between open states were excluded given electrophysiological and structural evidence that domain closure in the open state is so complete that it traps glutamate (Benveniste and Mayer, 1995; Armstrong and Gouaux, 2000). Simulations also showed that allowing dissociation from open states produced deactivation decays that deviated substantially from the simple exponential decays observed experimentally.

One simple explanation for the full desensitization produced by very low glutamate concentrations (Kiskin et al., 1986) is that the affinity of glutamate is higher for desensitized channels (Trussell and Fischbach, 1989; Patneau and Mayer, 1991; Raman and Trussell, 1995;Kessler et al., 1996). However, because the channels can open with two, three, or four subunits occupied, such a difference in affinity implies that the rate and extent of desensitization should vary with subunit occupancy (if microscopic reversibility is maintained). We therefore examined whether these properties varied as a function of glutamate concentration.

For both GluR1 and GluR4, currents evoked by a wide range of glutamate concentrations show similar decays (Fig. 3b–d), suggesting that the rate constants for entry and exit from desensitization (δ and γ) are relatively insensitive to subunit occupancy. These results agree with previous work on native channels (Colquhoun et al., 1992;Raman and Trussell, 1992; Hausser and Roth, 1997). As an additional test, we compared the decays of currents evoked by 5 mm glutamate in the absence and presence of the competitive antagonist NBQX. In these latter experiments, the rapid kinetics of glutamate binding should ensure that occupancy of all available sites precedes desensitization. As shown in Figure3e–g, the decays of the glutamate-evoked currents were similar over a 25-fold range of NBQX concentrations, even at concentrations that produced virtually complete blockade of the currents. The insensitivity of the current decays to receptor occupancy argues that glutamate binds to closed and desensitized states with similar affinity (k_-1/k₁≈k_-2/k₂).

Recovery from desensitization behaves as a two-step process

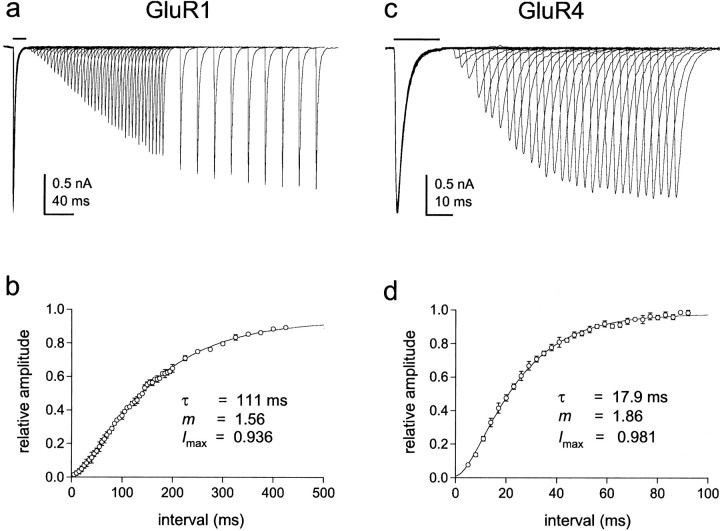
For the model in Figure 3a, there are many routes that a fully occupied desensitized channel (state D4) could take to exit from desensitization. To determine which of these possible routes is preferred, and to investigate the possibility that ligand dissociation contributes to the kinetics of recovery, we carefully mapped the time course of recovery with two-pulse protocols. A 20 msec application of 5 mm glutamate was made to desensitize the channels, and the peak current evoked by a second pulse was measured after various times in control solution. Results for GluR1 and GluR4 from single outside-out patches are shown in Figure4, a and c. Mean results from several patches are shown in Figure 4, b andd. The recovery time course is clearly sigmoid and was poorly described by single exponential fits. To estimate the number of kinetically similar steps that contribute to the time course of recovery, we fitted the mean data with Hodgkin-Huxley equations. The fits gave values for the exponent, m, of 1.56 for GluR1 and 1.86 for GluR4. These results suggest that there are two rate-limiting steps that contribute to the time course of recovery.

Fig. 4.

Recovery from desensitization follows a sigmoid time course. a, c, Currents evoked by 5 mm glutamate in outside-patches from cells expressing GluR1 (a) and GluR4 (c) channels. Two-step protocols were used in which an initial application of glutamate (bar) was paired with identical applications made at increasing interpulse intervals. Individual sweeps from the entire series are superimposed. b, d, For each patch, the peak amplitude of the current evoked by the second application of glutamate was expressed as a fraction of the peak amplitude of the current evoked by the first application with which it was paired. Circles show the mean (± SEM) results from five patches for GluR1 (b) and six patches for GluR4 (d) plotted as a function of the interpulse interval. Each set of data was fitted with a Hodgkin-Huxley equation. The fits (smooth curves) gave the indicated values for the time constant of recovery (τ), the number of equivalent rate-limiting steps (m), and the maximum fractional recovery (I_max). The values ofm suggest that there are two approximately equivalent steps along the route of recovery.

Receptor occupancy and the time course of recovery

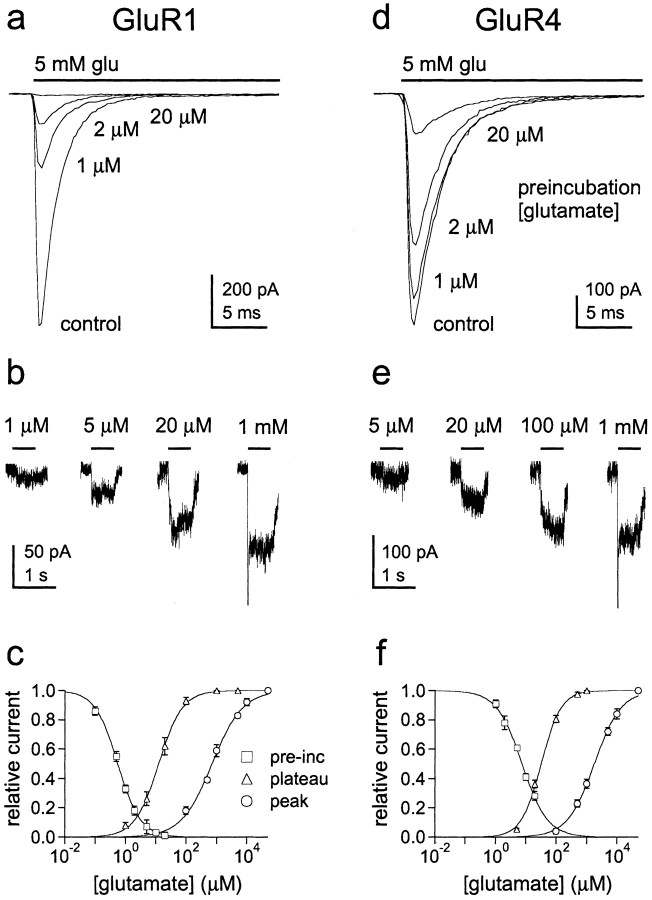
To determine how the time course of recovery depends on receptor occupancy, we measured recovery from desensitization at concentrations in which most occupied channels would have either one or two subunits occupied by glutamate. To obtain the first condition, outside-out patches containing GluR1 or GluR4 channels were equilibrated with concentrations of glutamate (2 μm for GluR1 and 8 μm for GluR4) that produced substantial desensitization but little channel activation (Fig. 1c,f). To obtain the second condition, outside-out patches containing GluR1 or GluR4 channels were equilibrated with 50 μmglutamate, a concentration that produced substantial plateau, but little peak current, and virtually complete desensitization (Fig.1c,f). Rapid switching between the three different solutions required for these experiments was achieved by using pipettes pulled from theta glass with two internal septa (Fig.2a).

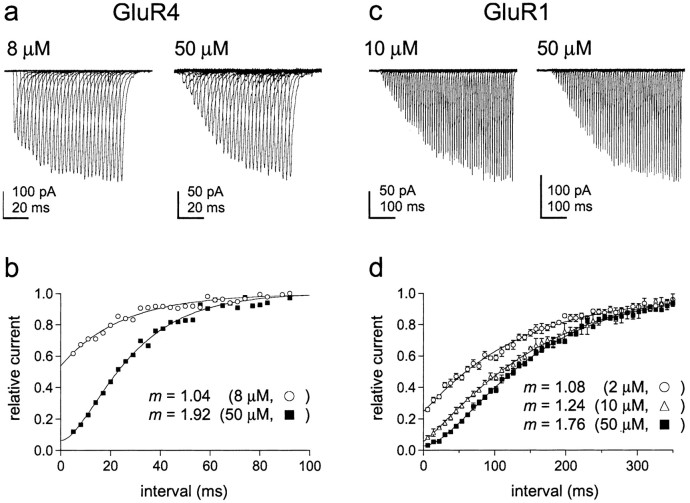
The results obtained for 8 and 50 μm glutamate from a patch containing GluR4 channels are shown in Figure5, a and b. Recovery from desensitization induced by 8 μmglutamate was nearly exponential (mean value of m from Hodgkin-Huxley fits, 0.99 ± 0.06; n = 5 patches), whereas the results obtained for 50 μmglutamate (m = 1.77 ± 0.13; n = 4 patches) were similar to those obtained for recovery from 5 mm glutamate. The time constants obtained at each concentration (20.9 ± 1.6 and 21.4 ± 1.7 msec) were similar to the time constant of recovery from 5 mmglutamate (Fig. 4). The results obtained for GluR1 are presented in Figure 5, c and d. The fits to the mean GluR1 recovery data show that the sigmoid nature of recovery increases in a graded manner as the concentration of glutamate is increased from 2 to 50 μm (Fig. 5d) (τ values: 120, 124, and 136 msec). Recovery is nearly exponential with 2 μm glutamate, whereas the results obtained for 50 μm glutamate are similar to those obtained with 5 mm glutamate. Together with the data shown in Figures 1 and 2, the concentration dependence of the kinetics of recovery indicates that the two rate-limiting steps during recovery proceed from doubly occupied channels and that channels with one glutamate bound recover with kinetics primarily determined by γ₁, the resensitization rate constant.

Fig. 5.

The time course of recovery from desensitization varies with receptor occupancy. a, Recovery from desensitization caused by 8 and 50 μm glutamate in an outside-out patch containing GluR4 channels. Currents are responses to 50 msec applications of 5 mm glutamate made at increasing intervals after switching from low glutamate to control solution.b, The peak currents were normalized to theI_max values obtained from Hodgkin-Huxley fits to each set of data. These fits (smooth curves) gavem values consistent with there being one and two rate-limiting steps for recovery from desensitization caused by pre-equilibration with 8 and 50 μm glutamate, respectively. c, Recovery from desensitization caused by 10 and 50 μm glutamate in outside-out patches containing GluR1 channels. d, Mean (± SEM) normalized recovery data obtained with 2, 10, and 50 μm glutamate (results from 4, 4, and 5 patches, respectively). The m values from the Hodgkin-Huxley fits to the data (smooth curves) are given on the figure. Time constants are given in Results.

Evidence for two types of desensitized states

We were able to reproduce the time course of recovery for both GluR1 and GluR4 channels with the model in Figure 3a, provided we assumed that the first rate-limiting step during recovery is glutamate dissociation from D2. The same set of rate constants also accurately predicted the concentration dependence of steady-state desensitization and the concentration–response curves for the plateau and peak currents for both channel types.

The model in Figure 3a, however, failed to reproduce two consistent experimental findings. First, over the time scale investigated, recovery was typically incomplete. TheI_max values obtained from the Hodgkin-Huxley fits to the recovery data at 5 mmglutamate were <1.0 (GluR1, 0.94; GluR4, 0.98), suggesting that a small fraction of the channels recover on a substantially slower time scale, as found in previous studies on native channels (Patneau and Mayer, 1991; Colquhoun et al., 1992). If the slow component of recovery reflects a qualitatively different type of desensitization, then it must correspond to states that are entered rapidly, because the desensitizing glutamate application was only 20 msec in duration. We tried a number of ways of creating such a rapidly filled “sink,” but for various reasons they all failed. However, we could reproduce the incomplete recoveries by including a constitutive desensitized state, D0. If glutamate can dissociate from state D1, albeit slowly, then during recovery some channels get stalled in state D0 (Fig.6a). The proportion of channels that accumulate in the D0 state is larger for GluR1 than GluR4 because the resensitization rate constant, γ₁, is smaller for the more slowly recovering GluR1 channels.

The second problem with the model in Figure 3a was the predicted decay of the plateau current at the end of a sustained glutamate application. At the end of such an application, most channels are desensitized and will begin to recover from desensitization on returning to control solution. If during this recovery glutamate dissociation is slow from state D2, then channels that linger in D2 will continue to generate plateau current, and the decay of the plateau current will be inversely related to the rate of glutamate dissociation. For glutamate dissociation rate constants (from state D2) that reproduced the rate and shape of the measured recovery time course, simulations predicted that the plateau currents should decay with time constants of 28 and 4.5 msec for GluR1 and GluR4, respectively. These predicted decays are 5–10 times slower than those observed experimentally. This problem can be solved if it is assumed that there is a second type of desensitized state and that recovery from desensitization for channels with two or more glutamate molecules bound requires two resensitization steps. This allows dissociation from state D2 to be rapid, because the sigmoid nature of recovery can be accounted for by two relatively slow resensitization steps. The black states in the kinetic model shown in Figure 6a incorporate this second type of desensitization.

Agreement between simulated and experimental data is often improved by adding states to kinetic schemes. The model in Figure 6awould therefore gain credibility if some physical meaning could be ascribed to the two hypothetical types of desensitization. The two types of desensitized states share the property that glutamate dissociation is rapid until reaching a state in which the number of glutamate molecules bound equals the number of transitions the channel is away from the equivalently occupied closed state. Only then is resensitization favored over glutamate dissociation. This suggests to us that glutamate dissociation is fast from some subunits and slow from others. Because binding domain closure likely precedes desensitization (Armstrong and Gouaux, 2000; Sun et al., 2002), one possible explanation for such different rates of dissociation is that they reflect differences in the extent of binding domain closure for individual subunits. We propose that desensitization is accompanied by conformational changes that stabilize binding domain closure on some subunits [and uncouple domain closure from channel opening (Sun et al., 2002)]. In the model shown in Figure 6a, desensitized states in successively “deeper” rows correspond to channels with an increasing number of subunits whose binding domains are partially closed, and the rate-limiting steps during recovery correspond to resensitization that occurs when glutamate dissociation becomes slow. If this interpretation of the results is correct, then the two-step nature of recovery indicates that desensitized channels with more than two partially closed binding domains are rare (or short lived). Because AMPA receptors are likely dimers of dimers, receptors with three and four closed binding domains are likely receptors in which the binding domains of both monomers in one dimer are closed. We therefore suggest that the rearrangements that accompany desensitization stabilize binding domain closure for one monomer in each dimer.

Although the kinetic scheme in Figure 6a has a large number of states, it reproduces a wide variety of experimental results with a small set of rate constants. If only the states in black are considered, there are two sets of binding constants (those for association and dissociation to open and partially closed binding domains), one set for channel opening and closing, and three sets for entry and exit from desensitized states. Table 1 gives values for these rate constants that we estimated for GluR1 and GluR4 channels from Monte Carlo simulations. The estimated rate constants give equilibrium dissociation constants for binding to closed states (k_-1/k₁) of 450 μm for GluR1 and 1 mm for GluR4. The rate at which glutamate dissociates from subunits with partially closed binding domains (k_-2) is slowed ∼10,000-fold. Although at high glutamate concentrations most desensitized channels will reside in states with more than one closed binding domain, for GluR1 the δ/γ ratio is much smaller for the second desensitizing transition, suggesting that the two desensitizing steps are not necessarily equivalent [in agreement with recent work (Bowie and Lange, 2002)].

As shown in Figure 6, the model accurately predicts the rate at which glutamate-evoked currents decay during sustained applications (Fig.6b), the time course of recovery from desensitization and its dependence on glutamate concentration (Fig.6c,d), and the concentration–response relationships for glutamate-induced desensitization and the peak and steady-state glutamate-evoked currents (Fig.6e,f). As noted above, the model also accounts for the small percentage of channels that recover on a slower time scale and our observation that this percentage is larger for GluR1 than GluR4 channels. Finally, the model reproduces the kinetics of entry into desensitization at low glutamate concentrations (Fig.2g,h), as well as the deactivation kinetics of both channel types (data not shown). At high glutamate concentrations, the model and the rate constants in Table 1 predict that approximately one-third of the GluR1 channels and one-fourth of the GluR4 channels will desensitize without ever opening. Manipulations that substantially slow entry into desensitization should therefore increase peak glutamate-evoked currents. For GluR1 these currents should be potentiated ∼35%, a prediction that agrees well with the effect of cyclothiazide on currents through GluR1 channels (Robert et al., 2001).

Although the kinetic model in Figure 6a accurately predicts a wide variety of experimental results, the experimental plateau currents for both GluR1 and GluR4 channels were approximately threefold larger at saturating glutamate concentrations than those for simulated currents. This discrepancy might be explained if desensitized channels conduct ions, as suggested recently for GluR1 channels (Bowie and Lange, 2002). However, if this is the explanation for the discrepancy, our results indicate that the unitary conductance of desensitized channels would be very small (<0.15% of the currents through fully occupied open channels).

Four features of the model in Figure 6a merit additional discussion. First, it has been proposed that binding domain closure precedes gating and results in short-lived closed states whose instability is relieved by channel opening or desensitization (Sun et al., 2002). Such short-lived transition states had little impact on the simulations that we performed, and they are excluded from the model in Figure 6a for the sake of simplicity. Second, states D₃3, D₃4, and D₄4 were not included in the simulations, but it is not necessary that their steady-state occupancy be small. All that is required is that resensitization from these states be fast and that the dissociation rate constants from states D₂3, D₂4, and D₃4 be substantially larger than the corresponding δ values. Third, the model assumes that glutamate binding to some desensitized states occurs at rates (k₁ andk_-1) identical to the rates for closed channels. We have no evidence that this is so. For example, during desensitization the binding domains of unstabilized subunits may oscillate between open and closed conformations (as they do during activation/deactivation gating), which would slow both the association and dissociation rate constants. Simulations showed that tenfold reductions in these rate constants (for binding to desensitized states) only modestly increased the values of m obtained from Hodgkin-Huxley fits to the recovery time courses (12% for GluR1 and 17% for GluR4). Changes of this magnitude are perfectly compatible with our results. Finally, although our results indicate that occupancy of a single subunit is sufficient to cause desensitization, we do not intend our scheme to imply that we believe individual subunits desensitize. Indeed the rearrangements at the dimer–dimer interface that we propose stabilize domain closure would involve all four subunits for fully occupied receptors (see below). In Figure6a, the rate constants for entry into desensitized states are integer multiples of each other, not because we believe desensitization involves subunit-independent rearrangements but because the likelihood of the structural rearrangements that we propose account for our results increases systematically with receptor occupancy (see below and last section of Materials and Methods).

Discussion

The model in Figure 6a is the first kinetic mechanism proposed for AMPA receptors that includes desensitization and incorporates four binding sites for glutamate and multiple concentration-dependent open levels. We show here that this model and a small set of rate constants can account for a wide variety of experimental results. In particular, the model clarifies the relationship between the affinity of glutamate for closed and desensitized states, the sensitivity of AMPA-type channels to glutamate-induced desensitization, and the rate of recovery from desensitization. We emphasize, however, that the large number of states and free parameters that the model contains make it likely that there are other sets of rate constants, or constraints on these values, that would account for the results equally well. As a result, our conclusions, although plausible, must be regarded as tentative.

Comparison with previous kinetic mechanisms

Although the model in Figure 6a has more states, it shares certain features with previous kinetic schemes. For example, when receptor occupancy is high, the first transition during recovery from desensitization will typically correspond to glutamate dissociation (Raman and Trussell, 1992, 1995; Partin et al., 1996). In our model, however, glutamate dissociation speeds recovery not because the rate of resensitization depends strongly on occupancy, but because some channels would otherwise cycle several times between the two types of desensitized states before escaping desensitization. As in previous work (Raman and Trussell, 1992, 1995; Partin et al., 1996), resensitization typically involves transitions to states that are not directly connected to open states of the channel. These resensitization transitions occur when glutamate dissociation becomes slow, which formally corresponds to an increase in the affinity of glutamate binding. In this sense, our model has some features of classic allosteric mechanisms (Monod et al., 1965), and at low glutamate concentrations the large δ/γ ratios for occupied channels and the slow rate of glutamate dissociation from the singly occupied desensitized state ensure that channels will spend most of their time desensitized. However, when channels are first exposed to glutamate, binding will almost always precede desensitization, and receptor occupancy will remain essentially constant once channels desensitize, because subsequent binding transitions are low affinity. This feature of our model differs substantially from previous schemes that include a subsequent high-affinity binding step to desensitized channels (Patneau and Mayer, 1991; Raman and Trussell, 1992, 1995; Partin et al., 1996;Banke et al., 2000). Unlike previous models (Raman and Trussell, 1992,1995; Jonas et al., 1993; Partin et al., 1996; Hausser and Roth, 1997), we also find no need to include negative cooperativity of binding to closed states. The inclusion of four binding sites for glutamate and multiple open levels, together with the different occupancy requirements for desensitization and activation, are sufficient to account completely for the concentration dependence of desensitization and activation.

Sensitivity to glutamate desensitization and the rate of recovery

In a previous study we noted that the IC₅₀for glutamate-induced desensitization was inversely correlated with the speed of recovery (Robert et al., 2001). This is also evident in our present results in which GluR1 channels are more sensitive to glutamate-induced desensitization than GluR4 channels and recover from desensitization more slowly. Although we suggested that both the IC₅₀ and the rate of recovery might reflect the affinity of glutamate for desensitized channels, our present results indicate that both parameters are primarily determined by the δ/γ ratios for channels with one and two glutamates bound. GluR1 channels are more sensitive to glutamate-induced desensitization than GluR4 channels, and recover more slowly, primarily because GluR1 channels enter desensitization more readily and resensitize more slowly.

Binding domain closure and desensitization

We conclude that recovery from desensitization involves two sequential resensitization transitions, a conclusion also reached from recent work on GluR1 channels at high glutamate concentrations (Bowie and Lange, 2002). The similar results obtained here with GluR4, as well as data for heteromeric GluR1/GluR4 channels (data not shown), indicate that the two-step nature of resensitization is likely a common property of AMPA receptors. This two-step nature probably accounts for previous observations on native channels that recovery follows an exponential time course only after an initial apparent delay (Raman and Trussell, 1995). Our results indicate that resensitization becomes preferred when glutamate dissociation becomes slow, and we suggest that this slowing reflects stabilization of binding domain closure for individual subunits.

AMPA receptors are likely dimers of dimers (Armstrong and Gouaux, 2000;Ayalon and Stern-Bach, 2001; Mansour et al., 2001; Robert et al., 2001), and two recent studies have concluded that desensitization involves concerted conformational changes within a dimeric unit (Bowie and Lange, 2002; Sun et al., 2002). Binding domain closure is probably the initial conformational change that triggers both activation and desensitization (Armstrong and Gouaux, 2000; Sun et al., 2002), and in Figure 7 we illustrate three possible relationships between receptor occupancy, desensitization, and binding domain closure that incorporate the dimeric nature of the tetrameric channel. In Figure 7, a andb, closure of both binding domains within a dimer is required to trigger desensitization, perhaps reflecting concerted rearrangement of the two anti-parallel monomer–monomer interfaces (Sun et al., 2002). In Figure 7c, occupancy and binding domain closure of a single subunit is sufficient, and desensitization is accompanied by structural rearrangements that stabilize one subunit in each dimer in a closed conformation.

Fig. 7.

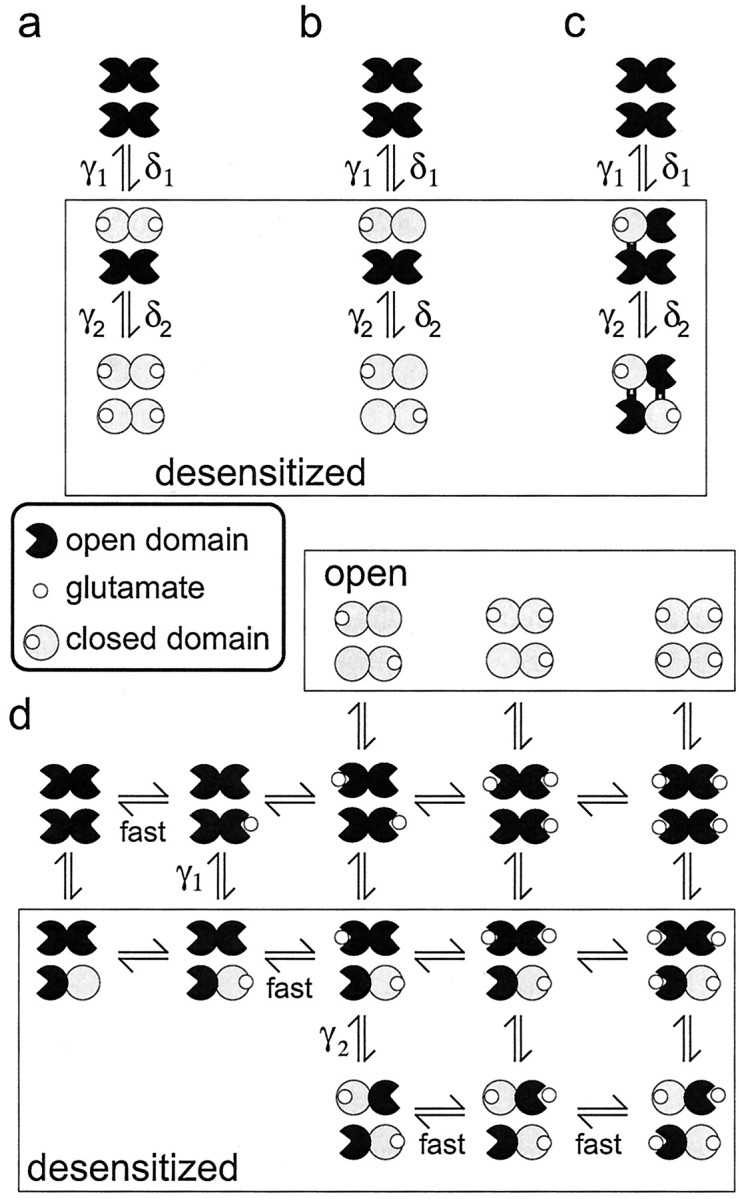
Desensitization stabilizes binding domain closure for one subunit per dimer. a–c, Three possible relationships between occupancy, desensitization, and binding domain closure. In each case, there are two types of desensitized states (those in the box) that are associated with sequential and equivalent changes in binding domain closure within each dimer.a, Binding is required for domain closure, and desensitization occurs after one dimer is doubly occupied. Simulations showed that this class of model requires that the two binding events be equivalent for one dimer and nonequivalent for the other. The double-occupancy requirement is also incompatible with the results in Figure 2. b, Occupancy of one subunit triggers concerted closure of both binding domains in the dimer. The similar desensitization seen in the presence of NBQX (Fig. 3) makes this proposal unlikely. c, Singly occupied channels can desensitize, and desensitization is accompanied by two interactions at the dimer–dimer interface that stabilize domain closure for one subunit in each dimer. d, Diagram illustrating the proposed relationship between binding, desensitization, and domain closure for the kinetic scheme in Figure 6a. For channels with two or more glutamates bound, the sigmoid time course of recovery reflects two sequential resensitization steps (characterized by the rate constants γ₂ and γ₁) that correspond to the disengagement of the interactions that stabilize domain closure. Glutamate dissociation is rapid from subunits with open domains and promotes recovery by greatly reducing the likelihood of domain closure.

In the example in Figure 7a, only doubly occupied dimers undergo desensitization, a constraint that is not consistent with the kinetics of entry into desensitization at low glutamate concentrations (Fig. 2). In addition, once channels desensitize, this class of model requires that subsequent glutamate binding to the remaining dimer be high affinity to one monomer and low affinity to the other. If this additional constraint is not introduced, either the separation between the EC₅₀ values for the plateau and peak currents is lost (both steps low affinity) or recovery is too slow (both steps high affinity). In Figure 7b, occupancy of one monomer results in the closure of both binding domains. However, concentrations of NBQX that produced nearly complete blockade of glutamate-evoked currents had little effect on desensitization (Fig. 3). Because NBQX binding is likely associated with minimal closure of the binding domain (Armstrong and Gouaux, 2000), the NBQX results suggest that concerted domain closure is not required for desensitization. NBQX also has little effect on channel activation, with the exception that it locks the channels in smaller conductance levels (Rosenmund et al., 1998;Smith and Howe, 2000). We therefore favor the proposal illustrated in Figure 7, c and d, in which desensitization involves conformational changes that stabilize binding domain closure of one subunit per dimer.

The recent crystallographic results of Sun et al. (2002) on the GluR2 binding core suggest a possible structural explanation for our conclusion that stabilization of domain closure occurs for only one subunit in each dimer. Although mutations or treatments that strengthen interactions at the monomer–monomer interface formed by helices J and D promote dimerization and reduce desensitization, a serine-to-aspartate mutation in helix J (N754D) that disrupts these interactions increases both the rate and extent of desensitization. Crystallographic analysis of this latter GluR2 S1S2J mutant revealed a different crystal packing in which helices F and G in domain 2 of one monomer interact with residues in loop 1 and the base of helix K in domain 1 of the other. The spatial relationship between the monomers in this crystal packing is that expected between adjacent subunits at the dimer–dimer interface in the complete tetrameric assembly (Sun et al., 2002). We suggest that interactions between domains 1 and 2 of adjacent subunits at the dimer–dimer interface both promote desensitization and stabilize binding domain closure. Because there is only one such potential interaction per dimer (Sun et al., 2002), only one monomer in each dimer is stabilized in a partially closed conformation.

Although our proposal is speculative, previous work on NMDA receptor channels identified loop 1 as a site mediating functionally important intersubunit contacts (Regalado et al., 2001). In addition, the interactions identified by Sun et al. (2002) involve the two structural elements, helix G and loop 1, that are missing in the bacterial glutamate-gated potassium channel, GluR0 (Chen et al., 1999; Mayer et al., 2001). Interestingly, currents through GluR0 channels show much slower and less complete desensitization than glutamate-evoked currents through mammalian AMPA receptors (Chen et al., 1999).

Conclusions

Our results confirm recent work showing that recovery from glutamate-induced desensitization behaves as a two-step process and that these steps correspond to sequential resensitization from two types of desensitized states (Bowie and Lange, 2002). For fully occupied channels, the initial transitions during recovery from desensitization correspond to the rapid dissociation of glutamate, events that hasten recovery by minimizing the likelihood of reentry into desensitized states. Both the kinetics of recovery and the sensitivity of AMPA-type channels to desensitization are determined primarily by the stability of desensitized states, as reflected by the resensitization rate constants. We conclude that desensitization involves conformational changes, likely at the dimer–dimer interface, that stabilize the binding domain of one subunit per dimer in a partially closed conformation. The time course of recovery is determined by the rate at which these stabilizing interactions disengage and allow the rapid dissociation of bound glutamate.