Abstract
The axons of dentate gyrus granule cells form synapses in the hilus. Ca2+ signaling was investigated in the boutons of these axons using confocal fluorescence imaging. Boutons were loaded with various concentrations of the Ca2+indicator Oregon Green BAPTA-1 by patch-clamping the cell bodies and allowing the dye to diffuse into the axon. Resting free [Ca2+] started at 74 nm, rose to ∼1 μm immediately after an action potential, and then decayed to rest with a time constant of 43 msec (all extrapolated to a dye concentration of zero). Action potential-induced [Ca2+] rises were smaller in larger boutons, consistent with a size-independent Ca2+ channel density of 45/μm2. Action potential-induced [Ca2+] changes varied with dye concentration in a manner consistent with κE ∼20 for the ratio of endogenous buffer-bound Ca2+ to free Ca2+. During trains of action potentials, [Ca2+] increments summed supralinearly by more than that expected from dye saturation. The amount of endogenous Ca2+ buffering declined as [Ca2+] rose, and this saturation indicated a buffer with a dissociation constant of ∼500 nm and a concentration of ∼130 μm. This is similar to the dissociation constant of calbindin-D28K, a Ca2+-binding protein that is abundant in dentate granule cells. Thus, calbindin-D28K is a good candidate for the Ca2+ buffer revealed by these experiments. The saturation of endogenous buffer can generate short-term facilitation by amplifying [Ca2+] changes during repetitive activity. Buffer saturation may also be relevant to the presynaptic induction of long-term potentiation at synapses formed by dentate granule cells.
Keywords: nerve terminals, calcium dynamics, calcium buffers, hippocampus, dentate gyrus, calbindin-d28K, mossy fibers
Introduction
Calcium ions enter a nerve terminal during presynaptic action potentials and bind to Ca2+ sensors to trigger neurotransmitter release. Cytoplasmic Ca2+ buffers compete for this Ca2+ to dampen the Ca2+ rise; Ca2+ sequestration and extrusion machinery restore Ca2+ to resting levels. By shaping the Ca2+ signal, the Ca2+-regulating systems of a nerve terminal play an important role in controlling synaptic function. Cytoplasmic Ca2+ signaling can be investigated by imaging with fluorescent dyes. Most previous fluorometric studies of presynaptic Ca2+fall into two distinct groups. Large nerve terminals are loaded by direct injection of Ca2+-sensitive dye (Smith et al., 1988; Jackson et al., 1991; Helmchen et al., 1997), affording a degree of control over the cytoplasm and membrane. This method cannot be applied to the far more abundant nerve terminals of smaller size. Alternatively, small nerve terminals can be loaded by extracellular application of membrane-permeable dyes (Regehr and Tank, 1991a; Melamed et al., 1993; Umbach et al., 1998). This overcomes the size obstacle, but the dye concentration is difficult to control. A promising new approach to the study of Ca2+ in nerve terminals is to fill the cell body with dye and allow it to diffuse into the axon (DiGregorio and Vergara, 1997; Cox et al., 2000; Koester and Sakmann, 2000; Emptage et al., 2001). The dye concentration can thus be controlled even in small nerve terminals, provided that they are close enough to the cell body to fill during a recording. In addition, by filling a selected cell, the origin of the axon is unambiguous.
We have applied this new loading technique to the granule cells of the dentate gyrus. These cells give rise to the well known mossy fiber pathway of the hippocampus (Henze et al., 2000). Mossy fiber synapses exhibit both short- and long-term plasticity. Long-term potentiation (LTP) at these synapses outlasts short-term changes in presynaptic Ca2+ (Regehr and Tank, 1991b); however, short-term changes in synaptic strength correlate well with Ca2+ (Regehr et al., 1994). Mossy fiber boutons vary in size over a wide range, and the largest of these were recently patch-clamped (Geiger and Jonas, 2000). Although mossy fiber terminals in the hippocampal CA3 region are ∼1 mm from the cell body and too far to be filled conveniently by this route, granule-cell axons branch extensively in the nearby hilus and display large numbers of boutons proximal to the cell body (Claiborne et al., 1986; Acsady et al., 1998). Granule cells form synapses in the hilus, indicating that these boutons constitute functional synaptic endings (Scharfman et al., 1990; Scharfman, 1993). Filling granule cells with Ca2+ indicators allowed us to follow the time course of [Ca2+] after action potentials and characterize the endogenous Ca2+ buffers.
A quantitative description of how Ca2+triggers neurotransmitter release depends on the knowledge of rapid spatially restricted transients in presynaptic Ca2+. Current Ca2+-imaging technology lacks the resolution to study these transients in small nerve terminals. Endogenous Ca2+ buffers are poorly understood, but they are likely to play an important role in shaping the spatiotemporal pattern of presynaptic Ca2+ (Yamada and Zucker, 1992; Roberts, 1994; Tank et al., 1995; Neher, 1998; Augustine, 2001; Burrone et al., 2002; Meinrenken et al., 2002). We analyzed the Ca2+ rises elicited by trains of action potentials and saw that the cytoplasmic buffering capacity declined as [Ca2+] rose. Thus, the Ca2+ buffers of granule-cell boutons saturate in a physiological range of intracellular [Ca2+].
Materials and Methods
Slice preparation. Animals that were 3–4 weeks of age were rendered unconscious with halothane and decapitated. The brain was removed; chilled in ice-cold cutting solution consisting of (in mm): 124 NaCl, 3.2 KCl, 1.25 NaH2PO4, 26 NaCO3, 1 CaCl2, 6 MgCl2, 2 pyruvate, 3 ascorbate, and 10 glucose; and saturated with 95% O2/5% CO2. Slices 400 μm thick were cut with a vibratome, maintained for 30 min at 34°C immediately after cutting, and subsequently maintained at room temperature (∼22°C) in artificial CSF (ACSF) for an additional 30 min before experiments. ACSF was identical to cutting solution but contained 2.5 mm CaCl2, lacked ascorbate and pyruvate, and contained 1.3 mm MgSO4 in place of MgCl2.
Electrophysiology. Recordings were made at 28–30°C while perfusing slices with ACSF saturated with 95% O2/5% CO2. Granule cells were identified in the stratum granulosa using a Zeiss (Thornwood, NY) microscope with infrared-differential interference contrast optics. Cells visualized with the aid of Ca2+-sensitive fluorescent dye (details below) showed the characteristic granule-cell morphology, with dendrites extending into the molecular layer and an axon extending into the hilus (see Fig. 1A). Granule cells were patch-clamped with an Axopatch 200C amplifier (Axon Instruments, Foster City, CA) using borosilicate glass patch pipettes filled with (in mm): 135 K-methylsulfate, 10 HEPES, 10 Na-phosphocreatine, 4 MgCl2, 4 Na-ATP, 0.4 Na-GTP, pH 7.3, and 12.5–100 μm Oregon Green BAPTA-1 (OGB1) or 100 μm Oregon Green BAPTA-6F (OGB6F) (Molecular Probes, Eugene, OR). Pipette resistance ranged from 3 to 8 MΩ before recording. Recordings were made in current-clamp, and the resting potential was regularly checked. Action potentials were evoked either singly or in trains (1–2 sec, 20 Hz) using 1 msec current pulses.
Fig. 1.
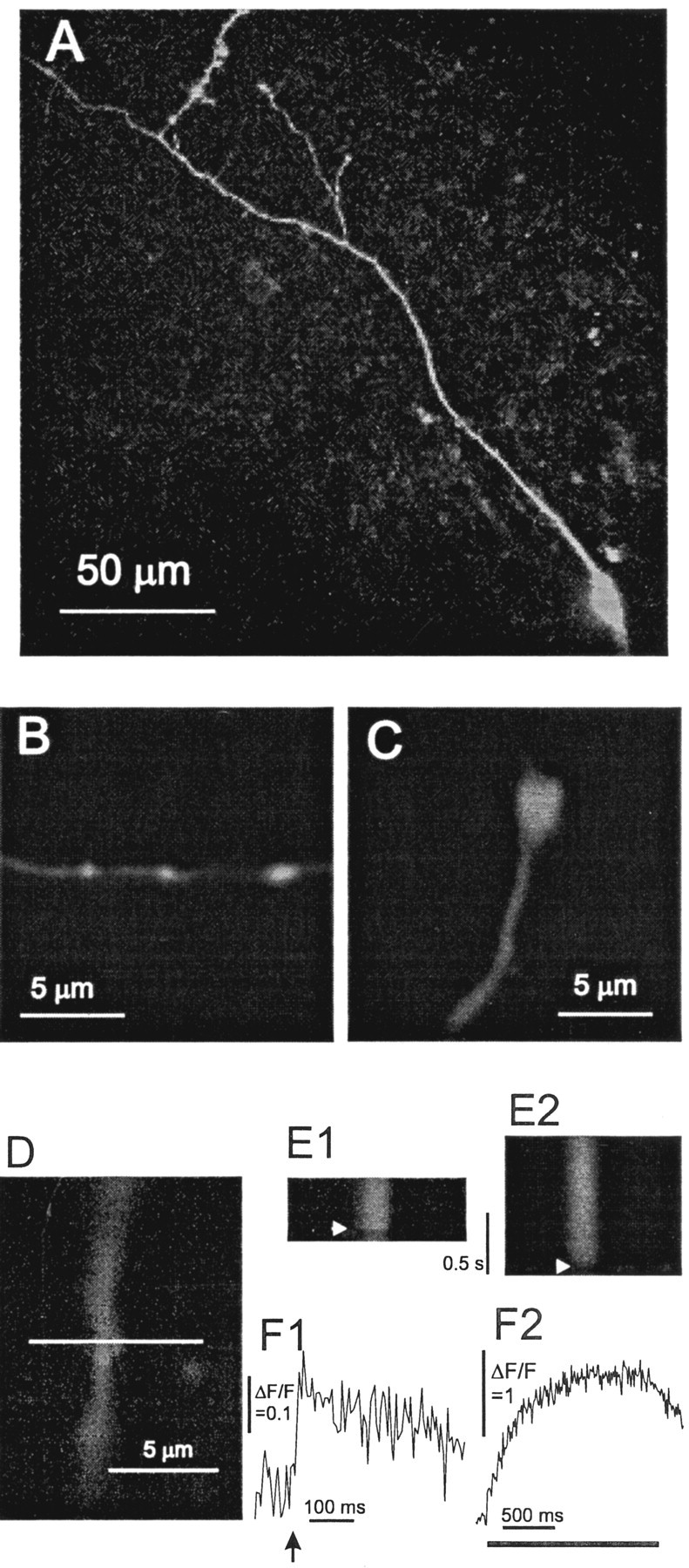
Confocal fluorescence micrographs of dentate granule cells filled with OGB1. A, A cell body and long-branched stretch of axon visualized from a z-stack projection spanning a depth of 40 μm. B, C, Segments of axon with three boutons (B) and one bouton (C) are shown. D, A bouton selected for recordings is shown with the line selected for scanning.E, Line scans show fluorescence increases evoked by an action potential (E1) and a train of action potentials at 20 Hz (E2). The horizontal axis is the position along the line in D. The vertical axis is time. The arrowhead indicates the time of the action potential in E1 and the start of the train in E2. F, Fluorescence in the segment spanning the bouton was averaged and plotted versus time for the action potential experiment in E1 and the train experiment inE2. The arrow in F1 shows the time of the action potential, and the bar inF2 shows the time for the train. Fluorescence traces were background subtracted and normalized to give ΔF/F. [OGB1]: A, B, 100 μm; C–F, 50 μm.
Imaging and microscopy. Imaging was performed with aZeiss LSM 510 laser-scanning confocal microscope. Light from an argon laser (488 nm) was used for illumination, and the FITC/GFP (green fluorescent protein) filter set prescribed for this microscope (dichroic, 488 nm; long-pass, 505 nm) selected fluorescent light and rejected laser lines. Before data acquisition, OGB1 was allowed to fill the axon for ≥15 and usually 30 min after break-in. When the time course of loading was followed, the dye fluorescence in proximal boutons reached a plateau within 15–30 min. Occasional checks of fluorescence intensity at ∼5 min intervals confirmed the stability of dye concentration. The axon was visualized as in Figure 1A and systematically traced from the cell body. Boutons such as those in Figure 1B–D were located and lines for scanning were drawn through boutons that were perpendicular to the axon (see Fig. 1D). Excitation parameters were adjusted to minimize photo damage (laser intensity, <0.5% of 6 mW; scan duration, <1 msec; pixel size, 0.02–0.05 μm). For single action potentials, line scans were taken every 5 msec, with an action potential evoked 0.1 sec after the start of a 0.5 sec sampling episode. For trains, line scans were performed at 10 msec intervals, with a 20 Hz, 1–2 sec train initiated 0.1 sec after the start of a 1–2 sec sampling episode. With these settings, photo damage, as evidenced by an increase in resting brightness and a decline in evoked responses, was generally not apparent until >10–20 recordings were made from the same bouton. Only two recordings were needed to obtain useful information from a single bouton: a spike and a train. Trials were often repeated, but nearly all of the data presented here were obtained with less than five recordings per bouton.
Data analysis. Measurements of [Ca2+] follow the method of Maravall et al. (2000). Recordings were initially examined with the software that was provided with the microscope. The segment of each scanned line, which included the entire cross-sectional extent of a bouton (see Fig.1E1, E2), was selected and averaged. Flanking segments well separated from the bouton on each side were used to estimate the background for each recording. Intracellular free [Ca2+] was calculated from background-subtracted fluorescence (f) as follows:
| Equation 1 |
The dissociation constant of OGB1 (Kd) was taken as 206 nm (Sabatini et al., 2002). The fluorescence under conditions in which all OGB1 is bound to Ca2+(fmax) was determined from a plateau in fluorescence during trains of action potentials (see Results). The fluorescence for free OGB1 (fmin) was calculated fromfmax assuming thatfmax/fmin= 6 (Sabatini et al., 2002). Although this ratio depends on poorly defined aspects of the cellular environment, estimates of [Ca2+] are relatively insensitive to the exact value as long asfmax/fminis a large value (Maravall et al., 2000).
For plotting and analysis of the decay kinetics of [Ca2+], fluorescence signals were transported to the computer program Origin (Microcal Software, Northampton, MA). [Ca2+] was computed from Equation 1, and the decay was fitted to a single exponential. Filtering was generally performed before fitting, although in several checks, filtering had no significant effect on the value of the time constant.
Endogenous Ca2+ buffers.Endogenous Ca2+ buffers were analyzed by a number of methods, starting with those of Neher and Augustine (1992), as adapted to a single-compartment model in which exchange of dye with the patch pipette or other regions of the cell is neglected (Helmchen et al., 1997; Sabatini et al., 2002). Buffers slow the decay of a [Ca2+] transient, and when the kinetic equations are linearized, the decay is exponential with a time constant:
| Equation 2 |
τ0 corresponds to γ/v from Neher and Augustine (1992) and reflects the activity of Ca2+ extrusion systems. This quantity can be thought of as the time constant for Ca2+ removal in the complete absence of buffering. κE and κDare the buffering capacities of the endogenous buffers (e.g., cytoplasmic Ca2+-binding molecules) and the Ca2+-sensitive dye (OGB1), respectively. These quantities represent the ratio of changes in concentrations of the Ca2+-buffer complex to free Ca2+. κDis computed from the dye concentration for a change from [Ca2+]1 to [Ca2+]2 as follows:
| Equation 3 |
The total dye concentration, [D]t, was taken as [OGB1] in the patch pipette, and as noted above, care was taken to allow time for the dye to diffuse into the bouton under study. With κD from Equation 3 and τ determined from the decay of a [Ca2+] rise, κE can be determined by plotting τ versus κD and fitting to a line. According to Equation2, the x-intercept is −1 − κE. κE can also be expressed in terms of [B]t and Kb, the concentration and dissociation constant of the endogenous buffer, by an analogy with Equation 3:
| Equation 4 |
An alternative method for determining κEuses a plot of the reciprocal of a [Ca2+] change versus κE, and is based on the following equation (Neher and Augustine, 1992):
| Equation 5 |
In the present study, Δ[Ca2+]t will always be taken as the increment in total [Ca2+] (free plus bound) induced by an action potential. According to Equation 5, a linear fit to a plot of 1/Δ[Ca2+] versus κD once again gives the x-intercept as −1 − κE.
We developed a different method for analyzing [Ca2+] changes that is more easily extended to the treatment of saturable endogenous buffers. For an action potential producing an increment in total [Ca2+] of Δ[Ca2+]t, the initial and subsequent concentrations obey the following relationship:
| Equation 6 |
[Ca2+]1 and [Ca2+]2 are the two measured concentrations before and after an action potential. The terms in parentheses in Equation 6, when multiplied by [Ca2+]1 or [Ca2+]2, are easily recognized as free endogenous buffer-bound and dye-bound Ca2+, respectively. Equation 6 thus expresses the conservation of Ca2+.
Equation 6 can be extended to a model with a single endogenous Ca2+ buffer, B:
| Equation 7 |
Kb and [B]t are as in Equation 4. Equation7 differs from Equation 6 in the replacement of κE by a term to reflect the saturation of the endogenous buffer.
The models represented by Equations 6 and 7 were fitted to data by comparing a measured value of [Ca2+]2 with a value of [Ca2+]2calculated from a measured value of [Ca2+]1 and the free parameters. The calculated value of [Ca2+]2 was obtained by solving the corresponding quadratic (Eq. 6) or cubic (Eq.7) equation. The sum-of-squares error between calculated and measured [Ca2+]2 was then minimized by varying the free parameters. For Equation 6, two free parameters, κE and Δ[Ca2+]t, were varied. For Equation 7, three parameters, Kb, [B]t, and Δ[Ca2+]t were varied. Both the solution of the equations (numerically) and the fitting were performed with the computer program Mathcad (Mathsoft, Cambridge, MA). Fitting with Mathcad does not provide the errors in parameters, but errors of the fit were computed as the square root of the sum-of-squares error of [Ca2+]2. Curve fits to simpler models performed within Origin yielded very similar values of parameters and also provided errors. The equations above were extended to the analysis of [Ca2+] rises during trains, but this analysis is best described together with the data in Results.
Results
When granule cells were patch-clamped with pipettes containing OGB1, a loaded axon became visible within a few minutes. In ∼50% of the recordings, the axon terminated at the surface of the slice <100 μm from the cell body, indicating that the axon was cut during slice preparation. In ∼25% of the recordings, a ∼100 μm segment of axon was visible. A few swellings were often found quite close to the cell body, and recordings from these swellings were included in this study. In the remaining ∼25% of granule cells, a long axon was visible with many irregularly distributed swellings and occasional branches (Fig. 1A). These fluorescence images resembled dentate granule-cell axons visualized by other histological techniques (Claiborne et al., 1986;Acsady et al., 1998), and the majority of the data presented here were from axons such as these. Closer examination of axonal segments under higher magnification revealed structures with the appearance ofen passant presynaptic boutons (Fig.1B–D), with diameters ranging from 0.5 to 3.5 μm.
An action potential evoked by a current pulse produced fluorescence increases in dendritic shafts, spines, axons, and boutons. Attention here focused on boutons; no effort was made to compare boutons with other regions. Figure 1D illustrates a bouton selected for study with the line of scanning indicated. The fluorescence change resulting from an action potential evoked in the cell body can be seen in the vertical succession of lines (Fig.1E1). A small fluorescence increase across the bouton follows the action potential nearly synchronously (indicated by thearrow). Averaging the fluorescence in the segment of the line spanning the bouton shows this fluorescence change more clearly (Fig. 1F1). When a current step applied to the cell body was subthreshold for action potential generation, no fluorescence change was detected in axonal swellings, indicating that passive spread of brief depolarizations cannot elicit detectable Ca2+ influx at these remote sites.
The following observations were not studied in depth but are noted here because they confirm previous studies of axons in other types of neurons. First, although most of the data collection was at 5 msec sampling intervals, a few recordings at 1–2 msec intervals indicated that the Ca2+ rise was complete within 1–2 msec. This is as rapid as that observed previously in boutons of cortical pyramidal cells (Cox et al., 2000; Koester and Sakmann, 2000). Second, in recordings at distal sites beyond initial boutons and branch points, fluorescence signals followed somatic action potentials with high fidelity. In no instance was a failure evident, either in a single action potential or the first few action potentials of 20 Hz trains. Thus, action potentials reliably invade the extensive arbors of granule-cell axons, as they do in pyramidal cell axons (Cox et al., 2000; Koester and Sakmann, 2000; Emptage et al., 2001)
Determination of fmax
Conversion of fluorescence to [Ca2+] with Equation 1 requires an estimate of fmax, the fluorescence when all of the OGB1 is Ca2+ bound. To saturate the dye, we used 20 Hz trains of action potentials. Figure1E2 shows a series of lines at 10 msec intervals with a train initiated after 100 msec. The fluorescence increase (Fig.1F2) exceeded that elicited by a single action potential (Fig. 1F1), by a factor of >20 in this case. The increments induced by individual action potentials were resolved early in the train. In this experiment, performed with 50 μm OGB1, fluorescence reached a plateau in slightly <1 sec after the start of the train and started to decay only when the train had terminated. When a lower concentration (25 μm) of OGB1 was used, the plateau was reached in ∼0.5 sec (Fig.2A). When a higher concentration (100 μm) was used, the time to reach a plateau was longer (Fig. 2B). These results indicate that the plateau in fluorescence with lower OGB1 concentrations is reached while [Ca2+] continues to rise. This supports the interpretation of the plateau as a saturation of the dye.
Fig. 2.
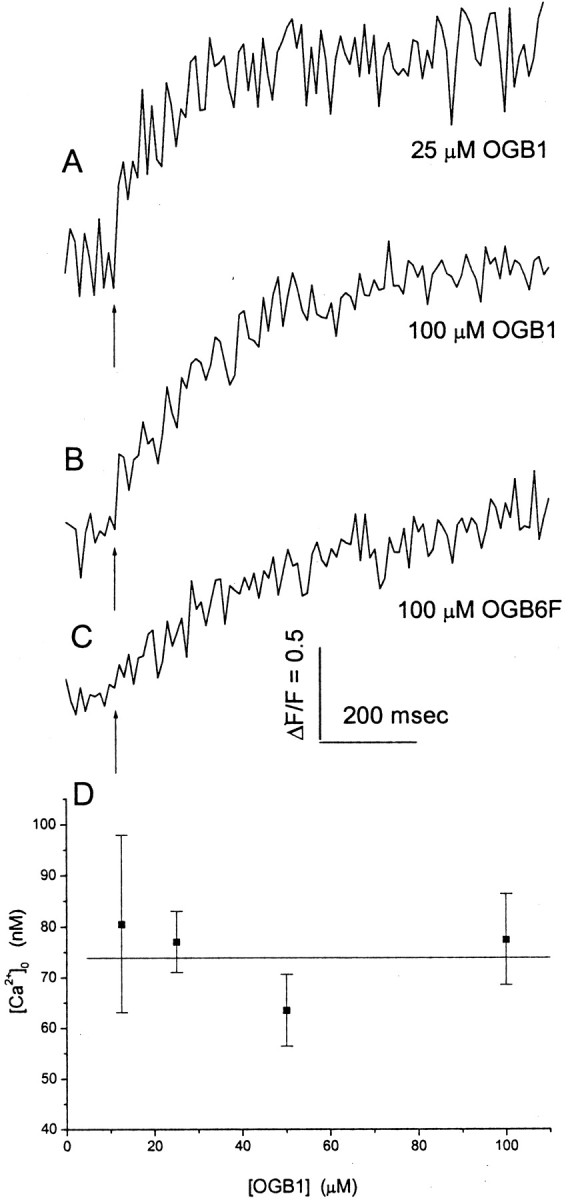
Fluorescence responses to trains of action potentials at 20 Hz illustrate the different rates of fluorescence rise for different intracellular dye solutions (indicated below eachtrace). Trains were initiated at thearrow. A–C, Recording of pipettes containing 25 μm OGB1 (A), 100 μm OGB1 (B), and 100 μm OGB6F (C). Fluorescence was averaged within a region of a bouton scanned by a lineas in Figure 1F2. D, Resting [Ca2+]0, computed from the initial and maximal fluorescence using Equation 1, is plotted versus patch pipette [OGB1]. SE is shown with 6–54 measurements.
A similar argument can be made using a lower affinity dye. When a train was applied to a bouton filled with 100 μm OGB6F (Kd, ∼3 μm), fluorescence continued to rise for >1 sec (Fig. 2C). This means that the saturation of fluorescence seen with OGB1 occurs as [Ca2+] continues to rise. Thus, the plateau in fluorescence reflects saturation of the dye rather than stabilization of [Ca2+] that might result from abatement of Ca2+ entry or compensation of Ca2+ entry by removal or sequestration. This supports the use of trains of action potentials to estimate fmax. This is confirmed by the results below on resting free [Ca2+], and by the observation that once the plateau is reached, deflections in fluorescence synchronous with action potentials cannot be detected, even in averages of many trains (see Fig. 5A).
Fig. 5.
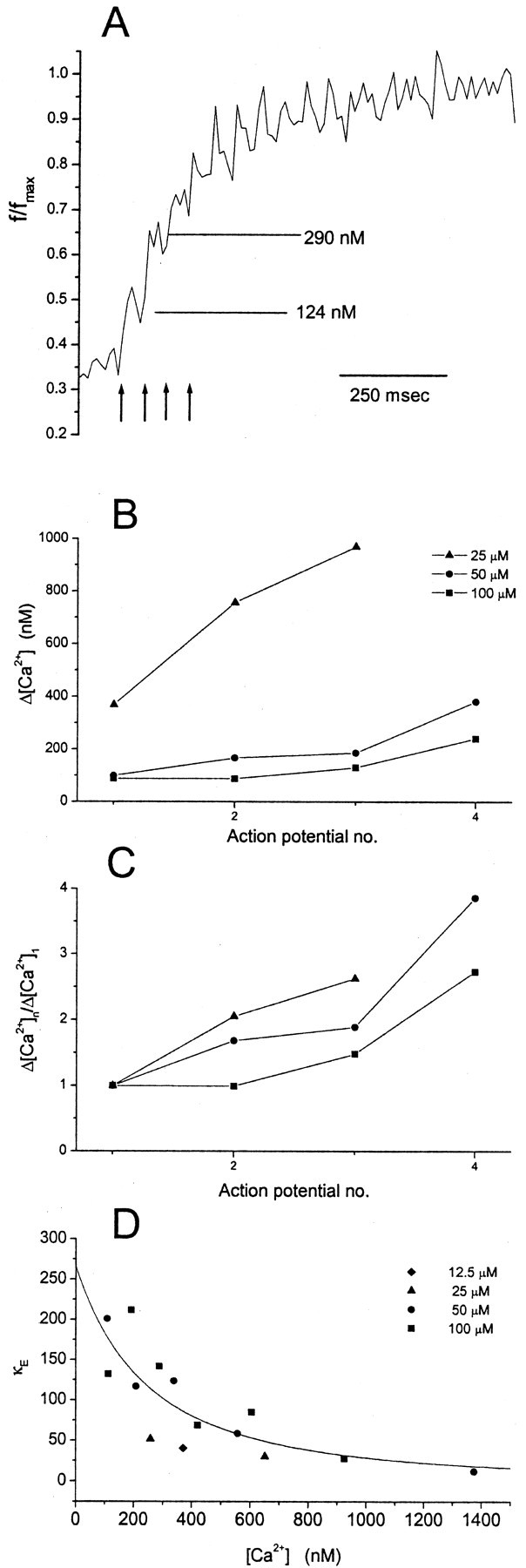
A, Fluorescence versus time during a train (arrows indicate the first four action potentials, continuing at 50 msec intervals). In 15 experiments with 50 μm OGB1, the fluorescence was normalized to the maximum and averaged. Computed free [Ca2+] immediately before and after the second action potential is shown to illustrate an example of [Ca2+]1 and [Ca2+]2 used to calculate κE in Equation 10. B, Increments in free [Ca2+] such as these are plotted versus action potential number in the train. Means similar to those inA were determined for seven boutons from three cells with 12.5 μm OGB1, 54 boutons from eight cells with 25 μm OGB1, and 11 boutons from eight cells with 100 μm OGB1. C, [Ca2+] increments normalized to the first increment of the train illustrate the supralinear summation of [Ca2+].D, Plot of κE versus [Ca2+]. κE was calculated from Equation 10 (Δ[Ca2+]t = 30 μm) for action potential-induced increases in [Ca2+]. [Ca2+] was 0.5([Ca2+]1 + [Ca2+]2). Thecurve is the fit of Equation 11, withKb = 490 nm and [B]t = 130 μm. Linear regression yielded p < 0.005 for this plot. Thepoints were derived from the first six action potentials in the train response with 100 μm OGB1, the first five action potentials in the train response with 50 μm OGB1, the first two action potentials in the train response with 25 μm OGB1, and the first action potential with 12.5 μm OGB1.
Resting free [Ca2+]
With fmax determined from a train, and fmin =fmax/6 (see Materials and Methods), we can use Equation 1 and the initial fluorescence to estimate [Ca2+]0, the resting free [Ca2+] within a bouton. [Ca2+]0 is plotted for four different values of [OGB1] in Figure 2D. All of the values are statistically indistinguishable, and a linear regression analysis showed no statistically significant correlation. This indicates that the dye does not alter [Ca2+]0. We can further say that the trains saturate OGB1 to a similar degree regardless of its concentration, supporting the measurement offmax from these trains. From these data, our best estimate of [Ca2+]0 is the [OGB1] = 0 intercept from a linear least-squares fit. This value was 74 ± 9 nm.
The value of [Ca2+]0 was independent of bouton size. Bouton diameter was estimated from a plot of the fluorescence versus the position in line scans. A plot with 54 measurements made with 25 μm OGB1 showed no significant correlation between [Ca2+]0 and bouton diameter (p = 0.21; data not shown).
Action potential evoked [Ca2+] changes
Both action potential-induced fluorescence changes (Fig.1F1) and train-induced fluorescence changes (Fig.1F2) were recorded from individual boutons.fmax was determined for each bouton and used to convert fluorescence to free [Ca2+] by Equation 1. Fluorescence and [Ca2+] versus time is shown in Figure3, A and C, for a bouton filled with 25 μm OGB1, and in Figure 3,B and D, for a bouton filled with 50 μm OGB1. The decays in [Ca2+] were well fitted by a single exponential function for both concentrations of OGB1 (Fig.3C,D). These results illustrate two important effects of dye on the shape of the Ca2+ signal. Increasing the dye concentration reduces the amplitude of the Ca2+ rise and slows the recovery. These features are well known consequences of increased Ca2+ buffering (Neher, 1995) and will be exploited in an analysis of endogenous Ca2+ buffers below.
Fig. 3.
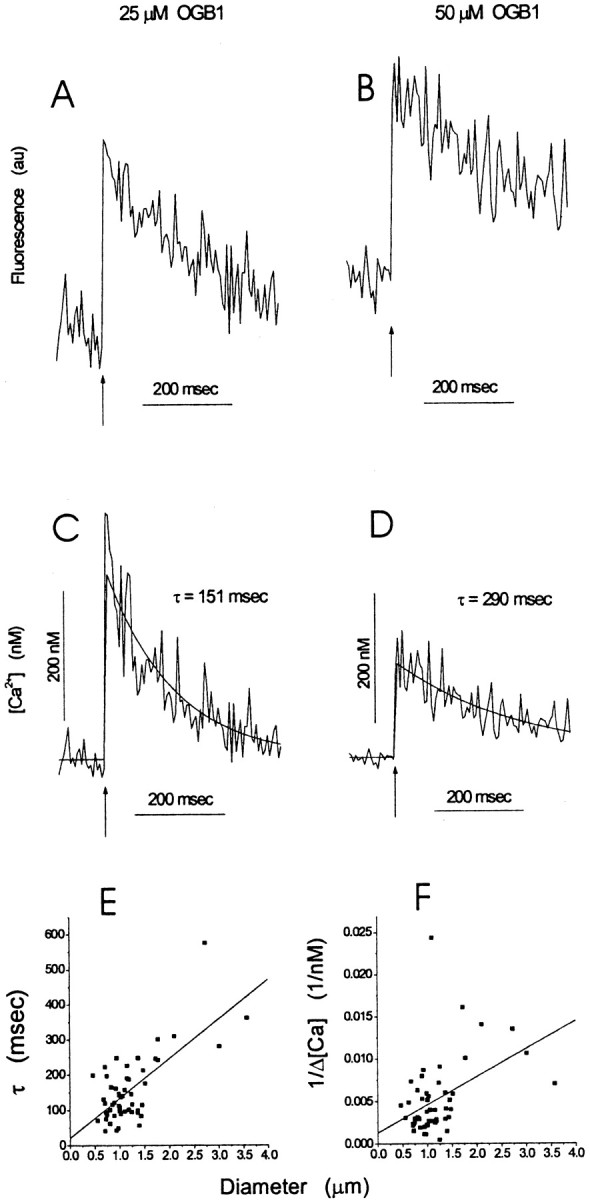
Fluorescence and [Ca2+] for two different values of [OBG1]. Action potentials were initiated at the arrow. A–D, Fluorescence traces in A and B were converted to [Ca2+] in C and D, respectively, using Equation 1. Exponential fits to [Ca2+] are shown together with estimates of τ.E, F, Plots of the time constant for [Ca2+] after an action potential (E) and the reciprocal of the peak change in [Ca2+] (F) versus bouton diameter; both plots were fitted to lines. The correlations were statistically significant with p< 0.001 for both plots. The slope of the line inF was used to calculate the Ca2+-channel density (see Results).
We made a larger number of measurements using 25 μm OGB1, because this concentration presented the best tradeoff between obtaining strong fluorescence signals and reducing dye-induced perturbations of [Ca2+]. With 54 such measurements, we could see that the time constant for decay (Fig.3E) as well as the reciprocal of the action potential-induced change in free [Ca2+] (Fig. 3F) varied with bouton size. Both plots showed highly significant correlations, with p < 0.001 from a linear least-squares fit. Thus, [Ca2+] rises are smaller and decays are slower in larger boutons. A similar correlation was obtained in dendritic spines for the amplitude of the change in free [Ca2+] and interpreted in terms of a fixed density of Ca2+ channels (Holthoff et al., 2002). Likewise, the correlation between the decay time constant and bouton size in Figure 3E could reflect a constant pump density.
A membrane Ca2+-channel density that is independent of bouton size predicts a linear relationship between the quantities plotted in Figure 3F; the slope can be used to estimate this density. The change in number of moles of Ca2+ (total) within a bouton, ΔmCa, is equal to the number of moles of Ca2+ that enters a bouton per Ca2+ channel, ϕ, times the number of Ca2+ channels, N, as follows:
| Equation 8 |
If the density of Ca2+ channels is denoted as ρCa and a spherical geometry is assumed, we can obtain the following:
| Equation 9 |
where d is diameter, and as defined in Materials and Methods, Δ[Ca2+]t is the sum of the concentration increases in free and bound Ca2+. Substituting Δ[Ca2+]t = Δ[Ca2+]free(1 + κE + κD) (from Eq.5) into Equation 9 then gives a linear relationship for interpreting Figure 3F with a slope of (1 + κE + κD)/6ϕρch. For ϕ we took the value used by Koester and Sakmann (2000) based on the estimate that each Ca2+ channel passes 0.2 pA for 0.2 msec during an action potential. This gave 125 Ca2+ ions or 2.1 × 10−22 mol of Ca2+. The slope in Figure 3Fwas 0.0033 nm−1μm−1. Equation 3 gave κD = 43 for these experiments. Based on the analysis of endogenous Ca2+ buffers presented below, we can take κE = 20 based on an analysis in terms of nonsaturable buffer, or κE = 124 computed with Equation 4 from our best estimates of the Kb and [B]t of the endogenous buffer. This gives a Ca2+ channel density of ρCa = 17/μm2 or ρCa = 45/μm2, respectively. Because data presented below indicate that the endogenous buffer is saturable, the second value is more reliable. The significance of different κE values for saturable and nonsaturable buffers will be discussed below.
[Ca2+] rises and endogenous Ca2+ buffers
To estimate the strength of endogenous Ca2+ buffers in bouton cytoplasm, we first examined a plot of the time constant for [Ca2+] decay from fits (Fig.3C,D) versus κD (Eq. 3) (Fig.4A). A linear fit based on Equation 2 yielded κE = 18 from the τ = 0 intercept. The reciprocal of the action potential-induced [Ca2+] rise was plotted versus κD, and a linear fit based on Equation 5yielded a similar value for a κE of 25 (Fig.4B). The prediction of a model involving buffer saturation to be discussed below is also shown (Figure4B, dotted curve).
Fig. 4.
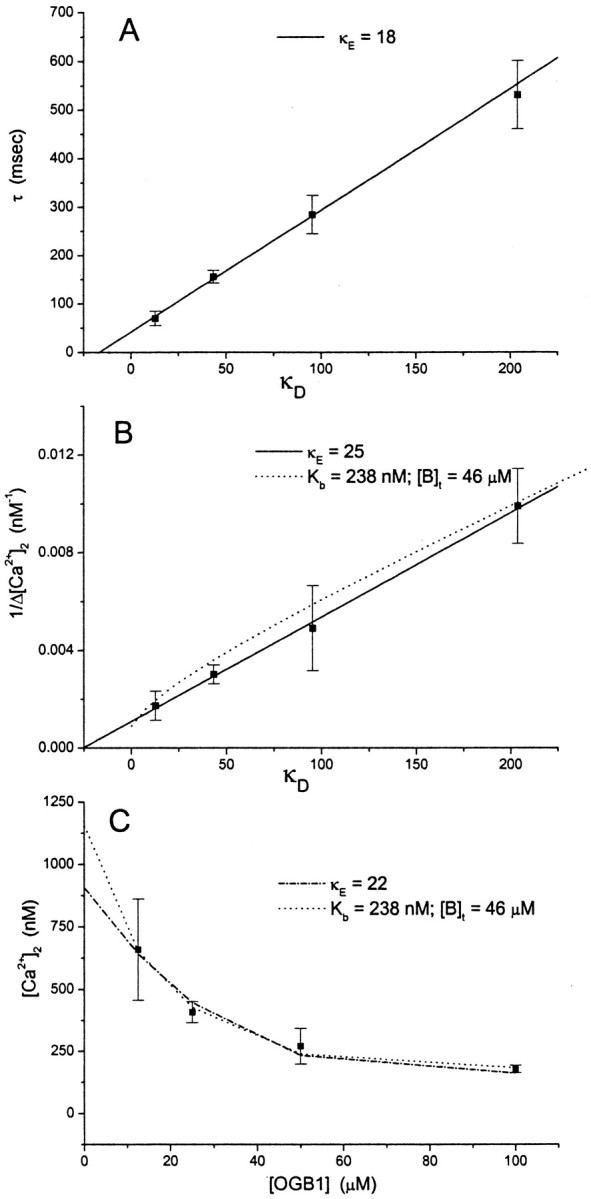
A, The time constant for [Ca2+] decay (from fits such as those in Fig. 3) was averaged for different values of [OGB1] and plotted versus average κD (from Eq. 3). The best fittingline (Eq. 2) gave κE = 18.B, Plot of the reciprocal of the action potential-induced Ca2+ change (1/Δ[Ca2+]) versus κD. The best fitting line (Eq. 5) gave κE = 25.Dotted curve, The prediction based on Equation 7, with Kb and [B]t obtained from the fit of Equation 7to the data in C. C, Plot of peak free [Ca2+] after an action potential versus [OGB1]. The dashed curve represents [Ca2+]2 from Equation 6, with κE = 22 and Δ[Ca2+]t = 19 μmfrom the best fits. The dotted curve represents the fit to Equation 7, which gave Kb = 238, [B]t = 46 μm, and Δ[Ca2+]t = 29 μm.
We introduced a new method of analyzing Ca2+ buffers based on Equation 6 from Materials and Methods, with resting free [Ca2+] as [Ca2+]1 and the peak free [Ca2+] after an action potential as [Ca2+]2. Given [Ca2+]1, Equation6 was solved for [Ca2+]2, and this value was compared with the measured value of [Ca2+]2. The parameters κE and Δ[Ca2+]t were then varied to minimize the error between calculated and measured [Ca2+]2. Measured [Ca2+]2 is plotted versus the dye concentration in Figure 4C. The calculated values of [Ca2+]2obtained from the fit are represented by the dashed curve. The model fits the data very well, yielding κE = 22 and Δ[Ca2+]t = 19 μm. Thus, the κEvalues determined by the three methods represented in Figure 4 are in reasonable agreement with one another. This comparison indicates that the decay time constants are reasonably well approximated by Equation 2and are therefore not distorted by factors such as diffusion of Ca2+ to neighboring regions.
We next analyzed the data in Figure 4C using a model that includes a single endogenous buffer species with a saturable binding site (Eq. 7). This model was fitted to the data, yielding [B]t = 46 μm, Kb = 238 nm, and Δ[Ca2+]t = 29 μm. The computed values of [Ca2+]2 (Fig.4C, dotted curve) are again in good agreement with this experiment. The error for the fit was reduced 40% compared with that achieved in Equation 6, but this model has one more free parameter. Both models give fits that fall close to the data points, so we conclude that the data presented in Figure 4C are consistent with either nonsaturating or saturating endogenous buffers.
Both saturating and nonsaturating models also fitted the plot of 1/Δ[Ca2+] versus κD in Figure 4B, in which the prediction of a saturable buffer based on Equation 7 is drawn as adotted curve. This plot indicates that a saturable endogenous Ca2+ buffer predicts nearly linear behavior over a wide range of κD values. It is thus once again difficult to distinguish models with saturating and nonsaturating buffers. Furthermore, the values of κE calculated from Equation 5 with endogenous buffer properties that generated the dotted curve in Figure4B range from 136 to 37 for [Ca2+] rises ranging from 0.1 to 1 μm. A saturable buffer with a much higher effective κE value can replicate the behavior of a nonsaturable buffer with a lower κE value. Thus, κE values derived from an analysis based on Equation 5 will be incorrect if a cell contains a buffer that saturates in the range of [Ca2+] under study (see Discussion).
The y-intercept in Figure 4A gives a dye-independent value for the time constant of Ca2+ removal τ0(1 + κE) = 43 ± 6 msec (from Eq. 2). τ0 is then computed as 2.4 msec, using the κE value obtained from the same plot. The magnitude of the rise in free [Ca2+], induced by an action potential for zero added dye, was computed with Equations 6 and 7 (using the parameters obtained from the fits) as 0.91 and 1.16 μm, respectively.
Summation of [Ca2+] rises and endogenous buffer saturation
During trains of action potentials we could resolve a series of steps in fluorescence associated with sequential action potential-induced [Ca2+] rises (Figs.1F2, 2A–C). The later steps in the train start from higher levels of [Ca2+], in which there should be fewer Ca2+-binding sites available within a bouton, because a greater fraction of those Ca2+-binding sites should be occupied. These data thus contain information about Ca2+ buffer saturation. To analyze these trains quantitatively, the fluorescence signals from many nerve terminals were normalized to their maxima and averaged together. Figure5A shows this average for all 15 bouton recordings made with 50 μm OGB1 (from four cells). This figure shows that the second action potential in the train elevated [Ca2+] from 124 to 290 nm. We could thus estimate the action potential-induced change in free [Ca2+] for a series of steps untilf/fmax exceeded ∼0.85 and free [Ca2+] exceeded ∼1 μm. Higher concentrations were subject to large errors because of the small value of the denominator in Equation 1.
The increases in free [Ca2+] are plotted in Figure 5B for 25, 50, and 100 μmOGB1. It can be seen that later action potentials always induce greater increases in free [Ca2+]. This is illustrated more clearly in Figure 5C, with the [Ca2+] increments normalized to the first for each concentration of OGB1. Thus, the [Ca2+] rises produced by successive action potentials were supralinear, and this trend was evident for all three values of [OGB1]. (With 12.5 μm OGB1, the fluorescence rise during a train was so rapid that [Ca2+] after the second action potential could not be accurately measured;f/fmax was 0.92.)
One possible explanation for these supralinear increases in [Ca2+] is the saturation of OGB1. With aKd of 206 nm, we would expect to see a reduction of buffering by this dye as [Ca2+] rises through its observed range. However, two other possibilities for the supralinear increases in [Ca2+] are changes in Δ[Ca2+]t and saturation of endogenous Ca2+ buffers. Because the effect of dye saturation can be calculated precisely, we can test the hypothesis of endogenous buffer saturation, subject to the assumption of constant Δ[Ca2+]t. The issue of variation in Δ[Ca2+]t will be considered in the Discussion.
Taking Equation 6, we can solve for κE:
| Equation 10 |
This equation can be used to calculate κEfor each pair of [Ca2+]1 and [Ca2+]2 in the progression of steps during a train (Fig. 5A), provided that we have an estimate of Δ[Ca2+]t. The analysis from Figure 4C yielded values for Δ[Ca2+]t of 19 and 29 μm, but the value of 19 μm was based on a model that assumes no saturation of the endogenous buffer (Eq. 6) and is therefore less reliable (see Discussion). Thus, we favor the value of 29 μm. This choice was confirmed by analysis of additional data from measurements with much higher dye concentration, in which the influence of endogenous buffers should be very small. We performed a limited set of measurements with 250 μm OGB1, from which we estimated [Ca2+]0 = 91 ± 15 nm and a peak action potential-induced free [Ca2+] change of 72 ± 15 nm (n = 5). From these values, Equation 6 and 7, without the endogenous buffer term, gave Δ[Ca2+]t = 34 μm. We therefore selected Δ[Ca2+]t = 30 μm for most of our analyses but conducted checks with other values as well.
κE computed from Equation 10 is plotted versus [Ca2+], taken as 0.5([Ca2+]1 + [Ca2+]2) in Figure5D. If the endogenous buffers failed to saturate in the range of [Ca2+] spanned in these experiments, the plot would be a horizontal line with no correlation between κE and [Ca2+]. Figure 5D reveals a strong inverse correlation between κE and [Ca2+], with p < 0.005. The decrease in κe with increasing [Ca2+] suggests that the endogenous buffers are saturated by rising [Ca2+].
To estimate the concentration and dissociation constant of the saturable Ca2+ buffer implicated in Figure5D, these data were analyzed in two ways. First, thepoints plotted in Figure 5D were fitted to the equation:
| Equation 11 |
κE is derived from Equation 4 using a single [Ca2+] = 0.5([Ca2+]1 + [Ca2+]2). The best fit is drawn in Figure 5D, with [B]t = 130 ± 28 μm and Kb = 490 ± 220 nm. The geometric mean of [Ca2+]1 and [Ca2+]2 was also used for [Ca2+] rather than the arithmetic mean because of the product in the denominator of Equation11. The fit produced the same results. When the analysis was performed with different values of Δ[Ca2+]t, the inverse correlation was still strong (p < 0.01 for all the plots), and values for [B]t andKb changed by less than a factor of 2. [B]t = 75 ± 33 μm and Kb = 850 ± 640 nm for Δ[Ca2+]t = 20 μm; [B]t = 191 ± 32 μm andKb = 414 ± 160 nm for Δ[Ca2+]t = 40 μm.
To avoid using the mean [Ca2+] in Figure5D and Equation 11, an analysis was conducted on the triplets of [Ca2+]1, [Ca2+]2, and κE (from Eq. 10). The constraint for fitting was set up with Equation 4. For the 14 points plotted in Figure 5D, the parameters [B]t andKb were varied to minimize the error between κE from Equation 4 (a theoretical value) and κE from Equation 10 (an experimental value). This fit yielded very similar results (Kb = 527 nm and [B]t = 130 μm with an Δ[Ca2+]t = 30 μm). Similar results were obtained with Δ[Ca2+]t = 20 μm (Kb = 906 nm and [B]t = 76 μm) and Δ[Ca2+]t = 40 μm (Kb = 450 nm and [Bt] = 190 μm). Because there is uncertainty about whether the affinity of the dye is altered by the cellular environment, we recalculated κE from Equation 10 usingKd = 170 and 240 nm for OGB1 instead of using 206 nm [the Kd of another Ca2+ indicator, fura-2, varies within this range in different in vivo environments (Neher, 1995)]. The inverse correlation between κE and [Ca2+] was maintained (p < 0.005) and the values forKb and [B]t were not affected significantly.
In summary, [Ca2+] rises during trains indicate that an endogenous cytoplasmic Ca2+ buffer saturates as [Ca2+] increases from rest to 1 μm. The saturation was clear and significant for a range of values of Δ[Ca2+]t and for several variations in the analysis. With 30 μm as our best estimate of Δ[Ca2+]t,Kb is ∼500 nmand [B]t is ∼130 μm.
Discussion
This study investigated Ca2+signaling in boutons on axons arising from dentate gyrus granule cells. Axons were filled with fluorescent dye through the cell body by a patch electrode. This made it possible to measure a number of important quantities associated with Ca2+ signaling in single boutons while controlling dye concentration. This work extends previous methodology (DiGregorio and Vergara, 1997; Cox et al., 2000; Koester and Sakmann, 2000; Emptage et al., 2001) and demonstrates that loading of axons through the cell body can serve as a powerful general approach for studying Ca2+signaling in nerve terminals. In principle, any neuron that forms synapses within a few hundred micrometers of the cell body should be amenable to this method.
Resting free Ca2+([Ca2+]0) was 74 nm and independent of dye concentration (Fig.2D). The added buffering of the dye altered the speed and magnitude of responses but left [Ca2+]0 unchanged. This supports the idea that resting Ca2+reflects the set point of a regulatory system that operates through a homeostatic response to free Ca2+. The bouton size independence of [Ca2+]0 suggests that the Ca2+ regulation machinery (pumps and channels) is distributed uniformly.
Extrapolations to zero dye indicated that [Ca2+] rises to ∼1 μmafter an action potential (Fig. 4C) and then decays with a time constant of 43 msec. In guinea pig mossy fibers loaded with fura-2 AM, the action potential-induced [Ca2+] rise was 10–50 nm and the decay time constant was ∼1 sec (Regehr et al., 1994). Although factors such as species, animal age, temperature, and methodology could contribute to the differences between these values and ours, we note that if the buffering strength of the fura-2 in the previous experiments exceeded the endogenous buffering strength by 25-fold, our estimates of both the [Ca2+] change and the time constant for decay would be in qualitative agreement.
Ca2+-channel density
The reciprocal of the action potential-induced [Ca2+] rise was correlated with the bouton diameter (Fig. 3F). The slope of this plot yielded an estimate for the Ca2+-channel density of 45/μm2, a value somewhat larger than that obtained for pyramidal-cell boutons (Koester and Sakmann, 2000). A fixed Ca2+-channel density provides a perspective on the issue of whether transiently high [Ca2+] in a microdomain or spatially averaged [Ca2+] is most relevant to neurotransmitter release. A constant Ca2+-channel density will produce lower spatially averaged Ca2+ rises for larger boutons, but Ca2+transients in microdomains should be independent of diameter. Thus, different-sized boutons with the same Ca2+-channel density would release transmitter with equal efficacy if the release site sees [Ca2+] within a microdomain.
Constancy of Δ[Ca2+]t
Our analysis of endogenous Ca2+buffers depends critically on the assumption of constant increments in total [Ca2+] (Δ[Ca2+]t) during the first few action potentials of a train. If [Ca2+]t decreases with successive action potentials, then Equation 10 would yield smaller values of κE. Figure 5D would then show an inverse correlation as observed but without endogenous buffer saturation. In contrast, increases in Δ[Ca2+]t would hide saturation or make it appear weaker. Thus, changes in Δ[Ca2+]t would introduce errors in our estimates of [B]t andKb, and for sufficiently large decreases, render our interpretation of buffer saturation incorrect.
Recordings from mossy fiber boutons in the hippocampus indicate that changes in Δ[Ca2+]t are in the positive direction and too small to produce significant errors in our analysis (Geiger and Jonas, 2000). Action potentials broaden during trains and Ca2+-entry increases, but these effects are quite small for the first several spikes. In 20 Hz trains, action potentials should broaden by ∼0.7% per action potential [based on the stated value of 1.3% at 50 Hz and visual examination of Fig. 3 from Geiger and Jonas (2000)]. The increases in Δ[Ca2+]t were smaller than the increases in action potential width, most likely because of Ca2+ channel inactivation. A repeat of our own analysis, in which κE was calculated with a large (3%) increase in Δ[Ca2+]t per spike, left the inverse correlation between κEand [Ca2+] strong (p = 0.017) and the parameter values from fitting Equation 11 essentially unchanged. In addition, the two data points in Figure 5D most vulnerable to changes in Δ[Ca2+]t were from the fifth and sixth action potentials of trains with 100 μm OGB1. Excluding these two points had essentially no effect (p = 0.019).
The assumption of constant Δ[Ca2+]t can be evaluated more directly with our data. With 100 μm OGB1, Δ[Ca2+] is the same for the first two spikes (Fig. 5C). The high dye concentration limits [Ca2+] to a narrower range in which Δ[Ca2+] is linear with Δ[Ca2+]t. Similarly, Regehr et al. (1994) observed constant fluorescence increments during trains for the first 10 impulses. In that study, the Δ[Ca2+] per action potential was very small, most likely because of buffering by a high dye concentration, which would make fluorescence linear with Δ[Ca2+]t. Ca2+-induced Ca2+ release is evoked by longer trains (Liang et al., 2002). However, these factors do not alter our interpretations, because they only become relevant after many action potentials. Thus, independent lines of reasoning support the assumption of constant Δ[Ca2+]t. Variations in Δ[Ca2+]t are too small to alter our conclusions regarding the saturation of endogenous Ca2+ buffer or influence our estimates ofKb and [B]t.
Endogenous Ca2+ buffer properties
Analysis with the aid of models that neglect endogenous Ca2+ buffer saturation showed κE ∼20 (Fig. 4). Only the recent estimate of κE in dendritic spines is this low (Sabatini et al., 2002). Values in other nerve terminals (Stuenkel, 1994; Tank et al., 1995; Koester and Sakmann, 2000) as well as cell bodies (Neher, 1995) are often >100. The lowest value obtained previously in a nerve terminal was 40 in the calyx of Held (Helmchen et al., 1997), and it is interesting to note that both these calyces and mossy fiber boutons are relatively large. However, the present analysis suggests that calculating κE using a nonsaturable buffer model may lead to a value that is erroneously small. A saturable buffer can give rise to a nearly linear plot of 1/Δ[Ca2+] versus κD (Fig. 4B), but the value of κE obtained by fitting Equation 5 is much lower than κE computed fromKb and [B]t with Equation 4. This can be visualized by noting that as κD is reduced, Δ[Ca2+] rises grow larger. The saturation of endogenous buffer enhances this effect, increasing the slope and shifting the x-intercept toward zero. Thus, the presence of a saturable buffer gives rise to a systematic error in the value of κE derived from a model based on nonsaturable buffer.
The analysis of [Ca2+] signals during trains indicated that endogenous Ca2+buffers are saturated as [Ca2+] rises (Fig. 5D). The reduction of buffering strength with increasing [Ca2+] indicates that the endogenous Ca2+-binding molecules have aKb of ∼500 nmand a concentration of ∼130 μm. Cytoplasmic molecules that bind Ca2+ include both small molecules such as ATP (Baylor and Hollingworth, 1998) and proteins such as parvalbumin, calretinin, and calbindin-D28K (Baimbridge et al., 1992). The Kb for ATP is ∼200 μm, so ATP cannot contribute to the saturable Ca2+ buffering seen here. Among the Ca2+-binding proteins, calbindin-D28K immunoreactivity is seen in dentate granule cells, is abundant by the age of the animals used here (3–4 weeks of age), and is distributed through the entire cell, including the mossy fibers (Baimbridge, 1992). Calbindin-D28K binds four Ca2+ ions (Veenstra et al., 1997) with dissociation constants ranging from 286 to 1790 nm (average, 400 nm) in 150 mm KCl and 2 mmMgCl2 (Berggard et al., 2002). Our estimate ofKb = 500 nm is consistent with these measurements. Granule-cell axons most likely contain a spectrum of Ca2+-binding molecules, but the anatomical distribution together with the binding properties make calbindin-D28K an excellent candidate for the saturable Ca2+ binding revealed by our experiments.
Implications for Ca2+-triggered release
An analysis of Ca2+ diffusion in the presence of mobile buffer yielded the following expression for free [Ca2+] as a function of radial distance (r) from a Ca2+ channel for a steady state that forms in a few microseconds of channel opening (Neher, 1998), as follows:
| Equation 12 |
The iCa is the single channel current (0.2 pA), F is Faraday's constant,DCa is the Ca2+ diffusion constant (2.2 × 10−6cm2/sec), and λ = with kon as the Ca2+-to-buffer binding rate constant and [B]f as the free buffer concentration. With [B]f = 110 μm from the present study andkon = 8 × 107m−1sec−1 (Nägerl et al., 2000), we obtain λ = 160 nm. With our estimate of the Ca2+ channel density of 45 μm2, the mean distance between channels is ∼150 nm. Because this is comparable with λ, Ca2+-channel microdomains would overlap and allow Ca2+ from different channels to summate at release sites, even without channel clustering. A release site in the center of a square of four Ca2+ channels would be ∼100 nm from each channel. Summation of [Ca2+] from Equation 12 for these four channels gave 15 μm. This represents an estimate for the minimum [Ca2+] at a release site. However, a release site that is close to a Ca2+channel, say 10 nm away, would see [Ca2+] = 70 μm; this value is insensitive to the buffer. Because single action potentials in granule cells evoke large synaptic responses (Henze et al., 2000), these estimates provide a range for [Ca2+] that triggers release from these boutons.
Implications for synaptic plasticity
Theoretical studies of Ca2+ dynamics have indicated that buffer saturation can play a role in synaptic facilitation (Neher, 1998). The introduction of exogenous buffers presynaptically results in facilitation of neocortical synapses, with synapse-specific differences that most likely reflect variations in the distance between Ca2+ channels and release sites (Rosov et al., 2001). For the maximum distance of 100 nm estimated above, Equation 12 suggests that buffer saturation could amplify [Ca2+] rises by up to twofold. This would enhance synaptic transmission during repetitive activity and provide a basis for the correlation between free [Ca2+] and short-term facilitation (Regehr et al., 1994).
Different laboratories have reported long-term potentiation of mossy fiber synapses that is triggered presynaptically (Ito and Sugiyama, 1991; Castillo et al., 1994; Mellor and Nicoll, 2001) and postsynaptically (Yeckel et al., 1999). The question of whether granule-cell synapses on hilar neurons also exhibit synaptic plasticity has yet to be studied. The amplification of Ca2+ signals by saturation of endogenous Ca2+ buffers would increase the effectiveness with which repetitive activity initiates Ca2+-dependent signaling cascades and thus contribute to the presynaptic induction of LTP.
Footnotes
We thank Garry Rodda for technical assistance.
Correspondence should be addressed to Meyer Jackson, Department Physiology, SMI 127, University of Wisconsin Medical School, 1300 University Avenue, Madison, WI 53706. E-mail:Mjackson@Physiology.wisc.edu.
References
- 1.Acsady L, Kamondi A, Sik A, Freund T, Buzsaki G. GABAergic cells are the major postsynaptic targets of mossy fibers in the rat hippocampus. J Neurosci. 1998;18:3386–3403. doi: 10.1523/JNEUROSCI.18-09-03386.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Augustine GJ. How does calcium trigger neurotransmitter release? Curr Opin Neurobiol. 2001;11:320–326. doi: 10.1016/s0959-4388(00)00214-2. [DOI] [PubMed] [Google Scholar]
- 3.Baimbridge KG. Calcium binding proteins in the dentate gyrus. In: Ribak CE, Gall CM, Mody I, editors. The dentate gyrus and its role in seizures. Elsevier Science; New York: 1992. pp. 211–220. [Google Scholar]
- 4.Baimbridge KG, Celio MR, Rogers JH. Calcium-binding proteins in the nervous system. Trends Neurosci. 1992;15:303–308. doi: 10.1016/0166-2236(92)90081-i. [DOI] [PubMed] [Google Scholar]
- 5.Baylor SM, Hollingworth S. Model of sarcomeric Ca2+ movements, including ATP Ca2+ binding and diffusion, during activation of frog skeletal muscle. J Gen Physiol. 1998;112:297–316. doi: 10.1085/jgp.112.3.297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Berggard T, Miron S, Onnerfjord P, Thulin E, Akerfeldt KS, Enghild JJ, Akke M, Linse S. Calbindin D28k exhibits properties characteristic of a Ca2+ sensor. J Biol Chem. 2002;277:16662–16672. doi: 10.1074/jbc.M200415200. [DOI] [PubMed] [Google Scholar]
- 7.Burrone J, Neves G, Gomis A, Cooke A, Lagnado L. Endogenous calcium buffers regulate fast exocytosis in the synaptic terminal of retinal bipolar cells. Neuron. 2002;33:101–112. doi: 10.1016/s0896-6273(01)00565-7. [DOI] [PubMed] [Google Scholar]
- 8.Castillo PE, Weisskopf MG, Nicoll RA. The role of Ca2+ channels in hippocampal mossy fiber synaptic transmission and long-term potentiation. Neuron. 1994;12:261–269. doi: 10.1016/0896-6273(94)90269-0. [DOI] [PubMed] [Google Scholar]
- 9.Claiborne BJ, Amaral DG, Cowan WM. A light and electron microscopic analysis of the mossy fibers of the rat dentate gyrus. J Comp Neurol. 1986;246:435–458. doi: 10.1002/cne.902460403. [DOI] [PubMed] [Google Scholar]
- 10.Cox CL, Denk W, Tank DW, Svoboda K. Action potentials reliably invade axonal arbors of rat neocortical neurons. Proc Natl Acad Sci USA. 2000;97:9724–9728. doi: 10.1073/pnas.170278697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.DiGregorio DA, Vergara JL. Localized detection of action potential-induced presynaptic calcium transients at a Xenopus neuromuscular junction. J Physiol (Lond) 1997;505:585–592. doi: 10.1111/j.1469-7793.1997.585ba.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Emptage NJ, Reid CA, Fine A. Calcium stores in hippocampal synaptic boutons mediate short-term plasticity, store-operated Ca2+ entry, and spontaneous transmitter release. Neuron. 2001;29:197–208. doi: 10.1016/s0896-6273(01)00190-8. [DOI] [PubMed] [Google Scholar]
- 13.Geiger JRP, Jonas P. Dynamic control of presynaptic Ca2+ inflow by fast-inactivating K+ channels in hippocampal mossy fiber boutons. Neuron. 2000;28:927–939. doi: 10.1016/s0896-6273(00)00164-1. [DOI] [PubMed] [Google Scholar]
- 14.Helmchen F, Borst GG, Sakmann B. Calcium dynamics associated with a single action potential in a CNS presynaptic terminal. Biophys J. 1997;72:1458–1471. doi: 10.1016/S0006-3495(97)78792-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Henze DA, Urban NN, Barrionuevo G. The multifarious hippocampal mossy fiber pathway: a review. Neuroscience. 2000;98:407–427. doi: 10.1016/s0306-4522(00)00146-9. [DOI] [PubMed] [Google Scholar]
- 16.Holthoff K, Tsay D, Yuste R. Calcium dynamics of spines depend on their dendritic location. Neuron. 2002;33:425–437. doi: 10.1016/s0896-6273(02)00576-7. [DOI] [PubMed] [Google Scholar]
- 17.Ito I, Sugiyama H. Roles of glutamate receptors in long-term potentiation at hippocampal mossy fiber synapses. NeuroReport. 1991;2:333–336. doi: 10.1097/00001756-199106000-00008. [DOI] [PubMed] [Google Scholar]
- 18.Jackson MB, Konnerth A, Augustine GJ. Action potential broadening and frequency-dependent facilitation of calcium signals in pituitary nerve terminals. Proc Natl Acad Sci USA. 1991;88:380–384. doi: 10.1073/pnas.88.2.380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Koester HJ, Sakmann B. Calcium dynamics associated with action potentials in single nerve terminals of pyramidal cells in layer 2/3 of the young rat neocortex. J Physiol (Lond) 2000;529:625–646. doi: 10.1111/j.1469-7793.2000.00625.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Liang Y, Yuan L-L, Johnston D, Gray R. Calcium signaling at mossy fiber presynaptic terminals in the rat hippocampus. J Neurophysiol. 2002;87:1132–1137. doi: 10.1152/jn.00661.2001. [DOI] [PubMed] [Google Scholar]
- 21.Maravall M, Mainen ZF, Sabatini BL, Svoboda K. Estimating intracellular calcium concentrations and buffering without wavelength ratioing. Biophys J. 2000;78:2655–2667. doi: 10.1016/S0006-3495(00)76809-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Meinrenken CJ, Borst JGG, Sakmann B. Calcium secretion coupling at calyx of Held governed by nonuniform channel-vesicle topography. J Neurosci. 2002;22:1648–1667. doi: 10.1523/JNEUROSCI.22-05-01648.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Melamed N, Helm PJ, Rahamimoff R. Confocal microscopy reveals coordinated calcium fluctuations and oscillations in synaptic boutons. J Neurosci. 1993;13:632–649. doi: 10.1523/JNEUROSCI.13-02-00632.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mellor J, Nicoll RA. Hippocampal mossy fiber LTP is independent of postsynaptic calcium. Nat Neurosci. 2001;4:125–126. doi: 10.1038/83941. [DOI] [PubMed] [Google Scholar]
- 25.Nägerl UV, Novo D, Mody I, Vergara JL. Binding kinetics of calbindin-D28k determined by flash photolysis of caged Ca2+. Biophys J. 2000;79:3009–3018. doi: 10.1016/S0006-3495(00)76537-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Neher E. The use of fura-2 for estimating Ca buffers and Ca fluxes. Neuropharmacology. 1995;34:1423–1442. doi: 10.1016/0028-3908(95)00144-u. [DOI] [PubMed] [Google Scholar]
- 27.Neher E. Usefulness and limitations of linear approximations to the understanding of Ca2+ signals. Cell Calcium. 1998;24:345–357. doi: 10.1016/s0143-4160(98)90058-6. [DOI] [PubMed] [Google Scholar]
- 28.Neher E, Augustine GJ. Calcium gradients and buffers in bovine chromaffin cells. J Physiol (Lond) 1992;450:273–301. doi: 10.1113/jphysiol.1992.sp019127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Regehr WG, Tank DW. Selective fura-2 loading of presynaptic terminals and nerve cell processes by local perfusion in mammalian brain slices. J Neurosci Methods. 1991a;37:111–119. doi: 10.1016/0165-0270(91)90121-f. [DOI] [PubMed] [Google Scholar]
- 30.Regehr WG, Tank DW. The maintenance of LTP at hippocampal mossy fiber synapses is independent of sustained presynaptic calcium. Neuron. 1991b;7:451–459. doi: 10.1016/0896-6273(91)90297-d. [DOI] [PubMed] [Google Scholar]
- 31.Regehr WG, Delaney KR, Tank DW. The role of presynaptic calcium in short-term enhancement at the hippocampal mossy fiber synapse. J Neurosci. 1994;14:523–537. doi: 10.1523/JNEUROSCI.14-02-00523.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Roberts WM. Localization of calcium signals by a mobile calcium buffer in frog saccular hair cells. J Neurosci. 1994;14:3246–3262. doi: 10.1523/JNEUROSCI.14-05-03246.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rosov A, Burnashev N, Sakmann B, Neher E. Transmitter release modulation by intracellular Ca2+ buffers in facilitating and depressing nerve terminals of pyramidal cells in layer 2/3 of the rat neocortex indicates a target cell-specific difference in presynaptic calcium dynamics. J Physiol (Lond) 2001;531:807–826. doi: 10.1111/j.1469-7793.2001.0807h.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sabatini BL, Oertner TG, Svoboda K. The life cycle of Ca(2+) ions in dendritic spines. Neuron. 2002;33:439–452. doi: 10.1016/s0896-6273(02)00573-1. [DOI] [PubMed] [Google Scholar]
- 35.Scharfman HE. Characteristics of spontaneous and evoked EPSPs recorded from dentate spiny hilar cells in rat hippocampal slices. J Neurophysiol. 1993;70:742–757. doi: 10.1152/jn.1993.70.2.742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Scharfman HE, Kunkel DD, Schwartzkroin PA. Synaptic connections of dentate granule cells and hilar neurons: results of paired intracellular recordings and intracellular horseradish peroxidase injections. Neuroscience. 1990;37:693–707. doi: 10.1016/0306-4522(90)90100-i. [DOI] [PubMed] [Google Scholar]
- 37.Smith SJ, Osses LR, Augustine GJ. Fura-2 imaging of localized calcium accumulation within squid “giant” presynaptic terminal. In: Grinnell AD, Armstrong D, Jackson MB, editors. Calcium and ion channel modulation. Plenum; New York: 1988. pp. 147–155. [Google Scholar]
- 38.Stuenkel EL. Regulation of intracellular calcium and calcium buffering properties of rat isolated neurohypophysial nerve endings. J Physiol (Lond) 1994;481:251–271. doi: 10.1113/jphysiol.1994.sp020436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tank DW, Regehr WG, Delaney KR. A quantitative analysis of presynaptic calcium dynamics that contribute to short-term enhancement. J Neurosci. 1995;15:7940–7952. doi: 10.1523/JNEUROSCI.15-12-07940.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Umbach JA, Saitoe M, Kidokoro Y, Gundersen CB. Attenuated influx of calcium ions at nerve endings of csp and shibire mutant Drosophila. J Neurosci. 1998;18:3233–3240. doi: 10.1523/JNEUROSCI.18-09-03233.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Veenstra TD, Johnson KL, Tomlinson AJ, Naylor S, Kumar R. Determination of calcium binding sites in rat brain calbindin D28K by electrospray ionization mass spectrometry. Biochemistry. 1997;36:3535–3542. doi: 10.1021/bi9628329. [DOI] [PubMed] [Google Scholar]
- 42.Yamada WM, Zucker RS. Time course of transmitter release calculated from simulations of a calcium diffusion model. Biophys J. 1992;61:671–682. doi: 10.1016/S0006-3495(92)81872-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yeckel MF, Kapur A, Johnston D. Multiple forms of LTP in hippocampal CA3 neurons use a common postsynaptic mechanism. Nat Neurosci. 1999;2:625–633. doi: 10.1038/10180. [DOI] [PMC free article] [PubMed] [Google Scholar]


