Coexistence of Excitatory and Inhibitory GABA Synapses in the Cerebellar Interneuron Network

Abstract

Functional GABA synapses are usually assumed to be inhibitory. However, we show here that inhibitory and excitatory GABA connections coexist in the cerebellar interneuron network. The reversal potential of GABAergic currents (E_GABA) measured in interneurons is relatively depolarized and contrasts with the hyperpolarized value found in Purkinje cells (−58 and −85 mV respectively). This finding is not correlated to a specific developmental stage and is maintained in the adult animal.E_GABA in interneurons is close to the mean membrane potential (−56.5 mV, as measured with a novel “equal firing potential” method), and both parameters vary enough among cells so that the driving force for GABA currents can be either inward or outward. Indeed, using noninvasive cell-attached recordings, we demonstrate inhibitory, excitatory, and sequential inhibitory and excitatory responses to interneuron stimulation [results obtained both in juvenile (postnatal days 12–14) and subadult (postnatal days 20–25) animals]. In hyperpolarized cells, single synaptic GABA currents can trigger spikes or trains of spikes, and subthreshold stimulations enhance the responsiveness to subsequent excitatory stimulation over at least 30 msec. We suggest that the coexistence of excitatory and inhibitory GABA synapses could either buffer the mean firing rate of the interneuron network or introduce different types of correlation between neighboring interneurons, or both.

Introduction

In mammals, postsynaptic effects of GABAergic synapses primarily result from the transient opening of GABA_A channels, which are permeant for Cl⁻ and bicarbonate ions. During embryonic life, neurons accumulate Cl⁻, probably through the Na⁺-K⁺-Cl⁻cotransporter (NKCC1; Vardi et al., 2000), resulting in a depolarized reversal potential (E_GABA). Later in development, however, Cl⁻ is extruded, probably through the K⁺-Cl⁻ cotransporter (KCC2; Rivera et al., 1999), so that the driving force for Cl⁻ ions is inverted [hippocampus (Ben-Ari et al., 1989), cortex (Owens et al., 1996), and cerebellum (Brickley et al., 1996; Eilers et al., 2001)]. For this reason, mature GABAergic and glycinergic synapses are generally viewed as inhibitory (Rivera et al., 1999).

However, recent results indicate more depolarizedE_GABA values for interneurons (INs, mature or immature alike) than for principal cells in the dorsal cochlear nucleus (Golding and Oertel, 1996) and in the sensory cortex and amygdala (Martina et al., 2001). These results suggest that the IN→IN synapses in these or in other central areas may be excitatory.

Determining E_GABA is not sufficient to know how the GABAergic postsynaptic potential (GPSP) affects the target neuron. A GPSP primarily drives the membrane potential of the cell (V_m) towardE_GABA. If the driving forceE_GABA –V_m is negative, this hyperpolarizes the cell and inhibits its firing, except when hyperpolarization-induced excitatory conductances are activated, giving rise to rebound excitation [as in deep cerebellar nuclei (Llinas and Mühlethaler, 1988; Aizenman and Linden, 1999) or thalamic relay cells (Bal et al., 1995)]. Conversely, if the driving force is positive, the GPSP depolarizes the cell and is expected to increase its firing; however, the neuron can still be inhibited through shunting, as long as the GABA_A conductances are active (Staley and Mody, 1992; Gao et al., 1998), or through longer-lasting, depolarization-induced Na⁺ channel inactivation (Zhang and Jackson, 1995) or K⁺ channel activation (Monsivais et al., 2000).

Sorting out these effects without perturbing the system is a challenge in a slice preparation. Recording methods (e.g., using sharp electrodes) may lead to a significant redistribution of Ca²⁺ and Cl⁻. In addition, application of a GABAergic agonist or extracellular electrical stimulation can lead to intracellular (Kaila and Voipio, 1987; Staley et al., 1995) or extracellular (Kaila et al., 1997) ion redistribution. Accordingly, the exact consequences of GPSPs on postsynaptic firing are often unclear or controversial [e.g., in immature CA3 pyramidal cells (compareLeinekugel et al., 1997; Lamsa et al., 2000)].

We addressed this question at the IN→IN synapses of the molecular layer in cerebellar slices. This is an attractive preparation because these INs include only two closely related cell types (Sultan and Bower, 1998); moreover, quantal sizes are very large (Llano and Gerschenfeld, 1993; Kondo and Marty, 1998a), so that firing of single presynaptic neurons induces marked changes in the firing of the postsynaptic cell (Häusser and Clark, 1997). Using a combination of gramicidin-perforated patch and cell-attached recordings, we found that IN→IN GPSPs display a variety of effects ranging from full inhibition to full excitation.

Materials and Methods

General methods

Slice preparation. Cerebella from young rats (12–14 d old) were prepared as described earlier (Llano and Gerschenfeld, 1993). For older rats [postnatal day 20 (P20)–P25 or P35-P40], the same procedure was used, except that animals were anesthetized with halothane (Sigma, St. Louis, MO), and that the cold solution used for cutting contained (in mm): 248d(+)-saccharose, 10 glucose, 4 KCl, 1 CaCl₂, 5 MgCl₂, 1.3 NaH₂PO₄, and 26 NaHCO₃, pH 7.4 when equilibrated with a 5% CO₂ and 95% O₂ mixture. These special procedures, including the elimination of sodium from the extracellular space during cutting, were designed to improve the condition of INs in slices of mature animals.

The experimental chamber was continuously perfused at a rate of 1–1.5 ml/min with physiological saline containing, except where otherwise stated (in mm): 125 NaCl, 2.5 KCl, 2 CaCl₂, 1 MgCl₂, 1.25 NaH₂PO₄, 26 NaHCO₃, and 10 glucose, pH 7.4 when equilibrated with a 5% CO₂ and 95% O₂mixture. All experiments were performed at room temperature (21°C; SD, 2°C). Liquid junction potentials were corrected.

Cell selection. INs of the molecular layer were identified as explained previously (Llano and Gerschenfeld, 1993). INs of the lower third and upper two-thirds of the molecular layer were considered basket cells and stellate cells, respectively.

Chemicals. The ionotropic glutamate receptor antagonists 6-nitro-7-sulfamoylbenzo[f] quinoxaline-2,3-dione (NBQX, 10 μm; Tocris) and d-APV (20 μm; Tocris) were applied to the recording chamber throughout the experiments except when stated otherwise. (−)-Bicuculline methochloride, (bicuculline, 10 μm; Tocris) or gabazine (10 μm; Research Biomedicals International, Natick, MA) were used to block GABA_A receptors.

Statistics. Values are mean ± SEM unless specified otherwise.

Whole-cell recordings

Pipette resistances used for whole-cell experiments were 3.5–5 MΩ. Series resistance values were kept in the range of 10–30 MΩ (R_s = 22 ± 4 MΩ), and were not compensated. The capacitance of the IN was in the range of 3–8 pF; this gives a maximum time constant of the clamp of 0.24 msec. The total input resistance observed at –60 mV was 1–10 GΩ (2.5 MΩ ± 1 GΩ) and was therefore of the same order of magnitude as typical pipette seal resistances. Indeed, the I–V curve reversed at a depolarized value (−35 ± 8 mV), confirming that the leak from the pipette to the extracellular solution is not negligible.

Whole-cell experiments were performed with a “physiological” intracellular solution containing (in mm): 144 K-gluconate, 6 KCl, 4.6 MgCl_2, 10 K-HEPES, 1 K-EGTA, 0.1 CaCl₂, 0.4 NaGTP, and 4 NaATP, pH = 7.2. With this solution, the Nernst equation gives –56 mV as the value forE_Cl, not significantly different from the value measured for E_GABA, the reversal potential of GPSPs, as determined in gramicidin-perforated patch recordings (−58 mV).

GABA-sensitive channels are permeable not only to Cl⁻ ions but also to HCO ${}_3^{-}$. Solving for the Goldman–Hodgkin–Katz equation, assuming E_Cl = −56 mV, E_HCO3 = −6 mV, and a permeability ratio of 0.2 between HCO ${}_3^{-}$ and Cl⁻(Bormann et al., 1987; Kaila and Voipio, 1987), gives a value of −53 mV for E_GABA. However, using the physiological intracellular solution in the whole-cell configuration, control muscimol (20 μm) puff experiments gave a reversal value of −56 ± 0.6 mV, the value ofE_Cl. Two factors explain that the contribution of bicarbonate ions is negligible: the relatively high value of the Cl⁻ concentration, which minimizes the impact of any additional bicarbonate, and the fact that the pipette solution, which equilibrates with the cell interior, did not contain any bicarbonate.

Gramicidin-perforated patch

Recording patch pipettes had a resistance of 6–11 MΩ. Experiments were started when series resistance was under 100 MΩ (80 ± 10 MΩ), giving a maximum time constant of the clamp of 0.8 msec. The total input resistance measured at –60 mV was 1–5 GΩ. The I–V curve reversed at –25 ± 5 mV. On the basis of these numbers, the maximum change of the membrane potential of the clamped cell attributable to the flow of current throughR_s was calculated as 0.5 mV.

The intracellular solution contained (in mm): 155 K-gluconate, 1 MgCl₂, 10 K-HEPES, 1 K-EGTA, 0.1 CaCl₂, 600 μm fura-2, and 50 μg/ml gramicidin D (Dubos; (Sigma), pH 7.2. This low-Cl⁻ solution was selected to ensure that the excitatory responses that were recorded were not caused by unwanted Cl⁻ exchange between the pipette and cell compartments (see below). A 50 mg/ml stock of gramicidin in DMSO was prepared freshly (<2 hr before recording) and sonicated. This was diluted with gramicidin-free solution, sonicated again for 10–30 sec, and centrifuged. The tip of the patch pipette was filled with the gramicidin-free solution. A gradual increase in pipette–cell conductance was observed 10–40 min after seal formation. Spontaneous passage to whole-cell recording was a very common occurrence in these experiments, particularly with mature animals. This was detected as a change in the polarity of GPSCs and by a somatic fluorescence increase (recorded with a high-resolution CCD camera; Fig. 1B) above the background level, reflecting the diffusion of fura-2 molecules from the pipette into the cell. Experiments were discontinued as soon as such changes were noticeable.

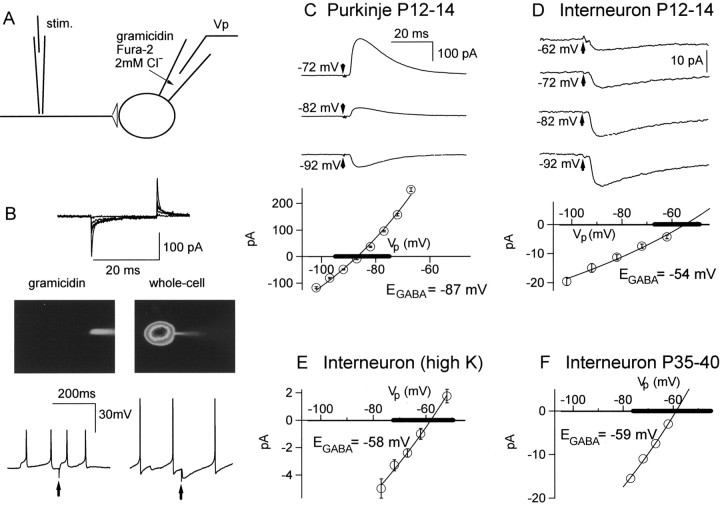
Fig. 1.

Determination of E_GABAin INs and Purkinje cells. A, Schematics of the experimental conditions. An interneuron or a Purkinje cell was studied using a gramicidin-perforated patch, with a recording pipette that contained a very low Cl⁻ concentration and 600 μm fura-2. An extracellular stimulation (stim.) pipette was positioned in the molecular layer to stimulate presynaptic INs. B, After seal formation, capacitive currents evolved with time over tens of minutes (top panel; from an interneuron recording), reflecting the incorporation of gramicidin channels in the patch. Inspection of the pipette–cell assembly allowed visualizationof spontaneous transitions to the whole-cell recording mode (middle panel). This was accompanied with a shift in the polarity of spontaneous and evoked GPSPs (bottom panel; arrows mark extracellular stimulations of presynaptic INs) as well as an increase of the apparent size of action potentials attributable to the sudden increase of the access conductance to the cell soma. C, Averaged GPSCs obtained at various holding potentials in a Purkinje cell experiment (P12–P14). Bottom panel,I–V curve for this experiment. There is a clear reversal at −87 mV. Pooled results gaveE_GABA = −85 ± 7 mV;n = 7; the thick line on theV_p axis indicates the corresponding voltage range). D, Similar experiment as performed on INs (P12–P14). The reversal potential is obtained by extrapolation with the Goldman–Hodgkin–Katz equation (−54 ± 4.5 mV in the example shown; −58 mV ± 4.5 mV for a series of 5 cells).E, Similar experiment as performed on P12–P14 INs, with a higher extracellular K⁺ concentration (5 mm instead of the standard 2.5 mm). Reversal potential, −58 ± 6 mV in the example shown; −61 ± 6 mV for a series of four cells. F, Similar experiment as performed on P35–P40 INs. Here, responses to short puffs of muscimol (10–30 msec; pipette concentration, 20 μm) were used instead of synaptic currents. Reversal potential, −59 ± 8 mV in the example shown; −60 ± 8 mV for a series of seven cells.Thick lines in C–F indicate the range comprising the mean ± 2 SD in each condition.

Cell-attached experiments

Cell-attached pipettes were small (10 MΩ) and filled either with a K⁺-rich solution (containing in mm: 150 K-gluconate, 4.6 MgCl_2, 10 K-HEPES, 1 K-EGTA, and 0.1 CaCl₂) or with a Na⁺-rich solution (containing in mm: 125 NaCl, 2.5 KCl, 0 or 2 CaCl₂, 1 MgCl₂, 1.25 NaH₂PO₄, 26 NaHCO₃, and 10 glucose, preequilibrated with O₂ and CO₂). The K⁺-rich solution was initially selected to allow the recording of GPSCs after breaking the seal at the end of the experiments, as explained below. However, with the Na⁺-rich solution, the cell was less perturbed while recorded in cell-attached mode, and GPSCs could still be recorded after breaking the seal.

With the K⁺-rich solution, it was observed that the firing frequency of the IN depends on the pipette potential, indicating the presence of a conductance link between the pipette and cell compartments. This was not observed when the pipette was filled with the extracellular saline solution. For this reason, the results of the experiments in the two conditions were kept apart in the analysis.

Extracellular stimulation (0.2 Hz; protocol described below) was performed at least 50 times (and up to 300 times) both in control conditions and in the presence of GABA_A blockers. For these experiments, the pipette potential was maintained at 0 mV.

At the end of most cell-attached experiments, GABA_A blockers were washed away, and whole-cell recordings were performed to verify the effectiveness of the presynaptic stimulation.

Extracellular stimulation

Extracellular stimulation was performed with glass pipettes similar to those used for whole-cell recording.

Stimulating presynaptic stellate and basket cells. It was essential for the interpretation of our cell-attached experiments that extracellular stimulation would not produce any subthreshold excitation of the recorded cell. Eventually the following protocol was adopted. In a first step, we searched for the location of the axon of the recorded cell by positioning the stimulation pipette at a distance of ∼100 μm of the recorded soma, in the proximal molecular layer (close to the Purkinje cell layer). The side where antidromic action potentials were evoked was the side of the axon (Pouzat and Marty, 1999). Having noted the value of the threshold for stimulation of antidromic action potentials, the pipette was moved to the other side, again at a distance of 100 μm of the recorded soma, and the stimulation potential was set at 30 V above this threshold value. When using whole-cell recording, this procedure does not result in any direct potential change in the interneuron soma (Pouzat and Marty, 1999). Under these conditions, any change in the firing pattern that was observed can be ascribed to synaptic effects and not to direct stimulation of the recorded cell. To verify this point, the same protocol was then repeated in the presence of GABA_A blockers. As a further control, in most experiments (including the examples shown in Fig. 5), a whole-cell recording was finally established with the original recording pipette, and it was verified (1) that the extracellular stimulation did not produce any cellular current change, and (2) that GABAergic currents were elicited after washing off bicuculline.

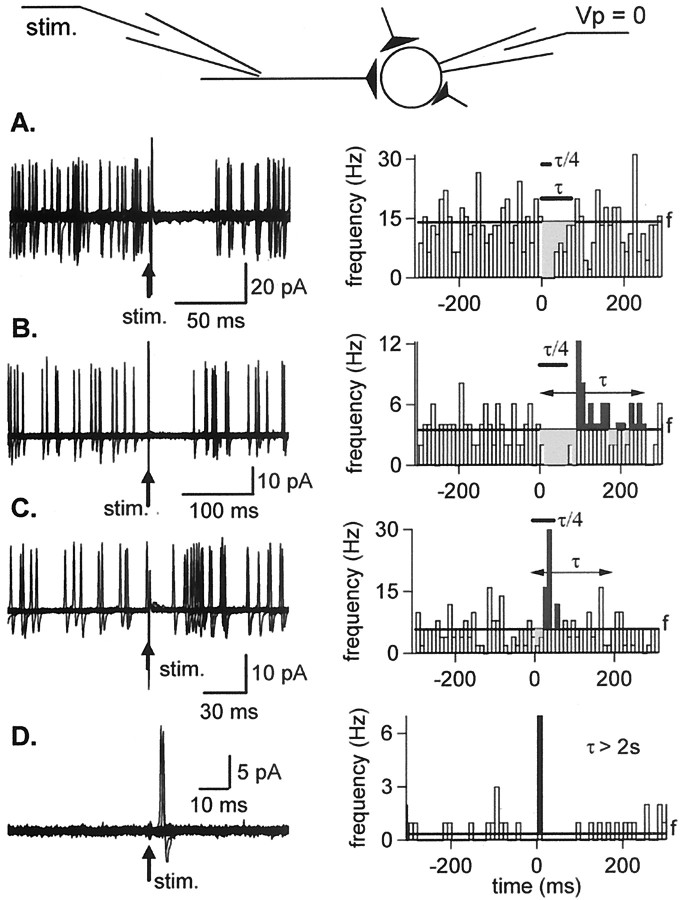
Fig. 5.

Variable effects of presynaptic stimulation on cell firing as measured in cell-attached recordings. All recordings were performed with a Na⁺-rich pipette solution.A, Pure inhibitory response. Left, Superimposed consecutive traces (n = 25) showing the effect of extracellular stimulation (stim.) on spontaneous action potentials as recorded in the cell-attached configuration. Right, Summary plot of instantaneous spiking frequency across the stimulation period. The mean control frequency, f, is represented by a thick horizontal line. Stimulation results in a transient frequency decrease (light gray area). B, Mixed inhibitory–excitatory response. Stimulation results in a transient frequency decrease (light gray area) followed by a frequency increase (dark gray area). C, Results from another experiment in which extracellular stimulation mainly resulted in a frequency increase after a delay of ∼20 msec.D, Excitatory response measured in a cell with very low resting frequency (0.3 Hz). Spikes were observed in 7 of 100 sweeps with a latency of ∼5 msec.

The number of presynaptic INs was estimated by counting failures in this last part of the experiments. We found a failure rate ranging from 0 to 0.92, with an average of 0.31 (n = 17). On the basis of the mean failure rate of individual connections as measured in paired recordings (0.615; calculated from Kondo and Marty, 1998a, their Table 1), and assuming independence, we obtain an average number of presynaptic neurons of 2.38.

Stimulating presynaptic granule cells. To stimulate presynaptic granule cells (or climbing fibers or both), a stimulating pipette was positioned in the granule cell layer ∼100 μm away from the recorded cell. Another pipette was positioned as explained above in the molecular layer to stimulate stellate and basket cells. With this arrangement, pure glutamatergic and GABAergic synaptic potentials could be elicited in the same experiment without resorting to pharmacological blockers.

Estimate of the bias in the measure of the mean resting potential of INs

Using the K⁺ channel reversal method. We compared several methods to determine the mean resting potential in unperturbed interneurons. We call this parameterV_CA because it applies to cell-attached recordings. We initially used the method of K⁺ channel reversal to measureV_CA (Zhang and Jackson, 1993;Verheugen et al., 1999; Lu and Trussell, 2001). In this method, the pipette is filled with a K⁺-rich solution (composition as above) so that the reversal potential of K⁺-sensitive channels is very close to 0 mV. The pipette potential for which K⁺-selective single-channel currents revert their polarity is the mean resting potential of the cell (V_d =V_CA –V_p = 0). In INs, this method seemed particularly convenient at first, because all somatic patches contained BK channels, which are highly selective for K⁺ ions and display very high unitary conductance. The seal conductance is irrelevant in these measurements, because it affects the holding current value registered at each potential but not the voltage for which reversal occurs. The pipette holding potential was 0 mV; voltage pulses were given with a duration of 500 msec, a frequency of 0.2 Hz, and amplitude increments of 10 mV. At each test potential, single-channel currents were individually measured, and an estimate of their amplitude was obtained by averaging. The reversal potential was calculated by fitting a straight line to the average single-current amplitude as a function of potential, yielding a value of −71 ± 7 mV (n = 11). This is 14.5 mV more hyperpolarized than the estimate ofV_CA determined by the equal firing method (V_eq; see below). However, while applying hyperpolarized steps in the pipette (V_p = −70–110 mV), although the quality of the seals was good (several gigaohms), action potentials were invariably stopped. This may have resulted in a change in the dynamics of the voltage-activated channels and consequently in a change in the membrane potential. A likely mechanism is provided by the evidence presented in Results, indicating that the high pipette K⁺ concentration used in these experiments induced a conductance link between cell and pipette. This conductance may have led to cell depolarization (because the pipette holding potential was 0 mV) and therefore to an elevation of the resting Ca²⁺ concentration. During the negative voltage pulses that were used to determine V_CA, the depolarizing current through the patch membrane was removed, but the counteracting K⁺ conductance attributable to Ca²⁺-dependent K⁺ channels presumably remained active, leading to a membrane potential measurement below the value that would apply for an undisturbed cell. Thus, the K⁺ channel reversal method gave a value that may have been too hyperpolarized.

Using the current-clamp gramicidin-perforated patch configuration. The mean membrane potential,V_m, for a given clamp current, was defined as the mean potential of the cell, spikes excluded. Spikes were identified with an automatic selection routine, and short sections were eliminated around each spike by using a threshold slope value of 1 mV/msec (both at the spike onset and at the end of the hyperpolarization potential). Similarly, the spike threshold was determined at the time position when the slope crossed the value 1 mV/msec before an action potential.

To measure V_CA, it is standard practice to determine the zero current potential in the current-clamp perforated patch configuration. But for compact cells, such as the INs studied here, which have a very high input resistance (1–10 GΩ), this measurement of V_CA is biased because of the leakage resistance through the seal. The associated bias may reach tens of millivolts (see , Eq. 4).

Therefore, another method was derived, in which the intensityi of the clamp is set such that the firing rate equals the mean spontaneous firing rate measured in the cell-attached configuration in the same preparation (as detailed in Results). Our estimation of V_CA (which we call the “equal firing potential,” V_eq) is the mean membrane potential measured in these conditions, excluding spikes. The bias V_eq −V_CA of such an estimate is a fraction of V_CA − T, whereT is the spike threshold and is on the order of a few millivolts (, Eq. 5). Therefore, the equal firing potentialV_eq appeared as the best estimate ofV_CA.

Results

Interneurons have more depolarized GABA_A reversal potentials than Purkinje cells

The E_GABA of GPSCs was measured using the gramicidin-perforated patch method, which allows voltage-clamp experiments but preserves the anionic conditions of the cell (Kyrozis and Reichling, 1995) (Fig.1A,B). Presynaptic stellate and basket cells were stimulated extracellularly (Vincent et al., 1992). Ionotropic glutamate receptors were blocked with a combination of NBQX and d-APV. In Purkinje cells (PCs) at P12–P14, a classical pattern of reversing GPSCs was observed, with a mean reversal potential of –85 ± 5 mV (n= 7; Fig. 1C), similar to that found for short applications of exogenous GABA (Eilers et al., 2001). However, in most of the IN recordings, only inward current responses were obtained in the potential range in which the postsynaptic cell could be held without firing action potentials, and E_GABAcould not be measured directly. Extrapolation from the points in the nonspiking voltage range (–100 to –60 mV), using the Goldman–Hodgkin–Katz equation, gave a mean reversal potential of −58 mV ± 5 mV (n = 5; Fig. 1D). Because the extracellular K⁺ concentration (K_o) can influence the intracellular Cl⁻ concentration (e.g., by interfering with Cl⁻ transporters; Rivera et al., 1999), we performed similar experiments with a K_oof 5 instead of 2.5 mm. This, however, did not significantly affect E_GABA in INs (−61 ± 6 mV; n = 4; Fig. 1E), showing that variations in K_o cannot explain the depolarized value of E_GABA observed in INs.

The above experiments, combined with published ones (Eilers et al., 2001), confirm that the negative shift ofE_GABA with age is complete for PCs by P12. However, it might not be the case for INs. To test this point, puff applications of muscimol were performed on fully adult INs (P35–P40; Fig. 1F), giving anE_GABA value of –60 ± 8 mV (n = 7). Therefore, the depolarized value ofE_GABA is not attributable to a late change in intracellular Cl⁻ concentration for this class of cells.

We conclude that, from P12, E_GABA is much more depolarized for INs than for PCs. The difference likely reflects a higher intracellular Cl⁻concentration in INs than in PCs. If the contribution of bicarbonate ions to the GABAergic conductance is neglected (see Materials and Methods), values of the intracellular Cl⁻concentration of 5.4 and 15 mm can be calculated for PCs and INs, respectively. In the remainder of this paper, we investigate the consequences of the latter value for GABAergic signaling at the IN→IN synapses. We shall focus our attention on the P12–P14 stage except when otherwise stated. Moreover, to restrict the possibility of variations linked to the nature of the postsynaptic cell, from this point on, we performed experiments exclusively on postsynaptic basket cells.

Estimate of the mean membrane potential in unperturbed cells

Given the depolarized value ofE_GABA for the INs, are GABAergic currents inhibitory or excitatory? The effect depends primarily, but not exclusively, on the driving forceE_GABA –V_m for GABAergic currents (see Introduction). Knowing the value ofE_GABA, we aimed next at estimating the value V_m in an unperturbed cell as accurately as possible.

At this stage, a distinction is needed between the mean membrane potential, designating the value that is experimentally measured (e.g., in current–clamp configuration) and that is notedV_m, and the actual mean membrane potential of unperturbed cells. The latter is notedV_CA because it applies to cells recorded in the cell-attached configuration.

To estimate V_CA, two main methods are available in the literature: the zero current potential measurement and the method of K⁺ channel reversal (Zhang and Jackson, 1993; Verheugen et al., 1999; Lu and Trussell, 2001). As explained in Materials and Methods, the first technique is clearly inappropriate for cerebellar interneurons. The second technique was performed on INs, but it turned out to yield seriously biased results as well (see Materials and Methods).

Therefore, another method was derived on the basis of the fact that INs are spontaneously active in our preparation (Llano and Gerschenfeld, 1993). In cell-attached recordings, INs fire irregularly at a mean firing rate, f, that varies among cells in the range of 0.1–20 Hz (Kondoand Marty, 1998a; results below). In gramicidin-perforated patch recordings, the intensity of the clamp, i, was set such that f equaled the mean spontaneous firing rate measured in the cell-attached configuration in the same preparation. Our estimate ofV_CA (which we called the equal firing potential) is the mean membrane potential,V_eq, measured in such a configuration, excluding spikes. A quantitative argument is presented in to show that the equal firing potential is a better estimate ofV_CA than the zero current potential.

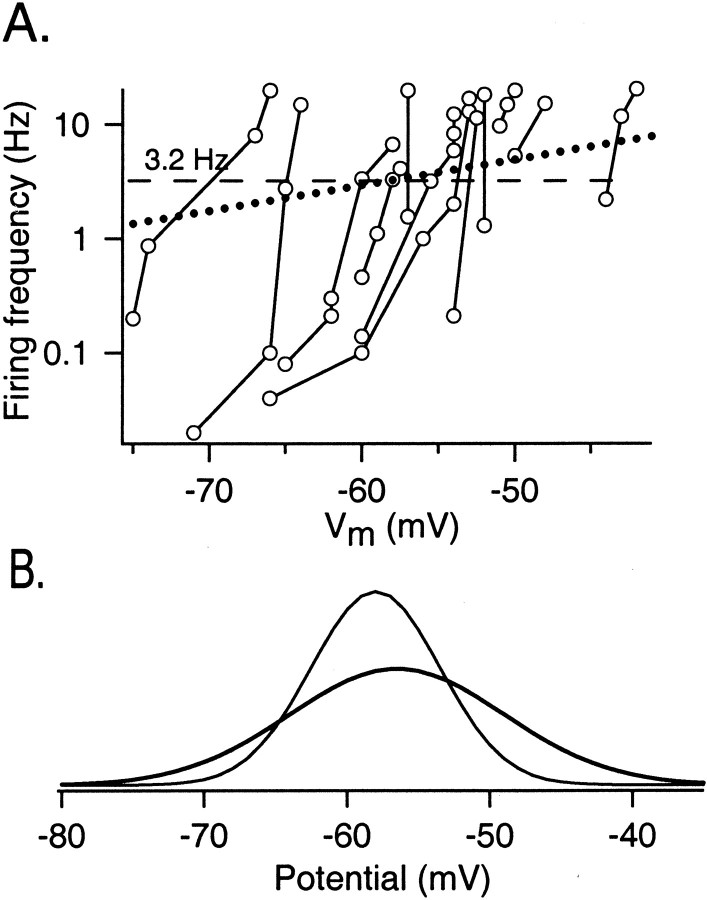
The determination of V_eq is illustrated in Figure 2. In each experiment, f and V_m values were obtained at various holding currents. Resultingf–V_m curves were very steep, particularly at f >1 Hz, so that the frequency range 0.1–20 Hz was obtained within a small potential range. However, the position of individualf–V_m curves varied markedly from cell to cell along the potential axis. On the basis of these results, V_eq was estimated by taking the intersects off–V_m curves with a horizontal line (Fig. 2, dashed line), which represented the mean firing frequency value obtained in cell-attached experiments (i.e., 3.2 Hz; calculated from Kondo and Marty, 1998a, their Table 1; results from cell-attached experiments described below are consistent with this value). This estimate is a first approximation, because it assumes that individual resting potentials of individual cells are not correlated with their resting firing frequency. In reality, some correlation exists, as shown in Figure 2, dotted slanted line, which was determined as explained in . Because of the steepness of individualf–V_m curves, it did not really matter whether V_eq was estimated by taking intersects with the dashed or dotted line: respective values were −56.5 ± 7.5 mV (n = 12) and −56.1 ± 7.8 mV (n = 12). These values are similar to E_GABA (–58 ± 5 mV). They are also similar to the values of the spike threshold, which were determined in whole-cell and perforated patch recordings alike at –53.7 ± 7.5 mV (n = 9).

Fig. 2.

Determination of the equal firing potential in interneurons. A,f–V_m curves. Interneurons were recorded in the current-clamp mode with the gramicidin-perforated patch configuration. The holding current was set in each cell so that its mean firing frequency lay in the range of 0.1–20 Hz. For each holding current, the mean frequency is plotted against the mean potential of the cell. Points joined by aline belong to the same cell. The equal firing potentialV_eq is the intersection of thef–V_m curve of each cell either with the line f = 3.2 Hz (dashed horizontal line), corresponding to the mean firing frequency as measured in cell-attached experiments, or with thef_CA–V_CA curve (dotted line; calculated according to Eq. 8; see). V_eq = –56.5 ± 7.5 mV (n = 12); this is our best measurement of the mean membrane potential of the interneurons in this preparation.B, Comparison of two Gaussian curves, with means and variances corresponding to the measurements ofE_GABA (thin line) and V_eq (thick line). Note that there is a high degree of overlap between the two curves. The curves have been scaled so that their integrals are identical.

The driving force E_GABA −V_m determines whether the synapse is excitatory or inhibitory

The fact that the membrane potentialV_CA and the reversal potentialE_GABA have a similar distribution would imply that IN→IN synapses can be both excitatory and inhibitory, assuming that the driving force is the main determinant of the sign of the synapse.

To examine this point, we performed whole-cell recording experiments with an intracellular Cl⁻ concentration of 15 mm to obtain a value ofE_Cl matching the mean value ofE_GABA, −58 mV.

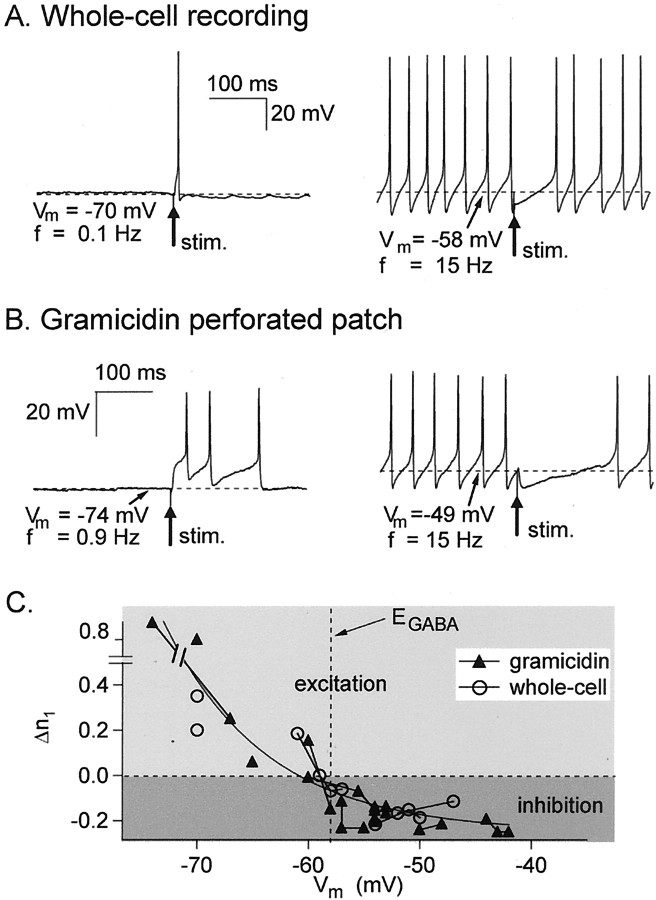
GPSPs were induced through extracellular stimulation of a presynaptic IN (see Materials and Methods). Figure3A, left, illustrates a cell with a low V_CA value (see Fig. 2), in which the holding current is adjusted so that the firing frequency is low (f = 0.1 Hz). In three of three experiments, the induced GPSPs resulted in the emission of action potentials. For these three cells, the probability values of inducing an action potential were, respectively, p = 0.2, 0.4, and 0.9. Thus, GPSPs are excitatory in these conditions. On the other hand, Figure 3A, right, illustrates a cell with a more depolarizedV_CA in which the holding current was adjusted to produce repetitive firing. In this case, the induced GPSPs resulted in a clear delay of the following spike compared with the position that would have been obtained without stimulation and were therefore inhibitory.

Fig. 3.

Positive and negative modulation of cell firing as measured in current-clamp experiments. A, Whole-cell experiments, Cl_i = 15 mm. Left panel, The holding current is set such thatV_m ∼ −70 mV; in these conditions, the resting firing frequency, f, is very small. An action potential can be induced by the extracellular stimulation of a presynaptic interneuron (stim. arrow; the probability to obtain a spike was p = 0.2 in this recording).Right panel, with a more depolarized cell (V_m ∼ −58 mV), the stimulation inhibits spontaneous firing (from another experiment). B, Same type of experiments in gramicidin-perforated patch recordings.C, Summary results. Closed triangles(n = 9) and open circles(n = 5) represent, respectively, gramicidin and whole-cell experiments. The y-axis represents Δn₁, the net gain or loss of spikes during the period of τ/4 after the stimulation, where τ = 1/f. Results originating from the same cells are connected with lines. The effect of a GPSP is shown to shift from inhibition to excitation forV_m ∼ −60 mV. Whole-cell and gramicidin results alike can be fitted with an exponential function, the equation of which is given in (Eq. 6).

The same types of experiments were then repeated in the gramicidin-perforated patch configuration. And the same types of results as in whole-cell recordings were obtained: at hyperpolarizing potentials, GPSPs were able to induce action potentials (either single spikes or bursts of up to three spikes), whereas at more depolarizing potentials, GPSPs were accompanied by an inhibition of the spontaneous firing (Fig. 3B).

Both whole-cell and gramicidin results are summarized in Figure3C. The response was quantified by measuring the difference between the observed number of spikes after the GPSP and that expected from the background activity. For consistency with later results, this difference, called Δn₁, was calculated over a period of τ/4, where τ is the mean control interspike interval (τ = 1/f). In a first approach, we call a synapse excitatory if Δn₁ > 0, and we call it inhibitory if Δn₁ < 0. The relation of Δn₁ on membrane potential has similar shapes in whole-cell recordings and in gramicidin experiments, and a sign reversal occurs in both cases near –58 mV (Fig.2C), which is at the value ofE_GABA that was derived earlier (Fig.1).

Note that most of the cells remained on one or the other side of the dividing line for the entire frequency range 0.1 <f < 20 Hz and gave therefore rise only to inhibitory or excitatory responses. Nevertheless, for a few recordings, sign reversal could be obtained in the frequency range 0.1 <f < 20 Hz simply by altering the holding potential [as previously shown using sharp electrode recordings in the INs of the dorsal cochlear nucleus (Golding and Oertel, 1996)].

Unitary excitatory GPSPs

An extracellular stimulation may simultaneously activate more than one presynaptic IN. We next asked whether unitary GPSPs can trigger spikes in the postsynaptic IN.

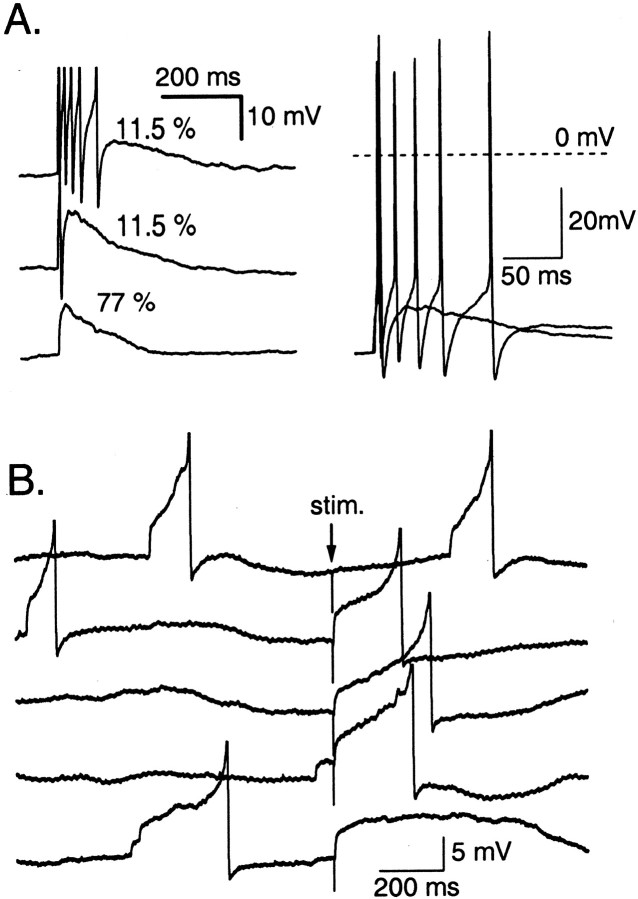
To this end, we reexamined gramicidin-perforated patch recordings between extracellular stimulations. If the holding potential was near –70 mV, spontaneous GPSPs were invariably depolarizing and often led to spikes or even bursts of spikes. An example is given in the recording of Figure 4A(holding current, −20 pA). Here the amplitude of spontaneous synaptic potentials was 6.7 ± 0.6 mV (events with spikes excluded), and the proportion of events leading to spikes and to bursts of spikes was 11.5% each. These results indicate that single-cell GPSPs can trigger action potentials.

Fig. 4.

Excitatory spontaneous synaptic potentials.A, Current-clamp recording with a gramicidin-perforated patch. The cell was maintained near –68 mV by injecting a hyperpolarizing current of 20 pA. Glutamatergic synaptic currents were blocked with CNQX and APV. Left, Examples of spontaneous synaptic potentials leading to a train of spikes (top), a single spike (middle), or subthreshold (bottom), with the corresponding occurrence rate.Right, Superimposed plot of the two events with spikes showing the full extent of the action potentials. B, Spontaneous currents recorded in another cell near –66 mV (holding current, −6.6 pA) led mostly to delayed single-spike discharges. Stimulation of INs (stim.) leads to similar excitatory responses. Action potentials are clipped for clarity.

The shape of spontaneous events and their ability to trigger action potentials were steeply voltage-dependent. In the cell illustrated in Figure 3B, GPSPs near –70 mV holding potential (holding current, −8.8 pA) were always subthreshold (results not shown), with a shape very similar to that illustrated in Figure 4A, bottom left record. However, when a slightly more depolarized holding potential was selected (approximately –66 mV; holding current, –6.8 pA), most spontaneous GPSPs led to delayed spike firing (Fig.4B). Similar events were triggered by electrical stimulation of presynaptic INs (Fig. 4B). They were blocked by bicuculline (results not shown). Even though an analysis of the cellular mechanisms underlying these events falls outside the scope of this study, the results at hand clearly suggest that the depolarization induced by the activation of GABA channels is enhanced by excitatory voltage-dependent conductances. Therefore, the depolarization is not limited to E_GABA; the record of Figure 4B suggests that the membrane potential exceeds E_GABA for tens of milliseconds before each spike.

Mixed inhibitory and excitatory effects of IN→IN synapses as measured in cell-attached experiments

Our main conclusion so far, that excitatory and inhibitory synapses between INs coexist in this preparation, rests mainly on current-clamp experiments. Because cerebellar INs have very large input resistance (several gigaohms), however, small current changes may have induced dramatic effects on the excitability of the cell; to confirm the above results, less invasive methods were required.

Therefore, we investigated the effects of GPSPs on basket cell firing in cell-attached experiments in which interference with cell excitability is minimized. Care was taken to stimulate one or a few presynaptic INs without injecting any significant current in the recorded cell (see Materials and Methods). The pipette was filled with high Na⁺ solution except in a series of experiments to be described below.

Four typical examples are illustrated in Figure5A–D. Left panelsshow superimposed consecutive traces centered on stimulation time (arrows), and right panels show analysis of the results in terms of action potential frequency. In Figure 5A, stimulation of GABAergic inputs resulted in a pure inhibition of the cell firing. The right panel reveals an inhibitory period (light gray, lasting 70 msec after the stimulation) during which the frequency was much lower than the control frequency f (horizontal line).

In Figure 5B, the stimulation resulted in biphasic inhibition–excitation sequences of cell firing. The right panel reveals an inhibitory period, lasting 90 msec after the stimulation, and a rebound excitatory period (dark gray, with a sharp peak at 90–110 msec after the stimulation, followed by a smaller tail) during which the frequency was clearly enhanced.

Figure 5C illustrates an experiment in which the main effect was an enhancement of firing observed 20–60 msec after extracellular stimulation. There was an indication of a short inhibitory period (lasting ∼20 msec), possibly reflecting shunt inhibition, but its statistical significance could not be guaranteed in view of the scatter of the control data. Thus the response of Figure 5C is rapid and almost purely excitatory, whereas that of Figure 5B is longer-lasting and of a mixed inhibitory and excitatory nature.

Whereas most recordings displayed a resting firing frequency between 0.5 and 20 Hz, allowing a simultaneous analysis of excitation and inhibition, one-third of the cells (8 of 24) had a very low resting firing frequency (f < 0.5 Hz), which precluded in practice any detection of inhibition. Three of these eight cells failed to manifest any response and will not be considered further. However, the remaining five displayed a clear excitatory response, as illustrated in Figure 5D. Here, single spikes were elicited shortly after the stimulation (mean latency, 5 msec in the case shown; range across cells, 5–80 msec). In two of the five responsive cells, trains of spikes (up to three spikes per train) were occasionally obtained (results not shown).

Spike balance after synaptic stimulation

The various effects of GABA_A stimulation on postsynaptic firing can be visualized by plotting Δn(t), the difference between the mean number of action potentials observed up to a certain time t after the stimulation and that expected from the control frequency observed before the stimulation. Δn(t) measures the spike balance, i.e., the integrated spike deficit or surplus after the stimulation.

Figure 6A shows plots of the spike balance for four experiments. To facilitate comparisons between cells, times have been normalized with respect to the mean control interspike interval, τ. Cell a shows an excitatory response (same recording as in Fig. 5C). Here there is a very short inhibitory period, presumably corresponding to the time of activation of GABA channels. This is followed by a sharp rise of Δn, which then stabilized at the level of 0.4, indicating a net increase in the number of action potentials. Cells band c display mixed inhibitory and excitatory action, in which an initial inhibition is more or less exactly compensated by a later excitation, so that at long times, the difference Δnis close to 0. For these examples, the effect of stimulation can be described as spike synchronization: after the stimulation, spikes are clustered around a rather precise time (the point of maximum slope in the plots of Fig. 6A) with a position that varied among cells between 0.4 ∗ τ and 0.8 ∗ τ. Finally, celld illustrates a pure inhibitory action. In this case, there is no late excitation, and the initial inhibition remains as a net loss of ∼0.6 spike.

Fig. 6.

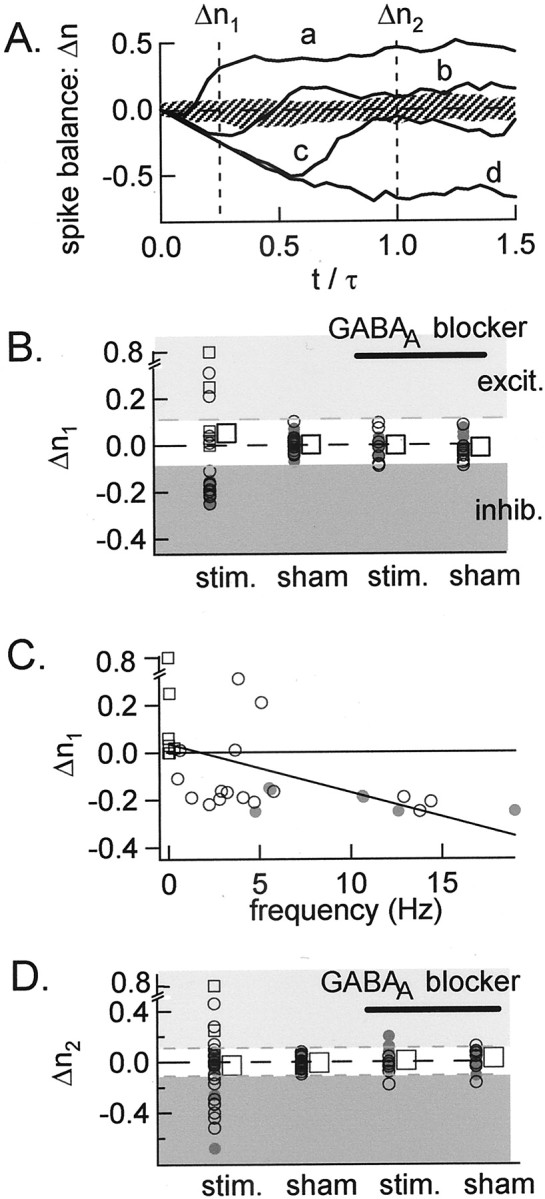
Spike surplus or deficit after synaptic stimulation at P12–P14. A, Plot of the spike balance as a function of time. The time is counted from the stimulation (stim.) and is normalized with respect to τ. They-axis shows at each time value the difference between the mean total number of observed spikes and the corresponding number expected from the firing frequency measured before the stimulation. The four traces show an almost purely excitatory response (a), mixed inhibitory–excitatory responses (b, c), and a pure inhibitory response (d). The hatched area represents the 95% confidence limit of such traces, measured starting from random points in standard saline solution.B–D, Summary results from 31 experiments.Open and closed symbols represent, respectively, experiments performed with pipettes filled with a Na⁺- and K⁺-rich solution.Circles and squares represent cells withf ≥ 0.5 and f < 0.5 Hz, respectively. Data represent the excess or deficit in the number of spikes, which was calculated during an early period of τ/4 after stimulation (B; Δn₁) and during a longer period of τ after stimulation (D; Δn₂). The first columns show results obtained after extracellular stimulation of GABAergic afferents. Second, third, and fourth columns show control results respectively obtained from data gathered after an arbitrarily chosen time point (located 300 msec before the actual stimulation), after the stimulus in the presence of a GABA_A blocker (bicuculline or gabazine), and after an arbitrarily chosen time point in the presence of a GABA_Ablocker. In B and D, dotted lines delimit the calculated 95% confidence interval on the value of Δn₁ and Δn₂, respectively.C, Δn₁ is significantly correlated (p < 0.01) to the resting firing frequency. Low-frequency cells tend to display excitatory responses, and high-frequency cells display inhibitory responses. Large squares in B and D indicate average values across all experiments. In C andD, dark gray areas contain cells significantly inhibited by a GPSP; light gray areascontain cells significantly excited by a GPSP (see Results).excit., Excitation; inhib., inhibition.

To characterize the early phase of the response, Δn was computed at a time of 0.25 ∗ τ, when the positive–negative effect of the stimulation on the spike balance was the strongest. We will note it Δn₁, so that Δn₁ = Δn(0.25 ∗ τ). If the stimulation has no average effect, Δn₁ should lie inside the 95% confidence interval (−0.09, 0.11) calculated on the assumption of a binomial distribution.

This procedure permits a provisional classification of the early responses in three groups (Fig. 6B). One group (four cells) had Δn₁ > 0.11, corresponding to excitation; a second group (five cells) with –0.09 < Δn₁ < 0.11, was considered neutral; and a third group (12 cells) had Δn₁ < −0.09, indicating inhibition.

A more refined analysis had to be performed with low-frequency cells (f < 0.5 Hz), represented in Figure 6,squares. Two of them had Δn₁ > 0.11 and were therefore already classified as “excited” cells. Three had –0.09 < Δn₁ < 0.11, and have been classified as “neutral” cells. However, low-frequency cells displayed effects in a time window (up to 100 msec) that was much shorter than 0.25 ∗ τ, so that the −0.09, 0.11 confidence interval did not apply. Within the 100 msec window, a significant excitatory effect could be demonstrated in all three neutral cells (including that of Fig. 5C) in addition to the two cells in which Δn₁ was >0.11.

Finally, to analyze late phases of the response to the stimulation, the spike balance was determined after the time τ. We note this overall balance Δn₂, with Δn₂ = Δn(τ). The time τ was chosen as the time after which the spike balance did not significantly change. Summary results are shown in Figure6D. The confidence interval for Δn₂ was determined as −2 ∗ SD, 2 ∗ SD, SD = 0.05 being the SD of the value of Δn₂ when there was no stimulation (sham stimulation; see below). At first sight, the results are similar to those of Figure 6B, but close inspection reveals interesting changes. Although the excitatory responses are not significantly modified from one analysis window to the other, the initially inhibitory responses display a variety of late changes, ranging from full compensation to increased inhibition. As a result of this, four early inhibitory responses were reclassified as neutral (inhibition followed by excitation), with no net effect on Δn₂.

Altogether, of the 21 cells that responded to stimulation, 7 (33%) gave an excitatory response, 8 (38%) gave an inhibitory response, and 6 (29%) gave mixed responses (including four inhibitory–excitatory sequential responses, as in Fig. 5B, and two cases in which the response was dependent on the spike frequency before stimulation) without any significant net gain or loss of action potentials.

Control cell-attached experiments

To test whether the frequency changes illustrated in Figure 6,A and B, were genuine, we compared the results with those obtained when starting the analysis from an arbitrary point in time without stimulation. For Δn₁, no significant departure from the control frequency f was observed, confirming that the changes were linked to the stimulation (Fig. 6B, second column of points). Likewise, the variations of Δn₂ were an order of magnitude smaller after a random point than after the stimulation (Fig.6D).

Next we asked whether the stimulation was producing its effect exclusively through activation of GABAergic fibers. To answer this question, we repeated the stimulations in each experiment after perfusion of bicuculline or gabazine in the bath (10 μmof either blocker). This invariably abolished the effects, as can be seen in the summary data of Figure 6B–D(third, fourth columns; the slightly larger scatter seen for these data in Fig. 6D is attributable to a reduced number of trials compared with the control runs). Thus, both the positive and negative frequency changes illustrated in Figure 6,A and B, are attributable to activation of GABA_A receptors. These results exclude any participation of direct subthreshold stimulation of the recorded cell through the stimulation pipette. They also exclude the participation of electrical junctions, which have been shown to play a significant role in IN networks of the hippocampus and cortex (Strata et al., 1997;Galarreta and Hestrin, 1999; Gibson et al., 1999) (for review, seeMcBain and Fisahn, 2001), as well as in the cerebellum of adult guinea pigs (Mann-Metzer and Yarom, 1999). We argued earlier that, in juvenile rats, electrical junctions are occasionally present but play a modest functional role (Pouzat and Marty, 1998).

Cell-attached experiments performed using a K⁺-rich pipette solution

Noteworthy additional results were obtained using a K⁺-rich pipette solution, which was used in an early set of experiments to obtain better whole-cell recordings at the end of the experiment as a check of the effectiveness of the extracellular stimulation (see Materials and Methods). However, in these conditions, it was noted that the frequency of firing depended on the pipette potential, indicating an electrical link between the pipette and the cell interior. Accordingly, because the pipette voltage was held at 0, the experiments performed with the K⁺-rich solution (Fig.6B–D, gray dots) tended to have a high resting frequency (> 5 Hz; Fig. 6C), and the stimulation uniformly led to an early inhibitory response (n = 10), whereas the experiments performed with the Na⁺-rich solution led to a variety of responses, including excitatory ones, as detailed above. Our interpretation of the results, in accordance with Figure 3,A and B, is that a K⁺-rich solution in the cell-attached pipette depolarizes the cell, thus shifting the GPSPs to their inhibitory mode.

P20–P25 cells

All experiments illustrated in Figures 2-6 have been performed at P12–P14, at a stage during which the molecular layer undergoes extensive synaptic development. Even thoughE_GABA does not appear to change with age (Fig. 1), it seemed possible that the basket cell excitability could change after P14, thus altering the proportion of cells that would respond in one or the other way to GABAergic stimulation. We therefore performed additional cell-attached experiments at a more advanced age (P20–P25) and compared the results with those at P12–P14.

The mean firing frequency of the interneurons was higher at P20–P25 (f_CA = 7.1 Hz;n = 15) than at P12–P14, but responses to a GABAergic input were similar at both ages. Figure7A illustrates a clear-cut case, obtained from a P24 animal, in which GPSPs led to an increased frequency of postsynaptic firing, peaking a few milliseconds after the presynaptic stimulation. This effect was abolished by bicuculline (results not shown). In general, P20–P25 experiments yielded all four classes of responses illustrated in Figure 5. Summary results are given in Figure 7, B and C. Of 15 P20–P25 basket cells, 5 (33%) gave excitatory responses; 5 (33%) gave inhibitory responses; and 5 (33%) gave mixed responses (including 3 inhibitory–excitatory sequential responses). Thus the proportions of the principal response types appear identical at P20–P25 and at P12–P14.

Fig. 7.

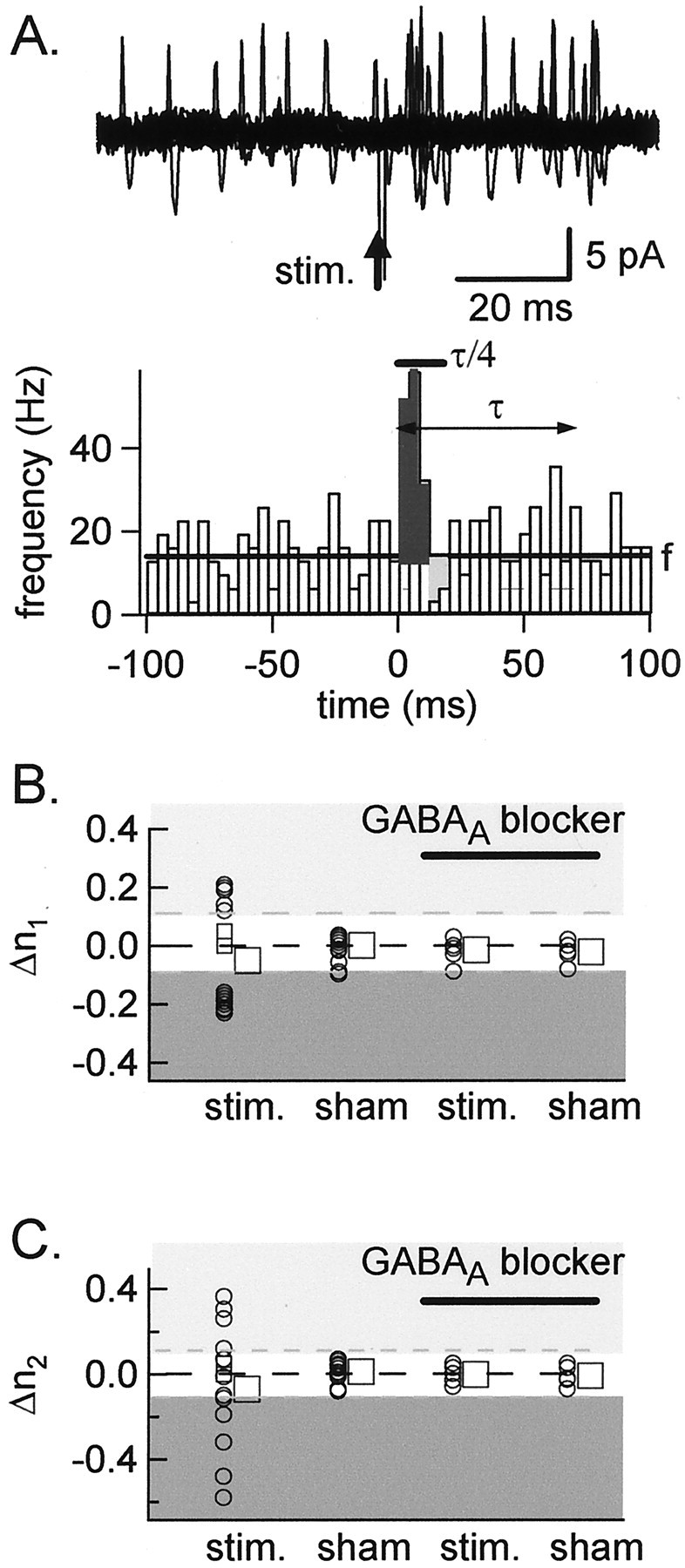
Effects of presynaptic stimulation measured in cell-attached recordings at P20–P25. Symbols are identical to those of Fig. 6. A, Example of a cell excited by a GPSP. Top, Superimposed consecutive traces(n = 25), showing the effect of a spontaneous GPSP on the cell firing as measured in a basket cell of a P24 animal.Bottom, Summary plot of instantaneous spiking frequency across the stimulation (stim.) period. Stimulation mainly results in a strong frequency increase (dark gray area). This was abolished by bicuculline (seeB). B, C, Summary results from 15 experiments. Both inhibition (dark gray areas) and excitation (light gray areas) are observed at τ/4 and τ. Note that the proportion of low-frequency cells (open squares) is lower at P20–P25 than at P12–P14 (compare with Fig. 6C,D).

Subthreshold excitatory GPSPs enhance the basket cell response to an excitatory input

The results illustrated in Figures 3-7 indicate that for hyperpolarized cells, slowly discharging cells, or both, activation of IN→IN synapses can lead to the firing of action potentials in the postsynaptic cell. In such recordings, however, effects of subthreshold depolarizations may still have been inhibitory because of depolarization-induced Na⁺ current inactivation or K⁺ current activation (Zhang and Jackson, 1995; Monsivais et al., 2000; Lu and Trussell, 2001). To address this issue, we tested how GPSPs would alter the postsynaptic excitability after a delay of 30 msec. This delay was chosen such that GABAergic currents were just over, as illustrated below, to avoid shunting inhibition (Gao et al., 1998).

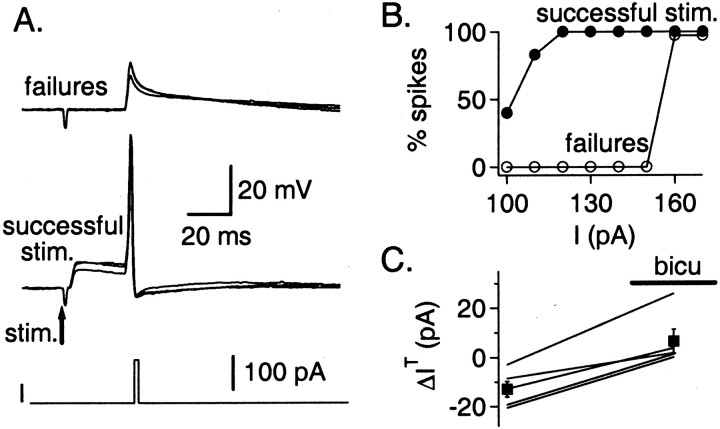
We examined the cell excitability by measuring the current threshold, i.e., the minimal amplitude of depolarizing current, using 2-msec-long pulses, which could induce an action potential. In the example shown (Fig. 8A), approximately half of the extracellular stimulations resulted in failures of synaptic transmission. The results were separated depending on the outcome of extracellular stimulation, and the current thresholds were compared after successful stimulations and after failures. As may be seen, in all cases of failures of the synaptic potential, the current injections resulted in a depolarization that did not induce an action potential, but after the induction of a synaptic potential, the same current injection led to an action potential, suggesting that GPSPs had a strong excitatory effect. Full analysis of the results obtained in this experiment revealed that GPSPs induced a 55 pA shift of the current threshold (Fig. 8B).

Fig. 8.

Enhanced excitability of the postsynaptic cell after presynaptic stimulation. A, A 1 msec current pulse is induced 30 msec after the stimulation (stim.) of a presynaptic interneuron. The current pulse does not reach threshold when synaptic transmission fails but always induces an action potential after a successful stimulation (whole-cell recording;V_m = −71 mV; Cl_i = 15 mm). B, For this cell, the current thresholdI_T for stimulation, defined as the current needed to induce an action potential with a probability ofp = 0.5, is 55 pA smaller after a successful GABAergic stimulation than after a failure. C, The mean difference ΔI_T between the current threshold measured after the stimulation and its control value measured before the stimulation is plotted for five cells in saline solution (ΔI_T = −12.9 ± 3.2 pA) and in bicuculline (bicu; ΔI_T= 6.5 ± 4.8 pA). In this plot, no distinction is made according to whether the stimulation elicited a synaptic current or led to a failure. On average, ΔI_T increases by 19.3 ± 3 pA between the two conditions (p < 0.005).

The results of five such experiments are summarized in Figure8C. To pool all results together, we compared the current thresholds with and without extracellular stimulation, instead of separating the traces obtained after extracellular stimulation according to the absence or presence of failures. In normal saline (containing NBQX and APV), the current threshold was on average smaller by 19 ± 3 pA (p < 0.005) with presynaptic stimulation than without stimulation. After perfusion of bicuculline in the bath, the difference in current threshold was abolished (Fig.8C). We conclude that, in whole-cell recordings performed under physiological conditions (with an intracellular Cl⁻concentration of 15 mm) at a holding potential negative of the firing range, the excitability of INs to depolarizing current injection is enhanced 30 msec after the GABAergic stimulation. These results are thus fully consistent with those of Figure 3,A and B, left panels, and Figure 5D, which all displayed enhanced firing under similar conditions.

Interactions between parallel fiber and interneuron synaptic inputs

We finally asked whether the effects shown in Figure 8 could result in significant interactions between interneuron and parallel fiber inputs. NBQX was omitted from the bath solution, and current injection in the postsynaptic cell was replaced by an extracellular stimulation of a presynaptic granule cell axon. One pipette was in the molecular layer, at ∼100 μm from the recorded cell, to recruit axons from presynaptic basket cells, stellate cells, or both. The other pipette was located in the granule cell layer, at the same level as the recorded cell, to recruit the ascending axon of presynaptic granule cells (Fig. 9A). In the example shown, stimulation of the granule cell axons alone (stim GC) triggered an action potential in 43% of the trials. If the same stimulus was preceded with a stimulation of presynaptic INs (stim IN), the percentage of action potentials increased to 72% (Fig. 9B). In two other cells, this percentage increased from 52 to 62%, and from 79 to 97% (n ≥ 60 stimulations).

Fig. 9.

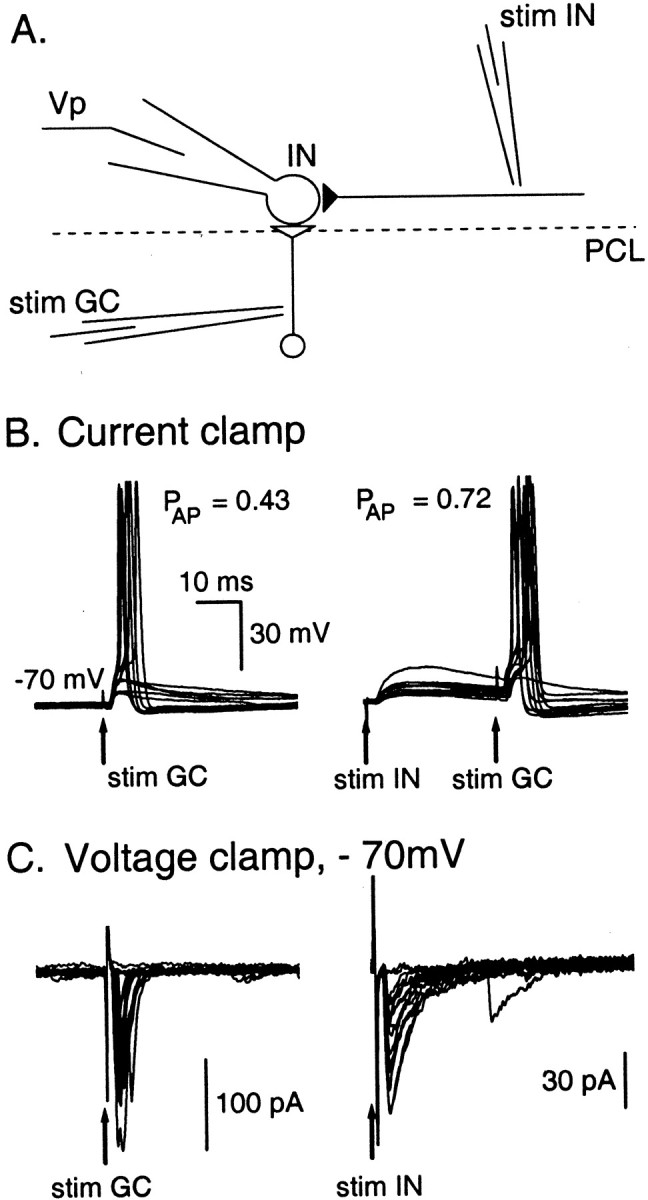
Interactions between glutamatergic and GABAergic synaptic inputs. A, Schematics of the experimental conditions: one extracellular stimulation pipette (stim IN) was positioned in the molecular layer near the Purkinje cell layer (PCL) to stimulate presynaptic INs, and another one (stim GC) was placed in the granular cell layer to stimulate ascending axons from granule cells or climbing fibers. The postsynaptic IN is recorded in whole-cell configuration using a physiological Cl⁻ concentration (Cl_i = 15 mm). B, Current-clamp experiment (V_m ∼ −70 mV). Superimposed traces (10 in eachpanel) show that the probability for a successful glutamatergic stimulation to induce an action potential increases fromp = 0.43 to p = 0.72 (n = 60 trials in each condition;p < 0.01) if it occurs 30 msec after a successful GABAergic stimulation. Therefore, 30 msec after a GPSP, the excitability of the cell is increased. C, Synaptic currents recorded under voltage-clamp conditions for the same cell as in B. The two panels show superimposedtraces of postsynaptic currents induced by stim GC and stim IN, respectively. Exponential fits to the decays of the synaptic currents gave time constants of 1 and 7 msec, respectively. The marked differences in the time courses of decay for the two sets of traces demonstrate that stim GC and stim IN respectively induce only EPSCs and only GPSCs. Note that at the time chosen for the second stimulus, GABAergic currents have fully subsided, so that shunting inhibition does not play a role here.

To ascertain that the stim GC and stim IN stimulations were indeed respectively purely glutamatergic and GABAergic, voltage-clamp recordings were performed in second parts of the experiments, and the synaptic currents elicited were examined (Fig. 9C). The results show that stim IN and stim GC were invariably associated with slow- and fast-decaying synaptic currents, respectively. Very distinct decay kinetics are associated with inhibitory and excitatory inputs, respectively (Llano and Gerschenfeld, 1993), demonstrating that the separation between the two kinds of input was fully effective.

In summary, the results show that under the conditions of these experiments (physiological intracellular Cl⁻ concentration, and holding potential near −70 mV), stimulation of IN afferences enhances the responsiveness to subsequent granule cell stimulation in a time range of tens of milliseconds.

Discussion

This study shows that, when taking into account the entire cell population, IN→IN synapses are globally neutral in the sense that they do not induce any net gain or loss of action potentials. However, individual synapses are not. According to our best estimate, approximately one-third of the synapses are excitatory; one-third are inhibitory; and one-third are mixed (mostly displaying an inhibitory–excitatory sequence). In the following, we examine various factors that can reverse the sign of individual synapses, and we discuss the possible consequences of such reversals.

Dependence of E_GABA on the nature of postsynaptic neurons

We find that the value of E_GABAis on average much more depolarized in INs (−58 mV) than in PCs (−85 mV). This observation is not related to a particular developmental stage and applies both to juvenile (P12–P14) and to fully adult (P35–P40) animals. Similar depolarizedE_GABA values have been obtained for INs in the dorsal cochlear nucleus (Golding and Oertel, 1996), in the hippocampus (Verheugen et al., 1999), and in the sensory cortex and amygdala (Martina et al., 2001). Thus a picture emerges suggesting thatE_GABA is more depolarized in INs than in principal cells. Because of this difference ofE_GABA in the postsynaptic cells, GABAergic INs can simultaneously trigger IPSPs in principal neurons and EPSPs in other local INs.

Sensitivity to recording conditions

Previous studies have indicated that cerebellar IN→IN synapses were inhibitory (Midtgaard, 1992; Häusser and Clark, 1997). Differences with the present work include animal species [turtle in the work of Midtgaard (1992) vs rat here] and experimental conditions [physiological temperature in the work of Häusser and Clark (1997) vs room temperature here]. However, it is unlikely that the excitatory responses would vanish at higher temperatures, because (1) energy-dependent accumulation of Cl⁻ is likely to be enhanced, if anything, by increasing the temperature; and (2) Martina et al. (2001) compared the reversal potentials for interneurons and principal cells in the cortex at 32°C and found values that were strikingly similar to those found for cerebellar interneurons and Purkinje cells at room temperature in the present study. These results, together with ours, suggest that the key factor responsible for the higher E_Cl is the nature of the cell (interneurons vs principal cells) and not temperature. In addition, the present results show that the system is very close to the critical point at which the net effect switches over from excitatory to inhibitory, and that small perturbations can affect the results dramatically. Fortunately, such perturbations can be minimized in an experimental approach combining cell-attached recordings and extracellular stimulations (Leinekugel et al., 1997; this work, Figs.5-7). In retrospect, experimental conditions used in previous studies may have favored inhibition. Thus Häusser and Clark (1997) used whole-cell recording to investigate IN→IN synapses, with an intracellular solution containing 9 mmCl⁻, lower than the 15 mm deduced from the present measurement ofE_GABA, and a resting firing frequency of 37.5 Hz (their Fig. 5), higher than their cell-attached measurement of 11 Hz.

Physiologically relevant factors that can reverse the sign of individual synapses

Because the excitatory and inhibitory effect of a GPSP mainly relies on the driving force V_m −E_GABA (Fig. 3C), the mechanisms that can set or modify the values ofE_GABA andV_m will set or reverse the effect of a GPSP.

Different values of E_GABA among INs could clearly be determined by different sets of Cl⁻ transporters such as KCC2 and NKCC, but past activity of the network could also be implicated in a change in E_GABA; for example, a strong activation of GABA_A channels, either alone or together with other conductances, is likely to bring about substantial changes in E_GABA (Kaila and Voipio, 1987; Thompson and Gähwiler, 1989). Likewise, activity-related elevation in intracellular calcium is likely to lowerE_GABA by simultaneously activating calcium-dependent Cl⁻ and K⁺ channels. In a similar manner, whereas different values of V_m among INs could be determined by different levels of expression of membrane channels, they could also result from the past activity of the cell or from the activation of metabotropic receptors.

These considerations raise the possibility that the effect of a GPSP can be reversed from inhibition to excitation (or conversely) through a previous burst of activity in the IN network or through a local release of neurotransmitters or of neuromodulators. It is worth noting that such reversal in a local group of INs would result in an alteration in the temporal correlation of the activities of neighboring Purkinje cells, the axons of which are the only output of the cerebellum.

Enhancement of depolarizing GABA effects by excitatory conductances

The time course of decay of GABAergic synaptic currents in INs is substantially slower than that of glutamatergic currents (Llano and Gerschenfeld, 1993). Nevertheless, 30 msec after stimulation, the GABAergic synaptic currents are over (Fig. 9C). However, both inhibitory and excitatory synaptic effects of GPSCs may last for hundreds of milliseconds, much longer than the duration of the synaptic currents. This can be explained by two factors. First, the very high input resistance of the INs (several gigaohms) translates to a long membrane time constant, leading to prolonged synaptic potentials (Figs.4A, 9B). Second, depolarizing GABA effects are apparently enhanced by slow excitatory conductances. Such a mechanism is needed to account for the trains of spikes (Figs.3B, 4A) and slow excitatory potentials (Fig. 4B), both lasting ≥100 msec, which are elicited by stimulation of GABA synapses. A recent study performed in the guinea pig confirms that such potentials exist in cerebellar INs and suggests that they are attributable to the activation of persistent, tetrodotoxin-sensitive Na⁺currents (Mann-Metzer and Yarom, 2001). During the slow excitatory potentials, the membrane potential may remain more depolarized thanE_GABA, so that the cell could now be in a mode in which another GPSP would be inhibitory. Because the mean frequency of spontaneous GPSPs is 4.7 Hz (Kondo and Marty, 1998b), excitatory GPSPs can induce a mode shift of the synapse during a substantial fraction of time.

A self-regulating network?

The ability of GPSPs to change signs depending on the state of the postsynaptic cell should have stabilizing effects on the cerebellar network by the following mechanism. INs are able to generate action potentials in the absence of any synaptic input (Llano and Gerschenfeld, 1993). However, there is a considerable variation among the rates of firing observed under normal conditions (0.3–9 Hz; Kondo and Marty, 1998a). Let us assume for a moment that the entire network is strongly inhibited such that most INs are silent. In this situation, reciprocal synapses are excitatory, according to the present results (Fig. 3, left panels). The few action potentials that are generated will therefore tend to spread to neighboring neurons. The mean number of presynaptic cells for one postsynaptic cell was estimated at 4.25 in this network (Kondo and Marty, 1998a). This is also the number of postsynaptic cells contacted by one presynaptic cell, because all INs can be regarded as equivalent, so that each neuron in the network has on average the same number of presynaptic and postsynaptic partners. If one considers a mean failure rate of 0.38 (calculated from Kondo and Marty, 1998a, their Table 1) and a probability to elicit a spike close to p = 1 for each successful GPSP, we obtain an average of 0.38 ∗ 4.25 = 1.6 postsynaptic action potentials for one presynaptic spike, suggesting that the system is divergent and will therefore spread in a regenerative manner. However, the increased firing and depolarization that are associated with each GPSP presumably alters the sign of the synapses for some time (Fig. 2). This effect introduces a negative feedback. Thus the IN network may regulate its firing rate, acting as a buffer.

Analyzing how such a flexible network differs from a fixed network relying exclusively on excitatory or inhibitory synapses will require quantitative modeling and falls outside the scope of this work. Nevertheless, it is possible to see that such a feature would allow the network to adjust its mean firing rate to external challenges. For example, when parallel fiber input is weak or absent (as in the present work), then a substantial proportion of GABAergic signals will be excitatory, thus maintaining a relatively high IN firing rate. If, on the other hand, the parallel fiber input is strongly activated (as it does in vivo after certain stimulation protocols;Jörntell and Ekerot, 2002), GABAergic synapses will turn inhibitory, and the overall effect on IN firing will be dampened. In this way, the ability of GABAergic synapses to change signs adds flexibility to the network and allows it to maintain its mean firing rate in the range in which it reacts best to new information. In anesthetized cats, stellate and basket cells fire at a relatively low rate, in the range of 7–30 Hz (Eccles et al., 1966; Armstrong and Rawson, 1979; Ekerot and Jörntell, 2001). This would appear as surprisingly close to the mean rate of 11 Hz found at the physiological temperature for P18–P35 rat slices (Häusser and Clark, 1997; a comparable rate was found at P20–P25 and room temperature in the present work), given the presumed massive difference in parallel fiber and climbing fiber inputs between the two preparations. The proposal of a buffering of the IN firing rate by the above mechanism provides an explanation for this paradox.

Comparison between two alternative methods to measure the mean resting potential of INs

Here we compare membrane potential measurements in current-clamp recordings using the zero current method or the equal firing potential method.

We model the membrane potential recording situation as a parallel combination of a battery v_CA and a conductance g_m, representing the resting conductance of the cell, and of a conductanceg_l and associated batteryE_l, representing the leak conductance through the seal. We further assume thatv_CA andg_m undergo small fluctuations around their mean values V_CA andG_m, and that these values are not affected by small applied currents through the cell. The recorded membrane potential may be calculated in this equivalent circuit as:

$$v_{\text{m}}=(g_{\text{m}}\ast v_{CA}+g\ast E_l+i)/(g_{\text{m}}+g_{\text{l}}),$$ Equation 1

where i is the applied current.

Let us consider first the zero current measurement method. Introducingi = 0 in Equation 1 gives:

$$v_0=(g_{\text{m}}\ast v_{CA}+g_{\text{l}}\ast E_l)/(g_{\text{m}}+g_{\text{l}}).$$ Equation 2

The bias introduced in the estimate ofv_CA can be derived from Equation 2 as:

$$v_0-v_{CA}=(E_l-v_{CA})/(1+g_{\text{m}}/g_{\text{l}}),$$ Equation 3

and, by taking means on both sides:

$$V_0-V_{CA}\sim (E_l-V_{CA})/(1+G_{\text{m}}/g_{\text{l}}).$$ Equation 4

Therefore, if g_l is of the same order of magnitude as g_m, as it is in the case in our whole-cell and gramicidin-perforated patch experiments (see Materials and Methods), such an estimation ofV_CA is biased to a more depolarized value by up to 30 mV (assuming V_CA = −60 mV; G_m =g_l; andE_l = 0 mV), which is not acceptable.

Let us consider now the equal firing method, in which the intensityi of the clamp is set such that the mean firing rate equals the mean spontaneous firing rate measured in the cell-attached configuration in the same preparation (as detailed in Results). We callv_eq andV_eq, respectively, the instantaneous and the mean membrane potentials in these conditions (spikes are excluded in the calculation of the mean). The cell fires each time thatv_eq reaches the threshold valueT, which we assume for simplicity to be independent of small injected currents. Although differences betweenv_eq andV_CA may be significant at hyperpolarized potentials, they must vanish near T to comply with the condition that the recorded cell has the same firing rate as the unperturbed cell. Making v_m =v_CA = T in Equation 1yields:

$$T=(g_{\text{m}}\ast T+g_{\text{l}}\ast E_l+i)/(g_{\text{m}}+g_{\text{l}}).$$

This gives the corresponding value of the current:

$$i=g_{\text{l}}\ast (T-E_l).$$

Inserting this into Equation 1 gives the following value ofv_eq:

$$v_{\text{eq}}=(g_{\text{m}}\ast v_{CA}+g_{\text{l}}\ast T)/(g_{\text{m}}+g_{\text{l}}).$$

The bias introduced in the estimate ofv_CA is:

$$v_{\text{eq}}-v_{CA}=(T-v_{CA})/(1+g_{\text{m}}/g_{\text{l}}),$$

and, provided that fluctuations ing_m are small:

$$V_{\text{eq}}-V_{CA}\sim (T-V_{CA})/(1+G_{\text{m}}/g_{\text{l}}).$$ Equation 5

Thus, the bias V_eq −V_CA is typically only 5 mV (by takingT − V_CA = 10 mV andG_m =g_l).

We conclude that, for compact cells that are spontaneously active, the equal firing potential V_eq is a better estimate of V_CA than the zero current potential V₀.

Calculation of the dependence of the firing frequency on the resting membrane potential

Here we show that the results of Figures 3 and 6 can be combined together to calculate the dependence between the firing frequencyf_CA and the mean membrane potentialV_CA for unperturbed cells.

Figure 3C shows the variation of the spike balance Δn₁ as a function ofV_m in current-clamp experiments. This can be fitted with an exponential function, with a constrained asymptotic value of −0.25 (the minimum value that Δn₁ can take):

$$\mathrm{\Delta }{n}_1=-0.25+0.00034\ast exp(-0.108\ast V_{\text{m}}).$$ Equation 6

Inversing this equation yields:

$$V_{\text{m}}=-0.108\ast ln((\mathrm{\Delta }{n}_1+0.25)/0.00034)).$$ Equation 7

Because all the points Δn₁(V_m) lie close to the fit, this equation also applies to the relation between Δn₁ andV_CA. Equation 7 may therefore be used to extract the relation between f_CAand V_CA from the plot of Δn₁ againstf_CA in cell-attached experiments (Fig.6C). By replacing in that plot each Δn₁ value with its correspondingV_m value, obtained with Equation 7, we obtain a plot of V_CA versusf_CA in cell-attached experiments. These two variables, V_CA andf_CA, are correlated (p < 0.0001, t test;n = 31). After inversion, the relation betweenf_CA andV_CA can be fitted with an exponential (with a constrained asymptotic value of 0), as follows:

$$f_{CA}=352\ast exp(-0.08\ast V_{CA}).$$ Equation 8

This is the equation in Figure 2, slanted dotted line.