Emergent Properties of Layer 2/3 Neurons Reflect the Collinear Arrangement of Horizontal Connections in Tree Shrew Visual Cortex

Abstract

The superficial layers of primary visual cortex, unlike layer 4, have an extensive network of long-range horizontal connections linking sites of similar orientation preference. To identify possible functional consequences of this distinct anatomy, we compared the receptive field properties of layers 2/3 and 4 neurons in tree shrew primary visual cortex with electrophysiological recordings. We found that elongated receptive fields, strong orientation tuning, and length summation (properties predicted by the anatomy of the horizontal connections) are present in layer 2/3 neurons, but not in layer 4 neurons. We further characterized the summation fields of layer 2/3 neurons and found axis and orientation-specific facilitation that matched the distribution of horizontal connections. The functional signature of horizontal connections was also evident in the population response of layer 2/3 neurons; the intrinsic signal activation pattern elicited by an array of collinear Gabor elements was significantly stronger than that elicited by a noncollinear array. Furthermore, our results showed that this enhancement of population response was achieved without compromising spatial resolution along the collinear axis, providing stimulus-specific facilitation without filling in between stimuli. Taken together, these results suggest that horizontal connections play a significant role in shaping the visual responses of layer 2/3 neurons.

Introduction

Pyramidal neurons in superficial layers of visual cortex are targets of two distinct types of intracortical circuits: feed-forward projections that originate from layer 4 neurons and recurrent projections that originate primarily from other layer 2/3 neurons. Feed-forward inputs, with a horizontal spread limited to <500 μm in any direction, are thought to provide much of the excitatory drive that shapes classical receptive field properties of layer 2/3 neurons (Hubel and Wiesel, 1968, 1977; Lund, 1973; Lund and Boothe, 1975; Mooser et al., 2001). In contrast, because they extend for several millimeters across the cortical surface, horizontal connections have been viewed as contributing to receptive field surround effects: facilitatory and inhibitory modulation of layer 2/3 activity by stimuli presented outside of the classical receptive field (Rockland and Lund, 1982; Gilbert and Wiesel, 1983; Gilbert, 1992,1998).

Although this functional distinction is appealing, evidence to support this strict dichotomy is incomplete. Horizontal connections do extend for long distances, but their field of influence includes many cells with overlapping receptive fields, suggesting the potential for a contribution to responses evoked by stimulation of the classical receptive field (Tucker and Fitzpatrick, 2003). Recent studies in macaque visual cortex provide evidence that horizontal connections may feed receptive field “center” responses, whereas other sources of input (notably feedback from extrastriate areas) are more suited to the properties of surround modulation (Angelucci et al., 2002; Cavanaugh et al., 2002) (but see Stettler et al., 2002). Furthermore, there have been few efforts to compare systematically the receptive field properties of neurons that participate in horizontal interactions with those that do not; if horizontal connections contribute significantly to responses of V1 neurons, differences in response properties that accord with these contrasting patterns of connectivity should be evident. Finally, much of the evidence that horizontal connections are limited to modulatory roles comes from tissue slice experiments in which electrical stimulation of horizontal inputs yielded relatively weak subthreshold changes in membrane potential (Hirsch and Gilbert, 1991; Weliky et al., 1995; Yoshimura et al., 2000). However, punctate stimulation in vitro may underestimate the capacity of horizontal connections to drive postsynaptic responses when large populations of interconnected neurons are activated in unison. Indeed, several perceptual phenomena in which horizontal connections have been implicated, such as “filling in” and “illusory contours,” seem to require that horizontal connections elicit spike discharges from target neurons (Fiorani et al., 1992; Grosof et al., 1993; Lee and Nguyen, 2001).

Tree shrew striate cortex offers a number of advantages for exploring questions about the function of horizontal connections. First, like primates, neurons in layer 4 lack substantial horizontal connections (Muly and Fitzpatrick, 1992); therefore, comparisons of response properties of layers 4 and 2/3 provide a strong assay for the impact of horizontal connections. Second, horizontal connections in the tree shrew are organized in a remarkably collinear manner, preferentially linking neurons with similar preferred orientations and for which the receptive fields are displaced along the axis of preferred orientation in visual space (Bosking et al., 1997). This anisotropy serves as a distinct signature, making it possible to assess whether differences in response properties of layers 4 and 2/3 neurons are consistent with (and likely to be derived from) the specific arrangement of horizontal connections. Additionally, by using optical imaging techniques to compare patterns of activity evoked by different stimulus configurations, we can use collinearity as a probe of the effectiveness of horizontal connections in driving responses of layer 2/3 neurons.

We find that neurons in layers 4 and 2/3 differ markedly in the size and shape of their receptive fields, orientation selectivity, and length tuning in ways consistent with the orderly arrangement of horizontal connections. However, even when large populations of layer 2/3 neurons are activated, the impact of the horizontal network appears to be dependent on activity from layer 4 inputs. These results suggest that horizontal connections play a significant role in shaping responses of layer 2/3 neurons without compromising the fine spatial resolution supplied by layer 4 inputs.

Materials and Methods

Animal preparation

All experimental procedures were approved by the Duke University Institutional Animal Care and Use Committee and performed in compliance with guidelines published by National Institutes of Health. Adult tree shrews (Tupaia belangeri) of both sexes were used for these experiments. Surgical procedures and animal preparation for both electrophysiology and optical imaging have been described previously (Bosking et al., 1997).

Electrophysiology

Extracellular recordings (single units and multiunits consisting of 2–4 units) were performed in striate cortex of 25 animals. We examined orientation tuning, minimum discharge field (MDF) size and shape, and length tuning for units in layers 2/3 and 4, and we also examined the axial tuning of layer 2/3 units. Seventy vertical and two oblique 45° posteroanterior angle penetrations were made through the cortical layers. Recordings were made from a total of 61 sites (30 single units and 31 multiunits) in layer 2/3, 35 sites (17 single units and 18 multiunits) in layer 4, and 10 sites (multiunits) in infragranular layers.

Tungsten electrodes, 61–70 mm in length, 75–125 μm in shank diameter, 14 MΩ in resistance (FHC, Bowdoinham, ME), were advanced into the cortex via a manual hydraulic micro-drive (Narishige, Tokyo, Japan). Activity was monitored by using a differential amplifier, displayed on an oscilloscope and audio monitor; the signals were sent to a personal computer via aCambridge Electronic Design (CED, Cambridge, UK) 1401plus Intelligent Laboratory Interface. The waveforms of individual cortical neurons were discriminated and tabulated with Spike2 software (CED).

For each site the binocular MDF was plotted by using a computer-assisted minimum response technique, and its location in visual space was checked systematically before each tuning measurement to insure that no eye movements had occurred. For multiunit aggregate receptive field plotting we considered both the spikes of individual units and the general “hash” response in determining the borders of the receptive fields. The waveforms obtained from the recordings were checked systematically to ensure that these sites showed biphasic spikes, characteristic of cell soma recordings (Bishop et al., 1962). At the end of each penetration two small lesions (4–5 μA, 6–7 sec) were made at different levels of the cortex to aid in the histological reconstruction of the recording sites and confirm that all recordings were made in V1.

Orientation tuning. Orientation tuning was performed for all sites by presenting a high-contrast bar stimulus (white bar on black background, 100% contrast, 1–2° in width, 20–40° in length) at 18 orientations (0–170°) moving back and forth through the receptive field at 10–20°/sec. Five repetitions of each stimulus were presented in randomly interleaved trials, and responses were averaged for each stimulus condition.

For all data analysis the average number of background spikes per trial was subtracted from the average number of stimulus-evoked spikes per trial. For orientation-tuning experiments an orientation selectivity index (OSI) was used as a measure of orientation tuning. The equation used to calculate the OSI was:

$$OSI=1-\text{orth}/\text{pref},$$ Equation 1

where pref is the response to the preferred orientation (i.e., the maximum response) and orth is the response to the orientation orthogonal to preferred. This results in OSI values between 0 and 1; an OSI close to 0 shows little to no selectivity, whereas a value close to 1 shows strong selectivity. This OSI has been used previously, with all values >0.7 being deemed selective (Gegenfurtner et al., 1997).

Position tuning. Position-tuning experiments were performed for 15 sites (7 single units and 8 multiunits) in layer 4. The stimulus used was a long (20–40° in length), thin (0.25° in width) bar panned back and forth within a 1° window at one of 16 positions (spaced 1° apart) centered on the previously measured MDF. Each stimulus was presented for 2 sec with a 500 msec interstimulus interval (ISI), and five repetitions of each stimulus were presented in randomly interleaved trials. The orientation of the stimuli corresponded to the preferred and orthogonal orientation for each site. A tuning curve was constructed for each position-tuning experiment, and a Gaussian curve was fit to the data.

Length tuning. Length-tuning experiments were performed in 37 sites (29 single units and 8 multiunits) in layer 2/3 and 33 sites (17 single units and 16 multiunits) in layer 4. Length tuning was measured by presenting a high-contrast bar of the same width and speed used for orientation tuning, set to the preferred orientation and drifting through the center of the MDF. This bar stimulus was presented at 18 different lengths from 2 to 36°. Five repetitions of each stimulus were presented in randomly interleaved trials. Responses tended to increase, decrease, or remain steady across all lengths; they were not seen to rise and then fall as if the site were tuned for midrange lengths. Therefore, to test for length tuning, we compared the responses to the shortest and longest stimuli for each site; sites that showed a significant difference were considered tuned for length. Tuned and untuned sites in each cortical layer were sorted and averaged, and the averages for tuned sites were fit with an exponential curve.

Axis tuning. Axis tuning was performed for 35 sites (13 single units and 22 multiunits) in layer 2/3. These experiments used Gabor stimuli (a sine-wave grating convolved with a Gaussian; Field et al., 1993). Our Gabor elements can be described as follows: diameter ∼5°, full width at half-height = 2.25°, period of the sine-wave grating = 2°, contrast = full range of pixel values (0 – 255). So that we could elicit strong, sustained cortical responses, the sine-wave grating was drifted back and forth within the stationary Gaussian window. Linear arrays of seven Gabor stimuli centered on the MDF and spaced 6° center to center were presented along eight different axes (0° to 157.5°) for 2 sec with a 4 sec ISI. The stimuli were presented on a medium gray background, which remained on the screen during the ISI. Two experiments were performed; in the first the stimuli were all iso-oriented Gabor elements, corresponding as nearly as possible to the preferred orientation of the site; in the second the stimuli consisted of a central Gabor element at the preferred orientation with orthogonally oriented Gabor elements in the surround. The central Gabor stimulus was positioned at the center of the defined receptive field. As part of each experiment a single Gabor stimulus (the central Gabor stimulus) also was presented individually as a control. For each condition there were five repetitions, and presentations were interleaved randomly.

Histology. At the conclusion of each experiment Nembutal was administered. Once the heart stopped beating, the animal was perfused transcardially with 0.9% saline, followed by 10% formalin in 0.1m sodium phosphate buffer, pH 7.4. The brain was postwashed in 10 and 20% cold sucrose for 6 and 24 hr, respectively. The posterior one-half of the brain containing the visual cortex was cut in 50 μm coronal or sagittal sections with a freezing microtome. The sections were mounted on glass slides, dried, dehydrated, stained with cresyl violet, and coverslipped.

Reanalysis of anatomy

Anatomic data from Bosking et al. (1997) were reanalyzed for comparison with the data presented here. For the previous study small biocytin injections were made in layer 2/3, and the locations of the resulting labeled axon boutons were plotted in 10 animals, recording the distance from the injection site for all boutons within 30° of the preferred and orthogonal axes. For the present study we used these data to create a cumulative percentage distribution of boutons along the two axes as well as to calculate the fall-off in density of boutons along each axis. For calculation of cumulative percentage distribution the boutons were binned according to distance from the injection site. Then bouton counts at each distance were converted to a percentage of total boutons for each case; cases were averaged and cumulative percentage was calculated. Binned bouton counts also were used for the density calculation; bin counts were normalized for total boutons per case (to correct for differences in injection size), density was calculated for each bin, and data were averaged across cases and plotted as the percentage of maximum density (our maximum was >15,000 boutons/mm²). Cortical distances were converted to visual space coordinates by using the average cortical magnification factor determined by Bosking et al. (2002) of 5.1°/mm to allow for comparison with MDF and summation field measures. Axis tuning of bouton distributions was established by creating an average axis-tuning curve from the 13 cases presented in Bosking et al. [(1997), their Fig. 10B] and by fitting with a Gaussian.

Optical imaging

To assess population responses to axial stimuli, we used intrinsic signal optical imaging in nine additional animals (all young adult females, age 2.5–5 months). Optical imaging of intrinsic signals was accomplished by an enhanced video acquisition system (Optical Imaging, Mountainside, NJ) that used techniques similar to those described previously (Bosking et al., 1997). Images of the left hemisphere area V1 were acquired through thinned bone, using an imaging chamber. Cortex was illuminated with a red light (700 ± 10 nm).

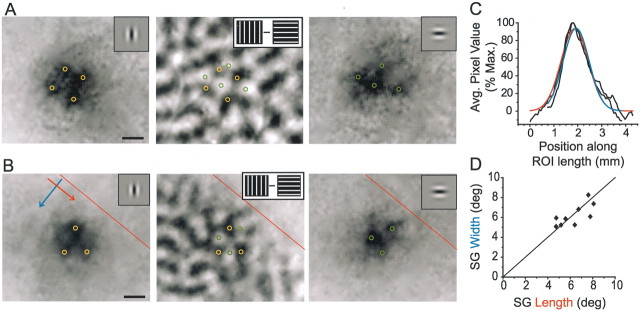
Stimuli consisted of Gabor elements that were the same as for the axis tuning described above in all respects except for their arrangements into rows. For imaging experiments the Gabor elements were arranged along either the vertical or the horizontal axes in visual space and separated by 5, 7.5, or 10° (center to center). All elements in a given stimulus were of the same orientation, either vertical or horizontal. If the orientation of the elements was the same as the orientation of the axis, the stimulus was referred to as “collinear.” If the orientation of the elements and the axis differed, the stimulus was referred to as “orthogonal.” Single Gabor stimuli (SG; horizontal and vertical) also were presented, as were blank (medium gray screen) stimuli. Stimuli were presented in sets of three or four and were ordered randomly for each presentation of the stimulus set; 20–25 repetitions of each set were performed. The order of stimulus sets was varied across animals. All possible stimulus sets were not completed in all animals, leading to variation in then for different analyses reported here.

A single trial consisted of the presentation of one stimulus for 9 sec, with acquisition of video images during the last 8 sec, an ISI of 8 sec during which the screen remained medium gray, and then presentation of the next stimulus in the set and so on until all stimuli had been presented once. Video images were acquired at a rate of 30 frames/sec, but all frames during the 8 sec acquisition were summed together before further processing. Image resolution was 655 × 480 pixels, with 75 pixels/mm as a result of the lens combination that was used. Trials with dominant stimulus artifact (caused by sudden changes in blood flow unrelated to the stimuli) were excluded. For all other trials the video images for the blank stimulus were subtracted from video images for each of the other stimuli, and the resulting images were summed across trials for each condition.

In our initial imaging experiments we noticed that responses to vertically oriented stimuli were often stronger than those to horizontal, regardless of stimulus arrangement. This vertical bias varied considerably in magnitude from animal to animal but would persist throughout the day-long set of experiments. The bias was found only for stimulus orientation, not stimulus axis, and the cause remains unknown. To avoid this confound, we always made comparisons between responses to arrays that contained Gabor stimuli of the same orientation presented along different axes in space; responses to horizontal and vertical Gabor stimuli were not directly compared in these analyses.

Imaging of orientation preference maps also was completed in all animals. Imaging procedures were identical to those described above. Stimuli consisted of high-contrast, full-screen (∼40°) drifting square wave gratings that were either vertical or horizontal. Video images for the horizontal stimulus were subtracted from images for the vertical stimulus, resulting in a map of orientation preference.

Images used for the analyses described below were either 32-bit floating point files or eight-bit files for which pixel values had been clipped to 3 SDs and rescaled from 0–255. These preparations were best for maintaining the full range of signal values necessary for quantitative analysis, and, although clipping was necessary for some analyses because not all of our software could process 32-bit files, there was virtually no difference in our results when unclipped and clipped images were compared. Because apparent contrast is very low with such preparations, contrast was enhanced to allow for a qualitative review of the images in the figures presented here. Brightness and contrast were adjusted equally for each set of images.

Analysis of spatial resolution. Images were clipped to 3 SDs for this analysis, which was more than sufficient to retain the full range of signal values without saturation. Images were mean filtered with a 7 × 7 pixel kernel to remove high-frequency noise. A vessel mask was created for V1 by tracing all large blood vessels on the reference image, and the pixel value of all pixels within the mask was replaced with the average value of the 100 nearest nonvessel pixels in the image (Bosking et al., 2000). To quantify the spatial distribution of signal in each image, we constructed an activity profile along the length (the axis in visual space parallel to the orientation of the stimulus) and width (the orthogonal axis) of each response. A region of interest (ROI) was selected that typically included signal from the central Gabor in the row as well as at least one or two flanking Gabor elements (identical ROIs were used for all relevant images within a given case). Typical size of the ROI was 90 pixels wide and 200–300 pixels long (1.2 × 2.67–4 mm). Pixel values across the width of the ROI were averaged row by row, producing an activity profile along the length of the ROI. This averaging removed some, but not all, of the modulations caused by orientation signal. Activity profiles were normalized by subtracting the average background value for each image (taken from a region of inactive cortex). Profiles were fit with Gaussians (a multipeak Gaussian fit was used for stimulus arrays, generating one multipeak fit as well as the component Gaussians), and the full width at half-height of the Gaussian fits was taken as a measure of the spatial extent of the signal. Length and width measures were converted from cortical space to visual space coordinates and corrected for the slight difference in magnification factor along the two axes (vertical, 4.8°/mm; horizontal, 5.5°/mm). The difference between peak and trough height also was measured for multipeak Gaussian fits; this was done by measuring the height of all peaks and troughs along the multipeak fit and subtracting the average trough from the average peak.

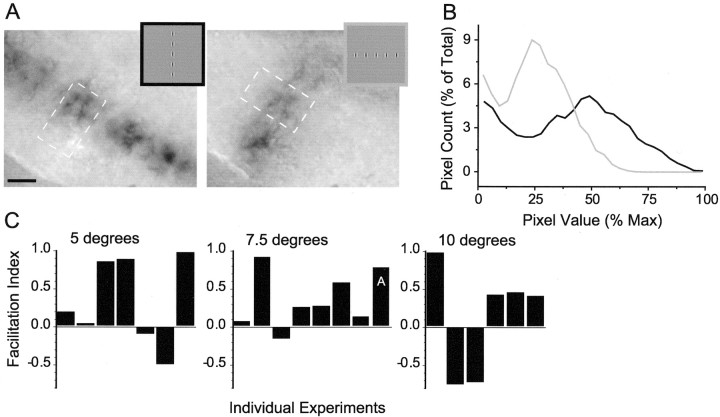
Histogram analysis. For this analysis floating point (unclipped) images were used. Images were mean filtered with a 5 × 5 pixel kernel to remove high-frequency noise. A vessel mask was created for V1 by tracing all large blood vessels on the reference image, and all pixel locations in the mask were excluded from further analysis. To quantify the signal in each image, we selected a ROI that included the signal from the central Gabor in the row as well as an approximately equal-sized region of the nonactive adjacent cortex. Typical size of the ROI was 100 × 165 pixels (1.33 × 2.2 mm) with occasional slight variation to keep the ROI in V1 or to avoid an imaging artifact. For each ROI a histogram was created counting the percentage of total pixels at each gray value. Histograms were multimodal, with the distribution of lighter colored pixels representing the background of each image. The background distribution was fit with a Gaussian, and the center of that Gaussian was set to zero, normalizing for any DC offset between images. Histogram values for collinear and orthogonal arrangements of stimuli of the same orientation (i.e., a vertical row of vertical stimuli and a horizontal row of vertical stimuli) were compared with each other. To normalize for differences in signal intensity across cases, we converted pixel values to a percentage of maximum pixel value within each collinear–orthogonal pair. The total pixel count for all pixel values >50% of max was calculated for each image, and from this value (P) a facilitation index was calculated for each image pair:

$$\text{Facilitation Index}=(P_{\text{collinear}}-P_{\text{orthogonal}})/(P_{\text{collinear}}+P_{\text{orthogonal}}).$$ Equation 2

This results in values ranging from –1 to 1, where a negative value indicates a greater orthogonal response and a positive response indicates a greater collinear response.

Results

Comparison of layer 2/3 and layer 4 receptive field properties

Orientation selectivity

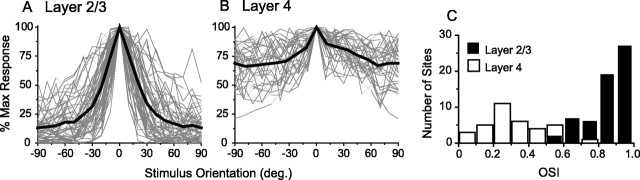
Orientation-tuning curves were established for 61 units in layer 2/3 (30 single units, 31 multiunits), 35 units in layer 4 (17 single, 18 multi), and 10 multiunits in infragranular layers, using a long bar stimulus presented at 18 different angles. Because there were no significant differences in the properties of the single and multiunit recordings measured in this study, we will continue to note the number of each type, but we will not distinguish between them in the analysis. In general, neurons in layer 2/3 were sharply tuned for orientation, with a clear peak in response to the preferred angle and a decrement in response to deviations away from the preferred angle (Fig.1A). The average full width at half-height of a Gaussian fit to the layer 2/3 orientation-tuning curves was 43 ± 20°, and responses to the preferred angle were always significantly greater than responses to the orthogonal. In contrast, neurons in layer 4 were generally poorly tuned for orientation, responding vigorously to all stimulus orientations (Fig. 1B). For those layer 4 tuning curves that were well fit with a Gaussian (n = 30), the average full width at half-height was 69.9 ± 38°, and in only 46% of layer 4 sites was the response to the preferred angle significantly greater than the response to the orthogonal. In none of the layer 4 recordings was it possible to identify a stimulus orientation that failed to elicit a response. An OSI that compares the response to the preferred angle with that of the orthogonal (0 = no selectivity for orientation; 1 = very selective for orientation) confirms the striking difference in tuning of layer 4 and layer 2/3 neurons. The distribution of OSI values for these two populations is mainly non-overlapping (Fig. 1C). The mean (± SD) OSI in layer 2/3 was 0.81 ± 0.12, which differed significantly from the mean layer 4 OSI of 0.31 ± 0.17 (Student's t test,p < 0.001). These OSI values indicate that, on average, the response of layer 2/3 neurons to the orthogonal angle was 81% less than the response to the preferred, whereas in layer 4 the response to the orthogonal angle was reduced by only 31% over that of the preferred.

Fig. 1.

Layer 2/3 neurons exhibit strong tuning for stimulus orientation, whereas layer 4 neurons are tuned only weakly.A, Orientation tuning for 61 layer 2/3 recording sites, with preferred orientation normalized to 0. Individual sites are shown in gray, with the average tuning curve shown inblack. B, Orientation tuning for 35 layer 4 recordings (gray) and average tuning curve (black), normalized as in A.C, Histogram of OSI values for layers 2/3 (black) and 4 (white). Values >0.7 are considered to be tuned for orientation.

MDF size and shape

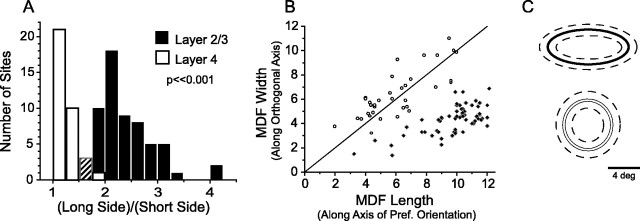
On average, layer 2/3 MDFs measured 9.8 ± 1.8° long and 4.3 ± 1.2° wide and were elongated significantly, with an average aspect ratio of 2.3:1 (ANOVA comparing length and width;p < 0.001; n = 61: 30 single units, 31 multiunits). The direction of elongation was always along the axis of preferred orientation. In contrast, layer 4 MDFs showed much smaller aspect ratios, and elongation, if present, was not necessarily in the direction of the most effective orientation. Aspect ratios calculated without regard to orientation bias (long side/short side) averaged 1.2:1 (Fig. 2A; 35 sites: 17 single units, 18 multiunits). When MDF length and width were defined as size along and orthogonal to the axis of the most effective orientation, respectively, aspect ratios averaged 0.95:1 (Fig.2B). The average size of the layer 4 MDF measured with respect to the most effective orientation was 6.1 ± 2.1° long and 6.4 ± 2.0° wide (ANOVA comparing length and width for layer 4, NS). The distribution of aspect ratios for the layer 4 recordings is significantly different from that of layer 2/3 (Fig.2A; t test, p < 0.001). Although the MDF measures for length and width varied across recording sites, a plot of MDF length versus width reveals two primarily non-overlapping distributions, with layer 4 values centered on the diagonal and the layer 2/3 distribution shifted to the right (Fig. 2B).

Fig. 2.

Layer 2/3 neuron MDFs are elongated along the axis of preferred orientation, whereas layer 4 neuron MDFs are radially symmetric. A, Histogram of MDF aspect ratios (long side/short side) for layer 2/3 neurons (black) and layer 4 neurons (white). In the third bin the counts for layers 2/3 and 4 were the same, represented by a hashed bar. B, MDF length versus width for layer 2/3 (black diamonds) and layer 4 (open circles), where length is measured along the axis of preferred orientation. C, Schematic of average MDF size and shape for layer 2/3 (top) and layer 4 (bottom) ± 1 SD (dashed lines).

To ensure the accuracy of our measures and the lack of significant elongation for layer 4 cells, we generated automated position-tuning curves for a subset of sites in layer 4 (7 single units and 8 multiunits), using bar stimuli presented at 16 positions spaced 1° apart. Position-tuning experiments were conducted both along and orthogonal to the axis of the most effective orientation, and tuning curves were fit with Gaussians. The median aspect ratio for these sites (calculated by using the full width at half-height of the Gaussian fits) was 1.2:1 (length and width were not significantly different), confirming our measurements by the hand plot technique. Position tuning was performed to determine the width of layer 2/3 receptive fields as part of a previous study (Bosking et al., 2002), and results confirm hand-plotted MDF widths found here: average full width at half-height of Gaussian fit to position-tuning data = 4.7 ± 2.5° (n = 39).

Summation fields

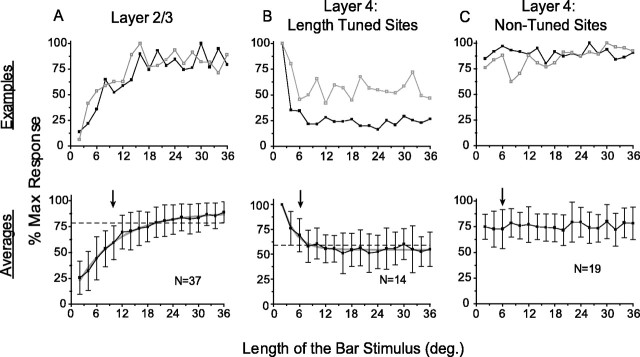
In addition to evaluating the MDF, we examined the length summation properties of neurons in layers 2/3 and 4 by comparing their response to bars of the preferred orientation varying in length from 2 to 36° drifting through the center of the MDF. Layer 2/3 (29 single units and 8 multiunits) showed length summation within and well beyond the area we had measured as the MDF (Fig.3A); on average, responses increased with length for all lengths shown. By fitting the average length-tuning curve with an exponential, we found that the stimulus length required to reach 90% of the response asymptote was 19.9°, which we took as a measure of the extent of length summation. In contrast, some layer 4 neurons (14 sites, 10 of them single units) gave a vigorous response for short stimulus lengths and then showed a decrease in response with increasing stimulus length, approaching an asymptote at 55%; the length required to reach 90% of the response asymptote was 8.8° (Fig. 3B). The remaining layer 4 sites showed no significant change in response to increasing stimulus length (19 sites, 7 of them single units; Fig. 3C).

Fig. 3.

Layer 2/3 neurons exhibit prominent length summation, whereas layer 4 neurons do not. The top rowshows two examples for each response type; blackindicates a single unit record, and gray indicates a multiunit record. The bottom row shows population average (error bars ± 1 SD), with arrowsindicating the extent of average MDF for each layer, gray lines showing exponential fits, and dashed linesindicating 90% of asymptote. A, Length summation in layer 2/3 neurons. B, Length suppression found in 14 of 33 recording sites in layer 4. C, Lack of prominent summation or suppression in 19 of 33 sites in layer 4.

Axis and orientation tuning of layer 2/3 summation fields

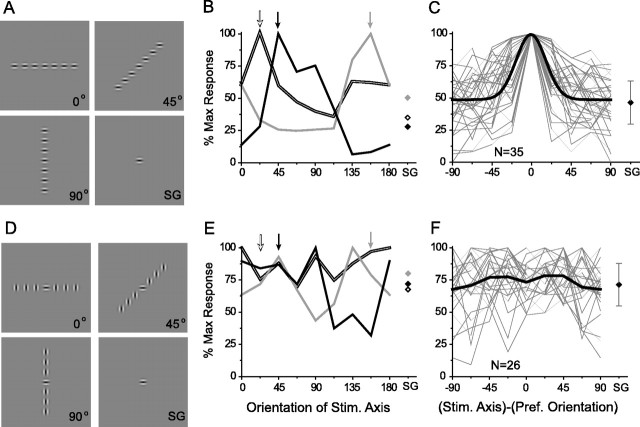
To evaluate the spatial organization of the summation field of layer 2/3 neurons (whether it is radially symmetric or elongated along the axis of preferred orientation) as well as to test its dependence on stimulus orientation, we designed a series of experiments that used linear arrays of Gabor stimuli in which we could vary the axis of the array independently of the orientation of the individual elements (Fig.4A,D). In these experiments the central Gabor stimulus was always centered on the MDF, whereas the flanking Gabor stimuli were arrayed along different axes for each trial [angles = (0–157.5°), incremented by 22.5°].

Fig. 4.

Collinear organization of summation fields in layer 2/3 neurons. A–C, Axis tuning assessed with iso-oriented Gabor stimuli. A, Example stimuli illustrating three of the eight axes that were tested and the single Gabor (SG) condition. B, Axis tuning for three sites. The arrows at the topindicate the preferred orientation for each site. Note correspondence between preferred orientation and peak of the axis-tuning curve for each site. Responses to SG stimuli are indicated bydiamonds on the right. Double line and black, Single units;gray, multiunit. C, Axis-tuning curves for all sites (thin gray lines) normalized to the preferred orientation of each site, with a Gaussian fit of the average tuning curve (black). Diamond atright, Average SG response (error bars ± 1 SD).D–F, Axis tuning assessed with cross-oriented Gabor stimuli. D, Examples of stimuli: a central Gabor of the preferred orientation surrounded by orthogonally oriented Gabors presented along different axes. E, Axis-tuning curves for the same sites illustrated in B showing a lack of orientation-specific axial facilitation. F, Axis tuning for all sites (thin gray lines) normalized to the preferred orientation. The black line represents average axis tuning; the black diamond depicts average SG response (error bars ± 1 SD).

Examples of axis tuning that use iso-oriented Gabor stimuli of the preferred orientation of the site are shown in Figure4B. In each example the responses to the Gabor arrays were tuned for the axis of the array, with the greatest response to the axis of the preferred orientation for the site. These peak responses significantly exceeded the response to the presentation of a SG in the receptive field center, but as the array deviated from the axis of preferred orientation, this facilitation diminished and was minimal (or below the response to the SG) for presentation of the array along the orthogonal axis. Similar results were obtained for all 35 sites (13 single units; 22 multiunits) in layer 2/3 (Fig. 4C); the optimal stimulus configuration was always a collinear row of Gabor stimuli aligned along the axis of the cell and its preferred orientation. On average, layer 2/3 neurons were well tuned for the axis of the array; normalized to the orientation preference of each recording site, the full width at half-height of the average axis-tuning curve was 33.7 ± 2.8°.

To test the orientation specificity of these facilitatory effects, we repeated the axis-tuning experiments, keeping the central Gabor at the preferred orientation but presenting the surrounding Gabors at the orthogonal orientation (Fig. 4D). The axis-tuning curves for these stimuli are illustrated in Figure 4Efor the same three sites that were shown in Figure4B. The axis tuning seen with Gabor stimuli of the preferred orientation was not present for orthogonal stimuli. Although there were both positive and negative deviations relative to the SG response, there was neither a significant nor consistent pattern of facilitation. Comparable results were found at all 26 sites (8 single units, 18 multiunits) that were tested with orthogonal orientations (Fig. 4F). Averaging the results from all of the sites after normalization to the preferred orientation of the recording site revealed no significant difference in the responses to different axes or to the average SG response.

The collinear Gabor array produced pronounced facilitation in every recording site tested in layer 2/3, exceeding the response to a SG in the receptive field center by 30–600% (mean, 154 ± 123%; Fig.5A). The consistent facilitation found with collinear stimulation contrasts sharply with the mixed effects (increments, decrements, or no change in response) found with presentation of iso-oriented Gabors along the orthogonal axis (Fig. 5B). Likewise, presentation of orthogonally oriented Gabors along either the preferred or orthogonal axis produced mixed effects in the population relative to the SG response (Fig.5C,D). As a population the noncollinear configurations do not differ significantly from the SG response; in contrast, the collinear configuration produced a significant change from the SG response (t test, p < 0.001).

Fig. 5.

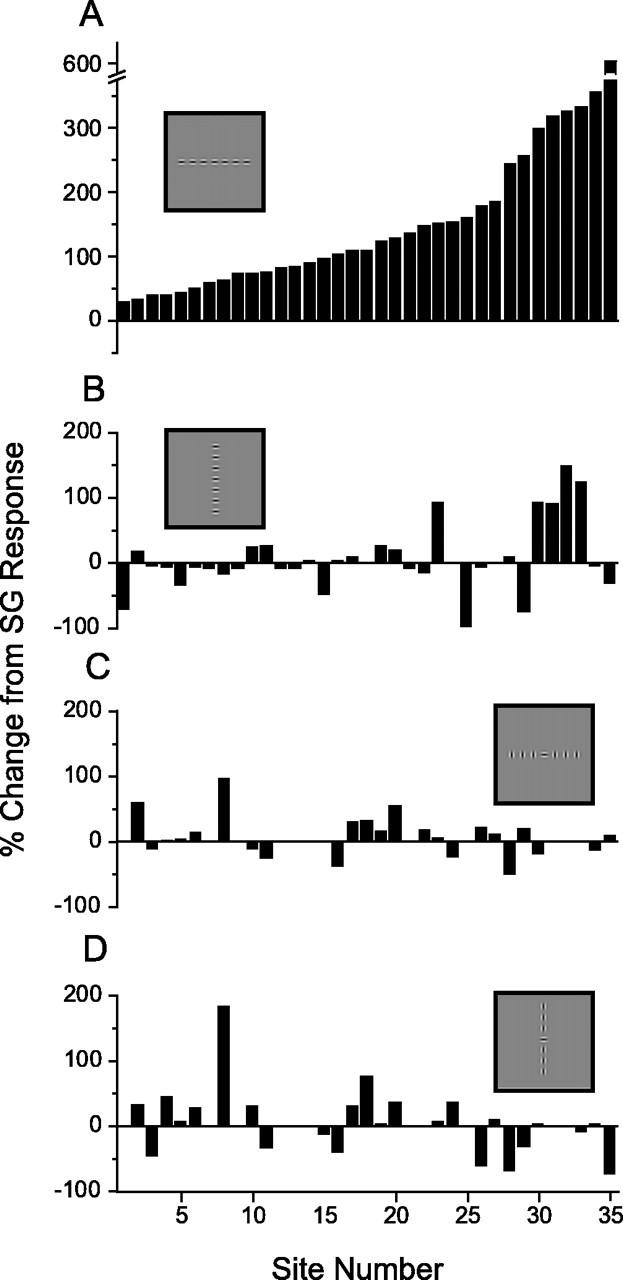
Magnitude of collinear facilitation revealed with axis-tuning experiments. A, Response to the collinear (preferred) stimulus configuration relative to the SG response shows facilitation for all sites (responses increased between 30 and 600%).B–D, Responses to noncollinear conditions (depicted with stimulus icons, insets) failed to produce consistent change from SG. For A,B, n = 35; for C,D, n = 26. Results for individual sites are aligned vertically for comparison across the four stimulus conditions.

Relationship of layer 2/3 MDF and summation fields to the distribution of horizontal connections

The elongated nature of the MDF and summation fields of layer 2/3 neurons are consistent with the spatial distribution of horizontal connections in layer 2/3 as revealed with small biocytin injections. To provide a more quantitative assessment of the distribution of horizontal connections and its relation to the minimum discharge and summation fields, we reevaluated the density and spatial distribution of horizontal connections along the collinear and orthogonal axes by using data from a previous study of the anatomy of horizontal connections (Bosking et al., 1997). The distance of each bouton from the injection site was measured for all boutons within 30° of the preferred or orthogonal axis in 10 cases (Fig.6A), allowing us to calculate the density of boutons at different distances and map the spatial extent of the bouton distribution.

Fig. 6.

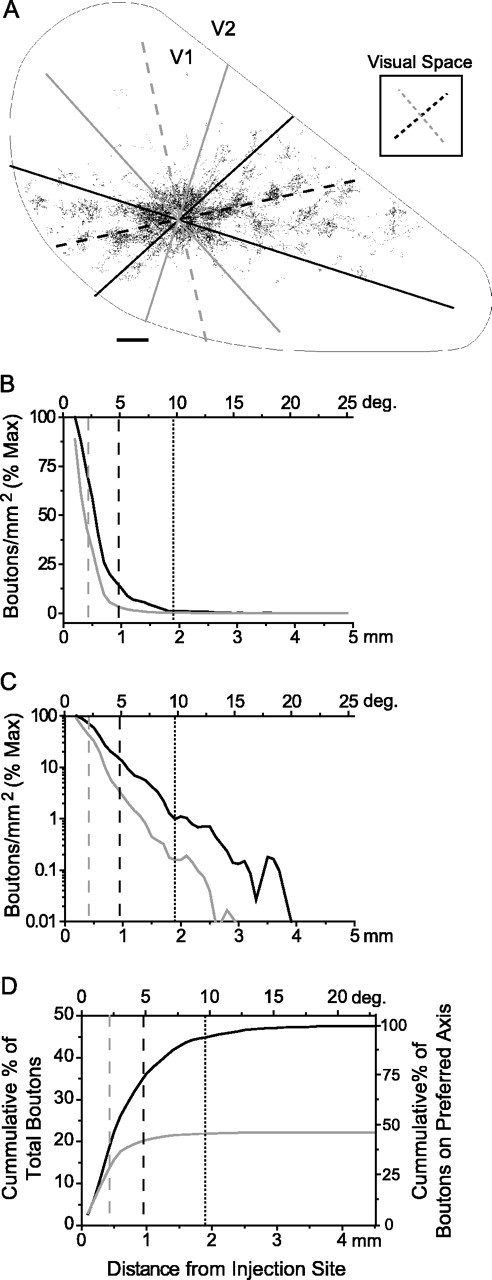
Horizontal connections in layer 2/3 and their relation to receptive field dimensions. A, A plot of labeled boutons within layer 2/3 of area V1 resulting from a biocytin injection into a site with an orientation preference of 40° (adapted from Bosking et al., 1997). The dorsal surface of V1 isoutlined, with the caudal pole to theleft, medial edge down, and V1/V2 border to the right. The axes of preferred (40°) and orthogonal (130°) orientation are indicated with blackand gray dashed lines, respectively, both in the icon of visual space to the right, and translated onto the cortical surface. Solid black and gray lines show the areas over which boutons were counted (± 30° from the two axes). Scale bar, 500 μm.B, Fall-off in bouton density with distance for the preferred (black) and orthogonal (gray) axes as a percentage of maximum density; distance is shown both in millimeters across cortex and degrees of visual space (average of 10 cases). C, The same data as plotted in B shown on a logarithmic scale to emphasize the extent of horizontal connections. D, The cumulative percentage of boutons measured along the preferred (black) and orthogonal (gray) axes (± 30°). Shown are average values for 10 experiments expressed as a percentage of total boutons (left axis) as well as percentage of boutons along collinear axis (right axis). In all graphs the dashed gray line indicates MDF width, the dashed black line indicates MDF length, and thedotted black line indicates the extent of the length summation field to 90% of asymptote.

The density of connections was greatest near the injection site and decreased dramatically with distance along both axes, falling to nearly 10% of maximum within 1 mm (Fig. 6B). Because of the exponential rate of decline the relative density for the more distant projections was better appreciated when it was plotted on a logarithmic scale (Fig. 6C); connections extended to 3–4 mm, but density was 10⁴ lower at these distances. Because of the orientation tuning of horizontal connections there were local regions with higher densities than depicted here at most distances; nevertheless, the drop in density with distance was still several orders of magnitude.

At comparable distances the density of boutons along the collinear axis in the map of visual space was significantly greater than along the orthogonal axis (t test, p < 0.001). This difference was evident at the shortest distance from the injection site for which boutons were counted (200 μm) and continued throughout the field of boutons. As a result, the total number of boutons found along the collinear axis was twice that observed along the orthogonal axis (Fig. 6D).

The length summation measurements derived from electrophysiological recordings bear a striking resemblance to the cumulative distribution curve for boutons along the collinear axis (Figs. 3A,6D). Stimulus lengths that yield 90% of maximum summation (19.9° total length or 10° from the injection site) occupy a cortical distance that encompasses 95% of the boutons that lie along the collinear axis (Fig. 6D). Moreover, the greatest extent of connections along the collinear axis (3.9 mm from injection site; Fig. 6C) corresponds to a distance in visual space of 38.9° (total length), a value that matches closely the maximum lengths over which summation was observed.

Although these results support the view that horizontal connections are a source of long-range facilitation, a consideration of their fall-off with distance suggests that horizontal connections are likely to exert stronger influence over events that occur within the dimensions of the MDF. Along the collinear axis, for example, ∼75% of the labeled boutons are located at distances in which the receptive field centers of the target neurons would overlap the MDF of neurons at the injection site (4.9° or 0.96 mm from the injection site; Fig. 6D). Furthermore, the projections to neurons for which the receptive fields lie outside the region of overlap (beyond 9.8° or 1.9 mm from the injection site) account for only 5% of the total number of boutons on this axis. At this distance the density of boutons is ∼100 times less than that near the injection site. Similar values are found along the noncollinear axis.

Population analysis of horizontal interactions in layer 2/3

The results presented above suggest that horizontal connections in layer 2/3 are responsible for the large and elongated summation fields that characterize layer 2/3 neurons as well as response features associated with the MDF. What is not clear is how this horizontal network acts to shape the spatial distribution of spiking activity in V1 that accompanies the presentation of discrete visual stimuli such as those used in the Gabor experiments. Horizontal connections alone could be capable of driving the responses of layer 2/3 neurons, in which case discrete oriented stimuli should produce patterns of activity in V1 that exhibit a collinear bias: an elongation along the orientation axis in the map of visual space. On the other hand, the absence of such a bias would be consistent with the view that horizontal connections operate at subthreshold levels, modifying, but not driving, the responses of other layer 2/3 neurons.

To address this issue, we used optical imaging techniques to visualize the pattern of activity evoked in V1 by SG stimuli. The presentation of these small Gabor stimuli reliably evoked restricted patches of activation ∼1 mm in diameter. Despite their small size, inhomogeneities in the magnitude of activity were often evident within these activated regions. Comparison with orientation maps derived from grating stimuli confirms that these “hot spots” accord with the local mapping of orientation preference (Fig.7A,B). Thus small stimuli that occupy less than the dimensions of the MDF and activate a small fraction of the horizontal network are still capable of evoking responses that are tuned to the orientation of the stimulus.

Fig. 7.

Population responses to SG stimuli display orientation specificity without anisotropic spread of activity.A, B, Intrinsic signal imaging of population responses to vertical (left panel) and horizontal (right panel) SG stimuli that were centered on the same location in visual space. Note the complementary distribution of activity peaks in these images (yellow and green circles) and their correspondence with dark and light regions, respectively, in the orientation difference map for the same region of cortex (middle panel). Scale bars, 0.5 mm. Images here and in subsequent figures are oriented such that caudal is leftand medial is down. The V1/V2 border is shown inred in B. C, Activity profiles along the length (axis of stimulus orientation) and width (orthogonal axis) of the SG response shown in the leftpanel of B (direction of activity profiles shown with colored arrows in B). The extent of activity along the two axes is very similar; raw profiles are shown in black, with Gaussian fits shown inred (length) and blue (width).D, Comparison of the extent of activity along the length and width of the SG responses (full width at half-height of Gaussian fits, as in C, converted to degrees) for nine experiments.

Overall, the patterns of activity evoked by single Gabors appeared symmetrical, with no consistent sign of elongation along the axis of preferred orientation. To assess this issue quantitatively, we constructed an activity profile along the length and width of each activity patch for nine separate experiments, including both horizontal and vertical Gabors, and fit each profile with a Gaussian (Fig.7C). Length/width ratios averaged 1.02 ± 0.2, showing no detectable aspect ratio (Fig. 7D). Thus discrete stimulation with single Gabors showed no sign of the collinear bias that is the signature of the horizontal network.

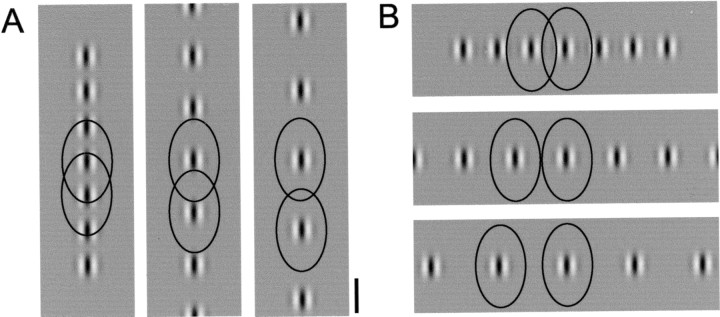
The failure to see signs of a collinear bias with single stimuli might have occurred because a single small stimulus failed to produce sufficient activity in the network to drive other layer 2/3 neurons. To test this possibility, we looked for signs of a collinear bias in the patterns of activation evoked by collinear and noncollinear arrays of Gabor stimuli, which should produce greater activity in the horizontal network. The horizontal network has the potential to integrate information over a large swath of visual space and do so in an axially biased way; whereas activity carried by horizontal afferents from sites of SG stimulation may not be sufficient to drive spiking activity several hundred micrometers away, convergent activity from multiple collinear Gabor stimuli may be able to drive responses (Fig.8). If so, we expected a filling in of activity between individual stimulus representations for collinear configurations. In contrast, we predicted the orthogonal configuration would produce well defined peaks and troughs of activity in response to the Gabor elements in the array.

Fig. 8.

Distribution of horizontal connections relative to collinear and orthogonal stimulus configurations. The distribution of horizontal connections in visual space coordinates (black lines represent 10% density threshold; see Fig. 6) relative to the size and spacing of Gabor arrays used for optical imaging (5, 7.5, and 10° center to center). Because of the collinear bias in the arrangement of horizontal connections, there will be greater convergence of horizontal inputs for the collinear configuration than for the orthogonal configuration at all stimulus distances. Scale bar, 5°.

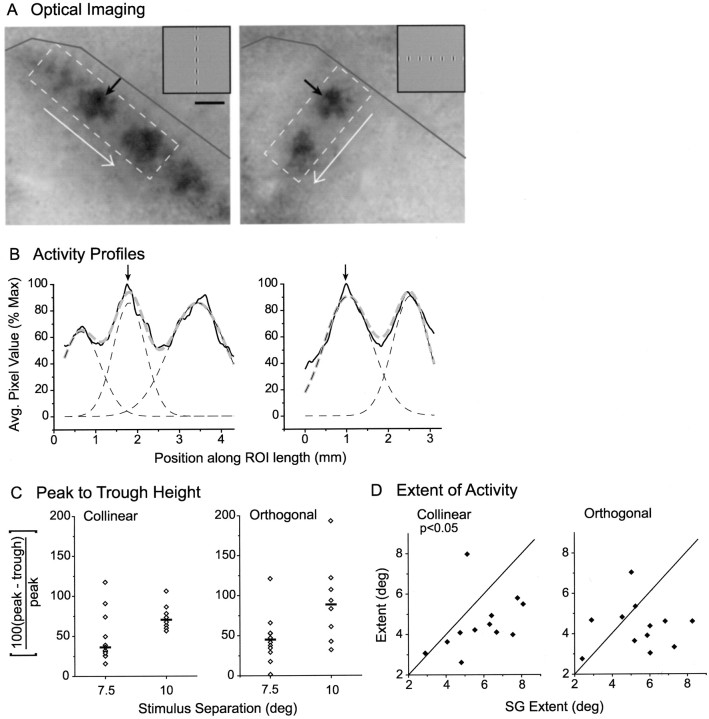
Rows of Gabor stimuli were presented on either the vertical or horizontal axes in visual space. All stimuli within these rows were of the same orientation, either collinear or orthogonal to the axis on which they were arrayed (examples of stimuli are shown in Figs. 8-10). At a spacing of 5°, peaks and troughs indicative of the location of each Gabor could not be distinguished from the modulation in response associated with orientation tuning. At 7.5 and 10° spacing, peaks and troughs associated with individual Gabor stimuli could be identified readily; however, we found no obvious difference between collinear and noncollinear configurations in the appearance of these peaks and troughs.

Fig. 9.

Population responses to collinear and orthogonal Gabor arrays display comparable spread of activity. A, Example of optical imaging of population response for collinear (left) and orthogonal (right) arrays (stimulus spacing = 7.5°). Black arrows point to the response associated with the Gabor stimulus common to both configurations. The dashed box defines a ROI used to create activity profile in the direction of the white arrow; a dark gray line marks the V1/V2 border. Scale bar, 1 mm. B, Activity profiles for images inA (black solid lines) were fit with a multipeak Gaussian (gray dashed lines) made up of component Gaussians that correspond to individual Gabor representations (black dashed lines); arrows point to the peak of the common Gabor response. C, Peak-to-trough heights for collinear and orthogonal stimulus configurations spaced at either 7.5 or 10°; black bars signify the median of each distribution. D, The extent of activity for a Gabor stimulus when that stimulus was a member of an array versus when it was present as a SG stimulus. Leftgraphplots the extent of activity along the collinear axis for collinear versus SG; rightgraph plots the extent of activity along the orthogonal axis for orthogonal versus SG. The full width at half-height of the relevant component Gaussian was used as the measure of extent.

Fig. 10.

Facilitation of population response to collinear arrays of Gabor stimuli. A, Example of imaging;insets show stimuli (stimulus spacing represents 7.5°). Dashed boxes represent ROIs used for analysis. Scale bar, 1 mm. B, Histograms generated from the images in A. More pixels show greater activity (i.e., darker signal/higher values) for the collinear condition (black) than the orthogonal (gray) for this example. C, Comparison of collinear and orthogonal histograms with the use of the facilitation index reveals that for most experiments greater activity was observed for the collinear condition (positive value for the facilitation index) than for the orthogonal (negative value). Results are broken down by stimulus spacing; the facilitation index for the example shown inA is marked accordingly.

To confirm this observation, we constructed an activity profile along the long axis of the stimulus array for the collinear and orthogonal conditions just as was done for the SG conditions, and we fit the activity pattern with a multipeak Gaussian (Fig.9A,B). As the separation distance was increased from 7.5 to 10°, the median peak-to-trough height deepened from 41 to 79% of max (7.5°,n = 14; 10°, n = 8). Thus there is significantly more activation between the centers of the Gabor representations at the shorter separation distance. However, we found no significant difference in the peak-to-trough height between the collinear and orthogonal conditions for either stimulus spacing (Fig.9C).

To test whether a more subtle effect may have been obscured by variation across animals, we compared the extent of activation evoked by a SG stimulus (full width at half-height of the Gaussian fit to the SG activity profile, as in Fig. 7) with the extent of activation evoked by the same stimulus in either the collinear or orthogonal configuration (full width at half-height of the corresponding component Gaussian within the multipeak fit; Fig. 9B). Our analysis was restricted to separation distances of 7.5°. The extent of an individual Gabor representation within a collinear array did differ significantly from the extent of the SG stimulus. Surprisingly, however, the collinear activation was actually lessextensive than that evoked by the SG stimulus (collinear mean = 0.89 ± 0.28 mm or 4.5 ± 1.4°, SG mean = 1.14 ± 0.29 mm or 5.8 ± 1.6°; paired t test,p < 0.02; Fig. 9D). The extent of response for the orthogonal condition was not significantly different from SG (orthogonal mean = 0.85 ± 0.24 mm or 4.3 ± 1.2°, SG mean = 1.07 ± 0.31 mm or 5.5 ± 1.7°, pairedt test, NS; Fig. 9D). Taken together, these results suggest that, even when the horizontal network is activated by multiple stimuli, the spatial spread of spiking activity is strikingly limited.

At first glance these results may seem at odds with the results of our unit recordings showing powerful collinear facilitation. However, facilitatory effects in the unit recording experiments were evoked with Gabor stimuli of the preferred orientation centered on the receptive field; at the population level this is the equivalent of looking only at the imaging signal in the center of a preferred orientation domain in the middle of a Gabor representation and disregarding the rest of the cortex. We may be able to detect a facilitation corresponding to that seen with physiology that does not involve spatial spread.

To test for a difference in signal magnitude between collinear and orthogonal conditions, we performed a histogram analysis that evaluated the number of active pixels and their level of activity for the single common Gabor element in collinear and orthogonal conditions. An example set of images of the population response and histograms is shown in Figure 10, A andB. By summing pixel counts for all pixel values >50% of the maximum with the use of a facilitation index, we found that the collinear condition produces more activation at these darkest pixel values for the vast majority of experiments: five of seven experiments at 5°, seven of eight experiments at 7.5°, and four of six experiments at 10° (Fig. 10D). When we combine all separation distances, the collinear condition produces significantly greater activation than the noncollinear condition (t test,p < 0.02).

Discussion

Layer 2/3 neurons receive a large proportion of their inputs from other layer 2/3 cells. In the past these inputs have been acknowledged primarily as a source of surround or contextual modulation, suppressing or facilitating the response of a cell to stimulation of the MDF, but not contributing to the response produced by stimuli that are limited to the MDF. Our results are consistent with a broader role for horizontal connections in shaping the response of a neuron to stimuli that fall within as well as beyond the MDF.

Summation properties of layer 2/3 neurons reflect the collinear arrangement of horizontal connections

Our results show that layer 2/3 neurons continue to increase their discharge rate for increasing stimulus lengths up to 36° or more. The absolute extent of summation fields in layer 2/3 accords well with the average extent of horizontal connections in the map of visual space (as shown previously in Bosking and Fitzpatrick, 1995); additionally, the shape of the physiological length-tuning curve and the cumulative bouton distribution curve match well. Furthermore, the responses to Gabor arrays reveal that these summation fields are elongated specifically along the axis of preferred orientation and are selective for orientation, properties consistent with the spatial arrangement of horizontal connections. Indeed, even the full widths at half-height of the average axis-tuning curves for unit recordings and bouton counts were nearly identical; the width of axis tuning physiologically was 33.7°, whereas the comparable axis-tuning width that was based on the distribution of axon boutons was 32.8°, using data from Bosking et al. (1997). Although we cannot rule out a contribution of layer 4 inputs to summation within the MDF, these inputs cannot account for the increase in response that occurs for stimuli for which the length exceeds ∼10°.

This correspondence between layer 2/3 summation fields and the horizontal network is consistent with several recent observations in cats and primates. Intracellular recordings in the cat indicate the presence of a subthreshold depolarizing zone surrounding the MDF that extends for distances commensurate with the spread of horizontal connections (Bringuier et al., 1999). This subthreshold field is likely to correspond to the summation field described here with extracellular recordings. Large summation fields similar in extent to the horizontal network also have been described in the macaque (Kapadia et al., 1999;Sceniak et al., 1999; Angelucci et al., 2002; Cavanaugh et al., 2002). Although the organization of horizontal connections in the macaque lacks the prominent orientation-specific anisotropy that is characteristic of tree shrew V1, this difference is consistent with the fact that summation fields of layer 2/3 neurons in this species are also generally isotropic (Angelucci et al., 2002). Although there may be species-specific features to the arrangement of the horizontal network, the available results suggest that, as a general rule, the extent of horizontal connections defines the dimensions of the summation field.

One difference between results in the tree shrew and previous studies in other species is the sensitivity of summation properties to stimulus contrast. The experiments reported here were run with high-contrast stimuli and revealed extensive summation zones in layer 2/3 without response suppression (end-stopping) that commonly is described in other species (Polat et al., 1998; Kapadia et al., 1999; Sceniak et al., 1999). We have not investigated the effect of contrast on the summation properties of layer 2/3 neurons, and it is possible that our results underestimate the full extent or magnitude of collinear summation. Nevertheless, the correspondence between summation field size and the distribution of horizontal connections is striking.

We found no consistent effect, facilitatory or suppressive, for noncollinear arrangements of Gabor stimuli. Some units showed no difference between SG and noncollinear array, whereas others showed distinct facilitation or suppression. This result is consistent with previous findings of asymmetric and variably positioned and tuned suppressive zones outside the classical receptive field (Levitt and Lund, 1997; Sengpiel et al., 1997; Das and Gilbert, 1999; Walker et al., 1999; Kapadia et al., 2000). It remains to be seen whether these effects are mediated by the less extensive horizontal connections from noncollinear sites or whether they depend on different inputs, such as feedback from extrastriate cortex.

A significant contribution of horizontal connections to the MDF

Previous studies have emphasized that horizontal connections extend far enough to link cells with non-overlapping MDFs. Indeed, this has been a principal reason for suspecting that horizontal connections are a source of receptive field surround effects (Gilbert and Wiesel, 1983, 1989; Gilbert, 1992). Our results show, however, that connections to sites with non-overlapping receptive fields account for a small percentage (well under 10%) of the contacts established. The vast majority of connections links neurons for which the MDFs overlap by at least 50%. This suggests that activity within the horizontal network is likely to play a significant role in shaping responses to stimuli confined to the MDF. The similarity between MDF elongation and the axially biased distribution of horizontal connections is further support for the idea that the MDF probably reflects both the activity of layer 4 inputs and the pattern of recurrent activity within layer 2/3.

The emergence of orientation selectivity in layer 2/3

The results presented here suggest that the generation of orientation-selective responses in tree shrew visual cortex departs significantly from the organization described in the cat, which figured so prominently in efforts to understand the mechanisms that underlie orientation selectivity. In the cat the orientation-selective responses arise in layer 4 neurons as a result of the selective arrangement of inputs from the lateral geniculate nucleus (LGN) (Hubel and Wiesel, 1962; Reid and Alonso, 1995; Ferster et al., 1996; Chung and Ferster, 1998; Ferster and Miller, 2000). Our results, supported by previous work in the tree shrew (Humphrey and Norton, 1980; Humphrey et al., 1980), show that layer 4 neurons in tree shrew are poorly tuned for orientation. Our finding is similar to the poor orientation tuning documented in layer 4cβ in macaque (Hubel and Wiesel, 1968, 1977;Blasdel and Fitzpatrick, 1984) (but see also Ringach et al., 2002). Thus orientation selectivity in layer 2/3 of the tree shrew appears to be more dependent on properties of intracortical circuits than on selective arrangement of LGN afferents in layer 4.

Although the circuits responsible for generating orientation selectivity differ from those in the cat, the fundamental mechanism may be the same: a bias in sampling from input neurons for which the receptive fields are displaced along the axis of preferred orientation in visual space. This classic feed-forward mechanism involves the selective convergence of LGN neurons onto layer 4 simple cells in the cat (Hubel and Wiesel, 1962; Ferster and Miller, 2000). In the tree shrew recent anatomic results demonstrate an orientation-specific anisotropy in the projections from layers 4 and 2/3 that is consistent with such a feed-forward mechanism (Mooser et al., 2001).

At the same time, however, an orientation-specific anisotropy is also present in the anatomic arrangement of horizontal connections, suggesting they too play a role in shaping orientation tuning in layer 2/3 neurons. The elongated distribution and collinear specificity of these connections (preferentially linking sites with similar orientation preference for which the receptive fields are displaced along the axis of preferred orientation) could provide a powerful amplification of an orientation bias supplied by feed-forward inputs. Although there has been considerable debate over the relative contribution of feed-forward and recurrent inputs to the generation of orientation selectivity (Martin, 2002), our observations suggest that both types of intracortical circuits have the requisite specificity to shape orientation-selective responses in the MDF.

Like cat layer 4 cells, neurons in tree shrew layer 2/3 have elongated MDFs. The elongation of simple cell receptive fields in the cat has been viewed as a direct outcome of the feed-forward mechanism and a significant factor in conferring orientation selectivity (Hubel and Wiesel, 1962; Gardner et al., 1999; Lampl et al., 2001; Usrey et al., 2003). Our imaging and anatomy results, however, suggest that receptive field elongation per se is not the critical factor in establishing orientation selectivity in layer 2/3 neurons. A SG stimulus that occupied only a portion of the MDF, for example, evoked an orientation-specific cortical response. Thus orientation selectivity must depend on a bias in inputs on a scale much finer than the dimensions of the MDF. Projections from both layers 4 and 2/3 show axis and orientation-specific differential density distributions on a scale much smaller than the MDF, and thus both appear to be capable of contributing to orientation tuning (for the layer 4 result, see Mooser et al., 2001).

The pattern of population activity for SG stimuli

Despite the extent and axial bias of horizontal connections in layer 2/3, optical imaging of SG stimuli produced remarkably punctate activation patterns restricted to diameters of ∼1 mm without detectable elongation. The activity associated with SG stimuli approximately corresponds to the cortical area that would be expected to receive strong activation from layer 4 neurons, only a fraction of the area linked by horizontal connections. Previous results from this lab have demonstrated that optical signal is correlated strongly with the distribution of spiking neurons (Bosking et al., 2002). Thus without sufficient activity in layer 4 afferents, horizontal inputs alone appear insufficient to drive the layer 2/3 population to spike (or at least to spike at a rate that is detectable with intrinsic signal imaging). These observations are consistent with previous reports that compared the strength of horizontal and vertical inputs in driving postsynaptic responses and with evidence that the effectiveness of horizontal connections is enhanced if the postsynaptic neuron is depolarized (Hirsch and Gilbert, 1991; Yoshimura et al., 2000).

The radial symmetry of the SG activation pattern is to be expected if horizontal connections require layer 4 inputs for their expression. Nevertheless, this pattern of population activity appears inconsistent with the elongated shape of the MDF of individual layer 2/3 neurons. Previous comparisons of the distribution of population activity derived by intrinsic signal imaging and predictions that were based on unit recordings (convolving receptive field size with cortical magnification factor) have shown remarkable correspondence between physiology and imaging measures. For example, the average MDF width of layer 2/3 neurons provides a close approximation of the width of the activity band evoked by a single line stimulus (Bosking et al., 2002). However, this comparison was based on measures of receptive field width, and it seems likely that the fall-off in response sensitivity is steeper across the width of the receptive field than along its length, consistent with both the axial bias in horizontal connections and the elongated summation fields. As such, the response of layer 2/3 neurons to punctate stimulation along the long axis of their receptive fields may provide a more sensitive comparison of unit recording and optical measures of neuronal activity; the optical recordings may not be sufficiently sensitive to detect small changes in spike rate from the weak ends of the MDF for just a portion of neurons in the population (i.e., those that respond to the stimulus orientation). Additionally, differences in the nature of the stimuli used in these experiments may contribute to this apparent inconsistency. The stimulus used to map the MDF was a 5–10° high-contrast bar, whereas the SG stimulus was smaller (full width at half-height 2.25°), round, and had soft edges; the latter stimulus simply may be less effective at driving the weak ends of the MDF.

The pattern of population activity for Gabor arrays: facilitation without filling in

A stronger test of the efficacy of horizontal connections came from presenting rows of Gabor stimuli at separation distances that should provide strong convergent activation via horizontal inputs to neurons for which the receptive fields lie in the gaps between stimulus elements. Consistent with unit recordings, optical imaging revealed facilitation for collinear stimuli. However, there was no spread of activity into regions representing stimulus gaps. Indeed, our results showed significantly less extensive activity for collinear stimuli than SG stimuli and no difference in activity at the stimulus gaps for collinear and noncollinear configurations.

These results suggest that facilitatory effects of horizontal connections are strongly gated by layer 4 activation or that inhibition within layer 2/3 suppresses responses in the stimulus gaps, or both. As suggested above, horizontal inputs may fail to reach threshold for spike discharge in the absence of layer 4 activation (Hirsch and Gilbert, 1991). The decreased extent of response compared with the SG condition, however, suggests the involvement of inhibitory circuitry. Just as axis and orientation-specific excitatory connections converge at points between stimuli, nonspecific inhibitory connections also converge; in the absence of layer 4 activation they may suppress filling in and preserve spatial resolution.

Although it may be possible to reveal horizontal spread of activity with other stimulus configurations (e.g., illusory contours), these results provide striking evidence for the role of horizontal connections in long-range facilitation without a loss of spatial resolution. Facilitation without filling in may be an important mechanism in V1 for representing the continuity of occluded objects without losing information about the occluding objects (Sugita, 1999;Albright and Stoner, 2002).